A numerical study of microfluidic droplet transport in a parallel-plate electrowetting-on-dielectric (EWOD) device

Abstract

The fluid dynamics of microwater droplet transport in a parallel-plate electrowetting-on-dielectric (EWOD) device have been investigated via a numerical model. The transient governing equations are solved by a finite volume scheme with a two-step projection method on a fixed computational domain. The interface between liquid and gas is tracked by a coupled level set and volume-of-fluid method. A continuum surface force model is employed to evaluate surface tension at the interface. A simplified model is adopted for the viscous stresses exerted by the parallel plates at the gas–liquid interface in conjunction with contact angle hysteresis implemented as a crucial element in EWOD modeling. Excellent agreement has been achieved between the numerical and published experimental results. Special attention has been focused on some localized areas near the ON/OFF electrode border where the transport process is primarily influenced. A dimensionless curvature has been introduced and a critical value has been identified beyond which the droplet would split during the transport. A parametric study has been performed in which the effects of several crucial parameters including initial droplet shape, static contact angles, contact angle hysteresis, viscous stress, channel height and electrode size on the transport process have been revealed.

1 Introduction

The concept of digital microfluidics emerged in the 1990s, and it has experienced rapid development due to the remarkable progress of various advanced microelectromechanical systems (MEMS) and lab-on-a-chip (LOC) devices (Berthier 2012; Fair 2007; Madou 2002). Meanwhile, the study of discrete droplet motion in microfluidic devices has been motivated as a crucial element of digital microfluidic applications. Microscale droplets are dominated by capillary forces which play a significant role in the overall fluid behavior. During the past 10 years, a number of physical mechanisms have been successfully employed to alter the surface tension force at the gas–liquid interface, which consequently creates a pressure difference across the droplet boundary and serves as the driving force for the droplet motion (Böhm et al. 2000; Darhuber et al. 2003; Jones et al. 2001; Nguyen et al. 2006; Pollack et al. 2002; Sammarco and Burns 1999).

The use of electrowetting effect as the driving mechanism for microfluidic droplet motion arose in the early 2000s. Electrowetting refers to the phenomenon whereby the wetting property of a conductive liquid droplet is modified with an applied electrical field at the triple contact line. This innovative technique has been widely applied in various microdroplet operations such as splitting, merging, dispensing and transport (Cho et al. 2003; Gong and Kim 2008; Guan and Tong 2015; Jang et al. 2007; Pollack et al. 2002; Walker et al. 2009; Wang et al. 2011). It has been discovered that the effectiveness of electrowetting devices can be improved by coating the bottom electrodes with a thin dielectric layer (Berge 1993; Moon et al. 2002), which leads to the increasing utilization of electrowetting-on-dielectric (EWOD) devices on microfluidic droplet motions in recent years.

Experimental studies of droplet transport in parallel-plate electrowetting-based microfluidic systems have been carried out over the last decade (Chang and Pak 2012; Cho et al. 2003; Jang et al. 2007; Pollack et al. 2000, 2002; Yaddessalage 2013). Pollack et al. (2000) performed a preliminary experimental study on electrowetting-induced discrete microdroplet transport using KCl solution as the working liquid. It was found that a voltage larger than 30 V was required to initiate the droplet movement and the voltage was mainly used to overcome the contact angle hysteresis effect. Pollack et al. (2002) extended the study to four fundamental microdroplet operations including transport, splitting, merging and dispensing with the same liquid and LOC devices. The transport process was successfully conducted with an average velocity exceeding 100 mm/s obtained at about 60 V beyond which the droplet was found to split during the transport. Cho et al. (2003) later conducted experiments on deionized (DI) water droplet transport in a parallel-plate EWOD device. Microdroplets were transported after being dispensed from a large liquid reservoir. It was discovered that the minimum voltage for initiating the droplet motion was only 18 V and that the average transport speed could go up to 250 mm/s at a higher AC voltage. Recently, Yaddessalage (2013) carried out EWOD-based droplet transport experiments in a parallel-plate LOC device with DI water as the working liquid. The effect of several parameters including working surface smoothness, electrode size and electrode geometry on droplet transport speed was examined. It was found that the transport speed was dependent on the working surface material and that a larger transport speed could be obtained when the electrode had a larger size or was separated into multiple equal-sized strips.

Due to the great difficulty of conducting experiments at such small scales, microdroplet transport process in parallel-plate electrowetting device has also been simulated with a number of numerical models (Arzpeyma et al. 2008; Bahadur and Garimella 2006; Clime et al. 2010; Keshavarz-Motamed et al. 2010; Lu et al. 2007; Mohseni et al. 2006; Zeng and Korsmeyer 2004). Mohseni et al. (2006) carried out numerical simulations of droplet transport in parallel-plate microchannels with the gas–liquid interface tracked by the volume-of-fluid (VOF) method. It was reported that the transport speed increased as the channel height became smaller and that the droplet would split during the transport if the actuation voltage was sufficiently high. An energy-based computational algorithm was formulated by Bahadur and Garimella (2006) for studying the droplet motion in parallel-plate electrowetting-based fluid actuation systems. It was found that the transport speed was significantly affected by actuation voltage but had negligible dependence on channel height. A coupled electrohydrodynamic numerical scheme was developed by Arzpeyma et al. (2008) for investigating the transport process induced by electrowetting force. It was shown that contact angle hysteresis was essential for modeling accuracy and that transport speed increased with applied voltage. Keshavarz-Motamed et al. (2010) recently performed a computational study on droplet transport process in parallel-plate microchannels with a molecular kinetic energy model. The dynamic behavior of the triple contact line was investigated, and the dynamic contact angles during the transport process were calculated. It was discovered that on average both the advancing and receding contact angles had a deflection of 8° compared with the static contact angle.

Several analytical models were also proposed for examining electrowetting-based fluid motion in parallel-plate microfluidic devices (Baird and Mohseni 2007; Ren et al. 2002; Bahadur and Garimella 2006; Walker et al. 2009). Governing equations of droplet motion were theoretically derived with the effects of electrical voltage, viscous stress, contact angle hysteresis, contact line friction force and other relevant terms included.

Even though the study of electrowetting-based microdroplet transport has been conducted for years, the important physics involved in the transport process is still not fully understood. Specifically, very few explanations have been offered for the commonly observed phenomena, such as droplet splitting when the electrical voltage is sufficiently high and droplet displaying different shapes during the transport as the channel height varies. The lack of explanation of such phenomena is perhaps a reflection of the technical difficulty of experimentally analyzing the droplet motion due to the complex two-phase flow patterns associated with the transport process which occurs at the microscale. Numerical methods, on the other hand, can provide crucial information such as the pressure and velocity profiles within the droplet at vital time instants which may otherwise be unavailable from experiments or other means. The objective of the present study is to numerically investigate microfluidic droplet transport process in a parallel-plate EWOD device. The results obtained from the numerical simulations are compared with the experimental data reported in the literature (Yaddessalage 2013). A parametric study which includes static contact angles, contact angle hysteresis, viscous stress, channel height, electrode size and droplet physical properties is also performed. A brief review of the parallel-plate EWOD model is given next followed by a description of the numerical formulation and results and discussion.

2 EWOD in a parallel-plate device

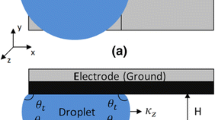
The schematics of the top and cross-sectional views of the EWOD device used in the present study are shown in Fig. 1. Note that the figure is not to scale with a much narrower channel height in the actual device. It consists of two parallel plates with the droplet sandwiched in between. The top electrode is one whole piece which remains grounded at all time, while the two disjointed square-shaped electrodes at the bottom can be switched ON and OFF independently as needed. There are two hydrophobic layers one each on the top and bottom plates which separate the droplet from the electrodes. The dielectric layer on the bottom plate is an insulating film which sustains the high electric field at the surface and allows a larger contact angle change upon the application of electrical voltage compared with the conventional electrowetting device (Moon et al. 2002).

Fig. 1

Top (a) and cross-sectional (b) views of the parallel-plate EWOD device

It has been found that the contact angle θ at the three-phase contact line is reduced by the addition of an electrical potential which leads to the Young–Lippmann’s equation given by:

$$\cos\theta \left(V \right) = \cos\theta_{0} + \frac{{\epsilon_{0}\epsilon}}{{2\sigma_{\text{LG}} d}}V^{2}$$

(1)

where θ is the contact angle at the triple contact line with nonzero electrical potential, θ ₀ the equilibrium contact angle with zero potential, $\epsilon_{0}$ the permittivity of vacuum, $\epsilon$ the dielectric constant of the dielectric layer, σ _LG the surface tension at the gas–liquid interface, d the thickness of the dielectric layer and V the magnitude of applied voltage. The Young–Lippmann equation is reasonably accurate in predicting the contact angle at low voltage. However, it has been discovered that the equation fails after the voltage reaches a certain threshold beyond which the contact angle θ only has a slight variation. This effect is referred to as contact angle saturation and has been addressed in the literature (Cho et al. 2003; Mugele and Baret 2005).

Since the contact angle at the triple contact line can be modified by applying electrical potential at the droplet boundary, this will alter droplet surface curvature and consequently surface tension induced pressure at the gas–liquid interface according to the Young–Laplace equation (Batchelor 2000):

$$\Delta p = \sigma_{\text{LG}} \left( {\kappa_{xy} + \kappa_{z} } \right)$$

(2)

where $\Delta p$ is the surface tension induced pressure at the gas–liquid interface and κ _xy and κ _z the mean curvatures in the x–y plane and along the z-direction, respectively. Since the channel height is very narrow compared with the device dimension and the Capillary number is much smaller than unity, the gas–liquid interface in the z-direction can be approximated as circular which yields

$$\kappa_{z} = \frac{{\left( { - \cos \theta_{\text{t}} - \cos \theta_{\text{b}} } \right)}}{H}$$

(3)

where θ _t and θ _b are the contact angles at the top and bottom plates, respectively, and H the channel height between the two parallel plates, see Fig. 1. Note that θ _t is always constant since the top electrode is grounded, but θ _b varies according to Eq. (1). Combination of Eqs. (2) and (3) gives the pressure difference at the droplet boundary across the ON and OFF regions as,

$$p_{\text{OFF}} - p_{\text{ON}} = \sigma_{\text{LG}} \left( {\frac{{\cos \theta_{{{\text{b}},{\text{ON}}}} - \cos \theta_{{{\text{b}}, {\text{OFF}}}} }}{H} + \kappa_{{xy,{\text{OFF}}}} - \kappa_{{xy,{\text{ON}}}} } \right)$$

(4)

As shown in Fig. 2, when electrical charges are applied, the surface tension at the interface is reduced due to the decreased contact angle $\theta_{{{\text{b}},{\text{ON}}}}$. This reduced surface tension on the electrowetted side leads to an imbalanced pressure force which moves the droplet from the OFF to the ON side. In the present study, a dimensionless curvature $\tilde{\kappa }$ is introduced, which is defined as,

$$\tilde{\kappa } = \frac{{\Delta \kappa_{z} }}{{k_{xy} }}$$

(5)

where $\Delta \kappa_{z}$ is given by

$$\Delta \kappa_{z} = \kappa_{{z,{\text{OFF}}}} - \kappa_{{z,{\text{ON}}}}$$

(6)

κ _z,OFF and κ _z,ON are the z-curvatures of the gas–liquid interfaces on the OFF and ON electrodes, respectively (Fig. 2). By incorporating the definition of κ _xy and Eq. (3), $\tilde{\kappa }$ becomes

$$\tilde{\kappa } = \frac{R}{H}\left( {\cos \theta_{{{\text{b}},{\text{ON}}}} - \cos \theta_{{{\text{b}}, {\text{OFF}}}} } \right)$$

(7)

where R is the initial droplet radius in the x–y plane, see Fig. 1. According to Eq. (5), $\tilde{\kappa }$ represents the relative significance between $\Delta \kappa_{z}$ and κ _xy in a particular droplet transport case, i.e., a larger value of $\tilde{\kappa }$ represents that $\Delta \kappa_{z}$ has a more dominant effect than κ _xy in the transport process.

Fig. 2

Pressure difference induced by the electrical actuation

An essential element in EWOD modeling is contact angle hysteresis, which refers to the difference in contact angles between the advancing and receding ends when the droplet is in motion (Mugele and Baret 2005; Walker and Shapiro 2006; Walker et al. 2009). When the droplet is stationary on a flat plate, a unique contact angle, referred to as static contact angle, is formed at the triple contact line. As the droplet moves, the contact angle on the advancing side increases, while that on the receding side decreases and are referred to as advancing and receding contact angles, respectively. It should be noted that the hysteresis phenomenon has a retarding effect on fluid motion (Walker and Shapiro 2006).

3 Numerical formulations

3.1 Governing equations

For incompressible flows with constant properties, the continuity and momentum equations are given by

$$\nabla \cdot \vec{\varvec{u}} = 0$$

(8)

$$\frac{{\partial \vec{\varvec{u}}}}{\partial t} + \vec{\varvec{u}} \cdot \nabla \vec{\varvec{u}} = - \frac{1}{\rho }\nabla P + \frac{1}{\rho }\nabla \cdot\varvec{\tau}+ \vec{\varvec{g}} + \frac{{\overrightarrow {{\varvec{F}_{\varvec{b}} }} }}{\rho }$$

(9)

where $\vec{\varvec{u}}$ is the velocity, ρ the density, P the pressure, τ the viscous stress tensor, $\vec{\varvec{g}}$ the gravitational acceleration and $\overrightarrow {{\varvec{F}_{\varvec{b}} }}$ the body force. A free surface flow model is adopted in this study in which the dynamic effect of the air is neglected. For Newtonian fluids, the viscous stress tensor $\varvec{\tau}$ can be written as:

$$\varvec{\tau}= 2\mu\varvec{S}\quad \varvec{S} = \frac{1}{2}\left[ {\left( {\nabla \vec{\varvec{u}}} \right) + \left( {\nabla \vec{\varvec{u}}} \right)^{T} } \right]$$

(10)

where S is the rate-of-strain tensor. Equation (9) is approximated in the finite difference form as:

$$\frac{{\vec{\varvec{u}}^{n + 1} - \vec{\varvec{u}}^{n} }}{\delta t} = - \vec{\varvec{u}}^{n} \cdot \nabla \vec{\varvec{u}}^{n} - \frac{1}{{\rho^{n} }}\nabla P^{n + 1} + \frac{1}{{\rho^{n} }}\nabla \cdot\varvec{\tau}^{n} + \vec{\varvec{g}}^{n} + \frac{1}{{\rho^{n} }}\overrightarrow {{\varvec{F}_{\varvec{b}} }}^{n}$$

(11)

A two-step projection algorithm is used where Eq. (11) is decomposed into the following two equations:

$$\frac{{\vec{\varvec{u}}^{ *} - \vec{\varvec{u}}^{n} }}{\delta t} = - \vec{\varvec{u}}^{n} \cdot \nabla \vec{\varvec{u}}^{n} + \frac{1}{{\rho^{n} }}\nabla \cdot\varvec{\tau}^{n} + \vec{\varvec{g}}^{n} + \frac{1}{{\rho^{n} }}\overrightarrow {{\varvec{F}_{\varvec{b}} }}^{n}$$

(12)

and

$$\frac{{\vec{\varvec{u}}^{n + 1} - \vec{\varvec{u}}^{ *} }}{\delta t} = - \frac{1}{{\rho^{n} }}\nabla P^{n + 1}$$

(13)

where $\vec{\varvec{u}}^{ *}$ represents an intermediate velocity. In the first step, $\vec{\varvec{u}}^{ *}$ is computed from Eq. (12) which accounts for incremental changes resulting from viscosity, advection, gravity and body forces. The second step involves taking the divergence of Eq. (13) while projecting the velocity field, $\vec{\varvec{u}}^{n + 1}$, to a zero-divergence vector field for mass conservation. This results in a single Poisson equation for the pressure field given by

$$\nabla \cdot \left[ {\frac{1}{{\rho^{n} }}\nabla P^{n + 1} } \right] = \frac{{\nabla \cdot \vec{\varvec{u}}^{ *} }}{\delta t}$$

(14)

which is used to obtain $\vec{\varvec{u}}^{n + 1}$ from Eq. (13).

As discussed in Kirby (2010), if a flow has a small and uniform depth in the z-direction and much larger dimensions in the x- and y-directions, it can be treated by the ‘Hele-Shaw cell’ model in which the pressure is uniform and the velocity component is negligible in the z-direction. For the current EWOD device, since the depth (gap) is much smaller than the dimensions in the other directions, it is modeled as ‘Hele-Shaw cell’ and the flow is reduced to two-dimensional in x and y. This Hele-Shaw cell 3D to 2D conversion has been applied in a number of numerical microfluidic droplet motion studies (Lu et al. 2007; Walker and Shapiro 2006; Walker et al. 2009).

3.2 Interface tracking methods

The main complexity of the numerical simulation is the dynamics of a rapidly moving free surface, the location of which is unknown and is needed as part of the solution. As the flow is surface tension driven, modeling of the surface tension force with a high degree of accuracy is critical. In recent years, a number of methods have been developed for modeling free surface flows (Hirt and Nichols 1981; Rudman 1998; Sussman et al. 1994; Scardovelli and Zaleski 1999), among which the volume-of-fluid (VOF) method and the level set (LS) method are two Eulerian-based methods that have been widely used. One of the advantages offered by these methods is the ease in which flow problems with large topological changes and interface deformations can be handled. These include droplet elongation and breakup, bubble merging and bursting, and microfluidic droplet operations. The VOF method has the desirable property of mass conservation. However, it lacks accuracy on the normal and curvature calculations due to the discontinuous spatial derivatives of the VOF function near the interface. This may lead to convergence problems (Meier et al. 2002; Renardy and Renardy 2002; Scardovelli and Zaleski 1999; Tong and Wang 2007), especially in the surface tension force dominant problems. As for the LS method, the normal and curvature can be calculated accurately from the continuous and smooth distance functions. However, one serious drawback of this method is the frequent violation of the mass conservation. To overcome such weaknesses of the LS and VOF methods, a coupled level set and volume-of-fluid (CLSVOF) method has recently been reported (Son and Hur 2002; Sussman 2003; Sussman and Puckett 2000; Yang et al. 2006). The coupled method offers improved accuracy on the surface curvature and normal calculations while maintaining mass conservation. A CLSVOF method is used in the present study with the interface reconstructed via a piecewise linear interface construction (PLIC) scheme on the VOF function (Rudman 1997) and the interface normal computed from the LS function. A brief overview of the CLSVOF scheme is given here.

The LS function, ϕ, is defined as a distance function given by

$$\phi (\vec{\varvec{x}},t)\left\{ {\begin{array}{*{20}l} { > 0 } \hfill & {{\text{outside}}\;{\text{of}}\;{\text{the}}\;{\text{interface}}} \hfill \\ { = 0} \hfill & {{\text{at}}\;{\text{the}}\;{\text{interface}}} \hfill \\ { < 0} \hfill & {{\text{inside}}\;{\text{of}}\;{\text{the}}\;{\text{interface}}} \hfill \\ \end{array} } \right.$$

(15)

i.e., negative in the liquid, positive in the air and zero at the interface. The VOF function, F, is defined as the liquid volume fraction in a cell with its value in between zero and one in a surface cell, and zero and one in air and liquid, respectively, i.e.,

$$F(\vec{\varvec{x}},t) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{in}}\;{\text{the}}\;{\text{fluid}}} \hfill \\ {0 < F < 1} \hfill & { {\text{at }}\;{\text{the }}\;{\text{interface}}} \hfill \\ 0 \hfill & {{\text{external}}\;{\text{to}}\;{\text{fluid}}} \hfill \\ \end{array} } \right.$$

(16)

The VOF and LS functions are advanced by the following equations, respectively:

$$\frac{{{\text{D}}F}}{{{\text{D}}t}} = \frac{\partial F}{\partial t} + \left( {\vec{\varvec{u}} \cdot \nabla } \right)F = 0$$

(17)

$$\frac{{{\text{D}}\phi }}{{{\text{D}}t}} = \frac{\partial \phi }{\partial t} + \left( {\vec{\varvec{u}} \cdot \nabla } \right)\phi = 0$$

(18)

It should be noted that since the VOF function is not smoothly distributed at the free surface, an interface reconstruction procedure is required to evaluate the VOF flux across a surface cell. In this study, the interface is reconstructed via a PLIC scheme and the interface unit normal is calculated from the LS function given by

$$\vec{\varvec{n}} = \frac{\nabla \phi }{{\left| {\nabla \phi } \right|}} = \nabla \phi$$

(19)

The LS function would fail to be a distance function after being advanced by Eq. (18), and a reinitialization (Sussman et al. 1994) process is needed for its return to a distance function. This can be achieved by obtaining a steady-state solution of the following reinitialization equation:

$$\frac{\partial \phi }{\partial \tau } = \frac{{\phi_{0} }}{{\sqrt {\phi_{0}^{2} + h^{2} } }}\left( {1 - \left| {\nabla \phi } \right|} \right)$$

(20)

where ϕ ₀ is the LS function at the previous time step, τ the artificial time and h the grid spacing. Finally, in order to achieve mass conservation, the LS functions have to be redistanced (Son and Hur 2002) prior to being used. The curvature, computed directly from the LS function, is given by

$$\kappa = \nabla \cdot \left( {\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right)$$

(21)

A flow chart for the CLSVOF algorithm is shown in Fig. 3. Details of the numerical formulation can be found in here (Tong and Wang 2007; Wang and Tong 2010).

Fig. 3

Flow chart of the CLSVOF scheme: coupling process in the dashed box

3.3 Surface tension modeling scheme

The continuum surface force (CSF) method (Brackbill et al. 1992) is used to model the surface tension in which the surface tension force is treated as a body force given by

$$\overrightarrow {{\varvec{F}_{\varvec{b}} }} = \sigma \delta \left( x \right)\kappa \vec{\varvec{n}}$$

(22)

where σ is the surface tension coefficient, δ(x) a delta function concentrated on the interface, κ the mean curvature and $\vec{\varvec{n}}$ the unit vector normal to the free surface. The body force $\overrightarrow {{\varvec{F}_{\varvec{b}} }}$ is distributed within a transition region near the free surface across which the fluid properties are assumed to change continuously from one grid to another. The discontinuous jump of fluid properties across the free surface is thus eliminated. By incorporating Eqs. (2) and (3), Eq. (22) becomes:

$$\overrightarrow {{\varvec{F}_{\varvec{b}} }} = \sigma \delta \left( x \right)\left( {\kappa_{xy} + \frac{{ - \cos \theta_{\text{t}} - \cos \theta_{\text{b}} }}{H}} \right)\vec{\varvec{n}}$$

(23)

3.4 Viscous stress exerted by the parallel plates

It should be noted that the ‘Hele-Shaw cell’ 3D to 2D simplification will forfeit the ability to include the viscous stresses on the z-plane. To account for the viscous stresses exerted by the parallel plates, the plane Couette flow model is considered. For fully developed Couette flows between two stationary planes, the velocity profile is parabolic for both u and v, with the shear stresses at both planes equal to $6\;\mu \frac{u}{H}$ and $6\;\mu \frac{v}{H}$ in the x- and y-directions, respectively. Since the transport process involves time-varying movement of the fluid, the flow is by no means steady and fully developed. The viscous stresses from the Couette flow model are modified with the incorporation of a multiplication factor λ _vs , which are given by

$$\tau_{zx} = \lambda_{vs} *\mu *\frac{u}{H}$$

(24)

$$\tau_{zy} = \lambda_{vs} *\mu *\frac{v}{H}$$

(25)

where μ is the dynamic viscosity and u and v the average velocities in the x- and y-directions, respectively.

3.5 Contact angle hysteresis

As mentioned earlier, contact angle hysteresis has an overall effect of reducing the droplet speed and its physics is still not completely understood. The fact that dynamic contact angles are influenced not only by the plate material (Gupta et al. 2011), but also by other factors such as temperature, ambient pressure, droplet speed and plate surface smoothness makes prediction of dynamic contact angles very challenging. The following scheme is used to determine whether the interface is advancing or receding at each time step before the dynamic contact angles are applied,

$$\vec{\varvec{u}} \cdot \vec{\varvec{n}}\left\{ {\begin{array}{*{20}l} { < 0} \hfill & {{\text{Receding}}\;{\text{interface}}} \hfill \\ { > 0} \hfill & {{\text{Advancing}}\;{\text{interface}}} \hfill \\ \end{array} } \right.$$

(26)

Once the direction is determined, the dynamic contact angles are computed by the following equations as:

$${\text{top}}\;{\text{receding}}\;{\text{angle}}\quad \theta_{{{\text{t}}, {\text{R}}}} = \theta_{\text{t}} -\Delta _{\text{R}}$$

(27)

$${\text{bottom}}\;{\text{receding}}\;{\text{angle}} \quad \theta_{{{\text{b}},{\text{R}}}} = \theta_{\text{b}} -\Delta _{\text{R}}$$

(28)

$${\text{top}}\;{\text{advancing}}\;{\text{angle}}\quad \theta_{{{\text{t}},{\text{A}}}} = \theta_{\text{t}} +\Delta _{\text{A}}$$

(29)

$${\text{bottom}}\;{\text{advancing}}\;{\text{angle}}\quad \theta_{{{\text{b}},{\text{A}}}} = \theta_{\text{b}} +\Delta _{\text{A}}$$

(30)

where $\Delta _{\text{R}}$ and $\Delta _{\text{A}}$ are the deflections of the receding and advancing contact angles from the static contact angle. By replacing θ _t and θ _b in Eq. (23) with the above dynamic contact angles, the hysteresis effect is properly implemented into the numerical model.

4 Results and discussion

4.1 Numerical simulations

Numerical simulations of microdroplet transport in a parallel-plate EWOD device have been performed. Deionized (DI) water is used as the working liquid without including any other liquid as the medium filler. The numerical setup and droplet physical properties given in Table 1 are same as the experiment performed by Yaddessalage (2013). The channel height between the two parallel plates is 0.1 mm unless specified otherwise. The computational domain used for the transport process is shown in Fig. 4 with dimensions 4.8 × 2.8 mm². Uniform square mesh with grid spacing of 0.05 mm is used based on the results of a grid refinement study which is reported in “Appendix”. No-slip boundary conditions are implemented at all sides of the domain. It should be noted that since the droplet is, by design, not expected to reach the boundary of the computational domain, the nature of the boundary condition is of no consequence. Note that the contact line would be unable to move if no-slip boundary condition is used everywhere on the solid surface (Huh and Scriven 1971). However, this boundary condition is not needed for the solution since a two-dimensional Hele-Shaw model is used for the current study. The time step for the numerical computations is automatically adjusted during the course of calculations, which is taken as the minimum of the time step constraints for numerical stability of capillarity, viscosity and the Courant condition (Brackbill et al. 1992; Harlow and Amsden 1971; Kothe et al. 1991). Due to lack of static contact angle values in the experimental results, 117° is used for $\theta_{{{\text{b}},{\text{OFF}}}}$ following a previous electrowetting-based water droplet splitting study (Guan and Tong 2015). The optimum value of $\theta_{{{\text{b}},{\text{ON}}}}$ is subsequently set to 54° by matching the droplet shape in the numerical simulation with the experiment.

Table 1 Parameters used in the current study

Fig. 4

Computational domain for droplet transport

The transport process with snapshots at various time instants is shown in Fig. 5. Two square electrodes of 2 × 2 mm² are set as ON and OFF from left to right for the entire transport process except for the initial condition in which the electrodes are set reversely instead to prevent the droplet from returning to circular shape (Fig. 5a). With the electrowetting force pinning the interface at the four corners, the droplet was stretched into square shape except the small curves at the corners as shown in the experiment. Since this quasi-square shape is difficult to prescribe as the initial condition in the numerical simulation, a square droplet with 2 mm length is used with the gas–liquid interface aligning with the electrode boundary and the size comparable to the experiment.

Fig. 5

Droplet transport: numerical (dark line) at t = 0 ms (a), t = 11 ms (b), t = 21 ms (c), t = 25 ms (d), t = 33 ms (e) and t = 40 ms (f); experimental (light line) (Yaddessalage 2013)

As soon as the left electrode is activated together with the right electrode deactivated simultaneously, the gas–liquid interface starts to deform due to the pressure difference across the droplet boundary as indicated by Eq. (4). The interfaces at the corners first develop into smooth curves instantaneously due to the extremely large surface tension force in the x–y plane. After the droplet deforms into circular shape, the interface on the left side starts moving toward the activated electrode due to the surface tension force induced by the electrowetting effect. Meanwhile, the interface close to the border of the two electrodes gradually changes from convex to concave shape, which leads to the formation of a neck (Fig. 5b). It is of great importance to note that the difference between curvatures κ _z,OFF and κ _z,ON not only creates the internal pressure gradient which drives the droplet from the OFF to the ON region, but also results in a pressure jump where the droplet interface cuts the ON/OFF electrode border. This pressure jump may lead to the formation of two localized areas, one on each side, adjacent to the border with a larger pressure gradient induced (Figs. 5b, 6). These localized areas directly determine the direction and speed of the fluid flow moving toward the activated electrode and consequently play a dominant role in the droplet deformation throughout the transport process. As the transport process continues, the liquid is gradually filling up the ON electrode with the droplet leading edge becoming wider than the trailing edge (Fig. 5c, d). With more liquid flowing to the activated electrode, a rapid increase in curvature κ _xy takes place at the tip of the trailing edge, which creates a larger pressure gradient and consequently a higher flow speed there (Fig. 5e). The fluid motion finally ceases when the liquid has completely settled on the ON electrode, which marks the end of the transport process (Fig. 5f). As shown in Fig. 5, the numerical results are in excellent agreement with the experiment. Note that the asymmetric shapes at the droplet trailing edge in the experimental results come from the non-uniform surface smoothness of the experimental device, which eventually leads to the slight disagreement between the experimental and numerical results.

Fig. 6

Pressure (top) and velocity fields (bottom) at t = 11 ms (only top half of the droplet is shown)

Certain key non-dimensional groups have been evaluated with the values listed in Table 1. U _R is the reference velocity which makes the maximum non-dimensional velocity close to unity. It is understood that certain aspects of microfluidic droplet motion induced by the electrowetting effect can be characterized by these non-dimensional numbers. There are three adjustable parameters in the numerical model: $\Delta _{\text{R}}$, $\Delta _{\text{A}}$ and λ _vs . Due to lack of information on contact angle hysteresis for the experiments, $\Delta _{\text{R}}$ and $\Delta _{\text{A}}$ are assumed to have the same value. The optimum hysteresis angles which best match the experiments are reported in Table 1. Optimum λ _vs is subsequently determined by matching the timescale of the numerical simulation with the experimental results.

It is discovered that the droplet transport process has little variation if the initial condition is set as circular with identical droplet volume instead (Fig. 7). Unlike the square-shaped case in which the curvature κ _xy has an extremely large magnitude at the corners, κ _xy is uniform with a much smaller magnitude for the circular-shaped case. However, it is found that the difference in κ _xy in the initial conditions only affects the opening stage of transport due to a much more dominant effect of Δκ _z on the transport process. Since Δκ _z is completely independent of initial droplet shape and has identical magnitude in these two cases, the pressure fields within the droplets have almost the same distributions (Fig. 8), which consequently leads to the very similar droplet shapes throughout the transport process.

Fig. 7

Droplet transport with different initial conditions: circular shape (a–d) and square shape (e–h)

Fig. 8

Pressure fields for different initial conditions: circular shape at t = 5 ms (a), t = 10 ms (b) and t = 20 ms (c) and square shape at t = 5 ms (d), t = 10 ms (e) and t = 20 ms (f)

4.2 Parametric study

A parametric study has been conducted in which the effects of static contact angles, contact angle hysteresis, viscous stress, channel height, electrode size and droplet physical properties on the transport process have been investigated. Droplets of circular shape are used as the initial conditions of all following cases for the purpose of eliminating the non-uniformity of κ _xy when square or other non-circular shapes are applied. As a consequence, the droplet motion is primarily controlled by Δκ _z at the opening stage of transport process.

4.2.1 Static contact angles

According to Eq. (3), the magnitude of κ _z can be modified by varying the static contact angles at the bottom plate, which will alter droplet shape and moving speed during the transport process (Fig. 9). When the static contact angles at the bottom plate are set as 44° and 127° for the ON and OFF electrodes, respectively, both Δκ _z and the pressure jump at the ON/OFF electrode border become larger than the reference case with 54° and 117° for θ _s,ON and θ _s,OFF, respectively. This change in static contact angles creates greater internal pressure gradient and more curved pressure contours in the localized areas as soon as the transport takes place (Fig. 10a). On the other hand, the pressure gradient away from the localized areas is much smaller, which results in a much slower flow speed at the trailing edge. As a consequence, the liquid flowing toward the activated electrode mostly comes from the area adjacent to the ON/OFF electrode border where a much higher flow speed is also induced. At the opening stage of transport, the interface near the ON/OFF electrode border keeps shrinking toward the center and swiftly deforms from convex to concave shape, while the interface at the trailing edge experiences only a slight deformation (Figs. 9a, 10b). As the transport process continues, the liquid near the ON/OFF electrode border maintains a much larger moving speed than the trailing edge. A neck is quickly formed at the ON/OFF electrode border (Fig. 9b, c) which ultimately breaks off and splits the droplet into two small ones staying separately on the ON and OFF electrodes (Fig. 9d). The pressure and velocity profiles at key time instants are shown in Figs. 10 and 11, which provides some vital information for this transport process.

Fig. 9

Droplet transport with different static contact angles: θ _s,ON = 44° and θ _s,OFF = 127° (a–d), θ _s,ON = 54° and θ _s,OFF = 117° (e–h) and θ _s,ON = 74° and θ _s,OFF = 97° (i–l)

Fig. 10

Pressure (top) and velocity fields (bottom) for θ _s,ON = 44° and θ _s,OFF = 127° at t = 0.1 ms (a), t = 5.0 ms (b), t = 10.0 ms (c) and t = 15.0 ms (d)

Fig. 11

Pinch-off of the droplet with θ _s,ON = 44° and θ _s,OFF = 127° at t = 17.0 ms (a) and t = 17.1 ms (b)

When θ _s,ON and θ _s,OFF are set as 74° and 97°, respectively, the magnitude of $\Delta \kappa_{z}$ is significantly reduced and κ _xy becomes more dominant. This switch of dominance from $\Delta \kappa_{z}$ to κ _xy considerably alters the pressure distributions within the droplet as well as the direction and speed of the fluid flow. As shown in Fig. 12a, the pressure contours near the ON/OFF electrode border are much less curved than the 44°/127° case at the opening stage of transport. As a result, the localized areas are absent here and the liquid flowing toward the ON electrode primarily comes from the center of the droplet rather than the area adjacent to the ON/OFF electrode border. This change in flow direction offers adequate explanations for the phenomenon that the droplet has an elliptical shape during the transport without the formation of a neck (Fig. 9i). As the transport process continues, the leading edge gradually becomes wider than the trailing edge where κ _xy has a larger magnitude than that at the droplet front (Fig. 9j). Since the transport process is primarily controlled by κ _xy in this case, the fluid flow at the trailing edge now has a larger speed (Fig. 12c), which rapidly pulls the interface remaining on the OFF electrode toward the activated area (Fig. 9k). With more fluid flowing onto the ON electrode, the droplet finally fills the activated area without splitting (Fig. 9l). Note that the transport process takes as long as 160 ms due to a much reduced pressure gradient within the droplet when the difference between θ _s,OFF and θ _s,ON is as small as 23°. The pressure and velocity profiles at key time instants are shown in Fig. 12.

Fig. 12

Pressure (top) and velocity fields (bottom) for θ _s,ON = 74° and θ _s,OFF = 97° at t = 0.1 ms (a), t = 40.0 ms (b), t = 80.0 ms (c) and t = 120.0 ms (d)

The transport process has also been carried out with different combinations of θ _s,ON and θ _s,OFF while keeping all other parameters unchanged. The results of droplet transport time versus dimensionless curvature $\tilde{\kappa }$ are shown in Fig. 13 in which $\tilde{\kappa }$ is computed from Eq. (7). It has been found that the droplet experiences a larger deformation as $\tilde{\kappa }$ increases and that a critical value of $\tilde{\kappa }$ exists somewhere between 12.612 and 13.240 beyond which splitting occurs during the transport. When $\tilde{\kappa }$ is smaller than this critical value, the transport time decreases as $\tilde{\kappa }$ increases from 4.485 to 10.934 and then slightly increases with $\tilde{\kappa }$ when $\tilde{\kappa }$ varies from 10.934 to 12.612. The reduction in the transport time when $\tilde{\kappa }$ is between 4.485 and 10.934 mainly results from the increasing pressure difference across the droplet boundary as the difference between θ _s,OFF and θ _s,ON becomes larger, which accelerates the transport speed. When $\tilde{\kappa }$ increases from 10.934 to 12.612, the slight increase in the transport time is primarily due to the narrower neck formed in the middle of the transport process (Fig. 14), which creates a smaller bottleneck for the flow trailing from the OFF electrode and consequently lengthens the transport time. When $\tilde{\kappa }$ further increases to beyond the critical value, $\Delta \kappa_{z}$ becomes much more dominant than κ _xy and splitting occurs as a result of a much larger pressure gradient and more curved pressure contours in the localized areas as explained previously.

Fig. 13

Droplet transport time versus dimensionless curvature for the parametric study of static contact angles

Fig. 14

Comparison of the necks of different static contact angle cases

The results of transport time versus static contact angle in the current study are in general agreement with the findings reported in the literature in which the droplet transport velocity was found to increase with the applied electrical voltage (Pollack et al. 2002; Ren et al. 2002; Bahadur and Garimella 2006; Arzpeyma et al. 2008; Lu et al. 2007). Since a higher voltage applied at the droplet boundary generally produces a smaller value of θ _s,ON and therefore a greater difference between θ _s,ON and θ _s,OFF, the same conclusion can be drawn from these findings that the transport speed increases with the difference between θ _s,ON and θ _s,OFF. Furthermore, the present results are in agreement with the phenomena observed by Lu et al. (2007) that the droplet shape experienced a larger deformation as the voltage increased. Additionally, it was discovered by Pollack et al. (2002) that the droplet would split when the voltage is beyond a certain voltage, which is also consistent with the results obtained in the present study.

4.2.2 Contact angle hysteresis

The effect of contact angle hysteresis on the transport process has been studied by altering the hysteresis angles in Eqs. (27)–(30) while keeping the assumption that $\Delta _{\text{R}}$ and $\Delta _{\text{A}}$ have the same value. In general, the difference between the receding and advancing contact angles will be decreased (or increased) if a larger (or smaller) hysteresis angle is applied, which will affect the pressure gradient within the droplet and eventually the overall transport process. However, as shown in Fig. 15, it has been found that hysteresis has only slight effects on both droplet shape and timescale of the transport process since hysteresis angle is much smaller than static contact angles and therefore only plays a minor role in the transport process.

Fig. 15

Droplet transport with different hysteresis angles: $\Delta _{\text{R}}$ = $\Delta _{\text{A}}$ = 0° (a–d), $\Delta _{\text{R}}$ = $\Delta _{\text{A}}$ = 4° (e–h) and $\Delta _{\text{R}}$ = $\Delta _{\text{A}}$ = 8° (i–l)

4.2.3 Viscous stress

The viscous stress exerted by the two parallel plates can be varied by adjusting the multiplication factor λ _vs in Eqs. (24) and (25). The transport processes for λ _vs  = 9, 18 (reference case) and 72 are shown in Fig. 16, which shows that the transport time increases with viscous stress, but the droplets display the same pattern during the entire process. Since both κ _xy and $\Delta \kappa_{z}$ are independent of the viscous force, the pressure distributions within the droplet are not affected by the variation of viscous stress (Fig. 17) even though the transport times differ by a factor of 6. The transport process has also been carried out with various viscous stress coefficients between 9 and 72, and it has been found that the transport time increases almost linearly with λ _vs .

Fig. 16

Droplet transport with different viscous stress coefficients: λ _vs  = 9 (a–d), λ _vs  = 18 (e–h) and λ _vs  = 72 (i–l)

Fig. 17

Pressure fields for different viscous stress coefficients: λ _vs  = 9 at t = 7 ms (a), t = 14 ms (b), t = 21 ms (c), λ _vs  = 72 at t = 39 ms (d), t = 78 ms (e) and t = 117 ms (f)

4.2.4 Channel height

The channel height is expected to affect the pressure gradient within the droplet as well as the viscous force exerted by the plates according to Eqs. (4), (24) and (25). The transport processes for H = 0.06, 0.1 mm (reference case) and 0.2 mm are shown in Fig. 18. When the channel height is reduced to 0.06 mm, both Δκ _z and the pressure jump at the ON/OFF electrode border increase according to Eq. (4). The pressure contours in the localized areas become more curved than the reference case, which further alters the speed and direction of the fluid flow adjacent to the ON/OFF electrode border. Even though the viscous force also becomes larger when channel height is reduced, the droplet shape is independent of the wall shear stress which only has the retarding effect on transport time as demonstrated previously. Therefore, similar to the case with 44°/127° static contact angles, the droplet interface experiences a large deformation at the localized areas during the transport (Fig. 18a–c), which eventually leads to the splitting at 37 ms (Fig. 18d). The entire transport process takes 40 ms, twice as long as the 44°/127° case due to the increased viscous force.

Fig. 18

Droplet transport with different channel heights: H = 0.06 mm (a–d), H = 0.10 mm (e–h) and H = 0.20 mm (i–l)

On the other hand, the droplet transports with an elliptical shape when the channel height is 0.2 mm instead (Fig. 18i), resulting from the less curved pressure contours within the droplet. The pressure gradient is also smaller near the ON/OFF electrode border due to a reduced pressure jump across the border when the channel height increases. The transport process is similar to the case with 74°/97° static contact angles except that the entire transport process only takes 20 ms since the viscous stress is significantly reduced (Fig. 18l).

Additional channel heights have also been studied for the 2 × 2 mm² electrode size, and the results of transport time versus channel height are given in Fig. 19. It has been found that the splitting does not occur when channel height is greater than a certain critical value between 0.08 mm and 0.09 mm. Beyond this critical value, the pressure jump is insufficient to bend the pressure contours near the ON/OFF electrode border to create the localized areas. When splitting is absent, the transport speed increases with the channel height due to the reduced viscous stress. Even though the pressure difference across the droplet boundary is also reduced as channel height increases, the decrease in wall shear stress is apparently more significant than the reduction in pressure difference. The transport time is found to reduce from 59 to 18 ms as the channel height increases from 0.09 to 0.25 mm. However, the decrease in transport time becomes very minimal when H is larger than 0.2 mm, which agrees with the findings of Bahadur and Garimella (2006) that the transport speed was of negligible dependence on the channel height when H varied between 0.3 and 0.7 mm. Moreover, it is discovered that the droplet shape experiences a larger deformation when channel height is reduced, which is consistent with the results obtained by Pollack (2001).

Fig. 19

Droplet transport time versus channel height for the 2 × 2 mm² electrode size

4.2.5 Electrode size

When the electrode size is altered with the droplet diameter maintained at the same ratio with the electrode length, the magnitude of κ _xy will vary reversely with the droplet size. The magnitude of κ _z , however, remains the same since neither the contact angles nor the channel height is modified. As a result, the effect of κ _z on the transport process becomes more (or less) dominant when the electrode size increases (or decreases), which changes the pressure distributions within the droplet and consequently affects the droplet shape. The transport processes for 1 × 1 mm², 2 × 2 mm² (reference case), 3 × 3 mm² and 4 × 4 mm² electrode sizes are shown in Fig. 20. When the electrode size increases from 1 × 1 mm² to 4 × 4 mm², $\Delta \kappa_{z}$ becomes increasingly dominant which results in more curved pressure contours in the localized areas and eventually the splitting for the same reason given for the 44°/127° and H = 0.06 mm cases. The localized areas which exist for the 3 × 3 mm² and 4 × 4 mm² electrode sizes are absent for the 1 × 1 mm² case due to a more dominant effect of κ _xy , which eventually leads to the elliptical shape during the transport.

Fig. 20

Droplet transport with different electrode sizes: 1 × 1 mm² (a–d), 2 × 2 mm² (e–h), 3 × 3 mm² (i–l) and 4 × 4 mm² (m–p)

The transport processes are also conducted with various channel heights for 1 × 1 mm², 3 × 3 mm² and 4 × 4 mm² cases. It has been found that the splitting does not occur when the channel height is larger than 0.045, 0.14 and 0.19 mm for 1 × 1 mm², 3 × 3 mm² and 4 × 4 mm² electrode sizes, respectively. The results of transport time versus dimensionless curvature are shown in Fig. 21. It has been found that the critical $\tilde{\kappa }$ value is around 13 for all electrode sizes, which is consistent with the value previously found in the parametric study of static contact angles. Below the critical $\tilde{\kappa }$ value, the transport time increases with $\tilde{\kappa }$ for all electrode sizes due to the increasing viscous stress as the channel height decreases.

Fig. 21

Droplet transport time versus dimensionless curvature for the parametric study of channel height and electrode size

4.2.6 Droplet physical properties

The results of the parametric study on droplet physical properties are shown in Fig. 22. It has been found that increase in density or viscosity reduces droplet speed and consequently delays the transport process since it is more difficult to move a droplet with the same pressure force if the fluid is heavier or more viscous. On the other hand, the capillary-induced pressure difference across the droplet boundary increases with the surface tension coefficient which accelerates the droplet motion and reduces the transport time. The droplet shape does not appear to vary much with density, viscosity or surface tension.

Fig. 22

Droplet transport time versus droplet physical properties

5 Conclusion

Microfluidic water droplet transport in a parallel-plate electrowetting-on-dielectric (EWOD) device has been numerically studied. The Navier–Stokes equations are solved using a finite volume formulation with a two-step projection method on a fixed grid. The free surface of the liquid is tracked by the CLSVOF method with the surface tension force determined by the CSF model. Contact angle hysteresis which is an essential feature in EWOD device has been implemented. A simplified model is adopted for the viscous stresses exerted by the parallel plates at the solid–liquid interface. The transport process obtained from the numerical results is in excellent agreement with the experiment. It has been discovered that the pressure jump at the ON/OFF electrode border may lead to the formation of two localized areas which directly determine the direction and speed of the fluid flow and consequently play a dominant role in the transport process. It has been found that the droplet experiences a larger deformation and even a splitting when the difference between θ _s,OFF and θ _s,ON is increased, when the channel height is reduced or when the electrode size is increased with the droplet diameter maintained at the same ratio with the electrode length. However, varying density, viscosity, surface tension coefficient or the viscous stresses exerted by the parallel plates appears to only alter the transport speed with the shape unchanged. A dimensionless curvature $\tilde{\kappa }$ has been introduced which represents the relative significance between $\Delta \kappa_{z}$ and κ _xy in a particular droplet transport case. The critical value of $\tilde{\kappa }$ beyond which the droplet splits during the transport has been found which appears to be universal for all the transport cases studied.

Appendix: Grid refinement study

Calculations of droplet transport have been conducted with three different mesh sizes for the grid convergence study. As shown in Fig. 23, the droplet shapes obtained from the three different grid sizes are very close, which indicates that grid convergence has been achieved. Based on the results of the grid refinement study, uniform square mesh of grid spacing of 0.05 mm is adopted for the present study.

Fig. 23

Droplet transport with different grid sizes: 0.05 × 0.05 mm², 0.025 × 0.025 mm² and 0.0125 × 0.0125 mm²