1 Introduction

The definition of nanocomposite (nanoparticulate-filled matrices) material has broadened significantly to encompass a large variety of systems such as one-dimensional, two-dimensional, and three-dimensional, made of distinctly dissimilar components and mixed at the nanometer scale. This rapidly expanding field is generating many exciting new materials with novel properties. The latter could be derived by combining properties from the parent constituents into a single material. There is also the possibility of new properties, which are unknown in the parent constituent materials. Numerical studies and models were established to predict the full potential of novel nanocomposites (Yang and Chen 2004; Valavala and Odegard 2005). There is a strong motivation to develop advanced heat transfer fluids (nanofluids) with higher thermal conductivity properties by using nanoparticle additives (Choi 1995; Lee and Choi 1996; Xuan and Li 2000; Eastman et al. 2001; Keblinski et al. 2002). In addition, from fluid dynamics point of view, nanofluids have a distinctive characteristic, which is quite different from those of traditional solid-liquid mixtures in which millimeter- and/or micrometer-sized particles are involved. Large particles can create pressure drop due to settling effects. In contrast, the nanoparticles exhibit significantly less additional pressure drop when flowing through the passages (Khanafer et al. 2003). Nevertheless, the possibility of clogging micrometric channels remains a challenge. For instance, this issue is magnified in case of Resin Transfer Molding (RTM) and other composite processes because of a high resin viscosity and a low preform permeability. Solving such problems is also considered as a challenge because the simulation and prediction of the characteristics of multiphase flows is very complex.

Changing from a single-phase model, where a single set of conservation equations for momentum, continuity, and energy is solved, to a multiphase model requires introducing additional sets of conservation equations. The modifications involve introducing the volume fractions for the multiple phases as well as introducing a mechanism for the exchange of momentum and energy between the phases. A total of six generic governing equations are required to model the mass, momentum, and energy fields. These six conservation equations, however, hold only within each phase; therefore three additional equations governing the interfacial transfer of mass, momentum, and energy between the phases are needed (Kleinstreuer 2003). In spite of the mentioned difficulties, significant progress has been made in different areas of multiphase computational fluid dynamics (CFD). Wachem and Almsted 2003, introduced different physical models for CFD predictions of multiphase flows, while (Kleinstreuer 2003) introduced their numerical solution tools. It was found that most computational models for multiphase flow on an application level describe both the continuous phase (fluid) and the dispersed phase (solid) by a so-called Eulerian model. In these models the dispersed phase, like the continuous phase, is described as a continuous fluid with appropriate closures. Hence, one calculates only the average local volume fraction, velocity, etc. and not the properties of each individual dispersed particle. In the case of well-dispersed phases, one can introduce the properties of the mixture (nanofluid) by considering the phasic volume approach (Kleinstreuer 2003). As an example for this formulation (Jackson 1997) used a formal mathematical definition of local variables to translate the point Navier–Stokes equations for the fluid and Newton’s equation for motion for a single particle directly into continuum equations representing momentum balances for the fluid and solid phases.

In the present paper, a two-dimensional simulation model based on the Eulerian multiphase approach for the flow of a carbon nanofluid around a carbon microfiber matrix is introduced to investigate and predict the flow characteristics. The concept of phasic volume fractions is utilized, while the effects of external body forces, lift forces, and virtual mass forces are introduced into the momentum equations. The phase coupled SIMPLE algorithm has been employed to solve the model.

2 Numerical formulation

2.1 System configuration and physical domain

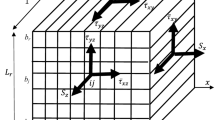
A nanofluid, which is composed of spherical carbon nanoparticles dispersed homogenously into a resin, is infiltrated into a two-dimensional carbon microfiber matrix as shown in Fig. 1a. The microfibers have the same diameter D and are arranged in a staggered configuration with a separate distance T = D from all directions. The used nanofluid is assumed to be Newtonian, incompressible, and laminar while the infiltration process is supposed to occur during a short period (in second scale). Due to the high viscosity of the used resin and the short duration time of the infiltration process, the particles’ Brownian motion and sedimentation will not be considered. A unit cell is taken as a representative unit cell for the system as shown in Fig. 1b, which illustrates that one-half of each side-by-side microfiber is only taken for symmetrical considerations, while the third microfiber, which is in a staggered orientation with the other two microfibers, is completely considered. As a case of study, carbon microfibers (8 μm in diameter) are considered, and a unit cell (16×38 μm2) represents the model. The carbon nanoparticles have a diameter of 100 nm.

Fig. 1
figure 1

a Carbon microfibers matrix configuration Fig. 1. b Model’s representative unit cell

Full size image

The thermophysical properties of the used fluid, resin, and the solid particles, carbon nanoparticles, are listed in Table 1.

Table 1 Thermophysical properties of the used fluid and solid particles
Full size table

2.2 Model description and governing equations

The present problem is classified as a multiphase flow problem. One of the most powerful models to simulate such problems is the Eulerian multiphase model (Kleinstreuer 2003). The Eulerian multiphase model solves a set of n momentum and continuity equations for each phase, and coupling between them is achieved through the pressure and interphase exchange coefficients. The concept of phasic volume fractions, which is utilized for nanofluid modeling (Khanafer et al. 2003), is considered in this model, and the laws of conservation of mass and momentum are satisfied by each phase individually. The derivation of the conservation equations is performed by using the mixture theory approach (Bowen 1976) as follows:

2.2.1 Continuity equations:

By considering no mass transfer between the two phases, the continuity equation for the fluid phase could be taken as given by (Kleinstreuer 2003) in the following form:

$$\frac{\partial}{{\partial t}}{\left({\alpha _{{\rm f}} \rho _{{\rm f}}} \right)} + \nabla {\left({\alpha _{{\rm f}} \rho _{{\rm f}} v_{{\rm f}}} \right)} = 0$$
(1)

where α f, ρ f, and v f are the fluid phase volume fraction, density, and velocity, respectively.

For the solid phase:

$$\frac{\partial}{{\partial t}}{\left({\alpha _{{\rm s}} \rho _{{\rm s}}} \right)} + \nabla {\left({\alpha _{{\rm s}} \rho _{{\rm s}} v_{{\rm s}}} \right)} = 0$$
(2)

where α s, ρ s, and v s are the solid phase volume fraction, density, and velocity, respectively.

2.2.2 Momentum equations

The conservation of momentum for the fluid phase is:

$$\begin{aligned}\frac{\partial}{{\partial t}}(\alpha _{{\rm f}} \rho _{{\rm f}} v_{{\rm f}}) + \nabla (\alpha _{{\rm f}} \rho _{{\rm f}} v_{{\rm f}} v_{{\rm f}}) & = - \alpha _{{\rm f}} \nabla p + \nabla \overline{{\tau _{{\rm f}}}} + \alpha _{{\rm f}} \rho _{{\rm f}} g \\ & \quad + \alpha _{{\rm f}} \rho _{{\rm f}} (F_{{\rm f}} + F_{{{\rm lift},{\rm f}}} + F_{{{\rm vm},{\rm f}}}) + K_{{{\rm sf}}} {\left({v_{{\rm s}} - v_{{\rm f}}} \right)}\end{aligned}$$
(3)

and for the solid phase, is:

$$\begin{aligned} \frac{\partial}{{\partial t}}(\alpha _{{\rm s}} \rho _{{\rm s}} v_{{\rm s}}) + \nabla (\alpha _{{\rm s}} \rho _{{\rm s}} v_{{\rm s}} v_{{\rm s}}) &= - \alpha _{{\rm s}} \nabla p + \nabla \overline{{\tau _{{\rm s}}}} + \alpha _{{\rm s}} \rho _{{\rm s}} g \\ & \quad + \alpha _{{\rm s}} \rho _{{\rm s}} (F_{{\rm s}} + F_{{{\rm lift},{\rm s}}} + F_{{{\rm vm},{\rm s}}}) + K_{{{\rm fs}}} {\left({v_{{\rm f}} - v_{{\rm s}}} \right)}\\ \end{aligned}$$
(4)

where p is the pressure shared by the two phases, \(\overline{\tau} \) is the phase stress tensor, F is the external body force, F lift is the lift force, F vm is the virtual mass force, K fs= K sf is the interphase momentum exchange coefficient between the two phases, and subscripts f and s denote the liquid and solid phases, respectively.

2.2.3 Stress tensors

The fluid phase stress tensor is taken as given by (Kleinstreuer 2003) in the form:

$$\overline{{\tau _{{\rm f}}}} = \alpha _{{\rm f}} \mu _{{\rm f}} {\left({\nabla v_{{\rm f}} + \nabla v^{{\rm T}}_{{\rm f}}} \right)}$$
(5)

where μf is the fluid viscosity.

On the other hand, the solid phase stress tensor contains shear and bulk viscosities arising from particle momentum exchange due to collision and translation (Gidaspow et al. 1992). The collision and kinetic parts are added to give the solids shear viscosity:

$$\mu _{{\rm s}} = \mu _{{{\rm s},{\rm collision}}} + \mu _{{{\rm s},{\rm kinetic}}} $$
(6)

The collisional part of the shear viscosity given by (Gidaspow et al. 1992) is in the form:

$$\mu _{{{\rm s},{\rm collision}}} = \frac{4}{5}\alpha _{{\rm s}} \rho _{{\rm s}} d_{{\rm s}} {\left({1 + e_{{\rm s}}} \right)}{\left({\frac{{\Theta _{{\rm s}}}}{\pi}} \right)}^{{0.5}} $$
(7)

where d s is the solid particle diameter, e s is the coefficient of restitution for particle collisions, and its value for the present case is 0.9, and Θ s is the granular temperature, which is proportional to the kinetic energy of the random motion of the particles and it has been derived by (Ding and Gidaspow 1990).

The kinetic part of the shear viscosity given also by (Gidaspow et al. 1992) is in the form:

$$\mu _{{{\rm s},{\rm kinetic}}} = \frac{{10\rho _{{\rm s}} d_{{\rm s}} {\sqrt {\Theta _{{\rm s}} \pi}}}}{{96\alpha _{{\rm s}} {\left({1 + e_{{\rm s}}} \right)}}}{\left[ {1 + \frac{4}{5}\alpha _{{\rm s}} {\left({1 + e_{{\rm s}}} \right)}} \right]}^{2} $$
(8)

Based on equations, 6, 7, and 8, the solid phase stress tensor will take the form:

$$\overline{{\tau _{{\rm s}}}} = \alpha _{{\rm s}} \mu _{{\rm s}} {\left({\nabla v_{{\rm s}} + \nabla v^{{\rm T}}_{{\rm s}}} \right)}$$
(9)

2.2.4 Lift forces

The lift force acts on the solid phase particles mainly due to velocity gradients in the fluid phase flow field. It could be computed from the formula derived by (Drew and Lahey 1993) in the form:

$$F_{{{\rm lift},{\rm f}}} = - 0.5\alpha _{{\rm s}} \rho _{{\rm f}} {\left| {v_{{\rm f}} - v_{{\rm p}}} \right|} \times {\left({\nabla \times v_{{\rm f}}} \right)}$$
(10)

and in this case, F lift, f= -F lift, s

2.2.5 Virtual mass forces

The virtual mass force occurs when the solid phase, s, accelerates relative to the fluid phase, f. The inertia of the fluid phase mass encountered by the accelerating particles of the solid phase exerts a virtual mass on the particles, and it could be taken as given by (Drew and Lahey 1993) in the form:

$$F_{{{\rm vm},{\rm f}}} = 0.5\alpha _{{\rm p}} \rho _{{\rm f}} {\left({{\left({\frac{{\partial v_{{\rm f}}}}{{\partial t}} + {\left({v_{{\rm f}} \nabla} \right)}v_{{\rm f}}} \right)} - {\left({\frac{{\partial v_{{\rm s}}}}{{\partial t}} + {\left({v_{{\rm s}} \nabla} \right)}v_{{\rm s}}} \right)}} \right)}$$
(11)

and in this case also, F vm, f=F vm, s

2.2.6 Interphase exchange coefficients

The fluid solid momentum exchange coefficient, K sf = K fs, could be introduced as given by (Gidaspow et al. 1992) in the following form:

$$K_{{{\rm sf}}} = \frac{3}{4}C_{{\rm D}} \frac{{\alpha _{{\rm s}} \alpha _{{\rm f}} {\left| {v_{{\rm s}} - v_{{\rm f}}} \right|}}}{{d_{{\rm s}}}}\alpha ^{{- 2.65}}_{{\rm f}} $$
(12)

where

$$C_{{\rm D}} = \frac{{24}}{{\alpha _{{\rm f}} {Re} _{{\rm s}}}}{\left[ {1 + 0.15{\left({\alpha _{{\rm f}} {Re} _{{\rm s}}} \right)}^{{0.687}}} \right]}$$
(13)

and Re s is the Reynolds number of the solid phase.

2.3 Numerical method

The numerical analysis is performed using Fluent as follows. The phase coupled SIMPLE algorithm (Vasquez and Ivanov 2000) is used for solving the pressure-velocity coupling, while the velocities are solved coupled by phases in a segregated fashion. The block algebraic multigrid scheme used by the coupled solver described by (Weiss et al. 1999) is used to solve the equation formed by the velocity components of all phases simultaneously. Then, a pressure correction equation is built based on total volume continuity rather than mass continuity. Pressure and velocities are then corrected so as to satisfy the continuity constraint.

2.4 Grid size

A grid size of 50×120 is applied on the unit cell illustrated in Fig. 1b. To test and assess grid independence of the solution scheme, the grid size was changed up to 50×120, and it is found that this grid size is sufficient for the present case of study.

2.5 Initial and boundary conditions

The numerical model was performed and solved under the following assumptions and boundary and initial conditions: the flow inlet is defined by its velocity components, while the flow outlet is defined by the outlet pressure. Since the flow thermal solution is assumed periodic, periodic boundary conditions are applied on the side boundaries of the flow inlets and outlets. The thermophysical properties of the used resin are introduced at a temperature level of 300°K. The inlet velocity of the flow is normal to the boundary and has a magnitude of 0.05 m/s. The flow outlet pressure will have the atmospheric pressure value. The carbon microfiber walls will have a temperature of 300°K with no internal heat generation and with no slip boundary condition. A condition of gravitational acceleration is also considered.

3 Results

The mentioned initial and boundary conditions have been applied on the proposed numerical model, which has been solved for different volume load ratios of the spherical carbon nanoparticles dispersed into the liquid phase; resin. The volume load ratios are 0, 0.5, 1, 1.5, and 2%; where the zero volume ratio corresponds to neat resin.

3.1 Neat resin flow characteristics

The predicted static pressure contours for neat resin are illustrated in Fig. 2a. This figure shows that the maximum static pressure is achieved over the upper ends of the upper two microfibers due to their reactions against the fluid head. Also from this figure, one can see that the static pressure at the upper half of the cell decreases gradually towards the radial direction, r, and it has a minimum value at the cell center between the side-by-side microfibers. Conversely, the static pressure decreases sharply from the upper end to the lower end along the axial direction, x, until it reaches a constant value at the lower half of the cell after passing the third microfiber.

Fig. 2
figure 2

Pressure contours for neat resin. a Static pressure contours. b Dynamic pressure contours

Full size image

The predicted dynamic pressure contours for neat resin are shown in Fig. 2b. Unlike the static pressure, the dynamic pressure increases from the wall sides toward the radial direction until it reaches maximum values at the center between the side-by-side microfibers. On the other hand, the dynamic pressure has less value around the third microfiber.

The predicted cell Reynolds number contours for the flow of neat resin are presented in Fig. 3a. The figure shows that the cell Reynolds number has minimum values around all microfiber walls as a result of high friction. The friction decreases gradually toward the center of the cell at the radial direction between the side-by-side microfibers where microfiber walls-fluid interaction diminished, while this friction decreases gradually around the third microfiber. Similarly, the shear stress is much higher at microfiber walls-fluid interface, Fig. 3b. The wall shear stress has been estimated with a thickness of 0.6 μm.

Fig. 3
figure 3

a Cell Reynolds number contours for neat resin. b Walls shear stress contours for neat resin

Full size image

3.2 Results for different carbon particles load ratios

The present numerical model has been performed and solved for different volume load ratios of the carbon particles into the resin to investigate and predict the effect of loading ratio on the flow characteristics. Due to their significant roles in the flow characteristics, the cell Reynolds number of the flow and shear stress of the walls will be taken as the assessment parameters between different cases. The predicted cell Reynolds number contours for the flow with different volume ratios of 0.5, 1, 1.5 and 2% are shown in Fig. 4. From this figure one can see that the magnitude of the cell Reynolds number decreases as the carbon particles volume load ratio increases in the resin. This trend could be explained by an increase in nanofluid effective viscosity. Similarly, the magnitude of the wall shear stresses increases by increasing the particles load ratio, Fig. 5. The relation between the load ratio and the maximum shear stress around the microfibers for all cases is illustrated in Fig. 6, which shows a quadratic relation between them.

Fig. 4
figure 4

Cell Reynolds number contours for different carbon nanoparticle volume load ratios. a 0.5%. b 1.0%. c 1.5%. d 2.0%

Full size image
Fig. 5
figure 5

Walls shear stress contours for different carbon nanoparticle volume load ratios a 0.5%. b 2%

Full size image
Fig. 6
figure 6

The relation between load ratio and maximum walls shear stress

Full size image

3.3 Energy imbalance approach

As was expected during the flow process, the interfacial fluid layers around the microfiber walls exhibits high friction. This friction tends to reduce the flows velocity, which may cause its sticking on the microfiber walls, and after sometime, perhaps the flow passages will be blocked.

To prevent any potential sticking of the adjacent fluid layers on the microfiber walls during the flow process, an energy imbalance technique could be created between the carbon microfiber walls and the fluid flow.

As reported by (Schwartz 2001) the temperature-induced surface stress will contribute to thermocapillary flow within the liquid layer. These thermocapillary effects give rise to various gravity independent phenomena including convective flows, interface distortions as well as interface rupture. Thermocapillary flows are driven by the imbalance of tangential stress on the interface caused by temperature dependence of surface tension (Jiang and Floryan 2003). This tangential stress is called Marangoni shear stress, and it has the following relation:

$$\tau _{{{\rm Marangoni}}} = \frac{{\partial \sigma}}{{\partial T}} \frac{{\partial T}}{{\partial s}}$$
(14)

where \(\frac{{\partial \sigma}}{{\partial T}}\) is the surface tension temperature coefficient, and \(\frac{{\partial T}}{{\partial s}}\) is the tangential vector of the local free surface. As is seen from the definition of Marangoni shear stress, it is a combination between a surface tension and a temperature gradient, which offers a wealth of possible responses.

To evaluate the Marangoni shear stress contribution in the present model, the governing integral equation for the conservation of energy for multiphase flow approach (Gidaspow 1994) has been performed and solved coupled with the continuity and momentum equations. After introducing several combinations of the surface tension temperature coefficient, ∂σ/∂T, and the temperature difference between fluid flow and carbon microfiber walls, it has been found that the interfacial fluid layers around the microfibers resulted in higher velocities when these two parameters were 0.4 N/m.K and 70°C, respectively. These higher velocities allow the interfacial fluid layers the potential to flow more smoothly around the microfiber walls, relative to its motion, before applying the energy imbalance technique. Thus the likelihood of sticking is less presumed.

The predicted cell Reynolds number contours for the flow with different volume load ratios after introducing the energy imbalance technique are shown in Fig. 7.

Fig. 7
figure 7

Cell Reynolds number contours after applying the energy imbalance technique for different carbon nanoparticle volume load ratios a 0.5%. b 1%. c 1.5%. d 2%

Full size image

In general, one can see that applying the proposed energy imbalance technique creates convective currents around the carbon microfiber walls, which cause kind of vortices around them. These vortices force the flow to move away from the carbon microfiber walls. From the figures we can also see that these vortices are stronger in the case of low loading ratios of the carbon nanoparticles in the resin, which means that in the case of higher load ratios, higher temperature differences may be needed.

4 Conclusions

The flow characteristics of carbon nanofluid around a staggered carbon microfiber matrix have been investigated and predicted numerically. Observations of the incident illustrate interactions between the microfiber sidewalls and the interfacial fluid layers. These interactions have a tendency to reduce the flow velocity, causing an attraction of the flow to the microfiber sidewalls. After some time, the flow passages will be blocked. To circumvent this tendency, an energy imbalance technique has been established between the fluid flow and microfiber walls. As a result of applying this technique, convective currents around the carbon microfiber walls have been produced causing vortices around them. The forces from these vortices cause the flow to move away from the carbon microfiber walls preventing the interfacial fluid layers to stick on the microfiber walls.