1 Introduction

Batch fabricated microfluidic platforms that can mimic conventional sample preparation techniques performed in laboratories hold great potential to enable both research and healthcare advances. Such miniaturized diagnostic devices have been termed micro total analysis systems (μTAS) or biochips and combine sensing mechanisms (physical, optical, electrical or chemical) with microfluidics. Such autonomous platforms have attracted considerable research interest due to opportunity to fabricate a highly integrated system able to perform all necessary processing steps required for the specific application. While microfluidics promises to have an impact in many research fields, one of the more attractive applications of microfluidics has been towards biomedical and life science diagnostics. A major research thrust in microfluidics has been the development of autonomous platforms for the extraction, purification and analysis of biological material from cells while using smaller reagent volumes with higher accuracy at a lower cost per device [1].

The motivation for the studies presented here is to create a miniaturized liquid extraction module for the purification of DNA from biological samples for genetic analysis. Genomic or plasmid DNA extraction using aqueous–organic liquid extraction is one of many standard techniques commonly performed in biology laboratories [2]. Briefly, the procedure consists of lysing cells in a basic lysis buffer (10 mM Tris, pH 8.0, 0.1 M EDTA, 20 μg/ml Pancreatic RNAase, 0.5% SDS and 100 μg/ml proteinase K) and adding an equal volume of phenol, chloroform and isoamyl alcohol (25:24:1 by volume) mixture to the aqueous solution. The organic (phenol) phase is immiscible with the aqueous phase and so the two phases separate in a gravitational field due to density differences. A vortexing step ‘mixes‘ the two phases and allows the different cellular components to partition into either the aqueous or organic phases. With effective mixing, the cell components naturally distribute themselves into the two phases in order to minimize interaction energies of the biological components with the surrounding solvents. The membrane components and protein partition to the organic–aqueous interface, while the DNA stays in the aqueous phase. This partitioning occurs over molecular dimensions at the aqueous–organic interface. Thus, effective mixing maximizes the surface area over which this partitioning occurs. Therefore, the smaller the discrete phase domains, the more effective is the DNA extraction procedure. After the mixing step, the two immiscible phases are allowed to separate and the aqueous phase is removed using a micropipette tool. The DNA is then concentrated by precipitation in ethanol and resuspended in an aqueous buffer. This technique has only been useful for a large number of cells and uses a large volume of liquid (∼1 ml) because of DNA loss during the aqueous phase removal and the size of micropipette tools. Recently, the use of DNA extraction columns has become more commonplace. Here, DNA is suspended within a gel matrix and other cellular components are passed through the column. The DNA is then eluted in an elution buffer and captured. DNA purification has been demonstrated using high-density silicon post arrays [3, 4], or by creating miniaturized silica columns [5–7]. First cells are lysed in a lysis buffer and the free protein is precipitated. The lysate is then loaded onto the column and the DNA is adsorbed onto the silica surfaces in a high salt buffer solution, the column is washed to remove proteins or cellular debris and finally the nucleic acids are eluted in a low salt buffer.

The long-term goal of these studies is to create an autonomous μTAS device that would perform all necessary biochemical DNA processing steps from whole cell sample introduction to obtaining a genetic profile of the sample in question. The device would have fluidic inlets for sample and enzyme introduction, specialized chambers for all necessary reactions (lysis, restriction endonuclease digest, PCR amplification) and DNA capillary electrophoresis separation. Of particular interest is to miniaturize the phenol extraction procedure for DNA purification. This requires an understanding of two phase flow mechanics in microgeometries. The stability criteria for obtaining stable stratified organic aqueous microflows has been experimentally examined [8]. This work is extended to study electrically enhanced mixing to increase the surface area over which liquid extraction occurs.

In most microfluidic devices, mixing occurs between two inlet streams of the same fluid where the two streams must be dispersed to remove any concentration gradients of dissolved components between the two streams. Mixing techniques can be classified into active and passive mixing categories. Passive mixing techniques usually involve modification or augmentation of the channel surfaces. Passive mixing schemes that has been reported include the use of successive lamination [9], mixing in serpentine microchannels [10], rotating block geometries where the geometry of the channel is used to induce secondary flow [11], placing obstacles within the flow path [12] and augmentation of the channel lower wall in a staggered herringbone pattern to promote chaotic advection [13]. Most passive mixing techniques require modification of the microfluidic channel and use of complex geometries. Alternatively, active mixers have been reported using temporally controlled flow profiles with sequential flow switching between two inlets [14], by superimposing low frequency sinusoidally fluctuating flow on a steady state flow [15] and using magnetic microstirrers [16]. A category of active mixing techniques has also been reported using conductivity gradients first in macroscale systems [17, 18] and more recently on the microscale using conductivity gradients that are perpendicular to the flow direction [19–21] and electrokinetically driven mixing [22] where an AC electric field is used to produce a flow instability that mixes the two phases. The use of electrohydrodynamic (EHD) instability for mixing between a single phase with spatially varying conductivity has also been reported [23, 24].

In this work, two phase mixing between an organic and aqueous phase is considered. Of particular interest is mixing between an aqueous phase and an organic phase consisting of phenol, chloroform and isoamyl alcohol (25:24:1) in a stratified three layer system where each layer is 50 μm wide. However, the analysis presented may be applied to any three layer organic/aqueous system where the two phases are immiscible and the aqueous phase is assumed to be a perfect conductor and the organic phase is assumed to be a perfect insulator. Since the organic and aqueous phases are immiscible, mixing in this context is defined as an increase in interfacial area between the two phases from droplet formation to dispersion of the two phases. Mixing is promoted by creating an unstable flow profile by electrically inducing the unstable motion of the interface between the two solution phases. The aqueous phase is assumed to be infinitely conducting due to dissolved salt ions, while the organic phase is assumed to be perfectly insulating. In the presence of an electric field, charge accumulates at the aqueous/organic interface. At a critical voltage the interface becomes unstable and the aqueous and organic layers mix.

2 Linear stability model

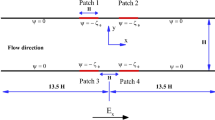
In order to understand how the mixing will proceed, it is important to understand the stability criteria at the organic–aqueous interfaces. The inviscid and viscous stability models presented here are used for comparison to experimental instability mixing, instability growth rates and wavenumber dependence of growth rates. The model consists of a non-conducting fluid sandwiched between two perfectly conducting layers maintaining an initially flat interface, with a DC potential, V o, applied across two parallel plate electrodes (Fig. 1). This setup very closely resembles the physical flow profile of an experimental stratified two phase flow, except that in the experimental work reported the fluids are moving under flow conditions and stratified due to viscous shear forces. Since the upper and lower fluids are assumed to be perfect conductors, the electric field in the middle organic layer is always normal to the fluid interfaces. V o can also be considered the root mean squared (RMS) value of an AC voltage where the frequency is sufficiently high that the interface cannot respond to the high-frequency interfacial stresses and only responds to the RMS value. When the relative impedance of the different fluids are considered, it is found that the magnitude of the impedance of the debye layer is much smaller than the magnitude of the aqueous layer which in turn is smaller than the magnitude of the impedance of the organic layer in the frequency range tested in this work. Therefore, the aqueous fluid acts as a perfect conductor (σ → ∞ ) at low input frequencies \({\left({({{\omega \varepsilon _{\text{p}}}}/{{\sigma _{\text{w}}}}})< < 1 \right)}\) where ɛp is the permittivity of the organic fluid (phenol) and σw is the conductivity of the aqueous fluid (water) so that the displacement current is much less than the conduction current with minimal voltage drop across the aqueous layer and essentially all of the electric field across the organic layer. At high frequencies \({\left({({{\omega \varepsilon _{p}}}/{{\sigma _{w}}}) > 1} \right)}\) the displacement current is larger than the conduction current so the water does not act as a perfect conductor and the electric field is not perpendicular to the interfaces and the deformation of the interfaces results in electrical interfacial shear stresses.

Fig. 1
figure 1

Schematic setup of rigid plane–parallel electrodes with three fluids layers having two interfaces. The top and bottom liquid layers are perfectly conducting relative to the insulating middle layer

Full size image

This configuration may be modeled using EHD linear stability analysis of the electrical and fluid interfacial boundary conditions using the transfer relations developed by Melcher [25]. A linearized perturbation analysis is performed by linearizing the flow and electrical field equations of the system shown in Fig. 1, where, the labels 1–6 denote regions just above or below interfaces where boundary conditions are applied to derive the stability requirements of the system. The labels 1 and 6 denote the electrodes, 2 and 5 denote the aqueous sides of the two interfaces and 3 and 4 denote the organic sides of the two interfaces. This process is modeled using both inviscid and viscous stability analyses applying the kinematic and stress conditions at the interface. It should be noted that this analysis neglects the effects of fluid flow and focuses on the electrical forces which destabilize the interfaces. Therefore, this preliminary stability analysis makes several simplifying assumptions and only predicts the incipience of instability and initial instability growth rate. As the system is driven beyond the small signal linear range, computational methods must be employed to further characterize instability progression into mixing.

2.1 Governing equations

The flow profiles of the two fluids are determined by conservation of mass and the Navier–Stokes equation.

$$\nabla \cdot \mathbf{u} = 0,$$
(1)
$$\rho {\left[ {\frac{{\partial \mathbf{u}}}{{\partial t}} + {\left({\mathbf{u} \cdot \nabla} \right)}\mathbf{u}} \right]} = - \nabla p + \rho \mathbf{g} + \mu \nabla ^{2} \mathbf{u} + \mathbf{F}_{\text{e}}, $$
(2)

where \(\mathbf{F}_{\text{e}}\) is the electrical volume force density. The volume force density is related to the divergence of the electrical stress tensor and for incompressible fluids is

$$ \mathbf{F} _{\text{e}} = \nabla \cdot \overline{\overline{{\mathbf{T}}^{{\text{e}}} }}= \rho _{\text{f}} \mathbf{E} - \frac{1}{2}{\left| {\mathbf{E}} \right|}^{2} \nabla \varepsilon, $$
(3)

where \({\overline{\overline{{\mathbf{T}}^{{\text{e}}}}}} \) is the electrical stress tensor, ρf is the free charge density, \(\mathbf{E} \) is the electric field and ɛ is the space varying dielectric permittivity. In the three layer system denoted in Fig.  1 the volume charge in each layer is zero (ρf=0), but there is a surface charge on each interface. The two incompressible liquids are assumed to be completely immiscible, so the dielectric permittivity is modeled as a step function across each interface so that the permittivity gradient is a dirac delta function right at the interface. Since the dielectric permittivity is constant in each layer, the polarization force density in each layer is zero except along the interface where the step change in permittivity contributes to an interfacial surface force density.

In electrostatic systems the electric field has zero curl so the electric field may be expressed in terms of a scalar electric potential

$$\nabla \times \mathbf{E} = 0 \Rightarrow \mathbf{E} = - \nabla \phi. $$
(4)

Since the fluid layers are assumed to contain no volume charge density and have constant permittivity, Gauss’s law may be written as

$$\nabla \cdot \mathbf{E} = 0.$$
(5)

Combining Eqs. 4 and 5, the governing electrical equation is Laplace’s equation

$$\nabla ^{2} \phi = 0.$$
(6)

2.2 Kinematic and stress conditions

In the presence of an electric field the surface charge density and polarization force density at the interface influences the interfacial force balance boundary condition and the electric field can affect fluid flow. The interfacial stress balance boundary condition in the i direction on a surface whose normal, \(\mathbf{n},\) is in the j direction is

$${\left\| {T^{\text{f}}_{{ij}} n_{j}} \right\|} + {\left\| {T^{\text{e}}_{{ij}} n_{j}} \right\|} + \gamma {\left({\nabla \cdot{\mathbf{n}} } \right)}n_{i} = 0,$$
(7)

where T ij is the stress tensor, γ is the interfacial tension between the phases, and the superscript refers to either the fluid (f) or electrical (e) contributions. Neglecting y-directed variations, for small displacements, the normal to an interface with a small displacement ξ is

$$\mathbf{n} = \mathbf{i} _{x} - \frac{{\partial \xi}}{{\partial z}}\mathbf{i} _{z}. $$
(8)

The fluid and electrical stress tensor components are

$$T^{\text{f}}_{{ij}} = - p\delta _{{ij}} + \mu {\left({\frac{{\partial u_{i}}}{{\partial x_{j}}} + \frac{{\partial u_{j}}}{{\partial x_{i}}}} \right)}$$
(9)

and

$$T^{\text{e}}_{{ij}} = \varepsilon E_{i} E_{j} - \frac{1}{2}\delta _{{ij}} \varepsilon E_{k} E_{k}.$$
(10)

The electrical stress tensor in Eq. 10 is derived from the volume force density in Eq. 3 due to coulombic and polarization force densities [25].

2.3 Equilibrium

In beginning the small signal linearized analysis the equilibrium stress balance must first be considered. In the absence of interfacial displacements shown in Fig. 1, (ξ1=ξ2=0) the equilibrium stress balances across the flat interfaces are

$$P_{{3{\text{o}}}} - P_{{2{\text{o}}}} - T^{\text{e}}_{{xx3{\text{o}}}} = 0,$$
(11)
$$P_{{5{\text{o}}}} - P_{{4{\text{o}}}} + T^{{\text{e}}}_{{xx4{\text{o}}}} = 0,$$
(12)
$$T^{{\text{e}}}_{{xx3{\text{o}}}} = T^{{\text{e}}}_{{xx4{\text{o}}}} = \frac{{\varepsilon _{{\text{b}}}}}{2}{\left({E^{2}_{{x{\text{o}}}} - E^{2}_{{z{\text{o}}}}} \right)} = \frac{{\varepsilon _{\text{b}}}}{2}E^{2}_{{\text{o}}}, $$
(13)

where \(E_{{x{\text{o}}}} = E_{{\text{o}}} = ({{V_{{\text{o}}}}}/b),\) b is the thickness of the organic layer, E zo is zero because in equilibrium the interfaces are flat and therefore the electric field E o is in the x direction. The equilibrium electrical normal stress is balanced by a jump in electrostatic pressure across the interface

$$P_{{2{\text{o}}}} - P_{{3{\text{o}}}} = {\left\| {\frac{1}{2}\varepsilon {\left({\mathbf{E} \cdot \mathbf{n}} \right)}^{2}} \right\|} = - \frac{1}{2}\varepsilon _{\text{b}} E^{2}_{\text{o}}, $$
(14)

where the subscript o corresponds to equilibrium values. Therefore

$$P_{{3{\text{o}}}} - P_{{2{\text{o}}}} = \frac{{\varepsilon _{\text{b}}}}{2}E^{2}_{{\text{o}}},$$
(15)
$$P_{{4{\text{o}}}} - P_{{5{\text{o}}}} = \frac{{\varepsilon _{\text{b}}}}{2}E^{2}_{{\text{o}}}. $$
(16)

2.4 Perturbation variables

The primary objective of this analysis is to test the stability of the fluid flow to infinitesimal disturbances. Here the two interfacial displacements are represented as

$$\xi _{1} {\left({z,t} \right)} = Re {\left[ {\hat{\xi}_{1} {\text{e}}^{{j{\left({\omega t - kz} \right)}}}} \right]},$$
(17)
$$\xi _{2} {\left({z,t} \right)} = Re {\left[ {\hat{\xi}_{2} {\text{e}}^{{j{\left({\omega t - kz} \right)}}}} \right]}.$$
(18)

where ω is the natural frequency of interfacial displacement, \(\hat{\xi}_{1} \) and \(\hat{\xi}_{2} \) are the complex amplitudes of interfacial displacements, k is the wavenumber components in the z direction and \(j = {\sqrt {- 1}}.\) The wavenumbers are related to the wavelengths (λ) of the interfacial displacements as

$$k = \frac{{2\pi}}{\lambda}.$$
(19)

Electrical perturbations may be described as

$$\phi {\left({z,t} \right)} = Re {\left[ {\hat{\phi}{\text{e}}^{{j{\left({\omega t - kz} \right)}}}} \right]}.$$
(20)

Similarly pressure and velocity perturbations may be described as

$$P{\left({z,t} \right)} = Re {\left[ {\hat{P}{\text{e}}^{{j{\left({\omega t - kz} \right)}}}} \right]},$$
(21)
$$U_{x} {\left({z,t} \right)} = Re {\left[ {\hat{U}_{x} {\text{e}}^{{j{\left({\omega t - kz} \right)}}}} \right]},$$
(22)
$$U_{z} {\left({z,t} \right)} = Re {\left[ {\hat{U}_{z} {\text{e}}^{{j{\left({\omega t - kz} \right)}}}} \right]}.$$
(23)

2.5 Perturbation electric field

For the nonconducting planar organic layer the perturbation potential distribution is nonzero while it is zero in the perfect conductors as each perfectly conducting layer contacts an electrode held at constant potential. The solution to Laplace’s equation relating the complex amplitude electric field interfacial perturbations on the insulating side of the interfaces, \(\hat{e}^{3}_{x} \) and \(\hat{e}^{4}_{x}, \) to the perturbation potentials, \(\hat{\phi}^{3} \) and \(\hat{\phi}^{4},\) at the equilibrium position of the interfaces is [25]

$$ {\left[ {\begin{array}{*{20}l} {{\hat{e}^{3}_{x} } \hfill} \\ {{\hat{e}^{4}_{x} } \hfill} \\ \end{array} } \right]} = k{\left[ {\begin{array}{*{20}l} {{ - \coth ka} \hfill} & {{{\text{1}/{\sinh ka}}} \hfill} \\ {{{-{\text{ 1}/{\sinh ka}}}} \hfill} & {{\coth ka} \hfill} \\ \end{array} } \right]}{\left[ {\begin{array}{*{20}l} {{\hat{\phi }^{3} } \hfill} \\ {{\hat{\phi }^{4} } \hfill} \\ \end{array} } \right]}. $$
(24)

Next, the electrical boundary conditions must be considered. The normals at the two interfaces are defined as

$$ \begin{aligned}{\mathbf{n _1}} & = {\mathbf{i _x}} - {\mathbf{i _z}} \frac{{\partial \xi _{1} }} {{\partial z}} \Rightarrow \hat{n}_{{1x}} = 1,\quad \hat{n}_{{1z}} = jk\hat{\xi }_{1} \\ {\mathbf{n _2}} & = {\mathbf{i _x}} - {\mathbf{i _z}} \frac{{\partial \xi _{2} }} {{\partial z}} \Rightarrow \hat{n}_{{2x}} = 1,\quad \hat{n}_{{2z}} = jk\hat{\xi }_{2}, \\ \end{aligned} $$
(25)

The electric field perturbation potentials at the electrodes are zero so

$${{\hat{\phi}^{1} = 0}}, \quad {{\hat{\phi}^{6} = 0}}.$$
(26)

In addition, the tangential components of the electric field must be continuous across each interface, and thus are zero since there is no field in the perfectly conducting layers. At the organic side of the top interface

$${\mathbf{n}} \times {\mathbf{E}} = 0 \Rightarrow {\mathbf{n}}_{\mathbf{1}} \times {\left(E_{o} {\mathbf{i}}_{\mathbf{1}} + e_{{x3}} {\mathbf{i}} _{\mathbf{x}} + e_{{z3}} {\mathbf{i}}_{\mathbf{z}} \right)}=0,$$
(27)

which expands to

$$\left(n_{{x3}} {\mathbf{i}} _{\mathbf{x}} + n_{{z3}} {\mathbf{i}} _{\mathbf{z}} \right) \times \left(E_{\rm o} {\mathbf{i}}_{\mathbf{x}} + e_{{x3}} {\mathbf{i}} _{\mathbf{x}} + e_{{z3}} {\mathbf{i}}_{\mathbf{z}} \right)=0.$$
(28)

Using the normals defined in Eq. 25 and neglecting second order contributions Eq. 28 reduces to

$$ - n_{1x} e_{{z3}} {\mathbf{i _y}} + n_1{z} E_{\text{o}} {\mathbf{i _y}} = 0 \Rightarrow \hat{e}_{{z3}} = jk\hat{\phi}^{3} = E_{o} jk\hat{\xi}_{1} \Rightarrow \hat{\phi}^{3} = E_{\text{o}} \hat{\xi}_{1}.$$
(29)

Similarly, it may be shown that at the lower interface

$$\hat{e}_{{z4}} = jk\hat{\phi}^{4} = E_{o} jk\hat{\xi}_{2} \Rightarrow \hat{\phi}^{4} = E_{o} \hat{\xi}_{2}.$$
(30)

These results may also be obtained by expanding the interfacial potentials to first order after interfaces 3 and 4 have moved a distance ξ1 and ξ2 by a Taylor series expansion about equilibrium interfacial positions x 3 and x 4

$$ \begin{aligned} \phi {\left( {x_{3} + \xi _{1} } \right)} & = \phi _{\text{o}}{\left( {x_{3} } \right)} + \left. {\frac{{\partial \phi }} {{\partial x}}} \right|_{{x_{3} }} \xi _{1} + \phi ^{3} \\ \phi {\left( {x_{4} + \xi _{2} } \right)} & = \phi_{\text{o}} {\left( {x_{4} } \right)} + \left. {\frac{{\partial \phi }} {{\partial x}}} \right|_{{x_{4} }} \xi _{2} + \phi ^{4} \\ \end{aligned}. $$
(31)

Now each interfacial potential is always the same as the equilibrium potential so ϕ(x 3+ξ1)=ϕ0(x 3)=0, ϕ(x 4+ξ2)=ϕ0(x 4)=V o . Since

$$\left. {\frac{{\partial \phi}}{{\partial x}}} \right|_{{x_{{3,4}}}} = - E_{\text{o}},$$

the perturbation potentials become

$$\phi ^{3} = E_{\text{o}} \xi _{1} \Rightarrow \hat{\phi}^{3} = E_{\text{o}} \hat{\xi}_{1}, $$
(32)
$$\phi ^{4} = E_{\text{o}} \xi _{2} \Rightarrow \hat{\phi}^{4} = E_{\text{o}} \hat{\xi}_{2},$$
(33)

which agree with the results derived in Eqs. 29 and 30.

2.6 Inviscid stability analysis

A linearized inviscid stability analysis is first performed in order to gain insight into the stability criteria and the initial incipience of instability and inviscid fastest growth wavenumber. Although, the instability demonstrated occurs in a viscous fluid, the incipience of instability occurs at a static interface and thus is the same in either an inviscid or viscous flow system. The inviscid analysis helps predict the incipience of instability with a minimum of complexity. For the inviscid analysis, because each layer is uncharged in the volume, only pressure forces must be considered. In the absence of electrical volume forces, and assuming gravitational forces are negligible, conservation of mass and the inviscid Navier–Stokes equation are written as

$$\nabla \cdot \mathbf{u} = 0, \quad \rho {\left({\frac{{\partial \mathbf{u}}}{{\partial t}} + \mathbf{u} \cdot \nabla \mathbf{u}} \right)} = - \nabla {\text{P}}.$$
(34)

For small perturbations, the convective term \(\mathbf{u} \cdot \nabla \mathbf{u} \) has no first order contribution, so combining the inviscid Navier Stokes equation and conservation of mass gives

$$\nabla ^{2} P = 0.$$
(35)

The pressure perturbations within the upper, middle and lower fluid layers are related to the interfacial velocities as [25]

$$ {\left[ {\begin{array}{*{20}l} {{\hat{P}_{1} } \hfill} \\ {{\hat{P}_{2} } \hfill} \\ \end{array} } \right]} = \frac{{j\omega \rho _{a} }} {k}{\left[ {\begin{array}{*{20}l} {{ - \coth ka} \hfill} & {{\text{1} /{{\sinh ka}}} \hfill} \\ {-{\text{{1}}/ {{\sinh ka}}} \hfill} & {{\coth ka} \hfill} \\ \end{array} } \right]}{\left[ {\begin{array}{*{20}l} {{\hat{U}^{1}_{x} } \hfill} \\ {{\hat{U}^{2}_{x} } \hfill} \\ \end{array} } \right]}, $$
(36)
$$ {\left[ {\begin{array}{*{20}l} {{\hat{P}_{3} } \hfill} \\ {{\hat{P}_{4} } \hfill} \\ \end{array} } \right]} = \frac{{j\omega \rho _{b} }} {k}{\left[ {\begin{array}{*{20}l} {{ - \coth kb} \hfill} & {{\text{1}/ {{\sinh kb}}} \hfill} \\ {-{\text{{1}}/ {{\sinh kb}}} \hfill} & {{\coth kb} \hfill} \\ \end{array} } \right]}{\left[ {\begin{array}{*{20}l} {{\hat{U}^{3}_{x} } \hfill} \\ {{\hat{U}^{4}_{x} } \hfill} \\ \end{array} } \right]}, $$
(37)
$$ {\left[ {\begin{array}{*{20}l} {{\hat{P}_{5} } \hfill} \\ {{\hat{P}_{6} } \hfill} \\ \end{array} } \right]} = \frac{{j\omega \rho _{a} }} {k}{\left[ {\begin{array}{*{20}l} {{ - \coth ka} \hfill} & {{\text{1}/ {{\sinh ka}}} \hfill} \\ {-{\text{{1}}/ {{\sinh ka}}} \hfill} & {{\coth ka} \hfill} \\ \end{array} } \right]}{\left[ {\begin{array}{*{20}l} {{\hat{U}^{5}_{x} } \hfill} \\ {{\hat{U}^{6}_{x} } \hfill} \\ \end{array} } \right]}. $$
(38)

At the rigid electrode boundaries the normal fluid velocities are zero

$$\hat{U}^{1}_{x} = \hat{U}^{6}_{x} = 0.$$
(39)

The interfacial velocities must be continuous across the interfaces because of the kinematic conditions and are related to the interfacial displacements as

$$\hat{U}^{2}_{x} = \hat{U}^{3}_{x} = j\omega \hat{\xi}_{1}.$$
(40)
$$\hat{U}^{4}_{x} = \hat{U}^{5}_{x} = j\omega \hat{\xi}_{2}.$$
(41)

The stress equilibrium in the x-direction across an interface is

$${\left\| P \right\|}n_{x} = {\left\| {T^{\text{e}}_{{_{{xj}}}}} \right\|}n_{j} - \gamma \nabla \cdot {{\mathbf {n} }}n_{x} $$
(42)

so at the upper interface

$${\left({P_{{2{\text{o}}}} + P_{2}} \right)} - {\left({P_{{3{\text{o}}}} + P_{3}} \right)} = \frac{{- \varepsilon _{{\text{b}}}}}{2}{\left({E_{{\text{o}}} + e_{x}} \right)}^{2} + \gamma \frac{{\partial ^{2} \xi _{1}}}{{\partial z^{2}}}$$
(43)

where P 2o and P 3o are the equilibrium pressures derived in Eq. 15 at the upper interface which balance the equilibrium Maxwell stress. Linearizing Eq. 43 and canceling out the equilibrium stress balance of Eq. 15, the perturbation stress equilibrium for the upper interface is

$$ - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{3} - \varepsilon _{\text{b}} E_{\text{o}} \hat{e}^{3}_{x} - k^{2} \gamma \hat{\xi}_{1} = 0.$$
(44)

Similarly, for the lower interface

$$ - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{4} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{5} + \varepsilon _{b} E_{o} \hat{e}^{4}_{x} - k^{2} \gamma \hat{\xi}_{2} = 0.$$
(45)

Now these force balance boundary conditions are combined into terms of \(\hat{\xi}_{1} \) and \(\hat{\xi}_{2} \) by inserting Eqs. 32 and 33 into Eq. 24 and then Eqs. 36, 37 and 38 are inserted into Eqs. 44 and 45 to yield

$$ {\left[ {\begin{array}{*{20}l} {{\frac{{\omega ^{2} \rho _{\text{a}} }} {k}\coth ka + \frac{{\omega ^{2} \rho _{\text{b}} }} {k}\coth kb + \varepsilon _{\text{b}} E^{2}_{{\text{o}}} k\coth kb - k^{2} \gamma } \hfill} & {{\frac{{ - \omega ^{2} \rho _{{\text{b}}} }} {{k\sinh kb}} - \frac{{\varepsilon _{b} E^{2}_{{\text{o}}} k}} {{\sinh kb}}} \hfill} \\ {{\frac{{ - \omega ^{2} \rho _{{\text{b}}} }} {{k\sinh kb}} - \frac{{\varepsilon _{{\text{b}}} E^{2}_{{\text{o}}} k}} {{\sinh kb}}} \hfill} & {{\frac{{\omega ^{2} \rho _{{\text{a}}} }} {k}\coth ka + \frac{{\omega ^{2} \rho _{{\text{b}}} }} {k}\coth kb + \varepsilon _{{\text{b}}} E^{2}_{{\text{o}}} k\coth kb - k^{2} \gamma } \hfill} \\ \end{array} } \right]}{\left[ {\begin{array}{*{20}c} {{\hat{\xi}_{1} }} \\ {{\hat{\xi}_{2} }} \\ \end{array} } \right]} = 0. $$
(46)

The dispersion equation solutions are obtained by setting the determinant of the coefficients to zero. Two modes may be derived from this relationship: a “kink” mode where the two interfaces displace in phase with each other \((\hat{\xi}_{1}=\hat{\xi}_{2})\) and a “sausaging” mode where the interfacial displacements are out of phase \((\hat{\xi}_{1}= - \hat{\xi}_{2}).\) The frequency–wavenumber dispersion relationship for the “kink” mode of the system is

$$\frac{{\omega ^{2}}}{k}{\left({\rho _{\text{a}} \coth ka + \rho _{\text{b}} \coth kb - \frac{{\rho _{\text{b}}}}{{\sinh kb}}} \right)} + \varepsilon _{\text{b}} E^{2}_{\text{o}} k{\left({\coth kb - \frac{1}{{\sinh kb}}} \right)} - k^{2} \gamma = 0,$$
(47)

which simplifies to

$$\frac{{\omega ^{2}}}{k}{\left[ {\rho _{\text{a}} \coth ka + \rho _{\text{b}} \tanh {\left({\frac{{kb}}{2}} \right)}} \right]} = k^{2} \gamma - \varepsilon _{\text{b}} E^{2}_{\text{o}} k\tanh {\left({\frac{{kb}}{2}} \right)},$$
(48)

where k is the wavenumber, ρ is the density of either fluid a or b, γ is the interfacial tension between the phases and ɛ b is the permittivity of the organic fluid and E o is the field strength across the non-conducting phase when the interface is flat, \(\hat{\xi}_{1} = \hat{\xi}_{2} = 0.\)

For the “necking” or “sausaging” mode

$$\frac{{\omega ^{2}}}{k}{\left({\rho _{\text{a}} \coth ka + \rho _{\text{b}} \coth kb + \frac{{\rho _{\text{b}}}}{{\sinh kb}}} \right)} + \varepsilon _{\text{b}} E^{2}_{\text{o}} k{\left({\coth kb + \frac{1}{{\sinh kb}}} \right)} - k^{2} \gamma = 0,$$
(49)

which simplifies to

$$\frac{{\omega ^{2}}}{k}{\left[ {\rho _{\text{a}} \coth ka + \rho _{\text{b}} \coth {\left({\frac{{kb}}{2}} \right)}} \right]} = k^{2} \gamma - \varepsilon _{\text{b}} E^{2}_{\text{o}} k\coth {\left({\frac{{kb}}{2}} \right)}.$$
(50)

Figure 2 plots ω 2 versus k for both the sausaging and kink modes for various applied field strengths using the physical fluid properties of the 50 μm wide aqueous and phenol–chloroform phases of interest, shown in Table 1. An instability will manifest if the conditions exist such that at least one wavenumber causes the system to become unstable. The criterion for interfacial stability is that ω must be real for all real values of k. The interface becomes unstable to infinitesimal perturbations when the imaginary part of ω is negative as the perturbation in Eqs. 17 and 18 will now grow exponentially and a chaotic flow pattern will develop. Since the coefficients of ω2 on the left side of Eqs. 48 and 50 are positive, stability is determined by the right hand side of the equation such that an instability will develop whenever ω 2 is negative. It is readily apparent from Fig. 2 that a variety of unstable wavenumbers will manifest for a given applied field greater than the electric field at the incipience. As the applied field increases, the width of this unstable wavenumber band increases as larger unstable wavenumbers become excited. The wavenumber corresponding to the fastest initial instability growth rate is determined from the minimum of this curve. Also, as the wavenumber increases, Eqs. 48 and 50 converge to the same equation.

Fig. 2
figure 2

Plot of ω2 versus wavenumber using the inviscid analysis for a variety of applied fields for both the sausaging (top) and kink (bottom) modes using layer thicknesses of a=b=50 μm and the physical parameters in Table 1. Unstable wavenumbers occur whenever ω2 is negative. The unstable wavenumber band increases as the applied field is increased. Insets show ω2 versus wavenumber for smaller wavenumber values to illustrate the differences between the stability of the kink and sausaging modes

Full size image
Table 1 Physical properties of proposed fluids (Lange’s Handbook of Chemistry, 10th edn)
Full size table

For the sausaging mode, a function is defined to represent the right side of Eq. 50

$$F(k) = \gamma k^{2} - \varepsilon _{\text{b}} E^{2}_{\text{o}} k\coth {\left({\frac{{kb}}{2}} \right)}.$$
(51)

As long as F(k) is greater than zero the system is stable. If F(k) is less than zero, then ω must be imaginary and the flow becomes unstable. Incipience occurs statically when ω=0. Consideration of EHD induced “sausaging” of a stratified insulating liquid surrounded by conducting fluid in the small wavenumber (infinite wavelength) limit shows the system is unstable to all perturbations as Eq. 51 is always negative when k=0.

The electric field to excite an unstable wavenumber, k, for the “sausaging” mode is

$$E_{\text{o}} = {\sqrt {\frac{{\gamma k}}{{\varepsilon _{\text{b}} \coth (kb/2)}}}}.$$
(52)

Similarly, the electric field to excite an unstable wavenumber, k, for the “kink” mode is

$$E_{o} = {\sqrt {\frac{{\gamma k}}{{\varepsilon _{b} \tanh (kb/2)}}}}.$$
(53)

One limit considered is the infinite wavelength limit (k→0). In this limit the effect of the electric field on the kink mode is equivalent to having a field-dependent interfacial tension given by

$$\gamma _{\text{eff}} = \gamma - \frac{1}{2}\varepsilon _{\text{b}} E^{2}_{\text{o}} b.$$
(54)

The system will be stable in the kink mode as long as γeff is greater than zero. The critical field for instability for the kink mode as k→0 (infinite wavelength), can be obtained using Eq. 53

$$E_{\text{o}} = {\sqrt {\frac{{2\gamma}}{{\varepsilon _{\text{b}} b}}}},$$
(55)

which is the condition for γeff=0. In the kink mode, the electric field thus acts at the interface as an electrically induced interfacial tension, reducing the overall interfacial tension between the two phases. In the zero wavenumber limit, the critical field for instability is calculated using Eq. 55 and the physical values in Table 1 for a 50 μm thick organic layer as 2.5×105 V/m.

2.7 Viscous stability analysis

Although, the preceding inviscid analysis provides insight into the incipience of instability and unstable wavenumbers as a function of applied electric field, the instability growth rate must be modeled considering the stabilizing effect of viscosity on constraining instability growth rates. Consideration of the effects of viscosity on EHD stability greatly complicates the analysis as now interfacial displacements in the x-direction may induce stresses having components in the z-direction. Therefore the interfacial stress balances become much more complicated than in the inviscid analysis as both x- and z-directed stresses are now present.

The velocity in each layer must obey the no-slip boundary conditions at the electrode boundaries and the interfaces together with the kinematic conditions. Therefore

$$\begin{array}{*{20}l} {{\hat{U}_{{x1}} = \hat{U}_{{x6}} = 0}}, &\quad {{\hat{U}_{{x2}} = \hat{U}_{{x3}} = j\omega \hat{\xi}_{1}}}, &\quad {{\hat{U}_{{z2}} = \hat{U}_{{z3}}}}, \\ {{\hat{U}_{{z1}} = \hat{U}_{{z6}} = 0}}, &\quad {{\hat{U}_{{x4}} = \hat{U}_{{x5}} = j\omega \hat{\xi}_{2}}}, &\quad {{\hat{U}_{{z4}} = \hat{U}_{{z5}}}}. \\ \end{array}.$$
(56)

Now the interfacial stress balances must be considered. Using the stress conditions in Eq. 7 and the definitions of fluid and electrical stress in Eqs. 9 and 10, the force balance at the top and bottom interfaces are

$${\left({T^{\text{f}}_{{ij2}} - T^{\text{f}}_{{ij3}}} \right)}n_{{1j}} - T^{\text{e}}_{{ij3}} n_{{1j}} + n_{{1i}} \gamma \frac{{\partial ^{2} \xi _{1}}}{{\partial z^{2}}} = 0,$$
(57)
$${\left({T^{\text{f}}_{{ij4}} - T^{\text{f}}_{{ij5}}} \right)}n_{{2j}} - T^{\text{e}}_{{ij4}} n_{{2j}} + n_{{2i}} \gamma \frac{{\partial ^{2} \xi _{2}}}{{\partial z^{2}}} = 0.$$
(58)

It was previously shown [25] that the perturbation x and z-directed first-order complex amplitude stresses may be described for a generic fluid layer of thickness Δ, density ρ, viscosity μ, with α denoting the upper interface and β denoting the lower interface are

$$\begin{aligned} {\left[ {\begin{array}{*{20}c} {{\hat{T}^{{f\alpha }}_{{xx}} }} \\ {{\hat{T}^{{f\beta }}_{{xx}} }} \\ {{\hat{T}^{{f\alpha }}_{{zx}} }} \\ {{\hat{T}^{{f\beta }}_{{zx}} }} \\ \end{array} } \right]} & = {\left[ {\begin{array}{*{20}c} {a} & {b} & {c} & {d} \\ {{ - b}} & {{ - a}} & {d} & {c} \\ {{ - c}} & {d} & {e} & {f} \\ {d} & {{ - c}} & {{ - f}} & {{ - e}} \\ \end{array} } \right]}{\left[ {\begin{array}{*{20}c} {{\hat{U}^{\alpha }_{x} }} \\ {{\hat{U}^{\beta }_{x} }} \\ {{\hat{U}^{\alpha }_{z} }} \\ {{\hat{U}^{\beta }_{z} }} \\ \end{array} } \right],} \\ a & = \frac{{ - \mu {\left( {\delta ^{2} - k^{2} } \right)}}} {{kD}}{\left( {\frac{k} {\delta }\coth \delta \Delta - \coth k\Delta } \right)}, \\ b & = \frac{{ - \mu {\left( {\delta ^{2} - k^{2} } \right)}}} {{kD}}{\left( {\frac{k} {\delta }csch\delta \Delta - \operatorname{csch} k\Delta } \right)}, \\ c & = \frac{{ - j\mu }} {D}{\left[ {\delta {\left( {1 + \frac{{3k^{2} }} {{\delta ^{2} }}} \right)}{\left( {\operatorname{csch} k\Delta csch\delta \Delta - \coth k\Delta \coth \delta \Delta } \right)} + k{\left( {3 + \frac{{k^{2} }} {{\delta ^{2} }}} \right)}} \right]}, \\ d & = \frac{{ - j\mu {\left( {\delta ^{2} - k^{2} } \right)}}} {{\delta D}}{\left( {\coth \delta \Delta \operatorname{csch} k\Delta - \coth k\Delta csch\delta \Delta } \right)}, \\ e & = \frac{{ - \mu {\left( {\delta ^{2} - k^{2} } \right)}}} {{\delta D}}{\left( {\frac{k} {\delta }\coth k\Delta - \coth \delta \Delta } \right)}, \\ f & = \frac{{\mu {\left( {\delta ^{2} - k^{2} } \right)}}} {{\delta D}}{\left( {csch\delta \Delta - \frac{k} {\delta }\operatorname{csch} k\Delta } \right)}, \\ D & = 1 + \frac{{k^{2} }} {{\delta ^{2} }} + \frac{{2k}} {\delta }{\left( {\operatorname{csch} k\Delta csch\delta \Delta - \coth k\Delta \coth \delta \Delta } \right)}, \\ \delta & = {\left[ {k^{2} + {\left( {{j\omega \rho } \mathord{\left/ {\vphantom {{j\omega \rho } \mu }} \right. \kern-\nulldelimiterspace} \mu } \right)}} \right]}^{\frac{1}{2}}. \\ \end{aligned} $$
(59)

Now by using Eq. 59 in Eqs. 57 and 58, a matrix relating the frequency ω to the interfacial perturbations may be derived. The x-directed stress balance has subscript i=x at the top (2/3) interface. Substituting into Eq. 57 yields

$${\left({T^{\text{f}}_{{xx2}} - T^{\text{f}}_{{xx3}}} \right)}n_{{1x}} + {\left({T^{\text{f}}_{{xz2}} - T^{\text{f}}_{{xz3}}} \right)}n_{{1z}} - T^{\text{e}}_{{xx3}} n_{{1x}} - T^{\text{e}}_{{xz3}} n_{{1z}} + n_{{1x}} \gamma \frac{{\partial ^{2} \xi _{1}}}{{\partial z^{2}}} = 0.$$
(60)

It is found that equilibrium stresses are T f xz20 =T f xz30 =T e xz30 =0, where the o subscript refers to equilibrium values, so the complex amplitude stress balance to first order becomes

$${\left({\hat{T}^{\text{f}}_{{xx2}} - \hat{T}^{\text{f}}_{{xx3}}} \right)} - \hat{T}^{\text{e}}_{{xx3}} - \gamma k^{2} \hat{\xi}_{1} = 0.$$
(61)

The perturbation electrical stress tensor is

$$\hat{T}^{\text{e}}_{{xx3}} = \frac{{\varepsilon _{\text{b}}}}{2}{\left[ {{\left({E_{\text{o}} + \hat{e}_{{x3}}} \right)}^{2} - \hat{e}^{2}_{{z3}}} \right]} - \frac{{\varepsilon _{\text{b}}}}{2}E^{2}_{\text{o}} \cong \varepsilon _{\text{b}} E_{\text{o}} \hat{e}_{{x3}}.$$
(62)

Using the relations in Eq. 59 and the small signal boundary conditions in Eq. 56

$$\hat{T}^{\text{f}}_{{xx2}} = - j\omega \hat{\xi}_{1} a_{2} + c_{2} \hat{U}_{{z2}}, $$
(63)
$$\hat{T}^{\text{f}}_{{xx3}} = j\omega \hat{\xi}_{1} a_{3} + j\omega \hat{\xi}_{2} b_{4} + c_{3} \hat{U}_{{z3}} + d_{4} \hat{U}_{{z4}}. $$
(64)

Similarly, at the lower (4/5) interface

$${\left({\hat{T}^{\text{f}}_{{xx4}} - \hat{T}^{\text{f}}_{{xx5}}} \right)} + \hat{T}^{\text{e}}_{{xx4}} - \gamma k^{2} \hat{\xi}_{2} = 0,$$
(65)
$$\hat{T}^{\text{e}}_{{xx4}} \cong \varepsilon _{\text{b}} E_{\text{o}} \hat{e}_{{x4}}, $$
(66)
$$\hat{T}^{\text{f}}_{{xx4}} = - j\omega \hat{\xi}_{1} b_{4} - j\omega \hat{\xi}_{2} a_{4} + d_{4} \hat{U}_{{z3}} + c_{4} \hat{U}_{{z4}}, $$
(67)
$$\hat{T}^{\text{f}}_{{xx5}} = j\omega \hat{\xi}_{2} a_{5} + c_{5} \hat{U}_{{z5}}. $$
(68)

Next, the z-directed interfacial stress balance when i=z at the top (2/3) interface is

$${\left({T^{\text{f}}_{{zx2}} - T^{\text{f}}_{{zx3}}} \right)}n_{{1x}} + {\left({T^{\text{f}}_{{zz2}} - T^{\text{f}}_{{zz3}}} \right)}n_{{1z}} - T^{\text{e}}_{{zx3}} n_{{1x}} - T^{\text{e}}_{{zz3}} n_{{1z}} + n_{{1z}} \gamma \frac{{\partial ^{2} \xi _{1}}}{{\partial z^{2}}} = 0,$$
(69)

which is further simplified to first-order and written in complex amplitude form as

$${\left({\hat{T}^{\text{f}}_{{zx2}} - \hat{T}^{\text{f}}_{{zx3}}} \right)} + {\left({T^{\text{f}}_{{zz2{\text{o}}}} - T^{\text{f}}_{{zz3{\text{o}}}}} \right)}\hat{n}_{{1z}} - \hat{T}^{\text{f}}_{{zx3}} - T^{\text{f}}_{{zz3{\text{o}}}} \hat{n}_{{1z}} = 0.$$
(70)

The equilibrium terms are reduced using Eqs. 9 and 10 so

$${\left({T^{\text{f}}_{{zz2{\text{o}}}} - T^{\text{f}}_{{zz3{\text{o}}}} - T^{\text{e}}_{{zz3{\text{o}}}}} \right)}\hat{n}_{{1z}} = {\left({P_{{3{\text{o}}}} - P_{{2{\text{o}}}} - T^{\text{e}}_{{zz3{\text{o}}}}} \right)}\hat{n}_{{1z}} = {\left({P_{{3{\text{o}}}} - P_{{2{\text{o}}}} + \frac{{\varepsilon _{\text{b}}}}{2}E^{2}_{\text{o}}} \right)}\hat{n}_{{1z}} = \varepsilon _{\text{b}} E^{2}_{0} jk\hat{\xi}_{1},$$
(71)
$$\hat{T}^{\text{e}}_{{zx3}} = \varepsilon _{\text{b}} E_{\text{o}} \hat{e}_{{z3}} = \varepsilon _{\text{b}} E^{2}_{0} jk\hat{\xi}_{1}.$$
(72)

Therefore, the stress balance of Eq. 70 becomes

$${\left({\hat{T}^{\text{f}}_{{zx2}} - \hat{T}^{\text{f}}_{{zx3}}} \right)} + \varepsilon _{\text{b}} E^{2}_{0} jk\hat{\xi}_{1} - \varepsilon _{\text{b}} E^{2}_{0} jk\hat{\xi}_{1} = 0 \Rightarrow {\left({\hat{T}^{\text{f}}_{{zx2}} - \hat{T}^{\text{f}}_{{zx3}}} \right)} = 0.$$
(73)

Using the fluid stress tensor relationships of Eq. 59, the interfacial stress condition becomes

$$j\omega \hat{\xi}_{1} {\left({c_{3} - c_{2}} \right)} - j\omega \hat{\xi}_{2} d_{3} - \hat{U}_{{z2}} {\left({e_{2} + e_{3}} \right)} - \hat{U}_{{z4}} f_{3} = 0.$$
(74)

Similarly at the lower (4/5) interface the stress balance relationship is

$$j\omega \hat{\xi}_{1} d_{4} - j\omega \hat{\xi}_{2} {\left({c_{4} - c_{5}} \right)} - \hat{U}_{{z4}} {\left({e_{4} + e_{5}} \right)} - \hat{U}_{{z3}} f_{4} = 0.$$
(75)

Combining the fluid and electrical stress contributions and the perturbation electric field relationships given in Eqs. 17 and 18, the requirement of x and z stress balance results in

$${\left[ {\begin{array}{*{20}c} {{- {\left({a_{\text{a}} + a_{\text{b}} - \frac{{\varepsilon _{\text{b}} E^{2}_{\text{o}} k}}{{j\omega}}\coth kb + \frac{{\gamma k^{2}}}{{j\omega}}} \right)}}} & {{- {\left({b_{\text{b}} + \frac{{\varepsilon _{\text{b}} E^{2}_{\text{o}} k}}{{j\omega \sinh kb}}} \right)}}} & {{{\left({c_{\text{a}} - c_{\text{b}}} \right)}}} & {{- d_{\text{b}}}} \\ {{- {\left({b_{\text{b}} + \frac{{\varepsilon _{\text{b}} E^{2}_{\text{o}} k}}{{j\omega \sinh kb}}} \right)}}} & {{- {\left({a_{\text{a}} + a_{\text{b}} - \frac{{\varepsilon _{\text{b}} E^{2}_{\text{o}} k}}{{j\omega}}\coth kb + \frac{{\gamma k^{2}}}{{j\omega}}} \right)}}} & {{d_{\text{b}}}} & {{- {\left({c_{\text{a}} - c_{\text{b}}} \right)}}} \\ {{- {\left({c_{\text{a}} - c_{\text{b}}} \right)}}} & {{- d_{\text{b}}}} & {{- {\left({e_{\text{a}} + e_{\text{b}}} \right)}}} & {{- f_{\text{b}}}} \\ {{d_{\text{b}}}} & {{{\left({c_{\text{a}} - c_{\text{b}}} \right)}}} & {{- f_{\text{b}}}} & {{- {\left({e_{\text{a}} + e_{\text{b}}} \right)}}} \\ \end{array}} \right]}{\left[ {\begin{array}{*{20}c} {{j\omega \hat{\xi}_{1}}} \\ {{j\omega \hat{\xi}_{2}}} \\ {{\hat{U}_{{z2}}}} \\ {{\hat{U}_{{z4}}}} \\ \end{array}} \right]} = 0$$
(76)

where a through f are the matrix elements defined in Eq. 59 and the subscript a or b relates to which layer, a or b, is used to evaluate the components. As with the inviscid analysis, the dispersion equations are obtained by setting the determinant of the coefficients to zero. The determinant of Eq. 76 separates into the product of two terms each of which may be zero

$$\begin{aligned} & {\left[{{\left({{\left({c_{\text{a}} - c_{\text{b}}} \right)} + d_{\text{b}}} \right)}^{2} + {\left({{\left({a_{\text{a}} + a_{\text{b}} - \frac{{\varepsilon _{\text{b}} E^{2}_{\text{o}} k}}{{j\omega}}\coth kb + \frac{{\gamma k^{2}}}{{j\omega}}} \right)} + {\left({b_{\text{b}} + \frac{{\varepsilon _{\text{b}} E^{2}_{\text{o}} k}}{{j\omega \sinh kb}}} \right)}} \right)}{\left({{\left({e_{\text{a}} + e_{\text{b}}} \right)} - f_{\text{b}}} \right)}} \right]} \\ & \times \quad\quad{\left[{{\left({{\left({c_{\text{a}} - c_{\text{b}}} \right)} - d_{\text{b}}} \right)}^{2} + {\left({{\left({a_{\text{a}} + a_{\text{b}} - \frac{{\varepsilon _{\text{b}} E^{2}_{\text{o}} k}}{{j\omega}}\coth kb + \frac{{\gamma k^{2}}}{{j\omega}}} \right)} - {\left({b_{\text{b}} + \frac{{\varepsilon _{\text{b}} E^{2}_{\text{o}} k}}{{j\omega \sinh kb}}} \right)}} \right)}{\left({{\left({e_{\text{a}} + e_{\text{b}}} \right)} + f_{\text{b}}} \right)}} \right]} = 0 \\ \end{aligned}.$$
(77)

The generalized analysis in [26] has proved that the incipience of instability occurs when ω=0. If the system is stable, ω is complex with a positive imaginary part and if unstable the real part of ω is 0 while the imaginary part is negative. This last condition is very helpful in numerically evaluating each of the functions in Eq. 77 to find instability growth rates as a function of electric field E o and wavenumber, k. Using the physical values given in Table I and layer thicknesses a=b=50 μm, negative imaginary roots of ω are found if the applied field is beyond the incipience of instability (Fig. 3). The fastest growth wavenumber is the minimum of the negative imaginary roots.

Fig. 3
figure 3

Plot of the negative imaginary (unstable) roots of ω versus wavenumber using the viscous analysis for a variety of applied fields. The flow is unstable as long as the root is negative imaginary

Full size image

Figure 4 shows a comparison of the fastest growth wavenumbers, k max, and growth rate at the fastest growth rate wavenumber, ω(k max), as a function of applied electric field for both the viscous and inviscid analyses presented. It is readily seen that the fastest growth wavenumber in the viscous model is much smaller than for the inviscid model and does not increase as quickly with increasing applied field. This is because the stabilizing effects of viscosity need to be overcome for the instability to grow. This requires a smaller wavenumber to be excited as viscosity constrains the fastest growth wavenumber.

Fig. 4
figure 4

(Top) Comparison of the fastest growth wavenumber, k max , as a function of applied electric field for the inviscid and viscous analyses. (Bottom) Magnitude of the imaginary instability growth rate at the fastest growth wavenumber, ω(k max), as a function of applied electric field for both the inviscid and viscous analyses

Full size image

3 Experimental

3.1 Device fabrication

The microfluidic channels used in this study are fabricated using polydimethylsiloxane (PDMS) replica molding using the soft lithography technique [27]. Briefly, the microfluidic channels are made by casting PDMS onto a negative SU-8 (SU-8 2050, MicroChem) structure that is fabricated on a glass slide. PDMS channels are fabricated by curing a two part mixture of Sylgard 184 Silicone Elastomer Base and Sylgard 184 Silicone Elastomer Curing Agent mixed at a 10:1 ratio which has been poured over the SU-8 structure and is allowed to cure for 4 h at 65°C. After curing, the PDMS is peeled off the SU-8 structure and holes are drilled through the PDMS using a carbide drill bit to define the inlets and outlets.

For electrical excitation, metal electrodes are patterned onto a glass slide using a lift off technique. The slide is lithographically patterned and developed using a 2-μm thick Shipley 1818 photoresist. The exposed area on the patterned glass slides is etched to a depth of 0.5 μm in 5:1 diluted hydrofluoric acid. The patterned slides are then transferred to a metal sputtering system to fabricate Cr/Au electrodes with thicknesses of 500 Å and 4,000 Å, respectively. After sputtering, the photoresist making layer is removed by dissolution in acetone. Once the photoresist is completely stripped, the glass slide with patterned metal electrodes is left behind.

The PDMS microchannel is bonded onto the glass slide with patterned electrodes by activating the bonding surfaces in oxygen plasma at 200 mTorr, 35 W, for 10 s [28]. The two components are aligned using a probe station stage and brought into contact to initiate the bonding process. The bonded device is further cured at 65°C overnight. The final daughter channel dimensions are 150 μm wide × 30 μm deep × 1 cm long and the device configuration is shown in Fig. 5. The electrodes are 2 mm long and have an interelectrode spacing of 75 μm and are designed to contact the upper and lower aqueous fluid phases and run tangentially to the fluid flow down the length of the microchannel.

Fig. 5
figure 5

Schematic of the three inlet geometry with electrodes and instability mixing. The channel height is 30 μm and the electrode to electrode spacing is 75 μm

Full size image

After the glass slide is bonded with the PDMS structure that has the channels, blunt end needles are inserted through the inlet and outlet holes into the reservoirs within the PDMS structure. The needles (Kontes Glass Company) guide the phenol and water phases to their respective reservoirs in the microfluidic structure.

3.2 Experimental procedure

The phenol and aqueous phases were co-infused through the microfluidic structure using a syringe pump (KD Scientific Inc.) with a flow rate for the water–phenol–water system of 5, 2.5, 5 μl/min corresponding to a total flow rate of 12.5 μl/min. This corresponds to an average velocity of 4.63 cm/s. A glass syringe (Whatman Laboratory Products) is connected to the microfluidic channel through a luer connection and rigid tubing. Phenol, chloroform and isoamyl alcohol at a 25:24:1 volume ratio was obtained through a vendor (USB Corp.) and used as received. For flow visualization the phenol phase is labeled with a lipophilic dye, DiI (1,1-dioctadecyl-3,3,3,3-tetramethylindocarbocyanine perchlorate) for phase contrast of the organic phase during flow. Due to the hydrophobic nature of DiI, it stays partitioned within the organic phase which appears bright using epifluorescent microscopy. The aqueous phase is a phosphate buffered saline (PBS) (10 mM phosphate buffer, pH 7.4, 140 mM NaCl, 3 mM KCl) (EMD Biosciences) solution with 0.5% sodium n-dodecyl sulfate (SDS) (CN Biosciences Inc). PBS is used so that the aqueous phase acts as a conducting medium with respect to the organic phenol phase which is non-conductive. SDS is used to improve the stability of the aqueous–organic–aqueous sheath flow profile by lowering the interfacial tension at the organic–aqueous interfaces [8].

Electrohydrodynamic instability was produced by biasing the electrodes with both AC voltages varying from 0 to 45 V RMS voltages over a frequency range of 250 kHz to 10 MHz. AC excitation is used to avoid electrolysis of the aqueous fluid phase. The electrical contacts to the coplanar electrodes were made by the use of microprobes. AC voltage excitation was provided by amplifying the function generator output (Agilent 33102A) through a power amplifier (Tucker, Model 310). The mixing events in the microfluidic channel were imaged using a conventional epifluorescent microscopy with a TRITC filter cube (Olympus IX71) using a 20× objective coupled to a 5 ns pulse width Nd:YAG (532 nm pulse wavelength) laser source to excite the fluorescent dye in the organic phase. Laser excitation allows visualization of the EHD instability events with minimal blurring. For each experiment between 15 and 70 image frames were recorded at a frame rate of 10 Hz using a 12 bit Cooke Sensicam QE (1,376×1,024 pixels) At the chosen magnification, the total CCD image size of corresponds to an image area of 461×340 μm.

4 Results and discussion

Onset of instability is seen at 40 V RMS at a frequency of 250 kHz \({\left[{({{\omega \varepsilon _{\text{p}}}}/{{\sigma _{\text{w}}}}) = 0.010} \right]}\) for saline and phenol. This corresponds to an electric field E o=8.0×105 V/m RMS across the 50 μm wide phenol phase. The instability is observed along the length of the electrodes. The applied voltage is increased and the representative images of the instability at different voltages and frequencies are shown in Fig. 6. As the applied field was increased to 8.4×105 V/m at 250 kHz, electrolysis of the aqueous phase was seen along the edges of the electrodes in the form of small bubbles. The frequency was then increased to 700 kHz \({\left[{{{\omega \varepsilon _{\text{p}}}}/{{\sigma _{\text{w}}}}) = 0.028} \right]}\) and 10 MHz \({\left[{{{\omega \varepsilon _{p}}}/{{\sigma _{w}}}) = 0.405} \right]}\) to allow higher fields while avoiding electrolysis. At an applied potential of 45 VRMS at 10 MHz dispersion of the two phases is seen (Fig. 6f). At this high frequency, however, there is a contribution from the displacement current and potential drop within the aqueous phase not considered in the theoretical model, so the validity of the stability model comes into question as the analysis assumes the aqueous layer is perfectly conducting. The system recovers the stratified flow profile (Fig. 6g) when the applied field is removed.

Fig. 6
figure 6figure 6

a A stable flow in the absence of an electric field. b The disruption of flow after a 40 VRMS potential (initial applied field E O=8×105 V/m) is applied at 250 kHz to the electrodes. c Further development of the dynamic unstable profile at 41 VRMS, 250 kHz (initial applied field E O=8.2×105 V/m). d Disruption of flow after a 42 VRMS potential is applied at 250 kHz to the electrodes. e EHD instability at 44 VRMS (initial applied field E O=8.8×105 V/m), 700 KHz. f Dispersion of the two phases at 45 VRMS (initial applied field E O=9×105  V/m) and 10 MHz. g Recovery after the field is removed. The electrodes are spaced 75 μm apart in the aqueous phase above and below the organic phase but appear dark in the epifluorescent images. All images were taken using a 20× microscope objective and each image window size is 340×461 μm2. The horizontal white lines delineate the channel boundaries. h A comparison of the power spectrum from the steady flow case and 44 VRMS where the pixel grayscale intensity is proportional to the logarithm of the power showing the higher power at longer spatial frequencies due to the EHD instability

Full size image

In order to visualize the instability, larger fields than are predicted for the onset of instability were required. Since the fluid is moving in the experiments conducted, if the instability growth rate is very slow (as when it is close to incipience) the instability may be convected away by the fluid movement before the interfacial disturbances are seen under the microscope. The instability growth rate corresponds to the negative imaginary value of ω. At an average flow rate of 4.63 cm/s and a frame width of 460 μm, the instability growth rate must be less than 0.01 s to be recorded within an image frame. At an applied electric field of 8.0×105 V/m the fastest growth wavenumber determined from the viscous stability model is expected to constrain the instability growth rate. At this wavenumber, the instability growth rate is determined to be 2.4×10−4 s which is several orders of magnitude faster than the required growth rate of 0.01 s. Thus, at this very fast growth rate, the instability has enough time to develop so that dramatic changes in the flow structure could be captured through the microscope.

In order to quantify the unstable wavenumbers during the mixing process a fast Hartley transform (FHT) analysis of the mixing images was conducted. A FHT is similar to a Fast Fourier Transform except that it works with real numbers instead of complex numbers and are therefore more computationally efficient over Fourier transforms when considering real data while producing the same frequency data. The FHT of the individual images was performed using ImageJ (NIH, Bethesda, MD, USA) with 2,048 pixel zero padding of the images. The power spectrums of the steady image and mixing image at 44 VRMS are shown in Fig. 6h, where the grayscale intensity of the image shows the logarithm of the power at a given spatial frequency. Since the fluorescent dye partitions only to the organic phase, fall off in pixel intensity delineate interfacial boundaries so the frequency components determined from the FHT analysis are attributed to interfacial displacements. As expected, at higher levels of mixing the power spectra has higher spatial frequency (wavenumber) components.

The excited wavenumbers for a given mixing run are estimated by comparing the ratio of the average FHT magnitude over all image frames at a given wavenumber to that of the average magnitude in the steady case. A plot of the logarithm of the FHT magnitude ratio from the steady case (Log(P mix/P steady)) where P refers to the power calculated from the FHT and the subscript refers to either the mixing case or the steady case as a function of wavenumber is shown in Fig. 7. As the applied field increases, the excited wavenumber band broadens and increases in intensity. The width of the band is determined by finding the wavelengths which contain a three standard deviation difference from the average high-frequency magnitude difference. The maximum of the wavenumber band is also compared to the predicted fastest growth wavenumber.

Fig. 7
figure 7

Plot of the wavenumber spectrum of the images at different initially applied fields compared to the steady spectra (Log(P mix/P steady)). The unstable wavenumber band width increases as the applied field is increased

Full size image

In order to quantify the level of mixing, the images are analyzed to determine the area of aqueous fluid entrainment into the organic layer. Since the two fluid phases are immiscible and the fluorescent dye used experimentally stays partitioned in the organic phase, the entrainment of the aqueous phase within the organic layer may be determined by intensity modulation of the image fluorescence within the organic layer. From the images, the entrainment area is measured as a percentage of the total organic layer area. This gives an estimation of the volume of organic fluid displaced due to the EHD instability. Figure 8 shows the entrainment area as a function of applied field. It is seen that the entrainment area increases from 1.9 to 28.6% as the applied field is increased from 8.0×105 to 9.0×105 V/m. It is also seen that at the applied field of 9.0×105 V/m, the variance of the entrainment area is very large. This is due to the wide level of entrainment seen during the instability ranging from 15% to as high as 66%.

Fig. 8
figure 8

Entrainment of conductive fluid into the organic layer as a percentage of image entrainment area into the total area of the organic layer as a function of applied field strength

Full size image

Table 2 summarizes a comparison of the unstable wavenumbers obtained from the images along with the predicted maximum field strength to excite a particular unstable wavelength from both the inviscid and viscous stability models using Eqs. 48, 50 and 77. A visual depiction comparing the theoretically predicted unstable wavenumbers and fastest growth wavenumbers with the experimental measurements is shown in Fig. 9. The largest measured wavenumber is assumed to be the least energetically favorable and requires the highest field for excitation. The maximum electric field that is required experimentally to produce the largest measured unstable wavenumber is calculated using both inviscid and viscous stability models and compared to the initially applied field. At low field strengths (40 and 41 VRMS) the applied field of 8.0 and 8.2×105 V/m for the two cases respectively, is slightly higher than the calculated maximum electric field strengths required for the instability of 4.6 and 5.3×105 V/m using the the viscous model (Eq. 77) with the largest measured wavenumbers of 0.137 and 0.165 μm−1 for each case respectively. In addition, the measured fastest growth wavenumbers for these two cases are 0.046 and 0.082 μm−1 versus 0.043 and 0.44 μm−1 predicted from the viscous model for the two cases respectively. However, there may be larger wavenumbers which are unstable but have a very slow growth rate so they are not experimentally observed as an increased power above the broad spectrum noise seen in the power spectrum plots. Therefore, the predicted maximum electric field for these cases is somewhat smaller than the initially applied fields.

Table 2 Comparison of the theoretical unstable wavenumbers, theoretical fastest growth wavenumbers and predicted maximum field strengths calculated from the largest unstable wavenumber measured using both the inviscid and viscous models with the experimentally measured values
Full size table
Fig. 9
figure 9

Comparison of theoretical unstable wavenumbers and theoretical fastest growth wavenumbers for both the inviscid and viscous models with the experimentally measured values

Full size image

At higher field strengths (42 VRMS and above) the experimentally applied field is smaller than the maximum field predicted using the largest measured wavenumbers. Similarly, the unstable wavenumber band which is measured is wider than theoretical predictions. The discrepancy between the predicted field and fastest growth wavenumber and the measured values is attributed to the fact that at higher field strengths the system is driven beyond the linear incipience limit in order to visualize the dramatic changes in the flow structure. At lower levels of mixing, the electric field within the organic layer is assumed to be uniform and the width of the non-conducting phenol phase is uniform. This assumption breaks down at higher field strengths as more profound mixing occurs. This is because the instability has grown beyond the linear range so the electric field is no longer uniform across the organic phase because of entrainment of the aqueous phase within the phenol layer due to large interfacial displacements. This results in an interfacial “sharpening” which increases the local electric field beyond the initially applied field. Further thinning of the phenol phase thickness during mixing increases the effective field across the phenol phase as the instability grows so larger wavenumbers are sampled leading to a larger predicted maximum field required for these wavenumbers.

5 Conclusion

Electrohydrodynamic mixing has been modeled in both inviscid and viscous flows using linear stability theory to predict the incipience of instability, and growth rates of the instability as a function of applied electric field and wavenumber. The analysis shown here serves as a guide to understanding the experimental system used in this work. Further consideration of instability under flow conditions requires using computational methods. Electrohydrodynamic mixing has also been experimentally demonstrated to increase the interfacial contact area between an organic and aqueous phase measured by the level of entrainment of conductive fluid into the nonconductive organic layer. The analytical results are compared with experimental demonstrations of EHD instability mixing within microfluidic devices. The simple fabrication procedure required to make the device and the use of electric fields to produce mixing makes this device desirable for multiphase mixing. The increase in interfacial area from the EHD instability will improve the biological material partitioning when the device is used to separate DNA from other cellular components.