1 Introduction

In order to realize the concept of Labs-on-a-chip for biomedical applications, integration and miniaturization are critical. There has been great success over the last decade in the development of microfluidic devices towards the integration of Lab-on-a-chip devices (McDonald et al. 2000; Reyes et al. 2002). It is a natural progression to extend these systems to the nanoscale regime with at least one of the dimensions on the nanometer scale since such devices offer unprecedented control over single cell transport, in manipulation as well as in detection (Jonas et al. 2001; Levene et al. 2003). A number of methods have been developed to fabricate nanofluidic devices in glass, silicon oxide, silicon nitride and polymide with good resolution (Guo et al. 2004; Kutchoukov et al. 2004; Eijkel et al. 2004). It has also been demonstrated that nanofluidic channels can be used for single cell analysis. Campbell et al. (2004) studied the electrophoretic behavior of single, fluorescently labelled DNA molecules in rectangular silicon nanochannels with a cross-sectional area down to 150×180 nm. The active control of single molecules of DNA in such small channels was achieved through electrokinetic transport. Han and Craighead (2000) separated long DNA molecules by electrokinetically pumping the molecules through a nanofluidic device consisting of alternating thin and thick regions with different depths. This alternative change in depth caused size-dependent trapping of DNA, which created an electrophoretic mobility difference enabling separation without the use of a gel matrix or pulsed electric field. Although a nanofluidic channel has great potential in single molecule analysis and the development of drug delivery systems, application of such devices in biomedical diagnosis and treatment is not yet practical. The bottleneck is the lack of fundamental understanding of transport phenomena in nanoscale devices, which has largely hindered the systematic design and precise control of such devices. To date, there are limited reports regarding fluid flow in nanofluidic channels, where electrical double layer is overlapped in most applications.

The first work on electroosmotic flow in a channel on the order of electrical double layer thickness (i.e. nanometer) was done by Burgeen and Nakache (1964). They produced results for the velocity field and potential field with the assumption of the Boltzmann distribution for species ionic concentration. However, as previous studies have shown (Ren and Li 2004), when the electrical double layer is overlapped, it is not proper to use the Boltzmann distribution for ionic concentration prediction. Recently, Jacobson et al. (2001) experimentally studied electroosmotic flow in channels with a height varying from 98 nm to 10.4 μm. Their experiments for the 98-nm-depth channel showed that electroosmotic mobility increased when the double layer thickness increased, however, when the double layer thickness extended significantly into the channel (44% of the half channel depth), electroosmotic mobility decreased. Pennathur and Santiago (2004) reported both numerical and experimental studies on electroosmotic flow in nanofluidic channels. In their experiments, it is found that the area-average velocity decreased nonlinearly when the channel dimensions approached the double layer thickness, which was also expected through analytical analysis (Rice and Whitehead 1965). In their numerical studies, finite but non-overlapped double layer was assumed and thus Poisson-Boltzmann equation was used to describe the applied electrical potential field. Their experimental data agreed with their numerical predictions for area-average velocity. Conlisk and McFerran (2002) solved a 1-D numerical model of mass transfer and fluid flow in rectangular micro- and nanochannels for ideal electrolytes (i.e. NaCl), where the channel height was down to 1 nm. In their numerical model, the wall boundary conditions for species ionic concentration were assumed. Their results showed that the continuum mechanics was valid for liquid flow in nanochannels through comparison between their numerical model predictions and the experimental data received from iMEDD, Inc.

In the above theoretical studies, either the Boltzmann distribution or the wall boundary conditions for species ionic concentration was assumed, which are not proper for overlapped double layer applications. The justification is detailed below. The derivation of the Boltzmann distribution requires an infinitely large aqueous phase so that the electrical potential is zero in the liquid far away from the charged surface and that the ionic concentrations in the region far away from the charged surface are equal to the original bulk ionic concentration (Hunter 1981; Masliyah 1994). Mathematically, this condition can be expressed as:

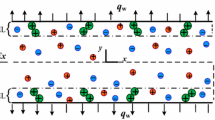
$$x = \infty,\quad\psi= 0, \quad {\text{and}} \quad n_i = n_i^0$$
(1)

where x is the distance in the normal direction to the channel wall, ψ is the electrical potential, and \(n_{\rm i}^{0}\) is the original bulk concentration. It is well known that the presence of charged solid–liquid interface will result in an excess of counter-ions and a deficit of co-ions in the EDL region. At neutral pH levels, the source of protons from the surface is low and can be neglected for this study; hence the counter-ions are supplied by the solution. Therefore, it should be expected that there is a deficit of counter-ions and a surplus of co-ions in the bulk liquid outside of the electrical double layer, as illustrated in Fig. 1. The conventional Boltzmann distribution cannot show this logical expectation. This is because a key underlying assumption of the Boltzmann distribution is an infinitely large liquid phase, as specified by the condition given in Eq. 1. It is understandable that if the size of the system is sufficiently large and/or bulk ionic concentration is sufficiently high, deficit and surplus are negligible and the Boltzmann distribution is acceptable.

Fig. 1
figure 1

Illustration of the net charge distribution in the liquid and the electroosmotic flow in a channel

Full size image

However, when the channel is scaled down to nanometer scale, the excess of counter-ions and the deficit of co-ions in the EDL region will result in significant changes in the concentrations of counter-ion and co-ion in the region outside the EDL. In order to satisfy the conservation condition that the total ion number is constant in a given system, the concentration of counter-ion in the bulk liquid region is expected to be lower than the original bulk concentration due to the accumulation of counter-ions in the EDL region; the concentration of co-ion in the bulk liquid region is expected to be higher than the original bulk concentration due to the deficit of co-ions in the EDL region. Consequently, neither the concentration of counter-ion nor the concentration of co-ion at the center of the microchannel is equal to the original bulk concentration. Therefore, the assumption that the ionic concentration in the bulk liquid region (far away from the EDL) is equal to the original bulk concentration, which is used to derive the Boltzmann distribution, is not correct and hence the Boltzmann distribution cannot be applied to such a system. In addition, the species ionic concentration at the channel wall is unknown and should be determined by satisfying the conservation condition that the total ion number is constant.

In this paper, a numerical model will be developed to examine electroosmotic flow in cylindrical nanochannels with radii R, and with the z-axis along the channel length. Pressure driven flow and electroosmotic driven flow are the commonly used methods for pumping liquid in microchannels. Each has its own advantages and disadvantages and the selection of pumping method is driven by applications. However, when the channel dimension is scaled down to nanometer, pressure driven flow is not feasible, which can be understood as follows. Consider a pressure driven flow in a nanochannel with a channel diameter d, where the area-average velocity can be evaluated by:

$$\vec u_{\text{ave}} = -\frac{{{\text{d}}^2}}{{32\mu}}\vec \nabla P$$
(2)

where μ is the viscosity of liquid and \(\vec \nabla P\) is the pressure gradient applied over the channel length. Assuming the viscosity is 1.0 ×10−3 kg/(m s) and the diameter, d, is chosen as 100 nm, in order to achieve a velocity on the order of mm/s, the required pressure gradient is as high as 3.2×109 Pa/m or 320 atm/cm (1.0 ×105 Pa is assumed to be 1 atm). It is not practical to integrate such a high pressure pump into Lab-on-a-chip devices. Electroosmotic driven flow offers great advantages over pressure driven flow for nanoscale devices such as: its ease of control, no dead volume, easy integration and plug-like velocity profile, and therefore is chosen as the pumping method in this study. The purpose of this study is to gain a better understanding of electrokinetic transport phenomena in nanoscale devices by examining the flow field, potential field and concentration field in nanochannels with the consideration of double layer overlapping and the application of continuum mechanics. Strong symmetric electrolytes such as KCl are considered as the working liquids although this model can easily be extended to asymmetric electrolytes.

2 Theoretical model

2.1 Electrical potential field

Consider a cylindrical channel and a simple symmetric (e.g., z:z = 1:1) electrolyte solution. According to the theory of electrostatics, the relationship between the electrical potential,ψ, and the net charge density per unit volume, ρ e , at any point in the liquid is described by the Poisson equation:

$$\frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}\left({r\frac{{{\text{d}}\psi}}{{{\text{d}}r}}} \right) = - \frac{{\rho_e}}{{\varepsilon_0 \varepsilon_r}}$$
(3)

where ɛ r is the dielectric constant of the solution and ɛ0 is the permittivity of vacuum. The net charge density is proportional to the ionic number concentration difference between positive ions and negative ions, via

$$\rho_e = e\left(n_{{\rm K}^{ +}} - n_{{\rm Cl}^{ -}} \right)$$
(4)

where e is the elemental charge, \(n_{\rm K}^{+}\) and \(n_{\rm Cl}^{-}\) are the number densities of K+ and Cl− ions, respectively. Substituting Eq. 4 into Eq. 3, the Poisson equation becomes,

$$\frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}\left({r\frac{{{\text{d}}\psi}}{{{\text{d}}r}}} \right) = - \frac{e}{{\varepsilon_r \varepsilon_0}}\left({n_ {+} - n_{-}} \right)$$
(5)

In order to numerically solve Eq. 5, the following boundary conditions are employed,

$$r = 0,\quad\frac{{{\text{d}}\psi}}{{{\text{d}}r}} = 0$$
(6a)
$$r = R,\quad\psi=\zeta$$
(6b)

where ζ is the electrical potential at the solid–liquid surface. Introducing dimensionless parameters:

$$r^* = \frac{r}{R},\quad\psi^* = \frac{{ze\psi}}{{k_b T}},\quad n_i ^* = \frac{{n_i}}{{n_i^0}},\quad u^* = \frac{u}{{U_{eo}}}$$

Equation 5 and the associated boundary conditions are reduced to:

$$\frac{1}{{r^*}}\frac{{\text{d}}}{{{\text{d}}r^*}}\left({r^* \frac{{{\text{d}}\psi^*}}{{{\text{d}}r^*}}} \right) = - \frac{{R^2 z^2 e^2 n^0}}{{k_b T\varepsilon_r \varepsilon_0}}\left({n_ + ^* - n_ - ^*} \right)$$
(7)
$$r^* = 0,\quad \frac{{{\text{d}}\psi^*}}{{{\text{d}}r^*}} = 0$$
(8a)
$$r^* = 1, \quad \psi^* = \zeta^* = \frac{{ze\zeta}}{{k_{\rm b} T}}$$
(8b)

where kb is the Boltzamnn constant, T is the temperature of the electrolyte solution, R is the radius of the channel, and Ueo is the velocity predicted by the Helmholtz-Smoluchowski model for electroosmotic flow with thin double layer thickness taking the form of

$$U_{{\rm eo}} = {{\varepsilon_r \varepsilon_0 \zeta E_x}/\mu},$$

where E x (V/m) stands for the external applied electrical field in the axial direction of the channel. Since we consider a symmetric electrolyte solution (z:z = 1:1) where the original bulk concentration for both positive and negative ions is the same \((n_ + ^0 = n_ - ^0 = n^0),\,n_i^0\) is replaced by n0 and it will be the same in the following discussions, except stated otherwise. For non-overlap double layers, the Boltzmann distribution is valid,

$$n_i = n_i^0 \hbox{exp}\left({- \frac{{z_i e\psi}}{{k_b T}}} \right)$$
(9)

which is derived based on the assumption

$$r = \infty,\quad \psi= 0 \quad {\text{and}} \quad n_i = n_i^0$$
(10)

As discussed above, the Boltzmann distribution is not valid when channel dimensions are scaled down to nanometer where the electrical double layer is overlapped because electroneutrality in the bulk liquid, which is used to derive the Boltzmann distribution, does not exist any more. Therefore, the Boltzmann distribution cannot be applied to such systems and the ionic number concentrations of species have to be obtained through the Nernst equation and the ionic number conservation equation. The derivation will be introduced in the following section.

2.2 Ionic concentration field

The relationship between the ionic concentration and the electrical double layer potential can be described by the Nernst equation,

$$\frac{1}{{n_i}}\frac{{{\text{d}}n_i}}{{{\text{d}}r}} = - \frac{{z_i e}}{{k_{\rm b} T}}\frac{{{\text{d}}\psi}}{{{\text{d}}r}}$$
(11)

Integrating Eq. 11 from the wall, where

$$r = R,\quad n_i = n_{i - \hbox{wall}},\quad \psi= \zeta$$
(12)

to a point in the bulk liquid, we get

$$n_i = n_{i - {\text{wall}}} \hbox{exp}\left({- \frac{{z_i e}}{{k_b T}}\left({\psi- \zeta} \right)} \right)$$
(13)

where ni−wall is the ionic concentration of the ith ionic species at the wall, which can be determined by satisfying the conservation condition of the ion number, given below,

$$\int_{0}^{{\text{R}}} {\text{n}}_{+\_\hbox{wall}}\hbox{exp}\left({- \frac{{ze}}{{k_{\rm b} T}}\left({\psi- \zeta}\right)}\right){\text{r{\text{d}}r}} = \frac{1}{2}n^{0} R^{2}$$
(14a)
$$\int_{0}^{{\text{R}}} {\text{n}}_{-\_\hbox{wall}}\hbox{exp}\left({\frac{{ze}}{{k_{\rm b} T}}\left({\psi- \zeta}\right)}\right){\text{r{\text{d}}r}} = \frac{1}{2}n^{0} R^{2}$$
(14b)

The dimensionless forms of the above equations are:

$$n_i^* = n_{{i - \hbox{wall}}}^* \hbox{exp}\left({- \frac{{z_i}}{z}\left({\psi^* - \zeta^*} \right)} \right)$$
(15)
$$\int_{0}^{R} {\text{n}}_{+ \_\hbox{wall}}^{*}\hbox{exp}\left({- \left({\psi^* - \zeta^*} \right)} \right)r{\text{d}}r = \frac{1}{2}R^{2}$$
(16a)
$$\int_{0}^{R} {\text{n}}_{{-\_\hbox{wall}}}^{*}\hbox{exp}\left({\psi^{*} - \zeta^{*}} \right)r{\text{d}}r = \frac{1}{2}R^{2}$$
(16b)

2.3 Flow field

Once the potential distribution and the ionic concentration distribution are found, the fluid motion equation can be solved. The general equation of motion for laminar flow of a liquid with constant density and viscosity is given by:

$$\rho \frac {\partial {\vec u}}{\partial t} + \rho \left({{\vec u} \cdot {\vec \nabla}}\right) {\vec u} = - {\vec \nabla} p + \mu \nabla ^{2} {\vec u} + {\vec F} $$
(17)

where ρ is the density of the liquid, \({\vec u}\) is the velocity vecor, p is the pressure, μ is the viscosity of the liquid, and \(\vec F\) represents the body force. Assuming the flow is steady, one-dimensional, and fully developed, the velocity components satisfy u=u(r), the velocity components in the r- and θ-direction are zero, and the transient term, \({\partial \vec u}/{\partial t},\) and the inertia term, \(\left({\vec u \cdot \vec \nabla} \right)\vec u,\) vanish as well. Also, no pressure difference is applied along the channel and the two reservoirs are open to air, therefore, the pressure gradient, dp/dx, disappears. If the gravity effect is negligible, the body force, \(\vec F,\) is only the external applied electrical driving force. Under the above conditions, Eq. 17 is reduced to:

$$\frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}\left({r\frac{{{\text{d}}u}}{{{\text{d}}r}}} \right) = -\frac{{\text{1}}}{\mu}E_x \rho_e$$
(18)

The above equation of motion is subjected to the following boundary conditions:

$$r = 0,\quad \frac{{{\text{d}}u}}{{{\text{d}}r}} = 0$$
(19a)
$$r = R,\quad {\text{u}} = 0$$
(19b)

The dimensionless form of the above equations is

$$\frac{1}{{r^*}}\frac{{\text{d}}}{{{\text{d}}r^*}}\left({r^* \frac{{{\text{d}}u^*}}{{{\text{d}}r^*}}} \right) = -\frac{{R^2}}{{U_{\text{eo}} \mu}}E_x \rho_e$$
(20)

The above equation of motion is subjected to the following boundary conditions:

$$r^* = 0,\quad \frac{{{\text{d}}u^*}}{{{\text{d}}r^*}} = 0$$
(21a)
$$r^{*} = 1,\quad {\text{u}}^{*} = 0$$
(22b)

The finite difference method was employed to numerically solve this model with the proper boundary conditions. A non-uniform grid system was applied (Anderson et al. 1984) with the minimum grid near the wall in order to capture the information of potential field and flow field inside the double layer. The EDL potential field, the ionic concentration field and the velocity field in nanochannels can be determined based on the simultaneous solution to the above governing equations.

3 Results and discussions

As discussed before, for a given solid-liquid system, when the channel height is sufficiently large, the accumulation of counter-ions in the EDL region has very little effect on the ionic concentrations in the bulk liquid region. In other words, the concentration of counter-ion in the bulk liquid region remains the same as the original bulk concentration. Mathematically, the ionic concentration can be predicted by the traditional Boltzmann distribution and it should satisfy the ionic number conservation condition as well. Therefore, there should be no difference in the potential field and ionic concentration fields predicted by the traditional P-B equation and the newly developed model here. This logic analysis is used to validate the developed model considering a case with a large channel. Figure 2 shows the comparisons of the model predicted potential field and ion concentration field between the conventional Poisson-Boltzmann model and the developed model for a 1 mM KCl solution in a 200 μm diameter channel. In this particular case, the Debye length, \(\lambda_d = \left({\sqrt{\frac{{2z^2 e^2 n^0}}{{k_{\rm b} T\varepsilon_r \varepsilon_0}}}} \right)^{- 1},\) is around 10 nm, which is 0.01% of the channel radius. The coincidence between the two model predictions of potential field and ionic concentration fields validated the developed model.

Fig. 2
figure 2

Comparison between the P-B theoretical model and the developed model simulation results for a non-dimensional ionic concentration, \(n_{i}*=n_{i}/n_{i}^{0},\) and net charge, n*K+−n*Cl−, distribution for 1 mM KCl solution in a 200 μm diameter cylindrical channel, b enlarged view of (a) near the channel surface, c corresponding potential field, ψ*, near the channel surface

Full size image

As the channel diameter is reduced, the non-dimensional Debye length, λd/d increases. The accumulation of counter-ions in the EDL region has significant effects on the ionic concentration distribution and potential distribution in the region outside the EDL. The excess positive net charges in the EDL, for a negative zeta potential, have to be balanced by negative net charges in the centre of the channel in order to conserve continuity. This phenomenon was observed in a 2 μm diameter channel with a 1 mM KCl solution and a corresponding zeta potential of −102 mV. The zeta potential value selected was the same as that reported by Pennathur and Santiago (2004) for the same non-dimensional Debye length. Figure 3a shows the non-dimensional potential field predicted by the traditional P-B equation and by the developed model for the above conditions. The potential field predicted by the P-B equation reaches zero outside the EDL, while a positive non-dimensional potential field of 0.0099 is observed by applying the developed model. Similarly, Fig. 3b illustrates the difference between the traditional P-B and the developed model for the ion distribution and net charge. A strong positive net charge density occurs in the EDL and a non-dimensional negative net charge density of −0.039 exists outside the EDL when the new model is applied.

Fig. 3
figure 3

Comparison of model predicted results between the P-B theory and newly developed model for a 1 mM KCl solution in a 2 μm diameter channel with −102 mV zeta potential. Shown are enlarged views of (a) non-dimensional potential field, ψ*, and b non-dimensional ion concentration, \(n_{\rm i}*=n_{\rm i}/n_{\rm i}^{0},\) and net charge, n*K+−n*Cl−

Full size image

Due to the presence of the net charges outside the EDL, when the electric potential is applied along the channel length for electro-osmotic driven flow, the negative net charges present in the region outside the double layer are attracted to the anode while the positive net charges within the EDL are drawn to the cathode, as illustrated in Fig. 1. As a result, the traditional plug-like electroosmotic velocity profile is distorted in the region outside the EDL. Figure 4 shows the distorted flow field predicted by the developed model for a 1 mM solution in a 2 μm diameter channel, where negative net charges are present in the centre of the channel. The driving force occurs in the EDL due to the net positive charges, resulting in a non-dimensional velocity at the edge of the EDL close to 1, observed for both the tradition P-B model and the newly developed model here. Outside the EDL, the excess negative ions cause a flow in a direction opposite to that within the EDL that alters the velocity profile and reduces the area-average velocity. The amplitude of this reduction is dependent on the applied electrical potential, the concentration of the electrolyte solution, the valences of the electrolyte ions, and surface properties. For the particular case studied here, the developed model predicted a reduction of 3.5% in the area-average velocity as compared to that predicted by the traditional P-B model.

Fig. 4
figure 4

Comparison of model predicted non-dimensional velocity field, u*=u/Ueo, between the P-B theory and the developed model for a 1 mM KCl solution in a 2 μm diameter channel with −102 mV zeta potential

Full size image

It was found that Poisson-Boltzmann theory can only be applied to accurately predict fluid flow in channels when the non-dimensional Debye length is small. For a 1 mM KCl solution in a 15 μm diameter channel with a −102 mV zeta potential, a small difference in the model-predicted potential field and concentration field between the P-B model and the developed model was observed. For dimensions below this the developed model should be applied to account for the ion distribution effects on the velocity field. The negative net charge density is very small outside the EDL for the 15 μm diameter channel (−0.005 non-dimensional charge density in the centre of the channel), and does not become a major factor until the non-dimensional Debye length reaches 0.02. Figure 5 shows the area-averaged velocity as a function of the non-dimensional Debye length predicted by the developed model. At non-dimensional Debye lengths above 0.02, the area–average velocity decreases significantly. A 19% decrease in area–average velocity is observed from a non-dimensional Debye length of 0.025 to a length of 0.25. This indicates that the ion distribution has an increasing effect on the velocity as the EDL thickness increases relative to the channel diameter. It also implies that the continuum mechanics might not be valid when the channel diameter is smaller than 1 μm. However, further validation of this statement requires extensive theoretical and experimental investigations later. At low non-dimensional Debye lengths, the average velocity becomes stable as the EDL effects are reduced in significance. This trend agrees with the experimental results reported by Pennathur and Santiago (2004). The simulation predicted area-average velocity for the same non-dimensional Debye length is higher than their experimental results. This may be attributed to the use of an ideal solution model instead of the buffer solution mixtures in the experiments. Buffer solutions normally have multivalent ions, which are found to reduce the electroosmotic flow significantly (Zheng et al. 2003).

Fig. 5
figure 5

Model prediction of area–averaged velocity as a function of non-dimensional Debye length for a 1 mM KCL solution in different channels with −102 mV zeta potential

Full size image

Increasing the non-dimensional Debye length can be achieved by decreasing the channel diameter while holding the solution concentration constant or by reducing the ionic concentration for a given channel diameter. Figure 6 displays the velocity field for the latter of the two methods for 1 mM, 5 mM, and 10 mM KCl solutions in a 100-nm channel diameter. The higher concentrations, with a lower zeta potential, attract less positive ions to the wall and therefore have a reduced number of negative net charges in the channel centre. This results in a velocity profile closer to that predicted by the P-B theory. A 4% decrease in area-averaged velocity is observed from the 10 mM KCl solution to the 1 mM solution.

Fig. 6
figure 6

Model predicted non-dimensional velocity field for 1 mM, 5 mM, 10 mM KCl solutions in a 100-nm diameter channel. The corresponding zeta potentials are −102-mV, −78-mV, and −68-mV (Mc Donald et al. 2000)

Full size image

4 Summary

The Boltzmann distribution is not valid for ionic concentration distribution of electrolyte solutions in a nanofluidic channel, where the double layer extends a significant distance into the channel. The Nernst equation for ionic distribution in nanometer scale cylindrical channels was applied in the developed model to determine the effects of excess negative ions outside the EDL layer on the velocity field of electroosmotic driven flow. Significant reductions in area-average velocity were observed at high non-dimensional Debye lengths (above 0.02). The velocity field for small channels differed from the conventional Poisson-Boltzmann theory with a reduced velocity profile in the centre of the channel. The area–average velocity reaches a steady value as the Debye length decreases and the EDL effects become less significant.