1 Introduction

Piezoelectric microstructures have gained significant attention in the field of micro-sized devices and systems, including micro energy harvesters, microsensors, and microactuators [1]. The performance of these microdevices relies on the electromechanical coupling properties of piezoelectric microcomponents. However, as the characteristic sizes of piezoelectric structures reach microns and sub-microns, their properties exhibit notable deviations from macro-scale behavior. Experimental studies have revealed size-dependent electromechanical coupling behaviors in piezoelectric microstructures. For instance, Bühlmann et al. [2] observed a significant increase in the piezoelectric response for lateral dimensions below 300 nm in lead zirconate titanate (PZT) films. Huang et al. [3] reported a substantial enhancement in the effective piezoelectric coefficient and electric energy density of barium strontium titanate (BST) cantilever microbeams with decreasing beam thickness. These size-dependent phenomena remain unexplained by classical continuum theories of piezoelectricity.

To explain the size-dependent mechanical behavior of microstructures, a variety of high-order continuum theories, including those of high-order elastic deformation, have been developed, such as couple stress theory and strain gradient theory. Couple stress analysis can be categorized into the initiated version and the modified version. As for the initiated couple stress theory, Mindlin [4] introduced rotation gradients into the strain energy of the structure. Subsequently, Yang [5] developed a modified couple stress theory, which considers only the symmetric components of rotation gradients on this basis. As for strain gradient theory, the earliest version was proposed by Mindlin [6] by introducing the first gradient of strain into the strain energy. On this basis, Lam et al. [7] put forward the modified strain gradient theory, where the components of strain gradients corresponding to the antisymmetric rotation gradients in the strain energy are ignored. In addition, Aifantis [8] established a simple strain gradient theory with only one material scale length parameter for isotropic materials. Zhou et al. [9] reformulated Mindlin’s first-order strain gradient elasticity theory and introduced an isotropic strain gradient model containing only three independent length parameters. Because this equation does not need any assumptions or approximation conditions, it can be regarded as a generalized strain gradient theory [10]. It should be pointed out that the couple stress theory, Aifantis’s simple theory and the modified strain gradient theory are specific cases of the generalized strain gradient theory [11]. The above-mentioned high-order theories have been widely used in the numerical simulation of microstructures, such as microbeams, microplates, and microshells.

Recently, high-order theories incorporating piezoelectric effects based on electromechanical formulation have been employed to model electromechanical responses in piezoelectric microstructures. For instance, Korayem et al. [12] applied the couple stress theory to model the performance of atomic force microscopy with a piezoelectric microcantilever. Arefi and Zenkour [13] analyzed the vibration, wave transmission, and static bending characteristics of Timoshenko sandwich microbeams made of functionally graded piezoelectric materials using the modified strain gradient theory.

All the aforementioned studies have primarily relied on simplified strain gradient theories that neglect certain components of strain gradients, leading to inaccurate predictions of size effects in small-scale structures [11]. In this study, a model based on the generalized strain gradient theory is proposed to investigate the size-dependent static characteristics of bilayer piezoelectric microbeams [9]. On this basis, the constitutive equations incorporating strain gradients for transversely isotropic piezoelectric materials are given. Basic equations for obtaining analytic solutions of bilayer piezoelectric cantilever beams are derived using the variational method. Then, the electromechanical responses of a piezoelectric–elastic bilayer cantilever under force load and voltage load are determined, respectively. The results obtained using different strain gradient theories are analyzed to reveal the contribution of strain gradient components.

2 Constitutive Relations for Piezoelectric Materials with Strain Gradient Effects

The present study develops a model for piezoelectric bilayer microbeams based on the general strain gradient theory in [9], which is appropriate for linear elastic materials. In the following, we recall the principal results of the constitutive relations in this theory. The expression for the strain energy density in the strain gradient elasticity theory is as follows:

$$ U_{0} = \frac{1}{2}\sigma_{ij} \varepsilon_{ij} + \frac{1}{2}\tau_{ijk} \eta_{ijk} $$
(1)

where σij is the classical Cauchy stress tensor, εij is the strain tensor, ηijk is the strain gradient tensor whose last two indices satisfy the subsymmetric condition, and τijk is the higher-order stress tensor work conjugated with the strain gradient tensor. The definitions of the strain tensor and the strain gradient tensor are as follows

$$ \varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right) $$
(2)
$$ \eta_{ijk} = \varepsilon_{jk,i} = \frac{1}{2}\left( {u_{j,ki} + u_{k,ji} } \right) $$
(3)

Here, \(u_{i}\) is the displacement vector, and the comma denotes partial differentiation of the coordinates. The constitutive relations derived from the strain energy density are as follows [9]

$$ \sigma_{ij} = \frac{{\partial U_{0} }}{{\partial \varepsilon_{ij} }} = C_{ijkl} \varepsilon_{kl} $$
(4)
$$ \tau_{ijk} = \frac{{\partial U_{0} }}{{\partial \eta_{ijk} }} = g_{ijklpq} \eta_{lpq} $$
(5)

in which Cijkl denotes the conventional material elastic tensor, and gijklpq represents the material elastic length-scale tensor linked with the strain gradient effects.

For isotropic materials, the convectional elastic tensor only has two Lame constants λ and μ, while the material elastic length-scale tensor only contains three independent length scale parameters l0, l1, and l2 for a general case. Thus, the expressions of constitutive relations (4) and (5) using Lame constants and the independent length-scale parameters can be rewritten, respectively, as follows [9]

$$ \sigma_{ij} = \lambda \delta_{ij} \varepsilon_{nn} + 2\mu \varepsilon_{ij} $$
(6)
$$ \begin{aligned} \tau_{ijk} = & \mu \Bigg[\left( {\frac{9}{5}l_{0}^{2} - \frac{4}{15}l_{1}^{2} - l_{2}^{2} } \right)\left( {\delta_{ij} \eta_{nnk} + \delta_{ik} \eta_{nnj} } \right) \\ & - \left( {\frac{3}{5}l_{0}^{2} + \frac{2}{15}l_{1}^{2} - l_{2}^{2} } \right)\left({\delta_{ij} \eta_{knn} + \delta_{ik} \eta_{jnn} + 2\delta_{jk} \eta_{inn} } \right) \\ &+ \left(\frac{12}{5}l_{0}^{2} - \frac{2}{15}l_{1}^{2} - 2l_{2}^{2}\right)\delta_{jk} \eta_{nni} + \left( {\frac{2}{3}l_{1}^{2} + 4l_{2}^{2} } \right)\eta_{ijk}\\ & + \left( {\frac{2}{3}l_{1}^{2} - 2l_{2}^{2} }\right)\left( {\eta_{kij} + \eta_{jik} } \right)\Bigg] \\ \end{aligned} $$
(7)

The above constitutive relations are the general form of strain gradient elasticity theory, involving all components of the strain gradient tensor. When ignoring certain parts of the strain gradient tensor, the current form can be reduced to various forms of simplified strain gradient elasticity theory [11]. For instance, by disregarding the symmetric components, the general theory with three length-scale parameters simplifies to the initial couple stress theory containing two parameters.

By introducing the electric term into the strain energy density (1) of the general strain gradient theory, we can obtain the electric enthalpy function of a piezoelectric solid which incorporates the effects of strain gradient as follows:

$$ H = \frac{1}{2}\sigma_{ij} \varepsilon_{ij} + \frac{1}{2}\tau_{ijk} \eta_{ijk} - \frac{1}{2}E_{i} D_{i} $$
(8)

where Di is the electric displacement vector, and Ei is the electric field vector defined by

$$ E_{i} = - \varphi_{,i} $$
(9)

in which φ denotes the electric potential function. Considering the coupling actions between strain and electric field, the constitutive relations of linear elastic piezoelectric materials based on the general strain gradient theory are derived from Eq. (8) as

$$ \sigma_{ij} = C_{ijkl}^{\text{E}} \varepsilon_{kl} - e_{kij} E_{k} $$
(10)
$$ \tau_{ijk} = g_{ijklpq} \eta_{lpq} $$
(11)
$$ D_{i} = e_{ikl} \varepsilon_{kl} + k_{ik}^{\text{S}} E_{k} $$
(12)

where \(C_{ijkl}^{\text{E}}\), \(e_{kij}\), \(g_{ijklpq}\), and \(k_{ik}^{\text{S}}\) denote the elastic, piezoelectric, elastic length-scale, and dielectric constant tensors, respectively. The independent parameters of these material constant tensors vary for different classes of piezoelectric crystalline materials and can be provided accordingly. For transversely isotropic piezoelectric materials, all tensors in the constitutive relations (10–12), both the variable tensors and material constant tensors, can be decomposed into two orthogonal parts in the main direction and plane of transverse isotropy, respectively. The complete representations of these components using elementary tensors attached to the main direction and plane of transverse isotropy are detailed in Appendix A. Then, the constitutive relations of these tensors are rewritten in component form as

$$ \sigma_{ij} = C_{ijkl}^{\text{En}} \varepsilon_{kl}^{\text{n}} + C_{ijkl}^{\text{Et}} \varepsilon_{kl}^{\text{t}} - e_{kij}^{\text{n}} E_{k}^{\text{n}} - e_{kij}^{\text{t}} E_{k}^{\text{t}} $$
(13)
$$ \tau_{ijk} = g_{ijklpq}^{\text{n}} \eta_{lpq}^{\text{n}} + g_{ijklpq}^{\text{t}} \eta_{lpq}^{\text{t}} $$
(14)
$$ D_{i} = e_{ikl}^{\text{n}} \varepsilon_{kl}^{\text{n}} + e_{ikl}^{\text{t}} \varepsilon_{kl}^{\text{t}} + k_{ik}^{\text{Sn}} E_{k}^{\text{n}} + k_{ik}^{\text{St}} E_{k}^{\text{t}} $$
(15)

in which the superscripts ‘n’ and ‘t’ denote the components of tensors attached to the main direction and plane of transverse isotropy, respectively. It turns out that the components with the superscript ‘t’ are isotropic because the material properties are isotropic in the plane of transverse isotropy.

3 Size-Dependent Models of Bilayer Microbeams

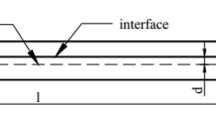
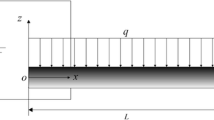
A rectangular bilayer microbeam composed of a transversely isotropic piezoelectric upper layer with a thickness of h1 and an isotropic elastic lower layer with a thickness of h2 is considered. As can be seen in Fig. 1, the size of the miniature beam is determined by its total thickness (H= h1 + h2), length L, and width B. In the Cartesian coordinate system, a transversely isotropic plane with the length and width aligning uniformly with the x- and y-axes, and the thickness along the z-axis. The zero-strain axis is indicated by the dashed line, also known as the physical neutral axis. For a slender beam with strain gradient effects, the location of the zero-strain axis is unknown. On this basis, a new method for locating the zero-strain axis is proposed. Therefore, in the Euler–Bernoulli beam method, a displacement component is used [14]

$$ u = u_{0} (x) - z\frac{{{\text{d}}w(x)}}{{{\text{d}}x}},\;v = 0,\;w = w(x) $$
(16)

where u, v, and w are displacements in the x-, y-, and z- directions, respectively, \(u_{0} (x) = - d(x)\), and dw(x)/dx is the axial displacement at z = 0, with d(x) representing the derivation from the physical neutral axis to the x-axis, and w(x) depicting beam deflection at the neutral axis. The non-vanishing parts of the strain and its gradients derived from Eqs. (2) and (3) are as follows:

$$ \varepsilon_{xx} = \frac{{{\text{d}}u_{0} }}{{{\text{d}}x}} - z\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} $$
(17)
$$ \eta_{xxx} = \frac{{{\text{d}}^{2} u_{0} }}{{{\text{d}}x^{2} }} - z\frac{{{\text{d}}^{3} w}}{{{\text{d}}x^{3} }} $$
(18)
$$ \eta_{zxx} = - \frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} $$
(19)
Fig. 1
figure 1

Schematic of a bilayer piezoelectric microbeam

Full size image

By substituting Eqs. (17–19) into Eqs. (6) and (7), the stress and the higher-order stress are obtained, respectively. On this basis, the energy density of the elastic lower layer is expressed as

$$ U_{0} = \frac{1}{2}E\varepsilon_{xx} \varepsilon_{xx} + \frac{1}{5}\mu \left( {9l_{0}^{2} + 2l_{1}^{2} } \right)\eta_{xxx} \eta_{xxx} + 2\mu \left( {\frac{6}{5}l_{0}^{2} + \frac{4}{15}l_{1}^{2} + l_{2}^{2} } \right)\eta_{zxx} \eta_{zxx} $$
(20)

where E is the material modulus. For the piezoelectric layer, non-vanishing terms of strain and strain gradients attached to the direction and plane of transverse isotropy are derived from Eqs. (A1–A6) in Appendix A as

$$ \varepsilon_{xx}^{\text{t}} = \varepsilon_{xx} ,\eta_{xxx}^{\text{t}} = \eta_{xxx} ,\eta_{zxx}^{\text{n}} = \eta_{zxx} $$
(21)

For a slender beam, the electric field Ez of the piezoelectric layer is mainly distributed in the thickness direction, while compositions in other directions can be ignored. Then, non-vanishing stress and electric displacement can be derived from Eqs. (10–12) as

$$ \sigma_{xx}^{\text{t}} = C_{11} \varepsilon_{xx} - e_{31} E_{z} $$
(22)
$$ D_{z}^{\text{n}} = e_{31} \varepsilon_{xx} + k_{33} E_{z} $$
(23)

and non-vanishing high-order stresses from Eq. (14) as

$$ \tau_{xxx}^{\text{t}} = g_{111111}^{\text{t}} \eta_{xxx} $$
(24)
$$ \tau_{zxx}^{\text{n}} = g_{311311}^{\text{n}} \eta_{zxx} $$
(25)

Following [9], we let \(g_{111111}^{\text{t}} = 2 (C_{11} - C_{12}) (9l_{\text{t}0}^{2} + 2l_{\text{t}1}^{2} )/5\) and \(g_{311311}^{\text{n}} = 2C_{44} l_{\text{n}}^{2}\), where \(l_{{{\text{t}}0}}\), \(l_{{{\text{t}}1}}\), and \(l_{{\text{n}}}\) are the length-scale parameters of the transversely isotropic piezoelectric materials in the isotropic plane and main direction of transverse isotropy, respectively.

Substituting Eqs. (21–25) into Eq. (8) yields the electric enthalpy of the piezoelectric upper layer as

$$ H_{0} = \frac{1}{2}C_{11} \varepsilon_{xx} \varepsilon_{xx} - e_{31} E_{z} \varepsilon_{xx} + \frac{1}{5}\left( {C_{11} - C_{12} } \right)\left( {9l_{{\text{t}}0}^{2} + 2l_{{\text{t}}1}^{2} } \right)\eta_{xxx} \eta_{xxx} + C_{44} l_{{\text{n}}}^{2} \eta_{zxx} \eta_{zxx} - \frac{1}{2}k_{33} E_{z} E_{z} $$
(26)

The total electric enthalpy of the bilayer beams is

$$ H = B\int_{0}^{L} {\int_{{ - h_{2} }}^{0} {U_{0} } } {\text{d}}z{\text{d}}x + B\int_{0}^{L} {\int_{0}^{{h_{1} }} {H_{0} } } {\text{d}}z{\text{d}}x $$
(27)

The work done by external force loads and electric loads is

$$ W = \int_{0}^{L} {pw} {\text{d}}x + Qw\left| {_{0}^{L} } \right. + Mw^{\prime}\left| {_{0}^{L} } \right. + M^{\text{h}} w^{\prime\prime}\left| {_{0}^{L} } \right. + Nu_{0} \left| {_{0}^{L} } \right. + N^{\text{h}} u_{0} ^{\prime}\left| {_{0}^{L} } \right. - B\int_{0}^{L} {q\varphi \left| {_{0}^{{{\text{h}}_{1} }} } \right.} {\text{d}}x $$
(28)

where p is the distributed load, Q, M, Mh, N, and Nh are the shear force, bending moment, higher-order bending moment, axial force, and higher-order axial force at the end of beams, and q is the electric charge density at the top and bottom surfaces of the piezoelectric layer. The apostrophe denotes the first derivative of x, and the double apostrophe denotes the second derivative of x.

The mechanical and electrostatic equilibrium of the bilayer beam requires the following variational equation

$$ \delta (H - W) = 0 $$
(29)

By substituting Eqs. (20) and (26) into Eq. (27) and calculating the variational equation, we obtain the governing equations

$$ k_{33} \varphi_{,zz} + e_{31} w^{\prime\prime} = 0 $$
(30)
$$ a_{5} u_{0}^{(5)} - a_{3} u_{0}^{(3)} + a_{4} w^{(4)} - a_{6} w^{(6)} - p = 0 $$
(31)
$$ a_{1} u_{0} ^{\prime\prime} - a_{2} u_{0}^{(4)} - a_{3} w^{(3)} + a_{5} w^{(5)} = 0 $$
(32)

and the boundary conditions as

$$ \left( {e_{31} u_{0} ^{\prime} - e_{31} \frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }}z - k_{33} \varphi_{,z} + q} \right)\delta \varphi \left| {_{0}^{{h_{1} }} } \right. = 0 $$
(33)
$$ \left( {a_{1} u_{0} ^{\prime} - a_{2} u_{0}^{(3)} - a_{3} w^{\prime\prime} + a_{5} w^{(4)} + Be_{31} \int_{0}^{{h_{1} }} {\varphi_{,z} {\text{d}}z} - N} \right)\delta u_{0} \left| {_{0}^{L} } \right. = 0 $$
(34)
$$ \left( {a_{2} u_{0} ^{\prime\prime} - a_{5} w_{{}}^{(3)} - N^{(\text{h})} } \right)\delta u_{0} ^{\prime}\left| {_{0}^{L} } \right. = 0 $$
(35)
$$ \left( {a_{3} u_{0} ^{\prime\prime} - a_{5} u_{0}^{(4)} - a_{4} w^{(3)} + a_{6} w^{(5)} - Q} \right)\delta w\left| {_{0}^{L} } \right. = 0 $$
(36)
$$ \left( { - a_{3} u_{0} ^{\prime} + a_{5} u_{0}^{(3)} + a_{4} w^{\prime\prime} - a_{6} w^{(4)} - Be_{31} \int_{0}^{{h_{1} }} {z\varphi_{z} } {\text{d}}z - M} \right)\delta w^{\prime}\left| {_{0}^{L} } \right. = 0 $$
(37)
$$ \left( {a_{6} w^{(3)} - a_{5} u_{0} ^{\prime\prime} - M^{\text{h}} } \right)\delta w^{\prime\prime}\left| {_{0}^{L} } \right. = 0 $$
(38)

in which \(u_{0}^{(n)}\) and \(w^{(n)}\) (n = 3, 4, 5, 6) are the n-th derivatives of \(u_{0}\) and \(w\) with respect to x, respectively, and the constants are

$$ a_{1} = C_{11} Bh_{1} + EBh_{2} ,\;a_{2} = b_{1} Bh_{1} + b_{2} Bh_{2} $$
$$ \begin{gathered} a_{3} = \frac{1}{2}C_{11} Bh_{1}^{2} - \frac{1}{2}EBh_{2}^{2} \hfill \\ a_{4} = 2C_{44} l_{n}^{2} Bh_{1} + b_{3} Bh_{2} + \frac{1}{3}C_{11} Bh_{1}^{3} + \frac{1}{3}EBh_{2}^{3} \hfill \\ a_{5} = \frac{1}{2}b_{1} Bh_{1}^{2} - \frac{1}{2}b_{2} Bh_{2}^{2} ,\;a_{6} = \frac{1}{3}b_{1} Bh_{1}^{3} + \frac{1}{3}b_{2} Bh_{2}^{3} \hfill \\ \end{gathered} $$
(39)

with

$$ b_{1} = \frac{2}{5}\left( {C_{11} - C_{12} } \right)\left( {9l_{\text{t0}}^{2} + 2l_{\text{t1}}^{2} } \right),\;b_{2} = \frac{2}{5}\mu \left( {9l_{0}^{2} + 2l_{1}^{2} } \right),\;b_{3} = 2\mu \left( {\frac{6}{5}l_{0}^{2} + \frac{4}{15}l_{1}^{2} + l_{2}^{2} } \right) $$
(40)

So far, a general model of the bilayer piezoelectric microbeams based on the general strain gradient theory has been established. The general strain gradient theory can be reduced to the simplified theory by ignoring certain components of strain gradient [11]. On this basis, the general model can be simplified further based on the simplified theory including only one length-scale parameter [8]. This simplification is achieved by appropriately selecting the constants in Eq. (39) as

$$ b_{1} = 2\left( {C_{11} - C_{12} } \right)l_{\text{st}}^{2} ,\;b_{2} = b_{3} = \frac{2\mu (1 - v)}{{(1 - 2v)}}l_{\text{s}}^{2} $$
(41)

where lst and ls are the length-scale parameters of the transversely isotropic piezoelectric layer and the isotropic elastic layer for the simplified strain gradient theory, respectively.

Moreover, if all material length-scale parameters for the general model are taken as zero, meaning that the strain gradient effects are neglected, the relations a2 = a5 = a6 = 0 and \(a_{4} = \tfrac{1}{3}C_{11} Bh_{1}^{3} + \tfrac{1}{3}EBh_{2}^{3}\) hold true. Additionally, the derivation between the zero-strain axis and the x-axis \(d = - a_{3} /a_{1}\) is a constant, and the axial displacement \(u_{0} \left( x \right)\) at \(z = 0\) is related to the deflection w(x) by \(- d \cdot {\text{d}}w(x)/{\text{d}}x\). In this case, the general model reduces to the model of bilayer piezoelectric beams based on conventional elastic and piezoelectric theories. The corresponding governing equations are given by

$$ k_{33} \varphi_{,zz} + e_{31} w^{\prime\prime} = 0 $$
(42)
$$ (EI)_{\text{e}} w^{(4)} - p = 0 $$
(43)

and the boundary conditions become

$$ [e_{31} \frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }}(d + z) + k_{33} \varphi_{,z} - q]\delta \varphi \left| {_{0}^{{h_{1} }} } \right. = 0 $$
(44)
$$ [(EI)_{\text{e}} w^{\prime\prime} - Be_{31} \int_{0}^{{h_{1} }} {(d + z)\varphi_{,z} } {\text{d}}z - M]\delta w^{\prime}\left| {_{0}^{L} } \right. = 0 $$
(45)
$$ [(EI)_{\text{e}} w^{(3)} + Q]\delta w\left| {_{0}^{L} } \right. = 0 $$
(46)

where \((EI)_{\text{e}} = \tfrac{1}{2}C_{11} Bh_{1}^{2} d - \tfrac{1}{2}EBh_{2}^{2} d + \tfrac{1}{3}C_{11} Bh_{1}^{3} + \tfrac{1}{3}EBh_{2}^{3}\) is the effective bending rigidity for bilayer microbeams of the classical piezoelectric theory.

4 Electromechanical Responses of Bilayer Cantilever Microbeams

This study focuses on the static bending of a bilayer piezoelectric cantilever microbeam subjected to force load at its free end and voltage load on its top surface, respectively.

4.1 A Bilayer Cantilever Piezoelectric Microbeam under a Force load at Its Free End

As shown in Fig. 1, a bilayer piezoelectric cantilever microbeam under force Q at the free end is considered. The zero point of electric potential is set at the interface between the upper and lower beams. For this case, the governing Eqs. (30–32) of the present model can be simply written as

$$ k_{33} \varphi_{,zz} + e_{31} w^{\prime\prime} = 0 $$
(47)
$$ a_{5} u_{0}^{(5)} - a_{3} u_{0}^{(3)} + a_{4} w^{(4)} - a_{6} w^{(6)} = 0 $$
(48)
$$ a_{1} u_{0} ^{\prime\prime} - a_{2} u_{0}^{(4)} - a_{3} w^{(3)} + a_{5} w^{(5)} = 0 $$
(49)

and the boundary conditions become

$$ \left( {e_{31} u_{0} ^{\prime} - e_{31} \frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }}z - k_{33} \varphi_{,z} } \right)\left| {_{{z = h_{1} }}^{{}} } \right. = 0,\quad \varphi \left| {_{z = 0}^{{}} } \right. = 0 $$
(50)
$$ \left( {a_{1} u_{0} ^{\prime} - a_{2} u_{0}^{(3)} - a_{3} w^{\prime\prime} + a_{5} w^{(4)} + Be_{31} \int_{0}^{{h_{1} }} {\varphi_{,z} {\text{d}}z} } \right)\left| {_{x = L}^{{}} } \right. = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} u_{0} \left| {_{x = 0}^{{}} } \right. = 0 $$
(51)
$$ \left( {a_{2} u_{0} ^{\prime\prime} - a_{5} w_{{}}^{(3)} } \right)\left| {_{x = L}^{{}} } \right. = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} u_{0} ^{\prime}\left| {_{x = 0}^{{}} } \right. = 0 $$
(52)
$$ \left( {a_{3} u_{0} ^{\prime\prime} - a_{5} u_{0}^{(4)} - a_{4} w^{(3)} + a_{6} w^{(5)} - Q} \right)\left| {_{x = L}^{{}} } \right. = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} w\left| {_{x = 0}^{{}} } \right. = 0 $$
(53)
$$ \left( { - a_{3} u_{0} ^{\prime} + a_{5} u_{0}^{(3)} + a_{4} w^{\prime\prime} - a_{6} w^{(4)} - Be_{31} \int_{0}^{{h_{1} }} {z\varphi_{,z} } {\text{d}}z} \right)\left| {_{x = L}^{{}} } \right. = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} w^{\prime}\left| {_{x = 0}^{{}} } \right. = 0 $$
(54)
$$ \left( {a_{6} w^{(3)} - a_{5} u_{0} ^{\prime\prime}} \right)\left| {_{x = 0}^{{}} } \right. = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} w^{\prime\prime}\left| {_{x = L}^{{}} } \right. = 0 $$
(55)

Solving the Gauss Eq. (47) with boundary conditions (50) gives the electric potential as follows

$$ \varphi = \frac{{e_{31} }}{{k_{33} }}\left( {u_{0} ^{\prime}z - \frac{1}{2}w^{\prime\prime}z^{2} } \right) = 0 $$
(56)

By solving the mechanical governing Eqs. (48) and (49), the solutions of displacements are obtained as:

$$ w = C_{1} + C_{2} x + C_{3} x^{2} + C_{4} x^{3} + C_{5} {\text{e}}^{{r_{1} x}} + C_{6} {\text{e}}^{{ - r_{1} x}} + C_{7} {\text{e}}^{{r_{2} x}} + C_{8} {\text{e}}^{{ - r_{2} x}} $$
(57)
$$ u_{0} = C_{9} + C_{10} x + \frac{{3a_{3} }}{{a_{1} }}C_{4} x^{2} + d_{1} C_{5} {\text{e}}^{{r_{1} x}} - d_{1} C_{6} {\text{e}}^{{ - r_{1} x}} + d_{2} C_{7} {\text{e}}^{{r_{2} x}} - d_{2} C_{8} {\text{e}}^{{ - r_{2} x}} $$
(58)

in which Ci (i = 1, 2 …10) are undetermined constants, and the parameters are

$$\begin{aligned} &r_{1} = [\frac{{ - g_{2} + (g_{2}^{2} - 4g_{1} g_{3} )^{{1/2}} }}{{2g_{1} }}]^{{1/2}} \\ &r_{2} = [\frac{{ - g_{2} - (g_{2}^{2} - 4g_{1} g_{3} )^{{1/2}} }}{{2g_{1} }}]^{{1/2}} \end{aligned}$$
(59)
$$ d_{1} = \frac{{a_{3} r_{1} - a_{5} r_{1}^{3} }}{{a_{1} - a_{2} r_{1}^{2} }},\;d_{2} = \frac{{a_{3} r_{2} - a_{5} r_{2}^{3} }}{{a_{1} - a_{2} r_{2}^{2} }} $$
(60)

with

$$ g_{1} = a_{5}^{2} - a_{2} a_{6} ,\;g_{2} = a_{2} a_{4} + a_{1} a_{6} - 2a_{3} a_{5} ,\;g_{3} = a_{3}^{2} - a_{1} a_{4} $$
(61)

Based on the reduced conditions of the general model to simplified models, the above solutions can also be reduced to those of simplified models. For example, the condition of setting material length scale parameters to be zero, that is, \(r_{1} = r_{2} = 0\), leads to the solution of the classical model as

$$ w_{\text{c}} = C_{1} + C_{2} x + C_{3} x^{2} + C_{4} x^{3} $$
(62)

For solutions (57) and (58) with strain gradient effects, the constants Ci (i = 1, 2 … 10) are determined using the boundary conditions (51–55). For the classical solution (62), the constants Ci (i = 1, 2 … 4) are determined using the boundary conditions (44–46). The results are given in Appendix B.

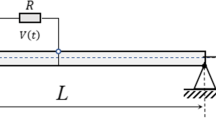
4.2 A Bilayer Piezoelectric Cantilever Microbeam Subjected to a Voltage on the Piezoelectric Layer

A bilayer piezoelectric cantilever microbeam is subjected to a voltage on the piezoelectric layer, as shown in Fig. 1. The zero point of electric potential is set at the interface between the upper and lower beams. In this scenario, the boundary conditions (50) and (53) are taken as follows, while the remaining boundary conditions and governing equations are the same as those of the previous problem.

$$ \varphi \left| {_{{z = h_{1} }}^{{}} } \right. = V,\begin{array}{*{20}c} {} & {} \\ \end{array} \varphi \left| {_{z = 0}^{{}} } \right. = 0 $$
(63)
$$ \left( {a_{3} u_{0} ^{\prime\prime} - a_{5} u_{0}^{(4)} - a_{4} w^{(3)} + a_{6} w^{(5)} } \right)\left| {_{x = L}^{{}} } \right. = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} w\left| {_{x = 0}^{{}} } \right. = 0 $$
(64)

The electric potential solution of Eq. (47) with condition (63) is obtained as

$$ \varphi = \frac{1}{2}\frac{{e_{31} }}{{k_{33} }}w^{\prime\prime}(h_{1} z - z^{2} ) + \frac{V}{{h_{1} }}z $$
(65)

The displacement solutions follow the same form as Eqs. (57) and (58). Different from the previous problem, in this case, the constants Ci (i = 1, 2 … 10) are determined using boundary conditions (51), (52), (54), (55), and (64). The result is also given in Appendix B.

5 Numerical Results and Discussion

To evaluate the bilayer piezoelectric cantilever microbeam models established in the previous section, this section presents some numerical examples. The material PZT-5H is chosen for the piezoelectric layer, with material constants e31 = − 6.5 N/(Vm), C11 = 126 GPa, C12 = 55 GPa, C44 = 35.3 GPa, and k33 = 13 × 10–9 N/V2. For the elastic layer made of Si, the material constants E = 166 GPa, μ = 166 GPa, and υ = 0.3 are considered. For simplicity, the material length scale parameters are taken as lt0 = lt1 = 1.2ln = lst = l for the piezoelectric layer and l0 = l1 = l2 = ls = 0.8 l for the elastic layer. The slenderness ratio L/h = 20 and width-to-thickness ratio B/h = 0.5 are considered, respectively.

5.1 Electric Responses of Bilayer Piezoelectric Beams under Mechanical Loads

The bilayer piezoelectric beam has the ability to generate electric potential when subjected to mechanical loads, making it an important feature for use in sensors and energy harvesting. To better understand the role of piezoelectricity and strain gradient, this study presents numerical results of the electric potential response of bilayer piezoelectric cantilevers subjected to free-end loading.

Figure 2 shows the relationship between normalized electric potential and piezoelectric layer thickness proportion while keeping total thickness constant. It can be seen that the changing trend of general strain gradient mode (GSGM) is similar to that of the classical mode in the change of induced electric potential. However, there is still a big difference. With the decrease of the maximum induced electric potential, the intrinsic thickness of the material does not change.

Fig. 2
figure 2

Induced electric potential of bilayer piezoelectric beams under force load

Full size image

In addition, the results also indicate that as the piezoelectric layer thickness increases, the normalized electric potential increases until achieving a maximum value when the zero-deviation is at the interface between the upper and lower beams, then decreases towards zero. This is because the deviation of the physical neutral axis from the interface decreases and approaches zero, then becomes more negative with the increase of piezoelectric layer thickness, as shown in Fig. 3. In the case of positive deviation, meaning the physical neutral axis is below the interface, the induced electric potential remains positive throughout the piezoelectric layer due to tension. In the case of negative deviation, where the physical neutral axis lies above the interface, part of the piezoelectric layer experiences compression. This leads to the generation of electric fields with opposite directions above and below the neutral axis, causing the overall electric potential to decrease.

Fig. 3
figure 3

Neutral axis derivation of bilayer piezoelectric beams

Full size image

Figure 4 displays dimensionless maximum induced electric potentials of various models versus dimensionless thickness, revealing noticeable size dependency in induced electric potential. Compared to classical methods, the induced electric potential of GSGM is lower, particularly at small H/l ratios. Additionally, the general model yields even smaller induced electric potentials than the simplified model.

Fig. 4
figure 4

Size-dependent electric potential of bilayer piezoelectric beams under force load (h1/H = 1:2)

Full size image

These findings suggest that the simplified model underestimates the size-dependent electromechanical response of microbeams due to neglecting partial strain gradients, while the general model effectively captures size dependence.

5.2 Mechanical Responses of Bilayer Piezoelectric Microbeams under Electric Loads

When a voltage is applied to the piezoelectric layer, the converse piezoelectric effect results in bending of bilayer piezoelectric beams. For a cantilever beam, the maximum deflection is at its free end.

To investigate the effect of piezoelectric layer thickness on the bending deformation, the maximum deflections predicted by different models versus the piezoelectric layer thickness are plotted in Fig. 5, where the applied voltage is 1 V. The results show that the deflections of both the GSGM and classical model rapidly increase in negative values with decreasing piezoelectric layer thickness. The GSGM exhibits smaller deflections than the classical model, particularly with decreasing dimensionless thickness, indicating size effects on the mechanical response of bilayer piezoelectric beams at small scales.

Fig. 5
figure 5

Variation of normalized maximum deflections with piezoelectric layer thickness when a 1 V voltage is applied

Full size image

Figure 6 presents the size dependency of deflection for a bilayer piezoelectric microbeam when a voltage is applied. Here, w(L) represents the deflections of GSGM and w0(L) represents the defection of the classical model. It is found that the deflection calculated by the strain gradient method is smaller than the traditional deflection as the dimensionless thickness H/l is small. For the strain gradient model, the deflection result of the general model is less than the simplified model.

Fig. 6
figure 6

Size dependency of normalized deflection for a bilayer piezoelectric microbeam

Full size image

6 Conclusions

In this study, we analyze the electromechanical properties of bilayer piezoelectric microbeams using the generalized stress gradient method. We describe the constitutive relations of transversely isotropic piezoelectric materials, which take into account the effects of strain gradient, represented by specific forms of transversely isotropic tensors. By utilizing the electric enthalpy variational approach, we derive the governing equations and boundary conditions for bilayer piezoelectric beams. We also develop formulas to calculate the induced potential and deformation of bilayer cantilever piezoelectric microbeams under force load and voltage load. Our findings show that the induced electric potential reaches its highest value at the intrinsic thickness under force load. In contrast, the generated deflection increases as the piezoelectric layer thickness decreases under a constant voltage. At small scales, the electric potential and deflection predicted by strain gradient models are lower than the classical model. The strain gradient models accurately capture the size-dependent electromechanical coupling characteristics of bilayer piezoelectric microbeams.