1 Introduction

The attraction of the solar power satellite system (SSPS) concept [1] designed to harvest clean energy from space-based solar-electric systems using wireless power transfer has captured the imagination of the government as well as private stakeholders because of its high efficiency, low operating cost as well as zero pollution. To realize the SSPS concept, many structural schemes for the SSPS have been proposed, which are comparable to one another.

Various studies of this concept were conducted during the 1970s, by NASA and the Department of Energy [2], which resulted in the 1979 Reference SPSS. The project named “Research on Concept, Structure and Technology of Space System” was set up in Europe, and the European Sail Tower concept—a gravity-gradient-stabilized, space-tether-based SSP concept—was proposed. The solar power satellite via arbitrarily large phased array [3] was proposed by NASA, and the associated project approachment studies were reported widely [4]. Recently, the \(\Omega \) concept was suggested by Prof. Duan [5], which has aroused considerable interest of the Qian Xuesen Laboratory of Space Technology.

However, there is no doubt that proposing a new SPSS concept is easier than demonstrating its feasibility. During the feasibility demonstration, the controllability and the control strategy design are two main tasks for the associated researchers before a new SPSS concept is proposed. Even if the proposed SPSS concept is controllable, the control energy determined mainly by the control strategy and the structural parameters should be minimal to save the fuel carried by the SPSS, which implies that optimizing the structural form and the control strategy to seek the minimum control energy is an important task in the structural/control design of the SPSS. However, the above SPSS concepts diverse in the structural forms, which suggests that it is difficult to develop a uniform approach to determine the minimum control energy for these SPSS concepts. Thus, in this work, only a typical structural component (beam) in the SPSS will be considered.

Certainly, the minimum control time is another objective considered in the process of the control strategy design. The minimum time control approach was developed and applied on spacecraft attitude tentatively to reduce the control time. Pao [6] considered the time-optimal control problem for rest-to-rest maneuvers of flexible spatial structures and presented some analytical results for the number of control switches for the one-bending-mode case. Liu et al. [7] proposed a near-minimum-time feedback control law for the agile satellite attitude control system. Zhu et al. [8] investigated the minimal time problem for the guidance of a rocket and revealed the existence of singular arcs of higher order in the optimal synthesis that causes the occurrence of a chattering phenomenon. Eldad et al. [9] developed a new algorithm for large-angle pitch maneuvers of deformable solar sails in minimum time recently.

Choosing the spatial beam as a typical component to study the minimum control energy in this work is based on the consideration that in the above SPSS concepts, there are many components that can be simplified as slender structures. For example, the long-span framework, the main load-carrying component of the solar receiver, can be simplified as the spatial flexible beam, which implies that the slender component is a basic model in the SPSS. Thus, the controllability and the control strategy of the slender component (such as the spatial beam) are important in the argument of the structural scheme for the SPSS.

There are amount of studies discussing the nonlinear dynamic behaviors of spatial beams. da Silva and Zaretzky [10] presented the nonlinear differential equations controlling the coupling motions of the beam capable of undergoing bending and pitching in space and studied the coupled nonlinear pitch-bending response of the beam in a circular orbit [11]. Chen and Agar [12] proposed an Lagrangian formulation of the spatial beam element for a purely geometric nonlinear analysis, in which the geometric stiffness matrix was expressed by either a one-dimensional integration of the stress resultants or a closed form of element-end forces. Quadrelli and Atluri [13] presented a general finite-element formulation for the dynamic analysis of spatial elastic beams with small strains in a multi-body configuration. Yang et al. [14] established a finite-element model for a flexible hub-beam system with a tip mass considering the viscous damping and the air drag force. Cai and Lim [15] studied dynamics of a flexible hub-beam system using a first-order approximation coupling model and the assumed mode discretization method. Zhang et al. [16] developed a two-node spatial beam element with the Euler–Bernoulli assumption for the nonlinear dynamic analysis of slender beams undergoing arbitrary rigid motions and large deformations. Yin et al. [17] presented a Hamiltonian formulation for the rigid model of the spatial beam and developed the symplectic method for it. Hu et al. [18,19,20,21,22,23] improved the above Hamiltonian formulation for the spatial flexible damping beam and developed the structure-preserving method for it based on the generalized multi-symplectic method.

In the above references, it has been proved that ignoring the flexibility and the damping effect of the spatial beam can accelerate the analysis speed of the method employed. Unfortunately, such simplifications may result in some deviations in the dynamic analysis of practical structures. In this work, the difference of the minimum control energy for the spatial beam model with the assumed attitude adjustment target between the models considering and ignoring the flexibility and the damping effect will be investigated in detail by the structure-preserving method.

Fig. 1
figure 1

Dynamic model of spatial beam

Full size image

2 Dynamic Model of Spatial Beam

In this section, the dynamic model of the spatial beam will be reviewed and the preliminary theoretical analysis on the minimum control energy of the spatial beam will be presented.

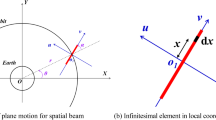
In our previous studies [18, 19, 24], a homogeneous spatial flexible beam moving in the XOY plane (with both the deformation and the motion out of the XOY plane ignored) was considered (see Fig. 1). In this paper, considering the flexibility as well as the non-sphere perturbation [19], the Lagrangian function of the spatial beam can be formulated by the state vector \([r,\;\alpha ,\;\theta ,\;u]^{\mathrm{T}}\),

$$\begin{aligned} L= & {} \frac{\rho l}{2}[{\dot{r}}^{2}+(r{\dot{\theta }})^{2}]\hbox {+}\frac{1}{2}\frac{\rho l^{3}}{12}({\dot{\theta }}+{\dot{\alpha }})^{2}+\frac{\rho }{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {[\partial _t^2 u+u^{2}({\dot{\theta }}+{\dot{\alpha }})^{2}]\hbox {d}x} \nonumber \\&+\,\frac{\mu \rho l}{r}-\frac{\mu \rho l^{3}}{24r^{3}}(1-3\cos ^{2}\alpha )+\frac{\mu J_2 R_e ^{2}\rho l}{2r^{3}}+\frac{3\mu J_{22} R_e ^{2}\rho l}{r^{3}}-\frac{EI}{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\partial _{xx}^2 u\hbox {d}x} \end{aligned}$$
(1)

in which \(r=r(t)=\left| {Oo_1 } \right| \) is the orbit radius, \(\theta =\theta (t)\) is the orbit true anomaly of the center of mass, \(\alpha =\alpha (t)\) is the attitude angle describing the attitude of the beam, \(u=u(x,t)\) is the transverse displacement in the local coordinate system \(uo_1 v\) denoting the transverse vibration induced by the plane motion of the beam when the flexibility of the spatial beam is considered, \(\rho \) and l represent the linear density and the length of the beam, respectively, \(\mu \) is the gravitational constant of the Earth, \(J_2 \) and \(J_{22}\) denote the coefficients of the Earth’s zonal harmonic term and tesseral harmonic term, respectively, \(R_e\) is the average equatorial radius of the Earth, and EI is the flexural stiffness when the flexibility of the spatial beam is considered.

Then, the plane motion and the transverse vibration of the spatial flexible beam with damping can be controlled by [19],

$$\begin{aligned}&\left\{ {\begin{array}{l}\displaystyle -\rho l\ddot{r}+\rho lr{\dot{\theta }}^{2}-\frac{\mu \rho l}{r^{2}}+\frac{\mu \rho l^{3}}{8r^{4}}(1-3\cos ^{2}\alpha )-\frac{3\mu J_2 R_e ^{2}\rho l}{2r^{4}}-\frac{9\mu J_{22} R_e ^{2}\rho l}{r^{4}}=0 \\ \displaystyle \rho lr^{2}\ddot{\theta }+2\rho lr{\dot{r}}{\dot{\theta }}+\frac{\rho l^{3}}{12}(\ddot{\theta }+\ddot{\alpha })+\rho \int _{-\frac{l}{2}}^{\frac{l}{2}} {[2u\partial _t u({\dot{\theta }}+{\dot{\alpha }})+u^{2}(\ddot{\theta }+\ddot{\alpha })]\hbox {d}x} =0 \\ \displaystyle \frac{\rho l^{3}}{12}(\ddot{\theta }+\ddot{\alpha })+\frac{\mu \rho l^{3}}{4r^{3}}\cos \alpha \sin \alpha +\rho \int _{-\frac{l}{2}}^{\frac{l}{2}} {[2u\partial _t u({\dot{\theta }}+{\dot{\alpha }})+u^{2}(\ddot{\theta }+\ddot{\alpha })]\hbox {d}x} =0 \\ \end{array}} \right. \end{aligned}$$
(2)
$$\begin{aligned}&\rho \partial _{tt} u+c\partial _t u-\rho u({\dot{\theta }}+{\dot{\alpha }})^{2}+EI\partial _{xxxx} u=0 \end{aligned}$$
(3)

Here c is the damping factor of the beam.

It has been proved that there are two stable attitude states for dynamic system (2)–(3). One is the stable attitude angle \(\alpha =0\), and the other is the stable attitude angle \(\alpha =\frac{\pi }{2}\) [18, 19] employing the structure-preserving method [20,21,22,23,24,25,26]. Only the stable attitude state \(\alpha =0\) is considered in this paper, because the subsequent simplified system only has this stable attitude state when the flexibility and damping of the spatial beam are ignored. For system (2)–(3), there are a variety of attitude adjustment strategies reported, which can be employed to unify the attitude of system (2)–(3) into one of the stable attitude states. The typical strategies include that reaction/momentum wheels are assembled to provide continuous control action according to the desired torque profile for attitude control, and as on-off devices, thrusters are normally capable of providing the fixed torque [27]. To simplify the practical engineering problems, the concrete attitude adjustment strategy will not be discussed in detail. However, the energy loss of the system during the transient process (i.e., the period from the initial state to the assumed stable attitude state) for system (2)–(3) with certain parameters is independent of the specific adjustment strategy and will be studied in this work, which is named the minimum control energy of the spatial beam with the assumed attitude adjustment target.

As mentioned above, the minimum control energy is the difference between the initial total energy and the total energy in the stable attitude state of system (2)–(3). If the flexibility and damping of the beam is considered, the minimum control energy is,

$$\begin{aligned} \Delta E_1= & {} \frac{\rho l}{2}[{\dot{r}}_0^2 +(r_0 {\dot{\theta }}_0 )^{2}]+\frac{1}{2}\frac{\rho l^{3}}{12}({\dot{\theta }}_0 +{\dot{\alpha }}_0 )^{2}+\frac{\rho }{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {[\left. {\partial _t^2 u} \right| _{t=0} +u_0^2 ({\dot{\theta }}_0+{\dot{\alpha }}_0 )^{2}]\hbox {d}x} \nonumber \\&-\,\frac{\mu \rho l}{r_0 }+\frac{\mu \rho l^{3}}{24r_0^3 }(1-3\cos ^{2}\alpha _0 )-\frac{\mu J_2 R_e ^{2}\rho l}{2r_0^3 }-\frac{3\mu J_{22} R_e ^{2}\rho l}{r_0^3 }+\left. {\frac{EI}{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\partial _{xx}^2 u\hbox {d}x} } \right| _{t=0} \nonumber \\&-\,\frac{\rho l}{2}[{\dot{r}}_s^2 +(r_s {\dot{\theta }}_s )^{2}]-\frac{1}{2}\frac{\rho l^{3}}{12}({\dot{\theta }}_s +{\dot{\alpha }}_s )^{2}-\frac{\rho }{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {[\left. {\partial _t^2 u} \right| _{t=t_s } -u_s^2 ({\dot{\theta }}_s +{\dot{\alpha }}_s )^{2}]\hbox {d}x} \nonumber \\&+\,\frac{\mu \rho l}{r_s }-\frac{\mu \rho l^{3}}{24r_s^3 }(1-3\cos ^{2}\alpha _s )+\frac{\mu J_2 R_e ^{2}\rho l}{2r_s^3 }+\frac{3\mu J_{22} R_e ^{2}\rho l}{r_s^3 }-\left. {\frac{EI}{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\partial _{xx}^2 u\hbox {d}x} } \right| _{t=t_s } \end{aligned}$$
(4)

where the subscript “0” represents the moment \(t=0\) and the subscript “s” represents the moment \(t=t_s \). The attitude angle tends to be \(\alpha =0\) when \(t=t_s \).

As the initial conditions employed in our previous studies [18, 19, 24], the initial state of the transverse vibration of the beam is assumed as \(u_0 =0,\;\left. {\partial _t u} \right| _{t=0} =0\). Then, the minimum control energy \(\Delta E_1 \) can be simplified as,

$$\begin{aligned} \Delta E_1= & {} \frac{\rho l}{2}[{\dot{r}}_0^2 +(r_0 {\dot{\theta }}_0 )^{2}]+\frac{1}{2}\frac{\rho l^{3}}{12}({\dot{\theta }}_0 +{\dot{\alpha }}_0 )^{2} \nonumber \\&-\,\frac{\mu \rho l}{r_0 }+\frac{\mu \rho l^{3}}{24r_0^3 }(1-3\cos ^{2}\alpha _0 )-\frac{\mu J_2 R_e ^{2}\rho l}{2r_0^3 }-\frac{3\mu J_{22} R_e ^{2}\rho l}{r_0^3 } \nonumber \\&-\,\frac{\rho l}{2}[{\dot{r}}_s^2 +(r_s {\dot{\theta }}_s )^{2}]-\frac{1}{2}\frac{\rho l^{3}}{12}({\dot{\theta }}_s +{\dot{\alpha }}_s )^{2}-\frac{\rho }{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {[\left. {\partial _t^2 u} \right| _{t=t_s } -u_s^2 ({\dot{\theta }}_s +{\dot{\alpha }}_s )^{2}]\hbox {d}x} \nonumber \\&+\,\frac{\mu \rho l}{r_s }-\frac{\mu \rho l^{3}}{24r_s^3 }(1-3\cos ^{2}\alpha _s )+\frac{\mu J_2 R_e ^{2}\rho l}{2r_s^3 }+\frac{3\mu J_{22} R_e ^{2}\rho l}{r_s^3 }-\left. {\frac{EI}{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\partial _{xx}^2 u\hbox {d}x} } \right| _{t=t_s } \end{aligned}$$
(5)

which contains the loss of potential energy resulting from the decrease in orbit radius and the loss of kinetic energy resulting from the transverse damping vibration as well as the plane state change of the beam.

It has been mentioned that, to simplify and accelerate the analysis process for system (2)–(3), the flexibility and the damping effect are always neglected. In this case, system (2)–(3) degrades into the following conservative system,

$$\begin{aligned} \left\{ {\begin{array}{l} \displaystyle -\rho l\ddot{r}+\rho lr{\dot{\theta }}^{2}-\frac{\mu \rho l}{r^{2}}+\frac{\mu \rho l^{3}}{8r^{4}}(1-3\cos ^{2}\alpha )-\frac{3\mu J_2 R_e ^{2}\rho l}{2r^{4}}-\frac{9\mu J_{22} R_e ^{2}\rho l}{r^{4}}=0 \\ \displaystyle \rho lr^{2}\ddot{\theta }+2\rho lr{\dot{r}}{\dot{\theta }}+\frac{\rho l^{3}}{12}(\ddot{\theta }+\ddot{\alpha })=0 \\ \displaystyle \frac{\rho l^{3}}{12}(\ddot{\theta }+\ddot{\alpha })+\frac{\mu \rho l^{3}}{4r^{3}}\cos \alpha \sin \alpha =0 \\ \end{array}} \right. \end{aligned}$$
(6)

This simplified system only owns one stable attitude state (\(\alpha =0)\) and is a conservative system obviously, which implies that the attitude adjustment cannot be performed by the dissipative effect of itself. The minimum control energy is the energy difference between the initial total energy and the total energy in the stable attitude state of system (6), that is,

$$\begin{aligned} \Delta E_2 =\frac{1}{2}\frac{\rho l^{3}}{12}{\dot{\alpha }}_0^2 +\frac{\mu \rho l^{3}}{8r_0^3 }(1-\cos ^{2}\alpha _0 ) \end{aligned}$$
(7)

which only contains the loss of kinetic energy resulting from the state change of plane motion of the rigid beam.

The difference between \(\Delta E_1 \) and \(\Delta E_2 \) is,

$$\begin{aligned} \Delta= & {} \Delta E_1 -\Delta E_2 \nonumber \\= & {} \frac{\rho l}{2}[{\dot{r}}_0^2 -{\dot{r}}_s^2 +(r_0 {\dot{\theta }}_0 )^{2}-(r_s {\dot{\theta }}_s )^{2}]+\frac{\rho l^{3}}{24}[{\dot{\theta }}_0 ({\dot{\theta }}_0 +2{\dot{\alpha }}_0 )-({\dot{\theta }}_s +{\dot{\alpha }}_s )^{2}]-\mu \rho l\left( \frac{1}{r_0 }-\frac{1}{r_s }\right) \nonumber \\&-\,\frac{\mu \rho l}{r_0^3 }\left( \frac{l^{2}}{12}+\frac{J_2 R_e ^{2}}{2}+3J_{22} R_e ^{2}\right) -\frac{\mu \rho l}{r_s^3 }\left[ \frac{l^{2}}{24}(1-3\cos ^{2}\alpha _s )-\frac{J_2 R_e ^{2}}{2}-3J_{22} R_e ^{2}\right] \nonumber \\&+\, \frac{\rho l}{2}u_s^2 ({\dot{\theta }}_s +{\dot{\alpha }}_s )^{2}-\frac{\rho }{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\left. {\partial _t^2 u} \right| _{t=t_s } \hbox {d}x} -\left. {\frac{EI}{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\partial _{xx}^2 u\hbox {d}x} } \right| _{t=t_s } \end{aligned}$$
(8)

When \(t\rightarrow t_s\), the attitude angle approaches the assumed stable attitude (in the following numerical experiments, the assumed stable attitude angle is \(\alpha =0)\), which implies that \(\alpha _s ={\dot{\alpha }}_s =0\). Then, Eq. (8) can be rewritten as,

$$\begin{aligned} \Delta= & {} \Delta E_1 -\Delta E_2 \nonumber \\= & {} \frac{\rho l}{2}[{\dot{r}}_0^2 -{\dot{r}}_s^2 +(r_0 {\dot{\theta }}_0 )^{2}-(r_s {\dot{\theta }}_s )^{2}]+\frac{\rho l^{3}}{24}[{\dot{\theta }}_0 ({\dot{\theta }}_0 +2{\dot{\alpha }}_0 )-{\dot{\theta }}_s^2 ]-\mu \rho l\left( \frac{1}{r_0 }-\frac{1}{r_s }\right) \nonumber \\&-\,\mu \rho l\left( \frac{l^{2}}{12}+\frac{J_2 R_e ^{2}}{2}+3J_{22} R_e ^{2}\right) \left( \frac{1}{r_0^3 }-\frac{1}{r_s^3 }\right) \nonumber \\&+\, \frac{\rho l}{2}u_s^2 {\dot{\theta }}_s^2 -\frac{\rho }{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\left. {\partial _t^2 u} \right| _{t=t_s } \hbox {d}x} -\left. {\frac{EI}{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\partial _{xx}^2 u\hbox {d}x} } \right| _{t=t_s } \end{aligned}$$
(9)

In Eq. (9), \((\frac{1}{r_0 }-\frac{1}{r_s })\gg (\frac{1}{r_0^3 }-\frac{1}{r_s^3 })\), that is, comparing with the term \(\mu \rho l(\frac{1}{r_0 }-\frac{1}{r_s })\), the term \(\mu \rho l(\frac{l^{2}}{12}+\frac{J_2 R_e ^{2}}{2}+3J_{22} R_e ^{2})(\frac{1}{r_0^3 }-\frac{1}{r_s^3 })\) is a higher-order infinitesimal quantity. In addition, the transverse vibration of the beam is very weak, which implies that the term \(\frac{\rho l}{2}u_s^2 {\dot{\theta }}_s^2 -\frac{\rho }{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\left. {\partial _t^2 u} \right| _{t=t_s } \hbox {d}x} -\left. {\frac{EI}{2}\int _{-\frac{l}{2}}^{\frac{l}{2}} {\partial _{xx}^2 u\hbox {d}x} } \right| _{t=t_s } \) is also an infinitesimal quantity. However, to investigate the effects of the initial conditions on the minimum control energy, all these infinitesimal quantities are taken into account in the following numerical experiments.

3 Numerical Results of Minimum Control Energy

In this section, the comparison between the minimum control energy (7) of the simplified system (6) ignoring both flexibility and damping of the spatial beam and the minimum control energy (5) of the coupled dynamic system (2)–(3) will be investigated by the proposed structure-preserving method [18, 19, 24] in detail.

The parameters of the beam, some initial conditions and constants are assumed as \(\rho =0.5\ {\hbox {kg}}/\hbox {m},\;l=2000\;\hbox {m,}\;E=6.9\times 10^{11}\ \hbox {Pa},\;I=1\times 10^{-4}\ \hbox {m}^{4},\;c=0.1,\;\mu =3.986005\times 10^{14}\ {\hbox {m}^{3}}/{\hbox {s}^{2}}\), \(r_0 =6{,}700{,}000\ \hbox {m},\;{\dot{r}}_0 =0,\;\theta _0 =0,\;{\dot{\theta }}_0 =\sqrt{\mu /{r_0^3 }}\ {\hbox {rad}}/\hbox {s},\;u(x,0)=\left. {\partial _t u(x,t)} \right| _{t=0} =0\). The minimum control energy of the rigid spatial beam can be obtained directly from Eq. (7).

In the following experiments, the minimum control energy of the spatial flexible damping beam will be obtained by the proposed structure-preserving method with different initial attitude angles and different initial attitude angle speeds. The constants associated with the non-sphere perturbation are assumed as \(J_2 =1.08263\times 10^{-3}\), \(J_{22} =1.81222\times 10^{-6}\) and \(R_e =6.371\times 10^{6}\ \hbox {m}\). The step lengths are fixed as \(\Delta x=1\ \hbox {m},\;\Delta t=1000\ \hbox {s}\) in the structure-preserving method, and the simulation time span is assumed as about three months (90 days) preliminarily, i.e., \(T_0 =7{,}776{,}000\ \hbox {s}\).

3.1 Are Three Months Long Enough for Spatial Flexible Damping Beam to Arrive at the Stable Attitude State?

If the attitude of the beam converges to the stable attitude state \(\alpha =\pi /2\), the results obtained in the following numerical simulations will not own the comparability with that of the simplified system (6) [19]. To avoid this and to judge whether or not the assumed interval (\(T_0 =7{,}776{,}000\ \hbox {s}\)) is long enough for the spatial flexible damping beam to arrive at the stable attitude state \(\alpha =0\), the initial attitude angle and the initial velocity of the attitude angle are, respectively, assumed as \(\alpha _0 =\pi /2\ \hbox {rad}, \;{\dot{\alpha }}_0 =0.000081\ {\hbox {rad}}/\hbox {s}\) in this section (which are the most rigorous initial conditions requiring almost the longest interval to arrive at the stable attitude state \(\alpha =0\), referring to the results presented in our previous study [19]).

In this case, the plane motion, the attitude angle evolution, as well as the transverse vibration of the spatial flexible damping beam are simulated by the proposed structure-preserving method deriving from the generalized multi-symplectic approach. Here, only the evolutions of the attitude angle, the attitude angle velocity and the transverse vibration at the end of the beam (\(x=1000\ \hbox {m}\)) are shown in Fig. 2.

Fig. 2
figure 2

The evolutions of the attitude angle, the attitude angle velocity and the transverse vibration at the end of the beam

Full size image

From Fig. 2, it can be found that the attitude angle, the attitude angle velocity and the transverse vibration at the end of the beam tend to be zero in about two months, which implies that three months is long enough for the spatial flexible damping beam to arrive at the stable attitude state \(\alpha =0\). In addition, similar to the results presented in our previous study [18], the transverse vibration at the end of the beam contains two periods obviously. During the first period, the vibrational amplitude increases rapidly. And during the second period, the vibrational amplitude decreases slowly.

3.2 Minimum Control Energy of Spatial Beam with Assumed Attitude Adjustment Target

In the above numerical experiments, we can confirm that three months is long enough for the spatial flexible damping beam to arrive at the assumed stable attitude state \(\alpha =0\); that is, the attitude of the spatial flexible damping beam tends to be stable and the transverse vibration of the spatial flexible damping beam decreases to the degree that is too weak to be detected after three months.

In this section, we set the initial attitude angle \(\alpha _0 \) and the initial attitude angle velocity \({\dot{\alpha }}_0 \) as independent variables. And then, the minimum control energy for the spatial rigid beam can be obtained from Eq. (7) directly. Subsequently, the plane motion and the transverse vibration of the spatial flexible damping beam are simulated. During the simulation, the minimum control energy for the spatial flexible damping beam can be recorded by referring to Eq. (5).

Firstly, the initial attitude angle velocity is fixed as \({\dot{\alpha }}_0 =0.000081\ {\hbox {rad}}/\hbox {s}\) (referring to the numerical results presented in our previous study [19], the attitude angle will not tend to be of the stable state \(\alpha =\pi /2\) when \({\dot{\alpha }}_0 =0.000081\ {\hbox {rad}}/\hbox {s})\), and the initial attitude angle \(\alpha _0 \) is assumed to increase from 0 to \(\pi /2\ \hbox {rad}\) with the step length \(\Delta \alpha _0 =\pi /{200}\ \hbox {rad}\). The comparison on the minimum control energy for this case between the spatial rigid beam and the spatial flexible damping beam is shown in Fig. 3. And then, the initial attitude angle is fixed as \(\alpha _0 =1.555\;\hbox {rad}\) (referring to the numerical results presented in our previous study [19], the attitude angle will not tend to be of the stable state \(\alpha =\pi /2\) when \(\alpha _0 =1.555\;\hbox {rad})\) and the initial attitude angle velocity \({\dot{\alpha }}_0 \) is assumed to increase from 0 to \({\dot{\alpha }}_0 =0.0001\ {\hbox {rad}}/\hbox {s}\) with the step length \(\Delta {\dot{\alpha }}_0 =0.000001\ {\hbox {rad}}/\hbox {s}\). The comparison on the minimum control energy for this case between the spatial rigid beam and the spatial flexible damping beam is shown in Fig. 4.

Fig. 3
figure 3

Minimum control energy of spatial beam with fixed initial attitude angle velocity

Full size image

From the numerical results shown in Fig. 3, it can be found that when \(\alpha _0 <0.15916\;\hbox {rad}\) or \(\alpha _0 >1.30578\;\hbox {rad}\), the minimum control energy for the spatial flexible damping beam is higher than that for the spatial rigid beam with the fixed initial attitude angle velocity \({\dot{\alpha }}_0 =0.000081\ {\hbox {rad}}/\hbox {s}\); when \(1.30578\;\hbox {rad}>\alpha _0 >0.15916\;\hbox {rad}\), the result is just the opposite. These conclusions imply that the energy loss of the spatial flexible damping beam is more acute than the energy loss of the spatial rigid beam when the initial attitude angle is close to the stable attitude state \(\alpha =0\) (\(\alpha _0 <0.15916\;\hbox {rad}\)) or is far away from the stable attitude state \(\alpha =0\) (\(\alpha _0 >1.30578\;\hbox {rad})\).

Although the initial attitude angle is not contained in Eq. (9) explicitly, it influences the necessary time for the spatial flexible damping beam to arrive at the assumed stable attitude state and affects the energy dissipation in the transverse vibration process of the damping beam. The above phenomena can be explained in detail as follows. The energy loss of the spatial beam is derived from the attitude control (as a result, both the attitude angle and the attitude angle velocity tend to be zero), the transverse flexible vibration attenuates, and the orbit radius decreases due to the damping dissipation if both flexibility and damping of the beam are considered. Obviously, if the coupling between the plane motion and the transverse vibration of the spatial flexible damping beam is ignored, the minimum control energy of the rigid spatial beam will be lower than that of the spatial flexible damping beam with random initial conditions. This is because the energy loss of the rigid spatial beam resulting from the attitude control is equal to that of the spatial flexible damping beam, and the energy loss resulting from the transverse flexible vibration attenuation and the orbit radius decrease is positive. Actually, the coupling effects between the plane motion and the transverse vibration cannot be neglected during the longtime dynamic simulation. When the initial attitude angle is close to the stable attitude state \(\alpha =0\) (\(\alpha _0 <0.15916\;\hbox {rad}\)), the time interval needed for the spatial flexible damping beam approaching the stable attitude state \(\alpha =0\) is short. In this case, both the orbit radius decrease and the damping dissipation are weak compared with the necessary attitude control energy. Thus, the minimum control energy for the spatial flexible damping beam is slightly higher than that for the spatial rigid beam. When the initial attitude angle is far away from the stable attitude state \(\alpha =0\) (\(\alpha _0 >1.30578\;\hbox {rad}\)), the time interval needed for the spatial flexible damping beam approaching the stable attitude state \(\alpha =0\) is up to two months. In this case, both the damping effect and the orbit radius decrease in the long interval are significant factors affecting the energy loss of the beam. Thus, the minimum control energy for the spatial flexible damping beam is much higher than that for the spatial rigid beam. When \(1.30578\;\hbox {rad}>\alpha _0 >0.15916\;\hbox {rad}\), the coupling between the plane motion and the transverse vibration is strong and the orbit true anomaly velocity \({\dot{\theta }}\) increases due to the orbit radius decrease, which implies that the total energy stored in the spatial flexible damping beam is high and the energy loss is small.

Fig. 4
figure 4

Minimum control energy of spatial beam with fixed initial attitude angle

Full size image

In Fig. 4, for the spatial rigid beam, the minimum control energy is almost independent of the initial attitude angle velocity, which results from \({\dot{\alpha }}_0^2 \ll 1-\cos ^{2}\alpha _0 \) in this case, and the term \(\frac{1}{2}\frac{\rho l^{3}}{12}{\dot{\alpha }}_0^2 \) is a higher-order infinitesimal quantity comparing with the term \(\frac{\mu \rho l^{3}}{8r_0^3 }(1-\cos ^{2}\alpha _0 )\) in \(\Delta E_2 \). However, for the spatial flexible damping beam, the minimum control energy increases slowly with the increase in the initial attitude angle velocity, which implies that the increase in the initial attitude angle velocity will increase the energy loss of the spatial flexible damping beam slightly.

Comparing the minimum control energy of the spatial flexible damping beam with that of the spatial rigid beam shown in Fig. 4, it can be found that the minimum control energy of the spatial flexible damping beam is much higher than that of the spatial rigid beam with the fixed initial attitude angle, which implies that ignoring the flexibility and damping of the spatial beam will underestimate the minimum control energy of the spatial beam when the initial attitude angle is fixed.

4 Conclusions

Estimating the minimum control energy for the attitude adjustment of the spatial structure is the prerequisite to the controller design process and determines the fuel or the control energy required for the attitude adjustment of the spatial structure. In this paper, the minimum control energy of the spatial rigid/flexible damping beam for the assumed stable attitude state is studied by the proposed structure-preserving method in detail.

From the numerical results presented in the experiments, it can be found that,

  1. (1)

    With the fixed initial attitude angle velocity (\({\dot{\alpha }}_0 =0.000081\ {\hbox {rad}}/\hbox {s})\), the minimum control energy for the spatial flexible damping beam is higher than that for the spatial rigid beam when \(\alpha _0 <0.15916\;\hbox {rad}\) or \(\alpha _0 >1.30578\;\hbox {rad}\).

  2. (2)

    The effect of the initial attitude angle velocity in the assumed range of this study on the minimum control energy is weak and can be ignored in the controller design process.

  3. (3)

    With the fixed initial attitude angle (\(\alpha _0 =1.555\;\hbox {rad})\), ignoring the flexibility and the damping effect will underestimate the minimum control energy obviously.