Introduction

The Real-Time Service (RTS) of the International GNSS Service (IGS) has been broadcasting satellite orbit and clock products in real-time since April 2013, with a latency of a few seconds only (Hadas and Bosy 2015). This makes possible real-time precise point positioning (PPP) serving time-critical applications such as earthquake or tsunami early warning (Bock and Melgar 2016; Hoechner et al. 2013) and commercial navigation (Malys and Jensen 1990; Zumberge, 1997). By now, precise orbit and clock corrections of GPS/GLONASS/Galileo/BDS have been regularly released in real time by several IGS analysis centers (AC) such as Centre National d’ Etudes Spatiales (CNES), Deutsches Zentrum für Luft- und Raumfahrt (DLR), GeoForschungsZentrum Potsdam (GFZ) and Wuhan University (WHU) (Kazmierski 2018). However, most of the ACs offer orbit and clock streams only. Available real-time code and carrier-phase bias products are required to achieve PPP ambiguity resolution (PPP-AR) that shows higher performance and reliability than typical PPP (Ge et al. 2008; Geng and Shi 2017).

It is demonstrated that integer recovery clock (IRC) products (also known as phase clock) can enable higher ambiguity-fixing performance than uncalibrated phase delays (UPDs) since the satellite clocks/phase biases are actually estimated under a rigorous ambiguity-fixed model (Laurichesse et al. 2009; Collins et al. 2010). Based on the IRC method, The National Centre for Space Studies (CNES) has released GPS dual-frequency IRC products since 2009 (Loyer et al. 2012) and GPS/Galileo products since 2015. To align the integer clocks to the time scale obtained from pseudoranges, Geng et al. (2019) proposed a modified phase bias/clock method where the inconsistency biases between pseudorange and carrier phases are modeled as a constant. Since 2019, Wuhan University has been releasing daily multi-GNSS phase bias/clock products at ftp://igs.gnsswhu.cn/pub/whu/phasebias/ (Geng et al. 2022a). In the same year, CODE also started issuing GPS/Galileo phase biases and clocks (Schaer et al. 2021). However, only dual-frequency ambiguities are resolved to obtain phase clocks in the published studies, while multi-frequency phase biases are still estimated using float ambiguities or Hatch–Melbourne–Wübbena (HMW) combinations (Hatch 1982). In contrast to the post-processing phase bias products, which are undergoing the product combination in IGS Repro3 (Geng et al. 2022b), estimating ambiguity-fixed multi-frequency satellite clocks and phase biases in real time always requires computational efficiency. Owing to the large number of parameters of the massive network, it is even hard to generate phase clocks based on the uncombined PPP model in real time, and estimate phase biases at the same time. Gong et al. (2018a, b) applied both carrier-range observations and blocked QR factorization (to express a matrix as the product of an orthogonal matrix and an upper triangular matrix) methods. They shortened the time consuming of one-epoch multi-GNSS satellite clock estimation from 31 to 0.5 s. Liu et al. (2019) proposed a 1-Hz real-time satellite clock estimation method with two parallel threads. However, phase biases were not discussed in their publications. Since 2016, CNES has been broadcasting real-time multi-frequency phase bias products (Laurichesse and Bolt, 2016). Similar to the post-processing case, CNES resolved dual-frequency ambiguities to generate phase clocks, while multi-frequency phase biases are still obtained by averaging ambiguity-float HMW combinations (Liu et al. 2020, 2021). Multi-frequency phase biases are calculated under an imperfect stochastic model. It is worth resolving all the ambiguities to improve the performance of real-time phase bias products.

In this study, we resolved multi-frequency ambiguities for the first time to directly estimate the observation-specific phase biases in real time. Besides, by applying carrier-range observations, phase biases are estimated from GNSS observable functions rather than float ambiguities or HMW combinations. We then apply this approach to calculate real-time multi-frequency GPS/Galileo/BDS phase biasSSR (State Spatial Representation) corrections in OSB (Observation-specific Signal Bias) forms (Schaer 2016). Finally, we initially accessed the phase bias streams shared through the IGS-RT service. This study is organized as follows: the second section derives the observation modeling and relative methods of generating ambiguity-fixed phase OSBs; the third section displays the data set and strategies of the real-time service; the fourth section demonstrates the data integrity of real-time carrier-range observations and analyzes the stability of the phase OSB products the performance of them in kinematic/static PPP-AR; the last section draws some conclusions.

Method

In this section, we derive the method to estimate multi-frequency ambiguity-fixed phase biases in real time commencing from the raw GNSS observable model. Typical UPD products are also given here as it is necessary for the method to resolve the undifferenced ambiguities.

All-frequency observation model

Generally, multi-frequency GNSS raw observations of pseudorange and carrier phase can be expressed as

$$\left\{ \begin{gathered} P_{i,j}^{k} = \rho_{i,j}^{k} + c(t_{i} - t^{k} ) + \gamma_{j}^{s} \cdot I_{i}^{k} + d_{i,j}^{s} - d_{j}^{k} + \varepsilon_{i,j}^{k} \hfill \\ L_{i,j}^{k} = \rho_{i,j}^{k} + c(t_{i} - t^{k} ) - \gamma_{j}^{s} \cdot I_{i}^{k} + \lambda_{j}^{s} (b_{i,j}^{s} - b_{j}^{\prime k} + N_{i,j}^{k} + \varphi_{i,j}^{k} ) \hfill \\ \end{gathered} \right.$$
(1)

where \(P_{i,j}^{k}\) and \(L_{i,j}^{k}\) are pseudorange and carrier-phase observations of frequency band \(j\) of satellite \(k\) measured by receiver \(i\). \(\rho_{i,j}^{k}\) denotes the non-dispersive geometric distance between the phase center of satellite and receiver antennas. \(t_{i}\) and \(t^{k}\) denote physical clock errors of receiver and satellite, respectively, while \(c\) is the speed of light in the vacuum. \(I_{i}^{k}\) is the ionosphere delay of the first band (\(j = 1\)) and \(\gamma_{j}^{s} = (\frac{{f_{1}^{s} }}{{f_{j}^{s} }})^{2}\), where \(f_{j}^{s}\) is the frequency of band \(j\) while \(\lambda_{j}^{s} = \frac{c}{{f_{j}^{s} }}\) denotes its wavelength. The symbol \(s\) denotes the code-division multiple access (CDMA) constellation, with G for GPS, E Galileo, C2 for BDS-2 and C3 for BDS-3. The terms \(d_{i,j}^{s}\) and \(d_{j}^{k}\) denote, respectively, the receiver and satellite-hardware biases of pseudorange observations. Similarly, \(b_{i,j}^{s}\) and \(b_{j}^{\prime k}\) are the receiver and satellite hardware biases of carrier-phase observations. \(N_{i,j}^{k}\) is the number of integer ambiguities in the \(L_{i,j}^{k}\) measurements. \(\varepsilon_{i,j}^{k}\) and \(\varphi_{i,j}^{k}\) denote the unmodeled errors of pseudorange and carrier-phase observations, respectively, including measurement noise and multipath errors. In the above equations, the phase biases \(b_{j}^{\prime k}\) can be separated into a constant part ( \(b_{j}^{k}\)) and a time-varying part (\(\delta b_{j}^{k}\)), also known as satellite inter-frequency clock bias (IFCB).

$$b_{j}^{\prime k} = b_{j}^{k} + \delta b_{j}^{k}$$
(2)

Note that \(\delta b_{j}^{k}\) is existing only on the third (or beyond three) frequencies of BLOCK IIF and BDS-2 satellites and is ignored for the other satellites (Montenbruck et al. 2013; Zhang et al. 2017).

The satellite hardware biases of pseudorange such as \(d_{j}^{k}\) can be pre-eliminated using the pseudorange OSB products, which are obtained from ionospheric observables based on two frequencies noted here with the subscripts 1 and 2. The pseudorange OSB products and pseudorange hardware biases satisfy the following functions (Geng et al. 2022a),

$$\left\{ \begin{gathered} D_{j}^{k} - d_{j}^{k} = D^{k} \hfill \\ \alpha \cdot D_{1}^{k} - \beta \cdot D_{2}^{k} = 0 \hfill \\ \end{gathered} \right.$$
(3)

with

$$\left\{ \begin{gathered} \alpha = \frac{{\gamma_{2}^{s} }}{{\gamma_{2}^{s} - 1}} \hfill \\ \beta = \frac{1}{{\gamma_{2}^{s} - 1}} \hfill \\ \end{gathered} \right.$$
(4)

where \(D_{j}^{k}\) denote the pseudorange OSB correction with respect to satellite \(k\) and frequency \(j\). \(D^{k}\) is a satellite-related constant. Owing to the correlation between hardware biases and clock errors, it is hard to obtain absolute bias corrections. \(D^{k}\) is introduced to make the observation-specific biases mathematically estimable (Wang et al. 2016). In the following, we apply the pseudorange OSB products \(D_{j}^{k}\) in the observation modeling.

Equation (1) displays the hardware biases clearly in the functions, but they cannot be solved due to the rank deficiency. In this study, we implement a typical re-parameterization of the clock, ionosphere delay, and ambiguity parameters (Zhang et al. 2011; Odijk et al. 2016), which also obeys the convention of IGS products based on dual-frequency ionosphere-free observables (noted with the subscripts 1 and 2). Then, the observation modeling for multi-frequency PPP presented in (1) can be written as:

$$\left\{ \begin{gathered} P_{i,1}^{k} + D_{1}^{k} = \rho_{i,1}^{k} + c(\overline{t}_{i} - \overline{t}^{k} ) + \gamma_{1}^{s} \cdot \overline{I}_{i}^{k} \hfill \\ P_{i,2}^{k} + D_{2}^{k} = \rho_{i,2}^{k} + c(\overline{t}_{i} - \overline{t}^{k} ) + \gamma_{2}^{s} \cdot \overline{I}_{i}^{k} \hfill \\ P_{i,j}^{k} + D_{j}^{k} = \rho_{i,j}^{k} + c(\overline{t}_{i} - \overline{t}^{k} ) + \gamma_{j}^{s} \cdot \overline{I}_{i}^{k} + C_{i,j}^{k} \hfill \\ L_{i,1}^{k} = \rho_{i,1}^{k} + c(\overline{t}_{i} - \overline{t}^{k} ) - \gamma_{1}^{s} \cdot \overline{I}_{i}^{k} + \lambda_{1}^{s} \cdot \overline{N}_{i,1}^{k} \hfill \\ L_{i,2}^{k} = \rho_{i,2}^{k} + c(\overline{t}_{i} - \overline{t}^{k} ) - \gamma_{2}^{s} \cdot \overline{I}_{i}^{k} + \lambda_{2}^{s} \cdot \overline{N}_{i,2}^{k} \hfill \\ L_{i,j}^{k} = \rho_{i,j}^{k} + c(\overline{t}_{i} - \overline{t}^{k} ) - \gamma_{j}^{s} \cdot \overline{I}_{i}^{k} + \lambda_{j}^{s} \cdot \overline{N}_{i,j}^{k} \hfill \\ \end{gathered} \right.$$
(5)

where

$$\left\{ \begin{gathered} \overline{t}^{k} = t^{k} + \frac{1}{c} \cdot D^{k} \hfill \\ \overline{t}_{i} = t_{i} + \frac{1}{c}(\alpha \cdot d_{i,1} - \beta \cdot d_{i,2} ) \hfill \\ \overline{I}_{i}^{k} = I_{i}^{k} - \beta (d_{i,1} - d_{i,2} ) \hfill \\ C_{i,j}^{k} = \gamma_{j}^{s} \cdot \beta (d_{i,1} - d_{i,2} ) - (\alpha \cdot d_{i,1} - \beta \cdot d_{i,2} ) + d_{i,j} \hfill \\ \hfill \\ \overline{N}_{i,1}^{k} = N_{i,1}^{k} + b_{i,1} - (b_{1}^{k} - \frac{1}{{\lambda_{1}^{s} }} \cdot D^{k} ) - \frac{1}{{\lambda_{1}^{s} }}\left( {(\alpha + \beta )d_{i,1} - 2\beta \cdot d_{i,2} } \right) \hfill \\ \overline{N}_{i,2}^{k} = N_{i,2}^{k} + b_{i,2} - (b_{2}^{k} - \frac{1}{{\lambda_{2}^{s} }} \cdot D^{k} ) - \frac{1}{{\lambda_{2}^{s} }}\left( {2\alpha \cdot d_{i,1} - (\alpha + \beta )d_{i,2} } \right) \hfill \\ \overline{N}_{i,j}^{k} = N_{i,j}^{k} + b_{i,j} - (b_{j}^{\prime k} - \frac{1}{{\lambda_{j}^{s} }} \cdot D^{k} ) - \frac{1}{{\lambda_{j}^{s} }}\left( {\gamma_{j}^{s} \cdot \beta (d_{i,1} - d_{i,2} ) + (\alpha \cdot d_{i,1} - \beta \cdot d_{i,2} )} \right) \hfill \\ \end{gathered} \right.$$
(6)

The dual-frequency parts of these equations are consistent with those used by IGS Analysis Centers (Kouba 2009). Satellite clock \(\overline{t}^{k}\), receiver clock \(\overline{t}_{i}\) and ionosphere delay \(\overline{I}_{i}^{k}\) are totally decided by dual-frequency observations after introducing a constant unknown \(C_{i,j}^{k} (j > 2)\) in the multi-frequency functions. At the same time, it is worth noting that (5) can easily include more frequencies without changing the composition of parameters (Geng and Guo 2020). In this study, we apply real-time SSR corrections provided by the Wuhan University to fix satellite orbits and clocks (Gu et al. 2018).

Real-time UPD determination.

Equation (6) shows that integer ambiguities are difficult to determine because of the high correlation between ambiguities and hardware biases. Ge et al. (2008) extracted the fractional parts of the float ambiguities and modeled them as UPD products, which can be used to recover the integer nature of ambiguities. UPD products can be calculated in high efficiency since they are free from network processing, and the satellite clocks are not required to be re-estimated. In this study, to resolve the multi-frequency ambiguities for the network processing in real-time, we calculated UPD products in advance. Starting from (6), the multi-frequency ambiguities can be rewritten as:

$$\left\{ \begin{gathered} \overline{N}_{i,1}^{k} = N_{i,1}^{k} + \overline{b}_{i,1} - \overline{b}_{1}^{k} \hfill \\ \overline{N}_{i,2}^{k} = N_{i,2}^{k} + \overline{b}_{i,2} - \overline{b}_{2}^{k} \hfill \\ \overline{N}_{i,j}^{k} = N_{i,j}^{k} + \overline{b}_{i,j} - \overline{b}_{j}^{k} \hfill \\ \end{gathered} \right.$$
(7)

where we have defined

$$\left\{ \begin{gathered} \overline{b}_{1}^{k} = b_{1}^{k} - \frac{1}{{\lambda_{1}^{s} }} \cdot D^{k} \hfill \\ \overline{b}_{2}^{k} = b_{2}^{k} - \frac{1}{{\lambda_{2}^{s} }} \cdot D^{k} \hfill \\ \overline{b}_{j}^{k} = b_{j}^{\prime k} - \frac{1}{{\lambda_{j}^{s} }} \cdot D^{k} \hfill \\ \end{gathered} \right.$$
(8)

\(\overline{b}_{i,j}\) denotes the receiver biases (including those from both pseudorange and carrier phase) in float ambiguities \(\overline{N}_{i,j}^{k}\). \(\overline{b}_{j}^{\prime k}\) denotes the nominal satellite phase biases which absorbs the constant \(D^{k}\). Receiver biases can be easily eliminated by forming single-differenced ambiguities in the same constellation:

$$\left\{ \begin{gathered} \overline{N}_{i,1}^{kq} = N_{i,1}^{kq} - \overline{b}_{1}^{kq} \hfill \\ \overline{N}_{i,2}^{kq} = N_{i,2}^{kq} - \overline{b}_{2}^{kq} \hfill \\ \overline{N}_{i,j}^{kq} = N_{i,j}^{kq} - \overline{b}_{j}^{kq} \hfill \\ \end{gathered} \right.$$
(9)

\(\overline{N}_{i,j}^{kq}\) denotes the single-differenced float ambiguity with respect to satellite \(k\) and \(q\). \(N_{i,j}^{kq}\) and \(\overline{b}_{j}^{kq}\) denote the single-differenced integer ambiguity and satellite-related phase bias, respectively. Though (9) seems simple enough to extract the raw phase biases, it cannot be used directly to calculate real-time UPDs. Generally, the raw ambiguities are transferred into ionosphere-free narrow-lane and wide-lane counterparts to decrease the influences of ionosphere delays. Specifically, for constellation \(s\), the transformation functions of triple-frequency raw ambiguities can be derived as

$$\left\{ {\begin{array}{*{20}c} {\overline{N}_{{i,{\text{nl}}}}^{kq} } \\ {\overline{N}_{i,w12}^{kq} } \\ {\overline{N}_{i,w32}^{kq} } \\ \end{array} } \right\} = M^{s} \left\{ {\begin{array}{*{20}c} {\overline{N}_{i,1}^{kq} } \\ {\overline{N}_{i,2}^{kq} } \\ {\overline{N}_{i,3}^{kq} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\tfrac{{f_{1}^{s} }}{{f_{1}^{s} - f_{2}^{s} }}} & { - \tfrac{{f_{2}^{s} }}{{f_{1}^{s} - f_{2}^{s} }}} & 0 \\ 1 & { - 1} & 0 \\ 0 & { - 1} & 1 \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}c} {\overline{N}_{i,1}^{kq} } \\ {\overline{N}_{i,2}^{kq} } \\ {\overline{N}_{i,3}^{kq} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\tfrac{{f_{2}^{s} }}{{f_{1}^{s} - f_{2}^{s} }} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq} } \\ 0 \\ 0 \\ \end{array} } \right\}$$
(10)

where \(\overline{N}_{i,w12}^{kq}\) and \(\overline{N}_{i,w32}^{kq}\) denote wide-lane ambiguities based on L1-L2 and L3-L2, respectively. \(\overline{N}_{{i,{\text{nl}}}}^{kq}\) is float narrow-lane ambiguity based on L1/L2 frequencies.\(M^{s}\) is the mapping matrix which can be extended to more frequencies by forming the other wide-lane ambiguities. \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq}\) is the nominal integer part of L1/L2 wide-lane ambiguity \(\overline{N}_{i,w12}^{kq}\). Note that narrow-lane ambiguities are formed after obtaining integer wide-lane ambiguities. In this section, we give the transformation of narrow-lane and wide-lane ambiguities together for brevity. Combined ambiguities in (10) can be further represented as

$$\left\{ \begin{gathered} \overline{N}_{{i,{\text{nl}}}}^{kq} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{{i,{\text{nl}}}}^{kq} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{{{\text{nl}}}}^{kq} \hfill \\ \overline{N}_{i,w12}^{kq} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w12}^{kq} \hfill \\ \overline{N}_{i,w32}^{kq} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w32}^{kq} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w32}^{kq} \hfill \\ \end{gathered} \right.$$
(11)

\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{{i,{\text{nl}}}}^{kq}\), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq}\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w32}^{kq}\) denote the nominal integer candidates of narrow-lane and wide-lane ambiguities. \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{{{\text{nl}}}}^{kq}\), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w12}^{kq}\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w32}^{kq}\) are the nominal fractional-cycle parts of phase biases. If we collect enough candidates of (11) from service-end stations, it is possible to extract the phase biases with reliable precision through the following steps:

$$\left\{ \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{{{\text{nl}}}}^{kq} = \frac{1}{m}\sum\limits_{i = 1}^{m} {\left\{ {\overline{N}_{{i,{\text{nl}}}}^{kq} - \left\langle {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{{i,{\text{nl}}}}^{kq} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{{{\text{nl}}}}^{kq} } \right\rangle } \right\}} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w12}^{kq} = \frac{1}{m}\sum\limits_{i = 1}^{m} {\left\{ {\overline{N}_{i,wl12}^{kq} - \left\langle {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w12}^{kq} } \right\rangle } \right\}} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w32}^{kq} = \frac{1}{m}\sum\limits_{i = 1}^{m} {\left\{ {\overline{N}_{i,w32}^{kq} - \left\langle {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w32}^{kq} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w32}^{kq} } \right\rangle } \right\}} \hfill \\ \end{gathered} \right.$$
(12)

where \(m\) is the number of ambiguity candidates of a specific satellite pair. “\(\left\langle { \, \cdot \, } \right\rangle\)” denotes the rounding option. Note that we will further align the fractional parts to avoid 1-cycle shift caused by the rounding option. After the averaging, the multi-frequency UPD products are obtained. In this study, they are further transferred into undifferenced forms by choosing a reference satellite.

Ambiguity-fixed phase OSB determination

After obtaining GPS/Galileo/BDS multi-frequency UPD products, it is possible to resolve multi-frequency ambiguities. Starting from (11), the integer nature of the float combined ambiguities can be recovered by applying UPD corrections calculated from (12). They become

$$\left\{ \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{{i,{\text{nl}}}}^{kq} = \overline{N}_{{i,{\text{nl}}}}^{kq} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{{{\text{nl}}}}^{kq} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq} = \overline{N}_{i,w12}^{kq} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w12}^{kq} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w32}^{kq} = \overline{N}_{i,w32}^{kq} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{b}}_{w32}^{kq} \hfill \\ \end{gathered} \right.$$
(13)

Generally, PPP ambiguities are resolved by adding constraints of (13) into the variance–covariance matrix to accelerate the convergence (Geng et al. 2020). However, for the server end that resolves the parameters of all stations at the same matrix, this would give rise to a huge matrix and render the ambiguity resolution impossible in real-time.

In this study, we rather choose to generate carrier-range observations, better adapted for real-time massive network data processing (Blewitt et al. 2010; Chen et al. 2014). The integer values of single-differenced raw ambiguities can be obtained by substituting (13) into (10), and as a result, we have

$$\left\{ {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,1}^{kq} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,2}^{kq} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,3}^{kq} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\tfrac{{f_{1}^{s} }}{{f_{1}^{s} - f_{2}^{s} }}} & { - \tfrac{{f_{2}^{s} }}{{f_{1}^{s} - f_{2}^{s} }}} & 0 \\ 1 & { - 1} & 0 \\ 0 & { - 1} & 1 \\ \end{array} } \right\}^{ - 1} \left\{ {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{{i,{\text{nl}}}}^{kq} + \tfrac{{f_{2}^{s} }}{{f_{1}^{s} - f_{2}^{s} }} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w32}^{kq} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{{i,{\text{nl}}}}^{kq} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{{i,{\text{nl}}}}^{kq} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{{i,{\text{nl}}}}^{kq} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w12}^{kq} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,w32}^{kq} } \\ \end{array} } \right\}$$
(14)

where we can see that the raw ambiguity of L1 and the L1/L2 narrow-lane ambiguity share the same integer value. The single-differenced raw ambiguities of (14) can be transferred into undifferenced form by selecting a satellite as the reference. In this study, we choose satellite \(q\) as the reference and define

$$\left\{ \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,1}^{kq} = N_{i,1}^{k} + \Delta N_{i,1} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,2}^{kq} = N_{i,2}^{k} + \Delta N_{i,2} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,3}^{kq} = N_{i,3}^{k} + \Delta N_{i,3} \hfill \\ \end{gathered} \right.$$
(15)

where \(\Delta N_{i,1}\),\(\Delta N_{i,2}\) and \(\Delta N_{i,3}\) denote frequency-specific constants which are introduced by fixing the reference ambiguity \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,j}^{q} (j = 1,2,3)\).

After obtaining the raw integer candidates of multi-frequency carrier-phase ambiguities, it is possible to do the carrier-phase observation modeling for phase OSB estimation. At the beginning, the unambiguous carrier-range observations can be derived as follows:

$$\overline{L}_{i,j}^{k} = L_{i,j}^{k} - \lambda_{j}^{s} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\overline{N}}_{i,j}^{kq} = L_{i,j}^{k} - \lambda_{j}^{s} \cdot (N_{i,j}^{k} + \Delta N_{i,j} )$$
(16)

Substituting (1) into (16), we get the following raw carrier-range function observations:

$$\overline{L}_{i,j}^{k} = \rho_{i,j}^{k} + c \cdot (t_{i} - t^{k} ) - \gamma_{j}^{s} \cdot I_{i}^{k} + \lambda_{j}^{s} \cdot (b_{i,j}^{s} - b_{j}^{\prime k} - \Delta N_{i,j} )$$
(17)

where \(\overline{L}_{i,j}^{k}\) denotes the carrier-range observations with respect to \(L_{i,j}^{k}\). To keep the consistency between pseudorange-based clocks and ambiguity-fixed OSBs, IGS legacy products shown in (5) are fixed in the above functions. Substituting \(\overline{t}^{k} = t^{k} + \frac{1}{c} \cdot D^{k}\) into (17), the carrier-range observations can be reparametrized as

$$\overline{L}_{i,j}^{k} + \overline{t}^{k} = \rho_{i,j}^{k} + c \cdot \overline{t}_{i,j}^{s} - \gamma_{j}^{s} \cdot I_{i}^{k} - \lambda_{j}^{s} \cdot B_{j}^{k}$$
(18)

and

$$\left\{ \begin{gathered} \overline{t}_{i,j}^{s} = t_{i} - \frac{1}{{f_{j}^{s} }}(b_{i,j}^{s} + \Delta N_{i,j} ) \hfill \\ B_{j}^{k} = b_{j}^{\prime k} - \frac{1}{{\lambda_{j}^{s} }}D^{k} \hfill \\ \end{gathered} \right.$$
(19)

where \(\overline{t}_{i,j}^{s}\) denotes a frequency-dependent parameter which absorbs physical receiver clock, hardware biases and the constant \(\Delta N_{i,j}\). \(B_{j}^{k}\) denote multi-frequency carrier-phase OSB estimates. Figure 1 shows one-epoch procedure of calculating the real-time ambiguity-fixed real-time phase OSB products in this study.

Fig. 1
figure 1

Flowchart of calculating ambiguity-fixed all-frequency real-time OSB products. Note that this shows only one epoch of the server-end data processing procedure

Full size image

Data processing

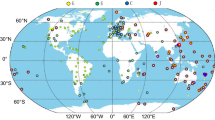
The ambiguity-fixed all-frequency phase OSB products have been continuously generated in the Wuhan IGS analysis center, routinely calculated by a workstation with 3.3 GHz, 8-cores CPU. The Intel math kernel library (MKL) is used to utilize the computing resources of the server fully. They can now be received from IGS ntrip casters with the mountpoint OSBC00WHU1. The real-time phase OSB products and clocks are also recorded and uploaded to ftp://igs.gnsswhu.cn/pub/whu/phasebias/ as standard product files with a latency of 3 h. The real-time observation streams of 180 globally distributed stations collected by BKG ntrip client (BNC) software are used for the products computation (shown in Fig. 2). Real-time orbit and clocks of Wuhan University are introduced as known products (Gu et al. 2018). Code OSB products released by the Chinese Academy of Sciences (CAS) are used to correct the hardware biases of pseudorange observations (Wang et al. 2016). GPS L1/L2/L5 and Galileo E1/E5a/E5b/E5/E6 pseudorange and carrier-phase observations are processed together in multi-frequency uncombined PPP. Antenna file IGS20.atx is applied to correct all-frequency antenna phase centers of both satellites and receivers (Rebischung and Schmid 2016). Troposphere delays are first corrected using the Saastamoinen, (1973) model, and then, the troposphere residuals are estimated based on the global mapping function (Boehm et al. 2006). To resolve GPS/Galileo/BDS multi-frequency ambiguities, the LAMBDA method is used to search for the optimal integer candidates (Teunissen 1994). The threshold of the ratio test is set as 3.0. A partial ambiguity resolution strategy is applied if the ratio test fails. If the partial ambiguity resolution cannot resolve ambiguities successfully, the ambiguity-float solutions are kept, meaning that no carrier-range observations can be generated in this epoch. More details of the server-end data processing are shown in Table 1.

Fig. 2
figure 2

Distribution of the stations used for real-time phase OSB computation and PPP-AR validation. Red circles denote the stations of the server end, while the green dots denote the stations used for PPP-AR

Full size image
Table 1 Details of the data processing of server-end PPP and OSB estimation
Full size table

To validate the real-time phase OSB products, simulated real-time PPP were implemented based on saved real-time orbit, clock and OSB products. This is because simulated real-time strategy is more convenient for implementing several PPP-AR experiments and free from maintaining lots of real-time procedures at the same time. Multi-frequency data collected from 82 IGS stations, covering day 68–74, 2023, are used for both kinematic and static PPP positioning.

Results

In this section, we first evaluate the time consumption of this method to demonstrate its efficiency in real-time network data processing. Next, we display the stability of the OSB products. Finally, the availability of those OSB products is validated through multi-frequency PPP-AR solutions.

Real-time computing efficiency

Calculation efficiency is important for a real-time phase bias service. In this study, we transferred raw observations to carrier-range observations first to achieve real-time network data processing. Figure 3 displays the time consumption of the typical UPD and ambiguity-fixed OSB methods based on carrier-range and raw observations, respectively. For the typical UPD method, the time consumption is linearly dependent on the number of stations since in this case PPP is carried out station by station. However, the computational burden is heavy to estimate ambiguity-fixed OSBs because all parameters are solved at once. Specifically, for a network processing of 100 stations, there will be about 10,000 parameters among the multi-GNSS and multi-frequency PPP observable matrix(as shown in Fig. 3), which take 120 s to be resolved in each epoch. At the same time, the requirement of computer memory grows exponentially with the number of parameters. In this case, carrier-range observations perfectly agree with the real-time task by eliminating integer ambiguities. After using carrier-range observations, the server takes 24 s only to process the data of 180 stations, which can meet a minimum product updating interval of 30 s.

Fig. 3
figure 3

Computation time consumption of different phase bias estimation methods of one epoch. The dashed gray line marks 30 s. The colored dashed lines denote the number of parameters of corresponding methods

Full size image

Real-time phase OSB products

The stability of real-time OSB products is important for the continuity of PPP-AR solutions. Cycle slips can be introduced in the observations when the OSB products have large or integer-cycle jumps. Figures 4 and 5 show the time series of phase OSBs of days 068–074 for GPS/Galileo and BDS-2/BDS-3, respectively. It is noted that BDS products of day 071 are missed due to the interruption of BDS orbit/clock streams at Wuhan University. All the GPS phase OSBs are continuous for one week without any integer-cycle jump. The mean standard deviations (STDs) of L1, L2 and L5 OSBs are 0.16, 0.23 and 0.24 ns, respectively, while the minimum STDs are about 0.1 ns. For Galileo, the performance of E5a/E5b/E5ab/E6 is comparable, achieving a mean STD of near 0.23 ns. A large jump of about over 1 cycle of E13 OSBs is detected at the end of day 074. BDS OSBs show a larger mean STD of about 0.3 ns for B1I/B1C and 0.4 ns for the other bands.

Fig. 4
figure 4

GPS/Galileo multi-frequency phase OSBs during days 068–074, 2023. In each panel, the minimum, maximum and mean STD of the time series are displayed in the bottom and satellites with the maximum OSB STD are colored as black. Panels i-j give the epoch-by-epoch OSB variations

Full size image
Fig. 5
figure 5

BDS-2/BDS-3 multi-frequency phase OSBs during the days 068–074, 2023. In each panel, the minimum, maximum and mean STD of the time series are displayed in the bottom and satellites with the maximum OSB STD are colored as black. Panels i-j give the epoch-by-epoch OSB variations

Full size image

Panels i and j of Figs. 4 and 5 display the epoch-by-epoch OSB variations. The OSB variations between adjacent epochs are plotted vertically in different colors and the variations before the 95th percentile are marked as black. Results show that the RMS of L1/E1 OSBs variations is 0.01 ns, while it is 0.02 ns for the other GPS/Galileo signals. About 97% of epoch-by-epoch variations of GPS L2/L5 and Galileo E5a/E5b/E5ab/E6 signals are within ± 0.05 ns, while 99% of the variations are within ± 0.1 ns. For BDS, mean RMSs of 0.03 ns and 0.05 ns are found with respect to B1I/B1C and B2I/B2a/B2b/B3I bands, respectively. About 95% of B1I/B1C OSB variations are within ± 0.05 ns, while those of B2I/B2a/B2b/B3I are 90% only. We should pay more attention when applying real-time BDS OSB products.

Multi-frequency kinematic PPP-AR

In this section, GPS/Galileo/BDS PPP-AR based on UPD products (WHU_UPD) and ambiguity-fixed phase OSB products (WHU_OSB) are carried out, respectively. At the same time, GPS/Galileo solutions based on CNES real-time orbit/clock/OSB products (CNES_OSB) are also presented. Figure 6 shows the horizontal positioning errors of real-time triple-frequency PPP-AR of 6 globally distributed stations from Fig. 2. It is shown that the ambiguity-fixed solutions of station BRUX, ALIC and USN7 are highly reliable and all of the epochs resolve the ambiguities correctly. In these areas, PPP-AR can converge in 5 min, achieving a positioning precision of 0.01 m in the horizontal directions. The performance of PPP-AR solution in the left area is weaker, indicating the comparably poor precision of the satellite phase OSBs in these areas. Multi-GNSS PPP-AR in these areas can converge in about 15 min and about 0.1–2.1% epochs could not resolve the ambiguities. Note that in this study the “convergence” of PPP solutions is recognized when the horizontal and vertical positioning errors fell into ± 5 cm and ± 20 cm for 20 min. For PPP-AR, we mark an epoch as “Failures” when the ratio test failed or the positioning errors are larger than the thresholds.

Fig. 6
figure 6

Horizontal positioning errors of GPS/BDS/Galileo kinematic PPP-AR. “Failures” represents the percentage of epochs for which the ambiguities are not successfully resolved

Full size image

Table 2 presents the statistics of the convergence time and positioning errors of PPP-AR solutions of all user stations among one week. GPS L1/L2/L5, Galileo E1/E5a/E6 and BDS-2 B1I/B2I/B3I, BDS-3 B1I/B2b/B3I signals are selected to carry out triple-/dual-frequency PPP. For solutions based on UPD products, results show clearly that triple-frequency GPS/Galileo/BDS PPP-AR can converge within 11.2 min. If ambiguity-fixed OSB products are applied instead, the mean convergence time of triple-frequency PPP-AR is only 7.2 min. As for GPS/Galileo triple-frequency PPP-AR, 14.8 min are required for solutions with respect to WHU UPD products to converge, which is 17% shorter than solutions based on CNES OSBs.

Table 2 Convergence time and positioning errors of PPP-AR with respect to UPD and ambiguity-fixed OSB products. For column “convergence time”, the mean convergence time of PPP-AR solutions is given to the left of “/”, while that of float PPP solutions is given to the right side. The percentages of solution which do not converge in 2 h are given in “()”. Positioning errors of east, north and up components of PPP-AR are divided by “/”
Full size table

Dual-frequency static PPP-AR

High-precision positioning performance of the real-time OSB products is validated in this section. The open-source software PRIDE PPP-AR is used for post-processing GPS/Galileo/BDS dual-frequency static PPP using real-time products of days 068–074, 2023. CNES products are also applied as a reference. GPS L1/L2, Galileo E1/E5a and BDS B1I/B3I signals are used for positioning. 126 IGS stations from Fig. 2 are included in the data processing. Figure 7 shows the mean narrow-lane ambiguity-fixing rates of globally distributed stations, which gives an overview of the product availability in different areas. The fixing rates represent the percentages of ambiguities which are resolved successfully in a post-processing strategy. It is obvious that GPS, Galileo and BDS-3 OSB products have good availability in Europe, Oceania and North America with a high narrow-lane ambiguity-fixing rate of more than 90%. As a regional system, BDS-2 can enable PPP-AR in the Asia Pacific area with the mean ambiguity-fixing rates of 60%.

Fig. 7
figure 7

Narrow-lane ambiguity-fixing rates of GPS/Galileo/BDS PPP-AR. a and b denote the results of GPS L1/L2 and Galileo E1/E5a, respectively, while c and d denote those of BDS-2 B1I/B3I and BDS-3 B1I/B3I, respectively

Full size image

Mean ambiguity-fixing rates and corresponding positioning errors of one-week solutions are given in Table 3. The RMS of positioning errors is calculated after the seven-parameter conversion by taking IGS weekly solutions as references. As we can see, CNES_OSB, WHU_UPD and WHU_OSB can achieve similar mean wide-lane fixing rates of about 88% for GPS satellites. However, the mean wide-lane fixing rate of Galileo satellites with respect to WHU products is 93%, while that of CNES is 99%. For narrow-lane ambiguities, the mean fixing rates of 79% and 77% for GPS and Galileo are achieved by WHU_UPD products, which are 6% and 5% higher than those of CNES. This can be understood by the better consistency between PRIDE PPP-AR and the software used in this study. Specifically, compared to WHU_UPD, WHU_OSB achieves the highest narrow-lane fixing rate of 82% and 85% for GPS and Galileo among the three products, which can at least indicate the significance of resolving ambiguities in the phase bias generation. For PPP combining BDS-2 and BDS-3, 60% and 76% percent of BDS-2 and BDS-3 narrow-lane ambiguities can be resolved successfully, achieving a positioning precision of 0.31, 0.30 and 0.60 cm for the east, north and up components.

Table 3 Mean ambiguity-fixing rates and positioning errors of static post-processing PPP-AR based on PRIDE PPP-AR software. Positioning errors of east, north and up components are divided by “/”
Full size table

All-frequency PPP-AR

To validate the flexibility of this multi-frequency OSB products, we designed three dual-frequency kinematic GPS/Galileo/BDS PPP-AR experiments based on different frequency choices: Solution I:GPS L1/L2 & Galileo E1/E5a & BDS B1I/B3I; Solution II:GPS L1/L5 & Galileo E1/E6 & BDS B1I/B2I(B2b) and Solution III: GPS L1/L5 & Galileo E1/E5b & BDS-3 B1C/B2a. Figure 8 shows three of the 2 h real-time PPP-AR positioning solutions of BRUX. It is clearly shown that the positioning errors of all three solutions converge rapidly in 5 min, indicating that ambiguities based on different frequency combinations could be resolved.

Fig. 8
figure 8

Horizontal positioning errors of three 2 h PPP-AR solutions of station BRUX. The gray dashed line marks 0.05 m

Full size image

Figure 9 shows the distribution of the fractional parts of wide-lane ambiguities. For brevity, results of Solution I and Solution II are displayed only. Residuals based on CNES OSBs are also displayed with green lines in the figures. We can see that more than 96% percent of residuals of Solution I are within ± 0.25 cycles. As for Solution II, the proportion of residuals falling into ± 0.25 cycles decreases to 89%, 75% and 82% for GPS, BDS-2 and BDS-3, respectively, while that of Galileo is still 99%.

Fig. 9
figure 9

Distribution of the fractional-cycle residuals of wide-lane ambiguities obtained from dual-frequency GPS/Galileo/BDS PPP based on WHU UPD and ambiguity-fixed OSB products. Results with respect to UPD products are colored black, while those with respect to ambiguity-fixed OSBs are colored red. Green lines mark the corresponding results based on CNES products

Full size image

The distribution of narrow-lane residuals is displayed in Fig. 10. Significant differences can be found with respect to UPDs (black) and ambiguity-fixed OSBs (red) residuals. For the results based on UPDs, 81% of GPS L1/L2 narrow-lane residuals fell into ± 0.15 cycles, while the proportion increases to 86.5% with ambiguity-fixed OSB products. Similar improvements can also be found on Galileo and BDS. Table 4 further gives the mean convergence time and positioning errors. We can see that Solution I PPP-AR can converge on average in 17.9 min, while those applying Solution II can also converge in 27.7 min. After resolving ambiguities successfully, a positioning precision of 0.01 m for the horizontal components can be achieved, demonstrating that all-frequency wide-lane and narrow-lane ambiguities are fixed correctly based on the same satellite clock/phase bias products.

Fig. 10
figure 10

Distribution of the fractional-cycle residuals of narrow-lane ambiguities obtained from dual-frequency GPS/Galileo/BDS PPP based on WHU UPD and ambiguity-fixed OSB products. Results with respect to UPD products are colored black, while those with respect to ambiguity-fixed OSBs are colored red. Green lines mark the corresponding results based on CNES products

Full size image
Table 4 Mean convergence time and positioning errors of all-frequency PPP-AR of Solution I, II and III. Refer to Table 3 for the other information
Full size table

Conclusions

In this study, we introduced a method to determine real-time multi-frequency phase OSB products based on IGS pseudorange-based satellite clocks. In this approach, the phase biases are estimated directly from GNSS observational model by resolving raw ambiguities rather than extracted from ambiguity estimates. The real-time OSB stream to IGS-RT service is initially assessed.

Together with satellite orbit/clock SSR corrections, one week of real-time phase OSB products were calculated and reserved first to implement PPP-AR experiments. GPS L1/L2/L5, Galileo E1/E5a/E5b/E5ab/E6 and BDS B1C/B1I/B2I/B2a/B2b/B3I OSBs are calculated reliably. The products were validated through triple-frequency kinematic PPP-AR experiments. Results show that GPS/Galileo/BDS PPP-AR can converge within several minutes in Europe, Oceania and North America. A mean convergence time of 7.2 min is achieved globally based on the ambiguity-fixed OSB products, showing an improvement of 36% compared to solutions based on UPD products.

PPP-AR using GPS L1/L5, Galileo E1/E6 and BDS B1I/B2I as the baseline frequencies were carried out successfully based on pseudorange-based satellite clocks. The narrow-lane ambiguities in the experiment are resolvable since about 95% of fractional-cycle residuals fell into ± 0.25 cycles. On average, the PPP-AR can converge successfully in 28 min.

Our results showed that BDS ambiguity-fixed OSBs are not as stable as GPS and Galileo ones, because of insufficient global observation streams and comparably weak precision of satellite orbit and clock products. As conclusion, it is encouraging to see that ambiguity-fixed OSB products enable higher ambiguity-fixing rates and faster convergence of PPP than UPD products, indicating that multi-frequency phase biases should be estimated from the observation modeling rather than from combined ambiguities such as MW combinations.