Introduction

As a timing base for Global Navigation Satellite Systems (GNSS), the performance of satellite-based atomic clocks directly affects navigation, positioning, and timing accuracy. Since the post-processed satellite clock bias (SCB) products provided by the International GNSS Service (IGS) have higher accuracy than those broadcasted by the broadcast ephemeris, it is important to use the IGS SCB product to establish a high-precision prediction model and improve the prediction accuracy of SCB. The commonly used prediction models include linear programming (LP) (Cernigliaro and Sesia 2012), quadratic polynomial (QP) (Huang et al. 2011; Huang et al. 2018), gray model (GM) (Liang et al. 2015; Lu et al. 2008), Kalman filter (KF) (Davis et al. 2012; Zhu et al. 2008), autoregressive integrated moving average (ARIMA) (Xi et al. 2014), and spectral analysis (SA) (Zheng et al. 2010; Zhao et al. 2021).

These prediction models have advantages and disadvantages: LP and QP models have the advantages of straightforward calculation and better short-term prediction accuracy. However, the accuracy and stability deteriorate significantly with time (Jonsson and Eklundh 2002). The GM model, ARIMA, and KF are affected by the characteristics of atomic clocks, the choice of key parameters, and the priori values of parameters (Zheng et al. 2009; Huang et al. 2014; Xu et al. 2013). The SA model requires a long time series of stable clock bias to implement its functionality (Heo et al. 2010). Since the time-varying properties of satellite-based atomic clocks are complex and are affected by many factors, neural network models have been applied to predict SCB. For example, the wavelet neural network (WNN) model (Wang et al. 2017) and supervised learning long short-term memory (SL-LSTM) model (Huang et al. 2021) have been used to predict the SCB of Global Positioning System (GPS) obtaining promising results.

The BeiDou Navigation Satellite System (BDS) differs from GPS in that its satellites operate on three types of orbits. The BDS-3 satellite constellation contains three Geostationary Orbit (GEO) satellites, three Inclined Geosynchronous Orbit (IGSO) satellites, and 24 Medium Earth Orbit (MEO) satellites. BDS provides worldwide basic navigation and satellite-based augmentation services. Two-way satellite-ground time transfer (TWSTF) is used for measuring SCB in BDS-2 broadcast ephemeris. BDS-3 increases inter-satellite link measurements compared to BDS-2 (Zhou et al. 2016; Liu et al. 2020) and generates SCB parameters in broadcast ephemeris using a combined short-term and long-term QP fit. IGS data centers, such as Wuhan University (WHU), Center for Orbit Determination in Europe (CODE), and German Research Center for Geosciences (GFZ), use observations from the multi-GNSS experiment (MGEX) to perform precise orbit determination of GPS, GLONASS, Galileo, and BDS, and provide precise orbit and clock bias products (Steigenberger et al. 2015; Zhao et al. 2013; Chen et al. 2014). The basic information on BDS satellites currently operating in orbit is listed in Table 1.

Table 1 BDS in-orbit satellites
Full size table

Neural networks in deep learning have developed rapidly (Dong et al. 2021), among which long short-term memory (LSTM) network has great potential and effectiveness in the prediction of nonlinear non-stationary time series. The BDS in-orbit satellite clock bias has complex characteristics whose prediction accuracy can still be improved. In this research, we apply the LSTM model for predicting the SCB of BDS-3 satellites and analyze the prediction performance of different in-orbit satellites over various time scales, to establish a reliable SCB prediction model.

In this research, the extraction process is applied to the dataset to form the input data and corresponding labels of the LSTM model. This method achieves multiple single-step predictions with the practical significance of avoiding the error accumulation problem caused by multi-step prediction. It improves processing speed by reducing matrix transposition and block division operations. In addition, the hyperparameters of the LSTM model are given for predicting 7-day BDS-3 SCB. Experiments on different types of BDS-3 satellites indicate that the model performance changes little when fine-tuning the model hyperparameters. Thus, a relatively robust LSTM model suitable for Beidou-3 SCB prediction is obtained.

Data sources and data pre-processing are introduced first. Next, the LSTM method is explained, and then, the results are shown. Furthermore, the results are compared in detail. The conclusion is given in the final part.

Data pre-processing

The 5-min interval high-precision SCB data for 70 days are selected as provided by the IGS Data Center of Wuhan University from August 30 to November 7, 2021. The SCB data of IGSO and MEO are analyzed since most IGS data centers do not currently provide the precise ephemeris data of BDS-3 GEO satellites.

The original SCB data are subject to anomalies such as data discontinuities, jumps, and gross errors (Feng 2009), which negatively impact the modeling and prediction of SCB. Data jumps are solved by using a moving window to find jump points (Zhou et al. 2016); the SCB data jump detection algorithm is based on the Hilbert transform (Guo 2013). For the problem of data discontinuity, a method of dividing the time-domain Allan variance by the Barnes deviation function was proposed to deal with data discontinuity (Riley and Howe 2008), and there exist methods for processing non-equidistant data (Hackman and Parker 1996). The methods described above can deal with these two types of problems. Maximum SCB data are selected without interruptions and jumps in the 70-day cycle. Gross errors are detected and eliminated necessarily since they always exist.

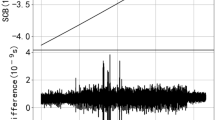
As shown in Fig. 1, PRN 35 and PRN 39 are the BDS-3 MEO and IGSO satellites, respectively. The abscissa “Epoch” represents the number of epochs, and the epoch interval is 5 min, while the ordinate represents the deviation of the satellite clock in the precise ephemeris relative to the ephemeris reference clock, i.e., SCB. The overall trend can be observed through the original SCB sequence, and the order of magnitude is μs. But the gross errors in the sequence are in the order of ns; thus, it is not easy to be observed.

Fig. 1
figure 1

Original SCB sequences of BDS-3 satellites in different orbits. Top: SCB of PRN 35 (BDS-3 MEO). Bottom: SCB of PRN 39 (BDS-3 IGSO)

Full size image

One of the most efficient ways to detect gross errors is to perform first differences on the original SCB sequence. For the SCB sequence \(L = \left\{ {l_{1} ,l_{2} ,...,l_{j} ...,l_{n} } \right\}\), the first-difference sequence is \(\Delta L = \left\{ {\Delta l_{1} ,\Delta l_{2} ,...,\Delta l_{j} ...,\Delta l_{n - 1} } \right\}\), where \(\Delta l_{j} = l_{j + 1} - l_{j}\), as shown in Fig. 2. It can be seen that there are some obvious abnormal data (in the order of 10 ns) called gross errors. The existence of gross errors will have a serious negative effect on the prediction accuracy of SCB, which has to be eliminated.

Fig. 2
figure 2

First differences of SCB sequences of BDS-3 satellites in different orbits. Top: First differences of PRN 35 (BDS-3 MEO). Bottom: First differences of PRN 39 (BDS-3 IGSO)

Full size image

The median absolute deviation (MAD) method is taken to replace the gross errors, whose mathematical model is expressed by

$$ \left| {\Delta l_{j} } \right| > (k + n \times {\text{MAD}}), $$
(1)

where \(k = Median\left\{ {\Delta L} \right\}\) is the median of first differences of SCB; \({\text{MAD}} = Median\left\{ {|\Delta l_{j} - k|/0.6745} \right\}\) is the absolute median deviation; the constant \(n\) is determined as needed. When \(\Delta l_{j}\) satisfies Eq. (1), it can be considered that \(\Delta l_{j}\) is a gross error. When gross errors are detected, the outlier can be replaced by a method such as the zeros padding or the cubic spline interpolation.

However, the traditional MAD method has limitations because the first-difference sequence still has a trend term. As shown in Fig. 3, the curve is the result of using the traditional MAD method to eliminate the gross errors, in which the first-difference sequences of PRN 35 and PRN 39 have very obvious trend terms. This can be seen from the expression:

$$ \Delta t^{s} = a_{0} + a_{1} \left( {t - t_{0} } \right) + a_{2} \left( {t - t_{0} } \right)^{2} + \Delta t_{r} , $$
(2)

where \(t_{0}\) is the initial moment (ephemeris reference time). \(a_{0} ,a_{1} ,and\,a_{2}\) are the clock bias, clock speed, and clock drift, respectively. \(\Delta t_{r}\) is the random term, whose statistical characteristics are only described by the clock stability. Ignoring the random term, the equation is a quadratic polynomial model. In practice, the magnitudes of \(a_{0} ,a_{1} ,and\,a_{2}\) are about 10−4, 10−10, and 10−20 s. For one satellite, only the influence of \(a_{1}\) and \(a_{2}\) remains after the first differencing. Since \(a_{2}\) is much smaller than \(a_{1}\), the traditional MAD method does not consider the influence of \(a_{2}\) so that the \(k\) value in the algorithm is a fixed constant. According to Eq. (1), data outside a certain range near the fixed \(k\) value will be eliminated and replaced, resulting in a serious loss of original data and a great increase in the prediction error, so the influence of \(a_{2}\) cannot be ignored.

Fig. 3
figure 3

Traditional MAD method to eliminate gross errors. Top: First differences after traditional MAD of PRN 35 (BDS-3 MEO). Bottom: First differences after traditional MAD of PRN 39 (BDS-3 IGSO)

Full size image

A straightforward idea is to make the sequence more “horizontal” by taking second differences and then take the traditional MAD method to eliminate gross errors. However, according to the principle of error propagation, it will cause the noise mean square error to be \(\sqrt 2\) times the original.

A dynamic MAD method (Huang et al. 2022) was proposed based on ridge regression (a modified least squares estimation method), where the trend term is fitted first, and then, the idea of MAD is applied to replace the gross errors. In this method, the authors redefine the expression for calculating \(k\). When \(\Delta l_{j}\) satisfies the following conditions:

$$ \left\{ {\begin{array}{*{20}c} {\left| {\Delta l_{j} - k} \right| > n \times {\text{MAD}}} \\ {k = \hat{\omega } = \left( {X^{T} X + \lambda I} \right)^{ - 1} X^{T} y} \\ \end{array} } \right., $$
(3)

it can be judged as a gross error. In Eq. (3), \(X\) is the time sequence; \(y\) is the first difference; \(I\) is the unit matrix; \(\lambda\) is the regularization coefficient, which needs to be determined from empirical values; and \(\hat{\omega }\) is the ridge regression value. \(k\) is the trend term contained in the first difference. The data outside a certain range near the \(k\) value are considered gross errors, which are eliminated and replaced by the cubic spline interpolation method, ensuring that as many original data are retained as possible, thus completing the data pre-processing step.

Methodology

Deep learning methods have been more widely used in solving nonlinear problems (Dong et al. 2021), and Recurrent Neural Network (RNN) is one of these approaches. RNN is a neural network with nodes directed to connect into a ring to find the series correlation by using the characteristics of its network structure, which is suitable for predictive filtering of time series and has been successfully applied in temporal data such as text, video, and speech.

Figure 4 shows the schematic diagram of RNN. The hidden node would have two parameters: weight and bias. However, a recurrent layer has three parameters to optimize: weight for the input, weight for the hidden unit, and bias. The parameters of the hidden layers in the RNN model inherit the output of the previous moment. It makes RNN that has the “memory” ability compared with other neural networks, so it can process the time series more effectively.

Fig. 4
figure 4

Schematic diagram of RNN. RNN has memory ability by using neurons with self-feedback, so it is suitable for processing time-series data

Full size image

LSTM is a variant of RNN that can solve the gradient disappearance and gradient explosion problems during the training of RNN models (Yu et al. 2019). A cell in the LSTM model has four gates, which enables the model to have long short-term memory and solves the gradient disappearance and gradient explosion problems. By introducing the “gate” mechanism, LSTM can give the network stronger memory ability and thus obtain better results for longer series. Figure 5 shows an LSTM neural network model. We provide a brief analysis of the applicability of the LSTM model based on the characteristics of the SCB sequence.

Fig. 5
figure 5

LSTM neural network model. Each cell of the LSTM model has four gates, which enable the model to have long short-term memory and solve the gradient disappearance and gradient explosion problems in RNN

Full size image

As the cell structure in the LSTM neural network model shown in Fig. 5, a cell has four gates: input gate \(i_{t}\), forget gate \(f_{t}\), select gate \(\tilde{C}_{t}\), and output gate \(o_{t}\), which are expressed as follows:

$$ f_{t} \, = \sigma \left( {W_{f} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{f} } \right), $$
(4)
$$ C_{t} \, = f_{t} *C_{t - 1} + i_{t} *\tilde{C}_{t} , $$
(5)
$$ i_{t} \, = \sigma \left( {W_{i} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{i} } \right), $$
(6)
$$ \tilde{C}_{t} \, = \tanh \left( {W_{C} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{C} } \right), $$
(7)
$$ o_{t} \, = \sigma \left( {W_{o} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{o} } \right), $$
(8)
$$ h_{t} \, = o_{t} *\tanh \left( {C_{t} } \right), $$
(9)

where \(\sigma\) denotes the sigmoid activation function. \(h_{t}\), \(C_{t}\), and \(x_{t}\) are the hidden state, the cell state, and the input at moment \(t\), respectively. \(W_{*}\) and \(b_{*}\) denote the weight matrix and bias of the current network layer, respectively. The information processing of LSTM is divided into three main stages:

  1. 1.

    Forgetting stage: In Eqs. (4) and (5), the input from the previous state node is selectively forgotten, that is, to control what needs to be remembered or forgotten in the previous state \(C_{t - 1}\) by \(f_{t}\).

  2. 2.

    Selective memory stage: In Eqs. (6) and (7), the inputs are remembered selectively, which important ones will be focused on and which unimportant ones will be remembered less. \(i_{t}\) is the input to the current cell, which can be selectively output by \(\tilde{C}_{t}\).

  3. 3.

    Output stage: In Eqs. (8) and (9), this stage is controlled by \(o_{t}\) and scaled using the tanh function on \(C_{t}\) to determine which outputs are used as the current state.

In Eq. (2), the random term \(\Delta t_{r}\) is affected by the physical characteristics of the atomic clock itself, which leads to the nonlinear and non-stationary characteristics of the SCB. The LSTM cell contains multiparameter nonlinear functions that can be automatically adjusted during training. Considering this characteristic, an LSTM neural network model is proposed for BDS-3 SCB prediction.

It is a fact that there exists the problem of prediction error accumulation. Time-series predicting includes single-step predicting and multi-step predicting. Single-step predicting refers to predicting one future value using all true values, while multi-step predicting refers to predicting multiple future values. In this case, numerous values are predicted in the future. If the multi-step predicting method is taken, the prediction error will be gradually accumulated because one predicted value may be affected by the previously predicted ones. In contrast, the single-step predicting method is taken to predict only one value without any error accumulation problem. So, the dataset is processed to make it into a multiple single-step predicting problem to avoid error accumulation.

For the whole time series \(\left\{ {x_{1} ,x_{2} ,...,x_{N} } \right\}\) in the training dataset, let \(p\) be the number of prediction days. In the training phase, all data are extracted with \(p\) as the sampling interval. The positive integer \(d\) is the dimension of the input data of the LSTM model and needs to satisfy:

$$ d \le \frac{N}{p} - 1, $$
(10)

then, it produces \(N - dp\) sequences:

$$ \left[ \begin{gathered} \left\{ {x_{1} ,x_{1 + p} ,x_{1 + 2p} , \ldots ,x_{1 + (d - 1)p} ,x_{1 + dp} } \right\} \hfill \\ \left\{ {x_{2} ,x_{2 + p} ,x_{2 + 2p} , \ldots ,x_{2 + (d - 1)p} ,x_{2 + dp} } \right\} \hfill \\ \ldots \hfill \\ \left\{ {x_{N - dp} ,x_{N - (d - 1)p} ,x_{N - (d - 2)p} , \ldots ,x_{N - p} ,x_{N} } \right\} \hfill \\ \end{gathered} \right], $$
(11)

The first \(d\) data of each sequence are used as input data during training, and the last ones are used as labels. Before training the LSTM model, all data need to be normalized first to improve the accuracy of the training model and the speed of model convergence. In the predicting stage, the latter \(d\) data of each sequence are taken as input to the trained LSTM model for predicting, and the output sequence \(\left\{ {x_{{1 + \left( {d + 1} \right)p}} ,x_{{2 + \left( {d + 1} \right)p}} ,...,x_{N + p} } \right\}\) are the values of \(N - dp\) single-step prediction results. Take the last \(p\) values, add the corresponding trend terms, and get the final SCB predictions by inverse difference (generate clock bias series using first differences).

By processing the dataset this way, the LSTM model does not have the problem of prediction error accumulation during predicting SCB, making the results more accurate and reliable. The implementation flowchart is shown in Fig. 6: (1) perform first differences on the original SCB data and take the ridge regression MAD method to eliminate gross errors, then subtract the fit trend term to obtain the pre-processed first differences of satellite clock bias (FDSCB). (2) Before training, the pre-processed data need to be normalized and dimensioned. The model parameters are saved at the end of the training. (3) Use the trained model for predicting. (4) The model outputs need to go through the reverse process of data pre-processing to obtain the final prediction results.

Fig. 6
figure 6

Implementation flowchart. The whole process is divided into three parts, data pre-processing (obtaining a stationary sequence), model training and predicting, and data post-processing (reconstructing the clock difference sequence)

Full size image

In this research, gross errors which will decline the prediction accuracy are detected first by performing first differences on the original SCB data, and then, the MAD method based on ridge regression is taken to replace the gross errors. Then, a more stable FDSCB series is obtained by subtracting the trend term, which is suitable as the input to the LSTM model. Next, it avoids the accumulation of the prediction error problem from multi-step predicting by processing the dataset and turning it into a multiple single-step predicting problem. Finally, the average root-mean-square errors (RMSEs) of all experimented satellites are calculated, and the SCB prediction accuracy of LSTM is compared with that of two traditional models (ARIMA and QP).

Results

The original SCB data are downloaded from the IGS Data Center of Wuhan University. The FDSCB data are generated after eliminating the gross errors as the input of the LSTM model to obtain the model output. The final SCB prediction data are obtained after data post-processing. All processing results for two satellites in different orbits during each step are shown.

Data pre-processing results

As shown in Fig. 7, the blue line represents the fitted results of the trend term \(k\), and the red one represents the fitted residuals, which are more stable and easier to fit and suitable to input into the LSTM model to predict. It completes the data pre-processing step. The range of FDSCB after pre-processing falls mostly between ± 0.5 ns, which means that the gross errors have almost been eliminated and replaced.

Fig. 7
figure 7

Fitting the trend term by ridge regression MAD (in blue) and pre-processed FDSCB (in red). Top: The fit trend term values and fitted residuals after ridge regression MAD of PRN 35 (BDS-3 MEO). Bottom: The fit trend term values and fitted residuals after ridge regression MAD of PRN 39 (BDS-3 IGSO)

Full size image

LSTM model output results

The LSTM model is established based on the Keras 2.7.0 deep learning environment with the specific parameters in Table 2. The 70-day FDSCB can be obtained through data pre-processing, after which 63 days of data are input as training data into the above-designed LSTM model for training. Some final losses during training are shown in Table 3.

Table 2 List of the LSTM model parameters
Full size table
Table 3 Final training error statistics based on the LSTM model for some satellites
Full size table

Then, the trained model is used for predicting, and the output series of the LSTM model is inverse normalized to obtain the FDSCB predictions. Figure 8 shows the comparison between the FDSCB predicted and true values for the next 7 days.

Fig. 8
figure 8

LSTM prediction output results. The blue curve is the true value of FDSCB, and the red one is the corresponding prediction. Top: The model output of PRN 35 (BDS-3 MEO). Bottom: The model output of PRN 39 (BDS-3 IGSO)

Full size image

SCB prediction results based on different models

The SCB prediction accuracy of the LSTM model is compared with two baseline models, ARIMA and QP. Figure 9 shows the deviations of the SCB predictions of BDS-3 satellites in short (0–6 h), medium (6 h–3 days), and long (3–7 days) terms based on LSTM, ARIMA, and QP.

Fig. 9
figure 9

Deviation diagram of short-, medium-, and long-term SCB predictions based on LSTM, ARIMA, and QP. Top: PRN 35 prediction error. Bottom: PRN 39 prediction error. Left: 0–6 h. Middle: 6 h–3 days. Right: 3–7 days. It means the prediction error at different stages

Full size image

Table 4 shows the statistical results of the average RMSE (\(\overline{{{\text{RMSE}}}}\)) of BDS-3 SCB predictions with good data continuity and no obvious jumps using the three models (results with 4 decimal places). For a single satellite \(i\), the RMSE is calculated as follows:

$$ {\text{RMSE}}_{i} = \sqrt {\frac{1}{p}\sum\nolimits_{k = 1}^{p} {(x_{k} - \hat{x}_{k} )} } , $$
(12)

where \(\hat{x}_{k}\) and \(x_{k}\) are the predicted and true values of SCB at the moment \(k\), respectively, and \(p\) is the number of predictions. For satellites of the same orbit, the \(\overline{RMSE}\) is calculated as follows:

$$ \overline{{{\text{RMSE}}}} = \frac{1}{m}\sum\limits_{i} {{\text{RMSE}}_{i} } , $$
(13)

where \(m\) is the number of satellites in the same orbit.

Table 4 \(\overline{{{\text{RMSE}}}}\) of SCB predictions of BDS satellites based on different models
Full size table

Discussion

Table 3 shows that the training loss values of the trained LSTM model using the MSE loss function for the data within 63 days are all less than 10–3, which tells us that the LSTM model has successfully performed regression fitting on the training dataset.

The 63-day pre-processed FDSCB is input into the trained LSTM model to predict the data for the next 7 days. It can be seen from the comparison results of the 7-day predicted values and the true values in Fig. 8 that the predicted curve is in good agreement with the true curve and reflects the trend and cycle characteristics of the true data. Therefore, the strong nonlinear fitting ability of the LSTM model is verified.

As shown from Fig. 9, the prediction accuracy of PRN 35 (BDS-3 MEO) in the short, medium, and long term is no more than 0.8, 8, and 27 ns, respectively. When it comes to PRN 39 (BDS-3 IGSO), they are no more than 3.2, 30, and 80 ns, respectively. The LSTM model has no obvious advantage in short-term predicting and is slightly worse than QP on satellite 35 and slightly worse than ARIMA on satellite 39. In medium- and long-term predicting, LSTM has the best effect, followed by QP, and ARIMA is the worst.

In Table 4, for all orbit types and all models, the SCB prediction errors increase as the prediction time increases. Compared with the other two models, the prediction ability of the LSTM model for the satellite clock errors of the two orbit types is optimal in the short, medium, and long term. For the BDS-3 IGSO satellites, the short-term prediction accuracy of LSTM is 0.4310 ns, which is 71.2% higher than ARIMA and 80.2% higher than QP; the medium-term prediction accuracy is 1.7874 ns, which is 91.5% higher than ARIMA and 81.7% higher than QP; and the long-term prediction accuracy is 19.1598 ns, which is 72.0% higher than ARIMA and 64.0% higher than QP. For the BDS-3 MEO satellites, the short-term prediction accuracy of LSTM is 0.2316 ns, which is 45.3% higher than ARIMA and 88.5% higher than QP; the medium-term prediction accuracy is 1.3899 ns, which is 88.1% higher than ARIMA and 86.6% higher than QP; and the long-term prediction accuracy is 8.5490 ns, which is 85.8% higher than ARIMA and 81.5% higher than QP.

Table 5 shows the accuracy improvement of the LSTM model compared with QP and ARIMA. As shown in Fig. 9, for the same type of single satellite, the short-term prediction accuracy may be slightly inferior to the other two traditional models, but after statistical processing of the experimental results, it can still show the advantage of the LSTM model in the performance of SCB prediction, especially in the long-term predicting.

Table 5 Accuracy improvement table of LSTM model compared with QP and ARIMA in percentage
Full size table

Experiments show that the LSTM model is comparable to the other two in short-term (within 6 h) prediction and performs better above 6 h. The average total time to process each satellite, i.e., train the model using 63 days of data and use the fitted model to predict SCB in the next 7 days, is about 20 min. With the same input data, the LSTM model takes longer to predict. This is a common problem of basic deep learning; that is, obtaining a neural network model through data-driven offline learning requires more computing time than traditional algorithms. Our operating environment is CPU R7 5800H and graphics card RTX3060. The time it takes about 20 min to predict SCB for the next 7 days is acceptable. In long-term predicting, when real-time broadcast ephemeris and precise ephemeris cannot be obtained in some cases, it is meaningful work to use the historical data of post-processed high-precision clock products to train the model to predict SCB.

While traditional QP and ARIMA models have achieved relatively good results in short-term predicting, prediction errors will diverge over time, resulting in poor predicting effects in medium- and long-term predictions. To date, there are relatively few studies on applying the LSTM neural network model to BDS-3 SCB prediction. The LSTM model in the field of deep learning realizes long sequence processing through a gating mechanism, which has considerable advantages in medium- and long-term predicting. Undeniably, the complexity of the deep learning neural network model is higher than that of traditional methods, but the LSTM method in this research can achieve better accuracy than QP and ARIMA in medium- and long-term SCB predicting.

Conclusions

This research applies an LSTM model for predicting BDS-3 SCB, including the data pre-processing and the cross-sectional comparison and analysis with two traditional models. To address the problem that the time series in engineering are nonlinear and non-smooth, which leads to the low accuracy of the predicting models in the traditional methods, we used a deep learning method to establish a multiple single-step predicting LSTM model using the precise ephemeris provided by the IGS Data Center of Wuhan University. The results are summarized and analyzed, which show that:

  1. 1.

    No matter which model is used, the clock difference prediction error will disperse with time. The LSTM model performs the short-, medium-, and long-term accuracy better than 0.5, 1.8, and 19.2 ns for the BDS-3 IGSO satellites. Meanwhile, it performs the short-, medium-, and long-term accuracy better than 0.3, 1.4, and 8.6 ns for the BDS-3 MEO satellites.

  2. 2.

    For satellites in the same orbit, the LSTM is the best, the ARIMA is the second best, and the QP is the worst for short-term SCB predicting in most cases; the LSTM is the best, the QP is the second best, and the ARIMA is the worst for medium- and long-term SCB predicting on all experimental satellites.

Basic deep learning is equivalent to the problem of function approximation, that is, the fitting of functions. Different from polynomial, B-spline, trigonometric, and wavelet functions used in traditional mathematics, nonlinear neural network functions are used as basis functions in deep learning. Among them, the LSTM neural network model is suitable for relatively long sequence prediction tasks, which improves the prediction accuracy of BDS-3 SCB. It positively impacts the reduction in positioning errors and is also expected to be applied to precise orbit determination.

Due to the limitation of the LSTM structure, the accuracy is not stable in short-term predicting. In future studies, the more popular attention-based transformer in recent years will be considered to model SCB prediction to achieve higher prediction accuracy.