A weighted mean temperature (T_m) augmentation method based on global latitude zone

Abstract

The weighted mean temperature (T_m) is a function of atmospheric temperature and vertical humidity profiles. It plays a crucial role in the progress of retrieving water vapor information from the tropospheric delay of GNSS signals. The T_m estimated by the empirical models is always used to convert the zenith wet delay (ZWD) to precipitable water vapor (PWV) in GNSS meteorology. However, these empirical T_m models used trigonometric functions, making it difficult to describe T_m in detail and leading to an obvious accuracy difference with latitude changes. Thus, a global latitude zone augmentation mode was adopted for the empirical T_m models; the augmentation coefficients for each latitude zone were obtained by introducing the measured surface temperature and using the least-squares method. Using the T_m data of 2011–2015 derived from radiosonde, the GPT3 model, UNB3m model, and GWTMD model were augmented and analyzed. The results show that all augmentation models can improve the accuracy of the estimated T_m compared with their corresponding original models, and their levels of improvement are different. The three augmentation models achieved an average RMSE of 2.79 K, 3.47 K, and 3.22 K, which correspond to 22%, 49%, and 8% improvement against the GPT3 model, UNB3m model, and GWTMD model. In addition, the comparisons with the T_m linear formula were carried out and showed the superiority of the augmentation models.

Introduction

In GNSS meteorology, the GNSS technique is regarded as an emerging and robust tool for remotely sensing precipitable water vapor (PWV) with advantages of high accuracy, all-weather capability, high spatial–temporal resolution, and cost-effective (Bevis et al. 1992; Duan et al. 1996; Chung et al. 2014; Yang et al. 2021a). The GNSS-derived PWV over a station is obtained by multiplying the zenith wet delay (ZWD) with a conversion factor II, which is a function of the weighted mean temperature (T_m) (Bevis et al. 1994; Dousa et al. 2018; Yang et al. 2021b). Thus, T_m has become a key parameter in the research of GNSS meteorology (Wang et al. 2016; Zhang et al. 2017; Yang et al. 2021c).

The weighted mean temperature, a function of atmospheric temperature and vertical humidity profiles, can be determined exactly using radiosonde data (Davis et al. 1985; Huang et al. 2021). But there is often no collocated radiosonde data available for the GNSS site since the radiosonde station is sparsely distributed, and the radiosonde balloon is launched fixed at several UTC epochs every day. The relationship between the surface temperature (T_s) and the weighted mean temperature (T_m) was adopted to estimate the value of T_m by constructing the T_s–T_m linear formula, such as the Bevis formula (Bevis et al. 1992). On the other hand, several empirical T_m models based only on the coordinates of the site and the time were proposed in recent years to achieve the T_m at any time at any GNSS site.

Yao et al. (2012) constructed the global weighted mean temperature (GWMT) model using radiosonde data from 135 global stations from 2005 to 2009. An updated model GT_m-II was proposed to solve the poor performance in the southern Pacific Ocean of the GWMT model (Yao et al. 2013). Taking into account the semi-annual and diurnal variations of T_m and considering the T_m lapse rate as a function of coordinates instead of a constant value, the GT_m-III and GWMT-IV models have been established (Yao et al. 2014a; He et al. 2013). Then, the developed GT_m-X model was built in a global resolution of a 1°*1° geographical grid (Chen et al. 2015). Focused on the diurnal variation and the lapse rate of T_m, He et al. (2017) proposed a voxel-based T_m model using T_m data over 4 years from 2010 to 2013. Huang et al. (2018) established the GGT_m model based on a sliding window algorithm. Sun et al. (2019) proposed the Gtrop model by considering the temporal variations by linear trends, annual, and semi-annual variations, and spatial variations. By exploring the time characteristics of the T_m lapse rate globally, Yang et al. (2020) proposed an improved T_m model. In addition, the empirical tropospheric delay models, such as the UNB3m and GPT3 models, can also give the T_m estimates at GNSS sites (Leandro et al. 2008; Bohm et al. 2015; Landskron et al. 2018). Meanwhile, some regional empirical models also have been established (Huang et al. 2019; Long et al. 2021). However, these empirical T_m models based on periodic function are difficult to describe T_m in detail, and their accuracy often shows obvious differences with the latitude changes. Thus, there is still room for improving the accuracy of these empirical models in T_m estimation.

We adopted an augmentation mode for the empirical T_m model, which acquires the augmentation coefficients by introducing the measured surface temperature to improve the accuracy of T_m estimation. Since the value of T_m mainly changes with latitude in space and the performance of the empirical T_m models is also affected by latitude (Yao et al. 2014b), we constructed the augmentation coefficients for different latitude zones. The T_m data of 2011–2015 derived from radiosonde were divided into twelve latitude zones, and 4/5 and 1/5 of the radiosonde sites in each latitude zone were utilized as the modeling and validated data. Considering that the ground meteorological sensors are becoming more common and economical in the GNSS community, surface temperature data are easily available along with the GNSS observations. It ensures the above augmentation method can be well used and promoted. In our experiment, the GPT3 model, UNB3m model, and GWTMD model were selected to conduct the augmentation due to their high grid resolution, open-source, and easy operation. The augmentation mode could be applied to each T_m empirical model.

Empirical T _m model and the augmentation method

As the latest version of the global pressure and temperature (GPT) series models, the GPT3 model established on monthly meteorological data of 10-year ERA-Interim can provide the surface temperature (T_s) and weight mean temperature I with a global resolution of 1° × 1° geographical grid. In this process, the mean value, as well as annual $\left( {A_{1} ,B_{1} } \right)$ and semi-annual $\left( {A_{2} ,B_{2} } \right)$ variations, are adopted in the following formula:

$$ \begin{aligned} r\left( t \right) = & A_{0} + A_{1} \cos \left( {\frac{{{\text{doy}}}}{365.25}2\pi } \right) + B_{1} \sin \left( {\frac{{{\text{doy}}}}{365.25}2\pi } \right) \\ & + A_{2} \cos \left( {\frac{{{\text{doy}}}}{365.25}4\pi } \right) + B_{2} \sin \left( {\frac{{{\text{doy}}}}{365.25}4\pi } \right) \\ \end{aligned} $$

(1)

where doy is the day of the year and $r\left( t \right)$ denotes the T_s or T_m, respectively.

In the UNB3m model, a look-up table for meteorological parameters derived from the U.S. Standard Atmosphere Supplement, 1966 (COESA 1966) is used. The parameters are pressure (P), temperature (T_s), relative humidity (Rh), temperature lapse rate (β), and water vapor pressure height factor (λ). Using the look-up table, the annual average and amplitude of these parameters can be computed as follows:

$$ A_{\phi } = \left\{ {\begin{array}{*{20}l} {A_{15} ,} \hfill & {{\text{if}}\;\varphi \le 15} \hfill \\ {A_{75} ,} \hfill & {{\text{if}}\;\phi \ge 75} \hfill \\ {A_{i} + \frac{{\left( {A_{i + 1} - A_{i} } \right)}}{15}\left( {\varphi - {\text{Lat}}_{i} } \right),} \hfill & {{\text{if}}\;15 < \varphi < 75} \hfill \\ \end{array} } \right. $$

(2)

where $A_{\varphi }$ stands for the computed average or amplitude, $\varphi$ denotes the latitude of interest, i is the index of the nearest lower tabled latitude and Lat stands for latitude. After the average and amplitude are computed for a given latitude, these five parameters can be estimated for the desired day of the year according to the following formula:

$$ X_{{\varphi ,{\text{doy}}}} = Avg_{\varphi } - Amp_{\varphi } \cos \left( {\left( {{\text{doy}} - 28} \right)\frac{2\pi }{{365.25}}} \right) $$

(3)

where $X_{\varphi ,doy}$ represents the computed five parameters for latitude $\varphi$ and day of the year. $Avg_{\varphi }$ and $Amp_{\varphi }$ are the computed average or amplitude using (2), respectively. Then, the T_m is estimated from the following formula:

$$ T_{m} = \left( {T_{0} - \beta H} \right)\left( {1 - \frac{\beta R}{{g_{m} \lambda^{\prime } }}} \right) $$

(4)

where $\lambda^{\prime } = \lambda + 1$, $T_{0}$, $\beta$ and $\lambda$ are the meteorological parameters computed according to (3). R is the gas constant for dry air (287.054 Jkg⁻¹ K⁻¹), $g_{m}$ is the acceleration of gravity at the atmospheric column centroid in $m \cdot s^{ - 2}$, and H denotes the orthometric height in m.

In the GWTMD model, the annual mean value and the coefficients of the annual and semi-annual variations of Tm are stored at the four reference height levels and the four reference times. To determine the T_m of the target location $\left( {\varphi ,\lambda ,h} \right)$, four steps are required: (1) to determine the two nearest reference height levels close to h and the other four vertical surfaces containing the eight voxels closest to $\left( {\varphi ,\lambda } \right)$, and to calculate the T_m values for the reference times on the eight voxels; (2) the T_m for the four grid points at the height of h are linearly interpolated from the T_m values on the two nearest reference heights; (3) The T_m at target point is horizontally interpolated by the T_m values on the four corners; (4) a spline interpolation in the time domain is carried out to find the T_m of the target location for the specific time of the day using the T_m values from the previous step.

For the GPT3 and UNB3m models, the T_s can be estimated as well as T_m. Thus, the augmentation mode for the two models is shown as the following formula:

$$ {\text{T}}_{{\text{m}}} = {\text{T}}_{{\text{m}}}^{{\text{M}}} + A \cdot \left( {{\text{T}}_{{\text{s}}} - {\text{T}}_{{\text{s}}}^{{\text{M}}} } \right) $$

(5)

where the $T_{m}^{M}$ and $T_{s}^{M}$ are the T_m and T_s values estimated by the GPT3 or UNB3m model, T_s is the measured surface temperature, T_m is the augmented T_m value, and A represents the augmentation coefficients for each model.

For the GWTMD model, only T_m value is estimated. Thus, the following formula was tried to conduct the augmentation:

$$ {\text{T}}_{{\text{m}}} = {\text{T}}_{{\text{m}}}^{{\text{M}}} + A \cdot {\text{T}}_{{\text{s}}} $$

(6)

where the parameters are similar to those in (5). $T_{m}^{M}$ refers to the T_m estimated by the GWTMD model, T_s is the measured surface temperature and T_m is the augmented T_m value. After achieving the T_m values from radiosonde and corresponding models, and T_s from observation data and the models, the least-squares method is applied to compute the augmentation coefficients A.

Experiment

The radiosonde that measured the atmospheric profiles is selected to conduct the augmentation mode for these three models. The globally distributed radiosonde sites can provide surface variables and pressure level parameters, including temperature, relative humidity, pressure, and other meteorological parameters. The daily data can be retrieved from the upper-air archive at the website of the University of Wyoming (available on http://weather.uwyo.edu/ypperair/sounding.html). The exact T_m value at each epoch of a certain site can be exactly calculated using the discretized formula as follows:

$$ T_{m} = \frac{{\sum\nolimits_{i = 1}^{N} {\left( {\frac{{e_{i} }}{{T_{i} }} + \frac{{e_{i + i} }}{{T_{i + 1} }}} \right)\frac{{\Delta z_{i} }}{2}} }}{{\sum\nolimits_{i = 1}^{N} {\left( {\frac{{e_{i} }}{{T_{i}^{2} }} + \frac{{e_{i + 1} }}{{T_{i + 1}^{2} }}} \right)\frac{{\Delta z_{i} }}{2}} }} $$

(7)

where i is the ith pressure level, N is the total number of layers and $\Delta z_{i}$ is the thickness of the ith layer. e and T represent the water vapor pressure and temperature at the corresponding layer, respectively.

The raw measurements of radiosonde are considered outliers in the following cases, such as the difference in height between two successive levels is greater than 10 km; the total number of valid pressure levels is less than 20; the height of the top pressure level is lower than 10 km; the gap between two successive atmospheric pressure levels is greater than 200 hPa; the number of radiosonde records in the site of interest is less than half a year (Long et al. 2021). These outliers were eliminated in a preprocessing to achieve the exact T_m value. After excluding the outliers and the unqualified sites, a total of 507 radiosonde sites from 2011 to 2015 were selected to compute the T_m using (7) and provide the measured T_s.

Considering that the accuracy of the empirical T_m models is affected by latitude, we tried to calculate the augmentation coefficients in different latitude zones. According to the differences in the distribution of radiosonde in the northern and southern hemispheres, twelve latitude zones are divided, i.e., 90°–70° N, 70°–60° N, 60°–50° N, 50°–40° N, 40°–30° N, 30°–20° N, 20°–10° N, 0°–10° N, 0°–10° S, 10°–20° S, 20°–30° S, 30°–90° S. In each latitude zone, the number of radiosonde sites is 16, 47, 95, 93, 97, 54, 15, 23, 17, 15, 17, 18, respectively, and 4/5 of the radiosonde sites are utilized to conduct the augmentation mode using (5) and (6), and the remaining 1/5 of radiosonde sites are used for validation. Figure 1 shows the distribution of the selected radiosonde sites, in which the blue circles and red triangles represent the sites for modeling and validation, respectively.

Fig. 1

Distribution of the selected radiosonde sites

Several statistical quantities including bias and root-mean-square error (RMSE) were chosen as criteria to assess the validation. The corresponding equations are described as follows:

$$ bias = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {T_{{m_{i} }} - T_{{m_{i} }}^{r} } \right)} $$

(8)

$$ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {T_{{m_{i} }} - T_{{m_{i} }}^{r} } \right)^{2} } } $$

(9)

where $T_{{m_{i} }}$ and $T_{{m_{i} }}^{r}$ are the T_m values from the different models and the reference, respectively. N refers to the number of samples.

Validation of the augmentation models

The 412 radiosonde sites were used to conduct the augmentation mode for the three models, and the new models are called GPT3-R, UNB3m-R, and GWTMD-R models. To assess their performances, the T_m from 2011 to 2015 derived from (7) at these 95 radiosonde sites were regarded as the references. The estimated T_m values derived from the six models and the corresponding reference T_m values at all validated sites are counted and shown as a scatter diagram in Fig. 2, in which the black dashed line refers to a 1:1 straight line and the red straight line represents a linear fit line between the estimated and reference T_m. It can be seen that the UNB3m model performs worst with the most scattered distribution of the points before the augmentation. The performances of the original three models are effectively improved by the corresponding augmentation models with more points concentrated near the fitted line. Specifically, the slopes of the linear fitting for the three original models increased from 0.85 to 0.92, from 0.94 to 0.99, and from 0.86 to 0.93 after the augmentation, respectively. Note that the scatter diagrams of the three original models are all truncated at both ends, indicating that the maximum and minimum values of the three models are limited. The GPT3-R and UNB3m-R model effectively improved this phenomenon, but the GWTMD-R model did not.

Fig.2

Scatter plots of estimated T_m and reference T_m for the six models

The T_m values at 95 validated sites are all counted, and the statistical results for the six models are listed in Table 1. The three augmentation models effectively improved the statistics of their original models in terms of bias, RMSE, and correlation coefficient, respectively. It showed that the UNB3m-R model has the most significant improvement compared with its original model, with the bias from − 5.05 to − 0.2 K, the RMSE from 7.89 to 4.06 K, and the correlation coefficient from 0.88 to 0.94. For the RMSE, the improvement of the UNB3m-R model is 3.83 K reaching approximately 49%, and the value and percentage of the improvement are 1.15 K/26% and 0.28 K/7% for the GPT3-R and GWTMD-R model, respectively. Although the improvement is not as large as the UNB3m-R model, the GPT3-R model still achieves the best accuracy for T_m estimation among the six models with the three best statistics of 0.07 K, 3.27 K, and 0.96.

Table 1 statistical results of all validate sites for the six models

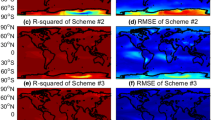
To assess the performances of the six models in different regions, the RMSE of T_m for each validated site is computed and illustrated in Fig. 3, in which the spatial variation in the accuracy of the six models can be seen. The accuracy of the three original models is affected by latitude, i.e., the RMSE in low latitudes is better than that in high latitudes. The accuracy of Tm in each latitude zone for the three augmentation models is improved compared with their original models. It can still be seen that the RMSE of the three augmentation models is slightly related to latitude. This is because the variation and fluctuation of T_m are more frequent in high latitudes, which is difficult to depict by models. The UNB3m model performs worst with most of the sites having RMSE greater than 5 K, and the percentage reaches 73%. For the UNB3m-R model, the sites with a value of RMSE greater than 5 K account only for 16%, and the largest improvement is 12.7 K from 16.2 K to 3.5 K. It is observed that the GPT3-R model achieves an accuracy of better than 5 K at all site, and the percentage of sites with a value of RMSE smaller than 4 K reaches 85%. The values become 39%, 43%, and 48% for the GPT3, GWTMD, and GWTMD-R models, respectively.

Fig. 3

Global distribution of T_m RMSE for the six models

The biases of T_m for each validated site are also counted and illustrated in Fig. 4. It can be seen that the biases of the UNB3m model and the GWTMD model show certain characteristics on a global scale, that is, the biases of the UNB3m model and the GWTMD model are negative and positive at most of the sites, respectively. The GPT3 model does not show this phenomenon and contains sites with warm and cold biases. After the augmentation, the large warm/cold biases are reduced, and more sites with bias close to 0 appear in these three augmentation models. The percentage of sites with absolute bias less than 1 K is 68%, 9%, and 45% for the three original models, respectively, and these values become to 86%, 40%, and 89% for the three augmentation models, respectively.

Fig. 4

Global distribution of T_m biases for the six models

Furthermore, the T_m RMSE of the six models in different latitude zones is counted and listed in Table 2. It is observed that the performance of each model in high latitudes is always worse than that in low latitudes, which is similar to Fig. 3. Compared with the UNB3m model, the improvement of the UNB3m-R model reaches the maximum in the latitude zone of 70°–90° N, close to approximately 67%, and the minimum improvement is 34% in the latitude zone of 20°–30° S; the average percentage of improvement by the UNB3-R model is 49%. For the GPT3-R and GWTMD-R models, the maximum, minimum, and average percentages are 33%, 8%, 22%, and 27%, 1%, 8%, respectively.

Table 2 Statistical results of T_m RMSE for the six models in different zones

The T_m residuals of all sites for the six models are represented by a histogram in Fig. 5, which also shows the mean, median, standard deviation (SD), and mode value. All the indicators of the augmentation models are better than those of the corresponding original models. The histograms of all models are normally distributed, only the symmetry axis of the UNB3m model deviates from the straight line of x = 0. The three augmentation models perform better than their corresponding original models with more residuals concentrated around zero. As for the absolute residuals smaller than 5 K, the GPT3-R model has the largest percentage of 89%, the UNB3m model has the smallest percentage of 49%, and the percentages are 76%, 80%, 78%, and 81% for the GPT3, UNB3m-R, GWTMD, and GWTMD-R model, respectively.

Fig. 5

Histogram of the T_m residuals for the six models

To analyze the improvement of the augmentation models to the T_m accuracy at different times, the RMSE for all sites is calculated daily and their time series are shown in Fig. 6. It is observed that the RMSE of six models has obvious annual cycles and seasonal changes, which experience a decrease from winter to summer and then an increase from summer to winter. The maximum RMSE appears generally in winter and the minimum values are in summer. The UNB3m model performs worst almost every day, its augmentation model achieves the greatest improvement. Among the six models, the GPT3-R model has the best performance and effectively improves the accuracy of its original model, while the daily improvement of the GWTMD-R model is not obvious compared to its original model. Note that the augmentation models have an effective improvement on the seasonal difference, especially the GPT3-R and UNB3m-R models.

Fig. 6

Time series of daily T_m for the six models

To further show the distribution of daily RMSE, the empirical distribution function of T_m RMSE for the six models is depicted in Fig. 7. Compared with the results of the three original models represented by the black, cyan, and green curves, the corresponding blue, red and yellow curves are closer to the position of 0 K and cover a relatively smaller range of the horizontal axis, showing a better distribution of the results of the augmentation model. The UNB3m model performs worst with most of the daily RMSE greater than 6 K, and its augmentation model effectively improves this phenomenon. When setting the daily RMSE with a value greater than 4 K, the cumulative probabilities are 65%, 9%, 100%, 41%, 53%, and 40% for the GPT3, GPT3-R, UNB3m, UNB3m-R, GWTMD and GWTMD-R model, respectively, which indicates the performance and improvement of each model in daily T_m estimation.

Fig. 7

Empirical distribution function of the daily RMSE in different models

Comparison with the T _s-T _m linear formula

Considering that the surface temperature is required in the augmentation methods, it is necessary to compare the accuracy of the proposed augmentation models with the T_s–T_m linear formulas. Therefore, the radiosonde sites used to construct the augmentation coefficients were again adopted to fit the T_s–T_m linear formula for each latitude zone, and the T_m values of the validated sites in each latitude zone were calculated based on these fitted formulas. In addition, the widely used Bevis formula was also added to this comparison.

The RMSE distribution in each latitude zone of the three augmentation models as well as those of the Bevis and the fitted T_s–T_m linear formula is shown in Fig. 8. The shapes with different colors represent these models and formulas, and the dashed lines refer to the average value of the RMSE for the corresponding methods. It can be seen that the Bevis formula performs the worst with an average RMSE of 3.80 K and a larger RMSE in each latitude zone. The fitted T_s–T_m linear formula achieved a better performance than the Bevis formula, with an average RMSE of 3.37 K. It illustrates that the Bevis formula is not suitable for the global application and accurate T_s–T_m linear formula needs to be fitted in the corresponding region of interest. Note that the UNB3m-R model outperforms the Bevis formula but is slightly worse than the fitted T_s–T_m linear formula, which may be due to the poor accuracy of UNB3m itself. The average RMSE of the other two augmentation models is smaller than those of the Bevis and the fitted T_s–T_m formula, indicating that using the augmentation model to calculate Tm is more accurate compared to using the T_s–T_m linear formula when the surface temperature is provided. Especially for the GPT3-R model, its RMSE in each latitude zone is significantly smaller than that of the Bevis and fitted T_s–T_m linear formula, and the improvement of the average RMSE reaches 27% and 17%, respectively. Specifically, the RMSE of T_m calculated by the Bevis formula and the fitted T_s–T_m linear formula in each latitude zone is counted and listed in Table 3, which can be compared with Table 2.

Fig. 8

RMSE distribution of the augmentation models and the linear formulas for each latitude zone

Table 3 Statistical results of T_m RMSE for the Bevis and fitted T_s–T_m linear formula in different latitude zones

Conclusion

The T_m, which acted as a key parameter in converting ZWD to PWV in GNSS meteorology, is generally estimated by using the global empirical models, such as GPT3, UNB3m, and GWTMD model, which are considered to be more convenient and more suitable for global application compared to the Bevis formula and the regional empirical models. These empirical T_m models are based on periodic function, they are difficult to describe T_m in detail and their accuracy often shows obvious differences with the latitude changes. Therefore, a global latitude zone augmentation mode was adopted for the three empirical T_m models, and their augmentation coefficients for each latitude zones were obtained by introducing the measured surface temperature and using the least-squares method.

The comprehensive comparisons between the three augmentation models and their corresponding original models were conducted using the 5 years of data derived from the radiosonde. The numerical results show that all the augmentation models can improve the accuracy of the T_m estimation compared with their corresponding original model, but their improvement degree is different. The UNB3m model performs the worst of the six models in terms of the scatter plots, the spatial distribution of RMSE and bias, the T_m residual analysis, and the results of daily T_m RMSE. After the augmentation, the slope of the linear fitting for the UNB3m-R model increased from 0.94 to 0.99, the average RMSE of different latitude zones for the UNB3m-R model decreased from 6.75 to 3.47 K, the SD of the T_m residuals for the UNB3m-R model decreased from 6.12 to 4.12 K, and the average value of daily T_m RMSE for the UNB3m-R model decreased from 7.78 to 4.03 K. It has the greatest improvement among the three augmentation models. The improvement of the GPT3-R model is not as large as the UNB3m-R model, but it achieves the best accuracy for T_m estimation in all types of comparisons. The GWTMD-R model only has a slight improvement in T_m estimation compared with its original model, since the GWTMD model cannot provide T_s estimates in the construction of the augmentation model. Moreover, the Bevis and the fitted T_s–T_m linear formula were compared with the proposed models, which demonstrated that it is more reasonable to use the augmentation model to calculate Tm than to use the T_s–T_m linear formula directly when the surface temperature is available. In the follow-up research, more detailed augmentation coefficients need to be explored, such as solving the augmentation coefficients at each model grid of the empirical T_m model.