Introduction

The level of stringency of positioning, navigation and timing (PNT) requirements is increasing with emerging mission-critical intelligent transportation system (ITS) applications in urban areas. As one of the main PNT sources, GNSS is widely used for vehicle positioning (Feng and Law 2002). GNSS signals, however, are prone to reflection, diffraction and blockage by surrounding buildings, resulting in multipath interference and non-line-of-sight (NLOS) reception in urban areas. This can result in pseudorange errors tens of meters in magnitude, leading to unacceptable positioning errors for ITS applications (MacGougan et al. 2002). To date, these effects are largely mitigated through hardware design (i.e., antenna design), signal processing and measurement-based modeling.

Among antenna design-based methods, choke-ring and dual-polarization antennas are commonly used to mitigate the effects of multipath and NLOS signals (Sun et al. 2021a; Li and Schwieger 2018). The cost and bulky size of the antennas limit the applications for ITS in urban environments, however. Signal processing methods can be used to reduce certain kinds of multipath error by improving the form of the receiver correlator structure design or correlator function, but they are not able to address NLOS effects (Yang 2016; Chen et al. 2020; He et al. 2020; Kumar and Singh 2020; Qi et al. 2021).

Measurement-based modeling methods improve the positioning accuracy in urban areas by combining GNSS measurements, observables and other information sources in the measurement domain to ameliorate the effects of NLOS reception and multipath. For example, data from additional sources, such as spatial information (i.e., 3D city models), inertial measurement units (IMU) and vision sensors, are used together with GNSS measurements to improve positioning accuracy in urban canyons (Sun et al. 2021c; Bhatti et al. 2007). The famous shadow matching method uses 3D city models to detect and exclude NLOS and therefore obtain improved urban positioning results (Groves 2011; Yozevitch and Ben Moshe 2015; Wang et al. 2015; Adjrad and Groves 2018; Xu et al. 2020; Zhang et al. 2020). Accurate positioning can also be achieved in urban areas by the weighted average of the candidate positions, which are generated by comparing the similarity between the simulated and actual pseudorange measurements with the assistance of the surrounding geospatial information (Miura et al. 2013, 2015; Hsu et al. 2016; Hsu 2017).

The extent to which the mentioned algorithms are able to improve positioning in urban areas by reducing the errors due to NLOS is constrained by some key issues, however. One of the main issues is the determination of the threshold of the variable (i.e., C/N0, elevation angle, etc.) for the NLOS detection. One recent proposal to address this is to use machine learning algorithms, where a training process is conducted to extract the rules for the input variables from raw GNSS measurements, including signal strength, satellite elevation angle, satellite azimuth angle, pseudorange residuals, pseudorange rate, number of visible satellites and dilution of precision (DOP) or their combinations and the corresponding output signal reception classifications (i.e., line-of-sight (LOS)/NLOS or LOS/multipath/NLOS). The rules extracted from the corresponding input and output variables are applied to newly collected GNSS data to predict the signal reception classifications. The position is then calculated by excluding the predicted NLOS/multipath signals (Yozevitch et al. 2016; Guermah et al. 2018; Quan et al. 2018; Sun et al. 2019, 2020). The positioning accuracy achievable through this approach is constrained, however, since the classification accuracy is affected by errors introduced from the offline labeling process needed for the machine learning algorithms (e.g., a 3D city model or camera-assisted labeling).

Unlike the above methods, which ultimately rely on the accuracy of signal reception classification, we have sought to address the problem through a machine learning-based algorithm to predict the pseudorange errors and thence correct the observed pseudoranges by considering the signal strength, satellite elevation angle and pseudorange residuals (Sun et al. 2021b). The proposed positioning method avoids the errors and costs arising from additional geospatial information during the labeling phase. Positioning tests in various urban canyons demonstrated that, when in static mode, the algorithm can deliver a 70% improvement in positioning accuracy compared to the conventional C/N0 and elevation angle-based multipath/NLOS exclusion and positioning algorithm.

In the dynamic mode, a Kalman filter is always used to integrate GNSS and IMU data to enhance the positioning accuracy, integrity, continuity and availability in urban environments. In general, the values of the filter parameters are fixed, but this may cause the filter to diverge in changing environments (Wang et al. 2006). Thus, a series of adaptive Kalman filters (AKF) have been developed to overcome the limitation of using a priori statistics to model errors that have time-varying characterized (Mohamed and Schwarz 1999; Hide et al. 2003; Xiao et al. 2010). The adaptive indicators may take on a range of roles, including adjustment of the covariance matrix of the state estimation vector, the covariance matrix of the process vector and the covariance matrix of measurement vector (Xia et al. 1994; Bian et al. 2006; Xian et al. 2013; Liu et al. 2018; Yan et al. 2020).

None of the adaptive indicators in the above fusion methods, however, have been adjusted specifically for the errors caused by multipath signals and NLOS that are common in urban areas. An effective method to update the measurement noise covariance in the filtering algorithm is therefore essential for integrated navigation performance in urban areas.

As demonstrated in our previous research, the pseudorange error can be used as an important indicator to evaluate measurement quality. Here, therefore, we propose a pseudorange error prediction-based adaptive Kalman filter (PEP-AKF) algorithm for GNSS/IMU integration in urban areas. The pseudorange error is predicted by an ensemble bagged regression tree model accounting for signal strength, satellite elevation angle and coordinate information. An adaptive indicator based on the predicted pseudorange errors is then proposed to update the measurement noise covariance in the tightly coupled integrated navigation system.

Algorithm framework

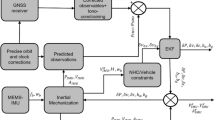
The framework of the proposed pseudorange error prediction-based adaptive tightly coupled GNSS/IMU integration algorithm (PEP-AKF) is presented in Fig. 1.

Fig. 1
figure 1

Framework of the proposed algorithm

Full size image

The main parts of the offline phase are variable selection, the labeling process and the ensemble bagged regression tree-based training process. First, offline reference positioning data are collected from the intended route using a high-grade GNSS/IMU integrated system with backward and forward post-processing. Every set of variables, from the raw GNSS measurement, which is obtained from the output data of the integrated system, including signal strength (\(C/N_{0}\)), satellite elevation angle (\(\theta\)) and coordinate information (\({\text{Lat}},{\text{Lon}}\)), is labeled with the corresponding pseudorange errors. The ensemble bagged regression tree model is then used to fit the pseudorange errors through the offline training process, thereby obtaining the prediction rules, that is, the relationship between the input variables (\(C/N_{0}\), \(\theta\), \({\text{Lat}}, {\text{Lon}}\)) and the corresponding labeled pseudorange errors.

The part outside the dashed box in Fig. 1 is the online tightly coupled GNSS/IMU navigation structure. The newly collected online GNSS variables from raw measurements and INS, including \(C/N_{0}\), \(\theta\), \({\text{Lat}}\) and \({\text{Lon}}\), are used together with the rules extracted from the offline phase to predict the pseudorange errors. The predicted pseudorange errors are then used to update the measurement noise covariance for the tightly coupled GNSS/IMU navigation.

Variable determination

The received GNSS signal contains various variables that can be used to predict the pseudorange error. Using too many variables, however, may increase the cost of computation. Following the trade-off between computational cost and training accuracy in Sun et al. (2019), we used four variables in this process: \(C/N_{0}\), \(\theta\), \({\text{Lat}}\) and \({\text{Lon}}\).

  1. (1)

    Signal strength (\(C/N_{0}\))

The signal strength can be determined by the ratio of carrier power to noise power per unit of bandwidth in decibel-hertz (dB-Hz) of the received signal. The \(C/N_{0}\) of NLOS/multipath signals is always lower than that of LOS signals, and since this can be used to measure the degree of multipath contamination of the signal, it represents for the pseudorange error prediction (Gu et al. 2016). In some cases, however, the receiver may output a high \(C/N_{0}\), such as when the signal is reflected by materials like glass curtain walls. This means that other input variables must be used in tandem with \(C/N_{0}\) in order to predict the pseudorange error accurately.

  1. (2)

    Satellite elevation angle (\(\theta\))

In general, the higher the elevation of a satellite, the less likely it is to be obstructed by objects, and the more likely it is to be received by a receiver in the form of LOS. This phenomenon, therefore, can also be used as a measure of the degree to which the signal has been contaminated by the multipath effect. Indeed, the technique of weighting measurements based on elevation angle to alleviate the multipath effect is widely used in positioning. The satellite elevation angle, \(\theta\), for the satellite \(\left( i \right)\) can be calculated by:

$$\theta^{\left( i \right)} = - \arcsin \left( {\frac{{z_{r} - z_{s}^{\left( i \right)} }}{{P_{r}^{\left( i \right)} }}} \right)$$
(1)

where \(z_{r}\) and \(z_{s}^{\left( i \right)}\) are the z-coordinates of the receiver and satellite \(\left( i \right)\) in an earth-centered earth-fixed (ECEF) coordinate system and \(P_{r}^{\left( i \right)}\) is the distance from the satellite \(\left( i \right)\) to the receiver position. The complexity of urban environments means, however, that reflected signals may also reach the receiver at a high elevation angle, so other features still need to be considered to assist the training rule extraction.

  1. (3)

    Latitude and longitude of the GNSS antenna (\({\text{Lat}}\) and \({\text{Lon}}\))

We select latitude and longitude as two input variables. Since the NLOS/multipath repeats in similar conditions, taking longitude and latitude as two variables can contribute to predict pseudorange errors more accurately (Margaria and Falletti 2016).

Pseudorange error labeling

The labeling of the pseudorange error is an important process in the offline phase. The pseudorange errors of the received signals can be calculated and labeled with their values from the offline reference data, obtained from the post-processing of a high-grade GNSS/IMU integrated system. The pseudorange \(\rho\) between the receiver and a satellite can be calculated as in the first term of (2) and (3):

$$\rho = P + c\left( {\delta t_{s}^{\left( i \right)} - \delta t_{r} } \right) + I + T + \varepsilon$$
(2)
$$P = \sqrt {\left( {x_{s}^{\left( i \right)} - x_{r} } \right)^{2} + \left( {y_{s}^{\left( i \right)} - y_{r} } \right)^{2} + \left( {z_{s}^{\left( i \right)} - z_{r} } \right)^{2} }$$
(3)

where \(P\) is the geometric range between the observed satellite \(\left( i \right)\) and the receiver; \(\left( {x_{r} ,y_{r} ,z_{r} } \right)\) and \(\left( {x_{s}^{\left( i \right)} ,y_{s}^{\left( i \right)} ,z_{s}^{\left( i \right)} } \right)\) are the coordinates of the receiver and the satellite \(\left( i \right)\) in an ECEF coordinate system; the constant \(c\) is the speed of light in a vacuum; \(\delta t_{s}^{\left( i \right)}\) and \(\delta t_{r}\) are the clock offset of satellite \(\left( i \right)\) and the receiver, respectively; \(I\) and \(T\) are, respectively, the delays caused by the ionosphere and troposphere; and \(\varepsilon\) represents the other errors, mainly from NLOS/multipath errors.

As mentioned earlier, the reference position is determined during the offline phase. The calculation of the corrected pseudorange \(\rho^{c}\) could then be expressed by considering the reference position and the error models applied on the related error sources, as in (4):

$$\rho^{c} = P + c\left( {\Delta \delta t_{s}^{\left( i \right)} - \Delta \delta t_{r} } \right) + \Delta I + \Delta T + \varepsilon$$
(4)

where the geometric range, \(P\), is calculated with the reference position and the position of the observed satellite from the broadcast ephemeris; \(\Delta \delta t_{s}^{\left( i \right)}\) represents the residual of the satellite errors of satellite \(i\) after applying the satellite clock offset corrections from the broadcast ephemeris; \(\Delta \delta t_{r}\) is the receiver clock offset after applying the calculated corresponding satellite and receiver clock error from the pseudorange positioning equations with the reference ground point position; and \(\Delta I\) and \(\Delta T\) are those residuals in the ionospheric and tropospheric delays that are not fully corrected by Klobuchar and Saastamoinen models, respectively. The pseudorange error \(\Delta \rho\) can be further derived as in (5):

$$\Delta \rho = \rho^{c} - P = c\left( {\Delta \delta t_{s}^{\left( i \right)} - \Delta \delta t_{r} } \right) + \Delta I + \Delta T + \varepsilon .$$
(5)

The calculated pseudorange error, \(\Delta \rho\), is then labeled as its value. Every set of variables from the raw GNSS measurements, including \(C/N_{0}\), \(\theta\), \({\text{Lat}}\) and \({\text{Lon}}\), will then have the corresponding value of \(\Delta \rho\) after the labeling process.

Ensemble bagged regression tree-based pseudorange error prediction

The ensemble decision tree is a popular machine learning method that is able to provide high accuracy prediction in many applications (Adler et al. 2011; Saeed et al. 2019). The ensemble bagged regression tree is composed of a combination of multiple regression decision trees established based on a subsample that comprises a training set. Thus, the ensemble model of multiple regression trees can bring a group of weak learners together to form a strong learner with the merit of not being sensitive to small perturbations or uncertainties in the training dataset. This makes it suitable for pseudorange error prediction. The process of establishing the ensemble bagged regression tree model is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of the ensemble bagged regression tree algorithm

Full size image

The discussed problem can be defined as follows: Given the training set \(\left\{ {x_{i} ,\Delta \rho_{i} } \right\}_{1}^{I}\) of known \(\left( {x,\Delta \rho } \right)\) values, the objective is to determine a function that maps \(x\) to \(\Delta \rho\), where \(x_{i} = \left( {C/N_{0i} ,\theta_{i} ,{\text{Lat}}_{i} ,{\text{Lon}}_{i} } \right),\,i = 1,2,3, \cdots ,I\). \(i\) is the sequence number of the sample, and \(I\) is the total number of the samples. \(\Delta \rho_{i}\) is the corresponding labeled pseudorange error of \(x_{i}\). The ensemble bagged regression tree model-based pseudorange error prediction is described as follows:

  1. (1)

    Single regression tree-based model generation

    In the input space of the subsample training set, each region is recursively divided into two subregions, and the output value of each subregion is determined so as to construct the regression tree.

    1. (a)

      Select the optimal segmentation variable \(j\) and the segmentation point \(s\) to solve:

      $$\mathop {\min }\limits_{j,s} \left[ {\mathop {\min }\limits_{{c_{1} }} \sum\limits_{{x_{i} \in R_{1} (j,s)}} {(\Delta \rho_{i} - c_{1} )^{2} + \mathop {\min }\limits_{{c_{2} }} \sum\limits_{{x_{i} \in R_{2} (j,s)}} {(\Delta \rho_{i} - c_{2} )^{2} } } } \right]$$
      (6)
      $$c_{1} = {\text{ave}}\left( {\left. {y_{i} } \right|x_{i} \in {\text{Reg}}_{1} \left( {j,s} \right)} \right)$$
      (7)
      $$c_{2} = {\text{ave}}\left( {\left. {y_{i} } \right|x_{i} \in {\text{Reg}}_{2} \left( {j,s} \right)} \right)$$
      (8)

      where \({\text{ave}}\) is the average function. Traverse the variable \(j\), scan the segmentation point \(s\) for the fixed segmentation variable \(j\) and determine the \(\left( {j, s} \right)\) that minimizes formula (6).

    2. (b)

      Divide the region with the selected \(\left( {j, s} \right)\) and determine the corresponding output value:

      $${\text{Reg}}_{1} \left( {j,s} \right) = \left\{ {\left. x \right|x^{\left( j \right)} \le s} \right\},{\text{Reg}}_{2} \left( {j,s} \right) = \left\{ {\left. x \right|x^{\left( j \right)} > s} \right\}$$
      (9)
      $$\hat{c}_{q} = \frac{1}{{N_{q} }}\sum\nolimits_{{x_{i} \in R_{q} \left( {j,s} \right)}} {\Delta \rho_{i} ,x \in R_{q} ,\quad q = 1,2}$$
      (10)

      where \({\text{Reg}}_{1} \left( {j,s} \right)\) and \({\text{Reg}}_{2} \left( {j,s} \right)\) mean the divided regions and \(\hat{c}_{q}\) is the corresponding output value. For each divide of the region, two new nodes will be created. A node is comprised of a sample of data and a decision rule.

    3. (c)

      Continue with steps (a) and (b) for the two subregions until the iteration stop conditions are met: i.e., where the sample size of the node is less than a user-specified value. Here, from the sensitivity analysis, the defined value is set as 8.

    4. (d)

      Divide the input space into \(L\) regions and generate a regression tree:

      $$h\left( x \right) = \sum\nolimits_{l = 1}^{L} {\hat{c}_{l} I\left( {x \in {\text{Reg}}_{l} } \right),\quad \left( {l = 1,2, \ldots ,L} \right)}$$
      (11)

      where \(h\left( x \right)\) is the predicted value of the regression tree; \(l\) is the number of the region; and \(I\) is a characteristic function.

  2. (2)

    Bagged regression tree-based training model generation

    The final output result of the bagged regression tree model is the average value of the predicted values of all the individual regression trees. The bagged regression tree model is expressed as:

    $$h_{{{\text{bag}}}} \left( x \right) = \frac{1}{N}\sum\nolimits_{n = 1}^{N} {h_{n} \left( x \right),{ }\quad \left( {1 \le n \le N} \right)}$$
    (12)

    where \(h_{n} \left( x \right)\) is the predicted value of the regression tree \(n\) for input \(x\) and \(n\) is the number of the regression trees.

  3. (3)

    Pseudorange error prediction

    The experiment in this paper uses only global positioning system (GPS) L1 data to train a bagged regression tree model. Since NLOS/multipath errors repeat in similar conditions of the surrounding environment and constellation, the rules from one constellation in the area may have a limited effectiveness on predicting pseudorange errors in other constellations in the same area. The pseudorange errors of the newly collected variables can be predicted based on the corresponding final predictor \(h_{{{\text{bag}}}} \left( x \right)\). The input \(x = \left( {C/N_{0} ,\theta ,{\text{Lat}},{\text{Lon}}} \right)\) can be used together with the output rules of the \(h_{{{\text{bag}}}} \left( x \right)\) to obtain the pseudorange errors.

Adaptive tightly coupled fusion scheme

The adaptive tightly coupled fusion scheme is based on the EKF structure. The state vector, \(X\), for the EKF is defined in (13).

$$X = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\delta r_{3 \times 1}^{T} } & {\delta v_{3 \times 1}^{T} } & {\Psi_{3 \times 1}^{T} } \\ \end{array} } & {b_{g3 \times 1}^{T} } & {b_{a3 \times 1}^{T} } \\ \end{array} } & {\nabla_{g3 \times 1}^{T} } & {\nabla_{a3 \times 1}^{T} } \\ \end{array} } & {t_{b} } & {\delta t_{b} } \\ \end{array} } \right]^{T}$$
(13)

where the first 21 dimensions of \(X\) are built on the IMU estimation errors, including the three-axis navigation parameters of position error \(\delta r_{3 \times 1}\), velocity error \(\delta v_{3 \times 1}\), attitude error \(\Psi_{3 \times 1}\), bias of gyroscope \(b_{g3 \times 1}\), bias of the accelerometer \(b_{a3 \times 1}\), scale factors of gyroscopes \(\nabla_{g3 \times 1}\) and scale factors of accelerometers \(\nabla_{a3 \times 1}\). The last two dimensions of \(X\) include the GNSS receiver clock bias \(t_{b}\) and GNSS receiver clock drift \(\delta t_{b}\).

The state transition equation for the state vector \(X\) is expressed in (14):

$$\dot{X} = AX + w$$
(14)

where \(\dot{X}\) is the first derivative of the state vector \(X\), \(A\) is the IMU dynamic transition model and \(w\) is the system noise. \(Q\) is defined as the covariance matrix of \(w\).

The measurement model \(Z\) is expressed in (15)

$$Z = HX + n$$
(15)

where \(Z\) is the measurement vector, \(H\) is the measurement mapping matrix and \(n\) is the measurement noise. \(R\) is defined as the covariance matrix of \(n\). If the number of visible satellites is \(M\), the measurement vector, \(Z\), is formed as:

$$Z = \left[ {\begin{array}{*{20}c} {\rho_{{{\text{IMU}},1}} - \rho_{{{\text{GNSS}},1}} } \\ \vdots \\ {\rho_{{{\text{IMU}},m}} - \rho_{{{\text{GNSS}},m}} } \\ \vdots \\ {\rho_{{{\text{IMU}},M}} - \rho_{{{\text{GNSS}},M}} } \\ \end{array} } \right]_{M \times 1}$$
(16)

where \(\rho_{{{\text{IMU}}}}\) is the pseudorange derived from the IMU and \(\rho_{{{\text{GNSS}}}}\) is the pseudorange decoded from GNSS observations; \(1 \le m \le M\).

An adaptive indicator is proposed based on the pseudorange error prediction in order to estimate the GNSS measurement noise covariance parameters in urban areas. The adaptive indicator \(f( \cdot )\) can be expressed in (17):

$$f( \cdot ) = \left( {\left| {h_{{{\text{bag}}}} ( \cdot )} \right| + \eta } \right)^{2}$$
(17)

where \(f( \cdot )\) is the proposed adaptive indicator function; \(h_{{{\text{bag}}}} ( \cdot )\) is the designed ensemble bagged regression tree model; \(\mathrm{and} \eta\) is the perturbation coefficient. Here, \(\eta = 0.1\). The measurement noise covariance matrix, \(R\), at epoch \(k\) can then be constructed based on the adaptive indictor function at epoch \(k\), as expressed in (18):

$$R_{k} = \left[ {\begin{array}{*{20}l} {f\left( {x_{{p_{1} }} } \right)} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & \ddots \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {f\left( {x_{{p_{m} }} } \right)} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & \ddots \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {f\left( {x_{{p_{M} }} } \right)} \hfill \\ \end{array} } \right]_{k}$$
(18)

where \(f\left( {x_{{p_{m} }} } \right)\) is the predicted results of the adaptive indicator function for the satellite \(p_{m} ,x = \left( {C/N_{0} ,\theta ,{\text{Lat,}}\,{\text{Lon}}} \right)\), and \(p_{m}\) \(\left( {m = 1 \ldots M} \right)\) is the \(m{\text{th}}\) satellite used for the positioning.

The final fusion results can then be obtained based on the following Kalman filter procedures.

Prediction stage:

$$\hat{X}_{k,k - 1} = \Phi_{k,k - 1} \hat{X}_{k - 1}$$
(19)
$$P_{k,k - 1} = \Phi_{k,k - 1} P_{k - 1} P_{k,k - 1}^{T} + Q_{k - 1}$$
(20)

Update stage:

$$K_{k} = P_{k,k - 1} H_{k}^{T} \left( {H_{k} P_{k,k - 1} H_{k}^{T} + R_{k} } \right)^{ - 1}$$
(21)
$$P_{k} = \left( {I - K_{k} H_{k} } \right)P_{k,k - 1} \left( {I - K_{k} H_{k} } \right)^{T} + K_{k} R_{k} K_{k}^{T}$$
(22)
$$\hat{X}_{k} = \hat{X}_{k.k - 1} + K_{k} \left( {Z_{k} - H_{k} \hat{X}_{k.k - 1} } \right)$$
(23)

where, \(\hat{X}_{k}\): state vector estimates at time epoch \(k\), \(\Phi_{k}\): state transition matrix at time epoch \(k\), \(P_{k}\): error covariance matrix at time epoch \(k\), \(Q_{k}\): system noise covariance matrix at time epoch \(k\), \(R_{k}\): measurement noise covariance matrix at time epoch \(k\), \(H_{k}\): measurement matrix at time epoch \(k\), \(K_{k}\): Kalman gain matrix at time epoch \(k\), ∎\(_{k,k - 1}\): matrix/vector ∎ propagation from time epoch \(k - 1\) to \(k\).

Experiment and results

In order to validate the proposed method, a vehicle-based field test was carried out in the urban areas in Taipei city of Taiwan, China. The training dataset was collected from about 10:00 in the morning in the Beijing time with the time duration of 2–3 h for consecutive 3 days. The total training dataset was collected for about seven hours at the experimental site. The data, including the raw GNSS measurement and fused positioning results, were collected using a high-grade GNSS/IMU integrated system (i.e., NovAtel SPAN-LCI). The variables extracted from the GPS L1 measurements were then used as the inputs for the training, and the post-processed GNSS/IMU positioning results were used for the pseudorange error labeling.

The testing data were collected around 11:00 in the morning in the Beijing time after one week, at the same experimental site, where the training data were collected. The testing trajectory is shown in Fig. 3, and the onboard navigation sensors used included: (1) a micro-electro-mechanical system (MEMS) IMU, STIM-300, with a sampling rate of 250 Hz. The corresponding IMU parameters are given in Table 1; (2) a GNSS receiver, NovAtel ProPak6, with a sampling rate of 1 Hz; and (3) a high-end GNSS/IMU integrated system, i.e., NovAtel SPAN-LCI, for high accuracy navigation solutions in the experiment. The corresponding IMU parameters are given in Table 2. The reference positions in the test were generated by the SPAN-LCI outputs with post-processing kinematic mode of the tightly coupled GNSS/IMU using NovAtel Inertial Explore software. A summary of the training dataset and testing dataset is shown in Table 3. The number of visible GPS satellites is depicted in Fig. 4, and the corresponding position dilution of precision (PDOP) and horizontal dilution of precision (HDOP) values are depicted in Fig. 5.

Fig. 3
figure 3

Vehicle trajectory

Full size image
Table 1 Sensor parameters of STIM-300
Full size table
Table 2 Sensor parameters of NovAtel SPAN-LCI
Full size table
Table 3 Summary of the datasets
Full size table
Fig. 4
figure 4

Number of visible GPS satellites

Full size image
Fig. 5
figure 5

PDOP and HDOP values

Full size image

Since the predicted pseudorange error affects the performance of the final positioning solutions, the evaluation of the fitting performance of the proposed ensemble bagged regression tree-based pseudorange error prediction compared with the other popular used fitting algorithms becomes essential. Here, the three other candidate fitting algorithms are the ensemble boosted trees model, the fine Gaussian support vector machine (SVM) model and the squared exponential Gaussian process regression model. The parameters used to evaluate the fitting performance are root mean square error (RMSE) of the residuals, R-squared and training time. The RMSE of the residuals is used to evaluate the accuracy of fitting results. The smaller the RMSE of the residuals, the closer the fitting result is to the reference pseudorange errors. The R-squared is another informative parameter for evaluating the fitting results. It can be any value between 0 and 1, with a higher value indicating a better fit for the regression model (Chicco et al. 2021). To prevent overfitting for some candidate machine learning algorithms, fivefold cross-validation was used for all models. The comparison results for the fitting algorithms are shown in Table 4.

Table 4 Comparison of ensemble bagged regression trees and other candidate models
Full size table

It is clear that the ensemble bagged regression tree model outperforms the other fitting methods based on the evaluation of the overall fitting performances. In particular, the RMSE of the ensemble bagged regression tree-based fitting results was 2.14 m, which is much smaller than the other fitting models, whose overall performance ranged from 2.36 to 3.01 m. In addition, the two highest R-squared values were the ensemble bagged regression tree model and the squared exponential Gaussian process regression model, with values of 0.70 and 0.64, respectively. The training time consumption for the squared exponential Gaussian process regression model was 1031.40 s, however, which was 22 times higher than that for the ensemble bagged regression tree model.

In order to evaluate the final algorithm positioning performance, the proposed PEP-AKF-based fusion algorithm was compared with two other candidate fusion algorithms: (1) traditional EKF-based fusion and (2) EKF-based fusion with pseudorange error correction. Also, the GPS L1 measurements are used for the candidate fusion algorithms. The detail steps of the candidate algorithms are shown in Table 5, and the fusion results are shown in Fig. 6.

Table 5 Summary of the algorithms
Full size table
Fig. 6
figure 6

Fusion results of the algorithms

Full size image

In Figs. 6 and 7, it is obvious that the positioning results of the proposed algorithm are closer to the reference than the other fusion algorithms, especially in densely built environment areas. The positioning accuracy for the candidate algorithms and the corresponding improvements compared to the traditional EKF-based fusion are shown in Table 6. The comparisons of the positioning error of the fusion results for the algorithms are depicted in Figs. 8 and 9.

Fig. 7
figure 7

Partial experimental results and experimental scenes

Full size image
Table 6 RMSE results comparison
Full size table
Fig. 8
figure 8

Positioning error in terms of the local-level coordinate system

Full size image
Fig. 9
figure 9

Horizontal and 3D positioning error in terms of the local-level coordinate system

Full size image

Table 6 indicates that the proposed fusion algorithm can provide a 3D position accuracy RMSE of 9.21 m, while it is 10.85 m for the EKF-based fusion with pseudorange error correction and 20.76 m for the traditional EKF-based fusion, corresponding to improvements of 15% and 55%. Meanwhile, the improvement in the horizontal positioning accuracy for the proposed algorithm compared to the EKF-based fusion with pseudorange error correction is also significant, with an improvement value of about 32%.

In the period between 1000 and 1100 s in Fig. 8, the surrounding urban environment is characterized by moderately dense development, with the received GPS signals experiencing medium multipath and NLOS. The surrounding urban environment is shown in Fig. 7, Part 1. In this condition, the measurement noise covariance matrix was adjusted by the generated adaptive indicator, alleviating the fused positioning error caused by the contaminated measurement arising from the multipath and NLOS. The use of the adaptive indicator, therefore, led to substantial improvements in the horizontal positioning results compared to the EKF-based fusion with pseudorange error correction model and the traditional EKF-based fusion model by 34% and 64%, respectively.

In the period between 1500 and 1600 s in Fig. 8, the environment was a dense urban area with taller and more closely packed buildings than in the moderately dense urban areas. This led to more significant NLOS and multipath effects, as shown in Fig. 7, Part 2. Strikingly, the improvement in performance offered by the proposed algorithm in this environment was even greater than in the moderately dense urban areas. Specifically, there was a 40% improvement in 3D positioning compared to the EKF-based fusion with pseudorange error correction model and a 76% improvement compared to the traditional EKF-based fusion model. Correspondingly, the maximum positioning error is also reduced to 16.30 m from 71.42 and 34.44 m.

In order to investigate the effectiveness of the proposed adaptive indicator further, the relationship for the adaptive indicator and the corresponding pseudorange errors was analyzed. An example of the typical adaptive indicator, and the corresponding pseudorange error for the satellite SV30, is shown in Table 7. This shows that, at 647 s, the satellite SV30 had a pseudorange error of 0.92 m, and the corresponding adaptive indicator was 0.799. At 1015 s, meanwhile, SV30 had a predicted pseudorange error of 18.95 m, and the corresponding adaptive indicator became 298.856. This means that the weighting of the pseudorange measurement for SV30 was significantly reduced by the severity of the pseudorange error, resulting in that the NLOS and multipath will have less effect on the fusion results.

Table 7 Examples of the typical adaptive indicator and the corresponding pseudorange error for satellite SV30
Full size table

The improvement in the 3D positioning results arising from the use of the proposed algorithm is also depicted in Fig. 10. This shows that the positioning results from the conventional EKF-based fusion and EKF-based fusion with pseudorange error correction comprise only about 0.7% and 3% of the epochs within 2 m. With the proposed PEP-AKF-based fusion model, however, this proportion increases significantly to 13%. In addition, with the proposed fusion model, the proportion of epochs with a positioning accuracy in the range of 2–4 m is much higher than that of the conventional EKF-based fusion and EKF-based fusion with pseudorange error correction. The EKF-based fusion with pseudorange error correction can improve the positioning accuracy to a certain extent, however. Due to the error present in the pseudorange error prediction for some epochs, using the incorrectly corrected pseudorange in the fusion will introduce errors in the positioning results. For the proposed algorithm, meanwhile, even when an incorrect pseudorange error is predicted for some epochs, the fusion algorithm is less sensitive to those errors because of the use of the corresponding adaptive indicator in the filter. This is why the proposed algorithm will return a smaller fusion error than the EKF-based fusion with pseudorange error correction model, even with the same predicted pseudorange error.

Fig.10
figure 10

3D positioning error distribution within 40 m

Full size image

Table 8 shows a comparison of the positioning accuracy analysis according to each epoch. This reveals that the proposed PEP-AKF-based fusion improved the horizontal and 3D positioning results in, respectively, 83.7% and 88.5% of the epochs, compared to the traditional EKF-based fusion. Although a deterioration in positioning accuracy was seen in about 13% of the epochs, this may have been due to the incorrect pseudorange error prediction results, and the algorithm is clearly still effective for most of the epochs. Compared to traditional EKF-based fusion, meanwhile, the EKF-based fusion with pseudorange error correction algorithm improved the horizontal and 3D positioning results in, respectively, 78.1% and 84.2% of the epochs. For both algorithms, the worse epochs for 3D positioning were fewer than the epochs for the horizontal positioning, since height errors tended to be more substantially corrected as the pseudorange errors were corrected. This is because NLOS and multipath signals affect height positioning results more severely than horizontal ones in urban areas.

Table 8 Algorithm performance compared to the traditional EKF-based fusion results with proportion of epochs
Full size table

Conclusion

We have developed a pseudorange error prediction-based adaptive Kalman filter algorithm for tightly coupled GNSS/IMU integration in urban areas. An adaptive indicator generated using a pseudorange error predicted by means of an ensemble bagged regression tree algorithm is used to optimize the measurement noise covariance parameters in the Kalman filter with the characteristics of GNSS measurement noise properties in urban areas. The experimental results show that the proposed PEP-AKF-based fusion algorithm delivers a better positioning performance in urban areas than other candidate fusion algorithms, providing a horizontal RMSE accuracy of 5.11 m, which represents a 52% improvement on traditional EKF-based fusion (RMSE of 10.67 m) and a 32% improvement on EKF-based fusion with pseudorange correction (RMSE of 7.53 m). The proposed algorithm can be used for the local urban positioning enhancement in the future, especially to provide the positioning accuracy improvement for incoming vehicles with low-cost onboard GNSS and IMU sensors. Further research is also needed to explore the added value of various aspects of multiple GNSS constellations.