Introduction

Due to the recent shift in focus of worldwide aviation from ground based to space based navigation systems, the safe use of GNSS and in particular GPS for such purposes has become the subject of global research. GPS performance available to the civilian community is specified in the standard positioning service (SPS) performance standard providing information on service accuracy, availability and reliability with respect to the signal-in-space (SIS).

To use GPS for aviation, stringent standards, established by the International Civil Aviation Organization (ICAO), have to be met. One of the requirements is integrity, a measure of the degree of trust that can be placed in the correctness of the navigation information. However, the GPS SPS does not provide real time integrity information. Hence, for safety and liability critical applications like aviation, GPS signals must be monitored. The vulnerability of GPS signals has been investigated for example, by Volpe (2001) and Ochieng et al. (2003).

GPS augmentations like GBAS (ground based augmentation systems) and SBAS (satellite based augmentation systems) monitor GPS signals in real time. They relay integrity information using signals which are themselves vulnerable to jamming and interference, a principal failure mode of GPS. Hence a potentially effective method to address the exposure to such risks is to integrate GPS with other navigation systems such as an INS. The INS is a self contained system with high short term stability, immune to jamming as well as interference. However, high grade systems are very expensive. The emergence of INS sensors exploiting MEMS (micro-electromechanical systems) technology is creating the potential for affordable integrated GPS/INS architectures if the problems associated with the performance could be overcome.

INS can be integrated synergistically with GPS so that short term and long term stabilities of INS and GPS, respectively, can be exploited. In order to realize an optimal integrated system, a number of issues related to system integrity need to be considered. This paper (the first part of two) reviews these including, integrated architectures, the corresponding failure modes and models, and the existing integrity monitoring methods. This information is used in Part II to develop a new integrity algorithm.

Integration architectures

Traditionally GPS and INS are coupled through a Kalman filter for the processing of raw measurements to obtain position, velocity and time. Initially, two broad classes of integration; loose and tight coupling were developed. However, in recent years a third class has emerged, referred to as deep integration or ultra-tight integration (Gautier 2003).

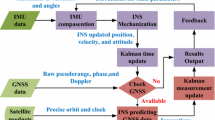
Figure 1 shows the three configurations at a high level. In the figure, the RF (radio frequency) front end refers to the electronic circuitry in the GPS receiver that is used to down-convert the GPS signal carrier frequency to a lower frequency called intermediate frequency (IF). This is done in order to avoid the use of expensive receivers that may be required to process signals in the GPS carrier frequency range. The acquisition and demodulator block tracks the input signal by monitoring the error between the received signal and the replica signal generated internally by the receiver. The received signal is also multiplied (demodulated) with the said replica signal. The integrate and dump (I and D) filter averages the signal obtained from the demodulator to produce the average in-phase and quadrature-phase components of the demodulated signal. This is done to perform the discriminator algorithm that can now decode the time delay between the internally generated code signal and the code signal obtained from the received signal. The pseudorange (PR) and delta pseudorange (DPR) measurements obtained from the discriminator are then used by the navigation filter to produce position, velocity and time of the host vehicle. In parallel, velocity and attitude increments are obtained from the IMU (inertial measurement unit) to act as forcing function in the navigation differential equations to generate attitude, velocity and position. Also in the navigation processor, error compensation equations are used to refine IMU measurements. The integration filter is used to combine the measurements from GPS and INS.

Fig. 1
figure 1

Loose, tight and ultra-tight GPS/INS navigation system (adapted from Babu and Wang (2004)

Full size image

Interconnections for different couplings are labelled (in Fig. 1) to clarify the depth of integration. In the case of loosely coupled systems, the position, velocity and time from the GPS receiver are combined with position, velocity and attitude from INS by the use of a truth model. The truth model is a mathematical depiction of the error characteristics of the systems that are to be combined by a Kalman filter. For the tightly coupled system, position, velocity and time from the INS are combined with the GPS PR measurements by using a Kalman filter. In a survey of integrated systems carried out by Wagner and Wieneke (2003), a new total state tightly coupled approach is presented that offers a simpler structure and better error estimation quality than conventional data fusion approaches. The approach uses an earth centred coordinate reference frame that leads to better accuracies and lower computation time. This has been adopted in Part II in the development of the simulation platform for the integrated system. In ultra-tight coupling, the measurements from the GPS receiver used are the in phase I and quadrature phase Q signal. There are variants of ultra-tight or deep integration. The salient difference between these couplings is the method of combining INS and GPS observables. In Gustafson and Dowdle (2003) a minimum variance non-linear filter is used, while Kim et al. (2003) and Gold and Brown (2004) employ an extended Kalman filter and a cascaded Kalman filter stages, respectively.

Failure modes and models

In order to assess the performance of the integrity algorithms we need to consider failure modes of the individual and the integrated systems. Table 1 groups the failure modes associated with GPS, INS and the integrated architectures into six classes and specifies a failure model for each based on the similarity of failure characteristics. The failure models are not meant to be rigorous but rather to capture the salient aspects of the behaviour of the failure modes so that their impact on integrity algorithms can be assessed.

Table 1 Failure mode characterization
Full size table

From the classification in Table 1, the worst case failure mode with regard to its detection by an integrity algorithm is the slowly growing (ramp type) errors (SGE). SGEs are typical of the GPS clocks and similar errors are present in INSs. A snapshot integrity algorithm would take a long time to detect these types of faults as they take time to reach the fault threshold, depending on the navigation requirements.

Integrated sensor level integrity monitoring

In general, the integrity monitoring of the integrated system followed in the footsteps of the integrity monitoring of GPS. Algorithms for monitoring the integrity of the integrated system were first proposed in the late 1980s (Brenner 1987). These follow the tradition of solution separation which has its roots in the GPS RAIM concept.

Integrity monitoring in the horizontal domain requires an alert to be raised whenever the horizontal position error is larger than the horizontal alert limit. However, in order to generate an alert, measurements must be relied upon. In general, the alert limit is defined in the position domain while the test statistics is formed in the measurement domain (Parkinson and Axelrad 1988). The noise level in the test statistic and the satellite geometry are the factors that affect the performance of an integrity algorithm.

Loosely coupled system

In this configuration, the outputs of the two systems are combined in the navigation processor, typically a Kalman filter using a truth model (Grewal et al. 2001). In essence, the position solution from GPS and INS are subtracted to provide the error to estimate the states of the integrated system that in turn, provide the required navigation variables. A disadvantage of the loosely coupled system is that the Kalman filter heavily depends upon the GPS solution. Hence, if the GPS solution is not available (e.g., when less than four satellites are available) the integrated solution is no longer possible. In such a case the performance of the integrated system is limited to its inertial coasting capability. The time for which a system can coast depends primarily on the quality of inertial sensors (Lee and Ericson 2004). Hence the loosely coupled system provides benefits in terms of the navigation performance i.e., accuracy, integrity, continuity and availability, over the individual systems. This means that the integrated system provides the following advantages over the individual systems.

  • It is more accurate.

  • More trust can be placed on its output because of the redundancy provided by an additional navigation system.

  • The integrated output is provided at a higher rate than GPS because of the higher data rate of INS.

  • The integrated system will be available even during GPS outage. The time of availability of accurate navigation solution is limited by the quality of the INS.

However, to get real benefits in integrity monitoring, measurement domain coupling methods are recommended.

Tightly coupled system

In the tightly coupled system, the Kalman filter processes the GPS raw measurements and their corresponding values predicted from INS measurements. The latter is made possible by using the current host vehicle position as determined by the INS and ephemeris data. In this way, even with less than four available satellites, the navigation solution can be maintained by the Kalman filter. A disadvantage of this filter is that it responds more slowly to INS errors than the loosely coupled system (Gautier 2003).

Sensor level integrity monitoring methods for the integrated system are based upon variations in the selection of test statistics, decision thresholds and horizontal protection limits (HPLs). There are two main approaches normally employed to determine the test statistic:

  • the use of the innovation of the Kalman filter (Nikiforov 2002; Diesel and King 1995), and

  • the use of the difference between the main filter solution and the subfilter solution (Brenner 1995).

The decision threshold against which the test statistic is compared is determined in one of two ways:

  • The threshold is a function of the standard deviation of the separation between the full solution and the sub-solutions, multiplied by a constant determined statistically. It is assumed that the test statistic is Gaussian in nature and hence the constant is calculated so that the given probability of false alert is not exceeded (Brenner 1995).

  • When the test statistic is a function of innovation that has multiple Gaussian distributed components, the threshold is chosen using the chi-square distribution. The probability of false alert is used to arrive at the value of the threshold (Diesel and King 1995).

The HPL can be determined either by using separation statistics between the full filter and sub-filters (Brenner 1995) or by fusing multiple terms as explained in the next section.

The three major current integrated system integrity algorithms are presented below.

Multiple solution separation (MSS) method

The selection of the test statistics for the MSS method is based on the difference of the full set solution and the subset solution (Brenner 1995).

Assuming that the full solution is given by,

$$\Delta x_{o} = S_{o} \Delta \rho$$
(1)

and the sub-solutions by,

$$\Delta x_{n} = S_{n} \Delta \rho \quad (n = 1,\ldots,\ N)$$
(2)

where Δρ is N the dimensional measurement vector relative to the initial estimate. S 0 and S n are the measurement matrices and Δx i the vector of three position components and the clock bias of the solution (i  =  0,..., n).

The test statistic or discriminator for the horizontal position is given by,

$$d_{n} = \sqrt{{(\Delta x_{o} (1) - \Delta x_{n} (1))^{2} + (\Delta x_{o} (2) - \Delta x_{n} (2))^{2}}}.$$
(3)

Building on this basic idea, sub-solutions, each based on a separate Kalman filter results in a number of Kalman filters, each excluding one satellite measurement at a time. The covariance matrix dP n (t), calculated at each time step, describes the statistics of the separation between the full filter and the sub-filters.

$${\rm d}P_{n} (k) = E[(\Delta x_{0} (t) - \Delta x_{n} (t))(\Delta x_{0} (t) - \Delta x_{n} (t))^{\rm T} ].$$
(4)

The errors are assumed to follow the Gaussian distribution yielding a frequency distribution for Gaussian variables given by,

$$f_{s} (s) = \frac{1}{{{\sqrt {2\pi}}}}{\rm e}^{{- ({1}/{2})s^{2}}} \quad - \infty < s < \infty$$
(5)

for a variable s.

When there is no satellite failure, an alert may be raised due to the presence of noise in the measurement. Therefore, the detection threshold should be chosen based upon the maximum permissible probability of false alert. Hence,

$$P_{{\rm fd}} = {P}(\xi > T_{D}) = \frac{1}{{{\sqrt {2\pi}}}}{\int\limits_{T_{D}}^\infty {{\rm e}^{{- {x^{2}}/{2\sigma ^{2}}}}}}{\rm d}x$$
(6)

where the mean of random variable x is zero, ξ noise, P fd the false alert probability and σ the standard deviation of x. As we are concerned with the magnitude of threshold T D and there are N measurements, we can write that:

$$T_{D} = {\sqrt {\lambda ^{{{\rm d}P_{n}}}}}Q^{{- 1}} {\left({\frac{{{P}_{{\rm fd}}}}{N}} \right)}$$
(7)

where \({\lambda ^{{{\rm d}P_{n}}}}\) is the largest eigenvalue of the horizontal position error covariance matrix and Q − 1 the inverse of

$$Q(x) = \frac{1}{{{\sqrt {2\pi}}}}{\int\limits_x^\infty {{\rm e}^{{- {t^{2}}/{2}}}}}{\rm d}t$$
(8)

where Q is the probability of variable t being greater than x.

As the horizontal position error has components in x and y axes, this ensures the usage of a standard deviation that is maximum, either in the x or y direction. In the case of a satellite with faulty measurements, the noise affecting the measurements can potentially reduce the magnitude of the fault. This happens when the sign of the noise is opposite to the true measurement. This could result in missed detection because the value of the test statistic will remain below the threshold. The faulty measurement is thus modelled as a Gaussian variable, so that the threshold is calculated based on the value of probability of missed detection, P md

$$a_{n} = {\sqrt {\lambda ^{{P_{n}}}}}Q^{{- 1}} {\left({{P}_{{\rm md}}} \right)}$$
(9)

where P n is the covariance matrix for the estimation of subfilter states. A matrix referred to as a dual propagation matrix is defined that is used to propagate P n and dP n with time so that the test statistic and HPL can be computed at each epoch.

The HPL for the algorithm is hence the sum of the two thresholds that acts as a strict upper bound:

$${\rm HPL} = {\rm max} (T_{{D_{n}}} + a_{n})\quad {\rm over}\ n = 1,\ldots,\ N.$$
(10)

Some modifications to the MSS method are suggested by Young and McGraw (2003). Instead of the dual propagation matrix, the covariance of solution separation matrix termed B n (k) is proposed in Young and McGraw (2003). This results in a saving in computation time. Furthermore, the inverse (Moore–Penrose) of this matrix is used in the calculation of the suggested test statistic. However, due to the reason of B n (k) being rank deficient, the usage of this in the calculation of the test statistics is not recommended. Furthermore, the calculation of the detection threshold and HPL are similar to the MSS approach but modifications are suggested therein. It is argued in Brenner (1995) that the limit for the threshold and HPL should be calculated using the maximum eigenvalues (Eqs. 7, 10) but this results in underestimation of both the values. This is due to the reason that horizontal position is a 2D variable and if the approach by Brenner (1995) is used, this limits the case to that of a 1D variable. However, a better approach is to cater for the second variable also (assuming it is a Gaussian variable) using a 2D approach. It is further suggested to use CEP tables for these calculations.

The approach by Young and McGraw (2003) while being credible, has two issues to be dealt with:

  • the assumption of position error being a Gaussian variable has not been resolved fully yet and there may not be any advantage of choosing it as a 1D or 2D variable, and

  • the calculation of the test statistics using a rank deficient matrix may create numerical instabilities as recognised by the same authors.

Hence, in this paper the MSS algorithm is pursued as a representative method for the solution separation approach.

Autonomous integrity monitoring by extrapolation method (AIME)

The AIME is effectively a sequential algorithm in which the measurements used are not limited to a single epoch (Diesel and King 1995). The test statistics are based on the innovation of the Kalman filter. The standard equations of the Kalman filter used are as follows (Grewal 2001).

$$x^{+} (k) = x^{-} (k) - K(k)r(k)$$
(11)

where K(k) is the Kalman gain, x(k) the filter state vector, − and + subscript show a priori and a posteriori estimates. The innovation r(k) is given by,

$$r(k) = z(k) - H(k)x^{-} (k).$$
(12)

The distribution of the components of r(k) is n dimensional normal with zero mean and known covariance, i.e.,

$$\begin{aligned} E[r(k)] &= 0 \\E[r(k) r^{\rm T} (k)] &= V(k). \\ \end{aligned} $$
(13)

The covariance of the innovation, V(k) is given by,

$$V(k) = H(k)P^{-} (k)H^{T} (k) + R(k)$$
(14)

where H(k) is the measurement matrix of the Kalman filter, P −(k) the covariance of state variables and R(k) the covariance matrix for measurements used in the Kalman filter.

The test statistic is then given by,

$$s^{2}_{{\rm avg}} = (r^{\rm T}_{{\rm avg}})(V^{{- 1}}_{{\rm avg}})(r_{{\rm avg}})$$
(15)

where,

$$r_{{\rm avg}} = (V^{{- 1}}_{{\rm avg}})^{{- 1}} \Sigma _{k} (V^{{- 1}} (k)r(k))$$
(16)

and

$$V_{\rm avg}^{-1}=\sum_{k}V^{-1}(k).$$
(17)

The test statistic exhibits central and non-central chi-square distributions for the no-fault and fault cases, respectively (Diesel and King 1995). Using the same formula, three test statistics s 1, s 2 and s 3 are formed; averaged over 150 s, 10 min and 30 min, respectively. The decision threshold is also based on the chi-square distribution. This is selected on the basis of a false alert rate of 10−5 per hour in a fault free environment (Diesel and Dunn 1996).

The HPL is the combination of three limits:

  • HPL1 is given by 5.33σ (position estimate uncertainty). The σ value is determined from elements of the horizontal position error covariance matrix. The value of 5.33 is chosen to reflect the probability of missed detection of 10−7.

  • HPL2 is the maximum value of the test statistics for all sub-filters. Hence, it varies as a function of GPS PR measurements.

  • HPL3 is based on a derivation similar to that of the traditional RAIM, which uses the slope of the satellite that is the most difficult to detect. The slope in this case is the ratio of the contribution of each satellite to the horizontal position error to the contribution to the test statistic (Brown and Chin 2002).

The slope calculation is carried out by the use of the Kalman filter gain matrix and measurement variance matrix. It is given by,

$${\rm slope}(i) = \frac{{{\rm d}R_{i}}}{{{\rm d}s_{i}}}$$
(18)

where,

$${\rm d}R_{i} = {\sqrt {({\rm d}x^{2}_{{i1}} + {\rm d}x^{2}_{{i2}})}}, {\rm d}x^{+}_{i} (k) = K(k)b_{i}\quad \hbox{and} \quad {\rm d}s_{i} = D^{{- \frac{1}{2}}} L^{\rm T} b_{i}$$

dR i is the horizontal position error due to measurement i, ds i the transformed residual formed by the introduction of range bias error \({b_{i}, {\rm d}x^{+}_{i}}\) the effect of the bias on the solution, D the diagonal matrix of the eigenvalues of the covariance matrix for the innovation and L the modal matrix.

HPL3 is given by,

$${\rm HPL}_{3} = {\rm slope}_{{\rm max}} s_{{\rm bias}}$$
(19)

where the value of s bias is determined by the use of non-central chi-square distribution. It is the square root of the non-centrality parameter of the chi-square distribution that would make the missed detection probability of the error equal to 0.001.

The overall HPL is then determined as:

$${\rm HPL} = {\rm root\hbox{-}sum\hbox{-}square} ({\rm max}({\rm HPL}_{1},{\rm HPL}_{2}), {\rm HPL}_{3}).$$
(20)

In a later extension of this method, HPL2 is removed from Eq. 20 (Lee and O‘Laughlin 2000). The reasons for this are that:

  • HPL2 is defined similarly to the HUL (horizontal uncertainty limit). By definition, HUL is an estimate of the horizontal position uncertainty that bounds the error with a probability of 0.999. Defining HPL in the same manner can result in a situation when the position error can exceed this value of the protection limit with a probability of 0.001. Hence inclusion of this 2nd term in the HPL violates the integrity requirement of 10−7 per hour.

  • HPL2 also fluctuates with measurements. Hence, if HPL is less than HAL at a particular time this does not provide enough assurance about the continuity of the flight operation as in a short time, a fluctuation in the measurement may increase the value of HPL above that of HAL.

In both the MSS and AIME approaches, the basic aim is to keep the value of the HPL below that of HAL. These methods use the detection threshold in the position and measurement domains, respectively. However, there is no provision for the detection of the error rate. This idea will be used to develop a new detection algorithm in Part II.

Optimal fault detection

Another approach that accounts in some detail for the theory of fault detection is presented in Nikiforov (2002). In this approach, the emphasis is on the early detection of a fault, with the positive result of minimizing the detection time. This is an important factor in cases where the time-to-alert is relatively short.

The approach divides navigation systems into two classes, those that can be described with regression-type models and others with state space models. For a GPS-only solution, the regression type approach suffices but for the integrated system, state space models have to be used, as described below. The fault detection algorithm is based on generalized likelihood ratio testing (GLRT) and can be explained as follows. Assuming a general method for the Kalman filter which is valid for typical loosely coupled and tightly coupled approaches, we have,

$$\begin{aligned} X_{{k + 1}} = FX_{k} + v_{k} + \gamma _{X} (k,t_{0}) \\ Y_{k} = HX_{k} + \xi _{k} + \gamma _{Y} (k,t_{0}) \\ \end{aligned}$$
(21)

where F is the system matrix, X k+1 and X k are the systems state vector at time k + 1 and k, respectively, v k the process noise, γ X the process fault whose onset time is \({t_{0}, Y_{k}}\) the measurement, H the measurement matrix and γ Y the fault in the measurement with onset time t 0.

The Kalman filter innovation is selected as the test statistic:

$$\varepsilon _{k} = Y_{k} - H_{k} \hat{X}_{{k|k + 1}}$$
(22)

where ɛ k is the innovation and \({\hat{X}_ {{k|k + 1}}}\) the state estimate based on Kalman filtering.

The test statistic is assumed to follow a Gaussian distribution with a zero mean in the fault free case and a non-zero mean in the faulty case, i.e.,

$$\varepsilon _{k} \sim \left\{{\begin{array}{*{20}c} {{N(0,\Sigma _{k})\quad \quad k < t_{0}}} \\ {{N(\eta (k,t_{0}),\Sigma _{k})\quad \quad k \geqslant t_{0}}} \\ \end{array}} \right.$$
(23)

where η(k,t 0) is the signature of the fault on the innovation and \({\Sigma _{k} = \operatorname{\rm cov} (\varepsilon _{k})}.\) To compare the test statistic with the decision threshold, a log likelihood ratio is formed as:

$$Z = \log \frac{{f_{l} (Y_{1}, \ldots Y_{k})}}{{f_{j} (Y_{1}, \ldots Y_{k})}}$$
(24)

where f j and f l are the probability distribution functions of measurements before and after the occurrence of a fault, respectively.

A change in the statistical model due to occurrence of a fault is reflected by a change in the sign of the mean of the log likelihood ratio (Nikiforov 1995). Hence, we can decide between the two hypotheses:

$$\begin{aligned} {\rm H}_{0} \quad : \quad {\left\{{\gamma (k,t_{0}) = 0} \right\}} \\ {\rm H}_{1} \quad : \quad {\left\{{\gamma (k,t_{0}) \ne 0} \right\}} \end{aligned}.$$
(25)

The alternate hypothesis results in the generation of an alert that indicates a failure. This algorithm is computationally complex and approximations need to be used for ease of implementation. Furthermore, the formula cannot be written recursively (Basseville and Nikiforov 1993). An approximate recursive solution is proposed in Nikiforov (2002).

Ultra-tightly coupled system

A RAIM method suggested for ultra-tightly coupled systems is the GI-RAIM (GPS inertial RAIM) method (Gold and Brown 2004). It is based on the BOPD (bounded probability of missed detection) concept. Based on a pre-filter, it is anticipated that a certain satellite is faulty. By excluding this satellite, a position solution is computed. From the comparison of this solution with the full solution, the contribution of the faulty satellite to the radial position error is estimated with a high probability. The algorithm ensures that this fault characterization minimizes the missed detection risk. However, the condition is that a sufficient number of satellites is available in a good geometrical configuration. It is claimed that HAL and VAL values close to 1 m can be achieved with this algorithm. But it should be noted here that this accuracy is achieved by using the GPS carrier phase observable. The availability of the carrier phase solution is limited by the resolution of integer ambiguity which is not always guaranteed. In the GI-RAIM integrity monitoring, a pre-filter is used to flag the faulty GPS signal. In this way, corrupt GPS data are prevented from propagating back into the main navigation filter.

Selection of integration architecture and integrity algorithm

The integrity performance of the loosely coupled system is restrictive in nature due to the fact that GPS measurements are not accessible. Hence, healthy GPS measurements are not of any use in the situation when the navigation solution is corrupted by a faulty measurement. In general, there are two advantages of the ultra-tightly coupled system over the tightly coupled system.

  • In case of corrupted GPS measurements as a result of either interference or jamming, the GPS solution obtained is better than the conventional GPS solution. The noise is effectively reduced by direct handling of the I and Q signals in the GPS receiver as shown in Gustafson and Dowdle (2003) and Kim et al. (2003).

  • The tracking loop of the GPS receiver is aided by the INS to lock onto the satellites.

As we want to analyze the behaviour of integrity algorithms in the case of SGEs for which the deep processing of the GPS receiver will not be of much advantage (as the SGE is not a kind of noise), it is the measurement redundancy that is paramount. Two scenarios arise in this respect.

  • If redundant satellite measurements are available, these can be fully exploited by the tightly coupled integrated systems, hence ultra tightly coupled systems are not superior in this case.

  • In case redundant satellite measurements are available but immersed in noise, ultra-tightly coupled systems have a better chance of utilizing them (for further detection of SGEs) than tightly coupled systems. However, the error detecting mechanism is not different as the test statistic for the GI-RAIM method is based on chi-square formulation as in AIME. Hence, the error detection strategy presented later in the second paper (Part II) is also applicable to ultra-tightly coupled systems.

The other benefit (aiding of the GPS tracking loop) of the ultra-tightly coupled system is limited by the fact that the INS has to be calibrated to provide aiding to the tracking loop. However, as shown later in Part II, it is not possible to calibrate INS in general, save for the usage of specific manoeuvres as in Groves et al. (2002) or by the usage of multiple antennae (Wagner 2005).

In summary, the tightly coupled architecture offers the best compromise (in the monitoring of SGEs) with regard to complexity of coupling and accessibility to the relevant measurements. Hence this architecture is selected for further study in Part II. With regard to the integrity algorithms for tightly coupled systems the optimal fault detection algorithm is not considered further because its characteristics are similar to that of the AIME algorithm. Furthermore, the need for knowledge of fault signatures precludes its use as a general integrity algorithm (Nikiforov 2002). Optimum fault detection is based on GLRT (generalized likelihood ratio testing) while AIME is based on chi-squared distribution. These testing mechanisms are similar. Hence Part II focuses on the AIME and MSS algorithms.

Conclusions

This paper has proposed models for various classes of failure modes and reviewed the existing sensor level integrity monitoring techniques for the integrated GPS/INS systems. The review of failure modes has identified the worst case class of potential failures to be those associated with slow growth over time. A subsequent review of the different architectures, has revealed that in the case of SGEs, the tightly coupled architecture offers the best compromise with regard to complexity of coupling and accessibility to the relevant measurements. Among the integrity algorithms for tightly coupled systems the MSS and AIME methods have been selected as candidate algorithms for further research (in Part II) because the optimal fault detection method has similar theoretical characteristics to AIME. This analysis (and the development of a new algorithm) will be presented in Part II.