Introduction

The conventional Kalman filtering (CKF) is an optimal estimation method that has been widely applied in navigation applications. For a normal operational situation, the model statistic noise levels are given before the filtering process starts and will maintain unchanged during the whole recursive process. Such priori statistical information is commonly determined beforehand using experiments and certain knowledge about the observation type. As long as the noise characteristics are correctly specified, the filter will produce optimal estimates for unknown system states. However, if the priori statistical information is inadequate to represent the real statistic noise levels, the Kalman filter estimation is not optimal and may cause unreliable results, sometimes even leading to filtering divergence (Mohamed and Schwarz 1999).

Fading Kalman filtering was proposed to overcome the shortcomings of the CKF (e.g., Fagin 1964), by assigning a constant fading factor. But its effect is not always ideal given an uncertain noise distributions. Accordingly various adaptive Kalman filters have been developed to estimate the fading factor (Lee 1988; Yang et al. 2001). An approach to estimate the fading factors adaptively was proposed by Xia and Rao (1994). Then a strong tracking Kalman filter was proposed and applied in nonlinear dynamic systems to identify states and parameters (Zhou and Frank 1996). In the field of surveying and navigation applications, Hu et al. (2003) presented an approach that uses an algorithm based on the magnitude of the predicted residuals to reduce the dynamic modeling errors. Zhang et al. (2003) used a strong tracking filter in DGPS/MEMS-IMU/Magnetic compass integrated navigation system for improving the robustness to the model uncertainties. Hide et al. (2003) also examined the use of three adaptive filtering techniques, including artificially fading Kalman filter covariance, the adaptive Kalman filter and multiple model adaptive estimation for a low-cost INS/GPS integrated system.

In this paper, we propose an adaptive method to estimate multiple fading factors in the Kalman filter for navigation applications. The algorithm makes use of the predicted residuals. Along with the statistical evaluation of the filter residuals using a Chi-square test, the fading factors are computed separately to increase the predicted variance components of the state vector. Land vehicle tests have been carried out to compare the performance of this algorithm with a conventional Kalman filter for vehicle navigation using GPS standalone and integrated GPS/INS system. The results demonstrate that the proposed algorithms can restrain the filtering divergence when system noise attributes are not accurate. The new approach is easy to implement and does not add a heavy computation burden to the system.

Kalman filter algorithm

Considering a linear dynamic system:

$$ x_{k} = \Upphi_{k/k - 1} x_{k - 1} + w_{k - 1} $$
(1)
$$ z_{k} = H_{k} x_{k} + v_{k} $$
(2)

where x k is the state vector at epoch k; ϕk/k−1 is the state transition matrix; w k−1 is the system noise; z k is the observation at epoch k; H k represents the observation matrix. The expectation and the covariance matrices of w k−1 and v k are written as

$$ \begin{aligned} E(w_{k - 1}) &= 0\\ \operatorname{var} (w_{k - 1}) &= Q_{k - 1}\\ E(v_{k - 1}) &= 0\\ \operatorname{var} (v_{k - 1}) &= R_{k - 1} \end{aligned} $$

respectively.

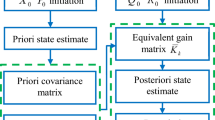
Basically, the Kalman filtering estimation algorithm comprises two steps, namely prediction and updating with external measurements. The main Kalman filtering equations are given below:

Prediction:

$$ {\hat{x}}_{k/k - 1} = \Upphi_{k/k - 1} {\hat{x}}_{k - 1} $$
(3)
$$ P_{k/k - 1} = \Upphi_{k/k - 1} P_{k - 1} \Upphi_{k/k - 1}^{T} + Q_{k-1} $$
(4)

Updating:

$$ K_{k} = P_{k/k - 1} H_{k}^{T} [H_{k} P_{k/k - 1} H_{k} + R_{k}]^{- 1} $$
(5)
$$ {\hat{x}}_{k} = {\hat{x}}_{k/k - 1} + K_{k} [z_{k} - H_{k} {\hat{x}}_{k/k - 1}] $$
(6)
$$ P_{k} = (I - K_{k} H_{k})P_{k/k - 1} $$
(7)

where \({\hat{x}}_{k/k - 1}\) is the predicted state vector; P k/k−1 is the variance matrix for \({\hat{x}}_{k/k - 1}; K_{k}\) is the gain matrix; \({\hat{x}}_{k}\) is the estimated states; and P k is the variance matrix for the estimated states.

Based on Eqs. (2) and (3), the predicted residual vector can be expressed as

$$ v_{k} = z_{k} - H_{k} \hat{X}_{k/k - 1} $$
(8)

For a linear dynamic system, when a filter is stable, we have

$$ v_{k} \sim N(0,H_{k} P_{k/k - 1} H_{k}^{T} + R_{k}) $$
(9)

Then

$$ \operatorname{var} (v_{k}) = H_{k} (\Upphi_{k/k - 1} P_{k - 1} \Upphi_{k/k - 1}^{T} + Q_{k - 1})H_{k}^{T} + R_{k} $$
(10)

We can construct a statistic:

$$ \gamma_{k} = v_{k}^{T} {\left[H_{k} (\Upphi_{k/k - 1} P_{k - 1} \Upphi_{k/k - 1}^{T} + Q_{k - 1})H_{k}^{T} + R_{k} \right]}^{- 1} v_{k} \sim\chi^{2} (m) $$
(11)

where γ k has a Chi-square distribution with m degrees of freedom, and m is the number of state variables which can be observed.

The testing criteria is

$$ \xi = \frac{\gamma_{k}}{\varepsilon} = \left\{{\begin{array}{*{20}c} {\geqslant 1\begin{array}{*{20}c} & {\begin{array}{*{20}c} {\rm test} & {\rm fails} \\ \end{array}} \\ \end{array}} \\ { < 1\begin{array}{*{20}c} &\ {\begin{array}{*{20}c} {\rm test}& {\rm passes} \\ \end{array}} \\ \end{array}} \\ \end{array}} \right. $$
(12)

where ζ is a scale factor for the statistical test, ɛ is the threshold value according to the Chi-square distribution table at a given confidential level. If the test tails then the assumption of multivariate normal distribution (9) is not valid.

Adaptive estimation of multiple fading factors in a Kalman filter

The Kalman filtering estimation at epoch k can be considered as ‘weighted’ adjustment between the new measurements (observation model) and the predicted ones based on the predicted state vector, the dynamic model, and all previous measurements. If too much “weight” were given to the dynamic model, the estimation would ignore the information from new measurements and causes the divergence of the filtering. To overcome this problem, a constant fading factor s is assigned,

$$ P_{k/k - 1} = \Upphi_{k,k - 1} (sP_{k - 1/k - 1})\Upphi_{k,k - 1}^{T} + Q_{k - 1}, \quad s > 1 $$
(13)

However, a constant fading factor can not guarantee optimal filtering. In actual applications, it is very difficult to determine the correct value of the fading factor. For the complicated multivariable systems, estimation performance of the Kalman filter varies for each variable. It is not enough to use only one fading factor to multiply the covariance matrices. To overcome the shortcomings of a single fading factor Kalman filter, a multiple fading factor Kalman filter is proposed to increase the predicted variance component for the state parameters individually. We write

$$ P_{k/k - 1} = S_{k} \Upphi_{k/k - 1} P_{k - 1} \Upphi_{k/k - 1}^{T} + Q_{k - 1} $$
(14)

Where S k  = diag(s 1, s 2,… s n ) is the matrix of fading factors.

Unfortunately Eq. (14) may lead to the asymmetry of P. To avoid this problem, the following new equation is used to replace Eq. (14)

$$ P_{k/k - 1} = S_{k} \Upphi_{k/k - 1} P_{k - 1} \Upphi_{k/k - 1}^{T} S_{k}^{T} + Q_{k - 1} $$
(15)

Now considering a new measurement matrix that satisfies the condition as follows:

$$ {\bar{H}}_{k} = {\left[\begin{array}{*{20}c} {\Lambda_{m \times m}}& {O_{m \times (n - l)}} \\ \end{array} \right]}_{m \times n}, \quad m \leq n $$
(16)

where, Λm×m = diag(λ1, λ2,…, λ m ). For many linear systems in control and estimation field, the condition above can be satisfied through rearranging the sequence of the state variables.

It is noted that when the filter is in a steady state processing, the predicted residual vector has an attribute as follows

$$ \gamma_{k} = v_{k}^{T} [{\bar{H}}_{k} (S_{k} \Upphi_{k/k - 1} P_{k - 1} \Upphi_{k/k - 1}^{T} S_{k}^{T} + Q_{k - 1}){\bar{H}}_{k}^{T} + R_{k}]^{- 1} v_{k} \sim\chi^{2} (m) $$
(17)

Where S k  = diag(s 1, s 2,… s n ) is the matrix of fading factors.

Given that

$$ A_{k} = {\bar{H}}_{k} S_{k} \Upphi_{k/k - 1} P_{k - 1} \Upphi_{k/k - 1}^{T} S_{k}^{T} {\bar{H}}_{k}^{T} $$
(18)
$$ B_{k} = {\bar{H}}_{k} Q_{k - 1} {\bar{H}}_{k}^{T} + R_{k} $$
(19)
$$ J_{k} = \Upphi_{k/k - 1} P_{k - 1} \Upphi_{k/k - 1}^{T} $$
(20)

Then

$$ \begin{aligned} A_{k} &= {\bar{H}}_{k} S_{k} \Upphi_{k/k - 1} P_{k - 1} \Upphi_{k/k - 1}^{T} S_{k}^{T} {\bar{H}}_{k}^{T}\\ &= {\left[ \begin{array}{*{20}c} {\Lambda_{m \times m}} & {O_{m \times (n - m)}} \\ \end{array} \right]}_{m \times n} {\left[\begin{array}{*{20}c} {S_{1,m \times m}} & {O_{m \times (n - m)}} \\ {O_{(n - m) \times m}} & {S_{2,(n - m) \times (n - m)}} \\ \end{array} \right]}_{n \times n} {\left[ \begin{array}{*{20}c} {J_{11,m \times m}}& {J_{12,m \times (n - m)}} \\ {J_{21,(n - m) \times m}} & {J_{22,(n - m) \times (n - m)}} \\ \end{array} \right]}_{n \times n}\\ &\quad {\left[\begin{array}{*{20}c} {S_{1,m \times m}} & {O_{m \times (n - m)}} \\ {O_{(n - m) \times m}} & {S_{2,(n - m) \times (n - m)}} \\ \end{array} \right]}_{n \times n} {\left[\begin{array}{*{20}c} {\Lambda_{m \times m}} \\ {O_{(n - m) \times m}} \\ \end{array} \right]}\\ &= {\left[\begin{array}{*{20}c} {S_{1,m \times m}}& {O_{m \times (n - m)}} \\ \end{array} \right]}_{m \times n} {\left[\begin{array}{*{20}c} {\Lambda_{m \times m}}& {O_{(n - m) \times m}} \\ {O_{(n - m) \times m}}& {O_{(n - m) \times (n - m)}} \\ \end{array} \right]}_{n \times n} {\left[ \begin{array}{*{20}c} {J_{11,m \times m}}& {J_{12,m \times (n - m)}} \\ {J_{21,(n - m) \times m}}& {J_{22,(n - m) \times (n - m)}} \\ \end{array} \right]}_{n \times n}\\ &\quad {\left[{\begin{array}{*{20}c} {\Lambda_{m \times m}}& {O_{(n - m) \times m}} \\ {O_{(n - m) \times m}}& {O_{(n - m) \times (n - m)}} \\ \end{array}} \right]}_{n \times n} {\left[ {\begin{array}{*{20}c} {S_{1,m \times m}} \\ {O_{(n - m) \times m}} \\ \end{array}} \right]}_{n \times m}\\ & = {\left[ {\begin{array}{*{20}c} {S_{1,m \times m}}& {O_{m \times (n - m)}} \\ \end{array}} \right]}_{m \times n} {\left[ {\begin{array}{*{20}c} {\Lambda_{m \times m} J_{11,m \times m} \Lambda_{m \times m}}& {O_{m \times (n - m)}} \\ {O_{(n - m) \times m}}& {O_{(n - m) \times (n - m)}} \\ \end{array}} \right]}_{n \times n} {\left[ {\begin{array}{*{20}c} {S_{1,m \times m}} \\ {O_{(n - m) \times m}} \\ \end{array}} \right]}_{n \times m} \\ & = S_{1,m \times m} \Lambda_{m \times m} J_{11,m \times m} \Lambda_{m \times m} S_{1,m \times m}\end{aligned} $$
(21)

From the above equation, the following equation can be derived

$$ a_{ii} = s_{i}^{2} \lambda_{i}^{2} j_{ii}, \quad (i = 1,2, \ldots, m) $$
(22)

where a ii (k) and j ii (k) are the ith diagonal element of matrix A k and J k respectively.

When a filter is stable, Eq. (9) is true. Each element of v k satisfies (Da 1994)

$$ \gamma_{i} (k) = \frac{[v_{i} (k)]^{2}}{a_{ii} (k) + b_{ii} (k)}\sim\chi (1) $$

where b ii (k) are the ith diagonal element of matrix B k .we can obtain that

$$ \frac{[v_{i} (k)]^{2}}{a_{ii} (k) + b_{ii} (k)}/\varepsilon_{i} < 1 $$
(23)

where v i (k) is the ith element of the v k .

Using inequality (23), the adaptive factors may satisfy the following condition

$$ s_{i}^{2} > \frac{[v_{i} (k)]^{2}}{\lambda_{i}^{2} j_{ii} (k)\varepsilon_{i}} - \frac{b_{ii} (k)}{j_{ii} (k)}, \quad (i = 1,2, \ldots, m) $$
(24)

Considering the sign of square root of s 2 i , if

$$ \frac{[v_{i} (k)]^{2}}{\lambda_{i}^{2} j_{ii} (k)\varepsilon_{i}} - \frac{b_{ii} (k)}{j_{ii} (k)} > 0, $$

then, one can obtain

$$ s_{i} = \max {\left(1,\sqrt{\frac{[v_{i} (k)]^{2}}{\lambda_{i}^{2} j_{ii} (k)\varepsilon_{i}} - \frac{b_{ii} (k)}{j_{ii} (k)}} \right)}, \quad (i = 1,2, \ldots, m) $$
(25)

If

$$ \frac{[v_{i} (k)]^{2}}{\lambda_{i}^{2} j_{ii} (k)\varepsilon_{i}} - \frac{b_{ii} (k)}{j_{ii} (k)} < 0, $$

then

$$ s_{i} = 1, \quad (i = 1,2, \ldots, m). $$

In this approach, only s 1, s 2,…, s m of matrix S k in Eq. (14) can be estimated adaptively. The other elements of the matrix S k cannot be estimated adaptively due to their un-observablilities, each of their values should be chosen as 1. The multiple fading factor matrix can be written as

$$ S_{k} = {\rm diag}(s_{1}, s_{2}, \ldots, s_{m}, 1, \ldots, 1, \ldots, 1) $$

This is because the only prior m state variables can be observed directly while other state variables cannot be observed. It is clear that the values of the observable states can be rectified, whereas the estimation performance of unobservable states cannot be rectified due to the lack of sufficient information.

Testing

Two examples from navigation, GPS standalone dynamic positioning and GPS/INS integrated navigation, are used to evaluate the performance of the adaptive algorithm proposed.

GPS dynamic positioning

A data set was collected using Leica 500 on a land vehicle in 2005. The available measurements are C/A code, P-code pseudoranges, L1 and L2 carrier phases and Doppler measurements with 1 Hz output rate.

The highly accurate double-differenced carrier measurements solutions were used as “reference” to compare with the Kalman filtering results from the code differential GPS measurements. The constant velocity model for the Kalman filter was employed. The system dynamic model is as follows

$$ {\left[{\begin{array}{*{20}c} {{\dot{x}}} \\ {{\dot{v}}} \\ \end{array}} \right]} = {\left[ {\begin{array}{*{20}c} {0} & {1} \\ {0} & {0} \\ \end{array}} \right]}{\left[ {\begin{array}{*{20}c} {x} \\ {v} \\ \end{array}} \right]} + {\left[ {\begin{array}{*{20}c} {0} \\ {w} \\ \end{array}} \right]} $$

The measurement equations is

$$ z = {\left[ {\begin{array}{*{20}c} {1} & {0} \\ \end{array}} \right]} {\left[ {\begin{array}{*{20}c} {x} \\ {v} \\ \end{array}} \right]} + n $$

where the variance for the position measurements was 0.2 m2 and the spectral density for the velocity measurements was chosen to be 0.01, 0.02, 0.05, 0.1 m2/s2, respectively.

We used the conventional Kalman filter and adaptive algorithm to estimate the GPS position and velocity. When using the adaptive filter, according to the Chi-square distribution table at the given confident level α = 0.99, the threshold value ɛ is 6.635. The positional errors are shown in Figs. 1 and 2.

Fig. 1
figure 1

The CKF

Full size image
Fig. 2
figure 2

The Adaptive algorithm

Full size image

Figure 1 shows the test results of the conventional Kalman filter. Because we do not know the exact spectral density for the velocity, we have to guess the noise covariance when using the CKF to estimate the state values. In Fig. 1a–d, we plot the result for different values of the noise covariance. It is can be seen that the dynamic noise level strongly affects the performance of conventional Kalman filter. We can also notice that the position errors become smaller when the noise covariance gets larger.

Under the same conditions, Fig. 2 shows the errors of position estimation using the proposed algorithm. Comparing with the results with Fig. 1, we can see that all the position errors in Fig. 2 are smaller. The proposed adaptive algorithm can estimate the position value accurately no matter what value of system noise covariance is chosen. Therefore the proposed algorithm is a robust approach and can effectively deal with state estimation for navigation applications.

GPS/INS integrated navigation

In GPS/INS integrated navigation application we consider a basic set of system parameters, the navigation parameters, and the accelerometer and gyroscope error states,

$$ \begin{aligned} \,& X = [\delta r_{N}, \delta r_{E}, \delta r_{D}, \delta V_{N}, \delta V_{E}, \delta V_{D}, \Uppsi_{N}, \Uppsi_{E}, \Uppsi_{D},\\ \,& \nabla_{bx}, \nabla_{by}, \nabla_{bz}, \nabla_{fx}, \nabla_{fy}, \nabla_{fz}, \varepsilon_{bx}, \varepsilon_{by}, \varepsilon_{bz}, \varepsilon_{fx}, \varepsilon_{fy}, \varepsilon_{fz}, \delta g_{N}, \delta g_{E}, \delta g_{D} ]^{T} \end{aligned} $$

The symbols δr N , δr E , δr D denote the position errors; δv N , δv E , δv D are the velocity errors; ψ N , ψ E , ψ D are the attitude errors; ∇ bx , ∇ by , ∇ bz are the accelerometer biases; ∇ bx , ∇ by , ∇ bz are the accelerometer scale factor errors; ɛ bx , ɛ by , ɛ bz are the gyro drifts. ɛ fx , ɛ fy , ɛ fz are the gyro scale factor errors; δg x , δg y , δg z represent the gravity uncertainty errors. The system noise vector is W(t) = [ω∇ bx ω ∇ by ω∇ bz ω∇ fx ω ∇ fy ω∇ fz ωɛ bx ω ɛ by ωɛ bz ω ɛ fx ωɛ fy ω ɛ fz ω gN ω gE ω gD ]T. The system errors model is presented as:

$$ {\dot{X}}(t) = F(t)X(t) + G(t)W(t) $$

The measurement model can be expressed as:

$$ Z(t) = {\left[P_{\rm INS} - P_{\rm GPS} \right]} = H(t)X(t) + V(t) = {\left[ {\begin{array}{*{20}c} {I_{3 \times 3}}& {O_{3 \times 21}} \\ \end{array}} \right]}X(t) + V(t) $$

Where Z(t) is the measurement vector; H(t) is the design matrix; and V(t) is the noise vector.

The test involved two Leica System 530 GPS receivers and one BEI C-MIGITS II (DQI-NP) INS unit. One GPS receiver was set up as the static reference station, and the other one mounted on top of the test vehicle together with the INS unit. The data were stored on the GPS receiver’s PCMCIA and a laptop computer for post processing.

Table 1 shows the DQI-NP’s technical data for reference. These values were used in setting up the Q estimation in the conventional Kalman filtering process. Using the same confident level α = 0.99 as in the first application, the threshold value ɛ is 6.635. Figure 3 shows the ground track of the test vehicle. Figure 4 shows the position errors obtained using the conventional Kalman filter. This result represents the best performance from the CKF using different values of system noise covariance. For the proposed algorithm, the initial noise levels were identical to those for the conventional Kalman filter. Figure 5 shows the position errors of the proposed algorithm.

Table 1 DQI-NP’s technical data
Full size table
Fig. 3
figure 3

Ground track of the test vehicle

Full size image
Fig. 4
figure 4

Position errors from the CKF

Full size image
Fig. 5
figure 5

Position errors from the adaptive algorithm

Full size image

From Fig. 4 it is seen that the maximum error in latitude and longitude were 0.4 m. The standard deviations of positioning errors are 0.0845 m and 0.1358 m for latitude and longitude respectively. The errors of position estimation are mainly caused by the unmodeled errors. In fact, it is very difficult to get the exact apriori information of navigation system, so we have to ‘guess’ the values of system noise covariance. Due to lack of adaptive estimation ability, the performance of the conventional Kalman filter is not satisfactorily.

Comparing Figs. 5 and 4, it is clearly demonstrated that the position errors with the proposed adaptive Kalman filters are significantly smaller than those of the CKF. For the proposed algorithm, the positioning errors are 0.0014 and 0.0016 m (standard deviation) for latitude and longitude, respectively. Better results can also be achieved with the proposed algorithm for the height. Hence the positioning errors are significantly reduced using the proposed multiple fading factor Kalman filter.

Conclusion

Inaccuracy in system models may degrade the performance of the conventional Kalman filter. To overcome these shortcomings of the Kalman filter, we have introduced a fading Kalman filtering algorithm. The algorithm uses the predicted residuals to compute multiple fading factors to scale the predicted covariance matrix.

The proposed algorithm has been tested using GPS standalone and GPS/INS integrated system examples. The comparisons have demonstrated that the proposed algorithm is much better than the conventional Kalman filter when the system noise characteristics are not exactly known. The proposed algorithm is a robust approach and insensitive to the levels of system noise. The characteristic of the new filter can overcome the shortcomings of the conventional Kalman filter as to robust estimation. Compared with the existing methods, the proposed new approach is easy to implement and without heavy computation burden.