Directional approach to gradual cover: a maximin objective

Abstract

The objective of original cover location models is to cover demand within a given distance by facilities. Locating a given number of facilities to cover as much demand as possible is referred to as max-cover, and finding the minimum number of facilities required to cover all the demand is referred to as set covering. When the objective is to maximize the minimum cover of demand points, the maximin objective is equivalent to set covering because each demand point is either covered or not. The gradual (or partial) cover replaces abrupt drop from full cover to no cover by defining gradual decline in cover. Both maximizing total cover and maximizing the minimum cover are useful objectives using the gradual cover measure. In this paper we use a recently proposed rule for calculating the joint cover of a demand point by several facilities termed “directional gradual cover”. The objective is to maximize the minimum cover of demand points. The solution approaches were extensively tested on a case study of covering Orange County, California.

1 Introduction

Cover location models constitute a main branch of location analysis. A demand point is covered by a facility within a certain distance (Church and ReVelle 1974; ReVelle et al. 1976). Facilities need to be located in the area to provide as much cover as possible. Such models are used for cover provided by emergency facilities such as ambulances, police cars, or fire trucks. They are also used to model cover by transmission towers for cell-phone, TV, radio, radar among others. For a review of cover models see Berman et al. (2010b), García and Marín (2015), Plastria (2002), Snyder (2011).

Gradual cover models (also referred to as partial cover) assume that up to a certain distance r the demand point is fully covered and beyond a greater distance R it is not covered at all. Between these two extreme distances the demand point is partially covered. There exist several formulations of the partial cover. Berman and Krass (2002) suggested a declining step function between r and R. Drezner et al. (2004) suggested a linear decline in cover between r and R, and Drezner et al. (2010) suggested a linear decline between random values of r and R. The original cover models are a special case of gradual cover models. When the two extreme distances are the same, cover drops abruptly at that distance.

Church and Roberts (1984) were the first to propose a discrete gradual cover model. The network version with a step-wise cover function is discussed in Berman and Krass (2002). The network and discrete models with a general non-increasing cover function were analyzed in Berman et al. (2003). The single-facility planar model with a linearly decreasing cover function between the distance of full coverage and the distance of no coverage was optimally solved in Drezner et al. (2004), and its stochastic version analyzed and optimally solved in Drezner et al. (2010). Additional references include (Berman et al. 2010b, 2019; Drezner and Drezner 2014; Eiselt and Marianov 2009; Karasakal and Karasakal 2004).

A main issue when several facilities partially cover a demand point is the estimation of the total cover, also referred to as joint cover. If the partial cover is interpreted as “the probability of cover”, then assuming independent probabilities, the probability of cover can be evaluated. If the probabilities are correlated, then the probability of total cover can be evaluated by a multivariate distribution. For a discussion of ways to estimate the joint cover see Berman et al. (2019), Drezner and Drezner (2014), Eiselt and Marianov (2009), Karasakal and Karasakal (2004).

Drezner et al. (2019) introduced a directional approach to gradual cover. Demand points are represented by circular discs rather than mathematical points and the facility covers points within a given distance. To find a demand point’s partial cover by one facility, the intersection area between two discs (the demand point’s disc and the facility’s coverage disc) is calculated. An explicit formula for the intersection area is given in Drezner et al. (2019). The partial cover of the demand point is the intersection area divided by the demand point’s disc area.

2 An illustrative example

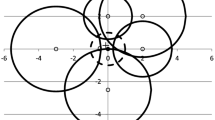
If several facilities exist in the area, the joint cover of a demand point is the union of the individual areas covered by the facilities. This joint cover depends on the distances to the facilities and on their directions. See Fig. 1 for an example. Six facilities are located in the area. Their coordinates and cover radii $D_j$ are depicted in Table 1. The demand point is located at (0, 0) and the disc of the “demand point” of radius 1 is marked by dots. The discs centered at the facilities are marked with thick circular lines.

Fig. 1

An illustrative example

Table 1 Parameters of six facilities

Each of the six facilities covers part of the demand point’s disc. The joint cover of the demand point is the union of intersection areas between the facilities’ discs and the unit disc surrounding the demand point.

The joint cover of several facilities depends on the directions of the facilities. To illustrate the effect of direction, consider in the illustrative example cover by two facilities as if the other four facilities are not in the area. Facility 2 is to the north of the demand point and facilities 4 and 6 are south of the demand point. The total area covered by facilities 2 and 4 is the sum of the cover areas. Facility 2 covers part of the northern region of the neighborhood while facility 4 covers part of the southern region and there is no overlap. The same is true for facilities 2 and 6 and also facilities 1 and 3. However, facilities 4 and 6 are both to the south and cover the southern part of the neighborhood. Because of the overlap between the cover areas, the total cover is the area covered by facility 4 and no additional cover is provided by facility 6. The total cover of facilities 1 and 4 is less than the sum of the areas and more than the largest area. There is an intersection area between the two cover areas which is counted only once. Contrary to all gradual cover models, the joint cover depends on the direction. In order to calculate the joint cover, it is not sufficient just to have for each facility the value of its partial cover.

Evaluating the union of the individual cover areas is quite complex. Drezner et al. (2019) suggested to estimate the union’s area by numerical integration using Gaussian quadrature based on Legendre polynomials (Abramowitz and Stegun 1972). For complete details the reader is referred to Drezner et al. (2019).

Drezner et al. (2019) experimented with the objective of maximizing the sum of the partial covers. In the present paper we maximize the minimum partial cover at all demand points. It turns out that maximizing the minimum cover is a much more difficult problem than maximizing the sum of partial covers. Even if only one demand point is not covered, the objective function is zero. Heuristic algorithms may be unable to improve it.

3 Heuristic approaches for maximizing the minimum cover

We constructed and tested two heuristic algorithms based on tabu search and simulated annealing which are similar to those proposed in Drezner et al. (2019) for the objective of maximizing the sum of the partial covers. However, contrary to the experience reported in Drezner et al. (2019), we found by computational experiments that for maximizing the minimum partial cover the quality of the results for large problems depends heavily on the starting solutions. We therefore constructed and tested five approaches for generating starting solutions. Some perform well when the number of facilities is small and the objective function is close to zero and others perform well for larger values of p when the objective function is close to full coverage. We were not able to find a starting solution approach that performs well for the whole range.

Consider a problem with n demand points and m potential facility’s locations. Note that co-location is not beneficial for cover. When two facilities are located at the same point, the intersection area for the facility with a smaller or equal cover radius is included in the intersection area of the facility with the larger radius. The union is the intersection area of the facility with a larger cover radius. Once the coverage by selecting p potential locations can be calculated, the problem reduces to selecting the best set of p out of m potential locations. If p and m are relatively small, the optimal solution can be found by total enumeration or a branch and bound algorithm. We constructed and tested two heuristic algorithms based on tabu search and simulated annealing which are similar to those proposed in Drezner et al. (2019). However, there are many implementation issues when applying these algorithms to the maximin objective. Detailed discussions of these issues are described in Sects. 4 and 5.

Tabu search and simulated annealing are based on evaluating moves. A move consists of removing one of the p selected potential locations and replacing it with one of the non-selected $m-p$ potential locations. There are $p(m-p)$ possible moves. We briefly summarize the two meta heuristics used in this paper.

3.1 Tabu search

Tabu search (Glover and Laguna 1997) allows downward moves in the hope of obtaining a better solution in subsequent iterations. A tabu list of forbidden moves is maintained. Tabu moves stay in the tabu list for tabu tenure iterations. To avoid cycling, the tabu list contains potential locations that were removed from the selected set during the recent tabu tenure iterations. The process continues for a pre-specified N iterations. Random range for the tabu tenure was suggested by Taillard (1991).

A vector $V=\{V_j,~1\le j\le m\}$ is maintained. $V_j$ is the last iteration number at which potential location j was removed from the selected set.

• 1. A starting solution is selected and is the best found solution. Set $iter=0$.

• 2. Set V to large negative numbers.

• 3. Set $iter=iter+1$.

• 4. If $iter>N$ stop with the best found solution as the result of the algorithm.

• 5. Otherwise, the tabu tenure, T, is randomly selected in the range $[T_{min},T_{\max }]$.

• 6. All moves are evaluated (one potential location is in and one is out) and the value of the objective function is calculated for each move.

• 7. If a move yields a better solution than the best found one, continue evaluating all the moves and perform the most improving move. Update the best found solution and go to Step 2.

• 8. If no move yields a solution better than the best found solution, select the non-forbidden move (moves for which $iter-V_{{in}}> T$) with the best value of the objective function, whether improving or not.

• 9. Set $V_{{out}}=iter$ and go to Step 3.

3.2 Simulated annealing

Simulated annealing (Kirkpatrick et al. 1983) simulates the cooling process of hot melted metals. Three parameters are required: the starting temperature $T_0$, the final temperature $T_F$, and the number of iterations N. Based on these three parameters, the temperature reduction factor $\alpha =\left( \frac{T_F}{T_0}\right) ^{1/N}$ is calculated.

• 1. A starting solution is selected and is the best found solution. Set $iter=0$ and $T=T_0$.

• 2. A random move is generated by randomly selecting a potential location from the solution to be removed, and a non-selected potential location to be added to the solution.

• 3. $\Delta F$ is the change in the value of the objective function by the move.

• 4. For $\Delta F\ge 0$: if the new solution is better than the best found solution, update the best found solution. Perform the move and go to Step 2.

• 5. For $\Delta F< 0$: perform the move with a probability $\pi =e^{\frac{\Delta F}{T}}$, and do not perform the move with a probability $1-\pi$.

• 6. Advance $iter=iter+1$ and multiply T by $\alpha$. If $iter\le N$, go to Step 2. Otherwise, stop with the best found solution as the result of the algorithm.

4 Implementation

When maximizing the total coverage, these algorithms performed well starting from a random solution (Drezner et al. 2019). However, when maximizing the minimum coverage the algorithms performed poorly, especially for a large number of demand points. Suppose that p facilities’ locations are randomly selected as a starting solution. It is quite common that at least one demand point is not covered at all and therefore the value of the objective function is zero. Furthermore, it is likely that all moves from this solution would also have an objective of zero. Simulated annealing will always accept the move regardless of the temperature thereby turning the process into a random walk of moves “hoping” to get a positive objective.

Tabu search will have all moves tied for the “best” move. Depending on the computer code used either the first or the last move will always be selected. When the “IF” statement selects a move as the best one if it is greater than the best found move, the first move is always selected (first checked facility will always be replaced and all others will not change). When the “IF” statement selects a move as the best one if it is greater than or equal to the best found move, the last move is always selected (last checked facility will always be replaced and all others will not change). In both cases the algorithm performs poorly.

It is therefore suggested to randomly select the “best” move if there are ties. This is good practice for any tabu search or ascent/descent algorithms. This can be done by either checking the moves in random order or by saving all tying moves in a list and once all moves are checked, randomly select one tying move from the list. A very simple approach to breaking ties was proposed in Drezner (2010).

4.1 Breaking ties

Tie Breaking Rule: The kth tying move replaces the selected move with probability $\frac{1}{k}$.

By this rule the first move (or a new best found move) is always selected ($k=1$). When a tying move is found, it replaces the selected move with probability $\frac{1}{2}$, and so on. When the process ends and K moves are tied for the best one, each of the tying moves is selected with probability $\frac{1}{K}$ (Drezner 2010).

4.2 Identifying optimal zero objective

When the number of facilities p is small, it is possible that there is no solution where all demand points have a positive cover. Therefore, the optimal value of the objective function for such a p is zero minimum cover. We can find the minimum value of p for which there exist a solution with all demand points having a positive cover. Demand point i has a radius $R_i$ and facility j has a cover distance $D_j$. We need to find the smallest value of p for which there exist a solution where all demand points are closer than $R_i+D_j$ to at least one facility. This is the original set covering problem that can be solved by an IP solver such as CPLEX (CPLEX, IBM ILOG 2009).

Let $d_{ij}$ be the distance between demand point i and potential location j. A matrix $\left\{ a_{ij}\right\}$ is defined:

$$\begin{aligned} a_{ij}=\left\{ \begin{array}{ll} 1\,|&{}d_{ij}< R_i+D_j\\ \\ 0\,|&{}\text{ otherwise }\end{array}\right. \end{aligned}$$

(1)

A vector of binary variables $x_j$ is defined. The IP formulation is

$$\begin{aligned}&p~=~\min \left\{ ~\sum _{i=1}^m x_j~\right\} \nonumber \\ \text{ Subject } \text{ to: }&\nonumber \\&\sum _{j=1}^m a_{ij}x_j\ge 1 \quad \text{ for } i=1,\ldots n\nonumber \\&x_j \in \{0,1\} \quad \quad \,\, \text{ for } j=1,\ldots m \end{aligned}$$

(2)

Once the minimum value of p is found, there is no need to solve problems with a smaller value of p because the optimal value of the objective function is zero and any selection of p potential locations is tied for the optimum.

4.2.1 Isolated demand points

It is possible that one or more demand points do not get partial (or full) cover by any potential location, i.e., being “isolated”. Such demand points cannot be even partially covered and the optimal value of the objective function is zero for any value of p. There is no feasible solution to the IP (2) because for such demand points $a_{ij}=0$ for all j. This is not a major issue when the objective is to maximize the total cover (Drezner et al. 2019), but even in this case full coverage of all demand points cannot be achieved for any value of p.

Another possibility is that there are no isolated demand points but one or more demand points are “semi-isolated”, meaning that they get partial (or full) cover by only one potential location. In this case, such potential locations must be selected for locating a facility in order to get a positive value of the objective function. Such demand points have $a_{ij}=0$ for all j except one and $\sum \nolimits _{j=1}^ma_{ij}=1$. The optimal value of the objective function cannot exceed the smallest partial cover (it can be full cover) of such demand points for any value of p. In the Orange County data set, that was tested in Sect. 6, there is one “semi-isolated” demand point that is covered by only one potential location which is the location of that demand point. See Fig. 2 where this demand point is marked with an arrow. In the case study, the set of potential locations are all the demand points. We used $r=2$ miles and $R=4$ miles. A facility located more than 4 miles from a demand point does not provide any cover. The demand point marked with an arrow is at least 4.18 miles away from all other demand points (which are also potential locations) and thus can be covered only by itself.

Fig. 2

Full cover of Orange County by 44 towers

This argument can be extended to any number of potential locations covering each demand point. For each demand point i there exist a list of all potential locations that partially (or fully) cover it. If all such potential locations are selected, the maximum possible cover of demand point i can be calculated. The minimum of these maximal covers is an upper bound for the optimal value of the objective function. Another way to interpret this property is that the value of the objective function when all potential locations are selected ($p=m$) is an upper bound for any value of p because the value of the objective function cannot increase when facilities are removed. This property is true also for the total cover objective.

5 Improved starting solutions

We experimented first with randomly generated starting solutions on two case studies detailed in the next section. The smaller instance has 131 demand points and 131 potential locations for facilities and the larger instance has 577 demand points and 577 potential locations for facilities. The results were disappointing for the larger instances. We therefore designed several ways to generate better starting solutions and obtain better results.

The following five approaches to generating starting solutions were tested:

• Random: Random starting solutions.

• Greedy: A greedy-like approach.

• Reverse: A reverse greedy-like approach.

• Set Covering: Solving set covering considering only cover by the closest facility.

• Set Covering2; Solving a variant of set covering based on the closest two facilities.

5.1 Greedy-like approach

Two lists are created. One includes all potential locations for facilities and the other one includes all demand points. The following is repeated until p potential locations are selected.

• 1. For each potential location in the list we find the number of demand points in the list which would be partially covered by a facility located there within a distance less than $D_j+R_i$.

• 2. The potential location that partially covers the largest number of demand points is selected.

• 3. The selected potential location and all demand points that are now partially covered are removed from the list of potential locations and the list of demand points. Go to Step 1.

Note: if there are several potential locations tied for the the largest number of partially covered demand points, ties are broken by the approach detailed in Sect. 4.1. Breaking ties this way will usually yield different starting solutions when the process is replicated with different random seeds.

When p is relatively large, it is possible that all demand points are partially covered before p potential locations are selected. In this case, all remaining potential locations are tied for the maximum of zero and the tie breaker rule in Sect. 4.1 selects one of the remaining potential locations with equal probability for each until p potential locations are selected.

5.2 The reverse greedy-like approach

We start with locating all m facilities and discard facilities one at a time until we are down to p facilities. Each iteration, a facility whose removal leads to the highest value of the objective function is removed. Ties are broken by the rule in Sect. 4.1. At the begining of the process when close to m facilties are selected, there are likely ties for full coverage. Since the tie breaking rule incorporates random draws, it is likely that different starting solutions are obtained when different initial random seeds are used.

5.3 Using set covering solutions

It is reasonable to assume that the demand point with the minimum cover is partially covered by only one facility. Using this assumption, if no such solution is found, the maximum value of the objective function is known to be zero. If such a solution is found, it has a positive value of the objective function. It may serve as a good starting solution. Such a solution may be optimal for small values of p when in the optimal solution the least covered demand point is indeed covered by only one facility.

For simplicity, we first show the analysis for the case when all radii of demand points are the same ($R_i=R$) and all cover distances by facilities are the same ($D_j=D$). The modification required for the general case is detailed in Sect. 5.3.4. The cover of a demand point by one facility is increasing when the facility is closer to that demand point. Therefore, maximizing the minimum cover by one facility is equivalent to minimizing, among all demand points, the minimum distance between the demand point and its closest selected facility. The minimum distance between a demand point and all the facilities is calculated for each demand point. The objective is to minimize the maximum among these values.

This problem can be solved in several ways. We propose the following IP formulation. Suppose that p potential locations are selected for locating facilities. Let d be the maximum of the minimum distances among all demand points. We would like to find the minimum possible d by selecting p potential locations. It can be done by a binary search in the range $D-R\le d\le D+R$. A value of $d=\overline{d}$ in the range is selected. We can find whether there is a selection of p potential locations that the maximum of the minimum distances among all demand points is less than or equal to $\overline{d}$. We propose two options to determine it:

5.3.1 Option 1

Solving problem (2) defining $a_{ij}$ by (1) replacing $d_{ij}< R_i+D_j$ by $d_{ij}\le \overline{d}$. If the solution is less than or equal to p such a solution exists. If it is greater than p no such solution exists.

5.3.2 Option 2

Add the constraint $\sum \nolimits _{i=1}^m x_j=p$ to the constraints in (2) and find whether there is a feasible solution to the formulation without an objective function.

5.3.3 Binary search

A desired accuracy $\epsilon >0$ is given.

• 1. Set the range $d_{\min }=D-R$, $d_{\max }=D+R$.

• 2. Select $\overline{d}=\frac{1}{2}(d_{\min }+d_{\max })$.

• 3. Find by Option 1 or Option 2 whether there is a selection of p potential locations such that the minimum distance for each demand point is less than or equal to $\overline{d}$.

• 4. If there is such a solution: set $d_{\max }=\overline{d}$, save this solution, and go to Step 6.

• 5. If there is no such solution: set $d_{\min }=\overline{d}$.

• 6. if $d_{\max }-d_{\min }>\epsilon$ go to Step 2. Otherwise, stop with the saved solution and the corresponding $\overline{d}$ as the result of the search.

5.3.4 Unequal radii and cover distances

It is shown in Drezner et al. (2019) that the proportion cover P by one facility of coverage distance $D_j$ of a demand point of radius $R_i$ for $D_j-R_i\le d\le D_j+R_i$ is:

$$\begin{aligned} P=\frac{1}{2\pi }\left[ 2\theta -\sin 2\theta +\frac{D_j^2}{R_i^2}\left( 2\phi -\sin 2\phi \right) \right] \end{aligned}$$

(3)

where

$$\begin{aligned} \theta =\arccos \frac{d^2+R_i^2-D_j^2}{2dR_i};~~~\phi =\arccos \frac{d^2+D_j^2-R_i^2}{2dD_j}~, \end{aligned}$$

(4)

The binary search is performed for $P\in [0,1]$. The value of $a_{ij}$ can be determined by substituting d into (3) because P is a monotonically decreasing function of d. Also, when $d\le D_j-R_i$, then $P=1$ and when $d\ge D_j+R_i$, then $P=0$. For example, when $d= D_j+R_i$,

• $\frac{d^2+R_i^2-D_j^2}{2dR_i}=\frac{2R_i^2+2D_jR_i}{2dR_i}=\frac{R_i+D_j}{d}=1$ and $\theta =0$,

• $\frac{d^2+D_j^2-R_i^2}{2dD_ji}=\frac{2D_j^2+2D_jR_i}{2dD_j}=\frac{R_i+D_j}{d}=1$ and $\phi =0$.

• Thus, $P=0$.

Similarly, when $d= D_j-R_i$, $\theta =\pi$ and $\phi =0$ and thus $P=1$.

5.4 Starting solutions with two covering facilities

Since the set covering starting solutions did not perform well for large values of p, we also experimented with finding a starting solution by the set covering approach but requiring each demand point to be at least partially covered by two facilities. This means changing the right hand side of the constraints in (2) from 1 to 2.

Since there might be “semi-isolated” demand points (see Sect. 4.2.1), we changed problem (2) to accommodate such cases. If demand point i is covered (partially or fully) by only one potential location j, we set $a_{ij}=2$. Such potential location must be selected. Also, if demand point i is fully covered by at least one potential location, we set $a_{ij}=2$ for all potential locations that provide full cover. If such a potential location is selected, there is no need for selecting a second potential location.

The binary search described in Sect. 5.3.3, is applied to find the best solution for a given p so that the second shortest distance to all selected potential locations is maximized.

6 Case study: transmission towers in Orange County, California

We investigate covering Orange County, California with transmission towers of cell phone, TV or radio. The data from the 2000 census for Orange County, California is given in Drezner (2004) and was also used in Berman et al. (2010a, 2019), Drezner and Drezner (2007, 2014), Drezner et al. (2006, 2019). There are 577 census tracts and their population counts are given. The total Orange County population is 2,846,289.

Computer programs were coded in Fortran using double precision arithmetic and were compiled by an Intel 11.1 Fortran Compiler using one thread with no parallel processing. They were run on a desktop with the Intel i7-6700 3.4 GHz CPU processor and 16 GB RAM.

Full cover within 2 miles and no cover beyond 4 miles were applied in Berman et al. (2019), Drezner and Drezner (2014), Drezner et al. (2019). To have comparable results we assign a radius of $R_i=1$ mile for each demand point and a cover radius of $D_j=3$ miles for each tower.

We tested simulated annealing and tabu search. The simulated annealing and tabu search were replicated 10 times for each p. The number of iterations for simulated annealing is $1000p(m-p)$ and for the tabu search $N=1000$. For simulated annealing we tested $T_0=0.1$ and $T_0=0.001$ and for both $T_F=0.00001$. We consider tying solutions for the best one if they are within $10^{-6}$ of the best found solution.

6.1 Covering north Orange County

We first selected the northernmost 131 census tracts, all with a y-coordinate of at least 30, that were tested in Berman et al. (2019), Drezner and Drezner (2014), Drezner et al. (2019). The total population residing in north Orange County is 639,958. Each census tract is a demand point and a potential location for a tower thus $m=n=131$.

For north Orange County the minimum value of p is 4 by solving (2). We solved the instances for $4\le p\le 12$ towers. Every solution approach and every starting solution matched the best known multiple times and in many cases for all ten runs. Since all approaches for solving the north Orange County instances performed very well and equally well, we do not see the need to report them.

It is interesting that ten towers cover all the demand while in Berman et al. (2019), Drezner and Drezner (2014) using linear decay, the solution for covering all demand is 13. The best found minimum cover for 10 towers is 0.96674 (Drezner and Drezner 2014). Run times using our procedure are quite short. For the largest instance ($p=12$) they are around 3–6 min for all runs.

Table 2 Covering Orange County from a random starting solution

Table 3 Covering Orange County from a greedy starting solution

Table 4 Covering Orange County from a reverse greedy starting solution

Table 5 Minimum cover at the set covering starting solution

Table 6 Covering Orange County from a set covering starting solution

Table 7 Summary of matched best known solutions

6.2 Covering all of Orange County

There are 577 demand points and equal number of potential locations in Orange County and thus $m=n=577$. The minimum value of p is 18 by solving (2). We tested $18\le p\le 44$ because full cover was found for $p=44$.

The results from the random starting solutions were unusually bad. For tabu search all results were zero except for $p=36$ for which a maximum of 0.75181 was found once while the best known solution is 0.91810. All results for simulated annealing for $p\le 32$ were also zero. Note that when the best found solution is zero for simulated annealing, the starting and ending temperatures do not affect the random walk because every move is accepted. We therefore report in Table 2 only results for the two versions of simulated annealing from the random starting solutions for $p\ge 33$. The best known solutions (marked in boldface) include results obtained by further experiments reported below. The algorithms did not perform well from random starting solutions. Only two instances yielded the best known solution for $T_0=0.1$ and three instances for $T_0=0.001$.

The results for the greedy-like starting solutions are reported in Table 3. Simulated annealing using $T_0=0.1$ performed poorly. The best known solution was not found even once. When the starting temperature is too high, most random moves during the early stages of the search are accepted, causing simulated annealing to perform like the random starting solution. We therefore re-ran the greedy-like starting solutions using $T_0=0.0001$, and used this starting temperature for the other starting solution approaches, and report these in Table 3. Simulated annealing performed better than tabu search.

The reverse greedy-like starting solutions results are reported in Table 4. The solution quality is similar to the quality of the greedy-like starting solutions. Simulated annealing performed much better than tabu search.

We then tested the set covering starting solution. In Table 5 we report the values of the objective function at the starting solution and the cover by only one facility. For 9 instances the value of the objective function is equal to the coverage by only one facility. In Table 6 We report the results from the set covering starting solution. We conclude from Table 6 that the quality of the solutions by the two versions of simulated annealing and tabu search are comparable with a slight edge to simulated annealing. The simulated annealing using $T_0=0.0001$ matched the best known solution 9 times, using $T_0=0.001$ matched it also 9 times and tabu search matched it 7 times. All of them matched the best known solution for the five smallest values of $p\le 22$. None of them matched the best known solution for the thirteen largest values of $p\ge 32$.

Since the set covering starting solutions did not perform well for large values of p, we also experimented with the starting solution described in Sect. 5.4. The minimum possible p is 29. The results for larger values of p are better than those reported in Table 6. They are much closer to the best known solution but failed to match it even once. We therefore do not report the results of these experiments.

The solution for $p=44$ facilities covering the whole demand is depicted in Fig. 2. There is one “semi-isolated” demand point (see Sect. 4.2.1) marked with an arrow. As expected, a facility is located there.

6.3 Summary of experiments

A summary of the results by four approaches for generating starting solutions and three meta heuristic applications (two simulated annealing with different starting temperatures and one tabu search) are summarized in Table 7. The number of times the results of each experiment matched the best known results are reported. To provide better visual assessment, when no results matched the best known one, the value is entered as blank rather than zero. The count and sum for each row and each column are also reported.

By inspecting Table 7 we conclude that simulated annealing performed better than tabu search. The random starting solution is not useful and can be ignored. For small values of p (especially for $p\le 21$) only the set covering starting solutions provided any best known results. The other three approaches yielded an objective of zero for these values of p. However, the set covering starting solutions did not match any of the best known solutions for $p\ge 32$.

The greedy-like starting solution performed best overall and the reverse greedy-like starting solution is second. There are 27 instances and each instance was solved ten times by twelve approaches for a total of 3240 runs. Less than 10% of the runs matched the best known solutions. The greedy-like approach matched the best known solutions in 33 cases for a total of 51 runs. The reverse greedy-like approach matched the best known solutions in 24 cases for a total of 66 runs. The set covering got 185 runs that matched the best known solutions, but 140 of them were obtained for the five smallest problems.

There are nine instances out of 27 for which only one of the twelve approaches matched the best known solution. In 13 instances only one starting solution approach yielded the best known solution and the three others did not. Most of the approaches are essential to get the best known solution. This suggests that better solutions may be found for many of the instances by other solution approaches to be developed in future research.

7 Conclusions

The objective of original cover location models is to cover demand within a given distance by facilities. The gradual (or partial) cover replaces abrupt drop from full cover to no cover by defining gradual decline in cover. We use a recently proposed rule for calculating the joint cover of a demand point by several facilities termed “directional gradual cover” (Drezner et al. 2019). Contrary to all gradual cover models, the joint cover depends on the direction. In order to calculate the joint cover, it is not sufficient just to have for each facility the value of its partial cover. The objective is to maximize the minimum cover of demand points by locating p facilities.

We constructed and tested two heuristic algorithms based on tabu search and simulated annealing. However, contrary to the experience reported in Drezner et al. (2019), we found out by computational experiments that the quality of the results depends heavily on the starting solutions. We therefore constructed and tested five approaches for generating starting solutions: (i) random starting solution; (ii) greedy-like starting solution; (iii) reverse greedy-like starting solution; and (iv) two variants based on solving the set covering formulation.

We tested the procedures on two case studies of covering Orange County, California by cell-phone towers. One is covering north Orange County (131 demand points) and one covering the entire Orange County (577 demand points).

The procedures performed well solving the smaller north Orange County instances. However, covering Orange County presents challenges that may be addressed by developing other solution approaches. We were not able to find a starting solution approach that performs well for the whole range of instances. For small values of p the set covering based starting solution considering the cover by the closest facility performed best. However, it performed poorly for large p instances. The greedy-like and reverse greedy-like approaches performed well for large values of p but very poorly on small values of p. The set covering based on the distances to the closest two facilities did not perform well but performed better than the other variant of set covering based on the closest facility for large values of p. The random starting solution performed poorly for all values of p and can be removed from consideration.