Optimal sample size for estimating the mean concentration of invasive organisms in ballast water via a semiparametric Bayesian analysis

Abstract

We consider the determination of optimal sample sizes to estimate the concentration of organisms in ballast water via a semiparametric Bayesian approach involving a Dirichlet process mixture based on a Poisson model. This semiparametric model provides greater flexibility to model the organism distribution than that allowed by competing parametric models and is robust against misspecification. To obtain the optimal sample size we use a total cost minimization criterion, based on the sum of a Bayes risk and a sampling cost function. Credible intervals obtained via the proposed model may be used to verify compliance of the water with international standards before deballasting.

1 Introduction

The D-2 standard of the International Maritime Organization (IMO) requires that deballasted water should contain fewer than 10 viable organisms (zooplankton and phytoplankton, referred to simply as organisms in the remainder) with maximum dimension 10 and $50\ \mu m$ per mL, among other restrictions. Such concerns with ballast water discharges are related to the possible introduction of invasive species in new environments and to the reduction of water quality in sensitive environments, causing diverse environmental, public health and economic problems. Given the amount of ballast water carried by large ships, compliance with such regulation must be verified via sampling processes that account for the inherent heterogeneous nature of the organism concentration in the ballast water tank (Murphy et al. 2002). Recently, Costa et al. (2015, 2016) proposed frequentist methods based on negative binomial models for such purposes. With the same objective, Costa et al. (2021) also used negative binomial models under a Bayesian approach to compute sample sizes controlling summaries of the credible intervals. The advantage of the Bayesian approach is that one may incorporate (if available) prior knowledge about the ballast water origin (coastal, oceanic or riverine), time of the water residence in the tank, etc (Aguirre-Macedo et al. 2008). This prior information can be obtained from preliminary analyses of ballast water taken at the port of origin and before its discharge at the destination.

Suppose that we collect n aliquots of ballast water with volume w and that the number of organisms in the i-th aliquot is $X_i$. Suppose additionally that the organism concentration in the region of the tank from which the i-th aliquot is sampled is $\lambda _i$, so that we expect to find $w\lambda _i$ organisms in the i-th aliquot. For $i = 1, \ldots , n$, suppose that, given $\lambda _i$, $X_i$ follows a Poisson distribution with mean $\mathbb {E}\left[ {X_i}\vert {\lambda _i}\right] = w\lambda _i$ and that $\lambda _i$ is governed by a probability measure F, partially or entirely unknown. Note that the model proposed in Costa et al. (2021) corresponds to the case where all $\lambda _i$ are equal to a quantity (namely, the organism concentration) and assumes a gamma prior distribution for this quantity.

To allow greater flexibility in the modeling and robustness against misspecification of a parametric form for F, we consider random probability measures (RPM), which are distributions in the space of probability measures (here, in $\mathbb {R}_+$). A popular RPM is based on the Dirichlet process introduced by Ferguson (1973) as a possible solution for the problem of prior specification in a nonparametric Bayesian approach, where the prior space is a set of probability distributions defined on a given space. For details, see Phadia (2016). Specifically, the parameters $\lambda _i$ are considered independent and identically distributed with an unknown distribution $F(\cdot )$ that in a third level follows a Dirichlet process. This prior process may be defined through a precision parameter $\alpha$ and a mean distribution $F_0(\cdot )$, here specified by a gamma distribution. In Sect. 2 we describe this semiparametric Bayesian model with more detail and the methodology required to obtain posterior distributions by simulation.

Under the light of the above considerations, our objective is to compute the number of aliquots (sample size), according to some optimality criterion, to estimate the mean concentration of organisms (zooplankton and phytoplankton) in ballast water tanks with reduced knowledge about their distribution in the tank.

An approach to the problem of determining an optimal sample size is to consider it as a decision problem (Müller and Parmigiani 1995; Lindley 1997; Parmigiani and Inoue 2009; Islam and Pettit 2014). Under this approach it is necessary to specify a loss function encompassing the parameter of interest and a decision $d_n$ based on a sample $X_1,\ldots ,X_n$. In an interval inference problem, a decision is specified by the lower and upper limits of a credible interval for the parameter of interest. Once the proper interval based on the optimal n is determined and real data is ensued, the terminal decision on compliance or not of a ship with the D-2 standard is established. Criteria and methodology for sample size determination and alternative loss functions are presented in Sections 3 and 4. We conclude with a discussion along with an illustration in Section 5.

2 The semiparametric Bayesian model and its simulation

Suppose that F follows a Dirichlet process with parameters $\alpha$ and $F_0$, symbolically, $F \sim \text {DP}(\alpha , F_0)$. Under this setting, we have $\mathbb {E}\left[ {F(A)}\right] =F_0(A)$ and $\text {Var}[F(A)]=F_0(A)[1-F_0(A)]/(\alpha +1)$, where A is an element of the $\sigma$-field associated to the parameter space of $\lambda _i$, namely $\Lambda$. In this setup, $F_0$ is the base-distribution and $\alpha$ is a precision parameter. For comparison with results obtained under parametric approaches, we consider $F_0$ to be a gamma distribution function with mean $\lambda _0$ and shape parameter $\theta _0$, both known, so that that the corresponding variance is $\lambda _0^2/\theta _0$. Noting that the Dirichlet process is the prior assigned to the unknown distribution of the mean concentrations associated with the conditional Poissonian observations, we may write the model hierarchically as

$$\begin{aligned}&X_i\vert \lambda _i{\mathop {\sim }\limits ^{\text {ind}}} \text {Poisson}(w\lambda _i),\quad i=1,2,\ldots ,n; \end{aligned}$$

(1)

$$\begin{aligned}&\lambda _i\vert F{\mathop {\sim }\limits ^{\text {iid}}} F, \quad i=1,2,\ldots ,n; \end{aligned}$$

(2)

$$\begin{aligned}&F\sim \text {DP}(\alpha , F_0). \end{aligned}$$

(3)

Given a random sample ${\varvec{x}}_n=(x_1,\ldots ,x_n)$ of counts and according to the Pólya urn representation of the Dirichlet process, the joint posterior distribution of the $\lambda _i$ is

$$\begin{aligned} \nu (d{\varvec{\lambda }}_n\vert {\varvec{x}}_n)\propto \prod _{i=1}^ng(x_i\vert \lambda _i)\left[ \alpha F_0(d\lambda _i)+\sum _{j=1}^{i-1}\delta _{\lambda _i}(d\lambda _j)\right] , \end{aligned}$$

where ${\varvec{\lambda }}_n=(\lambda _1,\ldots ,\lambda _n)$, $g(\cdot \vert \lambda )$ is the probability function of a Poisson distribution with mean $w\lambda$ and $\delta _{\lambda _i}(\cdot )$ is the degenerate distribution with point mass at $\lambda _i$ (Blackwell and MacQueen 1973; Escobar and West 1998).

Taking the discrete nature of the Dirichlet process into account, we may have identical values of $\lambda _i$ for different i due to the inherent clustering of these quantities (Escobar and West 1998; Müller et al. 2015). We group the $\lambda _i$ into $n^* (\le n-1)$ distinct values $\lambda _j^*$, and let $n_j$ denote the number of $\lambda _i$ taking this common value $\lambda _j^*$, $j=1,\ldots ,n^*$. For example, consider $n=5$ and the concentrations $\lambda _i$, $i=1,\ldots ,5$. If $\lambda _1=\lambda _2$ and $\lambda _3=\lambda _4=\lambda _5$, it follows that $\lambda _1^*=\lambda _1$, $\lambda _2^*=\lambda _3$, $n_1=2$, $n_2=3$ and $n^*=2$.

Given this clustering property, we may use the following full conditional probability distribution to draw samples of $\nu (d{\varvec{\lambda }}_n\vert {\varvec{x}}_n)$ using a Gibbs sampler (Escobar and West 1998, Section 1.3.1)

$$\begin{aligned} \nu (d\lambda _i\vert {\varvec{\lambda }}_{(-i)},{\varvec{x}}_n)\propto q_0g(x_i\vert \lambda _i)F_0(d\lambda _i)+\sum _{j=1}^{n^*}n_jq_j^*\delta _{\lambda _j^*}(d\lambda _i), \end{aligned}$$

(4)

where ${\varvec{\lambda }}_{(-i)}=\{\lambda _j\vert j\ne i, j=1,\ldots ,n\}$ with

$$\begin{aligned} q_0\propto \alpha \int _{\Lambda }g(x_i\vert \lambda _i)F_0(d\lambda _i)\quad \text{ and }\quad q_j^*\propto g(x_i\vert \lambda _j^*), \end{aligned}$$

such that $q_0+\sum _{j}n_jq_j^*=1$. In our problem $q_0$ is a mixture of a Poisson distribution by a gamma distribution, i.e., a negative binomial distribution. Escobar and West (1998) comment that when we use the above conditional distribution in a Markov chain Monte Carlo algorithm, there may occur problems if the sum of the $q_j^*$ becomes very large relatively to $q_0$ on any iteration. In order to prevent this problem it is helpful to “remix” the $\lambda _j^*$’s after every step. The cluster structure is defined by the set ${\varvec{s}}=\{s_1,\ldots ,s_n\}$ and the $n_j=\#\{s_i=j\}$ observations in cluster j that share the common value $\lambda _j^*$. Conditioning on $n^*$, consider $s_i=j$ if $\lambda _i=\lambda _j^*$ so that, given $s_i=j$ and $\lambda _j^*$, $X_i\sim \text {Poisson}(w\lambda _j^*)$. Define $J_j$ as the index set of the observations in cluster j, i.e., $J_j=\{i\vert s_i=j\}$. Let $x_{(j)}=\{x_i\vert s_i=j\}$ be the corresponding cluster of observations. Then, we use the following posterior distribution to “remix” the $\lambda _j^*$ in the Gibbs sampler

$$\begin{aligned} h(\lambda _j^*\vert {\varvec{x}}_n,{\varvec{s}},n^*)=h(\lambda _j^*\vert x_{(j)},{\varvec{s}},n^*)=\prod _{i\in J_j}g(x_i\vert \lambda _j^*)F_0(d\lambda _j^*), \end{aligned}$$

for $j=1,\ldots ,n^*$. In particular, we have

$$\begin{aligned} h(\lambda _j^*\vert {\varvec{x}}_n,{\varvec{s}},n^*)\propto (\lambda _j^*)^{\theta _0-1+\sum _{i\in J_j}x_i}\exp \left[ -\left( n_j+\frac{\theta _0}{\lambda _0}\right) \lambda _j^*\right] , \end{aligned}$$

(5)

which is a gamma distribution. To draw samples from $\nu (d{\varvec{\lambda }}_n\vert {\varvec{x}}_n)$ we use (4) in a Gibbs sampling process and (5) to “remix” the $\lambda _j^*$. Algorithm 1 designed for such purposes is outlined in the Appendix.

The parameter of interest is the mean of the unknown true concentration distribution in the tank, F, defined by the functional

$$\begin{aligned} \overline{\lambda }{:}=\overline{\lambda }(F)=\int _\Lambda uF(du). \end{aligned}$$

When a Dirichlet process prior is considered for F, this random variable enjoys some known features. For instance, the mean and variance of $\overline{\lambda }$ regarding $\text {DP}(\alpha ,F_0)$ are, respectively, the mean of $F_0$ and the variance of $F_0$ multiplied by $1/(\alpha +1)$ (Walker and Mallick 1997). For details on the probability distribution function of functionals of the Dirichlet process and its properties, the reader is referred to Cifarelli and Regazzini (1990), Cifarelli and Melilli (2000), James et al. (2008), Regazzini et al. (2002), among others. In our case we do not need to specify the probability distribution function of the functional; it is sufficient to know how to draw samples from the distribution of $\overline{\lambda }$ and this is possible by accounting for the stick-breaking representation (Müller et al. 2015; Phadia 2016) of the $\text {DP}(\alpha ,F_0)$. In effect, we may write

$$\begin{aligned} F=_dB\delta _{\xi }+(1-B)F, \end{aligned}$$

where the notation ‘$=_d$’ means “follows the same distribution as”, B denotes a random variable following a $\text {Beta}(1,\alpha )$ distribution and $\delta _\xi$ is the degenerate probability measure at $\xi \sim F_0$. This implies the distributional equation

$$\begin{aligned} \overline{\lambda }(F)=_d B\xi +(1-B)\overline{\lambda }(F), \end{aligned}$$

(6)

because $\overline{\lambda }(\delta _\xi )=\xi$ and under the condition that $\mathbb {E}\left[ {\log (1+\vert \xi \vert )}\right] <\infty$ (Hjort and Ongaro 2005). Given that we assume $F_0$ is a gamma distribution, this condition follows from Jensen’s inequality. The terms B, $\xi$ and $\overline{\lambda }$ in (6) are distributionally independent. The simulation strategy for estimating $\overline{\lambda }$ is based on (6) and on a Markov chain of the form

$$\begin{aligned} \overline{\lambda }_t=B_t\xi _t+(1-B_t)\overline{\lambda }_{t-1},\quad t\ge 2. \end{aligned}$$

(7)

Here we use the algorithm proposed by Guglielmi et al. (2002), which consists of simulating the following upper (u) and lower ($\ell$) chains over time

$$\begin{aligned} \overline{\lambda }_t^u=B_t\xi _t+(1-B_t)\overline{\lambda }_{t-1}^u,\quad t\ge 2, \end{aligned}$$

(8)

and

$$\begin{aligned} \overline{\lambda }_t^\ell =B_t\xi _t+(1-B_t)\overline{\lambda }_{t-1}^\ell ,\quad t\ge 2. \end{aligned}$$

(9)

The algorithm is initiated by choosing $\overline{\lambda }_1^u$ and $\overline{\lambda }_1^\ell$ for $t=2$. Guglielmi et al. (2002) set these quantities as the upper and lower bounds of the space parameter, respectively. For an unbounded parameter space as in the case under investigation, they suggest to set $\overline{\lambda }_1^u$ as the largest internal bit value of the computer being employed. We update these quantities using (8) and (9) until the difference is small, i.e., $\vert \overline{\lambda }_t^u-\overline{\lambda }_t^\ell \vert <\epsilon$, for a small $\epsilon >0$. Given that $\mathbb {E}\left[ {\log (1+\vert \xi \vert )}\right] <\infty$, then according Guglielmi & Tweedie (2001, Theorem 1) $\overline{\lambda }_t$ is geometrically ergodic and its limiting distribution is the distribution of $\overline{\lambda }$. Thus, we may draw from the distribution of $\overline{\lambda }$ through (7) for a large t. The corresponding procedure is outlined in Algorithm 2 in the Appendix.

Given a random sample ${\varvec{x}}_n=(x_1,\ldots ,x_n)$ of counts we may update the knowledge about $\overline{\lambda }$. Consider the posterior random mean given by

$$\begin{aligned} \overline{\lambda }^{(n)}=\int _\Lambda uF^{(n)}(du), \end{aligned}$$

with $F^{(n)}$ denoting the posterior distribution for F defined by

$$\begin{aligned} F\vert {\varvec{x}}_n\sim \int _{\Lambda ^n}\text {DP}(\alpha +n, G_n)\nu (d{\varvec{\lambda }}_n\vert {\varvec{x}}_n), \end{aligned}$$

where $G_n=(\alpha F_0+\sum _{i=1}^n\delta _{\lambda _i})/(\alpha +n)$. We may use the following representation to draw samples from the distribution of $\overline{\lambda }^{(n)}$ (Hjort and Ongaro 2005, Eq. 5.3)

$$\begin{aligned} \overline{\lambda }^{(n)}=_d B_* \sum _{i=1}^nD_iZ_i + (1-B_*) \overline{\lambda }, \end{aligned}$$

(10)

where $B_*\sim \text {Beta}(n, \alpha )$, $D_i$, $i=1,\ldots ,n$ are the elements of a vector with multivariate uniform distribution and $(Z_1,\ldots ,Z_n)\sim \nu (d{\varvec{\lambda }}_n\vert {\varvec{x}}_n)$. Taking all these features into account we are able to draw samples from the distribution of $\overline{\lambda }^{(n)}$. We may implement this process via Algorithm 3 outlined in the Appendix.

3 Sample size determination

An approach to the problem of determining the optimal sample size is to consider it as a decision problem (Müller and Parmigiani 1995; Lindley 1997; Parmigiani and Inoue 2009; Islam and Pettit 2014). Under this approach it is necessary to specify a loss function $L(\overline{\lambda }, d_n)$ based on a sample $X_1,\ldots ,X_n$ and a decision $d_n$. In the problem of interval inference, a decision corresponds to the determination of two quantities, the lower [say, $a=a({\varvec{x}}_n)$] and upper [say, $b=b({\varvec{x}}_n)$] limits of a credible interval for the parameter of interest $\overline{\lambda }$. A ship is declared not compliant with the D-2 standard mentioned in Sect. 1 if $a({\varvec{x}}_{n})>10$ or compliant, if $b({\varvec{x}}_{n})<10$. Otherwise, if $a({\varvec{x}}_{n})<10<b({\varvec{x}}_{n})$, more data are needed to make a decision. In this context, the posterior Bayes risk may be written as

$$\begin{aligned} r(F^{(n)},d_n)=\int _{\mathcal {X}^n}\mathbb {E}[L(\overline{\lambda },d_n)\vert \varvec{x}_n]g(\varvec{x}_n)d\varvec{x}_n, \end{aligned}$$

(11)

where $g(\varvec{x}_n)$ is the marginal distribution of the data. The decision $d_n^*$ which minimizes $r(F^{(n)},d_n)$ among all the possible decisions $d_n$ is the so-called Bayes rule. Then, the optimal sample size is the one which minimizes the total cost defined as

$$\begin{aligned} \text {TC}(n)=r(F^{(n)},d_n^*)+cn, \end{aligned}$$

where c is the cost of sampling an aliquot. It is not always possible to compute $r(F^{(n)},d_n^*)$ analytically. We use Monte Carlo simulations to estimate $r(F^{(n)},d_n^*)$, for each n in a set of specified sample sizes, by drawing samples of ${\varvec{x}}_n$, computing the expected value in (11) applied to $d_n^*$ and taking the mean of these values. With the estimates of $r(F^{(n)},d_n^*)$ for each n we fit the following curve, inspired from the one used in Müller and Parmigiani (1995)

$$\begin{aligned} \text {TC}(n)=\frac{E}{(1+n)^H}+cn, \end{aligned}$$

which may be linearized and viewed as a linear regression equation as follows

$$\begin{aligned} \log [\text {TC}(n)-cn]=\log E-H\log (1+n). \end{aligned}$$

(12)

This function leads to a closed form for the estimators of $\log E$ and H, and fits the data well, as indicated in Figure 1. The optimal sample size is the closest integer to

$$\begin{aligned} \left( \frac{\widehat{E}\ \widehat{H}}{c}\right) ^{1/(\widehat{H}+1)}-1, \end{aligned}$$

(13)

where $\widehat{E}$ and $\widehat{H}$ are the estimates of E and H, respectively, obtained via fitting the linear regression (12) (by least squares, for example).

An algorithm for the determination of the optimal sample size, say $n_o$, and for the decision with respect to D-2 standard follows.

• 1.

  • (a) Fixing a value for n, simulate a dataset ${\varvec{x}}_n=(x_1,\ldots ,x_n)$ from the prior predictive distribution

    $$\begin{aligned} g({\varvec{x}}_n)=\prod _{i=1}^ng(x_i\vert \lambda _i)\nu (\lambda _i)d\lambda _i, \end{aligned}$$

    with $X_i\vert \lambda _i\sim \text {Poisson}(w\lambda _i)$ and $\nu (\cdot )$ the DP prior for F parameterized by $\alpha F_0$.

  • (b) Given ${\varvec{x}}_n$, simulate m samples $Z^{(k)}=(Z_1^{(k)},\ldots , Z_n^{(k)})$, $k=1,\ldots ,m$ from the posterior distribution of $(\lambda _1,\ldots ,\lambda _n)$, say $\nu (\cdot \vert {\varvec{x}}_n)$, via Algorithm 1 in the Appendix.

  • (c) Let $\overline{\lambda }_k$ be a value sampled from the prior distribution of the random mean of F (generated via Algorithm 2 in the Appendix), $B^{(k)}$ be a value simulated from a $\text {Beta}(\alpha , n)$ distribution and $D^{(k)}=(D_1^{(k)},\ldots ,D_n^{(k)})$ be a vector of the symmetric Dirichlet distribution $\mathcal {D}$ $_{n-1}(1,\ldots ,1)$. Then,

    $$\begin{aligned} \overline{\lambda }_{k}^{(n)}=B^{(k)}\overline{\lambda }_k+(1-B^{(k)})\sum _{i=1}^nD_i^{(k)}Z_i^{(k)},\quad k=1,\ldots ,m, \end{aligned}$$

    is a m-tuple sample of the posterior distribution of the random mean of F (accounting for its stochastic representation).

  • (d) For a fixed decision rule $d_n$ (e.g., a credible interval for $\overline{\lambda }$), $L_k^{(n)}=L(\overline{\lambda }_k^{(n)}, d_n^*)$, $k=1,\ldots ,m,$ is the corresponding sample of the loss function L. The average of $L_k^{(n)}$ is an estimate of the posterior expected loss.

• 2. Repeat the steps in 1 a large number of times and take the empirical mean of every average of $L_k^{(n)}$. This represents an estimate of the posterior risk $r(F^{(n)}, d_n^*)$ for the fixed n.

• 3. Repeat steps 1 and 2 for a range of different values for n.

• 4. Compute the total cost $\text {TC}(n)=r(F^{(n)}, d_n^*)+cn$, and fit (12) via least squares to the points $\{(n, \text {TC}(n))\}$ obtaining estimates of E and H. This allows us to get the optimal n from the minimum of the corresponding approximation for $\text {TC}(n)$ via (13).

• 5. Once chosen the optimal n, say $n_o$, collect the real data ${\varvec{x}}_{n_o}=(x_1,\ldots ,x_{n_o})$ and determine the corresponding Bayes credible interval $[a^*({\varvec{x}}_{n_o}), b^*({\varvec{x}}_{n_o})]$, from which the terminal decision on compliance with the intended standard is made. Use the credible interval limits to decide for compliance with the D-2 standard as follows: declare compliance if $b^*({\varvec{x}}_{n_o})<10$, or non-compliance if $a^*({\varvec{x}}_{n_o})\ge 10$. Otherwise, if $a^*({\varvec{x}}_{n_o})<10< b^*({\varvec{x}}_{n_o})$, more data are required to make a decision.

We use the loss functions described in the following section and for simplicity of notation, we drop the argument ${\varvec{x}}_n$ in the limits $a({\varvec{x}}_n)$ and $b({\varvec{x}}_n)$ of the required credible intervals.

We implemented the algorithms and the required functions using R (R Core Team 2016). For the adopted model parameters, the running time to compute optimal sample sizes varied from 1.4 to 13 hours, depending on the setting. The running time may increase or decrease depending on the simulation settings and the number of core computers used; both are specified in the implemented functions. The computers that have been used have the following characteristics: (i) OS Linux Debian 11, RAM 216 GB and processor Intel Xeon CPU E5645 @2.40GHz; and (ii) OS Linux Ubuntu 20.04, RAM 7.7 GB, processor AMD PRO A8-8600B. The functions implemented in R may be obtained from the authors upon request.

4 Loss functions

The first loss function is

$$\begin{aligned} L(\overline{\lambda },d_n)=\rho \tau +(a-\overline{\lambda })^++(\overline{\lambda }-b)^+, \end{aligned}$$

(14)

where $0<\rho <1$ is a weight, $\tau =(b-a)/2$ is the half-width of the interval, the function $x^+$ is equal to x if $x>0$ and equal to zero, otherwise and a decision $d_n=d_n(a,b)$ corresponds to determination of the credible interval limits. Note that the loss function (14) is a weighted sum of two terms, $\tau$ and $(a-\overline{\lambda })^++(\overline{\lambda }-b)^+$, with weights $\rho$ and 1, respectively. In this context, Rice et al. (2008) argue that the second term of the loss function must receive the largest weight, i.e., $\rho <1$. The corresponding Bayes rule are the quantiles associated to probabilities $\rho /2$ and $1-\rho /2$ of the posterior distribution of $\overline{\lambda }^{(n)}$ (Rice et al. 2008). For this loss function applied to the Bayes decision, we have

$$\begin{aligned} \mathbb {E}\left[ {L(\overline{\lambda }^{(n)},d_n^*)}\right]= \mathbb {E}\left[ {\overline{\lambda }^{(n)}\delta _{\overline{\lambda }^{(n)}}(A_{b^*})}\right] -\mathbb {E}\left[ {\overline{\lambda }^{(n)} \delta _{\overline{\lambda }^{(n)}}(A_{a^*})}\right] , \end{aligned}$$

where $A_{b^*}=[b^*,\infty )$, $A_{a^*}=(0, a^*]$, $a^*$ and $b^*$ are the corresponding bounds of the Bayes decision $d_n^*$. The expected value is taken under the distribution of $\overline{\lambda }^{(n)}$, which is a mean functional computed over the posterior distribution $F\vert {\varvec{x}}_n$.

In Tables 1 and 2 we present optimal sample sizes computed using the total cost minimization criterion and loss function (14) with the weights $\rho =0.05$ and $\rho =0.25$, respectively.

Table 1 Optimal sample size ($n_o$) computed with $\rho =0.05$ under the Poisson/Dirichlet process (1)–(3) model with $F_0$ corresponding to a gamma distribution with mean $\lambda _0=10$ and shape parameter $\theta _0$ and loss function (14)

Table 2 Optimal sample size ($n_o$) computed with $\rho =1/4=0.25$ under the Poisson/Dirichlet process (1)–(3) model with $F_0$ corresponding to a gamma distribution with mean $\lambda _0=10$ and shape parameter $\theta _0$ and loss function (14)

The second loss function is

$$\begin{aligned} L(\overline{\lambda },d_n)=\gamma \tau +(\overline{\lambda }-m)^2/\tau , \end{aligned}$$

(15)

where $\gamma >0$ is a fixed constant and $m=(a+b)/2$ is the center of the credible interval. The first term involves the half-width of the interval and the second, the square of the distance between the parameter of interest and the center of the interval, which is divided by the half-width to maintain the same measurement unit of the first term. The weights attributed to each term are $\gamma$ and 1, respectively. If $\gamma <1$, we attribute the largest weight to the second term; if $\gamma >1$, the situation is reversed and if $\gamma =1$ the two terms have the same weight. In this case, the Bayes rule corresponds to the quantities which form the interval $[a^*,b^*]=[m-\text{ sd}_\gamma , m+\text{ sd}_\gamma ]$, where $(m,\text{ sd}_\gamma )=\left( \mathbb {E}\left[ {\overline{\lambda }^{(n)}}\right] ,\gamma ^{-1/2}\sqrt{\text {Var}[\overline{\lambda }^{(n)}]}\right)$. For more details see Rice et al. (2008). Under this loss function we have

$$\begin{aligned} \mathbb {E}\left[ {L(\overline{\lambda }^{(n)},d_n^*)}\right] =2\gamma ^{1/2}\sqrt{\text {Var}[\overline{\lambda }^{(n)}]}, \end{aligned}$$

where the expected value and the variance of $\overline{\lambda }^{(n)}$ are computed under the same conditions considered for the previous loss function. In Table 3 we present optimal sample sizes computed using the total cost minimization criterion and loss function (15).

To visualize the idea of the total cost minimization criterion, in Fig. 1 we present an example with estimates of TC(n) and the corresponding fitted curve using this loss function (14) with $\alpha = 0.5$, $\lambda _0 = 10$, $\theta _0 = 1$, $w = 0.5$, $c = 0.005$ and $\rho = 0.05$; loss function (15) with $\alpha = 0.5$, $\lambda _0 = 10$, $\theta _0 = 10$, $w = 1$, $c = 0.005$ and $\gamma =1$.

Fig. 1

Example with computed estimates of TC(n) with the fitted curve (in blue) and the optimal sample size indicated in the red line for loss functions (14) and (15), respectively

Table 3 Optimal sample size ($n_o$) computed under the Poisson/Dirichlet process (1)–(3) model with $F_0$ corresponding to a gamma distribution with mean $\lambda _0=10$ and shape parameter $\theta _0$, and loss function (15)

5 Discussion and illustration

According to international regulations, the ballast water of ships should be sampled and analysed to estimate the mean concentration of viable organisms in the ballast tank as a means of ascertaining the compliance with specified standards.

Although compliance with the D-2 standard may be viewed as a hypothesis testing problem, we decided to attack it via a credible interval approach for two main reasons. First the credible intervals may be employed to test the hypothesis that $\overline{\lambda } \le 10$ with the same spirit outlined in Costa et al. (2021), namely, the ship will be declared compliant with the D-2 standard if the upper limit of the posterior credible interval is smaller than 10 or non-compliant if the corresponding lower limit is larger than 10; otherwise, more data will be needed to make a decision. Second, the posterior credible interval accounts for the magnitude of the mean concentration $\overline{\lambda }$ and this may help regulators to establish more or less stringent remedial measures or compensation for possible environmental damage.

For planning and inference purposes, we propose a DP mixture of independent Poisson distributions for estimation of the quantity of interest, which is a mean functional of the unknown distribution, say F. Such estimation is accomplished from simulated values algorithmically generated through appropriate stochastic representations of these random quantities, with particular relevance for the posterior random mean of F.

The determination of $n_o$ (optimal number of aliquots of ballast water to be collected) follows criteria based upon decision rules corresponding to credible intervals. The related loss functions defined as weighted combinations of precision and bias measures and their respective Bayes intervals are determined from simulated samples of the posterior random mean distribution for each fixed value of n and each marginally generated vector of observations ${\varvec{x}}_n$. The $n_o$ is obtained by minimizing the sum of the cost of collecting all aliquots with the minimum Bayes risk estimates for fixed values of n, and fitted by a function wholly specified by a minimizing linearized regression structure.

The optimal sample size is directly affected when we vary $\theta _0$ with $\alpha$ fixed, or vary $\alpha$ with $\theta _0$ fixed (Tables 1, 2 and 3). This change in $n_o$ is more evident when loss function (15) is considered. In general, the sample sizes obtained via loss function (14) are smaller than those obtained via loss function (15) (see Tables 1, 2 and 3). A possible justification is that the Bayes rule associated with loss function (15) depends on the expected value and on the variance of the posterior distribution, whereas with loss function (14), the Bayes rule is based on the quantiles of the posterior distribution, which may provide wider intervals and therefore smaller sample sizes. From Tables 1 and 2, we may observe that $n_o$ increases as $\rho$ increases. In this case, as $\rho$ increases the fixed posterior probability decreases, which may provide intervals with shorter lengths but with smaller credibilities.

From Tables 1, 2 and 3, we may also observe that for a fixed $\theta _0$ the sample size increases with $\alpha$ until a certain value and then decreases, which is more evident in loss function (15). This may be explained by two facts: (i) Sethuraman and Tiwari (1982) showed that $\text {DP}(\alpha ,F_0)\rightarrow \delta _\lambda (\lambda ')$ in distribution as $\alpha \rightarrow 0$, where $\lambda '\sim F_0$, i.e., all the $\lambda _i$ are equal to a quantity $\lambda '$ with probability 1. In this sense, the model (1)–(3) approaches to the model of Costa et al. (2021); (ii) as $\alpha \rightarrow \infty$ the Dirichlet process tends to concentrate around $F_0$, which in our problem is a gamma distribution, i.e., the model (1)–(3) approaches to the following full parametric model:

$$\begin{aligned}&X_i\vert \lambda _i\sim \text {Poisson}(w\lambda _i),\quad i=1,\ldots ,n; \end{aligned}$$

(16)

$$\begin{aligned}&\lambda _i\sim F_0,\quad i=1,\ldots ,n, \end{aligned}$$

(17)

where $F_0$ is a gamma distribution with mean $\lambda _0$ and shape parameter $\theta _0$. Taking these features into account, it seems that the $n_o$ is smaller for extreme values of $\alpha$ because these situations correspond to models with only parametric components.

Also note that for $\theta _0$, $\alpha$ and c fixed, the value of the aliquot volume w does not considerably affect $n_o$, suggesting that one may choose smaller aliquot volumes w in order to decrease the total volume and the cost of sampling. On the other hand, when the cost c of obtaining an aliquot increases, $n_o$ decreases, which is more evident in loss function (15).

A practical concern with the use of a Dirichlet process for modeling observed data and for determining optimal sample sizes is the setting of the parameter $\alpha$. Walker & Mallick (1997, pg. 475) stated that a coherent prior choice for $\alpha$ is the quotient between the prior guess for the mean of the random variance defined as

$$\begin{aligned} \int _\Lambda u^2F(du)-\overline{\lambda }^2, \end{aligned}$$

and the prior guess for the variance of $\overline{\lambda }$. If we consider the same prior guess for these two quantities we obtain $\alpha =1$. In addition, a non-informative setup for $\overline{\lambda }$ is achieved by allowing $\text {Var}[\xi ]\rightarrow \infty$, where $\xi \sim F_0$. Since we considered a gamma distribution for $F_0$ in our model, it follows that $\text {Var}[\xi ]=\lambda _0^2/\theta _0$.

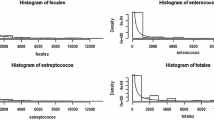
As an illustration, we consider a hypothetical data set to mimic a scenario with a vertical ballast tank like the one described in Murphy et al. (2002, Fig. 2), where there are two incomplete barriers forming almost three strata of water. To determine $n_o$ in a non-informative setup, we fix $\lambda _0=10$, the limit of the IMO standard, and $\theta _0=1$ so that $\text {Var}[\xi ]=100$ and consider loss function (15) with $w=1$, $c=0.010$, $\gamma =1/4$ and $\alpha =1.5$, leading to a sample size $n_o=52$ (see Table 3). Given that Murphy et al. (2002) indicate that for some organisms the concentration decreases as the tank depth increases, we consider two scenarios for the concentration in the strata: (i) concentrations of 20, 15 and 8, with overall mean of $14.33>10$; (ii) concentrations of 12, 7, and 4, with overall mean of $7.67<10$. Using three gamma distributions with the respective concentration means and shape parameter of 300, we simulated samples of 17 aliquots from two strata and 18 aliquots from the remaining one, in each scenario, and given the concentrations, we drew the number of organisms according to a Poisson distribution. The generated counts are displayed in Table 4. In Fig. 2, we depict an estimate of $\mathbb {E}\left[ {F}\vert {{\varvec{x}}_{n_o}}\right]$ for the generated counts in each case. These estimates are clearly non-continuous distribution functions, as expected from the stratified concentration scenarios considered, and suggests that a semiparametric approach should be preferred to analyze this data.

Table 4 Simulated counts for case 1 with strata concentrations 20, 5 and 8; and for case 2 with strata concentrations 12, 7 and 4. In each case the numbers in each line represent the simulated counts from the respective stratum

Fig. 2

Estimate of $\mathbb {E}\left[ {F}\vert {{\varvec{x}}_{n_o}}\right]$ for each case

For case 1 we drew 1000 values from the distribution of $\overline{\lambda }^{(52)}$, and using them, we computed the required interval according to the Bayes rule based on the loss function (15), i.e., $m\mp \text {sd}_\gamma$ with $\gamma =1/4$, obtaining [12.10, 15.38] which contains the true value 14.33 with credibility of 0.955. For case 2, we obtain the interval [6.90, 9.16] which contains the value 7.67 with credibility of 0.952. The histograms of the sampled values of $\overline{\lambda }^{(52)}$ for each case are presented in Fig. 3. These histograms, constructed with $n_o=52$, do not show large asymmetry. This might not be true for smaller sample sizes. However, construction of credible intervals based on small sample sizes might not be appropriate for the decision process under consideration. If on the other hand we consider $\alpha =1000$, which may be considered as an approximation to the full parametric model (16), (17), we obtain the intervals [9.63, 10.90] with 0.946 credibility and [9.43, 10.59] with 0.958 credibility, respectively for cases 1 and 2, which do not contain the overall mean. This suggests that the semiparametric approach may be a better alternative when little information is available on the heterogeneous organism distribution and/or the number of strata concentrations in the ballast water tank, given that the Dirichlet process embedded in the model (1)–(3) will naturally incorporate this lack of information. Details concerning the heterogeneity of this distribution are described in Murphy et al. (2002).

Fig. 3

Histogram of the sampled values of $\overline{\lambda }^{(52)}$ for each case

Even though the D-2 standard was proposed in 2004, only recently (2017) it has been enforced (Casas-Monroy et al. 2020). Data regarding details on the size and type of possible invasive organisms contained in ballast water as well as on their distributions in ballast water tanks which have different configurations are still scarce. Therefore estimation of the mean concentration of such organisms should be conducted with caution. We proposed an extremely flexible model that may take such features into account, although at the price of larger sample sizes. We believe that alternative and more specific models may be considered as more data become available.

Appendix A

Algorithm 1: :

Drawing samples from the joint posterior distribution of the $\lambda _i$.

Step 1. :

Simulate initial values for $\lambda _i$, $i=1,\ldots ,n$ from $F_0$;

Step 2. :

Under a Gibbs sampling scheme, update $\lambda _i$, $i=1,\ldots ,n$ using (4);

Step 3. :

Update the values obtained in Step 2 using (5);

Step 4. :

Repeat steps 2-3 a number of times as a burn-in; the values obtained in the last iteration are the required values.

Algorithm 2::

Drawing samples of the random mean $\overline{\lambda }$.

Step 1. :

Set a value for $\epsilon$, set $\overline{\lambda }_1^\ell =0$ and take $\overline{\lambda }_1^u$ as the largest internal bit value of the computer being employed (in our case, $1.79\times 10^{308}$);

Step 2. :

Update the upper and lower quantities using (8) and (9);

Step 3. :

If the absolute difference between the two quantities is smaller than $\epsilon$, the required value $\overline{\lambda }$ may be taken as either $\overline{\lambda }_t^u$ or $\overline{\lambda }_t^\ell$. Otherwise, return to step 2.

Algorithm 3: :

Drawing samples from the distribution of $\overline{\lambda }^{(n)}$

Step 1. :

Simulate $B_*$ from a $\text {Beta}(n, \alpha )$ distribution;

Step 2. :

Simulate $\overline{\lambda }$ using Algorithm 2;

Step 3. :

Simulate $D_i$, $i=1,\ldots ,n$ from a multivariate uniform distribution;

Step 4. :

Simulate $(Z_1,\ldots ,Z_n)$ from $\nu (d{\varvec{\lambda }}_n\vert {\varvec{x}}_n)$ using Algorithm 1;

Step 5. :

Obtain the required value using the quantities generated in steps 1-4 and (10) of the article.