1 Introduction

Skeletal muscles are involved in almost every human activity, including moving, speaking, and breathing. The study of their function is important because it is associated with a wide variety of conditions of physiological interest such as adaptation to training, disuse, aging or of pathological relevance, primary diseases like muscle dystrophy, and secondary diseases due to the involvement of muscles in respiratory, metabolic or nervous system diseases.

A thorough study of human muscle function is a challenging task. In fact, studies over the last century have recognized the existence of a multi-scale structure behind the macroscopic muscle function. The several newton forces and centimeter shortenings, which are required in our daily life, are actually generated by pico-newton forces and nanometer displacements at molecular level, where myosin motors cyclically interact with actin filaments, forming the cross-bridge cycle. Despite the multitude of papers aimed at the experimental characterization of myosin motors (Spudich 1994; Kitamura et al. 1999; Capitanio et al. 2012) and single muscle fibers in vitro (Marsh and Bennett 1986; Bottinelli et al. 1996; He et al. 2000), the impact of their results at macroscopic level, i.e., in whole muscles, is not yet fully understood. Actually, skeletal muscles exhibit a highly complex tri-dimensional architecture where thousands of muscle fibers, each with different properties, not only exert force on the tendons but also interact with each other and with surrounding connective sheaths, as endomysium, and perimysium, through transversal connections. With exception of few recent studies where single muscle fibers were visualized in vivo (Sanchez et al. 2015), most of the study on human muscle contraction are based on measurements of torque and angular rotation which are also dependent on the anatomy of bones and the joints. A gateway toward microscopic measurements in vivo has been opened by the recent development of muscle echography which allows the detection of movement of fiber bundles inside the muscle belly (Hauraix et al. 2015).

In this frame, mathematical modeling represents a useful tool to relate single molecule and single-fiber properties to whole muscle dynamics. Here, we focus in particular on mechanics of the relation between individual muscle fibers and fiber bundle. The fiber bundle relation has been the object of few experimental studies (Josephson and Edman 1988) and of some recent mathematical models (Sharafi and Blemker 2010), the latter being restricted to the analysis in resting conditions. In the present work, we adopted a finite element model, to study how different fibers in a bundle interact to generate the bundle force, shortening and power. In particular, we investigated the behavior of two main fiber types containing fast and, respectively, slow myosins isoforms, with different biochemical and biomechanical properties (Bottinelli and Reggiani 2000). Their selective recruitment in different tasks and their concomitant action in physiological situations is difficult to be assessed, since even the most refined and updated approach to human whole muscle mechanics in vivo can only reach the level of individual bundles inside a muscle (Hauraix et al. 2015).

Steady-state contractile properties of single muscle fibers were simulated with a Hill-type three-element model. This approach is among the most used in muscle modeling, since it combines good predictions of muscle behavior with a widely accessible computational power (Kojic et al. 1998). However, Hill-type models have limitations, in particular, because they usually represent whole muscle properties by means of a single contractile element where individual fiber properties are averaged. It has already been demonstrated, comparing models with one or two single Hill’s elements, that the fitting of muscle tension measured in situ and in vivo in animal muscles can be improved if two separated fiber pools, corresponding to slow- and fast-twitch fibers are considered (Hamouda et al. 2016; Wakeling et al. 2012; Levine et al. 2013; Holt et al. 2014). However, in those works all the fibers of the same type have been pooled in the same three elements and, consequently, the geometry and distribution of different muscle fibers have not been taken into account.

In this work, we adopted a finite element method (FEM) approach, to develop models for single fibers and, then, for a bundle of fibers. We started from the characterization of the parameters of Hill-type model to reproduce the experimental behavior of human slow and fast single fibers in vitro. To this end, we characterized both the contractile element and the elastic element in series in the Hill-type model, using available experimental data on human fibers (Bottinelli et al. 1996; He et al. 2000), and simulated the results of the experimental protocols with the predictions of the FE model of single fibers, comparing numerical simulations and experimental data. Then, we incorporated the FE models of individual fibers into the FE model of a bundle of fibers, whose geometry was based on an immunohistochemically stained cross sections of a muscle fiber bundle from a human diaphragm muscle biopsy, available in the literature (Hooijman et al. 2015).

Next, as a first application of our fiber bundle model, we generated the predicted force–velocity curve of the bundle and analyzed its relationship with the corresponding curves for the fast and slow fibers. This allowed us to define the parameters of the Hill’s three-element model that describe the bundle as a whole. The results obtained with the bundle model represent in turn the first step toward a physiologically defined, macroscopic FE model of a whole muscle. The bundle model could be also used in future to explore the effects of fiber selective submaximal activation under different external conditions or the relevance of transversal fiber–fiber interactions in physiological and pathological conditions such as Duchenne muscular dystrophy (DMD) (Sharafi and Blemker 2010; Virgilio et al. 2015).

Fig. 1
figure 1

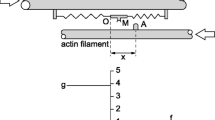
Hill-type model and FE model for single fiber and for bundle. a The three-element Hill-type model is formed by an elastic element (SE) in series with the contractile element (CE). These two elements are in parallel with a nonlinear elastic element (PE), which represents the passive or resting tension. b Single-fiber FE model. Each finite element is characterized by one Hill-type model with the same parameters, deduced for both fast and slow fiber type to fit single-fiber experimental behavior. c Immunohistochemically stained cross section of human diaphragm muscular tissue, with indication of the bundle and fibers modeled [black slow fibers and blue fast fibers; modified from Hooijman et al. (2015)]. d FE model of the bundle of fibers. Each finite element is characterized by one Hill-type model with parameters that are different for the fast and slow fiber type

Full size image

2 Material and methods

2.1 Design of the Hill’s three-element model

The properties that characterize muscle steady-state contraction are: the steady velocity of contraction reached against a constant load, the maximum isometric force generated at a given initial length of sarcomeres during isometric contraction, and the different forces generated at different activation levels. Hill-type three-element model is a useful approach to characterize these aspects of muscle mechanics because of its relative simplicity, which makes it suitable for implementing it into a FE model of whole muscle. Hill’s three-element model (Fig. 1a) is composed of a contractile element (CE), an elastic element (SE) in series with CE and an elastic element (PE) in parallel with CE and SE. The current lengths of these elements must fulfill the equation \(l_\mathrm{{PE}} =l_\mathrm{{SE}} +l_\mathrm{{CE}}\). The Hill’s model is a simplification of the actual structure of the sarcomeres, where both the SE and CE elements are affected by the cross-bridges properties. In this simplification, the relative length of SE and CE at a given sarcomere length cannot be defined by mechanical length perturbations and tension recordings, which give us a relationship only between the deformation and the SE contractile properties (Eq. 7 below). Therefore, a relationship between the initial lengths \(L_\mathrm{{SE}} \) and \(L_\mathrm{{CE}} \) is hypothesized, using \(L_\mathrm{{SE}} =k L_\mathrm{{CE}} \) with \(k=0.3\), as proposed by Kojic et al. (1998). The stretch on elements PE, CE and SE will be indicated with \(\lambda _f ={l_\mathrm{{PE}} }/{L_\mathrm{{PE}} }\), \(\lambda _m ={l_\mathrm{{CE}} }/{L_\mathrm{{CE}} }\) and \(\lambda _s ={l_\mathrm{{SE}} }/{L_\mathrm{{SE}} }\), respectively. Since CE and SE are in series, their stress must be equal at any time. In what follows, nominal stress (force per unit of undeformed area, P) is adopted. Therefore, the previous condition is expressed as \(P_\mathrm{{SE}} =P_\mathrm{{CE}} \), at any time of the analysis. The PE element is responsible for the passive elasticity of the surrounding component, whereas the CE element can be elongated freely in a non-activated state. Indicating with \(P_{0}\) the maximum isometric tension of the fiber, the stress response of the PE element is given by the equation:

$$\begin{aligned} P_\mathrm{{PE}} =\left\{ {\begin{array}{ll} 0&{} \lambda _f \le 0 \\ 4P_0 \left( {\lambda _f -1} \right) ^{2}&{} \lambda _f >0 \\ \end{array}} \right. \end{aligned}$$
(1)

The properties of the parallel element are assumed as proposed by Tang et al. (2009).

The CE element represents the active force generation of muscle and includes, in a phenomenological way, the above-mentioned characteristic of muscle contraction. Thus, its active tension \(P_\mathrm{{CE}} \) varies in time through the following components:

$$\begin{aligned} P_\mathrm{{CE}} =P_0 f_a \left( t \right) f_l \left( {\lambda _m } \right) f_v \left( {\dot{\lambda }_m } \right) \end{aligned}$$
(2)

The function \(f_a \left( t \right) \) represents the activation level of the fiber at any time t. Its description depends on the experimental protocol that one wants to simulate. In our case, it is characterized by two exponential functions representing the rise of activation and, respectively, its decay during relaxation. We assume a simplified form the activation function (Ehret et al. 2011), taking:

$$\begin{aligned} f_a \left( t \right) =\left\{ {\begin{array}{ll} a_0 &{}\quad t\le t_0 \\ a_0 +\left( {a_1 -a_0 } \right) \times h_t \left( {t,t_0 } \right) &{}\quad t_0<t\le t_1 \\ a_0 +\left( {a_1 -a_0 } \right) \times h_t \left( {t_1 ,t_0 } \right) \\ \quad \times \left[ {1-h_t \left( {t,t_1 } \right) } \right] &{}\quad t_1 <t \\ \end{array}} \right. \end{aligned}$$
(3)

where \(t_0\) and \(t_1\) are initial and final time instants of activation and the constants \(a_0\), \(a_1\) have been set as 0 and 1, respectively. The function \(h_t\) is defined as:

$$\begin{aligned} h_t \left( {t,t_i } \right) =1-\exp \left[ {-S\left( {t-t_i } \right) } \right] \end{aligned}$$
(4)

with S as time constant. The numerical values of all parameters used in this paper are reported in Table 1. The function \(f_l \left( {\lambda _m } \right) \) follows the force–length relationship as shown experimentally (Lieber and Ward 2011). We choose a length–force function proposed in the literature (Johansson et al. 2000):

$$\begin{aligned} f_l \left( {\lambda _m } \right) =\left\{ {\begin{array}{ll} \frac{\lambda _m -\lambda _\mathrm{{min}} }{\lambda _\mathrm{{opt}} -\lambda _\mathrm{{min}} }\\ \quad \times \exp \left[ {\frac{\left( {2\lambda _\mathrm{{min}} -\lambda _m -\lambda _\mathrm{{opt}} } \right) \left( {\lambda _m -\lambda _\mathrm{{opt}} } \right) }{2\left( {\lambda _\mathrm{{min}} -\lambda _\mathrm{{opt}} } \right) ^{2}}} \right] &{} \lambda _m >\lambda _\mathrm{{min}} \\ 0&{} \lambda _m \le \lambda _\mathrm{{min}} \\ \end{array}} \right. \end{aligned}$$
(5)

where the parameters \(\lambda _\mathrm{{min}} \) and \(\lambda _\mathrm{{opt}} \) are also reported in Table 1 (note that \(\lambda _\mathrm{{opt}} \) is slightly smaller than 1 to account for the extension of SE and the contraction of CE in isometric activation, see later).

Table 1 Model parameters
Full size table

The function \(f_v \left( {\dot{\lambda }_m } \right) \), where \(\dot{\lambda }_m \) is the rate of stretch of the CE element, generates the hyperbolic force–velocity relation as experimentally described by Hill (1938). In our model we define

$$\begin{aligned} f_v \left( {\dot{\lambda }_m } \right) =\left\{ {\begin{array}{ll} \frac{1-{\dot{\lambda }_m }/{\dot{\lambda }_\mathrm{{max}} }}{1+k_c {\dot{\lambda }_m }/{\dot{\lambda }_\mathrm{{max}} }}&{} \dot{\lambda }_\mathrm{{max}} <\dot{\lambda }_m \le 0 \\ 0&{} \dot{\lambda }_m \le \dot{\lambda }_\mathrm{{max}} \\ \end{array}} \right. \end{aligned}$$
(6)

in concentric contraction, where the parameter \(k_c\) is different for the fast and the slow fibers, as observed experimentally (see in the following and Table 1). The term \(\dot{\lambda }_\mathrm{{max}} \) represents the maximum stretch rate of the CE element and in a single fiber is associated with the maximum velocity of contraction through \(V_\mathrm{{max}} ={\dot{\lambda }_\mathrm{{max}} }/{(1+k)}\) (see next section). Finally, the characterization of SE is important as much as that of CE, since it is responsible of the fast response to abrupt changes in external load, which is quite common situation in several physiological conditions. Despite that, the relationship between its parameters and the experimental data in human muscle fibers is not clearly defined. Here, we propose to adopt a nonlinear relationship between its nominal stress and stretch, characterized through two variables \(\alpha \) and \(\beta \) (Table 1), as defined in (Kojic et al. 1998):

$$\begin{aligned} P_\mathrm{{SE}} =\beta \left\{ {\exp \left[ {\alpha \left( {\lambda _f -1} \right) -1} \right] } \right\} \end{aligned}$$
(7)

2.2 Experimental physiological data and identification of the Hill’s model parameters

We now use experimental data to characterize the parameters \(P_0\), \(\dot{\lambda }_\mathrm{{max}}\) and \(k_c\) for CE, as well as \(\alpha \) and \(\beta \) for SE. The parameters \(k_c\), S, \(\lambda _\mathrm{{min}}\) and the parameters for the isotropic term (see next section) will be obtained from previous models in the literature. Experimental data used for parameter identification are obtained from previous works (Bottinelli et al. 1996; He et al. 2000). In both studies, single muscle fibers used for this study were dissected from a biopsy sample of human Vastus lateralis muscle, permeabilized and maximally activated (\(\hbox {pCa}=4.6\)) at low temperature (\(12\,^{\circ }\hbox {C}\)) with initial sarcomere length adjusted at 2.6 \(\upmu \)m. Myosin heavy chain isoforms, fast and slow, were identified through gel electrophoresis. All experimental details concerning the mechanical experiments and the electrophoretic identification of myosin isoforms in each single fiber are reported in the above quoted papers.

Two experimental protocols are used to characterize the parameters for CE and SE, separately. The elastic component in series SE (parameters \(\alpha \) and \(\beta \)) can be characterized by the smallest rapid shortening needed to drop the isometric tension exactly to zero. This value can be extrapolated from the so-called slack test protocol (Edman 1979). Slack test procedure is based on small and rapid shortenings imposed to an isometrically contracting fiber. The rapid shortening drops tension to zero and moreover leads to a slacking of the fiber. The time required for the recovery of a linear geometry and a nonzero tension is related to both the unloaded shortening velocity \(V_{0}\) and the SE properties. The amount of shortening plotted versus the time needed to recover a nonzero tension (>1% of \(P_{0}\)) falls on a straight line (see Fig. 2). The intercept of the linear fitting is the amount of shortening which drops the tension to zero without slacking the fiber, and this is associated with the deformation of SE during isometric contraction.

Fig. 2
figure 2

Slack test: experimental data and simulations. Slack test has been used to characterize the series elasticity in muscle fibers (SE). a Typical experimental trace for the force versus time in a slack test. Skinned muscle fiber is allowed to contract in an isometric condition, then a rapid controlled shortening in length drops the tension to non-positive values. After the isometric conditions are restored, the tension rises toward original values. b Numerical simulation of the tension-time trace generated by the single-fiber FE model for fast isoform. The shortening \(\Delta L\) is reported relative to the initial length of the fiber \(L_0 \). The results of numerical simulation of fast fiber are reported for shortening \({\Delta L}/{L_0 }\) of 7, 9, 11, 13 and 15%. c The timing required to recover a positive tension is recorded and plotted in function of the imposed shortening, for both experimental data (circles) and simulation of fast and slow fiber type (triangles). The results from numerical simulation refer to shortening \({\Delta L}/{L_0 }\) of 7, 9, 11, 13 and 15%. The linear correlations are calculated from data points of the numerical simulation and extrapolated to time zero

Full size image

Parameters \(P_0 \), \(\dot{\lambda }_\mathrm{{max}} \) and \(k_c \) for the CE can be characterized by the experimental force–velocity curve, generated point by point by imposing a constant velocity of contraction and measuring the constant tension generated by the fiber (isovelocity shortening). From this pool of data, we determine the maximum isometric stress \(P_0\) and the maximum velocity \(V_\mathrm{{max}}\) (related to \(\dot{\lambda }_\mathrm{{max}}\) as described below) for the slow and fast fibers, and evaluate the parameter \(k_c\) through a least square fitting of experimental data with the curve described in Eq. (6). Notably, the slope of the fitting line in the slack test procedure (Fig. 2) represents maximum velocity of shortening in unloaded condition, usually indicated as \(V_0\). As shown in previous studies \(V_0\) and \(V_\mathrm{{max}}\) are similar but not identical (Bottinelli et al. 1996). In the data pool chosen for the slack test analysis, \(V_0 \) is equal to \(1.63L_0/\hbox {s}\) and \(0.3L_0/\hbox {s}\), while \(P_0\) is 97 and 83 kPa for fast and slow fibers, respectively. As stated above, we use the isovelocity data for defining \(P_0\), \(\dot{\lambda }_\mathrm{{max}}\) and \(k_c\). Values for \(P_0\) and \(V_0\) for this data pool is reported in Table 1.

The choice to fit the Hill’s model parameters to data obtained in muscle fibers in vitro has an impact on mechanical characterization of the model. In particular, non-muscle elasticity, which is present in vivo, for instance in relation to the tendon–fiber interaction, is lacking in vitro. The single fibers in vitro, considered in this work, are just segments of fibers clamped between the force transducer and the motor with displacement transducer, therefore the non-muscle extra-sarcomeric elasticity is negligible, and all the observed elasticity can be included into the SE. This, in turn, affects also the definitions of force-length and force–velocity relationship for the CE, since they are determined experimentally on the whole fiber and not on the CE alone. For instance, the maximum stretch rate \(\dot{\lambda }_\mathrm{{max}}\) imposed in Eq. (6) corresponds to the maximum contraction velocity referred to the initial length of the sole CE, while the whole finite element will contract at \(V_\mathrm{{max}} = {\dot{\lambda }_\mathrm{{max}}}/{(1+k)}\). In this work, the value of \(\dot{\lambda }_\mathrm{{max}}\) is adjusted correspondingly. Similarly, for an isometric contraction at a given total initial length \(L_\mathrm{{PE}} =L_\mathrm{{SE}} +L_\mathrm{{CE}}\), the current value \(l_\mathrm{{CE}}\) decreases while \(l_\mathrm{{SE}}\) increases. The component CE contracts till the forces generated by the two elements equilibrate, being \(P_\mathrm{{CE}} =P_\mathrm{{SE}} =P_0\). This effect is taken into account in this work, imposing \(\lambda _\mathrm{{opt}}\) equal to the equilibrium value of \(\lambda _m\) in isometric condition.

2.3 Single-fiber FE model

Based on the Hill’s three-element model, above described, a single-fiber three-dimensional FE model (Fig. 1b) aimed to simulate realistic experimental protocols is developed. The single-fiber model is defined to reproduce the average shape and dimension of experimentally tested segments of fibers (initial length \(L_0= 500~\upmu \hbox {m}\), diameter \(50{\div }100~\upmu \hbox {m}\)). The stretch of the fiber is given by:

$$\begin{aligned} \lambda _f =\sqrt{{\tilde{\mathbf{C}}}:\left( {\mathbf{n}_0 \otimes \mathbf{n}_0 } \right) } \end{aligned}$$
(8)

The second rank tensor \({\tilde{\mathbf{C}}}\) is the iso-volumetric part of the right Cauchy–Green strain tensor and \(\mathbf{n}_{0}\) is the unit vector that defines the initial disposition of the sarcomeric unit. It is defined \({\tilde{\mathbf{C}}}=J^{-2/3}{} \mathbf{F}^{T}{} \mathbf{F}\) where \(\mathbf{F}\) is deformation gradient and J the Jacobian of deformation. To account for possible three-dimensional stress states acting on the fibers (for example, in the clamped end regions), the first Piola–Kirchhoff stress tensor \(\mathbf{P}\) is defined as

$$\begin{aligned} \mathbf{P}=\mathbf{P}_\mathrm{{iso}} +\left( {P_\mathrm{{PE}} +P_\mathrm{{SE}} } \right) \mathbf{Fn}_0 \otimes \mathbf{n}_0 \end{aligned}$$
(9)

where the isotropic term \(\mathbf{P}_\mathrm{{iso}}\) is deduced via a standard derivate from the strain energy function:

$$\begin{aligned} w_\mathrm{{iso}} =\alpha _{m1} \exp \left[ {\alpha _{m2} \left( {\tilde{I}_1 -3} \right) } \right] +\frac{k_{mv} }{2}\left[ {J^{2}-1-2\hbox {ln}\left( J \right) } \right] \end{aligned}$$
(10)

In order to ensure the incompressibility, as generally assumed for muscle, the volumetric part is assumed as penalty term, setting its value in order to give an almost incompressibility but avoiding numerical instability (see Table 1). The above expression is similar to that proposed in the literature (Tang et al. 2009) for skeletal muscle fibers and the constitutive parameters \(\alpha _{m1}\) and \(\alpha _{m2}\) are set in order to obtain the same mechanical response of the isotropic matrix. In uniaxial tension the stress of the isotropic matrix is largely lower than the stress response given by the element PE. With the assumed parameters, for a stretch in the range of \(0.95{\div }1.05\) the isotropic term has a secant modulus of about 2.5 kPa. For a stretch in the range of \(1{\div }1.05\) the element PE shows a nonlinear response with a secant modulus of about 33 kPa.

The constitutive model for the muscle fiber is implemented via specific user subroutines in the general-purpose FE software ABAQUS Standard (Dassault Systémes) that have been adopted for all the analyses in this work. The model is developed with the software ABAQUS CAE (Dassault Systémes). The single-fiber model consists of 769 eight-node hexahedral elements and 1025 nodes. Finite elements with hybrid formulation are adopted in order to avoid numerical instabilities due to almost-uncompressible behavior.

2.4 Multi-fiber bundle FE model

The bundle FE model (Fig. 1d) is developed starting from an immunohistochemically stained cross section of human diaphragm bundle (Fig. 1c), available in the literature (Hooijman et al. 2015). In that work, fibers were identified by means of staining with specific antibodies against myosin isoform (M32). Adjacent fibers in the model are considered mutually connected at their interface, and therefore no sliding is allowed during any contraction. Both fast- and slow-type fibers are described by the same constitutive model, but assuming different numerical values of the parameters according to the experimental data obtained on the two fiber types (see above and Table 1). The bundle model is composed of 19 fibers (10 slow and 9 fast, see Fig. 1c) with a length of \(500~\upmu \hbox {m}\) and a constant section with irregular shape and “average” diameter of about \(180~\upmu \hbox {m}\). Also in this case, hybrid elements are adopted. The model consists of 24,495 linear elements with eight or six nodes and 25,064 nodes.

3 Results and discussion

3.1 Single-fiber modeling

Two sets of experimental data were used to identify the parameters of the single fiber model and to test its predictive power in slow and fast fibers: the slack test protocol and the steady-state shortening in load clamp or in isovelocity contractions. The nominal stress is calculated considering the resultant force at the free end of fiber/bundle and dividing this value for the area of the undeformed transversal section. This is consistent with the experimental approach, where force values are measured and nominal stresses are deduced according to the undeformed transversal section of the fiber.

Fig. 3
figure 3

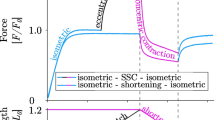
Numerical simulation of the experimental protocol for isotonic contraction (load clamp or isometric–isotonic protocol). a Simulated displacement versus time traces for a fast fiber in the following protocol: The fiber is activated with two fixed ends (isometric condition) till the full development of maximal force (rising phase not shown), then at time \(t=0\) one end is released and an external stress is applied at different values (isotonic condition, stresses \(P/{P_0}=0.2, 0.4, 0.6\) are shown in the figure). In full accordance with experimental records, the length initially drops for the rapid shortening of the SE, and then starts to shorten at a constant velocity. b Force versus velocity (F–v) curves predicted for the fast (red) and slow (blue) single fiber and comparison with the experimental data obtained from isokinetic experiments (iso-velocity). The values in abscissa are the velocity expressed as initial muscle fiber length \(L_0 \) per second. c F–v curve for the fast (red) and slow (blue) single fiber, compared to the F–v curve predicted from the bundle FE model. Dotted line is the average force predicted by fast and slow fibers contracting at the same velocity. The inset shows how the bundle behavior deviates from the dotted lines at high velocity

Full size image

Slack test protocol was adopted for characterization of the parameters of SE and for \(V_0\) determination. For both slow and fast fiber types, we plotted recovery times \(\Delta t\) corresponding to different shortenings \(\Delta L\). The data pairs were fitted through a linear regression to estimate the intercept at \(\Delta t=0\). This value was used to constrain the parameter \(\alpha \) in Eq. (7) imposing \(\beta =1.2P_0\) (Cleworth et al. 1972), where \(P_0\) refers to the value obtained in the pool of data used for the characterization of SE. As stated above, \(k={L_\mathrm{{SE}}}/{L_\mathrm{{CE}}}\) is assumed to be 0.3 as in (Kojic et al. 1998). To test the predictive ability of the single- fiber model, we simulated the slack test protocol, the fast shortening imposed during the isometric contraction and the subsequent recovery of tension after the period of slack (Fig. 2a). The model was able to reproduce the experimental behavior, showing a slacking of the whole fiber when the shortening of each element was higher than the stretch in the SE at the steady state of the isometric contraction (Fig. 2b and movie 1 in SI). Plotting the times required to recover a positive tension versus the imposed shortenings, we obtained a good fitting of the experimental data for both slow and fast fibers (Fig. 2c). The numerical model was able to overcome the experimental limits and to simulate the shortening needed to drop the tension exactly to zero and immediately start the tension recovery. The predicted values were in good agreement with the experimental intercept (SE extension) and slope \((V_0)\). In the simulation of the force–velocity curve (see below), a value of maximum shortening velocity \(V_\mathrm{{max}}\) will be obtained by extrapolation at zero load starting from the pairs of force and shortening values measured with isovelocity shortening.

The steady-state properties of the CE were characterized according to the force–velocity curve using the experimental data reported in (He et al. 2000), obtained during isovelocity shortening from the average of a number of fast and slow human fibers. The experimental procedure is described in (He et al. 2000). From these data, we defined the maximum isometric tension of the two types of fibers, \(P_0\), and the parameters of the force–velocity curve including the intercept on the velocity axis, i.e., the maximum velocity \((V_\mathrm{{max}})\) and the curvature, \(k_c\) (see Table 1). We then applied our single-fiber model to simulate the isometric–isotonic protocol (load clamp) where a constant load is imposed and velocity is recorded, and we compared the simulations with the experimental data. Notably, the load clamp experimental protocol was different from the isovelocity shortening where a constant velocity was imposed and the tension evaluated.

In the simulations, the tension shows a rapid drop due to the mechanical relaxation of the SE at the beginning of the isotonic phase, followed by a period of shortening at constant velocity (Fig. 3a), as in the experimental behavior. Then, we were able to construct the force–velocity curve and to compare it to the experimental data, for both the fast and the slow fibers (Fig. 3b), showing that the isotonic simulations also provide a good prediction of the isokinetic experimental data. Parameters deduced from published experimental data on human muscle fibers studied in vitro/ex vivo are reported in Table 1.

3.2 Fiber bundle modeling

The experimental studies on muscle mechanics are very often carried out on single fibers, which generally express a single myosin isoform and behave therefore as slow or fast fibers. How the combined action of fast and slow fibers affects the overall muscle behavior is hard to be assessed experimentally (Josephson and Edman 1988). A FE model of a fiber bundle, able to reproduce isometric tension and isotonic shortening, can be very helpful to address the problem of how fibers with different myosin isoforms cooperate to generate force and displacements in whole muscle. In fact, most human muscles are composed by a blend of slow- and fast-twitch fibers in various proportions (Bottinelli and Reggiani 2000; Levine et al. 2013). The fibers are finely intermingled to form bundles of hundreds of micrometers of diameter, kept together by extracellular matrix or endomysium, each bundle being separated from the adjacent bundles by sheaths of connective tissue or perimysium. The transversal connections between adjacent fibers inside each bundle are based on the multiprotein complex indicated as costamere, regularly spaced along the fibers with a periodicity corresponding to that of sarcomeres (Ervasti 2003). To characterize the behavior of a mixed fiber bundle we included our fiber models in a FE model of a bundle made of parallel fast and slow fibers (Fig. 1d), and we generated the force–velocity curve through a series of isometric–isotonic maneuvers (load clamps). The bundle mesh was developed starting from an immunohistochemically stained cross section of bundle taken from a biopsy of healthy human muscle present in literature (Hooijman et al. 2015), reproducing carefully the locations of fast and slow fibers and their relative cross-sectional areas with a total of \(12{,}752.3~\upmu \hbox {m}^{2}\) for the 9 fast fibers and \(13{,}765.0~\upmu \hbox {m}^{2}\) for the 10 slow fibers. Slow and fast fibers of the bundle were considered as perfectly bounded at their adjacent surfaces, and therefore, there were no relative displacements between fibers in the direction of the bundle long axis. The end sections of the bundle were also considered as rigid.

The FE model for the bundle was able to simulate the isometric–isotonic protocol and from a series of these simulated experiments a force–velocity curve was obtained (Fig. 3c). It was therefore interesting to compare the bundle force–velocity curve with the single fiber force–velocity curves, in the hypothesis that all the fibers were maximally activated in the same way. As seen in Fig. 3c, the force–velocity curve had intermediate values between the fast and the slow isoforms at higher loads, and as long as the predicted velocity of contraction is lower than the \(V_\mathrm{{max}}^s\), the maximum velocity of the slow isoform. At lower external loads, the predicted bundle velocity of contraction shifts to the one of the fast fiber. The more the external tension decreases, the closer the bundle velocity is to that specific of the fast fibers. The dotted line in Fig. 3c shows the mean tension generated at a given velocity from the slow and fast force–velocity curve.

The predicted behavior can be explained as follows: at high and intermediate external forces, both the fast and slow fibers contribute to contraction. Even though we imposed a constant external force, as in the experimental setup for isotonic contraction, the above-mentioned constraints of rigid link between fibers lead to the same velocity of contraction for every fiber. When different fibers contract at the same velocity they generate different forces, as predicted by the Hill’s force velocity curve imposed to CE (Fig. 3c, red and blue curves at the same abscissa). Consequently, fast fibers sustain a higher tension respect to slow fibers, while the total tension generated by the bundle equilibrates the one imposed as external condition. The different tension in the fibers of the bundle during isotonic contraction is shown in Fig. 4. Because of the almost-equal proportion of fast and slow fibers (51.9% slow and 48.1% fast), the force–velocity behavior is then similar to the average of the corresponding behaviors of the two types of fibers at any velocity until the slow fibers are still able to generate force. When the predicted velocity is higher than \(V_\mathrm{{max}}^s \), the tension generated by the slow fibers becomes zero and therefore the external tension is completely sustained by the fast fibers. This means that the effective tension acting on those fibers becomes actually twice than the nominal tension. The predicted velocity of contraction is then determined by the force–velocity curve of the fast fibers, computed on the effective tension acting on those fibers. In this phase, the slow fibers shorten without exerting forces on the surrounding fast fibers. The bundle force–velocity relationship could be interpolated with Eq. (6). The fitting curve (Fig. 3c dotted line) is characterized by a parameter \(k_c=11.9\).

Fig. 4
figure 4

Numerical simulation of the bundle during contraction against a constant external force. a Displacements (\(\upmu \)m) in the direction of the bundle U3 for an intermediate deformed configuration. Due to uneven distribution of slow and fast fibers inside the bundle, displacement shows a complex distribution. b Normal stress (MPa) along the direction of the bundle in a cross-section S33. When a constant external force, lower than the maximum force generated, is imposed to one end of the bundle, it starts to shorten. Despite the fact that the imposed condition is of constant force, the constraints between the fibers (corresponding to the effect of costameres) lead to a constant velocity of contraction of each fiber and, as a consequence, to different stress in different fiber types. The sum of the stress in the fast and slow type fibers equilibrates the external load imposed. Stress is higher in green than in blue fibers, according to color scale

Full size image

A prediction of how fast and slow fibers contribute to determine the bundle behavior has been previously done by means of validation methods (Wakeling et al. 2012; Lee et al. 2013; Holt et al. 2014; Biewener et al. 2014). In those works, one or two Hill-type models are adopted, with different hypotheses on the relative influence of the fast and slow fibers, and analyzed their fitting capabilities to deduce which one was the most reliable. Our work extended their analysis using a FEM approach and showed that a mixed bundle can be characterized by a force–velocity curve with \(V_\mathrm{{max}}\) close to the maximum shortening velocity of the fast fibers. Also, the bundle force–velocity curvature \((k_c =11.9)\) is slightly different from the average \((k_c =12.2)\) and closer to the faster fibers \((k_c=8.53)\). Such a difference has an interesting impact on the peak power generated by the bundle and on the velocity at which is reached, often indicated as optimal velocity (Bottinelli et al. 1996). Peak power of the bundle has a value \((0.035\times V/{L_0 }\times P/{P_0 })\) above the mean between the fast fiber \((0.053\times V/{L_0 }\times P/{P_0 })\) and the slow fiber \((0.013\times V/{L_0 }\times P/{P_0 })\) values. It is reached at an optimal velocity \((0.158\times V/{L_0 })\) closer to that of fast fibers \((0.221\times V/{L_0 })\) than that of slow fibers \((0.066\times V/{L_0 })\), see Fig. 5. Despite these differences are not very high, the model shows that in a bundle equally composed of slow and fast fibers, peak power, which is most relevant functional parameter in vivo, is determined more by fast fibers than by slow fibers. For further evaluation on muscle energetics, the model prediction should be validated against experimental data of bundle of fibers in vitro, which, at the best of our knowledge, are not present today. Our model makes a first step to overcome this experimental limit, predicting the parameters which characterize the force–velocity of a bundle. These parameters could be instrumental to the development of a FE model reproducing a whole muscle composed of thousands of bundles, each composed of tens or even hundred single muscle fibers. A FE model of a muscle accounting for the behavior of each individual fiber will likely be computationally too expensive. The parameters obtained in bundle model based on single-fiber model could then be used in a FE model of a (macroscopic) whole muscle maintaining the same physiological significance of models based on the single-fiber characterization.

Fig. 5
figure 5

Power–velocity data of slow fibers, fast fibers and a bundle equally composed of fast and slow fibers, as obtained by numerical analyses. Numerical values are interpolated by means of power-velocity curves obtained from the Hill’s Eq. (6). The arrows indicate the peak power and therefore the optimal velocity for each curve. The optimal velocity for slow fibers, fast fibers and bundle is 0.066, 0.221, 0.158 \(L_0\,\hbox {s}^{-1}\), respectively. Note that the bundle peak power is reached at an optimal velocity closer to that of fast fibers (0.221 \(L_0 \hbox {s}^{-1}\)) than to that of slow fibers (0.066 \(L_0\,\hbox {s}^{-1}\))

Full size image

4 Conclusions

In this work, we characterized the parameters in Hill’s model, based on experimental data of slow and fast fibers from human skeletal muscles in vitro, and reproduced the experimental behavior with single-fiber FE models. Then, we used these parameters to predict the behavior of a bundle of fibers contracting against a constant load, developing a force–velocity curve characteristic for the bundle. This allowed us to define the parameters for the Hill’s model of a bundle of fibers. These parameters could be used to reproduce the human whole muscle behavior, at least under our current assumptions: maximally activated fibers, same amount of fast and slow fibers, rigid connections between fibers.

The model could be improved to overcome these limits and explore how more physiological or pathological conditions affect the bundle behavior. In the first place, during their physiological activity, human muscles have a more complicated activation history. Fibers composing the same bundle often belong to different motor units and can thus experience different activation levels and, in some case, fibers completely inactive can be adjacent, side-by-side, to fully active fibers. Moreover, our experimental data for fast and slow fibers derive from experiments carried out at \(12\,^{\circ }\hbox {C}\). An extrapolation to physiological temperatures is required when the bundle characterization has to be applied to whole muscles in vivo. Finally, our constraints imposed on the interface between muscle fibers and at the bundle extremity where the myotendinous junction should be located, are the simplest hypothesis in a physiological situation. The constraints on the adhesion between adjacent fibers in the bundle FE model could be modified to explore how the transversal links might affect contraction force and velocity. This would acquire particular interest for those diseases which are related to mutations of sarcolemmal or sub-sarcolemmal proteins as DMD (Sharafi and Blemker 2010; Virgilio et al. 2015).

Despite the above limitations, the proposed FEM approach makes it possible to explore the interactions between single-fiber and multi-fiber contractile structures such as bundles, during contraction. Usually macroscopic muscle FE models define the parameters of the Hill’s elements in order to fit the known macroscopic behaviors. In other words, they deduce the single fibers/molecules properties from the macroscopic muscle behavior. As informative this top-down approach could be, it is limited in describing how different single-fiber alterations may affect the macroscopic muscle performance. In this work, we have proposed a method to deduce the macroscopic parameters from the single fibers, using a bottom-up approach. This method will lead to a more meaningful simulation of muscle mechanics in several patho-physiological conditions. The progress in muscle echographic recording will provide more and more data on mechanical behavior of bundles in situ and this might open a new chapter in the study of muscle modeling. The current limits of such techniques do not allow for an experimental validation of our results, but the definition of the parameters for an Hill curve representing the whole bundle fills the gap, though at the in silico level, between the experimental data on single fiber and the FEMs whose elements contain several fibers, of different types, at once.

Further works in this respect will lead to a more detailed characterization under a variety of physiological and pathological conditions. Muscle disorders and diseases are associated with severe alterations of single-fiber properties, such as contractile weakness, atrophy, or reduced cross-sectional area, which can affect differentially slow and fast fibers. As shown here, different muscle fiber types contribute in a different way to the bundle behavior and thus likely also to the whole muscle behavior. Our approach, based on the effective behavior of single fibers, will be particularly useful to predict how pathological alterations at fiber level can influence the whole muscle performance.