Sampling inspection to prevent the invasion of alien pests: statistical theory of import plant quarantine systems in Japan

Abstract

The establishment of appropriate import quarantine systems is the best known method for preventing the unintentional introduction of invasive alien pests. However, quarantine systems are sometimes judged as non-tariff barriers against trade by the World Trade Organization. The construction of a common scientific theory for quarantine systems is thus extremely important to prevent invasion without causing international conflict. We explain several statistical theories that have been adopted in import plant quarantine systems in Japan. Quarantine systems include three major components: (1) import sampling inspection, (2) early detection procedures, and (3) emergency control. We first explain the principle of risk management that was commonly adopted in these components. Then, we explain the method for calculating the required sample size in the import sampling inspection. We then explain hierarchical sampling inspection for detecting alien pests inside Japan. We further explain the theory for declaring the eradication of invasive alien pests as an emergency control. Actual examples of quarantine actions against the invasion of plum pox virus disease and citrus huanglongbing are discussed.

Introduction

Invasive alien species are divided into two categories: intentionally introduced species and unintentionally introduced species (McNeely et al. 2001; Wittenberg and Cock 2001; CBD 2014). Several alien mammals such as raccoons and mongooses became invasive after they were introduced intentionally. Small Indian mongoose Herpestes auropunctatus were intentionally introduced from India to Amami Island, Japan, to control the native poisonous snake called Habu, Trimeresurus flavoviridis. They became invasive afterwards, preying on other wild animals including the Amami rabbit Pentalagus furnessi, which is indigenous to the Amami and Tokuno Islands (Yamada and Sugimura 2004; Fukasawa et al. 2013). An appropriate assessment of invasiveness before the intentional introduction is important for preventing this kind of invasion. On the other hand, most species of alien agricultural pests including insect pests and plant diseases have been introduced unintentionally although their invasiveness was known beforehand (Kiritani 2001; Kiritani and Morimoto 2004). For example, Sharka disease that is caused by the plum pox virus (PPV) was found in Japan in 2009, although we have been taking precaution against the invasion of this disease (Kasugai 2010). The construction of appropriate import quarantine systems is the sole way to prevent this kind of invasion.

A quarantine system is sometimes judged as a non-tariff barrier against trade by the panel constructed by the World Trade Organization (WTO) (e.g., WTO 2003). World War II emerged from block economies that prevented international trade. The WTO is the 1995 successor to the General Agreement on Tariffs and Trade (GATT), established in 1948 to prevent international wars by removing barriers against trade (Takase 1997). However, the accelerated trade caused several problems including pest introduction (Kiritani 2001) as well as economic problems (Lang and Hines 1993; Fujii 2015). The WTO agreement on the application of sanitary and phytosanitary measures (SPS Agreement), which was enacted in 1995, permits member countries to enact phytosanitary measures including plant quarantines (WTO 1994). However, the phytosanitary measures are considered legal only if they satisfy several requirements such as transparency, sufficient scientific evidence, and an appropriate level of phytosanitary protection (ALOP). These requirements can be issues of international controversy as seen in the panel reports from WTO. The scientific theory adopted by the quarantine systems of the member countries must be disclosed to allow for a constructive and data-driven debate. The level of phytosanitary protection has been stated briefly in several countries (Venette et al. 2002; EPPO 2006; Ministry of Agriculture and Forestry 2010; USDA 2010, 2011; Robinson et al. 2011, 2012, 2013).

Japanese plant quarantine achieved the centenary in 2014 since the enactment of the import and export plant regulation in 1914. In this paper, we explain several statistical theories that have been adopted in the current official import plant quarantine systems in Japan. In the definition of International Plant Protection Convention (IPPC 2009a), plant quarantine generally indicates all activities designed to prevent the introduction and/or spread of quarantine pests or to ensure their official control. Import plant quarantine systems inside Japan contain the following three major components (Plant Protection Station 2014): (1) import sampling inspection, (2) early detection procedure, and (3) emergency control. We first explain the theory that is used to determine the sample size in the sampling inspection of the imported plant consignments at the port. We next explain the hierarchical sampling procedure that is used as an early detection procedure of alien pests inside Japan. We finally explain the procedure of sampling inspection to verify the eradication of alien pests in emergency control. Actual examples of eradication of alien plant diseases in Japan are described.

Theory for import plant quarantine sampling

Overview of the sampling procedure

The term ‘plant’ in plant quarantine conventionally indicates various items including plant parts such as fruits, timber, and cracked cereals. Three options are available for the importation of plants that may bring alien pests: complete ban of the importation of plants, inspection of all imported plants, and sampling inspection of imported plants. We discuss the third option, sampling inspection, in this paper. A sampling inspection does not completely eliminate the possibility of the unintentional introduction of alien pests. Hence, we must control some kind of ‘risk’ at this stage. The risk still remains even if all plants are inspected, because insect pests and plant diseases are not completely detected by the usual inspection in several situations. The remaining possibility of introduction should be eliminated by quarantine measures in the subsequent stages including early detection and an emergency control that will be discussed later. Generally, the term ‘risk’ is used by several different definitions. Several people define risk by the expectation of the severity, that is, the sum of the occurring probability of the event multiplied by the consequence of the event (Sueishi 2000; Society of Risk Analysis 2013). In 2009, the International Organization for Standardization (ISO) adopted a more ambiguous definition of risk as the ‘effect of uncertainty on objectives’ (ISO 2009). In this definition, the risk includes the positive risk that corresponds to desirable events in addition to the negative risk that corresponds to undesirable events. However, the Japanese plant quarantine adopted a classical definition that seems clearest (Upton and Cook 2008): a risk was defined by ‘the probability that an undesirable event would occur’. In performing risk management using this definition, we must provide answers for two questions:

• Which phenomenon should we consider as an undesirable event?

• Which probability of occurrence should we adopt as a limit in our risk management?

The import plant quarantine regulation was revised in 1992 in Japan. An ‘infested plant’ is defined by a unit of plants that is infested by specified quarantine pests. An ‘infested consignment’ is defined as ‘a consignment of which the proportion of infested units is not smaller than p _c’. The quantity of p _c indicates the critical proportion that is not permissible. An undesirable event is defined as the ‘introduction of an infested consignment into Japan’. Then, the sample size is determined so that the probability of occurrence of undesirable events is not larger than a specified quantity. We denote the quantity by β. In other words, the sample size is determined so that an infested consignment is detected by a probability not smaller than (1 − β). The limit of probability β corresponds to ‘consumer’s risk’ while a consignment corresponds to a ‘lot’ in the terminology of industrial sampling inspections (ISO 2006a). Several industrial standards such as those established by ISO and JIS (Japanese Industrial Standards) regulate two risks simultaneously: the consumer’s risk (β) and the producer’s risk (α) (e.g., Japanese Industrial Standards Committee 1956a). However, we considered that we need not regulate the producer’s risk because the principal purpose of our import plant quarantine inspection is to prevent the invasion of alien pests. If we ignore the producer’s risk, we can reduce the sample size and hence perform the import plant quarantine inspection more efficiently.

The actual procedure of inspection is as follows.

• 1. The sample size in weight is read from Annex Table 1 of Article 1 of the import plant quarantine regulation enacted in 1992.

• 2. The sample of a given weight is drawn at random, in principle, from each consignment. A systematic sampling is also allowed if appropriate.

• 3. All units in the sample are examined. The consignment is rejected if one or more infested units are included in the sample.

• 4. If a consignment is rejected, all units in the consignment are carried back to the ship or incinerated, in principle. The rejected units are permitted for importation only if they are treated by an appropriate method including sterilization.

Table 1 shows a part of Annex Table 1 of Article 1. The original table (in Japanese) is available from the web site of the Ministry of Agriculture, Forestry and Fisheries of Japan, http://www.maff.go.jp/j/kokuji_tuti/kokuji/k0000336.html or http://www.pps.go.jp/law_active/Notification/basis/5/9/html/9.html. The English translation, including all legislation about plant quarantine in Japan, can be purchased from Japan Plant Quarantine Association (Japan Plant Quarantine Association 2009). The original table consists of 40 categories of plants. Table 1 shows only two categories for convenience. The columns of p _c, β, and ‘Sample size in unit, s’ in Table 1 do not appear in the original Annex Table 1; these columns were added for this explanation. In the following sections, we explain the theory about how Annex Table 1 of Article 1 was constructed in 1992.

Table 1 A part of Annex Table 1 of Article 1 of the import plant quarantine regulation enacted in 1992, showing an example of regulation for the import plant quarantine inspection in Japan

Formulae for the calculation

Let p _i be the proportion of infested units in the ith consignment of a size n _i . Let s _i be the number of units drawn from the consignment at random. Let Y _i be the number of infested units in the sample. We can always reject the consignment if Y _i  > 0, because we are ignoring the producer’s risk as stated above. Then, the risk management principle in the sampling inspection described above is given by Pr(Y _i  = 0|p _i ) ≤ β for all p _i within 0 < p _c ≤ p _i  ≤ 1. The quantity of p _c corresponds to the lot tolerance percent defective (LTPD) in the definition of Dodge (1969). The probability of acceptance, Pr(Y _i  = 0|p _i ), is given by the zero-term of a hypergeometric distribution.

$$\Pr (\left. {Y_{i} = 0} \right|p_{i} ) = \frac{{\left( {\begin{array}{*{20}c} {n_{i} p_{i} } \\ 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {n_{i} - n_{i} p_{i} } \\ {s_{i} } \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {n_{i} } \\ {s_{i} } \\ \end{array} } \right)}} = \frac{{(n_{i} - n_{i} p_{i} )!(n_{i} - s_{i} )!}}{{n_{i} !(n_{i} - s_{i} - n_{i} p_{i} )!}} .$$

(1)

The minimum number of samples s _i that satisfy Pr(Y _i  = 0|p _i ) ≤ β for all p _i within p _c ≤ p _i  ≤ 1 is given by the following equation (Japanese Industrial Standards Committee 1956b, see Appendix for the derivation):

$$s_{i} = \left\lceil {\left( {n_{i} - \frac{{\left\lceil {n_{i} p_{\text{c}} } \right\rceil - 1}}{2}} \right)\left( {1 - \beta^{{1/\left( {\left\lceil {n_{i} p_{\text{c}} } \right\rceil } \right)}} } \right)} \right\rceil ,$$

(2)

where $\lceil \; \rceil$ indicates the ceiling function. Equation 2 is slightly different from the similar equation listed in the ISO standards (1995, p 12); a consignment having the proportion of infestation p _c is not allowed in our principle of risk management while it is allowed in ISO (1995).

If the sampling proportion (s _i /n _i ) is sufficiently small, we can approximately consider that each sampled unit is independently infested by a probability p _i . Hence, we can replace the hypergeometric distribution by a binomial distribution that is called p-binomial. We have Pr(Y _i  = 0|p _i ) = $(1 - p_{i} )^{{s_{i} }}$. Hence, we obtain

$$s_{i} = \left\lceil {\frac{{\log_{e} (\beta )}}{{\log_{e} (1 - p_{\text{c}} )}}} \right\rceil .$$

(3)

If the proportion of infested units p _i is sufficiently small, we can approximately consider that each infested unit is independently selected by a probability of s _i /n _i . Hence, we can replace the hypergeometric distribution by a binomial distribution that is called f-binomial (Stephens 2001). We have $\Pr (\left. {Y_{i} = 0} \right|p_{i} ) = (1 - (s_{i} /n_{i} ))^{{\left\lceil {n_{i} p_{i} } \right\rceil }}$. Thus, we obtain

$$s_{i} = \left\lceil {n_{i} (1 - \beta^{{1/(\left\lceil {n_{i} p_{\text{c}} } \right\rceil )}} )} \right\rceil .$$

(4)

We can alternatively obtain this equation by letting n _i p _c approach zero in Eq. 2. The f-binomial approximation was used by Kuno (1991) and Yamamura and Ishimoto (2009), but f-binomial approximation is not so widely known despite its potential usefulness in detecting a small proportion of contamination. We use f-binomial approximation in a later section in deriving the sample size required for confirming the eradication of invasive alien pests. If both of the sampling proportion (s _i /n _i ) and the proportion of infested units (p _i ) are sufficiently small, the hypergeometric distribution is approximately given by a Poisson distribution. We have Pr(Y _i  = 0|p _i ) = exp(−s _i p _i ) in this case. Hence, we obtain the simpler expression for the sample size:

$$s_{i} = \left\lceil { - \log_{e} (\beta )/p_{\text{c}} } \right\rceil ,$$

(5)

which is independent of n _i . In other words, the sample size is constant irrespective of the size of consignment. We can alternatively obtain Eq. 5 by a limiting case of Eq. 3 or Eq. 4. The sample size in Eq. 5 is not smaller than those of Eqs. 3 and 4. We can easily find it by using the inequality, −log _e (1 − z) > z or 1 − exp (−z) < z, for a positive z. On the other hand, the quantity of Eq. 4 is not smaller than that of Eq. 2. Hence, the Poisson approximation is the most conservative approximation in this sense (Yamamura and Sugimoto 1995). The conditions for Poisson approximation are usually satisfied in most of the import quarantine inspections except for small consignments. Hence, the Poisson approximation (Eq. 5) was used in calculating the sample size in the Annex Table 1 of the import plant quarantine regulation enacted in 1992. If we use β = 0.05, that is, if we want to detect the infestation by a probability of 95 %, Eq. 5 is approximately given by 3/p _c. Hence, we can easily calculate the sample size by a mental calculation in this case. This rule is sometimes called ‘the rule of three’ (Jovanovic and Levy 1997; van Belle 2002; Iwasaki 2005). We may not always correctly identify an infested unit. If an infested unit is identified as ‘infested’ by the probability of 1 − φ, the quantity of p _c should be replaced by (1 − φ)p _c in Eqs. 3 and 5, while the quantity of n _i should be replaced by n _i /(1 − φ) in Eq. 4.

Choice of consumer’s risk (β)

Two parameters appear in our definition of risk: p _c and β. The choice of these parameters is important in preventing the invasion of alien pests with an appropriate level of phytosanitary protection (ALOP). A great deal of discussion went into choosing the quantity of consumer’s risk (β) when the import plant quarantine regulation was revised in 1992. Most industrial standards such as ISO and JIS traditionally use the consumer’s risk β = 0.10 while using the producer’s risk α = 0.05 (e.g., Japanese Industrial Standards Committee 1956a; ISO 2006b). The source of this tradition is not clearly known but Deming (1950, p266) described the source as follows: “someone must decide what probability-levels α and β are most economical in view of the costs of sampling and testing and the consequences of the two types of risk. As a result of broad practice, Dodge and Romig place β = 0.10 and settle upon practicable sample sizes and values of AOQL (vide infra) that will be suitable under various conditions, thus settling upon α indirectly.” Average outgoing quality (AOQ) is defined as the average proportion of infestation after the sampling inspection. The average outgoing quality limit (AOQL) is then defined as the maximum possible quantity of AOQ over all possible values of the proportion of infestation of incoming products (ISO 2006a). Dodge (1969) noted, in his own review, as follows: “in the extended discussions of possible choices, probability-of-acceptance values, or risk values of 20, 15, 10, and 5 % were actively considered. A decision was reached to use a value of 10 %, chances of only 1 in 10, and to speak of it as a ‘Consumer’s Risk’, a ‘10 % Consumer’s Risk’”. However, we considered that the sampling cost discussed by Dodge and Romig is not an important problem in the quarantine sampling because we must pay a huge cost eternally if a serious pest species invaded Japan.

In testing the scientific hypotheses, most scientists use the threshold of significance probability P = 0.05 in the Fisherian school or the Type I error rate α = 0.05 in the Neyman-Pearson school. (See Hubbard and Bayarri 2003, for the difference between P and α). This 0.05-criterion was first used by Fisher (1926, p 504). Fisher noted that a rich harvest that occurs only once per 20 years is a rare event, and hence he used the criterion of P = 1/20 = 0.05. Most people seem to share the same feeling as Fisher; we also consider that 20 years is a sufficiently long period. This may be because 20–30 years corresponds to a generation time of humans, i.e., the age of childbirth of females. One event per 20 years means one event per one generation, and hence most people may consider that the event will surely occur but will occur only rarely. Events related to a twenty-year period (or 30-year period) appear frequently in our customs. For example, the wooden building of the Ise Shrine, which is the Japanese central shrine, is rebuilt every 20 years. The main shrine is rebuilt every 20 years for the purpose of transmitting the technique of constructing shrines to the next generation. This tradition has lasted for 1300 years from 690 AD (Sakurai 2012). Climatic normal, which was adopted by the International Meteorological Organization in 1935, is calculated by the average climate value of the past 30 years. For all of these reasons, we considered that β = 0.05 would be acceptable for consumers, and hence we adopted β = 0.05, in principle, in revising the import plant quarantine regulation in 1992.

Choice of impermissible proportion of infested units (p _c)

We previously defined an undesirable event as the ‘introduction of a consignment of which the proportion of infested units is not smaller than p _c’. The amount of undesirability will change depending on the invasiveness of pests. Therefore, the critical proportion of infested units (p _c) should be changed, depending on the amount of invasiveness of each pest species. Ideally, we should specify the quantity of p _c for each of the pest species. However, the actual inspection subject of import plant inspection is not pests but plants or plant parts. Hence, we must specify p _c for plants or plant parts, not for pests, by considering the pests that potentially accompany the corresponding plants or plant parts. In the revision of the import plant quarantine regulation in 1992, we empirically divided the plants into 12 categories as shown in Table 2. Plants were first divided into two categories by the types of associated pests: field crop pests and stored product pests. In each category, the plants were further divided into categories, considering the invasiveness of associated pests. Then, the critical proportion of infested units (p _c) was specified as listed in Table 3. Plants for planting such as seeds are directly placed in fields. Hence, the pests on these plants have a higher possibility of spreading. Therefore, the quantities of p _c in categories 1 and 2 were set at smaller quantities than those in categories 3, 4, and 5. International standards for phytosanitary measures (ISPM No. 32) recently recommended a similar categorization that considers the intended use of the plants (IPPC 2009b).

Table 2 Classification of plants by the invasiveness of accompanying pests (a document in the public hearing on April 30, 1992)

Table 3 Parameters, p _c and β, used in the import quarantine inspection in Japan (a document in the public hearing on April 30, 1992)

The consumer’s risk is mostly set at β = 0.05 in Table 3 as stated above, but the categories I and II are the exceptions. In category I, all units are examined and hence β equals 0. In category II, β is set at 0.01 to be intermediate between the categories I and III. However, the quantity of p _c in category II is essentially 0.33 % when β = 0.05; the corresponding p _c for β = 0.05 is calculated by 0.50 % × log _e (0.05)/log _e (0.01) ≈ 0.33 % by using Eq. 5.

Definition of sampling unit and consignment

The required sample size was specified by its total weight instead of the total number of units for convenience of inspection in the import plant quarantine regulation, in principle. Then, we must define the sampling unit by its weight, before calculating the required weight for sampling. The appropriate weight of one unit will change, depending on the combination of the type of plant, potential pests, and the form of transportation. We can use one plant as one unit of sampling if the corresponding pest is transported within a plant independently. However, if the corresponding insects and diseases occupy several adjacent plants, the cluster of adjacent plants should be treated as one unit of sampling. It will be troublesome if we use different sampling units for different combinations of plants and pests. Hence, we empirically classified the plants into 14 categories as shown by Table 4. For each category of plants, we specified a weight that should be regarded as one unit of sampling. Several inconsistencies inevitably arise from this simplification. For example, raw fruits of kiwi fruit, blueberry, and gooseberry are classified into the same group, and 50 g is allocated as a common unit of sampling. However, the actual weight of a kiwi fruit is around 100 g. Hence, one kiwi fruit is treated as two samples in calculating the sample size. We will discuss the sampling of kiwi fruits minutely in a later section.

Table 4 Table to transform the sample size to weight (a document in the public hearing on April 30, 1992)

We must also appropriately define a consignment, which is usually called a ‘lot’ in industrial sampling. Ideally, a consignment should be divided if the consignment contains different kinds of items that have much different amounts of infestation. For example, let us imagine a situation where several kinds of items are included in a consignment and only one kind of item has an extraordinary large proportion of infestation. In this case, we will discard many non-infested units as well as the infested units as a consequence of sampling inspection. We can avoid such a loss by appropriately dividing the consignment (Freeman 1948, p 42). However, the total sample size increases if we use a smaller size of consignments. Hence, we should not use too small a consignment unless we can suspect that the proportion of infestation is highly heterogeneous.

We should note that the heterogeneity within a consignment does not affect the consumer’s risk. Several researchers are considering the notion that the hypergeometric distribution given by Eq. 1 is applicable only if there is no heterogeneity within the consignment. For example, IPPC (2008) noted that “Aggregation of infested units of a commodity will always lower the likelihood of finding an infestation”. However, this is an incorrect statement. If we perform a random sampling, the number of infested units in a sample always follows the hypergeometric distribution given by Eq. 1, even if the proportion of infested units is highly heterogeneous within a consignment. Problems arise only if we perform a non-random sampling such as ‘increment sampling’ instead of a random sampling. In increment sampling, we draw several units from the same position in a consignment instead of drawing all units at random from different positions in a consignment. A cluster of units drawn from the same position of a consignment is called an ‘increment’. As we will show in a later section, increment sampling has been used in the early detection procedure of plum pox virus (PPV). We will explain the influence of heterogeneity in increment sampling in a later section.

Optimal allocation of samples among consignments

We should control the consumer’s risk for each consignment, but the control of consumer’s risk is not sufficient in light of the purpose of import plant quarantine inspection of consignments. The ultimate purpose of import quarantine inspection is not to control the consumer’s risk of consignments but to prevent the introduction of alien pests from any consignment imported during a specified period. Unlike industrial sampling, the size of consignments greatly varies in quarantine sampling; it ranges from the small baggage of tourists to the open hatch of a large cargo ship. Equation 2 indicates that the sample size should be almost constant irrespective of the size of the consignment in order to control the consumer’s risk. The Poisson approximation (Eq. 5), which was actually used in calculating the sample sizes in 1992, does not include the size of the consignment. However, if infested units are accidentally overlooked in a larger consignment, a larger number of infested units enter Japan. Therefore, we should use a larger sample size for a larger consignment if we want to reduce the total number of pests introduced during a specified period.

The problem of the size of consignments was implicitly discussed also in ISO 2859-1, which derives from the US Military Standard, MIL-STD-105 (Department of Defense 1963; ISO 1999). The sample size in these standards increases with the increasing size of the lot. However, in ISO 2859-1, the sample size increases in an arbitrary manner with the increase in the consignment size; the sample size becomes 10^1/5 times larger when the rank of consignment size increases by 1. Thus, the sample size is simply given by ‘R5 preferred numbers’ (Japanese Industrial Standards Committee 1954). On the other hand, the sampling procedure in the international standards for phytosanitary measures (ISPM No. 31) also implied that the sample size should be large for a larger consignment (IPPC 2008). IPPC (2008) described the situation as follows: “The choice of a constant level of detection may result in a varying number of infested units entering with imported consignments because lot size varies (for example, a 1 % infestation level of 1000 units corresponds to 10 infested units, while a 1 % infestation level of 10,000 units corresponds to 100 infested units). Ideally, the selection of the level of detection will reflect in part the number of infested units entering all consignments within a particular period of time.” However, ISPM No. 31 provided no idea about how we should determine sample sizes for consignments of various sizes.

In revising the import plant quarantine regulation in 1992, we calculated the optimal allocation of samples, which minimizes the total number of infested units entering Japan (Yamamura and Sugimoto 1995). Let g be the number of consignments imported during a specified period. Let n _i and s _i be the size of the ith consignment and the sample size, respectively (i = 1, 2,…, g). We approximately describe the distribution of the proportion (x) of infested units at the export region by a gamma distribution, assuming that the quantity of x is sufficiently small.

$$f(x) = \frac{1}{\varGamma (k)}\lambda^{k} x^{k - 1} \exp ( - \lambda x) ,$$

(6)

where k is the shape parameter and λ is a scale parameter (k > 0, λ > 0). The expectation and variance of the proportion of infestation are given by $\bar{x}$ = k/λ and V(x) = k/λ ², respectively. If x and the proportion of sampling (s _i /n _i ) are both sufficiently small, the probability that the consignment passes the inspection is given by the zero term of the Poisson distribution: exp(−s _i x). The expected number of infested units in the remaining part of this passed consignment is given by (n _i  − s _i )x ≈ n _i x. Hence, the expected number of infested units that are introduced by this consignment is given by the multiplication: n _i x exp(−s _i x). Then, the expectation of the total number of infested units after the sampling inspection, which is denoted by T, is given by integrating n _i x exp(−s _i x) over x, and by summing it over all consignments.

$$T = \sum\limits_{i = 1}^{g} {\int\limits_{0}^{\infty } {n_{i} x\exp ( - s_{i} x)f(x){\text{d}}x} } ,$$

(7)

where f(x) indicates the distribution of x defined by Eq. 6. We can obtain the combination of s _i that minimizes the above quantity for a fixed amount of total sample size S, using the Lagrange multiplier method. We want to minimize T under a constraint of Σs _i  = S, and hence we consider a function M(s) = T − L(S − Σs _i ) where L is a Lagrange multiplier that is determined when we specify the total sample size S under a given set of n _i ; and s is a vector that consists of s _i . Then, the optimal s _i is given by the following form by calculating the solution for ∂M(s)/∂s _i  = 0.

$$s_{i} = \lambda \left( {\left( {\frac{{k(k + 1)n_{i} }}{{\lambda^{2} L}}} \right)^{{\frac{1}{k + 2}}} - 1} \right) .$$

(8)

Equation 8 indicates that we should increase the sample size with increasing the size of consignment by a power of n _i with an exponent 1/(k + 2). If the degree of heterogeneity in the proportion of infested units in the export area is small, we can simplify Eq. 8 as follows, by increasing k and λ to infinity while keeping the mean (k/λ) constant:

$$s_{i} = c + \log_{e} (n_{i} )/\bar{x} ,$$

(9)

where c = (log _e ($\bar{x}$ ²) − log _e (L))/$\bar{x}$. In this case, the optimal sample size linearly increases with increasing log _e (n _i ) by a slope 1/$\bar{x}$; the slope becomes large if the average proportion of infestation ($\bar{x}$) is small.

We encounter a kind of dilemma: we should use the sample size given by Eq. 2 to manage the risk that an infested consignment is imported, while we should use the sample size given by Eq. 8 to minimize the total number of infested units that are imported. Equation 2 indicates a nearly constant sample size irrespective of n _i while Eq. 8 indicates the sample size that increases by a power of n _i . We adopted a stepwise sampling curve as a compromise solution to this dilemma in revising the import plant quarantine regulation in 1992. We first empirically specified a standard size of consignment for each category of invasiveness as specified in the last column of Table 3. Then, the standard sample size was calculated by Eq. 5 using the quantity of p _c and β specified in Table 3. We divided the size of consignments into several ranks as shown in the example in Table 1. Then, we specified a different p _c for each rank of consignment; a smaller p _c was used for a consignment that belongs to a larger rank, while a larger p _c was used for a consignment that belongs to a smaller rank. Examples of different p _c values are shown in Table 1. Consequently, we obtained a larger sample size for a larger-size consignment by using Eq. 5 as shown in the last column of Table 1. Finally, we calculated the required weight of samples for each sample size (s) using the weight of sampling unit specified in Table 4.

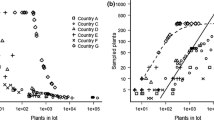
Figure 1 shows a comparison between the optimal allocation of sample size and the stepwise sample size specified by the import plant quarantine regulation for kiwi fruits. The invasiveness of kiwi fruits belongs to category VI in Table 2. In calculating the optimal allocation of samples given by Eq. 8, we used the parameters (k, λ, and n _i ) estimated by Yamamura and Sugimoto (1995). We considered the total number of samples to be Σs _i  = 100,000 to facilitate the comparison; the quantity of L was determined indirectly so that Σs _i becomes equal to 100,000. Figure 1 indicates that the overall slope of the specified stepwise sampling given by the bold line is close to that of the optimal allocation given by the dashed curve. A kiwi fruit is counted as two sampling units in Table 4, for the sake of simplicity in the categorization. In the import plant quarantine regulation, therefore, the sample size (s _i ) for a consignment of standard size is 2 × 300 = 600. Thus, the corresponding p _c is calculated by p _c = −log _e (β)/s _i  ≈ 3/600 = 0.50 % from Eq. 5. We can confirm that this quantity of p _c is equal to that listed in category VI of Table 3.

Fig. 1

Comparison between the optimal sample size and the sample size specified in the import plant quarantine regulation for kiwi fruits. Dashed curve indicates the optimal sample size calculated by Eq. 8 ($\hat{k}$ = 0.350, $\hat{\lambda }$ = 94.1). Bold line indicates the sample size in the import plant quarantine regulation enacted in 1992. Thin curves indicate the sample size calculated by Eq. 2. The corresponding p _c is shown in percent

For the smallest rank of consignment size, we cannot use the Poisson approximation (Eq. 5) because the proportion of sampled units (s _i /n _i ) becomes fairly large in this rank. We should use Eq. 2 in this rank. However, it is not practical for inspectors to use Eq. 2 directly. Therefore, we adopted a proportional sampling in which a specified proportion of units is sampled from each consignment. A proportional sampling is more easily applicable in the actual field of inspection in this case. We can perform the inspection by viewing the entire consignment if the size of the consignment is very small. Hence, we empirically judged that a proportional sampling would be permissible for the smallest rank of consignment. The example of proportional sampling appears in the first row in each plant category in Table 1.

Theory for early detection sampling

Hierarchical sampling recommended by NAPPO

Emergency control of Sharka disease caused by Plum pox virus (PPV, genus Potyvirus, family Potyviridae) is now in progress in several districts in Tokyo Metropolis, Aichi Prefecture, Osaka Prefecture, and Hyogo Prefecture. A sampling inspection is also performed in each of the 47 prefectures in Japan every year as an early detection procedure of PPV. Guidelines for phytosanitary action following detection of plum pox virus were published by the North American Plant Protection Organization (NAPPO 2004). In this document, NAPPO recommended a large-scale sampling plan as follows: “To determine if PPV is present in a large area such as a state or province, it is not necessary to survey the entire production range. A portion can be selected for survey by hierarchical sampling according to the procedures used by Hughes et al. (2002).” The procedures recommended in this document are as follows.

Let us consider the following hierarchical structure: each testing area (such a state, province, or prefecture) consists of many orchards, and each orchard consists of many plants. A prefecture is defined as an infected prefecture if the proportion of infected orchards in the prefecture is equal to or larger than q ₁, while an orchard is defined as an infected orchard if the proportion of infected plants in the orchard is equal to or larger than q ₂. We constructed a sampling scheme so that an infected prefecture was detected by a probability equal to or larger than 1 − γ. The parameter γ indicates the failure probability for the prefecture level, that is, the risk for the prefecture level. A prefecture corresponds to a consignment in the previous argument; our job is to manage the risk for the prefecture level. Let s ₁ be the number of orchards examined in a prefecture (primary sample size). Let s _2j be the number of plants examined in the jth orchard (secondary sample size). The secondary sample size s _2j is determined so that an infected orchard is detected by a probability equal to or larger than 1 − φ. The parameter φ indicates the failure probability for the orchard level, that is, the risk for the orchard level. We can calculate the secondary sample size s _2j by Eq. 2, where p _c and β are replaced by q ₂ and φ, respectively:

$$s_{2j} = \left\lceil {\left( {n_{2j} - \frac{{\left\lceil {n_{2j} q_{2} } \right\rceil - 1}}{2}} \right)\left( {1 - \varphi^{{1/\left( {\left\lceil {n_{2j} \,q_{2} } \right\rceil } \right)}} } \right)} \right\rceil ,$$

(10)

where n _2j is the number of plants in the jth orchard. In determining the primary sample size s ₁, Hughes et al. (2002) considered a situation where we can use the p-binomial approximation. In this approximation, we can consider that a sampled orchard in an infected prefecture is identified as an infected orchard by a probability equal to or larger than q ₁(1 − φ). Therefore, the required primary sample size s ₁ is given by Eq. 3 where p _c and β are replaced by q ₁(1 − φ) and γ, respectively.

$$s_{1} = \left\lceil {\frac{{\log_{e} (\gamma )}}{{\log_{e} (1 - q_{1} (1 - \varphi ))}}} \right\rceil .$$

(11)

When we perform early detection of pests, the proportion of infected orchards is usually very small, while the proportion of sampled orchards may become considerably large. In such cases, the f-binomial approximation is more appropriate than the p-binomial approximation. An infected orchard is sampled and judged as an infected orchard by a probability equal to or larger than (1 – φ)s ₁/n ₁, where n ₁ is the total number of orchards in the prefecture. Therefore, the required primary sample size s ₁ is given by a modification of Eq. 4:

$$s_{1} = \left\lceil {\frac{{n_{1} }}{1 - \varphi }(1 - \gamma^{{1/(\left\lceil {n_{1} q_{1} } \right\rceil )}} )} \right\rceil .$$

(12)

Early detection of plum pox virus in Japan

We can easily calculate the required primary sample size (s ₁) and secondary sample size (s _2i ) by using Eqs. 12 and 10, respectively, for a given set of risks, γ and φ, that is, for a given combination of the risk for the prefecture level (γ) and the risk for the orchard level (φ). However, we do not have enough empirical knowledge in determining the appropriate quantities of γ and φ. Therefore, we did not adopt the method of Hughes et al. (2002) in constructing the sampling inspection for the early detection of PPV in Japan. We instead used the same principle of risk management that we used in the import plant quarantine inspection of consignments. We defined an undesirable event as the ‘failure to detect infection in a prefecture in which the proportion of infected plants is not less than p _c’. We determined a sampling inspection so that the consumer’s risk would be no larger than β = 0.05.

The secondary sample of the size s _2j is drawn from the same position; we drew s _2j plants from the jth orchards instead of drawing them at random from the whole prefecture. This type of hierarchical sampling is essentially a kind of ‘increment sampling’ in which the size of the increment is s _2j . We described the spatial distribution of the proportion (p) of infected plants in a prefecture by a gamma distribution,

$$h(p) = \frac{1}{\varGamma (\kappa )}\eta^{\kappa } p^{\kappa - 1} \exp ( - \eta p) ,$$

(13)

where κ and η are constants. Equation 13 corresponds to the variability within a consignment. This should not be confused with Eq. 6, which describes the variability between consignments. Let x be the overall proportion of infected plants in a prefecture, given by x = κ/η. We again use a Poisson approximation in describing the number of infected plants in the sample obtained from an orchard. We assume that the secondary sample size is the same for all orchards for the sake of simplicity: s _2j  = s ₂ for all j. Let Y _j be the number of infected plants in the sample obtained from the jth orchard. Then, the distribution of Y _j is given by the following negative binomial distribution (Yamamura and Sugimoto 1995):

$$\Pr (Y_{j} = y) = \frac{\varGamma (\kappa + y)}{y!\varGamma (\kappa )}\left( {1 + \frac{{s_{2} }}{\eta }} \right)^{ - \kappa } \left( {\frac{{s_{2} }}{{\eta + s_{2} }}} \right)^{y} .$$

(14)

To control the consumer’s risk for a given set of κ and η, we must have $(\Pr (Y_{j} = 0))^{{s_{1} }}$ ≤ β. Then, the required number (s ₁) of sampled orchards for a given set of κ and η is given by the rearrangement of $(\Pr (Y_{j} = 0))^{{s_{1} }}$ = β.

$$s_{1} = \frac{{ - \log_{e} (\beta )}}{{\kappa \log_{e} \left( {1 + \frac{{s_{2} }}{\eta }} \right)}} ,$$

(15)

where we omitted the ceiling function for simplicity. The average proportion of infected plants, κ/η, is very small; i.e., κ is much smaller than η. Hence, we can replace η in the denominator by κ + η. IPPC (2008) indicated that this modified version of Eq. 15 should be used if we adopt cluster sampling, instead of random sampling, when the spatial distribution of pests is heterogeneous within a consignment.

We must satisfy $(\Pr (Y_{j} = 0))^{{s_{1} }}$ ≤ β for all existing combinations of κ and η that satisfy x ≥ p _c. Yamamura and Ishimoto (2009) proposed a practical solution for this calculation. The variance of p usually increases with increasing its mean (x). We can frequently express the variance of p by a power form, V(p) = ax ^b, where a and b are constants. This relation is called Taylor’s power law after Taylor (1961). Then, we have κ = p ^2−b_c /a and η = p ^1−b_c /a at x = p _c by the definition of Eq. 13. By substituting κ and η in Eq. 15, we obtain the following equation:

$$s_{1} = \frac{{ - ap_{\text{c}}^{b - 2} \log_{e} (\beta )}}{{\log_{e} (1 + ap_{\text{c}}^{b - 1} s_{2} )}} .$$

(16)

This sample size satisfies $(\Pr (Y_{j} = 0))^{{s_{1} }}$ ≤ β for all combinations of κ and η that satisfy x ≥ p _c if at least 1 < b < 2 (Yamamura and Ishimoto 2009). Figure 2 indicates the combinations of s ₁ and s ₂ that satisfy Eq. 16 for four levels of the impermissible proportion of infected plants (p _c = 0.15, 0.33, 0.50, and 1.00 %) that are used in import plant quarantine inspections in Japan (Table 3). We have a trade-off between s ₁ and s ₂; we can decrease the number of orchards sampled from a prefecture (s ₁) if we can increase the number of plants sampled in each orchard (s ₂). An infected plant may not be always correctly identified as an infected plant. If an infected plant is identified as infected by a probability of 1 − θ independently, we can obtain the required primary sample size by replacing s ₂ in Eq. 16 by s ₂(1 − θ).

Fig. 2

Combination of s ₁ and s ₂ (i.e., the number of sampled orchards in a prefecture and the number of sampled plants in an orchard) that is required for achieving the specified risk management in the early detection procedure of plum pox virus (PPV). Combinations are shown for four levels of the critical proportion of infestation (p _c = 0.15, 0.33, 0.50, and 1.00 %) that are adopted in the import plant quarantine inspection (Table 3). The consumer’s risk was set at β = 0.05. Dashed line indicates the quantity of s ₂ empirically determined (s ₂ = 45)

We must estimate two parameters (a and b) for using Eq. 16. We obtained estimates of parameters for the early detection of PPV from the preliminary examination: $\hat{a} = 39$ and $\hat{b} = 2$. The impermissible proportion of infected plants was set at p _c = 0.15 % that corresponds to the smallest quantity of p _c in the import plant quarantine inspection in Japan. The quantity of the number of sampled plants in an orchard was empirically determined as s ₂ = 45. Then, we obtained the required number of sampled orchards as s ₁ ≈ 90 from Eq. 16 as shown in Fig. 2. We roughly considered that the latent period required for the detection of PPV is about 3 years; an infected plant becomes visually detectable after 3 years. Therefore, we decided to perform the inspection every 3 years; the proportion of infected plants at the beginning year of inspection is controlled by the inspection of the next period. Actually, 30 orchards are examined every year to achieve 90 samples in one period of inspection. The total number of sampled plants is 45 × 90 = 4050. If we could perform a random sampling, the required number of sampled plants given by Eq. 5 is −log _e (0.05)/(0.15 %) = 1997. Thus, the total sample size in this increment sampling is about twice larger than that in a random sampling. This increase in sample size emerges from the heterogeneity among orchards within a prefecture. As was shown by Yamamura and Ishimoto (2009), the total sample size required for an increment sampling (Eq. 16) becomes equal to the sample size required for a random sampling (Eq. 5) if there is no heterogeneity within a prefecture.

We further adopted an adaptive management such as that used in ISO-2859-1 (ISO 1999) or MIL-STD-1916 (Department of Defense 1996). If no infected plants are detected in one period of inspection, we relax the protection level from p _c = 0.15 % to p _c = 0.33 %. Then, the required number of sampled orchards becomes 60 as shown in Fig. 2; hence, 20 orchards are examined every year to achieve 60 samples in one period of inspection of 3 years. An early detection procedure for PPV has been executed every year in each of the 47 prefectures in Japan using this system of hierarchical sampling.

Theory for emergency control in Japan

Spatial structure of emergency control

We conduct emergency controls to eradicate invading serious pests whenever they are found locally inside Japan. We construct two kinds of ranges, in principle, around the point where the pest was found (Fig. 3). First, there is the range within which the pest is completely eradicated by incinerating all related hosts or by completely spraying the hosts (Range A). Then, there is a range within which the movement of all related hosts is prohibited (Range B). Range A corresponds to the range of one colony of pests, while range B corresponds to the range that may contain other sources of colonies.

Fig. 3

Schematic illustration of the spatial structure of the emergency control. Upper panel indicates the horizontal view of the probability density of the pest existence. Lower panel indicates the vertical view of the probability density of the pest existence. Range A indicates the area having high probability density that derives from a known source of infestation. Range B corresponds to the area that is subject to the independent introduction of infested plants by human. The long tail of distribution of known colonies is also included in range B. If a new colony was found in the range B, we construct another range A surrounding the point of discovery of new colony

Successful emergency control results in the eradication of the pest in the local area. IPPC (1998) described that “When an eradication programme is completed, the absence of the pest must be verified. The verification procedure should use criteria established at the beginning of the programme and should be supported by adequate documentation of programme activities and results.” We again perform a risk management at this stage to verify the eradication. We must define two components of our risk management: an undesirable event, and the probability of its occurrence. By definition, eradication indicates a situation in which no infested plant exists in the entire field. Therefore, we define an undesirable event as a situation where ‘we do not detect the infestation when one or more infested plants exist in range B’. We again use the consumer’s risk β = 0.05 for the probability of occurrence.

Let us first consider the detection of plant diseases. It is quite difficult for us to detect infected plants directly if the proportion of infected plants is very small. Hence, we adopt an ‘incubation principle’ in detecting an infected plant from the field; we detect the disease after incubating it in the field instead of in the laboratory. We assume that an infected plant acquires infectiveness 1 year after the infection. We further assume that the infection becomes visually detectable for us d years after the infection, where d is the latent period for detection. Let R ₀ be the basic reproduction rate of infected plants per year; the number of infected plants becomes R ₀ times larger deterministically after a year if the infected plants are sufficiently sparse. If one or more plants are newly infected at 0 year or at a prior year, the number of infected plants becomes at least $R_{0}^{t}$ at t year. These plants become detectable at t + d years. Hence, the number of infected plants detectable at time t is at least $R_{0}^{t - d}$ for t ≥ d. Therefore, we should use the sample size to detect the $R_{0}^{t - d}$ plants by a probability (1 − β). We are detecting a very small proportion of infected plants (nearly zero) by sampling a considerably large proportion of plants, and hence we can use f-binomial approximation. Then, the required proportion of sampled plants f (=s/n) in the range B is given by replacing n _i p _c in Eq. 4 by $R_{0}^{t - d}$. If we omit the ceiling function for simplicity, we have

$$f = 1 - \beta^{{R_{0}^{d - t} }} .$$

(17)

If no infected plant is included in the sample, we can declare that the disease was successfully eradicated. We can modify Eq. 17 in various ways. For example, if N infected plants exist at t = 0, and if we conduct the sampling inspection of fraction f every year for w years from t = d, the probability that no infected plant is observed is not smaller than (1 − f)^N $(1 - f)^{{R_{0} N}} (1 - f)^{{R_{0}^{2} N}} \ldots (1 - f)^{{R_{0}^{(w - 1)} N}}$. Hence, the required proportion of sample to detect the infected plants by a probability (1 − β) is given by

$$f = 1 - \beta^{{\frac{{R_{0} - 1}}{{N(R_{0}^{w} - 1)}}}}$$

(18)

A similar formula is applicable for insect pests. Let us consider that the space consists of n quadrats. Let μ be the total number of insect pests in the space. The proportion (p) of quadrats occupied by insect pests can be described by the power of the mean density (μ/n) in most cases.

$$- \log_{e} (1 - p) = \omega (\mu /n)^{\rho } ,$$

(19)

where ω and ρ are constants. This empirical rule is called the Kono–Sugino equation after Kono and Sugino (1958); the rule was later rediscovered independently by other authors (Gerrard and Chiang 1970; Nachman 1984). The theoretical foundation of the rule was given by Yamamura (2000). If one reproductive insect exists at 0 years, the number of insects (μ) will become $R_{0}^{t}$ at t years by geometric growth under low density, where R ₀ is the basic reproduction rate defined in a manner similar to that for the plant disease. We have the relation −log _e (1 − p) ≈ p when p is small. Hence, Eq. 19 yields the following relation at t years:

$$p = \omega n^{ - \rho } R_{0}^{\rho t} .$$

(20)

Hence, the required proportion of the sampling survey f (=s/n) for confirming the eradication of insect pests is given by replacing p _c in Eq. 4 with $\omega n^{ - \rho } R_{0}^{\rho t}$. If we omit the ceiling function for simplicity, we obtain

$$f = 1 - \beta^{{1/(\omega n^{1 - \rho } R_{0}^{\rho t} )}} .$$

(21)

We must estimate three parameters, ω, ρ, and R ₀, to calculate the required proportion of the survey. Equation 19 assumes a linear form by the complementary log–log transformation about p: log _e (−log _e (1 − p)) = log _e (ω) + ρlog _e (μ/n). Hence we can estimate the parameters, ω and ρ, using linear regression from field data.

Emergency control of citrus huanglongbing

We briefly explain an actual example of successful eradication of citrus huanglongbing (HLB; citrus greening disease) by an emergency control. Huanglongbing is the most destructive citrus pathosystem worldwide (Gottwald 2010). This disease is caused by the bacteria Candidatus Liberibacter asiaticus, transmitted by the Asian citrus psyllid, Diaphorina citri Kuwayama. The latent period for detection is about d = 2 years (Gottwald 2010). We estimated R ₀ from the data in Gottwald et al. (1989). Figure 4 shows the progress of the disease incidence in the following three experimental plots: the Liuzhou Citrus Farm plot (LCF) that was established in October 1953, the Liuzhou Agricultural Research Institute plot (LARI) that was established in 1968, and the Reunion Island plot (RI) that was established in 1970. The former two plots were respectively located 20 and 22 km from Liuzhou City, Guangxi Province, People’s Republic of China. We assumed the logistic growth of the proportion of infected plants for convenience. We considered that the rate of infection would suffer a multiplicative error. Thus, we used a linear regression for the logit transformed rate of infection to estimate R ₀. The estimated R ₀ for LCF, LARI, and RI were 14.58, 6.50, and 2.68, respectively. Minimal insect control programs were practiced in two plots in China (LCF and LARI), while an insecticide program was practiced in the Reunion plot (RI) although psyllids were not a primary target insect. Therefore, we considered that the condition in RI is closest to that of Japan, and we adopted R ₀ = 3. Figure 5 indicates the required proportion of the sample (f) that is calculated by substituting d = 2, R ₀ = 3, and β = 0.05 into Eq. 17. We must examine 95 % of plants if we want to declare the eradication just after the latent period of detection; it is logically clear because we are using the consumer’s risk β = 0.05. However, it is practically impossible to examine 95 % plants in most cases. The required proportion of the sample decreases as the period of incubation lengthens. On the other hand, the cost required for emergency control increases as the period of incubation lengthens. Practically speaking, therefore, an optimal length for the period of incubation exists and needs to be determined.

Fig. 4

Estimation of R ₀ of huanglongbing disease from the curve of disease progress. Data from Gottwald et al. (1989). Open circles indicate the Liuzhou Citrus Farm plot (LCF). Open triangles indicate the Liuzhou Agricultural Research Institute plot (LARI). Closed circles indicate the Reunion Island plot (RI). Curves show the estimated logistic growth. The estimates of R ₀ are as follows. LCF: 14.58, LARI: 6.50, and RI: 2.68

Fig. 5

Required proportion of sample (f) to declare the eradication in the emergency control of huanglongbing disease. Open circle indicates the proportion of sampling that was actually adopted in the emergency control in Kikai Island in 2012. We cannot declare the eradication within the latent period of detection (2 years)

In Kikai Island (28°19′N, 129°56′E) in Kagoshima Prefecture, the disease was first found in 2003 (Shinohara et al. 2009). Emergency control was started in 2007. The range within a 500-m distance from an infected plant was defined as range A, while the remaining area of the entire island (56.87 km²) was defined as range B. The final infected plant was found in 2007. Then, the Moji Plant Protection Office executed a sampling inspection to confirm the eradication of disease in 2011. The duration from the last detection of disease to the sampling inspection to confirm the eradication was t = 2011–2007 = 4 years. Then, by substituting t = 4, d = 2, R ₀ = 3, and β = 0.05 into Eq. 17, we obtained the required proportion of samples f = 0.29. The total number of citrus host plants within range B was 36,975. Hence, the number of plants that should be examined by eye was calculated as 36,975 × 0.29 = 10,723 plants. Then, 12,521 plants were examined actually within range B by the Moji Plant Protection Office. Several suspected plants were further examined by real-time PCR and the conventional PCR method. No infected plant was detected by this sampling inspection. Therefore, the eradication of disease was declared by the Ministry of Agriculture, Forestry and Fisheries in March, 2012 (Kagoshima Prefecture 2012).

Systematic sampling to confirm the eradication

In confirming the eradication of citrus huanglongbing in Kikai Island, we used a systematic sampling instead of random sampling for the following practical reasons. Let n and s be the total number of plants and the sample size, respectively. In performing a systematic sampling, we examine the plants at a constant spatial interval along a route that covers the entire area of island excluding range A. The infected plants will exist in adjacent positions in most cases. Hence, we assumed the simplest deterministic case where τ infected plants exist in the adjacent position along the route of the systematic sampling. We consider a case where n/s is given by an integer, for simplicity. In this case of systematic sampling, we adopt one series of samples from the n/s series of samples at random; each series consists of s plants that are spaced by n/s intervals. If τ ≥ n/s, we can detect the infected plants by a probability of 100 %, because all n/s series of samples contain one or more infected plants. If τ < n/s, the probability of detection is τ/(n/s), because τ series of samples among the n/s series of samples contain infected plants. On the other hand, if we perform random sampling, the probability of detection is always 1 − (1 − (s/n))^τ, because we can use the f-binomial approximation (Eq. 4) in this case. We can show the inequality, τ/(n/s) ≥ 1 − (1 − (s/n))^τ, by using the binomial expansion if τ < n/s. Thus, systematic sampling yields a larger probability of detection than simple random sampling. Furthermore, the systematic sample is much less laborious than the random sampling, for which we must use random numbers in selecting each plant for inspection. For these reasons, we adopted systematic sampling to confirm the eradication of citrus huanglongbing on Kikai Island.

The probability of detection in a systematic sampling is thus larger than that in the corresponding random sampling if the spatial distribution of the disease is highly aggregated, but we should bear in mind the exception. If the probability of infection cyclically fluctuates along the route of systematic sampling and if this cycle exactly coincides with the cycle of the systematic sampling, the probability of detection may become lower than that of random sampling. If we want to avoid such kinds of inefficiency, we should use stratified random sampling, in which random sampling is performed in each stratum. Let us divide the field into ψ strata of equal size. Let p _j be the probability of infection in the jth stratum, and υ be the sample size in each stratum: υψ = s. We now consider that a plant in the jth stratum is independently infected by a probability p _j for convenience. Thus, we use the p-binomial approximation. The probability that no infected plant is found in the jth stratum is given by (1 − p _j )^υ. Hence, the probability of detection in the stratified random sampling is given by 1 − Π ^ψ _j=1 [(1 − p _j )^υ]. It is exactly expressed by 1 − (geometric mean of 1 − p _j )^s. On the other hand, if we perform simple random sampling, the probability of detection is exactly given by 1 − (arithmetic mean of 1 − p _j )^s. The geometric mean of 1 − p _j is smaller than the arithmetic mean of 1 − p _j unless all 1 − p _j values are the same. Therefore, stratified random sampling yields a larger probability of detection than simple random sampling if there is heterogeneity in the probability of infection. Stratified random sampling includes the characteristics of the two sampling procedures: the simple random sampling and the systematic sampling. Hence, the labor required for the stratified random sampling will be intermediate between those of simple random sampling and systematic sampling.

Discussion

We showed actual examples of the three components in the import plant quarantine systems in Japan: (1) sampling inspection of consignments at the port, (2) early detection by hierarchical sampling executed in every prefecture, and (3) emergency control to eradicate alien invasive pests. The classical definition of risk is used for the risk management in these procedures; it is defined as the probability of an undesirable event occurring. As for the probability of the occurrence i.e., the consumer’s risk, β = 0.05 is consistently used in most procedures in the quarantine procedures in Japan. The definition of the undesirable event differs depending on the invasiveness of the pest species. An appropriate evaluation of the invasiveness is important in protecting against its invasion.

The direct estimation of the probability of invasion requires complicated calculations such as indicated by Yamamura and Katsumata (1999a), and hence the import quarantine inspection is usually designed for controlling the proportion of sampling units infested by pests, instead of directly controlling the probability of invasion. The control criteria in the import quarantine inspection adopted by several countries can be roughly classified into two types: (1) control of the proportion of infestation of each consignment and (2) control of the proportion of infestation including all consignments. These criteria can be called ‘probability criterion’ and ‘average criterion’, respectively (Yamamura and Sugimoto 1995).

Most organizations are using the sampling inspection that controls the proportion of infestation of each consignment, that is, the sampling inspection of the first type. An example of the first type of inspection is seen in the National Agriculture Release Program (NARP) of the United States. The Bureau of Customs and Border Protection (CBP) implemented the NARP in 2007. It is a system that identifies high-volume agricultural imports known historically to be low-risk for the introduction of exotic plant pests and plant diseases into the United States. The hypergeometric sampling method is used to detect a 10 % actionable or reportable pest infestation rate with a 95 % confidence level for the importation of fresh fruits and vegetables (USDA 2010). The required sample size specified in their table can be calculated by Eq. 2 with p _c = 10 % and β = 0.05. The same table is also used in Agriculture Quarantine Inspection Monitoring (AQIM) Handbook (USDA 2011). Ministry of Agriculture and Forestry in New Zealand also used the first type of inspection in their standard 155.02.06 about the importation of nursery stock (Ministry of Agriculture and Forestry 2010). The standard specifies that “Infestation by visually detectable quarantine pests on inspection at the border must not exceed the Maximum Pest Limit (MPL) which is currently set at 0.50 %. To achieve a 95 % level of confidence that the MPL will not be exceeded, no infested units are permitted in a randomly drawn sample of 600 units (i.e., acceptance number = 0)”. Thus, the sample size was calculated by Eq. 5 with p _c = 0.50 % and β = 0.05.

Australian Centre of Excellence for Risk Analysis recommended the sampling inspection that controls the proportion of infestation including all consignments (Robinson et al. 2013), that is, the sampling inspection of the second type. Post-Intervention Compliance (PIC) was used as the indicator of performance, where PIC is defined as “the percentage of the units that arrive on the pathway that are compliant with quarantine regulations after quarantine intervention” (Robinson et al. 2011). They performed simulations in which the consignments are examined by using the Continuous Sampling Plans (CSP); CSP was originally developed for a situation where the series of units are not divided into lots (Dodge 1943; Dodge and Torrey 1951). Then, they recommended a plan called CSP-3 that has PIC >99.8 % in the inspection of dried and fresh dates; they recommended a sampling plan in which the proportion of infestation is smaller than 0.2 % after the inspection.

The Japanese import plant quarantine inspection is considered to belong to the third type of inspection because the inspection was designed to control both proportions: the proportion of infestation of each consignment and the proportion of infestation including all consignments. The basic level of phytosanitary protection for each consignment is explicitly specified in Tables 2, 3, and 4. Then, the p _c value was shifted from the basic level by a stepwise manner depending on the size of consignment. An example of shift is shown by the bold line in Fig. 1. Such a stepwise sampling effectively reduces the proportion of infestation including all consignments, as indicated by the optimal solution given by Eq. 8.

An important problem still remains to be solved; we cannot explicitly control the proportion of infestation including all consignments after the inspection if we do not know the distribution of the proportion of infestation before the inspection, that is, if we do not know f(x) in Eqs. 6 and 7. The proportion of infestation including all consignments after the inspection corresponds to the ‘average outgoing quality (AOQ)’ in industrial sampling (Dodge 1969). Under the absence of the knowledge about the proportion of infestation before the inspection, we should further consider the maximum possible quantity of the proportion of infestation after the inspection, which corresponds to the ‘average outgoing quality limit (AOQL)’ in industrial sampling (Dodge 1969). The probability of acceptance of a consignment is given by exp(−sx) if we can use the Poisson approximation, where s is the sample size and x is the proportion of infestation. If all units are disinfested when the consignment is rejected, the average proportion of infestation after the inspection is approximately given by x exp(−sx) if the proportion of sample is small. This quantity becomes the maximum at x = 1/s; the AOQL for a fixed sample size (s) is given by exp(−1)/s. The substitution of Eq. 5 indicates that AOQL for a fixed sample size is −p _c exp(−1)/log _e (β). If we use β = 0.05, therefore, AOQL for the fixed sample size is given by 0.12 p _c. As for the sampling inspection of kiwi fruits, for example, we can calculate the AOQL for each sample size, by multiplying p _c by 0.12 in Fig. 1; e.g., the AOQL is 0.06 % for a consignment that belongs to the largest class of size. AOQL including all consignments is given by the weighted sum of AOQL over all consignments: AOQL = $\left( {\sum\nolimits_{i = 1}^{g} {n_{i} \exp \left( { - 1} \right)/s_{i} } } \right)/ \sum\nolimits_{i = 1}^{g} {n_{i} }$, where n _i is the size of the ith consignment; g is the number of consignments imported during a specified period. By using a similar argument that was used to derive Eq. 8, we can find that we should change the sample size in proportion to the square root of the consignment size ($\sqrt {n_{i} }$) to minimize AOQL.

We may be able to estimate the possible maximum probability of invasion approximately by using AOQL. We can assure that the proportion of infestation including all consignments after the inspection never become larger than AOQL irrespective of the proportion of infestation at the export area. Let ζ be the probability of successful invasion of pests via one infested unit that passed the inspection. Let n be the total number of units imported per year. If ζn × AOQL is very small, ζn × AOQL will be nearly equal to the maximum possible probability of successful invasion, because the expectation of the number of occurrence is nearly equal to the probability of occurrence if the occurrence of events is extremely rare (Yamamura et al. 2001).

An appropriate index is crucially important in evaluating the invasiveness of pests. The probability of invasion may not be a useful index in determining the required level of quarantine inspection even if we could precisely estimate the probability of invasion, because the probability of invasion becomes close to 1 after a very long period of importation even if the probability of invasion per year is sufficiently small. Expected time required for invasion (ETI) may be more useful at this point. ETI is given as 1/R, where R is the probability of invasion per year (Yamamura et al. 2001). Kiritani and Yamamura (2003) assumed that the permissible expected time required for invasion is ETI = 1000 years, as an example, by considering the time scale of human nations. Then, they calculated the required strength of sampling inspection and disinfestation treatment to achieve ETI = 1000 years, against the invasion of Mexican fruit fly via citrus fruits. The problem of multiple pests should be also considered in determining the appropriate index for invasiveness. For example, apples can be potentially accompanied by codling moth and fire blight disease. Yamamura and Katsumata (1999b) and Yamamura et al. (2001) separately discussed the method of protection against codling moth and fire blight, respectively. Currently, we do not have an appropriate index to evaluate the joint risk of multiple pests including both the codling moth and fire blight. A weighted sum of risks, with an appropriate weight depending on the importance of pests, might be one of the practical indices to evaluate the joint risk. We should further accumulate the information for estimating the probability (ζ) of successful invasion of pests via one infested unit that passed the inspection. Then, we may be able to determine the appropriate level of phytosanitary protection (ALOP) by using ETI calculated from 1/(ζn × AOQ) or 1/(ζn × AOQL).

Appendix: Derivation of the required sample size (Eq. 2) for the hypergeometric distribution

Let p be the proportion of infested units in a consignment of a size n. Let s be the number of units drawn from the consignment at random. Let Y be the number of infested units in the sample. The probability that the sample contains no infested units for a given p is given by the zero-term of a hypergeometric distribution.

$$\Pr (\left. {Y = 0} \right|p) = \frac{{\left( {\begin{array}{*{20}c} {np} \\ 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {n - np} \\ s \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)}} = \frac{(n - np)!(n - s)!}{n!(n - s - np)!} .$$

(22)

We can rearrange the equation to yield Eq. 23 which is given by the multiplication of np components.

$$\begin{aligned} \Pr ( {Y = 0} |p) &= \frac{(n - np)!}{n!} \cdot \frac{(n - s)!}{(n - s - np)!} \\ &= \frac{1}{n(n - 1)(n - 2)\ldots(n - np + 1)}\frac{(n - s)(n - s - 1)(n - s - 2)\ldots(n - s - np + 1)}{1} \\ &= \left( {1 - \frac{s}{n}} \right)\left( {1 - \frac{s}{n - 1}} \right)\left( {1 - \frac{s}{n - 2}} \right)\ldots \left( {1 - \frac{s}{n - np + 1}} \right) \end{aligned}$$

(23)

We can interpret this expression by an intuitive manner. Let us attach a number on each infested unit sequentially. The first parenthesis in the right-hand side of Eq. 23 indicates the probability that the first infested unit is not included in the sample. The second parenthesis indicates the probability that the second infested unit is not included in the sample under the condition that the first infested unit is not included in the sample. The third parenthesis indicates the probability that the third infested unit is not included in the sample under the condition that the first and the second infested units are not included in the sample. Thus, Eq. 23 indicates the probability that none of the np units is included in the sample. The rearrangement in Eq. 23 may be called the f-binomial type rearrangement, because it is given by $\prod_{i = 1}^{np} \left( { 1 - f_{i} } \right)$, where f _i is the frequency of sample at the ith infested unit. If we replace the denominator in each parenthesis by the mean between the first denominator n and the last denominator n − (np − 1), the quantity becomes larger than or equal to the original quantity, because log _e (1 − (s/n)) is an upward-convex function of n, that is, the second derivative of log _e (1 − (s/n)) about n is negative. Thus, we obtain the following inequality.

$$\Pr (\left. {Y = 0} \right|p) \le \left( {1 - \frac{s}{{n - \frac{np - 1}{2}}}} \right)^{np} .$$

(24)

The equality holds if np = 1. We want to regulate the probability as Pr(Y = 0|p) ≤ β. Hence, we equate the right-hand side of inequality 24 to β. Then, the rearrangement yields the following sample size.

$$s = \left( {n - \frac{np - 1}{2}} \right)\left( {1 - \beta^{1/(np)} } \right) .$$

(25)

The actual number of infested units is an integer; a consignment is defined as an infested consignment if the number of infested units is equal to or larger than $\left\lceil {np} \right\rceil$, where $\lceil \; \rceil$ indicates the ceiling function. Hence we should express the equation by

$$s = \left\lceil {\left( {n - \frac{{\left\lceil {np} \right\rceil - 1}}{2}} \right)\left( {1 - \beta^{{1/(\left\lceil {np} \right\rceil )}} } \right)} \right\rceil .$$

(26)

The lot infested by the proportion p is not permitted in our risk management but it is permitted in ISO 2859-0. Hence Eq. 26 is slightly different from the corresponding formula given in ISO 2859-0 (ISO 1995, p 12).

In contrast to the f-binomial type rearrangement given by Eq. 23, we can alternatively consider another rearrangement which is given by Eq. 27.

$$\begin{aligned} \Pr ({Y = 0}|p) &= \frac{(n - s)!}{n!} \cdot \frac{(n - np)!}{(n - s - np)!} \\ &= \frac{1}{n(n - 1)(n - 2)\ldots (n - s + 1)}\frac{(n - np)(n - np - 1)(n - np - 2)\ldots (n - np - s + 1)}{1} \\ &= \left( {1 - \frac{np}{n}} \right)\left( {1 - \frac{np}{n - 1}} \right)\left( {1 - \frac{np}{n - 2}} \right)\ldots \left( {1 - \frac{np}{n - s + 1}} \right) \end{aligned}$$

(27)

This rearrangement may be called the p-binomial type rearrangement, because it is given by $\prod_{i = 1}^{s} \left( { 1 - p_{i} } \right)$, where p _i is the proportion of infested units at the ith sampled unit. Then, we obtain the inequality by a similar manner as Eq. 24.

$$\Pr (\left. {Y = 0} \right|p) \le \left( {1 - \frac{np}{{n - \frac{s - 1}{2}}}} \right)^{s}$$

(28)

This form of approximation was introduced by Cochran (1977) and later introduced by ISPM No. 31 (IPPC 2008). The approximation by the right-hand side of Eq. 28 is superior to that of Eq. 24 if the sample size is smaller than the number of infested units, i.e., if s < np. However, Eq. 28 seems not as useful as Eq. 24, because the sample size (s) is not given by an explicit form in Eq. 28.