Missing value estimation for microarray data through cluster analysis

Abstract

Microarray datasets with missing values need to impute accurately before analyzing diseases. The proposed method first discretizes the samples and temporarily assigns a value in missing position of a gene by the mean value of all samples in the same class. The frequencies of each gene value in both types of samples for all genes are calculated separately and if the maximum frequency occurs for same expression value in both types, then the whole gene is entered into a subset; otherwise, each portion of the gene of respective sample type (i.e., normal or disease) is entered into two separate subsets. Thus, for each gene expression value, maximum three different clusters of genes are formed. Each gene subset is further partitioned into a stable number of clusters using proposed splitting and merging clustering algorithm that overcomes the weakness of Euclidian distance metric used in high-dimensional space. Finally, similarity between a gene with missing values and centroids of the clusters are measured and the missing values are estimated by corresponding expression values of a centroid having maximum similarity. The method is compared with various statistical, cluster-based and regression-based methods with respect to statistical and biological metrics using microarray datasets to measure its effectiveness.

1 Introduction

DNA microarray techniques give an overall outlook of gene expression, observing the mRNA levels of thousands or more number of genes. Microarray dataset [7, 15] is basically a large matrix of expression levels of observations or genes under different experimental conditions or samples. The datasets generally contain missing values in time of preparation, such as dust or spotting or scratches on the slide, insufficient resolution, hybridization failures and image corruption [25]. But a good number of algorithms for gene dataset analysis take a complete dataset as input. Therefore, more accurate prediction of missing values is an important preprocessing step to form complete dataset and perform further experiments. Approximately 5% or more cell values of the matrix can often be missing unless extreme care is taken by the organization [36, 44].

1.1 Literature review

The researchers propose several methods [8, 24, 48, 49] to deal with missing values. The expensive and more time-consuming method presents in [5], where the original experiment is repeated until dataset without missing values is obtained. On the other hand, the method in [1] ignores missing value-related genes, which usually loses useful information and may bias the result if the remaining genes not capable to present the complete dataset. Some methods [1, 38] impute the missing values by a constant such as zero (0), or by the mean of the available sample values, which distort correlations among expression values. Another method [17] considers the relationships among gene expression values. It first measures the similarity between a gene with missing value and genes without missing values before predicting the missing values of the gene by observed values of the most similar genes. In the papers [19, 41], a missing value estimation method called singular value decomposition imputation (SVD-impute) is reported where missing values are estimated by identifying the K most significant Eigen genes. The paper [41] proposes a method called weighted KNN-impute that constructs the missing values using a weighted average of K most similar genes. Estimation ability of the method [41] is more robust than others, such as imputation by zero, row average or SVD-impute. In [30], a KNN-based missing data estimation algorithm is proposed based on the temporal and spatial correlation of sensor data. The methods discuss in [30, 41] have better performance than prior method, but drawback is that their estimation ability depends on parameter K (i.e., number of neighbor genes used to impute missing value) for which no theoretical way exists to determine them appropriately and thus needs to be specified by the user. In the paper [34], the missing values are estimated using fuzzy c-means clustering algorithm and semantic similarity among gene expression data, but the method requires gene oncology structure among several genes, which depend on biological knowledge, whereas, in the paper [4, 25, 46, 47], cluster-based algorithms have been proposed to deal with missing values which do not need such parameters but microarray dataset is very high dimensional and there exist large number of genes with large number of samples which may degrade the clustering performance. Also performance of these methods depends on number of clusters whose selection becomes very crucial. In the paper [37], the missing values are estimated to preprocess the datasets using fuzzy c-means clustering-based expectation maximization (EM) method.

The KNN-impute [41] method depends on the intuitive assumption that the genes closed to each other are potentially similar. The measurement considers both distance computation between genes and the number of nearest neighbors (K). As the missing gene may contain variant number of missing values, so the genes without missing values may have different lengths and their distances are inaccurate. The paper [21] proposes a sequential KNN imputation method (SKNN-impute) where missing values are estimated sequentially starting with a gene having the smallest missing rate. It uses the genes without any missing values for estimating the missing values of the genes. The SKNN-impute method iteratively estimates the missing values of the genes based on the ascending order of their missing rates. The paper [3] proposes an iterative KNN imputation method (IKNN-impute) which first replaces all missing values of a gene by the row average of all values in it. Then an iterative process is performed to obtain all missing values same as SKNN-impute method. The paper [31] proposes a similarity-based missing value estimation technique (PCM-impute), but it considers only single similar gene for estimating missing value. The improved version [32] (HCS-impute) of paper [32] is also a KNN-based algorithm that selects eight neighbors of a gene, but the demerit of the method is that it needs the value of K in advance.

The Bayesian principal component analysis (BPCA) [28] method estimates the missing values by linear combination of certain principal axis vectors, where the parameters are identified by Bayesian estimation method. On the other hand, local least squares (LLS) [22], sequential local least square (SLLS) [46, 47] and iterated local least square (ILLS) [6] methods utilize multiple regression models to impute the missing values from KNN genes of the missing value-related genes. Recently, bi-cluster-based estimation methods (BIC) [18] such as bi-cluster-based least square (bi-iLS) [8] and bi-cluster-based BPCA (bi-BPCA) [27] aim to estimate missing values with some integrated approaches and give acceptable results. Another method [16] estimates missing values with high accuracy using triple imputation strategies (TRIIM) based on BPCA, LLS and EM concepts.

1.2 Contribution and comparison

In the paper, a novel ‘Missing Value Estimation Technique through Cluster Analysis’ (MVETCA) has been proposed on microarray dataset for imputing missing values that not only overcomes the constraints of the existing methods but also gives significantly better statistical measures like less normalized root mean square error (NRMSE) [39], high conserved pairs proportion (CPP) [11] and high biomarker list concordance index (BLCI) [29].

The proposed method of missing value estimation consists of the following steps:

• i. The dataset is discretized to Z-score using transitional state discrimination (TSD) method [43], and the genes are characterized by N discrete sample values. The samples are divided into two disjoint classes, because they are collected from both normal and tumor patients. So, the frequencies of sample values are calculated separately in each class for each gene.

• ii. The whole gene set is partitioned into two clusters; one contains all genes without any missing values termed as ‘NOMISS’ and the other contains all genes with missing values termed as ‘MISS.’ Then missing values of genes in MISS is filled up using the mean gene value for all samples belonging to the same class, either normal or disease class. And finally, all genes in MISS are also replicated in NOMISS. Thus, all missing values are temporarily estimated.

• iii. Based on the frequencies of discrete sample values, the gene set NOMISS is partitioned into maximum 3N gene subsets, explained in Sect. 2.2. Now, N out of 3N clusters contains whole part (i.e., normal and cancerous samples) of the genes while each N of remaining 2N clusters contains only one part (i.e., either normal or cancerous samples) of the genes.

• iv. Each gene in gene set MISS is associated with one of the N subsets containing whole portion, or each of its two portions (i.e., normal and cancerous) is associated with one of the 2N respective subsets containing only one portion. The association of gene is determined by measuring the similarity of the gene expression values with the gene subsets, explained in Sect. 2.3.1.

• v. Now the 3N gene subsets are partitioned into optimal number of clusters (optimality is determined through validation indices) using similarity-based clustering algorithm where similarity factors are measured between centroid of each partition and associated portion of the missing value-related gene. The missing values of the associated portion of the gene are imputed by the respective values of the centroid with most similar partition. Thus, missing values of each gene are imputed by repeating steps (iv) and (v).

The pictorial representation of the proposed method is shown in Fig. 1.

Fig. 1

The overall work flow of proposed missing value estimation method

The HCS-impute method [32] uses eight similar genes, and SKNN-impute [21] and IKNN-impute [3] use twenty or less similar genes to estimate missing values, but the proposed method MVETCA has no such limitation. In KNN-impute [41], PCM-impute [31] and HCS-impute [32], the missing values are estimated only with the help of NOMISS genes. In SKNN-impute [21], sequentially the missing values are estimated according to the non-decreasing order of count of missing values of MISS genes and NOMISS dataset is updated after estimating the missing values one by one. But IKNN-impute [3], bi-BPCA [27], TRIIM [16] and proposed method use full dataset to estimate missing values. In IKNN-impute [3], row-average method considering all sample values of a gene is used to temporarily estimate the missing values of MISS and update the NOMISS set accordingly. Similarly, bi-BPCA [27] uses BPCA and TRIIM [16] uses BPCA, LLS and EM method to temporarily estimate the missing values of MISS and update the NOMISS set accordingly. But MVETCA uses cancerous or normal sample values, which is more logical with respect to expression values for a particular class. The MVETCA uses Hamming distance-based similarity function, whereas other methods use Euclidian distance metric for similarity measurement of genes, which is not so effective especially in case of high-dimensional datasets. The proposed MVETCA method is compared with some other imputation methods with the help of some statistical measures like NRMSE [39], CPP [11] and BLCI [29] considering six publicly available microarray datasets.

The paper is organized into four sections. Section 2 describes the proposed missing value estimation technique through cluster analysis. The experimental results and performances of the proposed method are evaluated for various benchmark microarray datasets in Sect. 3. Finally, the work is concluded in Sect. 4.

2 Missing value estimation

The efficient microarray technology [12] evaluates the gene expressions simultaneously under different experimental conditions. Generally, microarray dataset contains missing values for which almost (5–50%) genes are affected. Missing value is a crucial problem needs to handle before analysis of the microarray data in order to acquire important knowledge. Therefore, missing value imputation is a necessary preprocessing step to estimate proper expression values.

2.1 Gene expression discretization

Initially, dataset $\hbox {DS} = (U, C)$ has some missing values which are temporarily estimated by the mean gene value for all samples belong to the same class (either normal or disease), of a gene, where U the universe of discourse contains g genes and C the condition attribute set contains s samples. The gene subset with missing values is referred as MISS, and the initial estimated whole gene set is termed as NOMISS. The transitional state discrimination (TSD) method [43] is used to discretize MISS and NOMISS. The discretization factor $f_{ij}$, based on which the dataset is discretized, is computed for sample $C_{j} \in C$ of gene $g_{i} \in U$, using Eq. (1), for i = 1, 2,...,g and j = 1, 2, ..., s.

$$\begin{aligned} f_{ij} =\frac{M_i \left[ {C_j } \right] -\mu _{i}}{\delta _{i}} \end{aligned}$$

(1)

where $\mu _{i}$ and $\delta _{i}$ are the mean and standard deviation of gene $\hbox {g}_{i}$, respectively, and $M_{i}[C_{j}]$ is the sample value $C_{j}$ in gene $g_{i}$. Then, mean $(N_{i})$ of negative sample values and mean $(P_{i})$ of positive sample values of each gene $\hbox {g}_{i}$ are calculated and discretized to one of N (here, $N = 5$) fuzzy linguistic terms using Eq. (2).

$$\begin{aligned} f_{ij} =\left\{ \begin{array}{lll} {{}^\prime }VL^{\prime } &{}|if &{} f_{ij} \le N_{i} \\ {{}^\prime }L^{\prime }&{}|if&{} N_{i}<f_{ij}<0\\ {{}^\prime }Z^{\prime } &{}|if &{} f_{ij}=0\\ {{}^\prime }H^{\prime }&{}|if&{} 0<f_{ij} < P_i \\ {{}^\prime }VH^{\prime }&{}|if &{} f_{ij}\ge P_{i}\\ \end{array}\right. \end{aligned}$$

(2)

2.2 Structure of correlated gene subsets

Based on the frequencies of discrete sample values, the genes of NOMISS are partitioned into 3N different groups. N out of 3N groups contains whole (i.e., normal and cancerous samples) of the genes while each N of remaining 2N groups contains only one portion (i.e., either normal or cancerous samples) of the genes.

Either a gene of MISS is associated with one of the N groups containing whole gene or each of its two portions (i.e., normal and cancerous) is associated with one of the 2N respective groups containing only one portion.

Let the samples of the dataset are collected together from $s_{1}$ normal and $s_{2}$ cancerous patients and so each gene contains $s_{1}$ normal and $s_{2}$ cancerous samples. Let each gene $g_i \in NOMISS$ is represented as $g_i =\{g_{i1}^n ,g_{i2}^n , ,\ldots g_{is_1 }^n ,g_{i1}^c , g_{i2}^c ,\ldots ,g_{is_2 }^c \}$ where $g_{ij}^n$ for $j = 1, 2, {\ldots }, s_{1 }$ are normal samples and $g_{ik}^c$ for $k = 1, 2, {\ldots }, s_{2}$ are cancerous samples. Frequencies of discrete expression values for samples $\{g_{i1}^n , g_{i2}^n , {\ldots },g_{is_1 }^n \}$ and $\{g_{i1}^c , g_{i2}^c , {\ldots },g_{is_2 }^c \}$ of gene $g_{i}$ are computed as $\left\{ {f_{VL}^{ni} ,f_L^{ni} ,f_Z^{ni} ,f_H^{ni} ,f_{VH}^{ni} } \right\}$ and $\left\{ {f_{VL}^{ci} ,f_L^{ci} ,f_Z^{ci} ,f_H^{ci} ,f_{VH}^{ci} } \right\}$, respectively, where $f_{VL}^{ni}$ is the frequency of expression value ‘VL’ in normal samples of gene $g_{i}$, similar meaning of other terms. Let $f_\mathrm{max}^{ni} =\hbox {max}\left\{ {f_{VL}^{ni} ,f_L^{ni} ,f_Z^{ni} ,f_H^{ni} ,f_{VH}^{ni} } \right\}$ and $f_\mathrm{max}^{ci} =\hbox {max}\left\{ {f_{VL}^{ci} ,f_L^{ci} ,f_Z^{ci} ,f_H^{ci} ,f_{VH}^{ci} } \right\}$. The gene subsets are formed as follows:

If $f_\mathrm{max}^{ni}$ and $f_\mathrm{max}^{ci}$ are computed from:

(i) Same discrete expression value say ‘VL’ then the gene $g_{i }= \{g_{i1}^n , g_{i2}^n , {\ldots },g_{is_1 }^n ,g_{i1}^c , g_{i2}^c , {\ldots },g_{is_2 }^c \}$ is placed in subset $\hbox {GENE}\_\hbox {WHOLE}_{\mathrm{VL}}$ (abbreviated as $\hbox {GW}_{\mathrm{VL}}$, subsequently used throughout the paper). Similarly, considering other discrete values, total of five subsets $\hbox {GW}_{\mathrm{VL}}, \hbox {GW}_{\mathrm{L}}$, $\hbox {GW}_{\mathrm{Z}}$, $\hbox {GW}_{\mathrm{H}}$ and $\hbox {GW}_{\mathrm{VH}}$ are formed. Each of these five subsets contains genes of NOMISS, where maximum frequency of discrete value occurs for same discrete value in both normal and cancerous samples.

(ii) Different discrete expression value say $f_\mathrm{max}^{ni}$ occurs for ‘VL’ and $f_\mathrm{max}^{ci}$ occurs for ‘VH.’ In this case, the normal part $\{g_{i1}^n ,g_{i2}^n ,\ldots ,g_{id_1 }^n \}$ of $g_{i}$ is placed in subset $\hbox {GENE}\_\hbox {NORMAL}_{\mathrm{VL}}$ (abbreviated as $\hbox {GN}_{\mathrm{VL}}$), and same treatment takes place for other discrete values. And cancerous part $\{g_{i1}^c ,g_{i2}^c ,\ldots ,g_{id_2 }^c \}$ of $g_{i}$ is placed in subset $\hbox {GENE}\_\hbox {CANCER}_{\mathrm{VH}}$ (abbreviated as $\hbox {GC}_{\mathrm{VH}}$), same situation occurs for other discrete values. Thus, gene subsets $\hbox {GN}_{\mathrm{VL}}$, $\hbox {GN}_{\mathrm{L}}$,$\hbox {GN}_{\mathrm{Z}}$, $\hbox {GN}_{\mathrm{H}}$ and $\hbox {GN}_{\mathrm{VH}}$ are formed, each of which contains normal samples of genes whose maximum frequency discrete value differs from that of cancerous samples. Similarly, gene subsets containing only cancerous samples are formed which are $\hbox {GC}_{\mathrm{VL}}$,$\hbox {GC}_{\mathrm{L}}$,$\hbox {GC}_{\mathrm{Z}}$, $\hbox {GC}_{\mathrm{H}}$ and $\hbox {GC}_{\mathrm{VH}}$.

Thus, fifteen subsets are formed for the genes of NOMISS. These subsets are created according to the gene expression values of the dataset, and each subset contains similar nature of expression values.

2.3 Gene clustering and analysis

The ideal input for a clustering algorithm is a dataset without any noise. When the experimental data deviates from this property, it poses different problems for different types of clustering algorithms. Missing values in the dataset used during cluster analysis are a very crucial problem handled carefully for high-dimensional data.

2.3.1 Gene subset selection

The set NOMISS is partitioned into fifteen subsets without missing values, and each subset contains genes with similar nature according to their expression values. On the other hand, the set MISS contains genes with missing values need to be estimated prior to gene data analysis. Each gene $g_j \in MISS$ is denoted by $g_j =\left\{ {g_{j1}^n ,g_{j2}^n ,\ldots ,g_{js_1 }^n ,g_{j1}^c ,g_{j2}^c ,\ldots ,g_{js_2 }^c } \right\}$, where some missing normal and cancerous samples $g_{jk}^n$ and $g_{jl}^c$, for $k = 1, 2, {\ldots }, s_{1}$ and $l = 1, 2, {\ldots }, s_{2}$ need to be estimated. The method computes the frequency of discrete expression values in both normal and cancerous samples of gene $g_j \in MISS$. If maximum frequency occurs in both types of samples for same expression value, say ‘VH’, then $g_{j}$ is related to subset $\hbox {GW}_{\mathrm{VH}}$. But if maximum frequency occurs for different expression values, say ‘VL’ and ‘VH’ for normal class and cancerous class, respectively, then normal samples $\{g_{j1}^n ,g_{j2}^n ,\ldots ,g_{js_1 }^n \}$ of $g_{j}$ is associated with $\hbox {GN}_{\mathrm{VL}}$ and cancerous samples $\{g_{j1}^c ,g_{j2}^c ,\ldots ,g_{js_2 }^c \}$ of gene $g_{j}$ is associated with $\hbox {GC}_{\mathrm{VH}}$. Thus each gene $g_j \in MISS$ is either

• (i) Linked with any one subset of the set $\hbox {GW} = \{\hbox {GW}_{\mathrm{VL}}, \hbox {GW}_{\mathrm{L}}, \hbox {GW}_{\mathrm{Z}}, \hbox {GW}_{\mathrm{H}}, \hbox {GW}_{\mathrm{VH}}\}$ or

• (ii) Normal portion of it is linked with any one of $\hbox {GN} = \{\hbox {GN}_{\mathrm{VL}},\hbox {GN}_{\mathrm{L}}, \hbox {GN}_{\mathrm{Z}}, \hbox {GN}_{\mathrm{H}}, \hbox {GN}_{\mathrm{VH}}\}$ and cancerous portion of it is associated with any one of $\hbox {GC} = \{\hbox {GC}_{\mathrm{VL}}, \hbox {GC}_{\mathrm{L}}, \hbox {GC}_{\mathrm{Z}}, \hbox {GC}_{\mathrm{H}}, \hbox {GC}_{\mathrm{VH}}\}.$

2.3.2 Clustering of gene subset by splitting and merging

The most common distance metric used for distance measure is Euclidean distance. Though it is very useful in low dimensions, it does not work well in high-dimensional cancer dataset. It is observed that Euclidean distance does not capture the similarity of high-dimensional objects. Rather, bitwise similarity measurement, i.e., Hamming distance is more powerful for missing value estimation of genes. Here, gene subset associated with missing gene $g_j \in MISS$ is partitioned using similarity-based proposed clustering algorithm which provides set of K-clusters. If $g_j$ is associated with a subset of the set GW, then only that subset of genes is clustered to impute the missing values of $g_j$. And if missing values of $g_j$ arise both in normal portion and cancerous portion, the corresponding subsets of both the set GN and GC are clustered; otherwise, clustering algorithm is applied only on the corresponding subset of either GN or GC.

The gene subset is grouped into significant clusters capture the normal structure of the data to find genes with related functionality. Cluster analysis has been applied in different fields, like information science to social sciences [23] and biological science [33]. The relationships of genes are established from available information using clustering algorithms [13, 35, 40]. The aim of clustering algorithms is to collect the similar nature genes in a cluster and dissimilar genes in different clusters according to their expression values. The validity indices [2, 14] proposed by the researchers measure the goodness of clusters by checking entropies of the partition, membership distributions, clusters separation and compactness. The proposed method introduces merging and splitting procedure [9] on initial set of clusters, validates newly generated clusters using cluster validation indices and finally produces optimal set of clusters used to impute the missing values of the genes. Some notations and terms used in the algorithm are described below.

A. Notation and Definition

For convenience, following notations are used in proposed clustering algorithm:

• ${{\varvec{C}}}_{{\varvec{i}}}$: It is the ith cluster, where i = 1, 2, ..., k.

• ${{\varvec{x}}}_{{\varvec{k}}}$: It is the kth object of any cluster.

• ${{\varvec{n}}}_{{\varvec{i}}}$: Number of objects of ith cluster.

• ${{\varvec{S}}}\left( {{{\varvec{x}}}_{{\varvec{k}}} ,{{\varvec{C}}}_{{\varvec{i}}} } \right)$: It is the similarity function which computes bitwise matching of discrete sample values of ith cluster center to the kth object $x_k$ of ith cluster.

• ${{\varvec{S}}}({{\varvec{C}}}_{{\varvec{i}}} ,{{\varvec{C}}}_{{{\varvec{j}}}} )$: It is the similarity function which computes bitwise matching of the ith cluster center with jth cluster center.

Few terminologies are defined below for understanding the proposed clustering algorithm:

Definition 1

(Combine Center) Combine center $CCcomb_{ij}$ of two clusters $C_{\mathrm{i}}$ and $C_{\mathrm{j}}$ ($i, j = 1, 2,{\ldots },k$ and $i \ne j)$ is the weighted mean of centers of two clusters $C_{\mathrm{i}}$ and $C_{\mathrm{j}}$, computed using Eq. (3) and is considered as the center of combined cluster $C_{\mathrm{ij}}$, where $\overline{C_i}$ and $\overline{C_j }$ are the mean of $C_{\mathrm{i}}$ and $C_{\mathrm{j}}$, respectively.

$$\begin{aligned} CCcomb_{ij} =\frac{\left( {n_i \times \overline{C_i } } \right) +\left( {n_j \times \overline{{C}_j } } \right) }{n_i +n_j } \end{aligned}$$

(3)

Definition 2

(Similarity Factor) Similarity factor between two clusters $C_{\mathrm{i}}$ and $C_{\mathrm{j}}$ ($i, j =1, 2,{\ldots },k$ and $i \ne j)$ is denoted by $\hbox {CSF}_{ij}$ and is defined by Eq. (4).

$$\begin{aligned} \hbox {CSF}_{ij} =\frac{\mathop \sum \nolimits _{x_k \in C_i } S\left( {x_k ,CCcomb_{ij} } \right) +\mathop \sum \nolimits _{x_k \in C_j } S\left( {x_k ,CCcomb_{ij} } \right) }{n_i +n_j }+S(C_i ,C_j ) \end{aligned}$$

(4)

Definition 3

(Merging factor) Let $C_1 ,C_2 ,\ldots ,C_k$ be the k clusters. The merging factor MF is the cluster validation index for k clusters computed using Eq. (5) that is used to evaluate the clusters to obtain optimal set of clusters.

$$\begin{aligned} \hbox {MF}=\frac{\mathop \sum \nolimits _{i=1}^k \mathop \sum \nolimits _{x_j \in C_i } S\left( {x_j ,C_i } \right) }{\mathop \sum \nolimits _{i=1}^k \left( {\min \limits _{1\le j\le k,i\ne j} S(C_i ,C_j )} \right) } \end{aligned}$$

(5)

Definition 4

(Splitting Factor) It is the ratio of intra-cluster similarity to the minimum inter-cluster similarity of ith cluster to all other clusters. The Split Factor $\hbox {SF}_{\mathrm{i}}$ is calculated using Eq. (6) for each individual cluster.

$$\begin{aligned} \hbox {SF}_i =\frac{\mathop \sum \nolimits _{x_k \in C_i } S\left( {x_k ,C_i } \right) }{\min \limits _{1\le j\le k,i\ne j} S(C_i ,C_j )} \end{aligned}$$

(6)

Definition 5

(Mean of Split Factor) It is an average split factor of all clusters used as a threshold value ($\gamma$), calculated using Eq. (7) to split a cluster.

$$\begin{aligned} \gamma =\frac{1}{k}\mathop \sum \limits _{i=1}^k \hbox {SF}_i \end{aligned}$$

(7)

B. Merging of Clusters

Let there are n genes in a subset which need to be clustered. Initially, each gene is considered as a separate singleton cluster, and thus, n clusters $C_{1}$, $C_{2}$, ..., $C_{n}$ are formed. For any two clusters ${C}_{{i}}$ and $C_{{j}}\, (i$,$j =1, 2, {\ldots },n$ and $i \ne j)$ similarity factor $\hbox {CSF}_{ij}$ is computed using Eq. (4) with the implication that, if the similarity of the combine cluster $(C_{\mathrm{ij}})$ is high and at the same time the similarity of the two respective cluster centers is high, then the similarity factor $(\hbox {CSF}_{ij} )$ between the cluster is high and the clusters are much similar to each other according to the nature of objects of clusters. This implies that higher the similarity factor between the pair, more similar the clusters are. In Eq. (4), the weighted mean $(CCcomb_{ij} )$ representing the center of combined cluster $(C_{{ij}})$ is computed using Eq. (3) and original gene expression values of $C_{{i}}$ and ${C}_{{j}}$ are used, not the discrete values.

Thus, a similarity matrix $S = (\hbox {CSF}_{ij} )_{n\times n}$ is created using Eq. (4) which is a symmetric matrix with empty diagonal entries, as the similarity of a cluster with itself is not required. All the $\frac{n\left( {n-1} \right) }{2}$ similarity factors reside above the leading diagonal of S stored the information based on which clusters are merged. In every iteration, only the cluster pair with maximum similarity are merged and reducing the number of clusters by one.

Initially, the merging factor (MF) is computed using Eq. (5) and it is used while the merging process is over to measure the better clustering phenomenon that finally helps to form the stable set of clusters. In Eq. (5), if the numerator value is high (i.e., the points of each cluster are much more similar) and denominator is low (i.e., the cluster centers are more dissimilar), then the cluster qualities are good enough. High value of MF corresponds to clusters that are formed with more similar nature points and centers are more dissimilar with each other. So the larger the MF value better is the clustering. The merging procedure continues if MF value increases; otherwise, splitting procedure resumes, explained in Sect. 2.3.2C.

Let $C_1 ,C_2 ,\ldots ,C_n$ be the n number of clusters. After first merging, ($n- 1$) clusters are obtained whose MF value $\hbox {MF}_{n-1}$ is computed using Eq. (5). The process terminates if $\hbox {MF}_{n-1}$ is larger than $\hbox {MF}_{n}$ by a threshold value (set experimentally) and the system is rolled back to the previous state to preserve the previous set of n clusters; otherwise, same process is repeated with ($n - 1$) clusters.

The algorithm of merging process is given in detail below:

C. Splitting of clusters

There is some possibility that the objects are situated in dissimilar manner within the clusters. Such clusters are known as dissimilar clusters which need to be split into two or more clusters. In splitting process, the intra-cluster (within cluster) similarities are measured for each individual cluster. The measurement is performed with the comparison between cluster center and objects of corresponding cluster. Also inter-cluster (between clusters) similarity between each pair of clusters is measured comparing respective cluster centers. Now the split factor is calculated using Eq. (6) for each individual cluster. In Eq. (6), if numerator value is large and denominator value is small, then the split factor is high which implies that the cluster is compact with respect to its objects and other cluster centers; otherwise, the cluster is scattered. Now a threshold value $(\gamma )$ is calculated using Eq. (7) to measure the scattering of each individual cluster.

If split factor of any cluster is less than the $\gamma$ value, then the corresponding cluster is split into three clusters considering centroid of the cluster and two most dissimilar objects within the cluster as their centers. The other objects of the cluster are placed in one of the three newly formed clusters to which they are more similar. The algorithm of splitting process is described in detail below:

After splitting procedure, suppose n number of clusters is formed. The proposed method computes some cluster validity indices, such as (i) DB-index, (ii) Dunn-index, (iii) H-index and (iv) SC-index using Eqs. (8), (9), (12) and (13), respectively, of the obtained clusters. If two or more validity indices dominate the previous index values, then merging and splitting procedures are continued; otherwise, current k clusters are considered as stable clusters. The above-mentioned validity indices and their values for cluster validation are described below:

(i) :

DB-index: The Davies–Bouldin (DB) [10] index is defined in Eq. (8).

$$\begin{aligned} DB=\frac{1}{k}\mathop \sum \limits _{i=1}^k \mathop {\hbox {max}}\limits _{1\le i\le k\,\hbox {and}\,i\ne j} \left\{ {\frac{\sigma _i +\sigma _j }{\hbox {d}S\left( {C_i ,C_j } \right) }} \right\} \end{aligned}$$

(8)

where k is the number of clusters, $\sigma _i$ is the average dissimilarity of all patterns in cluster i to their cluster center $C_i$, $\sigma _j$ is the average dissimilarity of all patterns in cluster j to their cluster center $C_j$, and $dS\left( {C_i ,C_j } \right)$ is the dissimilarity of cluster centers $C_i$ and $C_j$. Small values of DB correspond to clusters that are compact, and whose centers are less similar from each other. The minimum of the DB-index determines the actual number of clusters.

(ii) :

Dunn’s index: The Dunn’s index (DN) [26] is defined in Eq. (9).

$$\begin{aligned} \hbox {DN}=\mathop {\min }\limits _{1\le i\le k} \left\{ {\mathop {\hbox {min}}\limits _{i+1\le j\le k} \left\{ {\frac{\delta \left( {C_i ,C_j } \right) }{\max \limits _{1\le l\le n} \partial \left( {C_l } \right) }} \right\} } \right\} \end{aligned}$$

(9)

where $\delta \left( {C_i ,C_j } \right) =\hbox {max}\left\{ {\hbox {d}S\left( {C_i ,C_j } \right) |x_i \in C_i ,x_j \in C_j } \right\}$ and $\partial \left( {C_l } \right) =\hbox {min}\left\{ \hbox {d}S\left( {C_i ,C_j } \right) \right. \left. |x_i ,x_j \in C_i \right\}$. The $S\left( {C_i ,C_j } \right)$ is the dissimilarity of two points of $C_i$ and $C_j$. The maximum of the DN-index determines the actual number of clusters.

(iii) :

H-index: The similarity within cluster (SSW) and similarity between clusters (SSB) are defined using Eqs. (10) and (11), respectively.

$$\begin{aligned} \hbox {SSW}=\frac{1}{n}\mathop \sum \limits _{i=1}^k \mathop \sum \limits _{j\in c_i } S\left( {x_j ,C_j } \right) \end{aligned}$$

(10)

where k is the total number of clusters, $C_j$ is the respective cluster centers and n is the total number of objects.

$$\begin{aligned} \hbox {SSB}=\frac{1}{n}\mathop \sum \limits _{i=1}^k n_i S\left( {C_i ,\bar{X}} \right) \end{aligned}$$

(11)

The Hartigan (H) [50] index is defined by Eq. (12).

$$\begin{aligned} H=-\hbox {log}\left( {\frac{\hbox {SSW}}{\hbox {SSB}}} \right) \end{aligned}$$

(12)

The minimum value of the H-index is determined as the desire number of clusters.

(iv) :

SC-index: The Silhouette Coefficient (SC) [45] is defined by Eq. (13).

$$\begin{aligned} SC=\frac{1}{k}\mathop \sum \limits _{i=1}^k \frac{\left( {b_i -a_i } \right) }{\hbox {max}\left( {a_i ,b_i } \right) } \end{aligned}$$

(13)

where $a_i$ is the average dissimilarity of ith objects with all other objects within the same cluster. $b_i$ is the lowest average dissimilarity of ith object to any other cluster. The maximum of the SC-index is determined as the desire number of clusters.

The overall flow diagram of cluster validation method is shown in Fig. 2:

2.4 Similarity measurement

As each gene in the dataset is of s-tuple (i.e., samples), so the centroids of k clusters are also of $s = (s_{1}+s_{2})$-tuples. Let the centroids of cluster t are CENTRE$_{t} = \{C_{t1}^n , C_{t2}^n , {\ldots },C_{ts_1 }^n ,C_{t1}^c , C_{t2}^c , {\ldots },C_{ts_2 }^c \}$, for $t = 1, 2, {\ldots },k$, where $C_{tj}^n$ is the centroid of jth normal samples in cluster t, for $j = 1,2,{\ldots },s_{1}$ and $C_{tj}^c$ is the centroid of jth cancerous samples of cluster t, for $j = 1, 2, {\ldots }, s_{2}$. Now the similarity $S_{jt}$ of gene $g_j \in MISS$ with cluster t is the number of samples matching the values to that of centroid of t. The procedure to measure the similarity of a gene with a cluster is described below:

Fig. 2

Overall flow diagram of cluster validation method

Thus, similarity of $g_{j}$ with all k clusters is obtained and if $S_{jP}$ is maximum for $1 \le P \le k$, then the missing $g_{jq}^n$ will be predicted by $C_{pq}^n$, $1 \le q \le s_{1}$ and missing $g_{jr}^c$will be estimated by $C_{pr}^c$, $1 \le r \le s_{2}$. Thus, the missing values are estimated for each gene $g_{j}$. The overall algorithm for missing value estimation through cluster analysis (MVETCA) is given below:

3 Experimental results and performance evaluation

Experimental studies presented provide an evidence of effectiveness of the proposed MVETCA method on gene expression datasets. Experiments are carried out on different kinds of microarray datasets [20]. Each dataset contains two or more types of samples, normal and cancerous. The numbers of genes, classes and samples contained in the various datasets are listed in Table 1.

Table 1 Summary of gene expression dataset

3.1 Efficiency of cluster analysis

To impute missing values, first the correlated gene subsets are identified, then the clustering algorithm is applied on appropriate gene subset and finally the missing values are estimated. To prove the efficiency of clustering algorithm, the algorithm applied on subsets of each dataset, optimal number of clusters are obtained and comparison is made with well-known K-means [35, 40] and Fuzzy C-means [13, 35] clustering techniques with same number of clusters by some validity indices [10, 26, 45, 50].

3.1.1 Comparative study

In the proposed method, initially all points are treated as individual clusters and after successive iteration of merging and subsequent splitting process, discussed in Sect. 3, optimal number of clusters is obtained. Considering same number of clusters obtained by the proposed method, K-means [35, 40] and Fuzzy C-means [13, 35] algorithm are applied on the same subsets and a comparison is made on six mentioned gene datasets (for some initial clusters) as listed in Tables 2, 3, 4, 5, 6, 7 and  8. The results show that DB, DN, SC and H indices produced by the proposed method are better than that produced by other methods in most of the cases (show in bolt and shaded font), which confirms the potentiality and superiority of the proposed method.

Table 2 Leukemia1 subsets with 10% missing values

Table 3 Lung cancer subsets with 20% missing values

Table 4 Prostate cancer subsets with 30% missing values

Table 5 Breast cancer subsets with 15% missing values

Table 6 DLBCL subsets with 10% missing values

Table 7 Colon subsets with 20% missing values

Table 8 Leukemia2 subsets with 5% missing values

3.1.2 Optimal cluster selection

The proposed method modifies the clusters iteratively, and finally, based on the validity indices optimal number of clusters is obtained. To demonstrate how the work finds the optimal number of clusters, one group of data (such as $\hbox {GW}_{\mathrm{Z}}$) for each dataset is selected and graph is plotted against ‘Cluster number’ and ‘validity indices.’ The following figures (Figs. 3, 4, 5, 6, 7, 8, 9) show the validity indices for different number of clusters. In figures, we have considered one group from each dataset and the validity indices are computed for different number of clusters obtained iteratively by our proposed clustering algorithm. It is noted that initially there are large number of clusters, which gradually become stable by splitting and merging procedures.

Fig. 3

Optimal no. of cluster for $\hbox {GW}_{\mathrm{Z}}$ set of Leukemia1 dataset

Fig. 4

Optimal no. of cluster for $\hbox {GC}_{\mathrm{L}}$ set of Lung cancer dataset

Fig. 5

Optimal no. of cluster for $\hbox {GW}_{\mathrm{Z}}$ set Prostate cancer dataset

Fig. 6

Optimal no. of cluster for $\hbox {GW}_{\mathrm{Z}}$ set of Breast cancer dataset

Fig. 7

Optimal no. of cluster $\hbox {GW}_{\mathrm{Z}}$ set for DLBCL dataset

Fig. 8

Optimal no. of cluster for $\hbox {GW}_{\mathrm{L}}$ set of Colon cancer dataset

Fig. 9

Optimal no. of cluster for $\hbox {GW}_{\mathrm{L}}$ set of Leukemia2 dataset

In all diagrams (Figs. 3, 4, 5, 6, 7, 8, 9), it is observed that DB and H value decreases and DN and SC value increases up to a certain number of clusters. According to proposed clustering algorithm, in any iteration if two or more validity indices dominate their previous values, then procedure is continued, and otherwise, the clusters used in this iteration are considered as the optimal clusters. For example, in case of $\hbox {GW}_{\mathrm{Z}}$ set of Leukemia1 dataset, DN-index, H-index and SC-index dominate their previous values (as shown in Fig. 3) in the iteration with 35 clusters, and so the process is continued. Finally the process terminates with six clusters when DN-index, H-index and SC-index dominate their previous values. Similar analysis is made for other datasets using Figs. 4, 5, 6, 7, 8, 9 to visualize optimal number of clusters obtained by the algorithm, as given in Tables 2, 3, 4, 5, 6, 7 and 8.

3.2 Performance analysis

Experimental results presented here provide an evidence of effectiveness of the proposed MVETCA algorithm on publicly available benchmark microarray datasets. The microarray dataset is divided into two subsets and in one set randomly missing values are provided at any random positions. Thus, two datasets NOMISS and MISS are formed from a given dataset. Then the missing values of genes in MISS are imputed by the proposed method using the genes in NOMISS.

In cluster-based methods, the number of nearest neighbors, K, must be selected. In KNN-impute, SKNN-impute and IKNN-impute, value of K is set by a value in between 10 and 20 and the best value of K is obtained. Here, we have decided to perform multiple estimation tests incorporating 5, 10, 15, 20, 25 and 30% missing values in the datasets.

3.2.1 Evaluation criteria

The performance of our missing values imputation algorithm is evaluated by three metrics such as ‘Normalized Root Mean Squared Error,’ ‘Conserved Pair Proportions’ and ‘Biomarker List Concordance Index.’

(a) Statistical index

We use the normalized root mean squared error (NRMSE) [39], a statistical index to evaluate the performance of the proposed and existing missing values estimation techniques, defined in Eq. (14). Lower the value of the NRMSE, better the method performs.

$$\begin{aligned} \hbox {NRMSE}=\frac{1}{\hbox {std}\_\hbox {dev}\left( {X_\mathrm{known} } \right) }\sqrt{\frac{\mathop \sum \nolimits _{i=1}^n \left( {X_\mathrm{predict} -X_\mathrm{known} } \right) ^{2}}{X}} \end{aligned}$$

(14)

where $X_\mathrm{known}$ is the original gene expression value and $X_\mathrm{predict}$ is the estimated value obtained by the proposed algorithm, $\hbox {std}\_\hbox {dev}\left( {X_\mathrm{known} } \right)$ is the standard deviation of original expression values and X is the total number of missing values. The number X is set randomly as 5, 10, 15, 20, 25 and 30% of total genes, and NRMSE is computed in all methods.

(b) Clustering index

Conserved pairs proportion (CPP) [11] one of the most promising clustering indices is used to evaluate the stability of the clusters against the missing values present in the genes. Here, the proposed ‘splitting and merging’ clustering algorithm is applied on the original dataset and the obtained clusters are say, $\hbox {OC} = \{C_{\mathrm{O1}}, C_{\mathrm{O2}}, {\ldots }, C_{\mathrm{Ok}}$}. Also, the same clustering algorithm is applied on dataset with generating and estimating the missing values and let the obtained clusters are, $\hbox {EC} = \{C_{\mathrm{E1}}, C_{\mathrm{E2}}, {\ldots }, C_{\mathrm{El}}\}$. The CPP index computed using Eq. (15) is used to compute the percentage of genes obtained associated with the clusters in OC and EC.

$$\begin{aligned} \hbox {CPP}=\frac{\mathop \sum \nolimits _{i=1}^K \left( {\max \limits _{1\le j\le l} \left( {\mathop \sum \nolimits _{x\in C_{Oi} } \mathop \sum \nolimits _{y\in C_{Ej} } \delta _{xy} } \right) } \right) }{n} \end{aligned}$$

(15)

where n is the total number of genes, $\delta _{{xy}} = 1$, if the genes x and y are identical and 0 otherwise. Higher the value of the CPP index, better the method performs.

(c) Differentially expressed genes index

We have used the biologically meaningful metric presented in [42] to express the biological impact of missing value imputation in gene datasets. The method [42] identifies differentially expressed genes for the original dataset and the imputed dataset. Then the biomarker list concordance index (BLCI) [29], defined in Eq. (16), is computed to evaluate the performance of different imputing methods.

$$\begin{aligned} \hbox {BLCI}=\frac{n\left( {D_\mathrm{OD} \cap D_\mathrm{ID} } \right) }{n\left( {D_\mathrm{OD} } \right) }+\frac{n\left( {D_\mathrm{OD}^C \cap D_\mathrm{ID}^C } \right) }{n\left( {D_\mathrm{OD}^C } \right) }-1 \end{aligned}$$

(16)

where $D_\mathrm{OD}$ and $D_\mathrm{ID}$ are the significantly differentially expressed genes in the original dataset (OD) and the imputed dataset (ID). $D_\mathrm{OD}^C$ and $D_\mathrm{ID}^C$ are the complement set of the $D_\mathrm{OD}$ and $D_\mathrm{ID}$, respectively, and $n\left( *\right)$ is the number of genes. A high BLCI value indicates that the list of the significantly differentially expressed genes of the OD is similar to that of the ID and the method is of high performance.

Fig. 10

NRMSE values for Leukemia1 dataset

3.2.2 Comparative study

The performance of MVETCA is compared with statistical methods (such as Zero-impute [1], Row-average [38], SVD-impute [19] and BPCA-impute [28]), cluster-based methods (such as KNN-impute [41], SKNN-impute [21], IKNN-impute [3] and HCS-impute [32], bi-BPCA-impute [27]), and regression-based methods (LLS-impute [22], SLLS- impute [46, 47], ILLS- impute [6] and TRIIM [16]).

(a) Statistical methods versus MVETCA

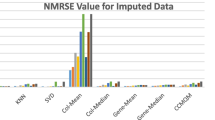
In Figs. 10, 11, 12, 13, 14, 15 and 16, the NRMSE values are plotted for various imputed datasets obtained by the proposed method MVETCA and well-known statistical methods, such as Zero-impute, Row-average, SVD and BPCA-impute.

Fig. 11

NRMSE values for Lung cancer dataset

Fig. 12

NRMSE values for Prostate cancer dataset

Fig. 13

NRMSE values for Breast cancer dataset

Fig. 14

NRMSE values for DLBCL dataset

Fig. 15

NRMSE values for Colon cancer dataset

Fig. 16

NRMSE values for Leukemia2 dataset

From the figures (Figs. 10, 11, 12, 13, 14, 15, 16), it is observed that MVETCA gives better results (i.e., minimum NRMSE) compare to other methods, which confirms the potentiality and superiority of the proposed method. Also, two popular biologically significant metrics such as CPP and BLCI are computed for all the considered datasets, as listed in Table 9. The result shows that for different percentage of missing values imputation, the proposed method always outperforms the others.

Table 9 CPP and LCI values for experimental datasets

(b) Cluster-based methods versus MVETCA

In Figs. 17, 18, 19, 20, 21, 22 and 23, the NRMSE values are plotted for various imputed datasets obtained by the proposed method MVETCA and some cluster-based methods, such as KNN-impute, SKNN-impute, IKNN-impute, HCS-impute and bi-BPCA.

Fig. 17

NRMSE values for Leukemia1 dataset

Fig. 18

NRMSE values for Lung cancer dataset

Fig. 19

NRMSE values for Prostate cancer dataset

Fig. 20

NRMSE values for Breast cancer dataset

Fig. 21

NRMSE values for DLBCL dataset

Fig. 22

NRMSE values for Colon cancer dataset

Fig. 23

NRMSE values for Leukemia2 dataset

From the figures (Figs. 17, 18, 19, 20, 21, 22, 23), it is observed that MVETCA gives better results (i.e., minimum NRMSE) compare to other methods in most of the cases, which confirms the potentiality and superiority of the proposed method. In some cases, like Leukemia1 dataset the IKNN method gives better result for 30% missing values and in Lung cancer dataset the SKNN and IKNN methods give better result for 15% missing values, but for rest of the cases the MVETCA gives the best results. The outstanding estimation ability of MVETCA is due to the accurate grouping of correlated genes, clustering of genes in stable and optimal way. Also, two popular biologically significant metrics such as CPP and BLCI are computed for all the considered datasets, as listed in Table 10. The result shows that for different percentage of missing values imputation, the proposed method outperforms the others in most of the cases.

(c) Regression-based methods versus MVETCA

In Figs. 24, 25, 26, 27, 28, 29 and 30, the NRMSE values are plotted for various imputed datasets obtained by the proposed method MVETCA and some regression-based methods, such as LLS-impute, SLLS-impute, ILLS-impute and TRIIM.

From the figures (Figs. 24, 25, 26, 27, 28, 29, 30), it is observed that MVETCA gives better results (i.e., minimum NRMSE) compare to other methods in most of the cases. Also, two popular biologically significant metrics such as CPP and BLCI are computed for all the considered datasets, as listed in Table 11.

Table 10 CPP and BLCI values for experimental datasets

Thus in general, the proposed method is evaluated estimating missing values by various performance evaluation indices and the results obtained by the proposed method outperform other statistical, cluster-based and regression-based methods, which shows the effectiveness of the proposed method.

4 Conclusion

Missing values can bring lots of complications in microarray data analysis because most of the existing methods are designed without any technique for handling them. But missing value estimation is one of the most significant preprocessing steps to deal with the missing values for further experiments. The existing cluster-based methods such as PCM, HCS, KNN, SKNN, IKNN, bi-BPCA and TRIIM estimate more erroneous values compare to the proposed MVETCA method. The PCM and HCS compute similarity between the missing gene and all other NOMISS genes and in time of imputation PCM takes information from only one gene, whereas HCS takes from eight neighbor genes. The KNN, SKNN and IKNN use different K values and taking best results among them. In time of estimation, all genes are not participated for all the above methods (except IKNN, bi-BPCA and TRIIM) and traditional Euclidian distance metric is used for similarity measurement, which is inefficient in case of high-dimensional datasets.

Fig. 24

NRMSE values for Leukemia1 dataset

Fig. 25

NRMSE values for Lung cancer dataset

Fig. 26

NRMSE values for Prostate cancer dataset

Fig. 27

NRMSE values for Breast cancer dataset

Fig. 28

NRMSE values for DLBCL dataset

Fig. 29

NRMSE values for Colon cancer dataset

Fig. 30

NRMSE values for Leukemia2 dataset

In this circumstance, MVETCA method totally depends on gene expression values and independent on number of genes and all genes are participated to estimating the missing values and use bitwise similarity matching instead of the Euclidian distance metric. To measure the correlation with respect to expression values between the normal and cancerous samples, the dataset is split into small subsets, which help to estimate the missing values effectively. In this paper, the gene dataset is initially divided into a group of correlated genes and then splitting and merging-based clustering algorithm gives the stable and optimal clusters of gene and finally the missing value of a gene is estimated by comparing it with the centroids of the final clusters of genes. The performance of proposed method is analyzed using publicly available microarray datasets, and the accuracy of the method is compared with some state of the art methods measuring NRMSE, CPP and BLCI values, which shows the goodness of proposed method. The proposed method is applicable for any dataset with two or more class labels for imputing the missing values. So, though the method is not suitable for a time series dataset of single class, it is equally applicable for multi-class time series microarray datasets.

Table 11 CPP and BLCI values for experimental datasets