Defining and evaluating network communities based on ground-truth

Abstract

Nodes in real-world networks organize into densely linked communities where edges appear with high concentration among the members of the community. Identifying such communities of nodes has proven to be a challenging task due to a plethora of definitions of network communities, intractability of methods for detecting them, and the issues with evaluation which stem from the lack of a reliable gold-standard ground-truth. In this paper, we distinguish between structural and functional definitions of network communities. Structural definitions of communities are based on connectivity patterns, like the density of connections between the community members, while functional definitions are based on (often unobserved) common function or role of the community members in the network. We argue that the goal of network community detection is to extract functional communities based on the connectivity structure of the nodes in the network. We then identify networks with explicitly labeled functional communities to which we refer as ground-truth communities. In particular, we study a set of 230 large real-world social, collaboration, and information networks where nodes explicitly state their community memberships. For example, in social networks, nodes explicitly join various interest-based social groups. We use such social groups to define a reliable and robust notion of ground-truth communities. We then propose a methodology, which allows us to compare and quantitatively evaluate how different structural definitions of communities correspond to ground-truth functional communities. We study 13 commonly used structural definitions of communities and examine their sensitivity, robustness and performance in identifying the ground-truth. We show that the 13 structural definitions are heavily correlated and naturally group into four classes. We find that two of these definitions, Conductance and Triad participation ratio, consistently give the best performance in identifying ground-truth communities. We also investigate a task of detecting communities given a single seed node. We extend the local spectral clustering algorithm into a heuristic parameter-free community detection method that easily scales to networks with more than 100 million nodes. The proposed method achieves 30 % relative improvement over current local clustering methods.

1 Introduction

Networks are a natural way to represent social [23], biological [26], technological [18], and information [9] systems. Nodes in such networks organize into densely linked groups that are commonly referred to as network communities, clusters, or modules [12]. There are many reasons why nodes in networks organize into densely linked clusters. For example, society is organized into social groups, families, villages, and associations [8, 14]. On the World Wide Web, topically related pages link more densely among themselves [9]. And, in metabolic networks, densely linked clusters of nodes are related to functional units, such as pathways and cycles [26].

In community detection, one aims to identify sets of nodes that correspond to communities. One way to formalize the process of community detection is to think of a scoring function that quantifies how much the connectivity pattern of a given set of nodes resembles the connectivity structure of a network community. Most scoring functions, like Modularity [25] and Conductance [31], are based on the intuition that sets of nodes that have many connections between its members correspond to communities. Once the scoring function is defined then one applies a procedure to find sets of nodes with high score. Such sets of nodes are then extracted and referred to as network communities.

Identifying such communities in networks [7, 10, 16, 29, 36] has proven to be a challenging task [11, 19, 20] due to several reasons: There exist a plethora of definitions, scoring functions, and methods for extracting network communities [6, 27]; even if we would agree on a single common structural definition (i.e., a single scoring function), the algorithmic formalizations of community detection lead to NP-hard problems [29]; And the lack of reliable ground-truth makes the evaluation of extracted communities and comparison of algorithms extremely difficult.

Currently, the performance of community detection methods is often evaluated by manual inspection. For each detected community, an effort is made to interpret it as a ‘real’ community by identifying a common property or external attribute shared by all the members of the community. For example, when examining communities in a scientific collaboration network, we might by manual inspection discover that many of detected communities correspond to groups of scientists working in common areas of science [25]. Such anecdotal evaluation procedures require extensive manual effort, are non-comprehensive, and limited to small networks.

A possible solution to this problem would be to find a reliable definition of explicitly labeled gold-standard ground-truth communities. Using such ground-truth communities would allow for quantitative and large-scale evaluation and comparison of network community detection methods. Such ability would enable the field to move beyond the current standard of anecdotal evaluation of communities to a comprehensive evaluation of community detection methods based on their performance to extract the ground-truth. Furthermore, it would allow for the development of new community detection methods and improve the understanding of how communities manifest themselves in networks.

1.1 Present work: structure and function

In this paper, we define a robust notion of ground-truth communities. We achieve this by distinguishing between structural and functional definitions of communities. We argue that the goal of network community detection is to extract functional communities based on the connectivity structure of the nodes in the network. We identify networks with explicitly labeled functional communities and then present a methodology that allows us to evaluate different structural definitions of communities.

Generally, after some community detection algorithm identifies communities based on the network structure, the essential next step is to interpret the communities by identifying a common external property or a function that the members of a given community share and around which the community organizes [8]. For example, given a protein–protein interaction network of a cell, one first identifies communities based on the structure of the network and then examines that these communities correspond to real functional units of a cell. Thus, the goal of community detection is to identify sets of nodes with a common (often external/latent/unobserved) function based on the connectivity structure of the network. In this context, a common function can be a common role, affiliation, or attribute [14]. In our protein interaction network example above, such common function of nodes would be ‘belonging to the same functional unit.’ Or, in a social network, common function would be ‘belonging to the same social circle.’

Thus, community detection methods identify communities based on the network structure, while the detected communities are then evaluated based on their function. Thus, we distinguish between structural and functional definitions of communities. Structural definitions are based on the structure of the connectivity between a set of nodes (e.g., a set of nodes with high Modularity score [25]). On the other hand, functional definitions of network communities are based on common function or role that the community members share (e.g., proteins of the same functional unit). Generally, the basic premise behind the network community detection is that functional communities have distinct structural patterns, and thus, one may be able to identify them based on the network structure.

1.2 Present work: networks with ground-truth communities

Our goal here is to obtain high-quality labels of ground-truth communities so that we can then devise a methodology to compare and evaluate various structural definitions of network communities.

While explicitly labeled structural communities are nearly impossible to obtain, our main insight here is that there exist networks where functional communities are explicitly declared in the data. Thus, we use sets of nodes with a common function to define ground-truth communities.

We gathered 230 networks from a number of different domains and research areas where nodes explicitly state their ground-truth functional community memberships. The size of the networks ranges from hundreds of thousand to hundreds of millions of nodes and edges. The networks represent a wide range of edge densities, numbers of explicitly defined communities, as well as sizes and amounts of community overlap.

Our collection consists of social, collaboration, and information networks for each of which we find a robust functional definition of ground-truth. For example, in online social networks (like Orkut, LiveJournal, and Friendster), we consider explicitly defined interest-based groups (e.g., fans of pop singer Lady Gaga, students of the same school) as ground-truth functional communities. Nodes in these networks explicitly join such groups that organize around specific topics, interests, and affiliations [8, 14]. We also consider the product co-purchasing network from Amazon where we define ground-truth using hierarchically nested product categories. Here, all members (i.e., products) of the same ground-truth community share a common function or purpose. Last, in the scientific collaboration network of DBLP, we use publication venues as proxies for ground-truth research communities. Our reasoning here is that in scientific collaboration networks, real communities would correspond to areas of science. Thus, we use journals and conferences as proxies for (heavily overlapping) scientific communities.

1.3 Present work: methodology and findings

The availability of ground-truth allows us to examine how well various structural definitions of network communities correspond to functional communities (i.e., ground-truth communities). A good structural definition of a community would be such that it would correspond to connectivity patterns that correspond to functional communities. Our experiments show a clear connection between functional and structural definitions: We show that functional communities exhibit distinct connectivity patterns. This means that we can evaluate different structural definitions based on their ability to identify ground-truth communities.

We study 13 commonly used structural definitions of communities and examine their quality, sensitivity, and robustness. Each such definition corresponds to a scoring function that scores a given set of nodes how ‘community-like’ it is, i.e., a scoring function assigns high score to sets of nodes that closely resemble functional communities. By comparing correlations of scores that different structural definitions assign to ground-truth communities, we find that the 13 definitions naturally group into four distinct classes. These classes correspond to definitions that consider: (1) only internal community connectivity, (2) only external connectivity of the nodes to the rest of the network; (3) both internal and external community connectivity, and (4) network modularity.

We then consider an axiomatic approach and define four intuitive properties that communities would ideally have. Intuitively, a ‘good’ community is cohesive, compact, and internally well connected while being also well separated from the rest of the network. This allows us to characterize which connectivity patterns a given structural definition detects and which ones it misses. Next, we also investigate the robustness of community scoring functions based on four types of randomized perturbation strategies. Overall, evaluation shows that among the scoring functions considered here those that are based on triadic closure [35] and the Conductance score [31] best capture the structure of ground-truth communities.

Last, we also investigate a task of discovering all members of a community given a single member node. We extend the local spectral clustering algorithm [3] into a parameter-free community detection method that scales to networks of hundreds of millions of nodes. Our method recovers ground-truth communities with 30 % relative improvement in the F1-score over the current local graph partitioning methods.

To the best of our knowledge, our work is the first to use social and information networks with explicit community memberships to define an evaluation methodology for comparing network community detection methods based on their accuracy on real data. We believe that the present work will bring more rigor to the standard for the evaluation of community detection methods. All our datasets can be downloaded at http://snap.stanford.edu.

The rest of the paper is organized as follows. Section 2 describes the datasets and defines the notions of ground-truth communities in each dataset. Section 3 shows the distribution of the properties of ground-truth communities and the structural characteristics of ground-truth communities. Section 4 describes the structural definitions of communities that we consider in this paper and discusses the relationship among the definitions. In Sect. 5, we evaluate the structural definitions of communities on two aspects. First, we study what connectivity patterns various definitions prefer and which they penalize. Second, we evaluate the robustness of community structure by using a set of randomized community perturbation strategies. Section 6 considers the problem of identifying ground-truth communities from seed nodes. Section 7 discusses related work. We conclude in Sect. 8.

Last, we also note that a shorter version of this paper appeared at the IEEE International Conference on Data Mining (ICDM) [38].

2 Ground-truth communities

We begin by explaining the intuition behind the definition the ground-truth communities. We distinguish between structural and functional definitions of communities. A structural definition of communities is a set of nodes with a particular connectivity structure (e.g., set of nodes with high edge density or set of nodes with high Modularity score). A functional definition of communities is a set of nodes with a common function, which can be common role, affiliation, or attribute [8, 14].

With these two definitions of communities, community detection process generally follows a two-step procedure: First one discovers communities based on a structural definition. And then one argues that the discovered communities correspond to functional communities. For example, Palla et al. [26] identified structural communities by identifying sets of overlapping $k$-cliques on protein–protein interaction networks. Then, they found that these structurally defined communities of proteins correspond to functional modules of proteins. In this example, communities are extracted based on the structural definition and then evaluated based on the functional definition by arguing that ‘belonging to the same functional module’ is the common function of nodes. An issue with this approach is that it is ad hoc and that the evaluation of extracted structural communities is manual—each extracted community has to be manually inspected.

Our approach takes the different direction: We first identify large-scale datasets where functional communities are already labeled, and then we evaluate community detection methods based on their ability to extract ground-truth functional communities.

Overall we consider 230 large social, collaboration and information networks, where for each network we have a graph and a set of functionally defined ground-truth communities. Members of these ground-truth communities share a common function, property or purpose. Networks that we study come from a wide range of domains and sizes. Table 1 lists the networks and their properties.

Table 1 230 Social, collaboration, and information networks with explicit ground-truth communities

2.1 Ground-truth communities in social networks

First, we consider three online social networks: the LiveJournal blogging community [5], the Friendster online network [23], and the Orkut social network [23]. In these networks, users create explicit functional groups to which other users then join. Such groups serve as organizing principles of nodes in social networks. Groups range from small to very large and are created based on specific topics, interests, hobbies, and geographical regions. For example, LiveJournal categorizes communities into the following types: culture, entertainment, expression, fandom, life/style, life/support, gaming, sports, student life, and technology. There are over 100 communities in LiveJournal with ‘Stanford’ in their name, and they range from communities based on different classes, student ethnic communities, departments, activity and interest-based groups, varsity teams, etc. Overall, there are over three hundred thousand explicitly defined communities in LiveJournal.

Similarly, users in Friendster as well as in Orkut define topic-based communities that others then join. Both networks have more than a million explicitly defined groups and each user can join to one or more such groups. We consider each group as a ground-truth community.

Last, we have a set of 225 different online social networks [15] that are all hosted by the Ning platform. It is important to note that each Ning network is a separate social network—an independent Web site with a separate user community. For example, the NBA team Dallas Mavericks and diabetes patients network TuDiabetes all use Ning to host their separate online social networks. After joining a specific network, users then create and join groups. For example, in TuDiabetes, Ning network groups form around specific types of diabetes, parenting children with diabetes, different geographical regions, age groups, and similar. Note that these are exactly the properties around which we expect communities to form in a network of diabetes patients. Again, we use such explicitly defined functional groups as ground-truth communities.

As we see in Table 1, ground-truth communities in social networks are quite diverse. For example, communities in Friendster are about twice smaller than communities in Ning or LiveJournal. Communities in Orkut overlap heavily as people are members of many communities at the same time, while for example, in Friendster, most nodes do not belong to any community.

2.2 Ground-truth communities in product networks

The second type of a network we consider is the Amazon product co-purchasing network [18]. The nodes of the network represent products and edges link commonly co-purchased products. Each product (i.e., node) belongs to one or more hierarchically organized product categories, and products from the same category define a group which we view as a ground-truth community. Note that here the definition of ground-truth is somewhat different. In this case, nodes that belong to a common ground-truth community share a common function or purpose.

Ground-truth communities in product networks (Table 1) are larger than in social networks and include around 100 nodes on the average. Given the hierarchical categorization of products, we also note that an average product belongs to 14 categories, i.e., ground-truth communities.

2.3 Ground-truth communities in collaboration networks

Finally, we also consider the DBLP scientific collaboration network [5], where nodes represent authors and edges connect authors that have co-authored a paper. To define ground-truth in this setting, we reason as follows. Functional communities in a scientific domain correspond to people working in common areas and subareas of science. However, note that publication venues serve as good proxies for scientific areas: People publishing in the same conference form a scientific community. Thus, we use publication venues (i.e., conferences, journals) as ground-truth communities, which serve as proxies for highly overlapping scientific communities around which the collaboration network then organizes.

Ground-truth communities in the DBLP network (Table 1) are the largest and moderately overlap with nodes being part of about 2.5 different communities on the average.

To conclude, we note that all our networks and the corresponding ground-truths are complete and publicly available at http://snap.stanford.edu. For each of these networks, we identified a sensible way of defining ground-truth communities that serve as organizational units of these networks. We were careful to define ground-truth communities based on common affiliation, social circle, role, activity, interest, function, or some other property around which networks organize into communities [8, 14]. Even though our networks come from very different domains and have very different motivation for the formation of communities, the results we present here are consistent and robust. Our work is consistent with the premise that is implicit in all network community literature: members of real communities share some (latent/unobserved) property or affiliation that serves as an organizing principle of the nodes and makes them well connected in the network. Here, we use these groups around which communities organize to explicitly define ground-truth. And, as we will later see, the ground-truth communities exhibit connectivity patterns that match our intuition of communities as densely connected sets of nodes.

2.4 Data preprocessing

To represent all networks in a consistent way, we consider each network as an unweighted undirected static graph. Because members of the group may be disconnected in the network, we consider each connected component of the group as a separate ground-truth community. However, we allow ground-truth communities to be nested and to overlap, i.e., nodes can be members of multiple communities at once.

3 Characteristics of ground-truth communities

In this section, we examine properties of ground-truth communities. First we study size and overlap distributions of communities and then proceed to examine finer structural properties of ground-truth communities.

3.1 Global properties of ground-truth communities

We start by analyzing the distribution of the properties of ground-truth communities. Figure 1 gives the distributions (complementary CDF) of community sizes which are the number of the nodes in the communities. Notice that all distributions are heavily skewed with most ground-truth communities being small, while large communities also exist. For example, largest social communities contain between one and ten thousand people, while product communities can be even larger.

Fig. 1

Ground-truth community size distribution. Complementary cumulative distribution function of the size of ground-truth communities. The size of a ground-truth community denotes the number of nodes belonging to the ground-truth community

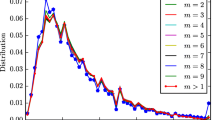
To get a sense of how much communities overlap, we also examine how many communities a node belong to. Figure 2 plots the distribution of the number of community memberships that a node belongs to. Again, we observe heavy tails with most nodes belonging to only a small number of communities and few nodes belonging to many.

Fig. 2

Node membership distribution. Complementary cumulative distribution function of the node memberships (the number of communities nodes belong to)

We further examine the properties of community overlaps. We focus on characterizing the overlap between pairs of ground-truth communities. We show the distribution of the absolute overlap sizes (the number of the nodes in the overlap) in Fig. 3. We observe that the distributions follow a power law, as also observed by Palla et al. [26] on detected (rather than ground-truth) communities.

Fig. 3

Community overlap distribution. Complementary cumulative distribution function of the size of overlaps between pairs of ground-truth communities. The size of an overlap is the number of the nodes that belong to the overlap

Last, we also study on the relative size of community overlaps. Relative sizes of overlaps are of our interest as they can characterize how ground-truth communities overlap: Do ground-truth communities overlap in a nested structure? Or, do they overlap only for a small fraction of members? We measure the fraction $f$ of the size of the overlap $A \cap B$ between two communities $A, B$ to the size of the smaller community, $\hbox {min} (|A|, |B|)$ ($f = |A \cap B| / \hbox {min} (|A|, |B|)$). If the fraction of overlap is close to 1, the network has a nested structure where the smaller community is included by the larger community. On the other hand, $f$ being close to 0 means that most communities are non-overlapping. We plot the histogram of the overlap fraction in Fig. 4. The Amazon network shows high probability at $f = 1$ because the ground-truth communities form a nested structure by construction. In social networks and the DBLP network, most overlaps take a small fraction of individual communities, which is reasonable as each community has its own special interests.

Fig. 4

Relative size of community overlaps. Histogram of the fraction of the relative overlap size. When ground-truth communities $A, B$ overlap $A \cap B$, then the fraction of the relative overlap size is $|A \cap B| / \hbox {min}(|A|, |B|)$, where $\hbox {min}(x,y)$ is the smaller of $x$ and $y$

3.2 Structural characteristics of ground-truth communities

In this subsection, we show that ground-truth communities that we defined have distinct connectivity properties. We show that our ground-truth communities, which are sets of nodes sharing common functions or properties (i.e., functional communities), also exhibit distinctive structural properties. The experiments confirm the premise that the functional communities exhibit distinct structural connectivity patterns and can thus be discovered based on the network connectivity structure.

We compare structural properties of a ground-truth community $C_i$ to those of a set of nodes that do not form a ground-truth community with the goal to establish how ground-truth communities structurally differ from non-communities. For each ground-truth community $C_i$, we sample a ‘non-community’ $\tilde{C_i}$, a set of nodes outside $C_i$ to which we compare $C_i$. To make our experiments realistic, we add three constraints to $\tilde{C_i}$:

• 1. $\tilde{C_i}$ has the same number of nodes as $C_i$

• 2. $\tilde{C_i}$ is connected

• 3. Members of $\tilde{C_i}$ have the same distribution of shortest path distances as $C_i$

The last constraint is an approximation for the ideal that we want $C_i$ and $\tilde{C_i}$ to have similar ‘compactness’ or ‘connectedness.’ To achieve these constraints, we proceed as follows. We take a node $u \in C_i$ uniformly at random and compute the distance histogram $H_u(k) = |\{v \in C_i: d(u, v) = k\}|$ that is the number of other member nodes who are $k$-hop away from $u$ $(k = 0, 1, 2,\ldots )$. Then, we pick $\tilde{u} \not \in C_i$ from which we generate $\tilde{C_i}$ by adding $H_u(k)$ nodes from the $k$-hop neighbors of $u'$. For example, if $H_u(0) = 1, H_u(1) = 3, H_u(2) = 5$, $\tilde{C_i}$ contains $\tilde{u}$, 3 neighbors of $\tilde{u}$, and 5 2-hop neighbors of $\tilde{u}$. At the same time, we only choose the nodes that are connected to at least one of the other members of $\tilde{C_i}$ to guarantee the connectedness of $\tilde{C_i}$.

We then measure the structural properties of $C_i$ and $\tilde{C_i}$. For a set of nodes $S$ ($S = C_i$ or $\tilde{C_i}$) that has $n_S$ member nodes and $m_S$ edges among its member nodes, we measure the following:

• Clustering coefficient (CCF) is the average clustering coefficient between the member nodes of $S$ [35].

• Average degree (AvgDeg) is the average number of node degree to other member nodes. ($2 m_S / n_S$) [27].

• Edge density (Density) is the fraction of pairs of member nodes that have an edge ($4 m_S / (n_S (n_S - 1) )$) [27].

• Cohesiveness captures the intuition that a good community should be internally well and evenly connected, i.e., it should be relatively hard to split a community into two subcommunities [19]. We capture this intuition by defining cohesiveness as the Conductance of the internal cut: $\max _{S' \subset S} \phi (S')$ where $\phi (S')$ is the Conductance of $S'$ measured in the induced subgraph by $S$. We will precisely define Conductance later, but intuitively, the more cohesive the community, the more edges have to be cut in order to further split the community and thus the higher the Conductance score of the internal cut.

Table 2 shows the ratio between the average value of $C_i$ and that of $\tilde{C_i}$ for the 3 properties. We observe that groups show 18 % higher clustering coefficient, 51 % higher average degree, 39 %higher edge density, and 102 % higher cohesiveness than sets of randomly chosen connected sets of nodes. This shows that the members of functional communities tend to be more cohesively and densely connected and thus exhibit distinct connectivity patterns.

Table 2 Comparison between ground-truth communities (functional communities) and sets of randomly chosen connected nodes

4 Community scoring functions

In community detection, one aims to identify sets of nodes that correspond to communities. One way to formalize this process is to design a scoring function that for a set of nodes outputs a quality score that characterizes how much the connectivity structure of a given set of nodes resembles that of a community. The idea then is that given a community scoring function, one can then find sets of nodes with high score and consider these sets as communities.

In practice, nearly all scoring functions build on the intuition that communities are sets of nodes with many connections between the members and few connections from the members to the rest of the network. There are many possible ways to mathematically formalize this intuition. We gather 13 commonly used scoring functions or, equivalently, 13 structural definitions of network communities. Some scoring functions are well known in the literature, while others are proposed here for the first time.

Given a set of nodes $S$, we consider a function $f(S)$ that characterizes the community quality of a given set of nodes $S$. Let $G(V,E)$ be an undirected graph with $n = |V |$ nodes and $m = |E|$ edges. Let $S$ be the set of nodes, where $n_S$ is the number of nodes in $S$, $n_S = |S|$; $m_S$ the number of edges in $S$, $m_S = |\{(u, v) \in E : u \in S, v \in S\}|$; $c_S$, the number of edges on the boundary of $S$, $c_S = |\{(u, v) \in E: u \in S, v \not \in S\}|$; and $d(u)$ is the degree of node $u$. We consider 13 scoring functions $f(S)$ that capture the notion of quality of a network community $S$. The experiments we will present later reveal that scoring functions naturally group into the following four classes:

(A) Scoring functions based on internal connectivity:

• Internal density: $f(S) = \frac{m_S}{n_S(n_S-1)/2}$ is the internal edge density of the node set $S$ [27].

• Edges inside: $f(S) = m_S$ is the number of edges between the members of $S$ [27].

• Average degree: $f(S) = \frac{2 m_S}{n_S}$ is the average internal degree of the members of $S$ [27].

• Fraction over median degree (FOMD): $f(S) = \frac{|\{u:u \in S, |\{(u,v):v \in S\}| > d_m\}|}{n_S}$ is the fraction of nodes of $S$ that have internal degree higher than $d_m$, where $d_m$ is the median value of $d(u)$ in $V$.

• Triangle participation ratio (TPR): $f(S) = \frac{|\{u:u \in S, \{(v,w):v,w \in S, (u,v) \in E, (u,w) \in E, (v,w) \in E\} \ne \varnothing \}|}{n_S}$ is the fraction of nodes in $S$ that belong to a triad.

(B) Scoring functions based on external connectivity:

• Expansion measures the number of edges per node that point outside the cluster: $f(S) = \frac{c_S}{n_S}$ [27].

• Cut ratio is the fraction of existing edges (out of all possible edges) leaving the cluster: $f(S) = \frac{c_S}{n_S(n-n_S)}$ [10].

(C) Scoring functions that combine internal and external connectivity:

• Conductance: $f(S) = \frac{c_S}{2m_S+c_S}$ measures the fraction of total edge volume that points outside the cluster [31].

• Normalized Cut: $f(S) = \frac{c_S}{2m_S+c_S} + \frac{c_S}{2(m-m_S)+c_S}$ [31].

• Maximum-ODF (Out Degree Fraction): $f(S) = \max _{u \in S} \frac{|\{(u,v) \in E:v \not \in S\}|}{d(u)}$ is the maximum fraction of edges of a node in $S$ that point outside $S$ [9].

• Average ODF: $f(S) = \frac{1}{n_S} \sum _{u \in S}\frac{|\{(u,v) \in E:v \not \in S\}|}{d(u)}$) is the average fraction of edges of nodes in $S$ that point out of $S$ [9].

• Flake ODF: $f(S) = \frac{|\{u:u \in S,|\{(u,v) \in E:v \in S\}|<d(u)/2\}|}{n_S}$ is the fraction of nodes in S that have fewer edges pointing inside than to the outside of the cluster [9].

(D) Scoring function based on a network model:

• Modularity: $f(S) = \frac{1}{4} (m_S - E(m_S))$ is the difference between $m_S$, the number of edges between nodes in $S$, and $E(m_S)$, the expected number of such edges in a random graph with identical degree sequence [24].

4.1 Experimental result: four classes of scoring functions

We examine relationship of the 13 community scoring functions we introduced. For each of the 10 million ground-truth communities in our networks, we compute a score using each of the 13 scoring functions. We then create a correlation matrix of scoring functions and threshold it. Figure 5 shows connections between scoring functions with correlation $\ge$0.6 on the LiveJournal network.

Fig. 5

Correlations of community scoring functions. Two scoring functions are connected by an edge if the values output by scoring functions are correlated with correlation coefficient $\ge$0.6. Notice four distinct classes of scoring functions

We observe that scores naturally group into four clusters. This means that scoring functions of the same cluster return heavily correlated values and quantify the same aspect of connectivity structure. Overall, none of the scoring functions are negatively correlated, which means that none of them systematically disagree. Interestingly, Modularity is not correlated with any other scoring function (average degree is the most correlated at 0.05 correlation).

We observe very similar results in all other network datasets that we considered in this study.

The experiment demonstrates that even though many different structural definitions of communities have been proposed, these definitions are heavily correlated. Essentially, there are only 4 different structural notions of network communities as revealed by Fig. 5. For brevity, in the rest of the paper, we present results for 6 representative scoring functions (denoted as blue nodes in Fig. 5): 4 from the two large clusters and 2 from the two small clusters.

We also note that here we computed the values of the 13 scores on ground-truth communities. In reality, the aim of community detection is to find sets of nodes that maximize a given scoring function. Exact maximization of these functions is typically NP-hard and leads to its own set of interesting problems. (Refer to [19] for discussion.)

5 Evaluation of community scoring functions

The second main purpose of our paper is to develop an evaluation methodology for network community detection. Based on ground-truth communities, we now aim to compare and evaluate different community scoring functions. We focus on two aspects of community scoring functions: how well the community scoring function can detect communities (Sect. 5.1) and how robust the community scoring function is to noise in network structure as well as node labeling (Sect. 5.2).

5.1 Detecting communities

Our goal is to rank different structural definitions of network communities (i.e., community scoring functions) by their ability to detect ground-truth communities. We adopt the following axiomatic approach. First, we define four community ‘goodness’ metrics that formalize the intuition that ‘good communities’ are both compact and well connected internally while being relatively well separated from the rest of the network.

The difference between community scoring functions from Sect. 4 and the goodness metrics defined above is that a community scoring function quantifies how community-like a set is, while a goodness metric in an axiomatic way quantifies a desirable property of a community. A set with high goodness metric does not necessarily correspond to a community, but a set with high community score should have a high value on one or more goodness metrics. In other words, the goodness metrics shed light on various (in many cases mutually exclusive) aspects of the network community structure.

Using the notation from Sect. 4, we define four goodness metrics $g(S)$ for a node set $S$:

• Separability captures the intuition that good communities are well separated from the rest of the network [10, 31], meaning that they have relatively few edges pointing from set $S$ to the rest of the network. Separability measures the ratio between the internal and the external number of edges of $S$: $g(S) = \frac{m_S}{c_S}$.

• Density builds on intuition that good communities are well connected [10]. It measures the fraction of the edges (out of all possible edges) that appear between the nodes in $S$, $g(S) = \frac{m_S}{n_S(n_S-1)/2}$.

• Cohesiveness characterizes the internal structure of the community. Intuitively, a good community should be internally well and evenly connected, i.e., it should be relatively hard to split a community into two subcommunities. We characterize this by the Conductance of the internal cut. Formally, $g(S) = \max _{S' \subset S} \phi (S')$ where $\phi (S')$ is the Conductance of $S'$ measured in the induced subgraph by $S$. Conductance essentially corresponds to the ratio of the edges in $S'$ that point outside the set and the edges inside the set $S'$. A good community should have high cohesiveness (high internal Conductance) as it should require deleting many edges before the community would be internally split into disconnected components [19].

• Clustering coefficient is based on the premise that network communities are manifestations of locally inhomogeneous distributions of edges, because pairs of nodes with common neighbors are more likely to be connected with each other [35].

5.1.1 Experimental setup

We are interested in quantifying how ‘good’ are the communities chosen by a particular scoring function $f(S)$ by evaluating their goodness metric. We formulate our experiments as follows: For each of 230 networks, we have a set of ground-truth communities $S_i$. For each community scoring function $f(S)$, we rank the ground-truth communities by the decreasing score $f(S_i)$. We measure the cumulative running average value of the goodness metric $g(S)$ of the top-$k$ ground-truth communities (under the ordering induced by $f(S_i)$).

The intuition for the experiments is the following. A perfect community scoring function would rank the communities in the decreasing order of the goodness metric, and thus, the cumulative running average of the goodness metric would decrease monotonically with $k$. Whereas if a hypothetical community scoring function would randomly rank the communities, then the cumulative running average would be a constant function of $k$.

5.1.2 Experimental results

We found qualitatively similar results on all our datasets. In this section, we only present results for the LiveJournal network. Results are representative for all other networks. We point the reader to the appendix of the paper for a complete set of results (Figs. 10 and 11).

Figure 6a shows the results by plotting the cumulative running average of separability score for LiveJournal ground-truth communities ranked by each of the six community scoring functions. Curve ‘U’ presents the upper bound, i.e., it plots the cumulative running average of separability when ground-truth communities are ordered by decreasing separability. If the scoring function would order communities exactly by their value of the goodness score, then optimal curve ‘U’ would be achieved.

Fig. 6

Cumulative average of goodness metrics for LiveJournal communities ranked by each of the six representative scoring functions. C conductance and T TPR, with high and monotonically decreasing values perform best

We observe that Conductance (C) and cut ratio (CR) give near optimal performance, i.e., they nearly perfectly order the ground-truth communities by separability. On the other hand, we observe Triad participation ratio (T) and Modularity (M) score ground-truth communities in the inverse order of separability (especially for $k <100$), which means that they both prefer densely linked sets of nodes.

Similarly, Fig. 6b, c, and d shows the cumulative running average of community density, cohesiveness, and clustering coefficient. We observe that all scoring functions (except Modularity) rank denser, more cohesive and more clustered ground-truth communities higher. For the density metric, the fraction over median degree (D) score performs best for high values of $k$ followed by Conductance (C) and Flake ODF (F). In terms of cohesiveness and clustering coefficient, the Triad participation ratio (T) score gives by far the best results. In all cases, the only exception is the Modularity, which ranks the communities in nearly reverse order of the goodness metric (the cumulative running average increases as a function of $k$). We note that these are all well-known issues of Modularity [11], but they get further attenuated when tested on ground-truth communities.

The curves in Fig. 6 illustrate the ability of the scoring functions to rank communities for the LiveJournal communities. To further quantify this, we perform the following experiment. For a given goodness metric $g$ and for each scoring function $f$, we measure the rank of each scoring function in comparison with other scoring functions at every value of $k$. For example, in Fig. 6a, the rank at $k=100$ of Conductance is 1, Cut ratio 2, Flake ODF 3, FOMD 4, Modularity 5, and TPR 6. For every $k$, we rank the scores and compute the average rank over all values of $k$, which quantifies the ability of the scoring function to identify communities with high goodness metric.

Table 3 shows the average rank for each score and each goodness metric. An average rank of 1 means that a particular score always outperforms other scores, while rank of 6 means that the score gives worst ranking out of all 6 scores. We observe that Conductance (C) performs best in terms of separability but relatively bad in the other three metrics. For density, cohesiveness, and clustering coefficient, Triad participation ratio (T) is the best. Perhaps not surprisingly, Triad participation ratio scores badly on separability of ground-truth communities. Thus, Conductance is able to identify well-separated communities, but performs poorly in identifying dense and cohesive sets of nodes with high clustering coefficient. On the other hand, triad participation ratio gives the worst performance in terms of separability but scores the best for the other three metrics.

Table 3 Average scoring function rank for each goodness metric

We conclude that depending on the network, different structural notions of network communities might be appropriate. When the network contains well-separated non-overlapping communities, Conductance is the best scoring function. When the network contains dense heavily overlapping communities, then the Triad participation ratio defines the most appropriate notion of a community. Further research is needed to identify most appropriate structural definitions of communities for various types of networks and functional communities. For example, in social networks, we have both identity-based and bond-based communities [28], and they may in fact have different structural signatures.

Figures 10 and 11 in the appendix show the results for all the networks, where we find similar trends. Interestingly, in Figs. 10 and 11, we also observe that the average goodness metric of the top $k$ communities remains flat but then quickly degrades. We observe the same pattern in all our datasets. Thus, for the remainder of the paper, we focus our attention on a set of the top 5,000 communities of each network based on the average rank over the 6 scores.

5.2 Robustness to perturbation

In this subsection, we evaluate community scoring functions using a set of perturbation strategies. We develop a set of strategies to generate randomized perturbations of ground-truth communities, which allows us to investigate robustness and sensitivity of community scoring functions. Intuitively, a good community scoring function should be such that it is stable under small perturbations of the ground-truth community but degrades quickly with larger perturbations.

Our reasoning is as follows. We desire a community scoring function that scores well when evaluated on a ground-truth community but scores low when evaluated on a perturbed community. In other words, an ideal community scoring function should give a maximal value when evaluated on the ground-truth community. If we consider a slightly perturbed ground-truth community (i.e., a node set that differs very slightly from the ground-truth community), we would want the score to be nearly as good as the score of the original ground-truth community. This would mean that the scoring function is robust to noise. However, if the ground-truth community is perturbed so much that it resembles a random set of nodes, then a good scoring function should give it a low score.

5.2.1 Community perturbation strategies

We proceed by defining a set of community perturbation strategies. To vary the amount of perturbation, each perturbation strategy has a single parameter $p$ that controls the intensity of the perturbation. Given $p$ and a ground-truth community defined by its members $S$, the community perturbation starts with $S$ and then modifies it (i.e., changes its members) by executing the perturbation strategy $p|S|$ times. We define the following perturbation strategies:

• NodeSwap perturbation is based on the mechanism where the community memberships diffuse from the original community through the network. We achieve this by picking a random edge $(u,v)$ where $u \in S$ and $v \not \in S$ and then swap the memberships (i.e., remove $u$ from $S$ and add $v$). Note that NodeSwap preserves the size of $S$ but if $v$ is not connected to the nodes in $S$, then NodeSwap makes $S$ disconnected.

• Random takes community members and replaces them with random non-members. We pick a random node $u \in S$ and a random $v \not \in S$ and then swap the memberships. Like NodeSwap, Random maintains the size of $S$ but may disconnect $S$. Generally, Random will degrade the quality of $S$ faster than NodeSwap, since NodeSwap only affects the ‘fringe’ of the community.

• Expand perturbation grows the membership set $S$ by expanding it at the boundary. We pick a random edge $(u,v)$ where $u \in S$ and $v \not \in S$ and add $v$ to $S$. Adding $v$ to $S$ will generally decrease the quality of the community. Expand preserves the connectedness of $S$ but increases the size of $S$.

• Shrink removes members from the community boundary. We pick a random edge $(u,v)$ where $u \in S, v \not \in S$ and remove $u$ from $S$. Shrink will decrease the quality of $S$ and result in a smaller community while preserving connectedness.

For a given $S$, let $h(S, p)$ denote a perturbed version of the community generated by the perturbation $h$ of intensity $p$.

We now quantify the difference of the score between the unperturbed ground-truth community and its perturbation. We use the $Z$-score, which measures in the units of standard deviation how much the scoring function changes as a function of perturbation intensity $p$. For ground-truth community $S_i$, the $Z$-score $Z(f, h, p)$ of community scoring function $f$ under perturbation strategy $h$ with intensity $p$ is as follows:

$$\begin{aligned} Z(f,h, p) = \frac{E_i[f(S_i) - f(h(S_i, p)) ]}{ \sqrt{Var_i[f(h(S_i, p))]}}, \end{aligned}$$

where $E_i[\cdot ], Var_i[\cdot ]$ are the mean and the variance over communities $S_i$, and $f(h(S_i, p))$ is the community score of perturbed $S_i$ under perturbation $h$ with intensity $p$. To measure $f(h(S_i, p))$, we run 20 trials of $h(S_i, p)$ and compute the average value of $f$. $Z$-score is the difference between the average community score of true communities $f(S_i)$ and the average community scores of perturbed communities $f(h(S_i, p))$ normalized by the standard deviation of community scores of perturbed communities. Since $f(h(S_i, p))$ are independent for each $i$, $E_i[f(h(S_i, p)) ]$ follows a normal distribution by the Central Limit Theorem. Thus, $P(z < Z(f, h, p))$ gives the probability that $E_i[f(h(S_i, p))] > E_i[f(S_i)]$ where $z$ is a standard normal random variable. We measure $f$ so that lower values mean better communities, i.e., we add a negative sign to TPR, Modularity and FOMD. High $Z$-scores mean that $E_i[f(S_i)]$ is likely to be smaller than $E_i[f(h(S_i, p))]$ and that $S_i$ is better than $h(S_i, p)$ in terms of $f$.

5.2.2 Experimental results

For each of the 6 community scoring functions, we measure $Z$-score for perturbation intensity $p$ ranging between 0.01 and 0.6. This means that we randomly swap between 1 and 60 % of the community members and measure the $Z$-score for each scoring function. For small $p$, small $Z$-scores are desirable since they indicate that the scoring function is robust to noise. For high perturbation intensities $p$, high $Z$-scores are preferred because this suggests that the community scoring function is sensitive, i.e., as the community becomes more ‘random,’ we want the scoring function to significantly increase its value.

Figure 7 shows the $Z$-scores as a function of perturbation intensity $p$ in the LiveJournal online social network. We plot the $Z$-score for each of the 6 community scoring functions. As expected, the $Z$-scores increase with $p$, which means that as the community gets more perturbed, the value of the score tends to decrease. The faster the increase the more sensitive and thus the better the score. For example, in LiveJournal, under the NodeSwap perturbation Conductance (C) exhibits the highest $Z$-score after $p > 0.2$, and it has the steepest curve. Triad participation ratio (T) also exhibits desirable behavior. On the other hand, Modularity (M) score does not change much as we perturb the ground-truth communities. This means that Modularity is not good at distinguishing true communities from randomized sets of nodes. Figure 12 and  13 in the appendix give the same plot for all other networks. We observe similar results.

Fig. 7

$Z$-scores as a function of the perturbation intensity. C conductance and T Triad participation ratio best detect the perturbations of LiveJournal ground-truth communities

Interestingly, Modularity (M) fails to achieve increasing $Z$-score as a function of perturbation intensity $p$ in all the networks except the Ning networks. We note that the key difference in Ning is the size of networks: Ning networks contain 3,000 nodes in average, whereas the other 5 networks contain at least almost a million nodes. Thus, our results show that, while Modularity works well in distinguishing true communities in small networks, it fails in large networks. Interestingly, this observation is consistent with the theoretical limitation of Modularity known as ‘the resolution limit’ [11]. Fortunato and Barthélemy [11] proved that Modularity is unable to distinguish communities when the network is too ‘large’ compared to community sizes, and this explains the failure of Modularity for 5 large networks other than Ning. Since the size of communities is generally less than 100 regardless of the network size (Table 1 and reference [20]), most communities are too ‘small’ for Modularity in these large-scale networks.

5.2.3 Sensitivity of community scoring functions

We also quantify the sensitivity of community scoring functions by computing the increase of the $Z$-score between small ($p=0.05$) and large perturbations ($p=0.2$). As noted above, we prefer a community scoring function with fast increase of the $Z$-score as the community perturbation intensity increases. Table 4 displays the difference of the $Z$-score between a large and a small perturbation: $Z(f,h,0.2)-Z(f,h,0.05)$. We compute the average increment across all the 230 networks. A high value of increment means that the score is both robust and sensitive. The score is robust because, at small perturbation ($p=0.05$), it maintains low $Z$-value, while at large perturbation ($p=0.2$), it has high $Z$-value and thus the overall $Z$-score increment is high.

Table 4 Average absolute increment of the $Z$-score between small and large community perturbations

Conductance is the most robust score under NodeSwap and Shrink. The Triad participation ratio (T) is the most robust under Random and Expand. In both cases, Conductance follows Triad participation ratio closely. We note that the clique percolation method (CPM) [26], which is the state-of-the-art overlapping community detection method, implicitly optimizes the Triad participation ratio. CPM will add a node to a community only if the node forms a clique (i.e., a triangle) in the community, and the Triad participation ratio of the detected communities will be $1$.

5.2.4 Bias of scoring functions

The experiments so far revealed surprisingly large differences in the robustness of different community scoring functions. Interestingly, we also observed that Modularity prefers large communities (score increases under Expand). To further investigate the bias of different community scoring functions on the size of the underlying network community, we perform the following experiment. We measure how the $Z$-score changes as a function of the size of the community while keeping perturbation intensity constant. In particular, we calculate the $Z$-score of each ground-truth community $S_i$ at perturbation intensity level $p=0.2$, and plot it as a function of the community size $|S_i|$. Figure 8 shows the results for the LiveJournal communities. Since $p=0.2$ represents relatively large perturbation, high $Z$-scores are desirable.

Fig. 8

$Z$-scores as a function of the community size

We observe that under NodeSwap Conductance is the most robust score and that as the community size increases, robustness of Conductance slightly decreases. For Random and Expand, the Triad participation ratio score performs best over the whole range of network community sizes. Generally, best performing scores tend to be more sensitive on small communities. The exception is Modularity. The results for Modularity are consistent with the resolution limit [11] mentioned previously. The $Z$-score of Modularity is very close to 0 for communities smaller than 100 members, i.e., Modularity cannot distinguish a community and a perturbed community when the community is smaller than around 100 nodes due to resolution limit. However, for large communities, Modularity score shows high $Z$-scores, except under the Expand perturbation, where it favors larger null communities in most networks. We note that we find similar results in other networks (Figs. 14 and 15 in the Appendix).

6 Discovering communities from a seed node

Now we focus on the task of inferring communities given a single seed node. We consider two tasks that build on two different viewpoints. The first task is motivated by a community-centric view where we discover all members of community $S$ given a single member $s \in S$. The second task is motivated by a node-centric view where we want to discover all communities that a single node $s$ belongs to. This means we discover both the number of communities $s$ belongs to and the members of these communities.

6.1 Proposed method

We extend the local spectral clustering algorithm [4, 32] into a scalable parameter-free community detection method. The benefits of our method are: First, the method requires no input parameters and is able to automatically detect the number of communities as well as the members of those communities. Second, the computational cost of our method is proportional to the size of the detected community (not the size of the network). Thus, our method is scalable to networks with hundreds of millions of nodes.

Our method (Algorithm 1) builds on the findings in Sect. 5: First, we aim to find sets of well-connected nodes around node $s$. We achieve this by defining a local partitioning method based on random walks starting from a single seed node [3]. In particular, we use the PageRank-Nibble random walk method that computes the PageRank vector with error $< \varepsilon$ in time $O(1/\varepsilon )$ independent of the network size [4]. The nodes with high PageRank scores from $s$ correspond to the well-connected nodes around $s$. Moreover, the random walk is ‘truncated’ as it sets PageRank scores $r_u$ to 0 for nodes $u$ with $r_u < \varepsilon$, for some small constant $\varepsilon$ [3]. This way the computational cost is proportional to the size of the detected community and not the size of the network.

After the PageRank-Nibble assigns the proximity scores $r_u$, we sort the nodes in decreasing proximity $r_u$ and proceed to the second step of our algorithm which extends the approach of Spielman and Teng [32]. We evaluate the community score on a set $S_k$ of all the nodes up to $k$th one (note that by construction $S_{k-1} \subset S_{k}$). This means that for a chosen community scoring function $f$, we compute $f(S_k)$ of the set $S_k$ that is composed of the top $k$ nodes with the highest random walk score $r_u$. The local minima of the function $f(S_k)$ then correspond to extracted communities.

We detect local minima of $f(S_k)$ using the following heuristic. For increasing $k = 1, 2, \ldots$, we measure $f(S_k)$. At some point $k^*$, $f(S_k)$ will stop decreasing and this $k^*$ becomes our candidate point for a local minimum. If $f(S_k)$ keeps increasing after $k^*$ and eventually becomes higher than $\alpha f(S_{k^*})$, we take $k^*$ as a valid local minimum. However, if $f(S_k)$ goes down again before it reaches $\alpha f(S_{k^*})$, we discard the candidate $k^*$. We experimented with several values of $\alpha$ and found that $\alpha =1.2$ gives good results across all the datasets.

For example, Fig. 9 plots $f(S_k)$ for two community scoring functions $f$ (Conductance) and $f'$ (Triad participation ratio). We identify the local optima (denoted by stars and squares) and use the nodes in the corresponding sets $S_k$ as the detected communities.

Fig. 9

Two community scoring functions $f$ (Conductance) and $f'$ (Triad participation ratio) evaluated on a set $S_k$ of top $k$ nodes with highest random walk proximity score to seed node $s$. Local optima of $f(S_k)$ correspond to detected communities (denoted by stars for Conductance and a square for TPR)

Note that our method can detect multiple communities that the seed node belongs to by identifying different local minima of $f(S_k)$. However, we assume that the communities are nested (smaller communities are contained in the larger ones) even though the ground-truth communities may not necessarily follow such a nested structure. Also, note that our method is parameter-free. Our method differs from local graph clustering approaches [3, 32] in two aspects. First, instead of sweeping only using Conductance, we consider sweeping using other scoring functions. Second, we find the local optima of the sweep curve instead of the global optimum—this change gives a large improvement over the conventional local spectral clustering approaches [3, 32].

6.2 Detecting a community from a single member

We first consider the task where we aim to reconstruct a single ground-truth community $S$ based on one member node $s$. For each community $S$, we pick a random member node $s$ as a seed node and compare the community we detect from $s$ with the ground-truth community $S$. Starting from node $s$, we generate a sweep curve $f(S_k)$. Let $k^*$ be the value of $k$ where $f(S_k)$ achieves the first local minima. We then use the set $S_{k^*}$ as the detected community. Now, given the ground-truth community $S$ and the detected community $S_{k^*}$, we evaluate how well-detected $S_{k^*}$ corresponds to ground-truth $S$. For this purpose, we compute precision, recall, and the F1-score between $S_{k^*}$ and $S$. For all metrics, the score of 1 means that detected $S_{k^*}$ perfectly matches ground-truth $S$. We consider 6 community scoring functions $f(\cdot )$ and compare the performance of our method to two standard community detection methods: local spectral clustering (LC) [3] and the 3-clique clique percolation method (CPM) [26].

Table 5 shows the performance of the proposed method for each scoring function and for the two baselines. First 5 rows show the F1-score for each of the datasets, and the last 3 rows show the average F1-score, precision and recall over all the datasets. We observe that the Conductance (C) gives the best average F1-score and outperforms all other scores on LiveJournal (LJ), Orkut, Amazon, and Ning. For Friendster (FS) and DBLP, the Triad participation ratio (T) performs best. This agrees with our intuition that for networks, like LiveJournal, that have fewer community overlaps scoring functions that focus on good separability perform well. In networks where nodes belong to multiple communities (like DBLP where authors publish at multiple venues), the Triad participation ratio (T) performs best. We also note that the average F1-score of Conductance is 0.46, while the baselines CPM and LC achieve F1-score of only 0.36 and 0.37, respectively. Note this is 10 % absolute and 30 % relative improvement over the baselines.

Table 5 Performance of our 6 methods and 2 baselines (LC, CPM) at detecting communities from a seed node

Last, we observe that some methods detect larger communities than necessary (higher recall, lower precision). Modularity (M) most severely overestimates community size. Conductance (C) and both baselines (CR and CPM) exhibit similar behavior but to a lesser extent. On the contrary, Flake ODF (F), Fraction over median (D), Triad participation ratio (T), and Cut ratio (CR) tend to underestimate the community size (higher precision than recall).

6.3 Detecting all communities that a seed node belongs to

We also explore the second task where we want to detect all the communities to which a given seed node $s$ belongs. In this task, we are given a node $s$ that is a member of multiple communities, but we do not know which and how many communities $s$ belongs to. We detect multiple communities by detecting all the local minima (and not just the first one) of the sweep curve. This way our method detects both the number and the members of communities.

For each dataset, we sample a node $s$, detect communities $\hat{S}_j$, and compare them to the ground-truth communities $S_i$ that node $s$ belongs to. To measure correspondence between the true and the detected communities, we match ground-truth communities to detected communities by the Hungarian matching method [17]. We then compute the average F1-score over the matched pairs. We use Conductance as the community scoring function and report results in Table 6.

Table 6 Average $F$-score between detected communities and the ground-truth communities to which a seed node belongs to, when the seed node belongs to $g$ different communities

Note that this task is harder than the previous one as here we aim to discover multiple communities simultaneously. Whereas the previous task evaluated our method for each ground-truth community, here, we first sample node $s$ and then search for the communities $S_i$ that $s$ belongs to. Therefore, larger ground-truth communities will be included in $S_i$ more often. Since larger ground-truth communities are less well separated [20], this makes the task harder.

Table 6 reports the average F1-score as a function of the number of communities $g$ that the seed node $s$ belongs to. Given that this is a harder task, we observe overall lower values of the F-score. Moreover, we also expect the performance to decrease as node $s$ belongs to more and more communities. In fact, we observe that the performance degrades with increasing the number of communities $g$. Interestingly, in LiveJournal and Amazon, it appears to be easier to detect communities of nodes that belong to 2 communities than to detect a community of a node that belongs to only a single community. This is due to the fact that single community nodes reside on the border of the community, and consequently, Conductance produces communities that are too small [20].

7 Related work

Generally, there are two approaches toward understanding the characteristics of network community structure and the community scoring functions (i.e., objective functions for community detection).

First way is theoretical analysis, which has been performed for a few most widely used functions such as Modularity [11] and Conductance [3, 13]. For example, Gleich and Seshadhri [13] mathematically proved the existence of node sets with high conductance in networks with high clustering coefficient. Fortunato and Barthelemy [11] showed that Modularity may not detect communities that have too few edges compared to the total number of edges in the network. More general theoretical analysis includes the work of Meilǎ [22], which studied the axiomatic criterion for community scores such as stability [34]. Although these theoretical attempts provide rigorous results, they cover only a few different scoring functions. To consider a broader range of community scoring functions, therefore, we take a different way, an empirical analysis, which allows us to evaluate any community scoring function.

Empirical approach analyzes how community scoring functions behave on real-world networks. One recent example is by Leskovec et al. [19], which evaluated a wide range of community scoring functions on large-scale real-world networks. However, there are two crucial differences in our work here. First, Leskovec et al. [19] used detected communities by the local spectral method [3] for the evaluation. Using communities detected by a specific community detection method would introduce a bias introduced by the detection method [1]. In this paper, our evaluation is free from such bias as we adopt ground-truth communities, which are explicitly declared by individual nodes. Second, Leskovec et al. [19] provides qualitative evaluation by showing the Network Community Profile plot [20] for each community scoring function. Here, we aim to quantify the robustness and sensitivity of community scoring functions to compare which scoring functions are better than others. We also note that empirical approach can be done with synthetic benchmarks such as in Shi et al. [30]; however, using synthetic benchmarks generates further biases due to natural deficiencies of synthetically generate networks.

Another related line of research is data-driven analysis of community detection algorithms. For example, Ahn et al. [2] employed community quality metrics based on the purity of node attributes to evaluate the performance of community detection methods. Abrahao et al. [1] showed that the communities detected by different communities exhibit fundamentally different structural properties. In this paper, however, we use data-driven evaluation metric to assess the performance of community detection on ground-truth communities. Our quality metrics directly focus on the correspondence between the detected and the ground-truth communities (as in Lin et al. [21], Sun et al. [33]).

8 Conclusion

The lack of reliable ground-truth gold-standard communities has made network community detection a very challenging task. In this paper, we studied a set of 230 different large social, collaboration, and information networks in which we defined the notion of ground-truth communities by nodes explicitly stating their group memberships.

We developed an evaluation methodology for comparing network community detection algorithms based on their accuracy on real data and compared different definitions of network communities and examined their robustness. Our results demonstrate large differences in behavior of community scoring functions. Last, we also studied the problem of community detection from a single seed node. We examined class of scalable parameter-free community detection methods based on Random Walks and found that our methods reliably detect ground-truth communities.

The availability of ground-truth communities allows for a range of interesting future directions. For example, further examining the connectivity structure of ground-truth communities could lead to novel community detection methods [37, 39, 40]. Overall, we believe that the present work will bring more rigor to the evaluation of network community detection, and the datasets publicly released as a part of this work will benefit the research community.

A Appendix

See Figs. 10, 11, 12, 13, 14, 15.

Fig. 10

Average metrics of top k communities by 6 scores. C conductance, T TPR, M modularity, F flake ODF, D FOMD, CR cut ratio

Fig. 11

Average metrics of top k communities by 6 scores. C conductance, T TPR, M modularity, F flake ODF, D FOMD, CR cut ratio

Fig. 12

$Z$-score of 6 scores versus the perturbation intensity for each null model. C conductance, T TPR, M modularity, F flake ODF, D FOMD, CR cut ratio

Fig. 13

$Z$-score of 6 scores versus the perturbation intensity for each null model. C conductance, T TPR, M modularity, F flake ODF, D FOMD, CR cut ratio

Fig. 14

$Z$-score of 6 scores versus the community size for each null model. C conductance, T TPR, M modularity, F flake ODF, D FOMD, CR cut ratio

Fig. 15

$Z$-score of 6 scores versus the community size for each null model. C conductance, T TPR, M modularity, F flake ODF, D FOMD, CR cut ratio