Characterization of TU games with stable cores by nested balancedness

Abstract

A balanced transferable utility game (N, v) has a stable core if its core is externally stable, that is, if each imputation that is not in the core is dominated by some core element. Given two payoff allocations x and y, we say that x outvotes y via some coalition S of a feasible set if x dominates y via S and x allocates at least v(T) to any feasible T that is not contained in S. It turns out that outvoting is transitive and the set M of maximal elements with respect to outvoting coincides with the core if and only if the game has a stable core. By applying the duality theorem of linear programming twice, it is shown that M coincides with the core if and only if a certain nested balancedness condition holds. Thus, it can be checked in finitely many steps whether a balanced game has a stable core. We say that the game has a super-stable core if each payoff vector that allocates less than v(S) to some coalition S is dominated by some core element and prove that core super-stability is equivalent to vital extendability, requiring that each vital coalition is extendable.

1 Introduction

In their seminal work on game theory, Von Neumann and Morgenstern [29] introduced the notion of stable sets as the main and most natural solution concept for cooperative games. Stable sets are based on the notion of dominance: A payoff vector x dominates another one y if there is a coalition S for which x is strictly better than y for every member of S but still remains affordable for them in the game under consideration. A set X of payoff vectors is said to be stable if no vector in X dominates another one of X (internal stability) and every payoff vector outside X is dominated by a vector of X (external stability).

Despite the attractive character of this definition, which has been disseminated to other domains like decision theory, the notion of stable sets has proved to be cumbersome. Stable sets are in general not unique, there may even be uncountably many of them, and, as shown by Lucas [16], there exist games with no stable sets. In addition, they are very difficult to find, and there is no known algorithm to find them. Deng and Papadimitriou [9] remarked that the problem of the existence of a stable set for a given game is undecidable. These unpleasant features made Aumann write in 1987: “Finding stable sets involves a new tour de force of mathematical reasoning for each game or class of games that is considered. Other than a small number of elementary truisms (e.g., that the core is contained in every stable set) there is no theory, no tools, certainly no algorithms [1]." This is why the main solution concept of cooperative game theory became the core.

There is, however, a close relationship between the core and stable sets. As mentioned above by Aumann, the core is contained in every stable set and, moreover, if the core is itself stable, then it becomes the unique stable set. Consequently, games with a stable core appear to be especially attractive, as they have a solution possessing the appealing properties of stable sets without having their drawbacks. The central question is then: For which games is the core a stable set? Are there simple sufficient conditions for core stability? Are there simple necessary conditions? The literature provided some answers to these questions, but not in full generality. An important notion here is the notion of extendability introduced by Kikuta and Shapley [13]. A game v is extendable if, for every coalition S, every core element of the subgame $v_{|S}$ (the restriction of v to the coalitions in S) can be extended to a core element of v. It turns out that extendable games have a stable core. Extendability is related to other well-known concepts in cooperative game theory. For example, subconvexity introduced by Sharkey [23], which is weaker than convexity, implies that the core is large, which in turn implies extendability, as proved by Van Gellekom et al. [27]. This leads to the conclusion that some well-known classes of games (convex, with a large core) have a stable core. However, extendability is far from being necessary for core stability. For example, for the case of assignment games that were introduced by Shapley and Shubik [22] and for which Balinski and Gale [2] described the geometric shape of the core, Solymosi and Raghavan [25] indeed showed that the core is stable if and only if the assignment game can be described by a payoff matrix that has a dominant diagonal. However, having a dominant diagonal does not imply that the assignment game is extendable, but it is possible to relax extendability so that it remains sufficient for core stability in general and becomes necessary for core stability in the case of assignment games. Indeed, according to Shellshear and Sudhölter [24] a coalition is strongly vital-exact if it is vital and, among all its subcoalitions that are not effective for all core elements, it is the unique coalition that is effective for some core element. Strongly vital-exact coalitions determine the core, and it turned out that it is sufficient to restrict extendability to these coalitions, which the authors call vital-exact extendability. They prove that vital-exact extendability is a sufficient and necessary condition for core stability for some classes of games, like matching games (an assignment game is a special matching game), simple flow games, and minimum coloring games. These results expand or reprove in a simple way the characterization results of [5, 25, 26], but vital-exact extendability still fails to be necessary in general. Moreover, it is not known whether a further weakening of extendability could lead to a necessary and sufficient condition of core stability. On the other hand, very few necessary conditions for core stability are known. It has been remarked by Gillies [12] that core stability implies that all singletons are exact.

In 1971, Kulakovskaja [14] published a note, giving a sufficient and necessary condition for core stability. This note was a short summary in English from her PhD dissertation in Russian from Leningrad State University (finished 1973). Unfortunately, T. E. Kulakovskaja died in 1996, and her work remained almost unnoticed. The second author of the present paper found a simple counterexample that disproves the published result. However, after inquiry, through the kind help of Natalia Naumova, he obtained an English translation by Professor Joseph Romanovsky of an extract of around 35 pages of the thesis [15]. We started our investigation from Kulakovskaja’s ideas and were able to build a sufficient and necessary condition for core stability, which is the main result of the present paper.

Indeed, Kulakovskaja’s idea was to strengthen the domination relation in such a way that (a) stability of the core remains unchanged and (b) the new relation is transitive. We have adopted this basic idea and say that a payoff vector x outvotes another payoff vector y via some feasible coalition S if x dominates y via S and assigns to each feasible coalition T that is not contained in S at least its worth v(T). Our notion of feasibility is of huge importance for the main result, and it is different from Kulakovskaja’s, though her thesis contains some version of our Theorem 5.1 (Theorem 2.9 in the thesis) [15]. The main result of the mentioned PhD thesis is only apparently similar to our main result, Theorem 6.1, and it only specifies a weak inequality. If we are not mistaken, she already tried to correct this main result for the English summary paper from 1971, where it appears as Theorem 2. In this theorem two cases are distinguished and one weak inequality appears as in our Theorem 6.1, but simple counterexamples show that this theorem does not hold. We believe that the second application of the duality theorem of linear programming (Kulakovskaja uses a theorem of Ky Fan instead) was not carried out carefully enough. Hence, we basically adopted only her idea to apply the mentioned transitive sub-relation of domination, called outvoting. The remaining sections of this paper are completely unrelated to her findings.

We briefly describe our construction and main result. Consider a balanced game (N, v). As the outvoting relation is transitive, the set M(v) of maximal elements w.r.t. the outvoting relation is nonempty, and we prove that it coincides with the core C(v) if and only if the core is stable. Checking the stability of the core amounts to finding a dominating core element x for every preimputation y outside the core. To get rid of both two quantifiers on uncountable sets and obtain a finite condition, the idea is to use a balancedness condition (one for each quantifier) as in the classical Bondareva-Shapley theorem, which yields a double balancedness condition. The first one is expressed by Theorem 5.1 and permits us to check if a preimputation outside the core can be outvoted via some coalition S. Then, the set $X(v){\setminus } C(v)$ of preimputations outside the core is divided into a finite number of blocks $X_\mathcal{S}(v)$, where $\mathcal{S}$ is the set of coalitions via which outvoting can be done. The second balancedness condition, which encompasses the first one, checks if all elements in $X_\mathcal{S}(v)$ can be dominated by a core element or not, for a given $\mathcal{S}$. The corresponding result is Theorem 6.1, and Corollary 6.2 summarizes by giving the final condition for core stability.

The paper is organized as follows. Section 2 introduces the main definitions and sets the framework. Section 3 generalizes the notion of balancedness, while Sect. 4 introduces a strengthening of the dominance relation, called the outvoting relation. Section 5 gives the general scheme of the construction as well as preparatory results, while the main result is presented in Sect. 6. In Sect. 7, we show that vital extendability characterizes a stronger form of stability of the core that we call super-stability. Finally, Sect. 8 is a discussion, giving additional results related to the complexity of using the condition of core stability. In the Appendix, we investigate the set of maximal elements w.r.t. the outvoting relation and conclude from its properties that it does not constitute a valuable solution concept.

2 Preliminaries

Stable sets and the core. A (cooperative TU) game is a pair (N, v) such that $N\ne \emptyset$ is finite and $v:2^N\rightarrow {\mathbb {R}}$, $v(\emptyset )=0$. We often identify (N, v) with its coalition function v. For $S\subseteq N$, we denote by ${\mathbb {R}}^S$ the |S|-dimensional Euclidean space of real functions on S. For $x,y\in {\mathbb {R}}^S$ we write $x\geqslant y$ if $x_i\geqslant y_i$ for all $i\in S$. Moreover we use $x>y$ for $x\geqslant y$ and $x\ne y$, and we write $x\gg y$ if $x_i>y_i$ for all $i\in S$. Let $X(v)=\{x\in {\mathbb {R}}^N\mid x(N)=v(N)\}$ and $I(v)=\{x\in X(v)\mid x_i\geqslant v(\{i\}) \text{ for } \text{ all } i\in N\}$, where $x(S)=\sum _{i\in S}x_i$ for each $x\in {\mathbb {R}}^N$ and $S\subseteq N$. That is, X(v) is the set of Pareto optimal allocations (preimputations) and I(v) is the set of imputations (individually rational preimputations). We also use $x_S=(x_i)_{i\in S}$ and denote, if $S\ne \emptyset$, the subgame of (N, v) restricted to the subsets of S, slightly abusing notation, by $\left( S,v_{|S}\right)$. The core of v is the set $C(v)=\{x\in X(v)\mid x(S)\geqslant v(S) \text{ for } \text{ all } S\subseteq N\}$. A coalition in N is a nonempty subset of N. Let $x,y\in {\mathbb {R}}^N$ and S be a coalition in N. We say that x dominates y via S (at v), written $x \text{ dom}_S~y$, if $x_S\gg y_S$ and $x(S)\leqslant v(S)$. We say that x dominates y ($x \text{ dom } y$) if $x \text{ dom}_S~y$ for some coalition S. We say that $X\subseteq {\mathbb {R}}^N$ is internally stable (at v) if $x\in X$, $y\in {\mathbb {R}}^N$, $x \text{ dom } y$ imply $y\notin X$. Moreover, X is externally stable (at v) if for all $y\in I(v){\setminus } X$ there exists $x\in X$ such that $x \text{ dom } y$. Finally, a set X is stable if it is internally and externally stable.

Note that C(v) is internally stable and that each externally stable set contains C(v). If $I(v)=\emptyset$, then $\emptyset =C(v)$ is a stable set. Hence we shall not further consider the case that $\sum _{i\in N}v(\{i\})>v(N)$.

The following remark formulates Proposition 2.1 and Corollary 2.1 of [24] (see also Gillies [12]).

Remark 2.1

Let (N, v) be a game with a stable core such that $I(v)\ne \emptyset$.

• (1) Then, for all $i\in N$, there exists $x\in C(v)$ such that $x_i=v(\{i\})$.

• (2) Hence, each preimputation that is not an imputation is dominated (via some singleton) by a core element.

We may use this remark to show that whether a game has a stable core is not only related to the geometrical properties of the core but also to the characteristic function itself because different games may have the same core. Hence “core stability” may not be a property of the core as a set, provided $|N|\geqslant 3$. Note that for each 1- and 2-person game its set of imputations coincides with its core, so that core stability is guaranteed. If, however, $|N|\geqslant 3$, then there exists a game (N, v) with a stable core and $I(v)\ne \emptyset$ such that the core is determined by the coalitions of at least two elements, i.e., $C(v)=\{x\in X(v)\mid x(S)\geqslant v(S) \text{ for } \text{ all } S\subseteq N \text{ with } |S|\geqslant 2\}.$ Hence, if (N, v) is replaced by a game $(N,v')$ that differs from (N, v) only inasmuch as $v'(\{k\})<v(\{k\})$ for some $k\in N,$ then $C(v')=C(v).$ If, moreover, $v'(\{k\})<\min _{x\in C(v)}x_k$, then $(N,v')$ does not possess a stable core by Remark 2.1. For completeness reasons we now present two explicit examples of the foregoing kind.

• Let $z\in {\mathbb {R}}^N$ and $(N,z(\cdot ))$ be the corresponding additive game. Then $C(z(\cdot ))=I(z(\cdot ))$ so that $(N,z(\cdot ))$ has a stable core. If $|N|\geqslant 3$, then

  $$\begin{aligned}&C(z(\cdot ))=\{z\}=\{x\in {\mathbb {R}}^N\mid x(N{\setminus }\{i\})\\&\quad =z(N{\setminus }\{i\}) \text{ for } \text{ all } i\in N \text{ and } x(N)=z(N)\}. \end{aligned}$$

  Hence, for $k\in N$ and each game (N, v) that satisfies $v(\{k\})<z_k$ and $v(S)=z(S)$ for all $S\in 2^N{\setminus }\{\{k\}\}$, we have that $C(v)=\{z\}$, but (N, v) does not have a stable core.

• Let (N, v) be defined by $v(S)=|S|-1$ for all $S\in 2^N{\setminus }\{\emptyset \}$. As the reader may easily verify, (N, v) has a stable core (because (N, v) is a convex game), and C(v) is determined by the non-singletons provided $|N|\geqslant 3$. Hence, if the worth of some singleton becomes negative, then the core is not changed, but the arising game does not possess a stable core.

Vital, exact, and core-determining coalitions. A coalition S in N is exact (at v) if it is effective for some core element, i.e., if there exists $y\in C(v)$ such that $y(S)=v(S)$. It is vital (at $v_{|S}$) if no proper subcoalition is effective for some core element of the corresponding subgame, i.e., if there exists $x_S\in C(v_{|S})$ such that $x(T)>v(T)$ for all $T\in 2^S{\setminus }\{S,\emptyset \}$. Note that S is vital if and only if the dimension of $C(v_{|S})$ is full, i.e., $|S|-1$. The coalition S is strictly vital-exact if there exists a core element for which S is effective but no proper subcoalition is, i.e., there exists $x\in C(v)$ such that $x(S)=v(S)$ and $x(T)>v(T)$ for all $T\in 2^S{\setminus }\{S,\emptyset \}$. Note that a strictly vital-exact coalition is necessarily vital and exact. Moreover, a property that is slightly weaker than strict vital-exactness is useful. The coalition S is called strongly vital-exact if it is vital, and there exists a core element for which S is effective but no proper subcoalition is, provided it is not effective for all core elements, i.e., S is vital and there exists $x\in C(v)$ such that $x(S)=v(S)$ and $x(T)>v(T)$ for all $T\in 2^S{\setminus }\{S,\emptyset \}$ for which there exists $y\in C(v)$ with $y(T)>v(T)$. Let $\mathcal{E}(v),$ $\mathcal{VE}^{\mathrm{strict}}(v),$ and $\mathcal{VE}^{\mathrm{strong}}(v)$ denote the set of exact, strictly vital-exact, and strongly vital-exact proper coalitions of N, respectively, i.e.,

$$\begin{aligned} \begin{array}{ll} \mathcal{E}(v)&{}=\{S\in 2^N{\setminus }\{\emptyset ,N\}\mid S \text{ is } \text{ exact } \text{ at } v\},\\ \mathcal{VE}^{\mathrm{strict}}(v)&{}=\{S\in 2^N{\setminus }\{\emptyset ,N\}\mid S \text{ is } \text{ strictly } \text{ vital-exact } \text{ at } v\}\text{, } \text{ and } \\ \mathcal{VE}^\mathrm{strong}(v)&{}=\{S\in 2^N{\setminus }\{\emptyset ,N\}\mid S \text{ is } \text{ strongly } \text{ vital-exact } \text{ at } v\}. \end{array} \end{aligned}$$

Note that $\mathcal{VE}^\mathrm{strict}(v)\subseteq \mathcal{VE}^{\mathrm{strong}}(v)\subseteq \mathcal{E}(v)$ and all inclusions may be strict. Finally, we say that a game (N, v) is exact if each coalition is exact.

Remark 2.2

As the aforementioned examples have shown, there exist “shapes of core” that can be both the core of a game with a stable core and the core of another game whose core is not stable. There are, however, two other extreme situations:

• (1) There are examples for which the core is always stable, i.e., each game with this core has a stable core. The reader may easily verify that $C=\Delta N=\{x\in {\mathbb {R}}^N_+\mid x(N)=1\}$ is the core of the unanimity game (N, u), defined by $u(N)=1$ and $u(S)=0$ for all $S\subsetneqq N$ and that, if (N, v) is an arbitrary game with $C(v)=C$, then $v(\{i\})=0$ for all $i\in N$, i.e., the singletons are needed to determine the core. Therefore, $I(v)=C(v)=C$, so that (N, v) has a stable core.

• (2) If a game (N, v) has a nonempty stable core, then the exact game $(N,v')$ with the same core (defined by $v'(S)=\min _{x\in C(v)}x(S)$ for all $S\subseteq N$) has a stable core as well. According to Theorem 3 of Biswas et al. [6], an exact game with at most four players has a stable core, but for five or more players there exist exact games that do not possess stable cores (see Example 6.4 below for the case $|N|=5$.) Hence, the core of such a game is never stable.

We elaborate on the collection of coalitions $\mathcal{F}(N,v)=\mathcal{F}(v)=\mathcal{F}$ which will serve as a basis for establishing our results. We impose the following properties for $\mathcal{F}$:

$$\begin{aligned} \mathcal{F}\subseteq & {} \mathcal{E}(v), \end{aligned}$$

(2.1)

$$\begin{aligned} C(v)= & {} \{x\in X(v)\mid x(S)\geqslant v(S)\forall S\in \mathcal{F}\}\text{, } \text{ and } \end{aligned}$$

(2.2)

$$\begin{aligned} \mathcal{F}\supseteq & {} \mathcal{VE}^\mathrm{strict}(v). \end{aligned}$$

(2.3)

The first condition is necessary, as the exactness property is needed in some proofs. The second condition says that the collection must be core-determining, an obvious requirement for studying core stability. Note that $\mathcal{E}(v)$ is core-determining but proper subcollections can be as well. The last condition is also related to this point: Let (N, v) be a game with a stable core such that $I(v)\ne \emptyset$. Then $\mathcal{VE}^{\mathrm{strict}}(v)$ satisfies (2.2), and, hence, it is necessary for core stability that the strictly vital-exact coalitions determine the core (i.e., that $\mathcal{VE}^\mathrm{strict}(v)$ satisfies (2.2)). Indeed, let $x\in X(v){\setminus } C(v)$. It remains to find a strictly vital-exact coalition S with $x(S)<v(S)$. To this end choose a core element y that dominates x (its existence is guaranteed because the core is stable) and a minimal coalition S w.r.t. inclusion such that y dominates x via S. Then $y(T)>v(T)$ for all $T\in 2^S{\setminus }\{\emptyset , S\}$ so that S is strictly vital-exact and $x(S)<v(S)$.

Let us present two examples of collections $\mathcal{F}$ satisfying the above three conditions. We assume that $C(v)\ne \emptyset$.

• (1) As remarked above, the set of exact coalitions, $\mathcal{F}(v)=\mathcal{E}(v)$, satisfies (2.1)–(2.3).

• (2) An often much smaller collection $\mathcal{F}(v)$ that also satisfies the three conditions is given by strongly vital-exact coalitions. Indeed, $\mathcal{VE}^{\mathrm{strong}}(v)$ satisfies (2.1), (2.2), and (2.3) by Lemma 3.7 of [24].

3 Balancedness

Let N be a finite nonempty set and S be a coalition in N. The vector $\mathbbm {1}^{S} \in {\mathbb {R}}^N$ denotes the indicator vector of S, i.e., $\mathbbm {1}^{S}_j=\left\{ \begin{array}{l}1\text{, } \text{ if } j\in S,\\ 0\text{, } \text{ if } j\in N{\setminus } S.\end{array}\right.$

Let $Z\subseteq {\mathbb {R}}^N_+{\setminus }\{0\}$ be a finite set. Define $F(Z)=\{\delta \in {\mathbb {R}}^Z_+\mid \sum _{z\in Z}\delta _z z=\mathbbm {1}^N\}$. Then F(Z) is a convex polyhedral set. By our assumption $z>0$ for all $z\in Z$, F(Z) is bounded and, hence, the convex hull of its extreme points (by the Krein-Milman theorem). Moreover, $\delta =(\delta _z)_{z\in Z}\in F(Z)$ is a vertex of F(Z) if and only if $\text{ supp } \delta =\{z\in Z\mid \delta _z>0\}$ is linearly independent. We say that $Z'\subseteq Z$ is balanced (in Z) if there is a system $(\delta _z)_{z\in Z'}$ of positive weights (called balancing weights) such that $\sum _{z\in Z'}\delta _z z=\mathbbm {1}^N$. A balanced set is minimal if and only if its system of balancing weights is unique. Hence, the vertices in F(Z) correspond to the minimal balanced sets. Each minimal balanced set is the support of a unique vertex and, vice versa, an element of F(Z) is a vertex if its support is a minimal balanced set in Z.

Recall that a collection $\mathcal{B}$ of coalitions (i.e., $\mathcal{B}\subseteq 2^N{\setminus }\{\emptyset \}$) is called balanced (in N) if $\{\mathbbm {1}^S\mid S\in \mathcal{B}\}$ is balanced. If $\mathcal{B}$ is a minimal balanced collection of coalitions, then we denote the unique system of balancing weights by $\left( \lambda ^\mathcal{B}_S\right) _{S\in \mathcal{B}}$ in this case.

Remark 3.1

Let (N, v) be a game.

• (1) $C(v)\ne \emptyset$ if and only if (N, v) is balanced, i.e., $v(N)\geqslant \sum _{S\in \mathcal{B}}\lambda ^\mathcal{B}_Sv(S)$ for all minimal balanced collections $\mathcal{B}$ in N [7, 21]. The result is “sharp” in the sense that, for each minimal balanced collection $\mathcal{B}\ne \{N\}$ in N there exists a game (N, v), which exclusively violates the foregoing inequality for this $\mathcal{B}$.

• (2) Let (N, v) be balanced. It is called totally balanced if, for all $\emptyset \ne S\subseteq N$, the subgame $(N,v_{|S})$ is balanced. The totally balanced cover $(N,{\bar{v}})$ is the totally balanced game such that ${\bar{v}}(S)\geqslant v(S)$ is minimal for all $S\subseteq N$. Note that $C(v)=C({\bar{v}})$ and that (N, v) has a stable core if and only if $(N,{\bar{v}})$ has [27].

• (3) It should be noted that [19] shows that a game is exact if it satisfies a certain balancedness condition. This result even applies to games with infinite player sets, whereas Csóka et al. [8] show that a game (with finitely many players) is exact if and only if it satisfies balancedness except that one of the balancing coefficients may be negative.

• (4) Let (N, v) be balanced and let $\mathcal{F}\subseteq 2^N{\setminus }\{N,\emptyset \}$ satisfy (2.2). If $|N|\geqslant 2$, then $\mathcal{F}$ is balanced and the linear span of $\{\mathbbm {1}^{S}\mid S\in \mathcal{F}\}$ is ${\mathbb {R}}^N$.

  This statement may be deduced from Corollary 6 of [10], but for the sake of completeness, we recall the proof. Let $x\in C(v)$ and $y\in {\mathbb {R}}^N$ satisfy $y(N)=0$ and $y(S)\geqslant 0$ for all $S\in \mathcal{F}$. Then $x+ty\in C(v)$ for all $t\geqslant 0$ so that $y=0\in {\mathbb {R}}^N$ by compactness of C(v). As $|N|\geqslant 2$, we also conclude that $\mathcal{F}\ne \emptyset$. Hence, the linear programming problem “$\max \sum _{S\in \mathcal{F}}y(S)$ subject to $y(S)\geqslant 0$ for all $S\in \mathcal{F}$ and $y(N)=0$” is feasible and its value is 0. By the duality theorem of linear programming [11, p. 62] there exist $\beta _S\geqslant 0,$ $S\in \mathcal{F}$, and $\beta _N\in {\mathbb {R}}$ such that $\beta _N\mathbbm {1}^N=\sum _{S\in \mathcal{F}}(1+\beta _S)\mathbbm {1}^S$. Hence, $\beta _N>0$ and $\mathcal{F}$ is balanced. We conclude that y is determined by $y\in {\mathbb {R}}^N$ and $y(S)=0$ for all $S\in \mathcal{F}$. Therefore, $\{\mathbbm {1}^S\mid S\in \mathcal{F}\}$ contains a vector space basis of ${\mathbb {R}}^N$.

4 The outvoting relation

Let (N, v) be a game and let $\mathcal{F}\subseteq 2^N{\setminus }\{N,\emptyset \}$. We now define a sub-relation of domination that is transitive.

Let $x,y\in {\mathbb {R}}^N$ and $P\in \mathcal{F}$. We say that x outvotes y via P (in $\mathcal{F}$), written $x\succ _P y$, if $x~\text{ dom}_P~y$ (i.e., $x_P\gg y_P$ and $x(P)\leqslant v(P)$), and $x(S)\geqslant v(S)$ for all $S\in \mathcal{F}{\setminus } 2^P$. Also, we say that x outvotes y ($x\succ y$) if there is $P\in \mathcal{F}$ such that $x\succ _P y$.

The outvoting relation is stronger than the domination relation, and the additional condition on x can be interpreted as follows: The payoff vector x must be acceptable for players outside P in the sense that any feasible coalition S involving players in $N{\setminus } P$ must receive at least its worth v(S).

Lemma 4.1

Let (N, v) be a game, $x,y,z\in {\mathbb {R}}^N$, and $P,Q\in \mathcal{F}$. If $x\succ _P y\succ _Q z$, then $P\subseteq Q$ and $x\succ _P z$.

Proof

As $y(S)\geqslant v(S)$ for all $S\in \mathcal{F}{\setminus } 2^Q$ and $y(P)<x(P)\leqslant v(P)$, $P\subseteq Q$. We conclude that $x\succ _Pz$. $\square$

Note that by Lemma 4.1 the binary relation $\succ$ is transitive. This fundamental property motivates to define M(v), the set of preimputations that are maximal w.r.t. the outvoting relation, i.e.,

$$\begin{aligned} M(v)=\{x\in X(v)\mid y\not \succ x\forall y\in X(v)\}. \end{aligned}$$

The two next lemmata are central. The first one shows that each non-maximal preimputation is outvoted by some element of M(v) and, in particular, that M(v) is nonempty, while the second proves that the dominance relation and outvoting relation are equivalent when dealing with the stability of the core. As a direct consequence, Proposition 4.4 below shows that the core coincides with the set of maximal elements of the outvoting relation if and only if it is stable.

Lemma 4.2

Let (N, v) be a balanced game and assume that $\mathcal{F}$ satisfies (2.2). For all $x\in X(v){\setminus } M(v)$ there exists $y\in M(v)$ such that $y \succ x$.

Proof

We may assume $|N|\geqslant 2$ (for $|N|=1$, $M(v)=X(v)$). For $Q\in \mathcal{F}$ let $Y(Q)=\{y\in X(v)\mid y\succ _Q x\}$. As $x\notin M(v)$, there exists $Q\in \mathcal{F}$ such that $Y(Q)\ne \emptyset$. Now, among those coalitions $Q\in \mathcal{F}$ satisfying $Y(Q)\ne \emptyset$, let P be a minimal (w.r.t. inclusion) one, and choose $y\in Y(P)$. Define $X=\{z\in X(v)\mid z_P\geqslant y_P,z(P)\leqslant v(P),z(S)\geqslant v(S) \text{ for } \text{ all } S\in \mathcal{F}{\setminus } 2^P\}$. Defined by weak inequalities, X is a closed polyhedral set. As $z_P\geqslant y_P$ implies $z(R)\geqslant y(R)$ for all $R\subseteq P$,

$$\begin{aligned}&X\subseteq \{z\in {\mathbb {R}}^N\mid z(N)=v(N),z(R)\geqslant y(R) \text{ for } \text{ all } R\in \mathcal{F}\cap 2^P,\\&\quad z(T)\geqslant v(T) \text{ for } \text{ all } T\in \mathcal{F}{\setminus } 2^P\}. \end{aligned}$$

A careful inspection of Remark 3.1 (3) shows that X contains neither lines nor rays, hence it is compact. As $y\in X$, X is nonempty. Hence, $t=\max \{z(P)\mid z\in X\}$ exists. Choose $z\in X$ such that $z(P)=t$. As $z\succ _P x$, it suffices to prove that $z\in M(v)$. For this purpose, assume, on the contrary, that there exists $z'\in X(v)$ such that $z'\succ _Q z$ for some $Q\in \mathcal{F}$. As $z\succ _P x$, by Lemma 4.1, we have $Q\subseteq P$ and $z'\succ _Q x$. By definition of P, we must have $Q=P$, implying that $z'\in X$, $z'_P\gg z_P$, and $z'_P\leqslant v(P)$ which is impossible by choice of z. $\square$

Lemma 4.3

Let $x\in C(v)$, $y\in X(v)$, and $\mathcal{F}$ satisfy (2.3). Then $x \text{ dom } y$ if and only if $x\succ y$.

Proof

If $x\succ _P y$ for some $P\in \mathcal{F}$, then $x \text{ dom}_P~y$. Conversely, if $x \text{ dom } y$, then let S be a minimal (w.r.t. inclusion) coalition such that $x \text{ dom}_S~y$. Then $S\ne N$ because $y(N)=v(N)$. By minimality of S, $x(T)>v(T)$ for all $T\in 2^S{\setminus }\{\emptyset ,S\}$. As $x\in C(v)$, $x(S)=v(S)$. Hence, S is strictly vital-exact so that $S\in \mathcal{F}$ by (2.3). Thus, $x\succ _S y$.$\square$

Proposition 4.4

Let (N, v) be a balanced game and let $\mathcal{F}$ satisfy (2.3) and (2.2). Then $M(v)=C(v)$ if and only if (N, v) has a stable core.

Proof

As $C(v)\subseteq M(v)$ is true in general, in view of Remark 2.1 (2), the if part follows from Lemma 4.3. Moreover, Lemma 4.2 and Lemma 4.3 imply the only-if part. $\square$

In view of the above results, we may consider the elements of M(v) as the “best” payoff vectors, so that one could think of M(v) as a solution of the game (N, v). However, in the Appendix we show that $M(\cdot )$ lacks some essential properties like convexity, boundedness, and upper hemicontinuity, which makes the use of $M(\cdot )$ as a solution concept questionable.

5 General scheme and first results

For the remainder, whenever a game (N, v) is given, $\mathcal{F}=\mathcal{F}(v)$ is always assumed to satisfy (2.1), (2.3) and (2.2).

Let (N, v) be a balanced game. This section describes the general idea of how to construct the finite test for core stability and serves as a preparation for the main result, namely Theorem 6.1 and its corollary.

Checking core stability of (N, v) amounts to check whether the following condition holds:

$$\begin{aligned} \forall y\in X(v){\setminus } C(v),\exists x\in C(v), x \text{ dom } y. \end{aligned}$$

The condition involves two nested quantifiers on uncountable sets, and a test of dominance which amounts to check linear strict inequalities and equality. Lemma 4.3 permits to replace the domination relation by the outvoting relation, i.e., to replace the previous condition by

$$\begin{aligned} \forall y\in X(v){\setminus } C(v),\exists x\in C(v), x\succ y, \end{aligned}$$

(5.1)

where the test is stronger and has better properties, but it still involves linear inequalities, some of them being strict, with the two quantifiers. Recall that the test of nonemptiness of the core reads

$$\begin{aligned} \exists x\in X(v),x(S)\geqslant v(S)\forall S \subseteq N, \end{aligned}$$

which involves one quantifier on an uncountable set and linear inequalities. It is well-known [7, 21] that the above problem is solved by means of the Farkas’ lemma and Krein-Milman theorem, and amounts to checking a finite set of linear inequalities (balancedness conditions, see Remark 3.1 (1)). Our approach to solve (5.1) is similar: We replace each test involving one quantifier on an uncountable set by a finite balancedness condition, hence leading to two nested (but finite) balancedness conditions. More precisely:

• Step 1: We solve for a given $y\in X(v){\setminus } C(v)$: $\exists x\in C(v), x\succ y$. This is done in Theorem 5.1 below, giving a first finite balancedness condition (5.2) on collections of $2^N$, close to the classical one.

• Step 2: We partition $X(v){\setminus } C(v)$ into a finite number of blocks $X_\mathcal{S}(v)$, where $\mathcal{S}\subseteq 2^N$. Hence, (5.1) becomes “for all $\mathcal{S}$ and all $y\in X_\mathcal{S}(v)$, (5.2) holds”.

• Step 3: The quantifier on the uncountable set $X_\mathcal{S}(v)$ is replaced by a balancedness condition, which also encompasses the first balancedness condition. This is given in Theorem 6.1.

Let $S\in \mathcal{F}$ and $\mathcal{B}\subseteq 2^N{\setminus }\{N,\emptyset \}$ be a minimal balanced collection. We say that $\mathcal{B}$ is associated with S if there exists $i\in S$ such that $\{i\}\in \mathcal{B}$ and $\mathcal{B}\subseteq \{\{j\}\mid j\in S\}\cup \{N{\setminus } S\}\cup \left( \mathcal{F}{\setminus } 2^S\right) .$ Let ${\mathbb {B}}_S$ denote the set of minimal balanced collections associated with S. Moreover, let $(N,v^S)$ be the game defined by $v^S(T)=v(T)$ for all $T\in 2^N{\setminus }\{N{\setminus } S\}$ and $v^S(N{\setminus } S)=v(N)-v(S)$.

Theorem 5.1

Let (N, v) be a balanced game, $y\in {\mathbb {R}}^N$, and $S\in \mathcal{F}$. Then y is outvoted by some preimputation via S (i.e., there exists $x\in X(v)$ such that $x \succ _S y$) if and only if, for every $\mathcal{B}\in {\mathbb {B}}_S$,

$$\begin{aligned} \sum \{\lambda ^\mathcal{B}_{\{i\}}y_i\mid i\in S,\{i\}\in \mathcal{B}\}+ \sum _{T\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^\mathcal{B}_Tv^S(T)<v(N). \end{aligned}$$

(5.2)

Proof

The only-if part: Let $S\in \mathcal{F}$ and $x\in X(v)$ such that $x\succ _S~y$. As $x(S)\leqslant v(S),$ $x(N{\setminus } S)=x(N)-x(S)\geqslant v(N)-v(S)=v^S(N{\setminus } S)$. As $x_S\gg y_S$ and $x(T)\geqslant v(T)$ for all $T\in \mathcal{F}{\setminus } 2^S$, we conclude that, for each $\mathcal{B}\in {\mathbb {B}}_S$,

$$\begin{aligned} v(N)= & {} x(N)=\sum _{T\in \mathcal{B}}\lambda ^\mathcal{B}_Tx(T)\\= & {} \sum \{\lambda ^\mathcal{B}_{\{i\}}x_i\mid i\in S,\{i\}\in \mathcal{B}\}+ \sum _{T\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^\mathcal{B}_Tx(T)\\> & {} \sum \{\lambda ^\mathcal{B}_{\{i\}}y_i\mid i\in S,\{i\}\in \mathcal{B}\}+ \sum _{T\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^\mathcal{B}_Tv^S(T). \end{aligned}$$

The if part: Let $S\in \mathcal{F}$ and assume that S satisfies (5.2) for each $\mathcal{B}\in {\mathbb {B}}_S$. As ${\mathbb {B}}_S$ is finite, there exists $\varepsilon > 0$ such that $v(N)\geqslant \sum \{\lambda ^\mathcal{B}_{\{i\}}(y_i+\varepsilon )\mid i\in S,\{i\}\in \mathcal{B}\}+ \sum _{T\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^\mathcal{B}_Tv^S(T)$ for all $\mathcal{B}\in {\mathbb {B}}_S$. It is sufficient to show that there exists $x\in {\mathbb {R}}^N$ such that $x_i\geqslant y_i+\varepsilon$ for all $i\in S$, $x(S) \leqslant v(S)$, $x(T)\geqslant v(T)$ for all $T\in \mathcal{F}{\setminus } 2^S,$ and $x(N)=v(N)$. As $x(N)=v(N)$, $x(S)\leqslant v(S)$ may be replaced by $x(N{\setminus } S)\geqslant v(N)-v(S)$. As $v(N{\setminus } S)\leqslant v(N)-v(S)$ by balancedness, $x\succ _S~y$ if the linear program

$$\begin{aligned} \begin{array}{l}\min x(N)\\ \text{ subject } \text{ to }\left\{ \begin{array}{l} x_i\geqslant y_i+\varepsilon \text{ for } \text{ all } i\in S,\\ x(N{\setminus } S)\geqslant v(N)-v(S),\\ x(T)\geqslant v(T) \text{ for } \text{ all } T\in \mathcal{F}{\setminus } (2^S\cup \{N{\setminus } S\})\text{, } \text{ and }\\ x(N)\geqslant v(N)\end{array}\right. \end{array} \end{aligned}$$

(5.3)

has an optimal solution and the value v(N). Hence, by the duality theorem [11, p. 62], it suffices to show that the dual program of (5.3) has an optimal solution and its value is also v(N). Now, the dual program is:

$$\begin{aligned}&\max \sum _{i\in S}\lambda _{\{i\}}(y_i+\varepsilon )+\lambda _{N{\setminus } S}(v(N)-v(S))+\sum _{T\in \mathcal{F}{\setminus } (2^S\cup \{N{\setminus } S\})}\lambda _T v(T)+\lambda _Nv(N) \nonumber \\&\text{ subject } \text{ to } \nonumber \\&\left\{ \begin{array}{l} \sum _{i\in S}\lambda _{\{i\}}\mathbbm {1}^{\{i\}}+\lambda _{N{\setminus } S}\mathbbm {1}^{N{\setminus } S}\!+\!\sum _{T\in \mathcal{F}{\setminus } (2^S\cup \{N{\setminus } S\})}\lambda _T \mathbbm {1}^{T}\!+\!\lambda _N\mathbbm {1}^{N}\!=\!\mathbbm {1}^{N} \text{ and }\\ \lambda _{\{i\}}\geqslant 0 \text{ for } \text{ all } i\in S, \lambda _{N{\setminus } S},\lambda _N\geqslant 0,\lambda _T\geqslant 0 \text{ for } \text{ all } T\in \mathcal{F}{\setminus } (2^S\cup \{N{\setminus } S\}).\end{array}\right. \end{aligned}$$

(5.4)

Now, with $\lambda _N=1$ and $\lambda _{R}=0$ for all other variables, we have a feasible solution (with value v(N)). Hence, we may assume that there is a further feasible solution. However, each further feasible solution satisfies $\lambda _N<1$, so that we just have to make sure that the value of the derived linear program

$$\begin{aligned}&\max \sum _{i\in S}\lambda _{\{i\}}(y_i+\varepsilon )+\lambda _{N{\setminus } S}(v(N)-v(S))+\sum _{T\in \mathcal{F}{\setminus } (2^S\cup \{N{\setminus } S\})}\lambda _T v(T)\nonumber \\&\quad \text{ subject } \text{ to } \nonumber \\&\left\{ \begin{array}{l} \sum _{i\in S}\lambda _{\{i\}}\mathbbm {1}^{\{i\}}+\lambda _{N{\setminus } S}\mathbbm {1}^{N{\setminus } S}+\sum _{T\in \mathcal{F}{\setminus } (2^S\cup \{N{\setminus } S\})}\lambda _T \mathbbm {1}^{T}=\mathbbm {1}^{N} \text{ and } \\ \lambda _{\{i\}}\geqslant 0 \text{ for } \text{ all } i\in S, \lambda _{N{\setminus } S},\lambda _T\geqslant 0 \text{ for } \text{ all } T\in \mathcal{F}{\setminus } (2^S\cup \{N{\setminus } S\})\end{array}\right. \end{aligned}$$

(5.5)

is not larger than v(N). Let $\mathcal{B}_0=\{\{i\}\mid i\in S\}\cup \{N{\setminus } S\}\cup ( \mathcal{F}{\setminus } (2^S\cup \{N{\setminus } S\}))$, let $(\lambda _T)_{T\in \mathcal{B}_0}$ be a feasible solution of (5.5), and let $\widetilde{\mathcal{B}}=\{T\in \mathcal{B}_0\mid \lambda _T>0\}$. Then $\widetilde{\mathcal{B}}$ is a balanced collection and $(\lambda _T)_{T\in \widetilde{\mathcal {B}}}$ is a system of balancing weights. Hence, $\widetilde{\mathcal{B}}$ is a union of minimal balanced collections $\mathcal{B}\subseteq \widetilde{\mathcal{B}}$ such that $(\lambda _T)_{T\in \widetilde{\mathcal{B}}}$ is a convex combination of the systems $(\lambda ^\mathcal{B}_T)_{T\in {\widetilde{\mathcal{B}}}}$, where $\lambda ^\mathcal{B}_T=0$ for all $T\in \widetilde{\mathcal{B}}{\setminus } \mathcal{B}$. If there exists $i\in S$ such that $\{i\}\in \mathcal{B}$, then $\mathcal{B}\in {\mathbb {B}}_S$ so that $\sum _{i\in S}\lambda ^\mathcal{B}_{\{i\}}(y_i+\varepsilon )+\lambda ^\mathcal{B}_{N{\setminus } S}(v(N)-v(S))+\sum _{T\in \mathcal{F}{\setminus } (2^S\cup \{N{\setminus } S\})}\lambda ^\mathcal{B}_T v(T)\leqslant v(N)$ by our assumption on $\varepsilon$. Otherwise $\mathcal{B}\subseteq \{N{\setminus } S\}\cup \mathcal{F}{\setminus } 2^S$. As S is exact, there exists $z\in C(v)$ with $z(S)=v(S)$ so that $z(N{\setminus } S)=v(N)-v(S)$. Therefore $v(N)=z(N)=\sum _{T\in \mathcal{B}}\lambda ^\mathcal{B}_T z(T)\geqslant \sum _{T\in \mathcal{B}}\lambda ^\mathcal{B}_T v^S(T)=\sum _{T\in \widetilde{\mathcal{B}}}\lambda ^\mathcal{B}_Tv^S(T)$. $\square$

We make some comments on this first important result. As is the case for every balancedness condition, balancing weights can be interpreted as time sharing of the players among the coalitions. We first note that the special form of the balanced collections considered (associated with S) comes from the definition of the outvoting relation: We pay attention to any coalition with players not in S, while singletons in S matter, as they should receive strictly more than $y_i$ (where y is the outvoted payoff vector), and $N{\setminus } S$ plays a special role because x (the outvoting payoff vector) should satisfy $x(N{\setminus } S)\geqslant v(N)-v(S)=v^S(N{\setminus } S)$. Therefore, if such an outvoting vector x exists and is “decomposed” by the balanced collection $\mathcal{B}$, i.e., $v(N)=x(N)=\sum _{T\in \mathcal{B}}\lambda ^\mathcal{B}_Tx(T)$, then Inequality (5.2) immediately follows, which can be easily deduced from the inequalities $x_i>y_i$ for all $i\in S$ and $x(T)\geqslant v^S(T)$ for all $T\in \mathcal{F}{\setminus } 2^S$. What is interesting and more difficult to obtain is that the converse is also true.

Another observation, which comes from the fact that S is exact, is that if v is balanced, then $v^S$ is also balanced. Indeed, take $x\in C(v)$ such that $x(S)=v(S)$. Then $x(N{\setminus } S)=v(N)-v(S)=v^S(N{\setminus } S)$. Hence, $x\in C(v^S)$. Now, since $v^S$ is balanced, we have for any $\mathcal{B}$ associated with S:

$$\begin{aligned} \sum \{\lambda ^\mathcal{B}_{\{i\}}v^S(\{i\})\mid i\in S,\{i\}\in \mathcal{B}\}+ \sum _{T\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^\mathcal{B}_Tv^S(T)\leqslant v(N) \end{aligned}$$

It follows that (5.2) is automatically satisfied whenever $y_i\leqslant v(\{i\})$ for all $\{i\}\in \mathcal{B}, i\in S$, with at least one strict inequality.

Let (N, v) be a balanced game. By (2.2), for each $x\in X(v){\setminus } C(v)$ there exists $P\in \mathcal{F}$ such that $x(P)<v(P)$. It follows that X(v) can be partitioned into blocks $X_\mathcal{S}(v)$, where $\mathcal{S}$ is the collection of all sets $S\in \mathcal{F}$ where strict inequality occurs. Formally:

$$\begin{aligned} X_\mathcal{S}(v)=\{x\in X(v)\mid x(S)<v(S)\forall S\in \mathcal{S},x(T)\geqslant v(T)\forall T\in \mathcal{F}{\setminus } \mathcal{S}\}, \end{aligned}$$

with $\mathcal{S}\subseteq \mathcal{F}$, and $X(v) = \bigcup _{\mathcal{S}\subseteq \mathcal{F}}X_\mathcal{S}(v)$. Note that $X_\emptyset (v)=C(v)$ and $X_\mathcal{S}(v)$ may be empty for some collections $\mathcal{S}\ne \emptyset$. Let us call $\mathcal{S}$ a feasible collection (for v) if $\mathcal{F}\supseteq \mathcal{S}\ne \emptyset \ne X_{\mathcal{S}}(v)$ so that

$$\begin{aligned} X(v){\setminus } C(v)=\mathop {\dot{\bigcup }}\{ X_{\mathcal{S}}(v)\mid \mathcal{S} \text{ is } \text{ a } \text{ feasible } \text{ collection } \text{ for } v\}. \end{aligned}$$

The previous considerations lead to the following result.

Lemma 5.2

Let (N, v) be a balanced game and $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}.$ Then $X_\mathcal{S}(v)\cap M(v)=\emptyset$ if and only if for every $y\in X_{\mathcal{S}}(v)$ there exists $S\in \mathcal{S}$ such that, for all $\mathcal{B}\in {{\mathbb {B}}}_S$, (5.2) holds.

Proof

Suppose that $X_\mathcal{S}(v)\cap M(v)=\emptyset$. Then, by Lemma 4.2, every $y\in X_\mathcal{S}(v)$ is outvoted by some preimputation x via some $S\in \mathcal{F}$. Since outvoting implies that $y(S)<x(S)\leqslant v(S)$, we deduce that $S\in \mathcal{S}$. By Theorem 5.1, (5.2) must hold for every $\mathcal{B}\in {{\mathbb {B}}}_S$.

Conversely, suppose that for each $y\in X_\mathcal{S}(v)$ there exists $S\in \mathcal{S}$ such that, for all $\mathcal{B}\in {{\mathbb {B}}}_S$, (5.2) holds. By Theorem 5.1, y is outvoted via S. Hence, $y\notin M(v)$. $\square$

The foregoing lemma implies the following corollary.

Corollary 5.3

The balanced game (N, v) has a stable core if and only if for each feasible collection $\mathcal{S}$ for v and for each $y\in X_\mathcal{S}(v)$ there exists $S\in \mathcal{S}$ such that, for all $\mathcal{B}\in {{\mathbb {B}}}_S$, (5.2) holds.

Proof

Suppose the core is stable. Then $M(v)=C(v)$ by Proposition 4.4 so that Lemma 5.2 finishes the only-if part.

Suppose now that for all feasible $\mathcal{S}$ and all $y\in X_\mathcal{S}(v)$ there exists $S\in \mathcal{S}$ such that (5.2) holds for all $\mathcal{B}\in {{\mathbb {B}}}_S$. Then, $X_\mathcal{S}(v)$ does not intersect M(v) by Lemma 5.2 so that $M(v)=C(v)$, i.e., the core is stable by Proposition 4.4. $\square$

We can slightly refine these results by eliminating some balanced collections $\mathcal{B}$ in each ${{\mathbb {B}}}_S$ for which (5.2) is automatically satisfied. Supposing (N, v) is balanced, consider some feasible $\mathcal{S}\subseteq \mathcal{F}$, some $S\in \mathcal{S}$, and $\mathcal{B}\in {{\mathbb {B}}}_S$ with the following property:

$$\begin{aligned} (\mathcal{B}{\setminus }\{\{i\}\mid i\in S\})\cap \mathcal{S}=\emptyset \ne (\mathcal{B}{\setminus }\{\{i\}\mid i\in S\})\cap \{N{\setminus } R\mid R\in \mathcal{S}\}. \end{aligned}$$

(5.6)

We claim that for each $x\in X_\mathcal{S}(v)$, $x(T)\geqslant v^S(T)$ for $T\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}$ and at least one of the inequalities is strict. To show our claim, note that for each $T\in \mathcal{B}{\setminus } \{\{i\}\mid i\in S\}$ that has the form $T=N{\setminus } R$ with $R\in \mathcal S$ we have, since $x\in X_\mathcal{S}(v)$, $x(T)>v(N)-v(N{\setminus } T)\geqslant v(T)$ by balancedness of (N, v). As there exists such a T, at least one of the mentioned inequalities is strict. For all $T\in \mathcal{B}{\setminus } \{\{i\}\mid i\in S\}$ that are not of the foregoing form, we have $T\in \mathcal{F}{\setminus }\mathcal{S}$, and hence $x(T)\geqslant v(T)$. Therefore,

$$\begin{aligned} v(N)= & {} x(N)=\sum _{T\in \mathcal{B}}\lambda ^{\mathcal{B}}_T x(T)\\= & {} \sum \{\lambda ^{\mathcal{B}}_{\{i\}}x_i\mid i\in S,\{i\}\in \mathcal{B}\}+\sum _{T\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^{\mathcal{B}}_Tx(T)\\> & {} \sum \{\lambda ^{\mathcal{B}}_{\{i\}}x_i\mid i\in S,\{i\}\in \mathcal{B}\}+\sum _{T\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^{\mathcal{B}}_Tv^S(T)), \end{aligned}$$

which is (5.2).

Let $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}$. The foregoing paragraph motivates to call $\mathcal{B}\in {{\mathbb {B}}}_S$ admissible for $\mathcal{S}$ if (5.6) is not satisfied, i.e., if $\mathcal{B}{\setminus } \{\{i\}\mid i\in S\}$ contains an element of $\mathcal{S}$ or does not contain a complement of an element of $\mathcal{S}$. Let ${{\mathbb {B}}}_S^{\mathcal{S}}$ denote the set of minimal balanced collections associated with S that are admissible for $\mathcal{S}$.

For each $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}$ we denote ${{\mathbb {C}}}(\mathcal{S})=\{(\mathcal{B}_S)_{S\in \mathcal{S}}\mid \mathcal{B}_S\in {{\mathbb {B}}}_S^{\mathcal{S}}\forall S\in \mathcal{S}\}.$ Thus, we have deduced that Lemma 5.2 and Corollary 5.3 are still valid if we require admissibility, so that we have the following corollary.

Corollary 5.4

Let (N, v) be a balanced game and $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}$. Then $M(v)\cap X_\mathcal{S}(v)\ne \emptyset$ if and only if there exist a system of balanced collections $(\mathcal{B}_S)_{S\in \mathcal{S}}\in {\mathbb {C}}(\mathcal{S})$ and $x\in X_\mathcal{S}(v)$ such that

$$\begin{aligned} \sum \{\lambda ^{\mathcal{B}_S}_{\{i\}}x_i\mid i\in S,\{i\}\in {\mathcal{B}_S}\}+ \sum _{T\in {\mathcal{B}_S}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^{\mathcal{B}_S}_Tv^S(T)\geqslant v(N)\forall S\in \mathcal{S}. \end{aligned}$$

6 Main result

Let (N, v) be a balanced game. Now, we express the necessary and sufficient condition for core stability in Corollary 5.4 by a certain balancedness condition.

Let $\emptyset \ne {\mathcal{S}}\subseteq \mathcal{F}$ and $(\mathcal{B}_S)_{S\in \mathcal{S}}\in {\mathbb {C}}(\mathcal{S})$. For $S\in \mathcal{S}$ let $z^S\in {\mathbb {R}}^N$ be given by

$$\begin{aligned} z^S_j=\left\{ \begin{array}{cl}\lambda ^{\mathcal{B}_S}_{\{i\}}&{}\text{, } \text{ if } j=i \text{ for } \text{ some } i\in S \text{ such } \text{ that } \{i\}\in \mathcal{B}_S,\\ 0&{}\text{, } \text{ for } \text{ all } \text{ other } j\in N.\end{array}\right. \end{aligned}$$

Define

$$\begin{aligned} Z:=Z\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right) :=\{\mathbbm {1}^{N{\setminus } S}\mid S\in \mathcal{S}\}\cup \{\mathbbm {1}^T\mid T\in \mathcal{F}{\setminus } \mathcal{S}\}\cup \{z^S\mid S\in \mathcal{S}\}. \end{aligned}$$

Moreover, for each $z\in Z$, define $a_z:=a_z\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}},v\right) :=\max (A\cup B\cup C),$ where

$$\begin{aligned} \begin{array}{ll}A&{}=\{v(N)-v(S)\mid S\in \mathcal{S},\mathbbm {1}^{N{\setminus } S}=z\},\\ B&{}=\{v(T)\mid T\in \mathcal{F}{\setminus } \mathcal{S},\mathbbm {1}^T=z\}\text{, } \text{ and }\\ C&{}=\left\{ \left. v(N)-\sum _{T\in \mathcal{B}_S{\setminus }\{\{i\}\mid i\in S\}}\lambda ^{\mathcal{B}_S}_Tv^S(T)\right| S\in \mathcal{S},z=z^S\right\} .\end{array} \end{aligned}$$

Note that A and B are empty or singletons. Moreover, note that by balancedness of v, $v(S)\leqslant v(N)-v(N{\setminus } S)$ for all $S\in 2^N$. By applying the exactness of the elements of $\mathcal{F}$, it may also be deduced that $\max \{B,C\}=\max C$ if $B\ne \emptyset \ne C$. Indeed, if $z^S=1^T$ for some $S\in \mathcal{S}$ and $T\in \mathcal{F}{\setminus } \mathcal{S}$, then $\mathbbm {1}^T+\sum _{R\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^{\mathcal{B}_S}_R\mathbbm {1}^R=\mathbbm {1}^N$. Choose $y\in C(v)$ such that $y(S)=v(S),$ and hence $y\in C(v^S)$. We conclude

$$\begin{aligned} v(N)=y(N)=y(T)+\sum _{R\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^{\mathcal{B}_S}_Ry(R)\geqslant v(T)+\sum _{R\in \mathcal{B}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^{\mathcal{B}_S}_Rv^S(R), \end{aligned}$$

so that $\max C\geqslant B.$ Hence,

$$\begin{aligned} a_z=\left\{ \begin{array}{cl}\max C&{}\text{, } \text{ if } C\ne \emptyset =A,\\ \max \{A,C\}&{}\text{, } \text{ if } C\ne \emptyset \ne A,\\ v(N)-v(S)&{}\text{, } \text{ if } z=\mathbbm {1}^{N{\setminus } S} \text{ for } \text{ some } S\in \mathcal{S}, C=\emptyset ,\\ v(T)&{}\text{, } \text{ if } z=\mathbbm {1}^T \text{ for } \text{ some } T\in \mathcal{F}{\setminus } \mathcal{S},A=\emptyset =C.\end{array}\right. \end{aligned}$$

Denote by ${\mathbb {B}}:={\mathbb {B}}\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right)$ the set of minimal balanced subsets in Z (see Sect. 3 for the definition of minimal balanced sets) and by ${\mathbb {B}}_0={\mathbb {B}}_0\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}},v\right)$ the subset of all $Z'\in {\mathbb {B}}$ for which there exists $S\in \mathcal{S}$ such that $z=\mathbbm {1}^{N{\setminus } S}\in Z'$ and $a_{z}=v(N)-v(S)$. Finally, for $Z'\in {\mathbb {B}}$, let $\delta ^{Z'}=(\delta ^{Z'}_z)_{z\in Z'}$ denote the system of balancing weights of $Z'$.

We now formulate our fundamental result.

Theorem 6.1

Let (N, v) be a balanced game and $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}$. Then the following conditions are equivalent.

• (1) $M(v)\cap X_\mathcal{S}(v)=\emptyset$.

• (2) For all $(\mathcal{B}_S)_{S\in \mathcal{S}}\in {\mathbb {C}}(\mathcal{S})$, with $a_z:=a_z\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}},v\right)$ for all $z\in Z\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right)$, one of the following conditions holds:

  $$\begin{aligned} \exists Z'\in {\mathbb {B}}\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right) {\setminus } \mathbb B_0\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right)&:&\sum _{z\in Z'}\delta ^{Z'}_za_z> v(N). \end{aligned}$$

  (6.1)
  $$\begin{aligned} \exists Z'\in \mathbb B_0\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right)&:&\sum _{z\in Z'}\delta ^{Z'}_za_z\geqslant v(N). \end{aligned}$$

  (6.2)

Proof

Let $(\mathcal{B}_S)_{S\in \mathcal{S}}\in {\mathbb {C}}(\mathcal{S})$. Let $\varepsilon \geqslant 0$ and consider the linear program

$$\begin{aligned}&\min x(N) \nonumber \\&\quad \text{ subject } \text{ to }\left\{ \begin{array}{l}x(T)\geqslant v(T) \text{ for } \text{ all } T\in \mathcal{F}{\setminus } \mathcal{S},\\ x(N{\setminus } S)\geqslant v(N)-v(S)+\varepsilon \text{ for } \text{ all } S\in \mathcal{S}\text{, } \text{ and }\\ \sum \{\lambda ^{\mathcal{B}_S}_{\{i\}}x_i\mid i\in S,\{i\}\in \mathcal{B}_S\}\geqslant v(N)-\sum _{T\in \mathcal{B_S}{\setminus }\{\{i\}\mid i\in S\}}\lambda ^{\mathcal{B}_S}_Tv^S(T) \text{ for } \text{ all } S\in \mathcal{S}.\end{array}\right. \end{aligned}$$

(6.3)

Note that (6.3) has feasible solutions. Hence, the linear program has either an optimal solution or it is unbounded from below. Therefore, its dual program must also have either an optimal solution with the same optimal value or it has no feasible solution. Now, with $Z=Z\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right)$ and

$$\begin{aligned} a^\varepsilon _z=\left\{ \begin{array}{l}a_z\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}},v\right) \text{, } \text{ if } z\in Z{\setminus } \{\mathbbm {1}^{N{\setminus } S}\mid S\in \mathcal{S}\},\\ \max \{a_z\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}},v\right) ,v(N)-v(S)+\varepsilon \}\text{, } \text{ if } z\in \{\mathbbm {1}^{N{\setminus } S}\mid S\in \mathcal{S}\},\end{array}\right. \end{aligned}$$

the dual program is

$$\begin{aligned}&\max \sum _{z\in Z}\delta _za^\varepsilon _z \nonumber \\&\text{ subject } \text{ to }\left\{ \begin{array}{l}\sum _{z\in Z}\delta _zz=\mathbbm {1}^N \text{ and } \\ \delta _z\geqslant 0 \text{ for } \text{ all } z\in Z.\end{array}\right. \end{aligned}$$

(6.4)

Sufficiency: Assume that $M(v)\cap X_\mathcal{S}(v)\ne \emptyset$. By Corollary 5.4 there exist $(\mathcal{B}_S)_{S\in \mathcal{S}}\in {\mathbb {C}}(\mathcal{S})$ and $\varepsilon >0$ such that there exists a feasible solution x of (6.3) such that $x(N)\leqslant v(N)$. Hence, for each $Z'\in {\mathbb {B}}\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right)$, $\sum _{z\in Z'}\delta ^{Z'}_za^\varepsilon _z\leqslant v(N)$. If $a^\varepsilon _z>a_z$ for some $z\in Z'$, $\sum _{z\in Z'}\delta ^{Z'}_za_z<v(N)$. Otherwise, $\sum _{z\in Z'}\delta ^{Z'}_za^\varepsilon _z=\sum _{z\in Z'}\delta ^{Z'}_za_z\leqslant v(N)$ so that this direction has been shown.

Necessity: Assume that, for some $(\mathcal{B}_S)_{S\in \mathcal{S}}\in {\mathbb {C}}(\mathcal{S})$, neither (6.1) nor (6.2) is valid. If ${\mathbb {B}}\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right) =\emptyset$, then, regardless of the choice of $\varepsilon >0$, (6.4) has no feasible solution so that there must be a feasible solution x of (6.3) such that $x(N)\leqslant v(N)$. If ${\mathbb {B}}\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right) \ne \emptyset$, then, for all $Z'\in {\mathbb {B}}\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right)$, $\sum _{z\in Z'}\delta ^{Z'}_za_z\leqslant v(N)$ and, if $Z'\in \mathbb B_0\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right)$, then $\sum _{z\in Z'}\delta ^{Z'}_za_z< v(N)$. Hence, we may select $\varepsilon >0$ such that $\sum _{z\in Z'}\delta ^{Z'}_za^\varepsilon _z\leqslant v(N)$. We conclude in any case that there must be a feasible solution x of (6.3) such that $x(N)\leqslant v(N)$. Therefore, there exists $x'\in {\mathbb {R}}^N$ with $x'\geqslant x$ and $x'(N)=v(N)$. Now, as $x'\geqslant x$, $x'$ is a feasible solution of (6.3) that satisfies $x'(N)=v(N)$. Hence, $x'\in X_{\mathcal{S}}(v)$ so that $\mathcal{S}$ is feasible for v. Thus, $M(v)\cap X_\mathcal{S}(v)\ne \emptyset$ by Corollary 5.4. $\square$

Let us try to explain the intuition behind this main result. Consider a given region $X_\mathcal{S}$, supposing for simplicity that $\mathcal{S}=\{S\}$. If there exists an undominated element $x\in X_\mathcal{S}$, by application of Corollary 5.4 (or Theorem 5.1), there exists a balanced collection $\mathcal{B}_S$ associated with S such that

$$\begin{aligned} \sum _{i\in S,\{i\}\in \mathcal{B}_S}\lambda _{\{i\}}^{\mathcal{B}_S}x_i+\sum _{T\in \mathcal{B}_S{\setminus }\{\{i\}\mid i\in S\}}\lambda _T^{\mathcal{B}_S}v^S(T)\geqslant v(N). \end{aligned}$$

Now, x being in $X_\mathcal{S}$, it satisfies all core inequalities except the one corresponding to S. In other words, x satisfies the system of inequalities in (6.3), which can be seen as similar to a core-defining system. Proceeding as in the classical Bondareva-Shapley proof, the balancedness condition is obtained by considering the dual program. The dual variables, denoted by $\delta _z$, are those corresponding to the coalitions $T\in \mathcal{F}{\setminus }\mathcal{S}$ ($z=\mathbbm {1}^T$), to $N{\setminus } S$ ($z=\mathbbm {1}^{N{\setminus } S}$), and to S ($z=z^S$). As the coefficients $\lambda ^{\mathcal{B}_S}_{\{i\}}$ of the $x_i$ in the inequality corresponding to S are not necessarily equal to 1 and do not have to coincide, a more general definition of a balanced collection is needed, and this yields the definition of Z. Now, the right-hand side of the system is not simply v(T) but a more involved expression, which is denoted by $a_z$. As the same left-hand side x(T) may appear in different lines of (6.12), $a_Z$ is defined as a maximum. In summary, the balancedness condition for the existence of an undominated element x in $X_\mathcal{S}$ would be given by $\sum _{z\in Z'}\delta _za_z\leqslant v(N)$ for all balanced collections $Z'$ in Z. Taking the negation of this statement yields the condition given in Theorem 6.1, up to some subtleties in strict or nonstrict inequalities caused by the inequality corresponding to $N{\setminus } S$.

Corollary 6.2

Let (N, v) be a balanced game. Then (N, v) has a stable core if and only if for all $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}$ and all $(\mathcal{B}_S)_{S\in \mathcal{S}}\in \mathbb C(\mathcal{S})$, with $a_z:=a_z\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}},v\right)$ for all $z\in Z\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}}\right)$, either (6.1) holds or (6.2) holds.

Remark 6.3

It should be noted that the condition “for all $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}$” in Corollary 6.2 can be replaced by “for all feasible collections $\mathcal{S}$ for v”, which would typically reduce the number of required tests for core stability, as often not all nonempty subsets of coalitions in $\mathcal{F}$ are feasible for v. On the other hand, the current form does not require to check in advance which of the nonempty subsets of $\mathcal{F}$ are feasible for v.

We now apply our main theorem to an illustrating example.

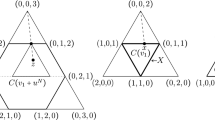
Example 6.4

Let $N=\{1,\ldots ,5\}$, $\lambda ^1=(2,1,0,0,0)$, $\lambda ^2=(0,0,1,1,1)$, and (N, v) be defined by $v(S)=\min \{\lambda ^1(S),\lambda ^2(S)\}$ for all $S \subseteq N$. Then (N, v) is exact, and C(v) is the convex hull of $\lambda ^1$ and $\lambda ^2$ [18, Example 4.3]. The shape of the core immediately shows that all strongly vital-exact coalitions are also strictly vital-exact:

$$\begin{aligned}&\mathcal{F}:=\mathcal{VE}^{\mathrm{strong}}(v)\\&\quad =\mathcal{VE}^{\mathrm{strict}}(v)= \{\{i\}\mid i\in N\}\cup \{\{1,k,\ell \}\mid k,\ell \in \{3,4,5\},k\ne \ell \}\cup \\&\quad \{\{2,i\}\mid i\in \{3,4,5\}\}. \end{aligned}$$

It is known that the core is not stable, and we now illustrate Theorem 6.1 by checking the condition for nonempty subsets $\mathcal{S}\subseteq \mathcal{F}$. The singletons and the 2-person coalitions in $\mathcal{F}$ are extendable. We remark that if S is extendable, then every preimputation x such that $x(S)<v(S)$ and $x(T)\geqslant v(T)$ for all $T\subsetneqq S$ can be outvoted via S by a core element. It follows that, for each $\mathcal{S}$ that contains at least one singleton or one 2-person coalition in $\mathcal{F}$, each element of $X_\mathcal{S}(v)$ is outvoted by a core element. Therefore, we now consider only the cases that $\mathcal{S}$ consists of one, two, or all 3-person coalitions in $\mathcal{F}$.

• (1) If $\mathcal{S}$ is the singleton of one 3-person coalition in $\mathcal{F}$, then we may assume, as players 3, 4, and 5 are substitutes, that $\mathcal{S}=\{\{1,3,4\}\}$. If $x\in X_{\mathcal{S}}(v)$, then we claim that $x=(2-a-b,1-a,a,a,b)$ for some $0\leqslant a<1$ and some $b>a$ such that $a+b\leqslant 2$. Indeed, for $j\in \{3,4\}$, $x_1+x_j+x_5\geqslant v(\{1,j,5\})=2$ and $x_2+x_{7-j}\geqslant v(\{2,7-j\})=1$. As $3=v(N)=x_1+x_j+x_5+x_2+x_{7-j}$, the foregoing inequalities are, in fact, equalities. Therefore, $x_3=x_4=:a$ and with $b:=x_5$, our claim follows because $x\geqslant 0$ and $x_1+x_3+x_4<2$. Therefore, for any $0<\varepsilon <\min \{1-a,\nicefrac {(b-a)}{2}\}$, $(2-2a-2\varepsilon ,1-a-\varepsilon ,a+\varepsilon ,a+\varepsilon ,a+\varepsilon )$ is a core element that outvotes x via $\{1,3,4\}$. (Note that $\mathcal{S}$ is feasible because, e.g., $(0,1,0,0,2)\in X_\mathcal{S}(v).$)

• (2) If $\mathcal{S}$ consists of two 3-person coalitions, then we may assume $\mathcal{S}=\{\{1,3,4\},\{1,3,5\}\}$. Choose $\mathcal{B}_{\{1,3,4\}}=\{\{4\},\{1,3,5\},\{2\}\}$, $\mathcal{B}_{\{1,3,5\}}=\{\{5\},\{1,3,4\},\{2\}\}$, and note that $B_{\{1,3,4\}}$ and $B_{\{1,3,5\}}$ are admissible for $\mathcal{S}$. Also $z^{\{1,3,4\}}=\mathbbm {1}^{\{4\}}$ and $a_{z^{\{1,3,4\}}}=v(N)-v(\{1,3,5\})-v(\{2\})=1$. Similarly, $z^{\{1,3,5\}}=\mathbbm {1}^{\{5\}}$ and $a_{z^{\{1,3,5\}}}=1$. The following table shows the resulting pairs $(z,a_z)$ such that $a_z$ is positive:

  $$\begin{aligned} \begin{array}{c|c}z&{}a_z\\ \hline (0,0,0,0,1)&{}1\\ (0,0,0,1,0)&{}1\\ (1,0,0,1,1)&{}2\\ (0,1,1,0,0)&{}1\\ (0,1,0,1,0)&{}1\\ (0,1,0,0,1)&{}1 \end{array} \end{aligned}$$

  Let $y=(0,0.5,0.5,1,1)$ and note that $y\cdot z\geqslant a_z$ for all $z\in Z$. Also, note that $y\cdot \mathbbm {1}^{N{\setminus } \{1,3,4\}}=1.5>a_{\mathbbm {1}^{N{\setminus }\{1,3,4\}}}=1$ and $y\cdot \mathbbm {1}^{N{\setminus } \{1,3,5\}}=1.5>a_{\mathbbm {1}^{N{\setminus }\{1,3,5\}}}=1$. Hence, for all minimal balanced subsets $Z'$ of Z, we have $\sum _{z\in Z'}\delta ^{Z'}_za_z\leqslant \sum _{z\in Z'}\delta ^{Z'}_z y\cdot z=y\cdot \sum _{z\in Z'}\delta ^{Z'}_z z=y\cdot \mathbbm {1}^N=3=v(N)$, and if $Z'$ contains $\mathbbm {1}^{N{\setminus } \{1,3,4\}}$ or $\mathbbm {1}^{N{\setminus } \{1,3,5\}}$ the inequality is strict. We conclude that M(v) intersects $X_\mathcal{S}(v)$. For instance, $(1,1,0,0.5,0.5)\in M(v)\cap X_\mathcal{S}(v)$. However, $(1,1,0,0.1,0.9)\in X_\mathcal{S}(v)$ is outvoted via $\{1,2,4\}$ by (1.2, 0.6, 0.4, 0.4, 0.4).

• (3) The case $\mathcal{S}=\{\{1,3,4\},\{1,3,5\},\{1,4,5\}\}$ is again treated “indirectly”. Let $x\in X_\mathcal{S}(v)$. In this case we may assume $x_3\leqslant x_4\leqslant x_5$. As $x\geqslant 0$, $x_4+x_5<2$ and, hence, $x_4<1$. As $x_4\leqslant x_5$, $x_1<2-2x_4$. Let $0<\varepsilon <\min \{1-x_4,\nicefrac {(2-2x_4-x_1)}{2}\}$. Then $(2-2x_4-2\varepsilon ,1-x_4-\varepsilon ,x_4+\varepsilon ,x_4+\varepsilon ,x_4+\varepsilon )\in C(v)$ outvotes x via $\{1,3,4\}$ so that the condition of our theorem is satisfied for $\mathcal{S}$. (Note that $\mathcal{S}$ is feasible because $(0.5,1,0.5,0.5,0.5)\in X_\mathcal{S}(v)).$

7 Core super-stability

Shellshear and Sudhölter [24] present several sufficient conditions for core stability, the weakest of which is called vital-exact extendability. Let (N, v) be a balanced game. A coalition $S\in 2^N{\setminus }\{N,\emptyset \}$ is called extendable if, for each $x\in C(v_{|S})$ (recall that $(S,v_{|S})$ is the subgame of (N, v) with player set S), there exists $y\in C(v)$ such that $y_S=x$. If all subcoalitions of N are extendable, then the core is stable [13]. However, extendability remains sufficient for core stability if it is weakened to vital-exact extendability, requiring just that all strongly vital-exact coalitions must be extendable. By means of examples, Shellshear and Sudhölter [24] show that core stability is less demanding than vital-exact extendability, which is less demanding than extendability of all vital exact coalitions, which in turn is less demanding than extendability of all coalitions. However, for several remarkable classes of games, vital-exact extendability is necessary (and sufficient) for core stability. Though it is not known if vital-exact extendability can be further relaxed so that it becomes necessary and remains sufficient for core stability in general, Corollary 6.2 allows the construction of a finite test for core stability. This section is devoted to study a more demanding property than core stability, called core super-stability. It is then shown that this property is equivalent to vital extendability requiring that all vital subcoalitions are extendable.

Let (N, v) be a game. A vector $x\in {\mathbb {R}}^N$ is N-feasible if $x(N)\leqslant v(N)$. Now, if $v(N)\geqslant \sum _{i\in N}v(\{i\})$, then, by Remark 2.1, the core is stable if and only if every preimputation that is not in the core may be dominated by a core element. Hence, the core is stable if and only if every N-feasible vector that is not in the core is dominated by a core element. Indeed, the if part is obvious. For the only-if part, let $y\in {\mathbb {R}}^N{\setminus } C(v)$ satisfy $y(N)\leqslant v(N)$. If there exists $S\subsetneqq N$ with $y(S)<v(S)$, then there exists $y'\in {\mathbb {R}}^N$ such that $y'_S=y_S$, $y'\geqslant y$, and $y'(N)=v(N)$. As the core is stable, $y'$ is dominated by some core element via some proper coalition so that y is dominated via the same coalition. If $y(S)\geqslant v(S)$ for all $S\in 2^N{\setminus }\{\emptyset ,N\}$, then $y(N)<v(N)$ and $y+\frac{v(N)-y(N)}{|N|}\mathbbm {1}^N$ is a core element that dominates y via N.

We now define the “super-stability” of the core by relaxing N-feasibility. A vector $x\in {\mathbb {R}}^N$ is aspiration-feasible [3] if, for each $i\in N$ there exists $S\subseteq N$ such that $i\in S$ and $x(S)\leqslant v(S)$. Note that Bennett [4] uses the word “anticipation” for a vector that is aspiration-feasible (and, in her context of a nonnegative game, nonnegative). An upper vector is a vector $x\in {\mathbb {R}}^N$ such that $x(S)\geqslant v(S)$ for all $S\subseteq N$ [27]. Let U(v) denote the set of upper vectors. An aspiration [4] is an aspiration-feasible upper vector, i.e., it is an upper vector x satisfying $x(S)=v(S)$ for all S in a covering of N. Let Asp(v) denote the set of aspirations. Observe that $C(v)\subseteq Asp(v)$.

Remark 7.1

• (1) Let $x\in {\mathbb {R}}^N{\setminus } U(v)$ and choose an arbitrary minimal coalition $P\subseteq N$ such that $x(P)<v(P)$. Then there exists $y\in U(v)$ such that y dominates x via P. Indeed, for $i\in P$, put $y_i=x_i+\frac{v(P)-x(P)}{|P|}$, and, for $j\in N{\setminus } P$, put $y_j$ large enough, e.g., $y_j=\max _{S\subseteq N}v(S)-\min _{S\subseteq N}v(S)$. For $S\subsetneqq P$, $y(S)\geqslant v(S)$ because $y_P \gg x_P$ and $x(S)\geqslant v(S)$. For $S\subseteq N$ with $S{\setminus } P\ne \emptyset$, $y(S)\geqslant (v(S)-v(S\cap P))+y(S\cap P)\geqslant v(S)$. Finally, $y(P)=v(P)$ so that y has the desired properties.

• (2) For each $y\in U(v)$ there exists $z\in Asp(v)$ such that $z\leqslant y$. Indeed, for each $z\in U(v)$ denote $T(z)=\bigcup \{S\subseteq N\mid z(S)=v(S)\}$. Now, let $z\in U(v)$ such that $z\leqslant y$ and T(z) is maximal (w.r.t. inclusion). It remains to show that $T(z)=N$. Assume, on the contrary, that there exists $j\in N{\setminus } T(z)$. Let $\widehat{z}\in {\mathbb {R}}^N$ differ from z only inasmuch as $\widehat{z}_j=z_j-\min \{z(S)-v(S)\mid S\subset N,j\in S\}$. Then $\widehat{z}\in U(v)$, $z\leqslant y$, and $T(\widehat{z})\supseteq T(z)\cup \{j\}$, which is impossible by the maximality of T(z).

The foregoing remark has the following implications. Recall that a game (N, v) has a large core if, for every $y\in U(v)$, there exists $x\in C(v)$ such that $x\leqslant y$ [23].

Corollary 7.2

• (1) Any $x\in {\mathbb {R}}^N{\setminus } U(v)$ is dominated by an aspiration.

• (2) The set of aspirations coincides with the core, i.e., $Asp(v)=C(v)$, if and only if (N, v) has a large core.

Say that the game (N, v) has a super-stable core if each aspiration-feasible vector that is not an aspiration is dominated by a core element.

Proposition 7.3

The game (N, v) has a super-stable core if and only if each $x\in {\mathbb {R}}^N{\setminus } U(v)$ is dominated by some core element.

Proof

The if part is true because an aspiration-feasible vector that is not an aspiration is also not an upper vector. For the converse, let $x\in {\mathbb {R}}^N{\setminus } U(v)$. Define the game (N, u) by $u(S)=\min \{x(S),v(S)\}$. Hence, $x\in U(N,u)$. By Remark 7.1 (2) there exists $y\in Asp(N,u)$ such that $y\leqslant x$. Hence, $y(S)=x(S)$ whenever $x(S)<v(S)$. As $u\leqslant v$, y is an aspiration-feasible vector of (N, v), but not an aspiration. Let $z\in C(v)$ dominate y via some coalition S. As $y(T)\geqslant v(T)$ whenever $x(T)\geqslant v(T)$, we deduce $x(S)<v(S)$, which implies $y(S)=x(S)$, which in turn implies $x_S=y_S$, so that z also dominates x via S. $\square$

Proposition 7.4

A TU game has a super-stable core if and only if the game is vital extendable.

Proof

To show the if part, assume that (N, v) is a vital extendable TU game and let $y\in {\mathbb {R}}^N{\setminus } U(v)$. Let S be a minimal (w.r.t. inclusion) coalition such that $y(S)<v(S)$. Define $x_S\in {\mathbb {R}}^S$ by $x_i=y_i+\frac{v(S)-y(S)}{|S|}$ for all $i\in S$. Then $x_S\in C(v_{|S})$ and $x(T)>v(T)$ for all proper subcoalitions T of S so that S is vital. Hence, $x_S$ can be extended to some $x\in C(v)$. Consequently, x dominates y via S.

For the remaining implication, assume that (N, v) has a super-stable core. Let S be a vital coalition and $x_S\in C(v_{|S})$. We first assume that $x(T)>v(T)$ for all proper subcoalitions T of S. Let $y^k_S\in {\mathbb {R}}^S$ be defined by $y^k_i=x_i-\frac{1}{k}$ for all $k\in {\mathbb {N}}$ and $i\in S$. Moreover, extend $y^k_S$ to some $y^k\in {\mathbb {R}}^N$ such that $y^k(P)\geqslant v(P)$ for all $P\in 2^N{\setminus } 2^S$. As $\lim _{k\rightarrow \infty } y^k_S=x_S$, there exists $K\in {\mathbb {N}}$ such that $y^k(P)\geqslant v(P)$ for all $P\in 2^N{\setminus }\{S\}$ and all $k\geqslant K$. By the super-stability of the core, for each $k\in {\mathbb {N}}$, as $y^k(S)<x(S)=v(S)$, there exists $z^k\in C(v)$ such that $z^k$ dominates $y^k$. Hence, for $k\geqslant K$, $z^k$ dominates $y^k$ via S. Moreover, as $\lim _{k\rightarrow \infty } y^k_S=x_S,$ $z_S>y_S^k$, and $z^k(S)=v(S)=x(S)$ for $k\geqslant K$, $\lim _{k\rightarrow \infty }z^k_S=x_S$. By compactness of the core, $(z^k)_{k\in {\mathbb {N}}}$ has a convergent subsequence. Let z be the limit of this subsequence. Hence, $z_S=x_S$ so that the extendability of $x_S$ has been verified.

Now we can finish the proof. Let $\widetilde{x}_S\in C(v_{|S})$ and $x_S\in C(v_{|S})$ such that $x(T)>v(T)$ for all proper subcoalitions T of S. Then, for all $k\in {\mathbb {N}}$, $x^k_S=\frac{1}{k}x_S+\frac{k-1}{k}\widetilde{x}_S\in C(v_{|S})$ and $x^k_S(T)>v(T)$ for all proper subcoalitions T of S so that $x^k$ can be extended to some $x^k\in C(v)$ as we have shown before. By compactness of the core the sequence $(x^k)_{k\in {\mathbb {N}}}$ has a convergent subsequence, and its limit extends $\widetilde{x}_S$ to a core element. $\square$

8 Discussion and concluding remarks

Corollary 6.2 allows to check if a balanced game has a stable core with the help of a finite number of tests. There are finitely many minimal balanced collections of coalitions (and we know how to inductively construct them [17]) so that there are just finitely many triples $\left( \mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}},Z'\right)$ that have to be checked. This solves a problem that has remained open for a long time.

This being said, still some further investigation seems to be necessary, mainly for two reasons: The test appears to be very combinatorial, and it involves a strict inequality: $\sum _{z\in Z'}\delta _z^{Z'}a_z>v(N)$. We discuss these points and some other ones in what follows.

Finding feasible collections. The first problem that arises is to find all feasible collections $\mathcal S$, in order to determine the partition of $X(v){\setminus } C(v)$. Indeed, recall that we may restrict our attention to feasible collections for v as explained in Remark 6.3. The following lemma permits us to avoid a naive enumeration of all the subcollections of $\mathcal F$.

Lemma 8.1

Let (N, v) be balanced and $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}$. Then the following statements are true.

• (1) If $\mathcal{S}$ is feasible, then it does not contain a balanced collection of N.

• (2) For $S,S'\in \mathcal{S}$, if $S\cup S'=N$, there is no $x\in X_\mathcal{S}(v)$ that can be dominated via S or $S'$.

Proof

(1) Consider a feasible $\mathcal{S}$ and suppose that a balanced collection $\mathcal{B}$ with balancing weights $(\lambda _S)_{S\in \mathcal{B}}$ is contained in $\mathcal{S}$. Then for every $x\in X_\mathcal{S}(v)$,

$$\begin{aligned} x(S) < v(S), \quad S\in \mathcal{B}. \end{aligned}$$

Multiplying the inequalities by $\lambda _S$ and summing them yields

$$\begin{aligned} v(N)=x(N)<\sum _{S\in \mathcal{B}}\lambda _Sv(S), \end{aligned}$$

which contradicts balancedness of (N, v).

(2) Suppose $S\cup S'=N$. If $X_\mathcal{S}(v)=\emptyset$, then nothing has to be shown. Otherwise take $y\in X_\mathcal{S}(v)$ and suppose that there is a core element x dominating y via S. Then the side-payment $z=y-x$ satisfies $z_S\ll 0_S$, $z(S)<0,$ and $z(S')<0$. As $S,S'\ne N$, we have $S\not \subseteq S'$ and $S'\not \subseteq S$. As z is a side-payment, we have $z(S)=-z(N{\setminus } S)=-z(S'{\setminus } S)$. It follows that

$$\begin{aligned} z(S')=z(S\cap S') + z(S'{\setminus } S) = \underbrace{z(S\cap S')}_{\geqslant z(S)}-z(S) \geqslant 0, \end{aligned}$$

which is a contradiction. $\square$

Note that a consequence of Lemma 8.1 (1) is that $S\in \mathcal{S}$ implies $N{\setminus } S\not \in \mathcal{S}$. Moreover, observe that (2) implies the following simple necessary condition for core stability: No feasible $\mathcal S$ can be of the form $\{S,S'\}$ with $S\cup S'=N$. But it may even be superfluous to check some feasible collections. For example, as we already mentioned in Example 6.4, every element of $X_\mathcal{S}$ is outvoted when $\mathcal{S}$ contains a minimal coalition S which is extendable.

On a sharp form of Corollary 6.2. Unlike the Bondareva-Shapley result on nonemptiness of the core (see (1) of Remark 3.1), we do not know if Corollary  6.2 (even with the condition “for all feasible collections $\mathcal{S}$ for v” rather than “for all $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}$”) is sharp or not, although we use only minimal admissible balanced collections. In particular, we do not know whether the condition $\sum _{z\in Z'}\delta _z^{Z'}a_z>v(N)$ is necessary or if only the $\ldots \geqslant$ suffices. So far, attempts to find examples where the strict inequality is used have failed. What we could establish, however, is that the set ${{\mathbb {B}}}_0$ is never empty when the core is stable. Incidentally, this gives another necessary condition for core stability.

Lemma 8.2

Let (N, v) be a balanced game with a stable core and $\emptyset \ne \mathcal{S}\subseteq \mathcal{F}$. Then ${{\mathbb {B}}}_0(\mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}})\ne \emptyset$ for all $(\mathcal{B}_S)_{S\in \mathcal{S}}\in {{\mathbb {C}}}(\mathcal{S})$.

Proof

1. We claim that for each $S\in \mathcal{S}$, there exists a minimal balanced collection $Z'$ containing $\mathbbm {1}^{N{\setminus } S}$. Indeed, all singletons being strictly vital-exact, they belong either to $\mathcal{S}$ or to $\mathcal{F}{\setminus } \mathcal{S}$. If $\{i\}$ is in $\mathcal{S}$, observe that $z^{\{i\}}=\mathbbm {1}^{\{i\}}$, because $\mathcal{B}_{\{i\}}\ni \{i\}$ and is a minimal balanced collection. Therefore, $Z'=\{\mathbbm {1}^{N{\setminus } S}\}\cup \{\mathbbm {1}^{\{i\}}\mid i\in S\}$ is a minimal balanced collection in Z, that we call S-canonical.

2. By core stability, Lemma 8.1(2) implies that there exists $S\in \mathcal{S}$ such that $S\cup T\subsetneqq N$ for all $T\in \mathcal{S}$. Let $Z'$ be the S-canonical minimal balanced collection. For all $T\in \mathcal{S}$, $z^T_j=0$ for all $j\in N{\setminus } T$. As $S\cup T\subsetneqq N$ for all $T\in \mathcal{S}$, $z^T\ne \mathbbm {1}^{N{\setminus } S}$. We conclude that the balancing weight $a_{\mathbbm {1}^{N{\setminus } S}}(\mathcal{S},(\mathcal{B}_T)_{T\in \mathcal{S}})$ must be $v(N)-v(S)$, i.e., $Z'\in {{\mathbb {B}}}_0(\mathcal{S},(\mathcal{B}_S)_{S\in \mathcal{S}})$. $\square$

The presence of a strict inequality in the test prevents us from easily answering questions like: Is the set of games with a stable core closed? Is core stability a strong prosperity property? We elaborate on the latter question. According to Van Gellekom et al. [27], a property P on a set of games is a (strong) prosperity property if for every game v, there exists a constant $\alpha (v^0)$, where $v^0$ is the restriction of v to $2^N{\setminus }\{N\}$, such that v has the property P if and only if v(N) is made greater or equal to $\alpha (v^0)$. P is a weak prosperity property if there exists a constant $\beta (v^0)$ such that v has property P if $v(N)\geqslant \beta (v^0)$. So far, it is known that core stability is a weak prosperity property, but it is not known whether it is a strong one. However, as vital extendability is a strong prosperity property, it follows that core super-stability is also a strong prosperity property.

On weak domination. An interesting fundamental question is whether replacing (usual) domination by weak domination, sometimes used in the literature, would have an impact on our construction and results. Given a game (N, v), a coalition S, and $x,y\in {\mathbb {R}}^N$, we say that x weakly dominates y via S if $x_S>y_S$ and $x(S)\leqslant v(S)$. Clearly, domination implies weak domination. The latter notion appears to be useful in the related problem of accessibility of the core: Given an imputation outside the core, how do we reach the core by successive improvements in the sense that the new imputation dominates the former. As shown by, e.g., Wu [30] or Vasil’ev [28], there exists a sequence of improvements that converges to a core element. However, in order to guarantee that such a sequence reaches the core after finitely many steps, the weak domination relation is employed [20] in another branch of the literature.

The following example shows that the core of a balanced game that does not possess a stable core may be stable w.r.t. weak domination. Indeed, let $N=\{1,\ldots ,5\}$ and $x=(2,1,0,0,0), z=(0,0,1,1,1)\in {\mathbb {R}}^N$, and (N, v) be defined, for each $S\subseteq N$, by $v(S)=\min \{x(S),z(S)\}$. Note that (N, v) is an “orthogonal game”—for a generalization of this example, see Biswas et al. [6]—that does not possess a stable core. Indeed, (1, 1, 1/2, 1/2, 0) cannot be dominated by a core element. On the other hand, if $y\in X(v){\setminus } C(v)$ is not dominated by a core element, then $y_i\geqslant 0$ because the singletons are exact (the game is exact). Also, $y_2+y_j\geqslant v(\{2,j\})$ because $\{2,j\}$ is extendable for $j=3,4,5$. Hence, $y_3+y_4+y_5\leqslant 3$, and we may assume that $y_3\geqslant y_4\geqslant y_5\geqslant 0$. Hence, $y_2\geqslant 1-y_5$ and, hence, $y_1\leqslant 2-y_3-y_4$. Therefore, $\widetilde{x}=(2-2y_4,1-y_4,y_4,y_4,y_4)\in C(v)$ and $\widetilde{x}$ weakly dominates y via $\{1,4,5\}$.

The foregoing example shows the structural difference between the concepts of “domination” and “weak domination”, and it follows that our characterization result of games with stable cores cannot simply be modified when we employ the notion of “weak domination”. We should also like to mention that the literature on von Neumann–Morgenstern stable sets relies on the concept of “ordinary” domination.

Concluding remarks. Obtaining a sharp form of Corollary  6.2 is a challenging task for future research, as well as establishing efficient algorithmic procedures to make the test easy to use in practice.

Appendix: The Solution \(M(\cdot )\) of Maximal Elements

Let U be a set with $U\supseteq \{1,2,3,4\}$ and $\Gamma ^b$ be the set of balanced games (N, v) such that $N\subseteq U$. For regarding $M(\cdot )$, assigning M(v) to each game $(N,v)\in \Gamma ^b$, as a solution on $\Gamma ^b_N$, we assume that $\mathcal{F}(N,v)=\mathcal{F}(N)$ just depends on N rather than on the considered game, say, $\mathcal{F}(N)=2^N{\setminus } \{N,\emptyset \}$. Hence, $\mathcal{F}(N)$ satisfies (2.3) and (2.2) for each $(N,v)\in \Gamma ^b_N$.

Note that, by its definition, $M(\cdot )$ satisfies some traditional properties like anonymity, covariance under strategic equivalence, and Pareto optimality. It also satisfies nonemptiness by Lemma 4.2. Finally, it satisfies the following weak dummy properties: Let $(N,u),(N\cup \{i\},v)\in \Gamma ^b$ with $i\in U{\setminus } N$ such that $u(S)=v(S)$ and $v(S\cup \{i\})=u(S)+v(\{i\})$ for all $S\subseteq N$.

• (1) Then, for each $y\in {\mathbb {R}}^{N\cup \{i\}}$ with $y_N\in M(u)$ and $y_i=v(\{i\})$, $y\in M(v)$. Indeed, assume, on the contrary, that there exists $z\in X(v)$ such that $z\succ ^v_S y$ for some $\emptyset \ne S\subsetneqq N\cup \{i\}$. If $i\in S$, then $z_i>y_i=v(\{i\})$, and if $i\notin S$, then $z_i\geqslant v(\{i\})$ because $\{i\}$ is supposed to be feasible for v. Hence, $S\ne \{i\}$ and, as $z_i\geqslant y_i$ and $z(N\cup \{i\})=y(N\cup \{i\})$, $S\ne N$. Therefore, there exists $z'\in X(u)$ with $z'\geqslant z_N$ and $z'_{S{\setminus }\{i\}}=z_{S{\setminus }\{i\}}$ so that $z'\succ ^u_{S{\setminus }\{i\}}y_N$ contradicting $y_N\in M(u)$.

• (2) Then, for each $y\in {\mathbb {R}}^{N\cup \{i\}}$ with $y\in M(v)$ and $y_i= v(\{i\})$, $y_N\in M(u)$. Indeed, if $z\succ ^u_S y_N$, then $z'\gg ^v_S y$, where $z'_i= v(\{i\}),z'_N=z$.

• (3) If $y\in M(v)$, then $y_i\geqslant v(\{i\})$. Indeed, each $x\in X(v)$ satisfying $x_i<v(\{i\})$ is outvoted via $\{i\}$ by any core element of v.

• (4) M(v) nevertheless does not satisfy the dummy (null player) property as shown by an example at the end of this section.

We now compute M(v) for all totally balanced (see (2) of Remark 3.1 ) symmetric 3-person games (N, v). By anonymity and covariance we may assume that $N=\{1,2,3\}$ and v is 0-normalized (i.e., $v(\{i\})=0$ for all $i\in N$). Now, if $v(N)=0$, then $v(S)=0$ for all $S\in \mathcal{F}$ because $C(v)\ne \emptyset$. Hence (N, v) is convex so that $M(v)=C(v)=\{(0,0,0)\}$. Hence, by covariance we may assume that $v(N)=1$. As $C(v)\ne \emptyset ,$ the symmetry of the game implies that $v(S)=\alpha$ for all $S\in \mathcal{F}$ with $|S|=2$ for some $\alpha \leqslant 2/3$. If $\alpha \leqslant 0$, then $C(v)=M(v)= \Delta (N):=\{x\in {\mathbb {R}}^N_+\mid x(N)=1\}$ by convexity of v. If $0<\alpha <1/2$, then, again by convexity of v, $C(v)=M(v)$ is the convex hull of

$$\begin{aligned} \{(0,\alpha ,1-\alpha ),\!(0,1-\alpha ,\alpha ),(\alpha ,0,1-\alpha ),\!(1-\alpha ,0,\alpha ),\!(\alpha ,1-\alpha ,0),\!(1-\alpha ,\alpha ,0)\}. \end{aligned}$$

For $\alpha =1/2$, the game is still convex so that $C(v)=M(v)$ is the convex hull of

$$\begin{aligned} \{(0,\nicefrac {1}{2},\nicefrac {1}{2}),(\nicefrac {1}{2},0,\nicefrac {1}{2}),(\nicefrac {1}{2},\nicefrac {1}{2},0)\}. \end{aligned}$$

If v is not convex (but balanced), then it has no stable core so that $C(v)\subsetneqq M(v)$.

To analyze the remaining cases, we write $v=v^\alpha$ to emphasize that we consider a one-parameter set of games.

• (1) $1/2<\alpha <2/3$ (see Fig. 1): Then $C(v^\alpha )$ is the convex hull of

  $$\begin{aligned} \{(1-\alpha ,1-\alpha ,2\alpha -1),(1-\alpha ,2\alpha -1,1-\alpha ),(2\alpha -1,1-\alpha ,1-\alpha )\}. \end{aligned}$$

  Let $X=\{x\in {\mathbb {R}}^N\mid x(N)=1,|\{i\in N\mid x_i\geqslant 1-\alpha \}|\geqslant 2\}$. We claim that $X\cup C(v^\alpha )=M(v^\alpha )$. In order to show that $M(v^\alpha ){\setminus } C(v)\subseteq X$ let $x\in X(v^\alpha ){\setminus } C(v^\alpha )$ such that $|\{i\in N\mid x_i>1-\alpha \}|<2$. By symmetry we may assume $x_1\leqslant x_2<1-\alpha < x_3$. Then x is outvoted via $\{1,2\}$ by a suitable convex combination of $(1-\alpha ,2\alpha -1,1-\alpha )$ and $(2\alpha -1,1-\alpha ,1-\alpha )$. For the other inclusion, let $y\in X$ and assume $y_1\leqslant y_2\leqslant y_3,y_2\geqslant 1-\alpha$, and $y\notin C(v^\alpha )$. Then y cannot be outvoted by some $z\in X(v^\alpha )$ via a singleton $\{i\}$ because $z(N)=1$ and $z(S)\geqslant \alpha$ for $S\in \mathcal{F}$ with $|S|=2$ implies $z\in C(v^\alpha )$, i.e., $z_i>0=v^\alpha (\{i\})$. Now, y cannot be outvoted via $\{2,3\}$ as this would imply $z_2+z_3> 2-2\alpha>2/3> v^\alpha (\{2,3\})$. Hence, it remains to prove that y can neither be outvoted via $\{1,2\}$ nor via $\{1,3\}$. To this end, assume that $z\succ _{\{1,2\}}y$. Hence, $z_1>y_1$, $z_2>y_2$, $z_1+z_3\geqslant \alpha$, $z(N)=1$. Therefore, $z_2=1-z_1-z_3\leqslant 1-\alpha \leqslant y_2$, a contradiction. Similarly we may show that y cannot be outvoted via $\{1,3\}$.

• (2) $\alpha =2/3$. Then $C(v^\alpha )=\{(\nicefrac {1}{3},\nicefrac {1}{3},\nicefrac {1}{3})\}.$ As under (1) we may show that $M(v^\alpha )=\{x\in X(v^\alpha )\mid |\{i\in N\mid x_i\geqslant 1/3\}|\geqslant 2\}$.

Fig. 1

$\alpha =0.6$. The triangle in dashed lines is I(v). Yellow (central triangle): $C(v^\alpha )$. Blue: X. $M(v^\alpha )$ is the union of the blue and yellow regions (color figure online)

The foregoing example permits to draw the following conclusions:

• M(v) may not be convex. Indeed, let $1/2<\alpha \leqslant 2/3$. For $\varepsilon >0$, $(1-\alpha +\varepsilon ,1-\alpha +\varepsilon ,2\alpha -1-2\varepsilon ),(1-\alpha +\varepsilon ,2\alpha -1-2\varepsilon ,1-\alpha +\varepsilon )\in M(v^\alpha ),$ but the midpoint $(1-\alpha +\varepsilon ,\nicefrac {(\alpha -\varepsilon )}{2},\nicefrac {(\alpha -\varepsilon )}{2})$ is not a member of $M(v^\alpha )$ (see Fig. 1).

• M(v) may not be bounded¹. Indeed, let $1/2<\alpha \leqslant 2/3$. Then $\{(1-\alpha +\varepsilon ,1-\alpha +\varepsilon ,2\alpha -1-2\varepsilon )\mid \varepsilon >0\}$ is an unbounded subset of $M(v^\alpha )$ (see Fig. 1).

• The correspondence $M(\cdot ): \Gamma ^b_N\rightrightarrows {\mathbb {R}}^N$ is not u.h.c. Indeed, let $(\alpha ^k)_{k\in {\mathbb {N}}}$ be an arbitrary real sequence with limit 1/2 and $1/2<\alpha ^k\leqslant 2/3$. Then $x^k=(2-\alpha ^k,2-\alpha ^k,2\alpha ^k-3)\in M(v^{\alpha ^k})$ for all $k\in {\mathbb {N}}$, $\lim _{k\rightarrow \infty } v^{\alpha ^k}=v^{1/2}$, and $\lim x^k=(\nicefrac {3}{2},\nicefrac {3}{2},-2)\notin M(v^{1/2})$.

Now we are able to show that a dummy player may receive more than her individual contribution in M. Let $(N\cup \{4\},w)$ be the game that arises from $(N,v^{2/3})$ by adding the null player 4. We claim that $x=(\nicefrac {2}{5},\nicefrac {2}{5},0,\nicefrac {1}{5})\in M(w)$. To this end, observe that $(\nicefrac {2}{5},\nicefrac {2}{5},\nicefrac {1}{5}), (\nicefrac {3}{5},\nicefrac {2}{5},0),(\nicefrac {2}{5},\nicefrac {3}{5},0)\in M(v^{2/3})$. Hence, x cannot be outvoted by a proper coalition of N. As x is individually rational, it cannot be outvoted by a 2-person coalition containing player 4. If it were outvoted by $z\in X(w)$ via N, then $z(\{1,2,4\}),z(\{1,3,4\}),z(\{2,3,4\})\geqslant 1$. Summing up these inequalities yields $2+z_4\geqslant 3$ so that $z_4\geqslant 1$ and, hence, $z(N)\leqslant 0$, which is impossible. It remains to show that x is neither outvoted via $S=\{1,3,4\}$ nor via $T=\{2,3,4\}$. Now, let $z\in X(w)$. If $x_S\ll z_S$, then $z(T)=1-z_1<3/5 < w(T)$, and, similarly, if $x_T\ll z_T$, then $z(S)< w(S)$.

Due to the foregoing “negative” properties we do not think that $M(\cdot )$ can be a valuable solution concept.