Facets of the cone of exact games

Abstract

The class of exact transferable utility coalitional games, introduced in 1972 by Schmeidler, has been studied both in the context of game theory and in the context of imprecise probabilities. We characterize the cone of exact games by describing the minimal set of linear inequalities defining this cone; these facet-defining inequalities for the exact cone appear to correspond to certain set systems (= systems of coalitions). We noticed that non-empty proper coalitions having non-zero coefficients in these facet-defining inequalities form set systems with particular properties. More specifically, we introduce the concept of a semi-balanced system of coalitions, which generalizes the classic concept of a balanced coalitional system in cooperative game theory. The semi-balanced coalitional systems provide valid inequalities for the exact cone and minimal semi-balanced systems (in the sense of inclusion of set systems) characterize this cone. We also introduce basic classification of minimal semi-balanced systems, their pictorial representatives and a substantial concept of an indecomposable (minimal) semi-balanced system of coalitions. The main result of the paper is that indecomposable semi-balanced systems are in one-to-one correspondence with facet-defining inequalities for the exact cone. The second relevant result is the rebuttal of a former conjecture claiming that a coalitional game is exact iff it is totally balanced and its anti-dual is also totally balanced. We additionally characterize those inequalities which are facet-defining both for the cone of exact games and for the cone of totally balanced games.

1 Introduction

The class of exact (transferable utility) games is one of the topics of interest in cooperative game theory; see Rosenmüller (2000, § V.1) or Grabish (2016, § 3.4). Exact games were introduced by Schmeidler (1972) within a wide framework of cooperative games with possibly infinite amount of players. In this paper we, however, consider the usual game-theoretical framework and assume that the set N of players (for considered cooperative games) is a (fixed) non-empty finite set. Mathematically equivalent concept of a coherent lower probability (to the one of an exact game) has later appeared in the context of imprecise probabilities (Walley 1991), where N has the interpretation of the sample space for considered (discrete) probability distributions. Exact games have various applications described in detail in (Csóka et al. 2011, § 1). For example, it was shown by Csóka et al. (2009) that exact games coincide with risk allocation games with no aggregate uncertainty and by Calleja et al. (2005) that non-negative exact games coincide with multi-issue allocation games.

1.1 Overview of former related results

It was shown already by Schmeidler (1972, § 2) that the exact games involve traditional convex (= supermodular) games (Shapley 1972) and form a subclass of a popular class of totally balanced games (Rosenmüller 2000, Chapter V). The latter class is then included in the class of balanced games (Shapley 1967), defined as the class of cooperative games with non-empty core polyhedron. Note that all these game-theoretical concepts have also their counterparts in the context of imprecise probabilities; see Miranda and Montes (2018) for more details about the correspondence.

In our framework of a finite set N of players, one can consider the geometric point of view on the situation. It follows from the results by Csóka et al. (2011) and Lohmann et al. (2012) that the set of (characteristic functions for) exact games over a fixed set N of players forms a polyhedral cone; the same is true for other three classes of cooperative games mentioned above. Thus, exact games over N can be characterized by means of a finite number of linear inequalities and a natural question of theoretical interest is what is the minimal set of such inequalities. Note in this context that we do not distinguish between an inequality and its multiple by a positive factor and that the uniqueness of the minimal defining set of linear inequalities for a polyhedral set is relative to the affine (= a shifted linear) space generated by the set; these are the so-called facet-defining inequalities for the polyhedral set.

Let us mention other related results. Balanced games were characterized in terms of linear inequalities already in the 1960s (Bondareva 1963; Shapley 1967) and the facet-defining inequalities for this cone correspond to certain systems of subsets of N, called the minimal balanced set systems (= collections). The facet-defining inequalities for the cone of supermodular games can also be assigned to set systems, namely to pairs of sets $S,T\subseteq N$ such that $S{\setminus } T$ and $T{\setminus } S$ are singletons (Kuipers et al. 2010, Corollary 11). The facet-defining inequalities for the cone of totally balanced games were recently characterized in (Kroupa and Studený 2019): they also correspond to set systems, called irreducible (minimal) balanced systems on subsets of N.

The existence of a finite system of linear inequalities characterizing exact games follows from the results by Lohmann et al. (2012). The inequalities reported by Lohmann et al. (2012) also correspond to systems of subsets of N; nevertheless, not all these inequalities are facet-defining for the exact cone. The problem of the characterization of facet-defining inequalities for this cone was then discussed in (Kroupa and Studený 2019, § 6) where a conjecture has been raised about their form. That conjecture, confirmed in case $|N|\le 5$, has an equivalent formulation saying that a game is exact iff it is totally balanced and its anti-dual game (Oishi et al. 2016) is totally balanced as well.

Recall that every polyhedral cone can be characterized by means of (finitely many) linear inequalities, which characterization is named the outer description. Nonetheless, every polyhedral cone can also alternatively be defined as the conic hull of finitely many vectors, which characterization is named the inner description. The latter approach leads to the task to characterize the extreme rays of (a pointed version of) the polyhedral cone. The generators of the extreme rays of the cones of (suitably) standardized cooperative games are named extreme games (Rosenmüller 2000, § V.4). Note in this context that the inner description for the cone of balanced games was presented in (Kroupa and Studený 2019, § 5.2). On the other hand, the number of extreme rays for the other three (standardized) cones seems to grow more than exponentially with |N|; this observation decreases the hope that they have manageable inner description. The available results here are the criteria to recognize extreme games: we have proposed simple and easily implementable such linear criteria based on the (vertices of the) corresponding core polyhedron both in the supermodular case (Studený and Kroupa 2016) and in case of exact games (Studený and Kratochvíl 2018).

1.2 Main results in this paper

This paper is devoted to the problem of characterization of facet-defining inequalities for the cone of exact games. We follow the line of research indicated above. More specifically, we introduce the concept of a (minimal) semi-balanced system of subsets of N, which generalizes the classic concept of a (minimal) balanced set system on N from (Shapley 1967). Linear inequalities assigned to these set systems are shown to characterize the cone of exact games (see Corollary 9). This result is analogous to Theorem 3.4 from (Lohmann et al. 2012) in which exact games are characterized by means of the so-called “exact balanced collections” of subsets of N, but there is one important difference. Our semi-balanced set systems technically differ from the collections of sets introduced by Lohmann et al. (2012), although the assigned sets of inequalities (as a whole) are necessarily equivalent.

The point is that our concept of a semi-balanced set system allows one to recognize easily certain hidden symmetry. More specifically, every game over N is exact iff its anti-dual game is exact and this fact is reflected in the linear inequalities for exact games: an inequality is valid/facet-defining for the exact cone iff the same holds for its conjugate inequality (see Sect. 5.1). Each semi-balanced set system ${{\mathcal {S}}}$ has a complementary semi-balanced set system ${{\mathcal {S}}}^{\star }$ and the inequality assigned to ${{\mathcal {S}}}^{\star }$ is conjugate to the inequality assigned to ${{\mathcal {S}}}$. We also introduce basic classification for minimal semi-balanced set systems, called briefly min-semi-balanced systems (on N), into four basic classes; the class of minimal balanced (= min-balanced) set systems on N is one of them (Sect. 5.2). In addition to that we introduce pictorial representatives for (permutational types of) min-semi-balanced systems (Sect. 5.3), which easily encode the assigned inequalities and reflect both the classification and complementarity relationships.

Besides that we establish a certain one-to-many correspondence between min-balanced systems on N involving at least 3 sets and purely min-semi-balanced set systems on N, that is, those that are not balanced (Sect. 6.1). This correspondence may be a basis for a procedure to generate the complete list of min-semi-balanced systems on N on basis of the list of all min-balanced systems on N. The point is that if $|N|\ge 3$ then every facet-defining inequality for the exact cone corresponds to a purely min-semi-balanced system. Note in this context that an analogous observation that the min-balanced systems are not needed for the minimal outer description of the exact cone was already made by Lohmann et al. (2012, § 5, Theorem 5.4).

Nonetheless, even purely min-semi-balanced set systems can be superfluous in the sense that the assigned inequalities are not facet-defining. We introduce a narrower concept of an indecomposable min-semi-balanced set system (see Sect. 7) and show that if $|N|\ge 3$ then any facet-defining inequality corresponds to an indecomposable set system. In fact, our main result is that the facet-defining inequalities for the exact cone are then just the inequalities assigned to indecomposable min-semi-balanced set systems (see Theorem 18).

We also put more light on the relation of the cones of exact and totally balanced games. Specifically, we first give a counterexample to a former conjecture from (Kroupa and Studený 2019, § 6) mentioned above in Sect. 1.1 (see Sect. 8.1). Then we derive, as a consequence of our main result, that those facet-defining inequalities for the cone of totally balanced games which concern strict subsets of N are also facet-defining for the cone of exact games (Sect. 8.2). In fact, these inequalities correspond to min-semi-balanced systems from one of four basic classes in our classification from Sect. 5.2. In particular, every irreducible min-balanced system on a strict subset of N from (Kroupa and Studený 2019) can be extended uniquely to a certain special indecomposable min-semi-balanced set system (on N).

1.3 Structure of the paper

In Sect. 2 we recall elementary concepts and basic facts. Our concept of a semi-balanced system is introduced in Sect. 3. We give several equivalent definitions of a minimal semi-balanced system, called a min-semi-balanced system, there and introduce the linear inequalities assigned to these set systems. The cone of exact games is characterized by means of these inequalities in Sect. 4. In Sect. 5 we then introduce the concept of a complementary set system and basic classification of min-semi-balanced systems. We also propose special pictures to represents these set systems and the inequalities assigned to them. In Sect. 6 we establish the correspondence of purely min-semi-balanced systems to min-balanced ones and shown that the inequalities assigned to min-balanced systems are superfluous if $|N|\ge 3$. The concept of an indecomposable min-semi-balanced set system is then defined formally in Sect. 7. We formulate our main result there saying that indecomposability is a necessary and sufficient condition for the assigned inequality to be facet-defining. Section 8 is devoted to the relation of the exact cone to the cone of totally balanced games. We first give a counterexample to the conjecture from (Kroupa and Studený 2019, § 6). Then we characterize those facet-defining inequalities for the totally balanced cone which are also facet-defining for the exact cone. In Conclusions (Sect. 9) we summarize our findings and give a reference to our catalogue of indecomposable min-semi-balanced systems over sets of low cardinality. Some of the longer technical proofs are moved to the “Appendix”.

2 Preliminaries

Throughout the paper the symbol N will denote a finite set of players and we restrict ourselves to the non-degenerate case $|N|\ge 2$. The power set $\mathcal{P}(N):= \{ S : S\subseteq N\}$ of the set of players is the set of coalitions. The symbol $\subset$ will denote strict inclusion of either sets or set systems, that is, $S\subset T$ iff $S\subseteq T$ and $S\ne T$. Given a set system ${{\mathcal {S}}}\subseteq \mathcal{P}(N)$ the union of sets in ${{\mathcal {S}}}$ will be denoted by $\bigcup {{\mathcal {S}}}$; analogously, $\bigcap {{\mathcal {S}}}$ will denote their intersection. The set of real numbers will be denoted by ${\mathbb R}$, the set of rational numbers by ${\mathbb Q}$.

2.1 Basic versions of linear combinations

We are going to deal with vectors in real Euclidean spaces ${\mathbb R}^{{{\mathcal {I}}}}$, where ${{\mathcal {I}}}$ is a non-empty finite index set. Our elementary linear algebraic operations will concern the space ${\mathbb R}^{N}$ in which case one has ${{\mathcal {I}}}=N$. But later on, some more advanced geometric considerations will be in the space ${\mathbb R}^{{{\mathcal {I}}}}$ where ${{\mathcal {I}}}$ will be a class of subsets of N, mostly ${{\mathcal {I}}}=\mathcal{P}(N)$.

The incidence vector of a coalition (= set) $S\subseteq N$ will be denoted by $\chi _{S}\in {\mathbb R}^{N}$:

$$\begin{aligned} \chi _{S}(i):= \left\{ \begin{array}{ll} 1~ &{} \hbox {if}\; i\in S,\\ 0~ &{} \hbox {if}\; i\not \in S, \end{array} \right. \qquad \hbox {for}\; i\in N. \end{aligned}$$

A vector whose components equal each other, that is, a vector of the form [r, ..., r] in ${\mathbb R}^{N}$, where $r\in {\mathbb R}$, will be called a constant vector in ${\mathbb R}^{N}$.

A special case of a constant vector in ${\mathbb R}^{N}$ is the zero vector in ${\mathbb R}^{N}$, denoted by ${\underline{0}}$. A finite set U of vectors in ${\mathbb R}^{N}$ is linearly independent if $\sum _{x\in U} \alpha _{x}\cdot x =\underline{0}$ with $\alpha _{x}\in {\mathbb R}$, $x\in \mathsf{U}$, implies $[\,\forall \, x\in \mathsf{U} ~~\alpha _{x}=0\,]$, otherwise it is called linearly dependent. Analogously, a finite set $\mathsf{U}\subseteq {\mathbb R}^{N}$ is affinely independent if

$$\begin{aligned} \left[ \,\, \sum _{x\in U} \alpha _{x}\cdot x = \underline{0}\quad \hbox {with}\; \alpha _{x}\in {\mathbb R}, x\in \mathsf{U}, \hbox {satisfying} \sum _{x\in \, \mathsf{U}} \alpha _{x}=0 \,\,\right] ~~\hbox {implies}~~ \left[ \,\forall \, x\in \mathsf{U} ~~\alpha _{x}=0\,\right] \,, \end{aligned}$$

otherwise it is called affinely dependent.

Other elementary concepts apply to any real Euclidean space ${\mathbb R}^{{{\mathcal {I}}}}$, $0<|{{\mathcal {I}}}|<\infty$. We are going to use the symbol

$$\begin{aligned} \langle \theta ,x\rangle ~:=~ \sum _{\iota \in \,{{\mathcal {I}}}}\, \theta (\iota )\cdot x(\iota )\qquad \hbox {for vectors}\; \theta ,x\in {\mathbb R}^{{{\mathcal {I}}}} \end{aligned}$$

to denote the respective scalar product in ${\mathbb R}^{{{\mathcal {I}}}}$. A (finite) linear combination $\sum _{i\in I} \uplambda _{i}\cdot x_{i}$ of vectors $x_{i}\in {\mathbb R}^{{{\mathcal {I}}}}$ with real coefficients $\uplambda _{i}\in {\mathbb R}$ is called

• non-zero if there is $i\in I$ with $\uplambda _{i}\ne 0$,

• affine if $\sum _{i\in I} \uplambda _{i}=1$,

• conic if $\uplambda _{i}\ge 0$ for all $i\in I$, and

• convex if it is both affine and conic.

The convex hull of a set $\mathsf{U}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is the collection of all convex combinations of vectors from $\mathsf{U}$; it will be denoted by $\hbox \mathrm{conv}\,(\mathsf{U})$. A set $\mathsf{U}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is convex if it is closed under convex combinations: $\mathsf{U}=\hbox \mathrm{conv}\,(\mathsf{U})$. The conic hull of $\mathsf{U}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is the set of all conic combinations of vectors from $\mathsf{U}$; it will be denoted by $\hbox {cone}\,(\mathsf{U})$.

Analogously, the affine hull of a set $\mathsf{U}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is the collection of all affine combinations of vectors from U. It is always an affine subspace of ${\mathbb R}^{{{\mathcal {I}}}}$, that is, a subset $\mathsf{A}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ closed under affine combinations. A non-empty affine subspace is always a shifted linear subspace of ${\mathbb R}^{{{\mathcal {I}}}}$, that is, a set of the form $\mathsf{A}=x+\mathsf{V}:=\{\, x+y\,:\ y\in \mathsf{V}\,\}$, where $x\in {\mathbb R}^{{{\mathcal {I}}}}$ and $V\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is a linear subspace (Brøndsted 1983, § 1); $\mathsf{V}$ is then uniquely determined by $\mathsf{A}$ while x is not unique.

The dimension of a set $\mathsf{U}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$, denoted by $\dim (U)$, is the dimension of its affine hull $\mathsf{A}$, defined as the dimension of V. Recall that the linear space V is determined uniquely by the set U through its affine hull $\mathsf{A}$.

A hyperplane in ${\mathbb R}^{{{\mathcal {I}}}}$ is an affine subspace $\mathsf{H}$ of ${\mathbb R}^{{{\mathcal {I}}}}$ of the dimension $|{{\mathcal {I}}}|-1$. An equivalent condition is that it is the set of solutions $x\in {\mathbb R}^{{{\mathcal {I}}}}$ to the equation $\langle \theta ,x\rangle =\beta$, where $\beta \in {\mathbb R}$ and $\theta \in {\mathbb R}^{{{\mathcal {I}}}}$ is a non-zero vector in ${\mathbb R}^{{{\mathcal {I}}}}$; see Brøndsted (1983, § 1).

2.2 Some concepts from polyhedral geometry

Throughout the paper we assume that the reader is familiar with standard concepts and basic facts from polyhedral geometry; see Brøndsted (1983), Schrijver (1998), Bachem and Kern (1992) and Ziegler (1995), for example. Nevertheless, for reader’s convenience, we recall those of them that are used (repeatedly) in our paper. On the other hand, those readers that are not interested in the proofs and technicalities can possibly skip the claims from Sect. 2.2 and consult it only when they encounter an unknown concept from polyhedral geometry.

Given distinct $x,y\in {\mathbb R}^{{{{\mathcal {I}}}}}$, the convex hull of $\{x,y\}$ is the closed segment, denoted by [x, y], while the open segment, denoted by ]x, y[, consists of convex combinations of x and y which have both coefficients non-zero:

$$\begin{aligned} ]x,y[ ~:=~ \{\, (1-\alpha )\cdot x+\alpha \cdot y\,:\ 0<\alpha <1\,\}\,. \end{aligned}$$

A polyhedron in ${\mathbb R}^{{{\mathcal {I}}}}$, $0<|{{\mathcal {I}}}|<\infty$, is the set of vectors $x\in {\mathbb R}^{{{\mathcal {I}}}}$ specified by finitely many linear inequalities $\langle \theta ,x\rangle \ge \beta$ for $x\in {\mathbb R}^{{{\mathcal {I}}}}$, where $\theta \in {\mathbb R}^{{{\mathcal {I}}}}$ and $\beta \in {\mathbb R}$. A polyhedron is called rational if, moreover, $\theta \in {\mathbb Q}^{{{\mathcal {I}}}}$ and $\beta \in {\mathbb Q}$ for these inequalities. A set $\mathsf{U}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is bounded if there are constants $c_{0},c_{1}\in {\mathbb R}$ such that $c_{0}\le x(\iota )\le c_{1}$ for any component $x(\iota )$, $\iota \in {{\mathcal {I}}}$, of any $x\in U$. A polytope (in ${\mathbb R}^{{{\mathcal {I}}}}$) is the convex hull of a non-empty finite set of vectors in ${\mathbb R}^{{{\mathcal {I}}}}$. A fundamental result in polyhedral geometry says that a subset of ${\mathbb R}^{{{\mathcal {I}}}}$ is a polytope iff it is a non-empty bounded polyhedron; see Brøndsted (1983, Theorem 9.2) or Ziegler (1995, Theorem 2.15).

A face of a polyhedron $\mathsf{P}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$, more precisely an exposed face of $\mathsf{P}$ (Brøndsted 1983, § 5), is a subset $\mathsf{F}\subseteq \mathsf{P}$ consisting of vectors $x\in \mathsf{P}$ satisfying $\langle \theta ,x\rangle =\beta$ for some $\theta \in {\mathbb R}^{{{\mathcal {I}}}}$, $\beta \in {\mathbb R}$, such that $\langle \theta ,y\rangle \ge \beta$ is a valid inequality for all $y\in \mathsf{P}$. In case of a polyhedron $\mathsf{P}$, this is equivalent to the condition that $\mathsf{F}\subseteq \mathsf{P}$ is a convex subset of it such that one has $[y,z]\subseteq \mathsf{F}$ whenever $y,z\in \mathsf{P}$ and $]y,z[\,\cap \, \mathsf{F}\ne \emptyset$; use Brøndsted (1983, § 8) or see Bachem and Kern (1992, Theorem 7.51). The number of faces of a polyhedron $\mathsf{P}$ is finite; see Brøndsted (1983, Corollary 8.5). The face-lattice of $\mathsf{P}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is the collection of its faces, ordered by inclusion relation $\subseteq$; it is indeed a lattice in usual sense (Brøndsted 1983, § 5).

Given a non-empty polyhedron $\mathsf{P}$, any of its faces of the dimension $\dim (\mathsf{P})-1$ is called a facet of $\mathsf{P}$. An equivalent definition is that a facet (of $\mathsf{P}$) is a maximal face $\mathsf{F}$ of $\mathsf{P}$ distinct from $\mathsf{P}$; use Brøndsted (1983, Corollary 8.6). A basic fact is that each full-dimensional proper polyhedron $\mathsf{P}\subset {\mathbb R}^{{{\mathcal {I}}}}$, that is, each polyhedron with $\dim (\mathsf{P})=|{{\mathcal {I}}}|$ and $\mathsf{P}\ne {\mathbb R}^{{{\mathcal {I}}}}$, is specified by those valid inequalities for $\mathsf{P}$ which define facets and the specification of $\mathsf{P}$ by facet-defining inequalities is the unique inclusion-minimal inequality description of $\mathsf{P}$ (up to positive multiples of inequalities); see Brøndsted (1983, Theorem 8.2).

A vertex (= an extreme point) of a convex set $\mathsf{P}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is a vector $x\in \mathsf{P}$ such that there is no open segment ]y, z[ with (distinct) $y,z\in \mathsf{P}$ and $x\in \,]y,z[$, which is, in case of a polytope $\mathsf{P}$, another way of saying that $\{x\}$ is a face of $\mathsf{P}$ (of the dimension 0). The set of vertices of (a polytope) $\mathsf{P}$ will be denoted by $\hbox \mathrm{ext}\,(\mathsf{P})$. A well-known consequence of famous Krein–Milman theorem is that every polytope $\mathsf{P}$ has finitely many vertices and equals to the convex hull of the vertex set: $\mathsf{P}= \hbox \mathrm{conv}\,(\hbox \mathrm{ext}\,(\mathsf{P}))$; see Brøndsted (1983, Theorem 7.2(c)) or Ziegler (1995, Proposition 2.2(i)).

One of easy observations is that if $\mathsf{U}=\hbox \mathrm{conv}\,(\mathsf{V})$ for $\mathsf{U},\mathsf{V}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ then $\hbox \mathrm{ext}\,(U)\subseteq \hbox \mathrm{ext}\,(V)$. Another immediate observation is that if $\mathsf{Q}\subseteq \mathsf{P}$ are two polytopes in inclusion in ${\mathbb R}^{{{\mathcal {I}}}}$ then $x\in \mathsf{Q}\cap \hbox \mathrm{ext}\,(\mathsf{P})$ implies $x\in \hbox \mathrm{ext}\,(\mathsf{Q})$. Every non-empty face $\mathsf{F}$ of a polytope $\mathsf{P}$ is again a polytope and $\hbox \mathrm{ext}\,(\mathsf{F})=\mathsf{F}\cap \hbox \mathrm{ext}\,(\mathsf{P})$; see Brøndsted (1983, Theorem 7.3) or Ziegler (1995, Proposition 2.3(i)). Further basic fact, which follows from the properties of the operator $\mathsf{U}\mapsto \hbox \mathrm{conv}\,(\mathsf{U})$ and Krein–Milman theorem, is the following one: if $\mathsf{P}_{j}$, $j\in J$, where J is a finite index set, are bounded polyhedrons in ${\mathbb R}^\mathcal{I}$ then $\mathsf{Q}:=\hbox \mathrm{conv}\,(\bigcup _{j\in J} \mathsf{P}_{j})$ is a bounded polyhedron in ${\mathbb R}^\mathcal{I}$ as well.

An edge of a polytope $\mathsf{P}$ is a closed segment $[y,z]\subseteq \mathsf{P}$ which is a face of $\mathsf{P}$ (of the dimension 1); then necessarily $y,z\in \hbox \mathrm{ext}\,(\mathsf{P})$. Further special fact is as follows. Given a polytope $\mathsf{P}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ and a hyperplane $\mathsf{H}$ in ${\mathbb R}^{{{\mathcal {I}}}}$ with $\mathsf{H}\cap \mathsf{P}\ne \emptyset$, the intersection $\mathsf{Q}:=\mathsf{H}\cap \mathsf{P}$ is a polytope and $x\in \hbox \mathrm{ext}\,(\mathsf{Q})$ iff either $x\in \mathsf{H}\cap \hbox \mathrm{ext}\,(\mathsf{P})$ or there is an edge [y, z] of $\mathsf{P}$ such that $x\in \,]y,z[$ and $[y,z]\cap \mathsf{H}=\{x\}$; use Brøndsted (1983, Theorem 11.1(d)).

A polyhedral cone in ${\mathbb R}^{{{\mathcal {I}}}}$ is a subset $\mathsf{C}$ of ${\mathbb R}^{{{\mathcal {I}}}}$ defined as the conic hull of a non-empty finite set $\mathsf{U}$ of vectors from ${\mathbb R}^{{{\mathcal {I}}}}$. An equivalent definition is that $\mathsf{C}$ is specified by finitely many inequalities $\langle \theta ,x\rangle \ge 0$ for $x\in {\mathbb R}^{{{\mathcal {I}}}}$ (Ziegler 1995, Theorem 1.3); thus, it is a non-empty polyhedron. A polyhedral cone $\mathsf{C}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is called pointed, if $-\mathsf{C}\cap \mathsf{C}=\{\mathbf{0}\}$, where $-\mathsf{C}:=\{-y\,:\ y\in \mathsf{C}\,\}$ and $\mathbf{0}$ denotes the zero vector in ${\mathbb R}^{{{\mathcal {I}}}}$. An equivalent condition is that there exists (non-zero) $\theta \in {\mathbb R}^{{{\mathcal {I}}}}$ such that $\langle \theta ,x\rangle >0$ for any $x\in \mathsf{C}{\setminus }\{\mathbf{0}\}$; see Studený (1993, Proposition 2). It makes no problem to observe that if, moreover, $\mathsf{C}{\setminus }\{\mathbf{0}\}\ne \emptyset$, then, for each $\beta >0$, the intersection of $\mathsf{C}$ with the hyperplane $\mathsf{H}:=\{ x\in {\mathbb R}^{{{\mathcal {I}}}}\,:\ \langle \theta ,x\rangle =\beta \,\}$ is a polytope; this is because one can find finite $\emptyset \ne \mathsf{U}\subset \mathsf{H}$ with $\mathsf{C}=\hbox {cone}\,(\mathsf{U})$. The reader can verify (using alternate definitions of a face) that then the mapping $\mathsf{F}\subseteq \mathsf{C} ~\mapsto ~\mathsf{F}\cap \mathsf{H}$ establishes a one-to-one correspondence between non-empty faces $\mathsf{F}$ of $\mathsf{C}$ and (all) faces of the polytope $\mathsf{P}:=\mathsf{C}\cap \mathsf{H}$: the inverse mapping is

$$ \begin{aligned} \mathsf{F}^{\prime }\subseteq \mathsf{C}\cap \mathsf{H} ~\mapsto ~ \hbox {cone}\,(\mathsf{F}^{\prime }\cup \{\mathbf{0}\}) \equiv \{\mathbf{0}\}\cup \{\alpha \cdot x\,:\ \alpha \ge 0 ~ \& ~ x\in \mathsf{F}^{\prime }\,\}. \end{aligned}$$

This correspondence preserves the inclusion ordering; thus, it is an isomorphism between the lattice of non-empty faces of $\mathsf{C}$ and the face-lattice of $\mathsf{P}$.

Every subset $\mathsf{U}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ can be assigned its dual cone

$$\begin{aligned} U^{*}:=\{\, \theta \in {\mathbb R}^{{{\mathcal {I}}}}\,:\ \langle \theta ,x\rangle \ge 0\quad \hbox {for any}~x\in \mathsf{U}\,\}\,, ~~\hbox {which is a closed convex cone.} \end{aligned}$$

A well-known elementary fact is that $\mathsf{C}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ is a non-empty closed convex cone iff $\mathsf{C}=\mathsf{C}^{**}$, which happens iff $\mathsf{C}=\mathsf{U}^{*}$ for some $\mathsf{U}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$; see for example Studený (1993, Consequence 1). Moreover, the dual cone to a polyhedral cone is also a polyhedral cone; use Bachem and Kern (1992, Corollary 7.12). Thus, if one shows, for a polyhedral cone $\mathsf{C}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$, and for a set $\mathsf{U}\subseteq {\mathbb R}^{{{\mathcal {I}}}}$ that $\mathsf{U}=\mathsf{C}^{*}$ then this fact already implies that $\mathsf{C}$ and $\mathsf{U}$ are mutually dual polyhedral cones, which means both $\mathsf{C}=\mathsf{U}^{*}$ and $\mathsf{U}=\mathsf{C}^{*}$. Another useful fact from polyhedral geometry is that the lattices of non-empty faces of mutually dual polyhedral cones are anti-isomorphic. More specifically, the mapping is as follows:

$$\begin{aligned} \mathsf{F}\subseteq \mathsf{C}~\hbox {a non-empty face of}~\mathsf{C} ~\mapsto ~~ \mathsf{F}^{\perp } := \{\, \theta \in \mathsf{U}\,:\ \langle \theta ,x\rangle =0~~ \hbox {for all} ~x\in \mathsf{F}\,\} \end{aligned}$$

and the inverse mapping is of the same form (exchange $\mathsf{C}$ for $\mathsf{U}$); use Bachem and Kern (1992, Theorem 7.41) to derive that. This particular one-to-one correspondence reverses the inclusion ordering and has the property that $\dim (\mathsf{F})+\dim (\mathsf{F}^{\perp })=|{{\mathcal {I}}}|$; use Bachem and Kern (1992, Theorem 7.42).

2.3 Some concepts from game theory

A (transferable utility coalitional ) game over (a set of players) N is modeled by a real function $m:\mathcal{P}(N)\rightarrow {\mathbb R}$ such that $m(\emptyset )=0$, called the “characteristic function" of the game. The class of all games over N will be denoted by $\mathcal{G}(N)$. Given $m\in \mathcal{G}(N)$ and $\emptyset \ne S\subseteq N$, the restriction $m_{S}$ of $m$ to ${{\mathcal {P}}}(S)$ is called a subgame of the game $m\in \mathcal{G}(N)$.

The core $C(m)$ of a game $m\in \mathcal{G}(N)$ is the polyhedron

$$ \begin{aligned} C(m) := \left\{ \,[x_{i}]_{i\in N}\in {\mathbb R}^{N} \,:\ \sum _{i\in N} x_{i}=m(N) ~ \& ~ \sum _{i\in S}x_{i} \ge m(S)\; \hbox {for all}~ S\subseteq N\right\} . \end{aligned}$$

We say that a game $m\in \mathcal{G}(N)$ is balanced if it has a non-empty core,

• totally balanced if every subgame of $m$ is balanced,

• exact if, for each coalition $S\subseteq N$, there exists a vector $[x_{i}]_{i\in N} \in C(m)$ in the core that is tight for S, which means that $\sum _{i\in S}x_{i} = m(S)$.

The set ${\mathcal {T}}(N)$ of all totally balanced games over N is known to be a polyhedral cone in ${\mathbb R}^{\mathcal{P}(N)}$; the same is true for the set ${\mathcal {E}}(N)$ of all exact games over N; see Kroupa and Studený (2019, § 2).

Recall from (Kalai and Zemel 1982, Theorem 1) that $m$ is totally balanced iff it has a finite min-representation, which means that there exists a non-empty finite $\mathcal{X}\subseteq {\mathbb R}^{N}$ such that

$$\begin{aligned} m(S)~=~\min _{x\in \mathcal{X}}\, \sum _{i\in S} x_{i}\qquad \hbox {for any }S\subseteq N. \end{aligned}$$

It is a well-known fact that $m$ is exact iff it has a min-representation $\emptyset \ne \mathcal{X}\subseteq C(m)$ consisting of the elements in the core; see Studený and Kratochvíl (2018, Proposition 1), for example. Hence, we know that every exact game is totally balanced.

Following Oishi et al. (2016), given $m\in \mathcal{E}(N)$, by the anti-dual of $m$ we call the game

$$\begin{aligned} m^{\diamond }(S) := m(N{\setminus } S)-m(N) \quad \hbox {for all}~S\subseteq N. \end{aligned}$$

Note that, by habitual terminology in cooperative game theory, the $(-1)$ multiple of $m^{\diamond }$ is named the dual game of $m$; see Peleg and Sudhölter (2007, Definition 6.6.3). Nonetheless, for our purpose the concept of an anti-dual is more relevant as $m\in {\mathcal {E}}(N)$ iff $m^{\diamond }\in {\mathcal {E}}(N)$, see Kroupa and Studený (2019, § 3.2). In particular, if $m$ is exact then both $m$ and $m^{\diamond }$ are totally balanced. On the other hand, $m\in {\mathcal {E}}(N) ~\not \Rightarrow ~ -m\in {\mathcal {E}}(N)$ in general; thus, duals of exact games need not be exact.

3 Balanced and semi-balanced set systems

We first recall a classic well-known concept in cooperative game theory (Shapley 1967).

Definition 1

(Non-trivial and balanced set system)  Let N be a finite set with $|N|\ge 2$. A system ${{\mathcal {S}}}$ of its subsets such that $\emptyset \ne {{\mathcal {S}}}\subseteq {\mathcal{P}(N)}{\setminus } \{\emptyset ,N\}$ will be called a non-trivial set system on N.

A balanced system (on N) is such a non-trivial set system ${{\mathcal {B}}}$ (on N) that $\chi _{N}$ is a conic combination of vectors $\{ \chi _{S}\,:\, S\in {{\mathcal {B}}}\}$ with all coefficients non-zero. A balanced system ${{\mathcal {B}}}$ on N is called minimal if there is no balanced system ${{\mathcal {C}}}$ on N with ${{\mathcal {C}}}\subset {{\mathcal {B}}}$; ${{\mathcal {B}}}$ will then be called briefly min-balanced (on N).

In other words, ${{\mathcal {B}}}$ is a balanced set system on N if $\chi _{N}$ is a linear combination of vectors $\{ \chi _{S}\,:\, S\in {{\mathcal {B}}}\}$ with strictly positive coefficients. In the sequel we are going to generalize this concept.

3.1 Semi-balanced set systems

Our generalization is based on the following elementary concept.

Definition 2

(Semi-conic combination) We shall say that a linear combination $\sum _{i\in I} \uplambda _{i}\cdot x_{i}$ in ${\mathbb R}^{N}$ is semi-conic if at most one of its coefficients $\uplambda _{i}$ is strictly negative, that is, $|\{j\in I\,:\ \uplambda _{j}<0\}|\le 1$.

While linear combination concepts recalled in Sect. 2.1 are standard in mathematics, the concept of a semi-conic combination is a specific concept relevant to the topic of our study. Our terminology is motivated by the fact that the remaining coefficients $\uplambda _{i}$, $i\ne j$, in a such a linear combination must be non-negative. Thus, any conic combination is also semi-conic. Nonetheless, despite this fact, the concepts of semi-conic and conic combination differ substantially from each other.

Remark 1

In this side note we explain the principal difference between conic and semi-conic combinations. Recall that the conic hull of a set $\mathsf{U}$ in a real Euclidean space is the collection $\hbox {cone}\,(\mathsf{U})$ of all conic combinations of vectors from $\mathsf{U}$ and it is always a convex cone. Another well-known fact is that the mapping $\mathsf{U}\mapsto \hbox {cone}\,(\mathsf{U})$ is a closure operator in sense of abstract algebra (Birkhoff 1995, § V.1); this means that it is extensive [$\mathsf{U}\subseteq \hbox {cone}\,(\mathsf{U})$], monotone [$\mathsf{U}\subseteq \mathsf{V}$ implies $\hbox {cone}\,(\mathsf{U})\subseteq \hbox {cone}\,(\mathsf{V})$] and idempotent [$\hbox {cone}\,(\hbox {cone}\,(\mathsf{U}))=\hbox {cone}\,(\mathsf{U})$]. One can analogously introduce the semi-conic hull $\hbox {semi-cone}\,(\mathsf{U})$ as the set of all semi-conic combinations of vectors from $\mathsf{U}$, but this set need not be convex. The operator $\mathsf{U}\mapsto \hbox {semi-cone}\,(\mathsf{U})$ is then extensive and monotone but it is not idempotent. Consider, for example, the case $\mathsf{U}=\{ (1,0),(0,1)\}\subseteq {\mathbb R}^{2}$. Thus, the mapping $\mathsf{U}\mapsto \hbox {semi-cone}\,(\mathsf{U})$ is not a closure operator.

Now, we are ready to introduce basic concepts in our treatise.

Definition 3

(Semi-balanced set system, exceptional set)  Assume that N is a finite set with $|N|\ge 2$. We shall say that a non-trivial set system ${{\mathcal {S}}}$ on N is semi-balanced (on N) if there is a constant vector in ${\mathbb R}^{N}$ which is a semi-conic combination of vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ with all coefficients non-zero. A semi-balanced system ${{\mathcal {S}}}$ on N will be called minimal if there is no semi-balanced system ${{\mathcal {C}}}$ on N with ${{\mathcal {C}}}\subset {{\mathcal {S}}}$. We will then say briefly that such a set system is min-semi-balanced (on N).

A semi-balanced set system ${{\mathcal {S}}}$ (on N) which is not balanced (on N) will be called purely semi-balanced (on N). Analogously, a minimal semi-balanced system which is not balanced will be called purely min-semi-balanced.

Given a non-trivial set system ${{\mathcal {S}}}$ on N, we will say that a set $T\in {{\mathcal {S}}}$ is exceptional within ${{\mathcal {S}}}$ if there exists a linear combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ with $\uplambda _{T}<0$ and $\uplambda _{S}\ge 0$ for $S\in {{\mathcal {S}}}{\setminus }\{T\}$.

It follows directly from the definition that any balanced system is also semi-balanced. Let us emphasize that both these concepts are relative to N despite one may have $\bigcup {{\mathcal {S}}}\subset N$ for a semi-balanced system ${{\mathcal {S}}}$ on N (see Example 1 below); this is because the constant vector is required to be in ${\mathbb R}^{N}$. Note that, for a semi-balanced system, all coefficients in any of the considered linear combinations must be strictly positive with one possible exception of a strictly negative coefficient (with an exceptional set).

If a set $T\subset N$ is exceptional within a system ${{\mathcal {S}}}$ then it is exceptional within any larger non-trivial system ${{\mathcal {T}}}\supseteq {{\mathcal {S}}}$: put $\uplambda _{S}:=0$ for $S\in {{\mathcal {T}}}{\setminus }{{\mathcal {S}}}$. Of course, every non-trivial set system with an exceptional set contains a semi-balanced system because the considered linear combination is semi-conic. Conversely, every purely semi-balanced system has at least one exceptional set. Note that, in case of a (purely) min-semi-balanced system, this exceptional set is uniquely determined; the uniqueness of this set follows from later Lemmas 1 and 2.

A set system containing a semi-balanced system need not be semi-balanced. In fact, even the union of two semi-balanced systems need not be a semi-balanced system (see Example 1 below). On the other hand, the union of a semi-balanced system and a balanced system has to be a semi-balanced system: consider a suitable non-trivial convex combination of the respective semi-conic combinations yielding constant vectors. The same argument implies that the union of two balanced systems on N is a balanced system on N.

Example 1

Given $N:=\{a,b,c,d\}$, consider two set systems ${{\mathcal {S}}}:=\{\,a,b,ab\,\}$ and ${{\mathcal {T}}}:=\{\,c,bc,acd\,\}$. The equalities $1\cdot \chi _{a}+1\cdot \chi _{b}+(-1)\cdot \chi _{ab}={\underline{0}}$ and $(-1)\cdot \chi _{c}+1\cdot \chi _{bc}+1\cdot \chi _{acd}=\chi _{N}$ imply that both ${{\mathcal {S}}}$ and ${{\mathcal {T}}}$ is semi-balanced on N. To show that their union ${{\mathcal {D}}}:={{\mathcal {S}}}\cup {{\mathcal {T}}}$ is not semi-balanced on N consider a linear combination $\sum _{S\in {{\mathcal {D}}}}\uplambda _{S}\cdot \chi _{S}=[r,r,r,r]\in {\mathbb R}^{N}$ having all coefficients non-zero. Realize that $\uplambda _{acd}=\sum _{S\in {{\mathcal {D}}}:\, d\in S}\uplambda _{S}=r$. The equality $\uplambda _{acd}=r=\sum _{S\in {{\mathcal {D}}}:\, c\in S}\uplambda _{S}=\uplambda _{c}+\uplambda _{bc}+\uplambda _{acd}$ then gives $\uplambda _{c}+\uplambda _{bc}=0$ and the assumption $\uplambda _{c}\ne 0\ne \uplambda _{bc}$ implies that [ $\uplambda _{c}<0$ or $\uplambda _{bc}<0$ ]. Analogously, $\uplambda _{acd}=r=\sum _{S\in {{\mathcal {D}}}:\, a\in S}\uplambda _{S}=\uplambda _{a}+\uplambda _{ab}+\uplambda _{acd}$ means $\uplambda _{a}+\uplambda _{ab}=0$, which implies that [ $\uplambda _{a}<0$ or $\uplambda _{ab}<0$ ]. Therefore, one has $\uplambda _{T}<0$ for at least two sets $T\in {{\mathcal {D}}}$ and the considered linear combination is not semi-conic.

The following lemma contains a few elementary observations valid for semi-balanced set systems; in fact, they hold for a wider class of systems containing semi-balanced ones. Its proof is shifted to “Appendix A”.

Lemma 1

Given $|N|\ge 2$ and $\emptyset \ne {{\mathcal {S}}}\subseteq {\mathcal{P}(N)}{\setminus } \{\emptyset ,N\}$, let $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}=\rho$ be a non-zero semi-conic combination yielding a constant vector $\rho =[r,\ldots ,r]\in {\mathbb R}^{N}$ (with zero coefficients allowed). Then one has $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\ge r\ge 0$; moreover, $r>0$ in case of a conic combination.

In any case $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}>0$ and by a positive factor multiplication one gets an affine semi-conic combination $\sum _{S\in {{\mathcal {S}}}} {\tilde{\uplambda }}_{S}\cdot \chi _{S}$ yielding a constant vector ${\tilde{\rho }}=[{\tilde{r}},\ldots ,{\tilde{r}}]\in {\mathbb R}^{N}$ with ${\tilde{r}}\in [0,1]$.

Finally, if the considered linear combination is not conic, then ${{\mathcal {S}}}$ has to contain at least three different sets and the existence of such a set system forces $|N|\ge 3$.

It follows from (the last claim in) Lemma 1 that every purely semi-balanced system contains at least three sets and, thus, there is no such a set system on a two-element set.

We now provide equivalent definitions of min-semi-balanced systems. Slightly longer proof of the next lemma is shifted to “Appendix B”.

Lemma 2

Given $|N|\ge 2$, let $\emptyset \ne {{\mathcal {S}}}\subseteq {\mathcal{P}(N)}{\setminus } \{\emptyset ,N\}$ be a non-trivial set system on N. Then the following conditions on ${{\mathcal {S}}}$ are equivalent:

(a):

${{\mathcal {S}}}$ is a minimal set system such that there is a constant vector in ${\mathbb R}^{N}$ which can be written as a non-zero semi-conic combination of vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$,

(b):

${{\mathcal {S}}}$ is a minimal semi-balanced set system on N,

(c):

${{\mathcal {S}}}$ is semi-balanced on N, the vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ are affinely independent and in case $\bigcup {{\mathcal {S}}}=N$ even linearly independent,

(d):

there is only one affine combination of vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ yielding a constant vector in ${\mathbb R}^{N}$ and this unique combination is semi-conic and has all coefficients non-zero,

(e):

there is only one affine semi-conic combination of vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ which is a constant vector in ${\mathbb R}^{N}$ and this unique combination has all coefficients non-zero.

Given (purely) min-semi-balanced system ${{\mathcal {S}}}$ on N with an exceptional set T, by Lemma 1 one can consider an affine combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector where $\uplambda _{T}<0$ and $\uplambda _{S}\ge 0$ for $S\in {{\mathcal {S}}}{\setminus }\{T\}$. Then, by Lemma 2(d), such a combination is unique. This implies that the exceptional set T within ${{\mathcal {S}}}$ is uniquely determined by ${{\mathcal {S}}}$.

The next Example 2 illustrates that the requirement concerning the case $\bigcup {{\mathcal {S}}}=N$ in the condition (c) of Lemma 2 cannot be removed.

Example 2

There exists a semi-balanced set system ${{\mathcal {S}}}$ on N with $\bigcup {{\mathcal {S}}}=N$ where vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ are affinely independent but not linearly independent. Take $N:=\{a,b,c,d\}$ and put ${{\mathcal {S}}}:=\{\, a,b,ab,abc, abd\,\}$. Then one has

$$\begin{aligned} 1\cdot \chi _{a} + 1\cdot \chi _{b} + (-2)\cdot \chi _{ab} + 1\cdot \chi _{abc} + 1\cdot \chi _{abd} =\chi _{N}\,, \end{aligned}$$

which implies that ${{\mathcal {S}}}$ is semi-balanced. The equality ${\underline{0}}=1\cdot \chi _{a} + 1\cdot \chi _{b}+ (-1)\cdot \chi _{ab}$ implies that $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ are linearly dependent. On the other hand, the condition

$$\begin{aligned} \alpha \cdot \chi _{a} + \beta \cdot \chi _{b} + \gamma \cdot \chi _{ab} + \delta \cdot \chi _{abc} + \varepsilon \cdot \chi _{abd} ={\underline{0}} \end{aligned}$$

together with $\alpha + \beta + \gamma + \delta + \varepsilon =0$ implies $\alpha =\ldots =\varepsilon =0$, which means that $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ are affinely independent. Indeed, take d first to derive $\varepsilon =0$, then c to get $\delta =0$, a to obtain $\alpha =-\gamma$ and b to obtain $\beta =-\gamma$; altogether, $0=\alpha + \beta + \gamma + \delta + \varepsilon =-\gamma$ gives the conclusion. Hence, by Lemma 2, the system ${{\mathcal {S}}}$ is not min-semi-balanced on N; two of its proper subsystems that are semi-balanced are $\{\,a,b,ab\,\}$ and $\{\,ab,abc, abd\,\}$.

The basic requirement in the condition (d) of Lemma 2 is a geometric one: it says that the affine subspace $\{\,\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}\in {\mathbb R}^{N}\,:\ \sum _{S\in {{\mathcal {S}}}} \uplambda _{S}=1\}$ intersects the line $\{[r,\ldots ,r]\in {\mathbb R}^{N}\,:\ r\in {\mathbb R}\}$ of constant vectors in precisely one vector. The following Example 3 shows that both additional requirements on this unique affine combination are necessary.

Example 3

There exists a non-trivial system ${{\mathcal {D}}}$ on N such that only one affine combination of $\{ \chi _{S}\,:\ S\in {{\mathcal {D}}}\}$ yields a constant vector in ${\mathbb R}^{N}$ and this unique combination is conic but has not all coefficients non-zero. Take $N:=\{a,b,c\}$ and put ${{\mathcal {D}}}:=\{\,a,b,bc\,\}$. Then

$$\begin{aligned} \frac{1}{2}\cdot \chi _{a} + 0\cdot \chi _{b} + \frac{1}{2}\cdot \chi _{bc}=\frac{1}{2}\cdot \chi _{N}\,, \end{aligned}$$

is the above-mentioned unique affine combination. Of course, this particular set system ${{\mathcal {D}}}$ is not semi-balanced but its subsystem ${{\mathcal {D}}}^{\prime }:=\{\,a,bc\,\}$ is even balanced.

There is also a non-trivial set system ${{\mathcal {C}}}$ on N with a unique affine combination of $\{ \chi _{S}\,:\ S\in {{\mathcal {C}}}\}$ yielding a constant vector in ${\mathbb R}^{N}$, where all the coefficients in this combination are non-zero but the combination is not semi-conic. Let us take $N:=\{a,b,c,d,e\}$ and consider ${{\mathcal {C}}}:=\{\,ab,ac,ad,abc,abce\,\}$. Then

$$\begin{aligned} (-1)\cdot \chi _{ab} + (-1)\cdot \chi _{ac} + 1\cdot \chi _{ad} + 1\cdot \chi _{abc} + 1\cdot \chi _{abce}=\chi _{N} \end{aligned}$$

is that unique combination. By Lemma 1, the system ${{\mathcal {C}}}$ is not semi-balanced on N.

A consequence of Lemma 2 is the observation that the concept of a min-semi-balanced system generalizes the one of a min-balanced system.

Corollary 3

Given $|N|\ge 2$, a balanced system ${{\mathcal {B}}}$ on N is minimal within the class of balanced systems on N if and only if it is minimal within the class of semi-balanced systems on N. In other words, ${{\mathcal {B}}}$ is min-balanced (on N) iff it is balanced and min-semi-balanced (on N).

Proof

The fact that ${{\mathcal {B}}}$ is balanced on N implies $\bigcup {{\mathcal {B}}}=N$. By Lemma 2(c), its minimality within semi-balanced systems means that $\{ \chi _{S}\,:\ S\in {{\mathcal {B}}}\}$ are linearly independent, while, by Lemma 2.1 in (Kroupa and Studený 2019), this condition characterizes its minimality within balanced systems. $\square$

Lemma 2(c) also sets a limit on the number of sets in a min-semi-balanced system.

Corollary 4

If $|N|\ge 2$ and $\mathcal{S}$ is a min-semi-balanced system on N then $|\mathcal{S}|\le |N|$.

Proof

If $\bigcup \mathcal{S}\subset N$ then affine independence of vectors $\{ \chi _{S} : S\in \mathcal{S} \}$ yields the inequalities $|{{\mathcal {S}}}|\le |\bigcup {{\mathcal {S}}}|+1\le |N|$ because affinely independent set in ${\mathbb R}^{M}$ has at most $|M|+1$ elements. In case $\bigcup {{\mathcal {S}}}=N$ the linear independence of the respective set of vectors implies directly $|{{\mathcal {S}}}|\le |N|$. $\square$

3.2 Inequalities assigned to semi-balanced systems

Given a non-trivial system ${{\mathcal {S}}}$ on N, any non-zero semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector $[r,\ldots ,r]\in {\mathbb R}^{N}$ gives an inequality

$$\begin{aligned} r\cdot m(N) ~\ge ~ \sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot m(S)\qquad \hbox {for}~m\in {\mathbb R}^{\mathcal{P}(N)}, \end{aligned}$$

which appears to be valid for all exact games $m$. To ensure one-to-one correspondence between the inequalities and semi-conic combinations we limit ourselves to affine combinations, which is possible owing to Lemma 1. The formal definition is as follows.

Definition 4

(Vectors of coefficients, inequalities induced by set systems)  Let ${{\mathcal {S}}}$ be a non-trivial set system on N, $|N|\ge 2$. Any affine semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector $[r,\ldots ,r]\in {\mathbb R}^{N}$ is assigned a vector $\theta \in {\mathbb R}^{\mathcal{P}(N)}$:

$$\begin{aligned} \theta (S)\!=\! -\uplambda _{S}~~\hbox {for }S\in {{\mathcal {S}}},\quad \theta (N)\!=\!r,~~ \theta (\emptyset )= 1-r, ~~ \theta (L)\!=\!0~~\hbox {for other}\ L\!\subseteq \! N. \end{aligned}$$

(1)

The vector $\theta$ is then interpreted as the coefficient vector in an inequality

$$\begin{aligned} 0\le \langle \theta ,m\rangle ~:=~ \sum _{S\subseteq N}\, \theta (S)\cdot m(S)\qquad \hbox {for vectors }m\in {\mathbb R}^{\mathcal{P}(N)} \hbox {with }m(\emptyset )=0. \end{aligned}$$

(2)

The symbol $\Theta _{{{\mathcal {S}}}}$ will denote the set of vectors $\theta$ for all such affine semi-conic combinations. Provided $|\Theta _{{{\mathcal {S}}}}|=1$, the only vector in $\Theta _{{{\mathcal {S}}}}$ will be denoted by $\theta _{{{\mathcal {S}}}}$.

Note that every coefficient vector $\theta$ is given by a suitable affine combination and that the values $\theta (S)$ for $S\in {{\mathcal {S}}}$ correspond to the coefficients in the combination; however, the remaining contingent non-zero values $\theta (N)$ and $\theta (\emptyset )$ are determined by them.

Here are some elementary observations on the set of coefficient vectors.

Corollary 5

Given $|N|\ge 2$ and a non-trivial set system ${{\mathcal {S}}}$ on N, one has $\Theta _{{{\mathcal {S}}}}\ne \emptyset$ iff ${{\mathcal {S}}}$ contains a semi-balanced system. The inclusion ${{\mathcal {T}}}\subseteq {{\mathcal {S}}}$ of two non-trivial systems on N implies $\Theta _{{{\mathcal {T}}}}\subseteq \Theta _{{{\mathcal {S}}}}$. The set $\Theta _{{{\mathcal {S}}}}$ is the union of sets $\Theta _{{{\mathcal {T}}}}$ for semi-balanced systems ${{\mathcal {T}}}$ with ${{\mathcal {T}}}\subseteq {{\mathcal {S}}}$. One has $|\Theta _{{{\mathcal {S}}}}|=1$ iff ${{\mathcal {S}}}$ contains just one semi-balanced system on N. In particular, every min-semi-balanced system ${{\mathcal {S}}}$ on N satisfies $|\Theta _{{{\mathcal {S}}}}|=1$.

These facts mean that the inequalities (2) from Definition 4 are just those that are assigned to semi-balanced systems. The last claim says that solely a non-minimal semi-balanced system ${{\mathcal {S}}}$ may have non-singleton $\Theta _{{{\mathcal {S}}}}$ and, thus, be assigned several inequalities.

On the other hand, the substantial inequalities appear to be those assigned to min-semi-balanced systems; see later Corollary 9(iii). Thus, the inequalities assigned to other non-trivial set systems are superfluous for the description of the exact cone. Nonetheless, in order to follow the analogy with former results by Lohmann et al. (2012), we have also assigned the inequalities to non-minimal semi-balanced set systems; see later Corollary 9(ii).

Proof

The first claim follows from Definition 3 and Lemma 1, further two ones are direct consequences of Definition 4. As concerns the fourth claim, the necessity of the uniqueness of a semi-balanced subsystem can be shown by contradiction with the help of Lemma 1. For its sufficiency realize that the unique semi-balanced system ${{\mathcal {T}}}$ on N with ${{\mathcal {T}}}\subseteq {{\mathcal {S}}}$ is necessarily minimal. Given vector $\theta \in \Theta _{S}$, the set system $\{S\subset N:\ S\ne \emptyset ~ \& ~ \theta (S)\ne 0\}\subseteq {{\mathcal {S}}}$ is semi-balanced on N, and, thus, it has to coincide with ${{\mathcal {T}}}$. The condition (e) in Lemma 2 (for ${{\mathcal {T}}}$) implies the uniqueness of $\theta \in \Theta _{{{\mathcal {S}}}}$; hence, $|\Theta _{{{\mathcal {S}}}}|\le 1$. This implies the last claim. $\square$

The following example shows that the set $\Theta _{{{\mathcal {S}}}}$ need not be convex.

Example 4

Take $N:=\{a,b,c,d\}$ and put ${{\mathcal {B}}}:=\{\,a,b,c,d,ab,cd\,\}$. The conic combination

$$\begin{aligned} \frac{1}{2}\cdot \chi _{a}+\frac{1}{2}\cdot \chi _{b} +\frac{1}{2}\cdot \chi _{c}+\frac{1}{2}\cdot \chi _{d} + \frac{1}{2}\cdot \chi _{ab}+ \frac{1}{2}\cdot \chi _{cd} = \chi _{N} \end{aligned}$$

means that ${{\mathcal {B}}}$ is balanced on N. A semi-conic combination $1\cdot \chi _{a}+1\cdot \chi _{b}+(-1)\cdot \chi _{ab}={\underline{0}}$ leads to a coefficient vector $\theta ^{1}\in \Theta _{{{\mathcal {B}}}}$:

$$\begin{aligned} \theta ^{1}(a)=-1, ~~\theta ^{1}(b)=-1,~~ \theta ^{1}(ab)=+1, ~~\theta ^{1}(\emptyset )=+1,\quad \theta ^{1}(L)=0 ~~\hbox {otherwise}. \end{aligned}$$

Analogously, $1\cdot \chi _{c}+1\cdot \chi _{d}+(-1)\cdot \chi _{cd}={\underline{0}}$ gives rise to the vector $\theta ^{2}\in \Theta _{{{\mathcal {B}}}}$:

$$\begin{aligned} \theta ^{2}(c)=-1, ~~\theta ^{2}(d)=-1,~~ \theta ^{2}(cd)=+1, ~~\theta ^{2}(\emptyset )=+1,\quad \theta ^{2}(L)=0 ~~\hbox {otherwise}. \end{aligned}$$

Their convex combination $\frac{1}{2}\cdot \theta ^{1}+\frac{1}{2}\cdot \theta ^{2}$, however, does not belong to $\Theta _{{{\mathcal {B}}}}$ because the corresponding affine combination $\frac{1}{2}(\chi _{a}+\chi _{b}+\chi _{c}+\chi _{d}-\chi _{ab}-\chi _{cd})=\underline{0}$ is not semi-conic.

On the other hand, $\Theta _{{{\mathcal {S}}}}$ is always the union of finitely many closed convex sets.

Corollary 6

Given a semi-balanced system ${{\mathcal {S}}}$ on N, $|N|\ge 2$, the set $\Theta _{{{\mathcal {S}}}}$ is the union of finitely many rational polyhedrons. In particular, if ${{\mathcal {S}}}$ is min-semi-balanced then the unique vector $\theta _{{{\mathcal {S}}}}$ in $\Theta _{{{\mathcal {S}}}}$ has rational components: $\theta _{{{\mathcal {S}}}}\in {\mathbb Q}^{\mathcal{P}(N)}$.

Proof

In fact, $\Theta _{{{\mathcal {S}}}}$ is the union over $T\in {{\mathcal {S}}}$ of sets $\Theta _{{{\mathcal {S}}}:T}$ consisting of $\theta \in {\mathbb R}^{\mathcal{P}(N)}$ such that

• $\theta (N)+\theta (\emptyset )=1=\sum _{S\in {{\mathcal {S}}}}-\theta (S)$,      $\sum _{S\in {{\mathcal {S}}}} -\theta (S)\cdot \chi _{S}=\theta (N)\cdot \chi _{N}$,

• $\forall \, S\in {{\mathcal {S}}}{\setminus }\{T\}\quad \theta (S)\le 0$,       $\forall \, L\in \mathcal{P}(N){\setminus } ({{\mathcal {S}}}\cup \{\emptyset ,N\})\quad \theta (L)=0$.

Indeed, the above conditions defining $\Theta _{{{\mathcal {S}}}:T}$ are the rewriting of (1) and of the requirements on the respective linear combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$, where $\uplambda _{T}$ is allowed to be negative. These constraints have clearly rational coefficients. In case of a minimal ${{\mathcal {S}}}$ one has $|\Theta _{{{\mathcal {S}}}}|=1$ by Corollary 5. Thus, $\{\theta _{{{\mathcal {S}}}}\}=\Theta _{{{\mathcal {S}}}:T}$ for some $T\in {{\mathcal {S}}}$ then. Because $\Theta _{{{\mathcal {S}}}:T}$ is specified by rational constraints it is a rational polyhedron. Another well-known fact from polyhedral geometry is that every vertex of a rational polyhedron has rational components; see Studený (1993, Statement 3) for example. This gives $\theta _{{{\mathcal {S}}}}\in {\mathbb Q}^{\mathcal{P}(N)}$. $\square$

Note that (the first claim in) later Lemma 7 implies that every set $\Theta _{{{\mathcal {S}}}:T}$ from the above proof is, in fact, a bounded polyhedron: the set $\Theta _{{{\mathcal {S}}}:T}$ with ${{\mathcal {S}}}:=\mathcal{P}(N){\setminus }\{\emptyset ,N\}$ coincides with the below-defined set ${\tilde{\Theta }}^{N}_{D}$ for $D=T$.

4 Characterization of exact games

Note that readers not interested in technicalities (or proofs) can possibly skip this section. The inequalities of the form (2) from Definition 4 allow one to delimit the cone of exact games. To this end we introduce the following convex sets.

Definition 5

(Auxiliary cones and polyhedrons)  Given $|N|\ge 2$ and $\emptyset \ne D\subseteq N$ we introduce

$$\begin{aligned}&{\Theta ^{N}_{D} := \{\,\theta \in {\mathbb R}^{\mathcal{P}(N)}\, :\ \theta (S)\le 0 \quad \mathrm{for\ any}\ S\subseteq N \ \mathrm{such \ that}\ S\not \in \{\emptyset , D, N\},}\\&~~\qquad \qquad ~~~~\sum _{L\subseteq N} \theta (L)=0 ~~~\mathrm{and}~ \sum _{L\subseteq N:\, i\in L} \theta (L)=0 ~~\mathrm{for\ any}\ i\in N\,\},\\&{\tilde{\Theta }}^{N}_{D} := \Theta ^{N}_{D}\,\cap \, \{\,\theta \in {\mathbb R}^{\mathcal{P}(N)}\,:\ \theta (N)+\theta (\emptyset )=1\,\},\\&\Delta ~ := \hbox \mathrm{conv}\,(\bigcup _{D:\,\emptyset \ne D\subseteq N} {\tilde{\Theta }}^{N}_{D}). \end{aligned}$$

Observe that ${\tilde{\Theta }}^{N}_{D} = \Theta ^{N}_{D}\,\cap \, \{\,\theta \in {\mathbb R}^{\mathcal{P}(N)}\,:\ \sum _{L:\,\emptyset \ne L\subset N} \theta (L)=-1\,\}$, which re-writing allows one to ignore the component for $\emptyset$ and interpret these convex sets as subsets of ${\mathbb R}^{\mathcal{P}(N){\setminus }\{\emptyset \}}$. It follows directly from the definition that ${\tilde{\Theta }}^{N}_{N}\subseteq {\tilde{\Theta }}^{N}_{D}$ for any $\emptyset \ne D\subset N$; thus, one can, alternatively, consider the union over $\emptyset \ne D\subset N$ in the definition of $\Delta$. The proof of the next lemma, based on some facts from (Kroupa and Studený 2019, § 5.1), is moved to “Appendix C”.

Lemma 7

 Given $|N|\ge 2$, every set ${\tilde{\Theta }}^{N}_{D}$, where $\emptyset \ne D\subseteq N$, is a bounded polyhedron. Every vector $\theta \in \Theta ^{N}_{D}$ satisfies both $\theta (N)\ge 0$ and $\theta (\emptyset )\ge 0$ and every non-zero vector $\theta \in \Theta ^{N}_{D}$ satisfies $\theta (N)+\theta (\emptyset )>0$. Given $m\in {\mathbb R}^{\mathcal{P}(N)}$ with $m(\emptyset )=0$, one has

$$\begin{aligned} m\in \mathcal{E}(N) ~~\Leftrightarrow ~~ \left[ \,\forall \, \theta \in \bigcup _{\emptyset \ne D\subseteq N}{\tilde{\Theta }}^{N}_{D}\qquad \langle \theta ,m\rangle \ge 0\right] . \end{aligned}$$

(3)

The first claim in Lemma 7 allows one to observe that $\Delta$ is a bounded polyhedron as well; this follows from basic facts in polyhedral geometry recalled in Sect. 2.2.

The second claim in Lemma 7 means that each set $\Theta ^{N}_{D}$, $\emptyset \ne D\subseteq N$, is a pointed polyhedral cone. An equivalent formulation is that every non-zero vector $\theta \in \Theta ^{N}_{D}$ satisfies $\sum _{L:\,\emptyset \ne L\subset N} \theta (L)<0$, which is relevant if $\Theta ^{N}_{D}$ is interpreted as a subset of ${\mathbb R}^{\mathcal{P}(N){\setminus }\{\emptyset \}}$.

Further auxiliary observation says that the vertices of the (bounded) polyhedrons from Definition 5 correspond to (certain) min-semi-balanced set systems on N. Thus, together with Lemma 7, it puts in relation exact games and semi-balanced systems. Its proof is also shifted to “Appendix D”.

Lemma 8

Given $|N|\ge 2$ and $\emptyset \ne D\subseteq N$, every vertex of ${\tilde{\Theta }}^{N}_{D}$ has either the form $\theta _{{{\mathcal {B}}}}$, where ${{\mathcal {B}}}$ is a min-balanced set system on N, or the form $\theta _{{{\mathcal {S}}}}$, where ${{\mathcal {S}}}$ is a min-semi-balanced system on N having D as the exceptional set.

Conversely, in case $\emptyset \ne D\subset N$, every vector $\theta _{{{\mathcal {S}}}}$, where ${{\mathcal {S}}}$ is a min-semi-balanced system on N having D as the exceptional set, is a vertex of ${\tilde{\Theta }}^{N}_{D}$: $\theta _{{{\mathcal {S}}}}\in \hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{D})$.

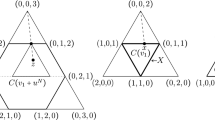
Note in this context that one can show, using the same arguments as in the proof of Lemma 8, that $\hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{N})$ consists just of the vectors $\theta _{{{\mathcal {B}}}}$ where ${{\mathcal {B}}}$ is a min-balanced set system on N; nonetheless, this observation is not necessarily needed to derive our results. On the other hand, the delimitation of $\hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{D})$ for $D\subset N$ in the first claim of Lemma 8 is not tight. Analogous arguments can be used to show that $\theta _{{{\mathcal {B}}}}\in \hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{D})$ for every min-balanced system ${{\mathcal {B}}}$ on N with $D\in {{\mathcal {B}}}$. For a min-balanced system ${{\mathcal {B}}}$ on N such that $D\not \in {{\mathcal {B}}}$, however, the vector $\theta _{{{\mathcal {B}}}}$ may or may not be a vertex of ${\tilde{\Theta }}^{N}_{D}$ as the next example shows.

Example 5

Take $N:=\{a,b,c\}$ and put $D:=\{ a,b\}$; the set system ${{\mathcal {B}}}:=\{\,a,b,c\,\}$ is then min-balanced on N. The corresponding vector $\theta _{{{\mathcal {B}}}}\in {\mathbb R}^{\mathcal{P}(N)}$ is given by

$$\begin{aligned} \theta _{{{\mathcal {B}}}}(N)= & {} +\frac{1}{3}, ~~\theta _{{{\mathcal {B}}}}(a)=\theta _{{{\mathcal {B}}}}(b)=\theta _{{{\mathcal {B}}}}(c)=-\frac{1}{3}, ~~\theta _{{{\mathcal {B}}}}(\emptyset )=+\frac{2}{3}, \\ \theta _{{{\mathcal {B}}}}(L)= & {} 0 ~~\hbox {otherwise}, \end{aligned}$$

evidently belongs to ${\tilde{\Theta }}^{N}_{D}$. Consider another min-balanced system ${{\mathcal {C}}}:=\{\,c,ab\,\}$ on N with

$$\begin{aligned} \theta _{{{\mathcal {C}}}}(N)=\theta _{{{\mathcal {C}}}}(\emptyset )=+\frac{1}{2}, ~~\theta _{{{\mathcal {C}}}}(c)=\theta _{{{\mathcal {C}}}}(ab)=-\frac{1}{2}, \quad \theta _{{{\mathcal {C}}}}(L)=0 ~~\hbox {otherwise}, \end{aligned}$$

and a min-semi-balanced system ${{\mathcal {D}}}:=\{\,a,b,ab\,\}$ on N with

$$\begin{aligned} \theta _{{{\mathcal {D}}}}(ab)=\theta _{{{\mathcal {D}}}}(\emptyset )=+1, ~~\theta _{{{\mathcal {D}}}}(a)=\theta _{{{\mathcal {D}}}}(b)=-1, \quad \theta _{{{\mathcal {C}}}}(L)=0 ~~\hbox {otherwise}\,. \end{aligned}$$

These two vectors both belong to ${\tilde{\Theta }}^{N}_{D}$ and one has $\theta _{{{\mathcal {B}}}}=\frac{2}{3}\cdot \theta _{{{\mathcal {C}}}}+\frac{1}{3}\cdot \theta _{{{\mathcal {D}}}}$. In particular, $\theta _{{{\mathcal {B}}}}$ is not a vertex of ${\tilde{\Theta }}^{N}_{D}$. On the other hand, the min-balanced system ${{\mathcal {B}}}^{\prime }:=\{\,a,bc\,\}$ on N with

$$\begin{aligned} \theta _{{{\mathcal {B}}}^{\prime }}(N)=\theta _{{{\mathcal {B}}}^{\prime }}(\emptyset )=+\frac{1}{2}, ~~\theta _{{{\mathcal {B}}}^{\prime }}(a)=\theta _{{{\mathcal {B}}}^{\prime }}(bc)=-\frac{1}{2}, \quad \theta _{{{\mathcal {B}}}^{\prime }}(L)=0 ~~\hbox {otherwise}, \end{aligned}$$

also complies with $D\not \in {{\mathcal {B}}}^{\prime }$ and it makes no problem to show that $\theta _{{{\mathcal {B}}}^{\prime }}\in \hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{D})$.

Lemmas 7 and 8 allow one to characterize exact games in terms of semi-balanced systems.

Corollary 9

Given $|N|\ge 2$, consider a set function $m\in {\mathbb R}^{\mathcal{P}(N)}$ such that $m(\emptyset )=0$. Then the following conditions on the game $m$ are equivalent:

(i):

   $m$ is an exact game over N, that is, $m\in {{\mathcal {E}}}(N)$,

(ii):

 for every semi-balanced set system $\mathcal{S}$ on N one has $\langle \theta ,m\rangle \ge 0$ for all $\theta \in \Theta _{{{\mathcal {S}}}}$,

(iii):

for every min-semi-balanced set system $\mathcal{S}$ on N one has $\langle \theta _{{{\mathcal {S}}}},m\rangle \ge 0$.

Note that one is entitled to write $\theta _{{{\mathcal {S}}}}$ in (iii) since, by Corollary 5, $|\Theta _{{{\mathcal {S}}}}|=1$ then.

Proof

The implication (i) $\Rightarrow$(ii) follows from (3) in Lemma 7, one only needs to realize that, given a semi-balanced system ${{\mathcal {S}}}$ on N, one has $\Theta _{{{\mathcal {S}}}}\subseteq {\tilde{\Theta }}^{N}_{D}$ for some non-empty set $\emptyset \ne D\subseteq N$. Indeed, any $\theta \in \Theta _{{{\mathcal {S}}}}$ is defined in (1) from an affine (semi-conic) combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$, which gives both $\theta (N)+\theta (\emptyset )=-\sum _{L:\emptyset \ne L\subset N} \theta (L)=+1$ and $\sum _{L\subseteq N:i\in L} \theta (L)=0$ for any $i\in N$. Thus, if it is a conic combination then $\theta \in {\tilde{\Theta }}^{N}_{N}$, otherwise one has $\theta \in {\tilde{\Theta }}^{N}_{T}$ for the only (exceptional) $T\in {{\mathcal {S}}}$ with $\uplambda _{T}<0$.

The implication (ii) $\Rightarrow$(iii) is immediate.

To verify (iii) $\Rightarrow$(i) we apply the first claim in Lemma 8 to observe that $\langle \theta ,m\rangle \ge 0$ for any $\theta \in \hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{D})$ and $\emptyset \ne D\subseteq N$. Hence, the same holds for any $\theta \in {\tilde{\Theta }}^{N}_{D}$ and arbitrary $\emptyset \ne D\subseteq N$. In particular, one can use (3) in Lemma 7 to derive (i). $\square$

Let us remark that the observations from Corollary 9 are analogous to former results by Lohmann et al. (2012), specifically to Theorem 3.4 in (Lohmann et al. 2012, § 3) and Theorem 5.1 in (Lohmann et al. 2012, § 5). The proviso is that Lohmann et al. used a different formal way to associate set systems with inequalities—see later Remark 2 for the explanation. We believe that our approach and presentation offers an elegant geometric interpretation and simpler arguments. Moreover, it can be extended to get the following characterization of facet-defining inequalities.

Corollary 10

Given $|N|\ge 2$, the inequality (2), that is, $0\le \langle \theta ,m\rangle$ for $m\in {\mathbb R}^{\mathcal{P}(N)}$, with a coefficient vector $\theta \in {\mathbb R}^{\mathcal{P}(N)}$, where $\sum _{S\subseteq N} \theta (S)=0$ and $\sum _{L:\,\emptyset \ne L\subset N} \theta (L)=-1$, is facet-defining for the cone of exact games ${{\mathcal {E}}}(N)$ iff $\theta \in \hbox \mathrm{ext}\,(\Delta )$.

Note that the above requirements $\sum _{S\subseteq N} \theta (S)=0$ and $\sum _{L:\,\emptyset \ne L\subset N} \theta (L)=-1$ on a coefficient vector $\theta$ are solely technical constraints which can, without loss of generality, be assumed to hold for any facet-defining inequality for the exact cone. The former requirement is related to the facts that $m(\emptyset )=0$ for any game $m\in \mathcal{G}(N)$ and that $\mathcal{E}(N)$ is a full-dimensional cone in ${\mathbb R}^{\mathcal{P}(N){\setminus }\{\emptyset \}}$: it is a convention on the value $\theta (\emptyset )$. The latter requirement is related to the fact that facet-defining inequalities are determined uniquely up to a positive multiple: it is a particular convention about the choice of the multiplicative factor.

The proof is based on a geometric consideration concerning the duality of polyhedral cones. It is more convenient technically to imagine both the cone of exact games and its dual cone within the space ${\mathbb R}^{\mathcal{P}(N){\setminus }\{\emptyset \}}$ because then the dual cone becomes pointed.

Proof

Consider the space ${\mathbb R}^{\mathcal{P}(N){\setminus }\{\emptyset \}}$ and interpret the polyhedrons ${\tilde{\Theta }}^{N}_{D}$ from Definition 5 as its subsets. Introduce a polyhedral cone ${\bar{\Delta }}\subseteq {\mathbb R}^{\mathcal{P}(N){\setminus }\{\emptyset \}}$ as the conic hull of $\Delta$. Since every $\theta \in \Delta$ satisfies $\sum _{\emptyset \ne L\subset N} \theta (L)=-1$ every non-zero $\theta \in {\bar{\Delta }}$ satisfies $\sum _{\emptyset \ne L\subset N} \theta (L)<0$ meaning that ${\bar{\Delta }}$ is pointed and its extreme rays are generated by vertices $\theta \in \hbox \mathrm{ext}\,(\Delta )$ (see Sect. 2.2). The first claim in Lemma 7 allows one to observe that $\Delta$ is a bounded polyhedron, while the third claim in Lemma 7 means that the cone ${{\mathcal {E}}}(N)$ is dual to ${\bar{\Delta }}$: ${{\mathcal {E}}}(N)=({\bar{\Delta }})^{*}$.

Hence, by the basic facts from polyhedral geometry recalled in Sect. 2.2, the cones ${\bar{\Delta }}$ and ${{\mathcal {E}}}(N)$ are mutually dual polyhedral cones and the lattices of their non-empty faces are anti-isomorphic. In particular, extreme rays of ${\bar{\Delta }}$ correspond to facets of ${{\mathcal {E}}}(N)$. Moreover, the lattice of non-empty faces of ${\bar{\Delta }}$ is isomorphic to the face-lattice of $\Delta$, which implies that the extreme rays of ${\bar{\Delta }}$ are just those rays that are generated by vertices of $\Delta$. In other words, a vector $\theta$ normalized by $\sum _{\emptyset \ne L\subset N} \theta (L)=-1$ yields a facet-defining inequality for ${{\mathcal {E}}}(N)$ iff $\theta$ is a vertex of $\Delta$. $\square$

Remark 2

Lohmann et al. (2012) introduced the concept of an exact balanced collection of sets with the intention to use such set systems to generate linear inequalities specifying the cone of exact games. These collections of sets often coincide with our semi-balanced set systems, but there is one (substantial) technical difference in their approach. It concerns the inequalities $\langle \theta ,m\rangle \ge 0$ for $m\in {{\mathcal {E}}}(N)$ with $\theta (N)=0$. They ascribe such inequalities to the so-called “minimal sub-balanced" collections which are certain set systems always involving the grand coalition N. To give an example of the difference consider the vector $\theta \in {\mathbb R}^{\mathcal{P}(N)}$, where $N=\{a,b,c\}$, given by

$$\begin{aligned} \theta (\emptyset )= & {} +1,\quad \theta (ab)=+1,\qquad \theta (a)=-1,\quad \theta (b)=-1, \\ \theta (L)= & {} 0~~\hbox {for other }L\subseteq N\,. \end{aligned}$$

One has $\theta \in \Theta ^{N}_{D}$ for $D=ab$ and $\langle \theta ,m\rangle \ge 0$ is facet-defining for $m\in {{\mathcal {E}}}(N)$. Our approach is to associate this inequality with a set system $\{\, a,b,ab\,\}$ while Lohmann et al. (2012) ascribe that inequality to the set system $\{\, a,b,ab, N\,\}$. We have two arguments why their approach is not appropriate for our purpose:

• There is no one-to-one correspondence between set systems and inequalities in their approach although technically all inequalities assigned to a minimal sub-balanced collection are equivalent [see Lohmann et al. (2012, Theorem 3.9)],

• Their approach does not allow one to reveal one important relation of complementarity among set systems which corresponds to the respective relation of conjugacy between facet-defining inequalities for ${\mathcal {E}}(N)$ [see Kroupa and Studený (2019, Lemma 3.4)]. The reader can find further details in Sect. 5.1.

That is why we believe our way of inequality description is more appropriate.

5 Properties of semi-balanced systems

In this section we discuss some structural relations among semi-balanced set systems.

5.1 Complementarity of set systems

A substantial fact about the cone of exact games is that its facet-defining inequalities come in pairs of mutually conjugate inequalities, as shown already in (Kroupa and Studený 2019, Lemma 3.4). Therefore, the corresponding set systems also come in pairs of mutually complementary systems.

Definition 6

(Conjugate inequality, complementary set system)  Assume $|N|\ge 2$. The conjugate inequality to the inequality (2), that is, to the inequality $0\le \langle \theta ,m\rangle$ for $m\in {\mathbb R}^{\mathcal{P}(N)}$ with a coefficient vector $\theta \in {\mathbb R}^{\mathcal{P}(N)}$, is the inequality

$$\begin{aligned} 0\le \langle \theta ^{\star },m\rangle ~~\hbox {for }m\in {\mathbb R}^{\mathcal{P}(N)},\qquad \hbox {where}~~ \theta ^{\star }(L):=\theta (N{\setminus } L) \ \hbox {for any}\ L\subseteq N. \end{aligned}$$

(4)

Given a non-trivial set system ${{\mathcal {S}}}$ on N, its complementary system is the set system

$$\begin{aligned} {{\mathcal {S}}}^{\star } := \{ N{\setminus } S\,:\ S\in {{\mathcal {S}}}\}\,. \end{aligned}$$

Of course, both concepts are relative to N. Here are the relevant observations.

Lemma 11

Given $|N|\ge 2$, let ${{\mathcal {S}}}$ be a non-trivial set system on N. Then ${{\mathcal {S}}}$ is semi-balanced iff ${{\mathcal {S}}}^{\star }$ is semi-balanced and $\Theta _{{{\mathcal {S}}}^{\star }}=\{ \theta ^{\star }\,:\ \theta \in \Theta _{{{\mathcal {S}}}}\}$. An analogous statement holds for balanced systems. In particular, ${{\mathcal {S}}}$ is min-semi-balanced iff ${{\mathcal {S}}}^{\star }$ is min-semi-balanced and the same holds for min-balanced systems on N. Moreover, one then has $\theta ^{\star }_\mathcal{S} := (\theta _\mathcal{S})^{\star } =\theta _{\mathcal{S}^{\star }}$.

Given $\theta \in {\mathbb R}^{\mathcal{P}(N)}$ with $\sum _{S\subseteq N} \theta (S)=0$ and $\sum _{\emptyset \ne L\subset N} \theta (L)=-1$, the inequality (2) is facet-defining for ${{\mathcal {E}}}(N)$ iff its conjugate inequality (4) is facet-defining for ${{\mathcal {E}}}(N)$.

Proof

By Lemma 1, ${{\mathcal {S}}}$ is semi-balanced if $r\cdot \chi _{N}=\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ with $r\in [0,1]$ and an affine semi-conic combination on the right-hand side (which has all its coefficients non-zero). One can multiply that by $(-1)$ and add to that the equality $\chi _{N}=\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{N}$ to get $(1-r)\cdot \chi _{N}=\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{N{\setminus } S}=\sum _{L\in {{\mathcal {S}}}^{\star }} \uplambda _{N{\setminus } L}\cdot \chi _{L}$, which means that ${{\mathcal {S}}}^{\star }$ is semi-balanced; one can then put $r^{\star }=1-r$ and $\uplambda ^{\star }_{L}=\uplambda _{N{\setminus } L}$ for $L\in {{\mathcal {S}}}^{\star }$. Thus, the relation $\Theta _{{{\mathcal {S}}}^{\star }}=\{ \theta ^{\star }\,:\ \theta \in \Theta _{{{\mathcal {S}}}}\}$ follows from Definition 4. The same argument works for balanced systems: the linear combination is even conic then. The relation of non-trivial systems ${{\mathcal {T}}}\subseteq {{\mathcal {S}}}$ iff ${{\mathcal {T}}}^{\star }\subseteq {{\mathcal {S}}}^{\star }$ then implies the consequences concerning minimal such systems.

The last claim in Lemma 11 can be derived from Corollary 10 using Definition 5. Note that $\theta \in {\tilde{\Theta }}^{N}_{N} ~\Leftrightarrow ~ \theta ^{\star }\in {\tilde{\Theta }}^{N}_{N}$, and, for every $\emptyset \ne D\subset N$, $\theta \in {\tilde{\Theta }}^{N}_{D} ~\Leftrightarrow ~ \theta ^{\star }\in {\tilde{\Theta }}^{N}_{N{\setminus } D}$, which allows one to deduce $\theta \in \Delta ~\Leftrightarrow ~ \theta ^{\star }\in \Delta$. Since $\theta \mapsto \theta ^{\star }$ is a linear mapping one has $\theta \in \hbox \mathrm{ext}\,(\Delta ) ~\Leftrightarrow ~ \theta ^{\star }\in \hbox \mathrm{ext}\,(\Delta )$ and the rest follows from Corollary 10. $\square$

Note that $T\in {{\mathcal {S}}}$ is exceptional within a non-trivial set system ${{\mathcal {S}}}$ on N (see Definition 3) iff $N{\setminus } T\in {{\mathcal {S}}}^{\star }$ is exceptional within ${{\mathcal {S}}}^{\star }$: given a combination $r\cdot \chi _{N}=\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ multiply it by $(-1)$ and add $(\sum _{S\in {{\mathcal {S}}}} \uplambda _{S})\cdot \chi _{N}$ to get $(\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}-r)\cdot \chi _{N}=\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{N{\setminus } S}=\sum _{R\in {{\mathcal {S}}}^{\star }} \uplambda _{N{\setminus } R}\cdot \chi _{R}$. In particular, a non-trivial system ${{\mathcal {S}}}$ on N is purely min-semi-balanced iff the same holds for its complementary system ${{\mathcal {S}}}^{\star }$.

5.2 Basic classification of min-semi-balanced systems

The uniqueness condition (d) in Lemma 2 on an affine combination yielding a constant vector allows one to classify min-semi-balanced systems by the values of the constant.

Lemma 12

Given $|N|\ge 2$ and a min-semi-balanced system ${{\mathcal {S}}}$ on N, let $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ be the unique affine (and semi-conic) combination yielding a constant vector $r\cdot \chi _{N}$, $r\in [0,1]$.

One has then $r=0$ iff there exists a min-balanced system ${{\mathcal {B}}}$ on $M\subset N$, $|M|\ge 2$, such that ${{\mathcal {S}}}={{\mathcal {B}}}\cup \{M\}$; another equivalent condition is $\bigcup {{\mathcal {S}}}\subset N$. Moreover, a min-balanced system ${{\mathcal {B}}}$ on $M\subset N$, $|M|\ge 2$, yields a min-semi-balanced one, namely the system $\mathcal{S}:={{\mathcal {B}}}\cup \{M\}$ on N with $r=0$.

One has $r=1$ iff ${{\mathcal {S}}}$ is a complementary system to a system ${{\mathcal {S}}}^{\star }$ with $\bigcup {{\mathcal {S}}}^{\star }\subset N$; another equivalent condition is $\bigcap {{\mathcal {S}}}\ne \emptyset$.

On the other hand, every min-balanced system ${{\mathcal {S}}}$ on N satisfies $0<r<1$.

The proof of Lemma 12 is shifted to “Appendix E”. Thus, one can distinguish at least three classes of min-semi-balanced systems ${{\mathcal {S}}}$:

• those with $\bigcup {{\mathcal {S}}}\subset N$, which are extensions of min-balanced systems on strict subsets,

• those with $\bigcap {{\mathcal {S}}}\ne \emptyset$, which can be viewed as their complementary systems, and

• min-balanced systems on N, which satisfy both $\bigcup {{\mathcal {S}}}=N$ and $\bigcap {{\mathcal {S}}}=\emptyset$.

Nevertheless, as the next example shows, there is the fourth class of min-semi-balanced systems: these satisfy both $\bigcup {{\mathcal {S}}}=N$ and $\bigcap {{\mathcal {S}}}=\emptyset$ but they are not balanced on N.

Example 6

Take $N:=\{a,b,c,d\}$ and ${{\mathcal {S}}}:=\{\,a,ab,bc,abd\,\}$. The semi-conic combination

$$\begin{aligned} 1\cdot \chi _{a}+ (-1)\cdot \chi _{ab}+ 1\cdot \chi _{bc}+ 1\cdot \chi _{abd} = \chi _{N} \end{aligned}$$

implies that ${{\mathcal {S}}}$ is semi-balanced on N. Since $\bigcup {{\mathcal {S}}}=N$ and $\{\chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ are linearly independent, by Lemma 2(c), ${{\mathcal {S}}}$ is min-semi-balanced. Clearly, the unique linear combination yielding $\chi _{N}$ is not conic; hence, ${{\mathcal {S}}}$ is not balanced.

Remark 3

We showed in Lemma 12 that every min-balanced set system ${{\mathcal {B}}}$ on a strict subset $M\subset N$ leads to a semi-balanced system ${{\mathcal {B}}}\cup \{M\}$ on N. Note in this context that ${{\mathcal {B}}}$ itself is never semi-balanced on N. This is because the vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {B}}}\}$ are then linearly independent (Kroupa and Studený 2019, Lemma 2.1). Thus, $\bigcup {{\mathcal {B}}}=M\subset N$ implies that a contingent semi-conic combination of $\{ \chi _{S}\,:\ S\in {{\mathcal {B}}}\}$ can only yield the zero constant vector $\underline{0}$, while the linear independence implies that only the zero linear combination yields $\underline{0}$.

5.3 Pictorial representation of min-semi-balanced systems

We propose to use certain special pictures to represent (permutational types of) minimal semi-balanced set systems. In fact, our diagrams additionally encode the corresponding linear inequalities (2). Corollary 6 says that, given a min-semi-balanced system ${{\mathcal {S}}}$ on N, the vector $\theta _{{{\mathcal {S}}}}$ has rational components, that is, it is given by an affine rational semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}=r\cdot \chi _{N}$. One can multiply this by a natural number $\ell$ so that $\alpha _{S}:=\ell \cdot \uplambda _{S}$, $S\in {{\mathcal {S}}}$, become integers with no common prime divisor. Then $\alpha _{N}:=\ell \cdot r\in {\mathbb Z}^{+}$ and one can introduce $\alpha _{\emptyset }:=-\alpha _{N}+\sum _{S\in {{\mathcal {S}}}} \alpha _{S}\in {\mathbb Z}^{+}$ (use Lemma 1). Thus, one gets

$$\begin{aligned} \sum _{S\in {{\mathcal {S}}}} \alpha _{S}\cdot \chi _{S}= \alpha _{\emptyset }\cdot \chi _{\emptyset } +\alpha _{N}\cdot \chi _{N}\,,\quad \hbox {where all the coefficients} \ \alpha _{S}\ \hbox {are integers.} \end{aligned}$$

One can have $\alpha _{\emptyset }=0$ or $\alpha _{N}=0$, while the remaining coefficients are non-zero. Provided there is $T\in {{\mathcal {S}}}$ with $\uplambda _{T}<0$ one can re-write that in the form

$$\begin{aligned} \sum _{S\in \mathcal{S}\setminus \{T\}} \alpha _{S}\cdot \chi _{S}= & {} \alpha _{\emptyset }\cdot \chi _{\emptyset }+ (-\alpha _{T})\cdot \chi _{T}+\,\alpha _{N}\cdot \chi _{N} \end{aligned}$$

with non-negative integers as coefficients.

A diagram representing a set system ${{\mathcal {S}}}$ has the form of a pair of two-dimensional arrays whose entries are colorful boxes; the arrays encode the sides of the above vector equality. The rows of these arrays correspond to the elements of the base set N (= players); they are labeled if the diagram represents a particular set system ${{\mathcal {S}}}$ and they are unlabeled if it represents a permutational type of such systems.

The columns of the arrays encode sets S from the enlarged system ${{\mathcal {S}}}\cup \{\emptyset , N\}$. Each of the sets has its own color; however, the black color is reserved for the grand coalition N, a fully blank (= white) column implicitly encodes the empty set and the grey color is reserved for a contingent set T with a negative coefficient $\uplambda _{T}<0$ (= an exceptional set in ${{\mathcal {S}}}$). The other sets from ${{\mathcal {S}}}$ have bright colors then. The column representing a set S has boxes of the respective color just in rows corresponding to elements of S. To express the value of the respective coefficient $\alpha _{S}\in {\mathbb Z}$ in the inequality the respective column is repeated $|\alpha _{S}|$-times.

The left array is composed of columns which correspond to sets with positive coefficients $\uplambda _{S}>0$, $S\in {{\mathcal {S}}}$, while the array on the right-hand side has either fully black columns, fully blank (= white) columns and possibly columns containing grey boxes.

Example 7

Take $N:=\{a,b,c,d,e\}$ and put ${{\mathcal {S}}}:=\{\,ab,ac,bc,abd,abe\,\}$. The relation

$$\begin{aligned} 1\cdot \chi _{ac}+ 1\cdot \chi _{bc}+ 2\cdot \chi _{abd}+ 2\cdot \chi _{abe} = 1\cdot \chi _{\emptyset } +3\cdot \chi _{ab} +2\cdot \chi _{N} \end{aligned}$$

Fig. 1

A picture representing the set system from Example 7

allows one to observe that ${{\mathcal {S}}}$ is semi-balanced on N. As the vectors $\{\chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ are linearly independent ${{\mathcal {S}}}$ is minimal. A picture representing this set system is in Fig. 1.

Note that, in any row, the numbers of boxes in the left and right array coincide: this is because of the equality $\sum _{S\in {{\mathcal {S}}}} \alpha _{S}\cdot \chi _{S}(i)=\alpha _{N}\cdot \chi _{N}(i)$ for any $i\in N$. Another interesting observation is that the diagram for the complementary system ${{\mathcal {S}}}^{\star }$ can easily by obtained by “reflection” from the diagram for ${{\mathcal {S}}}$: the boxes are interchanged with non-boxes and the colors for columns are kept, under a convention that the color for blank columns is black.

One can also easily recognize on basis of the diagram for ${{\mathcal {S}}}$ to which of the four basic classes it belongs. Systems ${{\mathcal {S}}}$ with $\bigcup {{\mathcal {S}}}\subset N$, that is, those with the constant $r=0$, have no black column. Their complementary systems ${{\mathcal {S}}}$ with $\bigcap {{\mathcal {S}}}\ne \emptyset$, that is, those with the constant $r=1$, have no blank (= white) column. The min-balanced systems on N have no grey column and other min-semi-balanced systems have blank, grey and black columns.

6 Purely min-semi-balanced systems

Let us first discuss the situation when only two players exist, that is, $|N|=2$. Then, as explained below Lemma 1, there is no purely semi-balanced system on N. In fact, the only semi-balanced system over $N=\{a,b\}$ is the min-balanced system ${{\mathcal {B}}}:=\{\, a,b\,\}$. Thus, by Corollary 9, a game $m\in {\mathbb R}^{\mathcal{P}(N)}$, $m(\emptyset )=0$, is exact iff $\langle \theta _{{{\mathcal {B}}}},m\rangle \ge 0$, and the cone of exact games is specified by a single inequality $m(ab)-m(a)-m(b)\ge 0$.

6.1 How to get purely min-semi-balanced systems

Therefore, in the sequel we limit our attention to a non-trivial case $|N|\ge 3$, when there exist purely semi-balanced systems on N. We first establish some relation between min-balanced and purely min-semi-balanced systems. The proof of the next lemma is shifted to “Appendix F”.

Lemma 13

Assume $|N|\ge 3$. If ${{\mathcal {B}}}$ is a min-balanced set system on N such that $|{{\mathcal {B}}}|\ge 3$ and $Z\in {{\mathcal {B}}}$ then $Y:=N{\setminus } Z$ is not in ${{\mathcal {B}}}$, the set system ${{\mathcal {S}}}:=({{\mathcal {B}}}{\setminus }\{Z\})\cup \{Y\}$ is purely min-semi-balanced on N and Y is the exceptional set within ${{\mathcal {S}}}$.

Conversely, if ${{\mathcal {S}}}$ is a (purely) min-semi-balanced system on N and $Y\in {{\mathcal {S}}}$ the exceptional set within ${{\mathcal {S}}}$ then $Z:=N{\setminus } Y$ is not in ${{\mathcal {S}}}$ and ${{\mathcal {B}}}:=({{\mathcal {S}}}{\setminus }\{Y\})\cup \{Z\}$ is a min-balanced system on N such that $|{{\mathcal {B}}}|\ge 3$.

Thus, by Lemma 13, there is one-to-many correspondence ${{\mathcal {B}}}\leftrightarrow {{\mathcal {S}}}$ between min-balanced systems ${{\mathcal {B}}}$ on N satisfying $|{{\mathcal {B}}}|\ge 3$ and purely min-semi-balanced systems ${{\mathcal {S}}}$ on N which is realized by the mutual exchange of a set $Z\in {{\mathcal {B}}}$ and of its complement $Y\in {{\mathcal {S}}}$. It allows one to generate a complete list of min-semi-balanced systems on N on basis of the list of all min-balanced systems on N. Note that the fact that balanced systems on N induce in this way other semi-balanced systems on N has already been recognized by Lohmann et al. (2012, § 4, Theorem 4.4). Nevertheless, the above correspondence was not revealed there in its full scope for the reason mentioned in Remark 2.

Let us remark in this context that the discussed transition from a min-balanced system ${{\mathcal {B}}}$ to a purely min-semi-balanced system ${{\mathcal {S}}}$ (and back) can be recognized easily on basis of their diagrams/pictures from Sect. 5.3. Indeed, if a diagram represents a min-balanced system ${{\mathcal {B}}}$ and has $\alpha _{Z}$ columns representing a set $Z\in {{\mathcal {B}}}$ then the diagram representing ${{\mathcal {S}}}:=({{\mathcal {B}}}{\setminus }\{Z\})\cup \{Y\}$, where $Y:=N{\setminus } Z$, can be obtained from it by removing those $\alpha _{Z}$ columns of bright color from the left array, $\alpha _{Z}$ blank columns and $\alpha _{Z}$ black columns from the right array and by adding $\alpha _{Z}$ grey columns representing the set Y to the right array. Of course, the transition back can be done by an inverse operation with the diagrams. The following example illustrates the procedure.

Fig. 2

Pictures representing the set systems ${{\mathcal {B}}}$ and ${{\mathcal {S}}}$ from Example 8

Example 8

Take $N:=\{a,b,c,d\}$ and put ${{\mathcal {B}}}:=\{\,ab,ac,bc,d\,\}$. One can observe that ${{\mathcal {B}}}$ is min-balanced on N using the equality relation

$$\begin{aligned} \frac{1}{2}\cdot \chi _{ab}+ \frac{1}{2}\cdot \chi _{ac}+ \frac{1}{2}\cdot \chi _{bc}+ 1\cdot \chi _{d}= \chi _{N}\,. \end{aligned}$$

The choice of a set $Z:=d$ from ${{\mathcal {B}}}$ leads, by Lemma 13, to a min-semi-balanced system ${{\mathcal {S}}}:=({{\mathcal {B}}}{\setminus }\{Z\})\cup \{Y\}=\{\,ab,ac,bc,abc\,\}$. The diagrams for both systems are in Fig. 2. We observe that two columns representing Z, $\emptyset$ and N from the diagram for ${{\mathcal {B}}}$ are missing in the diagram for ${{\mathcal {S}}}$ and replaced there by two columns representing $Y:=N{\setminus } Z= abc$.

6.2 The case of balanced systems

We now show that the inequalities corresponding to balanced systems on N, $|N|\ge 3$, are superfluous. The next observation follows from Lemma 13.

Corollary 14

Given $|N|\ge 3$, let ${{\mathcal {B}}}$ be a min-balanced set system on N with $|{{\mathcal {B}}}|\ge 3$. Then $\theta _{{{\mathcal {B}}}}$ is a (non-trivial) convex combination of $\theta _{{{\mathcal {D}}}}$ for a min-balanced system ${{\mathcal {D}}}$ on N with $|{{\mathcal {D}}}|=2$ and of $\theta _{{{\mathcal {S}}}}$ for a purely min-semi-balanced system ${{\mathcal {S}}}$ on N with $|{{\mathcal {S}}}|=|{{\mathcal {B}}}|$.

Proof

We take $Z\in {{\mathcal {B}}}$, put $Y:=N{\setminus } Z$ and observe, by means of Lemma 13, that $\mathcal{S}:=({{\mathcal {B}}}{\setminus }\{Z\})\cup \{Y\}$ is min-semi-balanced on N. Consider the unique affine conic combination $\sum _{S\in {{\mathcal {B}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$. Let us add $-\uplambda _{Z}\cdot \chi _{N}$ to that and obtain a semi-conic combination $\sum _{S\in {{\mathcal {B}}}{\setminus }\{Z\}} \uplambda _{S}\cdot \chi _{S} + (-\uplambda _{Z})\cdot \chi _{Y}$. By Lemma 1, applied to the latter combination, get $0<\sum _{S\in {{\mathcal {B}}}{\setminus }\{Z\}} \uplambda _{S} + (-\uplambda _{Z})=1-2\uplambda _{Z}$. Thus, $(1-2\uplambda _{Z})^{-1}$-multiple of it is an affine combination. Put ${{\mathcal {D}}}:=\{ Y,Z\}$, which is a min-balanced system on N, and the respective affine conic combination $\frac{1}{2}\cdot \chi _{Y}+\frac{1}{2}\cdot \chi _{Z}$ yields a constant vector in ${\mathbb R}^{N}$. Then

$$\begin{aligned}&{\sum _{S\in {{\mathcal {B}}}} \uplambda _{S}\cdot \chi _{S} = 2\uplambda _{Z}\cdot \left[ \frac{1}{2}\cdot \chi _{Y}+\frac{1}{2}\cdot \chi _{Z}\right] }\\&\quad +\, (1-2\uplambda _{Z})\cdot \left[ \sum _{S\in {{\mathcal {B}}}{\setminus }\{Z\}} (1-2\uplambda _{Z})^{-1}\cdot \uplambda _{S}\cdot \chi _{S} + (1-2\uplambda _{Z})^{-1}\cdot (-\uplambda _{Z})\cdot \chi _{Y} \right] , \end{aligned}$$

and using (1) derive that $\theta _{{{\mathcal {B}}}}=2\uplambda _{Z}\cdot \theta _{{{\mathcal {D}}}} +(1-2\uplambda _{Z})\cdot \theta _{{{\mathcal {S}}}}$. $\square$

Corollary 14 says that the vector $\theta _{{{\mathcal {B}}}}$ for a min-balanced system ${{\mathcal {B}}}$ with $|{{\mathcal {B}}}|\ge 3$ is a convex combination of vectors for min-semi-balanced systems of cardinality at most $|{{\mathcal {B}}}|$. The vector $\theta _{{{\mathcal {D}}}}$ for a min-balanced system ${{\mathcal {D}}}$ on N with $|{{\mathcal {D}}}|=2$ can also be written as a convex combination of other vectors. Nevertheless, the difference is that the summands in the combination correspond to set systems of higher cardinality.

Lemma 15

Assume $|N|\ge 3$. If ${{\mathcal {D}}}$ is a min-balanced system on N with $|{{\mathcal {D}}}|=2$ then $\theta _{{{\mathcal {D}}}}$ is a convex combination of $\theta _{{{\mathcal {S}}}}$ and $\theta _{{{\mathcal {T}}}}$ for purely min-semi-balanced systems ${{\mathcal {S}}}$ and ${{\mathcal {T}}}$ on N.

Proof

We have ${{\mathcal {D}}}=\{Y,Z\}$ where $Y\cap Z=\emptyset$, $Y\cup Z=N$, $\emptyset \ne Z$ and $|Y|\ge 2$. Thus, there exists a set $\emptyset \ne R\subset Y$ and one can put ${{\mathcal {S}}}:=\{\, Z,R,Z\cup R\,\}$ and ${{\mathcal {T}}}:=\{\, Z\cup R, Y, R\,\}$. The equalities $\chi _{Z}+\chi _{R}-\chi _{Z\cup R}=\underline{0}$ and $\chi _{Z\cup R}+\chi _{Y}-\chi _{R}=\chi _{N}$ together with affine/linear independence of involved vectors allows one to observe using Lemma 2 that both ${{\mathcal {S}}}$ and ${{\mathcal {T}}}$ is a min-semi-balanced system on N. The respective affine semi-conic combinations are related as follows:

$$\begin{aligned}&\left[ \frac{1}{2}\cdot \chi _{Y}+\frac{1}{2}\cdot \chi _{Z}\right] \,=\, \frac{1}{2}\cdot \left[ 1\cdot \chi _{Z}+1\cdot \chi _{R}+(-1)\cdot \chi _{Z\cup R}\right] \\&\quad +\, \frac{1}{2}\cdot \left[ 1\cdot \chi _{Z\cup R}+1\cdot \chi _{Y}+(-1)\cdot \chi _{R}\right] , \end{aligned}$$

which equality implies using (1) that $\theta _{{{\mathcal {D}}}}=\frac{1}{2}\cdot \theta _{{{\mathcal {S}}}} +\frac{1}{2}\cdot \theta _{{{\mathcal {T}}}}$. $\square$

The previous two results allow one to derive the following conclusion.

Corollary 16

 If $|N|\ge 3$ and ${{\mathcal {B}}}$ is a min-balanced system on N then the inequality given by $\theta =\theta _{{{\mathcal {B}}}}$ is not facet-defining for the exact cone ${{\mathcal {E}}}(N)$.

Recall that the fact that balanced systems provide superfluous inequalities has already been shown in (Lohmann et al. 2012, § 5, Theorem 5.4); we give our short proof for the sake of completeness.

Proof

By combining Corollary 14 with Lemma 15 observe that every vector $\theta _{{{\mathcal {B}}}}$ for a min-balanced system ${{\mathcal {B}}}$ on N is a non-trivial convex combination of vectors $\theta _{{{\mathcal {S}}}}$ for purely min-semi-balanced systems ${{\mathcal {S}}}$ on N. Then apply Corollary 10 to observe that the inequality (2) with $\theta =\theta _{{{\mathcal {B}}}}$ is not facet-defining for ${{\mathcal {E}}}(N)$. $\square$

7 Indecomposable semi-balanced systems

Nevertheless, even purely min-semi-balanced systems can induce superfluous inequalities. We give a simple sufficient condition for that.

Definition 7

(Decomposition, indecomposable system)  Assume $|N|\ge 3$. Given a purely min-semi-balanced set system ${{\mathcal {S}}}$ on N and $E\subseteq N$ with $E\not \in ({{\mathcal {S}}}\cup \{\emptyset ,N\})$ we say that E yields a decomposition of ${{\mathcal {S}}}$ if E is an exceptional set within the system $\mathcal{S}\cup \{E\}$ (see Definition 3). A purely min-semi-balanced set system on N will be called indecomposable if it has no decomposition.

Recall from Sect. 5.1 that a set is exceptional within a non-trivial set system iff its complement is exceptional within its complementary system. This implies that ${{\mathcal {S}}}$ has a decomposition iff its complementary system ${{\mathcal {S}}}^{\star }$ has a decomposition. Therefore, ${{\mathcal {S}}}$ is indecomposable iff the same holds for ${{\mathcal {S}}}^{\star }$. Our main result follows from the following lemma; its technical proof is moved to “Appendix G”.

Lemma 17

Let ${{\mathcal {S}}}$ be a purely min-semi-balanced system on N, $|N|\ge 3$, with exceptional set $T\in {{\mathcal {S}}}$ and ${{\mathcal {W}}}:= \mathcal{P}(N){\setminus } (\{\emptyset ,N\}\cup {{\mathcal {S}}})$. Then the following conditions are equivalent:

(a):

$\theta _{{{\mathcal {S}}}}\not \in \hbox \mathrm{ext}\,(\Delta )$, (see Definition 5)

(b):

there exists a convex combination $\theta _{{{\mathcal {S}}}}=\sum _{D\in {{\mathcal {W}}}\cup \{T\}} \alpha _{D}\cdot \theta ^{D}$ where $\alpha _{T}<1$ and $\theta ^{D}\in {\tilde{\Theta }}^{N}_{D}$ whenever $\alpha _{D}>0$,

(c):

the set $\Delta ({{\mathcal {S}}}):=\hbox \mathrm{conv}\,(\bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D}) \cap \{\,\theta \in {\mathbb R}^{\mathcal{P}(N)}\,:\ \theta (W)\ge 0 ~\hbox {for}\ W\in {{\mathcal {W}}}\,\}$ is non-empty,

(d):

there exists $E\in {{\mathcal {W}}}$ such that E is exceptional in ${{\mathcal {S}}}\cup \{E\}$, (= ${{\mathcal {S}}}$ has a decomposition)

(e):

there exists $E\in {{\mathcal {W}}}$ such that E is exceptional in $({{\mathcal {S}}}{\setminus }\{T\})\cup \{E\}$,

(f):

a min-semi-balanced system ${{\mathcal {D}}}$ on N exists such that ${{\mathcal {D}}}{\setminus }{{\mathcal {S}}}=\{E\}$ for some $E\in {{\mathcal {W}}}$, the set E is exceptional within ${{\mathcal {D}}}$, and $T\not \in {{\mathcal {D}}}$,

(g):

a min-semi-balanced system ${{\mathcal {D}}}$ on N exists with an exceptional set E such that $\mathcal{D}\setminus \mathcal{S}= \{E\}$.

Now, we are ready to state our main result.

Theorem 18

Given $|N|\ge 3$ the inequality $0\le \langle \theta ,m\rangle$ for  $m\in {\mathbb R}^{\mathcal{P}(N)}$ with a coefficient vector $\theta \in {\mathbb R}^{\mathcal{P}(N)}$, where $\sum _{S\subseteq N} \theta (S)=0$ and $\sum _{L:\,\emptyset \ne L\subset N} \theta (L)=-1$, is facet-defining for $m\in {{\mathcal {E}}}(N)$ iff $\theta =\theta _{{{\mathcal {S}}}}$ for an indecomposable min-semi-balanced system ${{\mathcal {S}}}$ on N.

Proof

By Corollary 10, facet-defining inequalities $0\le \langle \theta ,m\rangle$ for $m\in {{{\mathcal {E}}}}(N)$ correspond to vertices $\theta$ of the polytope $\Delta$. Each $\theta \in \hbox \mathrm{ext}\,(\Delta )$ must be a vertex of ${\tilde{\Theta }}^{N}_{D}$ for some $\emptyset \ne D\subseteq N$ (see Sect. 2.2). By Lemma 8, every vertex $\theta \in \hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{D})$ has the form $\theta =\theta _{{{\mathcal {S}}}}$ for a min-semi-balanced system ${{\mathcal {S}}}$ on N. Corollary 16 excludes the case that ${{\mathcal {S}}}$ is min-balanced. In case of a purely min-semi-balanced system ${{\mathcal {S}}}$ one applies Lemma 17, the equivalence of negations $\lnot \mathbf{(a)}\Leftrightarrow \lnot \mathbf{(d)}$, which says that $\theta =\theta _{{{\mathcal {S}}}}\in \hbox \mathrm{ext}\,(\Delta )$ iff ${{\mathcal {S}}}$ is indecomposable. $\square$

Note in this context that, by Lemma 17(f), a purely min-semi-balanced system ${{\mathcal {S}}}$ on N is indecomposable iff there is no min-semi-balanced system ${{\mathcal {D}}}$ with $T\not \in {{\mathcal {D}}}$, ${{\mathcal {D}}}{\setminus }{{\mathcal {S}}}=\{E\}$, and E exceptional within ${{\mathcal {D}}}$. Thus, provided one has all purely min-semi-balanced systems on N at disposal, the indecomposable ones among them can be determined by this criterion.

8 Relation of exact and totally balanced games

In this section we deal with the relation of the cone $\mathcal{E}(N)$ of exact games and the cone $\mathcal{T}(N)$ of totally balanced games. In (Kroupa and Studený 2019, § 6) a conjecture has been raised about what are the facets of $\mathcal{E}(N)$, which is equivalent to the condition that

a game $m$ over N is exact iff both $m$ and its anti-dual $m^{\diamond }$ are totally balanced.

We give a counterexample to the conjecture in case $|N|=6$. On the other hand, we show that every originally conjectured inequality from (Kroupa and Studený 2019, § 6) is indeed facet-defining for ${{\mathcal {E}}}(N)$ whenever $|N|\ge 3$.

8.1 Counterexample to a former conjecture

Here we present a counterexample to the conjecture from (Kroupa and Studený 2019, § 6). Despite we found our counterexample for $|N|=6$ computationally, by the method described in later Remark 4, the reader need not repeat those computations to check its validity. The values for coalitions in our counterexample $m$ are given in Table 1.

Table 1 Our counterexample $m$ over $N=\{a,b,c,d,e,f\}$

To show that $m\in \mathcal{T}(N)$ for the game $m$ from Table 1 we provide its min-representation in Table 2 (see Sect. 2.3 for the reason). It is boring and tedious but the reader can verify manually in a straightforward way that it is indeed a min-representation of $m$. As a hint we indicate already in Table 1 at least one vector from Table 2 which is tight for the respective coalition. The first 17 vectors in Table 2 are (all) the vertices of the core of $m$. None of them is tight for sets $\{c,e\}$ and $\{b,c,e\}$. This implies that there is no element in the core of $m$ which is tight for one of these two sets. This is because tight vectors for any set $S\subseteq N$ form a face of the core and, if this face is non-empty then, by arguments from Sect. 2.2, a vertex of the core exists that is tight for S. Thus, $m\not \in {{\mathcal {E}}}(N)$ (see again Sect. 2.3).

Table 2 The min-representation of our counterexample $m$

The anti-dual $m^{\diamond }$ of our game $m$ is given in Table 3, its min-representation in Table 4. The core of the anti-dual also has 17 vertices, presented in the first 17 lines of the table. None of them is tight for sets $\{a,d,f\}$ and $\{a,b,d,f\}$; in particular, $m^{\diamond }\not \in {{\mathcal {E}}}(N)$, which fact also follows from a former observation that $m\not \in {{\mathcal {E}}}(N)$. A min-representation of $m^{\diamond }$ can be obtained by adding one additional vector. The reader can verify manually that Table 4 indeed provides a min-representation of $m^{\diamond }$; for each coalition, we indicate in Table 3 at least one vector from Table 4 which is tight for it.

Table 3 The anti-dual $m^{\diamond }$ of our counterexample $m$

Table 4 The min-representation of the anti-dual $m^{\diamond }$

Remark 4

This is to describe the way we found our counterexample. Our method was based on the characterization of ${{\mathcal {E}}}(N)$ from Sect. 4. We have succeeded to compute the extreme rays of all the cones $\Theta ^{N}_{D}$, $\emptyset \ne D\subseteq N$, in case $|N|=6$. Thus, we got a finite set of linear inequalities characterizing the cone ${{\mathcal {E}}}(N)$ in this case, although a pretty big one. Additionally, on basis of the results from (Studený et al. 2019), we were able to get a complete list ${{\mathcal {L}}}$ of coefficient vectors for the conjectured facet-defining inequalities. Checking the validity of the conjecture in case $|N|=6$ was, therefore, reduced to checking whether, for every $\emptyset \ne D\subseteq N$, every generator of an extreme ray of $\Theta ^{N}_{D}$ is in the conic hull of ${{\mathcal {L}}}$.

This appeared not to be the case: we found an extreme ray of $\Theta ^{N}_{D}$ for $|D|=2$ which is not in the conic hull of $\mathcal{L}$. Specifically, it was an element of ${\hat{\theta }}\in \Theta ^{N}_{D}$ for $N=\{a,b,c,d,e,f\}$ and $D=\{c,e\}$ defined as follows (we write ce instead of $\{c,e\}$ here):

$$\begin{aligned}&{{\hat{\theta }}(\emptyset )=+1, \quad {\hat{\theta }}(ce)=+4,\quad {\hat{\theta }}(abcdef)=+3,}\\&{\hat{\theta }}(be)=-1, \quad {\hat{\theta }}(ace)=-3, \quad {\hat{\theta }}(bcf)=-1, \quad {\hat{\theta }}(bcde)=-1, \quad {\hat{\theta }}(cdef)=-2\,, \end{aligned}$$

and ${\hat{\theta }}(S)=0$ for remaining $S\subseteq N$. On basis of that objective vector ${\hat{\theta }}$ we found a game $m$ that satisfies $\langle {\hat{\theta }},m\rangle < 0$ while $\langle \theta ^{\prime },m\rangle \ge 0$ for any $\theta ^{\prime }\in \mathcal{L}$, which is just the game $m$ presented in Table 1. Note, however, that the vector ${\hat{\theta }}$ has appeared not to yield a facet-defining inequality for $m\in \mathcal{E}(N)$: the set $E=bce$ yields the decomposition of the respective min-semi-balanced system.

Remark in this context that an alternative idea of computing the extreme rays of the cone $\{m\in \mathcal{G}(N)\,:\ \langle \theta ,m\rangle \ge 0~~\hbox {for }\theta \in {{\mathcal {L}}}\}$ has appeared to be computationally infeasible. This is because the number of the extreme rays of $\mathcal{E}(N)$ grows very rapidly with |N| and we were not able to compute them even in case $|N|=5$.

8.2 Facets shared with the cone of totally balanced games

This is to relate our new concept of an indecomposable min-semi-balanced system to earlier concepts and results from (Kroupa and Studený 2019), where facet-defining inequalities for the cone ${\mathcal {T}}(N)$ of totally balanced games were characterized. The following is a simplified equivalent definition of a central concept from (Kroupa and Studený 2019, § 4); the equivalence of the original definition and the later simplified version of it was shown in (Studený et al. 2019, § 2.3).

Definition 8

(Reducible and irreducible balanced set system)  A min-balanced set system ${{\mathcal {B}}}$ on a finite set M, $|M|\ge 2$, will be called reducible if there exists a set $\emptyset \ne E\subset M$ such that $\chi _{E}$ is a conic combination of $\{\, \chi _{S}\,:\ S\in {{\mathcal {B}}}\,~ \& ~\, S\subset E\,\}$.

A min-balanced set system ${{\mathcal {B}}}$ on M which is not reducible is called irreducible.

It was shown in (Kroupa and Studený 2019, Lemma 2.1) that a balanced system ${{\mathcal {B}}}$ on M is minimal iff vectors $\{\chi _{S}\,:\ S\in {{\mathcal {B}}}\}$ are linearly independent. In particular, for a min-balanced set system ${{\mathcal {B}}}$ on M, there is a unique linear combination $\sum _{S\in {{\mathcal {B}}}} \gamma _{S}\cdot \chi _{S}$ yielding $\chi _{M}$ and this unique combination has all coefficients strictly positive: $\gamma _{S}>0$ for $S\in {{\mathcal {B}}}$. Standard interpretation of a min-balanced system ${{\mathcal {B}}}$ is then in terms of the assigned linear inequality

$$\begin{aligned} m(M)\ge \sum _{S\in {{\mathcal {B}}}}\, \gamma _{S}\cdot m(S)\,, \end{aligned}$$

which can be interpreted as an inequality for any game $m$ on a superset N of M. Recall that the main result from (Kroupa and Studený 2019, Theorem 5.1) says that the facet-defining inequalities for the cone ${\mathcal {T}}(N)$ of totally balanced games on N, $|N|\ge 2$, are just the inequalities assigned to irreducible min-balanced systems on subsets $M\subseteq N$, $|M|\ge 2$.

Table 5 Numbers of facets of ${{\mathcal {E}}}(N)$ and of its permutational types for $n=|N|\le 6$

Recall from Lemma 12 that every min-balanced set system ${{\mathcal {B}}}$ on a proper subset $M\subset N$, $|M|\ge 2$, corresponds to a min-semi-balanced system ${{\mathcal {S}}}:={{\mathcal {B}}}\cup \{M\}$. The unique affine combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector $\underline{0}\in {\mathbb R}^{N}$ is semi-conic with $\uplambda _{M}<0$ and can be written as $\sum _{S\in {{\mathcal {B}}}} \uplambda _{S}\cdot \chi _{S}=(-\uplambda _{M})\cdot \chi _{M}$. Therefore, the induced inequality (2) for $m\in {\mathbb R}^{\mathcal{P}(N)}$, $m(\emptyset )=0$, is equivalent to (= is a positive multiple of) the standard inequality assigned to the min-balanced system ${{\mathcal {B}}}$.

The next result says that every irreducible min-balanced system on a proper subset M of N yields an indecomposable min-semi-balanced system on N. Thus, by Theorem 18, this implies that the respective inequality is facet-defining for the exact cone $\mathcal{E}(N)$.

Lemma 19

Given a min-semi-balanced set system of the form ${{\mathcal {S}}}:={{\mathcal {B}}}\cup \{M\}$ on N, $|N|\ge 3$, where ${{\mathcal {B}}}$ is a min-balanced set system on $M\subset N$, $|M|\ge 2$, the next two conditions are equivalent:

(i):

 ${{\mathcal {B}}}$ is irreducible,

(ii):

${{\mathcal {S}}}$ is indecomposable.

Proof

We prove the equivalence of negations of those conditions.

To show $\lnot \mathbf{(i)}\Rightarrow \lnot \mathbf{(ii)}$ assume that ${{\mathcal {B}}}$ is a reducible min-balanced system on $M\subset N$. Consider $\emptyset \ne E\subset M$ and a conic combination $\sum _{S\in {{\mathcal {B}}}:S\subset E} \uplambda _{S}\cdot \chi _{S}=\chi _{E}$ and re-write that as a semi-conic combination $\sum _{S\in {{\mathcal {B}}}:S\subset E} \uplambda _{S}\cdot \chi _{S}+(-1)\cdot \chi _{E}=\underline{0}$ in the space ${\mathbb R}^{N}$. Then put $\uplambda _{S}:=0$ for remaining $S\in {{\mathcal {S}}}={{\mathcal {B}}}\cup \{M\}$, and, because $\underline{0}$ is a constant vector in ${\mathbb R}^{N}$, conclude that E is exceptional within ${{\mathcal {S}}}\cup \{E\}$. This means that ${{\mathcal {S}}}$ has a decomposition.

To verify $\lnot \mathbf{(ii)}\Rightarrow \lnot \mathbf{(i)}$ assume that ${{\mathcal {S}}}={{\mathcal {B}}}\cup \{M\}$ has a decomposition, that is, a linear combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}+\uplambda _{E}\cdot \chi _{E}=r\cdot \chi _{N}$ yielding a constant vector in ${\mathbb R}^{N}$ exists with $\uplambda _{S}\ge 0$ for $S\in {{\mathcal {S}}}$ and with $\uplambda _{E}<0$ for some $\emptyset \ne E\subset N$, $E\not \in {{\mathcal {S}}}$. Since it is a semi-conic combination, by Lemma 1, one has $r\ge 0$. In case $E{\setminus } M\ne \emptyset$ one can choose $i\in E{\setminus } M$ and its substitution to the equality gives a contradictory conclusion $r=\uplambda _{E}<0$. This gives $E\subseteq M$. Thus, as $E\not \in {{\mathcal {S}}}={{\mathcal {B}}}\cup \{M\}$, $E\subset M\subset N$, the choice of $j\in N\setminus M$ and its substitution to the equality gives $r=0$, that is, $\sum _{S\in {{\mathcal {B}}}\,\cup \{M\}} \uplambda _{S}\cdot \chi _{S}+\uplambda _{E}\cdot \chi _{E}=\underline{0}$. Hence, the non-negativity of the coefficients except for $\uplambda _{E}$ implies that, for any $S\in {{\mathcal {S}}}$ such that $S{\setminus } E\ne \emptyset$ (including $S=M$) one necessarily has $\uplambda _{S}=0$. Thus, $\uplambda _{S}>0$ forces $S\subset E$ for $S\in {{\mathcal {S}}}$, and one can write the equality in the form $\sum _{S\in {{\mathcal {B}}}: S\subset E} \uplambda _{S}\cdot \chi _{S}=(-\uplambda _{E})\cdot \chi _{E}$, which easily implies that ${{\mathcal {B}}}$ is reducible. $\square$

By Lemma 19 and Theorem 18, every facet-defining inequality for the totally balanced cone $\mathcal{T}(N)$ corresponding to a strict subset $M\subset N$ is also facet-defining for the exact cone $\mathcal{E}(N)$. These are facet-defining inequalities for both cones. Note that, by Lemma 11, also conjugate inequalities to these inequalities are facet-defining for $\mathcal{E}(N)$, but not for $\mathcal{T}(N)$. These two classes of inequalities induced by irreducible min-balanced systems on $M\subset N$ were originally conjectured in (Kroupa and Studený 2019, § 6) to be all facet-defining inequalities for $\mathcal{E}(N)$.

9 Conclusions

The main achievement in this paper is the observation that a linear inequality for games over N, $|N|\ge 3$, is facet-defining for the exact cone ${{\mathcal {E}}}(N)$ iff it corresponds to (uniquely determined) indecomposable min-semi-balanced set system on N (Theorem 18). At first we got these inequalities in case $|N|=6$ by computation and later we confirmed the conjecture that the correspondence holds in general. Because of the computation, we know what are the numbers of facets of ${{\mathcal {E}}}(N)$ in cases $2\le |N|\le 6$; they are shown in Table 5.

Note that the case $|N|=2$ is special in some sense: then the cone of exact games coincides with the cone of balanced games and the only facet-defining inequality corresponds to the only min-balanced set system on N with $|N|=2$. As concerns the case $|N|=3$, the cone of exact games coincides with the cone of supermodular (= convex) games, while for $|N|\ge 4$ these two cones already differ.

Min-semi-balanced systems and their induced inequalities can synoptically be described by means of special pictures/diagrams (see Sect. 5.3). A catalogue of permutational types of indecomposable min-semi-balanced set systems over N, $3\le |N|\le 6$, obtained as a result of our computation, is available:

http://gogo.utia.cas.cz/indecomposable-min-semi-balanced-catalogue/

Thus, it implicitly provides an overview of all facet-defining inequalities in these cases. Hence we know that every facet-defining inequality for ${{\mathcal {E}}}(N)$ in case $|N|\le 5$ corresponds to a min-semi-balanced system ${{\mathcal {S}}}$ satisfying either $\bigcup {{\mathcal {S}}}\subset N$ or $\bigcap {{\mathcal {S}}}\ne \emptyset$; on the other hand, this is not the case in case $|N|=6$.

Recall that the min-semi-balanced systems break into four basic classes (Sect. 5.2) and the pictorial representatives reflect this classification. They also reflect the fact that (indecomposable) min-semi-balanced systems are closed under complementarity transform (Sect. 5.1). Further relevant observation is that (purely) min-semi-balanced systems on N can be obtained on basis of min-balanced systems on N (Sect. 6.1), which fact suggests that one can possibly get all such systems for $|N|\ge 7$.

The second main result in this paper is an example of a game $m$ over N, with $|N|=6$, such that both $m$ and its anti-dual $m$ are totally balanced while $m$ is not exact (Sect. 8.1).

Appendices

Proof of Lemma 1

For reader’s convenience we recall the result.

Lemma 1    Given $|N|\ge 2$ and $\emptyset \ne {{\mathcal {S}}}\subseteq {\mathcal{P}(N)}{\setminus } \{\emptyset ,N\}$, let $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}=\rho$ be a non-zero semi-conic combination yielding a constant vector $\rho =[r,\ldots ,r]\in {\mathbb R}^{N}$. Then one has $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\ge r\ge 0$; moreover, $r>0$ in case of a conic combination.

In any case $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}>0$ and by a positive factor multiplication one gets an affine semi-conic combination $\sum _{S\in {{\mathcal {S}}}} {\tilde{\uplambda }}_{S}\cdot \chi _{S}$ yielding a constant vector ${\tilde{\rho }}=[{\tilde{r}},\ldots ,{\tilde{r}}]\in {\mathbb R}^{N}$ with ${\tilde{r}}\in [0,1]$.

Finally, if the considered linear combination is not conic, then ${{\mathcal {S}}}$ has to contain at least three different sets and the existence of such a set system forces $|N|\ge 3$.

Proof

The case of a conic combination is easy: choose $L\in {{\mathcal {S}}}$ with $\uplambda _{L}>0$, $i\in L$, and write $0<\uplambda _{L}\le \sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}(i)=r=\sum _{S\in {{\mathcal {S}}}:\,i\in S} \uplambda _{S}\le \sum _{S\in {{\mathcal {S}}}} \uplambda _{S}$. Thus, in the rest of the proof we assume that the combination is not conic.

Let $T\in {{\mathcal {S}}}$ be the set with $\uplambda _{T}<0$; note that $\emptyset \subset T\subset N$. The choice of an element $j\in N\setminus T$ gives $r=\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}(j)= \sum _{S\in {{\mathcal {S}}}:\,j\in S} \uplambda _{S}\ge 0$ because $\uplambda _{S}\ge 0$ whenever $S\in {{\mathcal {S}}}{\setminus }\{T\}$. Choose some $i\in T$ and observe implications for subsets of N: $i\not \in S\in {{\mathcal {S}}}~\Rightarrow ~ S\in {{\mathcal {S}}}{\setminus }\{T\}~\Rightarrow ~ \uplambda _{S}\ge 0$. This gives $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\ge \sum _{S\in {{\mathcal {S}}}:\,i\in S} \uplambda _{S}=\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}(i)=r$. For the verification of the claim $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}>0$ assume without loss of generality that $\uplambda _{S}\ne 0$ for any $S\in {{\mathcal {S}}}$, for otherwise one can replace ${{\mathcal {S}}}$ by ${{\mathcal {S}}}^{\prime }:=\{S\in {{\mathcal {S}}}\,:\ \uplambda _{S}\ne 0\}$. We distinguish two cases:

• In case [ $\exists \, L\in {{\mathcal {S}}}{\setminus }\{T\}$ with $T{\setminus } L\ne \emptyset$ ] we choose $k\in T{\setminus } L$. Then $\uplambda _{S}\ge 0$ whenever $k\not \in S\in {{\mathcal {S}}}$ and we get $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\ge \uplambda _{L}+ \sum _{S\in {{\mathcal {S}}}:\,k\in S} \uplambda _{S} > \sum _{S\in {{\mathcal {S}}}:\,k\in S} \uplambda _{S}= r\ge 0$.

• In case [ $\forall \, L\in {{\mathcal {S}}}{\setminus }\{T\}$ one has $T\subseteq L$ ] we first observe $\bigcup {{\mathcal {S}}}{\setminus } T\ne \emptyset$. Indeed, by contradiction: if $\bigcup {{\mathcal {S}}}\subseteq T$ then $\forall \, L\in {{\mathcal {S}}}{\setminus } \{T\}$ one has $L\subseteq T\subseteq L$, which means ${{\mathcal {S}}}=\{T\}$ contradicting $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\ge 0$. Thus, one can choose $k\in \bigcup {{\mathcal {S}}}{\setminus } T$, fix $K\in {{\mathcal {S}}}$ with $k\in K$ and write $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\ge r=\sum _{S\in {{\mathcal {S}}}:\,k\in S} \uplambda _{S}\ge \uplambda _{K}>0$.

Thus, in both cases we have $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}> 0$.

In particular, given a non-zero semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ we put $\ell :=\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}>0$ and observe that $\sum _{S\in {{\mathcal {S}}}} (\ell ^{-1}\cdot \uplambda _{S})\cdot \chi _{S}$ is the required affine semi-conic combination. The inequality $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\ge r$ applied to an affine combination $\sum _{S\in {{\mathcal {S}}}} {\tilde{\uplambda }}_{S}\cdot \chi _{S}$ with $\sum _{S\in {{\mathcal {S}}}} {\tilde{\uplambda }}_{S}=1$ yields ${\tilde{r}}\in [0,1]$.

To verify the last claim take $T\in {{\mathcal {S}}}$ with $\uplambda _{T}<0$ and assume for a contradiction $|{{\mathcal {S}}}|\le 2$. If $|{{\mathcal {S}}}|=1$ take $j\in T$ and get a contradictory conclusion: $0\le r=\sum _{S\in {{\mathcal {S}}}:\,j\in S} \uplambda _{S}=\uplambda _{T}<0$. In case $|{{\mathcal {S}}}|=2$ one has ${{\mathcal {S}}}=\{T,L\}$ and contingent choice of $j\in T{\setminus } L$ leads to an analogous contradiction. Hence, one must have $T\subset L$ and the choice of $j\in T$ and $k\in L{\setminus } T$ leads to another contradiction: $r=\sum _{S\in {{\mathcal {S}}}:\,k\in S} \uplambda _{S}=\uplambda _{L}>\uplambda _{L}+\uplambda _{T}= \sum _{S\in {{\mathcal {S}}}:\,j\in S} \uplambda _{S}=r$. Thus, $|{{\mathcal {S}}}|\ge 3$; since $|N|=2 ~\Rightarrow ~ |{\mathcal{P}(N)}{\setminus } \{\emptyset ,N\}|=2$, the existence of ${{\mathcal {S}}}$ forces $|N|\ge 3$. $\square$

Proof of Lemma 2

For reader’s convenience we recall the result.

Lemma 2    Given $|N|\ge 2$, let $\emptyset \ne {{\mathcal {S}}}\subseteq {\mathcal{P}(N)}{\setminus } \{\emptyset ,N\}$ be a non-trivial set system on N. Then the following conditions on ${{\mathcal {S}}}$ are equivalent:

(a):

${{\mathcal {S}}}$ is a minimal set system such that there is a constant vector in ${\mathbb R}^{N}$ which can be written as a non-zero semi-conic combination of vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$,

(b):

${{\mathcal {S}}}$ is a minimal semi-balanced set system on N,

(c):

${{\mathcal {S}}}$ is semi-balanced on N, the vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ are affinely independent and in case $\bigcup {{\mathcal {S}}}=N$ even linearly independent,

(d):

there is only one affine combination of vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ yielding a constant vector in ${\mathbb R}^{N}$ and this unique combination is semi-conic and has all coefficients non-zero,

(e):

there is only one affine semi-conic combination of vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ which is a constant vector in ${\mathbb R}^{N}$ and this unique combination has all coefficients non-zero.

Proof

To show (a) $\Rightarrow$(b) assume a non-zero semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ which is a constant vector in ${\mathbb R}^{N}$ and put ${{\mathcal {S}}}^{\prime }:=\{ S\in {{\mathcal {S}}}\, :\ \uplambda _{S}\ne 0\}$. Because of minimality of ${{\mathcal {S}}}$ in (a) one has ${{\mathcal {S}}}^{\prime }={{\mathcal {S}}}$, which implies that ${{\mathcal {S}}}$ is semi-balanced. The rest is evident.

To show (b) $\Rightarrow$(a) it is enough to verify the minimality of ${{\mathcal {S}}}$ in (a). Assume for a contradiction that a set system ${{\mathcal {C}}}\subset {{\mathcal {S}}}$ exists with a non-zero semi-conic combination $\sum _{S\in {{\mathcal {C}}}} \mu _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ and put ${{\mathcal {C}}}^{\prime }:=\{ S\in {{\mathcal {C}}}\, :\ \mu _{S}\ne 0\}$. Then ${{\mathcal {C}}}^{\prime }$ is semi-balanced on N and ${{\mathcal {C}}}^{\prime }\subset {{\mathcal {S}}}$ contradicts the minimality of ${{\mathcal {S}}}$ in (b).

To show (b) $\Rightarrow$(c) let us fix a semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ with $\uplambda _{S}\ne 0$ for $S\in {{\mathcal {S}}}$. We first consider the case when it is not a conic combination, that is, there is a unique set $T\in {{\mathcal {S}}}$ with $\uplambda _{T}<0$; hence, $\uplambda _{S}>0$ for $S\in {{\mathcal {S}}}{\setminus }\{T\}$.

We then verify that $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ are affinely independent. Assume for a contradiction that a non-zero linear combination $\sum _{S\in {{\mathcal {S}}}} \mu _{S}\cdot \chi _{S}=\underline{0}$ with $\sum _{S\in {{\mathcal {S}}}} \mu _{S}=0$ exists. One can assume without loss of generality $\mu _{T}\le 0$ for otherwise one can multiply the linear combination by $(-1)$. Moreover, $\sum _{S\in {{\mathcal {S}}}} \mu _{S}=0$ implies the existence of $L\in {{\mathcal {S}}}$ with $\mu _{L}<0$. In fact, there are at least two such sets: otherwise $\sum _{S\in {{\mathcal {S}}}} \mu _{S}\cdot \chi _{S}=\underline{0}$ is a semi-conic combination and, by Lemma 1, one has $\sum _{S\in {{\mathcal {S}}}} \mu _{S}>0$ which contradicts the assumption. In particular, there is $L\in {{\mathcal {S}}}{\setminus }\{T\}$ with $\mu _{L}<0$. For any $\varepsilon \ge 0$ and $S\in {{\mathcal {S}}}$ we put $\uplambda ^{\varepsilon }_{S}:= \uplambda _{S}+\varepsilon \cdot \mu _{S}$ and observe that $\sum _{S\in {{\mathcal {S}}}} \uplambda ^{\varepsilon }_{S}\cdot \chi _{S}$ yields the same constant vector, $\uplambda ^{\varepsilon }_{T}<0$, while $\uplambda ^{\varepsilon }_{S}>0$ for $S\in {{\mathcal {S}}}{\setminus }\{T\}$ and sufficiently small $\varepsilon$. Since $\uplambda ^{\varepsilon }_{L}$ tends to $-\infty$ with increasing $\varepsilon$ there is a maximal $\varepsilon ^{*}>0$ such that $\uplambda ^{\varepsilon ^{*}}_{S}\ge 0$ for all $S\in {{\mathcal {S}}}{\setminus }\{T\}$. There must be $K\in {{\mathcal {S}}}{\setminus }\{T\}$ with $\uplambda ^{\varepsilon ^{*}}_{K}=0$; then the system ${{\mathcal {C}}}:=\{S\in {{\mathcal {S}}}\,: \ \uplambda ^{\varepsilon ^{*}}_{S}\ne 0\}\not \ni K$ is semi-balanced on N, which contradicts the minimality of ${{\mathcal {S}}}$.

The second step is to show that if $\bigcup \mathcal{S}=N$ then the vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ are linearly independent. Note that this case involves the case of a conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}=r\cdot \chi _{N}\in {\mathbb R}^{N}$ because then, by Lemma 1, $r>0$, which enforces if $\bigcup \mathcal{S}=N$ then the vectors. In the sequel, let T denote a contingent set $T\in {{\mathcal {S}}}$ with $\uplambda _{T}<0$, which, however, need not exist. Recall that $\uplambda _{S}>0$ for $S\in {{\mathcal {S}}}{\setminus }\{T\}$.

Assume for a contradiction that a non-zero linear combination $\sum _{S\in {{\mathcal {S}}}} \mu _{S}\cdot \chi _{S}=\underline{0}$ exists. We then show that there exists such a linear combination which, additionally, satisfies $\mu _{T}\le 0$ if T exists and $\mu _{L}<0$ for at least one $L\in {{\mathcal {S}}}{\setminus }\{T\}$. This is easy in case T does not exist or $\mu _{T}=0$ because possible multiplication of the linear combination by $(-1)$ reaches the goal. In case $\mu _{T}\ne 0$ possible multiplication ensures $\mu _{T}<0$. To show then the existence of $L\in {{\mathcal {S}}}{\setminus }\{T\}$ with $\mu _{L}<0$ assume for a contradiction the opposite, which means that $\sum _{S\in {{\mathcal {S}}}} \mu _{S}\cdot \chi _{S}=\underline{0}$ is a semi-conic combination and the system $\mathcal{C} \,:=\, \{S\in \mathcal{S}\ : \, \mu _{S}\ne 0 \}$ is semi-balanced. The minimality of ${{\mathcal {S}}}$ then implies that $\mathcal{C}=\mathcal{S}$’ and, thus, $\mu _{S}>0$ for $S\in {{\mathcal {S}}}{\setminus }\{T\}$. Since $T\subset N$ there exists $i\in N{\setminus } T$ and $\bigcup {{\mathcal {S}}}=N$ implies the existence of $K\in {{\mathcal {S}}}$ with $i\in K$. Since [ $i\in S\in {{\mathcal {S}}}~\Rightarrow ~ \mu _{S}>0$ ], this leads to a contradictory conclusion $0=\sum _{S\in {{\mathcal {S}}}} \mu _{S}\cdot \chi _{S}(i)= \sum _{S\in {{\mathcal {S}}}: i\in S} \mu _{S}\ge \mu _{K}>0$.

Finally, having a linear combination $\sum _{S\in {{\mathcal {S}}}} \mu _{S}\cdot \chi _{S}=\underline{0}$ with $\mu _{T}\le 0$ and $\mu _{L}<0$ for some $L\in {{\mathcal {S}}}{\setminus }\{T\}$, one can repeat the construction used in the previous case (of affine independence) to get a contradiction with the minimality of ${{\mathcal {S}}}$.

To show (c) $\Rightarrow$(d) use Lemma 1 to obtain an affine semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ with all coefficients non-zero yielding a constant vector $\rho =[r,\ldots ,r]$ in ${\mathbb R}^{N}$ with $r\in [0,1]$. Let us fix this affine combination. Assume that $\sum _{S\in {{\mathcal {S}}}} \sigma _{S}\cdot \chi _{S}$ is an affine combination yielding a constant vector $\varsigma =[s,\ldots ,s]\in {\mathbb R}^{N}$. It is enough to show that these two combinations coincide. To this end we distinguish two cases.

In case $\bigcup {{\mathcal {S}}}\!\subset \! N$ we have $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}(i)\!=\!0\!=\!\sum _{S\in {{\mathcal {S}}}} \sigma _{S}\cdot \chi _{S}(i)$ for any $i\in N\setminus \bigcup \mathcal{S}$. This implies that both $\rho = \underline{0}$ and $\varrho = \underline{0}$. By subtracting we obtain the relation $\sum _{S\in {{\mathcal {S}}}} (\uplambda _{S}-\sigma _{S})\cdot \chi _{S}=\underline{0}$ with $\sum _{S\in {{\mathcal {S}}}} (\uplambda _{S}-\sigma _{S}) =0$ and by affine independence $\sigma _{S}=\uplambda _{S}$ for all $S\in {{\mathcal {S}}}$.

In case $\bigcup {{\mathcal {S}}}=N$ the linear independence of vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ implies both $r\ne 0$ and $s\ne 0$ because solely their zero linear combination yields the vector $=\underline{0}$. Hence, we have $\sum _{S\in {{\mathcal {S}}}} (r^{-1}\cdot \uplambda _{S})\cdot \chi _{S}=\chi _{N}$ and $\sum _{S\in {{\mathcal {S}}}} (s^{-1}\cdot \sigma _{S})\cdot \chi _{S}=\chi _{N}$. By subtracting we get $\sum _{S\in {{\mathcal {S}}}} (r^{-1}\cdot \uplambda _{S}-s^{-1}\cdot \sigma _{S})\cdot \chi _{S}=\underline{0}$ and by linear independence $r^{-1}\cdot \uplambda _{S}=s^{-1}\cdot \sigma _{S}$ for all $S\in {{\mathcal {S}}}$. Thus, $\uplambda _{S}=r\cdot s^{-1}\cdot \sigma _{S}$ for $S\in {{\mathcal {S}}}$ and, because both combinations are affine, by summing over $S\in {{\mathcal {S}}}$ one derives $1=r\cdot s^{-1}$. Hence, $s=r$ and $\sigma _{S}=\uplambda _{S}$ for all $S\in {{\mathcal {S}}}$.

The implication (d) $\Rightarrow$(e) is evident.

To show (e) $\Rightarrow$(b) consider the affine semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ with all coefficients non-zero yielding a constant vector in ${\mathbb R}^{N}$. Its existence implies that ${{\mathcal {S}}}$ is semi-balanced. To verify the minimality of ${{\mathcal {S}}}$ assume for a contradiction that ${{\mathcal {C}}}\subset {{\mathcal {S}}}$ exists which is semi-balanced on N. By Lemma 1 applied to ${{\mathcal {C}}}$ there exists an affine semi-conic combination $\sum _{S\in {{\mathcal {C}}}} \sigma _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$. We extend it by putting $\sigma _{S}=0$ for $S\in {{\mathcal {S}}}{\setminus }{{\mathcal {C}}}$. Thus, we get two different affine semi-conic combinations of $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ yielding a constant vector in ${\mathbb R}^{N}$, which contradicts the assumption. $\square$

Proof of Lemma 7

For reader’s convenience we recall what is claimed; see Definition 5 for notation.

Lemma 7    Given $|N|\ge 2$, every set ${\tilde{\Theta }}^{N}_{D}$, where $\emptyset \ne D\subseteq N$, is a bounded polyhedron. Every vector $\theta \in \Theta ^{N}_{D}$ satisfies both $\theta (N)\ge 0$ and $\theta (\emptyset )\ge 0$ and every non-zero vector $\theta \in \Theta ^{N}_{D}$ satisfies $\theta (N)+\theta (\emptyset )>0$. Given $m\in {\mathbb R}^{\mathcal{P}(N)}$ with $m(\emptyset )=0$, one has

$$\begin{aligned} \qquad \qquad \quad m\in \mathcal{E}(N) ~~\Leftrightarrow ~~ \left[ \,\forall \, \theta \in \bigcup _{\emptyset \ne D\subseteq N}{\tilde{\Theta }}^{N}_{D}\qquad \langle \theta ,m\rangle \ge 0\right] \,. \qquad \qquad \qquad \qquad \quad (3) \end{aligned}$$

Proof

Note that $\Theta ^{N}_{N}\subseteq \Theta ^{N}_{D}$ if $D\subset N$; therefore, one can assume without loss of generality $\emptyset \ne D\subset N$. To show $\theta (N)\ge 0$ for $\theta \in \Theta ^{N}_{D}$ choose $i\in N{\setminus } D$ and write $\theta (N)=-\sum _{L\subset N:i\in L} \theta (L)\ge 0$. Note that, for any $j\in N$,

$$\begin{aligned} \sum _{S\subseteq N{\setminus }\{j\}} \theta (S)= \sum _{S\subseteq N} \theta (S)-\sum _{L\subseteq N:j\in L} \theta (L) = 0-0 =0. \end{aligned}$$

Hence, to show $\theta (\emptyset )\ge 0$ for $\theta \in \Theta ^{N}_{D}$ take $j\in D$ and write $\theta (\emptyset )=-\sum _{\emptyset \ne S\subseteq N{\setminus }\{j\}} \theta (S)\ge 0$.

Thus, we have observed that every $\theta \in \Theta ^{N}_{D}$ satisfies both $\theta (N)\ge 0$ and $\theta (\emptyset )\ge 0$. In particular, if $\theta \in {\tilde{\Theta }}^{N}_{D}$ then $\theta (N)+\theta (\emptyset )=1$ gives both $0\le \theta (\emptyset )\le 1$ and $0\le \theta (N)\le 1$.

Let us show that, for $\theta \in {\tilde{\Theta }}^{N}_{D}$, if $S\subset N$ and $S{\setminus } D\ne \emptyset$ then $0\ge \theta (S)\ge -1$. Indeed, because of $S\not \in \{\emptyset ,D,N\}$, the choice of $i\in S{\setminus } D$ gives

$$\begin{aligned} 0\ge \theta (S)\ge \sum _{L\subset N:i\in L} \theta (L)=-\theta (N)+ \underbrace{\sum _{L\subseteq N:i\in L} \theta (L)}_{=0} =-\theta (N)\ge -1\,. \end{aligned}$$

To observe that $0\ge \theta (S)\ge -1$ for $\theta \in {\tilde{\Theta }}^{N}_{D}$ whenever $\emptyset \ne S\subset N$ and $D{\setminus } S\ne \emptyset$ introduce a vector $\theta ^{\star }\in {\mathbb R}^{\mathcal{P}(N)}$ by $\theta ^{\star }(L):=\theta (N{\setminus } L)$ for $L\subseteq N$. It is easy to observe that $\theta ^{\star }\in {\tilde{\Theta }}^{N}_{N{\setminus } D}$: to this end write for any $i\in N$

$$\begin{aligned} \sum _{L\subseteq N:i\in L} \theta ^{\star }(L)=\sum _{L\subseteq N:i\in L} \theta (N{\setminus } L)=\sum _{S\subseteq N:i\not \in S} \theta (S) =\sum _{S\subseteq N} \theta (S)-\sum _{S\subseteq N:i\in S} \theta (S)=0-0=0. \end{aligned}$$

Thus, because of $\emptyset \ne D{\setminus } S= (N{\setminus } S){\setminus }(N{\setminus } D)$, one has $0\ge \theta ^{\star }(N{\setminus } S)\ge -1$ by the previous observation applied to $\theta ^{\star }$, which, however, means $0\ge \theta (S)\ge -1$.

Altogether, we have $0\ge \theta (S)\ge -1$ for $\theta \in {\tilde{\Theta }}^{N}_{D}$ and $S\in \mathcal{P}(N){\setminus } \{\emptyset ,D,N\}$, which implies $0\ge \sum _{S: S\not \in \{\emptyset ,D,N\}} \theta (S)\ge 3-2^{|N|}$. Taking into consideration that

$$\begin{aligned} \sum _{S: S\not \in \{\emptyset ,D,N\}} \theta (S)= -\theta (\emptyset )-\theta (D)-\theta (N)+\underbrace{\sum _{L\subseteq N} \theta (L)}_{=0}= -\theta (N)-\theta (\emptyset )-\theta (D)=-1-\theta (D) \end{aligned}$$

one gets $2^{|N|}-4\ge \theta (D)\ge -1$. In particular, ${\tilde{\Theta }}^{N}_{D}$ is bounded and so is ${\tilde{\Theta }}^{N}_{N}$.

The fact that, for any $\emptyset \ne D\subseteq N$, every non-zero vector $\theta \in \Theta ^{N}_{D}$ satisfies $\theta (N)+\theta (\emptyset )>0$ follows directly from (Kroupa and Studený 2019, Lemma 5.1). In particular, every non-zero $\theta \in \Theta ^{N}_{D}$ is a positive multiple of a vector ${\tilde{\theta }}\in {\tilde{\Theta }}^{N}_{D}$. Further important fact, which follows from (Kroupa and Studený 2019, Lemma 5.3), is that a game $m$ is exact, that is, $m\in \mathcal{E}(N)$, iff $[\,\forall \,\emptyset \ne D\subseteq N ~~\forall \, \theta \in \Theta ^{N}_{D}\quad \langle \theta ,m\rangle \ge 0\,]$. The combination of these two observations gives (3). $\square$

Proof of Lemma 8

For reader’s convenience we recall what is claimed; see Definition 5 for notation.

Lemma 8    Given $|N|\ge 2$ and $\emptyset \ne D\subseteq N$, every vertex of ${\tilde{\Theta }}^{N}_{D}$ has either the form $\theta _{{{\mathcal {B}}}}$, where ${{\mathcal {B}}}$ is a min-balanced set system on N, or the form $\theta _{{{\mathcal {S}}}}$, where ${{\mathcal {S}}}$ is a min-semi-balanced system on N having D as the exceptional set.

Conversely, in case $\emptyset \ne D\subset N$, every vector $\theta _{{{\mathcal {S}}}}$, where ${{\mathcal {S}}}$ is a min-semi-balanced system on N having D as the exceptional set, is a vertex of ${\tilde{\Theta }}^{N}_{D}$: $\theta _{{{\mathcal {S}}}}\in \hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{D})$.

Proof

Given a vertex $\theta \in \hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{D})$, we first observe that there exists a min-semi-balanced system ${{\mathcal {S}}}$ on N such that $\theta =\theta _{{{\mathcal {S}}}}$. To this end we put

$$ \begin{aligned} {{\mathcal {S}}}~:=~ \{S\subseteq N\,:\ \emptyset \ne S\subset N ~~ \& ~~ \theta (S)\ne 0\,\}\qquad \hbox {and}~~ \uplambda _{S} ~:=~ -\theta (S)\quad \hbox {for} \ S\in {{\mathcal {S}}}. \end{aligned}$$

Thus, $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yields a constant vector $\theta (N)\cdot \chi _{N}$ and ${{\mathcal {S}}}$ is semi-balanced on N. To evidence that ${{\mathcal {S}}}$ is min-semi-balanced we use the condition (c) in Lemma 2. To verify affine independence of the vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ assume for a contradiction that there is a non-zero linear combination $\sum _{S\in {{\mathcal {S}}}} \sigma _{S}\cdot \chi _{S} =\underline{0}$ with $\sum _{S\in {{\mathcal {S}}}} \sigma _{S}=0$. Then we put $\sigma _{L}:=0$ for remaining $L\subseteq N$ and $\theta ^{\varepsilon }(S):=\theta (S)+\varepsilon \cdot \sigma _{S}$ for any $S\subseteq N$ and $\varepsilon \in {\mathbb R}$. Then one has $\theta ^{\varepsilon }\in {\tilde{\Theta }}^{N}_{D}$ whenever $|\varepsilon |$ is small; thus, the relation $\theta =\frac{1}{2}\cdot \theta ^{\varepsilon }+\frac{1}{2}\cdot \theta ^{-\varepsilon }$ then contradicts the assumption of extremity of $\theta$ in ${\tilde{\Theta }}^{N}_{D}$, because of $\sigma _{L}\ne 0$ for some $L\in {{\mathcal {S}}}$.

To verify linear independence of the vectors $\{ \chi _{S}\,:\ S\in {{\mathcal {S}}}\}$ in case $\bigcup {{\mathcal {S}}}=N$ we first realize that one has $\theta (N)>0$ then. Indeed, if $D=N$ then $\theta (S)<0$ for any $S\in {{\mathcal {S}}}$ and if $D\ne N$ then we choose $i\in N{\setminus } D$ and have $\theta (S)<0$ for any $S\in {{\mathcal {S}}}$ with $i\in S$; this allows us to use $\sum _{L\subseteq N:\, i\in L} \theta (L)=0$ for $i\in N$ to derive $\theta (N)>0$.

Assume for a contradiction that a non-zero linear combination $\sum _{S\in \mathcal{S}} \sigma _{S}\cdot \chi _{S}=\underline{0}$ exists and put $\varsigma :=\sum _{S\in {{\mathcal {S}}}} \sigma _{S}$. The case $\varsigma =0$ leads to a contradiction as shown in the case of affine independence. Thus, consider $\varsigma \ne 0$, put $\sigma _{\emptyset }:=-\varsigma$, $\sigma _{L}:=0$ for remaining $L\subseteq N$, and $\theta ^{\varepsilon }(S):=(1-\varepsilon \cdot \varsigma )^{-1}\cdot (\theta (S)+\varepsilon \cdot \sigma _{S})$ for any $S\subseteq N$ and $\varepsilon \in {\mathbb R}$, $\varepsilon \ne \varsigma ^{-1}$. One has $\theta ^{\varepsilon }\in {\tilde{\Theta }}^{N}_{D}$ for small $|\varepsilon |$. Moreover, $\theta =\frac{1-\varepsilon \cdot \varsigma }{2}\cdot \theta ^{\varepsilon }+ \frac{1+\varepsilon \cdot \varsigma }{2}\cdot \theta ^{-\varepsilon }$. Because of $\varsigma \ne 0$ we have $\theta ^{\varepsilon }(N)=(1-\varepsilon \cdot \varsigma )^{-1}\cdot \theta (N)\ne \theta (N)$ if $\varepsilon \ne 0$. Hence, we get a contradiction with the assumption of extremity of $\theta$ in ${\tilde{\Theta }}^{N}_{D}$.

We have thus shown that the set system ${{\mathcal {S}}}$ is min-semi-balanced on N and one clearly has $\theta =\theta _{{{\mathcal {S}}}}$. If ${{\mathcal {S}}}={{\mathcal {B}}}$ is min-balanced then the first option $\theta =\theta _{{{\mathcal {B}}}}$ occurs. If ${{\mathcal {S}}}$ has an exceptional set $T\in {{\mathcal {S}}}$ then $\theta (T)=\theta _{{{\mathcal {S}}}}(T)>0$ which forces $T=D$. Thus, D is the exceptional set in ${{\mathcal {S}}}$ in this case.

To verify the second claim assume that ${{\mathcal {S}}}$ is a min-semi-balanced set system on N and that D is the exceptional set within ${{\mathcal {S}}}$. It is straightforward to evidence that $\theta _{{{\mathcal {S}}}}\in {\tilde{\Theta }}^{N}_{D}$. To show that $\theta _{{{\mathcal {S}}}}\in \hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{D})$ assume for a contradiction that there is a non-trivial convex combination $\theta _{{{\mathcal {S}}}}=\alpha \cdot \theta ^{0}+ (1-\alpha )\cdot \theta ^{1}$ with $\theta ^{0},\theta ^{1}\in {\tilde{\Theta }}^{N}_{D}$, $\alpha \in (0,1)$, and $\theta ^{0}\ne \theta ^{1}$. We know that $\theta _{{{\mathcal {S}}}}(S)=0$ any $S\subseteq N$, $S\not \in \{\emptyset ,N\}\cup {{\mathcal {S}}}$ and observe that $\theta ^{0}(S)=0=\theta ^{1}(S)$ for any such $S\subseteq N$ as well. Indeed, the inclusion ${\tilde{\Theta }}^{N}_{D}\subseteq \Theta ^{N}_{D}$ implies $\theta ^{i}(L)\le 0$ for $L\subseteq N$, $L\not \in \{\emptyset ,D,N\}$, which forces $\theta ^{i}(S)=0$ for $S\subseteq N$, $S\not \in \{\emptyset ,N\}\cup {{\mathcal {S}}}$ .

For every $\varepsilon \ge 0$ we put $\theta ^{\varepsilon } := \theta ^{0} +\varepsilon \cdot (\theta ^{1}-\theta ^{0})$. Note that $\theta ^{\varepsilon }(S)=0$ for any $S\subseteq N$, $S\not \in \{\emptyset ,N\}\cup {{\mathcal {S}}}$. The fact that ${\tilde{\Theta }}^{N}_{D}$ is bounded (see Lemma 7) implies the existence of $\varepsilon ^{\diamond }:=\max \, \{\varepsilon \ge 1\,:\ \theta ^{\varepsilon }\in {\tilde{\Theta }}^{N}_{D}\,\}$. There exists $L\in {{\mathcal {S}}}$ with $\theta ^{\varepsilon ^{\diamond }}(L)=0$ because otherwise one gets a contradiction with maximality of $\varepsilon ^{\diamond }$. We put

$$\begin{aligned} {{\mathcal {C}}}:=\{ S\in {{\mathcal {S}}}\,:\ \theta ^{\varepsilon ^{\diamond }}(S)\ne 0\,\} \end{aligned}$$

and observe, using the fact $\theta ^{\varepsilon ^{\diamond }}\in {\tilde{\Theta }}^{N}_{D}$, that ${{\mathcal {C}}}$ is a semi-balanced system on N. Then the fact $L\in \mathcal{S}\setminus \mathcal{C}$ contradicts the minimality of ${{\mathcal {S}}}$. Thus, there is no non-trivial convex combination of $\theta ^{0},\theta ^{1}\in {\tilde{\Theta }}^{N}_{D}$ yielding $\theta _{{{\mathcal {S}}}}$, which means that $\theta _{{{\mathcal {S}}}}$ is a vertex of ${\tilde{\Theta }}^{N}_{D}$. $\square$

Proof of Lemma 12

For reader’s convenience we recall what is claimed.

Lemma 12    Given $|N|\ge 2$ and a min-semi-balanced system ${{\mathcal {S}}}$ on N, let $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ be the unique affine (and semi-conic) combination yielding a constant vector $r\cdot \chi _{N}$, $r\in [0,1]$.

One has then $r=0$ iff there exists a min-balanced system ${{\mathcal {B}}}$ on $M\subset N$, $|M|\ge 2$, such that ${{\mathcal {S}}}={{\mathcal {B}}}\cup \{M\}$; another equivalent condition is $\bigcup {{\mathcal {S}}}\subset N$. Moreover, a min-balanced system ${{\mathcal {B}}}$ on $M\subset N$, $|M|\ge 2$, yields a min-semi-balanced one, namely the system $\mathcal{S}:={{\mathcal {B}}}\cup \{M\}$ on N with $r=0$.

One has $r=1$ iff ${{\mathcal {S}}}$ is a complementary system to a system ${{\mathcal {S}}}^{\star }$ with $\bigcup {{\mathcal {S}}}^{\star }\subset N$; another equivalent condition is $\bigcap {{\mathcal {S}}}\ne \emptyset$.

On the other hand, every min-balanced system ${{\mathcal {S}}}$ on N satisfies $0<r<1$.

Proof

Recall that all coefficients $\uplambda _{S}$, $S\in {{\mathcal {S}}}$, are non-zero. If $r=0$ then there is $T\in {{\mathcal {S}}}$ with $\uplambda _{T}<0$, for otherwise $\uplambda _{S}>0$ for $S\in {{\mathcal {S}}}$ and ${{\mathcal {S}}}\ne \emptyset$ contradict $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S} =\underline{0}$. Given $i\in N{\setminus } T$ one has $\uplambda _{S}>0$ whenever $i\in S\in {{\mathcal {S}}}$ and $0=\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}(i)=\sum _{S\in {{\mathcal {S}}}: i\in S} \uplambda _{S}$ implies that there is no $S\in {{\mathcal {S}}}$ with $i\in S$. Hence, $\bigcup {{\mathcal {S}}}=T$ and $\sum _{S\in {{\mathcal {S}}}{\setminus }\{T\}} \uplambda _{S}\cdot \chi _{S}=(-\uplambda _{T})\cdot \chi _{T}$. This implies ${{\mathcal {S}}}{\setminus }\{T\}\ne 0$ and, thus, forces $|T|\ge 2$ (because $\bigcup {{\mathcal {S}}}=T$). The latter equality also means that ${{\mathcal {S}}}{\setminus }\{T\}$ is balanced on T and one can put $M:=T$ and ${{\mathcal {B}}}:={{\mathcal {S}}}{\setminus }\{T\}$. To show that ${{\mathcal {B}}}$ is minimal assume for a contradiction that ${{\mathcal {D}}}\subset {{\mathcal {B}}}$ exists which is balanced on T, that is, there are $\sigma _{S}>0$, $S\in {{\mathcal {D}}}$, with $\sum _{S\in {{\mathcal {D}}}} \sigma _{S}\cdot \chi _{S}=\chi _{T}$. Hence, $\sum _{S\in {{\mathcal {D}}}} \sigma _{S}\cdot \chi _{S}+ (-1)\cdot \chi _{T} =\underline{0}$ and, by Lemma 1, one has $-1+\sum _{S\in {{\mathcal {D}}}} \sigma _{S}>0$ and one can multiply it to get an affine combination (in ${\mathbb R}^{N}$) different from $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S} =\underline{0}$, which contradicts the minimality of ${{\mathcal {S}}}$ (use Lemma 2(d)). Thus, ${{\mathcal {B}}}$ has to be min-balanced on T.

The existence of such ${{\mathcal {B}}}$ then implies $\bigcup {{\mathcal {S}}}\subset N$. To complete the chain of implications realize that, if $\bigcup {{\mathcal {S}}}\subset N$ for a min-semi-balanced set system ${{\mathcal {S}}}$ on N then the choice of $i\in N{\setminus }\bigcup {{\mathcal {S}}}$ gives $r=\sum _{S\in {{\mathcal {S}}}:i\in S} \uplambda _{S}=0$.

To verify the additional claim assume that ${{\mathcal {B}}}$ is a min-balanced system on $M\subset N$, $|M|\ge 2$. By (Kroupa and Studený 2019, Lemma 2.1) $\{\chi _{S}\,:\ S\in \mathcal B\}$ is linearly independent (even in ${\mathbb R}^{N}$). Fix a combination $\sum _{S\in {{\mathcal {B}}}} \uplambda _{S}\cdot \chi _{S}=\chi _{M}$ with all coefficients strictly positive. Then $\sum _{S\in {{\mathcal {B}}}} \uplambda _{S}\cdot \chi _{S}+ (-1)\cdot \chi _{M} =\underline{0}$ is a semi-conic combination yielding a constant vector in ${\mathbb R}^{N}$ and ${{\mathcal {S}}}:={{\mathcal {B}}}\cup \{M\}$ is semi-balanced. We use the condition (d) in Lemma 2 to show that ${{\mathcal {S}}}$ is minimal. By Lemma 1 one has $k:=\sum _{S\in {{\mathcal {B}}}} \uplambda _{S}-1>0$ and $\sum _{S\in {{\mathcal {B}}}} k^{-1}\uplambda _{S}\cdot \chi _{S}+ (-k^{-1})\cdot \chi _{M} =\underline{0}$ is an affine semi-conic combination with all coefficients non-zero. We need to show that any affine combination $\sum _{S\in {{\mathcal {B}}}} \sigma _{S}\cdot \chi _{S}+ \sigma _{M}\cdot \chi _{M}=\rho$ yielding a constant vector in ${\mathbb R}^{N}$ coincides with the above mentioned affine combination. The substitution of some $i\in N{\setminus } M$ allows one to observe that $\rho = \underline{0}$.. One cannot have $\sigma _{M}=0$ because then $\sum _{S\in {{\mathcal {B}}}} \sigma _{S}\cdot \chi _{S} =\underline{0}$ contradicts linear independence of $\{\chi _{S}\,:\ S\in \mathcal B\}$. If $\sigma _{M}\ne 0$ then $\sum _{S\in {{\mathcal {B}}}} -\sigma _{M}^{-1}\sigma _{S}\cdot \chi _{S}=\chi _{M}$ and linear independence of $\{\chi _{S}\,:\ S\in \mathcal B\}$ gives $\uplambda _{S}=-\sigma _{M}^{-1}\sigma _{S}$ for all $S\in {{\mathcal {B}}}$. We substitute $\sigma _{S}=-\sigma _{M}\uplambda _{S}$ for $S\in {{\mathcal {B}}}$ to $\sum _{S\in {{\mathcal {B}}}} \sigma _{S}+ \sigma _{M}=1$ to get $\sigma _{M}=-k^{-1}$; hence, the considered affine combinations coincide.

As concerns the case $r=1$, by Lemma 11, ${{\mathcal {S}}}^{\star }$ is also min-semi-balanced and the respective unique affine combination for ${{\mathcal {S}}}^{\star }$ is $\sum _{L\in {{\mathcal {S}}}^{\star }} \uplambda _{N{\setminus } L}\cdot \chi _{L}=(1-r)\cdot \chi _{N}$. Thus, $r=1$ iff the previous case $r^{\star }=0$ occurs for ${{\mathcal {S}}}^{\star }$. The formula $\bigcap {{\mathcal {S}}}= N{\setminus } \bigcup {{\mathcal {S}}}^{\star }$ then gives the other equivalent condition.

The definition of a min-balanced system ${{\mathcal {B}}}$ on N implies $\bigcup {{\mathcal {B}}}=N$. By Lemma 11, the same is true for its complementary system: $\bigcup {{\mathcal {B}}}^{\star }=N$, which means $\bigcap {{\mathcal {B}}}=\emptyset$. Thus, one has both $\bigcup {{\mathcal {B}}}=N$ and $\bigcap {{\mathcal {B}}}=\emptyset$, and by previous claims, $r\ne 0$ and $r\ne 1$.

$\square$

Proof of Lemma 13

For reader’s convenience we recall what is claimed.

Lemma 13    Assume $|N|\ge 3$. If ${{\mathcal {B}}}$ is a min-balanced set system on N such that $|{{\mathcal {B}}}|\ge 3$ and $Z\in {{\mathcal {B}}}$ then $Y:=N{\setminus } Z$ is not in ${{\mathcal {B}}}$, the set system ${{\mathcal {S}}}:=({{\mathcal {B}}}{\setminus }\{Z\})\cup \{Y\}$ is purely min-semi-balanced on N and Y is the exceptional set within ${{\mathcal {S}}}$.

Conversely, if ${{\mathcal {S}}}$ is a (purely) min-semi-balanced system on N and $Y\in {{\mathcal {S}}}$ the exceptional set within ${{\mathcal {S}}}$ then $Z:=N{\setminus } Y$ is not in ${{\mathcal {S}}}$ and ${{\mathcal {B}}}:=({{\mathcal {S}}}{\setminus }\{Y\})\cup \{Z\}$ is a min-balanced system on N such that $|{{\mathcal {B}}}|\ge 3$.

Proof

I. :

Let ${{\mathcal {B}}}$ be a balanced system on N and $Z\in {{\mathcal {B}}}$ such that $Y:=N{\setminus } Z\not \in {{\mathcal {B}}}$. Then ${{\mathcal {S}}}:=({{\mathcal {B}}}{\setminus }\{Z\})\cup \{Y\}$ is semi-balanced on N. Indeed, there exists a conic combination $\sum _{S\in {{\mathcal {B}}}} \uplambda _{S}\cdot \chi _{S}=\chi _{N}$, $\uplambda _{S}>0$ for $S\in {{\mathcal {B}}}$. We add $-\uplambda _{Z}\cdot \chi _{N}$ to that and obtain a semi-conic combination $\sum _{S\in {{\mathcal {B}}}{\setminus }\{Z\}} \uplambda _{S}\cdot \chi _{S} + (-\uplambda _{Z})\cdot \chi _{Y}=(1-\uplambda _{Z})\cdot \chi _{N}$ yielding a constant vector.

II. :

Analogously, given a semi-balanced system ${{\mathcal {S}}}$ over N with an exceptional set $Y\in {{\mathcal {S}}}$ and $Z:=N{\setminus } Y\not \in \mathcal{S}$, the set system ${{\mathcal {B}}}:=({{\mathcal {S}}}{\setminus }\{Y\})\cup \{Z\}$ is balanced on N. Indeed, given a semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}=r\cdot \chi _{N}$ with $r\in {\mathbb R}$, where $\uplambda _{Y}<0$ and $\uplambda _{S}>0$ for $S\in {{\mathcal {S}}}{\setminus }\{Y\}$ we add $-\uplambda _{Y}\cdot \chi _{N}$ to that and get $\sum _{S\in {{\mathcal {S}}}{\setminus }\{Y\}} \uplambda _{S}\cdot \chi _{S} + (-\uplambda _{Y})\cdot \chi _{Z}=(r-\uplambda _{Y})\cdot \chi _{N}$, which is a conic combination yielding a constant vector. Then use Lemma 1.

III. :

Let ${{\mathcal {B}}}$ be a min-balanced system on N with $|{{\mathcal {B}}}|\ge 3$ and $Z\in {{\mathcal {B}}}$. Then one has $Y:= N{\setminus } Z \not \in {{\mathcal {B}}}$ as otherwise ${{\mathcal {D}}}:=\{Y,Z\}\subset {{\mathcal {B}}}$ is a balanced system contradicting the minimality of ${{\mathcal {B}}}$. Step I. implies that ${{\mathcal {S}}}:=({{\mathcal {B}}}{\setminus }\{Z\})\cup \{Y\}$ is semi-balanced on N, specifically, that there exists a semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ with $\uplambda _{Y}<0$. To show that ${{\mathcal {S}}}$ is minimal assume for a contradiction that a min-semi-balanced system ${{\mathcal {S}}}^{\prime }\subset {{\mathcal {S}}}$ exists. Then necessarily $Y\in {{\mathcal {S}}}^{\prime }$ as otherwise $\mathcal{S}^{\prime } \subset \mathcal{B}$ contradicts the minimality of ${{\mathcal {B}}}$ (use Corollary 3). Let $\sum _{S\in {{\mathcal {S}}}^{\prime }} \sigma _{S}\cdot \chi _{S}$ be the (unique) affine semi-conic combination yielding a constant vector in ${\mathbb R}^{N}$. Observe that $\sigma _{Y}<0$ as otherwise one can put $\sigma _{S}:=0$ for $S\in {{\mathcal {S}}}{\setminus }{{\mathcal {S}}}^{\prime }$, and then $\tau _{S}:=\alpha \cdot \sigma _{S}+(1-\alpha )\cdot \uplambda _{S}$ for $S\in {{\mathcal {S}}}$ with $\alpha :=-\uplambda _{Y}\cdot (\sigma _{Y}-\uplambda _{Y})^{-1}\in (0,1]$ to get a semi-conic combination $\sum _{S\in {{\mathcal {S}}}} \tau _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ where $\tau _{Y}=0$; this means that ${{\mathcal {E}}}:=\{S\in {{\mathcal {S}}}\,:\ \tau _{S}\ne 0\}\subset {{\mathcal {B}}}$ is a semi-balanced system which fact contradicts the minimality of ${{\mathcal {B}}}$, by Corollary 3. Thus, Y has to be an exceptional set within ${{\mathcal {S}}}^{\prime }$ and, by step II. applied to ${{\mathcal {S}}}^{\prime }$, the system ${{\mathcal {B}}}^{\prime }:=({{\mathcal {S}}}^{\prime }{\setminus }\{Y\})\cup \{Z\}\subset {{\mathcal {B}}}$ is a balanced system on N contradicting the minimality of ${{\mathcal {B}}}$. Thus, the first claim in Lemma 13 has been verified.

IV. :

Let ${{\mathcal {S}}}$ be a min-semi-balanced system on N with the exceptional set $Y\in {{\mathcal {S}}}$ within it. Then $Z:=N{\setminus } Y\not \in {{\mathcal {S}}}$ as otherwise ${{\mathcal {D}}}:=\{Y,Z\}\subset {{\mathcal {S}}}$ is a balanced system contradicting the minimality of ${{\mathcal {S}}}$ (note that $|{{\mathcal {S}}}|\ge 3$ by Lemma 1). Step II. implies that ${{\mathcal {B}}}:=({{\mathcal {S}}}{\setminus }\{Y\})\cup \{Z\}$ is balanced on N. To show that ${{\mathcal {B}}}$ is minimal assume for a contradiction that a balanced system ${{\mathcal {B}}}^{\prime }\subset {{\mathcal {B}}}$ on N exists. Then necessarily $Z\in {{\mathcal {B}}}^{\prime }$ as otherwise ${{\mathcal {B}}}^{\prime }\subset {{\mathcal {S}}}$ contradicts the minimality of ${{\mathcal {S}}}$. By step I. applied to ${{\mathcal {B}}}^{\prime }$, the set system ${{\mathcal {S}}}^{\prime }:=({{\mathcal {B}}}^{\prime }{\setminus }\{Z\})\cup \{Y\}\subset {{\mathcal {S}}}$ is semi-balanced on N, which contradicts the minimality of ${{\mathcal {S}}}$. Of course, $|{{\mathcal {B}}}|=|{{\mathcal {S}}}|\ge 3$, which concludes the proof of the second claim in Lemma 13. $\square$

Proof of Lemma 17

A key induction step in the proof is based on the following auxiliary observations.

Lemma 20

Given $|N|\ge 3$, let ${{\mathcal {S}}}$ be a purely min-semi-balanced system on N. Denote ${{\mathcal {W}}}:=\mathcal{P}(N){\setminus } (\{\emptyset ,N\}\cup {{\mathcal {S}}})$ and introduce the next special polytopes (see Definition 5):

$$\begin{aligned} \Sigma ({{\mathcal {S}}}):= & {} \hbox \mathrm{conv}\,\left( \bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D}\right) ,\\ \Delta ({{\mathcal {S}}}):= & {} \Sigma ({{\mathcal {S}}})\,\cap \, \{\theta \in {\mathbb R}^{\mathcal{P}(N)}\,:\ \theta (W)\ge 0 \quad \hbox {for any}\ W\in {{\mathcal {W}}}\,\}\,. \end{aligned}$$

Moreover, for any ${{\mathcal {Z}}}\subseteq {{\mathcal {W}}}$, we put:

$$\begin{aligned} \Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}}):= & {} \Sigma ({{\mathcal {S}}})\,\cap \, \{\theta \in {\mathbb R}^{\mathcal{P}(N)}\,:\ \theta (Z)= 0 \quad \hbox {for any} \ Z\in {{\mathcal {Z}}}\,\}\,,\\ \Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}}):= & {} \Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}})\,\cap \, \Delta ({{\mathcal {S}}})\,. \end{aligned}$$

Then, for any ${{\mathcal {Z}}}\subseteq {{\mathcal {W}}}$, one has:

(i):

$\Sigma ^{{{\mathcal {W}}}}({{\mathcal {S}}})=\emptyset$,

(ii):

if $\emptyset \ne \Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}})$ and $\Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}}){\setminus } \Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}})\ne \emptyset$  then  $\emptyset \ne \Delta ^{{{\mathcal {Z}}}\cup \{D\}}({{\mathcal {S}}})$ for some set $D\in \mathcal{W}\setminus \mathcal{Z}$

(iii):

if $\theta \in \hbox \mathrm{ext}\,(\Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}}))$ then $\theta \in \bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D}$.

Proof

To show (i) assume for a contradiction that $\theta \in \Sigma ^{{{\mathcal {W}}}}({{\mathcal {S}}})$ exists. Thus, $\theta (W)=0$ for any $W\in {{\mathcal {W}}}$ forces ${{\mathcal {B}}}:=\{ S\subset N\,:\ S\ne \emptyset ~ \& ~ \theta (S)\ne 0\,\}\subseteq {{\mathcal {S}}}$. Since, however, every $\eta \in \bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D}$ satisfies $\eta (S)\le 0$ for any $S\in {{\mathcal {S}}}$, one has $\theta ^{\prime }(S)\le 0$ for any $S\in {{\mathcal {S}}}$ and $\theta ^{\prime }\in \Sigma ({{\mathcal {S}}})$. Hence, $\theta (S)\le 0$ for any $S\in {{\mathcal {S}}}$ and for our vector $\theta \in \Sigma ^{{{\mathcal {W}}}}({{\mathcal {S}}})$. The fact that $\theta \in \Sigma ({{\mathcal {S}}})$ implies the equality constraints $\theta (N)+\theta (\emptyset )=0$, $\sum _{L\subseteq N} \theta (L)=0$, and $\sum _{L\subseteq N:\,i\in L} \theta (L)=0$ for $i\in N$ (use Definition 5). The relations imply $\sum _{S\in {{\mathcal {S}}}} \theta (S)\cdot \chi _{S}+\theta (N)\cdot \chi _{N} =\underline{0}$, and, using $\sum _{L:\emptyset \ne L\subset N} \theta (L)=-1$, also $\theta (N)>0$. Therefore $\theta (N)\cdot \chi _{N}=\sum _{S\in {{\mathcal {S}}}} -\theta (S)\cdot \chi _{S}$ is a conic combination, which allows one to observe that ${{\mathcal {B}}}$ is balanced on N. The minimality of ${{\mathcal {S}}}$ then implies that ${{\mathcal {B}}}={{\mathcal {S}}}$, contradicting the assumption that ${{\mathcal {S}}}$ is not balanced on N.

To show (ii) assume the existence of $\eta \in \Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}})$. By (i) one has ${{\mathcal {W}}}{\setminus }{{\mathcal {Z}}}\ne \emptyset$. If there is $D\in {{\mathcal {W}}}{\setminus }{{\mathcal {Z}}}$ with $\eta (D)=0$ then $\eta \in \Delta ^{{{\mathcal {Z}}}\cup \{D\}}({{\mathcal {S}}})$ and we are done. Thus, assume that $\eta (W)\ne 0$ for any $W\in {{\mathcal {W}}}{\setminus }{{\mathcal {Z}}}$, which implies, by definition of $\Delta ({{\mathcal {S}}})$, that $\eta (W)> 0$ for any $W\in {{\mathcal {W}}}{\setminus }{{\mathcal {Z}}}$. The second assumption in (ii) means that there exists $\theta \in \Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}}){\setminus } \Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}})$; thus, necessarily $\eta \ne \theta$. Put $\theta ^{\alpha }:=(1-\alpha )\cdot \eta +\alpha \cdot \theta$ for $0\le \alpha \le 1$; the convexity of $\Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}})$ gives $\theta ^{\alpha }\in \Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}})$. Take $\beta :=\max \, \{\,\alpha \ge 0\,:\ \theta ^{\alpha }\in \Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}})\,\}$ and $\theta ^{\prime }:=\theta ^{\beta }$. Note that there exists $D\in {{\mathcal {W}}}{\setminus }{{\mathcal {Z}}}$ with $\theta ^{\prime }(D)=\theta ^{\beta }(D)=0$ as otherwise one has $\theta ^{\beta }(W)>0$ for any $W\in {{\mathcal {W}}}{\setminus }{{\mathcal {Z}}}$, which contradicts the maximality of $\beta$. Thus, the facts $\theta ^{\prime }\in \Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}})$ and $\theta ^{\prime }(D)=0$ imply together that $\theta ^{\prime }\in \Delta ^{{{\mathcal {Z}}}\cup \{D\}}({{\mathcal {S}}})$.

The condition (iii) can be verified by induction on $|{{\mathcal {Z}}}|$. In case ${{\mathcal {Z}}}=\emptyset$ this follows directly from the definition of $\Sigma ({{\mathcal {S}}})$ using basic facts from polyhedral geometry recalled in Sect. 2.2. To verify the induction step assume that the claim is true for some ${{\mathcal {Z}}}\subset {{\mathcal {W}}}$, take $Z\in {{\mathcal {W}}}{\setminus }{{\mathcal {Z}}}$ and evidence the claim for ${{\mathcal {Z}}}\cup \{Z\}$. Note that the polytope $\mathsf{Q}:=\Sigma ^{{{\mathcal {Z}}}\cup \{Z\}}({{\mathcal {S}}})$ is the intersection of the polytope $\mathsf{P}:=\Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}})$ with the hyperplane $\mathsf{H}:=\{\,\theta \,:\ \theta (Z)=0\}$. The characterization of vertices of $\mathsf{Q}=\mathsf{P}\cap \mathsf{H}$ recalled in Sect. 2.2 says that any vertex $\theta \in \hbox \mathrm{ext}\,(\mathsf{Q})$ is either a vertex of $\mathsf{P}$, in which case one has $\theta \in \bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D}$ by the induction assumption, or there is an edge $[\eta ,\sigma ]$ of $\mathsf{P}$ such that $\theta \in \,]\eta ,\sigma [$ and $[\eta ,\sigma ]\cap \mathsf{H}=\{\theta \}$. Since $\eta ,\sigma \in \hbox \mathrm{ext}\,(\mathsf{P})$, by the induction hypothesis, one has $\eta ,\sigma \in \bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D}$. As $[\eta ,\sigma ]\cap \mathsf{H}=\{\theta \}$ one has $\eta (Z)\ne 0\ne \sigma (Z)$ and can assume without loss of generality that $\eta (Z)>0$ and $\sigma (Z)<0$. This forces that $\eta \in {\tilde{\Theta }}^{N}_{Z}$; assume that $\sigma \in {\tilde{\Theta }}^{N}_{E}$ for some $E\in {{\mathcal {W}}}$ (possibly $E=Z$). It makes no problem to observe that these facts imply that $\theta \in {\tilde{\Theta }}^{N}_{E}$ (see Definition 5). Hence, $\theta \in \bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D}$ and the induction step has been verified. $\square$

For reader’s convenience we recall what is claimed.

Lemma 17    Let ${{\mathcal {S}}}$ be a purely min-semi-balanced system on N, $|N|\ge 3$, with exceptional set $T\in {{\mathcal {S}}}$ and ${{\mathcal {W}}}:= \mathcal{P}(N){\setminus } (\{\emptyset ,N\}\cup {{\mathcal {S}}})$. Then the following conditions are equivalent:

(a):

$\theta _{{{\mathcal {S}}}}\not \in \hbox \mathrm{ext}\,(\Delta )$, (see Definition 5)

(b):

there exists a convex combination $\theta _{{{\mathcal {S}}}}=\sum _{D\in {{\mathcal {W}}}\cup \{T\}} \alpha _{D}\cdot \theta ^{D}$ where $\alpha _{T}<1$ and $\theta ^{D}\in {\tilde{\Theta }}^{N}_{D}$ whenever $\alpha _{D}>0$,

(c):

the set $\Delta ({{\mathcal {S}}}):=\hbox \mathrm{conv}\,(\bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D}) \cap \{\,\theta \in {\mathbb R}^{\mathcal{P}(N)}\,:\ \theta (W)\ge 0 ~\hbox {for }W\in {{\mathcal {W}}}\,\}$ is non-empty,

(d):

there exists $E\in {{\mathcal {W}}}$ such that E is exceptional in ${{\mathcal {S}}}\cup \{E\}$,

(e):

there exists $E\in {{\mathcal {W}}}$ such that E is exceptional in $({{\mathcal {S}}}{\setminus }\{T\})\cup \{E\}$,

(f):

a min-semi-balanced system ${{\mathcal {D}}}$ on N exists such that ${{\mathcal {D}}}{\setminus }{{\mathcal {S}}}=\{E\}$ for some $E\in {{\mathcal {W}}}$, the set E is exceptional within ${{\mathcal {D}}}$, and $T\not \in {{\mathcal {D}}}$,

(g):

a min-semi-balanced system ${{\mathcal {D}}}$ on N exists with an exceptional set E such that $\mathcal{D}\setminus \mathcal{S}= \{E\}$.

Proof

To show (a)$\Rightarrow$(b) realize that $\theta _{{{\mathcal {S}}}}\in {\tilde{\Theta }}^{N}_{T}\subseteq \Delta$ and assume that $\theta _{{{\mathcal {S}}}}\in \,]\eta ,\sigma [$ for $\eta ,\sigma \in \Delta$, $\eta \ne \theta _{{{\mathcal {S}}}}\ne \sigma$. By the definition of $\Delta$ a finite convex combination yielding $\eta$ exists: $\eta =\sum _{j\in J} \beta _{j}\cdot \eta _{j}$, where $\beta _{j}>0$ and $\eta _{j}\in \bigcup _{\emptyset \ne D\subseteq N} {\tilde{\Theta }}^{N}_{D}$ for $j\in J$. Since $\eta \ne \theta _{{{\mathcal {S}}}}$, there exists $j\in J$ with $\eta _{j}\ne \theta _{{{\mathcal {S}}}}$. An analogous convex combination exists for $\sigma$ and by combining them observe that a finite convex combination yielding $\theta _{{{\mathcal {S}}}}$ exists:

$$\begin{aligned} \theta _{{{\mathcal {S}}}}=\sum _{i\in I} \alpha _{i}\cdot \theta _{i},\qquad \hbox {where }\alpha _{i}>0\; \hbox {and}\; \theta _{i}\in \bigcup _{\emptyset \ne D\subseteq N} {\tilde{\Theta }}^{N}_{D}\; \hbox {for all }\;i\in I, \end{aligned}$$

and, moreover, $\theta _{i}\ne \theta _{{{\mathcal {S}}}}$ for at least one $i\in I$. Assume without loss of generality that $\theta _{i}$, $i\in I$, differ from each other and, if there is $i\in I$ with $\theta _{i}=\theta _{{{\mathcal {S}}}}$ then, by easy modification, one gets such a convex combination yielding $\theta _{{{\mathcal {S}}}}$ where $\theta _{i}\ne \theta _{{{\mathcal {S}}}}$ for all $i\in I$.

Observe that one can even assume without loss of generality that $\theta _{i}(S)\le 0$ for any $i\in I$ and $S\in {{\mathcal {S}}}{\setminus }\{T\}$. Indeed, if there exists $j\in I$ and $S\in {{\mathcal {S}}}{\setminus }\{T\}$ with $\theta _{j}(S)>0$ then the convex combination can be replaced by another convex combination $\theta _{{{\mathcal {S}}}}={\hat{\alpha }}_{j}\cdot {\hat{\theta }}_{j}+\sum _{i\in I{\setminus } \{j\}} {\hat{\alpha }}_{i}\cdot \theta _{i}$, where ${\hat{\theta }}_{j}(S)=0$. To observe that realize that $\alpha _{j}<1$, as otherwise $\theta _{j}=\theta _{{{\mathcal {S}}}}$. Thus, one can put $\alpha := 1-\alpha _{j}=\sum _{i\in I{\setminus }\{j\}} \alpha _{i}>0$ and

$$\begin{aligned} \theta ~:=~ \sum _{i\in I{\setminus }\{j\}} \frac{\alpha _{i}}{\alpha }\cdot \theta _{i}\,,\quad \hbox {which gives}\; \theta _{{{\mathcal {S}}}}=\alpha _{j}\cdot \theta _{j}+ \alpha \cdot \theta , \hbox {that is}, \theta _{{{\mathcal {S}}}}\in \,]\theta _{j},\theta [. \end{aligned}$$

On the other hand, since $\theta _{j}(S)>0$ and $\theta _{{{\mathcal {S}}}}(S)<0$ there exists unique ${\hat{\theta }}_{j}\in \,]\theta _{j},\theta _{{{\mathcal {S}}}}[$ such that ${\hat{\theta }}_{j}(S)=0$. Note that necessarily $\theta _{j}\in {\tilde{\Theta }}^{N}_{S}$ while $\theta _{{{\mathcal {S}}}}\in {\tilde{\Theta }}^{N}_{T}$ which facts together allow one to observe that ${\hat{\theta }}_{j}\in {\tilde{\Theta }}^{N}_{T}$. The vectors $\theta _{j},{\hat{\theta }}_{j},\theta _{{{\mathcal {S}}}}$ and $\theta$ are on the same line, which implies that $\theta _{{{\mathcal {S}}}}\in \,]{\hat{\theta }}_{j},\theta [$. Thus, $0<\gamma <1$ exists with $\theta _{{{\mathcal {S}}}}=\gamma \cdot {\hat{\theta }}_{j}+ (1-\gamma )\cdot \theta$ and the substitution gives

$$\begin{aligned} \theta _{{{\mathcal {S}}}} ~=~ \gamma \cdot {\hat{\theta }}_{j} + \sum _{i\in I{\setminus }\{j\}} \underbrace{\frac{(1-\gamma )\cdot \alpha _{i}}{\alpha }}_{{\hat{\alpha }}_{i}}\,\cdot \, \theta _{i}\,,\qquad \hbox {where it suffices to put}\; {\hat{\alpha }}_{j}:=\gamma . \end{aligned}$$

For any $i\in I$, one has $\theta _{i}\in {\tilde{\Theta }}^{N}_{E}$ for some $\emptyset \ne E\subseteq N$. In case $E\in {{\mathcal {S}}}{\setminus }\{T\}$ the above inequalities $\theta _{i}(S)\le 0$ for $S\in {{\mathcal {S}}}{\setminus }\{T\}$ give $\theta _{i}\in {\tilde{\Theta }}^{N}_{N}$ and (see Definition 5) the inclusion ${\tilde{\Theta }}^{N}_{N}\subseteq {\tilde{\Theta }}^{N}_{T}$ allows one to conclude that $\theta _{i}\in {\tilde{\Theta }}^{N}_{D}$ for some $D\in {{\mathcal {W}}}\cup \{T\}$. To summarize that: there exists a convex combination $\theta _{{{\mathcal {S}}}}=\sum _{i\in I} \alpha _{i}\cdot \theta _{i}$, where $\alpha _{i}>0$, $\theta _{i}\ne \theta _{{{\mathcal {S}}}}$ and $\theta _{i}\in \bigcup _{D\in {{\mathcal {W}}}\cup \{T\}} {\tilde{\Theta }}^{N}_{D}$ for all $i\in I$.

Further observation is that there exists $j\in I$ and $W\in {{\mathcal {W}}}$ such that $\theta _{j}(W)>0$. To show that assume for a contradiction the converse, that is, $\theta _{i}(W)\le 0$ for any $i\in I$ and $W\in {{\mathcal {W}}}$. That basically means, that, for any $i\in I$, the condition $\theta _{i}\in {\tilde{\Theta }}^{N}_{W}$ implies $\theta _{i}\in {\tilde{\Theta }}^{N}_{N}\subseteq {\tilde{\Theta }}^{N}_{T}$. In particular, one would have $\theta _{i}\in {\tilde{\Theta }}^{N}_{T}$, $\theta _{i}\ne \theta _{{{\mathcal {S}}}}$ for any $i\in I$, which contradicts the fact $\theta _{{{\mathcal {S}}}}\in \hbox \mathrm{ext}\,({\tilde{\Theta }}^{N}_{T})$ claimed by (the second claim in) Lemma 8.

Thus, any $i\in I$ can be assigned to some $D\in {{\mathcal {W}}}\cup \{T\}$ such that $\theta _{i}\in {\tilde{\Theta }}^{N}_{D}$; let us fix that choice and write $i\mapsto D$ to denote that. We already know that there exists $j\in I$ and $W\in {{\mathcal {W}}}$ with $\theta _{j}(W)>0$, which necessitates $j\mapsto W$. For any $D\in {{\mathcal {W}}}\cup \{T\}$ we put

$$\begin{aligned} \alpha _{D} ~:=~ \sum _{i\in I:\, i\,\mapsto D} \alpha _{i} \qquad \hbox {and, if }\alpha _{D}>0,\quad \theta ^{D} ~:=~ \sum _{i\in I:\, i\,\mapsto D} \frac{\alpha _{i}}{\alpha _{D}}\cdot \theta _{i}\in {\tilde{\Theta }}^{N}_{D}\,. \end{aligned}$$

Thus, one has $\theta _{{{\mathcal {S}}}}=\sum _{D\in {{\mathcal {W}}}\cup \{T\}} \alpha _{D}\cdot \theta ^{D}$, where $\theta ^{D}$ can be chosen arbitrarily in case $\alpha _{D}=0$. It is a convex combination and the existence of $j\in I$ and $W\in {{\mathcal {W}}}$ with $j\mapsto W$ implies $\alpha _{W}>0$. Hence, $\alpha _{T}<1$, which gives the condition (b).

To show (b)$\Rightarrow$(c) consider a convex combination $\theta _{{{\mathcal {S}}}}=\sum _{D\in {{\mathcal {W}}}\cup \{T\}} \alpha _{D}\cdot \theta ^{D}$ where $\alpha _{T}<1$ and $\theta ^{D}\in {\tilde{\Theta }}^{N}_{D}$ whenever $\alpha _{D}>0$. The fact $\theta _{{{\mathcal {S}}}}(T)>0$ forces both $\alpha _{T}>0$ and $\theta ^{T}(T)>0$ because $\eta (T)\le 0$ for any $\eta \in \bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D}$. Thus, one has some $\theta ^{T}\in {\tilde{\Theta }}^{N}_{T}$. Let us put

$$\begin{aligned} \theta ~:=~ \sum _{D\in {{\mathcal {W}}}}\,\, \frac{\alpha _{D}}{1-\alpha _{T}}\,\cdot \, \theta ^{D}\qquad \hbox {and observe that}\,\, \theta _{{{\mathcal {S}}}}=(1-\alpha _{T})\cdot \theta + \alpha _{T}\cdot \theta ^{T}. \end{aligned}$$

By definition, $\theta \in \hbox \mathrm{conv}\,(\bigcup _{D\in {{\mathcal {W}}}} {\tilde{\Theta }}^{N}_{D})$. The fact $\theta _{{{\mathcal {S}}}}\in \,]\theta ,\theta ^{T}[$ together with $\theta _{{{\mathcal {S}}}}(W)=0$ and $\theta ^{T}(W)\le 0$ for any $W\in {{\mathcal {W}}}$ forces $\theta (W)\ge 0$ for any such W. In particular, $\theta \in \Delta ({{\mathcal {S}}})$ and the condition (c) has been verified.

To show (c)$\Rightarrow$(d) we use Lemma 20; the condition (c) means, by notation from Lemma 20, that $\Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}})\ne \emptyset$ for empty ${{\mathcal {Z}}}=\emptyset$. By inductive application of Lemma 20(ii) we find ${{\mathcal {Z}}}\subseteq {{\mathcal {W}}}$ with $\Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}})=\Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}})\ne \emptyset$; indeed, by Lemma 20(i) one has $\Sigma ^{{{\mathcal {W}}}}({{\mathcal {S}}})=\emptyset$, which ensures that inductive enlarging of ${{\mathcal {Z}}}$ has to finish with some desired ${{\mathcal {Z}}}\subset {{\mathcal {W}}}$. Thus, $\emptyset \ne \hbox \mathrm{ext}\,(\Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}}))\subseteq \Delta ^{{{\mathcal {Z}}}}({{\mathcal {S}}})$ for some ${{\mathcal {Z}}}\subset {{\mathcal {W}}}$. One can take some $\theta \in \hbox \mathrm{ext}\,(\Sigma ^{{{\mathcal {Z}}}}({{\mathcal {S}}}))$ and, by Lemma 20(iii), there exists $E\in {{\mathcal {W}}}$ such that $\theta \in {\tilde{\Theta }}^{N}_{E}$. Hence, $\theta (W)\le 0$ for any $W\in {{\mathcal {W}}}{\setminus }\{E\}$ while $\theta \in \Delta ({{\mathcal {S}}})$ says $\theta (W)\ge 0$ for any $W\in {{\mathcal {W}}}$. That together means $\theta (W)=0$ for any $W\in {{\mathcal {W}}}{\setminus }\{E\}$ and $\theta (E)\ge 0$. One cannot have $\theta (E)=0$ for otherwise $\theta \in \Sigma ^{{{\mathcal {W}}}}({{\mathcal {S}}})$ contradicts the claim in Lemma 20(i). Thus, necessarily $\theta (E)>0$; note also that $\theta (S)\le 0$ for any $S\in {{\mathcal {S}}}$. The equality constraints $\sum _{L\subseteq N:\,i\in N} \theta (L)=0$ for any $i\in N$ and $\theta \in {\tilde{\Theta }}^{N}_{E}$ allow one to conclude that $\sum _{S\in {{\mathcal {S}}}\cup \{E\}} -\theta (S)\cdot \chi _{S}=\theta (N)\cdot \chi _{N}$ is a semi-conic combination yielding a constant vector in ${\mathbb R}^{N}$. Thus, by definition, E is exceptional in ${{\mathcal {S}}}\cup \{E\}$ and the condition (d) has been verified.

To show (d)$\Rightarrow$(e) assume that $E\in {{\mathcal {W}}}$ is exceptional within ${{\mathcal {S}}}\cup \{E\}$. This means that there exists a linear combination $\sum _{S\in {{\mathcal {S}}}\cup \{E\}} \nu _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ where $\nu _{E}<0$ and $\nu _{S}\ge 0$ for $S\in {{\mathcal {S}}}$. Observe that E is exceptional within a smaller set system $({{\mathcal {S}}}{\setminus }\{T\})\cup \{E\}$. In case $\nu _{T}=0$ we are done. In case $\nu _{T}>0$ we apply Lemma 2(d) to ${{\mathcal {S}}}$ which says that there exists (unique) affine combination $\sum _{S\in {{\mathcal {S}}}} \uplambda _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ with both $\uplambda _{T}<0$ and $\uplambda _{S}> 0$ for $S\in {{\mathcal {S}}}{\setminus }\{T\}$. Then we put $\uplambda _{E}:=0$ and

$$\begin{aligned} \kappa _{S} ~:=~ \frac{\nu _{T}}{\nu _{T}-\uplambda _{T}}\cdot \uplambda _{S} + \frac{-\uplambda _{T}}{\nu _{T}-\uplambda _{T}}\cdot \nu _{S} \qquad \hbox {for}\; S\in {{\mathcal {S}}}\cup \{E\}. \end{aligned}$$

Hence, $\sum _{S\in {{\mathcal {S}}}\cup \{E\}} \kappa _{S}\cdot \chi _{S}$ yields a constant vector in ${\mathbb R}^{N}$, $\kappa _{E}<0$, and $\kappa _{T}=0$. Thus, $({{\mathcal {S}}}{\setminus }\{T\})\cup \{E\}$ is a semi-balanced system on N and E is an exceptional set within it.

To show (e)$\Rightarrow$(f) we fix a semi-conic combination $\sum _{S\in {{\mathcal {S}}}\cup \{E\}} \kappa _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ with $\kappa _{E}<0$ and $\kappa _{T}=0$. In particular, one can choose a min-semi-balanced system ${{\mathcal {D}}}\subseteq ({{\mathcal {S}}}{\setminus }\{T\})\cup \{E\}$. One has $E\in {{\mathcal {D}}}$ as otherwise ${{\mathcal {D}}}\subset {{\mathcal {S}}}$ contradicts the minimality of ${{\mathcal {S}}}$. By Lemma 2(d), there exists (unique) affine combination $\sum _{S\in {{\mathcal {D}}}} \sigma _{S}\cdot \chi _{S}$ yielding a constant vector in ${\mathbb R}^{N}$ which is semi-conic and has all coefficients non-zero. Assume for a contradiction that $\sigma _{E}>0$. Then we put $\sigma _{S}:=0$ for $S\in {{\mathcal {S}}}{\setminus }{{\mathcal {D}}}$ and

$$\begin{aligned} \mu _{S} ~:=~ \frac{\sigma _{E}}{\sigma _{E}-\kappa _{E}}\cdot \kappa _{S} + \frac{-\kappa _{E}}{\sigma _{E}-\kappa _{E}}\cdot \sigma _{S} \qquad \hbox {for}~ S\in {{\mathcal {S}}}\cup \{E\}. \end{aligned}$$

Hence, $\sum _{S\in {{\mathcal {S}}}\cup \{E\}} \mu _{S}\cdot \chi _{S}$ yields a constant vector in ${\mathbb R}^{N}$ and $\mu _{E}=0=\mu _{T}$. Since it is a semi-conic combination ${{\mathcal {T}}}:=\{ S\in {{\mathcal {S}}}\,:\ \mu _{S}\ne 0\}\subset {{\mathcal {S}}}$ is a semi-balanced system on N, which contradicts the minimality of ${{\mathcal {S}}}$. As $\sigma _{E}\ne 0$, one necessarily has $\sigma _{E}<0$ and the set E is exceptional within ${{\mathcal {D}}}$. Thus, the condition (f) has been verified.

The implication (f)$\Rightarrow$(g) is evident.

To show (g)$\Rightarrow$(a) assume that ${{\mathcal {D}}}$ is the min-semi-balanced system with an exceptional set $E\in {{\mathcal {W}}}$ such that ${{\mathcal {D}}}{\setminus }{{\mathcal {S}}}=\{E\}$. Note that, by (1), one has both $\theta _{{{\mathcal {D}}}}(E)>0$ and $\theta _{{{\mathcal {D}}}}(W)=0$ for any $W\in {{\mathcal {W}}}{\setminus }\{E\}$. Then we put

$$\begin{aligned} \theta ^{\varepsilon } ~:=~ (1+\varepsilon )\cdot \theta _{{{\mathcal {S}}}} + (-\varepsilon )\cdot \theta _{{{\mathcal {D}}}} ~=~ \theta _{{{\mathcal {S}}}} +\varepsilon \cdot (\theta _{{{\mathcal {S}}}}-\theta _{{{\mathcal {D}}}})\qquad \hbox {for every }\varepsilon \ge 0. \end{aligned}$$

It makes no problem to observe that, for small $\varepsilon >0$, one has $\theta ^{\varepsilon }\in {\tilde{\Theta }}^{N}_{T}\subseteq \Delta$. Because of $\theta _{{{\mathcal {S}}}}\in \, ]\theta _{{{\mathcal {D}}}},\theta ^{\varepsilon }[$ and $\theta _{{{\mathcal {D}}}}\in {\tilde{\Theta }}^{N}_{E}\subseteq \Delta$ one gets $\theta _{{{\mathcal {S}}}}\not \in \hbox \mathrm{ext}\,(\Delta )$ and (a) has been verified. $\square$