1 Introduction

In the modern production/inventory management, the strategy of lead-time reduction has received a great deal of attention by the researchers. Due to Tersine (1982), lead time usually consists of the following components: order preparation, order transit, supplier lead time, delivery time and setup time.

Although most of the early literatures dealing with inventory problems viewed lead time as an uncontrollable variable [see, e.g., Naddor (1966) and Silver and Peterson (1985)], however in some practical situations, lead time can be reduced by controlling some or all of its components. To reduce lead time, Liao and Shyu (1991) first presented a continuous review inventory model in which the order quantity is predetermined and lead time is a unique variable that can be controlled by paying extra crashing cost. This model has been extended by Ben-Daya and Raouf (1994) to include both lead time and order quantity as decision variables. Later, Ouyang et al. (1996) developed a more general model, where they extended Ben-Daya and Raouf (1994) by allowing shortages and considered that only a fraction of the demand during the stock out period can be backordered. The lead time demand normally is considered as a random variable.

But due to changing scenario, it would be better to represent the mean lead time demand by a fuzzy number than to express it by a deterministic value. Thus the lead time demand is represented by a fuzzy random variable, based on the concept proposed by Puri and Ralescu (1986). Also, the annual average demand, due to the fact that it may fluctuate a little in an unstable environment and is difficult to assess by a crisp value, is represented as a fuzzy number (Chang et al. 2006a).

Due to the scarcity of the storage space at market places, retailers normally maintain two warehoses—one showroom (OW) at the market place and one rented warehouse (RW) little away from the market place to store the items. In the literature, a lot of work (cf. Hartely 1976; Sarma 1987; Bhunia and Maiti 1998; Kar et al. 2001; Zhou and Yang 2003) has been reported on two warehouse inventory system in crisp environment. Maiti and Maiti (2006, 2007), Rong et al. (2008a, b) have published papers on two warehouse system in fuzzy environment taking fuzzy constraints and fuzzy lead time. Recently, Rong et al. (2008a, b) has formulated and solved a single warehouse multi-retailers mixture inventory distribution model for a single item involving controllable lead-time with backorder and lost sales, considering lead-time demands of retailers to be uncertain in both stochastic and fuzzy sense.

In recent years some research work have been done based on lead time. Ouyang and Chuang (2000) considered a periodic review inventory model involving variable lead time with a service level constraint. Ouyang and Yao Ouyang and Yao (2002) developed a minimax distribution free procedure for mixed inventory model involving variable lead time with fuzzy demand. Huq et al. (2006) discussed a simulation study for a multi-product two echelon inventory replacement system with both one and two warehouse systems. Chang et al. (2006a, b) studied some integrated vendor-buyer cooperative inventory models with controllable lead time and ordering cost reduction. Wu et al. Wu et al. (2007) considered integrated vendor–buyer inventory system with sublot sampling inspection policy and controllable lead time. Recently, Rong and Maiti (2010) presented a two-warehouse inventory model with stochastic demand, controllable lead time and evaluated fuzzy present value of the profit.

Demand may be uncertain in both fuzzy and stochastic sense. Till now, researchers have considered lead time demand to be either fuzzy or stochastic in single warehouse model. A very few (Chang et al. 2006a etc.) researchers have considered fuzzy random lead time demand in single warehouse inventory problem. None has considered fuzzy-stochastic lead time demand for two warehouse inventory models. This research paper is prepared to fill up this gap.

In this paper, we consider a two warehouse inventory model with fuzzy-stochastic lead time demand. As usual, the replenishment is first placed in OW (i.e, the market warehouse) and after that, the rest amount is kept at the little away rented warehouse (RW). The item is transferred from RW to OW continuously. We consider two cases. In first case we discuss the models in crisp sense and in second case we discuss that in fuzzy sense. This paper has been developed by assumption that the expected value of the random lead time demand must be fuzzy because the lead time length is uncertain. For this assumption, the random lead time demand must be converted to fuzzy random lead time demand because realization of a fuzzy random variable is a fuzzy set/number. We solved the models without and with fuzzy-stochastic budget constraint. Here, shortages are fully backlogged. The fuzzy total cost is defuzzified using the centroid method of defuzzification and the crisp problems are solved using GRG method. For the case with constraint, the surprise function is used to convert the constrained optimization problem to the corresponding unconstrained problem. The optimum order quantities are obtained for discrete values of lead time and hence the optimal lead time and order quantities are obtained. The results, obtained in two different cases, are compared.

This article is organized as follows. In Sect. 2, assumptions and notations are given. In Sect. 3, we develop the model in two cases considering lead time demand as stochastic variable (i.e. crisp stochastic variable). In Sect. 4, we develop the fuzzy mixture inventory model involving fuzzy-stochastic lead time. Using the centroid method of defuzzification, we derive the estimate of total cost in the fuzzy sense. In Sect. 5, we derive the optimal order quantity and the optimal lead time by minimizing the estimate of total cost in the fuzzy/crisp senses. Numerical examples are provided to illustrate the models. In Sect. 6, results are discussed. In Sect. 7, a conclusion is given. The paper is concluded by citing some references.

2 Notations and assumptions

To develop the proposed two warehouse inventory model, the following notations and assumptions are used.

2.1 Notation

\(D\) :

Average annual demand

\(\mu \) :

Demand per day

\(\sigma \) :

Standard deviation of daily demand

\(p\) :

purchase price per unit

\(h_1\) :

Holding cost per unit per year in own warehouse (\(OW\))

\(h_2\) :

Holding cost per unit per year in rented warehouse (\(RW\))

\(\Pi \) :

Fixed penalty cost per unit short

\(Q\) :

Order quantity (decision variable)

\(L\) :

Length of lead time (decision variable)

\(A\) :

Fixed ordering cost per order

\(r\) :

Reorder point

\(X\) :

Lead time demand, which is normally distributed with finite mean \(\upmu \mathrm{L}\) and standard deviation \(\sigma \sqrt{L}\), where \(\mu \) and \(\sigma \) denote the mean and standard deviation of daily demand

\(x^{+}\) :

Maximum of \(x\) and 0 i.e, \(x^{+}=\max \{x,0\}\)

\(E(\cdot )\) :

Mathematical expectations

2.2 Assumptions

  1. (1)

    The retailer has two warehouses; one is own warehouse \((OW)\) at market place and another is rented warehouse \((RW)\) at a little distant place.

  2. (2)

    Shortages allowed and backlogged fully.

  3. (3)

    Inventory is continuously reviewed. Replenishment is made whenever the inventory level of \(OW\) falls to the reorder point \(r\).

  4. (4)

    The reorder point \(r\) in \(OW\) is the expected demand during lead-time plus safety stock (SS) and \(\text{ SS} = k\). (standard deviation of lead-time demand), i.e, \(r= \mu L + k\sigma \sqrt{L},\,k\) is the safety factor and satisfying \(P(X>r) = P(Z>k) = q,\,Z\) represents the standard normal random variable and \(q\) represents the allowable stock-out probability during lead-time \(L\).

  5. (5)

    The lead time L has n mutually independent components each having a different crashing cost for reducing lead time. The j-th component has a minimum duration \(a_j\) and normal duration \(b_j\) and a crashing cost per unit time \(c_j\). Furthermore, we assume that \(c_1 \le c_2 \le \cdots \le c_n\).

  6. (6)

    The components of lead time are crashed one at a time starting with the component of least \(c_i\) and so on.

  7. (7)

    If \(L_0 = \sum \nolimits _{j=1}^n {b_j}\) and \(L_i\) be the length of lead-time for buyer’s with components \(1,2,\ldots ,i\) crashed to their minimum duration, then \(L_i = \sum \nolimits _{j=1}^n {b_j} -\sum \nolimits _{j-1}^i {(b_j -a_j)}, \,i=1,2,{\ldots },n\); and the lead time crashing cost per cycle for buyer’s is \(C(L)\)for a given \(L \in [L_i, L_{i-1}\)] is given by

    $$\begin{aligned} C(L) = c_i [L_{i-1} -L] + \sum \limits _{j=i}^{i-1} {c_j} (b_j -a_j)\quad \text{ and}\quad C(L_0)=0 \end{aligned}$$
    (1)

3 Mathematical modeling in crisp sense

After purchasing the quantity \(Q,W\) amount is kept in \(OW\) and the remaining amount \(Q-W+X-r\) are transformed to \(RW\) which is located at some distant from the market place (\(OW\)). The supply is made from \(OW\) and it is replenished continuously transforming items from \(RW\) to \(OW\). In other words the release from \(RW\) to \(OW\) is continuous. When all items of \(RW\) are transferred to \(OW\), then the stock level of \(OW\) starts reducing to the level \(r\). The maximum and minimum inventory at \(RW\) are respectively \((Q-W+r-\mu L)\) and 0 (see Fig. 1); so the average inventory at \(RW\) is

$$\begin{aligned}&= \frac{1}{2}(Q-W+r-\mu L) \frac{(Q-W+r-\mu L)}{\mu } \frac{\mu }{Q}\\&= \frac{1}{2Q}(Q-W+r-\mu L)^{2}=\frac{1}{2Q}(Q-W+k\sigma \sqrt{L})^{2}. \end{aligned}$$

The average holding cost in \(RW\) is

$$\begin{aligned} \text{ AHCRW} =\frac{h_2}{2Q}(Q-W+k\sigma \sqrt{L})^{2}. \end{aligned}$$

The average holding cost in \(OW\) is

$$\begin{aligned} \text{ AHCOW}&= \frac{1}{T} \left[{WxT_1 x h_1 + \frac{1}{2} \{W+(r-\mu L)\}(T-T_1) x h_1} \right]\\&= \frac{\mu }{Q}\left[W\frac{(Q-W+r-\mu L)}{\mu } x h_1 \right.\\&\left.+\frac{1}{2\mu \left({W+r-\mu L} \right) x \left({W-r+\mu L} \right) x h_1} \right] [T\mu = Q]\\&= \frac{h_1}{Q}\left[{W\left({Q-W+k\sigma \sqrt{L}} \right)+\frac{1}{2}\left({W+r-\mu L} \right)\left({W-r+\mu L} \right)} \right]\\&= \frac{h_1}{Q}\left[{WQ-\frac{1}{2}(W-k\sigma \sqrt{L})^{2}} \right]. \end{aligned}$$
Fig. 1
figure 1

Level of inventory vs. time

Full size image

The above calculation is justified by the Remark 1 (see “Appendix 1”).

Total expected annual cost,

$$\begin{aligned} EAC&\!=\! A\frac{D}{Q}\!+\!\frac{h_2}{2Q}(Q\!-\!W\!+\!k\sigma \sqrt{L}) ^{2}\!+\!\frac{h_1}{Q}\left[{WQ\!-\!\frac{1}{2}(W\!-\!k\sigma \sqrt{L})^{2}} \right]\\&+ \frac{D}{Q}\left[{\Pi E(X-r)^{+} + C(L)} \right]\\ \text{ Now},\quad E(X-r)^+&= \int \limits _r^\infty {(x-r)f(x)dx}\,[\text{ By} \text{ definition}]\\&= \sigma \sqrt{L}\Psi (k)\,[\text{ using}\,r = \mu L + k\sigma \sqrt{L}]. \end{aligned}$$

where, \(\Psi (k)\equiv \phi (k)-k[1-\Phi (k)]\), and \(\phi , \Phi \) denote the standard normal p.d.f and cumulative distribution function (c.d.f), respectively (for proof, see “Appendix 2”).

3.1 Unconstrained stochastic (crisp) model

In this case, the problem is

$$\begin{aligned} \text{ Min}z&= A\frac{D}{Q}+\frac{h_2}{2Q}(Q-W+k\sigma \sqrt{L}) ^{2}+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}(W-k\sigma \sqrt{L})^{2}} \right]\nonumber \\&+ \frac{D}{Q}\left[{\Pi E(X-r)^{+} + C(L)} \right], \end{aligned}$$
(2)

with \(E(X-r)^{+}=\sigma \sqrt{L}\Psi (k),\,\Psi (k)\equiv \phi (k)-k[1-\Phi (k)]\).

3.2 Constrained stochastic (crisp) model

Let \(\mu _L=\mu L\) and \(\sigma _L = \sigma \sqrt{L}\), where \(\mu \) is an estimate(known value) i.e., \(\mu _L\) is an estimate. If the purchasing cost is paid at the time of order received, then the problem can be formulated by objective function with budget constraint,

$$\begin{aligned} \text{ Min}EAC&= A\frac{D}{Q}+\frac{h_2}{2Q}(Q-W+k\sigma \sqrt{L})^{2}+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}(W-k\sigma \sqrt{L})^{2}}\right]\\&+ \frac{D}{Q}\left[{\Pi E(X-r)^{+} + C(L)} \right] \end{aligned}$$

subject to

$$\begin{aligned} p(Q+r-X) \le B \end{aligned}$$
(3)

Since lead-time demand X is a random variable, we use the chance-constraint programming technique, developed by Charnes and Cooper (1959). Let \(\lambda \) be the probability of non-violation of the constraint (3), which is a real value chosen from [0,1]. Then the above constraint can be written as follows:

$$\begin{aligned}&\Pr ~ob\left[{p(Q+r-X) \le B} \right]\ge \lambda \\&\quad \Rightarrow \Pr ~ob \left[{B+pX \ge p(Q+r)} \right]\ge \lambda \\&\quad \Rightarrow \frac{E(B+pX)}{p(Q+r)} \ge \lambda \,[\text{ By} \text{ Markov} \text{ inequality;} \text{ see} \text{``Appendix} \text{3''}]\\&\quad \Rightarrow B+ pE(X)\ge \lambda p(Q+r)\\&\quad \Rightarrow p\{E(X)-\lambda r\}+ B\ge \lambda pQ\\&\quad \Rightarrow p \left({\mu L-\lambda \mu L-\lambda k\sigma \sqrt{L}} \right) +B\ge \lambda pQ\\&\quad \Rightarrow p(1-\lambda )\mu _L +B \ge p\lambda k\sigma _L +p\lambda Q \end{aligned}$$

Therefore the above constrainedcrisp stochastic problem is reduced to

$$\begin{aligned} \text{ Min}\,\,EAC&= A\frac{D}{Q}+\frac{h_2}{2Q}(Q-W+k\sigma \sqrt{L}) ^{2}+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}(W-k\sigma \sqrt{L})^{2}} \right]\nonumber \\&+ \frac{D}{Q}\left[{\Pi E(X-r)^{+} + C(L)} \right] \end{aligned}$$
(4)

subject to,

$$\begin{aligned} p(1-\lambda )\mu _L +B \ge p\lambda k\sigma _L +p\lambda Q. \end{aligned}$$

4 Mathematical modeling in fuzzy sense

4.1 Unconstrained fuzzy stochastic model: (ref. Chang et al. 2006a, b)

We consider the fuzzy mixture inventory model in this article. Let (\(\mathfrak R \), B, P) be the probability space, where \(\mathfrak R \) is the set of real numbers, B is the Borel field on \(\mathfrak R \), and P is a probability measure. The lead-time demand, \(X\), in Sect. 2 is a random variable on (\(\mathfrak R \), B, P), which is assumed to be normally distributed with mean \(\mu L\) and standard deviation \(\sigma \sqrt{L}\), i.e, X \(\sim \, N(\mu L,\sigma \sqrt{L})\). Using, \(\mu _L = \mu L\) and \(\sigma _L = \sigma \sqrt{L}\), we have pdf of X as

$$\begin{aligned} f(x) = \frac{1}{\sqrt{2\pi } \sigma _L} e^{-\frac{(x-\mu _L )^{2}}{2\sigma _L^2} },\; -\infty <x<\infty \end{aligned}$$
(5)

\(X\) is called the crisp random variable. Corresponding to \(X\), let \(\tilde{X}\) be a fuzzy random variable. From the definition of \(L_i\) (Assumption 7), we have \(\text{ min}_{0\le i\le n}\quad L_i =L_n\) and \(\text{ max}_{0\le i\le n}\quad L_i =L_0\) and hence \(L_n \le L\le L_0\). In the uncertain and/or unstable environments, for any \(L\in [L_i, L_{i-1}],i=1,2,\ldots ,n\), it is difficult for the decision-maker to determine the lead time demand (LTD) with a single value \(E(X) = \mu _L\), rather it may be easier to determine LTD by an interval \([\mu _L -\Delta _1, \mu _L +\Delta _2]\), where \(\Delta _1,\Delta _2\) are determined by the decision-maker and should satisfy the conditions: \(0<\Delta _1<\mu _{L_n}\) and \(0<k \sigma _{L_0} <\Delta _2\) (see Eqs. (8) and (9) in the following). Since \([\mu _L -\Delta _1, \mu _L+\Delta _2]\) is an interval, so the decision maker must take an appropriate value (we denote it by \(\hat{{\mu }}_L\)) from the inside of this interval as the estimate of LTD. If the chosen value is \(\mu _L\), it is the same as \(E(X) = \mu _L\) of the crisp case, and then the error of estimation \(\left| {\hat{{\mu }}_L -\mu _L} \right|\) is 0. Moreover, if the chosen value is located in the left-hand side (LHS) or right-hand side (RHS) of \(\mu _L\), then further the chosen value \(\hat{{\mu }}_L\) is away from \(\mu _L\), the larger the error of estimation \(\left|{\hat{{\mu }}_L-\mu _L}\right|\), and the largest errors will occur at the end points of the interval \([\mu _L -\Delta _1, \mu _L +\Delta _2]\).

In the fuzzy viewpoint, we may employ the confidence level instead of error. For the case of \(\hat{{\mu }}_L =\mu _L\) the error is 0, and the confidence level is the largest and we let it be 1. In contrast, the further the value \(\hat{{\mu }}_L\) is away from \(\mu _L\), the smaller the confidence level to be. At the end points of the interval, i.e., \(\hat{{\mu }}_L =\mu _L -\Delta _1\) and \(\hat{{\mu }}_L =\mu _L +\Delta _2\), the confidence level is in the smallest and we let it be 0.

Next, let us consider the following triangular fuzzy number,

$$\begin{aligned} \tilde{\mu }_L =(\mu _L -\Delta _1, \mu _L, \mu _L +\Delta _2) \end{aligned}$$
(6)

where \(0<\Delta _1 <\mu _{L_n}\) and \(0<k \sigma _{L_0} <\Delta _2\) [see Eqs. (8) and (9)]. The membership grade of \(\tilde{\mu }_L\) is 1 at point \(\mu _L\), decreases as the point is away from \(\mu _L\), and reaches 0 at the end points \(\mu _L -\Delta _1\) and \(\mu _L+\Delta _2\). Since the properties of membership grade and confidence level are same, consequently, when the membership grade is treated as the confidence level, corresponding to the interval \([\mu _L -\Delta _1, \mu _L +\Delta _2]\), it is reasonable to set the triangular fuzzy number \(\tilde{\mu }_L \) as Eq. (6). Utilizing the centroid method to diffuzzify \(\tilde{\mu }_L\), we obtain

$$\begin{aligned} C(\tilde{\mu }_L) = \mu _L + \frac{1}{3}(\Delta _2 -\Delta _1)= \frac{2}{3}\mu _L +\frac{1}{3}\Delta _2 +\frac{1}{3}(\mu _L-\Delta _1) >0. \end{aligned}$$
(7)

\(C(\tilde{\mu }_L)\) is regarded as the estimate of LTD in the fuzzy sense and \(C(\tilde{\mu }_L) \in [\mu _L -\Delta _1, \mu _L +\Delta _2]\). For the special case \(\Delta _{1} = \Delta _2\), we have \(C(\tilde{\mu }_L) = \mu _L\). Furthermore, from the assumption that the reorder point \(r = \mu _L +k\sigma _L\), we set \(\bar{{R}}\) is a fuzzy point with membership function \(m_{\tilde{r}} (x) = 1\) if \(x = r\), and \(m_{\tilde{r}} (x) = 0\) if \(x\ne r\). We then obtain the following triangular fuzzy number:

$$\begin{aligned} \tilde{\mu }_L (-) \tilde{r} = (\mu _L -r-\Delta _1, \mu _L -r, \mu _L -r+\Delta _2). \end{aligned}$$
(8)

Note that \(\tilde{r}\) is identical with the fuzzy number \(\tilde{r} = (r,r,r)\), and the arithmetic of fuzzy numbers can be found in several textbooks., e.g., Kaufmann and Gupta (1991).

From the above, \(0 < \Delta _1 <\mu _{L_n}\) and \(0<r-\mu _L =k\sigma _L <k\sigma _{L_0} <\Delta _2\), we have

$$\begin{aligned} \mu _L -r-\Delta _1 < \mu _L -r; \quad 0 < \mu _L -r+\Delta _2. \end{aligned}$$
(9)

From Puri and Ralescu (1986), the fuzzy random variable can be defined as a mapping from \(R\) of probability space (\(\mathfrak R \), B, P) to a family of membership functions. Corresponding to the crisp random variable\(X\), we set the fuzzy random variable \(\tilde{X}\) as

$$\begin{aligned} \tilde{X} : s(\in \mathfrak R )\rightarrow \tilde{X}(s), \end{aligned}$$
(10)

where \(\tilde{X}(s)\) is the membership function. Let the fuzzy set that has \(\tilde{X}(\mu _L)\) as membership function be \(\tilde{X}^{*}(\mu _L) = \tilde{\mu }_L\) [as defined in Eq. (6)].

Next, let us consider \(Y= X-r\), then we can obtain the pdf of random variable \(Y\) as:

$$\begin{aligned} g(y) = \frac{1}{\sqrt{2\pi } \sigma _L} e^{-\frac{(y+r-\mu _L)^{2}}{2\sigma _L^2}},\quad -\infty <y<\infty . \end{aligned}$$
(11)

Corresponding to the crisp random variable \(Y\), fuzzy random variable \(\tilde{Y}\)is defined as:

$$\begin{aligned} \tilde{Y} : t(\in \mathfrak R ) \rightarrow \tilde{Y}(t), \end{aligned}$$
(12)

where \(\tilde{Y}(t)\) is the membership function. Also, let the fuzzy set that has \(\tilde{Y}(\mu _L)\) as membership function be \(\tilde{Y}(\mu _L) = \tilde{X}^{*}(\mu _L) (-)\tilde{r} = \tilde{\mu }_L (-)\tilde{r}\) [as defined in Eq. (8)]. Then, we have

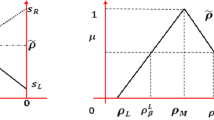
$$\begin{aligned} \tilde{Y}(\mu _L)(y) = \left\{ {\begin{array}{ll} \frac{y-(\mu _L -r-\Delta _1)}{\Delta _1},&\quad \mu _L -r-\Delta _1 \le y\le \mu _L -r \\ \frac{(\mu _L -r+\Delta _2)-y}{\Delta _2},&\quad \mu _L -r\le y\le \mu _L -r+\Delta _2, \\ 0,&\quad \mathrm{otherwise} \\ \end{array}}\right. \end{aligned}$$
(13)

The picture is shown in Fig. 2. \(\tilde{Y}(\mu _L)(y)\) is a continuous function on \(-\infty <y<\infty \). From the crisp probability theory, we note that \(\tilde{Y}(\mu _L)(Y)\) is a crisp random variable. From Fig. 1 and \(y\ge 0\), we can derive the expectation

$$\begin{aligned} E(\tilde{Y}(\mu _L)(Y))^{+} = \int \limits _0^{\mu _L -r+\Delta _2} {\left({\frac{\left({\mu _L -r+\Delta _2} \right)-y}{\Delta _2} x \frac{1}{\sqrt{2\pi } \sigma _L} e^{-\frac{(y+r-\mu _L)^{2}}{2\sigma _L^2}}}\right)} dy (>0)\nonumber \\ \end{aligned}$$
(14)

Let \(w = \frac{y+r-\mu _L}{\sigma _L},\,\phi (a) = \frac{1}{\sqrt{2\pi }}e^{-\frac{a^{2}}{2}}\), and \(\Phi (a) = \frac{1}{\sqrt{2\pi }}\int \nolimits _{-\infty }^a {e^{-\frac{w^{2}}{2}}} dw\), then from \(r = \mu _L +k\sigma _L\), we obtain (see “Appendix 4”)

$$\begin{aligned} E(\tilde{Y}(\mu _L)(Y))^{+}&= \frac{1}{\sqrt{2\pi } \Delta _2}\int \limits _k^{\frac{\Delta _2}{\sigma _L}} {(\Delta _2 -\sigma _L w)e^{-\frac{w^{2}}{2}}dw} \nonumber \\&= \Phi \left({\frac{\Delta _2}{\sigma _L}} \right)-\Phi \left(k \right)+\frac{\sigma _L}{\Delta _2} \left[{\phi \left({\frac{\Delta _2}{\sigma _L}}\right)-\phi (k)} \right], \end{aligned}$$
(15)

where \(\phi (\cdot )\) and \(\Phi (\cdot )\)is the pdf and the cumulative distribution function (cdf) of the standard normal distribution, respectively.

Fig. 2
figure 2

Triangular fuzzy number

Full size image

Let \(E(\tilde{Y})^{+} = E(\tilde{Y}(\mu _L)(Y))^{+}\), then when the term \(E({X-r} )^{+}\) in Eq. (2) is changed to be\(E(\tilde{Y})^{+}\), we obtain the following theorem.

Theorem 1

In Eq. (2), when the crisp random variable \(X\) with the probability distribution \(N(\mu _L, \sigma _L)\) is changed to be the fuzzy random variable \(\tilde{X}\) (as expressed in Eq. (10)), we obtain the total expected annual cost in the fuzzy sense

$$\begin{aligned} EAC_1 (Q,L; \Delta _1, \Delta _2)&= \frac{D}{Q}\left[{A+\Pi E(\tilde{Y})^{+}+C(L)} \right]+ \frac{h_2}{2Q}\left({Q-W+k\sigma \sqrt{L}} \right)^{2}\nonumber \\&+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}\left({W-k\sigma \sqrt{L}} \right)^{2}}\right], \end{aligned}$$
(16)

for \(Q>0, L\in [L_i, L_{i-1}], i = 1,2,\ldots ,n\).

As mentioned earlier, due to various uncertainties, the annual average demand may have a little fluctuation, especially in a perfect competitive market. Therefore, it is difficult for the decision-maker to assess the annual average demand by a crisp value \(D\), but easier to determine it by an interval \([D-\Delta _3, D+\Delta _4]\). Similar to the previous approach, corresponding to the interval \([D-\Delta _3, D+\Delta _4]\), we can set the following triangular fuzzy number

$$\begin{aligned} \tilde{D} = (D-\Delta _3, D, D+\Delta _4) \end{aligned}$$
(17)

where, \(\Delta _3\) and \(\Delta _4\) are determined by the decision-maker and should satisfy the conditions: \(0<\Delta _3 <D\) and \(0<\Delta _4\).

Now, we get the following by centroid method:

$$\begin{aligned} C\left({\tilde{D}} \right) = D+\frac{1}{3}\left({\Delta _4 -\Delta _3}\right) > 0, \end{aligned}$$
(18)

which is the estimate of total demand in the fuzzy sense.

Theorem 2

Fuzzifying the annual average demand D in Eq. (16) to be the triangular fuzzy number D as shown in Eq. (17), then we obtain:

  1. (i)

    the fuzzy total cost as

    $$\begin{aligned} F_{\left({Q,L} \right)} (\tilde{D})&= \frac{\tilde{D}}{Q}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C(L)} \right\} +\frac{h_2}{2Q}\left({Q-W+k\sigma \sqrt{L}} \right)^{2}\nonumber \\&+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}\left({W-k\sigma \sqrt{L}} \right)^{2}} \right] \end{aligned}$$
    (19)
  2. (ii)

    the estimate of total expected annual cost in the fuzzy sense as

    $$\begin{aligned} K\left({Q,L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} \right)&\equiv C\left({F_{\left({Q,L} \right)} \left({\tilde{D}} \right)} \right)= EAC_1 (Q,L; \Delta _1, \Delta _2)\nonumber \\&+ \frac{\Delta _4 -\Delta _3}{3Q}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C(L)} \right\} , \end{aligned}$$
    (20)

for \(Q>0, L\in [L_i, L_{i-1}], i = 1,2,\ldots ,n\).

Proof

  1. (i)

    For each \(Q>0, L\in [L_i, L_{i-1}], i = 1,2,\ldots ,n\), from Eq. (16), we set \(F_{\left({Q,L} \right)} \left(D \right) \equiv EAC1(Q,L; \Delta _1, \Delta _2)\) and fuzzyfy \(D\) to be the fuzzy number \(\tilde{D}\) as in Eq. (17), then the result shoed in Eq. (19) is obtained.

  2. (ii)

    Since \(Q>0\) and \(A+\Pi E\left({\tilde{Y}} \right)^{+}+C(L)>\)0, hence we can get the following triangular number:

    $$\begin{aligned} F_{\left({Q,L} \right)} (\tilde{D}) = (F_1, F_2, F_3), \end{aligned}$$
    (21)

   where

$$\begin{aligned} F_1&= \frac{D-\Delta _3}{Q}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C(L)} \right\} +\frac{h_2}{2Q}\left({Q-W+k\sigma \sqrt{L}} \right)^{2}\\&+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}\left({W-k\sigma \sqrt{L}} \right)^{2}} \right]\\&= EAC1(Q,L; \Delta _1, \Delta _2) - \frac{\Delta _3}{3Q}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C(L)} \right\} ,\\ F_2&= EAC1(Q,L; \Delta _1, \Delta _2),\\ F_3&= \frac{D+\Delta _4}{Q}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C(L)} \right\} +\frac{h_2}{2Q}\left({Q-W+k\sigma \sqrt{L}} \right)^{2}\\&+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}\left({W-k\sigma \sqrt{L}} \right)^{2}} \right]\\&= EAC_1 (Q,L; \Delta _1, \Delta _2) + \frac{\Delta _4}{3Q}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C(L)}\right\} . \end{aligned}$$

By centroid method \(F_{(Q,L)} (\tilde{D})\) is defuzzified to

$$\begin{aligned} C\left({F_{\left({Q,L} \right)} \left({\tilde{D}} \right)} \right) = \frac{1}{3}\left({F_1 +F_2 +F_3} \right). \end{aligned}$$
(22)

\(\square \)

Substituting the values of \(F_1,F_2\) and \(F_3\) in Eq. (22) we get the required result which is denoted by \(K({Q,L;\,\Delta _1, \Delta _2, \Delta _3, \Delta _4} )\), as shown in Eq. (20).

4.2 Constrained fuzzy-stochastic model

For the fuzzy random lead-time demand the inequality in the problem, described by (4), becomes

$$\begin{aligned} p(1-\lambda )\tilde{\mu } _L +B \ge p\lambda k\sigma _L +p\lambda Q. \end{aligned}$$

Then the problem (4) reduces to

$$\begin{aligned} \text{ Min} \,\,EAC&= A\frac{D}{Q}+\frac{h_2}{2Q}(Q-W+k\sigma \sqrt{L})^{2}+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}(W-k\sigma \sqrt{L})^{2}} \right]\nonumber \\&+\frac{D}{Q}\left[{\Pi E(X-r)^{+} + C(L)} \right] \end{aligned}$$
(23)

subject to,

$$\begin{aligned} p(1-\lambda )\tilde{\mu }_L +B \ge p\lambda k\sigma _L +p\lambda Q. \end{aligned}$$

Denoting \(p(1-\lambda )\tilde{\mu }_L +B\) by \(\tilde{\xi } =(\xi _1, \xi _2, \xi _3)\) and \(p\lambda k\sigma _L +p\lambda Q\) by \(a\) the above inequality becomes

$$\begin{aligned} \tilde{\xi } \ge a. \end{aligned}$$

Following possibility theory (cf. Liu and Iwamura 1998a, b), the fuzzy membership function is given as follows.

$$\begin{aligned} Pos\left({\tilde{\xi } \ge a} \right) = \left\{ {\begin{array}{ll} 1,&\quad a\le \xi _2\\ \frac{\xi _3 -a}{\xi _3 -\xi _2},&\quad \xi _2 \le a\le \xi _3 \\ 0,&\quad a\ge \xi _3\\ \end{array}} \right.. \end{aligned}$$

The surprise function \(s_\xi \) for the membership function \(Pos({\tilde{\xi } \ge a})\), is given by (cf. Neumaier 2003)

$$\begin{aligned} s_\xi = \left[{\left\{ {Pos\left({\tilde{\xi } \ge a} \right)} \right\} ^{-1}-1} \right]^{2}. \end{aligned}$$

Introducing the above surprise function, we have the above problem as follows

$$\begin{aligned} \text{ Min}\,\,EAC_c&= A\frac{D}{Q}+\frac{h_2}{2Q}(Q-W+k\sigma \sqrt{L})^{2}+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}(W-k\sigma \sqrt{L})^{2}} \right]\\&+ \frac{D}{Q}\left[{\Pi E(X-r)^{+} + C(L)} \right]+\left({\frac{a-\xi _2}{\xi _3 -a}} \right)^{2}, \end{aligned}$$

where,

$$\begin{aligned} (\xi _1, \xi _2, \xi _3)&\!=\!&\left\{ {p(1-\lambda )(\mu _L -\Delta _1) \!+\!B, p(1-\lambda )\mu _L \!+\!B, p(1-\lambda )(\mu _L \!+\!\Delta _2) +B} \right\} ,\\ a&= p\lambda k\sigma _L +p\lambda Q. \end{aligned}$$

Now considering annual demand as fuzzy as considered in the previous problem, the above problem becomes

$$\begin{aligned} \text{ Min}\,\,EAC_2&= A\frac{D}{Q}+\frac{h_2}{2Q}(Q-W+k\sigma \sqrt{L})^{2}+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}(W-k\sigma \sqrt{L})^{2}} \right]\nonumber \\&+ \frac{D}{Q}\left[{\Pi E(X-r)^{+} + C(L)} \right] + \frac{\Delta _4 -\Delta _3}{3Q}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C(L)} \right\} \nonumber \\&+\left({\frac{a-\xi _2}{\xi _3 -a}} \right)^{2}, \end{aligned}$$
(24)

where,

$$\begin{aligned} (\xi _1, \xi _2, \xi _3)&\!=\!&\left\{ {p(1-\lambda )(\mu _L -\Delta _1) \!+\!B, p(1-\lambda )\mu _L \!+\!B, p(1-\lambda )(\mu _L +\Delta _2) \!+\!B} \right\} \!,\\ a&= p\lambda k\sigma _L +p\lambda Q. \end{aligned}$$

5 Optimal solution of the models

5.1 Optimal solution of the unconstrained fuzzy stochastic model (cf. Sect. 4.1)

The solution technique (ref. Chang et al. 2006a, b) is discussed for finding the optimal order quantity and the optimal lead time giving the minimum value of the total expected annual cost in the fuzzy sense, while the decision-maker takes \(\Delta _1, \Delta _2, \Delta _3, \Delta _4 \) satisfying the conditions:

\(0<\Delta _1 <\mu _{L_n}, \Delta _2 > k \sigma _{L_0} >0, \quad 0<\Delta _3 <D\) and \(0<\Delta _4\).

Let \(S = \left\{ {L| L\in [L_i, L_{i-1}], i = 1,2,\ldots ,n} \right\} \). Also, from Eq. (1), let

$$\begin{aligned} C_i (L)&\equiv C(L)= c_i [L_{i-1} -L] + \sum \limits _{j=i}^{i-1} {c_j} (b_j -a_j),\\ i&= 1,2,\ldots ,n\quad \text{ and}\quad \sum \limits _{j=i}^0 {c_j} (b_j -a_j) = 0. \end{aligned}$$

From Eqs. (18) and (22), let

$$\begin{aligned} G_i \left({Q,L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} \right)&\!=\! \frac{D}{Q}\left[{A\!+\!\Pi E(\tilde{Y})^{+}\!+\!C_i (L)} \right]\!+\! \frac{h_2}{2Q}\left({Q-W+k\sigma \sqrt{L}} \right)^{2}\nonumber \\&+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}\left({W-k\sigma \sqrt{L}} \right)^{2}} \right] \nonumber \\&+ \frac{\Delta _4 -\Delta _3}{3Q}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C_i (L)} \right\} , \end{aligned}$$
(25)

for \(Q>0, L\in [L_i, L_{i-1}], i = 1,2,\ldots ,n\).

Then the mathematical expression of our problem is to find

$$\begin{aligned} MK&\equiv \mathop {\min } \limits _{Q>0,L\in S} K\left({Q,L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} \right) = \mathop {\min } \limits _{L\in S} \mathop {\min } \limits _{Q>0} K\left({Q,L;\, \Delta _1, \Delta _2, \Delta _3, \Delta _4} \right)\nonumber \\&= \mathop {\min } \limits _{1\le i\le n} \mathop {\min }\limits _{L\in [L_i, L_{i-1}]} \mathop {\min } \limits _{Q>0} G_i \left({Q,L;\,\Delta _1, \Delta _2, \Delta _3, \Delta _4} \right) \end{aligned}$$
(26)

We first find \( \mathop {\min } \nolimits _{Q>0} G_i ({Q,L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} )\).

For fixed \(i\in \{1,2,\ldots ,n\} \) and \(L\in [L_i, L_{i-1}]\), we take the first and second partial derivatives of Eq. (25) with respect to \(Q\), and obtain

$$\begin{aligned} \frac{\partial }{\partial Q} G_i&= -\frac{D}{Q^{2}}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C_i (L)} \right\} -\frac{h_2}{2Q^{2}}\left({Q-W+k\sigma \sqrt{L}} \right)^{2}\nonumber \\&+\frac{h_2}{Q}\left({Q-W+k\sigma \sqrt{L}} \right) -\frac{h_1}{Q^{2}}\left[{WQ-\frac{1}{2}\left({W-k\sigma \sqrt{L}} \right)^{2}} \right]\nonumber \\&+\frac{h_1 W}{Q}-\frac{\Delta _4 -\Delta _3}{3Q^{2}}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C_i (L)} \right\} \end{aligned}$$
(27)

and

$$\begin{aligned} \frac{\partial ^{2}}{\partial Q^{2}} G_i&= \frac{2D}{Q^{3}}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C_i (L)} \right\} +\frac{h_2}{Q^{3}}\left({Q-W+k\sigma \sqrt{L}} \right)^{2}\nonumber \\&-\frac{2h_2}{Q^{2}}\left({Q-W+k\sigma \sqrt{L}} \right)+\frac{h_2}{Q}+\frac{2h_1}{Q^{3}}\left[{WQ-\frac{1}{2}\left({W-k\sigma \sqrt{L}} \right)^{2}} \right]\nonumber \\&-\frac{2h_1 }{Q^{2}}W+\frac{2}{3}\frac{\Delta _4 -\Delta _3}{Q^{3}}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C_i (L)} \right\} \nonumber \\&= \frac{2H_i}{3Q^{3}}\left({3D+\Delta _4 -\Delta _3} \right)-\frac{h_1}{Q^{3}}\left({W-k\sigma \sqrt{L}} \right)^{2}\nonumber \\&+\frac{h_2}{Q^{3}}\left({W-k\sigma \sqrt{L}} \right)^{2},\,\text{ where}\,H_i =A+\Pi E\left({\tilde{Y}} \right)^{+}+C_i (L)\nonumber \\&= \frac{2H_i}{3Q^{3}}\left({3D+\Delta _4 -\Delta _3} \right)-\frac{h_1 -h_2}{Q^{3}}\left({W-k\sigma \sqrt{L}} \right)^{2} \end{aligned}$$
(28)

We choose \(\Delta _3, \Delta _4 \) such that

$$\begin{aligned} V = \frac{2H_i}{3}\left({3D+\Delta _4 -\Delta _3} \right) - \left({h_1 -h_2} \right)\left({W-k\sigma \sqrt{L}} \right)^{2}>0. \end{aligned}$$
(29)

Now under the condition (29), \(\frac{\partial ^{2}}{\partial Q^{2}} G_i ({Q,L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} ) > 0\). Thus for fixed \(i\in \{1,2,\ldots ,n\} \) and \(L\in [L_i, L_{i-1}]\), the minimum value of \(G_i (Q,L;\,\Delta _1,\Delta _2, \Delta _3, \Delta _4 )\) will occur at the point \(Q\) that satisfies \(\frac{\partial }{\partial Q} G_i ({Q,L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} ) = 0\). We solve this equation for \(Q\), which is denoted by \(Q_i^{(0)} (L)\), as follows:

$$\begin{aligned}&\frac{\partial }{\partial Q} G_i \left({Q,L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} \right) = 0\nonumber \\&\quad \Rightarrow \left({\frac{\Delta _4 -\Delta _3}{3}+D} \right)H_i +\frac{h_2}{2}\left({Q-W+k\sigma \sqrt{L}} \right)^{2}\nonumber \\&\qquad \quad +\,h_1 \left[{WQ-\frac{1}{2}\left({W-k\sigma \sqrt{L}} \right)^{2}} \right] = h_2 Q \left({Q-W+k\sigma \sqrt{L}} \right)+h_1 QW\nonumber \\&\quad \Rightarrow Q_i^{(0)} (L)= \sqrt{\frac{2H_i}{3h_2} \left({\Delta _4 -\Delta _3 +3D} \right)-\frac{\left({h_1 -h_2} \right)}{h_2} \left({W-k\sigma \sqrt{L}} \right)^{2}}\qquad \end{aligned}$$
(30)

The minimum value of \(G_i ({Q,L; \Delta _1, \Delta _2, \Delta _3, \Delta _4})\) is \(G_i ({Q_i^{(0)} (L), L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} )\) i.e, \(G_i ({Q_i^{(0)} (L), L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} )=\mathop {\min } \nolimits _{Q>0} G_i ({Q,L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} )\).

Therefore from Eq. (26), the problem is reduced to

$$\begin{aligned} MK= \mathop {\min } \limits _{1\le i\le n} \mathop {\min }\limits _{L\in [L_i, L_{i-1}]} G_i \left({Q_i^{(0)} (L), L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} \right). \end{aligned}$$
(31)

Next, for fixed \(i\in \{1,2,\ldots ,n\} \), by the numerical analysis method, we can find \(L_i^{(0)} \in [L_i, L_{i-1}]\) such that

$$\begin{aligned} G_i \left({Q_i^{(0)} ({L_i^{(0)}} ), L_i^{(0)} ; \Delta _1, \Delta _2, \Delta _3, \Delta _4} \right)=\mathop {\min } \limits _{L\in [L_i, L_{i-1}]} G_i \left({Q_i^{(0)} (L), L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} \right).\nonumber \\ \end{aligned}$$
(32)

Furthermore, for each \(i=1,2,\ldots ,n \), we evaluate the value of \(G_i ({Q_i^{(0)}({L_i^{(0)}}), L_i^{(0)}}\); \({\Delta _1, \Delta _2, \Delta _3, \Delta _4})\) and find \(\mathop {\min }\nolimits _{1\le i\le n} G_i ({Q_i^{(0)} ({L_i^{(0)}} ), L_i^{(0)};\,\Delta _1, \Delta _2, \Delta _3, \Delta _4} )\).

If \(G_m ({Q_m^{(0)} ({L_m^{(0)}} ), L_m^{(0)};\, \Delta _1, \Delta _2,\Delta _3, \Delta _4} )= \mathop {\min } \nolimits _{1\le i\le n} G_i ({Q_i^{(0)} ({L_i^{(0)} } ), L_i^{(0)};\, \Delta _1,}\) \({\Delta _2,\Delta _3, \Delta _4})\), then we have

$$\begin{aligned} MK= G_m \left({Q_m^{(0)} \left({L_m^{(0)}} \right), L_m^{(0)};\, \Delta _1, \Delta _2,\Delta _3, \Delta _4}\right). \end{aligned}$$
(33)

Thus the optimal lead time is \(L^{*} = L_m^{(0)}\) and the optimal order quantity is \(Q^{*}=Q_m^{(0)} (L_m^{(0)})\).

5.1.1 Numerical example of the unconstrained fuzzy stochastic model

We use the following data to find the results of the proposed model and compare them with those obtained from the crisp model. \(D= 730\) units /year; \(A =\$200\) per order; \(W =30;\,h_1 =\$25\) per unit per year; \(h_2 =\$20\) per unit per year; \(\Pi =\) $ 60 per unit short; \(\sigma = 7\) units /week; \(q = 0.2\) (hence \(k =0.8416\)) and the lead time, having three components, is given in Table 1.

Table 1 Lead time data
Full size table

Using the data given in Table 1, we get the following length of lead time with some components crashed to their minimum duration: \(L_0 = 70\) days, \(L_1=56\) days, \(L_2=42\) days, \(L_3 = 35\) days, \(L_4=28\) days, Hence \(L_4 = \text{ min}\,L_i = 28\) days(\(=\) 4 weeks), \(L_0 =\text{ max}\,L_i =70\) days(\(=\) 8 weeks), \(0<\Delta _1 <\mu L_4 =56\) and \(\Delta _2 > k \sigma _{L_0} =k\sigma \sqrt{L} =18.62\); \(0<\Delta _3 <D\,=\,730\) and \(0<\Delta _4 \). Also, the lead time crashing costs are as follows.

For fixed \(i\in \{1,2,\ldots ,n\} \) and \(L\in [L_i, L_{i-1}]\), from Eq. (30)

$$\begin{aligned} Q_i^{(0)} (L)&= \sqrt{\frac{2H_i}{3h_2} \left({\Delta _4 -\Delta _3 +3D} \right)-\frac{\left({h_1 -h_2} \right)}{h_2} \left({W-k\sigma \sqrt{L}} \right)^{2}}\\&= \sqrt{\frac{1}{30}\left({\Delta _4 \!-\!\Delta _3 \!+\!2190} \right)\left({200\!+\!60 E\left({\tilde{Y}} \right)^{+}\!+\!C_i (L)} \right)\!-\!\frac{1}{4}\left({30-18.62} \right)^{2}}. \end{aligned}$$

Corresponding total cost

$$\begin{aligned}&G_i \left({Q_i^{(0)} (L), L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} \right) = \frac{730}{Q_i^{(0)} (L)}\left[{200+60E(\tilde{Y})^{+}+C_i (L)} \right]\\&\qquad \!+ \frac{10}{Q_i^{(0)} (L)}\left({Q_i^{(0)} (L)\!-\!30\!+\!18.62} \right)^{2} \!+\! \frac{25}{Q_i^{(0)} (L)}\left[{30 Q_i^{(0)} (L)-\frac{1}{2}(30-18.62)^{2}} \right]\\&\qquad +\frac{\Delta _4 -\Delta _3}{3Q_i^{(0)} (L)}\left[{200+60E(\tilde{Y})^{+}+C_i (L)} \right], \quad L\in [L_i, L_{i-1}], i = 1,2,3,4, \end{aligned}$$

where

$$\begin{aligned} E(\tilde{Y})^{+} = \Phi \left({\frac{\Delta _2}{7\sqrt{L}}} \right)-\Phi (0.8416)+\frac{7\sqrt{L}}{\Delta _2} \left[{\phi \left({\frac{\Delta _2}{7\sqrt{L}}} \right)-\phi \left({0.8416} \right)} \right]. \end{aligned}$$

It is further noticed that \(\Delta _1, \Delta _2, \Delta _3\) and \(\Delta _4\) are given parameters. When \(L\) is specified, we can use the formulas listed in Table 2 to calculate \(U_i (L)\), and by checking the standard normal distribution table or using the software such as Microsoft Excel to find the values of \(\Phi ({\frac{\Delta _2}{7\sqrt{L}}} ),\,\Phi ({0.8416} ),\phi ({\frac{\Delta _2}{7\sqrt{L}}} )\) and \(\phi ({0.8416} )\), then calculate \(E(\tilde{Y})^{+}\). Once \(C_i (L)\) and \(E(\tilde{Y})^{+}\) are obtained, the values of \(Q_i^{(0)} (L)\) and \(G_i ({Q_i^{(0)} (L), L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} )\), can be found easily.

Table 2 Lead time crashing cost
Full size table

For example, consider a case where\(\Delta _1 = 10, \Delta _2 = 25, \Delta _3 = 30, \Delta _4 = 60\). For \(i \!=\! 1, L\in [L_1, L_0]\) \(=\) [56,70], using \(C_1 (L)=28-0.4L\) and above procedure, we obtain the results listed in Table 3. Here, for \(L\in \) [56,70], \(V>0\) is satisfied. From Table 3 we find that the minimum value of \(G_1 ({Q_1^{(0)} (L), L; \Delta _1, \Delta _2, \Delta _3, \Delta _4} )\), for \(L\in \) [56, 70], is $2952.81, which occurred at \(L=56\) days, and \(Q_1^{(0)} (L)=123.48\) units. From Eq. (32), this solution is denoted by \(L_1^{(0)}=56, Q_1^{(0)} ({L_1^{(0)}} )=123.48\) and \(G_1 ({Q_1^{(0)} ({L_1^{(0)}} ), L_1^{(0)};\,\Delta _1, \Delta _2, \Delta _3, \Delta _4}) = \$2952.81\).

Table 3 Optimal solutions of unconstrained fuzzy-stochastic model for different values of \(L\)
Full size table

For \(i \,{=}\, 2,\,L\in [L_2, L_1]=[42, 56],\,C_2 (L) \,{=}\, 72.80-1.2L\); for \(i \,{=}\, 3,\,L\in [L_3, L_2]= [35, 42], C_3 (L) \,{=}\, 232.4-5L\) and for \(i \,{=}\, 4,\,L\!\in \! [L_4, L_3]\,{=}\,[28, 35],\,C_4 (L) \,{=}\, 337.40-8L\), we use the same procedure and obtain the following results: \(L_2^{(0)}\,=\,56, Q_2^{(0)} ({L_2^{(0)}} )=123.48\) and \(G_2 ({Q_2^{(0)} ({L_2^{(0)}} ), L_2^{(0)};\, \Delta _1, \Delta _2, \Delta _3, \Delta _4} ) = \$2952.81; L_3^{(0)} \!=\!42, \,Q_3^{(0)} ({L_3^{(0)}} )\,=\,128.57\) and \(G_3 ({Q_3^{(0)} ({L_3^{(0)}}), L_3^{(0)} ; \Delta _1, \Delta _2, \Delta _3,}\) \({\Delta _4} ) = \$3010.04\,\,\text{ and}\,\,L_4^{(0)} =35, Q_4^{(0)} ({L_4^{(0)}} ) = 138.39\) and \(G_4 ({Q_4^{(0)} ({L_4^{(0)}} ), L_4^{(0)} ; \Delta _1,}\) \( {\Delta _2, \Delta _3, \Delta _4} ) = \$3181.25\).

By comparing the values of \(G_i ({Q_i^{(0)} (L), L; \Delta _1 ,\Delta _2, \Delta _3, \Delta _4} )\), for \(i = 1,2,3,4\), we get the minimum value \(MK = G_1 ({Q_1^{(0)} ({L_1^{(0)} } ), L_1^{(0)} ; \Delta _1, \Delta _2, \Delta _3, \Delta _4} ) = G_2 (Q_2^{(0)} ({L_2^{(0)}} ), L_2^{(0)} ; \Delta _1, \Delta _2, \Delta _3, \Delta _4 )\) = $2952.81. Thus the optimal lead time is \(L^{*}=L_1^{(0)} =L_2^{(0)} =\) 56 days (\(=\) 8 weeks)., and the optimal order quantity is \(Q^{*} = Q_1^{(0)} ({L_1^{(0)}} )=Q_2^{(0)} ({L_2^{(0)}} )=\) 124 units (truncated).

5.1.2 Optimal solution of the unconstrained crisp stochastic model

Now to compare the results with those obtained from crisp model (crisp random lead-time demand and crisp annual demand), we first find the optimal solution of crisp model in Table 4.

Table 4 The optimum solutions of unconstrained crisp model for different value of \(L\)
Full size table

From the results given in Table 5, we observe that the solution of the crisp model is given by \(L^{*} \mathbf{= 6 weeks;}\) \(Q^{*} = \mathbf{157 units (truncated)}; EAC(Q^{*},L^{*}) \mathbf{= \$ 3572.84}\).

Table 5 The results of solution of constrained fuzzy-stochasticmodel for different values of \(L\)
Full size table

5.2 Optimal solution of the constrained fuzzy stochastic model (cf. Sect. 4.2)

The problem (24) cannot be solved by the procedure used above, for the first order derivative with respect to \(Q\) considering \(L\) fixed wouldn’t give any explicit solution for \(Q\). Therefore in this case we follow the following indirect way.

We find the optimal value of \(Q_1 \) minimizing the function \(EAC_2 \) with the help of technique, GRG. The corresponding values of other parameters, the surprise function and objective function, \(EAC_3 \) are given in Table 6, where

$$\begin{aligned} EAC_3&= A\frac{D}{Q}+\frac{h_2}{2Q}(Q-W+k\sigma \sqrt{L}) ^{2}+\frac{h_1}{Q}\left[{WQ-\frac{1}{2}(W-k\sigma \sqrt{L})^{2}} \right]\\&+\frac{D}{Q}\left[{\Pi E(X-r)^{+} + C(L)} \right] + \frac{\Delta _4 -\Delta _3}{3Q}\left\{ {A+\Pi E\left({\tilde{Y}} \right)^{+}+C\left(L \right)} \right\} , \end{aligned}$$

Interestingly, it can be seen that for the optimal value of Q, surprise function’s contribution is zero.

Table 6 Optimal solutions of constrained crisp model for different values of \(L\)
Full size table

5.2.1 Numerical example of the constrained fuzzy stochastic model

Here, all data remain same as taken in the unconstrained model; only new data taken as \(B=1475\); \(p=12\); \(\lambda =0.95\).

From Tables 5 and 6 we see that the minimum value of the expected annual cost function is attained at \(L=L^{*} = \mathbf{8} \) weeks. The corresponding value of \(Q\,=\, Q^{*} = \mathbf{119(truncated);} EAC_3 \mathbf{*= \$ 2954.80;}\)

5.2.2 Numerical example of the stochastic model with budget constraint

Now to compare the results with those obtained from crisp model (crisp random lead-time demand and crisp annual demand), we first find the optimal solution of crisp model in Table 6.

6 Discussion

In Sect. 5.1.1, we find optimal solutions of unconstrained model with fuzzy-stochastic lead time as \(L^{*} = \mathbf{56\,days (8\,weeks);} Q^{*} =\mathbf{124\,units\,(truncated);} EAC(Q^{*},L^{*})= \$ 2952.80\) where as in Sect. 5.1.2, optimal solutions of unconstrained model with stochastic lead time (crisp) as \(L^{*} = \mathbf{42\,days (6\,weeks);} Q^{*}=\mathbf{157 units (truncated);} EAC(Q^{*},L^{*})= \$ 3572.84\).

In Sect. 5.2.1, we find optimal solutions of constrained model with fuzzy-stochastic lead time as \(L^{*} = \mathbf{56\,days (8\,weeks);} Q^{*} = \mathbf{119\,units (truncated);}\) \(EAC(Q^{*},L^{*}) = \$ 2954.80\) where as in Sect. 5.2.2, optimal solutions of constrained model with stochastic lead time (crisp) as \(L^{*}\) \(=\) 42 days (6 weeks); \(Q^{*} =\mathbf{120\,units (truncated);} EAC(Q^{*},L^{*})= \mathbf{\$ 3689.61}.\)

From the above results, it is observed that the models (both unconstrained and constrained type) with fuzzy-stochastic lead time give significantly less cost than the cost due to the model with stochastic lead time.

Moreover, from the above results it is verified that the constrained models give more costs than the corresponding unconstrained models, which are expected in the minimization problems.

7 Conclusion

In this article, fuzzy-stochastic lead time has been introduced in a two warehouse inventory model and the corresponding optimal results are obtained. As a particular case, the results for the two-warehouse inventory system with stochastic lead time (termed here as crisp model) are also obtained. Here, a methodology of introducing fuzziness on stochastic parameter has been presented. This process of treatment of fuzzy-stochastic parameters can be incorporated in the other fuzzy-stochastic inventory models such as models with inventory costs represented by fuzzy-stochastic parameters, fuzzy-stochastic demand, etc.