Introduction

Groundwater inflow into a tunnel may cause large drawdowns in the water table (Zhao et al. 2017; Li et al. 2018a; Wei et al. 2020). The energy-water balance of ecosystems is affected by these drawdowns and vegetation sustainability can be seriously compromised due to a lack of water when the drawdown exceeds the capacity of the ecological groundwater table (Sweetenham et al. 2017; Gokdemir et al. 2019, 2021). Limited discharge of groundwater was typically employed to reduce the drawdown and amount of groundwater inflow (Li et al. 2018b; Cheng et al. 2019a; Zhang and Sun 2019). Based on the goal of limited discharge, waterproofing and drainage systems (WDS) have been designed to control the amount of groundwater inflow (Farhadian and Nikvar-Hassani 2018; Li et al. 2021). Therefore, the prediction of groundwater inflow into water-rich mountain tunnels is a critical issue for the design of WDS (Ministry of Railways of the People's Republic of China 2004; Ding et al. 2007; Hassani et al. 2018). Various methods for estimating groundwater inflow into tunnels have been developed to provide a theoretical basis for the optimal design of WDS for tunnels and to minimize their adverse effects on the ecological environment. Examples of such methods include analytical solutions (Huang et al. 2010; Butscher 2012; Sedghi and Samani 2015; Tang et al. 2018; Cheng et al. 2019b), empirical methods (Katibeh and Aalianvari 2009; Zarei et al. 2013; Farhadian and Katibeh 2017), and numerical methods (Mikaeil and Doulati Ardejani 2009; Zhang et al. 2017; Farhadian et al. 2016; Nikvar-Hassani et al. 2016; Park et al. 2020).

Analytical solutions are useful because they can rapidly provide desirable approximations without requiring advanced computations (Maleki, 2018; Hassani et al. 2018). Furthermore, based on the simplification and practical theories of analytical solutions, these solutions have been widely utilized to calculate groundwater inflow into tunnels (Goodman et al. 1965; Bobet 2016; Su et al. 2017; Cheng et al. 2019a). For example, Goodman et al. (1965) and Heuer (2005) implemented the mirror image method developed by Harr (1962) to derive analytical solutions for groundwater inflow. El-Tani (2003), Kolymbas and Wagner (2007), Park et al. (2008), and Huang et al. (2010) applied the conformal mapping theory to derive analytical solutions for predicting groundwater inflow into drained tunnels under various tunnel boundary conditions. However, these analytical solutions were developed without the consideration of the tunnel lining. For the lined tunnel, discrepancies may exist between these solutions and actual values because groundwater inflow is sensitive to lining properties such as thickness and permeability (Tan et al. 2018).

In recent years, researchers have derived analytical solutions by assuming that composite lining is a single-layer lining and that groundwater uniformly penetrates the tunnel along the lining perimeter. For example, Wang (2003), Zhang (2006), Wang et al. (2008), and Tan et al. (2018) developed analytical solutions for estimating groundwater inflow into deeply buried lined tunnels. Yang et al. (2014) and Cheng et al. (2019b) derived analytical solutions for predicting groundwater inflow into lined tunnels considering grouting zone. However, composite tunnel linings contain an initial lining, secondary lining, and drainage system (Zhang and Sun 2019). Although some researchers have simplified composite lining as two-layer linings and assumed that groundwater uniformly penetrates the initial and secondary lining (Du et al. 2011; He et al. 2015; Xie et al. 2019), the effects of some WDS components (i.e., waterproof membranes, geotextiles, and blind pipes) on groundwater inflow are ignored in these analytical solutions. In practice, groundwater inflow is drained through blind pipes, rather than flowing uniformly along the lining perimeter, which is why there is always a gap between the predictions of existing analytical solutions and actual groundwater inflow data (He et al. 2015). Therefore, it is necessary to investigate the effects of an entire WDS on groundwater inflow into tunnels.

To the best of our knowledge, no analytical studies on the effects of WDS on groundwater inflow in tunnels have been reported in the existing literature. In this study, a water drainage seepage (WDSee) model was first established based on Darcy’s law. An analytical solution for estimating groundwater inflow into a composite-lined tunnel was then derived considering the effects of all components of a WDS (i.e., lining, grouting zone, waterproof membranes, geotextile, and blind pipes). The proposed analytical solution was compared to existing analytical solutions and validated using a numerical model. Finally, a parametric study was conducted to investigate the relationships between groundwater inflow and geometric/physical parameters. The findings of this study can provide a basis for analyzing the potential adverse environmental impacts caused by tunnel drainage and the optimal design of WDS for tunnels.

Theoretical model and analytical solution

In this section, a theoretical model that fully considers WDS is proposed firstly. The seepage path of the model is consistent with the actual tunnel condition. Then, an analytical solution for estimating groundwater inflow into a lined tunnel is derived according to the proposed model.

Proposed WDSee

Theoretical configuration of the model

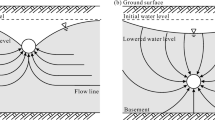
The WDSee model is illustrated in Fig. 1. This model consists of the surrounding rock, initial lining, geotextile, drainage system, waterproof membranes, and secondary lining.

Fig. 1
figure 1

WDSee model

Full size image

Groundwater flows from the surrounding rock into the initial lining, followed by the geotextile, and eventually reaches the circular drainage pipes. The seepage process of groundwater flow obeys Darcy’s law (Ying et al. 2018). After the groundwater flows into the circular drainage pipes, it is discharged through the longitudinal and lateral drainage pipes. Because water discharge is not a seepage process, it was excluded from our analytical model. Unlike existing models, geotextile, waterproof membranes, and circular drainage pipes, which are the main components of WDS, are considered in our model.

As shown in Fig. 1, the parameters r0 and r1 represent the inner and outer radii of the secondary lining, respectively; r2 is the outer radius of the initial lining; and r3 is the radius of the affected zone by the drainage. For the water head parameters, h2 is the water head outside the initial lining, hc is the water head at the geotextile, and H is the water head outside the affected drainage zone in the surrounding rock. For the permeability coefficients, k1 and kr are the permeability coefficients of the initial lining and surrounding rock, respectively. The distance between two adjacent circular drainage pipes is defined as L1. The thickness and permeability coefficient of the geotextile are denoted by t and kt, respectively.

Basic assumptions

The groundwater flowing into the initial lining from the surrounding rock is eventually discharged through the drainage pipes, regardless of leakage from cracks (Wang 2006; Wu and Xue 2006). The water pressure was assumed uniformly acted on the tunnel for the deeply buried tunnel (Wang et al. 2008; Zhang 2006), as shown in Fig. 2. The assumptions of the WDSee model are as follows.

Fig. 2
figure 2

Sketch of the assumption regarding water pressure loading on the tunnel

Full size image
  1. (1)

    The seepage of groundwater obeys the law of conservation of mass (Hassani et al. 2018; Wu and Xue 2006), indicating that the amount of groundwater flowing into the surrounding rock, initial lining, and geotextile are equal. The cross-section of the tunnel is circular. All groundwater is eventually discharged through circular drainage pipes (Wang 2006).

  2. (2)

    The surrounding rock and the initial lining are porous, homogeneous, and isotropic (Kolymbas and Wagner 2007; Su et al. 2017), and the water table is high, steady, and horizontal (Park et al. 2008; Tan et al. 2018). The seepage in the surrounding rock, initial lining, and geotextile obeys Darcy’s law (Ying et al. 2018; Murillo et al. 2014; Farhadian et al. 2017).

  3. (3)

    Groundwater flows along the radial direction in the surrounding rock and initial lining (Wang et al. 2008; Zhang 2006; Yang et al. 2014; Li et al. 2018b) (Fig. 1). Groundwater penetrates uniformly into the circular drainage pipes from the geotextile at a constant rate (Wang et al. 2004). Within the geotextile, groundwater flows along the tunnel axis (Wang 2006; Murillo et al. 2014; Liu 2017) (Fig. 3).

    Fig. 3
    figure 3

    Seepage path of groundwater

    Full size image

Governing equation

According to assumptions (1) and (2), the governing equation for steady-state groundwater flow in isotropic media is expressed in a Laplacian form as follows (Yang et al. 2014; Wu and Xue 2006; Xiao et al. 2009; Liu 2017):

$$\frac{\partial^2h}{\partial r^2}+\frac1r\frac{\partial h}{\partial r}+\frac1{r^2}\frac{\partial^2h}{\partial\theta^2}+\frac{\partial^2h}{\partial z^2}=0$$
(1)

where r is the radius, θ is the angle, z is the variable in the Z axis, and h is the water head.

Boundary conditions

According to the model configuration, four boundary conditions (BCs) can be defined: the BC at the radius of the affected zone by the drainage (BC1), BC at the outer radius of the initial lining (BC2), BC at the outer radius of the secondary lining (BC3), and BC at the inner radius of the secondary lining (i.e., the tunnel circumference) (BC4).

$$\begin{array}{c}\mathrm{BC}1\;:\;h\left|{}_{(r=r_3)}=H\right.\\\mathrm{BC}2\;:\;h\left|{}_{(r=r_2)}=h_2\right.\\\mathrm{BC}3\;:\;h\left|{}_{(r=r_1)}=h_c\right.\\\mathrm{BC}4\;:\;h\left|{}_{(r=r_0)}=0\right.\end{array}$$
(2)

The water head at the inner radius of the secondary lining is zero and the circular drainage pipe is connected to the tunnel boundary (BC4). Therefore, the water head in a circular drainage pipe is also zero (Wang 2006).

Derivation of an analytical solution

Seepage in surrounding rock

The seepage path in the surrounding rock is presented in Fig. 1. Based on assumptions (2) and (3), the groundwater flows along the radial direction in the surrounding rock. Therefore, the water head is constant along the Z axis as \(\frac{{{\partial^2}h}}{{\partial {z^2}}} = 0\) (Arjnoi et al. 2009; Su et al. 2017). Therefore, governing Eq. (1) can be simplified to the following equation (Huang et al. 2010):

$$\frac{{{\partial^2}h}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial h}{{\partial r}} + \frac{1}{{r^2}}\frac{{{\partial^2}h}}{{\partial {\theta^2}}} = 0.$$
(3)

According to the results reported by Bear (1972) and Zhang (2006), \(\frac{{{\partial^2}h}}{{\partial {\theta^2}}} = 0\). Therefore, the groundwater seepage in the surrounding rock obeys the continuity equation based on the symmetry of seepage flow (Yang et al. 2014; Li et al. 2018b).

$$\frac{d}{dr}(r\frac{dh}{{dr}}) = 0$$
(4)

The following expression is obtained by integrating Eq. (3):

$$r\frac{dh}{{dr}} = C,$$
(5)

where C is a constant.

Based on assumptions (1) and (2), the amount of groundwater inflow per meter Q can be expressed as follows (Wang et al. 2008; Yang et al. 2014):

$$Q = A \cdot k \cdot i = 2\pi rk\frac{dh}{{dr}}.$$
(6)

Therefore, the integral constants in Eq. (5) can be obtained as \(C = \frac{Q}{2\pi k}\). The amount of groundwater flowing per meter into the initial lining, Q1, can be expressed as:

$${Q_1} = 2\pi r{k_r}\frac{dh}{{dr}}$$
(7)

The boundary conditions for the surrounding rock are set to \({r_2} < r < {r_3},{h_2} < h < H\). The following equation can be obtained by integrating the variables:

$${Q_1} = \frac{{2\pi {k_r}(H - {h_2})}}{{\ln \frac{{r_3}}{{r_2}}}}.$$
(8)

Seepage in the initial lining

Consider an element of the initial lining in which the longitudinal length of the initial lining is dz and the circumferential length is r1dθ. Let QLi be the amount of groundwater flowing into the geotextile of the element. Based on Darcy’s law and the boundary conditions of the initial lining (BC2, BC3), QLi can be determined using the following equation:

$${Q_{Li}} = k \cdot i \cdot A = \frac{{{k_1}({h_2} - {h_c})}}{{{r_2} - {r_1}}}{r_1}d\theta dz.$$
(9)

Then, the amount of groundwater flowing per meter from the initial lining into the geotextile, Q2, can be obtained as:

$${Q_2} = \frac{{2\int_0^{\frac{{L_1}}{2}} {\int_0^{2\pi } {{Q_{Li}}} } }}{{L_1}}{ = }2\int_0^{\frac{{L_1}}{2}} {\int_0^{2\pi } {\frac{{{k_1}({h_2} - {h_c})}}{{({r_2} - {r_1}){L_1}}}{r_1}d\theta dz} }.$$
(10)

Seepage in the geotextile

The seepage in the geotextile also obeys governing Eq. (1). According to assumption (3) and the results reported by Murillo et al. (2014) and Liu (2017), \(\frac{\partial h}{\partial r}=0 \mathrm{and}\frac{{\partial }^{2}h}{\partial {\theta }^{2}}=0\). Therefore, governing Eq. (1) can be simplified to the following equation:

$$\frac{{{\partial^2}h}}{{\partial {z^2}}} = 0.$$
(11)

Consider an element of the geotextile in which the longitudinal length of the initial lining is L1/2. The maximum water head hm is assumed to be located in the middle of two adjacent circular drainage pipes. The circular drainage pipes are subjected to atmospheric pressure and the water head in the pipes is assumed to be zero (Wang 2006; He et al. 2015). Therefore, the boundary conditions for the geotextile are set to \(h\left| {_{(z = 0)} = 0,} \right.h\left| {_{(z = {L_1}/{2})} = {h_m}} \right.\), as shown in Fig. 4.

Fig. 4
figure 4

Water head distribution in the geotextile

Full size image

Therefore, the water head distribution in the geotextile, hc, (BC3) can be obtained by integrating Eq. (11) as follows:

$${h_c} = \frac{{2z{h_m}}}{{L_1}},$$
(12)

where L1 is the distance between two adjacent circular drainage pipes and \(0 < z < \frac{{L_1}}{2}\).

The velocity of the groundwater flowing into the circular drainage pipe q from the geotextile can be determined using the following expression according to Eq. (12):

$$q = k \cdot i = {k_t} \cdot \frac{{\partial {h_t}}}{\partial z} = \frac{{2{k_t}{h_m}}}{{L_1}},$$
(13)

where \(i\) is the hydraulic gradient.

Based on assumption (3), q is a constant rate, and the amount of groundwater flowing per meter into the circular drainage pipe, Q3, can be expressed as follows:

$${Q_3} = \frac{{2\int_0^{2\pi } {qt{r_1}d\theta } }}{{L_1}} = \frac{{4\pi {r_1}qt}}{{L_1}} = \frac{{8\pi {r_1}{k_t}{h_m}t}}{L_1^2}.$$
(14)

Furthermore, the amount of groundwater flowing per meter from the initial lining into the geotextile Q2 can be obtained by combining Eqs. (10) and (12) as follows:

$${Q_2} = \frac{{2\int_0^{\frac{{L_1}}{2}} {\int_0^{2\pi } {{Q_{Li}}} } }}{{L_1}} = 2\int_0^{\frac{{L_1}}{2}} {\int_0^{2\pi } {\frac{{{k_1}({h_2} - \frac{{2z{h_m}}}{{L_1}})}}{{({r_2} - {r_1}){L_1}}}{r_1}d\theta dz} } = \frac{{2\pi {k_1}{r_1}({h_2} - \frac{{h_m}}{2})}}{{{r_2} - {r_1}}}.$$
(15)

Analytical solution

According to assumption (1), Q1 = Q2 = Q3. Equations (8), (14), and (15) are combined and the analytical solution for groundwater inflow into a tunnel can be obtained as follows:

$$Q = \frac{{2\pi {k_r}H}}{{\ln \frac{{r_3}}{{r_2}} + \mu }},$$
(16)
$$\mu { = }\frac{{L_1^2{k_r}}}{{8{r_1}t{k_t}}} + \frac{{({r_2} - {r_1}){k_r}}}{{{r_1}{k_1}}},$$
(17)

where \(\mu\) is the drainage coefficient.

Verification

In the first part of this chapter, the analytical solution is reduced to solutions for unlined tunnels and various circular drainage pipe distances. Subsequently, the reduced solutions are compared to existing analytical solutions. In the second part of this chapter, a numerical model considering WDS is established and the results are used to verify the proposed analytical solution.

Comparisons to the existing analytical models

Analytical solution for an unlined tunnel

When the inner radius of the secondary lining, r0 approaches the outer radius of the initial lining, r2, the proposed analytical solutions can be reduced to the solution for an unlined tunnel. Equation (16) can be simplified as:

$${Q_c} = \frac{{2\pi {k_r}H}}{{\ln \frac{{r_3}}{{r_0}}}}.$$
(18)

According to Oshima (1983) and Zhang (2006), the radius of the drainage-affected zone r3 can be assumed as 2H. Therefore, Eq. (18) can be rewritten as follows:

$${Q_c} = \frac{{2\pi {k_r}H}}{{\ln \frac{2H}{{r_0}}}}.$$
(19)

It can be seen that Eq. (19) is identical to Goodman’s solution.

Analytical solutions for different distances between circular drainage pipes

  1. 1.

    Infinitesimal distance between two circular drainage pipes

    When the distance between two adjacent circular drainage pipes approaches an infinitely small value, the hydraulic behavior of the tunnel lining mimics that of a structure without a geotextile, waterproof membranes, or secondary lining. Under this condition, Eq. (16) can be simplified as.

    $$\begin{aligned}{Q_{Current}} &= \mathop {\lim }\limits_{{L_1} \to 0} Q \\ &= \mathop {\lim }\limits_{{L_1} \to 0} \frac{{2\pi {k_r}H}}{{\ln \frac{{r_3}}{{r_2}} + \frac{{L_1^2{k_r}}}{{8{r_1}t{k_t}}} + \frac{{({r_2} - {r_1}){k_r}}}{{{r_1}{k_1}}}}}\\ & = \frac{{2\pi {k_r}H}}{{\ln \frac{{r_3}}{{r_2}} + \frac{{({r_2} - {r_1}){k_r}}}{{{r_1}{k_1}}}}} \end{aligned}.$$
    (20)

    An existing analytical solution for the case of a tunnel structure without a geotextile, waterproof membranes, or circular drainage pipes has already been derived by Wang et al. (2008). This solution is expressed as follows:

    $${Q_{Wang}} = \frac{{2\pi {k_r}H}}{{\ln \frac{{r_3}}{{r_2}} + \frac{{k_r}}{{k_1}}\ln \frac{{r_2}}{{r_1}}}}.$$
    (21)

    The error between Eqs. (20) and (21) was defined as \(\eta\) using a set of parameters (Table 1) for verification, as shown in Eq. (5).

    $$\begin{aligned}\eta &=\frac{{{Q_{Wang}} - {Q_{Current}}}}{{{Q_{Wang}}}} \times 100\% \\&= (1 - \frac{{\ln \frac{{r_3}}{{r_2}} + \frac{{k_r}}{{k_1}}\ln \frac{{r_2}}{{r_1}}}}{{\ln \frac{{r_3}}{{r_2}} + \frac{{{k_r}({r_2} - {r_1})}}{{{k_1}{r_1}}}}}) \times 100\%\end{aligned}$$
    (22)
    Table 1 Notation for variables and values of parameters used in this study
    Full size table

    The error of the groundwater inflow between the two analytical solutions is less than 0.5% (Fig. 5). The larger the water head, the smaller this difference will be. Therefore, it can be concluded that the results of the reduced analytical solution and Wang’s solution (Wang et al. 2008) are nearly identical.

    Fig. 5
    figure 5

    Relative differences between reduced analytical solution and Wang’s solution

    Full size image
  2. 2.

    Infinite distance between two circular drainage pipes

    When the distance between two circular drainage pipes approaches infinity, the proposed analytical solution can be simplified as follows:

    $$\mathop {\lim }\limits_{{L_1} \to \infty } Q = \mathop {\lim }\limits_{{L_1} \to \infty } \frac{{2\pi {k_r}H}}{{\ln \frac{{r_3}}{{r_2}} + \frac{{L_1^2{k_r}}}{{8{r_1}t{k_t}}} + \frac{{({r_2} - {r_1}){k_r}}}{{{r_1}{k_1}}}}}{ = }0.$$
    (23)

    Equation (23) indicates that the groundwater flowing into the tunnel is equal to zero when the distance between two adjacent circular drainage pipes approaches infinity, implying that the composite lining serves as an impermeable lining. This result is consistent with the waterproofing mechanism in a real tunnel, where groundwater cannot penetrate the waterproof lining and secondary lining, and can only flow through the drainage pipes (Wang 2006).

    Figure 6 presents the relationship between groundwater inflow and the distance between two adjacent circular drainage pipes (0–350 m) derived by the proposed analytical method. When the distance is less than 30 m, the groundwater inflow into the tunnel rapidly decreases with an increasing distance. When the distance between two circular drainage pipes exceeds 100 m, the curve tends to flatten out and gradually approaches zero, implying that the lining is impermeable.

    Fig. 6
    figure 6

    Relationship between groundwater inflow and distance between two adjacent circular drainage pipes

    Full size image

    Based on the analysis above, the proposed analytical solution can generally be reduced to Goodman’s solution for an unlined tunnel. The difference between the proposed solution and Wang’s solution is less than 0.5% when the distance between two circular drainage pipes approaches infinitely small values. Therefore, both Goodman’s and Wang’s solutions can be considered specific cases of the proposed analytical solution.

Comparison to a numerical model

In this section, a three-dimensional numerical model is built using the FLAC3D. The numerical model consists of the surrounding rock, initial lining, circular drainage pipes, and geotextile (Fig. 7). The waterproof membranes and secondary lining serve as impermeable boundaries.

Fig. 7
figure 7

Numerical model

Full size image

The dimensions of the numerical model are 100 × 100 m in length and width and 20 m in thickness. The parameters of the numerical model are presented in Table 1. For the boundary conditions, the top of the model is permeable with a constant hydrostatic head. The bottom, front, and back hydraulic boundaries are assumed to be impermeable. The left and right hydraulic boundaries are permeable and the corresponding water pressure is linear. The ground below the water level is fully saturated, whereas the water pressure in the drainage pipes is zero. The seepage path of groundwater flows from the surrounding rock into the initial lining, followed by the geotextile, reaches the circular drainage pipes. The groundwater is finally discharged through the drainage pipes. The numerical results and errors, as well as the results of the proposed analytical method adopting the same parameter values, are listed in Table 2.

Table 2 Groundwater inflow results for numerical versus analytical solutions
Full size table

Table 2 reveals that the groundwater inflows obtained using the numerical and proposed analytical solutions are in good agreement. The error between the two methods ranges from 1.9 to 7.3%.

Prediction of groundwater inflow using the WDSee model

The permeability coefficient of the rock (kr) surrounding a tunnel is a critical parameter for estimating groundwater inflow (Farhadian and Katibeh 2015). Therefore, kr was adopted as a reference index to analyze the effect of WDS on groundwater inflow. Figure 8 presents the results of groundwater inflow from Goodman’s solution (for an unlined tunnel), Wang’s solution (for a lined tunnel without considering the waterproof membranes, geotextiles, and circular drainage pipes of WDS), and the proposed analytical solution (for a lined tunnel considering all components of WDS).

Fig. 8
figure 8

Comparison of groundwater inflows between three analytical solutions

Full size image

When kr is less than 1 × 10−8 m/s, the difference between the groundwater inflow obtained by Goodman’s solution and the other two solutions is less than 1%. This difference indicates that the tunnel lining has a small effect on groundwater inflow under this condition. Additionally, the maximum difference between Wang’s solution and the proposed analytical solution is only 0.6%. Therefore, the effects of WDS on groundwater inflow can be ignored. When kr ranges from 1 × 10−8 to 1 × 10−7 m/s, the differences among the three solutions remain insignificant. The difference between Wang’s solution and the proposed analytical solution increases to 5.7% at a permeability coefficient of 1 × 10−7 m/s, suggesting that the WDS effect on groundwater inflow can still be ignored. When kr is within the range of 1 × 10−7 to 1 × 10−6 m/s, the difference between Goodman’s solution and the other two solutions begins to increase and exceeds 43.9% at a permeability coefficient of 1 × 10−6 m/s, demonstrating that the effect of the lining on groundwater inflow is significant. The difference between Wang’s solution and the proposed analytical solution increases from 5.7 to 41.2%, demonstrating that the effects of WDS on groundwater inflow become more significant and cannot be ignored. Therefore, when kr exceeds 1 × 10−6 m/s, the WDS will significantly influence the amount of groundwater inflow and the effects of the WDS on groundwater inflow must be considered.

The percentage difference of the groundwater inflow between Wang’s solution and the proposed analytical solution (ξ=(Q − QWang) / Q×100%) was further analyzed to examine the effects of the WDS on groundwater inflow. Nine cases with varying permeability coefficients for the initial lining (k1) and outer radii of the initial lining (r2) were considered.

According to the results in Fig. 9, with an increase in kr, the difference in each case gradually increases to 10%. Furthermore, as k1 increases, the difference ξ becomes more significant and the maximum value exceeds 75%. This trend indicates that the effects of WDS on groundwater inflow are closely related to kr. Therefore, the influence of WDS is significant and cannot be ignored when kr exceeds 1 × 10−6 m/s.

Fig. 9
figure 9

The change on the percentage difference of groundwater inflow (ξ of Wang’s solution and the proposed analytical solution as a function of permeability coefficient of the surrounding rock

Full size image

Parametric analysis

In this chapter, the relationships between groundwater inflow and each model parameter are analyzed. The parameters of the WDSee model include the water head, distance between two adjacent circular drainage pipes, thickness and permeability of the initial lining, and geotextile thickness and permeability, which are listed in Table 1. The results are presented in Figs. 10 and 11.

Fig. 10
figure 10

Relationships between groundwater inflow and model parameters; (a) water head, (b) distance between two adjacent circular drainage pipes, (c) thickness of initial lining, (d) geotextile hydraulic conductivity

Full size image
Fig. 11
figure 11

Relationship between groundwater inflow and the permeability coefficient of the initial lining

Full size image

Water head and rock permeability

As shown in Fig. 10a, the groundwater inflow increases with an increase in the water head and rock permeability, indicating that H and kr have a significant effect on groundwater inflow. For example, when kr is 8 × 10−8 m/s, the groundwater inflow increases nine times as h increases from 50 to 500 m. When H is 100 m, the groundwater inflow increases from 1.19 to 4.56 m3/d/m when kr increases from 8 × 10−8 to 5 × 10−7 m/s.

Distance between two adjacent circular drainage pipes

The relationship between the groundwater inflow and L1 is presented in Fig. 10b, indicating that the groundwater inflow gradually decreases with an increase in L1. When kr is greater than 3 × 10−7 m/s, the groundwater inflow decreases by approximately 50% as L1 increases from 4 to 20 m. When kr is less than 1 × 10−7 m/s, the groundwater inflow decreases by approximately 25% as L1 increases from 4 to 20 m. This trend indicates that L1 significantly influences groundwater inflow. Additionally, the higher the rock permeability, the more sensitive the groundwater inflow is to L1.

Thickness of the initial lining

The relationship between the groundwater inflow and thickness of the initial lining (T = r2 − r1) is presented in Fig. 10c, where the parameter r1 remains the same and the outer radius of the initial lining r2 increases from 5.7 to 6.05 m. It can be seen that the thickness of the initial lining has a weak effect on groundwater inflow. When kr is less than 1 × 10−7 m/s, the groundwater inflow remains approximately constant. When kr is greater than 3 × 10−7 m/s, the groundwater inflow decreases by approximately 14.5% as T increases from 0.1 to 0.45 m.

Geotextile hydraulic conductivity

The geotextile hydraulic conductivity (ktt) is the product of the geotextile permeability coefficient and geotextile thickness. The relationship between the geotextile hydraulic conductivity and groundwater inflow is presented in Fig. 10d. When ktt increases from 1 × 10−7 to 1 × 10−6 m2/s, the groundwater inflow increases by more than 45%. When ktt is greater than 1 × 10−6 m2/s, each curve in the figure tends to be flat. This trend indicates that ktt has a significant effect on groundwater inflow when it is within the range of 1 × 10−7 to 1 × 10−6 m2/s.

Permeability coefficient of the initial lining

The relationship between the permeability coefficient of the initial lining and groundwater inflow is presented in Fig. 11. When k1 increases from 1 × 10−9 to 1 × 10–8 m/s, the groundwater inflow gradually increases. Figure 11 reveals that k1 has an apparent effect on groundwater inflow under this condition. When k1 is greater than 1 × 10−8 m/s, each curve tends to be flat and the groundwater inflow increases by approximately 5%, indicating that k1 has a weak effect on groundwater inflow under this condition.

Suggestions on the WDS design

For a deeply buried tunnel subjected to a high water table (e.g., H > 150 m), the limitation of tunnel discharge rate less than 5.0 m3/d-m (Zhang et al. 2007; Zhang and Sun 2019) has been suggested to protect the ecological environment of the tunnel area. The WDS layout should be optimized to limit the discharge for an environmentally acceptable rate. Based on the parametric analysis, the groundwater inflow would exceed the discharge limitation when the permeability coefficient of surrounding rock kr is greater than 3 × 10–7 m/s, independent from the WDS layout parameters. Thus, in this condition, engineering techniques such as grouting might be needed to limit groundwater discharge. Conversely, discharge limitation can be met with proper WDS layout design when kr is less than 3 × 10–7 m/s. For example, limited discharge can be provided when the permeability coefficient of initial lining is less than 3 × 10–7 m/s, the distance between two adjacent circular drainage pipes is set to 10 m, and the geotextile hydraulic conductivity is less than 1 × 10–6 m2/s.

Discussion

The proposed analytical solution was motivated by considering the effects of WDS on the groundwater inflow for a deeply buried tunnel subjected to a high water table. The proposed analytical solution was derived based on the assumption (assumption (1)) that the tunnel cross-section is circular. While it is often not true in practical engineering, an equivalent circle shape may be used. In addition, the surrounding rock is assumed (assumption (2)) to be a continuous porous medium. In practice, the fractured rock mass is often considered as continuous media when the tunnel size is larger than the representative elementary volume (Li 2018). For example, rock mass can be assumed to be the continuous porous medium when small fissures are densely distributed (Wang et al. 2008). Therefore, the proposed analytical solution can also be applied to tunnels in fractured rock with densely distributed fractures. However, when the tunnel is shallow buried, or the rock mass cannot be considered as continuous media, the proposed analytical solution may not be suitable. Finally, the seepage path of groundwater is assumed (assumption (3)) to flow from the surrounding rock to the circular drainage pipes, which can be achieved when the lining type is the composite lining. Therefore, the proposed analytical solution is suitable for the composite lining with WDS.

Conclusions

In this study, the WDSee model was developed to consider all components of WDS. A corresponding analytical solution for groundwater inflow into a composite lining tunnel was derived. WDS components were fully considered when deriving the proposed analytical solution, which was then validated using a numerical model. A parametric study was conducted to investigate the relationships between groundwater inflow, and geometric and physical parameters. The following conclusions can be drawn.

  1. 1.

    The proposed analytical solution is useful for estimating groundwater inflow into a tunnel with a composite lining. Such analytical solutions can be applied to deeply buried rock tunnels that are subjected to a high water table. The proposed analytical solutions can be reduced to Goodman’s solution for unlined tunnels. The difference between the proposed analytical solution and an existing solution (e.g., Wang’s solution) is less than 0.5% for an infinitesimal distance between two adjacent circular drainage pipes.

  2. 2.

    The effects of WDS on groundwater inflow are influenced by rock permeability. The higher the rock permeability coefficient, the more significant the effect. When the rock permeability coefficient of the surrounding rock exceeds 1 × 10−6 m/s, the effects of WDS cannot be ignored.

  3. 3.

    The groundwater inflow into a tunnel is closely related to the geometric and physical parameters of the tunnel. Geometric parameters include the initial lining thickness, radius of the affected zone by the drainage, distance between adjacent circular drainage pipes, and geotextile thickness. Physical parameters include the water head and permeability coefficients of the initial lining, surrounding rock, and geotextile. The groundwater inflow significantly decreases with an increase in the distance between adjacent circular drainage pipes. Furthermore, the higher the rock permeability coefficient, the more significant the effect of the geometric and physical parameters of the tunnel.

  4. 4.

    When the permeability coefficient of the surrounding rock kr is greater than 3 × 10−7 m/s, engineering techniques such as grouting might be needed to limit groundwater discharge under high water table (e.g., H > 150 m) to meet environment protection needs. Conversely, discharge limitation can be met with proper WDS layout design when kr is less than 3 × 10–7 m/s.