Introduction

In recent years, many probabilistic simulation methods have been developed for evaluating slope stability by considering the inherent spatial variability of soil properties. For example, Griffiths and Fenton (2004) studied the effect of spatial variability of the undrained shear strength on the failure probability of a slope using the random finite element method (RFEM). Cho (2007) presented the effect of spatially variable soil properties on the critical failure surface based on Monte Carlo simulation (MCS) to compute a probability distribution of the resulting factor of safety. Cho (2009) implemented a numerical procedure for probabilistic slope stability analysis, accounting for the uncertainties and spatial variation of the soil shear strength parameters, in which two-dimensional random fields were generated based on a Karhunen-Loeve expansion. Griffiths et al. (2011) described the effect of spatial variability of the soil shear strength on failure mechanisms of infinite slope assumptions. Jiang et al. (2014) used a non-intrusive stochastic finite element to investigate slope reliability analysis, in which the spatially variable shear strength parameters were modelled using cross-correlated non-Gaussian random fields. Nguyen et al. (2017, 2018) employed case studies of rainfall-induced slope failure to validate the effect of spatial variability of soil shear strengths and root cohesion due to infiltration. These studies indicated that ignoring the spatial variability of soil shear strength might lead to overestimation or underestimation in slope stability analysis.

In addition, several research studies have quantified the influence of spatial variability of the hydraulic conductivity function on saturated-unsaturated seepage analysis causing slope instability. Fenton and Griffiths (2008) implemented steady state seepage through a soil mass with spatially random saturated permeability. Srivastava et al. (2010) also studied the influence of spatially variable permeability properties on steady state seepage conditions and slope stability. Santoso et al. (2011) presented a probabilistic framework for evaluating unsaturated soil slope stability under rainfall infiltration by modelling the saturated hydraulic conductivity as a lognormal stationary random field using a modified Metropolis-Hasting algorithm. Zhu et al. (2013) explored a stationary random field model using the Fast Fourier Transformation (FFT) method to investigate the effect of saturated permeability on the distribution of matrix suction and factors of safety. Cho (2014) discussed various failure patterns of weathered residual soil slope caused by the spatial variability of saturated hydraulic conductivity in the rainfall infiltration based on a one-dimensional stationary random field of an infinite slope model. Dou et al. (2015) employed a series of seepage and stability analyses of an infinite slope using a one-dimensional non-stationary random field of the saturated hydraulic conductivity to study the effect of the trend component and its variability on the failure, due to rainfall infiltration, of an unsaturated slope. The results of these research studies have identified that hydraulic conductivity is one of the key parameters in seepage and slope stability analysis.

However, very few studies have incorporated the effect of hydraulic conductivity, soil water characteristic curves (SWCC) fitting parameters (hereafter a & n), and soil shear strength. Yang et al. (2012) accounted for the effect of SWCC and saturated hydraulic conductivity, ignoring spatial variability using the first order second moment (FOSM), showing increased uncertainty in the estimation of failure probability. Liu et al. (2017) investigated the impact of considering SWCC for a homogeneous embankment; the effect of spatial variability of the saturated hydraulic conductivity was investigated only by conducting a slope probabilistic analysis. The result indicated that saturated hydraulic conductivity plays a dominant role in slope stability.

In this paper, the effect of spatial variability of the saturated hydraulic conductivity (ks), the SWCC parameters (a & n), and the effective friction angle (ϕ’) are investigated to highlight the significance of each parameter on slope probabilistic analysis. The research presented in this paper is an extension of the original idea from Zhu et al. (2013), in which unsaturated seepage and stability analysis of a hypothetical slope is performed. The two-dimensional random field of the SWCC parameters and the effective friction angle are added in order to compare the result with the effect of a random field of saturated hydraulic conductivity due to rainfall infiltration. The objectives of this paper are: (1) to generate a series of independent random fields for saturated hydraulic conductivity and the effective friction angle and dependent random field for SWCC parameters using the Cholesky decomposition and Monte Carlo simulation; (2) by adopting the two modules of Geo-Studio (2012), and modifying the code in SEEP/W and SLOPE/W, to investigate the effect of spatial variability of random fields on the distribution of pore water pressure and slope stability analysis using both RFEM and the limit equilibrium method; (3) to evaluate the effect of spatial variability of random fields on statistical characteristics of safety factors and failure probability; (4) to summarise the most important parameters for probabilistic analysis of slope stability.

Deterministic analysis of infiltration and slope stability

Seepage analysis under rainfall conditions

For the seepage analysis in an unsaturated soil layer, Darcy’s law, originally derived for saturated soil, was modified for the flow of water through unsaturated soil (Richards 1931). The numerical codes were developed based on the theory of unsaturated flow. In this paper, the governing equation for two-dimensional steady-state flow in unsaturated soil is given by Papagianakis and Fredlund (1984).

$$ \frac{\partial }{\partial x}\left({k}_x\frac{\partial h}{\partial x}\right)+\frac{\partial }{\partial y}\left({k}_y\frac{\partial h}{\partial y}\right)+q=0 $$
(1)

where h is the total pressure head (m), kx and ky are the hydraulic conductivity in the horizontal direction x and vertical direction y (m/day), respectively, and q is the applied flux boundary (m/day). Several empirical and semi-empirical functions have been proposed to define the soil water characteristic curve and the hydraulic conductivity. The soil water characteristic curve that was developed by Fredlund and Xing (1994) [Eq. (2)], as shown in Fig. 1a, and hydraulic conductivity as an exponential equation [Eq. (3)] by Leong and Rahardjo (1997), as shown in Fig. 1b, are employed in this paper. These functions were also presented in the research of Zhu et al. (2013) for verifying the proposed seepage analysis.

$$ \theta ={\theta}_r+\frac{\theta_s-{\theta}_r}{{\left\{\mathit{\ln}\left[e+{\left(\psi /a\right)}^n\right]\right\}}^m} $$
(2)
$$ k={k}_s{\left(\frac{\theta -{\theta}_r}{\theta_s-{\theta}_r}\right)}^p $$
(3)

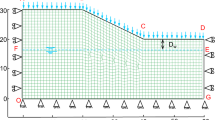
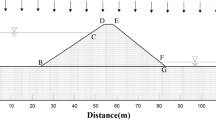
where θ is the volumetric water content; θr is the residual volumetric water content; θs is the saturated volumetric water content; ψ is the suction; a, n, and m are SWCC parameters, k is the hydraulic conductivity; ks is the saturated permeability; p is a constant, depending on the soil type. The steady-state nonlinear differential equation as in Eq. (1) was solved using an iterative finite element scheme implemented in the SEEP/W module (Geo-Studio 2012). Numerical modelling of the hypothestical slope under seepage presented by Zhu et al. (2013) is adopted in this study as shown in Fig. 2. A zero flux condition is imposed at the bottom of the slope (C-D). The left and right boundary conditions consists of a constant head boundary below the water table (B-C, D-E) and zero flux boundary above the water table (A-B, E-F). The vertical flux (q) can be applied to the slope surface where the flux corresponds to the rainfall intensity (Sainak 2004; Yeh et al. 2008; Oh and Lu 2015).

Fig. 1
figure 1

Soil property function used in unsaturated seepage analysis

Full size image
Fig. 2
figure 2

Geometry and boundary conditions for a hypothetical slope (after Zhu et al. 2013)

Full size image

Slope stability analysis

Previous studies have shown that the shear strength of saturated-unsaturated soils can be expressed by the Mohr-Coulomb failure criterion (Fredlund et al. 1978) and the suction stress (Lu and Likos 2006; Lu et al. 2010; Fredlund et al. 2012) as follows:

$$ {\tau}_f={c}^{\hbox{'}}+\left[\left(\sigma -{u}_a\right)+\frac{\theta -{\theta}_r}{\theta_s-{\theta}_r}\left({u}_a-{u}_w\right)\right]{tan\phi}^{\hbox{'}} $$
(4)

where c’ is the effective soil cohesion, ϕ’ is the effective friction angle, σ is the normal total stress, uw is the pore water pressure, and ua is the pore air pressure, which is zero at atmospheric conditions. As seen in Eq. (4), a decrease in matric suction or an increase in pore water pressure due to rainfall infiltration leads to a decrease in the shear strength, hence contributing to the slope instability.

The procedures of saturated-unsaturated soil slope stability analysis due to rainfall infiltration include two iterative steps: (1) computing pore water pressure and volumetric water content, and (2) computing the factor of safety along the failure surface. All these procedures are conducted using two modules of Geo-Studio (2012): the SEEP/W module is used to analyse hydrological behaviour due to infiltration [i.e., Eq. (1)], and the SLOPE/W module is employed to calculate the factor of safety. In this study, Bishop’s simplified method, known as the method of slices, is adopted. It is noted that this method was also used by Zhu et al. (2013). The effective normal stress and suction stress are incorporated into the shear strength in the SLOPE/W module, as shown in Eq. (4). The equation for calculating the factor of safety is given by:

$$ FS=\frac{\sum \limits_{i=1}^{n_s}\frac{1}{m_{\alpha }}\left[{c}^{\hbox{'}}{b}_i+\left({W}_i-{u}_a{b}_i\right){tan\phi}^{\hbox{'}}-\left(\frac{\theta -{\theta}_r}{\theta_s-{\theta}_r}\right){b}_i{tan\phi}^{\hbox{'}}\right]}{\sum \limits_{i=1}^{n_s}{W}_i\mathit{\sin}{\alpha}_i} $$
(5)
$$ {m}_{\alpha }=\left[1+\left({tan\phi}^{\hbox{'}}\mathit{\tan}{\alpha}_i\right)/ FS\right]\mathit{\cos}{\alpha}_i $$
(6)

where FS is the factor of safety; ns is the total number of slices; Wi is the weight of the ith slice; Wi = γibihi, in which γi, bi and hi are the average unit weight, width and height of the ith slice, respectively; and αi is the angle of the base of the ith slice.

Methodology of random field model and probabilistic analysis

Simulation of random field model

Random field theory has been widely adopted in geotechnical engineering to characterize the spatial variability of shear strength and saturated permeability (Phoon 2008; Fenton and Griffiths 2008; Cho 2014; Deng et al. 2017). Within the framework of random field theory, a domain of problems is required to generate sub-domains (elements), assigned according to different values of soil parameters. For any two elements, these values are assumed to be uncorrelated because of limited site investigation data; it is very difficult to accurately obtain specific soil properties. However, a soil parameter value in any element can correlate to others, based on absolute distance, instead of the location. In order to simulate the correlation of soil properties between any two discrete points, a 2-D exponential correlation function is used in this study (Fenton and Griffiths 2008; Srivastava et al. 2010) following as

$$ \rho \left({\tau}_x,{\tau}_y\right)=\mathit{\exp}\left(-\frac{2{\tau}_x}{l_x}\right)\mathit{\exp}\left(-\frac{2{\tau}_y}{l_y}\right) $$
(7)

where τx =  ∣ xi − xj∣ and τy =  ∣ yi − yj∣ are the absolute distances between two points in the horizontal and vertical directions, respectively; lx and ly are the horizontal and vertical correlation lengths of a random field, and (xi, yi) are the centroid coordinates of each element. To generate random fields in a soil profile, many methods can be applied, such as the Local Average Subdivision (Fenton and Griffiths 2008), the Fast Fourier Transformation (Zhu et al. 2013; Nguyen et al. 2017) and the K-L expansion (Cho 2012, 2014). In this study, the Cholesky decomposition method is employed, since this method is conceptually simple and easily implemented for both independent random fields (e.g., ks and φ’) and dependent random fields (i.e., SWCC parameters a & n) (Li et al. 2015; Jiang and Huang 2016).

A domain of problem is assumed to be discretized into ne random field elements; the correlation matrix \( {C}_{n_e\times {n}_e} \) can be built to define a correlation coefficient at each element as

$$ {C}_{n_e\times {n}_e}=\left[\begin{array}{cccc}1& \rho \left({\tau}_{x_{12}},{\tau}_{y_{12}}\right)& ...& \rho \left({\tau}_{x_{1{n}_e}},{\tau}_{y_{1{n}_e}}\right)\\ {}\rho \left({\tau}_{x_{21}},{\tau}_{y_{21}}\right)& 1& ...& \rho \left({\tau}_{x_{2{n}_e}},{\tau}_{y_{2{n}_e}}\right)\\ {}\vdots & \vdots & \ddots & \vdots \\ {}\rho \left({\tau}_{x_{n_e1}},{\tau}_{y_{n_e2}}\right)& \rho \left({\tau}_{x_{n_e2}},{\tau}_{y_{n_e2}}\right)& ...& 1\end{array}\right] $$
(8)

where \( \rho \left({\tau}_{x_{ij}},{\tau}_{y_{ij}}\right)=\rho \left({\tau}_{x_{ji}},{\tau}_{y_{ji}}\right) \), which is calculated using Eq. 7 for the ith element and jth element in the horizontal and vertical direction, respectively. Additionally, since two dependent parameters are used to generate the random field of a & n, the cross-correlation matrix R can be defined as

$$ R=\left[\begin{array}{cc}1& {\rho}_{n,a}\\ {}{\rho}_{a,n}& 1\end{array}\right] $$
(9)

where ρa, n = ρn, a (the cross-correlation coefficient between the SWCC parameters a & n). It is noted that R = 1 for an independent random field (i.e., ks and ϕ’). According to the Cholesky decomposition technique, two lower triangular matrices L1 and L2 can be decomposed from the correlation matrix \( {C}_{n_e\times {n}_e} \) and the cross-correlation matrix R, respectively, which are defined as

$$ {L}_1{L}_1^T={C}_{n_e\times {n}_e} $$
(10)
$$ {L}_2{L}_2^T=R $$
(11)

Subsequently, a typical realisation of the cross-correlation standard Gaussian random field can be generated as

$$ {X}_i^G\left(x,y\right)={L}_1{\xi}_i{L}_2^T $$
(12)

where the superscript G means cross-correlated Gaussian random fields, i is the number of simulations, ξi is the independent standard normal samples with the size of ne × ms obtained using an in-house MATLAB program, and ms is the random field numerical identifier. In this study, ms = 1 for an independent random field, and ms = 2 for a dependent random field. Based on field measurements, previous research has indicated that saturated permeability, SWCC parameters and shear strength parameters can be modelled as a lognormal random field (Phoon and Kulhawy 1999a, 1999b; Phoon et al. 2010). Thus, a lognormal distributed random field can be given by

$$ {Z}_i\left(x,y\right)=\mathit{\exp}\left[{\mu}_{lnz}+{\sigma}_{lnz}{X}_i^G\left(x,y\right)\right] $$
(13)

where μlnz and σlnz are mean and standard deviation following a normal distribution, which are converted to a mean of μz and a standard deviation of σz of a lognormal distribution (Fenton and Griffiths 2008). They are defined by

$$ {\sigma}_{lnz}^2=\mathit{\ln}\left(1+{\sigma}_z^2/{\mu}_z^2\right) $$
(14)
$$ {\mu}_{lnz}=\mathit{\ln}\left({\mu}_z\right)-\frac{1}{2}{\sigma}_{lnz}^2 $$
(15)

Probabilistic slope stability analysis

The problem of probabilistic slope stability analysis takes random fields of properties into consideration, representing a set of random variables. Let Z denote random variables of soil parameters; f(Z) is the joint probability density function of z, and FS(Z) is the factor of safety, known as the limit state function. The failure probability can be calculated using the following integral (Baecher and Christian 2003)

$$ {P}_f=P\left[ FS(Z)\le 1\right]={\int}_{FS(Z)\le 1}f(Z) dZ $$
(16)

Equation (16) usually includes large variability and strong non-linearity of the limit state function; therefore, the Monte Carlo simulation was adopted to calculate the failure probability for accurately solving slope stability problems

$$ {P}_f\approx \frac{1}{n_M}\sum \limits_{i=1}^{n_M}I\left[ FS\left({Z}_i\right)\right] $$
(17)

where nM is the number of realisations, and I[FS(Zi)] is an indicator function characterizing the failure domain defined as:

$$ I\left[ FS\left({Z}_i\right)\right]=\Big\{{\displaystyle \begin{array}{cc}1&\;FS\left({Z}_i\right)\le 1\\ {}0& FS\left({Z}_i\right)>1\end{array}} $$
(18)

In other words, the estimated failure probability of a slope is equal to the number of factor of safety, which is less than 1.0, divided by the total number of realisations.

Flowchart of probabilistic analysis

A probabilistic analysis procedure for the hypothetical slope, considering the effect of spatial variability of ks, a, n, and ϕ’ is schematically shown in the flow chart in Fig. 3 and is characterized as follows:

  1. (1)

    The finite element model of the hypothesis slope for both seepage and slope stability analysis with the same values of ks, a, n, and ϕ’ at all elements is created using the SEEP/W and SLOPE/W module, respectively. Deterministic analysis is firstly conducted with SEEP/W and SLOPE/W to define pore water pressure (suction), volumetric water content, and factor of safety. Then, the “PWP.xml” and “FS.xml” input files are generated from deterministic analysis containing all the necessary information of the SEEP/W and SLOPE/W modules. These input files can be modified according to the requirements of this study.

  2. (2)

    Identify the statistical characteristics of variables such as mean values suggested by Zhu et al. (2013), distribution function, coefficient of variation, and cross-correlation coefficient for the variables of SWCC parameters a & n based on previous research (Phoon and Kulhawy 1999a, 1999b; Phoon et al. 2010). Next, select an approximate range of correlation lengths to simulate the spatially varying variables in the horizontal and vertical direction for a 2D random field model. Then, nM random fields (corresponding to nM MCS) of variables are generated using Eq. (13), and different values of ks, a, n and ϕ’ are established in each random field for all elements in the domain of slope.

  3. (3)

    Perform iterative simulation and start from i = 1

    1. a)

      Replace the mean values of ks, a and n in the 1st step (i = 1) with the corresponding values generated in step (2) for “PWP.xml” as the input file, while a similar procedure is performed with the mean value of ϕ’ for the “FS.xml” input file. This process is implemented using a MATLAB coding program to make ith new “PWP.xml” and “FS.xml” input files. These input files have the same structure as the input files in step 1, except for the values of ks, a, n, and ϕ’ at each element.

    2. b)

      Run the ith “PWP.xml” input file to obtain the updated pore water pressure (suction) and volumetric water content.

    3. c)

      Run the “FS.xml” input file resulting from the ith “PWP.xml” input file in step 3(b) for random field of ks, a & n. This is because the ith generated random fields of ks, a & n cause differing seepage analysis results. For the random field of ϕ’, the initial analysis does not affect slope stability analysis; therefore, run the ith “FS.xml” input file with the result of the “PWP.xml” input file in step 1.

    4. d)

      Implement step 3(c) to calculate the FS. Such a process is executed automatically by a generated “Run.bat” file, and the FS is also automatically saved under “slip_surface.csv” output files. This process will produce nM different “slip_surface.csv” output files, which contain nM and different FS, respectively.

    5. e)

      Increase i by 1 and repeat steps 3(a) to 3(d) until i is equal to nM

  4. (4)

    Extract nM different FS values from the nM corresponding “slip_surface.csv” employed by the MATLAB coding program.

  5. (5)

    Estimate the statistical characteristics of FS such as mean, coefficient of variation, histogram, and probability density function for each random field ks, a & n, and ϕ’. Finally, the failure probability is approximated using Eq. (17).

    Fig. 3
    figure 3

    Flow chart of probabilistic analysis

    Full size image

Results and discussion

The research presented in this paper is an extension of the work of Zhu et al. (2013), in which the effect of the spatial variability of SWCC parameters (a & n) and the shear strength parameter (ϕ’) are studied and compared with the effect of spatial variability of saturated permeability (ks). For the deterministic analysis, the same mean values of soil parameters are used in this study as listed in Table 1. For probabilistic analysis, the coefficient of variation of ks has been suggested as 0.6–1.0 in the literature (Duncan 2000) and was mainly conducted at a value of 1.0 by Zhu et al. (2013). Since the sand is considered in the soil slope, according to Phoon et al. (2010), generic ranges of coefficient of variation of a and n are 0.81–1.19 and 0.09–0.19, respectively, and the range of cross-correlation coefficient (ρa, n) is from −0.409 to −0.251. In addition, the range of coefficient of variation of ϕ’ was also reported as 0.02–0.22 for sand (Phoon and Kulhawy 1999b). In order to comprehensively investigate the perfect spatial variability, the correlation length is extended to a range of 0.5–1000 m or 0.025–50 times the slope height (Zhu et al. 2013), and the average values of covs for a, n and ϕ’ are proposed in this study. To avoid the effect of slope dimension, a normalised correlation length is used, which is defined as δ = lx/H = ly/H (H is the height of slope). Table 2 summarises the statistical characteristics of all parameters used for the probabilistic analysis.

Table 1 Parameters for the hypothetic slope (after Zhu et al. 2013)
Full size table
Table 2 Statistical characteristic of parameters
Full size table

Deterministic analysis

In this section, the pore water pressure (suction) and volume water content at a steady state are calculated from SEEP/W and are then used as input in SLOPE/W to calculate the corresponding FS. As seen in Fig. 4, the pore water pressure within the entire soil slope varies from −40 kPa to 160 kPa, and linearly increases from the ground surface to the bottom of the domain. This is because the vertical infiltration flux applied to the slope surface is much smaller than the saturated permeability (more than 100 times, as seen Table 1). This value is employed to be able to influence soil parameters in the unsaturated zone, where a constant matric suction can be maintained (Zhang et al. 2004). Figure 4 also shows the critical surface, with FS = 1.230, which takes on the region of the unsaturated zone.

Fig. 4
figure 4

Pore water pressure and critical surface for deterministic analysis

Full size image

Probabilistic analysis

In order to create a random field of soil parameters, the domain of the slope is divided into sub-domains with a size of 2.0 m in square shape, including 800 elements. A random field is a series of random variables which is generated using Eq. (13) and iterations of the Monte Carlo simulation. All elements in the domain were then assigned various values from the generated random field; the value at one point of the field is correlated with values within a distance from other points. Figure 5 presents the convergence of analysis results with the number of realisations after approximately 1000 times. To avoid time-consuming numerical modelling, 1000 realisations are performed for the computational effort in this study, which can provide sufficiently accurate results, and is consistent with other studies, e.g. Griffiths and Fenton (2004); Hicks and Spencer (2010); Santoso et al. (2011). Figure 6 shows the range of ks, a, n, and ϕ’ within a slope taking an arbitrary realisation; for example, the correlation length of 1000 m (normalised correlation length, δ = 50). The approximate values of ks from 1.0 × 10−5 to 6.0 × 10−5 (Fig. 6a), of a from 3.5 to 9.7 (Fig. 6b), of n from 1.8 to 2.3 (Fig. 6c), and of ϕ’ from 270 to 31.50 (Fig. 6d). The effect of these random fields on the pore water pressure, slope stability, distribution of factors of safety, and failure probability are illustrated and discussed in the following sections.

Fig. 5
figure 5

Convergence with number of realisations of failure probability (δ = 25)

Full size image
Fig. 6
figure 6

Spatial variability of soil parameters for a typical realisation: a Saturated permeability; ba parameter of SWCC; cn parameter of SWCC; d Effective friction angle

Full size image

Influence of a typical realisation of random fields on distribution of pore water pressure and slope stability analysis

For each parameter listed in Table 2, the pore water pressure (suction) distribution is calculated by implementing the finite element method via the modified SEEP/W module for 1000 realisations. Figure 7 shows the pore water pressure profiles along section X-X at the crest, and section Y-Y at the middle of the slope (Fig. 2), for deterministic analysis and for considering a random field of ks, a and n. These pore water pressures are obtained for probabilistic analysis by taking the corresponding typical realisation of random fields, as presented in Fig. 6a to c. It can be seen that the typical realisation of random fields produces a higher negative pore water pressure above the water table when ignoring the spatial variability. At section X-X (Fig. 7a), the negative pore water pressure distribution considering random field a & n fluctuates more than that considering random field ks, which means that the random field a & n is more significant than the random field ks in unsaturated seepage analysis. The reason for this may be that the SWCC parameters a and n are fitting parameters related to unsaturated soil conditions, while ks is a permeability parameter related to saturated soil conditions. However, at section Y-Y (Fig. 7b), the pore water pressure distribution shows almost no fluctuation when considering random fields a and n. The explanation for this may be that the effect of unsaturated soil conditions, including the SWCC parameters (a & n), may not contribute at the middle of the slope where observation points are close to the water table. In addition, the spatial variability of a and n produces higher pore water pressure than the spatial variability of ks and approximates zero values above the water table (Fig. 7b). This may be because the a & n values generated from random fields in this case are more than the mean values at around the middle of the slope (Fig. 6b and c). These a & n values can cause overestimation compared with deterministic analysis, or the soil slope would become a part of saturation above the water table under steady state infiltration.

Fig. 7
figure 7

Pore water pressure for a typical realisation of random fields

Full size image

The effect of random fields on slope stability analysis is also provided in this section. The critical slip surfaces for the three random fields are depicted in Fig. 8, which are obtained using the resulting seepage analysis of the corresponding typical realisation of random fields as shown in Fig. 6a to d. The factors of safety from probabilistic analysis of all cases (Fig. 8) are less than the factor of safety from deterministic analysis (Fig. 4). These factors of safety evidently decrease with saturated permeability, SWCC parameters, and effective friction angle, respectively, as seen in Fig. 8a to c. It is clear that the effects of random fields ks, a & n producing the pore water pressure distribution along the critical slip surfaces increase, respectively (Fig. 8a and b). However, when considering random field ϕ’, it can be inferred that some smaller value of ϕ’ generated from the random field by the mean value of ϕ’ located at the crest of the slope (Fig. 6d) leads to significant reduction in the factor of safety, even though the pore water pressure distribution is the same as in the deterministic analysis (Fig. 8c).

Fig. 8
figure 8

Stability analysis for a typical realisation of random fields

Full size image

In the above assessments, the effect of each random field is based only on the typical realisation for another. No clear conclusion can be drawn about which random field has a greater impact or importance on slope stability analysis when taking into consideration a series of Monte Carlo simulations. The two following sub-sections will attempt to clarify the answer to this question.

Influence of random fields on distribution of factor of safety

The distribution of the factors of safety from 1000 realisations for each random field is presented in Fig. 9a to c. Considering random field ks, a & n, and ϕ’, the factors of safety range between 1.087–1.290, 0.922–1.690, and 0.916–1.998, respectively. In comparison, the factors of safety show the lowest variation in the case with random field ks, medium variation in the case with random field a & n, and the largest variation in the case with random field ϕ’. Figure 10 shows the histograms of factors of safety based on the three distributions of factor of safety depicted in Fig. 9. As can be expected from Fig. 9, the histograms of factor of safety for the three random fields are quite different from each other. For instance, the ranges of factor of safety tend to dramatically increase with the random field ks, a & n, and ϕ’, respectively, whereas the peak frequencies of FS value occurring approximately at the FS from deterministic analysis decrease, corresponding to random ks, a & n, and ϕ’.

Fig. 9
figure 9

Values of factor of safety from 1000 realisations

Full size image
Fig. 10
figure 10

Histogram of factors of safety from 1000 realisations

Full size image

Generally, the probabilistic analysis results could lead to overestimation or underestimation of deterministic analysis because each realisation is modelled with different values for every element in the whole domain assigned from the generated random field. Figure 11 shows the overestimation of deterministic factor of safety (similar for underestimation) that is calculated by a number of factors of safety which is higher than the deterministic factor of safety divided by the number of realisations (1000 realisations). For independent random fields ks and ϕ’, the curves have the same trend: rapid increase with normalised correlation length, whereas the curve of dependent random fields a & n shows a different trend of independent random fields ks and ϕ’, suddenly decreasing with normalised correlation length. However, almost all the curves remain constant when the normalised correlation length is more than 5.0. Another important point is that the results from random fields a & n, and ϕ’ are larger than those from random field ks at every normalised correlation length. The spatial variability of ks has less effect on the probabilistic analysis of unsaturated soil slopes. In comparison to random fields a & n and ϕ’, the probabilistic analysis results are more important if the normalised correlation length is higher than approximately 2.5 for both random field a & n and ϕ’.

Fig. 11
figure 11

Overestimation of deterministic factor of safety

Full size image

Influence of soil spatial variability on statistical characteristics of factor of safety and failure probability

Figure 12 shows the variation of mean and COVs of FS with normalised correlation length (listed in Table 2) estimated from the Monte Carlo simulation. Figure 12a shows different trends of the curves from the estimated mean values of FS depending on each considered random field. For relatively independent random fields (e.g. ks, ϕ’), the mean values of FS tend to increase with increasingly normalised correlation length, and approach a stable value when the normalised correlation length is higher than 5.0 and 25.0 for ks and ϕ’, respectively. This leads to the conclusion that the spatial variability of ϕ’ would have more effect than that of ks in slope probabilistic analysis. For relatively dependent random fields (e.g. a & n), the greatest reduction in mean value of FS occurs when the normalised correlation length is in a range between 0.025 and 5.0, and dramatically increases when the normalised correlation length is higher than 5.0. However, the COVs of FS show similar trends for the various normalised correlation lengths (Fig. 12b). Generally, the COVs of FS for all random fields increase rapidly when the normalised correlation length is less than 5.0, and then the COVs of FS increase slightly, and remain constant with the larger normalised correlation length. As seen in Fig. 12b, the COVs of FS with random field ϕ’ have the largest magnitude in all cases, while the COVs of FS with random field ks are smaller than those of the result obtained by random field a & n. This may be because random field ϕ’, a & n produces more variation for all normalised correlation lengths (i.e. a typical case is presented in Fig. 9a to c). This also indicates that random fields ϕ’, a & n have greater effect than random field ks, studied by Zhu et al. (2013).

Fig. 12
figure 12

Influence of spatial variability of random fields on statistical characteristics of FS

Full size image

The failure probability of a slope depends highly on variation in the factor of safety, which has values not greater than unity. In this section, the failure probability analysis is performed using Eq. (17) to investigate the effect of spatial variability of random fields. The failure probabilities obtained by all random fields ks, a & n, ϕ’ are also provided in Fig. 13. The results indicate that the curves of failure probability estimated from the three random fields for the various normalised correlation lengths have different trends. For random field ks, the failure probability remains zero at every normalised correlation length because the value of spatial variability of ks (i.e. cov, lx and ly) may not be enough to cause any failure event for unsaturated soil slope. This result is in agreement with the findings of Cho (2014) and Dou et al. (2015), that the spatial variability of ks is important only when the soil slope reaches saturated conditions under rainfall infiltration. For random fields a & n, the failure probability appears when the normalised correlation length is more than 5.0, increasing slightly until the normalised correlation length is equal to 25.0, and decreasing slightly for larger values. This is because this value of random field a & n allows SWCC functions that can generate many variations of pore water pressure and volumetric water content from unsaturated seepage analysis. It is clear that the factor of safety calculated from Eq. (5) would also vary as FS increases. The failure probability with random field ϕ’ appears at 0.4, when the normalised correlation length is less than that with random fields a & n. The failure probability increase rapidly with normalised correlation lengths between 0.4 and 25, and no longer changes with larger values. Based on the results in Fig. 12, random fields a & n, ϕ’ appear to be more important than random field ks for probabilistic analysis, considering unsaturated soil slope under rainfall infiltration.

Fig. 13
figure 13

Influence of spatial variability of random fields on failure probability

Full size image

Conclusion

The purpose of this study was to extend the work of Zhu et al. (2013); the spatial variability of random fields ks, a & n, and ϕ’ was incorporated in order to show how these parameters affect slope failure. The failure probability theory was modelled with RFEM for seepage analysis and with the limit equilibrium method for stability analysis. The key conclusions are highlighted as follows:

  1. 1.

    The pore water pressure distributions considering random field a & n have more fluctuation than those considering random field ks above the water table (unsaturated zone). This is because a and n are fitting parameters that were regressed by many SWCC functions of unsaturated soil samples, while ks was from the subject of field and/or laboratory experiments. In fact, the groundwater table, as well as pore water pressure distribution, could also be induced by the slope angle in seepage analysis. Therefore, the geometric variation should be considered in the future study as a random variable to compare with the influences of other parameters.

  2. 2.

    The variations of factor of safety obtained by Cholesky decomposition and Monte Carlo simulation increase with the corresponding random field ks, a & n, and ϕ’, as well as normalised correlation length. These results also lead to the increasing COVs of factor of safety with random field ks, a & n, and ϕ’, respectively (Fig. 12). In consideration of hydraulic condition analysis, it was found that the spatial variability of random field a & n has greater importance than that of random field ks. However, when the spatial variability of soil strength parameter (ϕ’ in this study) is used for slope stability analysis, the random field ϕ’ is the most important of the three random fields. The reason is that the COVs of ks, a and n are large values (Duncan 2000; Phoon et al. 2010), whereas they are small values for ϕ’(Phoon and Kulhawy 1999b).

  3. 3.

    Comparing the effect between the independent random fields ks and ϕ’ and the dependent random field a & n on the distribution of factor of safety, the results obtained by ks, ϕ’ show the same trends, increasing with increased normalised correlation length. Otherwise, they have different trends of ks, ϕ’ for a & n, decreasing rapidly with smaller normalised correlation length, and increasing slightly with larger normalised correlation length. Consequently, the effect of the dependent random fields is more complicated than that of the independent random field.

  4. 4.

    The failure probability calculated by random field ks is always zero at every normalised correlation length. This result is consistent with the research of Zhu et al. (2013), where most of factors of safety are more than 1.0. The failure probabilities, ignoring random fields a & n and ϕ’, are underestimated for different normalised correlation lengths. The random fields a & n and ϕ’ predicted a higher failure probability than random field ks. This seems to be the expected result in this study, as the spatial variability of random fields a & n have more influence on the probability framework with modelling RFEM of seepage analysis. However the spatial variability of random field ϕ’ would have the most influence on this using the limit equilibrium method of stability analysis. Thus, further research into RFEM for both seepage and stability analysis is suggested for the future.

  5. 5.

    Although the effect of spatial variability of hydraulic and shear strength parameters are investigated through a hypothetical slope, the proposed method used in this study does not require the user to rewire existing finite element codes, and could provide a practical tool for reliability analysis involving complex problems. Hence, the proposed method can apply in the reliability analysis of practical slopes. Further research shall be required to study the effect of random fields in other parameters or advanced probabilistic approaches.