Introduction

Rainfall-induced slope failure is one of the major causes of natural landslides. The rainfall infiltration could increase unit weight of soil and contribute positive pore water pressure to the soil slope (Ng and Shi 1998; Rahardjo et al. 2007). Mostly, the landslides start taking the form of shallow failure (typically 1–3 m depth) with potential slip surface parallel to original slope surface during heavy rainfall (Lu and Godt 2008; Ray et al. 2010; Li et al. 2013; Kanjanakul et al. 2016). Landslides usually occur because of the shallow impermeable bedrock type of soil slope, in which the water table raising from the rainfall accelerates the slope failure process (Ng and Shi 1998; Cho 2009; Han et al. 2014). Stability analysis of rainfall-induced slope failure generally employs a deterministic analysis, which does not consider the spatial variability of soil properties. However, it is important that the variation of soil properties from one point to another might affect the analysis results, particularly in the case of slope failure caused by reduction in soil shear strength due to rainfall infiltration. Therefore, the spatial variability of soil properties framework of random field to simulate non-homogeneous of soil profiles was proposed (Vanmarcke 1983).

A probabilistic slope stability analysis considered the random field of shear strength parameters was presented by Fenton and Griffiths (2008). There are several studies on seepage analysis using the spatial variability of a saturated permeability in the random field model (Srivastava et al. 2010; Cho 2012). Griffiths et al. (2011) analyzed the failure probability of infinite slope assuming a random field model of the shear strength parameters. The results indicated that the critical failure surface can happen at weak layers where the minimum factor of safety against sliding occurs. Another study also considered a one-dimensional random field of the saturated permeability combined with transient seepage analysis to study a shallow landslide of an infinite slope of the weathered residual soil (Cho 2014). The slope failure occurs only when pore water pressure reaches a positive value, and the most critical failure surface always take place at the interface between the weathered soil layer and the underlying bedrock. These studies demonstrate the effect of the spatial variability of soil shear strength and the saturated permeability on the slope stability analysis. However, all the studies described above used an assumption of the mean values of shear strength parameters to analyze the slope stability, and the slope failures occur at the critical depth where the soil became fully saturated. In practice, slopes may fail due to reduction in soil shear strength caused by increasing volumetric moisture content; therefore, either positive pore water pressure or rising water table will not necessarily contribute to slope failure.

In this paper, a probabilistic stability analysis considering random fields of shear strength parameters was implemented for a rainfall-induced slope failure problem. Assumptions of reducing soil shear strength and increasing unit weight of the soil were made in the analysis. An infinite slope assumption can be reasonably applied to rainfall-induced slope failure problem because the failure mechanism can be characterized as shallow landside with potential failure surface parallel to slope surface (Cho and Lee 2002; Lu and Godt 2008; Ray et al. 2010; Santoso et al. 2011; Li et al. 2013). A one-dimensional seepage analysis was performed to define variable suction and volumetric moisture content of soil due to rainfall infiltration. This is because of simplicity, and the vertical flow plays a more dominant role than the lateral flow (Lee et al. 2011; Lu and Godt 2013). A case study of rainfall-induced slope failure in Japan was used to verify the framework. Results of analysis were compared with the field data to illustrate the proposed method.

Unsaturated seepage

For seepage analysis in an unsaturated soil layer, Darcy’s law originally derived for saturated soil was modified to accommodate the flow of water through unsaturated soil (Richards 1931). The only difference is that under condition of unsaturated flow, the hydraulic conductivity is no longer a constant. The governing equation for one-dimensional flow in unsaturated soil is given by

$$ \frac{\partial }{\partial z}\left({k}_z\frac{\partial h}{\partial z}\right)+q=\frac{\partial \theta }{\partial t} $$
(1)

where z is the depth of soil layer (m), h is the total pressure head (m), k z is the hydraulic conductivity in the vertical direction (m/h), θ is the volumetric moisture content, q is the applied flux boundary (m/h), and t is time (h).

There are some empirical and semi-empirical functions which have been proposed to present hydraulic conductivity. In this analysis, non-linear functions of the volumetric moisture content and the coefficient of permeability of the unsaturated soil were adopted based on the Mualem-van Genuchten model (van Genuchten 1980) as

$$ {S}_e=\frac{\theta -{\theta}_r}{\theta_s-{\theta}_r}=\frac{1}{{\left[1+{\left(\alpha h\right)}^n\right]}^m} $$
(2)

where \( m=1-\frac{1}{n} \), n > 1 are dimensionless parameters, and

$$ {k}_z={k}_s{S}_e^{1/2}{\left[{\left(1-{S}_e^{1/m}\right)}^m\right]}^2 $$
(3)

in which S e is the effective water saturation, θ r is the residual volumetric moisture content, θ s is the saturated volumetric moisture content, k s is the saturated permeability (m/h), and α is the fitting parameter (1/m).

In this study, the one-dimensional finite element method was applied using SEEP/W module of Geo-Slope (2012) to solve the Eq. (1). To obtain the result, time step increment and element size should be defined in the advantage (Pan et al. 1996; Van Dam and Feddes 2000; Caviedes-Voullième et al. 2013). Therefore, the small time step increment of 1 s, and element size of 0.05 m were used in the analysis.

Infinite slope stability

The rainfall-induced slope failure is normally categorized as a shallow failure, in which the infinite slope assumption can be reasonably used to analyze the slope stability. Therefore, the infinite slope stability model was adopted in this study, as shown in Fig. 1. The factor of safety of the infinite slope can be expressed as

$$ FS=\frac{\tau_f}{\tau_m}=\frac{\tau_f}{W\sin \beta \cos \beta } $$
(4)

where τ f is the shear strength of soil, τ m is the shear stress at any point along the potential failure surface, W is the weight of the soil slice per unit base area, and β is the slope angle.

Fig. 1
figure 1

Stability analysis of an infinite slope model

Full size image

The shear strength of unsaturated soil can be expressed based on the extended Mohr-Coulomb failure criterion (Fredlund et al. 1978) as

$$ {\tau}_f={c}^{\prime }+\left({\sigma}_n-{u}_a\right)\tan {\phi}^{\prime }+\left({u}_a-{u}_w\right)\tan {\phi}^b $$
(5)

where c′ is the effective cohesion, σ n is the total normal stress on failure surface, u a is the pore air pressure, u w is the pore water pressure, ϕ′ is the effective angle of internal friction, and ϕ b is the contribution to the shear strength due to soil suction. The equation can be simplified (Fredlund et al. 2012) as

$$ {\tau}_f=C+\left({\sigma}_n-{u}_a\right)\tan {\phi}^{\prime } $$
(6)

where C = c ′ + (u a  − u w ) tan ϕ b is the total cohesion under unsaturated soil condition.

The shear strength parameters from the direct shear tests conducted by Matsushi et al. (2006) were adopted in this study. During the test, a single-staged direct shear was performed under different normal stresses. The moisture conditions of soil specimens varied from an oven-dried condition to a capillary saturated condition. The results indicate that the total cohesion can be expressed using an exponential decay function of the apparent soil cohesion at dry condition (c), reduction coefficient (μ), and volumetric moisture content (θ) as

$$ C={ce}^{-\mu \theta} $$
(7)

However, the observations from the direst shear tests indicated that the friction angle is rather constant at the various test conditions from oven-dried to capillary saturated; so in this study, the friction angle is assumed to be constant (i.e., ϕ = ϕ′).

The unit weight of the soil slice increases with the moisture content from rainfall infiltration. The weight of a vertical soil column per unit cross-sectional area (W) from the slope surface to the potential failure surface can be expressed as

$$ W=\sum_{i=1}^m\left({\gamma}_d+{\theta}_i{\gamma}_w\right)\varDelta z $$
(8)

where m is the total number of elements, Δz is the thickness of the soil, γ d is the dry unit weight of soil, and θ i is the volumetric moisture content of each soil element.

In addition, the unstable slope is still affected by the increase in pore water pressure (Fig. 1) causing a decrease in effective stress. If u a  = 0 at atmospheric pressure, the safety factor of the slope can be expressed as

$$ FS=\frac{ce^{-\mu \theta}}{\sum_{i=1}^m\left({\gamma}_d+{\theta}_i{\gamma}_w\right)\varDelta z\sin \beta \cos \beta }+\frac{\tan \phi }{\tan \beta }-\frac{\max \left({u}_w,0\right)\tan \phi }{\sum_{i=1}^m\left({\gamma}_d+{\theta}_i{\gamma}_w\right)\varDelta z\sin \beta \cos \beta } $$
(9)

Probabilistic method

Probabilistic slope stability analysis

The probabilistic framework for stability analysis is formulated using a set of random variables. Let x denotes random variables; f X (x) is the joint probability density function of x, and FS(x) is the factor of safety function of slope. The failure probability can be calculated by the following integral (Baecher and Christian 2003)

$$ {P}_f=P\left[ FS(x)\le 1\right]={\int}_{FS(x)\le 1}{f}_X(x) dx $$
(10)

A Monte Carlo Simulation (MCS) is adopted to calculate the failure probability due to the variability of soil shear strength as (Fenton and Griffiths 2008)

$$ {P}_f\approx \frac{1}{n}\sum_{1=1}^nI\left[ FS\left({x}^i\right)\right] $$
(11)

where x i is the ith sample of random variable x, n is the number of generated samples, and I[FS(x)] is an indicator function characterizing the failure domain defined as

$$ I\left[ FS(x)\right]=\left\{\begin{array}{cc}\hfill 1\hfill & \hfill FS(x)\kern0.62em \le \kern0.62em 1\hfill \\ {}\hfill 0\hfill & \hfill FS(x)\kern0.62em >\kern0.62em 1\hfill \end{array}\right. $$
(12)

Random field

In order to describe the spatial variability of soil, the Markov correlation function is used in this study (Fenton and Griffiths 2008; Phoon 2008) as follows

$$ \rho \left(\tau \right)=\exp \left\{-\frac{2\left|\tau \right|}{l}\right\} $$
(13)

where ρ(τ) is a correlation coefficient indicating a relationship between two random variables (i.e., 0 ≤ ρ ≤ 1), τ is the vertical distance between two data points in meter, and l is the actual correlation length in meter. A high correlation length implies a smoothly varying field while a small correlation length indicates a ragged field.

In this study, a normal random field in one-dimensional space was generated using the one-sided spectral approach. A continuous random field can be obtained from Eq. (13) based on calculating the spectral function. In the geotechnical engineering application, the random variable is always positive; thus, the random variables of soil properties are usually assumed to be a lognormal distribution. A transformation approach is used to obtain lognormal random variable. A detailed description of this approach can be found in Fenton and Griffiths (2008).

Case study

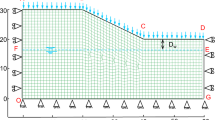
The studied site is located in the southwest central Japan, Boso Peninsula including sandstone and mudstone slopes (Fig. 2). A 1989 rainstorm which caused landslides along the sandstone and mudstone slopes was recorded at four meteorological stations (Yokohama, Kisarazu, Sakuma, and Sakahata) within a 30 km radius from the study site (Fig. 3). The sandstone slope S-1, which has an angle of β = 38.4°, slip depth of 1.6 m, sliding area of 620 m2, and volume of 990 m3 was selected in this study (Matsushi et al. 2006). Figure 4 shows the longitudinal section and failure surface of the S-1 slope. It is noted that the shallow failure was a transitional type, so the assumption of infinite slope can be reasonably used in this study. The properties of the upper 1.5 m soil layer were evaluated and summarized in Table 1 (Matsushi 2006). The soil profile of slope S-1 was classified using a dynamic cone penetration test (DCPT) value (Nc) as shown in Fig. 5. According to the ASTM D6951 (2003), the penetrometer consists of a penetration rod with a cone tip of 25-mm diameter and 60° tip angle, guide rods, and a 5-kg weight. When performing the test, the weight falls from a height of 50 cm along the guide rod to the cone. Wakatsuki et al. (2005) classified the ground into four soil layers: 0 ≤ Nc < 5 (upper layer), 5 ≤ Nc < 10 (middle layer), 10 ≤ Nc < 30 (lower layer), and Nc ≥ 30 (bedrock). In the classification of weathered rock by the Geological Society (1995), the upper layer and the middle layer correspond to “grade V/VI” (completely weathered soil), the lower layer corresponds to “grade IV” (highly weathered rock), and the bedrock corresponds to “grades I-III” (slightly weathered rock and fresh rock). According to the Unified Soil Classification System (USCS), the upper layer can be classified as silty sand (SM) based on grain-size distribution (Table 1).

Fig. 2
figure 2

Site location (after Matsushi 2006)

Full size image
Fig. 3
figure 3

Rainfall intensity of the 1989 storm recorded at four meteorological stations (after Matsushi 2006)

Full size image
Fig. 4
figure 4

Longitudinal section and failure surface of slope S-1 (adapted from Matsushi 2006)

Full size image
Table 1 Physical soil properties
Full size table
Fig. 5
figure 5

Soil profile of slope S-1

Full size image

The soil suction and volumetric moisture content of the upper layer were obtained from pressure plate tests. The soil water characteristic curve (SWCC) and its curve-fitting van Genuchten model are presented in Fig. 6. In this study, the types of middle and lower layer of soil can be reasonably assumed to be the same as the upper layer based on the DCPT; therefore, the same set of SWCC parameters were used for all soil layers. The saturated permeability was determined from a constant head permeability test with the specimen size of 75 mm in diameter and 260 mm in height (ASTM D2434-68, 2000) which was almost remained from the upper layer down to the bedrock, as shown in Fig. 7. Table 2 summarizes the fitting parameters of the soil-water characteristic curve and the average saturated permeability of all soil layers as input parameters for seepage analysis.

Fig. 6
figure 6

Soil water characteristic curve of the upper layer

Full size image
Fig. 7
figure 7

Saturated permeability varied with depth from a constant head permeability test

Full size image
Table 2 SWCC parameters and saturated permeability
Full size table

The shear strength of soils determined under four different normal stresses with various volumetric moisture contents (Matsushi et al. 2006) was used in the analysis. The best fitting curves of shear strength versus volumetric moisture content for normal stress of 10, 20, 30, and 40 kPa are presented in Fig. 8. The apparent soil cohesion (soil cohesion in dry condition), the friction angle, and the reduction coefficient were calculated as the input shear strength parameters for the stability analysis, as summarized in Table 3. It is noted that the direct shear tests were performed for the upper layer (i.e., < 2 m depth). The analysis was then focused on the upper layer.

Fig. 8
figure 8

Best-fitted shear strength versus volumetric moisture content curves for four normal stresses

Full size image
Table 3 Soil shear strength parameters
Full size table

In this study, a one-dimensional transient seepage analysis was conducted to study the effect of the 1989 rainstorm causing the shallow slope failure in the Japan. For the S-1 slope, the bedrock located at 4.5 m depth (Fig. 5) was designated the bottom undrained boundary (zero flux boundary), while the top boundary of the model should be designated a flux boundary (q), which is equivalent to the desired rainfall intensity. The average rainfall intensity from four recorded stations (Fig. 3) which was equivalent to a flux of 0.032 m/h was defined as the top boundary condition. The linear pressure head (zero at bedrock and − 4.5 m at the surface slope) was set as the initial condition. No ponding on the top surface of the soil column can be reasonably assumed due to the fact that when the rainwater exceeds the infiltration capacity of soil the excess water will drain away as surface runoff. A one-dimensional transient seepage analysis model of the S1-slope is presented in Fig. 9. The volumetric moisture content extracted from the transient seepage analysis was used to calculate the factor of safety using Eq. (9).

Fig. 9
figure 9

One-dimensional seepage model of the S1-slope (element size, Δz = 0.05 m)

Full size image

To analyze the probability of rainfall-induced slope failure, the total soil cohesion under unsaturated condition (C) and the frictional resistance (tanϕ) were considered as the random fields. The mean values of C and tanϕ were determined from the direct shear test results (Fig. 8). It is noted that the mean value of C is not constant, but it tends to decrease with increasing volumetric moisture content due to rainfall infiltration. According to Retheti (1988), the covariance coefficient of the effective cohesion (COVc′) for sandy soils and clayish soils were usually greater than 0.2. Since the effective soil cohesion is the same as the total soil cohesion in the saturated condition, the covariance coefficient of the total soil cohesion (COVC) can be set as the same value of COVc′ (Fenton and Griffiths 2008). The covariance coefficient of the frictional resistance (COVtanϕ) was between 0.02 and 0.22 (Phoon and Kulhawy 1999). In order to verify slope failure during the rainstorm and evaluate the effect of each shear strength parameter, the slope failure probability was calculated using the same value of covariance coefficient corresponding to COVC = COVtanϕ = 0.2. In addition, to simulate the effect of heterogeneous soil characteristics on the probabilistic calculation, the correlation length l is varied from 0.02 to 2.0 m for the description of the spatial correlation length of random fields C and tanϕ. Table 4 summarizes the statistical characteristics of soil shear strength parameters used for probabilistic analysis.

Table 4 Statistical properties of soil shear strength parameters used for probabilistic analysis
Full size table

A series of random fields of C and tanϕ are carried out using the random model and MCS. Figure 10 shows the convergence of the estimated probability of failure for the slope, which indicates that the failure probability can be converged when the generated samples exceed 2000. In this study, 5000 sets of the random fields C and tanϕ were used as input shear strength parameters for probabilistic stability analysis. Then, the factor of safety and critical depth were recorded for each generated random fields C and tanϕ; the failure probability was approximated based on Eq. (11).

Fig. 10
figure 10

Convergence of the failure probability at different times

Full size image

Analysis results

Deterministic analysis

In this section, a deterministic seepage and slope stability analysis was performed to investigate slope stability during rainfall. The resulting volumetric moisture content calculated from SEEP/W was then used with the infinite slope stability model to determine the corresponding factor of safety. Figure 11a shows the vertical distribution of volumetric moisture content with the duration of rainfall. The results show that the volumetric moisture content of ground surface rapidly increased at the beginning of rainfall. Then, the volumetric moisture content increased with depth as rainfall infiltrated the soil. When infiltration remained constant after 12 h, the volumetric moisture content nearly reached saturation, and there was no generation of positive pore water pressure in the upper layer. Figure 11b shows that the factor of safety varied with depth for the different rainfall durations. It can been seen that by increasing volumetric moisture content with depth, the factor of safety first decreased dramatically, increased slightly, and then decreased again. For the case of the 6 h rainfall, the factor of safety decreased due to soil shear strength deceased and the unit weight of the soil slice increased with increasing depth. The minimum factor of safety, close to 1.21, occurred at the depth of 1.05 m. However, as shown in Fig. 11a, the volumetric moisture content decreases at a depth of approximately 1.1–1.3 m; therefore, the factor of safety began to increase slightly. Subsequently, the unit weight of the soil slice increases with increasing depth, and the factor of safety began to decrease. This is because the main factor controlling the factor of safety is the reduction in soil shear strength at the early stage of rainfall. A similar phenomenon can be observed at 3 and 9 h of rainfall. The factor of safety only continuously decreases with depth after 12 h of rainfall because the increase in volumetric moisture content is almost constant in the upper layer (the top 2 m) (Fig. 11a). A factor of safety of less than one can be observed from a depth below 1.7 m. The slope stability analysis demonstrates that failure of the S-1 slope occurred during the 1989 rainstorm with failure surfaces below 1.6 m in the upper layer. Results indicate that the simulation of the failure surface agrees well with the observation of actual slip surface.

Fig. 11
figure 11

Results of deterministic analysis. a Volumetric moisture content profiles. b Variation of the factor of safety with time

Full size image

Probabilistic analysis

Effect of correlation length

In this section, probabilistic analysis of rainfall-induced slope failure is illustrated. The correlation lengths between 0.02 to 2.0 m were implemented for both random fields of C and tanϕ in this study. Figure 12 shows the histogram of frequency of each critical failure surface which occurred at different depth for the correlation lengths of 0.02 and 2.0 m at 9 and 12 h of rainfall duration. Figure 12a, b indicates that the critical failure surface most likely occurred at a depth of approximately 1.0–1.7 m after 9 h of rainfall. This finding means that the wetting front due to rainfall infiltration only decreases the shear strength of soil at the slope’s upper portion in the early stage of infiltration. As infiltration progresses and the wetting front moves down, the critical surface continuously increases in depth until the wetting front reaches the base of the upper layer. Finally, the highest frequency of critical surface failure occurred at the base of the upper layer, as shown Fig. 12c, d. Since the highest frequency of critical surface failure took place between 1.5 and 2.0 m depths of the upper layer after 9 h of rainfall, as seen Fig. 12, the failure mechanism can be characterized as a shallow failure, where the critical failure surfaces were located above the interface between the weathered soil and bedrock. Comparing the previous studies of Cho (2014) and Dou et al. (2015), the failure mechanism always occurs at the interface between the weathered soil and bedrock during rainfall infiltration. Figure 12 also indicates that the frequency of the critical surface failure was affected by the correlation length. In the histogram shown in Fig. 12a, c, l = 0.02 m displays smaller frequencies at the critical failure surface than the histogram in Fig. 12b, d for l = 2.0 m. This is because the lower correlation length, which exhibits highly non-homogeneous soil, has the critical surface moving upward. Conversely, the higher correlation length provided an increased frequency probability that the critical failure surface would be located at the weakest part of the upper layer as the random field becomes more spatially uniform.

Fig. 12
figure 12

Histogram of the critical depth at two different times (COVC = 0.2; COVtanϕ = 0.2). a After 9 h, l = 0.02 m. b After 9 h, l = 2.0 m. c After 12 h, l = 0.02 m. d After 12 h, l = 2.0 m

Full size image

Figure 13 shows the influence of correlation length l in the range of 0.02 ≤ l ≤ 2.0 m on the failure probability at different points in rainfall duration. The failure probability was calculated at the critical failure surface corresponding to the minimum factor of safety of the deterministic analysis. The results indicate that the failure probability increases dramatically as infiltration progresses, and soil slope with smaller values of correlation length has a smaller failure probability at the early stages of infiltration. However, the failure probability for cases with smaller values of correlation length is greater than those with larger values of correlation length after the rainfall duration exceeded approximately 9.5 h. This can be referred to as a critical rainfall duration causing slope failure. It should be emphasized that all curves cross over at the failure probability of P f  = 0.5 occurring at the critical rainfall duration. This is because the cumulative probability of FS for all correlation lengths equal to 0.5 at the corresponding safety factor of FS = 1.0, as shown Fig. 14. Therefore, the location of the failure surface can be derived from probabilistic analysis, in which P f  = 0.5.

Fig. 13
figure 13

Effect of l on failure probability at critical depth (COVC = 0.2; COVtanϕ = 0.2)

Full size image
Fig. 14
figure 14

Cumulative probability of FS at critical rainfall duration (COVC = 0.2; COVtanϕ = 0.2)

Full size image

In order to obtain the failure surface, the failure probability distributions were calculated at the point of critical rainfall duration. Figure 15 shows the distribution of failure probability with depth for all correlation lengths. The corresponding failure surface was also obtained at the failure probability of P f  = 0.5, with the failure surface located at the depth of 1.7 m of slope while the actual failure surface during the 1989 storm occurred at the depth of 1.6 m, which approximates the analysis result indicating that the probabilistic analysis with random fields is an effective predictor to locate critical failure surfaces and determine critical rainfall durations.

Fig. 15
figure 15

Failure probability distribution at critical rainfall duration (COVC = 0.2; COVtanϕ = 0.2)

Full size image

Effects of random field of shear strength parameters

In the previous assessment, two random fields of C (total soil cohesion under unsaturated condition) and tanϕ (frictional resistance) were considered for the failure probability calculation. One might want to identify which random field greater effect on the slope failure. In order to evaluate the influence of each random field, a series of FS for each random field alone and both random fields were calculated at the failure surface which occurred at the critical rainfall duration, and the cumulative probability curves of FS for these cases were obtained at a different correlation lengths. Figure 16 compares the cumulative probability curve of FS considering two random fields together with the curve obtained by ignoring one random field at a different correlation length. The difference between the curves considering two random fields and the curve neglecting one random field reflects the importance of that random field for failure probability calculation. As shown in Fig. 16, when random field tanϕ was ignored, the difference of probability was more than the difference by neglecting random field C. It turns out that shallow failure is mainly caused by reduction in soil cohesion during rainfall infiltration. In addition, this difference tends to increase with the increase of correlation length. This finding indicates that the influence of each random field for non-homogeneous soil is somewhat important.

Fig. 16
figure 16

Effect of random field C and tanϕ on the slope failure at the critical rainfall duration (COVC = 0.2; COVtanϕ = 0.2). a l = 0.02 m. b l = 0.05 m. c l = 0.25 m. d l = 2.0 m

Full size image

Conclusion

This paper examined the spatial variability of shear strength parameters on rainfall-induced landslides. A case study of a sandstone slope with deep impermeable bedrock in a site in Japan was selected for comparison. An unsaturated seepage and infinite slope stability analysis were applied using a probabilistic method. To simulate shallow failure, the reduction in soil shear strength due to the increase in volumetric moisture content was considered. A series of Monte Carlo simulations were conducted to investigate the effect of a random field on C and tanϕ parameters. The analysis results were then compared to an actual occurrence of slope failure during a storm in 1989. The study results can be concluded as follows

  1. 1.

    The probabilistic analysis results indicate that the critical failure surface was located at the depth of approximately 1.0–2.0 m belowground surface depending on the rainfall duration. The failure surface occurred at 1.7 m depth at the critical rainfall duration of 9.5 h. The actual soil slope also failed at 1.6 m depth belowground in the period of the 1989 storm. However, the deterministic approach with infinite slope assumption reported the location of the failure surface at the base of the upper layer (i.e., 2.0 m in this study).

  2. 2.

    The critical failure surface is not necessarily fixed at the base of the upper layer but changed due to the migration of wetting front as rainfall progressed. The results show that the frequency of the critical failure surface that occurs at the weakest part of the upper layer increase with increased correlation length. This also agrees well with previous studies by Cho (2014) and Dou et al. (2015).

  3. 3.

    The probability framework can be used to find the critical rainfall duration corresponding to the location of the slip surface occurring at a depth of 1.7 m of the upper layer. In this study, the critical rainfall duration was obtained to indicate the slope failure during the 1989 rainstorm. The results confirm that the random field model is an essential technique to predict the slope failure due to rainfall.

  4. 4.

    A probabilistic stability analysis of rainfall-induced slope failure depends on the contribution of random fields on the shear strength parameters C and tanϕ. However, the study found that the random field of C is more important than the random field of tanϕ for failure probability estimation of shallow landslides. This finding can be used to verify the significance of effect of uncertain shear strength parameters of a shallow failure.