Introduction

Flow-like landslides are typical earth surface geophysical flows. They are recognized as one of the most dangerous natural hazards on the earth for their high mobility and catastrophic consequences (Evans et al. 2009a; Yin et al. 2011; Hungr et al. 2014; Iverson et al. 2015; Haque et al. 2016). Flow-like landslides can be triggered by heavy rainfall (Iverson 2000; Wang and Sassa 2003), earthquake (Okada et al. 2008; Evans et al. 2009b), snowmelt (Meyer et al. 2012), or some other factors (Hou et al. 2018; Rossano et al. 1996). In their propagation processes, these landslides run quickly on hill slopes or along narrow valleys, and the volumes of them increase dramatically by entraining the loose materials along the traveling paths. This phenomenon is called bed entrainment or basal erosion/scour (Hungr and Evans 2004; McDougall and Hungr 2005; Pastor et al. 2009).

Previous studies (Iverson 1997; Mangeney 2011; Crosta et al. 2017) illustrate that bed entrainment is a very complex physical process. This process normally consists of the shearing, thrusting, and plowing of the basal materials and the materials mixing between the sliding mass and the entrained mass. Bed entrainment has at least three important impacts on flow-like landslides: (1) increasing the volume of a flow-like landslide; (2) changing the physical properties (e.g., water content, bulk density, rheology, etc.) of the sliding mass; (3) reshaping the topography of the sliding surface. The first impact has been observed in many flow-like landslides. Some flow-like landslides originated from a small volume of unstable debris or soil mass, but their final volumes expanded more than ten times by entraining loose materials (Hungr and Evans 2004; Breien et al. 2008). For example, the 1990 Tsing Shan debris flow in Hong Kong had an initial volume of only 400 m3, but its volume finally increased to about 20,000 m3 (King 1996). The volume bulking caused by bed entrainment has been demonstrated to be an important factor influencing the propagation of flow-like landslides (Pirulli and Pastor 2012; Cuomo et al. 2016). The importance of the second impact has also been noticed for decades. The results of flume experiments show that the mobility of a flow-like landslide can be significantly altered by bed entrainment (Mangeney et al. 2010; Iverson et al. 2011). Generally, entraining saturated materials will increase the run-out distance of a landslide, while entraining dry erodible materials will decrease the mobility of the landslide. This phenomenon is easy to understand, but how to quantify it is still a difficult problem. Therefore, most previous studies (Ouyang et al. 2015; Cuomo et al. 2014; Pirulli and Pastor 2012; McDougall and Hungr 2005) either neglected this impact or oversimplified it in numerical modeling. The third impact appears naturally in the bed entrainment process. The topography change may alter the traveling path of a flow-like landslide; this impact is noticeable especially for some debris flows whose traveling directions rely heavy on the topography. However, the importance of the third impact also has not been deeply explored.

Tens of numerical models have been proposed to simulate the propagation of flow-like landslides. These models can be divided into continuous medium models (CMM) and discrete medium models (DMM). CMM take sliding mass as a continuous material, using numerical methods like smoothed particle hydrodynamics (McDougall and Hungr 2005; Pastor et al. 2009; Dai et al. 2014; Huang et al. 2015), the finite difference method (Chen et al. 2006; Sassa et al. 2010; Pirulli and Pastor 2012; Ouyang et al. 2015; Shen et al. 2018), and the modified finite element method (Crosta et al. 2009; Zhang et al. 2015) to solve the governing equations. In comparison, DMM take sliding mass as a discrete block system, adopting the discrete element method or discontinuous deformation analysis (Peng et al. 2018) to calculate the motion of each block. These models have been widely implemented in the back analysis of real events. For most CMM, bed entrainment is considered by modifying the depth-integrated governing equations for shallow water flows. Some recent papers have provided state-of-the-art reviews of the existing bed entrainment models (Pirulli and Pastor 2012; Iverson and Ouyang 2015). According to these reviews, plenty of bed entrainment models have been adopted in the abovementioned numerical models. These bed entrainment models generally fall into two categories: empirical models (Takahashi and Kuang 1986; Egashira et al. 2001; Pitman et al. 2003; McDougall and Hungr 2005; Blanc et al. 2011) and physically based models (Fraccarollo and Capart 2002; Sovilla et al. 2006; Medina et al. 2008). Empirical models associate the entrainment rate with some parameters of a flow-like landslide, such as slope angle, velocity, thickness, grain concentration, etc. These models are usually constructed by using statistical methods to analyze the data from past events or experiments. Therefore, they do not have clear physical meaning and need to be calibrated in practice. In comparison, physically based models are deduced according to some physical principles, such as the momentum conservation of the erodible mass. The physical meaning of the model proposed by Fraccarollo and Capart (2002) is clear and the parameters in this model can be determined by laboratory tests, making it very easy to use. Therefore, this model is adopted in the present study.

According to the abovementioned research works, this paper aims to further explore the roles of the bed entrainment-induced rheology and topography changes on the propagation of flow-like landslides. The Fraccarollo and Capart model and a new rheology change method are incorporated into a quasi-3D finite difference code developed by Shen et al. (2018) to conduct this numerical investigation. The main contribution of this study is that it advances the techniques in modeling the bed entrainment phenomenon of flow-like landslides to some extent. In the following sections, the governing equations for flow-like landslides are briefly introduced; then, two widely used bed entrainment models are remarked and a new approach is proposed to quantify the rheology change; following that, the code is used to analyze one ideal case and two real cases; finally, the simulation results are presented and discussed.

Governing equations

The governing equations of flow-like landslides consist of the momentum equations and the continuity equation. These equations are deduced in Eulerian coordinates based on the shallow water assumption, and bed entrainment is considered by the entrainment rate E. The shallow water assumption is suitable here, since, for most flow-like landslides, the thickness of the sliding mass is much smaller than the length and width. These equations are briefly introduced here, and the detailed derivation can be found in Shen et al. (2018).

The momentum equations represent the momentum conservation in a fixed soil column, and are given by:

$$ \frac{\partial {Q}_x}{\partial t}+\frac{\partial {Q_x}^2/h}{\partial x}+\frac{\partial {Q}_x{Q}_y/h}{\partial y}=-\left({k}_x hg\frac{\partial h}{\partial x}+g\frac{h^2}{2}\frac{\partial {k}_x}{\partial x}\right)+\left( Ag+B\right)\frac{h\tan \alpha }{G}-\frac{hDxS}{m} $$
(1)
$$ \frac{\partial {Q}_y}{\partial t}+\frac{\partial {Q}_x{Q}_y/h}{\partial x}+\frac{\partial {Q_y}^2/h}{\partial y}=-\left({k}_y hg\frac{\partial h}{\partial y}+g\frac{h^2}{2}\frac{\partial {k}_y}{\partial y}\right)+\left( Ag+B\right)\frac{h\tan \beta }{G}-\frac{hDyS}{m} $$
(2)

where Qx and Qy are the flow quantities in the x and y directions, respectively; h is the thickness of the sliding mass; kx and ky are the lateral pressure coefficients in the x and y directions, respectively; g is the acceleration of gravity; A and B are the parameters related to the static and centrifugal supporting forces on the sliding surface, respectively; α and β are the dip angles of the sliding mass in the x and y directions, respectively; G is a geometric parameter related to α and β; S is the shear resistance on the sliding surface; Dx and Dy are the operators projecting S in the x and y directions, respectively; and m is the mass of the soil column. The expressions of G, A, and B are given as:

$$ G={\tan}^2\alpha +{\tan}^2\beta +1 $$
(3)
$$ A=1+\left({k}_x\frac{\partial h}{\partial x}+\frac{h}{2}\frac{\partial {k}_x}{\partial x}\right)\tan \alpha +\left({k}_y\frac{\partial h}{\partial y}+\frac{h}{2}\frac{\partial {k}_y}{\partial y}\right)\tan \beta $$
(4)
$$ B=\frac{C_x}{\cos \alpha }{\left(\frac{v_x}{\cos \alpha}\right)}^2+\frac{C_y}{\cos \beta }{\left(\frac{v_y}{\cos \beta}\right)}^2 $$
(5)

where Cx and Cy are the curvatures of the sliding surface in the x and y directions, respectively, and vx and vy are the velocities in the x and y directions, respectively.

The lateral pressure coefficient k is a continuous function of the strain rate. For example, the lateral pressure coefficient in the x direction is given by:

$$ {k}_x=\Big\{{\displaystyle \begin{array}{c}{k}_{pas},\\ {}\left(\frac{\partial {v}_x}{\partial x}/\varepsilon \right)\left({k}_{pas}-{k}_0\right)+{k}_0,\\ {}{k}_0-\left(\frac{\partial {v}_x}{\partial x}/-\varepsilon \right)\left({k}_0-{k}_{act}\right),\\ {}{k}_{act},\end{array}}\kern0.5em {\displaystyle \begin{array}{c}\frac{\partial {v}_x}{\partial x}\le -\varepsilon \\ {}-\varepsilon <\frac{\partial {v}_x}{\partial x}<0\\ {}0\le \frac{\partial {v}_x}{\partial x}<\varepsilon \\ {}\frac{\partial {v}_x}{\partial x}\ge \varepsilon \end{array}} $$
(6)

where kpas, k0, and kact are the passive, static, and active lateral pressure coefficients of the soil column, respectively, and ε is the threshold which is related to the minimum strain rate changing the soil column from the static state to the passive or active state. kpas and kact are determined according to the equation suggested by Savage and Hutter (1989):

$$ {\displaystyle \begin{array}{c}{k}_{pas}\\ {}{k}_{act}\end{array}}\Big\}=\frac{2}{\cos^2{\varphi}_i}\left(1\pm \sqrt{1-{\cos}^2{\varphi}_i\left(1+{\tan}^2{\varphi}_b\right)}\right)-1 $$
(7)

where φi and φb are the internal and basal friction angles of the soil column, respectively.

The shear resistance S is calculated by the Mohr–Coulomb criterion considering that the sliding mass is a frictional material:

$$ S=N\tan {\varphi}_a+ c\varDelta \mathrm{x}\varDelta \mathrm{y}\sqrt{G} $$
(8)

where N is the supporting force in the normal direction of the sliding surface; c is the effective cohesion; Δx and Δy are the widths of the soil column in the x and y directions, respectively; and φa is the apparent friction angle. The expression of φa is given by:

$$ \tan {\varphi}_a=\left(1-{r}_u\right)\tan \varphi $$
(9)

where ru is the pore pressure coefficient representing the ratio of the pore pressure and total stress, and φ is the effective basal friction angle.

The continuity equation refers to the mass conservation in the fixed soil column, and is given by:

$$ \frac{\partial h}{\partial t}+\frac{\partial {Q}_x}{\partial x}+\frac{\partial {Q}_y}{\partial y}=E $$
(10)

where E is the entrainment rate. The governing equations of flow-like landslides consist of Eqs. (1), (2), and (10). These equations are solved by a quasi-3D finite difference code developed by Shen et al. (2018).

Bed entrainment

The abovementioned governing equations are not closed because E is unknown. Two widely used bed entrainment models which can be used to close these equations are introduced and remarked in this section. Furthermore, a new method is proposed to consider the rheology evolution of the sliding mass during the bed entrainment process.

Bed entrainment models

As mentioned above, many bed entrainment models have been proposed currently. Among them, the empirical model proposed by McDougall and Hungr (2005) and the physically based model proposed by Fraccarollo and Capart (2002) may be the most widely used.

The empirical model proposed by McDougall and Hungr (2005) is a simple and effective model. This model assumes that the entrainment rate E is the product of the landslide growth rate Er, thickness h, and velocity v. The equation of this model is given by:

$$ E=-\frac{\partial Z}{\partial t}={E}_r hv $$
(11)

where Z is the elevation of the sliding surface and Er is an empirical constant which is independent of h and v. Er needs to be calibrated to make the simulated landslide volume match the measured data. The primary value of Er is estimated based on the assumption that the volume of a flow-like landslide shows a natural exponential growth with the displacement (McDougall and Hungr 2005). In Eq. (11), E is proportional to v because the above assumption associates E with the displacement of the sliding mass. Er can be estimated by Eq. (12):

$$ {E}_r=\frac{\ln \left({V}_f/{V}_o\right)}{L} $$
(12)

where Vo and Vf are the volumes of the landslide before and after bed entrainment, respectively, and L is the approximate average path length of the entrainment zone.

The physically based model proposed by Fraccarollo and Capart (2002) is deduced from the Rankine–Hugoniot condition, which represents the momentum conservation across a shock-like discontinuity. Since the velocities, bulk densities, and stresses at the two sides of this surface are different, the interface between the sliding mass and the erodible mass is a discontinuous surface. The expression of E in this model is given by:

$$ E=-\frac{\partial Z}{\partial t}=\frac{\tau_s-{\tau}_b}{\rho_ev} $$
(13)

where τs is the shear stress of the sliding mass on the sliding surface; τb is the resistant shear stress in the erodible mass; and ρe is the bulk density of the erodible mass.

Equation (13) can be interpreted by Fig. 1. Since the sliding mass exerts a shear stress τs on the erodible mass, the erodible mass will resist shear deformation by a resistant shear stress τb. When τs is larger than τb, the original static erodible mass will accelerate. Suppose that the sliding mass is moving at a velocity v. To be entrained, the erodible mass needs to accelerate to v within a short period of time. According to momentum conservation, only the top erodible mass with a thickness of dZ can be accelerated to v by the external force τs − τb at the same time. This explains why E is reciprocal to v in Eq. (13).

Fig. 1
figure 1

Schematic diagram of the mechanism of the Fraccarollo and Capart bed entrainment model

Full size image

The form of the empirical model is simpler than the physically based one, so this empirical model is very popular in practice. On the other hand, the empirical model does not have physical meaning, so it cannot correctly capture the evolution of the sliding surface topography. In addition, this empirical model does not have a certain relation with the rheology of the sliding mass, so it cannot consider the entrainment-induced rheology change. The topography change of the sliding surface and the rheology change may significantly influence the propagation direction of a flow-like landslide, so it is necessary to correctly reflect these changes in the model. In comparison, the physically based model can explain the mechanism of bed entrainment, making it more reliable in simulating the topography evolution of the sliding surface. This model also links the entrainment rate with the parameters τb and τs that are related to the rheology of flow-like landslides. Therefore, the physically based model is selected to conduct the present study.

The topography change can be easily determined by E. According to Eq. (13), the entrainment rate E is the partial derivate of the sliding surface elevation Z to time t, so its integration is the local elevation change of the sliding surface. To explore the influence of topography change, two bed entrainment scenarios are considered here, as shown in Fig. 2. Figure 2a, b represent the bed entrainment scenarios with a thin erodible mass and a thick erodible mass, respectively. The influences of topography change in these two scenarios are different. In Fig. 2a, the erodible mass is thin, so the topography change is not obvious after entrainment. For this scenario, the topography of the underneath fixed bed plays the dominant role. However, when the erodible mass is thick, the topography of the sliding surface may be uncertain after entrainment, as shown in Fig. 2b. Under such a circumstance, the sliding surface topography can be significantly reshaped by bed entrainment. The propagation of a flow-like landslide may, thus, be influenced by the reshaped topography.

Fig. 2
figure 2

Schematic diagram of two bed entrainment scenarios: a erodible mass is thin and b erodible mass is thick

Full size image

Rheology change

The erodible mass has distinct property with the sliding mass. Therefore, when it is entrained and mixes with the sliding mass, the rheology of the sliding mass must change. The rheology of the sliding mass changes gradually in the bed entrainment process, and, in turn, this change affects the entrainment rate and alters the mobility of flow-like landslides. In the previous studies (Ouyang et al. 2015; Cuomo et al. 2014; Pirulli and Pastor 2012; McDougall and Hungr 2005), the rheology change due to entrainment was neglected or not properly considered. A simple approach to consider this change is to modify the parameters in the rheology models. Since bed entrainment is a progressive process, the rheology change of the sliding mass should also evolve gradually. A basic principle adopted here is that the rheology of the sliding mass will be closer to that of the erodible mass when more erodible mass is entrained. Therefore, the following equation is proposed to estimate the rheology change during bed entrainment:

$$ {f}_a=\frac{f_o{V}_o+{f}_bw{V}_e}{V_o+w{V}_e} $$
(14)

where fa represents the rheology parameters of the sliding mass after entrainment (i.e., ru, c, and φ, etc.); fo represents the rheology parameters of the sliding mass before entrainment; fb represents the rheology parameters of the erodible mass; Vo is the volume of the original sliding mass; Ve is the volume of the entrained mass; and w is an empirical weight coefficient. Equation (14) is a weighted average between the rheology parameters of the original sliding mass and that of the erodible mass. The sliding mass and erodible mass have different weights because their contributions to the rheology of the mixed sliding mass may be different. For instance, the rheology of the mixed sliding mass should be closer to that of the erodible mass when the entrained mass is entrapped at the bottom of the landslide. In such a situation, the erodible mass should play a dominate role even if the volume of the entrained mass is small. For a flow-like landslide, the w value is normally between 10 and 50. When the entrained mass is saturated and entrapped at the bottom of the sliding mass, it takes a high value. By contrast, if the entrained mass is not fully saturated and mixes well with the sliding mass, it takes a low value. The rheology of the sliding mass which passes the erodible zone will be modified by Eq. (14).

Ideal case study

Setup of the ideal case

In this section, a simple ideal case is simulated to explore the bed entrainment-induced topography and rheology changes on the propagation of flow-like landslides. The schematic diagram of this case is shown in Fig. 3. In this case, the initial sliding surface consists of two planes with different dip angles. An ideal landslide is released from the upper plane and then propagates downwards under gravity. On the upper plane, an erodible zone is set to consider bed entrainment. The sliding mass can entrain material from the erodible zone when it moves within this zone. The case presented here is similar to those cases studied by Cuomo et al. (2014) and McDougall and Hungr (2005), but the setup of the present case is different to those in previous studies since different research purposes. The setup of the present case is shown in Fig. 4. The ideal landslide is initially placed at the middle of the upper plane in the y direction. The length and width of the sliding mass is Bx and By, respectively. The original landslide is identical in thickness of Hs. The erodible zone is next to the sliding mass; the width of this zone is Be and the thickness of the erodible mass is He. A point P located at the center of the erodible zone is selected to record the entrainment rate in the simulation. The simulated run-out distance (Ls) and lateral spreading width (Ws) of the landslide will also be recorded. In total, 11 groups of simulations are carried out. The detailed setups for these groups are shown in Table 1, and the initial parameters for the sliding mass and the erodible mass are given in Table 2. In these groups, only the parameters related to the rheology and topography are set to be variables.

Fig. 3
figure 3

Schematic diagram of the ideal bed entrainment case study

Full size image
Fig. 4
figure 4

Setup of the ideal bed entrainment case study

Full size image
Table 1 Setup of the 11 groups of simulations of the ideal case study
Full size table
Table 2 Parameters used in the simulations of the ideal case study
Full size table

In Table 1, T1 represents the situation in which bed entrainment is not considered, T2–T6 represent the bed entrainment scenario with a thick erodible mass, and T7–T11 represent the bed entrainment scenario with a thin erodible mass. For all groups, the computational region is 2200 m in the x direction and 2000 m in the y direction, the intersection line of the upper and lower planes is located at x = 500 m, the size of the computational cells is 10 m in both the x and y directions, and the initial time step is 0.01 s.

Results of the ideal case

Figure 5 shows the simulated final topography of the deposits obtained in T1–T5. It shows that the run-out distance (Ls = 670 m) and lateral spreading width (Ws = 300 m) of T1 (Fig. 5a) are the smallest in these groups. This illustrates that the mobility of a landslide may be underestimated without considering bed entrainment. T2 represents the situation that the rheology change is not considered. Ls and Ws of T2 are only slightly larger than that of T1, demonstrating that volume bulking is not likely to significantly increase the mobility of a landslide alone. The run-out distance of T3 (Ls = 1390 m) and T4 (Ls = 1300 m) are much larger than that of T1 (Ls = 670 m), indicating that the rheology change can significantly increase the run-out distance of a flow-like landslide (Fig. 5c, d). In addition, the results of T3 and T4 also show that the topography change may constrain the lateral spreading. The lateral spreading width of T3 (Ws = 620 m) is obviously bigger than that of T4 (Ws = 440 m). When the sliding mass moves on a thick erodible mass, a deep concave trench may be created by bed entrainment, thus impeding the lateral spreading of the sliding mass. This result suggests that the lateral spreading of a flow-like landslide may be greatly overestimated if the topography change is not considered when the erodible mass is thick. In comparison, the result of T5 (Fig. 5e) shows that the run-out distance of the landslides will increase if the erodible mass has a stronger ability to soften the sliding mass.

Fig. 5
figure 5

Simulated thickness of the final deposit of the ideal case: a–e the results of T1–T5, respectively

Full size image

The simulated Ls, Ws, entrained volume Ve, and duration t in T1–T11 are presented in Table 3. The results of T7–T11 show that the rheology change still has a significant influence on the run-out distance of a flow-like landslide when the erodible mass is thin. However, the simulated values of Ws in T7–T11 (Ws = 320–340 m) are only slightly larger than that of T1 (Ws = 300 m), reflecting that the influence of the topography change on the lateral spreading is not significant when the erodible mass is thin. For both entrainment scenarios (T2–T6 and T7–T11), the rheology change also alters the duration of the propagation of a landslide. It shows that the duration is proportional to the run-out distance.

Table 3 Simulated run-out (Ls), lateral spreading width (Ws), entrainment volume (Ve), and duration (t) of the ideal case in groups T1–T11
Full size table

Figure 6 depicts the bed entrainment rate obtained in T2 and T4–T6 at point P. As shown in this figure, with the increase of the weight coefficient w, the bed entrainment rate decreases gradually, while the duration of entrainment shows a reverse tendency. This phenomenon is in accord with the principle indicated by Eq. (13). A larger w means that the rheology of the sliding mass changes quickly after entraining a small volume of erodible mass. The value of τs − τb decreases quickly when w goes up, thus decelerating the bed entrainment rate E. The total thickness of the erodible mass at P is a constant here, so the entrainment duration will increase when E reduces. This phenomenon also indicates that the rheology change will influence the topography change. In the propagation process of a flow-like landslide, the rheology change and topography change interact with each other, finally determining the run-out distance, propagation duration, lateral spreading, and topography of the final deposit. The simulated Ve in T2 and T4–T6 are shown in Fig. 7. The change rate of Ve will also decrease when w increases. The change rate of Ve is proportional to E, so this result agrees with the above analysis.

Fig. 6
figure 6

Evolution of the simulated bed entrainment rate E of the ideal case at point P in groups T2 (w = 0), T4 (w = 2), T5 (w = 20), and T6 (w = 30)

Full size image
Fig. 7
figure 7

Evolution of the simulated entrainment volume Ve of the ideal case at point P in groups T2 (w = 0), T4 (w = 2), T5 (w = 20), and T6 (w = 30)

Full size image

In summary, the results of this ideal case show that both the rheology and topography changes can significantly influence the propagation of flow-like landslides. The rheology change plays a dominant role in altering the run-out distance and duration of a flow-like landslide, no matter whether the thickness of the erodible mass is thick or thin, while the topography change is likely to constrain the lateral spreading when the erodible mass is thick. In addition, the rheology change and topography change are two interactive procedures; they influence each other in the bed entrainment process, finally determining the run-out distance, lateral spreading, velocity, and duration of flow-like landslides.

Case study of two flow-like landslides

Introduction of the Dabaozi landslide

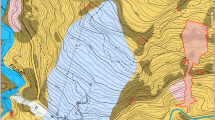
The Dabaozi landslide is a typical flow-like landslide in the Chinese Loess Plateau. This landslide is located in the side of a loess tableland in Jinyang County, Shaan’xi Province, China (N 34°29′8.76″, E 108°52′10.08″). Previous studies (Shen et al. 2016; Peng et al. 2017; Hou et al. 2018) show that irrigation on the top of the tableland is the main triggering factor of the landslides in this region. These landslides have caused serious damages to the local infrastructures and environment. In this region, landslide entrainment is a very common phenomenon. The original sliding mass of the landslides is the loess from the side of the loess tableland. After a landslide occurs, the sliding mass will entrain a large volume of saturated gravel from the first terrace of the Jinghe River. Since the saturated gravel is likely to become liquefied under the huge impact of a landslide, entraining saturated terrace gravel may contribute to the high mobility of the flow-like landslides in this region. The Dabaozi landslide happened on April 10, 2012. This landslide originated from a 72-m-high slope and traveled about 275 m on the terrace of the Jing River (Shen et al. 2016). The panorama and topography of this landslide is shown in Fig. 8. The original volume of this loess landslide was about 206,000 m3, and about 82,000 m3 of terrace gravel was entrained by this landslide. The thickness of the gravel on the terrace was about 4 m before being entrained, while the thickness of the loess landslide was about 10–20 m. For this landslide, the thickness of the erodible mass is deemed to be relatively thick, since the change of the sliding surface may have a significant influence on the propagation of this landslide. Therefore, it is selected as the case to represent the bed entrainment scenario with a thick erodible mass.

Fig. 8
figure 8

a Satellite picture of the Dabaozi landslide, b the measured final topography of the Dabaozi landslide

Full size image

The parameters used in the simulation of this case are shown in Table 4. The c, φ, and ρ values of the loess and gravel are given based on the laboratory test results of Shen et al. (2016). The ru value is determined according to the saturation and drainage condition of the soil. The static lateral pressure coefficient k0 is estimated by k0 = 1 − sin φa, where φa is the apparent friction angle in Eq. (8). For the saturated gravel, the drainage condition tends to be poor in the high-speed propagation of the landslide, so its ru value takes 0.98 here, while part of the loess is unsaturated in this landslide, so it takes a relatively low ru value. Using the parameters shown in Table 4, three simulations of different situations are carried out. The computational dimension for this case is 500 m in the x direction and 440 m in the y direction. The size of each cell is 5 m in both the x and y directions, and the initial time step Δt is 0.01 s. The thickness of the erodible mass is 4 m. The weight coefficient w takes a relative high value of 50, considering that the erodible mass is entrapped on the bottom of the loess sliding mass.

Table 4 Parameters used in the simulation of the Dabaozi landslide
Full size table

Simulation results of the Dabaozi landslide

Figure 9 shows the simulated thickness of the sliding mass and entrainment depth at different times (t = 4.6, 16.1, and 28.0 s). These times represent the early, middle, and final stages of the propagation process, respectively. It shows that the result in Fig. 9e agrees best with the measured trimline. In comparison, the situation without considering topography change (Fig. 9g) overestimated the lateral spreading and run-out distance of this landslide, while neglecting rheology change (Fig. 9h) significantly reduces the final run-out distance. This result is in accord with the analysis of the ideal case in the above section. The simulated final topography in Fig. 9e also agrees well with the field survey data: the thickest part of the final deposit is the rear part (about 20 m) and the thickness part of the final deposit in the middle part is about 5–10 m. Figure 9b–f show that the entrainment depth in the middle of the entrained zone is the deepest (4 m), and the entrainment depth decreases gradually from the middle of this zone to the margin. It indicates that the topography after entrainment is concave; such a concave topography tends to impede the propagation of this landslide.

Fig. 9
figure 9

Simulated thickness and entrainment depth of the Dabaozi landslide at different times and simulation situations (S1: neglecting rheology change; S2: considering rheology and topography change; S3: neglecting topography change). a Thickness and b entrainment depth at t = 4.6 s in S2. c Thickness and d entrainment depth at t = 16.1 s in S2. e Thickness (final deposit) and f entrainment depth at t = 28.0 s in S2. g Final thickness in S3 and h final thickness in S1

Full size image

Five points (P1–P5 in Fig. 9f) in the erodible zone are selected to analyze the evaluation of the entrainment rate E at different run-out distances. The locations of these points are shown in Table 5. The simulated E at these points are recorded and presented in Fig. 10. It shows that E decreases gradually with the increase of the run-out distance. With the increase of the run-out distance, more erodible mass will be entrained, so the rheology of the sliding mass will be closer to that of the erodible mass, leading to the decrease of E. This result indicates that the bed entrainment-induced rheology change is a progressive process. The new rheology method (Eq. (14)) can naturally reflect such a process.

Table 5 Coordinates setup for the measured points P1–P5 in the simulation of the Dabaozi landslide
Full size table
Fig. 10
figure 10

Simulated bed entrainment rate E at points P1–P5 in the simulation of the Dabaozi landslide

Full size image

Figures 11 and 12 show the evolution of the simulated entrainment volume Ve and average velocity v obtained in the three situations. Figure 11 shows that the entrainment volume of S1 (Ve = 39,000 m3) is the lowest, while that of S3 (Ve = 119,000 m3) is the largest. The result of S2 (Ve = 89,000 m3) agrees best with the estimated entrainment volume (82,000 m3). Figure 12 shows that the maximum average velocities of these three situations are almost the same. However, without considering the rheology change, the sliding mass will decelerate quickly after it reaches the terrace, leading to a short run-out distance. In comparison, if the topography change is not considered, the additional energy consumption caused by the concave topography cannot be considered, resulting in a larger lateral spreading and run-out distance. In addition, the duration of this landslide is also greatly affected by the sliding mass rheology and the sliding surface topography.

Fig. 11
figure 11

Simulated entrainment volume of the Dabaozi landslide in different simulation conditions (S1: neglecting rheology change; S2: considering rheology and topography change; S3: neglecting topography change)

Full size image
Fig. 12
figure 12

Simulated average velocity of the Dabaozi landslide in different simulation conditions (S1: neglecting rheology change; S2: considering rheology and topography change; S3: neglecting topography change)

Full size image

Introduction of the Dagou landslide

The Dagou landslide is a loess–mudstone flow-like landslide induced by heavy rainfall in Tianshui City, Gansu Province, China (N 34°31′59.90″, E 105°55′54.50″). This landslide occurred on July 23, 2013, and turned into a debris flow by entraining loose saturated materials along the Dagou galley. Figure 13 shows the panorama of the deposit two months after the landslide. The landslide formed a fan-shaped deposit at the exit of the galley after traveling about 1100 m along the meandering galley, and, finally, destroyed ten houses in the deposition zone (Shen et al. 2018). Field survey indicates that 151,000 m3 of loess–mudstone (mainly mudstone) was involved in this event, and more than 43,000 m3 of loose mass was entrained by the landslide (Shen et al. 2018). In comparison with the Dabaozi landslide, the erodible mass along the traveling path is relatively thin, with an average thickness of only 1 m. Therefore, this landslide is selected as another case to study the bed entrainment scenario with thin erodible mass.

Fig. 13
figure 13

Satellite picture of the Dagou landslide two months after its occurrence (modified from Google Earth)

Full size image

In the simulation of this case, the computational dimensions are 1150 m and 330 m in the x and y directions, respectively, the cell size is 10 m in both the x and y directions, the initial time step Δt is 0.01 s, 1 m of erodible mass is distributed along the galley, and w takes a relatively high value of 30 considering the high mobility of the landslide. The parameters used in this simulation are given in Table 6. The initial c and φ values of the sliding mass are given according to the laboratory test results of the mudstone samples (Shen et al. 2018), while that of the erodible mass are set to have much lower values, considering that the erodible mass is soft and loose. Since the erodible mass is saturated, its ru value takes 0.98, while that of the mudstone takes a relatively low value, considering that part of the mudstone is unsaturated. The density of the mudstone is determined by laboratory testing, while the density of the erodible mass is assumed to have the same ρ as the mudstone. Similarly, three situations are simulated here to explore the influence of the bed entrainment-induced rheology and topography changes on the propagation of this landslide.

Table 6 Parameters used in the simulation of the Dagou landslide
Full size table

Simulation results of the Dagou landslide

Figure 14 shows the simulated distribution of the sliding mass at different times and the final topography of the three situations. The simulated final deposit in Fig. 14d, e are very close, indicating that the topography change only has a slight influence on the propagation of this landslide. However, the rheology change still plays a dominant role in determining the final run-out distance. As can be seen in Fig. 14d, f, without considering rheology change, the landslide will stop moving after a run-out distance of only 500 m (almost half of the measured value). The simulated results using the new method proposed in this paper can properly reflect the rheology change-induced high mobility of this landslide. The whole propagation of this landslide can be accurately depicted by the modified model: starting from a landslide (Fig. 14a); transforming into a debris flow (Fig. 14b); propagating quickly along the meandering galley (Fig. 14c); and, finally, stopping in the deposition zone (Fig. 14d). In addition, the simulated final topography (Fig. 14d) agrees well with the measured data, with an average thickness of 10 m in both the landslide zone and the deposition zone.

Fig. 14
figure 14

Simulated thickness of the Dagou landslide at different times and simulation situations (S1: neglecting rheology change; S2: considering rheology and topography change; S3: neglecting topography change). a Thickness at t = 7.5 s in S2. b Thickness at t = 18.5 s in S2. c Thickness at t = 34.5 s in S2. d Final deposit in S2. e Final deposit in S3. f Final deposit in S1

Full size image

The simulated evolutions of Ve and v of these three situations are presented in Figs. 15 and 16, respectively. The final entrainment volumes of S2 (Ve = 47,300 m3) and S3 (Ve = 47,800 m3) are very close, and the evolution of v of S2 and S3 are also very similar. These results indicate that topography change does not have a significant influence on the propagation of a flow-like landslide when the erodible mass is relatively thin. By contrast, the rheology change increases the entrainment volume (Fig. 15), duration (Fig. 16), velocity (Fig. 16), and run-out distance (Fig. 14f) of a flow-like landslide.

Fig. 15
figure 15

Simulated entrainment volume of the Dagou landslide in different simulation conditions (S1: neglecting rheology change; S2: considering rheology and topography change; S3: neglecting topography change)

Full size image
Fig. 16
figure 16

Simulated average velocity of the Dagou landslide in different simulation conditions (S1: neglecting rheology change; S2: considering rheology and topography change; S3: neglecting topography change)

Full size image

Discussion

By analyzing the propagation of one ideal case and two real flow-like landslides, the present study explores the influence of the bed entrainment-induced rheology and topography changes on the propagation of flow-like landslides. The results of the ideal case and the two real cases show the same patterns: the rheology change determines the final run-out distance of a flow-like landslide no matter whether the erodible mass is thin or thick, while the topography change mainly influences the lateral spreading of the landslide when the erodible mass is thick; the rheology change and topography change interact with each other in the propagation of a flow-like landslide, making bed entrainment a very complex process. In previous studies, rheology change due to bed entrainment was not deeply studied. Some studies considered rheology change by directly replacing the rheology rules of the sliding mass (McDougall and Hungr 2005; Pirulli and Pastor 2012). The main problem of such a method is that it considers the rheology change as an abrupt event, which is obviously in contrast to the fact that the rheology of the sliding mass should change gradually by mixing with the entrained materials. Furthermore, some other studies did not consider the rheology change caused by bed entrainment entirely (Chen et al. 2006; Cuomo et al. 2014; Ouyang et al. 2015). Although these previous studies have realized the importance of the rheology change, they still neglected it for simplification. The importance of the bed entrainment-induced topography change has also long been noticed. However, since most depth-integrated models adopt empirical methods (Takahashi and Kuang 1986; Egashira et al. 2001; Pitman et al. 2003; McDougall and Hungr 2005; Blanc et al. 2011), to estimate the entrainment rate, the topography change determined by these empirical bed entrainment models tends to be questionable. Although empirical methods are simple and effective approaches in evaluating the bed entrainment problems in flow-like landslides, their drawbacks are also obvious. In most empirical bed entrainment models, the entrainment rate does not have a relation to the rheology of the sliding mass. However, in nature, the rheology change influences the topography by altering the entrainment rate, while the topography influences the rheology of the sliding mass in turn by altering the stresses on the sliding surface. In comparison with previous studies, the proposed new method here modifies the sliding mass rheology according to the entrainment volume, so this method can naturally reflect the progressive evolution of the rheology. By combining our new method with the physically based bed entrainment model proposed by Fraccarollo and Capart (2002), analyzing the interaction between the rheology change and topography change becomes very easy. The results of the two real landslides show that considering rheology and topography change can produce better simulation accuracy. The progressive bed entrainment phenomena in flow-like landslides can be effectively depicted by the modified finite difference code in this paper.

On the other hand, the mechanism of bed entrainment is far from being fully understood; thus, it still needs to be explored further. Although many empirical and physically based models have been proposed to quantify bed entrainment, none of these models can fully capture the mechanism of such a phenomenon. The present study is just a preliminary attempt to quantify the bed entrainment-induced rheology and topography change in flow-like landslides, while the interplay of bed entrainment, landslide rheology, and topography is more complex in nature. Nevertheless, this study may be helpful in improving the bed entrainment simulation techniques for the existing depth-integrated models. In addition, some other complicated phenomena associated with landslide entrainment, such as the frontal plowing effect of the erodible mass, liquefaction of the sliding mass, and thermodynamic response of the landslide, are out of the scope of this paper, although they also have a close relationship with the present topic. Currently, it may be too difficult to consider these phenomena in a numerical model simultaneously, so they may need to be addressed in future works.

Conclusion

In this paper, a new method is proposed to consider the rheology change caused by bed entrainment. This method and a physically based bed entrainment model are incorporated into a finite difference code to investigate the influence of the rheology and topography changes on the propagation of flow-like landslides. An ideal case and two-real landslides are analyzed by the modified code. According to the simulation results, the following results are obtained:

  1. (1)

    The rheology change and the topography change caused by bed entrainment interplay with each other in the propagation of a flow-like landslide; they determine the run-out distance, lateral spreading, velocity, and duration of the landslide.

  1. (2)

    The rheology change plays a dominant role in determining the run-out distance of a flow-like landslide no matter whether the erodible mass is thick or thin; without considering rheology change, the run-out of a flow-like landslide may be significantly underestimated. In comparison, the topography change of the sliding mass mainly influences the lateral spreading of a flow-like landslide. When the erodible mass is thick, the sliding surface tends to be reshaped by bed entrainment into a concave shape, thus impeding the lateral spreading of the sliding mass.

  2. (3)

    A finite difference code is modified by combining with the proposed new rheology change method and the Fraccarollo and Capart model. This modified finite difference code can effectively reflect the progressive evolution of the landslide rheology and the sliding surface topography in the propagation of flow-like landslides.