1 Introduction

The problem of dimensionality reduction arises in many fields, such as pattern recognition [1, 2] and computer vision tasks [3, 4], which always have to deal with high-dimensional data. High-dimensional data are noisy usually. There are many problems while processing high-dimensional data such as excessive computational complexity and time consumption. Therefore, it is necessary to find low-dimensional representations of high-dimensional data.

Many dimensionality reduction algorithms have been proposed recently. The dimensionality reduction algorithms are usually categorized into two kinds, i.e., linear and nonlinear. The linear method assumes that the internal structure of the data is linearly distributed. Among the linear dimensionality reduction algorithms, the three most famous methods are principal component analysis (PCA) [5], linear discriminant analysis (LDA) [6], and independent component analysis (ICA) [7].

Although linear methods are simple and easy to implement, linear methods may fail to model nonlinear data structure. This promotes the development of nonlinear dimensionality reduction algorithms, i.e., kernel-based methods and manifold learning-based methods. The kernel method is to map linear inseparable data to a high-dimensional feature space so that the data are linearly separable on the high-dimensional space. However, this method can cause the dimension of data extremely high. The main algorithms based on kernel learning are kernel principal component analysis (KPCA) [8, 9] and kernel discriminant analysis [10, 11].

The basic assumption of manifold learning is that high-dimensional data samples lie on or close to a low-dimensional smooth manifold embedded in the ambient Euclidean space [12]. With this significant assumption, the goal of manifold learning-based methods is to extract intrinsic dimensionalities hidden in the input high-dimensional dataset. Since manifold learning was first proposed in 2000 [13,14,15], many manifold learning-based algorithms are raised gradually, such as locally linear embedding (LLE) [14], ISOMap [16], Laplacian eigenmap (LE) [17], neighborhood-preserving embedding (NPE) [18], locality-preserving projection (LPP) [19] and local tangent-space alignment (LTSA) [20]. These models are well known and have been applied to many real-life applications [21,22,23]. Besides these classical and well-known embedding methods, other novel algorithms for dimension reduction have been proposed recently. In [24], auto-encoder is utilized to extract the local deep features. In some other dimension reduction algorithms, nonlinear mapping for manifold learning was first proposed to search for the low-dimensional embedding representations [25]. Besides, the global geometrical structure is also taken into consideration to well preserve the data structure [26].

Local tangent-space alignment (LTSA) is one of the classical and well-known dimension reduction algorithms. LTSA computes a linear transformation for the data to align the local tangent-space coordinates of each neighborhood with the low-dimensional representations in a global coordinate system. The low-dimensional data point can be predicted by transferring the local tangent-space coordinates. However, the prediction of the target data point is only via one locality and ignores the fact that the target data point may belong to multiple localities. Therefore, the geometric information may be lost when constructing low-dimensional data features.

This paper proposes an unsupervised dimensionality reduction algorithm based on multi-local linear regression and global subspace projection distance minimum. This algorithm fully considers the neighborhood relationship between the original high-dimensional data and maintains the local geometric structure. After the original high-dimensional data is divided into individual parts, the local data information is mapped to the low-dimensional tangent space, which is also called local coordinates. Each locality has overlapping parts. In other words, each data point may belong to several localities. Therefore, our algorithm takes into account the fact that the target prediction point belongs to multiple localities. Based on this characteristic, each local coordinate is aligned, and then, linear regression is performed on the local data points to learn the linear pattern on the locality, which is significantly different from LTSA. For each real low-dimensional data, there are different predicted values in each locality. We require that each predicted data should be as close to the real data as possible, and the variance between each predicted value should be as small as possible, which helps to maintain the geometric relationship between the localities. Figure 1 shows the schematic diagram of multi-locality.

Fig. 1
figure 1

The schematic diagram of multi-locality. We assume that the data point in red belongs to locality 1, locality 2, and locality 3. Then, the local linear regression of the data point in these three localities can be obtained via local homeomorphism

Full size image

For real-world applications, we assume that high-dimensional data has a manifold distribution. The proposed algorithm can extract and maintain the structure well in the low-dimensional space. Besides, we also consider the global distribution of the data. It is assumed that the low-dimensional data and the high-dimensional data have a linear mapping relationship. By finding the projection matrix, the high-dimensional data and its projection in the subspace have the smallest distance. In this way, the dimensionality reduction and the separability of low-dimensional data are achieved.

In general, the algorithm takes account both local and global information of the original data and has the following characteristics:

  1. 1.

    In this paper, dimensionality reduction is performed under the principle of local homeomorphism, and the continuous dependency relationship of the original high-dimensional data in each locality is maintained after dimensionality reduction.

  2. 2.

    Considering the linear relationship of the local coordinates, the affine transformation of the local coordinates is used to perform linear regression on the target data with the remaining data to learn the local linear pattern.

  3. 3.

    Because the division of data parts needs to follow the principle of overlap, each target prediction point belongs to multiple localities. Therefore, this article performs linear prediction on each locality to which the target point belongs, which fully considers the geometric relationship between the localities.

  4. 4.

    By searching for the subspace, the distance between the projection of the high-dimensional data on the subspace and the high-dimensional data is minimized, and the coordinates of the projection are used as the low-dimensional data to achieve dimensionality reduction and maintain global information.

The remainder of this paper is organized as follows: Section 2 reviews several related works. Then, the proposed algorithm of dimensionality reduction is presented in Sect. 3. Section 4 describes the experiments. Conclusions are given in Sect. 5.

2 Related works

In this section, the mathematical models of the related unsupervised dimension reduction algorithm are first outlined. For notational convenience, let us denote the matrix and the vector as capital and lower letters in boldface, respectively. Matrix dimensions are shown as \((m\times n)\), where m and n are the number of rows and columns, respectively. For a matrix \(\mathbf {X}=[x_{ij}]\), \(x_{i}\) denotes its ith column. The trace of matrix \(\mathbf {X}\) is \(\mathbf{Tr} (\mathbf {X})=\sum \limits _{i=1}^{n}x_{ii}\). Note that the dimensionality of the high-dimensional and the low-dimensional dataset is D and d, respectively. The goal of the dimension reduction algorithm is to extract the low-dimensional dataset \(\mathbf {Y}\in \mathbb {R}^{d\times M}\) from the original high-dimensional dataset \(\mathbf {X}\in \mathbb {R}^{D\times M}\).

2.1 PCA

Principal components analysis (PCA) [5] is a global linear dimensionality reduction algorithm. The embedding result of PCA is determined by the covariance matrix of the high-dimensional dataset and the corresponding principal eigenvectors. To compute PCA, we first find the mean vector in high-dimensional data space as \(\bar{\mathbf {x}}=\dfrac{1}{M}\sum \limits _{i=1}^{M}{{\mathbf {x}_{i}}}\). Then, the covariance matrix of high-dimensional space can be written as

$$\begin{aligned} \mathbf {C}=\sum \limits _{i=1}^{M}(\mathbf {x}_{i}-\bar{\mathbf {x}})(\mathbf {x}_{i}-\bar{\mathbf {x}})^{T} \end{aligned}$$
(1)

Next, compute eigenvalues and corresponding eigenvectors on the covariance matrix and extract \(\mathbf {U}\in {{\mathbb {R}}^{D\times d}}\) composed of the m eigenvectors corresponding to the first largest eigenvalues. Finally, the low-dimensional data \(\mathbf {y}_{i}\) can be obtained by \(\mathbf {y}_{i}=\mathbf {U}^{T}\mathbf {x}_{i}\). PCA is a linear dimensionality reduction algorithm to consider the global distribution of the data and therefore cannot extract the nonlinear structure well.

2.2 LE

Laplacian eigenmap (LE) is also a manifold algorithm that considers the local structure. LE uses undirected graphs to establish the relationship between data points, that is, adjacent data points in high-dimensional space maintain a consistent approximative relationship after dimensionality reduction. The property is achieved by solving the following optimization problem. The LE algorithm can better maintain the relationship between the data points, but requires a higher sparseness of the Laplacian matrix.

$$\begin{aligned} \begin{aligned}&\mathop {\mathbf{{min}}}\limits _\mathbf{{Y}} {} {} {} {} {} {} {} \frac{\mathrm{{1}}}{\mathrm{{2}}}\sum \limits _{i,j}^M {\left\| {{\mathbf{{y}}_i} - {\mathbf{{y}}_j}} \right\| _\mathrm{{2}}^\mathrm{{2}}} {\mathbf{{w}}_{ij}} \\&s.t.\ \sum \limits _{i=1}^{M}{{\mathbf {D}}_{i}{{\mathbf {y}}_{i}}\mathbf {y}_{i}^{T}={{\mathbf {I}}_{d}}} \\ \end{aligned} \end{aligned}$$
(2)

where \({\mathbf{{w}}_{\mathbf{{ij}}}}\) is used to measure the similarity of high-dimensional data points \({\mathbf{{x}}_i}\) and \({\mathbf{{x}}_j}\). If \({\mathbf{{x}}_j}\) is the neighbor of \({\mathbf{{x}}_i}\) , then \({\mathbf{{w}}_{ij}} = 1\) or \({\mathbf{{w}}_{ij}} = {\mathrm{{e}}^{ - \left( {{{\left\| {{\mathbf{{x}}_i} - {\mathbf{{x}}_j}} \right\| }^2}} \right) /\left( {{t^2}} \right) }}\), where t is a constant. \({\mathbf{{y}}_i}\) and \({\mathbf{{y}}_j}\) is the low-dimensional representation of \({\mathbf{{x}}_i}\) and \({\mathbf{{x}}_j}\) . The model of LE can be rewritten as \(\mathop {{min}}\limits _{{\mathbf{{Y}}^T}{} \mathbf{{Y}} = \mathbf{{I}}} {tr}\left( {{\mathbf{{Y}}^T}{} \mathbf{{LY}}} \right) \), where \(\mathbf{{L}} = \mathbf{{D}} - \mathbf{{W}}\) is the Laplacian matrix of the neighborhood graph with the connection weight matrix \(\mathbf{{W}}\) , and \(\mathbf{{D}}\) is the diagonal matrix with column sums of \(\mathbf{{W}}\) as its diagonal entries.

2.3 LTSA

Local tangent-space alignment (LTSA) [20] utilizes tangent coordinates to represent the local geometry. Each data point and its neighbors form a patch \(\mathbf {X}_{i}\). LTSA acquires the optimal tangent coordinates by optimizing the following objective function on each patch

$$\begin{aligned} \begin{aligned}&\min \limits _{\mathbf {Y}}\sum \limits _{i=1}^{M}{\left\| {{\bar{\mathbf {Y}}}_{i}}-{\mathbf {A}_{i}}{\mathbf {\Theta }_{i}} \right\| _{{}}^{2}}\ \ \\&s.t.\ \mathbf {YY}^{T}=\mathbf {I}_{d} \\ \end{aligned} \end{aligned}$$
(3)

where \(\bar{\mathbf {Y}_{i}}\) is the centralized data, i.e., \(\bar{\mathbf {Y}}_{i}=\mathbf {Y}_{i}\left( {\mathbf {I}_{k+1}}-\dfrac{1}{k+1}{\mathbf {\Gamma }_{k+1}}\mathbf {\Gamma } _{k+1}^{T} \right) ={\mathbf {Y}_{i}}{\mathbf {C}_{K+1}}\); \(\mathbf {I}_{k+1}\) is an identity matrix; \(\Gamma _{k+1}\) is a vector with all the elements equal to one; \(\mathbf {\Theta }_{i}\in \mathbb {R}^{d\times \left( k\text {+}1 \right) }\) is the tangent coordinates; \(\mathbf {A}_{i}\in \mathbb {R}^{D\times d}\) is the orthogonal basis matrix of the tangent space and is used to rotate and scale \(\mathbf {\Theta }_{i}\).

To obtain the low-dimensional coordinates, the projection between the high-dimensional and the low-dimensional data can be expressed as:

$$\begin{aligned} {\mathbf {\Theta }_{i}}=\mathbf {U}_{i}^{T}\bar{{{\mathbf {X}}_{i}}}\in {{\mathbb {R}}^{d\times \left( k+1 \right) }} \end{aligned}$$
(4)

where \(\mathbf {U}_{i}^{T}\) denotes the matrix of d left singular vectors of \(\bar{{{\mathbf {X}}_{i}}}\) corresponding to its d largest singular values.

Since \(\mathbf {\Theta }_{i}\) is acquired, Eq.(3) can then be further simplified to

$$\begin{aligned} \begin{aligned}&\underset{\mathbf {YY}^{T}={\mathbf {I}_{d}}}{\mathop {arg min}}\,{{\sum \limits _{i=1}^{M}{\left\| \mathbf {Y}{\mathbf {S}_{i}}{\mathbf {C}_{K+1}}\left( {\mathbf {I}_{K+1}}-\mathbf {\Theta } _{i}^{\dagger }\mathbf {\Theta }_{i} \right) \right\| }}^{2}}\ \\&=\ \underset{\mathbf {YY}^{T}={\mathbf {I}_{d}}}{\mathop {arg min}}\,{{\sum \limits _{i=1}^{M}{\left\| \mathbf {Y}{\mathbf {L}_{i}} \right\| }}^{2}}\ \\&=\underset{\mathbf {YY}^{T}={\mathbf {I}_{d}}}{\mathop {arg min}}\,\mathbf{Tr} \left( \mathbf {YL}{\mathbf {Y}^{T}} \right) \ \end{aligned} \end{aligned}$$
(5)

where \(\mathbf {S}_{i}\) is a selecting matrix; \(\mathbf {I}_{K+1}\) is an identity matrix; \(\mathbf {L}=\sum \limits _{i=1}^{M}\mathbf {L}_{i}\mathbf {L}_{i}^{T}\) and \(\mathbf {L}_{i} = \mathbf {S}_{i}{\mathbf {C}_{K+1}}\left( {\mathbf {I}_{K+1}}-\mathbf {\Theta } _{i}^{\dagger }\mathbf {\Theta }_{i} \right) \). Then Eq.(5) is actually a Rayleigh quotient problem. Therefore, the embedding results can be obtained by computing the eigenvectors of matrix \(\mathbf {L}\) corresponding to the d smallest eigenvalues. The local coordinate of each data point is just computed in one locality in LTSA, which is significantly different from our proposed method. The proposed method fully considers the localities containing the same data point to extract local structures.

2.4 LDFA

Local deep-feature alignment (LDFA) [24] is an unsupervised deep-learning dimensionality reduction algorithm. First, the neighborhood for each data sample is constructed. Then, a local stacked contractive auto-encoder (SCAE) from the neighborhood is learned to extract the local deep features. Next, an affine transformation to align the local deep features of each neighborhood with global features is exploited. The objective function of LDFA in the low-dimensional data space is similar to LTSA as

$$\begin{aligned} \begin{aligned}&\min \limits _{\mathbf {Y}}\sum \limits _{i=1}^{M}{\left\| {{{\bar{Y}}}_{i}}-{\mathbf {A}_{i}}\mathbf {H}_{i}^{L} \right\| _{F}^{2}}\ \ \\&s.t.\ \mathbf {YY}^{T}={\mathbf {I}_{d}} \end{aligned} \end{aligned}$$
(6)

where \(\mathbf {H}_{i}^{L}\) is the top-layer local deep feature. The following procedures are similar to LTSA. LDFA learns discriminative local features well via stacked contractive auto-encoder. However, the neural network increases the complexity and executed efficiency of the model.

2.5 SNPPE

Simplify neighborhood-preserving embedding (SNPPE) [25] is an explicit nonlinear manifold learning algorithm based on the assumption that there exists a polynomial mapping between high-dimensional data samples and their low-dimensional representations. The polynomial mapping between high- and low- dimensional representations of SNPPE is defined as:

$$\begin{aligned} y_{i}^{k}=\sum \limits _{{\begin{matrix} {{l}_{1}},{{l}_{2}},\ldots ,{{l}_{n}}\ge 0 \\ 1\le {{l}_{1}}+{{l}_{2}}+\ldots +{{l}_{n}}\le p \end{matrix}}}{\mathbf {v}_{k}^{l}{{(\mathbf {x}_{i}^{1})}^{{{l}_{1}}}}}{{(\mathbf {x}_{\text {i}}^{2})}^{{{l}_{2}}}}\cdots {{(\mathbf {x}_{\text {i}}^{n})}^{{{l}_{n}}}} \end{aligned}$$
(7)

where \(y_{i}^{k}\) is the kth component of \(\mathbf {y}_{i}\), \({l}_{1},{{l}_{2}},\ldots ,{{l}_{n}}\) are integers. The superscript \(\mathbf {l}\) stands for the n-tuple indexing array \(\left( {l}_{1},{{l}_{2}},\ldots ,{{l}_{n}}\right) \), and \(\mathbf {v}_{k}\) is the vector of polynomial coefficients, which can be expressed as:

$$\begin{aligned} {{\mathbf {v}}_{k}}=\left( \begin{aligned}&v_{k}^{l}\left| _{{{l}_{1}}=p,{{l}_{2}}=0,\ldots ,{{l}_{n}}=0} \right. \\&v_{k}^{l}\left| _{{{l}_{1}}=p-1,{{l}_{2}}=1,\ldots ,{{l}_{n}}=0} \right. \\&\begin{matrix}{}{} & {} {}{} & {} \vdots \end{matrix} \\&v_{k}^{l}\left| _{{{l}_{1}}=1{{,}_{2}}=0,\ldots ,{{l}_{n}}=0} \right. \\&\begin{matrix}{}{} & {} {}{} & {} \vdots \end{matrix} \\&v_{k}^{l}\left| _{{{l}_{1}}=0,{{l}_{2}}=0,\ldots ,{{l}_{n}}=1} \right. \\ \end{aligned} \right) \end{aligned}$$
(8)

To obtain the embedding results of the high-dimensional data samples, the optimization problem can be expressed as:

$$\begin{aligned} \begin{aligned}&\underset{{{y}_{i}}}{\mathop {min}}\,\dfrac{1}{2}\sum \limits _{i,j}^{M}{{{\mathbf {W}}_{ij}}\left\| {{\mathbf {y}}_{i}}-{{\mathbf {y}}_{j}} \right\| _{2}^{2}}\ \ \ \\&\ s.t.\ \sum \limits _{i=1}^{M}\mathbf {D}_{i}\mathbf {y}_{i}\mathbf {y}_{i}^{T}=\mathbf {I}_{d} \\ \end{aligned} \end{aligned}$$
(9)

where \(\mathbf {W}_{ij}\left( i,j=1,2,\ldots ,M\right) \) are symmetrical and positive matrixes, which can be derived from the input data samples similar to LLE and \(\mathbf {D}_{i}=\sum \limits _{j=1}^{M}{\mathbf {W}}_{ij}\).

Then, further derivation of Eq. (9) leads to a Rayleigh quotient problem as

$$\begin{aligned} {\mathbf {X}_{p}}(\mathbf {D}-\mathbf {W})X_{p}^{T}{{\mathbf {v}}_{i}}=\lambda {\mathbf {X}_{p}}\mathbf {DX}_{p}^{T}{{\mathbf {v}}_{i}},\ i=1,2,\ldots ,m \end{aligned}$$
(10)

where \(\mathbf {W}=\left( \mathbf {W}_{ij}\right) \); \(\mathbf {D}\) is a diagonal matrix whose ith diagonal entry is \(\mathbf {D}_{i}\) and \({\mathbf {X}_{p}}=\left[ \mathbf {X}_{p}^{\left( 1 \right) }\ \mathbf {X}_{p}^{\left( 2 \right) }\ \cdots \ \mathbf {X}_{p}^{\left( N \right) } \right] \) is achieved by

$$\begin{aligned} \mathbf {X}_{p}^{\left( i \right) }=\left( \begin{array}{c} \overbrace{{\mathbf {x}_{i}}\odot {\mathbf {x}_{i}}\odot \cdots \odot {\mathbf {x}_{i}}}^{p} \\ \begin{matrix} \vdots \\ {\mathbf {x}_{i}}\odot {\mathbf {x}_{i}} \\ \end{matrix} \\ {\mathbf {x}_{i}} \\ \end{array} \right) \end{aligned}$$
(11)

Once \({\mathbf {v}_{i}},\ i=1,2,\ldots ,m\) is determined, the embedding results can be acquired by:

$$\begin{aligned} \mathbf {y}=\left( \begin{matrix} \sum \nolimits _{l}{v_{1}^{l}{{\left( {{x}^{1}} \right) }^{{{l}_{1}}}}{{\left( {{x}^{2}} \right) }^{{{l}_{2}}}}\cdots {{\left( {{x}^{n}} \right) }^{{{l}_{n}}}}} \\ \vdots \\ \sum \nolimits _{l}{v_{m}^{l}{{\left( {{x}^{1}} \right) }^{{{l}_{1}}}}{{\left( {{x}^{2}} \right) }^{{{l}_{2}}}}\cdots {{\left( {{x}^{n}} \right) }^{{{l}_{n}}}}} \\ \end{matrix} \right) \end{aligned}$$
(12)

where \(\mathbf {y}\) is the low-dimensional representation. SNPPE assumes that there is a polynomial mapping between the high-dimensional data and their low-dimensional representations, which may destroy the nonlinear structure, and the polynomial operation also significantly increases the complexity.

2.6 ULG

Local regression and global information-embedded dimension reduction (ULG) [26] preserve both local information and global information. First, ULG applies PCA to denoise the local data. Besides, a regularization is added to solve the ill-posed problem \((D\gg M)\). Furthermore, a linear regression model is used to capture the local geometrical structure. The objective function of ULG is as follows:

$$\begin{aligned} \begin{aligned}&\underset{\mathbf {W}}{\mathop {\min }}\,\mathbf{Tr} \left( \dfrac{{\mathbf {U}^{T}}\mathbf {XL}{\mathbf {X}^{T}}\mathbf {U}}{{\mathbf {U}^{T}}\mathbf {X}{\mathbf {H}_{{n}}}{\mathbf {X}^{T}}\mathbf {U}} \right) \ \ \\&s.t.\ {\mathbf {U}^{T}}\mathbf {U}={\mathbf {I}_{d}} \\ \end{aligned} \end{aligned}$$
(13)

where \(\mathbf {L}\) is related to the local geometrical information and \(\mathbf {H}_{n}\) contains information about global geometrical information. Similarly, Eq. (13) is also solved by eigenvalue decomposition. Then, the low-dimensional representations can be computed by \(\mathbf {y}=\mathbf {U}^{T}\mathbf {x}\). ULG assumes that there is a linear mapping between high- and low-dimensional data space, which makes it difficult for ULG to capture the nonlinear structure of the original high-dimensional dataset. At the same time, ULG also ignores the multi-local property.

3 Proposed method

In this section, we propose an unsupervised dimensionality reduction method based on multi-local linear pattern preservation. The purpose of the algorithm is to fully consider the existence of multiple local characteristics for each data point, correct the prediction error of a local data point, and extract the geometric structure of the data so that more effective features to be maintained during the dimensionality reduction process.

The algorithm proposed in this paper can be divided into the following three steps: (1) We use the KNN algorithm to find the nearest k points of each high-dimensional sample point to form the locality. (2) After performing the SVD decomposition on the centralizing locality, we obtain the local coordinates of each locality. The linear prediction coefficient of each local is obtained by the affine transformation of local coordinates. (3) Since each data point may belong to several different localities at the same time, we require that the predicted values of each locality are as similar as possible and the variance between each predicted value is the smallest.

3.1 Local decomposition

For a given high-dimensional dataset \(\mathbf {X}=\left[ {{\mathbf {x}}_{1}} , \ldots , {{\mathbf {x}}_{N}} \right] \in {{\mathbb {R}}^{D\times N}}\), \(\mathbf {X}\) is decomposed into several localities \({\mathbf {X}}_{1} , \ldots , {{\mathbf {X}}_{M}}\), where \(\mathbf {X}_{m}\in \mathbb {R}^{D\times N_{m}}\) and \(N_{m}\) represents the number of high-dimensional data contained in \(\mathbf {X}_{m}\), \(m=1,\ldots ,M\). The decompositions must overlap each other, that is, one locality at least overlaps the other locality. In addition, the decomposition must include all data, that is \(\mathbf {X}\text {=}\bigcup \limits _{m=1}^{M}{{{\mathbf {X}}_{m}}}\).

The decomposition of high-dimensional datasets can be determined according to various principles. The simplest decomposition method of a high-dimensional dataset is that each high-dimensional data and its neighbors constitute a locality. \(\mathbf {Y}=\left[ {{\mathbf {y}}_{1}} , \ldots , {{\mathbf {y}}_{N}} \right] \in {{\mathbb {R}}^{d\times N}}\) represents the low-dimensional data of \(\mathbf {X}\), where \(d\ll D\). Because the dimensionality reduction data and the high-dimensional data have a one-to-one correspondence, the dimensionality-reduced dataset is also decomposed into several localities \({\mathbf {Y}}_{1} , \ldots , {{\mathbf {Y}}_{M}}\) accordingly where the locality of the reduced-dimensional data \(\mathbf {Y}_{m}\in \mathbb {R}^{d\times N_{m}}\) includes the corresponding data of \(\mathbf {X}_{m}\), \(m=1,\ldots ,M\).

3.2 Learning the local linear pattern based on local homeomorphism

The assumption of manifold learning is that the high-dimensional dataset \(\mathbf {X}\in \mathbb {R}^{D\times N}\) is collected from a sub-manifold embedded in a D-dimensional Euclidean space \(\mathbb {R}^{D}\) and the dimension of the sub-manifold is d, where \(D\gg d\). According to the mathematical definition of the manifold, each locality \(\mathbf {X}_{m}\in \mathbb {R}^{D\times N_{m}}\) of the high-dimensional dataset \(\mathbf {X}\) is said to be locally homeomorphic with an open set \(\mathbf {\Theta }_{m}\in \mathbb {R}^{d\times N_{m}}\) of the Euclidean space \(\mathbb {R}^{d}\). This open set \(\mathbf {\Theta }_{m}\) is the local coordinate of \(\mathbf {X}_{m}\). The local coordinate lies in low-dimensional Euclidean space, so it can be used as the dimensionality reduction representation of the high-dimensional data.

There are several solutions to solve the local coordinates. The most common one is to project the locality \(\mathbf {X}_{m}\) on the manifold to the tangent space centered at \(\mathbf {X}_{m}\). The coordinate of the projection is the local coordinate of \(\mathbf {X}_{m}\). In numerical calculations, \(\mathbf {\Theta }_{m}\) is the PCA result of \(\mathbf {X}_{m}\). The specific steps are as follows.

  1. 1.

    Centralization of \(\mathbf {X}_{m}\) Centralize the locality \(\mathbf {X}_{m}=\left[ \mathbf {x}_{m_{1}},\ldots ,\mathbf {x}_{m_{N_{m}}}\right] \) of high-dimensional data, that is

    $$\begin{aligned} \hat{\mathbf {X}}_{m}=\left[ \mathbf {x}_{m_{1}}-\bar{\mathbf {x}}_{m},\ldots ,\mathbf {x}_{m_{N_{m}}}-\bar{\mathbf {x}}_{m}\right] \end{aligned}$$
    (14)

    where \({{\mathbf {C}}_{{{N}_{m}}}}={{\mathbf {I}}_{{{\text {N}}_{m}}}}-\dfrac{1}{{{N}_{m}}}{{\mathbf {\Gamma }}_{{{N}_{m}}}}\mathbf {\Gamma }_{{{N}_{m}}}^{T}\in {{\mathbb {R}}^{{{N}_{m}}\times {{N}_{m}}}}\) is the centralized matrix and \({{\mathbf {{\bar{x}}}}_{m}}=\dfrac{1}{{{N}_{m}}}\sum \limits _{i=1}^{{{N}_{m}}}{{{\mathbf {x}}_{{{m}_{i}}}}}\) is the center of \(\mathbf {X}_{m}\).

  2. 2.

    Singular value decomposition of \(\hat{\mathbf {X}}_{m}\)

    $$\begin{aligned} {{\mathbf {{\hat{X}}}}_{m}}={{\mathbf {U}}_{m}}{{\mathbf {\Sigma }}_{m}}\mathbf {V}_{m}^{T} \end{aligned}$$
    (15)

    where \({{\mathbf {U}}_{m}}\in {{\mathbb {R}}^{D\times D}}\) and \({{\mathbf {V}}_{m}}\in {{\mathbb {R}}^{N_{m}\times N_{m}}}\) are both standard orthogonal matrices.

  3. 3.

    Local coordinates \({{\mathbf {U}}_{m,d}}\in {{\mathbb {R}}^{D\times d}}\) is a matrix consisting of the first d column vectors of \({{\mathbf {U}}_{m}}\), the column vectors of \({{\mathbf {U}}_{m,d}}\) are the standard orthogonal bases of the midpoint \({{\mathbf {{\bar{x}}}}_{m}}\) of \({{\mathbf {{\bar{X}}}}_{m}}\) in the tangent space. Therefore, the coordinate of the projection in the tangent space is

    $$\begin{aligned} {{\mathbf {\Theta }}_{m}}=\mathbf {U}_{m,d}^{T}{{\mathbf {{\hat{X}}}}_{m}}=\left[ {{\mathbf {\theta }}_{m,1}} , \ldots , {{\mathbf {\theta }}_{m,{{N}_{m}}}} \right] \in {{\mathbb {R}}^{d\times {{N}_{m}}}} \end{aligned}$$
    (16)

    The center of the local coordinate \({{\mathbf {\Theta }}_{m}}\) is 0, which is the origin of the Euclidean space \(\mathbb {R}^{d}\).

  4. 4.

    Local linear pattern: The local coordinate \({{\mathbf {\Theta }}_{m}}\) is obtained by considering a single locality \({{\mathbf {X}}_{m}}\). The relationship between \({{\mathbf {X}}_{m}}\) and other localities is ignored during the dimensionality reduction process. Therefore, \({{\mathbf {\Theta }}_{m}}\) is not the global coordinate \({{\mathbf {Y}}_{m}}\) of \({{\mathbf {X}}_{m}}\). However, both \({{\mathbf {\Theta }}_{m}}\) and \({{\mathbf {Y}}_{m}}\) are data in the d-dimensional Euclidean space \(\mathbb {R}^{d}\), and both are derived from \({{\mathbf {X}}_{m}}\). Therefore, we assume that there is an affine relationship between \({{\mathbf {Y}}_{m}}\) and \({{\mathbf {\Theta }}_{m}}\), i.e.,

    $$\begin{aligned} {{\mathbf {{\hat{Y}}}}_{m}}={{\mathbf {A}}_{m}}{{\mathbf {\Theta }}_{m}} \end{aligned}$$
    (17)

    where \({{\mathbf {{\hat{Y}}}}_{m}}={{\mathbf {Y}}_{m}}{{\mathbf {C}}_{{{N}_{m}}}}\) which means \({\mathbf {Y}}_{m}\) is centralized. Geometrically, it is equivalent to translate \({\mathbf {Y}}_{m}\), so that the center of \(\mathbf {{\hat{Y}}}\) coincides with the center of the d-dimensional Euclidean space \(\mathbb {R}^{d}\). \(\mathbf {A}_{m}\in \mathbb {R}^{d\times d}\) is the rotation and scaling matrix and can be approximated as \({{\mathbf {A}}_{m}}={{\mathbf {{\hat{Y}}}}_{m}}\mathbf {\Theta }_{m}^{\dagger }\). Therefore, \(\mathbf {{\hat{Y}}}_{m}\) is obtained by:

    $$\begin{aligned} {{\mathbf {{\hat{Y}}}}_{m}}={{\mathbf {{\hat{Y}}}}_{m}}\mathbf {\Theta }_{m}^{\dagger }{{\mathbf {\Theta }}_{m}}={{\mathbf {Y}}_{m}}{{\mathbf {C}}_{{{N}_{m}}}}\mathbf {\Theta }_{m}^{\dagger }{{\mathbf {\Theta }}_{m}} \end{aligned}$$
    (18)

    where \(\mathbf {\Theta }_{m}^{\dagger }\) is the pseudo-inverse of \(\mathbf {\Theta }_{m}\). For any data point \(\mathbf {y}_{m_{i}}\), we have

    $$\begin{aligned} \begin{aligned}&{{\mathbf {y}}_{{{m}_{i}}}}-\dfrac{1}{{{N}_{m}}}\sum \limits _{j=1}^{{{N}_{m}}}{{{\mathbf {y}}_{{{m}_{j}}}}}={{\mathbf {y}}_{{{m}_{i}}}}\left( 1-\dfrac{1}{{{N}_{m}}} \right) -\dfrac{1}{{{N}_{m}}}\sum \limits _{{\begin{matrix} j=1 \\ j\ne i \end{matrix}}}^{{{N}_{m}}}{{{\mathbf {y}}_{{{m}_{j}}}}} \\&={{\mathbf {y}}_{{{m}_{i}}}}\left( 1-\dfrac{1}{{{N}_{m}}} \right) -\dfrac{1}{{{N}_{m}}}\sum \limits _{{\begin{matrix} j=1 \\ j\ne i \end{matrix}}}^{{{N}_{m}}}{{{\mathbf {Y}}_{m}}{{\mathbf {s}}_{m,j}}} \\&={{\mathbf {Y}}_{m}}{{\mathbf {C}}_{{{N}_{m}}}}\mathbf {\Theta }_{m}^{\dagger }{{\mathbf {\Theta }}_{m}}{{\mathbf {s}}_{m,i}} \\ \end{aligned} \end{aligned}$$
    (19)

    where \({{\mathbf {s}}_{m,i}}\in {{R}^{{{N}_{m}}}}\) is to select a specific data point from the locality. The i-th element is 1 and others are 0 for \(i=1,\ldots ,N_{m}\). Thus, the local linear pattern of \(\mathbf {y}_{m_{i}}\) is

    $$\begin{aligned} \begin{aligned}&{{\mathbf {y}}_{{{m}_{i}}}}=\dfrac{{{N}_{m}}}{{{N}_{m}}-1}{{\mathbf {Y}}_{m}}\left( {{\mathbf {C}}_{{{N}_{m}}}}\mathbf {\Theta }_{m}^{\dagger }{{\mathbf {\Theta }}_{m}}{{\mathbf {s}}_{m,i}}+\dfrac{1}{{{N}_{m}}}\sum \limits _{{\begin{matrix} j=1 \\ j\ne i \end{matrix}}}^{{{N}_{m}}}{{{\mathbf {s}}_{m,j}}} \right) ={{\mathbf {Y}}_{m}}{{\mathbf {w}}_{m,i}},\\&i=1,\ldots ,{{N}_{m}}\\ \end{aligned} \end{aligned}$$
    (20)

    where \(\left\{ {{\mathbf {w}}_{m,i}} | i=1,\ldots ,{{N}_{m}} \right\} \) is the local linear pattern obtained according to the local homeomorphic criterion, and

    $$\begin{aligned} {{\mathbf {w}}_{m,i}}=\dfrac{{{N}_{m}}}{{{N}_{m}}-1}\left( {{\mathbf {C}}_{{{N}_{m}}}}\mathbf {\hat{\Theta }}_{m}^{\dagger }{{{\mathbf {\hat{\Theta }}}}_{m}}{{\mathbf {s}}_{m,i}}+\dfrac{1}{{{N}_{m}}}\sum \limits _{{\begin{matrix} j=1 \\ j\ne i \end{matrix}}}^{{{N}_{m}}}{{{\mathbf {s}}_{m,j}}} \right) \in {{\mathbb {R}}^{{{N}_{m}}}}. \end{aligned}$$

3.3 Learning the local geometrical structure

For any low-dimensional data point \({{\mathbf {y}}_{m}}\in \mathbf {Y}\), \({\mathbf {y}}_{m}\) may belongs to several localities simultaneously due to the overlapping rule of the locality decomposition, i.e., \({{\mathbf {y}}_{m}}\in \mathbf {Y}_{m_{j}}\), \(1\le m_{j}\le M\) for \(j=1,\ldots , J_{m}\). To illustrate the multi-locality situation intuitively, a schematic diagram of multi-locality is shown in Fig. 2. The black solid lines in Fig. 2 denote the weighted connections between data point 9 and the remaining points in that locality. In Fig. 2, data point 9 belongs to the pink, green, and blue localities concurrently. Obviously, each locality will provide a prediction to data point 9. For instance, in Fig. 2a, data point 9 will be reconstructed by data points 3, 4, 5, 6 in the green locality with the linear regression coefficients calculated in Sect. 3.2. Similarly, the pink and blue localities will provide another two predictions to data point 9, as shown in Fig. 2b, c.

Therefore, there are several predictions to the low-dimensional data point \({\mathbf {y}}_{m}\). Each prediction is predicted linearly by one locality and can be expressed as:

$$\begin{aligned} {{\mathbf {y}}_{m,j}}={\mathbf {Y}_{{{m}_{j}}}}{{\mathbf {w}}_{{{m}_{j}},id\left( m,{{m}_{j}} \right) }}=\mathbf {Y}{\mathbf {S}_{{{m}_{j}}}}{{\mathbf {w}}_{{{m}_{j}},id\left( m,{{m}_{j}} \right) }} \end{aligned}$$
(21)

where \({{\mathbf {w}}_{{{m}_{j}},id\left( m,{{m}_{j}} \right) }}\) is the linear regression coefficients of locality \({\mathbf {Y}_{{{m}_{j}}}}\), \(id\left( m,{{m}_{j}} \right) \) is the order of \(\mathbf {y}_{m}\) in \(\mathbf {Y}_{m_{j}}\) and \(\mathbf {S}_{m_{j}}\in \mathbb {R}^{N\times N_{m}}\) is a selecting matrix with \({{\mathbf {s}}_{j,{{m}_{j}}}}=1\) for \(j=1,\ldots ,N_{m}\) and zero for remaining elements. Then, the linear predictions of \(\mathbf {y}_{m}\) are denoted as \(\left\{ \left. {{\mathbf {y}}_{m,j}} \right| j=1,\ldots ,{{J}_{m}} \right\} \). The goal is to reconstruct data points \(\mathbf {y}_{m}\) with these predictions, and the derivation of the final objective function in low-dimensional space is departed into three steps as follows:

  1. 1.

    Approximating \(\mathbf {y}_{m}\) to the average of \(\left\{ \left. {{\mathbf {y}}_{m,j}} \right| j=1,\ldots ,{{J}_{m}} \right\} \) The average of all the predictions is \(\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{{{\mathbf {y}}_{m,j}}}\) and the function can be denoted as:

    $$\begin{aligned} \begin{aligned}&\underset{{{\mathbf {y}}_{m}},\left\{ \left. {{\mathbf {y}}_{m,j}} \right| j=1,\ldots ,{{J}_{m}} \right\} }{\mathop {arg min}}\,{{\left\| {{\mathbf {y}}_{m}}-\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{{{\mathbf {y}}_{m,j}}} \right\| }^{2}} \\&=\underset{\mathbf {Y}}{\mathop {arg min}}\,{{\left\| \mathbf {Y}{{\mathbf {s}}_{m}}-\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{\mathbf {Y}{\mathbf {S}_{{{m}_{j}}}}{{\mathbf {w}}_{{{m}_{j}},id\left( m,{{m}_{j}} \right) }}} \right\| }^{2}} \\&=\underset{\mathbf {Y}}{\mathop {arg min}}\,{{\left\| \mathbf {Y}\left( {{\mathbf {s}}_{m}}-\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{{\mathbf {S}_{{{m}_{j}}}}{{\mathbf {w}}_{{{m}_{j}},id\left( m,{{m}_{j}} \right) }}} \right) \right\| }^{2}} \\&=\underset{\mathbf {Y}}{\mathop {arg min}}\,{{\left\| \mathbf {Y}{\mathbf {l}_{m}} \right\| }^{2}}=\underset{\mathbf {Y}}{\mathop {arg min}}\,\mathbf{Tr} \left( \mathbf {Y}{\mathbf {l}_{m}}\mathbf {l}_{m}^{T}{\mathbf {Y}^{T}} \right) \\&=\underset{\mathbf {Y}}{\mathop {arg min}}\,\mathbf{Tr} \left( \mathbf {Y}{\mathbf {L}_{m}}{\mathbf {Y}^{T}} \right) \end{aligned} \end{aligned}$$
    (22)

    where \({\mathbf {s}_{m}}\in {{\mathbb {R}}^{N}}\) is a selecting vector that the m-th element is one and the remaining elements are zeros, \({\mathbf {l}_{m}}={{\mathbf {s}}_{m}}-\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{{\mathbf {S}_{{{m}_{j}}}}{{\mathbf {w}}_{{{m}_{j}},id\left( m,{{m}_{j}} \right) }}}\in {{\mathbb {R}}^{N}}\) and \({\mathbf {L}_{m}}={\mathbf {l}_{m}}\mathbf {l}_{m}^{T}\in {{\mathbb {R}}^{N\times N}}\).

  2. 2.

    Minimize the variance of each prediction: We require that the variance of the prediction by different localities is minimum, that is

    $$\begin{aligned} \underset{{{\mathbf {y}}_{m}},\left\{ \left. {{\mathbf {y}}_{m,j}} \right| j=1,\ldots ,{{J}_{m}} \right\} }{\mathop {arg min}}\,\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{{{\left\| {{\mathbf {y}}_{m,j}}-{{\mathbf {y}}_{m}} \right\| }^{2}}} \end{aligned}$$
    (23)

    Similarly, substituting (21) into (23) yields

    $$\begin{aligned} \begin{aligned}&\underset{{{\mathbf {y}}_{m}},\left\{ \left. {{\mathbf {y}}_{m,j}} \right| j=1,\ldots ,{{J}_{m}} \right\} }{\mathop {arg min}}\,\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{{{\left\| {{\mathbf {y}}_{m,j}}-{{\mathbf {y}}_{m}} \right\| }^{2}}} \\&=\underset{\mathbf {Y}}{\mathop {arg min}}\,\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{{{\left\| \mathbf {Y}{{\mathbf {h}}_{m,j}} \right\| }^{2}}} \\&=\underset{\mathbf {Y}}{\mathop {arg min}}\,\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}\mathbf{Tr \left( \mathbf {Y}{{\mathbf {h}}_{m,j}}\mathbf {h}_{m,j}^{T}{\mathbf {Y}^{T}} \right) } \\&=\underset{\mathbf {Y}}{\mathop {arg min}}\,\mathbf{Tr} \left( \mathbf {Y}\left( \dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{{{\mathbf {h}}_{m,j}}\mathbf {h}_{m,j}^{T}} \right) {\mathbf {Y}^{T}} \right) \\&=\underset{\mathbf {Y}}{\mathop {arg min}}\,\mathbf{Tr} \left( \mathbf {Y}{\mathbf {H}_{m}}{\mathbf {Y}^{T}} \right) \\ \end{aligned} \end{aligned}$$
    (24)

    where \({{\mathbf {h}}_{m,j}}={\mathbf {S}_{{{m}_{j}}}}{{\mathbf {w}}_{{{m}_{j}},id\left( m,{{m}_{j}} \right) }}-{{\mathbf {s}}_{m}}\) and \({\mathbf {H}_{m}}=\dfrac{1}{{{J}_{m}}}\sum \limits _{j=1}^{{{J}_{m}}}{{{\mathbf {h}}_{m,j}}\mathbf {h}_{m,j}^{T}}\).

  3. 3.

    Multi-local Linear Regression Considering the two constraints above, we obtain the objective function, that is

    $$\begin{aligned} \begin{aligned}&\mathbf{Tr} \left( \mathbf {Y}{\mathbf {L}_{m}}{\mathbf {Y}^{T}} \right) \text {+}{} \mathbf{Tr} \left( \mathbf {Y}{\mathbf {H}_{m}}{\mathbf {Y}^{T}} \right) \\&\text {=}{} \mathbf{Tr} \left( \mathbf {Y}\left( {\mathbf {L}_{m}}\text {+}{\mathbf {H}_{m}} \right) {\mathbf {Y}^{\text {T}}} \right) \text {=}{} \mathbf{Tr} \left( \mathbf {Y}{\mathbf {W}_{m}}{\mathbf {Y}^{\text {T}}} \right) \\ \end{aligned} \end{aligned}$$
    (25)

    where \({\mathbf {W}_{m}}\text {=}{\mathbf {L}_{m}}\text {+}{\mathbf {H}_{m}}\). \({\mathbf {W}_{m}}\) is a symmetric matrix due to the fact that both \({\mathbf {L}_{m}}\) and \({\mathbf {H}_{m}}\) are symmetric matrixes. Take all the data points into consideration and the final objective function can be written as

    $$\begin{aligned} \begin{aligned}&\underset{\mathbf {Y}}{\mathop {argmin}}\,\sum \limits _{m=1}^{N}\mathbf{Tr \left( \mathbf {Y}{\mathbf {W}_{m}}{\mathbf {Y}^{T}} \right) } \\&=\underset{\mathbf {Y}}{\mathop {argmin}}\,\mathbf{Tr} \left( \mathbf {Y}\left( \sum \limits _{m=1}^{N}{{\mathbf {W}_{m}}} \right) {\mathbf {Y}^{T}} \right) \\&=\underset{\mathbf {Y}}{\mathop {argmin}}\,\mathbf{Tr} \left( \mathbf {YW}{\mathbf {Y}^{T}} \right) \\ \end{aligned} \end{aligned}$$
    (26)

    where \(\mathbf {W}=\sum \limits _{m=1}^{N}{{\mathbf {W}_{m}}}\) and obviously, \(\mathbf {W}\) is also a symmetric matrix.

Fig. 2
figure 2

Schematic diagram of multi-local linear predictions

Full size image

3.4 Global projection distance minimum

We also considered the global distribution of the data. As mentioned above, for a given high-dimension dataset \(\mathbf {X}\in {{\mathbb {R}}^{D\times N}}\), the task is to determine a low-dimensional representation \(\mathbf {Y}\in {{\mathbb {R}}^{d\times N}}\), where \(D\gg d\) and \(\mathbf {Y}\) is the dimensionality reduction result of \(\mathbf {X}\). Since the product of \(\mathbf {X}\) and a matrix can change the size of \(\mathbf {X}\), we want to determine a matrix \(\mathbf {A}\in {{\mathbb {R}}^{D\times d}}\) and take the product of \(\mathbf {A}\) and \(\mathbf {X}\) as the dimensionality reduction result, i.e., \(\mathbf {Y}=\mathbf {A}^{T}\mathbf {X}\).

From the perspective of data dimensionality reduction, the meaning of \(\mathbf {Y}=\mathbf {A}^{T}\mathbf {X}\) is that the column vectors of matrix \(\mathbf {A}\) expand into a subspace \(span\mathbf {A}\), and the column vectors of matrix \(\mathbf {A}\) are the standard orthogonal bases of this subspace. The coordinates of the projection are \(\mathbf {Y}=\mathbf {A}^{T}\mathbf {X}\). The projection of high-dimensional data in the subspace is still high-dimensional data, but the coordinates of the projection are low-dimensional data. The objective function for finding \(\mathbf {A}\) can be written as:

$$\begin{aligned} \begin{aligned}&\underset{\mathbf {A}}{\mathop {\min }}\,{{\left\| \mathbf {X-AY} \right\| }^{2}}=\underset{\mathbf {A}}{\mathop {\min }}\,{{\left\| \mathbf {X-A}{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X} \right\| }^{2}} \\&s.t.\ {\mathbf {A}^{T}}\mathbf {A}=\mathbf {I} \end{aligned} \end{aligned}$$
(27)

where \(\mathbf {AA}^{T}\mathbf {X}\) is the projection of \(\mathbf {X}\) on the subspace \(span\mathbf {A}\). The optimization problem can be simplified as:

$$\begin{aligned} \begin{aligned}&{{\left\| \mathbf {X}-\mathbf {A}{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X} \right\| }^{2}}=\left\langle \mathbf {X}-\mathbf {A}{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X},\mathbf {X}-\mathbf {A}{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X} \right\rangle \\&=\left\langle \mathbf {X},\mathbf {X} \right\rangle +\left\langle \mathbf {A}{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X},\mathbf {A}{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X} \right\rangle -2\left\langle \mathbf {X},\mathbf {A}{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X} \right\rangle \\&=\left\langle \mathbf {X},\mathbf {X} \right\rangle +tr\left( \mathbf {A}{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X}{{\mathbf {X}}^{\mathbf {T}}}\mathbf {A}{{\mathbf {A}}^{\mathbf {T}}}\right) -2tr\left( \mathbf {X}{{\mathbf {X}}^{\mathbf {T}}}\mathbf {A}{{\mathbf {A}}^{\mathbf {T}}} \right) \\&={{\left\| \mathbf {X} \right\| }^{2}}-tr\left( {{\mathbf {A}}^{\mathbf {T}}}\mathbf {X}{{\mathbf {X}}^{\mathbf {T}}}\mathbf {A} \right) \\ \end{aligned} \end{aligned}$$
(28)

Therefore, the optimization problem is transformed to:

$$\begin{aligned} \begin{aligned}&\underset{\mathbf {A}}{\mathop {\max }}\,tr\left( {{\mathbf {A}}^{\mathbf {T}}}\mathbf {X}{{\mathbf {X}}^{\mathbf {T}}}\mathbf {A} \right) \\&s.t.\ {\mathbf {A}^{T}}\mathbf {A}=\mathbf {I} \\ \end{aligned} \end{aligned}$$
(29)

3.5 Multi-local linear regression and the global subspace projection distance minimum

In order to mine the structural information of the data better, the proposed algorithm considers both local information and global information of the original data. The model of the algorithm is:

$$\begin{aligned} \begin{aligned}&\underset{\mathbf {A}}{\mathop {\min }}\,tr\left( \dfrac{\mathbf {YW}{{\mathbf {Y}}^{\mathbf {T}}}}{{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X}{{\mathbf {X}}^{\mathbf {T}}}\mathbf {A}} \right) \underset{\mathbf {Y=}{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X}}{\mathop {=}}\,\underset{\mathbf {A}}{\mathop {\min }}\,tr\left( \dfrac{{{\mathbf {A}}^{\mathbf {T}}}\mathbf {XW}{{\mathbf {X}}^{\mathbf {T}}}\mathbf {A}}{{{\mathbf {A}}^{\mathbf {T}}}\mathbf {X}{{\mathbf {X}}^{\mathbf {T}}}\mathbf {A}} \right) \\&s.t.\ {\mathbf {A}^{T}}\mathbf {A}=\mathbf {I} \end{aligned} \end{aligned}$$
(30)

Since we denote \(\mathbf {Y}=\mathbf {A}^{T}\mathbf {X}\), once the subspace \(\mathbf {A}\) is selected, the dimension reduction data \(\mathbf {Y}\) is also determined. The selection of subspace \(\mathbf {A}\) needs to consider both criteria, that is, the distance between the high-dimensional dataset \(\mathbf {X}\) and its projection \(\mathbf {AA}^{T}\mathbf {X}\) in the subspace \(span\mathbf {A}\) is the smallest, and the coordinate \(\mathbf {Y}\) of the projection is the most conducive to multi-locality linear embedding principle. Under orthogonal constraint of \(\mathbf {A}\), the optimization problem in (26) transforms into a generalized Rayleigh entropy problem. The procedure of the proposed method is summarized in Algorithm 1.

figure a

3.6 Computational complexity analysis

The high-dimensional dataset \(\mathbf {X}\in {{\mathbb {R}}^{D\times N}}\) contains N data points, and the dimension of the data point is D. As shown in the proposed framework, we need to find the locality of each sample \(\mathbf {x}_{m}\) utilizing the k-nearest neighborhood method. The computational complexity of finding k nearest neighbors by calculating the distance is \(\mathcal {O}\left( ND\right) \), and for all N data points to find the k nearest neighbors, the corresponding computational complexity is \(\mathcal {O}\left( N^{2}D\right) \). To calculate the reconstructed coefficient of each sample, the computational complexity of singular value decomposition on each locality \(\mathbf {X}_{m}\in {{\mathbb {R}}^{D\times N_{m}}}\) is \(\mathcal {O}\left( D^{3}\right) \) for \(N_{m}\ll D\). For the convenience of analysis, we assume that the number of localities containing \(\mathbf {x}_{m}\) for \(m=1,\ldots ,N\) is the same fixed value, i.e., \(J_{m}=J, m=1,2,\ldots , N\). Therefore, the total computational complexity required for SVD is \(\mathcal {O}\left( NJD^{3}\right) \). The computational complexity of the proposed algorithm is \(\mathcal {O}\left( NJD^{3}+N^{2}D\right) \).

4 Experiments

In this section, we compare our proposed method with other unsupervised dimensionality reduction algorithms on real-world datasets. We tested the proposed algorithm and compared the results with five different dimensionality reduction algorithms based on manifold learning, i.e., LTSA, LE, ULG, SNPPE, and LDFA. Among these algorithms, LE and LTSA are two classical manifold learning-based dimensionality reduction algorithms. ULG and SNPPE are two representative dimension reduction algorithms devised recently. LDFA is a novel dimension reduction algorithm based on deep learning.

4.1 Datasets’ description

In this section, we list several real-world datasets that are utilized to verify the performance of our proposed method. These datasets are widely used to test the performance of the dimensionality reduction algorithms. The detailed description of these datasets is presented below, and Table 1 shows the statistics of the experimental data.

  1. 1.

    Faces94 [27] [28]: The dataset contains images of 153 subjects. Each subject has 20 images with different facial expressions. Out of 153 subjects, 20 subjects are female, 113 are male subjects, and 20 male staff subjects. In our experiment, we randomly choose images of 10 males. Each sample is with a size of \(64 \times 64\). All the images are resized to \(50 \times 45\) in our experiment.

  2. 2.

    Olivetti [29]: Olivetti Faces is a relatively small face database of New York University. It consists of 400 pictures of 40 people, that is, each person has 10 faces. The gray level of each picture is 8 bits, and the gray level of each pixel is between 0 and 255, and the size of each picture is \(64 \times 64\).

  3. 3.

    MNIST [30] [31]: The MNIST dataset is from the National Institute of Standards and Technology (NIST). Handwritten Arabic numerals are written by different people. From 0 to 9, each number contains 100 images, a total of 1,000, each of which is \(28\times 28\) in size.

  4. 4.

    COIL20 [32] [33]: The dataset is an object dataset with 20 subjects. There are 72 images for each object with different orientations. Each image is resized to \(32 \times 32\) in our experiment.

  5. 5.

    USPS [25, 34]: The USPS (United States Postal Service) dataset is a handwriting dataset. This dataset has 10 classes corresponding to the digits 0 to 9 with 1100 samples per class. Based on the size of the dataset itself and the consideration of the high complexity of some algorithms, we only randomly choose four digits as our experimental data. A total of 800 samples in four categories.

Table 1 Statistics of the experimental data
Full size table

4.2 Parameter selection

In this section, we first evaluate the effect of parameter k, i.e., the number of neighbors in the proposed algorithm, and compare the results with LTSA, ULG, SNPPE, LE, and LDFA. We refer to [38] [39] for the experimental settings. We apply the proposed method and compare the algorithms on the USPS, MNIST and COIL20 datasets followed by the k-means clustering method on the embedding results. The performance of clustering results is evaluated by clustering accuracy. And the clustering accuracy is defined as:

$$\begin{aligned} Clustering\ Accuracy=\dfrac{1}{M}\sum \limits _{j=1}^{M}{\delta ({{l}_{j}},l_{j}^{*})} \end{aligned}$$

where \(l_{j}^{*}\) and \(l_{j}\) are the truth label and cluster label provided by the clustering approaches for the data point \(\mathbf {x}_{j}\), respectively. \(\delta \left( \cdot ,\cdot \right) \) is set to 1 if and only if \(l_{j}^{*}=l_{j}\), and 0 otherwise.

In addition to the parameter k, our algorithm also includes another parameter, i.e., the embedding dimension d. Therefore, we fix the value of parameter d and observe the influence of the change of parameter k on the experimental results. There are many algorithms proposed to estimate the intrinsic dimensionality of a dataset, such as the maximum likelihood estimator (MLE) [35], minimum neighbor distance (MiND) [36], and the geodesic minimum spanning tree estimator (GMST) [37]. The range of the estimated dimensionality of the experimental data is usually between 5 and 25, so we fixed the embedding dimension to 15. We test the clustering performance with \(k\in \left\{ 10,20,\ldots ,80 \right\} \). The results are presented in Fig. 3.

Fig. 3
figure 3

Clustering accuracy versus k of algorithms on datasets. a USPS, b MNIST, c COIL20

Full size image

From the experimental results, it can be seen that the proposed algorithm shows strong robustness for the parameter k. As the increase of k, the clustering accuracy of the proposed algorithm is quite stable. The parameter k represents the number of neighbors to perform linear regression. Our model contains two parts: multi-local linear regression and global subspace projection distance minimum. Therefore, for different datasets, the effect of these two parts in the model may be different. Our algorithm takes into account both global information and local information, which may be the reason for its high robustness. In the future, it would be better to adjust the proportion of these two parts of the model via a parameter.

In general, the clustering accuracy of the proposed algorithm on these three datasets is relatively good when k takes different values. The clustering accuracy of the proposed algorithm is the best on the USPS dataset (Fig. 3a). For the COIL20 dataset (Fig. 3c), MLLRGPD is also superior to LTSA due to the utilization of multiple predictions during the feature extraction procedure. As the increase of the number of neighbors, the clustering accuracy of LDFA decreases significantly. As is illustrated in [24], LDFA learns discriminative local features well with relatively small neighborhood size, which explains the tendency of the curve for LDFA in Fig. 3.

We hope to set the parameters k with the same physical meaning in different algorithms to be the same value. However, the experimental results show that we cannot choose a value to optimize the performance of all algorithms. The performance of most algorithms is relatively good when k is 60. To simplify the discussion of the following experiments, we set the parameter k of MLLRGPD to 60, as well as other compared algorithms involving k.

4.3 Visualization experiment

To show the dimensionality reduction results intuitively, we reduce the high-dimensional data to two-dimensional data and show the distribution of data in the low-dimensional plane. In this section, we perform a visualization experiment on the COIL20 dataset and the Faces94 dataset. The experimental results are compared with the algorithms introduced above. The parameters’ setting of all algorithms is shown in Table 2. Figures 4 and 5 show the experimental results of all algorithms on the COIL20 and the Faces94 datasets, respectively.

Table 2 Parameters’ setting for algorithms
Full size table
Fig. 4
figure 4

The 2D visualization result of the COIL20 dataset by a MLLRGPD, b ULG, c LTSA, d LDFA, e SNPPE, f LE

Full size image

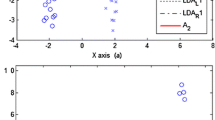
Although there are only two feature dimensions in the dimension-reduced data, the low-dimensional data are also obviously separable (Figs. 4a, 5a). The criterion of global projection distance minimum indicates that the low-dimensional data are with large variance. Therefore, the dimensionality-reduced data can achieve high separability. In addition, data belonging to the same category still show aggregation distribution after dimensionality reduction. This phenomenon shows that the MLLRGPD algorithm can effectively keep the original distribution information of the high-dimensional data. The MLLRGPD algorithm considers the relationship between multiple localities that contain the same data point and effectively maintains the spatial structure of the original high-dimensional data in low-dimensional space. The performance of LTSA and LDFA is relatively poor. Data points of different categories are mixed, which means that the original structure in the high-dimensional space is destroyed. The dimensionality reduction effect of LE is relatively good. The basic idea of LE is to keep the adjacency relationships between data points via an undirected graph. However, the data of different categories also overlap obviously. On the Faces94 dataset, most algorithms achieve good performance. However, the distribution of the low-dimensional data obtained by LDFA has a relatively obvious aliasing phenomenon, which may be caused by the SCAE during the feature extraction procedure.

Fig. 5
figure 5

The 2D visualization result of the Faces94 dataset by a MLLRGPD, b ULG, c LTSA, d LDFA, e SNPPE, f LE

Full size image

To quantitatively analyze the dimensionality reduction effect of the algorithms, we show the clustering accuracy of two-dimensional features in Fig. 6. Among them, MLLRGPD performs better than other compared algorithms on the COIL20 dataset. On Faces94, MLLRGPD is 2% higher than LTSA, and the dimensionality reduction effects of ULG, SNPPE, and LE are similar. The accuracy of clustering is consistent with the result of the visualization.

Fig. 6
figure 6

The clustering accuracies base on the dimension reduction in a COIL20 and b Faces94

Full size image

4.4 Clustering experiment

In this section, we evaluate the performance of the proposed algorithm by conducting a clustering experiment on the dimensionality-reduced dada. The experiment results are compared with several algorithms, such as LE, LTSA, ULG, LDFA, and SNPPE. The k-means approach with the Euclidean distance metric is applied to cluster the embedding results. Since the k-means algorithm is sensitive to the initial point, we repeat the clustering procedure 50 times, and the final scores are computed by averaging the scores. We evaluate the clustering performance of the proposed algorithm and other algorithms with two scores, i.e., clustering result and normalized mutual information (NMI) [12]. NMI between two sets \(l^{*}\) and l is defined as

$$\begin{aligned} NMI\left( l_{{}}^{*},l \right) =\dfrac{MI\left( l_{{}}^{*},l \right) }{max\left( H\left( l_{{}}^{*} \right) ,H\left( l \right) \right) } \end{aligned}$$

where \(H\left( l^{*} \right) \) and \(H\left( l \right) \) denote the entropy of \(l^{*}\) and l, respectively, and

$$\begin{aligned} MI\left( l^{*},l \right) =\sum \limits _{{{l}_{i}}\in l,l_{j}^{*}\in l^{*}}^{n}{p\left( {{l}_{i}},l_{j}^{*} \right) }{{\log }_{2}}\dfrac{p\left( {{l}_{i}},l_{j}^{*} \right) }{p\left( {{l}_{i}} \right) p\left( l_{j}^{*} \right) } \end{aligned}$$

\(p\left( l_{j}^{*} \right) \) and \(p\left( {{l}_{i}} \right) \) are the marginal probability distribution of \(l^{*}_{j}\) and \(l_{i}\), respectively, and \(p\left( {{l}_{i}},l_{j}^{*} \right) \) denote the joint probability function of \(l^{*}_{j}\) and \(l_{i}\).

The parameter settings of all algorithms are shown in Table 2. In the process of dimensionality reduction, we cannot predict the embedding dimension of data in advance. The dimensionality of the reduced data for all algorithms is searched in [5, 21] for the datasets. The detailed clustering results are shown in Figs. 7, 8, 9, 10, and 11.

Fig. 7
figure 7

USPS dataset. a Clustering accuracy, b NMI

Full size image
Fig. 8
figure 8

Faces94 dataset. a Clustering accuracy, b NMI

Full size image

For the embedding results of the USPS, Faces94, and COIL20 dataset, the clustering accuracy of the proposed algorithm is the best with different embedding dimensions. For NMI, the proposed algorithm is superior to other methods too. On the USPS dataset, the curve of the proposed method is quite stable, while the clustering accuracy of LTSA decreases with the increase of the embedding dimension. The reason may be that low-dimensional data contain redundant information and cause interference. LDFA fails to extract the intrinsic dimensionalities of USPS and MNIST datasets totally, which may due to the error brought by SCAE during the feature extraction procedure. Besides, maybe it is not suitable for LDFA to deal with the problem of a small number of samples since LDFA contains a neural network. Compared with LTSA and ULG, MLLRGPD shows stronger robustness for embedding dimension.

Fig. 9
figure 9

COIL20 dataset. a Clustering accuracy, b NMI

Full size image
Fig. 10
figure 10

MNIST dataset. a Clustering accuracy, b NMI

Full size image
Fig. 11
figure 11

Olivetti dataset. a Clustering accuracy, b NMI

Full size image

On Faces94, COIL20, MNIST, and Olivetti datasets, the curves of the clustering accuracy and NMI of most algorithms have a similar trend. As the reduced dimension increases, the clustering accuracy rises first and then remains stable. This is because too much information is lost when the dimension is too low and the performance deteriorates. When the reduced dimension is increased enough to represent the effective information of the original data, the increase of the dimension will not improve the performance. The increase of the embedding dimension makes the data information mining more sufficient, but at the same time, it will also bring more redundant information, which will cause interference to the data processing. The curves of LE on the Faces94 dataset and LTSA on the USPS dataset reflect this problem.

Overall, the proposed algorithm performs well on five datasets, which shows that the effectiveness of information retention through multiple localities. Besides, we take the global distribution of the data into account to avoid huge interference caused by special local structures. The experimental results of the proposed algorithm have obvious improvements compared with LTSA, which confirms the conclusion.

To consider the overall clustering performances on all embedding dimensionalities, we average the clustering accuracy and clustering NMI. The average results are summarized in Tables 3 and 4. The proposed algorithm performs better than other algorithms on almost datasets, which illustrates the effectiveness of our proposed method in terms of clustering tasks.

Table 3 Average clustering accuracy
Full size table
Table 4 Average NMI
Full size table

5 Conclusion

In recent years, computer vision, pattern recognition, and other technologies have been widely used in face recognition, object recognition, speech processing, and biological fields. These fields involve a large amount of high-dimensional data. Therefore, the multi-local linear regression and global subspace projection distance minimum algorithm proposed in this paper are of great significance in practical application. Under the local homeomorphic criterion, the algorithm fully maintains the internal continuous dependency relationship of high-dimensional data. Besides, the proposed algorithm fully considers the fact that each target point belongs to multiple localities. To maintain the internal data relationship of each locality, we have learned the linear pattern of each locality through linear regression. We require that each predicted data should be as close to the ideal data as possible, and the variance of all predicted values obtained from several localities should be as small as possible to maintain the geometric relationship between the overlapping localities.

At the same time, we consider the global distribution of the data. We want to learn a subspace so that the distance between the high-dimensional data and its projection on the subspace is the smallest. Combining the multi-local linear regression and the minimum global projection distance, the proposed algorithm maintains both the local homeomorphism characteristics and the global structure of the data. Experiments show that the proposed algorithm can well maintain the structural relationship of high-dimensional data during the dimensionality reduction process. On most datasets, the clustering effect is significantly better than other algorithms.

Our model actually contains two parts: multi-local linear regression and global subspace projection distance minimum. These two parts describe the local and global information of the data, respectively. Therefore, we may add a parameter to adjust the proportion of these two parts to improve the robustness of the algorithm. Besides, the idea of multi-localities may be applied to more manifold learning algorithms.