Domain adaption based on source dictionary regularized RKHS subspace learning

Abstract

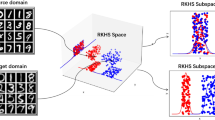
Domain adaption is to transform the source and target domain data into a certain space through a certain transformation, so that the probability distribution of the transformed data is as close as possible. The domain adaption algorithm based on Maximum Mean Difference (MMD) Maximization and Reproducing Kernel Hilbert Space (RKHS) subspace transformation is the current main algorithm for domain adaption, in which the RKHS subspace transformation is determined by MMD of the transformed source and target domain data. However, MMD has inherent defects in theory. The probability distributions of two different random variables will not change after subtracting their respective mean values, but their MMD becomes zero. A reasonable method should be that the MMD of the source and target domain data with the same label should be as small as possible after RKHS subspace transformation. However, the labels of target domain data are unknown and there is no way to model according to this criterion. In this paper, a domain adaption algorithm based on source dictionary regularized RKHS subspace learning is proposed, in which the source domain data are used as a dictionary, and the target domain data are approximated by the sparse coding of the dictionary. That is to say, in the process of RKHS subspace transformation, the target domain data are distributed around the mostly relevant source domain data. In this way, the proposed algorithm indirectly achieves the MMD of the source and target domain data with the same label after RKHS subspace transformation. So far there has been no similar work reported in the published academic papers. The experimental results presented in this paper show that the proposed algorithm outperforms 5 other state-of-the-art domain adaption algorithms on 5 commonly used datasets.

1 Introduction

In the era of big data, it is very crucial to learn the discriminative information of the auxiliary dataset and transfer it to the target dataset or other tasks. In order to ensure the precision and reliability of the model after training, the traditional machine learning algorithms are usually established under two basic assumptions: (1) The training samples and test samples are in the same feature space, independent of each other, and they should obey the same probability distribution[1]; (2) there should be sufficient training samples. However, these two basic assumptions are often not satisfied in many real-world applications. First, the heterogeneity and timeliness of data are increasingly prominent in the era of big data. Thus, the original training samples and newly collected test samples are often subject to different distributions, and sometimes they are even located in different feature spaces. On the other hand, due to the expensive cost of data collection and sample labeling, labeled data are relatively scarce and difficult to obtain. In order to solve these problems and improve the efficiency and reliability of data utilization, a large number of transfer learning algorithms have been proposed and attracted wide attention.

Transfer learning (TL) is a kind of machine learning method that uses existing knowledge to solve the tasks across different but related domains[2, 3]. Domain and task[1] are two important concepts in transfer learning. Data samples in the same feature space and with the same probability distribution are categorized into the same domain. If two tasks share the same label space and obey the same posterior conditional probability distribution, then they can be regarded as one task. The purpose of transfer learning is to apply the knowledge extracted from source domain and source task to the target domain and target task. Domain adaptive learning (DAL) belongs to the category of transfer learning[4,5,6], yet sharing the same source task and target task. The research of DAL focuses on how to use labeled source domain data, unlabeled or partially labeled target domain data and target domain prior knowledge to learn and reliably complete the tasks in target domain when the probability distribution of source domain and target domain is different but relevant. Domain adaptation can be divided into three types: supervised[7, 8], semi-supervised[9,10,11], and unsupervised[12,13,14,15,16,17]. One solution of DAL is to map the source domain data and the target domain data into a new feature space by finding a suitable feature mapping function, so that the distribution of the source domain and the target domain in this space is as similar as possible. Kernel function is a category of suitable feature mapping function which can implicitly map the data to the high-dimensional RKHS and explicitly provide the inner product of the data in the space. Another method is to use neural networks to solve the domain adaptation problem, such as the literature[18,19,20]. Cai [18] proposed a new model, named domain adaption using cross-domain homomorphism, to identify intrinsic homomorphism hidden in mixed data from all domains. Long [19] proposed joint adaptation networks (JAN), which learn a transfer network by aligning the joint distributions of multiple domain-specific layers across domains based on a joint maximum mean discrepancy criterion. Bousmalis [20] proposed a new approach that learns, in an unsupervised manner, a transformation in the pixel space from one domain to the other. And their model is based on generative adversarial network (GAN).

Maximum mean discrepancy[21] is a common metric in domain adaptive learning. MMD measures the mean value of source domain data and target domain data mapped to the RKHS through kernel function. By minimizing the mean discrepancy between source domain data and target domain data in RKHS, the distribution of data from two domains will tend to get closer. If the mean discrepancy is lower than the tolerable threshold value, it can be claimed that data from two different domains in RKHS follow the same probability distribution. Otherwise, the source domain data and the target domain data are not subject to the same probability distribution, and they are not similar.

In MMD criterion, data need to be mapped into RKHS, so kernel function is essential during the process of MMD. The choice of kernel function determines the characteristics of the feature space to which the source domain data and target domain data will be mapped and also affects the effect of domain adaptive learning. The kernel function is fixed and cannot learn the geometric structure of the data. Therefore, many researchers divide a subspace from RKHS and map the source domain data and target domain data to the subspace. And subspace learning needs to adopt the MMD criterion to minimize the mean difference between source domain data and target domain data, so as to obtain a suitable subspace. In the process of subspace learning, researchers put forward various regularization items, such as manifold regularization and variance maximization regularization, so that the performance of the model is more superior.

The main contributions of this thesis are as follows: A domain adaption algorithm based on source dictionary regularized RKHS subspace learning is proposed, in which the source domain data are used as a dictionary, and the target domain data are approximated by the sparse coding of the dictionary. That is to say, in the process of RKHS subspace transformation, the target domain data are distributed around the mostly relevant source domain data. In this way, the proposed algorithm indirectly achieves the MMD of the source and target domain data with the same label after RKHS subspace transformation. The algorithm requires the target domain data to be distributed around the source domain data with the strongest linear correlation, thereby indirectly reflecting the requirement that the spatial distribution of the source domain data and target domain data of the same category is as consistent as possible.

The following parts of this paper are organized as follows. In Sect. 2, we briefly introduce the related mathematical theories, including reproducing Kernel Hilbert space (RKHS), domain adaptive learning (DAL), maximum mean discrepancy (MMD), and dictionary learning (DL). We give an overview about the global research trends of domain adaptive learning and dictionary learning in Sect. 3. Then, in Sect. 4, we introduce our Domain Adaption Based on Source Dictionary Regularized RKHS Subspace Learning (SDRKHS-DA) in detail. In Sect. 5, we briefly introduce the comparison algorithm model and its corresponding characteristics. In Sect. 6, a series of experiments are carried out to verify the effectiveness and practicability of our algorithm through five cross-domain tasks. Finally, we summarize our work in Sect. 7.

2 Notations and preliminaries

2.1 Notations

In this paper, $X_{\mathrm{s}}$ and $X_{\mathrm{t}}$ represent, respectively, the source domain and target domain data, and the set of source domain and target domain data is $X=[X_{\mathrm{s}},X_{\mathrm{t}}]$. $y^{s}$ is the source domain data projected to the subspace, and $y^{t}$ is the target domain data projected to the subspace (shown in Table 1).

Table 1 The basic notations

2.2 Reproducing Kernel Hilbert Spaces

Hilbert space is the complete inner product space, while the reproducing kernel Hilbert space is a special kind of Hilbert space which introduces the definition of reproducing kernel. Let H be a Hilbert space composed of functions that satisfy certain conditions (such as square integrability) defined on the set $\varOmega$, i.e., $f\in H$, $f:\varOmega \rightarrow \mathbb {R}$, if there exists a function $k: \varOmega \times \varOmega \rightarrow \mathbb {R}$ which satisfies the following conditions:

• 1. For any $x\in \varOmega$, $k(\bullet ,x)\in H$;

• 2. For any $x\in \varOmega$, and any $f\in H$, $f(x)=\langle f, k(\bullet ,x)\rangle$. Here, $\langle \bullet ,\bullet \rangle$ refers to the inner product in H.

Then, H is a RKHS, and k is the reproducing kernel of H.[22] The reproducing kernel holds the properties of symmetry, positive semi-definition, uniqueness, etc. Using the reproducing kernel k, we can define the transformation: $\phi : \varOmega \rightarrow H$, for any $x\in \varOmega$, $\phi (x)=k(\bullet ,x)\in H$. And with the properties of reproducing kernel, it can be proved that, for any $x,y\in \varOmega$, $\langle \phi (x),\phi (y)\rangle =k(x,y)$.

According to Moore–Aronszajn theorem, RKHS can be generated uniquely by kernel function. The definition of kernel function[23] is: $k: \varOmega \times \varOmega \rightarrow \mathbb {R}$ which satisfies:

• 1. Symmetry: for any $x,y\in \varOmega$, $k(x,y)=k(y,x)$;

• 2. Positive definition: for any finite elements $\left\{ {\mathrm{{x}}_1 , \cdots ,x_N } \right\}$ $\subseteq {} \varOmega$, the matrix K below is a positive definite matrix:

  $$\begin{aligned} K = \left[ {\begin{array}{*{20}c} {k\left( {x_1 ,x_1} \right) } &{} \cdots &{} {k\left( {x_1 ,x_N } \right) } \\ \vdots &{} \ddots &{} \vdots \\ {k\left( {x_N ,x_1 } \right) } &{} \cdots &{} {k\left( {x_N ,x_N } \right) } \\ \end{array}} \right] \end{aligned}$$

The process of generating RKHS with kernel function is as follows:

• 1. Generate the linear space with kernel function:

  $$\begin{aligned} \begin{aligned} H_\mathrm{k}= & {} span\left\{ {\left. {k\left( { \bullet ,x} \right) } \right| x \in \varOmega } \right\} \\= & {} \left\{ {\left. {\sum \limits _{i = 1}^n {\alpha _\mathrm{{i}} k\left( { \bullet ,x_i } \right) } } \right| x_i \in \varOmega ,\alpha _i \in R,n \in Z^ + } \right\} \end{aligned} \end{aligned}$$

  where $Z^+$ represents all positive integers.

• 2. Define inner product in $H_k$: $\left\langle { \bullet , \bullet } \right\rangle :H_k \times H_k \rightarrow \mathbb {R}$, for any $f,g\in H_k$,

  $$\begin{aligned} f\left( \bullet \right)= & {} \sum \limits _{i = 1}^n {\alpha _i k\left( { \bullet ,x_i } \right) } ,\quad g\left( \bullet \right) = \sum \limits _{j = 1}^m {\beta _j k\left( { \bullet ,y_j } \right) } ,\\ \langle f,g\rangle= & {} \begin{bmatrix} \alpha _1&\cdots&\alpha _N \end{bmatrix} \begin{bmatrix} k(x_1,y_1) &{} \cdots &{} k(x_1,y_m) \\ \vdots &{} \ddots &{} \vdots \\ k(x_n,y_1) &{} \cdots &{} k(x_n,y_m) \end{bmatrix} \begin{bmatrix} \beta _1 \\ \vdots \\ \beta _m \end{bmatrix} \end{aligned}$$

• 3. Complete $H_\mathrm{k}$ and thus obtain $\bar{H_\mathrm{k}}$, then $\bar{H_\mathrm{k}}$ is a RKHS and k is the reproducing kernel of $\bar{H_\mathrm{k}}$. Because a certain kernel function only produces a certain RKHS, learning a RKHS is also the process of learning a kernel function.

2.3 Domain adaptive learning and MMD

There is a special scenario that often occurs in the field of machine learning. There are two datasets in data space $\varOmega$: source domain dataset $X^s = \left\{ {x_1^s , \cdots ,x_{N_\mathrm{s} }^s } \right\} \subseteq \varOmega$ and target domain dataset $X^t = \left\{ {x_1^t , \cdots ,x_{N_\mathrm{t} }^t } \right\} \subseteq \varOmega$. The source domain data $X^s$ are labeled, while target domain data $X^t$ are unlabeled, and the distributions of $X^s$ and $X^t$ in data space are different. However, now we need to utilize the label of $X^s$ to classify the label of $X^t$. This problem is what we call Domain Adaptation Learning problem, and it belongs to transfer learning problems. Note that the data space $\varOmega$ is usually Euclidean space, but it may also be Riemannian manifold or Grossmann manifold that has gained increasing popularity in machine learning. To articulate this issue, for example, in the application of face recognition, the photographs on various certificates stored by the public security organs are the source domain data. The faces in these photographs are in a state of upright posture and neutral expression and are under good lighting condition, while the photographs captured from video monitoring are the target domain data. The faces in these photographs may contain different oblique postures and exaggerated expressions or are under unsatisfying lighting condition. Obviously, the distribution of ID photographs (source domain data) and those captures by real-time cameras (target domain) is different in image space. But we only know the identity of the faces on the ID photographs, and we have to recognize the identity of the face on those real-time photographs with the available labels.

Among various DAL methods, MMD is a commonly used and helpful criterion. DAL focuses on the scenario that the distributions of source domain data $X^s$ and target domain data $X^t$ in data space $\varOmega$ are not the same. Then, MMD wants to learn a RKHS composed of functions in data space $\varOmega$ and utilize the reproducing kernel k of this space to transform the source domain data $X^s$ and target domain data $X^t$ in data space $\varOmega$ to this RKHS H, i.e.,

$$\begin{aligned} \phi \left( {\mathrm{{X}}^s } \right)= & {} \left\{ {\phi \left( {x_1^s } \right) , \cdots ,\phi \left( {x_{N_\mathrm{s} }^s } \right) } \right\} \subseteq H,\\ \phi \left( {\mathrm{{X}}^t } \right)= & {} \left\{ {\phi \left( {x_1^t } \right) , \cdots ,\phi \left( {x_{N_\mathrm{t} }^t } \right) } \right\} \subseteq H. \end{aligned}$$

such that the distributions of $\phi (X^s)$ and $\phi (X^t)$ in RKHS H can be as similar as possible. And the similarity here can exactly be measured by MMD, i.e.,

$$\begin{aligned} \left\| {\frac{1}{{N_\mathrm{s} }}\sum \limits _{i = 1}^{N_\mathrm{s} } {\phi \left( {x_i^s } \right) } - \frac{1}{{N_\mathrm{t} }}\sum \limits _{j = 1}^{N_\mathrm{t} } {\phi \left( {x_j^t } \right) } } \right\| ^2 \xrightarrow {\phi } \min \end{aligned}$$

where $\phi$ is the mapping defined by reproducing kernel k, and the optimization of $\phi$ also means the process of choosing k. As we know, k relies on the RKHS H. Therefore, this process can be attributed to the choice of RKHS H.

In practice, it is not easy to learn an optimal RKHS H according to MMD. As a result, most methods based on MMD do not choose to learn RKHS H, but a linear subspace W of it, so that the mean values of $\phi (X^s)$ and $\phi (X^t)$ can be similar after they are projected once again into the linear subspace W:

$$\begin{aligned} \left\| {\frac{1}{{N_\mathrm{s} }}\sum \limits _{i = 1}^{N_\mathrm{s} } {\phi _{W} \left( {x_i^s } \right) } - \frac{1}{{N_\mathrm{t} }}\sum \limits _{j = 1}^{N_\mathrm{t} } {\phi _{W} \left( {x_j^t } \right) } } \right\| ^2 \xrightarrow {\phi }\min \end{aligned}$$

where $\phi _W (X^s)$ and $\phi _W (X^t)$ mean the projection of $\phi (X^s)$ and $\phi (X^t)$ in the subspace, respectively.

2.4 Dictionary learning

The premise of sparse coding is to have a suitable dictionary. The dictionary mentioned in this paper is learned based on samples of specific applications. After collecting a certain number of representative samples, the dictionary is obtained after optimization.

Let $X=\{ x_{1},\cdots ,x_{N} \}$ be a sample, and find a suitable dictionary $\{ d_{1},\cdots ,d_{L} \}$ through the N samples. The objective function of dictionary learning can be expressed as follows:

$$\begin{aligned} \mathop {\min }\limits _{d_{1},\cdots ,\mathrm{d}_{L}} \sum \limits _{i=1}^{N}\left[ \left\| x_{i}-\sum _{j=1}^{L}a_{ij}\mathrm{d}_{j}\right\| ^{2}+\lambda \mathbf{sparse} (A_{iRow})\right] \end{aligned}$$

(1)

where $A = \left[ {\begin{array}{*{20}c} a_{11} &{} \cdots &{} a_{1L} \\ \vdots &{} \ddots &{} \vdots \\ a_{11} &{} \cdots &{} a_{NL} \\ \end{array}} \right]$ is called the sparse coding matrix. In the above objective function, the sparse coding matrix A is a by-product that is not needed in the next algorithm, but the trained dictionary $\{\mathrm{d}_{1},\cdots ,\mathrm{d}_{L} \}$ is needed.

After the dictionary $\{\mathrm{d}_{1},\cdots ,\mathrm{d}_{L} \}$ has been learned, each trusted data point x can be roughly represented by this set of dictionaries. The function of sparse coding is to make the coefficient components of x linearly represented by this set of dictionaries $\{\mathrm{d}_{1},\cdots ,\mathrm{d}_{L} \}$ tend to 0 as much as possible. The objective function of sparse coding can be expressed as follows

$$ J(w) = \left\| {x - \sum\limits_{{j = 1}}^{L} {\alpha _{j} } {\text{d}}_{j} } \right\|^{2} + \lambda {\text{sparse}}(\alpha ){\text{ }} $$

(2)

Here, $\alpha =[ \alpha _{1}, \cdots , \alpha _{L} ]^{T}$, $\text {sparse}(\alpha )$ is the sparse regular term of sparse coding and makes the component tend to 0 as much as possible. We usually use the 1 norm to represent the sparse regular term of sparse coding

$$\begin{aligned} \mathbf{sparse} (\alpha )=\left\| \alpha \right\| _{1}=\sum _{j=1}^{L} | \alpha _{j} | \end{aligned}$$

(3)

And $\text {sparse}(\alpha )$ is the feature vector after sparse coding. Without $\text {sparse}(\alpha )$, it will become a problem of solving subspace projection. If $\{\mathrm{d}_{1},\cdots ,\mathrm{d}_{L} \}$ is orthogonal to each other, then

$$\begin{aligned} \mathop {\min }\limits _{\alpha } \left\| x-\sum _{j=1}^{L}\alpha _{j}\mathrm{d}_{j} \right\| ^{2} \rightarrow \alpha _{j}=x^{T}d_{j}, j=1,\cdots ,L \end{aligned}$$

(4)

3 Related works

3.1 Domain adaptive learning

Domain adaptive learning is an active new research field which has been successfully applied to various fields including text classification, object recognition, face recognition, event recognition, indoor location, target location, video concept detection, etc.[24]. The purpose of domain adaptive learning is to solve the problem of inconsistent distribution of source domain data and target domain data. There are many ways to solve this problem, and the most common one is to use MMD as the criterion of domain adaptation, such as TCA [15], SSTCA[15]], and IGLDA [16]. In recent years, some researchers have also proposed other domain adaptation criteria. Li et al.[11] proposed covariance as a criterion for domain adaptive learning, which minimizes the difference between the variance of the source domain data and the target domain data to make the source domain data and target domain data as consistent as possible. Moreover, the learning subspace is optimized by minimizing the intra-class distance and maximizing the inter-class distance. At the same time, manifold regularization is used to maintain the geometric structure of the data. Wang [25] et al. proposed that the distribution of target domain data projected to the subspace can be approximated to the distribution of source domain data of the same category through a transformation matrix, and the correlation between different label categories in the projection matrix is minimized.

In addition to different criteria in domain adaptation, researchers have also proposed many other methods. In order to simultaneously extract cross-domain information of emotion and topic vocabulary, Li et al.[26] first generate emotion and topic ‘seeds’ in the target domain and then use a method called Relational Adaptive bootstraPping (RAP) to expand ‘seeds.’ RAP is a DAL algorithm based on specific relationship so as to complete the extraction task in the target domain according to the extracted information. Long et al.[27, 28] proposed a Deep Adaptation Network (DAN) to learn the transferable features, which started the research of deep learning-based adaptive learning. The research of adversarial adaptive learning[29] utilized a binary domain discriminator to realize domain confusion in a supervised way, thus minimized the differences between domains.

Gong et al.[30] proposed geodesic flow kernel (GFK), and it used the source domain data and target domain data to construct a geodesic flow and a geodesic flow kernel. The geodesic flow represents the incremental changes between the two domains, while the geodesic flow kernel maps numerous subspaces on the geodesic flow. GFK integrates numerous subspaces on the geodesic flow from the source domain subspace to the target domain subspace and extracts the domain-invariant subspace direction.

Fernando et al.[31] proposed the method of subspace alignment (SA) to solve the DAL problems. SA learns a mapping function that aligns the subspace of source domain and target domain. Specifically, it aims to learn a transformation matrix M and construct the target function:

$$\begin{aligned} \mathop {\min }\limits _M \left\| {X^s M - X^t } \right\| _F^2 \end{aligned}$$

(5)

$X^s$ and $X^t$ are the subspace representations of source domain data and target domain data constructed by principal component analysis (PCA) according to data from both domains and the pre-defined subspace dimension. Equation (5) can be solved by the least square method. According to the subspace representation after alignment, we can train classifiers on the source domain data and then apply it to the target domain.

Pan et al.[32] put forward Maximum Mean Discrepancy Embedding algorithm (MMDE), and MMDE first learns a kernel matrix K, so that the data in the source domain and the target domain could follow the consistent distribution in the embedding RKHS corresponding to the kernel matrix. At the same time, the variance of the data can be preserved for better classification. Then, MMDE conducts PCA to K to learn a low-dimensional feature subspace of RKHS and select the main feature vectors to construct the low-dimensional representation of the data. The limitation of MMDE is that it learns the kernel matrix in a transductive way, so the kernel matrix must be re-learned when out-of-sample data are introduced. Moreover, the process of PCA after optimizing the kernel matrix may lose the potential useful information in the kernel matrix.

Transfer component analysis (TCA) proposed by Pan et al.[15] also focuses on learning a low-dimensional subspace of RKHS under the principle of reducing the distribution differences between domains and maintaining the internal structure of data. TCA uses empirical kernel trick to combine kernel method and subspace learning. And its constraint is used to maintain the linear independence of the transformation matrix and preserve the data variance mapped to the subspace. Based on TCA, semi-supervised transfer component analysis[15] (SSTCA) maximizes the correlation between the data and label information and preserves the data locality. Furthermore, Integration of Global and Local Metrics for Domain Adaptation Learning[16] (IGLDA) introduces category information of the data, so that the intra-class distance of the projected data can be as small as possible.

Liu et al.[33, 34] proposed an approach called low-rank representation (LRR) to identify the subspace structure of noisy data. Based on this, Jhuo et al.[35] proposed a robust DAL algorithm based on low-rank reconstruction. Shekhar et al.[36, 37] proposed a method using shared dictionaries to represent source domain data and target domain data in a latent subspace. And domain-specific dictionary learning[38, 39] aims to learn a dictionary for each domain and then use domain-specific or domain-common representation coefficients to represent the data of each domain.

Li et al.[40] proposed a method for judging feature learning based on categories. The algorithm first uses the basic classifier to identify a pseudo-label on the target domain data and minimizes the distance between the source data of the same class and maximizes the distance between the source data of the different class. The method also minimizes the distance between the target data of the same class and maximizes the distance between the target data of the different class. Zhang et al.[41] proposed a Manifold Criterion guided Transfer Learning. The algorithm uses the source domain to generate an intermediate domain, so that the generated intermediate domain data approximate the distribution of the target domain data from both local and global aspects.

3.2 Dictionary learning

Before sparse coding, a dictionary is first generated, so sparse coding methods are usually associated with dictionary learning. Traditional dictionary learning methods are unsupervised, and the dictionary has no category labels. In order to learn more discriminative dictionaries, in recent years, researchers have proposed supervised dictionary learning methods. Ramirez and Castrodad proposed a dictionary determined for each type of data learning category[42, 43]. Zhou proposed to learn a dictionary with certain categories by minimizing the divergence between classes of similar data and learning a shared dictionary by maximizing the divergence between classes of different types of data[44]. Perronnin proposed to adaptively generate a category-determined dictionary from a common dictionary through the GMM model[45]. Gao proposed to simultaneously learn the category-determined dictionary and the shared dictionary and apply it to fine-grained image classification tasks[46]. The above-mentioned supervised dictionary learning methods are all methods based on vector space. Among the dictionary learning methods on the SPD manifold, most of the dictionary learning methods are unsupervised. Sivalingam proposed a Tensor Dictionary Learning algorithm based on Logdet divergence[47]. When training each type of dictionary, the inconsistency between this type of dictionary and other types of dictionaries is used as a regular term to learn a dictionary of discriminative category determination. The criterion used by Sivalingam to measure the coherence between two SPD matrices is the matrix inner product:

$$\begin{aligned} Q(X,Y)=\mathrm{tr}(XY),X,Y\in \mathrm{Sym}_{++}^{d} \end{aligned}$$

(6)

where $\mathrm{Sym}_{++}^{d}$ is d$\times$d symmetric positive definite matrix. The larger the Q(X, Y), the greater the continuity between X and Y. Hrandi learns both the dictionary and the classifier by minimizing the classification error[48]. In general, the supervised dictionary learning method on SPD manifold needs further research.

4 Domain adaption based on source dictionary regularized RKHS subspace learning

4.1 The framework of RKHS subspace learning

In the existing domain adaptive algorithms, many researchers will use the RKHS subspace learning framework to solve the domain discrepancy problem. The common RKHS subspace learning framework is to use the RKHS reproducing kernel to transform the data from the original data space to RKHS and then transform to a finite-dimensional RKHS subspace by the subspace projection and finally transform to the Euclidean space by the standard orthonormal basis of the subspace and isomorphic transformation. This paper also uses this framework.

Below, we will give the structure of the RKHS subspace, the constraints that must be met, and the data representation of the subspace dependence in the Euclidean space. The specific choice of RKHS subspace is open and can be determined according to the specific application of machine learning.

4.1.1 Construction and constraints of RKHS subspace

Let $(H,\langle \bullet ,\bullet \rangle )$ be the RKHS on the data space $\varOmega$, and use the reproducing kernel k of H to define the transformation from the data space $\varOmega$ to RKHS $H:\varphi :\varOmega \rightarrow H$, for any $x \in \varOmega$, $\varphi (x)=k(\bullet ,x)\in H$. For any x, y in $\varOmega$, $\langle \varphi (x),\varphi (y) \rangle =k(x,y)$

Give a dataset in the data space $\varOmega$

$$\begin{aligned} X=\left\{ x_{1},\cdots ,x_{N} \right\} \subseteq \varOmega \end{aligned}$$

(7)

Use $\varphi$ to transform X to H:

$$\begin{aligned} \phi (X)=\left\{ \varphi (x_{1}),\cdots ,\varphi (x_{N}) \right\} \subseteq H \end{aligned}$$

(8)

And we record K as

$$\begin{aligned} \begin{aligned} K&= \left[ {\begin{array}{*{20}{c}} {\left\langle \varphi (x_1),{\varphi ( x_1 )} \right\rangle }&{} \cdots &{}{\left\langle \varphi ( x_1 ),\varphi ( x_\mathrm{N} ) \right\rangle }\\ \vdots &{} \ddots &{} \vdots \\ {\left\langle \varphi ( x_\mathrm{N} ),\varphi ( x_1 ) \right\rangle }&{} \cdots &{}{\left\langle \varphi ( x_\mathrm{N} ),\varphi ( x_\mathrm{N} ) \right\rangle } \end{array}} \right] \\&=\left[ {\begin{array}{*{20}{c}} {k\left( {{x_1},{x_1}} \right) }&{} \cdots &{}{k\left( {{x_1},{x_\mathrm{N}}} \right) }\\ \vdots &{} \ddots &{} \vdots \\ {k\left( {{x_\mathrm{N}},{x_1}} \right) }&{} \cdots &{}{k\left( {{x_\mathrm{N}},{x_\mathrm{N}}} \right) } \end{array}} \right] \\&= \left[ {\begin{array}{*{20}{c}} {{K_{1Col}}}&\cdots&{{K_{\mathrm{NCol}}}} \end{array}} \right] \in {R^{N \times N}} \end{aligned} \end{aligned}$$

(9)

where $K_{\mathrm{iCol}}$ represents the $i^{th}$ column of $K,i=1,\dots ,N$.

Now, we use $\varphi \left( X \right)$ to structure a subspace of H, Let

$$\begin{aligned} {\theta _i} = \sum \limits _{j = 1}^N {{w_{j\mathrm{{i}}}}\varphi \left( {{x_j}} \right) } \;,i = 1, \cdots ,d \end{aligned}$$

(10)

And we denote W as

$$\begin{aligned} W=\begin{bmatrix} w_{11}&{}\cdots &{}w_{1d}\\ \vdots &{} \ddots &{} \vdots \\ w_{N1}&{} \cdots &{}w_{\mathrm{Nd}} \end{bmatrix} = \begin{bmatrix} {W_{1\mathrm{Col}}}&\cdots&{W_{\mathrm{dCol}}} \end{bmatrix} \in {R^{N \times d}} \end{aligned}$$

(11)

where $W_{iCol}$ represents the $i^{th}$ column of $W,i=1,\dots ,d$.

We use $\varTheta =\left\{ {{\theta _1}, \cdots ,{\theta _d}} \right\}$ to span a subspace of H

$$\begin{aligned} span\varTheta =\left\{ \sum ^{d}\limits _{i=1} \alpha _i\theta _i\Bigg |\alpha _i\in R ,i=1,\dots ,d \right\} \end{aligned}$$

We hope that $\varTheta$ constitutes the standard orthogonal basis of $span\theta$ and then

$$\begin{aligned} \begin{bmatrix} \left\langle {{\theta _1},{\theta _1}} \right\rangle &{} \cdots &{}{\left\langle {{\theta _1},{\theta _d}} \right\rangle }\\ \vdots &{} \ddots &{} \vdots \\ {\left\langle {{\theta _d},{\theta _1}} \right\rangle }&{} \cdots &{}{\left\langle {{\theta _d},{\theta _d}} \right\rangle } \end{bmatrix}={I_\mathrm{d}} \end{aligned}$$

(12)

For all

$$\begin{aligned} \begin{aligned} \left\langle {{\theta _i},{\theta _j}} \right\rangle&=\left\langle \sum ^{N}\limits _{p=1} w_{p\mathrm{{i}}}\varphi ({x_p}) ,\sum ^{N}\limits _{q=1} w_{q\mathrm{{i}}}\varphi ({x_q}) \right\rangle \\&=\sum ^{N}\limits _{p=1}\sum ^{N}\limits _{q=1}{w_{p\mathrm{{i}}}}{w_{q\mathrm{{i}}}}\left\langle {\varphi \left( {{x_p}}\right) ,\varphi \left( {{x_q}}\right) } \right\rangle \\&=\sum ^{N}\limits _{p=1}\sum ^{N}\limits _{q=1}{w_{p\mathrm{{i}}}}{w_{q\mathrm{{i}}}}k\left( x_p,x_q\right) =W^T_{iCol}KW_{jCol} \end{aligned} \end{aligned}$$

(13)

, we have

$$\begin{aligned} \begin{aligned} \begin{bmatrix} {\left\langle {{\theta _1},{\theta _1}} \right\rangle }&{} \cdots &{}{\left\langle {{\theta _1},{\theta _d}} \right\rangle }\\ \vdots &{} \ddots &{} \vdots \\ {\left\langle {{\theta _d},{\theta _1}} \right\rangle }&{} \cdots &{}{\left\langle {{\theta _d},{\theta _d}} \right\rangle } \end{bmatrix}&= \begin{bmatrix} {W_{1Col}^TK{W_{1Col}}}&{} \cdots &{}{W_{1Col}^TK{W_{dCol}}}\\ \vdots &{} \ddots &{} \vdots \\ {W_{dCol}^TK{W_{1Col}}}&{} \cdots &{}{W_{dCol}^TK{W_{dCol}}} \end{bmatrix}\\&=W^TK{W} = {I_d} \end{aligned} \end{aligned}$$

(14)

Obviously, the subspace $span\varTheta$ is a d-dimensional subspace and completely determined by the combinational coefficient W, and W must satisfy the above constraints.

4.1.2 Data representation of RKHS subspace

$$\begin{aligned} \begin{aligned} {y}&= \begin{bmatrix} {\left\langle {\varphi \left( {{x}} \right) ,{\theta _1}} \right\rangle }\\ \vdots \\ {\left\langle {\varphi \left( {{x}} \right) ,{\theta _d}} \right\rangle } \end{bmatrix} = \begin{bmatrix} \left\langle \varphi (x),\sum \limits _{j = 1}^N w_{j1}\varphi (x_j) \right\rangle \\ \vdots \\ \left\langle \varphi (x),\sum \limits _{j = 1}^N w_{jd}\varphi (x_j) \right\rangle \end{bmatrix}\\&= \begin{bmatrix} \sum \limits _{j = 1}^N w_{j1}\left\langle \varphi (x),\varphi (x_j)\right\rangle \\ \vdots \\ \sum \limits _{j = 1}^N w_{jd}\left\langle \varphi (x),\varphi (x_j)\right\rangle \end{bmatrix}\\&=\begin{bmatrix} {\sum \limits _{j = 1}^N {{w_{j1}}k\left( {{x},{x_j}} \right) } }\\ \vdots \\ {\sum \limits _{j = 1}^N {{w_{jd}}k\left( {{x},{x_j}} \right) } }\ \end{bmatrix} \end{aligned} \end{aligned}$$

According to the projected theorem, if $\left\{ \theta _1,\dots ,\theta _d\right\}$ is the standard orthogonal basis of the subspace $span\theta$ , the coordinate of $\varphi \left( x_i\right)$ projected on the subspace $span\theta$ is

$$\begin{aligned} \begin{aligned} {y_i} =\begin{bmatrix} {\sum \limits _{j = 1}^N {{w_{j1}}k\left( {{x_i},{x_j}} \right) } }\\ \vdots \\ {\sum \limits _{j = 1}^N {{w_{jd}}k\left( {{x_i},{x_j}} \right) } } \end{bmatrix} =\begin{bmatrix} {W^{T}_{1\mathrm{Col}}K_{\mathrm{iCol}} }\\ \vdots \\ {W^{T}_{\mathrm{dCol}}K_{\mathrm{iCol}} } \end{bmatrix} \end{aligned} \end{aligned}$$

(15)

where $i=1,\dots ,d$. Through the RKHS subspace, we realize the data transformation from the original data space $\varOmega$ to the European space $R^d$:

$$\begin{aligned} X=\left\{ x_1,\dots ,x_N\right\} \subseteq \varOmega \Rightarrow Y=\left\{ y_1,\dots ,y_N\right\} \in R^d \end{aligned}$$

(16)

The original data space $\varOmega$ can be varied according to the specific situation, e.g., European space, Riemannian Manifold, Grassmann Manifold, etc., but the working space is all European space $R^d$, where W will be determined according to the specific machine learning task.

4.2 Domain adaption based on RKHS subspace learning

This paper studies the domain adaptive problem. Given a source domain dataset and a target domain dataset in the original data

$$\begin{aligned} X_\mathrm{s}=\left\{ x^s_1,\dots ,x^s_{N_\mathrm{s}}\right\} \subseteq \varOmega \end{aligned}$$

(17)

where the source domain data $X_\mathrm{s}$ is labeled, and the labels of the unlabeled target domain data $X_\mathrm{t}$ need to be identified by the label of $X_\mathrm{s}$. However, the distribution of $X_\mathrm{s}$ and $X_\mathrm{t}$ in $\varOmega$ is different, and identifying directly on $\varOmega$ will inevitably cause a larger error.

The domain adaptive algorithm based on RKHS subspace learning transforms the source domain data and target domain data from the original data space to the RKHS subspace, and through subspace learning, the distribution of source domain data and target domain data can converge after transforming from the original data space to RKHS subspace.

Let

$$\begin{aligned} X=X_6\cup X_6=\left\{ x_1,\dots ,x_\mathrm{N}\right\} =\left\{ x_1^s,\dots ,x_{N_\mathrm{s}}^s,x_1^t,\dots ,x_{N_\mathrm{t}}^t\right\} \subseteq \varOmega , N=N_\mathrm{s}+N_\mathrm{t} \end{aligned}$$

Using the RKHS subspace learning framework proposed in Section 4.1, we have

$$\begin{aligned} Y_\mathrm{s}=\left\{ y^s_1,\dots ,y^s_{N_\mathrm{s}}\right\} \subseteq R^d ,y^s_i=W^\mathrm{TK}_{\mathrm{iCol}}, i=1,\dots ,N_\mathrm{s} \end{aligned}$$

$$\begin{aligned} Y_\mathrm{t}=\left\{ y^t_1,\dots ,y^t_{N_\mathrm{t}}\right\} \subseteq R^d ,y^t_j=W^\mathrm{TK}_{\left( N_\mathrm{s}+j\right) \mathrm{Col}}, j=1,\dots ,N_\mathrm{t} \end{aligned}$$

In the expressions of $Y_\mathrm{s}$ and $Y_\mathrm{t}$, the matrix W is unknown and represents the RKHS subspace. Through the learning of W, $Y_\mathrm{s}$ and $Y_\mathrm{t}$ are converged in the distribution of Euclidean space $R^d$. How to measure the convergence of the distribution? The common criterion is the maximum mean difference (MMD) criterion:

$$\begin{aligned} \mathop {\mathrm{arg}\ \mathrm{min}}\limits _{W} \left\| \frac{1}{N_\mathrm{s}}\sum \limits _{i=1}^{N_\mathrm{s}}W^\mathrm{TK}_{\mathrm{iCol}}-\frac{1}{N_\mathrm{t}}\sum \limits _{j=1}^{N_\mathrm{t}}W^\mathrm{TK}_{(N_\mathrm{s}+j)\mathrm{Col}}\right\| ^2 \end{aligned}$$

(18)

4.3 Domain adaption based on source dictionary regularized RKHS subspace learning (SDRKHS-DA)

4.3.1 Dictionary learning

Given a source domain dataset and a target domain dataset in the original data space $\varOmega$:

$$\begin{aligned} X_\mathrm{s}=\left\{ x^s_1,\dots ,x^s_{N_\mathrm{s}}\right\} \subseteq \varOmega , X_\mathrm{t}=\left\{ x^t_1,\dots ,x^t_{N_\mathrm{t}}\right\} \subseteq \varOmega \end{aligned}$$

We hope to use the source domain data $X_\mathrm{s}$ as a dictionary, and the data $X_\mathrm{t}$ as a training sample. The training sample will be linearly represented by a dictionary. The linear representation is expressed as z. In the process of dictionary learning, we need to learn the coding coefficients z. We hope that each target domain data can be obtained by a suitable linear representation of the original data. At the same time, we hope that the coding coefficients are sparse, i.e., the target domain data can only be derived from a few source domains. In terms of data, this can force the model to learn the relationship between the target domain data and the source domain data as much as possible and select the source domain data most relevant to the target domain, so the L1 regularity is used for the coding coefficients. The model of dictionary learning is as follows

$$\begin{aligned} \mathrm{DIC}^2\left( X_\mathrm{s},X_\mathrm{t}\right) =\mathop {\mathrm{arg}\ \mathrm{min}}\limits _{z}\sum \limits _{j=1}^{N_\mathrm{t}}\left\| y^t_j -\sum \limits _{i=1}^{N_\mathrm{s}} y^s_iz_{ij}\right\| ^2+\lambda \sum \limits _{j=1}^{N_\mathrm{t}}\left\| z_j\right\| _1 \end{aligned}$$

(19)

4.3.2 Modeling

As mentioned in 4.1, we use the RKHS regeneration kernel to transform the data from the original data space to RKHS and then transform to a finite-dimensional RKHS subspace by subspace projection and finally transform to the Euclidean space by the subspace standard orthogonal basis and isomorphic transformation. In the selection of subspace, this paper adopts MMD most commonly used in domain adaptation, which is to minimize the mean difference between the source domain and target domain data, to reduce the distribution difference between them. And based on the above, this paper proposes a novel regular term, i.e., the source domain dictionary regularization, which constitutes a new RKHS subspace learning method based on the source domain dictionary regularization. This method aims to learn the relationship between the source domain data and the target domain data by the model so that the target domain data can be represented by the few most relevant source domain. Our model is as follows:

$$\begin{aligned} \begin{aligned}&\mathop {arg}\, \mathop {\mathrm{min}}\limits _{W,z} \left\| \frac{1}{N_\mathrm{s}}\sum \limits _{i=1}^{N_\mathrm{s}}{y^s_i}-\frac{1}{N_\mathrm{t}}\sum \limits _{j=1}^{N_\mathrm{t}}{y^t_j}\right\| ^2 +\eta \sum \limits _{j=1}^{N_t}{\left\| y^t_j - \sum \limits _{i=1}^{N_\mathrm{s}}{y^s_i z_{ij}}\right\| ^2}\\&\quad +\lambda \sum \limits _{j=1}^{N_\mathrm{t}}{\left\| z_j\right\| _1}+\mu \left\| W\right\| _2 \end{aligned} \end{aligned}$$

(20)

$y^s$ is the source domain data, $y^t$ is the target domain data, and W is the projection matrix. z is the coding coefficient, that is, the linear representation of the source domain data mentioned above. The first part of the model is MMD, and the second is the source domain dictionary criterion. $\left\| z\right\| _1$ controls the sparsity of z, and $\left\| W\right\| _2$ is used to control the complexity of W.

4.3.3 Objective function

Our model is available through section 4.3.1.

For $\left\| \frac{1}{N_s}\sum \limits _{i = 1}^{N_\mathrm{s}} {y_i^s} - \frac{1}{N_\mathrm{t}}\sum \limits _{j = 1}^{N_\mathrm{t}} {y_j^t} \right\| ^2$ , we get

$$\begin{aligned} \begin{aligned} \left\| \frac{1}{N_\mathrm{s}}\sum \limits _{i = 1}^{{N_\mathrm{s}}} {y_i^s} - \frac{1}{N_\mathrm{t}}\sum \limits _{j = 1}^{N_\mathrm{t}} {y_j^t} \right\| ^2&= \left\| \frac{1}{N_s}\sum \limits _{i = 1}^{N_s} {{W^T}{K_{\mathrm{iCol}}}} - \frac{1}{N_\mathrm{t}}\sum \limits _{j=1}^{N_{\mathrm{t}}} {{W^T}{K_{(N_\mathrm{s}+j)\mathrm{Col}}}} \right\| ^2 \\&=tr\left( W^\mathrm{TKLKW}\right) \end{aligned} \end{aligned}$$

(21)

where

$$\begin{aligned} \varGamma _s= & {} \begin{bmatrix} \frac{1}{N_\mathrm{s}}\\ \vdots \\ \frac{1}{N_\mathrm{s}}\\ 0\\ \vdots \\ 0 \end{bmatrix}\in R^{N_\mathrm{s} + N_\mathrm{t}}\quad \varGamma _t= \begin{bmatrix} \frac{1}{N_\mathrm{t}}\\ \vdots \\ \frac{1}{N_\mathrm{t}}\\ 0\\ \vdots \\ 0 \end{bmatrix}\in R^{N_\mathrm{s} + N_\mathrm{t}}\quad \varGamma =\varGamma _s -\varGamma _t\nonumber \\ {{K_s}}= & {} \left[ {\begin{array}{*{20}{c}} {{k}\left( {{x_1^s},{x_1^s}} \right) }&{} \cdots &{}{{k}\left( {{x_1^s},{x_N^s}} \right) }\\ \vdots &{} \ddots &{} \vdots \\ {{k}\left( {{x_N^s},{x_1^s}} \right) }&{} \cdots &{}{{k}\left( {{x_N^s},{x_N^s}} \right) } \end{array}} \right] {{K_{st}}}\mathrm{{ = }}\left[ {\begin{array}{*{20}{c}} {{k}\left( {{x_1^s},{x_1^t}} \right) }&{} \cdots &{}{{k}\left( {{x_1^s},{x_N^t}} \right) }\\ \vdots &{} \ddots &{} \vdots \\ {{k}\left( {{x_N^s},{x_1^t}} \right) }&{} \cdots &{}{{k}\left( {{x_N^s},{x_N^t}} \right) } \end{array}} \right] \nonumber \\ {{K_{ts}}}= & {} \left[ {\begin{array}{*{20}{c}} {{k}\left( {{x_1^t},{x_1^s}} \right) }&{} \cdots &{}{{k}\left( {{x_1^t},{x_N^s}} \right) }\\ \vdots &{} \ddots &{} \vdots \\ {{k}\left( {{x_N^t},{x_1^s}} \right) }&{} \cdots &{}{{k}\left( {{x_N^t},{x_N^s}} \right) } \end{array}} \right] {{K_t}}\mathrm{{ = }}\left[ {\begin{array}{*{20}{c}} {{k}\left( {{x_1^t},{x_1^t}} \right) }&{} \cdots &{}{{k}\left( {{x_1^t},{x_N^t}} \right) }\\ \vdots &{} \ddots &{} \vdots \\ {{k}\left( {{x_N^t},{x_1^t}} \right) }&{} \cdots &{}{{k}\left( {{x_N^t},{x_N^t}} \right) } \end{array}} \right] \nonumber \\ K= & {} \begin{bmatrix} {K_\mathrm{s}}&{}{K_{\mathrm{st}}}\\ {K_{\mathrm{ts}}}&{}{K_{t}} \end{bmatrix}, L=I_\mathrm{N}-\frac{1}{N}\varGamma _{N}\varGamma _{N}^{T} \end{aligned}$$

(22)

For $\sum \limits _{j=1}^{N_t}{\left\| y^t_j - \sum \limits _{i=1}^{N_s}{y^s_i z_{ij}}\right\| }^2 +\lambda \sum \limits _{j=1}^{N_t}{\left\| z_j\right\| _1}$, we get

$$\begin{aligned} \begin{aligned}&\sum \limits _{j=1}^{N_\mathrm{t}}\left\| y^t_j - \sum \limits _{i=1}^{N_\mathrm{s}}{y^s_i z_{ij}}\right\| ^2 +\lambda \sum \limits _{j=1}^{N_\mathrm{t}}{\left\| z_j\right\| _1}\\&\quad =\sum \limits _{j=1}^{N_t}\left\| W^T\left( K_{\left( N_s+j\right) \mathrm{Col}}-\sum \limits _{i=1}^{N_\mathrm{s}}{K_{\mathrm{iCol}}z_{ij}}\right) \right\| ^2+\lambda \sum \limits _{j=1}^{N_\mathrm{t}}{\left\| z_j\right\| _1}\\&\quad =tr\left( W^T\left( \sum \limits _{j}\left( K_{\left( N_s+j \right) \mathrm{Col}}-\sum \limits _{i=1}^{N_s}{K_{\mathrm{iCol}}z_{ij}} \right) \left( K_{\left( N_s+j \right) \mathrm{Col}}\right. \right. \right. \\&\qquad \left. \left. \left. -\sum \limits _{i=1}^{N_\mathrm{s}}{K_{\mathrm{iCol}}z_{ij}}\right) ^T\right) W\right) +\lambda \sum \limits _{j=1}^{N_\mathrm{t}}{\left\| z_j\right\| _1}\\&\quad =\mathrm{tr}\left( W^T\varPhi W\right) +\lambda \sum \limits _{j=1}^{N_t}{\left\| z_j\right\| _1} \end{aligned} \end{aligned}$$

where $\varPhi =\sum \limits _{j}(K_{(N_\mathrm{s}+j)\mathrm{Col}}-\sum \limits _{i=1}^{N_\mathrm{s}}{K_{\mathrm{iCol}}z_{ij}} ) (K_{(N_\mathrm{s}+j)\mathrm{Col}}-\sum \limits _{i=1}^{N_\mathrm{s}}{K_{\mathrm{iCol}}z_{ij}})^T$

We hope to use dictionary learning as regular terms for the target domain data distribution to approach the source domain. Therefore, our final objective function is as follows:

$$\begin{aligned}&\mathop {arg}\, \mathop {min}\limits _{W,z} \mathrm{tr}\left( W^\mathrm{TKLKW}\right) +\eta tr\left( W^T\varPhi W\right) +\lambda \sum \limits _{j=1}^{N_t}{\left\| z_j\right\| _1}+\mu tr\left( W^\mathrm{TW}\right) \nonumber \\&\quad Subject\ to\ W^\mathrm{TKW}=I_\mathrm{d} \end{aligned}$$

(23)

4.4 Solution to SDRKHS-DA

For SDRKHS-DA , the idea of dictionary learning needs to be applied to domain adaptation. Therefore, we need to optimize the projection matrix W and coding coefficients z in the final objective function. The iterative alternate optimization strategy is commonly used. Each round is divided into the update of the projection matrix W and the update of the coding coefficients z.

4.4.1 Solution to W

In the process of updating the projected matrix W, we first fix the value of the coding coefficient, and the problem becomes an ordinary problem of solving the projected matrix W. The objective function of the projected matrix W update is

$$\begin{aligned} \begin{aligned}&\mathop {min}\limits _{W} \mathrm{tr}\left( W^TKLKW\right) +tr\left( W^T\varPhi W\right) \\&\quad =\mathop {min}\limits _{W} tr\left( W^TK^{1/2}K^{1/2}\mathrm{LK}^{1/2}K^{1/2}W\right) +\mathrm{tr}\left( W^TK^{1/2}K^{-1/2}\varPhi K^{-1/2}K^{1/2} W\right) \\&\quad \mathop {=}\limits _{V=k^{1/2}W}\mathop {min}\limits _{W} \mathrm{tr}\left( V^TK^{1/2}LK^{1/2}V\right) + \mathrm{tr}\left( V^TK^{-1/2}\varPhi K^{-1/2}V\right) \end{aligned} \end{aligned}$$

Similarly, $W^TKW=W^TK^{1/2}K^{1/2}W\mathop {=}\limits _{V=k^{1/2}W}V^TV=I_\mathrm{d}$

Then,

$$\begin{aligned} \begin{aligned}&\mathop {min}\limits _{W} tr\left( V^TK^{1/2}LK^{1/2}V\right) + tr\left( V^TK^{-1/2}\varPhi K^{-1/2}V\right) \\&\quad =\mathop {min}\limits _{W} tr\left( V^T\left( K^{1/2}LK^{1/2}+K^{-1/2}\varPhi K^{-1/2}\right) V\right) \\&\quad =\mathop {min}\limits _{W}tr\left( V^T\varTheta V\right) \\&\quad V^TV=I_\mathrm{d} \end{aligned} \end{aligned}$$

(24)

We use the Rayleigh entropy to solve and perform eigenvalue decomposition of $K^{1/2}LK^{1/2}+K^{-1/2}\varPhi K^{-1/2}$. The eigenvector of the first d dimension can be taken as the projected matrix W.

4.4.2 Solution to z

In updating the coding coefficients z, we first fix the value of the projection matrix W, and the problem becomes the most primitive sparse coding problem. The objective function for updating the coding result is

$$\begin{aligned} \begin{aligned}&\mathop {min}\limits _{W} {\left\| W^TK_{j\mathrm{Col}}-\sum \limits _{i=1}^{N_\mathrm{s}}{W^TK_{i\mathrm{Col}}z_{ij}}\right\| }+{\left\| z_j\right\| _1}\\&\quad =\mathop {min}\limits _{W} \left( W^TK_{j\mathrm{Col}}-\sum \limits _{i=1}^{N_\mathrm{s}}{W^TK_{i\mathrm{Col}}z_{ij}}\right) ^T\left( W^TK_{jCol}-\sum \limits _{i=1}^{N_\mathrm{s}}{W^TK_{i\mathrm{Col}}z_{ij}}\right) +{\left\| z_j\right\| _1}\\&\quad =\mathop {min}\limits _{W}K_{j\mathrm{Col}}^TWW^TK_{jCol}+\sum \limits _{i=1}^{N_\mathrm{s}}{K_{jCol}^TWW^TK_{i\mathrm{Col}}z_{ij}} +\sum \limits _{i=1}^{N_\mathrm{s}}{z_{ij}^TK_{i\mathrm{Col}}^TWW^TK_{j\mathrm{Col}}}\\&\qquad +\sum \limits _{i=1}^{N_\mathrm{s}}\sum \limits _{p=1}^{N_\mathrm{s}}{z_{ij}^TK_{i\mathrm{Col}}^TWW^TK_{p\mathrm{Col}}z_{pj}}+{\left\| z_j\right\| _1} \end{aligned} \end{aligned}$$

(25)

The above problem is a typical Lasso optimization problem, and SPAMS[49] and CVX[50] toolboxes can quickly solve this problem.

The pseudo-code for solving the projected matrix is shown in Algorithm 1.

Algorithm 1
Input: source domain data sample${X_\mathrm{s}}$ and target domain data sample${X_t}$
Output: the projection matrix W
1. Calculation matrix: K and $C_\mathrm{N}$, randomly initialize coding coefficients z;
2. Calculate matrix $\varPhi$ by coding coefficient;
3. Perform eigenvalue decomposition on $K^{1/2}LK^{1/2}+K^{-1/2}\varPhi K^{-1/2}$, and take
the d eigenvectors corresponding to the first d largest eigenvalues to form $W^T$;
4. Solve coding coefficients z by mexlasso;
5. Iteratively solve steps 3 and 4, and stop iterating until the loss value
is less than the set threshold;
6. Get the projection matrix W.

4.5 Complexity analysis

We use $O_1$ and $O_2$ to represent our time complexity and space complexity. In the algorithm, we need to update the parameter W through SVD algorithm. For each SVD algorithm, the time complexity is $O_1\left( N^3\right)$ and the space complexity is $O_2\left( N^2\right)$, $N=N_s+N_t$; then, the sparse matrix Z is updated through mexlasso, the time complexity is $O_1\left( N^4\right)$, and the space complexity is $O_2\left( N^2\right)$; at the same time, the parameter $\varPhi$ needs to be updated. The time complexity of the update process is $O_1\left( N_sN_t\right)$, and the space complexity is $O_2\left( N+N_tN\right)$. If the number of the algorithm update iterations is k, then the time complexity of our algorithm is $O_1\left( k\left( N^4+N^3+N_\mathrm{s}N_\mathrm{t}\right) \right) =O_1\left( kN^4\right)$, and the space complexity is $O_2\left( k\left( N^2+N^2+N+N_\mathrm{t}N\right) \right) =O_2\left( kN^2\right)$.

5 Comparison to other related state-of-the-art algorithm

In this chapter, we will introduce 5 state-of-the-art algorithms related to the algorithm proposed in the paper. These five algorithms all use subspace learning methods to solve the domain adaptation problem, and they all have their own advantages and disadvantages in domain adaptation. This chapter mainly elaborates the theoretical difference between the algorithm proposed in this paper and the comparison algorithm, and the difference in experimental effects will be explained in the next chapter.

5.1 Comparison to TCA

The model of TCA[15] is as follows:

$$\begin{aligned}&\mathop {min}\limits _{W} {\left\| \frac{1}{N_\mathrm{s}}\sum \limits _{i=1}^{N_\mathrm{s}}W^TK_{i\mathrm{Col}}-\frac{1}{N_\mathrm{t}}\sum \limits _{j=1}^{N_\mathrm{t}}W^TK_{\left( N_\mathrm{s}+j\right) \mathrm{Col}}\right\| ^2}+\mu {\left\| W\right\| ^2_2}\\&\quad s.t. W^TKHKW=I_\mathrm{d} \end{aligned}$$

where W is the projected matrix and K is kernel matrix. $K_{i\mathrm{Col}}$ represents the ith column of K. TCA uses MMD as the criterion of domain adaptation and maps the data to RKHS through a kernel function and then maps the data to the RKHS subspace through a projection matrix. In the process of constructing the subspace, the distance between the source domain data and the target domain data is required to be minimized. $\left\| W\right\| ^2_2$ controls the complexity of W. The role of $W^TKHKW=I_\mathrm{d}$ is to maximize the variance of the mapped data, which helps to retain the attributes useful for classification tasks.

The main difference between SDRKHS-DA algorithm and TCA algorithm is that SDRKHS-DA algorithm adds source domain dictionary regularization on the basis of TCA. The SDRKHS-DA algorithm adopts the source domain dictionary regularization, so that the spatial distribution of the source domain data and the target domain data in the same category in the subspace overlaps as much as possible.

5.2 Comparison to SSTCA

SSTCA[15] adds the optimization term of manifold regularization on the basis of TCA, and its model is:

$$\begin{aligned} \begin{aligned}&\mathop {min}\limits _{W} {\left\| \frac{1}{N_\mathrm{s}}\sum \limits _{i=1}^{N_s}W^TK_{i\mathrm{Col}}-\frac{1}{N_t}\sum \limits _{j=1}^{N_t}W^TK_{\left( N_s+j\right) Col}\right\| ^2}\\&\quad +\frac{\lambda }{N^2}\sum \limits _{j,l=1}^{N}{\left\| W^TK_{j\mathrm{Col}}-W^TK_{lCol}\right\| P_{jl}}+\mu {\left\| W\right\| ^2_2}&\qquad s.t. W^TKH\tilde{k}_{\mathrm{yy}}\mathrm{HKW}=I \end{aligned} \end{aligned}$$

SSTCA has made some improvements on the basis of TCA, in which $W^TKH\tilde{k}_{\mathrm{yy}}\mathrm{HKW}=I$ uses HSIC to enhance the correlation between labels and data; $\sum \limits _{j,l=1}^{N}{\left\| W^TK_{j\mathrm{Col}}-W^TK_{l\mathrm{Col}}\right\| P_{jl}}$ is a manifold regular term that retains the geometric structure of the data.

The difference between the SDRKHS-DA algorithm and the SSTCA algorithm is that SSTCA uses a manifold regular, and it hopes that all data mapped to the subspace are as close as possible. The source domain dictionary is combined with the idea of linear discrimination, and it is hoped that the spatial distribution of the source domain data and the target domain data in the same category in the subspace overlaps as much as possible.

5.3 Comparison to TIT

TIT[51] obtained pseudo-labels through multiple experiments to improve the final accuracy rate. Its model is:

$$\begin{aligned} \begin{aligned}&\mathop {min}\limits _{W} {\left\| \frac{1}{N_\mathrm{s}}\sum \limits _{i=1}^{N_\mathrm{s}}W^TK_{i\mathrm{Col}}-\frac{1}{N_\mathrm{t}}\sum \limits _{j=1}^{N_t}W^TK_{\left( N_s+j\right) Col}\right\| ^2}\\&\quad +\frac{1}{2}\lambda \sum \limits _{j,l=1}^{N}\left\| W^TK_{j\mathrm{Col}}-W^TK_{l\mathrm{Col}}\right\| ^2P_{jl} +\beta \left\| K_\mathrm{t}-W_tW_t^TK_\mathrm{t}\right\| ^2_F+\mu {\left\| W\right\| _{2,1}}&\qquad s.t. W^TKHKW=I_\mathrm{d} \end{aligned} \end{aligned}$$

where W is the projected matrix, $K_\mathrm{t}$ represents the target domain data on RKHS, and $W_\mathrm{t}$ is the projected matrix of $K_\mathrm{t}$. The TIT model is the same as the previous models, using MMD as the domain adaptation criterion, and also using manifold regularization to preserve the geometric structure of the data. But this model $\left\| W\right\| _{2,1}$ uses in the construction subspace, which means that the elements of W are as sparse as possible.

TIT has one more regular term on the basis of SSTCA. The function of the regular term $\left\| K_t-W_tW_t^TK_t\right\| ^2_F$ is similar to the PCA algorithm. If KNN is used as the classifier, the regular term has no effect. Compared with TIT, SDRKHS-DA maps both the source domain and target domain data to the same subspace, so that the target domain data are distributed around the linearly related source domain data, which is theoretically better than TIT.

5.4 Comparison to IGLDA

The IGLDA[16] model is as follows:

$$\begin{aligned} \begin{aligned}&\mathop {min}\limits _{W} {\left\| \frac{1}{N_\mathrm{s}}\sum \limits _{i=1}^{N_s}W^TK_{i\mathrm{Col}}-\frac{1}{N_\mathrm{t}}\sum \limits _{j=1}^{N_\mathrm{t}}W^TK_{\left( N_\mathrm{s}+j\right) \mathrm{Col}}\right\| ^2}\\&\quad +\mu {\left\| W\right\| ^2_2}+\frac{1}{c}\sum \limits _{l=1}^{c}{\frac{2}{N_l(N_l-1)}}\sum \limits _{i=1}^{N_l}\sum \limits _{j=i+1}^{N_l}\left\| W^TK^s_{l_i\mathrm{Col}}-W^TK^s_{l_j}\mathrm{Col}\right\|&\qquad s.t. W^TKHKW=I_\mathrm{d} \end{aligned} \end{aligned}$$

where is the number of categories and is the number of data in each category. It can be seen from the above model that IGLDA is similar to TCA. IGLDA uses MMD as the domain adaptation criterion, and $\left\| W\right\| ^2_2$ controls the complexity of W. $W^TKHKW=I_\mathrm{d}$ maximizes the variance of the mapped data.

The difference between SDRKHS-DA and IGLDA is the regular terms used by the two algorithms. The regular term used by IGLDA is similar to the inter-class divergence of the source domain data, but it does not require the distance between the source domain data of different categories as far as possible, which may lead to misjudgment of the label of the target domain data. The source domain dictionary is combined with the idea of linear discrimination, and it is hoped that the target domain data can be distributed around the source domain data that is linearly related to it. In general, the strongest linear correlation is the data of the same category, so the source domain dictionary regularization can improve the classification accuracy.

5.5 Comparison to GSL

The model of GSL[52] is as follows:

$$\begin{aligned} \begin{aligned}&\mathop {min}\limits _{W_\mathrm{s},W_\mathrm{t},M,Z} \beta \left\| W_\mathrm{s}-W_\mathrm{t}\right\| ^2_F+\left\| W_\mathrm{t}^TX_\mathrm{t}-W_\mathrm{s}^TX_\mathrm{s}Z\right\| ^2_F +\lambda \left\| Z\right\| _*+\left\| W_t^TX-\hat{Y}\circ M\right\| ^2_F&\quad s.t. M \ge 0 \end{aligned} \end{aligned}$$

The GSL model maps the source domain data and target domain data to two different subspaces through two different projection matrices. And Z is used to solve the problem that the number of source domain data and target domain data is not equal, so that the source domain data and target domain data projected to the subspace are closer. This paper hopes that the learning of the subspace $W_\mathrm{s}$ of the source domain can guide the learning of the subspace $W_\mathrm{t}$ of the target domain, so it is achieved by minimizing the Bregmans divergence between $W_\mathrm{s}$ and $W_\mathrm{t}$. And $\left\| W_\mathrm{t}^TX-\hat{Y}\circ M\right\| ^2_F$ plays the role of training a classifier.

The difference between the SDRKHS-DA and GSL algorithms is that, first, the GSL algorithm does not look for a subspace on RKHS, but for a subspace on the original space. SDRKHS-DA searches for a subspace on RKHS and maps the data to the subspace. Second, the $\left\| W_t^TX_\mathrm{t}-W_\mathrm{s}^TX_\mathrm{s}Z\right\| ^2_F$ used in the GSL algorithm and the source domain dictionary regularity proposed in this article both use source domain data to approximate the target domain data, but the GSL algorithm does not require z to be sparse. And the literature of GSL algorithm does not mention that it is dictionary learning. From the point of view of mathematical formula, this algorithm is similar to the source domain dictionary regularity proposed in this paper, so this paper adopts GSL as one of the comparison algorithms.

6 Experimental results

This paper uses SDRKHS-DA algorithm to train and predict classification tasks on five standard datasets, including face data, handwritten digital data, and text data. This article compares SDRKHS-DA with the TCA, SSTCA, IGLDA, TIT, GSL algorithms mentioned in the article and verifies the effectiveness of SDRKHS-DA.

6.1 Face classification on AR dataset

In this experiment, AR Face Database is used for face recognition. There are more than 4000 colored frontal face images in the AR Face Database, involving 126 people, including 70 men and 56 women. We select a subset of AR Face Database which contains 2600 face pictures, involving 100 people, including 50 men and 50 women. Each identity has 26 pictures that were collected from two samplings at a two-week interval. During each sampling, 13 pictures in different modes were collected according to different light brightness, light angle, facial expression, and partial occlusion. During the preprocessing stage, each face image is organized into a 43$\times$60 pixel gray image, and the vectorized gray value of the image is directly used as the training set and test set without any additional preprocessing. According to different sampling and condition, each person’s 26 face pictures correspond to 26 modes, numbered as 1.a-1.m and 2.a-2.m, respectively. Figure1 depicts some examples of the organized gray pictures in AR Face Database, showing 26 face pictures of one person. The first and the second row is the pictures taken during two samplings, respectively. (Fig. 2)

Mode 1.a and 2.a are the natural expressions. In this experiment, we combine mode 1.a and 2.a into one domain as the source domain dataset and use mode 1.b-1.j and 2.b-2.j from the rest as the target domain dataset. We totally set up 18 tasks according to the different target domain. For each experiment of each task, all source domain data are used as the training set, and the target domain data are used as the test set. The SDRKHS-DA algorithm and the comparison algorithm are used to train on the training set to obtain the low-dimensional representation in the subspace of the training set. The training set data and the test set data are, respectively, multiplied by the low-dimensional representation to obtain the training data and the test data after dimensionality reduction. This experiment uses SVM as the classifier and trains the SVM model based on the low-dimensional representation of the training set data and its labels. The SVM model predicts the low-dimensional representation of the test set. The same experiment was repeated 20 times. SDRKHS-DA algorithm parameter settings: $\mu =1$, $\lambda =0.001$, $\eta =1$. The kernel function uniformly uses linear kernels. The subspace projection dimension is 90.

Fig. 1

Example of AR dataset

Table 2 Classification accuracy of different target domains(%)

The experimental results are shown in Table 2. The bolded data in the table mark the best results in each target domain. According to the results of the table, the algorithms with the highest accuracy in different target domains are not the same, but the average classification accuracy of SDRKHS-DA is the highest. Compared with TCA, SSTCA, IGLDA, TIT, and GSL, SDRKHS-DA has 5.5%, 5.73%, 15.34%, 1.12%, and 11.76% improvement in average classification accuracy, respectively. In the classification accuracy of specific tasks, some algorithms are higher than SDRKHS-DA, but SDRKHS-DA algorithm is the best in most tasks. It can be seen that the SDRKHS-DA algorithm has the highest accuracy in the target domain of 1.b, 1.c, 2.b, and 2.c compared to other algorithms. We believe that the four target domains are not very different from the source domain data. Therefore, when the source domain data are used as a dictionary, the model can learn the characteristics of the source domain data well, so that the edge distribution of the target domain data is close to the source domain data. In the 1.h-1.j and 2.h-2.j target domains, the TIT algorithm and the SDRKHS-DA algorithm have similar effects, and the two algorithms are the best. We consider that the reason is that TIT retains the geometric structure of the target domain data on RKHS in the process of constructing the subspace, so that the classification accuracy of these target domains is greatly improved compared with other algorithms. The SDRKHS-DA algorithm chooses 1.a and 2.a as the dictionary. From the point of view of image pixels, the target domain 1.h-1.j, 2.h-2.j is not very different from the dictionary. Only the pixels at the position of the glasses and the brightness of the lower right corner of the picture are different, which makes the model learn better features and makes the classification accuracy better.

Next, we study the effects of our proposed algorithm in different dimensions. In the experiment to study the influence of different dimensions, we choose 2.i as the target domain. The dimensions are set to 30, 50, 70, 90, 110, 130, 150 in 7 dimensions. We do 10 experiments in each dimension, for a total of 70 experiments. From Table 3, we can see that as the dimension increases, the accuracy of the comparison algorithm first increases and then decreases, while the accuracy of SDRKHS-DA will not change after 50 dimensions. It can be seen that our algorithm has good stability and is suitable for different dimensions. And the accuracy rate is also the highest in different dimensions

Table 3 Classification accuracy of different dimensions in the target domain 2.i(%)

6.2 Face classification on ORL dataset

The ORL face database consists of a series of face images taken by the laboratory from 1992 to 1994. There are 40 objects of different ages, genders, and races. Each person has 10 images, a total of 400 grayscale images, the image size is 92$\times$112, and the image background is black. There are changes in facial expressions and details, such as smiling or not, eyes open or closed, and wearing or not wearing glasses, and the posture of the face also changes. The depth rotation and plane rotation can reach 20 degrees. The size can also vary by up to 10%. We processed the pictures of the ORL dataset into a size of 32$\times$32 and marked photographs with 10 patterns for each person as 1.a-1.j. In this experiment, we use 1.a and 1.b as the source domain data, and the remaining 8 patterns as 8 domains, respectively, as the target domain dataset. Therefore, a total of 8 tasks are set up according to the different target domains. For each experiment of each task, we use a total of 80 photographs in 1.a and 1.b as the training set, and the remaining 40 photographs in each domain as the test set. The SDRKHS-DA algorithm and the comparison algorithm are used to train on the training set to obtain the low-dimensional representation in the subspace of the training set. The training set data and the test set data are, respectively, multiplied by the low-dimensional representation to obtain the training data and the test data after dimensionality reduction. This experiment uses SVM as the classifier and trains the SVM model based on the low-dimensional representation of the training set data and its labels. The SVM model predicts the low-dimensional representation of the test set. The same experiment was repeated 20 times. SDRKHS-DA algorithm parameter settings: $\mu =1$, $\lambda =0.001$, $\eta =1$. The kernel function uniformly uses linear kernels. The subspace projection dimension is 30.

Table 4 Classification accuracy of different target domains(%)

Fig. 2

Classification effect diagram of different algorithms on ORL dataset

The experimental results are shown in Table 4. The bolded data in the table mark the best results in each target domain. According to the results of the table, the algorithms with the highest accuracy in different target domains are not the same, but the average classification accuracy of SDRKHS-DA is the highest. Compared with TCA, SSTCA, IGLDA, TIT, and GSL, SDRKHS-DA has an improvement of 0.4%, 4.81%, 4.68%, 1.31%, and 2.81% in average classification accuracy, respectively. In terms of the classification accuracy of specific tasks, SDRKHS-DA algorithm is the best among 5 tasks. In tasks 1.g, 1.h, and 1.e, the classification effect of TCA, TIT, and GSL algorithms is the best, respectively.

Next, we study the effects of our proposed algorithm in different dimensions. In the experiment to study the influence of different dimensions, we choose 1.j as the target domain. The dimensions are set to 5, 10, 15, 20, 25, and 30 in 6 dimensions. We do 10 experiments in each dimension, for a total of 60 experiments. From Table 5, we can see that as the dimensions increase, the accuracy of the comparison algorithm first increases and then decreases, while the accuracy of SDRKHS-DA will not change after 20 dimensions. It can be seen that our algorithm has good stability. In the 5-15 dimension, SDRKHS-DA is less effective than other algorithms, which may be because the data are seriously distorted when the dimension is too low. The target domain cannot find a more suitable source domain to represent it, which reduces the accuracy.

Table 5 Classification accuracy of different dimensions in the target domain 1.j(%)

6.3 Face classification on YALE dataset

This section uses the YALE face dataset for classification experiments. The YALE dataset has a total of 165 face color pictures, involving 15 people, and each person has 11 pictures of different modes. The 11 modes are center light, with glasses, happy, left light, without glasses, normal, right light, sadness, drowsiness, surprise, and blink, marked as 1.a-1.k. In this experiment, we use central light and glasses as the source domain data, and the remaining 9 modes are, respectively, regarded as 9 domains as the target domain dataset. So according to the different target domains, a total of 9 tasks are set up. For each experiment of each task, we use a total of 30 photographs in 1.a and 1.b as the training set, and 15 photographs in each domain as the test set. The SDRKHS-DA algorithm and the comparison algorithm are used to train on the training set to obtain the low-dimensional representation in the subspace of the training set. The training set data and the test set data are, respectively, multiplied by the low-dimensional representation to obtain the training data and the test data after dimensionality reduction. This experiment uses SVM as the classifier and trains the SVM model based on the low-dimensional representation of the training set data and its labels. The SVM model predicts the low-dimensional representation of the test set. The same experiment was repeated 20 times. SDRKHS-DA algorithm parameter settings: $\mu =1$, $\lambda =0.001$, $\eta =1$. The kernel function uniformly uses linear kernels. The subspace projection dimension is 30.

Table 6 Classification accuracy of different target domains(%)

The experimental results are shown in Table 6. The bolded data in the table mark the best results in each target domain. According to the results of the table, the algorithms with the highest accuracy in different target domains are not the same, but the average classification accuracy of SDRKHS-DA is the highest. Compared with TCA, SSTCA, IGLDA, TIT, and GSL, SDRKHS-DA has 1.85%, 15.18%, 1.26%, 7.41%, and 18.52% improvement in average classification accuracy, respectively. In terms of the classification accuracy of specific tasks, SDRKHS-DA algorithm performed the best in 6 tasks, TCA performed best in 1.i task, and IGLDA performed best in 1.f and 1.g tasks .

Fig. 3

Classification accuracy of each algorithm in different dimensions in the target domain 1.e

Fig. 4

Classification accuracy of each algorithm in different dimensions in the target domain 1.h

Then, we explored the model effect when using algorithms to map data to subspaces of different dimensions. We also use the 30 pictures in 1.a and 1.b as the source domain according to the previous preprocessing and choose the 1.e and 1.h data as the two target domains. The subspace dimension is set from 5 to 30, and the step size is 5. The experiment uses SVM as the classifier, trains the SVM model according to the low-dimensional representation of the training set data and its labels, and then predicts the low-dimensional representation of the test set. The same experiment is repeated 20 times.

The experimental results are shown in Figs. 3 and 4. It can be seen that the SDRKHS-DA algorithm has a better classification accuracy in different dimensions than the other five domain adaptive algorithms. In the target domain 1.e, the classification accuracy of the SDRKHS-DA algorithm in 5–30 dimensions is the best. As far as the SDRKHS-DA algorithm is concerned, when the dimension is 5, the classification effect is the worst, with an accuracy rate of only 73.33%. When the dimension is 15–30, the classification accuracy rate stabilizes, reaching 93.33%. In the target domain 1.h, the classification effect of SDRKHS-DA algorithm is not ideal when the dimensions are 5 and 10, and the accuracy is lower than IGLDA and SSTCA. When the dimension is 5, the classification accuracy of IGLDA, SSTCA, and SDRKHS-DA is 79.33%, 82.00%, and 73.33%, respectively. When the dimension is 10, the classification accuracy of IGLDA, SSTCA, and SDRKHS-DA is 84.67%, 83.33%, and 80.00%, respectively. When the dimension is 15 to 30, SDRKHS-DA has the highest accuracy rate, which has been maintained at 86.67%. It can be seen that the classification accuracy of the SDRKHS-DA algorithm increases with the increase of the dimension and reaches the peak in a certain dimension.

6.4 Handwritten digit classification

The MNIST+USPS dataset is a very commonly used dataset in the field of machine learning. This section uses this dataset for handwritten digit classification experiments. The MNIST and USPS dataset images contain 10 kinds of grayscale images of handwritten Arabic numerals, and they have been standardized to place the numbers in the center of the image and make the image size consistent. The MNIST dataset is a subset of the NIST database. It contains 60,000 images in the training set and 10,000 images in the test set. The image size is 28$\times$28 pixels. The USPS dataset contains 7291 training set picture data and 2007 test set picture data, and the picture size is 16$\times$16 pixels. The sample of the MNIST+USPS dataset is shown in Fig.5. It can be seen that USPS and MNIST follow different distributions.

The experiment in this section uses a subset of the MNIST+USPS dataset, which contains 2000 pictures randomly selected from MNIST and 1800 pictures randomly selected from USPS. We uniformly scale all pictures in the subset to the pixel size and use the gray value of the pixel as a feature vector to represent each picture, so the samples of MNIST and USPS are located in the same 256-dimensional feature space. In addition, no additional preprocessing was performed on the samples.

Fig. 5

An example of MNIST+USPS dataset. Left: USPS, Right: MNIST

We take the samples of MNIST and USPS as two domains, respectively, and set up two tasks, namely MNIST$\rightarrow$USPS and USPS$\rightarrow$MNIST, where the arrow points to the target domain. For each experiment of each task, 50 samples are randomly selected from each category of the source domain as the source domain data of the training set, a total of 500; then, 20% of the target domain samples are randomly selected as the target domain data of the training set, and 80% of the domain samples are used as the test set. The SDRKHS-DA algorithm and the comparison algorithm are used to train on the training set to obtain the low-dimensional representation in the subspace of the training set. The training set data and the test set data are, respectively, multiplied by the low-dimensional representation to obtain the training data and the test data after dimensionality reduction. This experiment uses SVM as the classifier and trains the SVM model based on the low-dimensional representation of the training set data and its labels. The SVM model predicts the low-dimensional representation of the test set. The same experiment was repeated 10 times. SDRKHS-DA algorithm parameter settings: $\mu =1$, $\lambda =0.001$. The kernel function uniformly uses RBF kernels.

Table 7 Classification accuracy of task MNIST$\rightarrow$USPS(%)

The experimental results are shown in Table 7. The data in bold in the table mark the best results of each task. According to the results of the table, the algorithms with the highest accuracy in different subspace dimensions are not the same, but the average classification accuracy of SDRKHS-DA is the highest. Compared with TCA, SSTCA, IGLDA, TIT and GSL, SDRKHS-DA has 3.97%, 12.85%, 3.51%, 1.89% and 2.65% improvement in average classification accuracy respectively. In terms of classification accuracy in different dimensions, the SDRKHS-DA algorithm has the best performance in 5 different dimensions. IGLDA performs best when the dimension is 25, TIT performs best when the dimension is 70, and GSL performs best when the dimension is 15.

Table 8 Classification accuracy of task USPS$\rightarrow$MNIST(%)

The experimental results are shown in Table 8. The bolded data in the table mark the best results in each subspace dimension. According to the results of the table, the algorithms with the highest accuracy in different subspace dimensions are not the same, but the average classification accuracy of SDRKHS-DA is the highest. Compared with TCA, SSTCA, IGLDA, TIT and GSL, SDRKHS-DA has an increase of 4.28%, 5.52%, 3.82%, 2.45%, and 6.5% in average classification accuracy, respectively. In terms of classification accuracy in different dimensions, SDRKHS-DA algorithm performs best in 7 different dimensions, and TIT performs best when the dimension is 50. The SDRKHS-DA algorithm has the highest classification accuracy rate of 49.11% in all dimensions, which is 1.91% higher than the TCA algorithm with the second highest accuracy rate. Figure 6 is a synthesis of the classification accuracy of each algorithm of the two tasks in different dimensional subspaces. It can be seen that the SDRKHS-DA algorithm has a certain improvement effect compared with the five comparison algorithms, and the improvement of the proposed algorithm in more than half of the subspace dimensions is at least 2 percent.

Fig. 6

The average classification accuracy of two tasks in different dimensional subspaces

6.5 Text classification

The Reuters-21578 dataset is often used in information retrieval, machine learning, and other corpus-based research. It was collected from the documents on the Reuters news line in 1987. There are five category sets in Reuters-21578 dataset; that is, there exist five attributes which can determine the category of a document sample, namely ‘exchanges,’ ‘orgs,’ ‘people,’ ‘places,’ and ‘topics.’ The attribute ‘topics’ is an economic-related attribute, and the other four are all specific attributes. For example, the values of the attributes ‘exchange,’ ‘orgs,’ ‘people,’ and ‘places’ are Nasdaq, GATT, Perez-de-Cuellar, and Australia, respectively.

In this experiment, the preprocessed Reuters-21578 dataset is used for text classification. In this dataset, all the data samples belong to at least one specific attribute, namely ‘org,’ ‘place,’ or ‘people.’ At the same time, these samples are divided into positive and negative classes. The different attributes of the sample have specific relationship but cannot be compared directly. Thus, according to the three kinds of attributes those samples hold, all the sample data are divided into three different domains. Therefore, we set three tasks called ‘people vs. places,’ ‘orgs vs. people,’ and ‘orgs vs. places,’ respectively. The specific information about samples in different domains is shown in Table 9.

Table 9 The preprocessing Reuters-21578 dataset

For each experiment of each task, 50% of the source domain samples are randomly selected as the source domain data of the training set, and 30% of the target domain samples are randomly selected as the target domain data of the training set. Another 65% of the target domain samples are randomly selected as the test set. The SDRKHS-DA algorithm and the comparison algorithm are used to train on the training set to obtain the low-dimensional representation in the subspace of the training set. The training set data and the test set data are, respectively, multiplied by the low-dimensional representation to obtain the training data and the test data after dimensionality reduction. This experiment uses SVM as the classifier and trains the SVM model based on the low-dimensional representation of the training set data and its labels. The SVM model predicts the low-dimensional representation of the test set. The same experiment was repeated 20 times. SDRKHS-DA algorithm parameter settings:$\mu =1$, $\lambda =0.001$. The kernel function uniformly uses linear kernels.

Table 10 Classification accuracy of Reuters-21578 dataset (%)

Fig. 7

The average classification accuracy of the three tasks in different dimensional subspaces

The experimental results are shown in Table 10. The bolded data in the table mark the best results in each subspace dimension. According to the results of the table, SDRKHS-DA performs very well in the classification. Combining the average classification accuracy rates under all dimensions of the three tasks, TCA, SSTCA, IGLDA, TIT, GSL, and SDRKHS-DA are 58.88%, 61.21%, 60.46%, 60.39%, 61.98%, and 65.72%, respectively. Compared with TCA, SSTCA, IGLDA, TIT, and GSL, SDRKHS-DA has an improvement of 6.84%, 4.51%, 5.26%, 5.33%, and 3.74% in average classification accuracy, respectively. It can also be seen from the classification accuracy rates of the different dimensions of the three different tasks that the SDRKHS-DA algorithm basically performs the best, especially in the orgs vs. places and orgs vs. people tasks. The classification accuracy of different dimensions exceeds the other five comparison algorithms. Figure 7 shows the average classification accuracy of each algorithm for the three tasks in the same dimension. It can be seen from the figure that the SDRKHS-DA algorithm has a greater improvement in classification accuracy than the comparison algorithm, and the improvement of the proposed algorithm in more than half of the subspace dimensions is at least 3 percent.

7 Conclusion

In this paper, in order to solve the problem of the mismatch of data distribution between the source domain and the target domain, we propose a domain adaptive algorithm based on source dictionary regularized RKHS subspace learning. We first map the source domain data and target domain data to RKHS through the kernel function and then find a suitable subspace on RKHS to map the source domain data and target domain data to the subspace and learn the subspace. In the process of subspace learning, we use MMD as the basic criterion of the model to make the difference between the mean value of the source domain data and the target data as small as possible. The source domain data are used as a dictionary, and the target domain data are linearly represented by the source domain data, and the linear representation is required to be sparse; that is, the target domain data can only be represented by a few source domain data. This can force the model to learn the relationship between the target domain data and the source domain data as much as possible and select the source domain data most relevant to the target domain. The purpose of domain adaptation is to allow the target domain data to approximate the source domain data so that the distribution of the two is similar. In general, the source domain data related to the target domain data should be of the same kind. Then, using the source domain data to linearly represent the target domain data will make the distribution of the source domain data and target domain data of the same category in the learned subspace as consistent as possible, thereby improving the classification effect of the target domain data. Sufficient experiments show that our algorithm far exceeds the classification effect of several state-of-the-art algorithms, thus proving the effectiveness of our algorithm. In the current algorithm, when we map data to RKHS, we use a fixed kernel function. In the future, we can try to use some learnable kernel functions to keep the geometric structure of the data when the data are mapped to RKHS.