Gaussian kernel width exploration and cone cluster labeling for support vector clustering

Abstract

The process of clustering groups together data points so that intra-cluster similarity is maximized while inter-cluster similarity is minimized. Support vector clustering (SVC) is a clustering approach that can identify arbitrarily shaped cluster boundaries. The execution time of SVC depends heavily on several factors: choice of the width of a kernel function that determines a nonlinear transformation of the input data, solution of a quadratic program, and the way that the output of the quadratic program is used to produce clusters. This paper builds on our prior SVC research in two ways. First, we propose a method for identifying a kernel width value in a region where our experiments suggest that clustering structure is changing significantly. This can form the starting point for efficient exploration of the space of kernel width values. Second, we offer a technique, called cone cluster labeling, that uses the output of the quadratic program to build clusters in a novel way that avoids an important deficiency present in previous methods. Our experimental results use both two-dimensional and high-dimensional data sets.

1 Introduction

1.1 Clustering overview

Clustering is an unsupervised classification of data into natural groups [17]. It has applications in fields such as bioinformatics, where the data tends to have high dimensionality. Many different types of clustering criteria and algorithms exist (see [5, 9, 10, 11, 17] for clustering surveys). However, it is generally agreed that good clustering maximizes intra-cluster similarity and minimizes inter-cluster similarity.

Clustering algorithms typically employ one or more of the following approaches: graph-based [12, 14, 16, 28], density-based [8], model-based methods using either a statistical approach or a neural network approach, or optimization of a clustering criterion function. Efficient clustering algorithms tend to rely heavily on parameter selection. For example, the K-means algorithm [3] is faster than some other methods but requires the number of clusters and each cluster center’s starting location as an input. If no prior information about the data set is available, argument-free clustering algorithms like that of [7] can be used. Since those algorithms use proximity graphs such as Delaunay diagrams, they are not appropriate for high-dimensional data sets.

Constructing cluster boundaries is another popular technique [6, 12]. Support vector clustering (SVC) is similar to a boundary-finding clustering method except that it only identifies certain points on the boundary of each cluster; these points are support vectors. SVC does not require prior knowledge about the data. It is based on concepts from support vector machines. A support vector machine is a classifier that is used widely in many machine learning applications [2, 27]. It constructs a nonlinear classification boundary by creating a linear boundary in a high-dimensional space that is a transformation of the original data space [15]. This paper is based on SVC, whose foundation is summarized below in Sect. 1.2.

1.2 Support vector clustering

The basic idea of SVC is similar to that of a support vector machine. In fact, one can view SVC as a one-class support vector machine classifier. In both SVC and support vector machines, data are transformed by a nonlinear mapping into a high-dimensional feature space. This space is a Hilbert space for which a kernel function defines an inner product. The kernel function allows certain operations on data point images to be carried out in the feature space. The operations are executed without explicit knowledge of the nonlinear mapping or direct calculations on the data point images in feature space.

Support vector machines use a linear separator in feature space in order to separate and classify points. In contrast, SVC uses a minimal hypersphere surrounding feature space images of data points. The minimal hypersphere yields contours in the data space that form cluster boundaries [1, 13]. The cluster labeling task associates each data point with a cluster, using only the available operations, without explicitly constructing the contours in data space. An important advantage of SVC over other clustering methods is its ability to produce irregularly shaped clusters. Another advantage is its ability to handle outliers by allowing the minimal hypersphere to exclude some data point images.

Given a finite set ${\mathcal{X}} \subseteq {\mathbb{R}} ^d$ of N distinct data points, the radius R of the minimal hypersphere enclosing all data points’ images in the feature space is governed by Eq. 1, as in [1]:

$$ \left\Vert{\Upphi (x)-a}\right\Vert^2 \leq R^2 \quad \forall x \in {\mathcal{X}}, $$

(1)

where $\Upphi$ is a nonlinear mapping from data space to feature space, $\Upphi(x)$ is the feature space image of data point $x, \left\Vert{\cdot}\right\Vert$ is the Euclidean norm, and a is the center of the sphere. A slack variable ξ _x can be added to the right-hand side of Eq. 1, combined with a multiplicative penalty constant C, to form a soft constraint. Images on the surface of the sphere correspond to points on contour boundaries in data space, and images inside the sphere map to points within contours. Data points can be categorized into three groups based on the location of their feature space images: (1) points whose images are on the surface of the minimal hypersphere are Support Vectors (SVs), (2) points whose images are outside of the minimal hypersphere are Bounded Support Vectors (BSVs, controlled by penalty constant C), and (3) points whose images are inside the minimal hypersphere.

The mapping from data space to feature space is specified by a kernel function, ${K:\mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}, }$ that defines the inner product of image points. We use a Gaussian kernel given by Eq. 2 below [1, 13, 22]:

$$ K(x_i,x_j) = \hbox{e}^{-q\parallel x_i - x_j \parallel ^2} = \langle \Upphi(x_i) \cdot \Upphi(x_j) \rangle, $$

(2)

where q is the width parameter of the Gaussian kernel. From Eq. 2, it follows that,

$$ K(x_i,x_i) = 1. $$

(3)

All data point images are therefore on the surface of the unit ball in feature space [2]. From Eqs. 1 to 3, the Lagrangian W in Eq. 4 below can be derived. It must be maximized in order to find the minimal hypersphere.

$$ \begin{aligned} \max W &= \sum_j K(x_j,x_j)\beta_j - \sum_{i,j}\beta_i\beta_jK(x_i,x_j)\\ &= 1 - \sum_{i,j}\beta_i\beta_jK(x_i,x_j)\\ \end{aligned} $$

(4)

where β _i is a Lagrange multiplier, 1 ≤ i ≤ N, and ∑ _i β _i  = 1. A soft margin constraint β _i  ≤ C, where C is the penalty constant, controls the number of BSVs and therefore allows exclusion of some outliers. When C ≥ 1 no BSVs can exist. Note that Eq. 4 is quadratic in the β values. Solving Eq. 4 using quadratic programming yields β values corresponding to the minimal hypersphere in feature space. These β values are used for cluster labeling.

The high-level SVC strategy is outlined below:

SVC(${\mathcal{X}}, q, C$)
$K \leftarrow$ computeKernel(${\mathcal{X}}, q$) using Eq. 2
$\beta \leftarrow$ solveLagrangian(K, C) using Eq. 4
return $\leftarrow$ clusterLabeling(${\mathcal{X}}, \beta$)

1.3 Parameter selection

SVC’s running time depends directly on the number of q and C combinations explored. Since clustering is subjective, multiple (q, C) pairs might be required in order to provide an acceptable result. Minimum and maximum q values q _min and q _max can be easily established by forcing all off-diagonal kernel values to be close to 1 or 0, respectively. The minimum q value typically produces a single cluster, while the number of support vectors N _sv is expected to be N at the maximum q value. The former case yields

$$ 1-\hbox{e}^{-q*\max\{\left\Vert{x_i-x_j}\right\Vert^2\}} \leq \epsilon_{\min},\quad \hbox{where }\ 0 \leq \epsilon_{\min} \leq 1 \Rightarrow q_{\min} = \frac{\ln(\frac{1}{1-\epsilon_{\min}})}{\max\{\left\Vert{x_i-x_j}\right\Vert^2\}}. $$

(5)

In the latter case we obtain

$$ \hbox{e}^{-q*\min\{\left\Vert{x_i-x_j}\right\Vert^2\}} \leq \epsilon_{\max}, \hbox{where }0 \leq \epsilon_{\max} \leq 1 \Rightarrow q_{\max} = \frac{\ln(\frac{1}{\epsilon_{\max}})}{\min\{\left\Vert{x_i-x_j}\right\Vert^2\}}. $$

(6)

The value of q _min can be chosen such that $\ln(\frac{1}{1-\epsilon_{\min}})=1;$ thus $q_{\min}= \frac{1}{\max\{\left\Vert{x_i-x_j}\right\Vert^2\}}.$ This is used as an initial q value in [1]. Similarly, q _max can be selected such that $\ln(\frac{1}{\epsilon_{\max}})=1;$ this produces $q_{\max}= \frac{1}{\min\{\left\Vert{x_i-x_j}\right\Vert^2\}}.$

A procedure is needed to select intervening q values. An ideal sequence would produce only critical q values where the clustering structure changes. Furthermore, these q values would be sorted by their clustering quality. That is, values corresponding to the most natural clustering results would appear early in the sequence.

The SVC literature has not yet offered a procedure for generating such a sequence. Grid sampling can produce a list of q values, but it suffers from the need to guess an appropriate $\Updelta q$ value. Also, it does not necessarily yield a good ordering of the q values. Our secant-like algorithm, introduced in [18, 19, 21], behaves similar to successive doubling of the initial q value. Like a secant method, this algorithm starts with two initial values and finds subsequent values by using secant lines but stops when the slope of the line is close to flat. Experiments with q values generated in this fashion suggest that critical q values often occur in the sequence and the length of the sequence depends only on spatial characteristics of the data set rather than the dimensionality of the data set or the number of data points. However, this approach still does not produce the most desirable q values early in the sequence.

Indeed, identifying critical q values and determining a good ordering of them is a very challenging problem. While we do not completely solve this problem here, we offer some progress using fresh insight into the behavior of R ² as a function of q. This builds on our earlier observations in [18, 19, 21] about conditions in which this function is monotonic. Monotonicity, convexity, and appropriate scaling allow the function to have a unique radius of curvature [23] minimum that tends to correspond to a q value at which clustering structure changes are the most significant. This serves as a starting point for our q sequence. Successive doubling produces the remaining q values. The radius of curvature technique is new and its new clustering results are presented in this paper.

For each (q, C) pair, computing the kernel matrix followed by solving the Lagrangian together require O(N ²) space and O(N ³) running time in the worst case. Our method is efficient because it uses information that is already needed by SVC. In this paper, we set C to 1 so that no data point images are outside the minimal hypersphere. Systematically identifying a sequence of critical C values is beyond the scope of this paper. This is also a difficult problem for which little guidance appears in the SVC literature.

1.4 Cluster labeling

Cluster labeling, the second focus of this paper, has a goal of grouping together data points that are in the same contour associated with the minimal hypersphere. Recall that the grouping must be done without the ability to explicitly construct the contour boundaries; this greatly complicates the task.

Prior cluster labeling work is summarized in [21, 20] and discussed below. In the literature, cluster labeling has been an SVC performance bottleneck. Dominant SVC cluster labeling algorithms are Complete Graph (CG) [1], Support Vector Graph (SVG) [1], Proximity Graph (PG) [28], and Gradient Descent (GD) [22]. These algorithms group together data points by representing pairs of data points using an adjacency structure, which is usually a matrix. Each element signifies whether there is adequate justification to decide that the associated pair of data points is in the same contour and therefore in the same cluster. Each connected component of the associated graph is a cluster. CG needs a O(N ²) sized adjacency structure because it represents all data point pairs. SVG represents pairs in which one point is a support vector, so its adjacency structure only uses O(N _sv N) space where N _sv is the number of support vectors. Once the support vectors are clustered, SVG clusters the remaining data points in a second phase. PG forms an adjacency structure from a proximity graph that has only O(N) edges. The GD method finds Stable Equilibrium Points (SEPs) that are the nearest minimum point of Eq. 7 below for each data point and then tests pairs of SEPs. Consequently, GD’s adjacency structure uses O(N ²_sep ) space, where N _sep is the number of SEPs.

Because data space contours cannot be explicitly constructed, the algorithms mentioned above use an indirect method to determine if a pair of data points x _i and x _j are in the same contour. The strategy is a sampling approach based on the fact that each possible path connecting two data points in distinct data space contours leaves the contours in data space and the image of the path in feature space exits the minimal hypersphere. The aforementioned algorithms use the straight line segment $\overline{x_ix_j}$ connecting x _i and x _j as a path. This path is sampled. For sample point x in data space, $\Upphi(x)$ is outside the minimal hypersphere if R ²(x) > R ², where R ²(x) is defined by Eq. 7 below. If the image of each sample point along $\overline{x_ix_j}$ is inside the minimal hypersphere, then x _i and x _j are put into the same cluster.

$$ \begin{aligned} R^2(x) &= \left\Vert{\Upphi(x) - a}\right\Vert^2\\ &= 1 - 2\sum_j\beta_jK(x_j,x)+\sum_{i,j}\beta_i\beta_jK(x_i,x_j), \end{aligned} $$

(7)

where $x \in \mathbb{R}^d$ and $a = \sum_i \beta_i \Upphi(x_i)$ is the center of the minimal hypersphere [1]. (Note that since support vectors are on the boundary of the minimal hypersphere, R ²(x) = R ² in their case.)

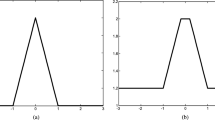
The sampling approach induces a problematic running time versus accuracy tradeoff. If m is the number of sample points along a line segment, then solving Eq. 7 for each sample point generates a multiplicative factor of mN _sv beyond the time proportional to the size of the adjacency data structure. The algorithms restrict m to be a small constant in order to limit running time; this is typically 10–20. However, small values of m can cause false positive and false negative errors, as depicted in Fig. 1.

Fig. 1

Problems in using line segment $\overline{x_ix_j},$ illustrated in two-dimensional data space: a all sample points on $\overline{x_ix_j}$ are inside the minimal hypersphere, while x _i and x _j are in different contours; b some sample points are outside the minimal hypersphere although x _i and x _j are in the same contour

The problem illustrated in Fig. 1a can be partially solved if we base the number of sample points along the line segment on the distance between data points. However, this method may still suffer from the same problem. The disadvantage shown in Fig. 1b can be ameliorated by enhancing connectivity among data points. However, as the number of data points to be checked increases, the time complexity of cluster labeling becomes more expensive.

Different cluster labeling algorithms use line segments between different numbers of data points and therefore suffer from the above problems to varying degrees. For example, CG uses line segments for all data pairs while SVG only uses line segments for all data pairs in which one data point is a support vector. SVG’s smaller number of pairs exacerbates the problem depicted in Fig. 1b, causing the probability of breaking a cluster into several clusters to be higher. Thus SVG, PG, and GD have weaker cluster connectivity than CG.

This paper takes a very different approach to cluster labeling that does not sample a line segment between a pair of data points. Our strategy approximates the contours in data space using the union of a set of hyperspheres centered on the support vectors. All of the hyperspheres have the same radius, which is derived from cones in the feature space. The radius is based on the β values obtained from the quadratic programming model in Eq. 4. The cones are designed with the goal of approximating part of the feature space associated with the intersection of the surface of the unit ball with the minimal hypersphere surrounding the images of the data points. This cone cluster labeling (CCL) scheme is fast and provides excellent clustering results for our data sets.

1.5 Overview

Section 2 describes the data sets used in this paper. In Sect. 3, we offer a new heuristic for exploring SVC Gaussian kernel widths for a fixed value of the outlier parameter C. Kernel width values are ordered using the radius of curvature of the function that specifies the radius of the minimal hypersphere in feature space in terms of kernel width. Values close to the critical curvature point appear to often correspond to critical changes in clustering structure. An estimate is provided for the number of kernel width values generated by the strategy.

This paper circumvents the cluster labeling problems listed in Sect. 1.4 by using a novel approach that decides if two data points are in the same cluster without sampling a path between them. The main idea is to cover an important portion of the minimal hypersphere in feature space using cones that correspond to hyperspheres in data space. Each support vector is associated with one feature space cone and one data space hypersphere. The radius of the hypersphere is based on the output of the quadratic programming model of Eq. 4. The union of the hyperspheres in data space need not be explicitly constructed. Pairs of support vectors can be quickly tested during the cluster labeling process and then the remaining data points can be easily clustered. Our CCL algorithm, presented in Sect. 4, does not use sample points. An earlier version of this work appears in [20, 21]. Lee and Daniels [20] states our CCL claims and briefly outlines the main ideas of the proofs. Lee [21] provides additional detail for the proofs. In the current paper, we provide final versions of the preliminary drafts of proofs from [21]. CCL is able to efficiently recover known clustering structure in our data sets. Its clustering results are similar in quality to the best results we have seen using CG. (Recall from Sect. 1.4 that CG has the strongest clustering connectivity of the existing sampling-based SVC cluster labeling techniques.) Furthermore, our new algorithm is faster than traditional cluster labeling algorithms and appears to work well even in high dimensions. Section 4’s comparison with existing cluster labeling algorithms contains our new CCL results using our new kernel width selection process. Section 5 concludes the paper.

2 Data sets

This section describes data sets that are used in this paper. (Additional data sets are discussed in [21].) In each case 1 and N are extreme values for the number of possible clusters. We identify the most natural number(s) of clusters in between these values, where appropriate. This provides known clustering structure that is used in our paper for assessing the quality of our clustering approach.

2.1 Two-dimensional data

Table 1 depicts eight illustrative two-dimensional data sets. In Table 1, (a) shows five clusters with clear separation. We created (b) to test data with no specific clustering structure. Data set (c) has two blocks (upper and lower) of the same non-convex shape; 2 is therefore a reasonable number of clusters for this case. It can also be construed as having four clusters, with two clusters inside each block. Data set (d) shows two interleaved, highly non-convex clusters. This is a subset of data from the authors of [12]. Even though these data do not have outliers, it is not easy to obtain two clusters. Data set (e) has one cluster with 28 outliers. We consider each outlier to be a distinct cluster; this results in 29 clusters. Data set (f) can be viewed as two or three clusters as in [12]. Data set (g) is the same data as used in [1]; it has four clusters. Data set (h) shows three nested clusters.

Table 1 Two-dimensional data

2.2 High-dimensional data

As described in [21], we first generated some high-dimensional test data sets with different dimensions and known clustering structure. For d dimensions and N _cl clusters, we created N _cl linearly independent vectors, each containing d/N _cl consecutive $1^{\prime}s.$ We then created d additional vectors using small perturbations of each vector. This yielded data sets HD1(dim = 9, N = 12), HD2(dim = 25, N = 30), and HD5(dim = 200, N = 205), with 3, 5, and 5 clusters, respectively, where dim represents dimensions. Points in these data sets were shuffled by random.

Other high-dimensional data sets were obtained from the block-type data set that is introduced in Table 1(c). We appended additional dimensions to the block data by adding a new attribute for each dimension that has similar variation to its first two dimensions. We created a 3D nonconvex data set HD3 containing 81 data points using one block with two clusters. We also used some data sets from the UCI Repository [24]. The Iris data set contains 150 points in 4-dimensional space (except cluster label) and 33.3% of the points are in each of the three classes. We used 147 points after removing three duplicated points and we call that data set HD4.

3 Automatic generation of Gaussian kernel widths

In this section we suggest a natural method to automatically generate SVC parameter values using the way that the radius of the minimal hypersphere in feature space changes as q (Gaussian kernel width) increases. Section 3.1 introduces characteristics of the minimal hypersphere in feature space. We provide a heuristic in Sect. 3.2 to generate q values automatically for a given outlier parameter value C. The q values are generated in an order that is more consistent with the goals of Sect. 1.3 than methods in the existing SVC literature. Section 3.3 assesses our new strategy. The length of the q list is analyzed and is shown to be independent of the dimensionality of the data and number of data points. We show that, when used with the CCL scheme of Sect. 4, excellent clustering results are achieved that recover the known clustering structure of the data.

3.1 Characteristics of minimal hypersphere radius

This section provides background for our work on a heuristic that generates an increasing sequence of kernel width values that supports the goals stated in Sect. 1.3. The Gaussian kernel of Eq. 2 is used throughout this section. The main idea is to locate a q value, denoted by q*, that minimizes the radius of curvature of the graph of R ²(q). Our approximation $\hat{q}^*$ to this q* value is used as the starting point for a sequence of q values. Studying our previous experimental work in [18, 19, 21] on generating q values provided the inspiration for our new observation that significant changes in clustering structure occur at a critical point in the R ²(q) function.

From [18, 19, 21], we know some characteristics of the behavior of the R ²(q) function. To characterize the function, we first recall that, as R is the radius of the minimal hypersphere enclosing data point images, R ²(q) ≥ 0 for $0 \leq q \leq \infty.$ Furthermore, since the kernel is Gaussian, the entire data space is embedded onto the surface of the unit ball in feature space [2]. Therefore, R ²(q) ≤ 1 for $0 \leq q \leq \infty$ and hence 0 ≤ R ²(q) ≤ 1 for $0 \leq q \leq \infty.$

The results of [18, 19, 21] establish that R ²(q) = 0 for q = 0, 0 ≤ R ²(q) ≤ 1 − 1/N for $0 \leq q \leq \infty, R^2(q) = 1 - 1/N$ if and only if $q = \infty,$ and provide a condition under which R ²(q) is a monotonically increasing function of q. Under the condition the horizontal line R ²(q) = 1 − 1/N is an asymptote for the function. In our experiments in [18, 19, 21], the condition was satisfied, providing monotonicity. Furthermore, the slope was monotonically decreasing, implying convexity of the R ²(q) function in those cases. Convexity together with monotonicity imply at most one critical point (minimum) for the radius of curvature of the R ²(q) function; let this q value be q ^*. See Fig. 2 for an example.

Fig. 2

Example of convex and monotonic R ²(q) curve for two-dimensional data set (g) of Table 1 with interval containing q ^* identified

3.2 Curvature-based heuristic for kernel width list

Our heuristic to generate an increasing sequence of q values, starting with an approximation $\hat{q}^*$ to q ^*, requires a small amount of preprocessing to scale the data. We scale the data so that the largest coordinate value is equal to N. In practice, this usually makes the initial slope of our approximation to the R ²(q) curve at least equal to one, which makes the radius of curvature achieve a minimum over the range of q values generated.

We use the origin and $q_{\min} =\frac{1}{\max \{\left\Vert{x_i - x_j}\right\Vert^2 \}}$ as the first two q values in our search for $\hat{q}^*$ (see the derivation of q _min in Sect. 1.3). Since R ²(q) ≥ 0 for q ≥ 0 and R ² = 0 for q = 0, the origin is an appropriate starting q value for the search in the heuristic. The next q value in the search is from [1] and is expected to yield one cluster. For each additional value of q that is searched, the associated R ²(q) value is calculated using the SVC steps of updating a kernel matrix, solving the Lagrangian, and computing the radius of the minimal hypersphere. To generate each subsequent q search value, the current q value is doubled. Our experiments show that successive doubling approximates the behavior of our successful secant-like q generation algorithm from [18, 19, 21]. The radius of curvature of the R ²(q) function is approximated as the q values are generated. The q value minimizing the radius of curvature of the function’s approximation becomes our approximation $\hat{q}^*$ to q*. It is important to note that $\hat{q}^*$ is generated without performing any SVC cluster labeling. This is a significant efficiency consideration.

We output $\hat{q}^*$ as the most significant q value. Each additional q value in the output is produced using repeated doubling. The stopping condition can be chosen in various ways. The simplest condition is q = q _max, as derived in Sect. 1.3. This often produces N clusters, beyond which there is no change in clustering structure. However, we have achieved better results by checking the β values for the data points and stopping when either every data point is a support vector or the slope of the R ²(q) curve falls below a small tolerance value.

The pseudocode for our new qListGenerator() procedure is given in Tables 2 through 5. The slope tolerance termination test is omitted for clarity. Procedure checkBetas(), whose pseudocode is omitted, returns the number of data points whose β values are greater than 1; this is the number of support vectors N _sv. Procedure append(), whose pseudocode is also omitted, appends its second argument to the end of the list given by the first argument. Procedure findQStar() is listed separately below in Table 3. It searches for the approximate minimum radius of curvature of the R ²(q) curve using successive q doubling. It uses the procedure computeRadiusOfCurvature(), which approximates the first and second derivatives of the R ²(q) function at the most recent q value and uses them within a standard radius of curvature formula. We omit the pseudocode for this procedure. If we denote R ²(q) by f(q), then the curvature formula is (assuming $f^{\prime\prime}(q) \neq 0$):

$$ \frac{[1+(f^{\prime}(q))^2]^{3/2}}{f^{\prime\prime}(q)} $$

(8)

Table 2 Heuristic for q generation

Table 3 Heuristic for $\hat{q}^*$ generation

Table 4 R ²(q) calculation

Table 5 N _sv calculation

The worst-case running time of qListGenerator() is in O(|Q|N ³), where |Q| is the set of q values produced and the factor of O(N ³) is due to Eq. 4. To derive a rough estimate of |Q|, we use q _min from Eq. 5 and q _max from Eq. 6 in Sect. 1.3. Successive doubling of q values yields:

$$ |Q| \approx lg(\max\{\left\Vert{x_i-x_j}\right\Vert^2\})-lg(\min\{\left\Vert{x_i-x_j}\right\Vert^2\}). $$

(9)

Note that Eq. 9 depends only on spatial characteristics of the data set and not on the dimensionality of the data set or the number of data points. This is the same q list length estimate that was obtained for the secant-like procedure of [19, 18, 21]. See Sect. 3.3.1 for results on how well this estimates the actual length of the q list for our data.

3.3 Quality assessment

Our implementations use MATLAB ^{TM 1} and Java and are run on an Intel Core 2 Duo T5200, 1.6GHz processor with 2GB of RAM. We use SMO [25] to solve the Lagrangian (Eq. 4). To address the floating point precision problems of determining positive β values, we use an epsilon of 10⁻⁶. The outlier parameter C is set equal to 1 throughout the experiment.

Data sets from Sect. 2 are used. For all of our data sets the slope of the R ²(q) curve is monotonically decreasing and the curve approximation is convex. With our scaling, the radius of curvature of the R ²(q) curve attains a single minimum. The $\hat{q}^*$ value often corresponds to the most natural clustering of the data. In our experiments, values of q less than $\hat{q}^*$ frequently produce only one cluster and can therefore safely be omitted from the q list.

Section 3.3.1 examines the length of the q list. Sections 3.3.2 and 3.3.3 discuss two and higher-dimensional data sets, respectively. The cone cluster labeling method CCL, described in Sect. 4 is used here for cluster labeling due to its strong cluster connectivity. We compare these results with the existing automatic q list generation algorithm, which is our secant-like algorithm from [18, 19, 21]. This is used with both CG and CCL.

3.3.1 List length

Table 6 shows Eq. 9 of Sect. 3.2 applied to our data sets. For our two-dimensional data sets, the number of actual q values is always smaller than the estimated number. In most cases the difference is large; on average the actual number is 32% of the estimated number. For our high-dimensional datasets, the actual number is close to the estimated one but sometimes exceeds it. The actual number is, on average, 112% of the estimated one.

Table 6 Number of kernel values output by qListGenerator()

In order to provide a comparison with existing q generation methods, we include the best results from a combination of the research in [18, 19, 21]. This uses a secant-like method whose behavior is similar to successive doubling. For our two-dimensional data sets, the length of our new q list is an average of 22% of the length of the secant-like method’s list. For our high-dimensional data sets, the average is 82%.

3.3.2 Two-dimensional clustering

Table 7 shows clustering results for $\hat{q}^*$ for the two-dimensional data sets of Sect. 2.1. In each case unclustered data are shown on the left and clustered data appear on the right, with clusters differentiated by color. See Table 8 for the complete list of q values produced by qListGenerator() for the two-dimensional data.

Table 7 Cluster results for $\hat{q}^{*}$ with C = 1 for data from Table 1

Table 8 Sequence of q values produced by qListGenerator() for two-dimensional data from Table 1, with $\hat{q}^*$ as the first value in each case

In most of the cases $\hat{q}^*$ correctly recovers the known clustering structure. Examples (c) and (d) are of particular note due to the highly nonconvex nature of those data sets. Example (e), containing outliers, is clustered by using C = 1 and then considering each singleton cluster as an outlier. While the correct answer of 29 clusters is not produced by $\hat{q}^*,$ the fourth value in the list is correct. For example (h) the $\hat{q}^*$ value does not produce the desired result of three clusters. However, the second value in the q list yields the correct result.

The secant-like method is also able to recover known clustering structure, but the best q values do not appear early in the sequence and no automatic identification of the best q value is available. For example, when that method is used with the CG cluster labeling technique, the best q value yields excellent clustering quality for all but example (d). That value appears in between the second and tenth values and, on average, is the seventh q value in the list. Similar behavior occurs when CCL is used with the secant-like method. Unlike CG, CCL is able to correctly cluster example (d). However, CCL requires an average of 3.6 more q values in the secant-like list in order to achieve good clustering results. (This average takes into account high-dimensional as well as two-dimensional cases.)

3.3.3 High-dimensional clustering

Table 9 shows the result of clustering our high-dimensional data sets from Sect. 2.2 using the q values generated from qListGenerator(). As introduced in Sect. 2.2, we have four synthetic data sets and the Iris data (HD4). In all but one case (HD3) our q list includes at least one value that corresponds to a natural number of clusters. In the HD1, HD2, and HD5 cases $\hat{q}^*$ recovers the known clustering structure. For the Iris data set, a reasonable result of 2 clusters is associated with the third value in our q list. In the N = 81 three-dimensional block data case HD3, the q list terminates when only one cluster has been found. In this exceptional nonconvex case a different stopping condition of R ²(q) curvature equal to 0 achieves the correct clustering result. This adds an extra three q values to the list.

Table 9 Sequence of q values produced by qListGenerator() for high-dimensional data from Sect. 2.2, with $\hat{q}^*$ as the first value in each case

While it is true that the “curse of dimensionality” poses a challenge for high-dimensional clustering, we note that, prior to our high-dimensional SVC clustering work, the SVC literature did not contain reasonable clustering results for high-dimensional data without using dimensionality reduction techniques such as Principal Component Analysis.

One intriguing observation is that N _sv is greater than or equal to the dimension of the data for all q values. This observation suggests that N _sv heavily depends on the dimension of the data even for the initial q value.

As in Sect. 3.3.2, it is fruitful to compare our results with the secant-like q generation method. Again, with CG the first q value does not produce the best result. The best value occurs between the third and ninth positions in the list. It appears fifth on average. However, we note that CG with the secant-like method has one quality advantage over CCL with our new method for the Iris data set. In the CG case the correct answer of three clusters was achieved, whereas only two clusters were found by CCL.

4 Cone cluster labeling

4.1 High-level approach

We present a novel cluster labeling algorithm that is significantly different from other SVC cluster labeling methods. An earlier version of this work appears in [20, 21], which introduces our CCL approach and provides some initial results. Here we summarize the strategy and include final versions of proofs whose preliminary drafts appeared in [21]. Experimental coverage is examined, convergence is informally discussed, and clustering quality is assessed. Furthermore, execution times are compared across cluster labeling methods, and our new q list generator is used in our experiments.

As described in Sect. 1.4, existing methods [1, 22, 28] decide if two data points are in the same cluster by sampling a path connecting the two data points. If every sample point’s image is inside the minimal hypersphere in feature space, then the two data points are put into the same cluster. As noted in Sect. 1.4, this induces an execution time versus clustering accuracy tradeoff.

For a given kernel width value, our algorithm does not sample a path between two data points in order to decide if they should be assigned to the same cluster. Rather, we use the geometry of the feature space to identify clusters in the data space. The key observation is that a hypersphere about a point x _i in data space corresponds to a cone in the feature space. As explained below, the cone has the feature space origin as its apex, and its axis is the vector through the origin and the point $\Upphi(x_i)$ (recall that $\Upphi(x_i)$ is the feature space image of x _i ). We derive the cone’s base angle in Sect. 4.2. This correspondence is the basis of our approach. We call our algorithm Cone Cluster Labeling because of its reliance on cones.

The algorithm first finds an approximate cover of part of the minimal hypersphere in feature space using cones associated with the images of support vectors. This is described in Sect. 4.2. The cover is for part of the intersection P of the surface of the unit ball with (the interior and boundary of) the minimal hypersphere. The approximate cover is part of a union of cone-shaped regions. One region is associated with each support vector’s feature space image. Let $V=\{v_i|v_i\ \hbox{is \ a \ support \ vector},\ 1\leq i \leq N_{\rm sv}\}$ be the set of SVs for a given q value. The region for support vector v _i is called a support vector cone and is denoted by ${{\mathcal{E}}_{v_i}.}$

Cone ${{\mathcal{E}}_{v_i}}$ in feature space is associated with a hypersphere ${{\mathcal{S}}_{v_i}}$ centered on v _i in the data space. Section 4.3 derives the radius of ${{\mathcal{S}}_{v_i}, }$ which is the same for all support vectors. The radius is based on the minimal hypersphere’s radius R in feature space (obtained from Eq. 7, which requires the β values from the quadratic programming model of Eq. 4). Having only one radius contributes to the speed of CCL. The union ${\cup_i ({\mathcal{S}}_{v_i})}$ is an approximate covering of the data space contours $P^{\prime},$ where $\Upphi(P^{\prime}) \subseteq P.$ This union is not explicitly constructed. Instead, cluster labeling is done in two phases, as described in Sect. 4.4. The first phase clusters support vectors whereas the second clusters the remaining data points. Two support vectors v _i and v _j are put into the same cluster if their hyperspheres overlap: ${({\mathcal{S}}_{v_i} \cap {\mathcal{S}}_{v_j}) \neq \emptyset. }$ Forming the transitive closure of the connected relation yields a set of support vector clusters. The second step clusters data points that are not support vectors. Each such data point inherits the closest support vector’s cluster label.

Section 4.5 provides experimental CCL results. Section 4.5.1 gives experimental coverage figures. Section 4.5.2 discusses the clustering quality of CCL as compared with that of CG, which is the most accurate of the SVC techniques that sample line segments for cluster labeling. Section 4.5.3 compares the execution time performance of CCL with existing cluster labeling methods. CCL is successful because it is fast and, without actually constructing the data space contours, it tends to give a clustering answer that is close to the actual number of connected components of the contours.

4.2 Approximate covering in feature space

This section forms support vector cones that cover part of P. Recall that P is the intersection of the surface of the unit ball with the minimal hypersphere. As we introduce in [20, 21], let $\Uptheta_i = \angle ( \Upphi(v_i)Oa),$ where O is the origin of the feature space and a is the center of the minimal hypersphere enclosing all data point images. In feature space, each support vector has its own cone ${{\mathcal{E}}_{v_i}. }$ Let ${{\mathcal{E}}_{v_i}}$ be the cone with axis $\overrightarrow{\Upphi(v_i)}$ and base angle $\Uptheta_i,$ so that the cone is generated by rotation of vector $\overrightarrow{Oa}$ about the axis formed by vector $\overrightarrow{\Upphi(v_i)}$ at an angle of $\Uptheta_i$ between vector $\overrightarrow{Oa}$ and vector $\overrightarrow{\Upphi(v_i)}.$ Lemma 4.1 below shows that $\Uptheta_i=\Uptheta_j$ for all $v_i,v_j \in V.$

Lemma 4.1

$\angle(\Upphi(v_i)Oa) = \angle(\Upphi(v_j)Oa), \forall v_i,v_j \in V.$

Proof

For each support vector image $\Upphi(v_i),$ consider the triangle with vertices $\Upphi(v_i), O,$ and a. We claim that there is side-side-side congruence for the set of such triangles. For, the line segment $\overline{Oa}$ is common to all the triangles. Also, the definition of a support vector guarantees that all the support vector images are equally distanced from the center of the minimal hypersphere; thus all the line segments of the form $\overline{\Upphi(v_i)a}$ have the same length. Finally, because each support vector’s image is on the surface of the unit ball in feature space, all the line segments of the form $\overline{\Upphi(v_i)O}$ have the same length. This establishes the side-side-side congruence, which guarantees the equivalence of angles $\angle(\Upphi(v_i)Oa)$ and $\angle(\Upphi(v_j)Oa)$ for each pair of support vectors $\Upphi(v_i)$ and $\Upphi(v_j).$ □

Due to Lemma 4.1, hereafter we denote $\Uptheta_i$ by $\Uptheta$ (see Fig. 3a to illustrate a two-dimensional example). We also denote by $a^{\prime}$ the intersection of $\overrightarrow{a}$ with the surface of the unit ball (see Fig. 3b). The point $a^{\prime}$ is a common point of intersection for all the support vector cones. This commonality suggests to us that these cones might provide good coverage of P. Mathematically, we do not have a guarantee of complete coverage. However, we show experimentally in Sect. 4.5.1 that all of the data points’ feature space images are contained within ${(\cup_{i} ({\mathcal{E}}_{v_i})) \cap P}$ for q values from our qListGenerator(). Thus, empirical data suggest that the union of cones provides an approximate cover in feature space.

Fig. 3

Inner product between a or a′ and SV image (illustrated for two dimensions): v _i and v _j are support vectors and $\Upphi(v_i)$ and $\Upphi(v_j)$ are their feature space images, respectively. a $\Uptheta = \angle(aO\Upphi(v_i)) =\angle(aO\Upphi(v_j)).$ b $a^{\prime}$ is projection of a onto the surface of the unit ball. c the length $\left\Vert{a}\right\Vert$ is $\langle \Upphi(v_i) \cdot a^{\prime}\rangle.$ d $\Updelta = \langle\Upphi(v_i) \cdot a\rangle = 1-R^2 = \left\Vert{a}\right\Vert^2.$

It is instructive to consider what happens for the extreme cases of q = 0 and $q = \infty.$ For q = 0, the minimal hypersphere in feature space is degenerate. It consists of a single point, which is equal to ${\Upphi({\mathcal{X}})}$ and also equal to ${(\cup_{i} ({\mathcal{E}}_{v_i})) \cap P. }$ Thus, the cones perfectly cover P and also the images of the data points. For $q = \infty,$ every data point is a support vector, the angle between each pair of support vector images is equal to π/2, and the cones cover ${\Upphi({\mathcal{X}})}$ completely. For q values greater than 0, it is possible for the union of cones to cover parts of the unit ball outside of P. It is also possible for some data point images to be outside the union of cones. However, our experience shows that these problems fade rapidly as q increases.

4.3 Approximate covering in data space

Our CCL algorithm places all data points whose images have smaller base angle than $\Uptheta$ with respect to $\overrightarrow{\Upphi(v_i)}$ in the same cluster as v _i . The goal of this section is to find $\Uptheta$ and then identify such data points in the data space. This task is complicated by the lack of an inverse mapping for $\Upphi.$ In particular, there is not necessarily a single point in the data space whose feature space image is the point of cone commonality $a^{\prime}.$

Our approach circumvents this issue using distances in data space corresponding to constant angles in feature space. That is, we rely on the fact that a cone with apex at the feature space origin whose axis intersects a support vector’s image corresponds to a hypersphere about the support vector in the data space.

To approximately cover the contours $P^{\prime}$ in data space using information derived from support vector cones, we associate ${({\mathcal{E}}_{v_i} \cap P)}$ with a hypersphere ${{\mathcal{S}}_{v_i}}$ in data space. Since Lemma 4.1 guarantees that all support vector cones have the same base angle $\Uptheta,$ all ${{\mathcal{S}}_{v_i}}$ have the same radius and each ${{\mathcal{S}}_{v_i}}$ is centered at v _i . The radius of ${{\mathcal{S}}_{v_i}}$ is based on the results of Lemma 4.2 below. (Note that the Gaussian kernel in Eq. 2 limits feature space angles: $0 \leq \angle(\Upphi(v_i)O \Upphi(v_j)) \leq \pi/2.$)

Lemma 4.2

Each data point whose image is inside ${({\mathcal{E}}_{v_i} \cap P)}$ is at distance $\leq \left\Vert{v_i-g_i}\right\Vert$ from v _i , where ${g_i \in {\mathbb{R}}^d}$ is such that $\angle(\Upphi(v_i)O\Upphi(g_i))=\Uptheta.$

Proof

Consider $u \in {\mathbb{R}}^d$ such that $\Upphi(u) \in ({\mathcal{E}}_{v_i} \cap P).$ Point $\Upphi(u)$ in $({\mathcal{E}}_{v_i} \cap P)$ has an angle with respect to $\Upphi(v_i)$ which is at most equal to $\Uptheta.$ Since $\Uptheta=\angle (\Upphi(v_i)Oa)=\angle (\Upphi(v_i)Oa^{\prime}),$ this implies that:

$$ \begin{aligned} &\angle(\Upphi(u)O\Upphi(v_i)) \leq \angle(\Upphi(v_i)Oa^{\prime})\\ & \Rightarrow \hbox{cos}(\angle(\Upphi(u)O\Upphi(v_i))) \geq \hbox{cos}(\angle(\Upphi(v_i)Oa^{\prime}))\\ & \Rightarrow \langle \Upphi(v_i) \cdot \Upphi(u)\rangle \geq \langle \Upphi(v_i) \cdot a^{\prime}\rangle\\ &\Rightarrow K(v_i,u) \geq K(v_i,g_i)\\ &\Rightarrow \hbox{e}^{-q\left\Vert{v_i-u}\right\Vert^2} \geq \hbox{e}^{-q\left\Vert{v_i-g_i}\right\Vert^2}\\ &\Rightarrow \left\Vert{v_i-u}\right\Vert^2 \leq \left\Vert{v_i-g_i}\right\Vert^2.\end{aligned} $$

□

Lemma 4.2 implies that $({\mathcal{E}}_{v_{i}} \cap P)$ corresponds to a hypersphere ${\mathcal{S}}_{v_{i}}$ in the data space centered at v _i with radius $\left\Vert{v_i-g_i}\right\Vert.$ We now must obtain $\left\Vert{v_i-g_i}\right\Vert$ in data space. Because $\left\Vert{\Upphi(v_i)}\right\Vert=1=\left\Vert{a^{\prime}}\right\Vert,$ we have

$$ \cos(\Uptheta)=\cos(\angle(\Upphi(v_i)Oa^{\prime}))=\langle \Upphi(v_i) \cdot a^{\prime}\rangle. $$

(10)

Thus, we solve for $\left\Vert{v_i-g_i}\right\Vert$ as follows:

$$ \left\Vert{v_i-g_i}\right\Vert = \sqrt{-\frac{\ln(\cos(\Uptheta))}{q}}. $$

(11)

All ${\mathcal{S}}_{v_{i}}$ have the same radii because $\Uptheta=\angle(\Upphi(v_i)Oa^{\prime})$ is the same for all $v_i \in V.$ We therefore denote $\left\Vert{v_i-g_i}\right\Vert$ by Z. The next step is to obtain $\langle \Upphi(v_i) \cdot a^{\prime}\rangle$ in order to calculate $\cos(\Uptheta).$ To do this, we first show in Lemma 4.3 below that $\langle \Upphi(v_i) \cdot a^{\prime}\rangle=\left\Vert{a}\right\Vert, \forall v_i \in V$ (see Fig. 3c). We then show in Lemma 4.4 that $\left\Vert{a}\right\Vert=\sqrt{1-R^2}.$ The final result will be that $\cos(\Uptheta)=\sqrt{1-R^2}.$

Lemma 4.3

$\langle \Upphi(v_i)\cdot a^{\prime} \rangle=\left\Vert{a}\right\Vert, \forall v_i \in V.$

Proof

Let z be the point obtained by orthogonally projecting $\Upphi(v_i)$ onto $\overrightarrow{Oa^{\prime}}.$ Thus, $\langle \Upphi(v_i)\cdot a^{\prime} \rangle=\left\Vert{z}\right\Vert.$ All the images of support vectors are projected to z because of Lemma 4.1 and the fact that, since all $\Upphi(v_i)$ are on the surface of the unit ball in feature space, $\left\Vert{\Upphi(v_i)}\right\Vert = \left\Vert{\Upphi(v_j)}\right\Vert=1.$ Since all other data images have smaller angle between their vector and $\overrightarrow{Oa^{\prime}},$ the distances between them and z is smaller than the distance between $\Upphi(v_i)$ and z. Therefore, a hypersphere centered at z with radius $\overline{z\Upphi(v_i)}$ encloses all data images. Now, the distance between z and a support vector image $\Upphi(v_i)$ is the shortest between $\Upphi(v_i)$ and $\overrightarrow{Oa^{\prime}}.$ Therefore, the hypersphere centered at z is the minimal hypersphere enclosing all the data images. Thus, z is a, the center of the minimal hypersphere. Consequently, $\langle \Upphi(v_i)\cdot a^{\prime} \rangle=\left\Vert{z}\right\Vert=\left\Vert{a}\right\Vert.$ □

Corollary 4.1 below is used in the proof of Lemma 4.4 immediately after the corollary.

Corollary 4.1

$\langle \Upphi(v_i)\cdot a \rangle =\left\Vert{a}\right\Vert^2, \forall v_i \in V.$

Proof

From the definition of cosine, we obtain $\cos(\Uptheta)=\frac{\langle \Upphi(v_i)\cdot a \rangle}{\left\Vert{\Upphi(v_i)}\right\Vert\left\Vert{a}\right\Vert}=\frac{\langle \Upphi(v_i)\cdot a^{\prime} \rangle}{\left\Vert{\Upphi(v_i)}\right\Vert\left\Vert{a^{\prime}}\right\Vert}.$ This results in $\langle \Upphi(v_i)\cdot a \rangle=\left\Vert{a}\right\Vert \langle \Upphi(v_i)\cdot a^{\prime} \rangle=\left\Vert{a}\right\Vert^2$ by Lemma 4.3. $\square$

Lemma 4.4

$\left\Vert{a}\right\Vert = \sqrt{1-R^2}.$

Proof

Let $\Updelta = \langle \Upphi(v_i)\cdot a \rangle$ where $v_i \in V$ (see Fig. 3d). Let $\Upgamma$ denote the shortest distance between a and $\overrightarrow{\Upphi(v_i)}.$ Then by the Pythagorean theorem², we have $R^2=\Upgamma^2+(1-\Updelta)^2$ and $\left\Vert{a}\right\Vert^2=\Upgamma^2+\Updelta^2.$ Therefore, $R^2=\Upgamma^2+1-2\Updelta+\Updelta^2=\left\Vert{a}\right\Vert^2+1-2\Updelta.$ Now we have $\left\Vert{a}\right\Vert^2=R^2-1+2\Updelta.$ Solving for $\Updelta$ yields $\Updelta=\frac{\left\Vert{a}\right\Vert^2-R^2+1}{2}.$ Now, applying Corollary 4.1 yields $\Updelta=\left\Vert{a}\right\Vert^2$ and $\left\Vert{a}\right\Vert^2=1-R^2=\Updelta.$ □

Equation 10 and Lemmas 4.3 and 4.4 together show that $\cos(\Uptheta)=\sqrt{1-R^2}.$ Consequently, Eq. 11 becomes

$$ Z = \sqrt{\frac{-\ln(\sqrt{1-R^2})}{q}}. $$

(12)

As in Sect. 4.2, we consider the extremes of q = 0 and $q = \infty.$ Equation 12 fails at these extremes. For q = 0 division by 0 is problematic. However, Z tends toward $\infty$ for small q values, where the entire data space is covered by each ${\mathcal{S}}_{v_{i}}.$ In this case, the cover of the data space contours and $\Upphi({\mathcal{X}})$ is complete. Additionally, the number of connected components of $\cup_{i} ({\mathcal{S}}_{v_{i}})$ equals 1, which is the same value as the number of connected components of the data space contours. The number of clusters is therefore equal to 1.

For $q = \infty, \ln(0)$ is undefined. Z tends towards 0 as q approaches $\infty.$ In this case, the cover of ${\mathcal{X}}$ and $P^{\prime}$ is perfect. That is, $\cup_{i} ({\mathcal{S}}_{v_{i}}) = {\mathcal{X}} = P^{\prime}.$ The number of connected components of $\cup_{i} ({\mathcal{S}}_{v_{i}})$ equals N _sv = N, which is the same value as the number of connected components of the data space contours. The number of clusters is therefore equal to N.

In our experiments, Z is a monotonically decreasing function of q; see Sect. 4.5.1. As with the question of feature space coverage, for q values greater than 0, it is possible for the union of hyperspheres to cover parts of the data space outside of $P^{\prime}.$ It is also possible for some data point images to be outside the union of hyperspheres. However, our experience again shows that these problems diminish quickly as q increases. In particular, for values at least as large as $\hat{q}^*,$ our experiments suggest that the number of clusters found by CCL is close to the number of data space contours. The success of the method is due to the fact that Z is chosen based on characteristics of the minimal hypersphere in feature space.

4.4 Assign cluster labels

Table 10 below shows the CCL algorithm. For the given q value, it first computes Z using Eq. 12. Next, support vectors are clustered using procedure ConstructConnectivity() (see Table 11) followed by finding connected components in the resulting adjacency structure. Connected components can be efficiently found using a standard algorithm such as Depth-First Search (DFS). Each connected component corresponds to a cluster. Therefore, the output of FindConnComponents() is an array of size N that contains cluster labels. Finally, the remaining data points are clustered by using the cluster label of the nearest support vector.

Table 10 Main algorithm of CCL

Table 11 ConstructConnectivity(V, Z)

Figure 4 shows evolution of circles for some increasing q values. Some data points may not be covered by the circles when q is close to the initial q value. However, since there is a small number of support vectors for those cases and they are connected to each other, all data points are clustered together. As q is increased, we get smaller spheres and eventually we obtain some reasonable cluster results for some q values.

Fig. 4

Cone Cluster Labeling example for data sets (a) and (e) in Table 1

The worst-case asymptotic running time complexity for ConstructConnectivity() and FindConnComponents() is in O(N ²_sv ). The time complexity of the CCL for loop is in O((N − N _sv)N _sv). Therefore, this algorithm uses time in O(NN _sv) for each q value. Unlike previous cluster labeling algorithms, this time does not depend on a number of line sample points which are along the line segment connecting two data points. Detailed execution time comparisons are provided in Sect. 4.5.3.

4.5 Results

As in Sect. 3.3, our implementations use MATLAB ^{TB 3} and Java and are run on an Intel Core 2 Duo T5200, 1.6GHz processor with 2GB of RAM.

In this section we first show that, for our data sets, the SV hyperspheres in cone cluster labeling capture all of our data points and they increasingly conform to the data points as q increases (Sect. 4.5.1). Next, we discuss CCL’s high-quality clustering (Sect. 4.5.2) that uses less computation time than existing SVC-based cluster labeling algorithms (Sect. 4.5.3). The four algorithms for comparison are CG, SVG, PG, and GD; these were introduced in Sect. 1.4.

4.5.1 Approximate cover

There is not yet a mathematical guarantee regarding conditions under which the SV hyperspheres cover all the data points in data space. Therefore, we present empirical data on the number of covered data points for different q values produced by our qListGenerator(). All of our data points are covered, and this applies not only to the data space but also to the covering in feature space of data points’ images by the union of cones.

In our experiments, the radius Z of the data space hyperspheres is a monotonically decreasing function of q. Since $\ln(\sqrt{1-R^2})$ is negative, if we assume that R ² is a monotonically nondecreasing function of $q, -\ln(\sqrt{1-R^2})$ increases logarithmically as q is increased. Consequently, the hyperspheres converge to the data points as q approaches infinity. Figure 5 shows a typical graph of Z ² versus q. This new result uses q values beyond those generated by our qListGenerator() in order to illustrate behavior for extreme values of q.

Fig. 5

Z ² versus q example with CCL for two-dimensional data set of Table 3a

4.5.2 Quality comparison

Sections 3.3.2 and 3.3.3 showed that CCL with qListGenerator() recovers known clustering structure for most of our data sets, with the best result typically occurring at the first q value ($\hat{q}^*$). This provides some validation of CCL’s results.

Sections 3.3.2 and 3.3.3 also compare CCL with CG. Of all the cluster labeling algorithms that use some sample points on a line segment joining two data points, CG creates the most consensus with the contours of the minimal hypersphere mapping. Therefore, comparing cluster quality results with CG is sufficient to validate CCL with respect to existing cluster labeling algorithms.

As an example of the strength of CCL, Fig. 6 compares our best CG clustering with that of CCL for the highly interleaved data set of Table 1d of Sect. 2.1. CCL correctly separates the data into two clusters, whereas CG does not.

Fig. 6

CCL example for two-dimensional data set of Table 3d. Left CG result, Right CCL result

4.5.3 Execution time comparison

In this section we compare three different types of execution times as well as total time of CG, SVG, PG, GD, and CCL: (1) constructing the adjacency matrix, (2) finding connected components from the adjacency matrix (this clusters some data points), and (3) clustering remaining data points.

Worst-case asymptotic time complexity is given in Table 12 below. In the table, m denotes the number of sample points tested along a line segment between two data points (see Sect. 1.4). As usual, N is the number of data points and N _sv is the number of support vectors. For GD, N _sep is the number of SEPs and k is the number of iterations to converge to a SEP. (Recall from Sect. 1.4 that a SEP is a stable equilibrium point.)

Table 12 Worst-case asymptotic running times for a single q value

Worst-case asymptotic time analysis is supplemented by actual running time comparisons. The total of the three actual execution times is measured and divided by the length of the q list to compute average times. Since a cluster labeling algorithm receives q as an input and produces a cluster result, the average time is appropriate as a measurement for execution time comparison. Below we compare running times of our implementations of the five cluster labeling algorithms for the two-dimensional and high-dimensional data sets of Sect. 2. Running times do not include time to solve the Lagrangian of Eq. 4, which is common to all the algorithms.

4.5.3.1 Comparisons for two-dimensional data

This section compares the three different running times listed at the start of Sect. 4.5.3. Theoretical times are shown in Table 12 and actual execution times are compared in Fig. 7.

Fig. 7

Two-dimensional execution time: a Comparison of adjacency matrix construction time (plus preprocessing). b Comparison of time for finding connected components in adjacency matrix. c Comparison of time for clustering of non-SV data points. d Comparison of total time of cluster labeling (Note different scale in b, c)

Preprocessing and constructing adjacency matrix Each cluster labeling algorithm constructs an adjacency matrix for cluster labeling. Preprocessing time is included in this discussion and in the actual running times of Fig. 7. Three of the algorithms have preprocessing: PG, GD, and CCL.

PG constructs a Delaunay Triangulation (DT) [26] by calling delaunay() that is a function provided by MATLAB. PG constructs an adjacency matrix by checking all edges in the DT. GD [22] is the newest SVC cluster labeling algorithm that we compare CCL with. GD obtains a SEP by searching for a minimum of R ²(x) (Eq. 7) for each data point $x \in {\mathcal{X}}.$ GD calls a gradient descent function fminsearch() provided by MATLAB’s optimization toolbox. We round the result to gather together SEPs that are close to each other. By doing this, we can obtain fewer SEPs. It makes GD faster without any observable loss of accuracy. CCL computes the Z value (Eq. 12) and converts it to a Gaussian kernel value to compare it with the kernel matrix directly. By doing this, we can save memory space and construct an adjacency matrix even faster.

CG, SVG, and GD require the most asymptotic running time for preprocessing plus adjacency matrix construction. Figure 7a shows actual running times when m is 20. The vertical axis gives the time for preprocessing plus adjacency matrix construction. As expected from the asymptotic analysis, CG, SVG, and GD are the most expensive. Both CG and GD are more expensive than SVG, PG, and CCL. Since the time complexity of GD for this part of SVC is O(mN ² k + mN ²_sep N _sv) versus O(mN ² N _sv) for CG, GD is more expensive in some cases for small values of N. As expected from the analysis, PG shows better performance than SVG, while CCL requires a very small amount of time compared with the other algorithms.

Finding connected components Connected components can be found using DFS in time proportional to the size of the adjacency matrix (see Table 12). The actual running times shown in Fig. 7b are consistent with the worst-case asymptotic times, except for PG. Since PG’s matrix is sparsely populated, its actual running time is significantly smaller than CG or SVG.

Labeling remaining data points CG clusters all data points during previous steps, so it is excluded from this comparison. To assign cluster labels to unclustered data points, SVG, PG, and CCL find the nearest SV and assign its cluster label; this requires O((N − N _sv)N _sv) time. In GD non-SV cluster labeling is done by taking the corresponding SEP’s cluster label. This requires O(N − N _sep) time if we keep a SEP index for each data point. Figure 7c shows a comparison result for four cluster labeling algorithms. Although the theoretical time of SVG, PG, and CCL is the same for this task, we do see some variation in running time. However, for all algorithms shown here, this task requires only a very small amount of time compared with the former two tasks. Note that the scale of this graph is in units of 10⁻³ s.

Total execution time comparisons To show the total performance of each cluster labeling algorithm, Table 12 shows asymptotic time while Fig. 7d sums the actual running time across the SVC tasks. As expected from Table 12, CCL shows the best performance. SVG is more expensive than PG. Although PG has reasonably small running time, it has the worst accuracy of all of the cluster labeling algorithms. CG’s expense prevents it from being practical for large data sets, even for 250 data points. Although GD’s worst-case asymptotic time exceeds CG, GD’s actual performance relative to CG depends on the data set. It appears that the performance of GD depends on the shape of clusters. This is suggested by the fact that the N = 180 data set includes clusters that are very close to each other.

4.5.3.2 Comparisons for high-dimensional data

PG using Delaunay triangulation does not appear in this section since it is not practical in high dimensions (>10). Table 12 shows worst-case asymptotic running times for the remaining four algorithms. These times contain an implicit dimensionality factor due to distance calculations in ${{\mathbb{R}}^d. }$ Figure 8 shows actual execution times for all of our high-dimensional data sets except for the N = 205, 200-dimensional case when m is 20. The trends in the graphs remain the same for that dataset.

Fig. 8

High-dimensional data: a Comparison of total time to construct adjacency matrix (plus preprocessing). b Comparison of total time of cluster labeling

Figure 8a represents CPU times to construct an adjacency matrix for high-dimensional data sets. CG shows the worst performance of all, followed by GD. Dimensionality highly affects GD’s performance, especially when finding SEPs. This is because the gradient descent algorithm is trying to find a minimum point in a high-dimensional space. In fact, for our 200-dimensional data set GD exceeded the maximum number of iterations for finding each SEP during fminsearch(). We note that this example greatly exceeds the maximum of 40 dimensions for the examples reported in [22]. CCL shows the best performance.

The comparison for finding connected components is omitted because, except for GD, the results are as expected from Table 12. The asymptotic cluster labeling time of non-SV data points is the same for both SVG and CCL. Since there is no difference between them and CG is excluded from this comparison, we omit the comparison.

Table 8(b) shows total execution time for cluster labeling. CCL shows the best performance for high-dimensional data while CG and GD show the worst performance.

5 Conclusion and future work

This paper provides two new advances in support vector clustering for a constant outlier parameter value: (1) a heuristic that explores Gaussian kernel width values, with values that empirically correspond to significant changes in clustering structure appearing early in the resulting list and (2) a strong cluster labeling method, based on cones in the feature space that correspond to hyperspheres in data space. Our estimate of the number of kernel width values depends on spatial characteristics of the data but not on the number of data points or the dimensionality of the data set. Future work on this method would automatically generate varying outlier parameter values.

Existing SVC cluster labeling algorithms, such as Complete Graph [1], Support Vector Graph [1], Proximity Graph [28], and Gradient Descent [22], sample a line segment to decide whether a pair of data points are in the same cluster. This creates a tradeoff between cluster labeling time and clustering quality. Our CCL method uses a novel covering approach that avoids sampling. Using the geometry of the feature space, we employ cones to cover part of the intersection of the minimal hypersphere with the surface of the unit ball. This maps to a partial cover of the contours in data space. The approximate cover uses hyperspheres in data space, centered on support vectors. Without constructing the union of these hyperspheres, data points are clustered quickly and effectively. The radius of the hyperspheres is generated using the results of the SVC quadratic programming model.

Experiments with data sets of up to 200 dimensions suggest that our new method generates clusterings whose quality is at least that of the most accurate sampling-based cluster labeling algorithm. All of our data points are covered by the union of support vector hyperspheres in data space. This reflects strong coverage of feature space image points by the union of cones. Furthermore, our approach is efficient compared with existing SVC methods. The worst-case asymptotic running time of our technique for a single kernel width value is less than that of the aforementioned algorithms. Our experiments support this by showing that its actual running time is also faster than these methods for our data sets. Our experiments suggest that it operates well even in high dimensions. The Complete Graph algorithm is expensive for large data sets. Neither Proximity Graph nor Gradient Descent appears practical in high dimensions.

Solving the Lagrangian optimization problem to find the radius of the minimal sphere is currently an SVC bottleneck that limits the number of data points for which SVC can be efficiently applied. However, SVC bears resemblance to a one-class Support Vector Machine (SVM), and the machine learning community has been working to increase the efficiency of SVM methods for kernel matrix handling and quadratic programming optimization. (See [4] for a comprehensive treatment of recent approaches to SVM for large datasets.) This similarity offers hope that SVM advances will improve the efficiency of SVC Lagrangian computation, thereby improving overall SVC performance on large datasets.