A novel look-ahead optimization strategy for trie-based approximate string matching

Abstract

This paper deals with the problem of estimating a transmitted string X ^* by processing the corresponding string Y, which is a noisy version of X ^*. We assume that Y contains substitution, insertion, and deletion errors, and that X ^* is an element of a finite (but possibly, large) dictionary, H. The best estimate X ⁺ of X ^*, is defined as that element of H which minimizes the generalized Levenshtein distance D(X, Y) between X and Y such that the total number of errors is not more than K, for all X ∈H. The trie is a data structure that offers search costs that are independent of the document size. Tries also combine prefixes together, and so by using tries in approximate string matching we can utilize the information obtained in the process of evaluating any one D(X _i , Y), to compute any other D(X _j , Y), where X _i and X _j share a common prefix. In the artificial intelligence (AI) domain, branch and bound (BB) schemes are used when we want to prune paths that have costs above a certain threshold. These techniques have been applied to prune, for example, game trees. In this paper, we present a new BB pruning strategy that can be applied to dictionary-based approximate string matching when the dictionary is stored as a trie. The new strategy attempts to look ahead at each node, c, before moving further, by merely evaluating a certain local criterion at c. The search algorithm according to this pruning strategy will not traverse inside the subtrie(c) unless there is a “hope” of determining a suitable string in it. In other words, as opposed to the reported trie-based methods (Kashyap and Oommen in Inf Sci 23(2):123–142, 1981; Shang and Merrettal in IEEE Trans Knowledge Data Eng 8(4):540–547, 1996), the pruning is done a priori before even embarking on the edit distance computations. The new strategy depends highly on the variance of the lengths of the strings in H. It combines the advantages of partitioning the dictionary according to the string lengths, and the advantages gleaned by representing H using the trie data structure. The results demonstrate a marked improvement (up to 30% when costs are of a 0/1 form, and up to 47% when costs are general) with respect to the number of operations needed on three benchmark dictionaries.

1 Introduction

We consider the traditional problem involved in the syntactic pattern recognition (PR) of strings, namely that of recognizing garbled words (sequences), and present a novel recognition strategy which involves tries, branch and bound (BB) pruning, and dictionary-based (as opposed to string-based) dynamic programming (DP).

Let Y be a misspelled (noisy) string, of length M, obtained from an unknown word X ^*, of length N, which is an element of a finite (but possibly, large) dictionary H, where Y is assumed to contain substitution, insertion, and deletion (SID) errors. Various algorithms have been proposed to obtain an appropriate estimate X ⁺ of X ^*, by processing the information contained in Y, and the literature contains hundreds (if not thousands) of associated papers. We include a brief review here.

The trie is a data structure that offers search costs that are independent of the document size. Tries also combine prefixes together, and so by using tries in approximate string matching [15, 27], we can utilize the information obtained in the process of evaluating any one D(X _i , Y), to compute any other D(X _j , Y), where X _i and X _j share a common prefix. As opposed to this, in the field of artificial intelligence (AI) Branch and Bound (BB) techniques [12] are well known, and have been used to prune paths for game trees etc. They are used when we want to prune paths that have costs above a certain threshold.

In this paper, we attempt to use the same data structure, the trie, for storing the strings in the dictionary so as to take advantage of the compact calculations for the distance matrix, by utilizing the common paths for the common prefixes. We then introduce a new BB pruning strategy that makes use of the fact that the length of the strings to be compared is known a priori. We thus propose to apply this new pruning strategy to the trie-based approximate search algorithm, which we call the look-ahead branch and bound (LHBB) scheme. By using these four features (the trie, BB, look-ahead, and dictionary-based dynamic programming), we can demonstrate a marked improvement, because this pruning can be done before we even start the edit distance calculations. LHBB helps us to search in portions of the dictionary where the word lengths are acceptable, without actually having to partition the dictionary, and at the same time make use of the effective properties of tries. The experimental results presented later shows improvements of up to 30%, and up to 47% when costs are general with small and large benchmark dictionaries. This high improvement is at the expense of just storing two extra memory locations for each node in the trie. Also, if the length of the noisy word is very far from all the acceptable words in the dictionary, i.e., those which can give an edit error smaller than K, the edit distance computations for this noisy word can be totally pruned with only a single comparative test. All of these concepts will be illustrated presently.

The organization of the paper is as follows. Section 2 presents a brief background for the work done in the paper. Section 3 describes, in detail, the new LHBB scheme when costs are of 0/1 form, while sect. 4 describes the technique when costs are general. Section 5 presents the experiments done and provides the results that demonstrate the benefits of the new method. Section 6 concludes the paper.

2 Background

Damerau [5, 20, 26] was probably the first researcher to observe that most of the errors found in strings were either a single substitution, insertion, deletion or a reversal (transposition) error. In much of the existing literature, the transposition operation has been modeled as a sequence of a single insertion and deletion. The first breakthrough in comparing strings using the three (the SID) edit transformations was the concept of the Levenshtein metric introduced in coding theory [16], and its computation. The Levenshtein distance, D(X, Y), between two strings, X and Y is defined as the minimum number (or the associated weights) of edit operations required to transform one string to another. This distance is intricately related to the costs associated, with the individual edit operations, typically the SID operations. These inter-symbol distances can be of a 0/1 sort, parametric [6, 23] or entirely symbol dependent [15, 26], in which case, they are usually assigned in terms of the confusion probabilities. In this case it is named general Levenshtein distance (GLD). In all of these cases, the primary DP rule used in computing the inter-string distance D(X,Y) is

$$\begin{aligned} D(x_1 \dots x_N,\quad y_1 \dots y_M) &= \min \left[ \left\{D(x_1 \dots x_{N-1}, \quad y_1 \dots y_{M-1}) + d(x_N,y_M) \right\},\right.\\ &\qquad\quad\; \left\{D(x_1 \dots x_{N},\quad y_1 \dots y_{M-1}) + d(\lambda,y_M) \right\},\\ &\qquad\quad\; \left.\left\{D(x_1 \dots x_{N-1},\quad y_1 \dots y_{M}) + d(x_N, \lambda) \right\} \right], \\ \end{aligned}$$

(1)

where d(a,b) is the inter-symbol distance between the two symbols a and b, and λ is the null symbol.

Wagner and Fischer [30] and others [26] also proposed an efficient algorithm for computing this distance by utilizing the concepts of DP. This algorithm is optimal for the infinite alphabet case and it has O(MN) worst case. Various amazingly similar versions of the algorithm are available in the literature, a review of which can be found in [5, 26, 28]. Masek and Paterson [17] improved the algorithm for the finite alphabet case, and Ukkonen [29] designed solutions for cases involving other inter-substring edit operations which runs in O(KN) worst case. Related to these algorithms are the ones used to compute the longest common subsequences (LCS) of two strings [5, 13, 14, 26, 28]. String correction using GLD-related criteria has been done for noisy strings [5, 9, 25, 26, 28], substrings [26, 28], and subsequences [20], and also for strings in which the dictionaries are treated as grammars [26, 28, 31]. A new approach to rapid sequence comparison, basic local alignment search tool (BLAST) [1], directly approximates alignments that are based on the optimization of a local similarity measure, the maximal scores pair (MSP). It yields the results that would approximate a DP algorithm for optimizing this measure. The direct applications of this tool are stated in [1] and include DNA and protein sequence database searches, motif searches, gene identification searches, and the analysis of multiple regions of similarity in long DNA sequence. Besides these, various probabilistic methods have also been studied in the literature [4, 25]. Indeed, more recently, probabilistic models which attain the information theoretic bound have also been proposed [22, 24]. The most recent survey on approximate string matching can be found in [18].

All early algorithms proposed for estimating X ⁺ requires the separate evaluation of the edit distance between Y and every element of X ∈H, and would thus unnecessarily repeat the same comparisons and minimizations for a substring and all its prefixes. Thus, most previous algorithms usually have many redundant computations.

The first pioneering attempt to avoid the repetitive computations for a finite dictionary was the one which took advantage of this prefix information, as proposed by Kashyap and Oommen [15]. The authors of [15] proposed a set-based algorithm to compute X ⁺ ∈ H. It calculated D(X,Y) for all X ∈ H simultaneously, and this was done by treating the dictionary as one integral unit and by using “dictionary-based” DP principles. They proposed a new intermediate edit distance called the “pseudo-distance”, from which the final edit distance can be calculated by using only a single operation. However, the algorithm in [15] was computationally expensive, because it required set-based operations in its entire execution. This work has been recently extended by Oommen and Badr [21], by presenting a feasible implementation for the concepts introduced in [15]. This was achieved by the introduction of a new data structure called the Linked Lists of Prefixes (LLP), which can be constructed when the dictionary is represented by a trie. The LLP, which in one sense actually implements a modified breadth first search (BFS) of the trie, rendered the solution proposed by Kashyap and Oommen [15] both feasible and practical.

2.1 Tries and cutoffs

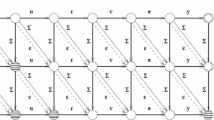
Tries offer text searches with costs which are independent of the size of the document being searched. The data are represented not in the nodes but in the path from the root to the leaf. Thus, all strings sharing a prefix will be represented by paths branching from a common initial path. Figure 1 shows an example of a trie for a simple dictionary of words {for, form, fort, forget, format, formula, fortran, forward}. Shang and Merrettal [27] used the trie data structure for exact and approximate string searching. They presented a trie-based method whose cost is independent of the document size. They proposed a K-approximate match algorithm on a text represented as a trie, which performs a depth first search (DFS) on the trie. The insight they provided was that the trie representation of the text drastically reduces the DP computations. The trie representation compresses the common prefixes into overlapping paths, and the corresponding column (in the DP matrix) needs to be evaluated only once.

Fig. 1

An example of a dictionary stored as a trie with the words {for, form, fort, fortran, forma, forget, format, formula, forward}

In [27], the authors applied a known pruning strategy called Ukkonen’s cutoff [29] to abort unsuccessful searches. For example, in Fig. 1, if the noisy word is Y = “fwt”, Ukkonen’s cutoff will force searching in any path to terminate prematurely, whenever the prefixes to be examined cannot lead to Y with an error less than K. This means that the paths that cannot lead a solution can be pruned, and thus the method limits the search to a portion of the search space. So, for example, if K  =  2, the path for the word “fortran” will be cut off after doing the calculations at node r, and so no more search will be done at the trie rooted at node r. Figure 2 shows the pruning done when applying Ukkonen’s cutoff technique. Chang and Lawler [7] showed that Ukkonen’s algorithm evaluated O(K) DP table entries. If the fanout of the trie is Σ, the trie method needs to evaluate only O(K| Σ |^K) DP table entries, which is independent of the number of noisy words we are searching for. Their experiments showed that their method significantly out-performs the nearest competitor for K = 0 and K = 1, which are arguably the most important cases. They also compared their work experimentally with agrep, a software package for Unix that implements the algorithm presented in [32], which is an extension (for a numeric scheme) for the exact string matching algorithm developed by Baeza-Yates and Gonnet [2]. Also, a similar cutoff technique, called the edit distance cutoff, was used in [19], to devise error-tolerant finite-state recognizers.

Fig. 2

The cutoff done for the trie example when applying Ukkonen’s cutoff, for Y = “fwt” and K = 2

Most of the dictionaries used in string correction contain strings of different lengths. This variation in the string lengths could help in excluding many strings from the computation of the corresponding edit distances when compared against the noisy word, as strings of this length could not have possibly given rise to the given noisy string. Indeed, this conclusion is because the difference in their lengths is more than the number of errors allowed. This property was used in [11] to partition the dictionary and eliminate the words to be compared in the dictionary. A set is built from all possible partitions, and a string-to-string correction technique was used to get the best match. The authors of [11] limited their discussion to cases where the error distance between the given string and its nearest neighbors in the dictionary was small. The problem with this method is that this set can be quit large for larger values of K, and can thus include the whole dictionary. This could lead to string-to-string comparisons for a large partition of the dictionary, or even the whole dictionary itself. Another drawback of this method is that two words sharing common prefixes, but which reside in different partitions, will necessitate redundant computations for the entire common segments.

3 Look-ahead branch and bound scheme

Given the fact that the dictionary is stored in a trie, any PR-related search for a word in H will have to search the entire trie. To minimize the computational burden, we shall now show how we can use concepts in AI to “reduce” the portion of the search space investigated. We do this by invoking the principles of BB strategies.

In AI, whenever we encounter a search space, the latter can be searched in a variety of ways such as by invoking a BFS, a DFS, or even a best-first search scheme, where, in the latter, the various paths are ranked by using an appropriate heuristic function. But if the search space is very large, BB techniques can be used to prune the search space. This is done by estimating the costs of the various potential paths with a suitable heuristic, and if the cost of any path exceeds a pre-set threshold, this path (or branch) is pruned, and the search along this path is aborted. What we pay are that we need more processing operations per node, and possibly additional storage for storing some local indices. But what we gain is that we can prune numerous unneeded paths, and thus save enormous redundant computations.

In the present case, we now investigate how we can eliminate searching along some of the paths of the trie. Thus, we effectively map the trie into the “search tree” of an AI algorithm, and seek a suitable heuristic to achieve the pruning. The heuristic that we propose has three characteristics, namely, it has a static component, a dynamic component, and finally, it must be of a look-ahead sort, as opposed to the cut-off methods already proposed [19, 29]. Indeed, the edit distance cutoff used in [19] and Ukkonen’s cutoff used in [27] depend on the a posteriori evaluation of the edit distances even as we process more characters from prefixes of strings in the dictionary. In other words, in these schemes, the pruning is invoked only after calculating the edit distance of the prefix being currently processed, and results only when there is no possible conversion from this prefix to the noisy word in hand. We will now examine each of the components of our BB heuristic.

3.1 The look-ahead component

The idea that we advocate is to prune, from the calculations, the sub-tries in which the strings stored are not within a pre-defined acceptable condition. The lengths of the string stored in subtrie(c) can be directly related to the maximum edit distance allowed, and thus can simplify the equations and the condition that has to be tested per node even before we traverse the path. The maximum edit distance or error can give an indication about the maximum and minimum lengths of the strings allowed.

We propose a strategy by which we will not traverse the subtrie(c) unless there is a “hope” of determining a suitable string in it, where the latter is defined as the string that could be garbled into Y with less than K errors. Stating that a subtrie(c) has to be pruned, implies that the minimum possible errors of all the substrings (to transform them into Y) that are stored in subtrie(c) is bigger than K. So, in our new heuristic, because the maximum edit distance or error can be known a priori, and because the lengths ¹ of the strings in H are also known a priori, we can look ahead at each node, c, and decide whether we have to prune the subtrie(c). If we do, we are guaranteed that all the strings stored will not possibly lead to Y with less than K errors.

3.2 The dynamic component

The lengths of the prefixes to be processed can also be directly related to the maximum edit distance error K. The maximum and minimum allowed lengths for all strings stored in a subtrie(c) are easily related to the length of Y, M, and to the error K, as

$$ {\rm max}({\rm length}(X^+)) \leq M + K. $$

Further, if we are at node c and the length of the prefix calculated so far is N′, and the length of any string in subtrie(c) is N′′, this constraint can be re-written as

$$ {\rm max}\left(N^{\prime} + N^{\prime\prime} \right) \leq M + K. $$

Since N′ is constant per node c, this means

$$ {\rm max}\left(N^{\prime\prime} \right) \leq M - N^{\prime} + K. $$

(2)

Similarly, since K is the absolute number of errors,

$$ {\rm min}\left(N^{\prime\prime} \right) \geq M - N^{\prime} - K. $$

(3)

Using these dynamic equations for the minimum and maximum lengths allowed for string eligible to be X ⁺, we can easily test at each node if the lengths of the suffixes stored are within these acceptable ranges, namely, min(N′′), max(N′′). The corresponding inequalities which involve generalized edit distances are currently being derived.

3.3 The static component

To test if we are within acceptable ranges for the potential candidates for X ⁺, we need to store the information needed for these calculations within each node, so that the conditions can be tested locally (and quickly) within the corresponding node. Fortunately, this information is already known a priori and is easily calculated and stored. More specifically, we need to store two values at each node of the trie, which are:

• Maxlen: A value stored at a node which indicates the length of the path between this node and the most distant node representing an element of the dictionary H. This is actually the length of the largest suffix for all the suffixes stored in the subtrie rooted at this node.

• Minlen: A value stored at a node which indicates the length of the path between this node and the least distant node representing an element in H. This is actually the length of the smallest suffix for all the suffixes stored in the trie rooted at this node.

3.4 The overall heuristic

At each node of the trie, before we do any further computations, we test the following conditions, referred to as the LHBB conditions:

• (a) Minlen  >  M  −  N′  +  K obtained by negating Eq. 2, or

• (b) Maxlen  <  M  −  N′  −  K obtained by negating Eq. 3.

If (a) or (b) is true, it means that there is no hope of finding a solution within the present subtrie, and so we prune the calculations for the subtrie. The LHBB, as its name implies, first looks forward at each node, and sees if it is expected to perform any further calculations. If at any time we reach a string X in the dictionary (which is thus an accepting node), we accept the string if the D(X,Y) ≤  K.

Consider, for example, the same trie in Fig. 1, where the noisy word Y = “fwt”. By applying the LHBB, for K  =  2, the path for the word “fortran” will be pruned before doing the edit distance calculations at node t, and so no further search will be done at the trie rooted at node t. But since node t is an accepting node, we need to calculate its edit distance. This thus saves two levels of computations for the edit distance for the trie rooted at node t with respect to the previous method. The path for the word “forget”, however, will be pruned before doing edit distance calculations at node g. Since g is not an accepting node, it will be also pruned from further calculations. Figure 3 shows the pruning done when applying the LHBB technique only.

Fig. 3

The cutoff done for the trie example when applying only the LHBB technique, for Y = “fwt” and K  =  2

The LHBB can also be used in combination with Ukkonen’s cutoff used earlier for tries. The LHBB requires only the testing of the above conditions using the values stored locally within each node. Figure 4 shows the pruning when applying both techniques.

Fig. 4

The cutoff done for the trie example when applying both Ukkonen’s cutoff and the LHBB technique, for Y = “fwt” and K  =  2

3.5 Algorithm for obtaining X ⁺ using LHBB

In this section, we present the algorithm for obtaining X ⁺, by pruning using LHBB in trie-based calculations. The algorithm follows the steps of the trie method except that it includes the LHBB pruning (see Algorithm 1). The lines indicated by asterisks show the modified part. Also, computing the Maxlen and Minlen values is fairly straightforward, and can be done during the construction of the trie, as the strings are inserted one by one. When inserting a string in the trie, we already know the length of this string, and hence the values of Maxlen and Minlen need to be adjusted only for the nodes along the path included in the insertion, which can be done by comparing their old values with the length of the newly inserted string.

Algorithm 1

Algorithm LHBB

4 A look-ahead BB scheme for general costs

When general costs are used, relating the computed (or anticipated) edit distance to the maximum edit distance or the maximum number of errors is not possible, and so Ukkonen’s cutoff cannot be used. In this case, as far as we know, the only available technique that can be used to prune the trie is the one we propose. This is because the new technique can serve as a direct link between the length of the strings in the dictionary and the maximum number of errors, independent of the costs that are assigned for the errors, while similarly using the same LHBB conditions.

In this scenario, we again encounter the three components of the LHBB as follows:

• The look-ahead component: The lengths of the string stored in subtrie(c) can still be directly related to the maximum edit distance allowed. This is because the LHBB technique builds a relation between the lengths of the strings and the maximum number of errors. Thus, independent of the costs we are using, we will still be able to apply the technique. We can still look ahead at each node, c, and decide whether we have to prune the subtrie(c). By doing this, we are guaranteed that all the strings stored will not possibly lead to Y with less than K errors.

• The dynamic component: At each node of the trie, before we do any further computations, we can still test the same LHBB conditions obtained by negating Eqs. 2 and 3. As we see, the calculations for the proposed LHBB technique do not depend on the costs for the inter-symbols at all. It only depends on the length of the noisy word Y, the length of the prefix calculated so far N′, and the maximum number of errors K, that is known a priori. If any of the LHBB conditions is true, it still implies that there is no hope of finding a solution within the present subtrie, and so we can prune the calculations for the subtrie.

• The static component: We still need to store two values Minlen and Maxlen at each node of the trie to be able to calculate the LHBB conditions.

When the maximum number of errors is used as a criterion, a further improvement can be done by pruning the paths if the length of the prefix calculated so far is larger than M + K, and this (as a replacement for Ukkonen’s cutoff) can be used in conjunction with the LHBB technique. Other enhancements can be applied when only the best match is required. In this case, we can “cut off” the subtrie at any node if the min value (the minimum edit distance value in any column during the calculation, which is the minimum edit distance value to change any prefix in H to Y) is larger than the edit distance of the nearest neighbor word found so far, and if it is, we can prune the trie at this node. An analogous technique was also applied in [27] when the best match was required. We shall see that when applying the new technique, the enhanced algorithm yields an even better performance.

5 Experimental results

To investigate the power of our new method with respect to computation we conducted various experiments. The results obtained were remarkable with respect to the gain in the number of computations needed to get the best estimate X ⁺. By computations we mean the addition and minimization operations needed, including the minimization operations required for calculating the LHBB criterion ². The LHBB scheme was compared with the original trie-based work for approximate matching [27] when the edit distance costs were of a 0/1 form and of a general form.

Three benchmark data sets were used in our experiments. Each data set was divided into two parts: a dictionary and the corresponding noisy file. The dictionary was the words or sequences that had to be stored in the Trie. The noisy files consisted of the strings which were searched for in the corresponding dictionary. The three dictionaries we used were as follows:

• Eng ³ This dictionary consisted of 964 words obtained as a subset of the most common English words [10] augmented with words used in the computer literature.

• Dict ⁴ This is a dictionary file used in the experiments done by Bentley and Sedgewick in [3].

• Webster’s unabridged dictionary This dictionary was used by Clement et al. [8] to study the performance of different trie implementations. The alphabet size is 54 characters.

The statistics of these data sets are shown in Table 1.

Table 1 Statistics of the data sets used in the experiments

Three sets of corresponding noisy files were created using the technique described in [24], and in each case, the files were created for a specific error value. The three error values tested were for K  =  1, 2, and 3, as are typical in the literature [19, 27].

The two methods, Trie (the original method) [27] and our scheme, LHBB, were tested for the three sets of noisy words. We report below a summary of the results obtained in terms of the number of computations (additions and minimizations) in millions.

We conducted two sets of experiments: The first set of experiments was when the costs were of a 0/1 form, and the second set of experiments was when the costs were general and were generated from the table of probabilities for substitution (typically called the confusion matrix), which was based on the proximity of character keys on the standard QWERTY keyboard and is given in [22] ⁵. The conditional probability of inserting any character given that an insertion occurred was assigned the value 1/26; and the probability of deletion was set to be 1/20. All the experiments were done on a Pentium 4 machine with 3.2 GHZ, 1 GB RAM, and 80 GB hard disk.

5.1 Experimental setup I: 0/1 costs

In Tables 2, 3, and 4, the results show the significant benefits of the LHBB scheme with up to 30% improvement. For example, for the Webster’s dictionary, when K  =  1, the number of computations is 6,849 and 4,776 millions, respectively, which represents an improvement of 30.26%. The improvement decreases as the number of errors increases, which can be expected because as K increases, more neighbors have to be tested, which, in turn, implies that more parts of the trie have to be examined. By studying the results we see that the improvements are quite prominent even for K  =  2 and 3. The improvement is more than 20%, which is considerable compared to what can be achieved by the state-of-the-art trie methods. Additionally, observe that the search is still bounded by the O(K| Σ |^K) DP table entries, because we use the trie to store the dictionary. This is in contrast to the method discussed in [11], where the set of all possible partitions will become so large as K increases, and the method is reduced to the tedious corresponding sequential string-to-string comparison techniques.

Table 2 The results obtained in terms of the number of operations (additions and minimizations) needed when the maximum number of errors K  =  1, and the costs are of a 0/1 form

Table 3 The results obtained in terms of the number of operations (additions and minimizations) needed when the maximum number of errors K  =  2, and the costs are of a 0/1 form

Table 4 The results obtained in terms of the number of operations (additions and minimizations) needed when the maximum number of errors K  =  3, and the costs are of a 0/1 form

Further improvement can be obtained when the algorithm is only searching for the best match. We can then apply the same strategy for the same dictionaries when K  =  1, 2, and 3. The results are shown in Table 5 for the Dict dictionary, as the results for the other dictionaries are almost identical. The results show the significant benefits of the LHBB scheme with up to 26% improvement (compare with Table 2). For example, when K  =  1, the number of computations is 1,120 and 819 millions respectively, which represents an improvement of 26.87%. The improvement decreases as the number of errors increases.

Table 5 The results obtained in terms of the number of operations (additions and minimizations) needed when maximum number of errors, K is 1, 2, and 3, the costs are of 0/1 from, the best match optimization is applied, and the Dict dictionary is used

5.2 Experimental setup II: general costs

The second set of experiments was conducted when the costs were general as explained above. In this case Ukkonen’s cutoff cannot be applied as the maximum number of errors cannot be related to the edit distance costs any more. The results are shown in Table 6 for the Dict dictionary, and not included for the other dictionaries as the results for the other dictionaries are relatively the same. The results show the significant benefits of the LHBB scheme with up to 47.98% improvement. For example, when K  =  1, the number of computations is 66,545 and 34,614 millions, respectively, which represents an improvement of 47.98%.

Table 6 The results obtained in terms of the number of operations (additions and minimizations) needed when maximum number of errors, K is 1, 2, and 3, the costs are general, and the Dict dictionary is used

When the best match is required and the inter-symbols costs are general, we can apply the same strategy for the same dictionaries for the cases when K  =  1, 2, and 3. The results are shown in Table 7 for the Dict dictionary (the results for the other dictionaries are omitted). The results show the significant benefits of the LHBB scheme with up to 42.59% improvement. For example, when K  =  1, the number of computations is 16,827  and 9,661 millions respectively, which represents an improvement of 42.59%. If we compare the results of Tables 6 and 7, we will find that the best match optimization add further improvement of 72% for the LH when K  =  1 and the costs are general. This best match improvement is not significant when the costs are of a 0/1 form because in this case Ukkonen’s cutoff is already applied.

Table 7 The results obtained in terms of the number of operations (additions and minimizations) needed when maximum number of errors K is 1, 2, and 3, the costs are general, the best match optimization is applied, and the Dict dictionary is used

6 Conclusion

In this paper, we presented a new BB scheme that can be applied to approximate string matching using tries, which we called a Look-Ahead Branch and Bound scheme or the LHBB-trie pruning strategy. The new scheme made use of the information about the lengths of the strings stored in the dictionary and assumed that the maximum number of errors was known a priori. The heuristic that we proposed, worked specifically on a trie and had three characteristics, namely a static component, a dynamic component, and finally, was of a look-ahead sort, as opposed to the cutoff methods already proposed in [19, 29]. Several experiments were conducted using three benchmarks dictionaries for noisy sets involving different error values, K =  1, 2, and 3.

The results demonstrated a significant improvement, with respect to the number of operations needed, for approximate searching using tries which could be even as high as 30%. The new LHBB pruning could also be used together with Ukkonen’s cutoff technique [29]. We also demonstrated how we could extend the latter for the case when the costs were general, in which case improvements of up to 47% were obtained. Finally, further results were also obtained when the algorithm utilized the additional best match optimization.