Introduction

Long-term leakage from hydraulic/water conveyance tunnels affects the safe operation and economic benefits of a reservoir. These tunnels are often reinforced by a steel lining to resist high internal pressures—examples include Qinglong hydropower station, Jinping-II hydropower station, and Liyang pumped storage power station in China; La Grande-II hydropower station in Canada; Goina hydropower station in India, etc. However, steel linings are complicated and costly to construct and are only used in areas with branch pipes under high internal water pressure in the lower horizontal section in front of some underground powerhouses. The upper horizontal and inclined shaft sections of water conveyance tunnels are constructed of reinforced concrete; therefore, some leakage is inevitable owing to the partial cracking of the lining under high internal water pressures (Yi et al. 2011; Shin et al. 2012). The estimation of leakage from these tunnels under high internal water pressure during water-filling tests, or normal operation of the reservoir, is deemed necessary.

More research has concentrated on water inflow into such tunnels (Hwang and Lu 2007; Zarei et al. 2011; Chiu and Chia 2012; Russo et al. 2013; Chen et al. 2016; Rezae 2017; Su et al. 2017). Many methods, such as analytical solutions and numerical analyses, have been employed to calculate water inflow to conveyance tunnels. Goodman et al. (1965) proposed a steady-state analytical solution to calculate groundwater inflow into a circular tunnel. Based on the Goodman equations, some modified solutions have been presented (Lei 1999; El Tani 2003, 2010; Karlsrud 2001; Moon and Fernandez 2010; Liu et al. 2018). Numerical models of fluid flow into tunnels have also been presented (Molinero et al. 2002; Masset 2011; Farhadian et al. 2016; Nikvar Hassani et al. 2016). Comparisons, in relation to prediction of groundwater inflow into a circular tunnel, between analytical solutions and numerical modeling were conducted by Farhadian et al. (2017) and Nikvar Hassani et al. (2018). The results showed that numerical simulation was more reliable in complex geomechanical and hydrogeological conditions. Some geological factors involved in and/or prior to tunnel construction—fracture or fault zones, fracture aperture width and length, the depth of cover above the tunnel, and the permeability of fractured rocks—have been considered to estimate water inflows (Kitterød et al. 2000; Kværner and Snilsberg 2011; Nilsen and Palmström 2001; Huang et al. 2013; Sharifzadeh et al. 2013; Holmøy and Nilsen 2014; Farhadian et al. 2017).

For a completed tunnel, with its lining, the leakage is mainly related to the permeability of the reinforced concrete lining, the surrounding rock, grouted zones, and fault zones across the tunnel. The groundwater inflow into the tunnel can decrease by 90–95% when using tunnel grouting (Zhang et al. 2015); furthermore, the permeability of the lining and grouting zones will increase with rising water pressure in the tunnel, in particular in the presence of cracks in the lining (Yi et al. 2011).

However, little attention has been paid to the research of leakage from hydraulic pressure tunnels. For unlined water tunnels, the leakage has been estimated by Panthi and Nilsen (2010) and found to be mainly affected by the hydrostatic head and the geometric characteristics of the rocks—such as joint connectivity rate, joint roughness, and joint orientation (Lyu et al. 2018). However, the method could not be applied to lined water tunnels subjected to high internal water pressure because the joints therein were grouted; thus, the leakage only occurs through cracks formed in the concrete lining (Ren et al. 2009). A reinforced concrete lining’s design is often based on the assumption that the water pressure acts on the inner surface of the concrete lining. Leakage through the lining will increase with increasing water pressure due to a possible gap between the lining and the grouting zone (Fernandez and Alvarez Jr. 1994; Bobet and Nam 2007). Additionally, with the increase in internal pressure, the width of the cracks in the lining, and the permeability thereof, may be changed due to deformation of the surrounding rocks (Schleiss 1997); therefore, leakage from the tunnel depends on the width of the cracks (Yi et al. 2011). Some coupling processes based on elastic damage theory and groundwater flow theory have been developed (Schleiss 1997; Rong et al. 2006; Bian and Xiao 2010; Shin et al. 2012; Hu et al. 2013). These studies were mainly focused on the analysis of cracks in tunnel linings, and the design of, and loads acting on, the lining. The calculation of leakage was rarely discussed because it was difficult to determine the position, distribution, and number of cracks. In this study, the tunnel, with its reinforced concrete lining, was treated as a homogeneous weak permeable medium without considering the development of cracks in its lining.

The aim of this research was to deduce an analytical solution with which to estimate leakage from a hydraulic pressure tunnel by considering the effects of tunnel length, the intersection angle between the tunnel and the horizontal plane, the permeability of the lining, and the water filling level. The leakage calculated by using the analytical method was validated using observation data, and sensitivity analysis of the parameters is discussed. The leakage was estimated with the verified analytical method during normal operation of the reservoir, which can provide some basis for subsequent leakage control measurements in hydraulic pressure tunnels.

The work involved analysis of the leakage from a tunnel. Firstly, the location, scale, and configuration of the tunnel, as well as the permeability of the rock surrounding it, were determined; secondly, an analytical solution was developed considering the tunnel as being completely, and partially, filled with water. Finally, the analytical solution was verified and used to assess the amount of leakage from the water-conveyance tunnels in a case study based on Heimifeng Pumped Storage Power Station (HPSPS) in China.

Research area

Study site

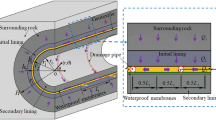
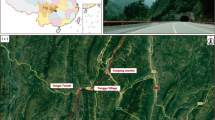
HPSPS is situated in Wangcheng County, Hunan Province, around 25 km from Changsha City, China. It includes four reversible pumped storage units, and each unit has an installed capacity of 300 MW. It is composed of upper and lower storage reservoirs, an underground powerhouse, and two water-conveyance tunnels (Fig. 1). Water levels above sea level (a.s.l.) for the upper and lower storage reservoirs are 400 and 103.7 m, respectively. The nominal productive head, the minimum water head required for the rated output of a hydraulic turbine under normal operation, is 295 m. The underground powerhouse is located at the tail of the water-conveyance tunnels and close to the lower storage reservoir.

Fig. 1
figure 1

a Location of Heimifeng Pumped Storage Power Station (HPSPS), China. b Layout of the hydraulic structures and c geological cross-section

Full size image

The two water-conveyance tunnels are arranged in parallel at a separation of 46 m and each tunnel has a radius of 4.25 m. Each tunnel corresponds to two pumped storage units, and each unit has two functions: power generation and pumping. Each of the water-conveyance tunnels consists of an upper horizontal section, an inclined shaft section, and a lower horizontal section (Fig. 2a), whereby the upper horizontal section was drilled over a length of 280 m at a slope of 8% from an elevation of 365.5 to 343.25 m a.s.l, while the inclined shaft section was drilled over a length of approximately 420 m at a slope of 50° from an elevation of 341.51. to 17.85 m a.s.l. The lower horizontal section consists of a horizontal segment, a Y-type branch tunnel, and two tailrace tunnels. The lengths of the horizontal segments of the two diversion tunnels (Nos. 1 and 2) are 193.93 and 208.93 m, respectively. A Y-type branch tunnel was arranged to connect the horizontal segment and the corresponding tailrace tunnels for each diversion tunnel (Fig. 2b). Both of the Y-type branch tunnels have a bifurcation angle of 60° and are 24.31 m long and were designed with variable radii from 4.25 m (main tunnel) to 2.65 m (branch tunnel). These branch tunnels were reinforced by using steel plate lining with very low permeability, so that the branch tunnels are deemed almost impermeable. The two diversion tunnels were strengthened using a reinforced concrete lining with a thickness of 0.5–0.8 m. The chainages covered by the reinforced concrete lining range from 1Y0 + 118.354 to 1Y0 + 933.552, where ‘1Y’ refers to the No. 1 diversion tunnel, ‘0’ denotes the centre of the upper storage reservoir, and ‘118.354’ represents the distance to the centre (Fig. 2a) and from 2Y0 + 118.354 to 2Y0 + 948.552 for the diversion tunnels Nos.1 and 2, respectively.

Fig. 2
figure 2

Location of water-conveyance tunnels: a No. 1 diversion tunnel, and b Branch tunnel

Full size image

Geological framework

The area is situated in an area containing low mountains, of which the elevations of the ground surface in the east are generally about 300 m greater than those in the west. Granite in the late Yanshan and Quaternary strata (Q) are revealed across the study site. As shown in Fig. 1a, Monzonitic granite is widely distributed around the water-conveyance tunnels and underground powerhouse. The Quaternary strata such as the eluvial layer (Qedl), riverbed alluvium (Qal), and colluvial deposit (Qcol + dl), are mainly distributed near the ground surface with thicknesses ranging from 2 to 5 m.

The faults revealed in the upper storage reservoir strike N50–70°E and incline NW with a dip angle of 54–78°, whereas the faults shown in the lower storage reservoir strike N43–65°W and incline NE with a dip angle of 55–82°. Additionally, some granitic pegmatite veins lie close to the lower horizontal section with a strike of NE and a width of 0.2 m. Many fractures with steep dip angles of 65° have developed in the area of the underground powerhouse and some of these fractures are filled by granitic pegmatite and quartz veins. Cross-cutting of fractures and faults constitutes the groundwater storage space and conducting pathways. Groundwater is recharged by precipitation and discharged to the gulley in the form of spring water through a fractured aquifer system.

Types and permeability of surrounding rock

According to data from exploratory adits, boreholes, and geophysical tests, the rocks surrounding the tunnels are divided into five types based on the Standard for Engineering Classification of Rock Masses (GB50218-94). Integrity and strength indices of rocks become weaker from classes Ι–V; however, the permeability of the rocks gradually increases from classes I–V. The types of surrounding rocks around two water-conveyance tunnels in HPSPS are displayed in Table 1: the rocks surrounding the No. 1 diversion tunnel exhibit better integrality than those around the No. 2 diversion tunnel. The horizontal segments for the two diversion tunnels are about 215 m below ground surface and a fault, F15, is close to two branch tunnels of the ‘Y’-type tunnel. The distance from F15 to the intersection of the main and branch tunnels is 14 m for the No. 1 diversion tunnel and 4 m for the No. 2 diversion tunnel (Fig. 2b); hence, the percentage of rock class IV is larger in the lower horizontal sections due to the effect of F15.

Table 1 Percentage by type of rocks surrounding the two water-conveyance tunnels
Full size table

According to results from high water-pressure tests and pumping tests in the field and penetration tests conducted on rock blocks in the laboratory, hydraulic conductivity can be calculated for the different surrounding rocks (Xu et al. 2012; Ma et al. 2014; Wu et al. 2015a, b, 2016, 2017). Hydraulic conductivities of surrounding rocks for types II-IV are i × 10−6 cm/s, i × 10−4 to i × 10−6 cm/s, and i × 10−4 cm/s, respectively, under natural conditions, where i is an arbitrary constant between 1 and 10; however, cement and chemical grouts have been used in different types of surrounding rocks. The permeability is increased by between two and four orders of magnitude relative to that prevailing before grouting.

Methods

Analytical solution of tunnel leakage

During the normal operation of the reservoir, groundwater in the rock, originating from leakage from the water-conveyance tunnels, has a gradually varying flow rate owing to the changes in the upper and lower reservoir water levels. Eventually, a steady-state flow regime is established. The leakage was governed by the boundary conditions imposed by the reservoirs. Because the minimum thickness of the unsaturated zone is about 60 m, the travel time of groundwater from the top of the unsaturated zone to the groundwater level is long due to the low permeability of the surrounding rock. The change in groundwater level caused by precipitation is less than that caused by leakage; therefore, it is assumed that (1) rainfall recharge does not need to be considered for this aquifer, (2) the rocks surrounding the tunnels are homogeneous isotropic media, (3) the bottom of the aquifer is horizontal, (4) the groundwater is a gradually varying flow and satisfies Darcy’s law, and (5) water flow along the water-conveyance tunnels from the upper to lower storage reservoirs can be regarded as one-dimensional (1D) owing to the small hydraulic gradient between the two reservoirs. Based on these assumptions, the upper reservoir can be regarded as the left river, and the lower storage reservoir as the right river. The formula for steady flow under a phreatic aquifer between two reservoirs can be expressed as (Bear 1972):

$$ {h}^2={h}_{\mathrm{u}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}{l}x $$
(1)

where hu and hl refer to the upper and lower storage reservoir water levels respectively, h is the phreatic water level at an arbitrary position between the upper and lower storage reservoirs, l is the horizontal distance between two reservoirs, and x denotes the position or horizontal coordinate (Fig. 3a).

Fig. 3
figure 3

Conceptual models for an underground water pipe. a Underground water pipe filled with water, b underground water pipe part-filled with water, and c schematic diagram of tunnel section

Full size image

According to Darcy’s law, leakage or discharge per unit width from water-conveyance tunnels under water filling condition can be given by:

$$ {q}_1={K}_1\cdot \frac{h_{\mathrm{u}}-{h}_{\mathrm{c}}}{d_1}\cdot 2\uppi R $$
(2)
$$ {q}_2={K}_2\cdot \frac{h_{\mathrm{c}}-h}{d_2}\cdot 2\uppi \left(R+{d}_1\right) $$
(3)

where q1 and q2 represent the leakage per unit width with a concrete lining and the grouting zone in the surrounding rock, K1 and K2 denote the hydraulic conductivities of the two grouting zones, d1 and d2 represent the thicknesses of the two grouting zones respectively, hc is the water-table head above the concrete lining, and R is the radius of the water-conveyance tunnel (Fig. 3c). The leakage in any section should be equal under steady flow conditions, and q1 = q2; hence, using Eqs. (2) and (3), hc can be calculated as:

$$ {h}_{\mathrm{c}}=\frac{\uppi {Rd}_2{K}_1{h}_{\mathrm{u}}+\uppi \left(R+{d}_1\right){d}_1{K}_2h}{\uppi \left(R+{d}_1\right){d}_1{K}_2+\uppi {Rd}_2{K}_1} $$
(4)

The leakage, q, can be rewritten as:

$$ q={K}_1\cdot \frac{h_{\mathrm{u}}-h}{d^{\prime }}\cdot 2\uppi R $$
(5)
$$ {d}^{\prime }=\frac{\left(R+{d}_1\right){d}_1{K}_2+{Rd}_2{K}_1}{\left(R+{d}_1\right){K}_2} $$
(6)

where d′ is defined as an effective hydraulic path. If K1 = K2 = K, d′ can be rewritten as:

$$ {d}^{\prime }={d}_1+\frac{R}{R+{d}_1}\cdot {d}_2 $$
(7)

For a hydraulic conveyance tunnel, the ratio of R/d1 is often close to, or greater than, 10, so d′ = d1 + d2, and the leakage can be expressed as:

$$ q=K\cdot \frac{h_{\mathrm{u}}-h}{d_1+{d}_2}\cdot 2\uppi R $$
(8)

Substituting h from Eq. (1) into Eq. (5), the leakage from a water-conveyance tunnel can be given by:

$$ q={K}_1\cdot \left({h}_{\mathrm{u}}-\sqrt{h_{\mathrm{u}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}{l}x}\right)\cdot \frac{2\uppi R}{d^{\prime }} $$
(9)

Thus, for filled (1) and part-filled (2) tunnels:

  1. 1.

    When a water-conveyance tunnel is filled with water, the total leakage from the tunnel is the sum of the leakages from the upper horizontal section, inclined shaft section, and lower horizontal section (Fig. 3a). Therefore, the total leakage, Q, can be expressed as:

$$ Q={Q}_1+{Q}_2+{Q}_3={\int}_0^{l_1\cos \alpha } qdx+{\int}_{l_1\cos \alpha}^{l_1\cos \alpha +{l}_2\cos \beta } qdx+{\int}_{l_1\cos \alpha +{l}_2\cos \beta}^{l_1\cos \alpha +{l}_2\cos \beta +{l}_3\cos \gamma } qdx $$
(10)

where Q1, Q2, and Q3 denote the leakages from the upper horizontal, inclined shaft, and lower horizontal sections l1, l2, and l3 represent the lengths of those three sections, α, β, and γ are the intersection angles between the horizontal plane and each of the three sections, respectively.

Substituting Eq. (9) into Eq. (10), Q1, Q2, and Q3 can be rewritten as:

$$ {\displaystyle \begin{array}{c}{Q}_1={\int}_0^{l_1\cos \alpha }{K}_1\cdot \left({h}_{\mathrm{u}}-\sqrt{h_{\mathrm{u}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}{l}x}\right)\cdot \frac{2\uppi R}{d^{\prime }} dx\\ {}={K}_1\cdot \frac{2\uppi R}{d^{\prime }}\cdot \left[{h}_{\mathrm{u}}{l}_1\cos \alpha -\frac{2}{3}\cdot \frac{l}{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}\cdot \left({H}_1^3\hbox{--} {h}_{\mathrm{u}}^3\right)\right]\end{array}} $$
(11)
$$ {\displaystyle \begin{array}{c}{Q}_2={\int}_{l_1\cos \alpha}^{l_1\cos \alpha +{l}_2\cos \beta }{K}_1\cdot \left({h}_{\mathrm{u}}-\sqrt{h_{\mathrm{u}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}{l}x}\right)\cdot \frac{2\uppi R}{d^{\prime }} dx\\ {}={K}_1\cdot \frac{2\uppi R}{d^{\prime }}\cdot \left[{h}_{\mathrm{u}}{l}_2\cos \beta -\frac{2}{3}\cdot \frac{l}{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}\cdot \left({H}_2^3\hbox{--} {H}_1^3\right)\right]\end{array}} $$
(12)
$$ {\displaystyle \begin{array}{c}{Q}_3={\int}_{l_1\cos \alpha +{l}_2\cos \beta}^{l_1\cos \alpha +{l}_2\cos \beta +{l}_3\cos \gamma }{K}_1\cdot \left({h}_{\mathrm{u}}-\sqrt{h_{\mathrm{u}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}{l}x}\right)\cdot \frac{2\uppi R}{d^{\prime }} dx\\ {}={K}_1\cdot \frac{2\uppi R}{d^{\prime }}\cdot \left[{h}_{\mathrm{u}}{l}_3\cos \gamma -\frac{2}{3}\cdot \frac{l}{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}\cdot \left({H}_3^3\hbox{-} {H}_2^3\right)\right]\end{array}} $$
(13)

where

$$ {H}_1=\sqrt{h_{\mathrm{u}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}{l}\cdot {l}_1\cos \alpha } $$
(14)
$$ {H}_2=\sqrt{h_{\mathrm{u}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}{l}\cdot \left({l}_1\cos \alpha +{l}_2\cos \beta \right)} $$
(15)
$$ {H}_3=\sqrt{h_{\mathrm{u}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{u}}^2}{l}\cdot \left({l}_1\cos \alpha +{l}_2\cos \beta +{l}_3\cos \gamma \right)} $$
(16)
  1. 2.

    When a water-conveyance tunnel is part-filled with reservoir water (Fig. 3b), if 0 < x ≤ l1 cos α, Q1, Q2, and Q3 can be rewritten as:

$$ {\displaystyle \begin{array}{c}{Q}_1={\int}_{l_1\cos \alpha \hbox{-} \left({h}_{\mathrm{f}}-l{}_2\mathrm{s}\mathrm{in}\beta -z\right)/\tan \alpha}^{l_1\cos \alpha }{K}_1\cdot \left({h}_{\mathrm{f}}-\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{\prime }}x}\right)\cdot \frac{2\uppi R}{d^{\prime }} dx\\ {}={K}_1\cdot \frac{2\uppi R}{d^{\prime }}\cdot \left[{h}_{\mathrm{f}}\left({h}_{\mathrm{f}}-{l}_2\sin \beta -z\right)/\tan \alpha -\frac{2}{3}\cdot \frac{l^{\prime }}{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}\cdot \left({I}_1^3\hbox{--} {I}_0^3\right)\right]\end{array}} $$
(17)
$$ {\displaystyle \begin{array}{c}{Q}_2={\int}_{l_1\cos \alpha}^{l_1\cos \alpha +{l}_2\cos \beta }{K}_1\cdot \left({h}_{\mathrm{f}}-\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{\prime }}x}\right)\cdot \frac{2\uppi R}{d^{\prime }} dx\\ {}={K}_1\cdot \frac{2\uppi R}{d^{\prime }}\cdot \left[{h}_{\mathrm{f}}{l}_2\cos \beta -\frac{2}{3}\cdot \frac{l^{\prime }}{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}\cdot \left({I}_2^3\hbox{-} {I}_1^3\right)\right]\end{array}} $$
(18)
$$ {\displaystyle \begin{array}{c}{Q}_3={\int}_{l_1\cos \alpha +{l}_2\cos \beta}^{l_1\cos \alpha +{l}_2\cos \beta +{l}_3\cos \gamma }{K}_1\cdot \left({h}_{\mathrm{f}}-\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{\prime }}x}\right)\cdot \frac{2\uppi R}{{\mathrm{d}}^{\prime }} dx\\ {}={K}_1\cdot \frac{2\uppi R}{d^{\prime }}\cdot \left[{h}_{\mathrm{f}}{l}_3\cos \gamma -\frac{2}{3}\cdot \frac{l^{\prime }}{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}\cdot \left({I}_3^3\hbox{-} {I}_2^3\right)\right]\end{array}} $$
(19)

where

$$ {l}^{\prime }=\left({h}_{\mathrm{f}}-l{}_2\mathrm{s}\mathrm{in}\beta -z\right)/\tan \alpha +{l}_2\cos \beta +{l}_3\cos \gamma $$
(20)
$$ {I}_0=\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{\prime }}\cdot \left[{l}_1\cos \alpha \hbox{-} \left({h}_{\mathrm{f}}-l{}_2\mathrm{s}\mathrm{in}\beta -z\right)/\tan \alpha \right]} $$
(21)
$$ {I}_1=\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{\prime }}\cdot {l}_1\cos \alpha } $$
(22)
$$ {I}_2=\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{\prime }}\cdot \left({l}_1\cos \alpha +{l}_2\cos \beta \right)} $$
(23)
$$ {I}_3=\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{\prime }}\cdot \left({l}_1\cos \alpha +{l}_2\cos \beta +{l}_3\cos \gamma \right)} $$
(24)

If l1 cos α < x ≤ l1 cos α + l2 cos β, Q1 = 0, and Q2 and Q3 can be rewritten as:

$$ {\displaystyle \begin{array}{c}{Q}_2={\int}_{l_1\cos \alpha +{l}_2\cos \beta \hbox{-} \left({h}_{\mathrm{f}}-z\right)/\tan \beta}^{l_1\cos \alpha +{l}_2\cos \beta }{K}_1\cdot \left({h}_{\mathrm{f}}-\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{\prime \prime \prime }}x}\right)\cdot \frac{2\uppi R}{d^{\prime }} dx\\ {}={K}_1\cdot \frac{2\uppi R}{d^{\prime }}\cdot \left[{h}_{\mathrm{f}}\left({h}_{\mathrm{f}}-z\right)/\tan \beta -\frac{2}{3}\cdot \frac{l^{\prime \prime }}{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}\cdot \left({J}_2^3\hbox{--} {J}_1^3\right)\right]\end{array}} $$
(25)
$$ {\displaystyle \begin{array}{c}{Q}_3={\int}_{l_1\cos \alpha +{l}_2\cos \beta}^{l_1\cos \alpha +{l}_2\cos \beta +{l}_3\cos \gamma }{K}_1\cdot \left({h}_{\mathrm{f}}-\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{{\prime\prime} }}x}\right)\cdot \frac{2\uppi R}{d^{\prime }} dx\\ {}={K}_1\cdot \frac{2\uppi R}{d^{\prime }}\cdot \left[{h}_{\mathrm{f}}{l}_3\cos \gamma -\frac{2}{3}\cdot \frac{l^{\prime \prime }}{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}\cdot \left({J}_3^3\hbox{--} {J}_2^3\right)\right]\end{array}} $$
(26)

where

$$ {l}^{{\prime\prime} \prime }=\left({h}_{\mathrm{f}}-z\right)/\tan \beta +{l}_3\cos \gamma $$
(27)
$$ {J}_1=\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{{\prime\prime} \prime }}\cdot \left[{l}_1\cos \alpha +{l}_2\cos \beta \hbox{-} \left({h}_{\mathrm{f}}-z\right)/\tan \beta \right]} $$
(28)
$$ {J}_2=\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{{\prime\prime} \prime }}\cdot \left({l}_1\cos \alpha +{l}_2\cos \beta \right)} $$
(29)
$$ {J}_3=\sqrt{h_{\mathrm{f}}^2+\frac{h_{\mathrm{l}}^2-{h}_{\mathrm{f}}^2}{l^{{\prime\prime} \prime }}\cdot \left({l}_1\cos \alpha +{l}_2\cos \beta +{l}_3\cos \gamma \right)} $$
(30)

where hf is the water level in the tunnel, and z is the distance between the bottom of the inclined shaft section and the bottom of the aquifer. The water level in the tunnel, hf, changed over time during impoundment, and hu and hl will also change during the operation of the reservoir, so the water levels are therefore a function of time. This proposed formula can also be applied to transient flow.

Leakage calculation under a variable filling level

The water-filling level with an effect on total leakage, Q, is an instantaneous water level at time t. If the change in filling level is a piecewise function, the total leakage can be given by:

$$ Q=\sum \limits_{i=1}^n{\int}_{t_i}^{t_{i+1}}{Q}_t dt $$
(31)

where Qt is the leakage at t, i is a time period number, and n is the total number of time periods.

Numerical solution

In addition to analytical solutions, the leakage from the tunnels was also calculated by using FEFLOW (Finite Element Subsurface FLOW and Transport Simulation System) software, which was developed by DHI-WASY GmbH, Institute for Water Resources Planning and Systems Research Ltd. It is a three-dimensional (3D) variably saturated subsurface flow and solute transport model that can describe the spatial and temporal distribution of groundwater. FEFLOW has been universally applied to the simulation of groundwater flow in porous and fractured media (Sefelnasr et al. 2014; Hu and Jiao 2015; Malott et al. 2016; Kavour et al. 2017). To compare this with the analytical solution, a 2D numerical model based on FEFLOW was employed to calculate the leakage. The left and right-hand sides of the model have the first-type (Dirichlet) boundary, which corresponds to the upper and lower reservoir water levels, respectively. The bottom of model has the second-type (Neumann) boundary. It has weak permeability and is considered to be an aquiclude. The top of the model is a free surface boundary. The hydraulic pressure tunnels form the first-type boundary.

Method of error estimation

The difference between the measured and calculated leakages was estimated by use of root mean squared error (RMSE) measurement. This is the mean average of the squared differences between measured and calculated leakages. Thus,

$$ \mathrm{RMSE}={\left[\frac{1}{n}\sum \limits_{i=1}^n{{\left({Q}_{\mathrm{m}}-{Q}_{\mathrm{c}}\right)}_i}^2\right]}^{1/2} $$
(32)

where n is the number of time steps, and Qm and Qc are the measured and calculated leakages, respectively.

Results and discussion

Water-filling tests

Two groups of water-filling tests have been conducted to verify the reliability of the water-conveyance tunnels. The test of the No. 1 diversion tunnel ran from 4 April 2009 to 14 May 2009. Water levels in the lower and upper storage reservoirs remained at 87.26 and 381.5 m, respectively, upon test completion. The test of the No. 2 diversion tunnel ran from 16 to 30 November 2009. At this time, water levels in the lower and upper storage reservoir remained at 78.61 and 388.25 m, respectively. Test records are listed in Table 2. The time between the two tests is about half a year; thus, the design condition means that No. 1 diversion tunnel was filled with water and No. 2 diversion tunnel was emptied. The water levels and fluxes could be observed in the No. 2 diversion tunnel. When the No. 2 diversion tunnel was filled with water, the normal operation of the HPSPS could be simulated.

Table 2 Test records: Nos. 1 and 2 diversion tunnels
Full size table

Osmometer data

An osmometer is a sensor for measuring pore water pressure in structures. The purpose of using an osmometer is to estimate the leakage in the tunnels. Osmometers P1-1 to P1-4 are located at chainage 1Y0 + 912, F15, and No. 1-2 branch tunnel for monitoring the No. 1 diversion tunnel (Fig. 2b). At F15, the elevations of P1-2 and P1-3 are 22 and 36.94 m, respectively; however, P2-1, P2-2, P2-3, and P2-4 are located at chainage 2Y0 + 948.5, F15, and No. 2-1 branch tunnel for the No. 2 diversion tunnel (Fig. 2b). The elevations of P2-2 and P2-3 are 22 and 35.44 m. Measured data from the eight osmometers are illustrated in Fig. 4. The water table at P1-1 is at about 96 m a.s.l. with an increase of 75 m after the water-filling test of the No. 1 diversion tunnel (the first test). The water table remained stable even during the second test period, which means that the water-filling test of No. 2 diversion tunnel (the second test) has not affected the water table at P1-1. Measured data from P1-2 increase over the two tests, but the extent of the increase in the second test is smaller than that of the first test. The water table at P1-3 rises after the first test by more than 300 m, which indicates leakage under the high water pressure; however, P1-3 is unaffected by the second test. For P1-4, there are two peak values of groundwater level during testing, but the increase during the first test exceeds that in the second test. Water tables at P2-1, P2-2, and P2-4 increase after the second test, but the first test has no distinct effect thereon and the first test has little effect on P2-3, whereby the water table increases by about 280 m, and the increase during the second test exceeds that in the first test. The preceding analysis shows that the tunnels will leak during water filling and that the leakages are mainly distributed around the tunnels; thus, the leakage can be calculated using the proposed method.

Fig. 4
figure 4

Osmometer data versus time: water-filling tests

Full size image

Monitoring and calculating leakage around the tunnels

Some measurement points such as drainage ditches, measuring weirs, drainage galleries around the tunnels, and the No. 2 diversion tunnel, were used to monitor leakage during the first test. When the second test was performed, the Nos. 1 and 2 diversion tunnels were filled with water. The main measurement points for leakage determination were drainage ditches, measuring weirs, and drainage galleries. Measured data from the first test show leakage rates ranging from 1.0 to 3.32 L/s with an average value of 2.1 L/s. The minimum value was measured at 12:00, 3 May 2009, and the maximum value was measured at 6:00, 14 May 2009. Leakage increases with increasing water level (Fig. 5a). The leakage increases from 0.66 to 1.29 L/s with an average valve of 0.89 L/s. The measured leakage increases until 28 November 2009, and then decreases and remains stable (Fig. 5b). Comparison between the first and second tests indicates that the leakage from the former is larger than that from the latter. This may be caused by water pressure around the No. 1 diversion tunnel, where the leakage from the No. 1 diversion tunnel increases the external water pressure in the No. 2 diversion tunnel, which reduces leakage at the No. 2 diversion tunnel.

Fig. 5
figure 5

Comparison of calculated and measured leakage for the a first test, and b second test

Full size image

The leakage was calculated by using the proposed analytical formula and its numerical solution. Values of hydraulic conductivity and tunnel parameters are listed in Table 3. The absolute errors and RMSE were used to estimate how well the calculated leakages agree with the observed values. Also, the Nash-Sutcliffe model efficiency coefficient (NSMEC) was used to assess the goodness of fit (Nash and Sutcliffe 1970). The calculated leakage was similar to the changes in water level in the first test, which underestimated the measured leakage (Fig. 5a). The absolute errors range from 0.01 to 0.42 L/s and the RMSE is 0.241 L/s with an NS coefficient of 0.928 (Table 4). In the second test, the calculated leakage exceeds that measured (Fig. 5b) with the absolute errors ranging from 0.01 to 0.18 L/s and the RMSE indicated as 0.11 L/s with an NS coefficient of 0.84 (Table 4). The differences between measured leakages and the numerical results are listed in Table 4. Compared with the analytical solution, the numerical solution differs slightly in terms of the absolute errors, RMSE, and large NSMEC, but the difference between them is negligible as it lies within pre-specified tolerances. The analytical solution can, therefore, be used to estimate the leakage from a tunnel during reservoir operations.

Table 3 Parameters of calculating the leakage
Full size table
Table 4 Errors between the measured and calculated leakages
Full size table

Sensitivity analysis

Effect of β on leakage

β denotes the intersection angle between the inclined shaft section and horizontal plane. For many waterpower projects, it is designed to have differing values. The values are here assumed to lie within the range from 30–80° during sensitivity analysis. When the distance between the upper and lower storage reservoirs (l) and l2 is constant, l1 will change owing to the different value of β; therefore, l1/l2 is also considered to be a variable, but other parameters in Table 3 remain unchanged. A dimensionless ratio, Q/Q0, is used to evaluate the effect of β on leakage, where Q0 is the leakage at β = 50°. The relationship between Q/Q0 and β is plotted in Fig. 6: leakage decreases with increasing β when l1/l2 is a constant and the decrease ranges from 0.035 to 0.052 L/s per increment in β. The average decrement in leakage is about 2.8% compared with that at β = 50°; consequently, β affects the leakage. When β is a constant, leakage decreases with increasing l1/l2, but the decrease diminishes and the average decrement in leakage changes from 2.8 to 0.09% with increasing l1/l2, so the leakage will increase for small l1 and large l2. This may be correct for a single tunnel, but if there are two parallel distributed tunnels, and one tunnel has an effect on the other, and the leakage may change in the opposite direction—for example, the leakage from the second test is smaller than that of the first test although l1 from the No. 2 diversion tunnel is less than that from the No. 1 diversion tunnel (Table 3).

Fig. 6
figure 6

Relationship between Q/Q0 and β

Full size image

Effect of hydraulic conductivity

During testing and in the operation of the reservoir, the reinforced concrete lining around the tunnel may be cracked under the high water pressure. The hydraulic conductivity of the reinforced concrete lining will increase compared to its design value. Its effect on the leakage is discussed from the perspective of the results of water-filling tests. The ratio of hydraulic conductivity for reinforced concrete lining to that of the grouting zone (K1/K2) is taken as the independent variable (X-axis), and Q/Q0 plotted on the Y-axis (Fig. 7); the solid triangles denote calculated leakage, and the dotted line is a fitting curve. The K2 value is 1 × 10−5 cm/s, but K1 values are 1 × 10−7, 5 × 10−7, 1 × 10−6, 5 × 10−6, and 1 × 10−5 cm/s, respectively. Figure 7 illustrates that the leakage increases with increasing K1/K2. The leakage increment is large for small K1/K2; however, if the K1 value is doubled, the leakage is increased 2.5-fold. When K1 is close to K2, the leakage increment becomes very small—for example, when the K1 value is doubled, the leakage is only increased 1.05-fold. The relationship between them is nonlinear. The fitting curve may be described by a single logarithmic relationship: Q/Q0 = 2.25 ln (K1/K2) + 11.03 with a correlation coefficient of 0.99. Therefore, as predicted, the hydraulic conductivity of the reinforced concrete lining is an important factor affecting the leakage.

Fig. 7
figure 7

Relationship between Q/Q0 and hydraulic conductivity of the reinforced concrete lining

Full size image

Furthermore, the leakage also increases with increasing difference in the water levels between the upper and lower storage reservoirs. The leakage increases with rising water levels in the tunnel. The values of α and γ are usually smaller than 5°, showing no obvious effect on the leakage.

Prediction of the leakage with the analytical formula

After the water-filling tests were completed in 2009, two pumped storage units, Nos. 1-1 and 1-2 from the No. 1 diversion tunnel, have been run since 1 June 2010. The other two pumped storage units, Nos. 2-1 and 2-2 from the No. 2 diversion tunnels, have been run since 6 October 2010. Some measured data from osmometers (numbered P1-1 to P1-4 and P2-1 to P2-4) are shown in Fig. 4. Furthermore, other osmometers were installed in the diversion tunnels between the grouting zone and surrounding rock in August 2008 (Fig. 2a). The osmometer readings are recorded in Table 5) where it can be seen that the water level is decreased by 80 to −130 m when the water in the diversion tunnels leaks into the surrounding rock through the reinforced concrete lining and grouting zone.

Table 5 Observed water level from osmometers during normal operation of the reservoir
Full size table

Based on the analytical method, the leakage around these two tunnels was estimated during normal operation of the reservoir. For a pumped storage power station, pumping and emptying water are conducted alternately. It is assumed that water from the lower storage reservoir was pumped into the upper storage reservoir from 9:00 pm to 7:00 am the following morning, due to the lower cost of electricity during those hours. The water filling level ranges from the dead storage level (376.5 m) to the normal impounded level (400 m; Fig. 8). Then water from the upper storage reservoir was discharged to generate electricity from 7:00 am to 9:00 pm owing to the high cost of electricity during those hours. The lowest water level is no less than 376.5 m during the generation period. After a period of reservoir operation, one tunnel needs to be examined and repaired, and the other tunnel will keep running. The leakage for this scenario was also calculated (Fig. 8).

Fig. 8
figure 8

Estimation of leakage during reservoir operation

Full size image

The leakage increases during pumping and decreases during emptying (Fig. 8). When the two tunnels are running at the same time, the leakage ranges from 4.48 L/s (387.07 m3/day) to 8.85 L/s (764.64 m3/day), which is very close to the maximum measured value of 8.0 L/s. When the No. 1 diversion tunnel is filling and No. 2 is emptying, the leakage is between 3.30 L/s to 5.05 L/s, which is more than the leakage when No. 1 is emptying and No. 2 is filling. The total leakage for these two cases is greater than 0.5 L/s for water filling in both tunnels. This leakage is approximately 8.5% of the total leakage and indicates that, when the two tunnels are running simultaneously, one tunnel has little effect on the leakage of the other. The effect indicates a small increase of water pressure and a small decrease in the leakage.

Conclusions

The analytical formulae for calculating leakage from tunnels with variable water filling levels and an arbitrary angle were deduced, according to Darcy’s law and the formula for steady flow under phreatic aquifer conditions, between two reservoirs. The leakage calculated using the analytical method has been validated by the calculated leakage and the measured values from two water-filling tests undertaken at the HPSPS site. The small discrepancies indicated that the calculated leakage matched measured values and the proposed method can be used to estimate leakage from the tunnels during reservoir operations. The effects of parameters such as the intersection angle (β), the hydraulic conductivity of the reinforced concrete lining, and water level, on the leakage have been discussed based on the dimensionless expressions Q/Q0, K1/K2, and l1/l2. The results show that the average decrement in leakage is about 2.8% per increment in β, which implies β does influence the leakage. For different values of the ratio K1/K2, if the K1 value is doubled, the increase in leakage is 1.05–2.5 times the original leakage. Therefore, the hydraulic conductivity of the reinforced concrete lining is also an important factor influencing the leakage in these cases; furthermore, the leakage increases with rising water level in the tunnels. The effects of other parameters (l1, l2, α, and γ) are negligible.

The leakage was estimated during normal reservoir operation by using the proposed analytical method. When both tunnels were running simultaneously, the estimated leakage ranges from 4.48 to 8.85 L/s. If one tunnel is filling and the other tunnel is emptying, the calculated total leakage is more than 0.5 L/s for water filling in both tunnels, which reveals that the running tunnel has little effect on the leakage when the other tunnel is emptying. When the reservoir level is 376.5 m, the corresponding reservoir capacity is 152.6 × 104 m3. The estimated total leakage from the reservoir is about 700 m3 (0.046% of reservoir capacity by volume), which indicates that the leakage control measures are relatively effective.