Non-Darcian flow to a well in a leaky aquifer using the Forchheimer equation

Abstract

Non-Darcian flow to a well in a leaky aquifer was investigated using a finite difference method. Flow in the leaky aquifer is assumed to be non-Darcian and horizontal, while flow in the aquitard is assumed to be Darcian and vertical. The Forchheimer equation was employed to describe the non-Darcian flow in the aquifer. The finite difference solution was compared with the solution of Birpinar and Sen (2004). The latter overestimates the drawdown at early times and underestimates the drawdown at late times; also, the impact of β _D on the drawdown depends on the value of B _D, where β _D is a dimensionless turbulent factor in the Forchheimer equation and B _D is the dimensionless leakage parameter. The impact of leakage on drawdown is similar to that of Darcian flow. A sensitivity analysis indicated that the drawdown is very sensitive to the change in the dimensionless well radius r _cD when B _D is relatively large, while it is sensitive to the change in B _D when B _D is relatively small. The numerical solution has been applied to analyze the pumping test data in Chaj-Doab area of Pakistan. Birpinar ME, Sen Z (2004) Forchheimer groundwater flow law type curves for leaky aquifers. J Hydrol Eng 9(1):51–59

Résumé

Un écoulement non Darcien vers un puits dans un aquifère semi-perméable a été étudié en utilisant la méthode des éléments finis. Un écoulement dans un aquifère semi-captif est considéré comme non Darcien et horizontal, tandis que l’écoulement dans un aquitard est supposé être darcien et vertical. L’équation de Forchheimer a été employée pour décrire l’écoulement non Darcien dans l’aquifère. La solution avec éléments finis a été comparée avec la solution de Birpinar et Sen (2004). Cette dernière surestime le rabattement au début de pompage et sous estime celui-ci en fin de pompage; par suite, l’impact de β _D sur le rabattement dépend de la valeur de B _D où β _D est un facteur de turbulence sans dimension dans l’équation de Forchheimer et B _D est le paramètre de drainance sans dimension. L’incidence de la drainance sur le rabattement est similaire à celle d’un écoulement Darcien. Une analyse de sensibilité montre que le rabattement est très sensible à la variation de rayon r _cD du puits quand B _D est grand, alors qu’il est sensible à la variation de B _D quand B _D est relativement petit. La solution numérique a été appliquée pour analyser le test de pompage, secteur de Chaj-Doab, Pakistan. Birpinar ME, Sen Z (2004) Forchheimer groundwater flow law type curves for leaky aquifers [Courbes de Forchheimer type écoulement de nappe en aquifères semi-perméables]. J Hydrol Eng 9(1):51–59

Resumen

Se investigó el flujo no Darciano hacia un pozo en acuífero semiconfinado usando un método de diferencias finitas. El flujo en el acuífero semiconfinado se supone Darciano y horizontal, mientras que el flujo en el acuitardo se supone Darciano y vertical. Se empleó la ecuación de Forchheimer para describir el flujo no Darciano en el acuífero. La solución a diferencias finitas fue comparada con la solución de Birpinar y Sen (2004). Esta última sobreestima la depresión en los primeros tiempos y subestima la depresión en los tiempos posteriores, además, el impacto de β _D en la depresión depende del valor de B _D, donde β _D es un factor adimensional de turbulencia en la ecuación de Forchheimer y B _D es el parámetro adimensional de filtración. El impacto de la filtración en la depresión es similar al del flujo Darciano. Un análisis de sensibilidad indicó que la depresión es muy sensible al cambio en el radio adimensional r _cD cuando B _D es grande, mientras que es sensible al cambio en B _D cuando B _D es relativamente pequeño. La solución numérica se aplicó para analizar los datos de ensayos de bombeo en el área Chaj-Doab de Pakistan. Birpinar ME, Sen Z (2004) Forchheimer groundwater flow law type curves for leaky aquifers [Curvas tipo de la ley de flujo de aguas subterráneas de Forchheimer para acuíferos semiconfinados]. J Hydrol Eng 9(1):51–59

摘要

本文采用有限差分方法研究了越流含水层中抽水井附近的非达西流问题。越流含水层中的水流假定为非达西流, 且方向为水平方向; 弱透水层中的水流假定为达西流, 且方向为竖直方向。本文所获得的有限差分解与Birpinar和Sen (2004)所得到的解进行了比较, 结果表明后者在抽水初期会高估水位降深而在抽水后期会低估水位降深。此外还发现β _D对水位降深的影响取决于B _D的大小, 其中β _D为Forchheimer定律中无量纲紊动因子, B _D为无量纲越流因子。越流对水位降深的影响与达西流情况下的结果一致。对各个参数进行敏感性分析发现当B _D取值较大时, 水位降深对无量纲井径r _cD比较敏感, 当B _D取值较小时, 水位降深对B _D比较敏感。最后本文还利用所得到的数值解对巴基斯坦Chaj-Doab地区的某一抽水试验数据进行了分析。Birpinar ME, Sen Z (2004) Forchheimer groundwater flow law type curves for leaky aquifers [基于Forchheimer定律的越流含水层中地下水流动井函数标准曲线]. J Hydrol Eng 9(1):51–59

Resumo

Investigou-se o fluxo não darciano para um furo num aquífero semiconfinado utilizando um método de diferenças finitas. Assume-se que o fluxo no aquífero semiconfinado é não darciano e horizontal enquanto no aquitardo é darciano e vertical. Aplicou-se a equação de Forchheimer para descrever o fluxo não darciano no aquífero. Comparou-se a solução de diferenças finitas com a solução de Birpinar e Sen (2004). Esta solução sobrestima o rebaixamento para tempos curtos de ensaio e subestima o rebaixamento para tempos longos; também, o impacte de β _D no rebaixamento depende do valor de B _D, onde β _D é um factor de turbulência adimensional na equação de Forchheimer e B _D é o parâmetro de drenância adimensional. O impacte da drenância no rebaixamento é semelhante àquele do fluxo de Darcy. Uma análise de sensibilidade indicou que o rebaixamento é muito sensível à mudança do raio adimensional do poço r _cD quando B _D é grande, enquanto é sensível à mudança de B _D quando B _D é relativamente pequeno. A solução numérica foi aplicada para analisar os dados do ensaio de bombagem na área de Chaj-Doab, no Paquistão. Birpinar ME, Sen Z (2004) Forchheimer groundwater flow law type curves for leaky aquifers [Curvas-tipo da lei Forchheimer de escoamento de água subterrânea para aquíferos semiconfinados]. J Hydrol Eng 9(1):51–59

Introduction

Darcy’s law has been used for over one and a half centuries for solving groundwater problems (Wen et al. 2009). However, flow can be non-Darcian under certain conditions as long as the flow velocity is relatively high or low (Forchheimer 1901; Dudgeon 1966; Basak 1977; Sen 1990; Choi et al. 1997; Bordier and Zimmer 2000). The limitations of Darcy’s law for solving flow problems have long been recognized and even Darcy himself realized that the linear relationship only worked for a certain range of grain size under a certain range of hydraulic gradient (Darcy 1856).

Many scientists have investigated the relationship between the hydraulic gradient and specific discharge for non-Darcian flow (e.g., Forchheimer 1901; Rose 1951; Polubarinova-Kochina 1962; Muskat 1937; Harr 1962; Izbash 1931; Escande 1953; Wilkinson 1956; Slepicka 1961), as summarized by Basak (1978). As can be seen from Table 1 in the paper of Basak (1978), all the relationships can be classified into two types: i.e., polynomial and power functions. Among these empirical (or theoretical) equations, two were commonly used. The first is the Forchheimer equation, which states that the hydraulic gradient is a second-order polynomial function of the specific discharge. The second is the Izbash equation which states that the hydraulic gradient is a power function of the specific discharge. Both equations have advantages and disadvantages. The Forchheimer equation has two terms, the first term represents the viscous term and the second term represents the inertial term. The physical meaning of the Forchheimer equation is evident and it has been validated theoretically by several scientists (Irmay 1958; Whitaker 1996; Giorgi 1997; Sorek et al. 2005). When the velocity is relatively low, the second term, as opposed to the first term, can be ignored. In this case, the Forchheimer equation becomes Darcy’s law. The Izbash equation is a fully empirical equation based on numerous experimental data. However, because of the mathematical convenience, it also has been commonly used (e.g., Wen et al. 2006, 2008a, 2008b). In many cases, these two equations can describe non-Darcian flow equivalently well (Bordier and Zimmer 2000; Li et al. 2008).

Table 1 Definition of the dimensionless variables

Because of the high velocities, non-Darcian flow is likely to occur near pumping wells (Wu 2002a, b; Sen 1987, 1988, 1989, 1990; Wen et al. 2006, 2008a, b, c, 2009). Based on the Forchheimer or Izbash equations, many studies have been carried out to investigate the non-Darcian flow near the pumping well. A careful review of existing publications about the non-Darcian flow to a pumping well indicates that three methods have commonly been used to solve this type of non-linear problem: the Boltzmann transform, the linearization method and numerical modeling. Sen (1987, 1988, 1989, 1990) has done extensive studies on non-Darcian flow to a pumping well by using the Boltzmann transform method. Recently, Wen et al. (2008a, b) have proposed a linearization procedure for solving non-Darcian flow to a well based on the assumption that the flow can be described by the Izbash equation. Meanwhile, numerical methods have also been used to solve non-Darcian flow problems (e.g., Ewing et al. 1999; Ewing and Lin 2001; Wu 2002a, b; Mathias et al. 2008; Wen et al. 2009). As commented by many scientists (e.g., Camacho-V and Vasquez-C 1992; Mathias et al. 2008), the Boltzmann transform cannot be used to solve such non-Darcian flow problems in a rigorous mathematical sense. The linearization procedure also has some limitations such as the discrepancies associated with early-time solutions. From this viewpoint, it seems that the present analytical methods can not solve such non-Darcian problems very well and numerical modeling might be a good approach in this area.

Up to now, most models on non-Darcian flow to a well are for confined aquifers such as, e.g., Sen (1987, 1990) and Wen et al. (2006, 2008a). Research on non-Darcian flow in leaky aquifers is too limited. Sen (2000) used a volumetric approach to investigate non-Darcian flow in leaky aquifers with the Izbash equation, and that study has been extended by Birpinar and Sen (2004) to investigate a similar problem with the Forchheimer equation. These two studies were based on the solutions obtained by the Boltzmann transform which was found to be problematic in a rigorous mathematical sense (Camacho-V and Vasquez-C 1992; Mathias et al. 2008). Therefore, the solutions in these two studies might be questionable. Recently, Wen et al. (2008c) used a linearization procedure and finite difference method to solve non-Darcian flow in a leaky aquifer with the Izbash equation. As mentioned before, the Izbash equation has some disadvantages for describing radial non-Darcian flow. To the authors’ knowledge, the investigations about non-Darcian flow in leaky aquifers with the Forchheimer equation are still very limited.

In this paper, a finite difference method will be used to investigate the non-Darcian flow to a pumping well in a leaky aquifer. The wellbore storage is also considered. The flow in the aquifer is assumed to be horizontal and non-Darcian, and the flow in the aquitard is assumed to be vertical and Darcian. The Forchheimer equation will be used to describe the non-Darcian flow in the aquifer. Sensitivity analysis for different parameters under non-Darcian flow conditions will be done in this study and the numerical solution will be applied to analyze the pumping test data in Chaj-Doab area of Pakistan. As Wen et al. (2008b) have investigated non-Darcian flow to a well in an aquifer-aquitard system with the Izbash equation, this study can be regarded as an extended work of Wen et al. (2008b).

Problem statement

Governing equations

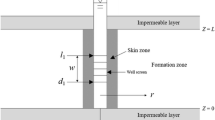
The system discussed here is similar to that of Hantush and Jacob (1955), as shown in Fig. 1 (Wen et al. 2008b). The following assumptions have been used in this study to make the problem mathematically tractable. First, the aquifer and the bounded upper aquitard are assumed to be homogeneous, isotropic, and horizontally infinite. Second, the flow in the aquifer is assumed to be non-Darcian while the flow in the upper aquitard is assumed to be Darcian, and the flow direction in the aquifer is horizontal while the flow direction in the aquitard is vertical. Third, the aquitard storage is not considered and, fourth, the well fully penetrates the aquifer and the pumping rate is assumed to be constant. Under these assumptions, the mathematical model can be generated as follows:

$$ \frac{1}{r}\frac{{\partial \left[ {rq\left( {r,t} \right)} \right]}}{{\partial r}} - \frac{{s\left( {r,t} \right)}}{B} = \frac{S}{m}\frac{{\partial s\left( {r,t} \right)}}{{\partial t}}, $$

(1)

$$ s\left( {r,0} \right) = 0, $$

(2)

$$ s\left( {\infty, t} \right) = 0, $$

(3)

$$ 2\pi rmq\left( {r,t} \right)\left| {_{{r \to 0}}} \right. = - Q, $$

(4)

in which r is radial distance from the center of the pumping well [L]; t is pumping time [T]; q(r,t) is specific discharge [L/T]; s(r,t) is drawdown [L]; S is storage coefficient of the aquifer; m is aquifer thickness [L]; Q is pumping rate, which is constant [L³/T]; B is the leakage parameter defined as $m \times {m_1}/{k_1}$, [LT], where m ₁ and k ₁ are thickness and hydraulic conductivity of the aquitard, respectively. It is notable that a greater value of B, meaning that a larger aquitard thickness m ₁ or a smaller aquitard hydraulic conductivity k ₁, indicates smaller leakage effect. If the hydraulic conductivity of the aquitard k ₁ goes to zero, the leakage parameter B goes to infinity, then the problem investigated here is similar to the Theis model for confined aquifers.

Fig. 1

A schematic diagram of the leaky confined aquifer system (Wen et al. 2008b, with permission from Elsevier)

If the wellbore storage cannot be ignored, the boundary condition Eq. (4) should be replaced by

$$ 2\pi {r_{{\rm{w}}}}mq\left( {r,t} \right)\left| {_{{r = {r_{{\rm{w}}}}}}} \right. - \pi r_{{\rm{c}}}^{2}\frac{{d{s_{{\rm{w}}}}\left( t \right)}}{{dt}} = - Q, $$

(5)

where r _w is the radius of the well screen [L], r _c is the radius of the well casing [L]. In most cases, r _c is larger than, instead of equal to r _w. s _w(t) is drawdown inside the well [L], which is dependent of the pumping time t.

The Forchheimer equation will be used to describe the non-Darcian flow in the aquifer. The Forchheimer equation can be expressed as:

$$ q + \beta q\left| q \right| = k\frac{{\partial s}}{{\partial r}}, $$

(6)

in which β [T/L] is a non-Darcian factor representing the turbulence of the non-Darcian flow. If β is equal to zero, Eq. (6) becomes the well-known Darcy’s law, k [L/T] can be regarded as the apparent hydraulic conductivity of the aquifer.

Dimensionless transform

Similar to the analysis of the Theis type curves for Darcian flow, one can define the following dimensionless variables, as listed in Table 1. Notice that a minus sign was included in the definition of the dimensionless specific discharge q _D. It is necessary to emphasize two important dimensionless variables, i.e., B _D and β _D. B _D is a dimensionless variable representing the leakage and a larger B _D means smaller leakage. β _D is a dimensionless parameter representing the non-Darcian effect and a larger β _D indicates greater turbulence. With these definitions, the problem proposed here can be expressed in dimensionless form as:

$$ - \frac{{\partial \left[ {{r_{{\rm{D}}}}{q_{{\rm{D}}}}} \right]}}{{{r_{{\rm{D}}}}\partial {r_{{\rm{D}}}}}} - \frac{{{s_{{\rm{D}}}}}}{{{B_{{\rm{D}}}}}} = \frac{{\partial {s_{{\rm{D}}}}}}{{\partial {t_{{\rm{D}}}}}}, $$

(7)

$$ {s_{{\rm{D}}}}\left( {{r_{{\rm{D}}}},0} \right) = 0, $$

(8)

$$ {s_{{\rm{D}}}}\left( {\infty ,{t_{{\rm{D}}}}} \right) = 0, $$

(9)

$$ \frac{1}{2}\left( {{r_{{\rm{D}}}}{q_{{\rm{D}}}}} \right)\left| {_{{{r_{{\rm{D}}}} \to 0}}} \right. = 1. $$

(10)

The boundary condition considering wellbore storage can also be expressed in dimensionless format as:

$$ \frac{1}{2}\left( {{r_{{\rm{D}}}}{q_{{\rm{D}}}}} \right)\left| {_{{{r_{{\rm{D}}}} = {r_{{{\rm{wD}}}}}}}} \right. + \frac{{r_{{cD}}^{2}}}{{4S}}\frac{{d{s_{{{\rm{wD}}}}}\left( {{t_{{\rm{D}}}}} \right)}}{{d{t_{{\rm{D}}}}}} = 1. $$

(11)

The Forchheimer equation will be changed to:

$$ {q_{{\rm{D}}}} + {\beta _{{\rm{D}}}}q_{D}^{2} = - \frac{{\partial {s_{{\rm{D}}}}}}{{\partial {r_{{\rm{D}}}}}}. $$

(12)

Solutions for the problem

Numerical solution

The finite difference method was used to simulate the problem investigated here. It should be pointed out that only the case with wellbore storage was considered when doing the simulation. The case without wellbore storage can be easily solved by setting very small values (close to zero) to the dimensionless radii r _w and r _c. First, one needs to discretize the dimensionless spatial domain [r _wD, r _eD], where r _eD is a very large value which is used to approximate the outer boundary condition at which the drawdown is equal to zero. The value of r _D at the ith node can be referred as r _i, where the subscript represents the node of interest. For any node of r _i, r _wD < r _i < r _eD, i = 1, 2,…,N, and r ₀ = r _wD and r _n+1 = r _eD. As the drawdown changes rapidly near the pumping well, the dimensionless domain was discretized logarithmically (Wu 2002a; Mathias et al. 2008):

$$ {r_{{\rm{i}}}} = \left( {{r_{{{\rm{i}} - 1/2}}} + {r_{{{\rm{i}} + 1/2}}}} \right)/2,\; \;\;\;i = {\hbox{1}},{\hbox{ 2}}, \ldots ,N, $$

(13)

with respect to

$$ {\log _{{10}}}\left( {{r_{{{\rm{i}} + 1/2}}}} \right) = {\log _{{10}}}\left( {{r_{{{\rm{wD}}}}}} \right) + i\left[ {\frac{{{{\log }_{{10}}}\left( {{r_{{{\rm{eD}}}}}} \right) - {{\log }_{{10}}}\left( {{r_{{{\rm{wD}}}}}} \right)}}{N}} \right],\;i = 0,\;{\hbox{1}}, \ldots ,N. $$

(14)

The governing equation, Eq. (7), can also be reduced to the following differential equation with respect to the dimensionless time t _D:

$$ \frac{{d{s_{{\rm{i}}}}}}{{d{t_{{\rm{D}}}}}} \approx \frac{{{r_{{{\rm{i}} - 1/2}}}{q_{{{\rm{i}} - 1/2}}} - {r_{{{\rm{i}} + 1/2}}}{q_{{\operatorname{i} + 1/2}}}}}{{{r_{{\rm{i}}}}\left( {{r_{{{\rm{i}} + 1/2}}} - {r_{{{\rm{i}} - 1/2}}}} \right)}} - \frac{{{s_{{\rm{i}}}}}}{{{B_{{\rm{D}}}}}},\;i = {\hbox{1}},\;{\hbox{2}}, \ldots ,N, $$

(15)

in which s _i and q _i are the dimensionless drawdown s _D and dimensionless specific discharge q _D at node i, respectively. From the Forchheimer equation, one has:

$$ {q_{{\rm{D}}}} = \frac{{\text{1}}}{{{\hbox{2}}{\beta _{{\rm{D}}}}}}\left\{ { - 1 + {{\left[ {1 - 4{\beta _{{\rm{D}}}}\frac{{\partial {s_{{\rm{D}}}}}}{{\partial {r_{{\rm{D}}}}}}} \right]}^{{1/2}}}} \right\}. $$

(16)

Therefore, the dimensionless specific discharge that goes into and out of each cell can be expressed as:

$$ {q_{{{\rm{i}} - 1/2}}} \approx \frac{{\text{1}}}{{{\hbox{2}}{\beta _{{\rm{D}}}}}}\left\{ { - 1 + {{\left[ {1 + 4{\beta _{{\rm{D}}}}\left( {\frac{{{s_{{{\rm{i}} - 1}}} - {s_{{\rm{i}}}}}}{{{r_{{\rm{i}}}} - {r_{{{\rm{i}} - 1}}}}}} \right)} \right]}^{{1/2}}}} \right\},\;i = {\hbox{2}},\;{\hbox{3}}, \ldots ,N, $$

(17)

$$ {q_{{{\rm{i}} + 1/2}}} \approx \frac{{\text{1}}}{{{\hbox{2}}{\beta _{{\rm{D}}}}}}\left\{ { - 1 + {{\left[ {1 + 4{\beta _{{\rm{D}}}}\left( {\frac{{{s_{{\rm{i}}}} - {s_{{{\rm{i}} + 1}}}}}{{{r_{{{\rm{i}} + 1}}} - {r_{{\rm{i}}}}}}} \right)} \right]}^{{1/2}}}} \right\},\;i = {\hbox{1}},{\hbox{ 2}}, \ldots ,N - {\hbox{1}}, $$

(18)

. At the inner and outer boundaries, one has:

$$ {q_{{{\rm{1}} - 1/2}}} \approx \frac{{\text{1}}}{{{\hbox{2}}{\beta _{{\rm{D}}}}}}\left\{ { - 1 + {{\left[ {1 + 4{\beta _{{\rm{D}}}}\left( {\frac{{{s_{{{\rm{wD}}}}} - {s_{1}}}}{{{r_{1}} - {r_{{{\rm{wD}}}}}}}} \right)} \right]}^{{1/2}}}} \right\}, $$

(19)

$$ {q_{{{\rm{N}} + 1/2}}} \approx \frac{{\text{1}}}{{{\hbox{2}}{\beta _{{\rm{D}}}}}}\left\{ { - 1 + {{\left[ {1 + 4{\beta _{{\rm{D}}}}\left( {\frac{{{s_{{\rm{N}}}} - 0}}{{{r_{{{\rm{eD}}}}} - {r_{{\rm{N}}}}}}} \right)} \right]}^{{1/2}}}} \right\}, $$

(20)

where s _wD is the dimensionless drawdown inside the well, which can be approximated as follows by considering Eq. (11):

$$ \frac{{d{s_{{{\rm{wD}}}}}}}{{d{t_{{\rm{D}}}}}} \approx \frac{{4S}}{{r_{{cD}}^{2}}}\left( {1 - \frac{1}{2}{r_{{{\rm{wD}}}}}{{\hbox{q}}_{{{\rm{1 - 1/2}}}}}} \right). $$

(21)

After these preparations, the problem can be solved with the MATLAB software by using the stiff integrator ODE15s (Mathias et al. 2008). A MATLAB program named LeakyForch was developed to do this calculation. For all the simulations, N was chosen to be 5000 and r _eD was chosen to be 10⁸. These values are found to be sufficiently large for this study.

The solution of Birpinar and Sen (2004)

Birpinar and Sen (2004) proposed an analytical solution for the same problem by using the Forchheimer equation. They obtained the analytical solution for the type curves in leaky aquifers by using the volumetric approach proposed by Sen (1985), and on the basis of their previous study (Sen 1989). It is notable that the solution of Sen (1989) for the type curves in confined aquifers was obtained by the Boltzmann transform. Here the point is that the Boltzmann transform cannot be used to derive the type curves for non-Darcian flow problems, as pointed out by several scientists (e.g., Camacho-V and Vasquez-C 1992; Mathias et al. 2008; Wen et al. 2008a). In this study, the numerical solution will be used to verify the analytical solution obtained by Birpinar and Sen (2004) for the same problem. As stated by Birpinar and Sen (2004), the analytical solution (see Eq. (11) in their study) obtained by the volumetric approach can be changed to the following equation by using the dimensionless variables defined in this study:

$$ {s_{{\rm{D}}}} = \int_{{\frac{{r_{D}^{2}}}{{4{t_{{\rm{D}}}}}}}}^{\infty } {\frac{{\exp \left( { - x - \frac{{r_{D}^{2}}}{{4{B_{{\rm{D}}}}}}\frac{1}{x}} \right)}}{{\left( {1 + \frac{{2\sqrt {\pi } {\beta _{{\rm{D}}}}\sqrt {x} }}{{{r_{{\rm{D}}}}}}} \right)x}}} dx + \frac{{2{\beta _{{\rm{D}}}}}}{{{r_{{\rm{D}}}}}}\int_{{\frac{{r_{D}^{2}}}{{4{t_{{\rm{D}}}}}}}}^{\infty } {\frac{{\exp \left( { - 2x - \frac{{r_{D}^{2}}}{{4{B_{{\rm{D}}}}}}\frac{1}{x}} \right)}}{{{{\left( {1 + \frac{{2\sqrt {\pi } {\beta _{{\rm{D}}}}\sqrt {x} }}{{{r_{{\rm{D}}}}}}} \right)}^{2}}x}}} dx, $$

(22)

in which x is a dummy variable. The aforementioned equation can be integrated easily by using a MATLAB program.

Results and discussion

In order to check the numerical solution proposed in this study, first the numerical solution was compared with the analytical solution of Hantush and Jacob (1955) for the Darcian flow case (β _D = 0). Three typical dimensionless distances were chosen as r _D = 0.5, 1, and 5 and the dimensionless leakage parameter was given as 10. As shown in Fig. 2, the numerical solution agrees perfectly with the analytical solution during the entire pumping period. This indicates that the numerical error caused by the finite difference method probably can be ignored and the numerical solution in this study is sufficiently accurate.

Fig. 2

Comparison of the numerical solution and the solution of Hantush and Jacob (1955) for the Darcian flow case

Dimensionless drawdown without wellbore storage

Figure 3 shows the comparison of the numerical solution used in this study and the solution of Birpinar and Sen (2004). The analytical solution of Birpinar and Sen (2004) was calculated from Eq. (22). The parameters used in Fig. 3 were given as β _D = 10, B _D = 10, r _D = 0.5 and 5. As can be seen from Fig. 3, it is evident that the solution obtained by Birpinar and Sen (2004) is not reliable. The method of the volumetric approach associated with the Boltzmann transform overestimates the dimensionless drawdown at early times and underestimates the dimensionless drawdown at late times. It can also be found that when the dimensionless distance is larger, the discrepancy between the analytical solution and the numerical solution is smaller, as expected.

Fig. 3

Comparison of the numerical solution and the solution of Birpinar and Sen (2004) with B _D = 10, β _D  = 10, r _D  = 0.5 and 5

The sensitivity analysis of the dimensionless turbulent factor β _D on the dimensionless drawdown is shown in Fig. 4. Two typical dimensionless leakage parameters B _D = 100 and 1 were used in this figure, as shown in Fig. 4a and b. The other parameters were given as: r _D = 0.5, β _D = 1, 10 and 50. The solution of Hantush and Jacob (1955) has also been depicted as a reference. Interestingly enough, the features of these two figures are quite different. For the case B _D = 100, a relatively large value for the dimensionless leaky parameter which indicates a relatively small leakage effect, a larger β _D results in a smaller dimensionless drawdown at early times and leads to a larger dimensionless drawdown at late times. This phenomenon can be explained as follows. The Forchheimer equation can be rewritten as: $q = {K_{\beta }}\left( {\partial s/\partial x} \right)$, in which${K_{\beta }} = k/\left( {1 + \beta \left| q \right|} \right)$, and K _β can be regarded as apparent “Darcian” hydraulic conductivity. If β _D is larger, which also means a larger β, then K _β is smaller. At early times, the flow has not approached the steady state and the specific discharge q increases from zero to the stationary q ₀ at steady state. A smaller K _β indicates that it will take a longer time for the flow to approach the steady state. Thus, at the same time, a smaller K _β has a smaller specific discharge. Consequently, a smaller drawdown can be found from the equation $q = {K_{\beta }}\left( {\partial s/\partial x} \right)$. At late times, the flow approaches the steady state and the specific discharge does not change any more, which is only proportional to the pumping rate Q. From the equation $q = {K_{\beta }}\left( {\partial s/\partial x} \right)$, one can see a smaller K _β will result in a larger drawdown. As reflected in Fig. 4a, a larger K _β results in a larger dimensionless drawdown at late times. For the case B _D = 1 shown in Fig. 4b, a relatively small value for the dimensionless leaky parameter which indicates a relatively great leakage effect, a larger β _D results in a smaller dimensionless drawdown during the entire pumping period. This might be because a large leakage from the aquitard will result in the system approaching the quasi steady state earlier. Therefore, the “early-time” behavior of the type curve is very short and not long enough to be shown in the figure. Figure 4b might only reflect the “large-time” behavior of the type curve; therefore, it is no wonder that a larger β _D results in a smaller drawdown during the entire pumping period, as shown in Fig. 4b.

Fig. 4

Drawdown-time behavior for different values of the turbulent factor β _D with r _D  = 0.5, β _D = 1, 10 and 50. a B _D  = 100; b B _D  = 1

It is also worthwhile to analyze the effect of the leakage on the drawdown. Figure 5 is about the dimensionless drawdown versus dimensionless time for different dimensionless leakage parameters. The parameters were given as: r _D = 0.5, β _D = 10, B _D = 1, 10 and 100. The case without the leakage (Mathias et al. 2008) has also been depicted in this figure as a reference. As shown in Fig. 5, all the curves for different B _D values approach the same asymptotic value at early times, as well as the case of Mathias et al. (2008). This is because water from the leakage has not arrived at the confined aquifer at early times; therefore, the leakage has little impact on the drawdown at early times. As the pumping time increases, great differences have been found for different B _D. When B _D is larger, the dimensionless drawdown is larger. This is because a larger B _D means a smaller leakage effect, thus a larger dimensionless drawdown at late times. It can also been found that when B _D is larger, the curve is closer to that obtained by Mathias et al. (2008), as expected.

Fig. 5

Drawdown-time behavior for different values of the leakage factor B _D with r _D  = 0.5, β _D = 10, B _D  = 1, 10 and 100

Type curves

It is useful to generate a series of type curves for the hydrology community to conduct well testing analysis. When conducting a pumping test, the position of the observation well r and the aquifer thickness m are usually known. This means one can obtain r _D before analyzing the pumping test data. For a specific value of r _D, one can obtain a series of type curves for different dimensionless parameters. Taking r _D = 0.5 as an example, the corresponding type curves for different values of the dimensionless parameters are shown in Fig. 6. For a specific pumping test, if r _D happens to equal 0.5, one can use these type curves to estimate the aquifer parameters (an example will be given in the following section). The type curves for different r _D values can also be obtained by the MATLAB program, but it is impossible to report all the type curves in this paper. For the hydrology community use, one can get the MATLAB program upon request.

Fig. 6

Type curves for r _D  = 0.5, B _D  = 0.5, β _D = 0.5, 10 and 50

Dimensionless drawdown with wellbore storage

When the wellbore storage is considered, the dimensionless drawdowns inside the well for different turbulent factor β _D and different leakage parameter B _D were analyzed. As shown in Figs. 7 and 8, all the curves for different turbulent factor β _D and different leakage parameter B _D approach the same asymptotic value at early times while significant differences have been found at late times. Similar to the features of the drawdowns in the aquifer without the wellbore storage, a larger β _D (or B _D) results in a larger drawdown inside the well. The drawdowns in the aquifer when considering the wellbore storage have also been analyzed. As the features are similar to those without the wellbore storage, it is not repeated here.

Fig. 7

Drawdown-time behavior inside the well when considering the wellbore storage for different values of the turbulent factor β _D with r _D  = 0.1, r _wD  = r _cD  = 0.1, S = 0.001, B _D  = 10, β _D = 1, 10, 20 and 50

Fig. 8

Drawdown-time behavior inside the well when considering the wellbore storage for different values of the leakage factor B _D with r _D  = 0.1, r _wD  = r _cD  = 0.1, S = 0.001, β _D = 10, B _D = 1, 10 and 100

Sensitivity analysis

In order to assess the influence of different parameters on the results, the sensitivity analysis was done on different parameters, i.e., B _D, β _D, r _wD, and r _cD. This analysis is useful in assessing how a conceptual model responds to the change in certain variables. As proposed by Liou and Yeh (1997) and Huang and Yeh (2007), the sensitivity of a dependent variable can be defined as:

$$ {X_{{{\rm{i,j}}}}} = \frac{{\partial {R_{{\rm{i}}}}}}{{\partial {P_{{\rm{j}}}}}}, $$

(23)

in which X _i,j is the sensitivity coefficient of the jth parameter P _j at the ith time. R _i is the dependent variable at the ith time, which is the dimensionless drawdown in this study. Huang and Yeh (2007) have proposed a normalized sensitivity method to assess the effect of different variables on the dependent variable, which is defined as:

$$ X_{{{\rm{i,j}}}}^{\prime} = {P_{{\rm{j}}}}\frac{{\partial {R_{{\rm{i}}}}}}{{\partial {P_{{\rm{j}}}}}}, $$

(24)

where $X_{{i,j}}^{\prime}$ is the normalized sensitivity of the jth parameter P _j at the ith time. Notice that there is a partial derivative on the right hand of the Eq. (24), which is always difficult to obtain for a specific case. A finite difference formula will be used to approximate this differentiation (Yeh 1987), that is

$$ \frac{{\partial {R_{{\rm{i}}}}}}{{\partial {P_{{\rm{j}}}}}} = \frac{{{R_{{\rm{i}}}}\left( {{P_{{\rm{j}}}} + \Delta {P_{{\rm{j}}}}} \right) - {R_{{\rm{i}}}}\left( {{P_{{\rm{j}}}}} \right)}}{{\Delta {P_{{\rm{j}}}}}}, $$

(25)

in which ΔP _j is a small increment, which will be chosen as 10^–2 × P _j (Yang and Yeh 2009). The two most important dimensionless parameters used in this study are β _D and B _D. When the wellbore storage is considered, r _cD is also an important parameter which reflects the water stored in the wellbore. Thus, normalized sensitivities of these parameters will be analyzed in the following. The hypothetical data used were β _D = 10, r _wD = r _cD = 0.1, r _D = 1, S = 0.001, and B _D = 100 (or 1). The reason for not analyzing the sensitivities of r _wD and S are as follows: (1) r _wD is the dimensionless radius of the well screen which is assumed to be equal to r _cD in this study; (2) the storage coefficient S has been used in the definition of the dimensionless variable t _D.

Figure 9a and b plot the dimensionless time-drawdown curve and the normalized sensitivities of the parameters β _D, B _D and r _cD in semi-log scales. Figure 9a is for a case with a relatively small leakage B _D = 100, while Fig. 9b is for a case with a relatively large leakage B _D = 1. It can be seen that the normalized sensitivity of the drawdown with respect to B _D has a positive effect from both parts a and b of Fig. 9. This feature is quite distinct in Fig. 9b and this is because when B _D is larger, the leaky rate is smaller, resulting in a larger drawdown. For B _D = 1, the leakage is very large, then this positive phenomenon is evident. A relative change in β _D has a positive effect for B _D = 100 in Fig. 9a, while it has a negative effect for B _D = 1 in Fig. 9b. This is consistent with the features of Fig. 4a and b. The normalized sensitivity with respect to r _cD produces a negative effect at early times and stabilizes at zero after a relatively large dimensionless time t _D (say, 10⁴). This can be easily understood by considering the physics of the wellbore storage. Comparing parts a and b of Fig. 9, one can see that r _cD produces the largest normalized sensitivity in the magnitude when B _D is relatively large (B _D = 100), while B _D produces the largest normalized sensitivity in the magnitude when B _D is relatively small (B _D = 1). Those results indicate that the drawdown is very sensitive to the change in r _cD when B _D is large, while it is sensitive to the change in B _D when B _D is relatively small.

Fig. 9

Drawdown-time curve and the normalized sensitivities of the parameters β _D , B _D and r _cD . a B _D  = 100; b B _D  = 1

It seems that a relative change of these three parameters has no effect on the drawdown at early times (say, t _D < 10⁰), as shown in Fig. 9a. The truth is that the value of the dimensionless drawdown at early times is very small (see Fig. 4), consequently, the corresponding normalized sensitivity is a very small value around zero.

Application

The numerical solution developed in this study can be used to determine the aquifer parameters associated with the pumping test data. In order to show the applications of the solutions, the data from Ahmad (1998) was used, who did a pumping test in the Chaj-Doab area near Gujrat water distributory in Pakistan. The pumping rate is fixed at Q = 3.77m³/min, the thickness of the aquifer is measured as m = 76 m, and the observation well is about r = 122 m away from the pumping well. Therefore, the corresponding dimensionless distance r _D is equal to 1.61. As stated by Ahmad (1998), the aquifer in that area can be classified as a mixture of leaky and unconfined aquifers (Birpinar and Sen 2004). Therefore, it is possible to use the type curves developed in this study to estimate the aquifer parameters. The observation data of time-drawdown was plotted in log-log scale as shown in Fig. 10. After a trial and error process, the curve with r _D = 1.6053, B _D = 25 and β _D = 0.4 matched the observation data perfectly, as shown in Fig. 10. A matching point was chosen in the common area so that one could obtain the corresponding coordinates: s = 0.1 m, t = 10 min, s _D = 0.36 and t _D = 5.68. When the matching procedure is done, one can do the following calculations.

• 1. From the definitions of the dimensionless drawdown ${s_{{\rm{D}}}} = \frac{{4\pi km}}{Q}s$, one can obtain the apparent hydraulic conductivity $k = \frac{{{s_{{\rm{D}}}}Q}}{{4\pi ms}} = \frac{{0.36 \times 3.77}}{{4 \times 3.14 \times 76 \times 0.1}} = 0.014\left[ {{\hbox{m}}/{\hbox{min}}} \right].$

• 2. When k is known, the storage coefficient S can be calculated as: $S = \frac{{kt}}{{m{t_{{\rm{D}}}}}} = \frac{{0.014 \times 10}}{{5.68 \times 76}} = 3.24 \times {10^{{ - 4}}}.$

• 3. With the dimensionless definition ${\beta _{{\rm{D}}}} = \frac{{\beta Q}}{{4\pi {m^{2}}}}$, one has: $\beta = \frac{{4\pi {m^{2}}{\beta _{{\rm{D}}}}}}{Q} = \frac{{4 \times 3.14 \times {{76}^{2}} \times 0.4}}{{3.77}} = 7697\left[ {{\hbox{min}}/{\hbox{m}}} \right].$

• 4. Finally, the leakage parameter B can be calculated as: $B = \frac{{{B_{{\rm{D}}}}{m^{2}}}}{k} = \frac{{25 \times {{76}^{2}}}}{{0.014}} = 1.031 \times {10^{7}}$. As B is defined as $m \times {m_1}/{k_1}$, if the thickness of the aquitard is known, the hydraulic conductivity of the aquitard can be obtained subsequently.

Fig. 10

Type curve and field data matching sheets. The field data were obtained from Birpinar and Sen (2004)

As discussed in section Type curves, for a specific given distance r _D, one can generate a series of type curves. When the pumping data are available, one can estimate the aquifer parameters through the matching processes described in the previous with the type curves and the observed data.

Summary and conclusions

A numerical solution for non-Darcian flow to a well in leaky aquifers has been obtained by using the finite difference method in this study. The Forchheimer equation has been used to describe the flow in the aquifer. The impacts of the turbulent factor and the leakage parameter on the drawdowns have been analyzed. The results were also compared with the solution of Birpinar and Sen (2004) who investigated a similar problem with a volumetric approach. The solutions obtained in this study can also be used to estimate the aquifer parameters when the groundwater flow is non-Darcian. Several findings can be presented from this study:

• 1. The method of the volumetric approach associated with the Boltzmann transform (Birpinar and Sen 2004) overestimates the dimensionless drawdown at early times and underestimates the dimensionless drawdown at late times. When the dimensionless distance is larger, the discrepancy between the analytical solution and the numerical solution becomes smaller.

• 2. For a relatively larger dimensionless leakage parameter, e.g., B _D = 100, a larger turbulent factor β _D results in a smaller drawdown at early times and a larger drawdown at late times. While for a relatively smaller dimensionless leakage parameter, e.g., B _D = 1, a larger β _D results in a smaller drawdown during the entire pumping period.

• 3. The impact of the leakage on the drawdown is similar to that of Darcian flow; the leakage has little impact on the drawdown at early times, while a greater leakage parameter B _D leads to a larger drawdown at late times.

• 4. The drawdown is very sensitive to the change in r _cD reflecting the importance of wellbore storage when B _D is large, while it is sensitive to the change in B _D when B _D is relatively small.