1 Introduction

Let \(\mathcal H\) be a real Hilbert space with inner product \(\langle \cdot ,\cdot \rangle \) and its deduced norm \(\Vert \cdot \Vert \). Denote \(x^k\rightharpoonup x\) to indicate that the sequence \(\{x^k\}\) converges weakly to x, and \(x^k\rightarrow x\) to indicate that the sequence \(\{x^k\}\) converges strongly to x. Let C be a nonempty convex closed subset of \(\mathcal H\) and a bifunction \(f:\mathcal H\times \mathcal H\rightarrow \mathcal R\) such that the equilibrium condition \(f(x,x)=0\) holds for all \(x\in \mathcal H\) and \(f(x,\cdot )\) is lower semicontinuous, convex for each \(x\in \mathcal H\). In this paper, we consider an equilibrium problem, shortly \(\textrm{EPs}(C,f)\), first suggested by Nikaido and Isoda in [29] for non-cooperative convex games and the term “equilibrium problem” first used by Blum and Oettli in [9] as follows:

$$ \text {Find } x^*\in C\text { such that } f(x^*,y)\ge 0,\quad \forall y\in C. $$

The solution set is denoted by \(\textrm{Sol}(C,f)\). In recently years, the problem \(\textrm{EPs}(C,f)\) is an attractive field that has been investigated in many research papers due to its applications in a large variety of fields arising in structural analysis, economics, optimization, operations research and engineering sciences (see some interesting books [12, 13, 21] and many references therein).

It is worth to mention that during the recent years several solution algorithms came in the existence to solve the problem \(\textrm{EPs}(C,f)\) and its generalizations. The solution mapping \(E: C\rightarrow C\) was first introduced by Moreau in [28] as the form:

$$\begin{aligned} Ex=\arg \min \left\{ \lambda f(x,y)+\frac{1}{2}\Vert y-x\Vert ^2: y\in C\right\} ,\quad \forall x\in C, \end{aligned}$$
(1.1)

where \(\lambda >0\). Note that Ex is the unique solution of a strongly convex problem under proper lower semicontinuous and convex assumptions of f. It is originated by the fact that a point \(x^*\in C\) is a solution of the problem \(\textrm{EPs}(C,f)\) if and only if it is a fixed point of the solution mapping E [25, Proposition 2.1]. The solution mapping has become a useful tool in solving the problem \(\textrm{EPs}(C,f)\). Under some conditions onto \(\lambda \), the mapping E has some the following properties:

  • If the cost bifunction f is strongly monotone and Lipschitz-type continuous, then E is contractive [14, 25, Proposition 2.1].

Then, by using Banach’s contraction mapping principle, the unique solution of the problem \(\textrm{EPs}(C,f)\) is evaluated by the fixed point iteration sequence:

$$ x^0\in C,\quad x^{k+1}=Ex^k,\qquad \forall k\ge 0. $$

The authors showed that the sequence \(\{x^k\}\) converges strongly to a unique solution of the problem \(\textrm{EPs}(C,f)\). To avoid strongly monotone assumption of f, as an extension of Kraikaew and Saejung in [22], Hieu used a solution mapping [15] as follows:

$$ Fx=\arg \min \left\{ \lambda f(Ex,y)+\frac{1}{2}\Vert y-x\Vert ^2: y\in C\right\} ,\quad \forall x\in H_x, $$

where \(H_x=\{w\in \mathcal H: \langle x-\lambda w_x-Ex,w-Ex\rangle \le 0\}\), \(w_x\in \partial f(x,\cdot )(x)\) and Ex is defined in (1.1). Then, for each \(x^*\in \textrm{Sol}(C,f)\), we have

$$ \Vert Fx-x^*\Vert ^2\le \Vert x-x^*\Vert ^2-(1-2\lambda c_1)\Vert Ex-x\Vert ^2-(1-2\lambda c_2)\Vert Fx-Ex\Vert ^2,\quad \forall x\in \mathcal H, $$

where f is pseudomonotone and Lipschitz-type continuous. However, F can not be quasi-nonexpansive on \(\mathcal H\) such as \(\textrm{Sol}(C,f)\ne \textrm{Fix}(T)\).

For solving the monotone problem \(\textrm{EPs}(C,f)\), there are various instances of the computational algorithms with combining the solution mapping E with other iteration techniques. It is worth mentioning to very interesting results such as the extragradient algorithms proposed by Quoc et al. [31, 32], inexact proximal point methods of Iusem et al. [17, 18], extragradient-viscosity methods of Maingé and Moudafi [24], auxiliary principles of Mastroeni and Noor [25, 26, 30], extragradient methods of Anh et al. [2, 5, 6] and many other computational methods in [4, 7, 8, 10, 11, 16, 19, 20, 27, 33, 34] and the references cited therein.

Inspired and motivated by the ongoing research, we are aiming to suggest a new approach to the equilibrium problem \(\textrm{EPs}(C,f)\). First, we introduce a new solution mapping and prove its strongly quasi-nonexpansiveness. Second, we use the solution mapping for solving the problem \(\textrm{EPs}(C,f)\) via a Lipschitz continuous and strongly monotone mapping, and another Lipschitz continuous mapping. By the way, we can prove that the strong cluster point of the sequence constructed by our algorithm is the unique solution of a variational inequality problem where the constraint is the solution set of the problem \(\textrm{EPs}(C,f)\) under quasimonotone and Lipschitz continuous assumptions of the cost bifunction f. This constitutes a new approach which is called solution mapping approach and the fundamental difference of our algorithm with respect to current computational methods.

Our paper is organized as follows. In Section 2, we present some useful definitions, technique lemmas and a new solution mapping. A new algorithm and its convergent analysis for solving the problem \(\textrm{EPs}(C,f)\) are presented in Section 3. In Section 4, several numerical experiments are provided to illustrate the efficiency and accuracy of our proposed algorithm.

2 Solution Mappings

For each \(x\in \mathcal H\), the metric projection of x onto C is denoted by \(\varPi _C(x)\) which is the unique solution to the strongly convex problem:

$$ \min \{\Vert x-y\Vert ^2: y\in C\}. $$

Given a bifunction \(f: \mathcal H\times \mathcal H\rightarrow \mathcal R\) and \(\emptyset \ne K\subset \mathcal H\). The bifunction f is called to be:

  • \(\beta \)-strongly monotone if

    $$ f(x,y)+f(y,x)\le -\beta \Vert x-y\Vert ^2,\quad \forall x,y\in \mathcal H. $$

  • monotone if

    $$ f(x,y)+f(y,x)\le 0,\quad \forall x,y\in \mathcal H. $$

  • pseudomonotone if

    $$ f(x,y)\ge 0\quad \Rightarrow \quad f(y,x)\le 0,\quad \forall x,y\in \mathcal H. $$

  • \(\eta \)-strongly quasimonotone on K where \(\eta >0\) if

    $$ f(x,y)+f(y,x)\le -\beta \Vert x-y\Vert ^2,\quad \forall x\in K,y\in \mathcal H. $$

  • quasimonotone on K if

    $$ f(x,y)\ge 0\Rightarrow f(y,x)\le 0,\quad \forall x\in K,y\in \mathcal H. $$

  • Lipschitz-type continuous on \(\mathcal H\) with constants \(c_1>0\) and \(c_2>0\) if

    $$ f(x,y)+f(y,z)\ge f(x,z)-c_1\Vert x-y\Vert ^2-c_2\Vert y-z\Vert ^2,\quad \forall x,y,z\in \mathcal H. $$

Let a mapping \(S: \mathcal H\rightarrow \mathcal H\) and the fixed point set of S be \(\textrm{Fix}(S):=\{x\in \mathcal H: Sx=x\}\). The operator S is called to be:

  • \(\eta \)-strongly quasi-nonexpansive, where \(\eta >0\), if

    $$ \Vert Sx-z\Vert ^2\le \Vert x-z\Vert ^2-\eta \Vert Sx-x\Vert ^2,\quad \forall x\in \mathcal H,~ z\in \textrm{Fix}(S). $$

  • quasi-nonexpansive if

    $$ \Vert Sx-z\Vert \le \Vert x-z\Vert ,\quad \forall x\in \mathcal H,~ z\in \textrm{Fix}(S). $$

  • quasicontractive with constant \(\eta \in [0,1)\) if

    $$ \Vert Sx-z\Vert \le \eta \Vert x-z\Vert ,\quad \forall x\in \mathcal H,~z\in \textrm{Fix}(S). $$

    When \(\textrm{Fix}(S)=\mathcal H\), the mapping S is called contractive with constant \(\eta \).

For each \(x\in \mathcal H\) and \(\xi >0\), we consider the solution mapping \(S: \mathcal H\rightarrow C\) of the problem \(\textrm{EPs}(C,f)\) defined in the form:

$$\begin{aligned} Sx=\arg \min \left\{ \xi f(x,y)+\frac{1}{2}\Vert x-y\Vert ^2: x\in C\right\} . \end{aligned}$$
(2.1)

It is well-known that \(x\in C\) is a solution of the problem \(\textrm{EPs}(C, f)\) if and only if it is a fixed point of the mapping S [25, Proposition 2.1]. Let \(\gamma >0\). We introduce a new half space as follows:

$$\begin{aligned} H_x=\left\{ w\in \mathcal H: \langle x-\xi w_x-Sx, w-Sx\rangle \le \gamma \Vert x-Sx\Vert ^2\right\} , \end{aligned}$$
(2.2)

where \(w_x\in \partial f(x,\cdot )(Sx)\). Using the well-known necessary and sufficient condition for optimality of the convex programing (2.1), we see that Sx solves the strongly convex program

$$ \min \left\{ \xi f(x,y)+\frac{1}{2}\Vert x-y\Vert ^2: x\in C\right\} $$

if and only if

$$ 0\in \xi \partial f(x,\cdot )(Sx)+Sx-x+N_C(Sx), $$

where \(N_C(Sx)\) is the (outward) normal cone of C at \(Sx\in C\). Since \(f(x,\cdot )\) is subdifferentiable for each \(x\in \mathcal H\), so there exists \(w_x\in \partial f(x,\cdot )(Sx)\) such that

$$ x-Sx-\xi w_x\in N_C(Sx),\quad \forall x\in \mathcal H. $$

Consequently

$$ \langle x-Sx-\xi w_x,y-Sx\rangle \le 0,\quad \forall y\in C. $$

From \(\gamma >0\), it follows that

$$ \langle x-\xi w_x-Sx,y-Sx\rangle \le \gamma \Vert x-Sx\Vert ^2,\quad \forall y\in C. $$

By (2.2), it yields \(C\subset H_x\) for all \(x\in \mathcal H\).

Now we propose a new solution mapping \(T:\mathcal H\rightarrow \mathcal H\) for the problem \(\textrm{EPs}(C,f)\) as follows:

$$\begin{aligned} Tx=\arg \min \left\{ \nu \xi f(Sx,y)+\frac{1}{2}\Vert y-x\Vert ^2: y\in H_x\right\} , \end{aligned}$$
(2.3)

where regular parameter \(\nu >0\) is very important for strongly quasi-nonexpansiveness of T. In the case \(f(x,y)=\langle F(x),y-x\rangle \), set \(z=x-\nu \xi F(x)\). It is easy to evaluate that Tx is the projection of z onto \(H_x\) and presented in an explicit formula:

$$\begin{aligned} Tx=\varPi _{H_x}(z)= \left\{ \begin{array}{ll} z-\frac{\langle d_x, z-Sx\rangle -\gamma \Vert x-Sx\Vert ^2}{\Vert d_x\Vert ^2}d_x& \quad \text { if }z\notin H_x,\\ z & \quad \text { otherwise}, \end{array}\right. \end{aligned}$$

where \(d_x=x-\xi w_x-Sx\). Note that, if \(d_x=0\) then obviously \(z\in H_x\) and \(Tx=x-\nu \xi F(x)\).

The following result will present some important properties of the operators T and S that will be needed in the sequel.

Lemma 2.1

Suppose that f is Lipschitz-type continuous with constants \(c_1>0\) and \(c_2>0\). Under conditions \(\xi >0\), \(\nu >0\) and \(\gamma >0\), the following inequality holds

$$\begin{aligned} \Vert Tx-t\Vert ^2\le & \Vert t-x\Vert ^2-(1-\nu )\Vert x-Tx\Vert ^2-\nu (1-2\gamma -2\xi c_1)\Vert x-Sx\Vert ^2\\ & -\nu (1-2\xi c_2)\Vert Tx-Sx\Vert ^2+2\nu \xi f(Sx,t),\quad \forall t\in C, x\in \mathcal H. \end{aligned}$$

Proof

By using the definition of \(w_x\in \partial f(x,\cdot )(Sx)\), we get

$$\begin{aligned} f(x,z)-f(x,Sx)\ge \langle w_x,z-Sx\rangle ,\quad \forall z\in \mathcal H. \end{aligned}$$
(2.4)

Combining (2.4) and \(Tx\in H_x\), it implies

$$\begin{aligned} \langle x-Sx,Tx-Sx\rangle - \gamma \Vert x-Sx\Vert ^2\le & \xi \langle w_x,Tx-Sx \rangle \\\le & \xi [f(x,Tx)-f(x,Sx)]. \end{aligned}$$

From the necessary and sufficient condition for the strongly convex problem (2.3), there exists \(v_x\in \partial f(Sx,\cdot )(Tx)\) such that

$$ 0\in \nu \xi v_x+Tx-x+N_{H_x}(Tx). $$

Thus,

$$ \langle \nu \xi v_x+Tx-x, t-Tx\rangle \ge 0,\quad \forall t\in H_x, $$

and hence

$$\begin{aligned} \nu \xi \langle v_x, t-Tx\rangle \ge \langle x-Tx, t-Tx\rangle ,\quad \forall t\in H_x. \end{aligned}$$
(2.5)

By the definition of \(v_x\in \partial f(Sx,\cdot )(Tx)\) and \(\nu \xi >0\), it implies

$$ f(Sx,y)-f(Sx,Tx)\ge \langle v_x,y-Tx\rangle ,\quad \forall y\in \mathcal H. $$

This together with (2.5) implies

$$\begin{aligned} \langle x-Tx, t-Tx\rangle\le & \nu \xi \langle v_x, t-Tx\rangle \nonumber \\\le & \nu \xi [f(Sx,t)-f(Sx,Tx)],\quad \forall t\in H_x. \end{aligned}$$
(2.6)

Since f is Lipschitz-type continuous with \(c_1\) and \(c_2\), we deduce

$$ f(x,Sx)+f(Sx,Tx)\ge f(x,Tx)-c_1\Vert x-Sx\Vert ^2-c_2\Vert Tx-Sx\Vert ^2. $$

Combining this and (2.6), we get that, for each \(t\in \mathcal H_x\),

$$\begin{aligned} & \langle x-Tx, t-Tx\rangle -\nu \xi f(Sx,t)\nonumber \\ & \le -\nu \xi f(Sx,Tx)\nonumber \\ & \le \nu \xi \big [f(x,Sx)-f(x,Tx)+c_1\Vert x-Sx\Vert ^2+c_2\Vert Tx-Sx\Vert ^2\big ],\quad \forall t\in \mathcal H_x\nonumber \\ & \le \nu \langle Sx-x, Tx-Sx\rangle +\nu \gamma \Vert x-Sx\Vert ^2+\nu \xi c_1\Vert x-Sx\Vert ^2+\nu \xi c_2\Vert Tx-Sx\Vert ^2. \end{aligned}$$
(2.7)

By using the relation

$$ 2\langle a,b\rangle =\Vert a\Vert ^2+\Vert b\Vert ^2-\Vert a-b\Vert ^2,\quad \forall a,b\in \mathcal H, $$

we obtain

$$\begin{aligned} 2\langle x-Tx, t-Tx\rangle= & \Vert x-Tx\Vert ^2+\Vert t-Tx\Vert ^2-\Vert t-x\Vert ^2,\\ 2\langle Sx-x, Tx-Sx\rangle= & \Vert x-Tx\Vert ^2-\Vert Sx-x\Vert ^2-\Vert Tx-Sx\Vert ^2. \end{aligned}$$

This together with (2.7) implies that

$$\begin{aligned} \Vert Tx-t\Vert ^2\le & \Vert t-x\Vert ^2-(1-\nu )\Vert x-Tx\Vert ^2-\nu (1-2\gamma -2\xi c_1)\Vert x-Sx\Vert ^2\\ & -\nu (1-2\xi c_2)\Vert Tx-Sx\Vert ^2+2\nu \xi f(Sx,t),\quad \forall t\in C. \end{aligned}$$

The proof is complete.\(\square \)

Lemma 2.2

Assume that f is Lipschitz-type continuous with constants \(c_1>0\) and \(c_2>0\). Let parameters \(\nu \), \(\xi \) and \(\gamma \) satisfy the following conditions:

$$\begin{aligned} \xi \in \left( 0,\frac{1}{c_1+c_2}\right) ,\quad \gamma \in \left( 0,1-\xi (c_1+c_2)\right) ,\quad \nu \in \left( 0,\frac{1}{\xi c_2}\right) . \end{aligned}$$
(2.8)

Then, \(x^*\in C\) is a solution of the problem \(\textrm{EPs}(C,f)\) if and only if it is a fixed point of the solution mapping T.

Proof

Assume that \(\bar{x}\in C\) is a fixed point of T, i.e., \(T\bar{x}=\bar{x}\). Substituting \(x=\bar{x}\) into Lemma 2.1, we obtain

$$\begin{aligned} \Vert \bar{x}-t\Vert ^2\le & \Vert t-\bar{x}\Vert ^2-(1-\nu )\Vert \bar{x}-T\bar{x}\Vert ^2-\nu (1-2\gamma -2\xi c_1)\Vert \bar{x}-S\bar{x}\Vert ^2\\ & -\nu (1-2\xi c_2)\Vert T\bar{x}-S\bar{x}\Vert ^2+2\nu \xi f(S\bar{x},t),\quad \forall t\in C. \end{aligned}$$

Consequently

$$ \xi f(S\bar{x},t)\ge (1-\gamma -\xi c_1-\xi c_2)\Vert \bar{x}-S\bar{x}\Vert ^2,\quad \forall t\in C. $$

From (2.8), it follows

$$ f(S\bar{x},t)\ge 0,\quad \forall t\in C. $$

Thus, \(S\bar{x}\in C\) is a solution of the problem \(\textrm{EPs}(C,f)\). Since \(x\in C\) is a solution of the problem \(\textrm{EPs}(C,f)\) if and only it is a fixed point of S, so \(\bar{x}=S\bar{x}\in \textrm{Sol}(C,f)\).

Now we assume \(\hat{x}\in \textrm{Sol}(C,f)\). Then, \(S\hat{x}=\hat{x}\). Substituting \(t=\hat{x}\) and \(x=\hat{x}\) into Lemma 2.1 and using \(f(x,x)=0\) for all \(x\in C\), we get

$$ (1-\nu \xi c_2)\Vert T\hat{x}-\hat{x}\Vert ^2\le 0. $$

By (2.8), it yields \(T\hat{x}=\hat{x}\). Thus, the solution \(\hat{x}\in \textrm{Sol}(C,f)\) is a fixed point of T. This implies the proof. \(\square \)

Lemma 2.3

Suppose that f is quasimonotone on \(\textrm{Sol}(C,f)\) and Lipschitz-type continuous with constants \(c_1>0\), \(c_2>0\). The parameters satisfy the following restrictions:

$$\begin{aligned} \left\{ \begin{array}{l} \xi \in \left( 0,\min \left\{ \frac{1}{2c_1},\frac{1}{2c_2}\right\} \right) , \\ \gamma \in \left( 0,1-\xi (c_1+c_2)\right) , \\ \nu \in \left( 0,\min \left\{ 1,\frac{1}{\xi c_2}\right\} \right) . \end{array}\right. \end{aligned}$$
(2.9)

Then, the solution mapping T is strongly quasi-nonexpansive with constant \((1-\nu )\).

Proof

Let \(x^*\in \textrm{Sol}(C,f)\), i.e., \(f(x^*,x)\ge 0\) for all \(x\in C\). By replacing \(t=x^*\) into Lemma 2.1, we get

$$\begin{aligned} \Vert Tx-x^*\Vert ^2\le & \Vert x-x^*\Vert ^2-(1-\nu )\Vert x-Tx\Vert ^2-\nu (1-2\gamma -2\xi c_1)\Vert x-Sx\Vert ^2\nonumber \\ & -\nu (1-2\xi c_2)\Vert Tx-Sx\Vert ^2+2\nu \xi f(Sx,x^*). \end{aligned}$$
(2.10)

Since \(Sx\in C\), f is quasimonotone and (2.10), we deduce \(f(Sx,x^*)\le 0\) and

$$\begin{aligned} \Vert Tx-x^*\Vert ^2\le & \Vert x-x^*\Vert ^2-(1-\nu )\Vert x-Tx\Vert ^2-\nu (1-2\gamma -2\xi c_1)\Vert x-Sx\Vert ^2\nonumber \\ & -\nu (1-2\xi c_2)\Vert Tx-Sx\Vert ^2+2\nu \xi f(Sx,x^*)\nonumber \\\le & \Vert x-x^*\Vert ^2-(1-\nu )\Vert x-Tx\Vert ^2-\nu (1-2\gamma -2\xi c_1)\Vert x-Sx\Vert ^2\nonumber \\ & -\nu (1-2\xi c_2)\Vert Tx-Sx\Vert ^2. \end{aligned}$$
(2.11)

Combining this and conditions (2.9), we have

$$ \Vert Tx-x^*\Vert ^2\le \Vert x-x^*\Vert ^2-(1-\nu )\Vert x-Tx\Vert ^2,\quad \forall x^*\in \textrm{Sol}(C,f), x\in \mathcal H. $$

By the definition and Lemma 2.2, we get that \(\textrm{Fix}(T)=\textrm{Sol}(C,f)\) and the solution mapping T is \((1-\nu )\)-strongly quasi-nonexpansive.\(\square \)

Remark 2.4

In [14, Theorem 3.7], the author showed that if \(f:C\times C\rightarrow \mathcal R\) is \(\zeta \)-strongly monotone and there exist functions \(\alpha _i:C\times C\rightarrow \mathcal H\), \(\beta _i: C\rightarrow \mathcal H\) \((i=1,\ldots ,p)\) such that

$$ f(x,y)+f(y,z)\ge f(x,z)+\sum _{i=1}^p\langle \alpha _i(x,y),\beta _i(y-z)\rangle ,\quad \forall x,y,z\in C, $$

where \(\beta _i\) is \(K_i\)-Lipschitz continuous, \(\alpha _i(x,y)+\alpha _i(y,x)=0\) and \(|\alpha _i(x,y)|\le L_i\Vert x-y\Vert \) for all \(x,y\in C\), \(i=1,\ldots ,p\). Under condition \(\xi \in (0, \frac{2\zeta }{M^2})\) where \(M=\sum _{i=1}^pK_iL_i\), the mapping S defined by (2.1) is contractive with constant \(\delta =\sqrt{1-\xi (2\zeta -\xi M^2)}\in (0,1)\).

Lemma 2.5

[23, Remark 2.1] Let \(T:\mathcal H\rightarrow \mathcal H\) is quasi-nonexpansive and \(T_{\omega }=(1-\omega )\textrm{Id}+\omega T\) with \(\omega \in (0,1]\) such that \(\textrm{Fix}(T)\ne \emptyset \), where \(\textrm{Id}\) is an identify operator. Then, the following statements hold:

  1. (i)

    \(\textrm{Fix}(T)=\textrm{Fix}(T_{\omega })\).

  2. (ii)

    \(T_{\omega }\) is quasi-nonexpansive.

  3. (iii)

    \(\Vert T_{\omega }x-v\Vert ^2\le \Vert x-v\Vert ^2-\omega (1-\omega )\Vert Tx-x\Vert ^2\) for all \(x\in \mathcal H\) and \(v\in \textrm{Fix}(T)\).

  4. (iv)

    \(\langle x-T_{\omega }x,x-u\rangle \ge \frac{\omega }{2}\Vert x-Tx\Vert ^2\) for all \(x\in \mathcal H\) and \(u\in \textrm{Fix}(T)\).

3 Subgradient Auxiliary Principle Algorithm

Let \(G:\mathcal H\rightarrow \mathcal H\) be \(L_G\)-Lipschitz continuous and \(\beta _G\)-strongly monotone, and \(g:\mathcal H\rightarrow \mathcal H\) is \(L_g\)-Lipschitz continuous. In this section, we propose a new algorithm which is called Subgradient Auxiliary Principle Algorithm for solving the problem \(\textrm{EPs}(C,f)\) via the mappings G and g. Under certain conditions we obtain the desired convergence for the algorithm. First, we give the restrictions governing the cost bifunction \(f: \mathcal H\times \mathcal H\rightarrow \mathcal R\) and the sequence of parameters below.

\((R_1)\):

The solution set \(\textrm{Sol}(C,f)\) of the problem \(\textrm{EPs}(C,f)\) is nonempty.

\((R_2)\):

The cost bifunction f is quasimonotone and Lipschitz-type continuous with constants \(c_1>0\) and \(c_2>0\). f is jointly weakly continuous on \(\mathcal H\times C\) in the sense that, if \(\{x^k\}\), \(\{y^k\}\) converge weakly to \(\hat{x}\), \(\hat{y}\), respectively, then \(f(x^k,y^k)\rightarrow f(\hat{x}, \hat{y})\) as \(k\rightarrow \infty \).

\((R_3)\):

For every integer \(k\ge 0\), all the positive parameters satisfy the following restrictions:

$$ \left\{ \begin{array}{l} \xi _k\in \left( 0,\min \left\{ \frac{1}{2c_1},\frac{1}{2c_2}\right\} \right) ,~\lim _{k\rightarrow \infty }\xi _k=\xi >0, \\ \gamma _k\in \left( 0,1-\xi _k(c_1+c_2)\right) , \\ \nu \in \left( 0,\min \left\{ 1,\frac{1}{\xi _k c_2}\right\} \right) ,\\ \omega \in \left( 0,\frac{1}{2}\right) ,~\mu \in \left( 0,\frac{2\beta _G}{L_G^2}\right) ,~\gamma \in \left( 0,\frac{\mu }{L_g}\left( \beta _G-\frac{\mu L_G^2}{2}\right) \right) ,~\tau \in \left( \gamma L_g,\mu \beta _G\right) ,\\ \alpha _k\in \left( 0,\min \left\{ 1,\frac{2(\mu \beta _G-\tau )}{\mu ^2 L_G^2-\tau ^2},\frac{1}{\tau -\gamma L_g}\right\} \right) ,~\sum _{k=0}^{\infty }\alpha _k=\infty ,~\lim _{k\rightarrow \infty }\alpha _k=0. \end{array}\right. $$

Let the mappings S and T be defined by (2.1)–(2.3). Now we present the Subgradient Auxiliary Principle Algorithm for solving the problem \(\textrm{EPs}(C,f)\).

Algorithm 1
figure a

Subgradient Auxiliary Principle Algorithm (SAPA).

Full size image

For each \(k\ge 0\) and \(x\in \mathcal H\), set

$$\begin{aligned} S_k x= & \arg \min \left\{ \xi _k f(x,y)+\frac{1}{2}\Vert y-x\Vert ^2: x\in C\right\} ,\end{aligned}$$
(3.1)
$$\begin{aligned} T_k x= & \arg \min \left\{ \nu \xi _k f(S_kx,y)+\frac{1}{2}\Vert y-x\Vert ^2: x\in H_k\right\} , \end{aligned}$$
(3.2)

where \(H_k=\{w\in \mathcal {H}: \langle x-\xi _k w_x-S_kx,w-S_kx\rangle \le \gamma _k\Vert x-S_kx\Vert ^2\}\) and \(w_x\in \partial f(x,\cdot )(S_kx)\).

Remark 3.1

  1. (i)

    Since \(x^*\) is a solution of the problem \(\textrm{EPs}(C,f)\) if and only if it is a fixed point of the mapping \(S_k\) defined by (3.1). Therefore, if \(y^k=x^k\) in Algorithm 1, i.e., \(x^k=S_kx^k\) under the assumption \(\xi _k>0\), then \(x^k\) is a solution of the problem \(\textrm{EPs}(C,f)\). The stopping criterion in Step 1 is valid.

  2. (ii)

    By Lemma 2.2, \(x^k\) is a solution of the problem \(\textrm{EPs}(C,f)\) if and only if it is a fixed point of the solution mapping \(T_k\) defined by (3.2) under the assumptions \((R_1)\)–\((R_3)\). Thus, if \(z^k=x^k\) in Algorithm 1, i.e., \(x^k=T_kx^k\), then \(x^k\) is a solution of the problem \(\textrm{EPs}(C,f)\). The stopping criterion in Step 2 is valid.

  3. (iii)

    As usual, for each \(\varepsilon >0\), an iteration point \(x^k\) defined in Algorithm 1 is \(\varepsilon \)-solution of the problem \(\textrm{EPs}(C,f)\), if \(\Vert y^k-x^k\Vert \le \varepsilon \) or \(\Vert z^k-x^k\Vert \le \varepsilon \). Equivalently, \(\max \{\Vert y^k-x^k\Vert ,\Vert z^k-x^k\Vert \}\le \varepsilon \).

The next lemma is crucial for the proof of our convergent theorem.

Lemma 3.2

Let \(\{x^k\}\) and \(\{y^k\}\) be the two sequences generated by Algorithm 1 and let \(x^*\in \textrm{Sol}(C,f)\). Under assumptions \((R_2)\) and \((R_3)\), the following claim holds

$$\begin{aligned} \Vert z^k-x^*\Vert ^2\le & \Vert x^k-x^*\Vert ^2-(1-\nu )\Vert x^k-z^k\Vert ^2-\nu (1-2\gamma _k-2\xi _k c_1)\Vert x^k-y^k\Vert ^2\\ & -\nu (1-2\xi _k c_2)\Vert z^k-y^k\Vert ^2. \end{aligned}$$

Proof

From (2.1) and Step 1, it follows \(y^k=S_kx^k\), where the mapping \(S_k\) is defined in (3.1). Combining (3.2) and Step 2, it yields that \(x^{k+1}=T_kx^k\). By using the \((1-\nu )\)-strongly quasi-nonexpansive property of the mapping \(T_k\) in Lemma 2.3, (2.11), assumptions \((R_2)\) and \((R_3)\), we obtain

$$\begin{aligned} \Vert z^k-x^*\Vert ^2= & \Vert T_kx^k-x^*\Vert ^2\\\le & \Vert x^k-x^*\Vert ^2-(1-\nu )\Vert x^k-T_kx^k\Vert ^2-\nu (1-2\gamma _k-2\xi _k c_1)\Vert x^k-S_kx^k\Vert ^2\\ & -\nu (1-2\xi _k c_2)\Vert T_kx^k-S_kx^k\Vert ^2. \end{aligned}$$

which completes the proof.\(\square \)

Theorem 3.3

Let the cost bifunction f and the parameters satisfy assumptions \((R_1)\)–\((R_3)\). Then, two iteration sequences \(\{x^k\}\) and \(\{y^k\}\) generated by Algorithm 1 converge strongly to the unique solution \(x^*\in \textrm{Sol}(C,f)\) of the following variational inequality:

$$\begin{aligned} \langle (\mu G-\gamma g)(x^*),x-x^*\rangle \ge 0,\quad \forall x\in \textrm{Sol}(C,f). \end{aligned}$$
(3.3)

Proof

Let \(x^*\) satisfy the inequality (3.3). Then, \(x^*\in \textrm{Sol}(C,f)\). From Lemma 2.2, it follows that \(x^*\) is a fixed point of \(T_k\) defined by (3.2). By Lemma 2.3, the mapping \(T_k\) is strongly quasi-nonexpansive on \(\mathcal H\). Since (3.2) and Step 2, we have \(z^k=T_kx^k\). For every \(x\in \mathcal H\), since G is \(\beta _G\)-strongly monotone and \(L_G\)-Lipschitz continuous, we have

$$\begin{aligned} & \Vert (\textrm{Id}-\alpha _k\mu G)(x)-(\textrm{Id}-\alpha _k\mu G)(y)\Vert ^2\nonumber \\ & \qquad =\Vert x-y\Vert ^2-2\alpha _k\mu \langle x-y,G(x)-G(y) \rangle +\alpha _k^2\mu ^2\Vert G(x)-G(y)\Vert ^2\nonumber \\ & \qquad \le (1-2\alpha _k\mu \beta _G+\alpha _k^2\mu ^2L_G^2)\Vert x-y\Vert ^2\nonumber \\ & \qquad \le (1-\alpha _k\tau )^2\Vert x-y\Vert ^2,\quad \forall x,y\in \mathcal H, \end{aligned}$$
(3.4)

where the last inequality is deduced from the condition \(\alpha _k\in \left( 0,\min \left\{ 1,\frac{2(\mu \beta _G-\tau )}{\mu ^2 L_G^2-\tau ^2}\right\} \right) \) and \(\tau \in (0,\mu \beta _G)\) of \((R_3)\). Since g is \(L_g\)-Lipschitz continuous, (3.4) and Lemma 2.5(iii), we obtain

$$\begin{aligned} \Vert x^{k+1}-x^*\Vert= & \Vert \alpha _k\gamma g(x^k)+(\textrm{Id}-\alpha _k\mu G)(h^k)-x^*\Vert \nonumber \\= & \Vert \alpha _k\gamma [g(x^k)-g(x^*)]+\alpha _k[\gamma g(x^*)-\mu G(x^*)]\nonumber \\ & +(\textrm{Id}-\alpha _k\mu G)(h^k)-(\textrm{Id}-\alpha _k\mu G)(x^*)\Vert \nonumber \\\le & \alpha _k\gamma \Vert g(x^k)-g(x^*)\Vert +\alpha _k\Vert \gamma g(x^*)-\mu G(x^*)\Vert \nonumber \\ & +\Vert (\textrm{Id}-\alpha _k\mu G)(h^k)-(\textrm{Id}-\alpha _k\mu G)(x^*)\Vert \nonumber \\\le & \alpha _k\gamma L_g\Vert x^k-x^*\Vert +\alpha _k\Vert \gamma g(x^*)-\mu G(x^*)\Vert +(1-\alpha _k\tau )\Vert h^k-x^*\Vert \nonumber \\= & \alpha _k\gamma L_g\Vert x^k-x^*\Vert +\alpha _k\Vert \gamma g(x^*)-\mu G(x^*)\Vert \nonumber \\ & +(1-\alpha _k\tau )\Vert (1-\omega )x^k+\omega T_kx^k-x^*\Vert \\\le & \alpha _k\gamma L_g\Vert x^k-x^*\Vert +\alpha _k\Vert \gamma g(x^*)-\mu G(x^*)\Vert +(1-\alpha _k\tau )\Vert x^k-x^*\Vert \nonumber \\= & [1-\alpha _k(\tau -\gamma L_g)]\Vert x^k-x^*\Vert +\alpha _k(\tau -\gamma L_g)\frac{\Vert \gamma g(x^*)-\mu G(x^*)\Vert }{\tau -\gamma L_g}\nonumber \\\le & \max \left\{ \Vert x^k-x^*\Vert ,\frac{\Vert \gamma g(x^*)-\mu G(x^*)\Vert }{\tau -\gamma L_g}\right\} \nonumber \\\le & \cdots \nonumber \\\le & \max \left\{ \Vert x^0-x^*\Vert ,\frac{\Vert \gamma g(x^*)-\mu G(x^*)\Vert }{\tau -\gamma L_g}\right\} ,\nonumber \end{aligned}$$
(3.5)

where \(\alpha _k(\tau -\gamma L_g)\in (0,1)\) is deduced from the conditions \((R_3)\). Therefore, \(\{x^k\}\) is bounded. Applying Lemma 2.5(iv) for \(T_{\omega }:=(1-\omega )\textrm{Id}+\omega T_k\), using the Cauchy–Schwarz inequality and (3.4), we have

$$\begin{aligned} & \langle x^{k+1}-x^k+\alpha _k [\mu G(x^k)-\gamma g(x^k)], x^k-x^*\rangle \\ & \quad = \langle (\textrm{Id}-\alpha _k\mu G)(h^k)-(\textrm{Id}-\alpha _k\mu G)(x^k), x^k-x^*\rangle \\ & \quad =\langle (\textrm{Id}-\alpha _k\mu G)(T_{\omega }x^k)-(\textrm{Id}-\alpha _k\mu G)(x^k), x^k-x^*\rangle \\ & \quad =(1-\alpha _k)\langle T_{\omega }x^k-x^k,x^k-x^*\rangle +\alpha _k\langle (\textrm{Id}-\mu G)T_{\omega }x^k-(\textrm{Id}-\mu G)x^k,x^k-x^*\rangle \\ & \quad \le (1-\alpha _k)\langle T_{\omega }x^k-x^k,x^k-x^*\rangle +\alpha _k\langle (\textrm{Id}-\mu G)T_{\omega }x^k-(\textrm{Id}-\mu G)x^k,x^k-x^*\rangle \\ & \quad \le -(1-\alpha _k)\frac{\omega }{2}\Vert T_kx^k-x^k\Vert ^2+\alpha _k(1-\alpha _k\tau )\Vert T_{\omega }x^k-x^k\Vert \Vert x^k-x^*\Vert \\ & \quad = -\frac{(1-\alpha _k)\omega }{2}\Vert T_kx^k-x^k\Vert ^2+\omega \alpha _k(1-\alpha _k\tau )\Vert T_kx^k-x^k\Vert \Vert x^k-x^*\Vert . \end{aligned}$$

Then, using the relation

$$ 2\langle x,y\rangle =\Vert x+y\Vert ^2-\Vert x\Vert ^2-\Vert y\Vert ^2,\quad \forall x,y\in \mathcal H, $$

we get

$$\begin{aligned} 2\langle x^{k+1}-x^k,x^k-x^*\rangle= & \Vert x^{k+1}-x^*\Vert ^2-\Vert x^{k+1}-x^k\Vert ^2-\Vert x^k-x^*\Vert ^2\nonumber \\\le & 2\alpha _k \langle \mu G(x^k)-\gamma g(x^k), x^*-x^k\rangle -(1-\alpha _k)\omega \Vert T_kx^k-x^k\Vert ^2\nonumber \\ & +2\omega \alpha _k(1-\alpha _k\tau )\Vert T_kx^k-x^k\Vert \Vert x^k-x^*\Vert . \end{aligned}$$
(3.6)

From Step 3, it follows that

$$\begin{aligned} \Vert x^{k+1}-x^k\Vert ^2= & \Vert \alpha _k\gamma g(x^k)+(\textrm{Id}-\alpha _k\mu G)(h^k)-x^k\Vert ^2\nonumber \\= & \Vert \alpha _k\gamma g(x^k)+(\textrm{Id}-\alpha _k\mu G)(T_{\omega }x^k)-x^k\Vert ^2\nonumber \\= & \Vert \alpha _k[\gamma g(x^k)-\mu G(x^k)]+(\textrm{Id}-\alpha _k\mu F)T_{\omega }x^k-(\textrm{Id}-\alpha _k\mu G)(x^k)\Vert ^2\nonumber \\\le & 2\alpha _k^2\Vert \gamma g(x^k)-\mu G(x^k)\Vert ^2+2\Vert (\textrm{Id}-\alpha _k\mu F)T_{\omega }x^k-(\textrm{Id}-\alpha _k\mu G)(x^k)\Vert ^2\nonumber \\\le & 2\alpha _k^2\Vert \gamma g(x^k)-\mu G(x^k)\Vert ^2+2(1-\alpha _k\tau )^2\Vert T_{\omega }x^k-x^k\Vert ^2\nonumber \\= & 2\alpha _k^2\Vert \gamma g(x^k)-\mu G(x^k)\Vert ^2+2(1-\alpha _k\tau )^2\omega ^2\Vert T_kx^k-x^k\Vert ^2. \end{aligned}$$
(3.7)

Set \(a_k:=\Vert x^k-x^*\Vert \). Combining (3.6) and (3.7), it yields

$$\begin{aligned} a_{k+1}\le & a_k+\Vert x^{k+1}-x^k\Vert ^2+2\alpha _k [\mu G(x^k)-\gamma g(x^k)], x^*-x^k\rangle \nonumber \\ & -(1-\alpha _k)\omega \Vert T_kx^k-x^k\Vert ^2+2\omega \alpha _k(1-\alpha _k\tau )\Vert T_kx^k-x^k\Vert \Vert x^k-x^*\Vert \nonumber \\\le & a_k+2\alpha _k \langle \mu G(x^k)-\gamma g(x^k), x^*-x^k\rangle -(1-\alpha _k)\omega \Vert T_kx^k-x^k\Vert ^2\nonumber \\ & +2\alpha _k^2\Vert \gamma g(x^k)-\mu G(x^k)\Vert ^2+2(1-\alpha _k\tau )^2\omega ^2\Vert T_kx^k-x^k\Vert ^2\nonumber \\ & +2\omega \alpha _k(1-\alpha _k\tau )\Vert T_kx^k-x^k\Vert \Vert x^k-x^*\Vert \nonumber \\= & a_k+2\alpha _k \langle \mu G(x^k)-\gamma g(x^k), x^*-x^k\rangle -\omega [1-\alpha _k-2\omega (1-\alpha _k\tau )^2]\Vert T_kx^k-x^k\Vert ^2\nonumber \\ & +2\alpha _k^2\Vert \gamma g(x^k)-\mu G(x^k)\Vert ^2+2\omega \alpha _k(1-\alpha _k\tau )\Vert T_kx^k-x^k\Vert \Vert x^k-x^*\Vert . \end{aligned}$$
(3.8)

Let us consider two following cases:

Case 1. There exists a positive integer \(k_0\) such that \(a_{k+1}\le a_k\) for all \(k\ge k_0\). Then, the limit \(\lim _{k\rightarrow \infty }a_k=A<\infty \) exists. Passing to the limit into (3.8) as \(k\rightarrow \infty \), using the boundedness of \(\{x^k\}\) and \(\lim _{k\rightarrow \infty }\alpha _k=0\), we obtain \(\lim _{k\rightarrow \infty }\Vert T_kx^k-x^k\Vert =0\). From (3.8), it follows

$$ \alpha _k\varGamma _k\le a_k-a_{k+1},\quad \forall k\ge k_0, $$

where \(\varGamma _k:=-2\langle \mu G(x^k)-\gamma g(x^k), x^*-x^k\rangle -2\alpha _k\Vert \gamma g(x^k)-\mu G(x^k)\Vert ^2-2\omega \alpha _k(1-\alpha _k\tau )\Vert T_kx^k-x^k\Vert \Vert x^k-x^*\Vert \). By the condition \(\sum _{k=0}^{\infty }\alpha _k=\infty \) in \((R_3)\), we deduce \(\liminf _{k\rightarrow \infty }\varGamma _k\le 0\) and hence

$$ \liminf _{k\rightarrow \infty }\langle \mu G(x^k)-\gamma g(x^k), x^k-x^*\rangle \le 0. $$

Combining this with the relation

$$ \langle (\mu G-\gamma g)(x)-(\mu G-\gamma g)(y),x-y\rangle \ge (\mu \beta _G-\gamma L_g)\Vert x-y\Vert ^2,\quad \forall x,y\in \mathcal H, $$

yields

$$\begin{aligned} 0\ge & \liminf _{k\rightarrow \infty }\langle \mu G(x^k)-\gamma g(x^k), x^k-x^*\rangle \nonumber \\\ge & \liminf _{k\rightarrow \infty }\left[ \langle \mu G(x^*)-\gamma g(x^*), x^k-x^*\rangle +(\mu \beta _G-\gamma L_g)\Vert x^k-x^*\Vert ^2\right] . \end{aligned}$$
(3.9)

From (3.5), it follows

$$\begin{aligned} \Vert x^{k+1}-x^*\Vert\le & \alpha _k\gamma L_g\Vert x^k-x^*\Vert +\alpha _k\Vert \gamma g(x^*)-\mu G(x^*)\Vert \\ & +(1-\alpha _k\tau )\Vert (1-\omega )x^k+\omega T_kx^k-x^*\Vert \\\le & \alpha _k\gamma L_g\Vert x^k-x^*\Vert +\alpha _k\Vert \gamma g(x^*)-\mu G(x^*)\Vert \\ & +(1-\alpha _k\tau )(1-\omega )\Vert x^k-x^*\Vert +(1-\alpha _k\tau )\omega \Vert z^k-x^*\Vert . \end{aligned}$$

Passing to the limit as \(k\rightarrow \infty \), we have

$$ A\le \lim _{k\rightarrow \infty }\Vert z^k-x^*\Vert . $$

By Lemma 3.2, we also have

$$ \lim _{k\rightarrow \infty }\Vert z^k-x^*\Vert \le A. $$

Thus,

$$ \lim _{k\rightarrow \infty }\Vert z^k-x^*\Vert = A. $$

Using Lemma 3.2 yields

$$ \lim _{k\rightarrow \infty }\Vert y^k-x^k\Vert = 0. $$

Since \(\{x^k\}\) is bounded, there exists a subsequence \(\{x^{k_j}\}\) such that \(x^{k_j}\rightharpoonup \bar{x}\) as \(j\rightarrow \infty \) and

$$ \liminf _{k\rightarrow \infty }\langle \mu G(x^*)-\gamma g(x^*),x^k-x^*\rangle = \lim _{j\rightarrow \infty }\langle \mu G(x^*) - \gamma g(x^*),x^{k_j}-x^*\rangle . $$

Then, \(y^{k_j}\rightharpoonup \bar{x}\). Since C is closed and convex, C is weakly closed. Thus, from \(\{y^k\}\subset C\), we obtain \(\bar{x}\in C\). By the proof of [1, Lemma 3.1],

$$ \xi _k[f(x^k,y)-f(x^k,y^k)]\ge \langle x^k-y^k, y-y^k\rangle ,\quad \forall y\in C. $$

Passing to the limit in the last inequality as \(k\rightarrow \infty \) and using the assumption \((R_2)\) and \(\lim _{k\rightarrow \infty }\xi _k=\xi >0\), we get \(f(\bar{x},y)\ge 0\) for all \(y\in C\). Thus, \(\bar{x}\in \textrm{Sol}(C,f)=\textrm{Fix}(T_k)\). Since \(x^*\) is the solution of (3.3) and (3.9), we have

$$\begin{aligned} (\mu \beta _G-\gamma L_g)\lim _{k\rightarrow \infty }a_k= & (\mu \beta _G-\gamma L_g)\lim _{k\rightarrow \infty }\Vert x^k-x^*\Vert ^2\\\le & -\liminf _{k\rightarrow \infty }\langle \mu G(x^*)-\gamma g(x^*), x^k-x^*\rangle \\= & -\lim _{j\rightarrow \infty }\langle \mu G(x^*)-\gamma g(x^*), x^{k_j}-x^*\rangle \\= & -\langle \mu G(x^*)-\gamma g(x^*), \bar{x}-x^*\rangle \\\le & 0. \end{aligned}$$

Using \(\gamma \in \left( 0,\frac{\mu }{L_g}\left( \beta _G-\frac{\mu L_G^2}{2}\right) \right) \), it implies \(\lim _{k\rightarrow \infty }a_k=0\). Thus, both \(\{x^k\}\) and \(\{y^k\}\) converge strongly to \(x^*\).

Case 2. There does not exist any integer \(k_0\) such that \(a_{k+1}\le a_k\) for all \(k\ge k_0\). Then, consider the sequence of integers as follows:

$$ \phi (k)=\max \{j\le k:a_j<a_{j+1}\},\quad \forall k\ge k_0. $$

By [23], \(\{\phi (k)\}\) is a nondecreasing sequence verifying

$$\begin{aligned} \lim _{k\rightarrow \infty }\phi (k)=\infty , \quad a_{\phi (k)}\le a_{\phi (k)+1},\quad a_k\le a_{\phi (k)+1},\qquad \forall k\ge k_0. \end{aligned}$$
(3.10)

Replacing k by \(\phi (k)\) into (3.8), it follows that

$$\begin{aligned} & \omega [1-\alpha _{\phi (k)}-2\omega (1-\alpha _{\phi (k)}\tau )^2]\Vert T_{\phi (k)}x^{\phi (k)}-x^{\phi (k)}\Vert ^2\nonumber \\ & \quad \le a_{\phi (k)}-a_{{\phi (k)}+1}+2\alpha _{\phi (k)} \langle \mu G(x^{\phi (k)})-\gamma g(x^{\phi (k)}), x^*-x^{\phi (k)}\rangle \nonumber \\ & \qquad +2\alpha _{\phi (k)}^2\Vert \gamma g(x^{\phi (k)})-\mu G(x^{\phi (k)})\Vert ^2\nonumber \\ & \qquad +2\omega \alpha _{\phi (k)}(1-\alpha _{\phi (k)}\tau )\Vert T_{\phi (k)}x^{\phi (k)}-x^{\phi (k)}\Vert \Vert x^{\phi (k)}-x^*\Vert \nonumber \\ & \quad \le 2\alpha _{\phi (k)} \langle \mu G(x^{\phi (k)})-\gamma g(x^{\phi (k)}), x^*-x^{\phi (k)}\rangle +2\alpha _{\phi (k)}^2\Vert \gamma g(x^{\phi (k)})-\mu G(x^{\phi (k)})\Vert ^2\nonumber \\ & \qquad +2\omega \alpha _{\phi (k)}(1-\alpha _{\phi (k)}\tau )\Vert T_{\phi (k)}x^{\phi (k)}-x^{\phi (k)}\Vert \Vert x^{\phi (k)}-x^*\Vert . \end{aligned}$$
(3.11)

Taking the limit as \(k\rightarrow \infty \) in (3.11) and using the boundedness of \(\{x^k\}\), we obtain

$$\begin{aligned} \Vert T_{\phi (k)}x^{\phi (k)}-x^{\phi (k)}\Vert \rightarrow 0\quad \text { as }~ k\rightarrow \infty . \end{aligned}$$
(3.12)

From (3.11), it implies

$$\begin{aligned} & \langle \mu G(x^{\phi (k)})-\gamma g(x^{\phi (k)}), x^{\phi (k)}- x^*\rangle \\ & \le \alpha _{\phi (k)}\Vert \gamma g(x^{\phi (k)})-\mu G(x^{\phi (k)})\Vert ^2 + 2\omega (1-\alpha _{\phi (k)}\tau )\Vert T_{\phi (k)}x^{\phi (k)}-x^{\phi (k)}\Vert \Vert x^{\phi (k)}-x^*\Vert .\nonumber \end{aligned}$$
(3.13)

Consider (3.9) again, we have

$$ \langle \mu G(x^{\phi (k)})-\gamma g(x^{\phi (k)}), x^{\phi (k)}-x^*\rangle \ge \langle \mu G(x^*)-\gamma g(x^*), x^{\phi (k)}-x^*\rangle +(\mu \beta _G-\gamma L_g)a_{\phi (k)}. $$

Combining this and (3.13), it leads

$$\begin{aligned} & \langle \mu G(x^*)-\gamma g(x^*), x^{\phi (k)}-x^*\rangle +(\mu \beta _G-\gamma L_g)a_{\phi (k)}\\ & \le \alpha _{\phi (k)}\Vert \gamma g(x^{\phi (k)})-\mu G(x^{\phi (k)})\Vert ^2+2\omega (1-\alpha _{\phi (k)}\tau )\Vert T_{\phi (k)}x^{\phi (k)}-x^{\phi (k)}\Vert \Vert x^{\phi (k)}-x^*\Vert . \end{aligned}$$

Then, by using \(\lim _{k\rightarrow \infty }\alpha _k=0\) and (3.12), we have

$$\begin{aligned} (\mu \beta _G-\gamma L_g)\limsup _{k\rightarrow \infty } a_{\phi (k)} \le -\liminf _{k\rightarrow \infty } \langle \mu G(x^*)-\gamma g(x^*), x^{\phi (k)}-x^*\rangle . \end{aligned}$$
(3.14)

We recall the fact that \(\{x^{\phi (k)}\}\) is bounded, we can choose a subsequence \(\{x^{\phi (k_j)}\}\) such that

$$ x^{\phi (k_j)}\rightharpoonup \hat{x} \quad \text { as }~ j\rightarrow \infty $$

and

$$ \liminf _{k\rightarrow \infty } \langle \mu G(x^*)-\gamma g(x^*), x^{\phi (k)}-x^*\rangle = \langle \mu G(x^*)-\gamma g(x^*), \hat{x}-x^*\rangle . $$

By a similar way as in Case 1, we also have \(\hat{x} \in \textrm{Sol}(C,f)\). It means \(\langle \mu G(x^*)-\gamma g(x^*), \hat{x}-x^*\rangle \ge 0\). Then, using (3.14) and \(\mu \beta _G-\gamma L_g>0\) in \((R_3)\), we deduce

$$ (\mu \beta _G-\gamma L_g)\limsup _{k\rightarrow \infty } a_{\phi (k)} \le - \langle \mu G(x^*)-\gamma g(x^*), \hat{x}-x^*\rangle \le 0, $$

and hence \(\limsup _{k\rightarrow \infty } a_{\phi (k)}=0\). However, from (3.8) and (3.12), it follows

$$ \limsup _{k\rightarrow \infty } a_{\phi (k)+1} \le \limsup _{k\rightarrow \infty }a_{\phi (k)}. $$

Consequently

$$ \limsup _{k\rightarrow \infty } a_{\phi (k)+1}=0. $$

Recalling \(a_k\le a_{\phi (k)}\) for all \(k\ge k_0\) in (3.10), we immediately obtain \(\lim _{k\rightarrow \infty } a_k=0\). Thus, both \(\{x^k\}\) and \(\{y^k\}\) converge strongly to a unique solution \(x^*\) of the variational inequality problem (3.3). Which completes the proof. \(\square \)

Remark 3.4

Theorem 3.3 showed that the strongly cluster point of the sequences \(\{x^k\}\) and \(\{y^k\}\) constructed by the algorithm (SAPA) is a unique solution of the variational inequality problem (3.3). This result is a fundamental difference of our algorithm with respect to existing algorithms. However, the set \(\textrm{Sol}(C,f)\) is not given explicit. So, the problem (3.3) is not easy to solve.

4 Numerical Experiments

An important application of the problem \(\textrm{EPs}(C,f)\) is the noncooperative n-person games. The problem is to find \(x^*\in C\) such that

$$ f_i(x^*[y^i])\rightarrow \max ,\quad \forall y^i\in C_i, $$

where

  • The ith player’s strategy set is a closed convex set \(C_i\) of the Euclidean space \(\mathcal R^{s_i}\) for all \(i\in I:=\{1,2,\ldots ,n\}\).

  • The \(f_i: C:=C_1\times C_2\times \cdots \times C_n\rightarrow \mathbb {R}\) is the loss function of player i.

  • The \(x[y^i]\) stands for the vector obtained from \(x = (x^1,\ldots ,x^n)\in C\) by replacing \(x^i\) with \(y^i\).

By [21], a point \(x^*\in C\) is said to be a Nash equilibrium point on C if and only if

$$ f_i(x^*) \le f_i(x^*[y^i]),\quad \forall y^i\in C_i, i\in I. $$

Then, we set

$$ f(x,y)=\sum _{i=1}^n[f_i(x[y^i])-f_i(x)]. $$

We can see that the problem of finding a Nash equilibrium point of f on C can be formulated equivalently to the problem \(\textrm{EPs}(C,f)\).

Now we provide some computational results for solving the problem \(\textrm{EPs}(C,f)\) to illustrate the effectiveness of Subgradient Auxiliary Principle Algorithm (SAPA), and also to compare this algorithm with two well-known algorithms using the solution mapping S defined in the form (2.1): Extragradient Algorithm (EA) introduced by Quoc et al. [32, Algorithm 1] with the auxiliary bifunction \(L(x,y)=\frac{1}{2}\Vert y-x\Vert ^2\) for all \(x,y\in \mathcal H\) and Halpern Subgradient Extragradient Algorithm (HSEA) proposed by Hieu [15, Algorithm 3.2]. As we know, the iteration point \(x^k\) defined by S is a solution of the problem \(\textrm{EPs}(C,f)\) if and only if \(y^k=x^k\). Therefore, we have used the sequence \(\{S_k= \Vert x^k -y^k\Vert : k=0,1,\ldots \}\) to consider the convergent rate of all above algorithms. And, we can say that \(x^k\) is an \(\varepsilon \)-solution to the problem \(\textrm{EPs}(C,f)\) where \(\varepsilon >0\), if \(S_k\le \varepsilon \).

To test all above algorithms, the parameters are chosen as follows.

  • Subgradient Auxiliary Principle Algorithm (SAPA):

    $$\begin{aligned} \xi _k= & \frac{1}{4c_1}+\frac{1}{5k+400},\quad \gamma _k=\frac{1}{2}(1-\xi _k(c_1+c_2)),\quad \nu =\frac{1}{2}\min \left\{ 1,\frac{1}{\xi _k c_2}\right\} ,\\ \omega= & \frac{1}{4},\quad \mu =\frac{\beta _G}{L_G},\quad \gamma =\frac{\mu }{2L_g}\left( \beta _G-\frac{\mu L_G^2}{2}\right) ,\quad \tau =\frac{1}{2}\min (\gamma L_g,\mu \beta _G),\\ \alpha _k= & \frac{a}{k+1}\quad \text { where }~a=\min \left\{ 1,\frac{2(\mu \beta _G-\tau )}{\mu ^2 L_G^2-\tau ^2},\frac{1}{\tau -\gamma L_g}\right\} . \end{aligned}$$

  • Extragradient Algorithm (EA):

    $$ \beta :=\frac{1}{2},\quad \rho :=\frac{1}{2\Vert z\Vert (h|e_1|+g|p_1|)}\in \left( 0,\min \left\{ \frac{\beta }{2c_1},\frac{\beta }{2c_2}\right\} \right) . $$

  • Halpern Subgradient Extragradient Algorithm (HSEA):

    $$ \lambda :=\frac{1}{4c_1}\in \left( 0,\min \left\{ \frac{1}{2c_1},\frac{1}{2c_2}\right\} \right) ,\quad \alpha _n:=\frac{1}{5n+10},\quad \forall n\ge 0. $$

Auxiliary convex problems in the algorithms are computed effectively by the function fmincon in Matlab 2018a Optimization Toolbox. All the programs are performed on a PC Desktop Intel(R) Core(TM) i7-12700F CPU @ 2.10 GHz 2.50 GHz, RAM 32.00 GB.

Let \(\mathcal H\) be a real Hilbert space. We introduce a new cost bifunction \(f: \mathcal H\times \mathcal H\rightarrow \mathcal R\) and the constraint C are given in the forms

$$\begin{aligned} C= & \{x\in \mathcal H:\Vert x\Vert ^2\le R^2,~\langle r,x\rangle \le l\},\end{aligned}$$
(4.1)
$$\begin{aligned} f(x,y)= & \langle [g\sin (p_1\Vert x\Vert +p_2)+h\cos (e_1\Vert y\Vert +e_2)+m]z,y-x\rangle , \end{aligned}$$
(4.2)

where \(x,y\in \mathcal H\), \(R,p_1,p_2,e_1,e_2\in \mathcal R\), \(l>0\), \(g>0\), \(h>0\), \(m\in (g+h,\infty )\), \((z,r)\in \mathcal H\times \mathcal H\). Then, the C is nonempty closed convex, and the f has the following properties.

Proposition 4.1

Let the bifunction \(f:\mathcal H\times \mathcal H\rightarrow \mathcal R\) be defined by (4.2). Then,

  1. (i)

    f is pseudomonotone;

  2. (ii)

    f is Lipschitz-type continuous with constants \(c_1=c_2=\frac{\Vert z\Vert (h|e_1|+g|p_1|)}{2}\).

Proof

Assume that \(f(x,y)\ge 0\) for each \(x,y\in \mathcal H\). Then, we have

$$\begin{aligned} 0\le & f(x,y) = \langle [g\sin (p_1\Vert x\Vert +p_2)+h\cos (e_1\Vert y\Vert +e_2)+m]z, y-x\rangle \\= & [g(\sin (p_1\Vert x\Vert +p_2)+1)+h(\cos (e_1\Vert y\Vert +e_2)+1)+(m-g-h)]\langle z, y-x\rangle . \end{aligned}$$

From \(m\in (g+h,+\infty )\), it yields that \(\langle z, y-x\rangle \ge 0\) and

$$\begin{aligned} f(y,x)= & \langle [g\sin (p_1\Vert y\Vert +p_2)+h\cos (e_1\Vert x\Vert +e_2)+m]z,x-y\rangle \\= & [g(1+\sin (p_1\Vert y\Vert +p_2))+h(1+\cos (e_1\Vert x\Vert +e_2))+(m-g-h)]\langle z,x-y\rangle \\\le & 0. \end{aligned}$$

By definition, the bifunction f is pseudomonotone on \(\mathcal H\times \mathcal H\).

Since (4.2), it follows that, for every \(x,y,t\in \mathcal H\),

$$\begin{aligned} & f(x,y)+f(y,t)-f(x,t)\\ & \quad =\langle [g\sin (p_1\Vert x\Vert +p_2)+h\cos (e_1\Vert y\Vert +e_2)+m]z, y-x\rangle \\ & \qquad + \langle [g\sin (p_1\Vert y\Vert +p_2)+h\cos (e_1\Vert t\Vert +e_2)+m]z, t-y\rangle \\ & \qquad -\langle [g\sin (p_1\Vert x\Vert +p_2)+h\cos (e_1\Vert t\Vert +e_2)+m]z, t-x\rangle \\ & \quad =\langle [g\sin (p_1\Vert x\Vert +p_2)+h\cos (e_1\Vert y\Vert +e_2)+m]z, y-x\rangle \\ & \qquad + \langle [g\sin (p_1\Vert y\Vert +p_2)+h\cos (e_1\Vert t\Vert +e_2)+m]z, t-y\rangle \\ & \qquad -\langle [g\sin (p_1\Vert x\Vert +p_2)+h\cos (e_1\Vert t\Vert +e_2)+m]z, t-y\rangle \\ & \qquad -\langle [g\sin (p_1\Vert x\Vert +p_2)+h\cos (e_1\Vert t\Vert +e_2)+m]z, y-x\rangle \\ & \quad =h[\cos (e_1\Vert y\Vert +e_2)-\cos (e_1\Vert t\Vert +e_2)]\langle z, y-x\rangle \\ & \qquad + g[\sin (p_1\Vert y\Vert +p_2)-\sin (p_1\Vert x\Vert +p_2)]\langle z, t-y\rangle \\ & \quad =-2h\sin \left( e_1\frac{\Vert y\Vert +\Vert t\Vert }{2}+e_2\right) \sin \left( e_1\frac{\Vert y\Vert -\Vert t\Vert }{2}\right) \langle z, y-x\rangle \\ & \qquad + 2g\cos \left( p_1\frac{\Vert y\Vert +\Vert x\Vert }{2}+p_2\right) \sin \left( p_1\frac{\Vert y\Vert -\Vert x\Vert }{2}\right) \langle z, t-y\rangle \\ & \quad \ge -2h\left| \sin \left( e_1\frac{\Vert y\Vert +\Vert t\Vert }{2}+e_2\right) \right| \left| \sin \left( e_1\frac{\Vert y\Vert -\Vert t\Vert }{2}\right) \right| \Vert z\Vert \Vert y-x\Vert \\ & \qquad - 2g\left| \cos \left( p_1\frac{\Vert y\Vert +\Vert x\Vert }{2}+p_2\right) \right| \left| \sin \left( p_1\frac{\Vert y\Vert -\Vert x\Vert }{2}\right) \right| \Vert z\Vert \Vert t-y\Vert \\ & \quad \ge -2h\left| \sin \left( e_1\frac{\Vert y\Vert -\Vert t\Vert }{2}\right) \right| \Vert z\Vert \Vert y-x\Vert - 2g\left| \sin \left( p_1\frac{\Vert y\Vert -\Vert x\Vert }{2}\right) \right| \Vert z\Vert \Vert t-y\Vert \\ & \quad \ge -h|e_1|\left| \Vert y\Vert -\Vert t\Vert \right| \Vert z\Vert \Vert y-x\Vert - g|p_1|\left| \Vert y\Vert -\Vert x\Vert \right| \Vert z\Vert \Vert t-y\Vert . \end{aligned}$$

where the last inequality is deduced from the relation

$$ |\sin \theta |\le |\theta |,\quad \forall \theta \in \mathcal R. $$

By using the relation

$$ |\Vert a_1\Vert -\Vert a_2\Vert |\le \Vert a_1-a_2\Vert ,\quad \forall a_1,a_2\in \mathcal H, $$

we obtain

$$\begin{aligned} & f(x,y)+f(y,t)-f(x,t)\\ & \quad \ge -h|e_1|\big |\Vert y\Vert -\Vert t\Vert \big |\Vert z\Vert \Vert y-x\Vert - g|p_1|\big |\Vert y\Vert -\Vert x\Vert \big |\Vert z\Vert \Vert t-y\Vert \\ & \quad \ge -h|e_1|\Vert y-t\Vert \Vert z\Vert \Vert y-x\Vert - g|p_1|\Vert y-x\Vert \Vert z\Vert \Vert t-y\Vert \\ & \quad \ge -\frac{h|e_1|\Vert z\Vert }{2}\Vert y-t\Vert ^2-\frac{h|e_1|\Vert z\Vert }{2}\Vert y-x\Vert ^2- \frac{g|p_1|\Vert z\Vert }{2}\Vert y-x\Vert ^2- \frac{g|p_1|\Vert z\Vert }{2}\Vert t-y\Vert ^2\\ & \quad =-\frac{\Vert z\Vert (h|e_1|+g|p_1|)}{2}\Vert y-x\Vert ^2-\frac{\Vert z\Vert (h|e_1|+g|p_1|)}{2}\Vert y-t\Vert ^2. \end{aligned}$$

Thus, the f is Lipschitz-type continuous with \(c_1=c_2=\frac{\Vert z\Vert (h|e_1|+g|p_1|)}{2}\). The proof is complete. \(\square \)

Test 1

First, let us run the algorithm (SAPA) in \(\mathcal {R}^s\) with \(s=5\). The starting point is \(x^0=(1,0,1,100,25)^{\top }\). The parameters R, g, p, q, h, e, f, m, l and the vectors r, z are randomly chosen as follows:

$$\begin{aligned} R= & 5,~~l=2,~~g=3,~~p_1=-5,~~p_2=7,~~h=3,~~e_1=8,~~e_2=2,~~m=g+h+5,\\ r= & (2,-3,5,8,4)^{\top },\quad z=(10,5,3,-7,12)^{\top }. \end{aligned}$$

Consider the mappings \(G:\mathcal R^s\rightarrow \mathcal R^s\), \(g:\mathcal R^s\rightarrow \mathcal R^s\):

$$\begin{aligned} g(x)=10x,\quad G(x)=Qx+q,\qquad \forall x\in \mathcal R^s, \end{aligned}$$

where \(q\in \mathcal R^s\), \(Q=AA^{\top }+B+D\), A is a \(s\times s\) matrix, B is a \(s\times s\) skew-symmetric matrix, and D is a \(s\times s\) diagonal matrix with its nonnegative diagonal entries (so Q is positive semidefinite). It is obviously that G is \(\beta _G\)-strongly monotone and \(L_G\)-Lipschitz continuous, where \(\beta _G=\min \{t: t\in \text {eig}(Q)\}\) is the smallest eigenvalue of Q and \(L_G=\Vert Q\Vert \). The matrics A, B, D of the mapping G are chosen randomly as follows:

$$\begin{aligned} A= & \begin{bmatrix} 1& -2 & 3 & 4& 0\\ 2 & 1& 0& 5& -3\\ 4& 0 & 7 & 9& 1\\ 2& 5& 0& -5& 3\\ -1 & 9 & 4 & 2 & 3\\ \end{bmatrix}_{(5\times 5)},\quad B=\begin{bmatrix} 0& 2& 3& 4& 5\\ -2& 0 & -5& 7& 9\\ -3& 5 & 0 & 6& -8\\ -4& -7 & -6& 0& 1\\ -5& -9& 8& 1& 0\\ \end{bmatrix}_{(5\times 5)},\\ D= & \begin{bmatrix} 1& 0& 0& 0& 0\\ 0& 3& 0& 0& 0\\ 0& 0& 7& 0& 0\\ 0& 0& 0& 10& 0\\ 0& 0& 0& 0& 5\\ \end{bmatrix}_{(5\times 5)},\quad q=(1,7,-3,22,6)^{\top }. \end{aligned}$$

Then, the eigenvalue and the norm of Q are evaluated as follows:

$$ \text {eig}(Q)=\{221.2357,144.1649,3.3983,24.9611,22.2399\},\quad \Vert Q\Vert = 222.3145. $$

This implies that the strongly monotone constant of G is \(\beta _G=3.3983\) and the Lipschitz continuous constant of G is given in \(L_G=222.3145\).

It is easy to evaluate that

$$ c_1=c_2=\frac{1}{2}(g|p_1|+h|e_1|)\Vert z\Vert \approx 352.6213, $$

and

$$ \partial f(x^k,\cdot )(y^k)= \left\{ \begin{array}{ll} \Big \{ [g\sin (p_1\Vert x^k\Vert +p_2)+h\cos (e_1\Vert y^k\Vert +e_2)+m]z\\ \qquad -\frac{h e_1\sin (e_1\Vert y^k\Vert +e_2)}{\Vert y^k\Vert }\langle y^k,z\rangle (y^k-x^k)\Big \}& \quad \text { if } y^k\ne 0,\\ \Big \{ [g\sin (p_1\Vert x^k\Vert +p_2)+h\cos (e_2)+m]z\\ \qquad +h e_1\sin (e_2)\langle u^k,z\rangle x^k: \Vert u^k\Vert \le 1\Big \},& \quad \text { otherwise}. \end{array}\right. $$

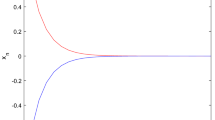
With the tolerance \(\max \{\Vert y^k-x^k\Vert ,\Vert x^{k+1}-x^k\Vert \}\le \varepsilon =10^{-3}\), the computational results of the algorithm (SAPA) are showed in Fig. 1 and Table 1.

Fig. 1
figure 1

Performance of the sequence \(\{x^k\}\) in the algorithm (SAPA) with the tolerance \(\varepsilon =10^{-3}\). The approximate solution is \(x^{196}=(-1.5086,-0.5649,-0.1058,1.0853,-1.8301)^{\top }\)

Full size image
Table 1 Iterations (Iter.) and CPU times (Times) with randomly different parameters, where \(a=\min \left\{ 1,\frac{2(\mu \beta _G-\tau )}{\mu ^2 L_G^2-\tau ^2},\frac{1}{\tau -\gamma L_g}\right\} ,\bar{\gamma _k}=1-\xi _k(c_1+c_2),\bar{\nu _k}=\min \left\{ 1,\frac{1}{\xi _k c_2}\right\} \) and \( \bar{\gamma }=\frac{\mu }{L_g}\left( \beta _G-\frac{\mu L_G^2}{2}\right) \)
Full size table

Test 2

Consider in an infinite-dimensional Hilbert space \(\mathcal H=L^2[0,1]\) with inner product

$$ \langle x,y\rangle =\int _0^1 x(t)y(t)dt,\quad \forall x,y\in \mathcal H, $$

and its induced norm

$$ \Vert x\Vert =\sqrt{\int _0^1 x^2(t)dt},\quad \forall x\in \mathcal H. $$

The constraint C and the cost bifunction f are defined in the forms (4.1) and (4.2). We compare the algorithm (SAPA) with three above algorithm with different starting points \(x_0\). The numerical results are showed in Table 2.

Fig. 2
figure 2

Comparison results of the algorithm (SAPA) with two algorithms (EA) and (HSEA), where \(x^0=(1,0,1,100,25)^{\top }\)

Full size image
Table 2 Comparative results with different starting points in \(L^2[0,1]\)
Full size table

From the comparative results in Fig. 2 and Table 2 of the Subgradient Auxiliary Principle Algorithm (SAPA) with two other agorithms: the Extragradient Algorithm (EA) and the Halpern Subgradient Extragradient Algorithm (HSEA), and the preliminary numerical results reported in Table 1 and Fig. 1, we observe that

  • The convergence speed of our algorithm (SAPA) is the most sensitive to all the parameters. The CPU time and iteration number depend very much on the parameter sequence \(\{\xi _k\}\).

  • The CPU time (second) and the number of iterations of our algorithm are less than those of the algorithms (EA) and (HSEA).

Conclusions

In this paper, we introduce a new solution mapping to equilibrium problems in a real Hilbert space. We show that this mapping is strongly quasi-nonexpansiveness under quasimonotone and Lischitz continuous assumptions of the cost bifunction. Then, the Subgradient Auxiliary Principle Algorithm is constructed by the solution mapping and classical auxiliary principle. Finally, the stated theoretical results are verified by several preliminary numerical experiments.