1 Introduction

Malignant gliomas are highly invasive and heterogeneous brain tumors. Their treatment is still elusive, in spite of the development and diversification of the therapeutic approaches [51]. The differentiated response of tumor cell subpopulations to treatment and the infiltrative growth throughout the brain tissue [23, 39, 41] are two main causes for the lack of surgical, radio-, and chemotherapeutical cure. Indeed, it is largely accepted that cells with a highly proliferating phenotype are more sensitive to both chemo and radiotherapy, whereas the migratory phenotype is attended by reduced treatment sensitivity, see, e.g., [41, 45, 63] and the references therein. Moreover, because of the high affinity of glioma cells to myelinated fiber tracts in the white matter [24, 26], in more than 90 % of cases, the recurrent tumor develops immediately adjacent to the resection margin or within several centimeters of the resection cavity [23, 41].

In this work, we address both the modeling of (infiltrative) glioma spread and growth, and the response to surgical resection and radiotherapy. Concerning the treatment, we use the idea of reducing tumor cell migration by inhibiting the binding of cell surface receptors to the tissue fibers in the peritumoral region (see, e.g., [11, 23] and the references therein), hence also rendering the cancer cells more sensitive against radiotherapy, in view of the go-or-grow hypothesis stating that the tumor cells can either migrate or proliferate [9, 23, 25, 29]. On the other hand, however, the receptor-binding inhibition can also impair cell proliferation, as the latter is known to be influenced by cell-matrix (and cell-cell) adhesion [14, 27, 32, 42, 48, 67]; hence, the balance between increasing proliferation through stopping migration and reducing mitotic activity through inhibiting adhesion will be the driving factor for enhancing radiosensitivity. Mathematical models for the therapy of glioma have also been considered, e.g., in [2, 36, 37, 54, 55], however in a much simplified monoscale case not able to account for the highly infiltrative behavior of this type of cancer. Here, we start from the multiscale setting introduced in [19] to describe the evolution of a heterogeneous tumor consisting of migrating and proliferating glioma cells moving along white matter tracts. The anisotropic structure of the brain is assessed from diffusion tensor imaging (DTI) data and—as in [17]—the model involves on the microscopic, subcellular scale the receptor binding dynamics to the tissue fibers, while the individual cell dynamics are modeled on the mesoscale via kinetic transport equations. A parabolic scaling allows to deduce effective equations for the tumor growth on the macroscopic (population) scale, carrying the information from the lower scales. This model permits to account for the infiltrative behavior of glioma, and in this work, we extend it to also consider therapy in the sense stated above. Another multiscale model involving intracellular (microscale) and extracellular pH dynamics along with the evolution of tumor cells and normal tissue (macroscale) has been proposed in [64] and extended in [47] to include the issue of treatment with sensitization against radiotherapy via alkalinization of the tumor microenvironment and depletion of cancer cells via chemotherapy and radiotherapy. The tumor heterogeneity was addressed there by considering a population of active and one of quiescent tumor cells, with their corresponding transitions controlled by the pH dynamics, another important issue in determining the extent and aggressiveness of a tumor. In the present work, we consider two cancer cell subpopulations, one of which is moving (and less sensitive against therapy) and the other is proliferating (and infers higher therapy sensitivity), the transitions and depletions being regulated by the therapeutic doses. Our model accounts for a single chemotherapeutic agent (some peptidomimetic, see Section 2) in combination with radiotherapy. An (a priori) micro-macro version of the approach in this paper has recently been addressed and analyzed in [65], where the transitions were controlled by the amount of receptors bound to the tissue. In all these works—including the present one—the chemotherapy is not aiming at direct cell kill but rather at rendering the cells more sensitive towards radiotherapy and (this applies to [65] and this paper) at reducing their motility and whence the tumor invasion.

This paper is organized as follows: In Section 2, we present the mathematical model and describe the way in which therapy is considered and implemented, then use a parabolic scaling to re-deduce (with the changes due to modeling therapy) the effective equations for glioma spread involving the DTI information for the patient specific brain structure and encompassing the subcellular receptor-binding dynamics in the diffusion, transport, and haptotaxis coefficients. The well posedness of both formulations (multiscale and population level, respectively) is proven as well. Section 3 is concerned with the (heuristic) estimation of the functions and parameters employed in the model, and Section 4 presents the numerical method and the simulations obtained from our setting, along with observations about which of the therapy approaches considered therein seems to be the most adequate one. In the absence of reliable biological as well as medical data, both due to this type of chemotherapeutic agents being still in clinical trials, the model presented here could not be validated. However, the simulations advise that the combination of chemotherapy (although non-lethal for the cells) and radiotherapy will improve the outcome. The results suggest a reduction of the peak tumor density using adjuvant chemotherapy of around 50 % compared to radiotherapy alone. Eventually, Section 5 offers some comments about the potential of this modeling approach and further issues to be addressed in this context.

2 Mathematical Modeling

2.1 Equations on the Mesoscopic and Microscopic Levels

In [19], we considered a model for glioma invasion relying on the go-or-grow hypothesis. In this work, we extend that setting in order to account for therapy. Thereby, in view of the migratory/proliferative phenotype of cancer cells significantly influencing the response of tumors to various treatments like radiotherapy and chemotherapy, we will characterize this differentiated response by considering two tumor subpopulations: proliferative (hence non-motile) and migrating cells, respectively.

We consider the density function p(t,x,v,y) of moving cells at time t and position \(\textbf {x} \in \mathbb R^{n}\), with velocity \(\textbf {v} \in V\subset \mathbb R^{n}\) and receptor state \(y\in \mathbb R_{+}\), and the density function r(t,x,y) of resting cells. Thereby, the receptor state y is a subcellular scale (microscale) variable and refers to the volume fraction of cell surface receptors bound to insoluble ligands in the surrounding tissue. While it is clear that integrins (a family of heterodimeric cell adhesion molecules playing a crucial role in cell–cell and cell-matrix interaction [32, 33, 48]) with their binding to the ECM are essential for glioma migration [15, 67] and it has been found that glioma cells follow the anisotropic brain structure along the white matter tracts [24, 26], the mechanism of adhesion to the myelinated axons is still not elucidated, but integrins alone do not seem to be responsible for such bindings [24]. Hence, there might be some further receptors involved or the interaction is rather indirect; adapting the description in [67] one can imagine the glioma cells “climbing” along a ladder whose long “rails” are myelinated axons and whose “rungs” are made up of the ECM fibers present in the space between myelinated axons, oligodendrocytes, astrocytes, etc. It is those ECM components to which the crucial process of integrin binding takes place. In the following, we will use the syntagma “cell surface receptors” for all kinds of receptors involved in cell-tissue adhesion and will concentrate on integrins when referring to some chemotherapeutical agent which aims at inhibiting migration and proliferation. For further discussions on the issue of glioma-tissue adhesion we refer to [17, 19].

The two cancer cell densities of interest satisfy on the mesoscale the system of partial integro-differential equations

$$\begin{array}{@{}rcl@{}} &&\partial_{t}p +\nabla_{\mathbf{x}}\cdot(\mathbf{v}p)+\partial_{y}\left( G(y,Q,d_{c},d_{r})p\right) \end{array} $$
$$\begin{array}{@{}rcl@{}} &&\qquad=\mathcal{L}[\lambda (y)]p -a(\mathbf{x},d_{c})p+b (\mathbf{x},d_{c}) \frac{q(\hat{\mathbf{v}})}{\omega}r-(l_{1}(N)+R_{1}(\alpha_{1},d_{r}))p, \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} &&~~\partial_{t} r = a(\mathbf{x},d_{c}) {\int}_{V} p(\mathbf{v}) d\mathbf{v} -b(\mathbf{x},d_{c})r+g(N,d_{c})r-(l_{2}(N)+R_{2}(\alpha_{2},d_{r}))r, \end{array} $$
(2)

where \(\mathcal {L}[\lambda (y)] p:= -\lambda (y)p+\lambda (y){\int }_{V} K(\textbf {x},\textbf {v})p(\textbf {v}^{\prime })d\textbf {v}^{\prime }\) is the turning operator modeling the cell velocity innovations due to contact guidance, environmental cues, etc. Here, the turning kernel K accounting for such influences is taken for simplicity to be of the form (see [30]) \(K(\textbf {x}, \textbf {v}):=\frac {q(\hat {\mathbf {v}})}{\omega }\) , where \(\hat {\mathbf {v}}\) is the normalized velocity, \(q(\textbf {x},\hat {\mathbf {v}})\) is the directional distribution of tissue fibers, and \(\omega ={\int }_{V}q(\hat {\mathbf {v}})d\textbf {v}\) is a scaling constant (we assume \(V=s\mathbb {S}^{n-1}\), with s given) such that K is indeed a kernel. The function λ(y) denotes as in [17–19] the turning rate of the cells. Motivated by existing experimental evidence (see, e.g., [43, 49]) that integrins expressed by resting cells do not in general bind their ligands in a dynamic way (i.e., the binding/detachment steady-state is maintained), we assume this also for our model, as we did in [19].Footnote 1

In (1) and (4) below Q(t,x) denotes the (macroscopic) volume fraction of tissue (including as in [17, 19] ECM and neuron bundles). The functions a(x,d c ) and b(x,d c ) denote the rates with which cells stop and proliferate, respectively start moving after a resting (proliferating) phase. The cells which exit proliferation and become motile are doing this by interacting with the tissue, which motivates the factor \(\frac {q(\hat {\mathbf {v}})}{\omega }\) in the corresponding term of (1). Both a and b can depend on the position x and are supposed to also depend on the dose d c of the chemotherapeutic agent. g(N,d c ) and l i (N) (i=1,2) are functions representing gain and loss due to cell proliferation and death, respectively. Thereby, the gain is impaired by the effect of chemotherapy and the loss is amplified by radiotherapy. The effects of the latter are described by the terms R j (α j ,d r ), where

$$ R_{j}(\alpha_{j},d_{r})=\sum\limits_{i=1}^{\nu} (1-S(\alpha_{j},d_{r})) \eta_{\delta}(t-t_{i}),\qquad t_{i} \in \text{radiotherapy} $$
(3)

with j=1,2,3 and “radiotherapy” denoting the set of times at which ionizing radiation is applied to the patient (with dose d r ). Here, ν is the number of fractions, η δ is a \(C^{\infty }_{0}\) function with unit mass and support in (−δ,δ), δ<<1, and \(S(\alpha _{j},d_{r})=\exp (- \alpha _{j} d_{r}-\beta _{j} {d_{r}^{2}} )\) models the survival fraction of each subpopulation p (for j=1), r (for j=2) or normal tissue (for j=3), respectively, after application of radiotherapy with a dose d r (in Gy). Thus, we adopted the linear quadratic (LQ) model [21, 28, 57], which in spite of its shortcomings [10, 35, 69] is still the standard choice in radiation treatments (see, e.g., [53, 62]). The parameter α j represents lethal lesions produced by a single radiation track (they are linearly related to the dose: α j d r , cell kill per Gy), while β j characterizes lethal lesions produced by two radiation tracks (quadratically related to the dose: \(\beta _{j}{d_{r}^{2}}\), cell kill per Gy 2). The relevant parameter in the LQ model is actually the radiation sensitivity \(\frac {\alpha _{j}}{\beta _{j}}\), which correlates to the cell cycle length: late responding tissues with a slow cell cycle have a small \(\frac {\alpha _{j}}{\beta _{j}}\) ratio, while it is large for early responding, highly aggressive cancers [62]. In clinical practice, the total dose d r is given in ν fractions of size \(\hat d_{r}\); hence,

$$S(\alpha_{j},d_{r})=\exp(-\nu (\alpha_{j}\hat d_{r}+\beta_{j}{\hat{d}}_{r}^{2}))=\exp (-\alpha_{j}d_{r}(1+\hat d_{r}/(\alpha_{j}/\beta_{j}))). $$

Concerning chemotherapy, we concentrate on reducing invasion and proliferation and not necessarily on achieving cell kill. In our model, the latter is supposed to be due to ionizing radiation; however, the setting can be easily extended to include a further chemotherapeutic agentFootnote 2 triggering cell death. Most types of cells depend on integrin-mediated adhesion to ECM for migration, proliferation, and survival. In particular, glioma cells have highly migrating potential, which accounts for glioma recurrence, often far away from the primary tumor site [15]. Moreover, integrin-ECM interactions have been shown to increase cell survival after radiation exposure [13]. Supplementary to their role in cancer cells, integrins on the surface of host cells (e.g., endothelial cells, perivascular cells, fibroblasts, etc.) in the neoplastic microenvironment can boost the malignant potential of a tumor by mediating angiogenesis, lymphangiogenesis, and desmoplasia [16]. These facts make integrins an attractive target for anti-tumor therapy, the potential effects being on curtailing angiogenesis, invasion, and tumor growth, see, e.g., [16, 66]. Among the types of integrin inhibitors evaluated in preclinical or clinical studies, peptidomimetics (RGDFootnote 3-based small protein-like chains designed to mimic peptides and blocking ligand binding) are aimed at treating glioblastoma [11]. Examples of pseudomimetics are cilengitide (targets α v β 3|α v β 6 integrins), ATN 161 (targets α 5 β 1 integrins), and HYD1 (targets β 1 integrins) [11]. In our model, we will consider the action of such chemotherapeutic agents.

The effects of chemotherapy are described in our equations by way of dependence on the chemotherapeutic dose d c . Hence, the influences are on the transition rates between proliferating and migrating phenotypes, on the growth function of the (resting) tumor cells, and on the binding of free receptors to the tissue fraction surviving irradiation (attachment and detachment rates k +(d c ) and k −(d c ), respectively, in (4)).

The microscale dynamics of receptor binding is characterized by

$$ \dot y=G(y,Q,d_{c},d_{r}) = k^{+}(d_{c})(1-y)Q~S(\alpha_{3},d_{r})-k^{-}(d_{c})y. $$
(4)

In equations (1) and (2) above, the function N denotes the total glioma cell density and is given by

$$N(t,\mathbf{x}) = {\int}_{V} {\int}_{Y} p(t,\mathbf{x},\mathbf{v},y)dy~d\mathbf{v} + {\int}_{Y} r(t,\mathbf{x},y) dy. $$

2.2 Derivation of the Effective Equations on the Macroscopic Level

The model ((1) and (2)) in Section 2.1 is a system coupling a partial differential equation of first order with an ordinary differential equation. Its well posedness will be addressed in Section 2.3, along with that of the macroscale equation for N obtained in this subsection via parabolic scaling. Before doing this scaling, however, we normalize the subcellular dynamics as in [17–19]. The explicit equation becomes

$$ \dot y = k^{+}(d_{c})(1-y)QS(\alpha_{3},d_{r}) - k^{-}(d_{c})y = -(k^{+}QS+k^{-})y + k^{+}QS. $$

The unique steady state of this equation is given by

$$y^{*} = \frac{k^{+}QS}{k^{+}QS+k^{-}} =: f(k^{+},k^{-},Q,S). $$

As in [19], we introduce the deviation z: = y ∗−y from the steady state and consider the path of a single cell starting in x 0 and moving with velocity v through a time-invariant density field Q(x). Then, with the notation x = x 0 + v t, it follows that z satisfies the equation

$$\dot z = \dot f -\dot y = -(k^{+}QS+k^{-})z + F(t) + f^{\prime}(Q) \mathbf{v} \cdot \nabla Q(\mathbf{x}), $$

where

$$F(t):=\dot d_{c} \left( \frac{\partial f}{\partial k^{+}} ({k^{+}})'(d_{c}) + \frac{\partial f}{\partial k^{-}} ({k^{-}})'(d_{c})\right) + \dot d_{r} f^{\prime}(S) S^{\prime}(\alpha_{3},d_{r}). $$

Thus, choosing (as in [17, 19]) the turning rate to be of the form λ(z) = λ 0−λ 1 z≥0, where λ 0 and λ 1 are some positive constants, the transformed system of equations reads:

$$\begin{array}{@{}rcl@{}} \partial_{t} p + \nabla \cdot (\mathbf{v} p) &-&\frac{\partial}{\partial z}\left( \left( (k^{+}QS+k^{-})z - F(t) -f^{\prime}(Q) \mathbf{v} \cdot \nabla Q\right)p\right) \end{array} $$
$$\begin{array}{@{}rcl@{}} &=&-\lambda_{0} p +\lambda_{0}\frac{q(\hat{\mathbf{v}})}{\omega }\bar p + \lambda_{1} zp-\lambda_{1}z\frac{q(\hat {\mathbf{v}})}{\omega}\bar p-a(\mathbf{x},d_{c}) p \end{array} $$
$$\begin{array}{@{}rcl@{}} &&+ b(\mathbf{x},d_{c}) \frac{q(\hat {\mathbf{v}} )}{\omega }r - L_{1}(N,\alpha_{1},d_{r})p, \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} \partial_{t} r &=& a(\mathbf{x} ,d_{c})\bar p -b(\mathbf{x} ,d_{c}) r + g(N,d_{c}) r- L_{2}(N,\alpha_{2},d_{r}) r, \end{array} $$
(6)

where \(\bar p(t,\mathbf {x},y):={\int }_{V} p(\textbf {v} )d\textbf {v}\) and L i (N,α i ,d r ): = l i (N) + R i (α i ,d r ), i=1,2.

Now doing the parabolic scaling x→𝜖 x, t→𝜖 2 t, we obtain

$$\begin{array}{@{}rcl@{}} \epsilon^{2} \partial_{t} p +\epsilon \nabla \cdot (\mathbf{v} p) &-&\frac{\partial}{\partial z}\left( \left( (k^{+}QS+k^{-})z - \epsilon^{2} F(t) -\epsilon f^{\prime}(Q) \mathbf{v} \cdot \nabla Q\right)p\right) \end{array} $$
$$\begin{array}{@{}rcl@{}} &=&-\lambda_{0} p +\lambda_{0}q\bar p + \lambda_{1} zp-\lambda_{1}z\frac{q}{\omega }\bar p-a(d_{c}) p \end{array} $$
$$\begin{array}{@{}rcl@{}} && + b(d_{c}) \frac{q}{\omega }r - \epsilon^{2} L_{1}(N, \alpha_{1},d_{r})p, \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} \epsilon^{2}\partial_{t} r &=& a(d_{c})\bar p -b(d_{c}) r + \epsilon^{2} g(N,d_{c}) r- \epsilon^{2} L_{2}(N, \alpha_{2},d_{r}) r. \end{array} $$
(8)

Thereby, we scaled with 𝜖 2 the quantity F(t) involving time derivatives of the different doses and the survival fraction S and accounting for fast dynamics.

In the next step, we set up a moment system w.r.t. the involved distribution functions and introduce the notations

$$\begin{array}{@{}rcl@{}} m(t,\mathbf{x},\mathbf{v}) &=& {\int}_{Z} p(t,\mathbf{x},\mathbf{v},z)dz,\qquad\quad M(t,\mathbf{x}) = {\int}_{V} m(t,\mathbf{x},\mathbf{v}) d\mathbf{v}, \\ m^{z}(t,\mathbf{x},\mathbf{v}) &=& {\int}_{Z} zp(t,\mathbf{x},\mathbf{v},z) dz,\qquad M^{z}(t,\mathbf{x}) = {\int}_{V} m^{z}(t,\mathbf{x},\mathbf{v}) d\mathbf{v},\\ W(t,\mathbf{x}) &=& {\int}_{Z} r(t,\mathbf{x},z) dz,\qquad\quad~ W^{z}(t,\mathbf{x}) = {\int}_{Z} zr(t,\mathbf{x},z)dz, \end{array} $$

where Z⊆[y ∗−1,y ∗] is our new domain for the internal dynamics. The higher order moments are neglected, in virtue of the subcellular dynamics being much faster than the events on the higher scales, which permits to assume z to be close to zero (i.e., the steady state of the subcellular dynamics is rapidly reached). As in [17–19], we assume the functions to have a relatively compact support in this interval and be compactly supported in the (x,z)-space, which allows to perform the subsequent calculations. With the moment notations, we get (after integrating (7) and (8) w.r.t. z)

$$\begin{array}{@{}rcl@{}} \epsilon^{2} \partial_{t} m +\epsilon \mathbf{v} \cdot \nabla m \!&=&\! -\lambda_{0} m +\lambda_{0} \frac{q}{\omega }M + \lambda_{1} m^{z} -\lambda_{1} \frac{q}{\omega }M^{z}-a m + b \frac{q}{\omega}W - \epsilon^{2} L_{1} m,\qquad \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} \epsilon^{2} \partial_{t} W \!&=&\! a M - b W +\epsilon^{2} (g-L_{2})W, \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} \epsilon^{2} \partial_{t} m^{z} +\epsilon \mathbf{v} \cdot \nabla m^{z} \!&=&\! -(k^{+}QS+k^{-})m^{z} +\epsilon f^{\prime}(Q) \mathbf{v} \cdot \nabla Q m + \epsilon^{2} F m \end{array} $$
$$\begin{array}{@{}rcl@{}} &&-\lambda_{0} m^{z} +\lambda_{0}\frac{q}{\omega }M^{z} -a m^{z}+b \frac{q}{\omega } W^{z} - \epsilon^{2} L_{1} m^{z}, \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} \epsilon^{2} \partial_{t} W^{z} &=& aM^{z} - bW^{z} +\epsilon^{2} (g-L_{2}) W^{z}. \end{array} $$
(12)

Now we consider the Hilbert expansions \({\Xi } = {\sum }_{k=0}^{\infty } {\Xi }_{k} \epsilon ^{k}\) for Ξ∈{m,m z,M,M z,W,W z} and collect corresponding powers of 𝜖:𝜖 0:

$$\begin{array}{@{}rcl@{}} 0&=& -(\lambda_{0} +a) m_{0} + \lambda_{0} \frac{q}{\omega }M_{0} + \lambda_{1} {m_{0}^{z}} -\lambda_{1} \frac{q}{\omega }{M_{0}^{z}} +b \frac{q}{\omega } W_{0},\\ 0&=&aM_{0}-bW_{0},\\ 0&=&-(k^{+}QS+k^{-}+\lambda_{0}+a){m_{0}^{z}} +\lambda_{0}\frac{q}{\omega }{M_{0}^{z}} +b\ \frac{q}{\omega } {W_{0}^{z}},\\ 0&=&a{M_{0}^{z}} -b {W_{0}^{z}}. \end{array} $$

From these equations, we deduce by integrating w.r.t. v (where appropriate) that \({M_{0}^{z}} = 0\), \({W_{0}^{z}}=0\), \({m_{0}^{z}}=0\), \(m_{0} = \frac {q}{\omega }M_{0}\), and \(W_{0}=\frac {a}{b}M_{0}\). 𝜖 1:

$$\begin{array}{@{}rcl@{}} \mathbf{v} \cdot \nabla m_{0} &=& -(\lambda_{0}+a) m_{1} +\lambda_{0} \frac{q}{\omega }M_{1}+\lambda_{1} {m_{1}^{z}} -\lambda_{1} \frac{q}{\omega }{M_{1}^{z}}+b \frac{q}{\omega} W_{1}, \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} 0&=& a M_{1} - b W_{1}, \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} \mathbf{v} \cdot \nabla {m_{0}^{z}}&=& -(k^{+}QS+k^{-}+\lambda_{0} +a){m_{1}^{z}} +f^{\prime}(Q) \mathbf{v} \cdot \nabla Q m_{0} + \lambda_{0} \frac{q}{\omega }{M_{1}^{z}} + b \frac{q}{\omega} {W_{1}^{z}},\quad \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} 0&=& a {M_{1}^{z}} -b {W_{1}^{z}}. \end{array} $$
(16)

Using the above deduced facts in (16), then in (15) (integrated w.r.t. v) and (13), we obtain \({M_{1}^{z}}={W_{1}^{z}}=0\)

$$\begin{array}{@{}rcl@{}} {m_{1}^{z}} &=& \frac{1}{\gamma (\mathbf{x})} f^{\prime}(Q) \mathbf{v} \cdot \nabla Q m_{0}, \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} m_{1} &=& \frac{1}{\lambda_{0}+a}\left( \frac{\lambda_{1}}{\gamma }f^{\prime}(Q)\mathbf{v} \cdot \nabla Qm_{0}-\mathbf{v} \cdot \nabla m_{0}+\frac{aq}{\omega}M_{1} \right), \end{array} $$

where γ(x): = k + Q S + k − + λ 0 + a .

By (13) and (14), we can write

$$\mathbf{v} \cdot \nabla m_{0} =\mathcal L[\lambda_{0}+a]m_{1}+\lambda_{1}{m_{1}^{z}}. $$

Then, \(\mathcal L[\lambda _{0}+a]\) defined on the weighted L 2-space \({L^{2}_{q}}(V)\) with the weight function \(q^{-1}(\hat {\mathbf {v}})\) is a compact Hilbert–Schmidt operator (see [30]) with pseudoinverse \(\mathcal {L}[\lambda _{0} +\alpha ]^{-1}_{|\langle q\rangle ^{\bot }}\zeta =-\frac {1}{\lambda _{0} + \alpha }\zeta \). As in [19], this leads to

$$ m_{1}= -\frac{1}{\lambda_{0}+\alpha}(\mathbf{v}\cdot \nabla m_{0}-\lambda_{1} {m_{1}^{z}}). $$
(18)

We also have the set of equations𝜖 2:

$$\begin{array}{@{}rcl@{}} \partial_{t}m_{0}+\mathbf{v} \cdot \nabla m_{1}&=&\mathcal{L}[\lambda_{0}]m_{2}+\lambda_{1}{m_{2}^{z}}-\lambda_{1}\frac{q}{\omega }{M_{2}^{z}}-am_{2}+b\frac{q}{\omega } W_{2}-L_{1}(N_{0})m_{0}, \end{array} $$
(19)
$$\begin{array}{@{}rcl@{}} \partial_{t}W_{0}&=&aM_{2}-bW_{2}+(g(N_{0})-L_{2}(N_{0}))W_{0}. \end{array} $$
(20)

From (20), we have

$$\frac{b}{\omega }W_{2}=\frac{1}{\omega }[aM_{2}+(g(N_{0})-L_{2}(N_{0}))W_{0}-\partial_{t}W_{0}], $$

which plugged into (19) leads to

$$\begin{array}{@{}rcl@{}} \partial_{t} m_{0} + \mathbf{v}\cdot \nabla m_{1} &=&\mathcal{L}[\lambda_{0}+a]m_{2}-\mathcal{L}[\lambda_{1}]{m_{2}^{z}}\\ && +\frac{q}{\omega}\left[\frac{a}{b}M_{0}(g(N_{0})-L_{2}(N_{0}))-\partial_{t}(W_{0})\right]-L_{1}(N_{0})m_{0}. \end{array} $$

After integrating w.r.t. v and rearranging, this becomes

$$\partial_{t}M_{0} + {\int}_{V} \mathbf{v}\cdot \nabla m_{1}~ d\mathbf{v} =\left( g(N_{0})-L_{2}(N_{0}) \right)W_{0}- \partial_{t} W_{0}-L_{1}(N_{0})M_{0}. $$

Hence, with \(N_{0}=M_{0}+W_{0}=(1+\frac {a}{b})M_{0}\), we get

$$\begin{array}{@{}rcl@{}} \partial_{t}N_{0}+\nabla \cdot {\int}_{V}(\mathbf{v} m_{1})d\mathbf{v} &=&\left( g(N_{0})-L_{2}(N_{0})\right)W_{0}-L_{1}(N_{0})M_{0} \end{array} $$
$$\begin{array}{@{}rcl@{}} &=&\frac{a}{a+b} N_{0}\left( g(N_{0}) - L_{2}(N_{0})\right)-\frac{b}{a+ b} N_{0}L_{1}(N_{0}). \end{array} $$
(21)

It remains to express \({\int }_{V} \mathbf {v} m_{1}~ d\textbf {v} \) in terms of N 0. From (18), we have

$$m_{1}= -\frac{1}{\lambda_{0}+\alpha}\left( \mathbf{v}\cdot \nabla \left( \frac{q}{\omega}M_{0}\right)-\lambda_{1} {m_{1}^{z}}\right), $$

and from (17), we know \({m_{1}^{z}}= \frac {1}{\gamma (\textbf {x} )}f^{\prime }(Q)\textbf {v}\cdot \nabla Q\ \frac {q}{\omega }M_{0}\); hence,

$$\begin{array}{@{}rcl@{}} \nabla \cdot {\int}_{V}\mathbf{v}m_{1}~d\mathbf{v} &=&\nabla\cdot \left( -\frac{1}{\lambda_{0} +a}\nabla\cdot \left( \frac{1}{\omega} {\int}_{V} \mathbf{v}\mathbf{v}^{t} q~d\mathbf{v} M_{0}\right) \right)\\ &&+ \nabla\cdot\left( \frac{\lambda_{1}}{\lambda_{0}+a} \frac{1}{\gamma (\mathbf{x} )}f^{\prime}(Q)\frac{1}{\omega} {\int}_{V} \mathbf{v}\mathbf{v}^{t} q ~d\mathbf{v} \nabla Q M_{0} \right). \end{array} $$

Now denote

$$\mathbb D_{T}(\mathbf{x} ):=\frac{1}{\omega} {\int}_{V} \mathbf{v}\mathbf{v}^{t} q ~d\mathbf{v} $$

to obtain

$$\begin{array}{@{}rcl@{}} \nabla \cdot {\int}_{V}\mathbf{v}m_{1} ~d\mathbf{v} &=&\nabla\cdot \left( -\frac{1}{\lambda_{0} +a}\nabla \cdot \left( \frac{b}{a+b}\mathbb D_{T}(\mathbf{x})N_{0}\right)\right)\\ &&+ \nabla \cdot \left( \frac{\lambda_{1}}{\lambda_{0}+a} \frac{1}{\gamma (\mathbf{x} )}\frac{b}{a+b}f^{\prime}(Q)\mathbb D_{T}(\mathbf{x} )\nabla QN_{0}\right). \end{array} $$

Plug this into (21) to obtain the macroscopic equation for N 0:

$$\begin{array}{@{}rcl@{}} &&\partial_{t} N_{0} -\nabla\cdot \left( \frac{1}{\lambda_{0} +a}\nabla \cdot \left( \frac{b}{a+b}\mathbb D_{T}(\mathbf{x}) N_{0}\right)\right)\\ &&\qquad+ \nabla \cdot \left( \frac{\lambda_{1} f^{\prime}(Q)}{\gamma (\mathbf{x} )}\frac{b}{(\lambda_{0}+a)(b+a)} \mathbb D_{T}(\mathbf{x})\nabla Q N_{0}\right)\\ &&\quad = \left( \left( g(N_{0}) - L_{2}(N_{0})\right)\frac{a}{a+b} - L_{1}(N_{0})\frac{b}{a+b}\right) N_{0}. \end{array} $$
(22)

Throughout the rest of this paper, we will assume for simplicity that the functions a and b depend only on time.

2.3 Well Posedness of the Settings

2.3.1 Micro-meso System

The system (1), (2), and (4) fits in the more general framework handled in [44]; hence, its well posedness follows (with corresponding initial conditions) like in that reference.

2.3.2 Macroscopic Equation

For the well posedness of the macroscopic equation (22) set in a bounded space-time domain, we rely on the theory of monotone operators for nonlinear parabolic equations (see, e.g., [56]).

Let Ω be a bounded domain in \(\mathbb {R}^{3}\) with the Lipschitz boundary ∂Ω. We want to verify the existence of a solution to the nonlinear parabolic initial-boundary-value problem

$$\begin{array}{@{}rcl@{}} \partial_{t} u - \nabla\cdot \left( D(\mathbf{x},t)\nabla u - H(\mathbf{x},t)u\right) + G(u) &=& 0\qquad\text{ in }~{\Omega} \times (0,T), \\ \left( D(\mathbf{x},t)\nabla u - H(\mathbf{x},t)u\right) \cdot \mathbf{n} &=& 0 \qquad\text{ on }~ \partial {\Omega} \times (0,T),\\ u(0) &=& u_{0} \qquad\text{on }~{\Omega} \times \{0\}, \end{array} $$
(23)

where

$$\begin{array}{@{}rcl@{}} D(\mathbf{x},t) &=& \frac{b(t)}{(\lambda_{0}+a(t))(a(t) +b(t))}\mathbb{D}_{T}(\mathbf{x}),\\ H(\mathbf{x},t) &=& \frac{\lambda_{1} f^{\prime}(Q)}{\gamma (t,\mathbf{x})}\frac{b(t)}{(\lambda_{0}+a(t))(b(t)+a(t))} \mathbb{D}_{T}(\mathbf{x})\nabla Q\\ && - \frac{b(t)}{(\lambda_{0}+a(t))(a(t)+b(t))}\text{div}(\mathbb D_{T}(\mathbf{x})),\\ G(u,t) &=& -\left( (g(u,t) - L_{2}(u,t))\frac{a(t)}{a(t) +b(t)} - L_{1}(u,t)\frac{b(t)}{a(t) + b(t)}\right)u. \end{array} $$

Assumptions

  1. (A.i)

    The functions D and H are continuous in time and essentially bounded in space. Moreover, D satisfies the condition ξ T D(x,t)ξ≥𝜃(t)|ξ|2 with a positive 𝜃(t) bounded away from zero: 0<c 𝜃 ≤𝜃(t)≤C 𝜃 <∞ for all t≥0.

  2. (A.ii)

    G is continuous w.r.t. time and the solution variable. Moreover, G satisfies the condition G(0,t)=0, the growth condition |G(u,t)|≤C(1+|u|2), with a constant C independent of time and space, and the coercivity condition \(\inf _{\zeta \in \mathbb {R}^{+}} G(\zeta ,t)\zeta >-\infty \).

For our concrete setting above, we require that:

  1. (i)

    The diffusion tensor \(\mathbb {D}_{T}\) is uniformly positive definite and lies in the space W 1,∞(Ω).

  2. (ii)

    The volume fraction of tissue fibers Q has to lie in the space W 1,∞(Ω), as well.

  3. (iii)

    The rates a,b,k + and k − are continuous in the variable d c (which has to be continuous in time) and uniformly bounded.

  4. (iv)

    The gain and loss functions g and l (the latter is contained in the expression of L i , i=1,2) are continuous and bounded.

Remark 1

Assumptions (i) and (ii) express the fact that the intrinsic properties of the brain structure are smooth. This can be justified at a reasonable level of detail. Moreover, the diffusion tensor \(\mathbb D_{T}\) is (re)constructed in such a way that the uniform positive definiteness is assured in every computational voxel.

Lemma 1

For non-negative initial data u 0 a solution of ( 23 ) remains non-negative for all future times.

Proof

This follows immediately from our assumptions, by applying the parabolic comparison principle. □

As we are only interested in non-negative initial values, leading to non-negative solutions, we assume in the following that G(t,u)=0 for u<0.

Define the spaces V: = H 1(Ω) and H: = L 2(Ω) and the corresponding Gelfand triple (V,H,V ⋆). We look for a solution to (23) in the space W:={v∈L 2(0,T;V),v ′∈L 2(0,T;V ⋆)}, with T>0 fixed.

Now define the operators

$$\begin{array}{@{}rcl@{}} \langle A(t)u,v\rangle &:=& {\int}_{\Omega} (D(\mathbf{x},t)\nabla u - H(\mathbf{x},t)u)\cdot \nabla v~d \mathbf{x},\\ \langle B(t)u,v\rangle &:=& {\int}_{\Omega} G(u,t) v~d \mathbf{x} \end{array} $$

for u,v∈W.

Remark 2

The operators A and B defined above are continuous w.r.t. time, due to (iii).

Lemma 2

The family of operators A(t) is continuous from V to V ⋆ and satisfies Garding’s inequality

$$\langle A(t)u,u\rangle \geq c_{1} \|u\|_{V}^{2} - c_{2} \|u\|_{H}^{2} $$

with the constants c 1 >0 and c 2 ≥0.

Proof

The claim follows straightforwardly by usual estimates. □

Remark 3

We assume without loss of generality that c 2=0. Otherwise, we transform (23) into an equivalent problem by \(\hat u = \exp (c_{2}t)u\). Note that after this transformation the operators A and B remain continuous in time.

The following result is obtained (as a particular case) by a simple adaptation of the proofs in Section 3.3.6, [56] (or of Section III.4, [61]):

Theorem 1

Let u 0 ∈H. Under the previous assumptions about the function G and the coefficients involved in A there exists a solution u∈W to ( 23 ), in the sense that

$$-{{\int}_{0}^{T}}\langle v^{\prime}(t),u(t)\rangle_{V}dt+{{\int}_{0}^{T}}\langle A(t)u(t),v(t)\rangle_{V}dt+{{\int}_{0}^{T}}\langle B(t)u(t),v(t)\rangle_{V}=(u_{0},v(0))_{H} $$

for all v∈W with v(T)=0. If G is strictly monotone, then the solution u is unique.

3 Assessing the Parameters and Coefficient Functions

3.1 Fiber Density q

To determine the diffusion tensor \(\mathbb D_{T}\), we need to determine the fiber orientation distribution q. As in [17–19], we could select q to be the peanut distribution proposed by Hillen and Painter in [31]:

$$ q(\mathbf{x},\boldsymbol{\theta}) = \frac{n}{|\mathbb{S}^{n-1}| \text{tr}(\mathbb{D}_{W}(\mathbf{x}))}\boldsymbol{\theta}^{t} \mathbb{D}_{W} \boldsymbol{\theta}, $$
(24)

where \(\mathbb {D}_{W}\) denotes the DTI-measured water diffusion tensor and \(\boldsymbol {\theta } \in \mathbb {S}^{n-1}\) gives the fiber orientation. The major problem occurring with this choice is that the tumor diffusion tensor may not reproduce the brain structure in enough detail, as it consists of only six gradient directions and cannot resolve crossing fiber tracts [8]. Different other choices try to overcome this drawback. One is to use a bimodal von Mises–Fisher distribution (see [46]) as proposed in [50]

$$ q(\mathbf{x},\boldsymbol{\theta}) = \frac{k(\mathbf{x})}{8\pi \sinh(k(\mathbf{x}))}(\exp(k(\mathbf{x}) \phi \cdot \boldsymbol{\theta})+\exp(-k(\mathbf{x}) \phi\cdot \boldsymbol{\theta})), $$
(25)

where k(x) = κ F A(x), with the measured fractional anisotropy FA and a real constant κ to be determined. The vector ϕ represents the leading eigenvector of the diffusion tensor for each voxel. This choice, however, has several disadvantages: On the one hand, the parameter κ cannot be measured and has to be assessed by using different clinical DTI data sets. On other hand, the fractional anisotropy is a not satisfactory enough indicator for anisotropy (see [70]), as well as for the fiber density. Moreover, the leading eigenvector does not resemble the fiber orientation in all voxels [34]. Another way to enhance the quality of the diffusion tensor description is to use the concept of an orientation distribution function (ODF) [1, 8] which describes the probability of diffusion in a direction 𝜃. The usual definition of this probability is

$$ODF(\boldsymbol{\theta}) = {\int}_{0}^{\infty} \mathcal P(r\boldsymbol{\theta}) r^{2}~ dr, $$

where \(\mathcal P(r\boldsymbol {\theta })\) denotes the displacement probability of a spatial point in spherical coordinates.Footnote 4 For more details we refer to the cited paper. Hence, we may set our fiber orientation density to the orientation distribution function

$$ q(\boldsymbol{\theta}) = ODF(\boldsymbol{\theta}). $$
(26)

For diffusion tensor imaging, the fiber orientation q in (26) can be computed explicitly ([1]):

$$ q(\mathbf{x},\boldsymbol{\theta}) = \frac{1}{4\pi |\mathbb D_{W}(\mathbf{x})|^{\frac{1}{2}} \left( \boldsymbol{\theta}^{t} \mathbb D_{W}(\mathbf{x})^{-1}\boldsymbol{\theta}\right)^{\frac{3}{2}}}; $$
(27)

thus, we do not need reconstruction procedures involving the integral expression to obtain this quantity. The ODF is available for different medical imaging techniques [1, 8], among them also the high quality imaging procedures Q-Ball and HARDI. This is a major advantage allowing to include different medical data in the model. For our test dataFootnote 5, we use here this ODF; the issue of comparison between this and the peanut distribution for the tumor diffusion tensor setup will be addressed in a forthcoming work.

3.2 Estimation of Q

We estimated the volume fraction of tissue fibers Q as in [18]. Hence, we chose

$$Q = 1 - \frac{{l_{c}^{3}}}{h^{3}}, $$

where h is the side length of one voxel and the characteristic length l c is estimated via

$$l_{c} = \sqrt{\frac{\text{tr}(\mathbb{D}_{W})h^{2}}{4l_{1}}}, $$

using l 1 as the leading eigenvalue of the diffusion tensor \(\mathbb {D}_{W}\). The determination of an unbiased estimator for the fiber volume fraction is ongoing work.

3.3 Coefficient Functions

First, we have to select the transition rates a and b between the migrating population p in (1) and the proliferating population r in (2). These functions depend on the space variable and the dose of chemotherapeutic agent; however, as mentioned before, we choose the constant w.r.t. x, as there is no known procedure to quantify this dependency. As mentioned in Section 2, the chemotherapeutic drug modeled in this paper concentrates its impact on the integrin bindings. These are essential for cell migration; thus, this has to be taken into account for the choice of a and b. The rate a models the cell transition from the migrating to the resting (and hence proliferating) regime. As migrating cells seem to be responsible for the infiltrative behavior of the tumor and its recurrence, we aim at inhibiting the migratory phenotype of the cell population. Hence, a should be monotonically increasing in its only variable d c . The rate b describes the transition rate to migratory behavior, so it has to be monotonically decreasing in d c . Therefore, a possible choice is

$$\begin{array}{@{}rcl@{}} a(d_{c}) &=& 0.05 \cdot (1+d_{c}),\\ b(d_{c}) &=& 0.1 \cdot \left( 1+\frac{d_{c}}{1+{d_{c}^{2}}}\right). \end{array} $$

As there is no quantitative information available for these rates, they cannot be fit to measurements. Therefore, we concentrate on their qualitative behavior. This also applies to the rates k + and k −. However, there is some indication that this choice is reasonable, because it is of the same order as the constants α and β [19] modeling the same rates. The unit of these rates is \(\frac {1}{\text {s}}\).

Next, we address the receptor-binding rates k + and k −, the first of which describes the rate of a cell binding to unsoluble ligands (fibers) in its environment, while k − is the detachment rate. Since the chemotherapeutical agent under consideration is meant to inhibit receptor bindings, we assume the function k + to be monotonically decreasing, while k − is supposed to be monotonically increasing. This means that it is more likely for a cell under the influence of the chemotherapeutical substance to detach from the ECM than to attach to it. Thus, our choices are

$$\begin{array}{@{}rcl@{}} k^{+}(d_{c}) &=& 0.1\cdot \left( 1+\frac{d_{c}}{1+{d_{c}^{2}}}\right),\\ k^{-}(d_{c}) &=& 0.1\cdot (1+d_{c}). \end{array} $$

This corresponds to the rates selected in [18, 19]. The rate k − could be determined to be around 0.1 in absence of the chemotherapeutical substance [40]. The rate k + should be larger than k −, since the attachment of the cell to the surrounding fibers should be more probable then detachment, if no further (bio)chemical information is available. Like for the rates a and b, the unit of k + and k − is \(\frac {1}{\text {s}}\).

Eventually, we have to adjust the functions included in the nonlinear term G and describing radiotherapy and proliferation. Like in [18, 19], we model the growth in a logistic way and select

$$\begin{array}{@{}rcl@{}} g(s) &=& c_{g},\\ L_{1}(d_{c},d_{r},u) &=& c_{g} u + \sum\limits_{i=1}^{\nu} \left( 1-S(\alpha_{1},d_{r})\right) \eta_{\delta}(t-t_{i}),\\ L_{2}(d_{c},d_{r},u) &=& c_{g} u + \sum\limits_{i=1}^{\nu} \left( 1-S(\alpha_{2},d_{r})\right) \eta_{\delta}(t-t_{i}). \end{array} $$

As in (3), ν is the number of therapy fractions. Altogether, we have

$$\begin{array}{@{}rcl@{}} -G(w) &=& \frac{a}{a+b} c_{g} w - c_{g} w^{2} - \left( \frac{b}{a+b}\sum\limits_{i=1}^{\nu} \left( 1-S(\alpha_{1},d_{r})\right) \eta_{\delta}(t-t_{i})\right.\\ &&\left. + \frac{a}{a+b}\sum\limits_{i=1}^{\nu} \left( 1-S(\alpha_{2},d_{r})\right) \eta_{\delta}(t-t_{i})\right)w. \end{array} $$
(28)

Note that this G satisfies the requirements of Assumption (A.ii). The growth rate c g has to be measured as a density growth rate. This is different from the commonly considered cell doubling rates or even volume growth rates, targeting the size of individual cells. Both are not appropriate for a cell density variable, therefore we estimated in [18] the density growth rate c g to be approximately \(8\cdot 10^{-7}\frac {1}{\text {s}}-10^{-6}\frac {1}{\text {s}}\) by using information about the cell cycle.

3.4 Constants

We selected the necessary constants as in Table 1 below. The necessary therapy parameters change from scenario to scenario, so we will specify them where occurring.

Table 1 Model parameters
Full size table

4 Numerical Simulations

We solve the equation (22). While all necessary data, i.e., the diffusion tensor \(\mathbb D_{T}\) and the volume fraction of tissue fibers Q, are computed in advance from the DTI measurements using C++ and the Armadillo linear algebra library [58], we implemented the simulation of the PDE via the numerical framework DUNE [3–5, 7]. The coefficients and the drift term depend on time and space, so we expect time dependent regions of the computational domain that are dominated by the diffusion term and others dominated by the drift term. Thus, we need numerical methods capable to handle both diffusion dominated and degenerate parabolic equations. Moreover, the selected method has to handle full tensors and it should be locally mass conservative and positivity preserving.

4.1 Implementation

For the simulations, we use a parallel structured quadrilateral mesh as implemented in YaspGrid of DUNE. The cells are chosen in such a way that we have a subset of the voxel mesh given by the medical data set consisting of the regions occupied by gray and white matter. These were given by a segmentation of the brain in the data set. On this mesh, we use a cell-centered finite volume method as described in [20]. For the time discretization, we employ an implicit Euler scheme with a step size τ satisfying a CFL-condition near 1. In our case, we considered τ to be one half of a day.

4.2 Results

We performed numerical simulations for different scenarios. The coefficients are those given in Section 3. Different therapy strategies are to be compared, all of which involve resection followed after 21 daysFootnote 6 by radio- and chemotherapy, the latter applied in a concurrent way. The starting point is considered the detection of the tumor. Recall that here the chemotherapy is aiming merely at inhibiting receptor binding to the tissue fibers; the cell kill is achieved by radiotherapy.

  1. Strategy 1:

    Resection (2 weeks after start), no further therapy.

  2. Strategy 2:

    Resection (2 weeks after start), followed after 3 weeks by radiotherapy (a daily dose of 2 Gy—except on weekends) for 6 weeks.

  3. Strategy 3:

    Resection (2 weeks after start), followed after 3 weeks by concurrent chemotherapy (a normalized dose of 5.0 in our model) and radiotherapy (a daily dose of 2 Gy—except on weekends) for 6 weeks.

As therapies with inhibitors of receptor/integrin binding to unsoluble ligands in the environment of tumor cells are not yet approved for clinical practice, we relied on some clinical trials when designing the strategies 1 to 3, thereby intentionally omitting the effect of a chemotherapeutic agent (like temozolomide) directly aiming at cell kill. Hence, these strategies (and the involved parameters) are motivated by the trials NCT01165333 (Cilengitide in Combination With Irradiation in Children With Diffuse Intrinsic Pontine Glioma) and NCT00689221 (Cilengitide, Temozolomide, and Radiation Therapy in Treating Patients With Newly Diagnosed Glioblastoma and Methylated Gene Promoter Status) at ClinicalTrials.gov.

In our simulations, the resection is numerically obtained by setting to zero the actual tumor density above a threshold of 0.2, in each computational cell and during the corresponding time step. This is of course not a mathematical, but a computational way to proceed. The effect of this procedure is that after resection there is no tumor left in the resected area. The main problem with modeling the resection mathematically in a continuous manner is the nonlinearity of this process (no simple loss term can describe it) and the sharp discontinuity of the solution in this time step. Since here we do not focus on modeling resection, but rather on a novel therapy approach (involving a chemotherapeutic agent from the class of peptidomimetics, for which clinical studies are ongoing), we consider this simplified computational approach, which is nevertheless able to solve the problem and to capture to a reliable extent the effect of resection. Moreover, it preserves the non-negativity of the solution. The maximal chemotherapeutical dose is selected such that the upper value of k − is of the order chosen in [17–19].

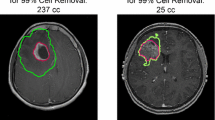
Figure 1 shows the starting point (when the tumor has been assessed by medical imaging), the time point of resection (2 weeks after start), and the result of surgical resection. Observe in Fig. 1b the heterogeneous structure of the tumor, which corresponds to the known fact that glioma expand according to the brain structure, exhibiting a highly anisotropic behavior, as commented in Section 1. Due to this infiltrative growth, the resection is less successful at the tumor margins (Fig. 1c).

Fig. 1
figure 1

Tumor at starting point, before, and after resection

Full size image

Figure 2 shows the time point at the end of therapy in strategies 2 and 3 (i.e., 9 weeks after resection), follow-up pictures after 2 months for the different strategies, and scaled versions of these pictures. Notice the tumor recurrence which is more pronounced at the marginal region of the original neoplastic bulk. As expected, resection alone (first column in Fig. 2) provides the poorest therapeutic outcome; the spread of glioma along white matter tracts of the brain tissue leads to the scattered shape of the tumor. This behavior is in line with clinically observed patterns (see e.g., [23, 60] and the references therein). Subsequent radiotherapy (middle column in Fig. 2) is expected to enhance tumor eradication, and concurrent chemotherapy aiming at impairing cell-tissue adhesion by inhibiting receptor binding provides in our simulations an even better outcome (last column in Fig. 2). However, complete eradication seems to be out of reach, as the scaled pictures in Fig. 2b, d show. This is due to the high proliferation and migration ability of the glioma cells. We also compared adjuvant and neo-adjuvant chemotherapy (where the same chemotherapeutic agent was used) with surgery and radiotherapy, but the most significant differences were achieved with the strategies presented here in more detail. Whenever merely small improvements were obtained we opted for the less expensive and more conservative strategy.

Fig. 2
figure 2

Comparison of strategy 1 (left column), strategy 2 (middle), and strategy 3 (right)

Full size image

5 Conclusions and Outlook

In this note, we started from previous multiscale models for glioma invasion and proposed some descriptions of therapy approaches, partly involving the already standard one of surgery followed by radiotherapy, but also considering more recent therapeutic ideas connected to inhibition of cell-tissue attachment and its effects on migration and proliferation. Our multiscale setting with explicit subcellular dynamics seems particularly well suited to account for such features. Although we eventually work with the effective equations deduced on the macroscopic level, they carry in their coefficients the information from the lower (subcellular and individual cell) levels and assimilate DTI data allowing for a patient-specific description of the brain structure. Notice that on the macroscale, we are merely interested in the tumor bulk (as assessed by medical imaging), therefore the macroscopic limit does no longer feature two different subpopulations, as they could not be distinguished by the imaging procedures which are clinical standard. Nevertheless, the influence of the two subpopulations is still contained in the coefficients of (22), in particular also visible in the growth/decay term on the right hand side, which contains the main therapy effects. We also stress out that the spatiality is an essential feature and that an ODE model with two compartments for the two cell subpopulations would not be able to properly account for the tumor heterogeneity w.r.t. migration and proliferation: The very notion of migration is tightly connected to the question of how far do the cells invade into the tissue and not explicable by proliferation/growth alone. Moreover, an ODE setting is neither able to describe the highly anisotropic spread of glioma nor to include haptotaxis, which is crucial in tumor invasion. As observed in [17–19], the latter is obtained in the macroscopic equations as a consequence of taking into account the subcellular level of information in our multiscale model.

Several issues are yet to be addressed in future works; here, we mention just a few: (i) When describing resection we set to zero all densities above 0.2. While this is convenient to do in the computer, in clinical practice it is hardly possible to zoom (rescale) and assess the tumor heterogeneity at this level of detail; only the regions with high cell density can be observed by medical imaging and the tumor volume to be resected/irradiated (i.e., the CTV-PTV marginFootnote 7) is established by following some general guidelines. However, our modeling approach opens the way for assessing the evolution of the tumor on the particular brain structure obtained by DTI and to account thereby for the infiltrative growth of glioma, which is a main factor in tumor recurrence. Hence, in forthcoming works more attention will be paid to tumor delineation and treatment planning. (ii) Throughout the simulations we used the same DTI-assessed tissue structure via the functions q and Q. Including an equation for characterizing the evolution of normal tissue would be desirable, but difficult to realize in this framework and with the available data, as the tissue structure would need to be assessed after each stage of therapy (resection and irradiation), which is expensive (if at all possible, at this level of detail). (iii) The parameters involved in our simulations have been taken from literature or empirically estimated. Determining them in a more precise way would mean to combine medical imaging techniques with biopsy and cell tracking; we refer, e.g., to [52] for DTI image-guided biopsy studies. (iv) The effects of supplementary cell sensitization towards therapy and even enhancement of tumor cell degradation can be addressed by considering another chemotherapeutic agent, like temozolomide. It is one of the great advantages of mathematical modeling to be able to investigate a large variety of therapeutic approaches and to compare them.