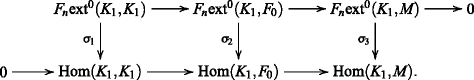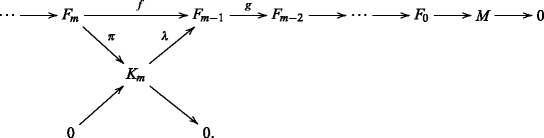Derived Functors of Hom Relative to n-Flat Covers

Abstract

In this paper, we introduce the notion of n-flat covers of modules and prove that every module over any ring admits an n-flat cover. Then, we give some criteria for computing left and right $\mathcal {F}_{n}$-dimensions in terms of the properties of the derived functor of Hom.

1 Introduction

The notions of (pre)covers and (pre)envelopes of modules were introduced by Enochs [2] in 1981. Since then, the existence and the properties of (pre)covers and (pre)envelopes relative to certain submodule categories have been studied widely. The theory of (pre)covers and (pre)envelopes, which plays an important role in Homological algebra and representation theory of algebras, becomes now one of the main research topics in relative homological algebra.

In 2001, Bican et al. [1] proved that every module over any ring admits a flat cover. After introducing the notion of an n-flat module, it is natural to ask the following question: For any ring R, do all modules have n-flat covers? In this paper, we introduce the notion of n-flat covers of modules and show that over any ring R, every module admits an n-flat cover. Further, using this result, we study the derived functors of Hom.

In what follows, we write R−Mod (resp. Mod−R) and $\mathcal {F}_{n}$ for the categories of all left (resp. right) R-modules and all n-flat left R-modules, respectively. We prove that every left R-module has an n-flat cover over any ring R (see Theorem 3), so every left R-module M has a left $\mathcal {F}_{n}$-resolution, that is, there is an exact sequence ${\cdots } \rightarrow F_{1} \rightarrow F_{0} \rightarrow M \rightarrow 0$ with each F _i n-flat such that $\text {Hom}(\mathcal {F}_{n}, -)$ leaves the sequence exact. Write K ₀=M, $K_{1} = \ker (F_{0} \rightarrow M)$, $K_{i} = \ker (F_{i-1} \rightarrow F_{i-2})$ for i≥2. The mth kernel K _m (m≥0) is called the mth $\mathcal {F}_{n}$-syzygy of M.

Recall that a ring R is called right n-coherent (for integers n>0 or $n=\infty$) if every finitely generated submodule of a free right R-module whose projective dimension is ≤n−1 is finitely presented. It is known that every left R-module M has an n-flat pre-envelope over the right n-coherent ring (see [8, Theorem 3.1]). Thus, M has a right $\mathcal {F}_{n}$-resolution, that is, there is an exact complex $0 \rightarrow M \rightarrow F^{0} \rightarrow F^{1} \rightarrow {\cdots }$ with each F ⁱ n-flat such that $\text {Hom}(-,\mathcal {F}_{n})$ leaves the sequence exact. Let L ⁰=M, $L^{1} = \text {coker}(M \rightarrow F^{0})$, $L^{i} = \text {coker} (F^{i-2} \rightarrow F^{i-1})$ for i≥2. The mth cokernel L ^m (m≥0) is called the mth $\mathcal {F}_{n}$-cosyzygy of M. Note that Hom(−,−) is left balance on R−Mod×R−Mod by $\mathcal {F}_{n} \times \mathcal {F}_{n}$ for a right n-coherent ring R (see [3, Definition 8.2.13]). Thus, the ith left derived functor of Hom(−,−), which is denoted by $F_{n} \text {ext}^{i}(-,-)$, can be computed using a right $\mathcal {F}_{n}$-resolution of the first variable or a left $\mathcal {F}_{n}$-resolution of the second variable. Following [3, Definition 8.4.1], the left $\mathcal {F}_{n}$-dimension of a left R-module M, denoted by left $\mathcal {F}_{n}$-$\dim (M)$ (or $\mathcal {F}_{n}$-$\dim (M)$), is defined as $\inf${m: there is a left $\mathcal {F}_{n}$ -resolution of the form $0 \rightarrow F_{m} \rightarrow {\cdots } \rightarrow F_{0} \rightarrow M \rightarrow 0~ \text {of}~ M\}$. If there is no such m, set left $\mathcal {F}_{n}$-$\dim (M) = \infty$. The right versions can be defined similarly.

This paper is divided into four sections. In Section 2 of this paper, we introduce the notion of n-flat covers of modules. In Section 3, we prove that over any ring R, every module admits an n-flat cover. In Section 4, we investigate the left derived functor $F_{n} \text {ext}^{i} (-,-)$. Let R be a right n-coherent ring. We first show that every left R-module M has a left $\mathcal {F}_{n}$-resolution. Next, we prove that $F_{n} \text {ext}^{i} (-,-)$ is well defined, and finally, we prove that the right $\mathcal {F}_{n}$-$\dim (N) \leq m-2$ (m≥2) if and only if $F_{n} \text {ext}^{m+k}(N,M) =0$ for all left R-modules M and k≥−1 if and only if $F_{n} \text {ext}^{m-1}(N,M) =0$ for all left R-modules M.

Throughout this paper, R is an associative ring with identity and all R-modules are, if not specified otherwise, left R-modules. For an R-module M, we use M ⁺ to denote the character module $\text {Hom}_{\mathbb {Z}}(M,\mathbb {Q}/\mathbb {Z} )$ of M. Let M and N be R-modules. Hom(M,N) (resp. Extⁱ(M,N)) means Hom _R (M,N) (resp. ${\text {Ext}_{R}^{i}}(M,N)$), and similarly, M⊗N (resp. Tor _i (M,N)) denotes M⊗ _R N (resp. ${\text {Tor}_{i}^{R}}(M,N)$) for an integer i≥1. A left R-module M is called n-flat [5] if Tor₁(N,M)=0 holds for all finitely presented right R-modules N with projective dimension (p.d) ≤n and a left R-module M is called n-absolutely pure [5] if Ext¹(N,M)=0 holds for all finitely presented left R-modules N with projective dimension ≤n.

For unexplained terminology and basic results, we refer to [6, 7].

2 n-Flat Covers

In this section, we generalize the definition of flat cover [2] and cotorsion for a fixed positive integer n and we study some basic results.

Definition 1

If $\phi : F \rightarrow M$ is a homomorphism between left R-modules with F n-flat, then ϕ is called n-flat cover of M if for every F′ n-flat and every homomorphism $F^{\prime } \rightarrow M$ the diagrams

• (a)  

  

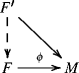
  can always be completed to a commutative diagram or equivalently $\text {Hom}(F^{\prime },F) \rightarrow \text {Hom}(F^{\prime },M)\rightarrow 0$ is exact and

• (b)  

  

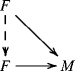
  can be completed to a commutative diagram only by automorphisms of n-flat module F. If (a) is satisfied (and perhaps not (b)), then $\phi : F \rightarrow M$ is called n-flat precover of M.

The notion of n-flat (pre)envelope can be defined dually.

Theorem 1

$\mathcal {F}_{n}$ is closed under direct limits.

Proof

Since the functor Tor _n commutes with direct limits, it follows that the direct limit of n-flat modules is n-flat. □

Given a class $\mathcal {C}$ of R-modules, let $^{\bot } \mathcal {C}$ be the class of R-modules K such that Ext¹(K,C)=0 for every $C \in \mathcal {C}$ and let $\mathcal {C}^{\bot }$ be the class of R-modules K such that Ext¹(C,K)=0 for every $C \in \mathcal {C}$.

Definition 2

Recall that a left R-module U is said to be cotorsion if Ext¹(F,U)=0 for all flat left R-modules F, i.e., $U \in \mathcal {F}^{\bot }$, where $\mathcal {F}$ is the class of all flat modules.

A left R-module U is said to be n-cotorsion if Ext¹(F,U)=0 for all n-flat left R-modules F, i.e., $U \in \mathcal {F}_{n}^{\bot }$.

Theorem 2

For any ring R and any R-module M, if M has an n-flat precover, then it has an n-flat cover.

Proof

It follows from Theorem 1 and [7, Theorem 2.2.8]. □

By Theorem 2, in order to find an n-flat cover for a module M, we only need to find an n-flat precover of M.

3 All Modules have n-Flat Covers

In this section, we show that over any ring R, every module M has an n-flat cover.

Consider the classes of modules

$$\begin{array}{@{}rcl@{}} \mathcal{G} &=& \{M \in \text{Mod}-R ~|~ M~ \text{ is finitely presented with p.d }~\leq n\},\\ \mathcal{F}_{n} &=& \{ M \in R-\text{Mod} ~|~ \text{Tor}_{1}(N,M) = 0~~\forall \, N \in \mathcal{G}\} \end{array} $$

and

$$\mathcal{C}_{n} = \{ M \in R-\text{Mod} ~|~ \text{Ext}^{1}(F,M) = 0~~ \forall \, F \in \mathcal{F}_{n}\}. $$

Clearly, $\mathcal {F}_{n}^{\bot } = \mathcal {C}_{n}$.

Proposition 1

$\mathcal {F}_{n}$ is closed under pure submodules.

Proof

Let $B \in \mathcal {F}_{n}$ and let $A \subseteq B$ be a pure submodule. Then, we have an exact sequence $0 \rightarrow A \rightarrow B \rightarrow B/A \rightarrow 0$. Therefore, the exact sequence $0 \rightarrow (B/A)^{+} \rightarrow B^{+} \rightarrow A^{+} \rightarrow 0$ is split and hence B ⁺≅(B/A)⁺⊕A ⁺. By [5, Lemma 5], B ⁺ is n-absolutely pure and so (B/A)⁺ and A ⁺ are n-absolutely pure. Therefore, $B/A, A \in \mathcal {F}_{n}$ by [5, Lemma 5]. □

Lemma 1

$^{\bot }\mathcal {C}_{n} = \mathcal {F}_{n}$ , i.e., $\mathcal {F}_{n}$ = $^{\bot }(\mathcal {F}_{n}^{\bot })$.

Proof

Clearly, $\mathcal{F}_n \subset^\bot(\mathcal{F}_n^\bot) = ^\bot\mathcal{C}_n$. On the other hand, for any finitely presented right R-module N with $\mathrm {p.d} \leq n, N^{+} = \text {Hom}_{\mathbb {Z}}(N, \mathbb {Q}/\mathbb {Z})$ is pure injective as a left R-module. Then, by the mixed isomorphism theorem, we have

$$0 = \text{Ext}^{1}(F, N^{+}) = \text{Ext}^{1}(F,\text{Hom}_{\mathbb{Z}}(N, \mathbb{Q}/\mathbb{Z})) \cong \text{Hom}_{\mathbb{Z}}(\text{Tor}_{1}(F,N), \mathbb{Q}/\mathbb{Z}). $$

This shows that Tor₁(F,N)=0 for any finitely presented right R-module N with p.d≤n. Hence, F is n-flat. □

Note that $(\mathcal {F}_{n}, \mathcal {F}_{n}^{\bot }(=\mathcal {C}_{n}))$ is a cotorsion theory.

Definition 3

A cotorsion theory $(\mathcal {F}_{n}, \mathcal {C}_{n})$ with $\mathcal {F}_{n}$ the class of all n-flat modules (and so $\mathcal {F}_{n}^{\bot }$ = $\mathcal {C}_{n}$ the class of all n-cotorsion modules) is called the n-flat n-cotorsion theory.

The following proposition is an analog version of Proposition 2 in [1].

Proposition 2

Let R be any ring. The n-flat n-cotorsion theory $(\mathcal {F}_{n}, \mathcal {C}_{n})$ of the category of R-modules is cogenerated by a set.

Proof

Let $F \in \mathcal {F}_{n}$. By [3, Lemma 5.3.12], Card(R)≤ℵ _β . Then, we can write F as a union of a continuous chain (F _α ) _α<λ of pure submodules of F such that Card(F ₀)≤ℵ _β and Card(F _α+1/F _α )≤ℵ _β whenever α+1<λ. If N is an R-module such that Ext¹(F ₀,N)=0 and Ext¹(F _α+1/F _α ,N)=0 whenever α+1<λ, then Ext¹(F,N)=0 by [3, Theorem 7.3.4]. Since F _α is a pure submodule of F for any α<λ, we have $F_{\alpha } \in \mathcal {F}_{n}$ by Proposition 1. On the other hand, F _α is a submodule of F _α+1 whenever α+1<λ; hence, $F_{\alpha + 1}/F_{\alpha } \in \mathcal {F}_{n}$ by Proposition 1. Let K be a set of representatives of all modules $X \in \mathcal {F}_{n}$ with Card(X)≤ℵ _β . Then, $\mathcal {F}_{n}^{\bot }$ = K ^⊥, but then, this just says that the n-flat n-cotorsion theory is cogenerated by the set K. □

Thus, the following result is a consequence of [4, Theorem 3.2.15].

Theorem 3

Over any ring R, every module admits an n-flat cover.

Proof

It follows immediately from Proposition 2 and Theorem 2. □

4 Derived Functors

In this section, we obtain some results using the main result in Section 3. Throughout this section, we assume R is a right n-coherent ring.

Theorem 4

Given an R-module M, there is an exact sequence

$$\begin{array}{@{}rcl@{}} {\cdots} \rightarrow F_{2} \rightarrow F_{1} \rightarrow F_{0} \rightarrow M \rightarrow 0 \end{array} $$

with the F _i ’s n-flat, which remains exact if we apply any functor Hom(F,−) where F is n-flat (such a sequence will be called an n-flat left resolution of M).

Proof

Given an R-module M, take F ₀ to be an n-flat precover of M. Since F ₀ and F are n-flat, we have the commutative diagram

so that $\text {Hom}(F, F_{0}) \rightarrow \text {Hom}(F, M) \rightarrow 0$ is exact. Now, we have the exact sequence $0 \rightarrow K_{1} \rightarrow F_{0} \rightarrow M \rightarrow 0$. Take F ₁ to be an n-flat precover of K ₁ which gives the commutative diagram

Thus, $\text {Hom}(F, F_{1}) \rightarrow \text {Hom}(F, F_{0}) \rightarrow \text {Hom}(F, M) \rightarrow 0$ is exact. Continuing this procedure, we obtain the exact sequence

$${\cdots} \rightarrow \text{Hom}(F, F_{2}) \rightarrow \text{Hom}(F, F_{1}) \rightarrow \text{Hom}(F, F_{0}) \rightarrow \text{Hom}(F, M) \rightarrow 0. $$

Therefore, ${\cdots } \rightarrow F_{2} \rightarrow F_{1} \rightarrow F_{0} \rightarrow M \rightarrow 0$ is an n-flat left resolution of M and Hom(F,−) is exact. □

Remark 1

Similarly, using the result [8, Theorem 3.1], we can prove for an R-module M that there is an exact sequence $0 \rightarrow M \rightarrow F^{0} \rightarrow F^{1} \rightarrow \cdots$ with F ⁱ’s n-flat, which remains exact if we apply any functor Hom(−,F) where F is n-flat (such a sequence will be called an n-flat right resolution of M).

By the method described above, we can get an n-flat resolution ${\cdots } \rightarrow F_{2} \rightarrow F_{1} \rightarrow F_{0} \rightarrow M \rightarrow 0$ for any R-module M. Using a similar argument to that for projective modules, we can show that this complex is unique up to homotopy. This leads us to get new derived functors, which are well defined. We call these $F_{n} \text {ext}^{i}(N, M)$.

Theorem 5

The $F_{n} \text {ext}^{i}(N, M)$ are well defined.

Proof

Take two different n-flat resolutions and a map $\phi \in \text {Hom}(\overline {M}, M)$. We need to show that there is a commutative diagram

and that the associated map of n-flat resolutions is unique up to homotopy. Now, F ₀ is a precover of M, so there exists $\phi _{0} : \overline {F_{0}} \rightarrow F_{0}$ which makes the following diagram commutative

Next, we find ϕ ₁ using ϕ ₀. We have the following commutative diagrams

and F ₁ is a precover of K ₁; there exists a $\phi _{1} : \overline {F_{1}} \rightarrow F_{1}$. Assume that $\phi _{0}, \phi _{1},\dots , \phi _{m-1}$ are defined. Complete the following diagram

to get a ψ _m which makes this diagram commutative, and since F _m is a precover of K _m , we have a $\phi _{m} : \overline {F_{m}} \rightarrow F_{m}$ making the diagram

commutative. This tells us that we complete the diagram. We now argue uniqueness up to homotopy, that is, from the following diagram

we can find $s_{0}, s_{1}, \dots , s_{m}, \dots ,$ with $s_{m} : \overline {F_{m}} \rightarrow F_{m+1}$, such that $\overline {\phi _{m}} - \phi _{m} = d_{m+1}s_{m} + s_{m-1} \overline {d_{m}}$, where $s_{-1} : M \rightarrow F_{0}$ is the zero map.

We know that $d_{0} \circ \overline {\phi _{0}} = \overline {d_{0}} = d_{0} \circ \phi _{0}$; thus, $d_{0} (\overline {\phi _{0}} - \phi _{0}) = 0$. Therefore, we have the diagram

which can be completed since F ₁ is an n-flat precover. Call this map s ₀, which gives $\overline {\phi _{0}}- \phi _{0} = d_{1} \circ s_{0}$.

The next step is to create an s ₁ which will complete the following diagram commutatively.

Let s ₁ be the map which completes the following diagram

Therefore, we have that

$$\begin{array}{@{}rcl@{}} d_{1}(\overline{\phi_{1}}-\phi_{1} - s_{0} \overline{d_{1}}) &=& d_{1}(\overline{\phi_{1}}- \phi_{1}) - d_{1}(s_{0} \overline{d_{1}}) \\ &=& d_{1}(\overline{\phi_{1}}- \phi_{1}) - (d_{1}s_{0}) \overline{d_{1}}\\ &=& d_{1}(\overline{\phi_{1}}- \phi_{1}) - (\overline{\phi_{0}}- \phi_{0})\overline{d_{1}}\\ &=& 0 \end{array} $$

as desired. Now, suppose that $s_{0}, \dots , s_{m-1}$ are determined. Define s _m as the completion of the following diagram

This gives the commutative diagram

Now, as desired, we have

$$\begin{array}{@{}rcl@{}} d_{m}(\overline{\phi_{m}}-\phi_{m} - s_{m-1} \overline{d_{m}}) &=& d_{m}(\overline{\phi_{m}}- \phi_{m} - s_{m-1}\overline{d_{m}})\\ &=& d_{m}(\overline{\phi_{m}}- \phi_{m}) - d_{m}(s_{m-1} \overline{d_{m}}) \\ &=& d_{m}(\overline{\phi_{m}}- \phi_{m}) - (d_{m}s_{m-1}) \overline{d_{m}}\\ &=& d_{m}(\overline{\phi_{m}}- \phi_{m}) - (\overline{\phi_{m-1}}- \phi_{m-1} - s_{m-2} \overline{d_{m-1}}) \overline{d_{m}}\\ &=& d_{m}(\overline{\phi_{m}}- \phi_{m}) - (\overline{\phi_{m-1}}- \phi_{m-1}) \overline{d_{m}} + s_{m-2} \overline{d_{m-1}d_{m}}\\ &=& 0+0, \end{array} $$

since our diagram has exact rows. Then, the similar argument for that of projective modules gives the process of proving the choice of maps and then of n-flat resolutions is unique up to homotopy. □

Let ${\cdots } \rightarrow F_{1} \stackrel {f} \rightarrow F_{0} \stackrel {g} \rightarrow M \rightarrow 0$ be an n-flat resolution of M. Applying Hom(N,−), we obtain the deleted complex

$${\cdots} \rightarrow \text{Hom}(N, F_{1}) \stackrel{f_{*}} \rightarrow \text{Hom}(N, F_{0}) \rightarrow 0. $$

Then, $F_{n} \text {ext}^{i}(N,M)$ is exactly the ith homology of the complex above. There is a canonical map

$$\sigma : F_{n}\text{ext}^{0}(N,M)=\frac{\text{Hom}(N, F_{0})}{\text{im}(f_{*})} \longrightarrow \text{Hom}(N,M) $$

defined by σ(α+im(f _∗))=g α for α∈Hom(N,F ₀).

Proposition 3

Assume M has a left $\mathcal {F}_{n}$ -resolution. Then, the following statements are equivalent:

• (1) M is n-flat.

• (2) The canonical map $\sigma : F_{n}\text {ext}^{0}(N,M) \rightarrow \text {Hom}(N,M)$ is an epimorphism for any left R-module N.

• (3) The canonical map $\sigma : F_{n}\text {ext}^{0}(M,M) \rightarrow \text {Hom}(M,M)$ is an epimorphism.

Proof

(1) ⇒ (2) is obvious by letting F ₀=M.

• (2) ⇒ (3) is trivial.

• (3) ⇒ (1) By (3), there exists α∈Hom(M,F ₀) such that σ(α+im(f _∗))=g α=1_Hom(M,M).

Thus, M is a direct summand of F ₀, and hence, it is n-flat. □

Proposition 4

The following statements are equivalent for a left R-module M:

• (1) $\mathcal {F}_{n}$ - $\dim (M) \leq 1$;

• (2) The canonical map $\sigma : F_{n}\text {ext}^{0}(N,M) \rightarrow \text {Hom}(N,M)$ is a monomorphism for any left R-module N.

Proof

(1) ⇒ (2). By (1), M has an n-flat resolution $0 \rightarrow F_{1} \rightarrow F_{0} \rightarrow M \rightarrow 0$. Thus, we get an exact sequence

$$0 \rightarrow \text{Hom}(N, F_{1}) \rightarrow \text{Hom}(N, F_{0}) \rightarrow \text{Hom}(N,M) $$

for any left R-module N. Hence, σ is a monomorphism.

• (2) ⇒ (1) Consider the exact sequence $0 \rightarrow K_{1} \rightarrow F_{0} \rightarrow M \rightarrow 0$ with F ₀ n-flat. We only need to show that K ₁ is n-flat. By [3, Theorem 8.2.3], we have the commutative diagram with exact rows:

  

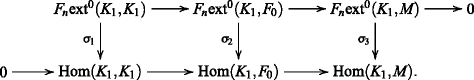
Note that σ ₂ is an epimorphism by Proposition 3 and σ ₃ is a monomorphism by (2). Thus, σ ₁ is an epimorphism by Snake lemma (see [6, Theorem 6.5]). Thus, K ₁ is n-flat by Proposition 3 and so (1) follows. □

Remark 2

From Proposition 3 and Proposition 4, we get that the canonical map

$$\sigma : F_{n}\text{ext}^{0}(N,M) \longrightarrow \text{Hom}(N,M) $$

is an isomorphism when M is n-flat and $\mathcal {F}_{n}$-$\dim (M) \leq 1$.

Proposition 5

The following statements are equivalent for a left R-module M and an integer m ≥ 2:

• (1) $\mathcal {F}_{n}$ - $\dim (M) \leq m$,

• (2) $F_{n}\text {ext}^{m+k}(N,M) = 0$ for all left R-modules N and k≥−1, and

• (3) $F_{n}\text {ext}^{m-1}(N,M) = 0$ for all left R-modules N.

Proof

(1) ⇒ (2). Let $0 \rightarrow F_{m} \rightarrow {\cdots } \rightarrow F_{0} \rightarrow M \rightarrow 0$ be an n-flat resolution of M, which induces an exact sequence $0 \rightarrow \text {Hom}(N, F_{m}) \rightarrow \text {Hom}(N, F_{m-1}) \rightarrow \text {Hom}(N, F_{m-2})$ for any left R-module N. Hence, $F_{n}\text {ext}^{m}(N,M) = F_{n}\text {ext}^{m-1}(N,M) =0$. However, it is clear that $F_{n}\text {ext}^{m+k}(N,M) = 0$ for all k≥1. Then (2) holds.

• (2) ⇒ (3) is trivial.

• (3) ⇒ (1) Let ${\cdots } \rightarrow F_{m} \rightarrow F_{m-1} \rightarrow {\cdots } \rightarrow F_{0} \rightarrow M \rightarrow 0$ be an n-flat resolution of M with $K_{m} = \ker (F_{m-1} \rightarrow F_{m-2})$. We only need to show that K _m is n-flat. In fact, we have the following exact commutative diagram:

  

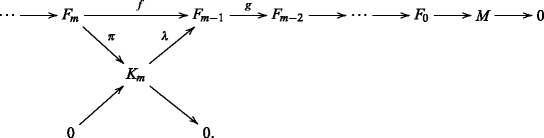
By (3), $F_{n}\text {ext}^{m-1}(K_{m}, M) =0$. Thus, the sequence

$$\text{Hom}(K_{m}, F_{m} ) \stackrel{f_{*}} \rightarrow \text{Hom}(K_{m}, F_{m-1}) \stackrel{g_{*}} \rightarrow \text{Hom}(K_{m}, F_{m-2}) $$

is exact. Since g _∗(λ)=g λ=0, $\lambda \in \ker (g_{*}) = \text {im}(f_{*})$. Thus, there exists h∈Hom(K _m ,F _m ) such that λ=f _∗(h)=f h=λ π h, and hence, π h=1 since λ is monic. Therefore, K _m is n-flat. □

Proposition 6

The following statements are equivalent for a left R-module N and an integer m ≥ 2:

• (1) The right $\mathcal {F}_{n}$ - $\dim (N) \leq m-2$,

• (2) $F_{n}\text {ext}^{m+k}(N,M) = 0$ for all left R-modules M and k≥−1, and

• (3) $F_{n}\text {ext}^{m-1}(N,M) = 0$ for all left R-modules M.

Proof

(1) ⇒ (2). Let $0 \rightarrow N \rightarrow F^{0} \rightarrow F^{1} \rightarrow {\cdots } \rightarrow F^{m-2} \rightarrow 0$ be a right $\mathcal {F}_{n}$-resolution of N. Then, we have the following complex

$$0 \rightarrow \text{Hom}(F^{m-2}, M) \rightarrow \text{Hom}(F^{m-3},M) \rightarrow {\cdots} \rightarrow \text{Hom}(F^{0},M) \rightarrow 0 $$

for any left R-module M. Hence, $F_{n}\text {ext}^{m+k}(N,M) = 0$ for all k≥−1.

• (2) ⇒ (3) is trivial.

• (3) ⇒ (1) There exists a right $\mathcal {F}_{n}$-resolution of N:

  $$0 \rightarrow N \rightarrow F^{0} \rightarrow F^{1} \rightarrow {\cdots} \rightarrow F^{m-4} \stackrel{j} \rightarrow F^{m-3}\stackrel{h} \rightarrow F^{m-2} \stackrel{f} \rightarrow F^{m-1} \stackrel{g} \rightarrow F^{m} \rightarrow \cdots $$

  with each F ⁱ n-flat. Let $\pi : F^{m-1} \rightarrow L^{m} = F^{m-1}/\text {im}(f)$ be the canonical projection, $i : L^{m} \rightarrow F^{m}$ the induced map and let f and h factor through im(f) and $\ker (f)$ respectively in obvious ways, that is, $f = \lambda f^{\prime }$ and $h = \gamma h^{\prime }$. Then, we have the following commutative diagram:

  

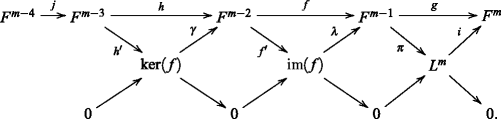
By (3), $F_{n}\text {ext}^{m-1}(N, L^{m}) = 0$. Thus, the sequence

$$\text{Hom}(F^{m}, L^{m}) \stackrel{g^{*}} \rightarrow \text{Hom}(F^{m-1}, L^{m}) \stackrel{f^{*}} \rightarrow \text{Hom}(F^{m-2}, L^{m}) $$

is exact. Since f ^∗(π)=π f=0, $\pi \in \ker (f^{*}) = \text {im}(g^{*})$. So π=g ^∗(l)=l g for some l∈Hom(F ^m,L ^m), but g=i π, and hence, π=l i π. Thus, l i=1 since π is epic, and so L ^m is n-flat. It follows that im(f) and $\ker (f)$ are n-flat. We claim that the complex

$$0 \rightarrow N \rightarrow F^{0} \rightarrow F^{1} \rightarrow {\cdots} \stackrel{j} \rightarrow F^{m-3} \rightarrow \ker(f) \rightarrow 0 $$

is a right $\mathcal {F}_{n}$-resolution of N. In fact, it is enough to show that the complex

$$0 \rightarrow \text{Hom}(\ker(f), G) \stackrel{(h^{\prime})^{*}} \rightarrow \text{Hom}(F^{m-3}, G) \stackrel{j^{*}} \rightarrow \text{Hom}(F^{m-4}, G) $$

is exact for any n-flat left R-module G. Note that we have the following exact commutative diagram:

Therefore, $\ker ((h^{\prime })^{*}\gamma ^{*}) = \ker (h^{*}) = \text {im}(f^{*}) = \text {im}((f^{\prime })^{*}\lambda ^{*}) = \text {im}(f^{\prime })^{*} = \ker (\gamma ^{*})$. Let $\alpha \in \ker (h^{\prime })^{*}$. Since γ ^∗ is epic, α=γ ^∗(β) for some β∈Hom(F ^m−2,G). Thus, $(h^{\prime })^{*}\gamma ^{*}(\beta ) = (h^{\prime })^{*}(\alpha ) = 0$, and hence, α=γ ^∗(β)=0. It follows that $(h^{\prime })^{*}$ is monic. On the other hand, $\ker (j^{*}) = \text {im}(h^{*}) = \text {im}((h^{\prime })^{*})$, so we obtain the desired exact sequence. This completes the proof. □