Abstract
This article addresses the question of what properties can be monitored over an unreliable communication channel. We model unreliable communications as mutations to finite traces and define what it means for a property to be immune to such a mutation. We also introduce the idea of a trustworthy verdict, which is a verdict guaranteed to be correct in the presence of a trace mutation. We show that the trustworthiness of a verdict or immunity of a property for a single mutation is equivalent to the trustworthiness or immunity for any number of mutations. We classify trustworthy verdicts on \(\omega \)-regular properties by updating a recently proposed monitorability-focused refinement of the safety-liveness taxonomy. The article also includes a fixed-parameter tractable algorithm to test an \(\omega \)-regular property for immunity to a trace mutation. Our results show that many of the most common properties can be monitored over unreliable channels.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In Runtime Verification (RV), the correctness of a program execution is determined by another program, called a monitor. In some cases, monitors run remotely from the systems they monitor, either due to resource constraints or for dependability. For example, ground stations monitor a spacecraft, while an automotive computer may monitor emissions control equipment. In both cases, the program being monitored must transmit data to a remote monitor.
Communication between the program and monitor may not always be reliable, however, leading to incorrect or incomplete results. For example, data from the Mars Science Laboratory (MSL) rover are received out of order, and some low priority messages may arrive days after being sent [29]. Even dedicated debugging channels like ARM Embedded Trace Macrocell (ETM) have finite bandwidth and may lose data during an event burst [6]. Some works in the field of (RV) have begun to address the challenges of imperfect communication, but the problem has been largely ignored in the study of monitorability.
Our recent work introduced a definition for a property to be considered monitorable over an unreliable channel [41]. We defined common mutations that may occur to a trace and provided a decision procedure to test \(\omega \)-regular properties for monitorability over a channel with such a mutation. This article expands on that work by defining when a property can be unmonitorable over an unreliable channel but still have value to monitor. We also provide a classification of properties that may be monitored over certain unreliable channels.
The article is organized as follows. We first define notation used throughout the article in Sect. 2. We then introduce foundations necessary for understanding the article in Sect. 3, first examining the concept of uncertainty in monitoring in Sect. 3.1 and then reviewing common notions of monitorability in Sect. 3.2. We then define common trace mutations due to unreliable channels in Sect. 4. In Sect. 5, we describe what makes a property immune to a trace mutation and how that relates to monitorability. Section 6 expands on that idea by defining how a verdict for a property may be trustworthy over an unreliable channel even when the property is not immune to the channel’s mutation. We then review and augment the Finitely Refutable/Finitely Satisfiable property classification in Sect. 7 by adding subclasses relevant to common mutations. We use this augmented classification to categorize properties with trustworthy verdicts over those mutations in Sect. 8 including a discussion of the utility of such properties in Sect. 8.5. We work toward a decision procedure for the immunity of an \(\omega \)-regular property by mapping the definition of immunity to a property of derived monitor automata in Sect. 9. Finally, we present a decision procedure for the immunity of an automaton to a mutation and prove it correct in Sect. 10. We then present related work in Sect. 11. Section 12 discusses some of the conclusions from the article and possible future work.
2 Preliminary notation
We use \(\mathbb {N}\) to denote the set of all natural numbers including zero and \(\infty \) to denote infinity. We write \(\bot \) to denote \(\textit{false}\) and \(\top \) to denote \(\textit{true}\).
In this work, we consider both finite and infinite sequences. A finite sequence \(\sigma \) of n values is written \(\sigma = \langle v_1, \ldots , v_n \rangle \) where both \(v_i\) and \(\sigma (i)\) mean the i’th item in the sequence. In this work, sequence index numbers begin at one. The notation \(\langle v_1, v_2, \cdots \rangle \) is used to denote either an infinite sequence or a finite sequence of indeterminate length. A value x is in a sequence \(\sigma \), denoted by \(x \in \sigma \), iff \(\exists \ i\ \in \ \mathbb {N}\) such that \(\sigma (i) = x\). The length of a sequence \(\sigma \) is written \(|\sigma | \in \mathbb {N}\cup \{\infty \}\). The suffix of a sequence \(\sigma \) beginning at the i’th item in the sequence is written \(\sigma ^i\). The concatenation of two sequences \(\sigma , \tau \) is written \(\sigma \cdot \tau \) where \(\sigma \) is finite and \(\tau \) is either finite or infinite. A finite sequence u is a prefix of a finite or infinite sequence \(\sigma \), written \(u \sqsubseteq \sigma \), iff there exists a sequence v such that \(u \cdot v = \sigma \).
We denote the cross product of A and B as \(A \times B\) and the set of total functions from A to B as \(A \rightarrow B\). Given a set S, \(S^*\) denotes the set of finite sequences over S where each sequence element is in S, \(S^{\omega }\) denotes the set of infinite sequences of such elements, and \({S^{\infty } = S^* \cup S^\omega }\). Given a set S, we write \(2^{S}\) to mean the set of all subsets of S. The cardinality of a set S is written |S|. A map is a partial function  where K is a domain of keys mapped to the set V of values. We write \(M(k) \leftarrow v\) to denote M updated with k mapped to v. AP is a finite, non-empty set of atomic propositions. Throughout the work, we assume an alphabet, denoted \(\varSigma = 2^{\text {AP}}\). An element of the alphabet is a symbol \(s \in \varSigma \). A trace, word, or string is a sequence of symbols. A language, or a property, is a set of words. A trace \(\sigma \in \varSigma ^\infty \) satisfies a property \(\mathcal {L}\subseteq \varSigma ^\infty \) if \(\sigma \in \mathcal {L}\) or violates it if \(\sigma \notin \mathcal {L}\).
where K is a domain of keys mapped to the set V of values. We write \(M(k) \leftarrow v\) to denote M updated with k mapped to v. AP is a finite, non-empty set of atomic propositions. Throughout the work, we assume an alphabet, denoted \(\varSigma = 2^{\text {AP}}\). An element of the alphabet is a symbol \(s \in \varSigma \). A trace, word, or string is a sequence of symbols. A language, or a property, is a set of words. A trace \(\sigma \in \varSigma ^\infty \) satisfies a property \(\mathcal {L}\subseteq \varSigma ^\infty \) if \(\sigma \in \mathcal {L}\) or violates it if \(\sigma \notin \mathcal {L}\).
In this work, we use Finite Automaton (FAs) to represent both regular and \(\omega \)-regular languages. We use (NBAs) to represent \(\omega \)-regular languages, which accept infinite strings, and (NFAs) to represent regular languages, which accept finite strings. Both NBA and NFA are written \(\mathcal {A} = (Q, \varSigma , q_0, \delta , F)\), where Q is the set of states, \(\varSigma \) is the alphabet, \(q_0 \in Q\) is the initial state, \(\delta : Q \times \varSigma \rightarrow 2^{Q}\) is the transition function, and \(F \subseteq Q\) is the set of accepting states. The two types of FAs differ in their accepting conditions.
A path (or run) through FA \(\mathcal {A}\) from a state \({q \in Q}\) over a word \({\sigma \in \varSigma ^\infty }\) is a sequence of states \({\pi = \langle q_1, q_2, \cdots \rangle }\) such that \({q_1 = q}\) and \({q_{i+1} \in \delta (q_i,\sigma _i)}\). We write \({\mathcal {A}(q, \sigma )}\) to denote the set of all runs on \(\mathcal {A}\) starting at state q with the word \(\sigma \). The set of all reachable states in FA \(\mathcal {A}\) from a starting state \(q_0\) is denoted  .
.
A finite run on NFA \(\pi = \langle q_1, q_2, \ldots , q_n \rangle \) is considered accepting if \(q_n \in F\). For an infinite run \(\rho \) on NBA, we use \(\textit{Inf}(\rho ) \subseteq Q\) to denote the set of states that are visited infinitely often, and the run is considered accepting when \(\textit{Inf}(\rho ) \cap F \ne \varnothing \). \(\text {L}(\mathcal {A})\) denotes the language accepted by FA \(\mathcal {A}\). The complement or negation of FA \(\mathcal {A} = (Q, \varSigma , q_0, \delta , F)\) is written \(\overline{\mathcal {A}}\) where \(\text {L}(\mathcal {\overline{A}}) = \varSigma ^* \setminus \text {L}(\mathcal {A})\) for NFAs and \(\text {L}(\mathcal {\overline{A}}) = \varSigma ^\omega \setminus \text {L}(\mathcal {A})\) for NBAs.
NFA is Deterministic Finite Automaton (DFA) iff  . Given DFA \((Q,\varSigma ,q_0,\delta ,F)\), a state \(q \in Q\), and a finite string \({\sigma \in \varSigma ^*}\) where \({|\sigma | = n}\), the terminal (nth) state of the run over \(\sigma \) beginning in q is given by the function \({\delta ^* : Q \times \varSigma ^* \rightarrow Q}\).
. Given DFA \((Q,\varSigma ,q_0,\delta ,F)\), a state \(q \in Q\), and a finite string \({\sigma \in \varSigma ^*}\) where \({|\sigma | = n}\), the terminal (nth) state of the run over \(\sigma \) beginning in q is given by the function \({\delta ^* : Q \times \varSigma ^* \rightarrow Q}\).
We use Linear Temporal Logic (LTL) formulae throughout the article to illustrate examples of properties because it is a common formalism in the RV area. The syntax of these formulae is defined by the following inductive grammar where p is an atomic proposition, U is the Until operator (\(\varphi \ U \psi \) means \(\psi \) must eventually hold and \(\varphi \) must hold until then), and X is the Next operator (\(X \varphi \) means \(\varphi \) must hold in the next state, which must exist).
We use the following inductive semantics for the infinite case, where \({\sigma \in \varSigma ^\omega }\). The reader should assume the use of infinite-trace semantics unless otherwise specified where LTL is found in this article.

The language of LTL formula \(\varphi \) is given in the infinite case by \({L[\![\varphi ]\!] = \{ \sigma \in \varSigma ^\omega : \sigma \models \varphi \}}\).
For the finite case, where \({\sigma \in \varSigma ^*}\), we use the following inductive semantics.

The language of LTL formula \(\varphi \) is given in the finite case by \({L_{F}[\![\varphi ]\!] = \{ \sigma \in \varSigma ^* : \sigma \models \varphi \}}\).
For both infinite and finite-trace semantics we also define the standard notation: \(\textit{true} = p \vee \lnot p\) for any proposition p, \(\textit{false} = \lnot \textit{true}\), \(\varphi \wedge \psi = \lnot (\lnot \varphi \vee \lnot \psi )\), \(\varphi \rightarrow \psi = \lnot \varphi \vee \psi \), \(F \varphi = \textit{true}\ U \varphi \) (eventually \(\varphi \)), and \(G \varphi = \lnot F \lnot \varphi \) (globally \(\varphi \)).
Example
Consider an infinite trace \(\sigma \) where p holds for the entire trace except the tenth symbol, which is the only symbol where q holds. The LTL formula Gp is violated for \(\sigma \) in the infinite case, and it is violated in the finite case for prefixes of \(\sigma \) of at least length ten. The formula is satisfied; however, in the finite case for prefixes of \(\sigma \) of length less than ten. Likewise, the LTL formula Fq is satisfied for \(\sigma \) in the infinite case and in the finite case for prefixes of \(\sigma \) of at least length ten. It is violated for prefixes of \(\sigma \) of length less than ten.
3 Foundations of monitoring
In this section, we establish definitions from previous works referenced in the article. We begin with the truth domains we use and how they relate to monitoring. We then provide traditional definitions of monitorability.
3.1 Uncertainty
In RV, there are two prevailing options for checking that a trace of a program’s execution satisfies a property: offline and online. In offline RV, we consider a finite trace produced by a program that has terminated. In this case, properties are specified as languages of finite words, for example, using a finite-trace semantics to interpret LTL formulae. In online RV, we consider a continuously expanding finite prefix produced by a running program. In this case, properties are specified as languages of infinite words, for example, using an infinite-trace semantics to interpret LTL formulae.
In this work, we are interested in checking finite prefixes of execution traces against properties specified as languages of infinite words. We say a finite string determines inclusion in (or exclusion from) a language of infinite words only if all infinite extensions of the prefix are in (or out of) the language. If some infinite extensions are in the language and some are out, then the finite prefix does not determine inclusion and the result is uncertainty. The problem appears with an LTL property such as Fa, which is satisfied if an a appears in the string. However, if no a has yet been observed, and the program is still executing, it is unknown if the specification will be satisfied in the future.
To express notions of uncertainty in monitoring languages of infinite words, extensions to the Boolean truth domain \(\mathbb {B}_{2}= \{\top , \bot \}\) have been proposed. \(\mathbb {B}_{3}\) adds a third verdict of \({{\varvec{?}}}\) to the traditional Boolean notion of \(\textit{true}\) or \(\textit{false}\) to represent the idea that the specification is neither satisfied nor violated by the current finite prefix [13]. \(\mathbb {B}_{4}\) replaces \({{\varvec{?}}}\) with presumably true (\(\top _p\)) and presumably false (\(\bot _p\)) to provide more information on what has already been seen [14].
The verdicts \(\top _p\) and \(\bot _p\) differentiate between prefixes that would satisfy or violate the property interpreted with finite trace semantics. The intuition is that \(\bot _p\) indicates that something is required to happen in the future, while \(\top _p\) means there is no such outstanding event. For example, if the formula \(G(a \rightarrow Fb)\) is interpreted as four-value LTL (LTL4) (also called Runtime Verification LTL (RV-LTL) [14], which uses \(\mathbb {B}_{4}\)), the verdict on a trace \(\langle \{c\} \rangle \) is \(\top _p\) because a has not occurred, and therefore, no b is required, while the verdict on \(\langle \{a\} \rangle \) is \(\bot _p\) because there is an a but as yet no b. If the same property is interpreted as three-value LTL (LTL3) (which uses \(\mathbb {B}_{3}\)), the verdicts on both traces would be \({{\varvec{?}}}\).
The above intuitions are formalized in Definition 1. Here, we define a property \(\mathcal {L}\) to be a set of both finite and infinite traces. The infinite words determine the permanent verdicts of \(\top \) and \(\bot \) while the finite words are used in the \(\mathbb {B}_{4}\) case to choose between \(\top _p\) and \(\bot _p\). For both \(\mathbb {B}_{3}\) and \(\mathbb {B}_{4}\), Definition 1 includes a function that evaluates a finite trace prefix with respect to \(\mathcal {L}\).
Definition 1
(Evaluation Functions) Given a property \(\mathcal {L}\subseteq \varSigma ^\infty \) for each of the truth domains \({\mathbb {V}\in \{ \mathbb {B}_{3}, \mathbb {B}_{4}\}}\), we define evaluation functions of the form  as follows.
as follows.
For \(\mathbb {B}_{3}= \{\bot , {{\varvec{?}}}, \top \}\),

For \(\mathbb {B}_{4}= \{\bot , \bot _{p}, \top _{p}, \top \}\),

Example
Suppose we would like to monitor the LTL formula \({\varphi = G(a) \vee b}\) using the \(\mathbb {B}_{4}\) truth domain. The language (property) to monitor is \(\mathcal {L}= L[\![\varphi ]\!] \cup L_{F}[\![\varphi ]\!]\). The following are the evaluations for given finite prefixes:

Monitors also exist for properties that cannot be specified in LTL or other common temporal logics. This work uses language-theoretic formalisms that allow for the monitoring of any language of finite and infinite words. For example, it is possible to monitor a property consisting of an infinite repetition of every valid C program. Clearly, such a language is not representable in LTL since recognizing it requires a stack. For the verdicts specified in Definition 1 for  to make intuitive sense, the infinite and finite words in the language must be related. For an LTL formula \(\varphi \), the infinite words are defined by \(L[\![\varphi ]\!]\) and the finite words by \(L_{F}[\![\varphi ]\!]\). Given a language of finite words, Falcone et al. defined how to construct both the finite words and infinite words in [31]. In the general case, however, the precise relationship between the two subsets has not been defined. This relationship remains a subject for future work on monitoring non-\(\omega \)-star-free languages.
to make intuitive sense, the infinite and finite words in the language must be related. For an LTL formula \(\varphi \), the infinite words are defined by \(L[\![\varphi ]\!]\) and the finite words by \(L_{F}[\![\varphi ]\!]\). Given a language of finite words, Falcone et al. defined how to construct both the finite words and infinite words in [31]. In the general case, however, the precise relationship between the two subsets has not been defined. This relationship remains a subject for future work on monitoring non-\(\omega \)-star-free languages.
Introducing the idea of uncertainty in monitoring causes the possibility that some properties might never reach a definite, \(\textit{true}\) or \(\textit{false}\) verdict. A monitor that will only ever return a \({{\varvec{?}}}\) result does not have much utility. The monitorability of a property captures this notion of the reachability of definite verdicts.
3.2 Monitorability
In this section, we examine the four most common definitions of monitorability. To define monitorability for properties over unreliable channels, we must first define monitorability for properties over ideal channels. Rather than choose one definition, we introduce established definitions and allow the reader to select that of their preference.
We begin with the definition of \(\sigma \)-Monitorability, which depends not only on the monitored property but also on the already-seen trace prefix. For each definition of monitorability that depends only upon the monitored property \({\mathbb {M}\in \{\text {C(lassical), W(eak), A(lternative)}\}}\), we introduce an evaluation predicate of the form  that returns \(\textit{true}{}\) iff the input property is monitorable. We say that an LTL formula \(\varphi \) is monitorable if its language \(L[\![\varphi ]\!] \cup L_{F}[\![\varphi ]\!]\) is monitorable.
that returns \(\textit{true}{}\) iff the input property is monitorable. We say that an LTL formula \(\varphi \) is monitorable if its language \(L[\![\varphi ]\!] \cup L_{F}[\![\varphi ]\!]\) is monitorable.
3.2.1 \(\sigma \)-Monitorability
Pnueli and Zaks introduced the first formal definition of monitorability in their work on Property Specification Language (PSL) for model checking in 2006 [52]. They define monitorable properties given a trace prefix \(\sigma \). Subsequent works all define monitorability for a property without assuming knowledge of any part of the trace.
Definition 2
(\(\sigma \)-Monitorability) Given a finite sequence \(\sigma \in \varSigma ^*\), a property \({\mathcal {L}\subseteq \varSigma ^\infty }\) is \(\sigma \)-monitorable iff  or \({\sigma \cdot \eta \cdot s \not \models \mathcal {L})}\).
or \({\sigma \cdot \eta \cdot s \not \models \mathcal {L})}\).
That is, there exists another finite sequence \(\eta \) such that \(\sigma \cdot \eta \) determines inclusion in or exclusion from \(\mathcal {L}\).
For example, the LTL formula GFp is non-\(\sigma \)-monitorable for any finite prefix, because the trace needed to determine the verdict must be infinite. Other properties are \(\sigma \)-monitorable for some prefixes but not others. For example, there is no point to continuing to monitor \(GFp \vee q\) if q does not hold in the first symbol of the trace.
3.2.2 Classical monitorability
Bauer, Leuker, and Schallhart reformulated this definition of monitorability and proved that safety (e.g., Gp) and guarantee (e.g., Fp) properties represent a proper subset of the class of monitorable properties [15]. It was already known that the class of monitorable properties was not limited to safety and guarantee properties from the work of d’Amorim and Roşu on monitoring \(\omega \)-regular languages [24], however that work did not formally define monitorability. Diekert and Leuker have also defined a purely topological version of this definition of monitorability [26].
The definition of monitorability given by Bauer et al. is identical to Definition 2, except that it considers all possible trace prefixes instead of a specific prefix [30, 31] and it excludes languages with finite words. The restriction to infinite words is due to their interest in defining monitorable \(\hbox {LTL}_{3}\) properties, which only considers infinite traces.
Bauer et al. use Kupferman and Vardi’s definitions of good and bad prefixes of an infinite trace [42] to define what they call an ugly prefix. That is, given a language of infinite strings \(\mathcal {L}\subseteq \varSigma ^\omega \),
-
a finite word \(b \in \varSigma ^*\) is a bad prefix for \(\mathcal {L}\) iff
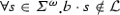 , and
, and -
a finite word \(g \in \varSigma ^*\) is a good prefix for \(\mathcal {L}\) iff
 .
.
Bauer et al. use good and bad prefixes to define ugly prefixes and then use ugly prefixes to define Classical Monitorability.
Definition 3
(Ugly Prefix) Given a language of infinite strings \(\mathcal {L}\subseteq \varSigma ^\omega \), a finite word \(u \in \varSigma ^{*}\) is an ugly prefix for \(\mathcal {L}\) iff  is either a good or bad prefix.
is either a good or bad prefix.
Definition 4
(Classical Monitorability) Given a language of infinite strings \(\mathcal {L}\subseteq \varSigma ^{\omega }\),

Many works have explored decision procedures for Classical Monitorability. Diekert, Muscholl, and Walukiewicz proved that the problem is PSPACE-Hard and can be solved in EXPSPACE [27] for \(\omega \)-regular languages. This result was most recently refined by Peled and Havelund, who showed that deciding Classical Monitorability for these languages is EXPSPACE-Complete [49].
3.2.3 Weak monitorability
Recently, both Chen et al. [21] and Peled and Havelund [49] proposed a weaker definition of monitorability that includes more properties than the Classical definition. They observed that there are properties that are classically non-monitorable, but that are still useful to monitor. For example,  because any trace that begins with a must then satisfy or violate GFa, which is not possible. However, \(a \wedge GFa\) is violated by traces that do not begin with a, so it may have some utility to monitor.
because any trace that begins with a must then satisfy or violate GFa, which is not possible. However, \(a \wedge GFa\) is violated by traces that do not begin with a, so it may have some utility to monitor.
Definition 5
(Weak Monitorability) Given a language of infinite strings \(\mathcal {L}\subseteq \varSigma ^{\omega }\),

Deciding that an \(\omega \)-regular property is Weakly Monitorable requires testing that no information may be obtained from the monitor. Peled and Havelund gave an algorithm for deciding Weak Monitorability for these languages and showed that it is EXPSPACE-Complete [49].
3.2.4 Alternative monitorability
Falcone et al. observed that the class of monitorable properties should depend on the truth domain of the monitored formula. However, they noticed that changing from \(\mathbb {B}_{3}\) to \(\mathbb {B}_{4}\) does not influence the set of monitorable properties under classical monitorability [30, 31]. To resolve this perceived shortcoming, the authors of [30, 31] introduce an alternative definition of monitorability. They introduce the notion of an r-property (runtime property) which separates the property’s language of finite and infinite traces into disjoint sets. We do not require this distinction and treat the property as a single set containing both finite and infinite traces. Falcone et al. then define an alternative notion of monitorability for a property using a variant of Definition 1.
Definition 6
(Alternative Monitorability) Given a truth domain \(\mathbb {V}\) and an evaluation function for \(\mathbb {V}\),  and a property \({\mathcal {L}\subseteq \varSigma ^\infty }\),
and a property \({\mathcal {L}\subseteq \varSigma ^\infty }\),



Definition 6 says that, given a truth domain, a property with both finite and infinite words is monitorable if evaluating the finite strings in the property always yield different verdicts from evaluating the finite strings out of the property. By Definition 6, only properties with finite words are considered monitorable and its results must be understood in the same context as  , where finite words identify prefixes where no outstanding event precludes satisfaction.
, where finite words identify prefixes where no outstanding event precludes satisfaction.
Procedures for deciding if an \(\omega \)-regular property is Alternatively Monitorable depend on the truth domain. For \(\mathbb {B}_{3}\), monitorable properties are exactly the union of Safety and Guarantee properties (see Sect. 8) [31]. Determining inclusion in these classes is known to be PSPACE-Complete [55]. For \(\mathbb {B}_{4}\), monitorable properties are the Reactivity properties, which are all properties representable in LTL [31]. Deciding if a language represented as an NBA is a Reactivity property is PSPACE-Complete [25].
4 Unreliable channels
For a property to be monitorable over an unreliable channel, it must be monitorable over ideal channels, and it must reach the correct verdict despite the unreliable channel. To illustrate this, we introduce an example.
4.1 An example with unreliable channels
Consider the LTL formula \(\varphi = Fa\) over the alphabet \({\varSigma = \{\{a\},\{\lnot a\}\}}\). That is, all traces that contain at least one symbol with a satisfy \(\varphi \). We assume that the trace is monitored remotely, and, for this example, we will adopt a \(\mathbb {B}_{3}\) truth domain. Using  from Definition 1, the verdict on finite prefixes without an a, is \({{\varvec{?}}}\), while the verdict when an a is included is \(\top \). Figure 1a shows the NBA for such a property.
from Definition 1, the verdict on finite prefixes without an a, is \({{\varvec{?}}}\), while the verdict when an a is included is \(\top \). Figure 1a shows the NBA for such a property.
4.1.1 Monitorability under reordering
Suppose that the channel over which the trace is transmitted may reorder events. That is, events are guaranteed to be delivered, but not necessarily in the same order in which they were sent.
We argue that Fa should be considered monitorable over a channel that reorders the trace. First, the property is monitorable over an ideal channel (see Sect. 3.2). Second, given any trace prefix, reordering the prefix would not change the verdict of a monitor. Any a in the trace will cause a transition to state \(q_2\), regardless of its position.
Note that we are not concerned with when the verdict occurs. For example, assume a trace \(\langle \{a\},\{\lnot a\} \rangle \) that is reordered to \(\langle \{\lnot a\},\{a\} \rangle \). Both traces result in a \(\mathbb {B}_{3}\) verdict of \(\top \), but in the reordered case it comes one symbol later. This article considers these results to be equivalent, but future work could consider the implications of such a change in timing.
4.1.2 Monitorability under loss
Now suppose that, instead of reordering, the channel over which the trace is transmitted may lose events. That is, the order of events is guaranteed to be maintained, but some events may be missing from the trace observed by the monitor.
We argue that Fa should not be considered monitorable over a channel that loses events, even though the property is deemed to be monitorable over an ideal channel. It is possible for the verdict from the monitor to be different from what it would be given the original trace. For example, assume a trace \(\langle \{a\}, \{\lnot a\} \rangle \). For this trace, the verdict from \(\hbox {ltl}_3\) monitor would be \(\top \). However, if the first symbol (containing a) is lost, the verdict would be \({{\varvec{?}}}\).
Note that there may still be some utility to monitor Fa when symbols may be lost because a \(\top \) verdict is actionable. That is, if the monitor receives a trace \(\langle \{a\} \rangle \) then a must have held in the original trace as well. In this case, we call \(\top \) a trustworthy verdict. We explore the concept of trustworthy verdicts in Sect. 6.
4.2 Trace mutations
To model unreliable channels, we introduce trace mutations. A mutation represents the possible modifications to traces from communication over unreliable channels. These mutations are defined as relations between unmodified original traces and their mutated counterparts. Trace mutations include only finite traces because only finite prefixes may be mutated in practice.
There are four trace mutations \({\mathcal {M}^k \subseteq \varSigma ^* \times \varSigma ^*}\) where \(\mathcal {M}\) denotes any of the relations in Definitions 7, 8, 9, and 10 or a union of any number of them, and k denotes the number of inductive steps.
Definition 7
(Loss Mutation)

Definition 8
(Corruption Mutation)

Definition 9
(Stutter Mutation)

Definition 10
(Out-of-Order Mutation)

Definition 11
(Inductive \(k\)-Mutations) Given any mutation or union of mutations \(\mathcal {M}\), we define \(\mathcal {M}^{k}\) inductively as follows.

These mutations are based on Lozes and Villard’s interference model [48]. Other works on the verification of unreliable channels, such as [19], have chosen to include insertion errors instead of \(\textit{Corruption}\) and \(\textit{OutOfOrder}\). We prefer to define \(\textit{Corruption}\) and \(\textit{OutOfOrder}\) because the mutations more closely reflect our real-world experiences. For example, packets sent using the User Datagram Protocol (UDP) may be corrupted or arrive out-of-order, but packets must be sent before these mutations occur.
In this work, we assume that the monitor has no information about how a received trace has been modified by an unreliable channel. Instead, we only permit that the channel is known to sometimes mutate traces in a certain manner (e.g., losing symbols). This differs from and is a weaker assumption than some other works, where trace modifications are marked [11, 34, 40, 45].
We say a mutation M is prefix-assured when \(\forall (\sigma ,\sigma ') \in M\) such that \(|\sigma | > 1\), \(\exists (\sigma _p,\sigma _p') \in M\), where \(\sigma _p \sqsubseteq {} \sigma \) and \(\sigma _p' \sqsubseteq {} \sigma '\). All mutations \(\mathcal {M}^1\) are prefix-assured. Combining mutations is possible under Definition 11, and it is possible to form any combination of strings by doing so. This capability is important to ensure the mutation model is complete.
Definitions 7 through 10 include every possible mutation. That is, it is possible to apply a combination of these mutations to a trace to transform it into any other trace.
Theorem 1
(Completeness of Mutations) Given any two sets of non-empty traces \({S,S' \subseteq \varSigma ^* \setminus \{\varepsilon \}}\),  .
.
Proof
First, Definition 8 allows an arbitrary symbol in a string to be changed to any other symbol. Thus, \({\forall \sigma ' \in \varSigma ^*}\) there exists \({\sigma : (\sigma , \sigma ') \in \textit{Corruption}^{n}}\) where \({|\sigma | = |\sigma '|}\) and \({n \ge |\sigma |}\). A string can also be lengthened or shortened arbitrarily, so long as it is non-empty. Definition 9 allows lengthening, because \({\textit{Stutter}(\sigma , \sigma ') \implies |\sigma | < |\sigma '|}\), while Definition 7 allows shortening, because \({\textit{Loss}(\sigma , \sigma ')\!\implies |\sigma |{>}|\sigma '|}\). \(\square \)
These mutations are general and it may be useful for practitioners to define their own, more constrained mutations based on domain knowledge. For example, if a communications protocol guarantees delivery of high priority messages but allows low priority messages to be lost, this can be modeled as a mutation. Some properties may be monitorable over this more-precise mutation when they would not be monitorable over the \(\textit{Loss}\) mutation, which permits losing any message.
Even Definition 10 (\(\textit{OutOfOrder}\)) is a more-constrained version of the \(\textit{Corruption}\) mutation. That is, \(\textit{OutOfOrder}^n \subset \textit{Corruption}^{2n}\ \forall n \in \mathbb {N}\). \(\textit{OutOfOrder}\) is unnecessary for the completeness of the mutation model, as can be seen in Theorem 1. However, we consider the mutation to be general enough to include here, and a combination of Definitions 7, 8, and 9 can only over-approximate the \(\textit{OutOfOrder}\) relation.
5 Immunity to trace mutations
The two requirements for a property to be monitorable over an unreliable channel are that the property is monitorable over an ideal channel and that the property is immune to the effects of the unreliable channel. A monitor must be able to reach a meaningful, actionable verdict for a trace prefix, and the verdict must also be correct. If a monitored property is immune to a mutation, then we can trust the monitor’s verdict whether or not the observed trace is mutated.
The notion of immunity to a mutation is related to the concept of monotonicity of entailment of a logical system. For a monotonic logic, anything that could be concluded before information is added can still be concluded after. In this case, however, mutations to a trace may remove or modify information as well as add. Monotonicity of a property with regard to past events was also previously defined by Joshi, Tchamgoue, and Fischmeister for channels with \(\textit{Loss}\) to mean that the property’s monitor cannot change its verdict if lost information is added to the trace [40]. Monotonicity has also been used in RV in the sense of a monotone function to describe how verdicts like \(\top \) and \(\bot \) may not change once reached [22]. Here, we use the term immunity to avoid overloading the word monotonic further in the field of RV.
Definition 12 characterizes properties where the given trace mutation will have no effect on the evaluation verdict. For example, the LTL formula Fa from Fig. 1a is immune to \(\textit{OutOfOrder}^{1}\) (an LTL formula \(\varphi \) is immune to a mutation \(\mathcal {M}^k\) if its language \(L[\![\varphi ]\!] \cup L_{F}[\![\varphi ]\!]\) is immune to \(\mathcal {M}^k\)) with truth domain \(\mathbb {B}_{3}\) or \(\mathbb {B}_{4}\) because reordering the input trace cannot change the verdict.
Definition 12
(Full Immunity to Unreliable Channels) Given a property \(\mathcal {L}\subseteq \varSigma ^\infty \), a trace mutation \({\mathcal {M}^k \subseteq \varSigma ^* \times \varSigma ^*}\), a truth domain \(\mathbb {V}\), and an evaluation function  is immune to \(\mathcal {M}^k\) iff
is immune to \(\mathcal {M}^k\) iff  .
.
Example
We want to check if the LTL formula \({\varphi = Ga}\) is immune to the \(\textit{Stutter}^1\) mutation for truth domain \(\mathbb {B}_{4}\). The property for this formula is \({\mathcal {L}= L[\![\varphi ]\!] \cup L_{F}[\![\varphi ]\!]}\). \(\mathcal {L}\) is immune to \(\textit{Stutter}^1\) for \(\mathbb {B}_{4}\) iff the verdict from  is always the same when applied to both the left and right sides of every pair in \(\textit{Stutter}^1\). Where \(\varSigma = \{\{a\},\{\lnot a\}\}\), we check the following:
is always the same when applied to both the left and right sides of every pair in \(\textit{Stutter}^1\). Where \(\varSigma = \{\{a\},\{\lnot a\}\}\), we check the following:
-

-

-

-

-
\(\cdots \)
If every pair has an equal verdict, then \(\mathcal {L}\) (and \(\varphi \)) is immune to \(\textit{Stutter}^1\) for \(\mathbb {B}_{4}\).
Definition 12 specifies a \(k\)-Mutation from Definition 11, but a property that is immune to a mutation for some k is immune to that mutation for any k. This significant result forms the basis for checking for mutation immunity in Sect. 10. The intuition is that, since we assume any combination of symbols in the alphabet is a possible ideal trace, and a mutation could occur at any time, one mutation is enough to violate immunity for any vulnerable property.
Theorem 2
(Single Mutation Immunity Equivalence) Given a property \(\mathcal {L}\subseteq \varSigma ^\infty \), a trace mutation \(\mathcal {M} \subseteq \varSigma ^* \times \varSigma ^*\), and a number of applications of that mutation k, \(\mathcal {L}\) is immune to \(\mathcal {M}^k\) iff \(\mathcal {L}\) is immune to \(\mathcal {M}^1\).
Proof
Since \(k\)-Mutations are defined inductively, Theorem 2 is equivalent to the statement that \(\mathcal {L}\) is immune to \(\mathcal {M}^{k+1}\) iff \(\mathcal {L}\) is immune to \(\mathcal {M}^{k}\). Now assume by way of contradiction a property \({\mathcal {L}_{\text {bad}} \subseteq \varSigma ^\infty }\) such that \(\mathcal {L}_{\text {bad}}\) is immune to some \(k\)-Mutation \(M^k\) but not to \(M^{k+1}\). That is, given a truth domain \(\mathbb {V}\), there exists a pair of traces \((\sigma _{1},\sigma _{3}) \in M^{k+1}\) such that  . From Definition 11, either \((\sigma _{1},\sigma _{3}) \in M^k\), or there exists both \((\sigma _1,\sigma _2) \in \mathcal {M}^k\) and \((\sigma _2,\sigma _3) \in \mathcal {M}^1\) such that
. From Definition 11, either \((\sigma _{1},\sigma _{3}) \in M^k\), or there exists both \((\sigma _1,\sigma _2) \in \mathcal {M}^k\) and \((\sigma _2,\sigma _3) \in \mathcal {M}^1\) such that  . It cannot be true that \((\sigma _1,\sigma _3) \in M^k\) since \({\mathcal {L}_{\text {bad}}}\) is immune to \(M^k\) so there must exist pairs \({(\sigma _1,\sigma _2) \in \mathcal {M}^k}\) and \({(\sigma _2,\sigma _3) \in \mathcal {M}^1}\). Since \(\mathcal {L}_{\text {bad}}\) is immune to \(\mathcal {M}^k\),
. It cannot be true that \((\sigma _1,\sigma _3) \in M^k\) since \({\mathcal {L}_{\text {bad}}}\) is immune to \(M^k\) so there must exist pairs \({(\sigma _1,\sigma _2) \in \mathcal {M}^k}\) and \({(\sigma _2,\sigma _3) \in \mathcal {M}^1}\). Since \(\mathcal {L}_{\text {bad}}\) is immune to \(\mathcal {M}^k\),  so it must be true that
so it must be true that  . However, it is clear from Definition 11 that \(M^k \subseteq M^{k+1}\), so \(M^1 \subseteq M^k\) for any k, which is a contradiction.
. However, it is clear from Definition 11 that \(M^k \subseteq M^{k+1}\), so \(M^1 \subseteq M^k\) for any k, which is a contradiction.
For the reverse case, assume a property \(\mathcal {L}_{\text {sad}} \subseteq \varSigma ^\infty \) such that \(\mathcal {L}_{\text {sad}}\) is not immune to some \(k\)-Mutation \(M^k\) but is immune to \(M^{k+1}\). However, as we saw before, \(M^k \subseteq M^{k+1}\) so \(\mathcal {L}_{\text {sad}}\) must not be immune to \(M^{k+1}\), a contradiction. \(\square \)
Immunity under Definition 12 is too strong to be a requirement for monitorability over an unreliable channel, however. Take, for example, the property \(G(a \rightarrow F\lnot a) \vee Fb\), as shown in Fig. 1b. By Definition 12 with truth domain \(\mathbb {B}_{4}\) this property is vulnerable (not immune) to \(\textit{OutOfOrder}^{1}\) because reordering symbols may change the verdict. For example, the trace \({\langle \{a,\lnot b\},\{\lnot a,\lnot b\} \rangle }\) results in a verdict of \(\top _p\), but reordering the trace to \({\langle \{\lnot a,\lnot b\},\{a,\lnot b\} \rangle }\) changes the verdict to \(\bot _p\). However, this property is monitorable under all definitions in Sect. 3.2, because it is always possible to reach a \(\top \) verdict if a b appears. We would like a modified definition of immunity that only considers the parts of a property that affect its monitorability.
To achieve this modified definition of immunity, we consider only the determinization of the property to be crucial. Definition 13 characterizes properties for which satisfaction and violation are unaffected by a mutation. We call this true-false immunity, and it is equivalent to immunity with truth domain \(\mathbb {B}_{3}\). The intuition is that \(\mathbb {B}_{3}\) treats all verdicts outside \(\{\top ,\bot \}\) as the symbol \({{\varvec{?}}}\) so immunity with this truth domain does not concern non-\(\textit{true}\)-\(\textit{false}\) verdicts.
Definition 13
(True-False Immunity to Unreliable Channels) Given a trace mutation \({\mathcal {M}^k \subseteq \varSigma ^* \times \varSigma ^*}\), a language \({\mathcal {L}\subseteq \varSigma ^\infty }\) is true-false immune to \(\mathcal {M}^k\) iff \(\mathcal {L}\) is immune to \(\mathcal {M}^k\) for the truth domain \(\mathbb {B}_{3}\).
The true-false immunity of a property to a mutation is necessary but not sufficient to show that the property is monitorable over an unreliable channel. For example, the LTL formula GFa is true-false immune to all mutations because  for any prefix \(\sigma \in \varSigma ^*\), but the property is not monitorable. We can now define monitorability over unreliable channels in the general case.
for any prefix \(\sigma \in \varSigma ^*\), but the property is not monitorable. We can now define monitorability over unreliable channels in the general case.
Definition 14
(Monitorability over Unreliable Channels) Given a language \({\mathcal {L}\subseteq \varSigma ^\infty }\), a trace mutation \(\mathcal {M}^k \subseteq \varSigma ^* \times \varSigma ^*\), and a definition of monitorability  , \(\mathcal {L}\) is monitorable over \(\mathcal {M}^k\) iff
, \(\mathcal {L}\) is monitorable over \(\mathcal {M}^k\) iff  and \(\mathcal {L}\) is true-false immune to \(\mathcal {M}^k\).
and \(\mathcal {L}\) is true-false immune to \(\mathcal {M}^k\).
The question of what languages are considered monitorable by Definitions 4, 5, and 6 has largely been answered by prior work. To understand what languages are monitorable over an unreliable channel, we must understand what languages are true-false immune to the given mutation.
6 Trustworthy verdicts
Some properties that are unmonitorable over an unreliable channel may still have some utility. A property that is not true-false immune to a trace mutation may still yield trustworthy verdicts when monitored. This idea is similar to that of weak-monitorability, defined in Sect. 3.2.3, in that some properties may be interesting to monitor despite being classically unmonitorable. In this section we define trustworthy verdicts and examine their practical consequences.
A trustworthy verdict for a property over an unreliable channel implies the same verdict for the property over an ideal channel. For example,  (the NBA for the LTL formula Fa is shown in Fig. 1a) when there exists a symbol in \(\sigma \) where a holds. Over a channel with the \(\textit{Loss}\) mutation, a \(\top \) verdict guarantees that a held in the original as well as the mutated trace, since \(\textit{Loss}\) cannot add such a symbol.
(the NBA for the LTL formula Fa is shown in Fig. 1a) when there exists a symbol in \(\sigma \) where a holds. Over a channel with the \(\textit{Loss}\) mutation, a \(\top \) verdict guarantees that a held in the original as well as the mutated trace, since \(\textit{Loss}\) cannot add such a symbol.
Definition 15
(Trustworthy Verdicts) Given a property \(\mathcal {L}\subseteq \varSigma ^\infty \), a trace mutation \({\mathcal {M}^k \subseteq \varSigma ^* \times \varSigma ^*}\), a truth domain \(\mathbb {V}\), and an evaluation function  , a verdict \(v \in \mathbb {V}\) is trustworthy for \(\mathcal {L}\) over a channel with \(\mathcal {M}^k\) iff
, a verdict \(v \in \mathbb {V}\) is trustworthy for \(\mathcal {L}\) over a channel with \(\mathcal {M}^k\) iff  .
.
Definition 15 specifies a \(k\)-Mutation from Definition 11, but a property that is immune to a mutation for some k is immune to that mutation for any k. This result follows from Theorem 2, which specifies single mutation immunity equivalence.
Corollary 1
(Single Mutation Trustworthy Verdict Equivalence) Given a property \(\mathcal {L}\subseteq \varSigma ^\infty \), a truth domain \(\mathbb {V}\), a trace mutation \(\mathcal {M} \subseteq \varSigma ^* \times \varSigma ^*\), and a number of applications of that mutation k, a verdict \(v \in \mathbb {V}\) is trustworthy from \(\mathcal {L}\) over a channel with \(\mathcal {M}^k\) iff v is trustworthy for \(\mathcal {L}\) over a channel with \(\mathcal {M}^1\).
Proof
Corollary 1 is implied by Theorem 2. Theorem 2 specifies that a property \(\mathcal {L}\subseteq \varSigma ^\infty \) is immune to a mutation \(M^k \subseteq \varSigma ^* \times \varSigma ^*\) iff \(\mathcal {L}\) is immune to \(M^1\). By Definition 12, if the property is immune to \(M^1\) for a truth domain \(\mathbb {V}\) and an evaluation function  then for all pairs \({(\sigma ,\sigma ') \in \mathcal {M}^k}\) and for all verdicts \({v \in \mathbb {V}}\)
then for all pairs \({(\sigma ,\sigma ') \in \mathcal {M}^k}\) and for all verdicts \({v \in \mathbb {V}}\)  . Therefore, the same result applies for a specific verdict \(v \in \mathbb {V}\) and one-way implication instead of two. \(\square \)
. Therefore, the same result applies for a specific verdict \(v \in \mathbb {V}\) and one-way implication instead of two. \(\square \)
If all verdicts in a truth domain are trustworthy for a property and a trace mutation, then that property is immune to the trace mutation. This equivalence allows us to apply the study of trustworthy verdicts to that of mutation immunity. In Sect. 8, we classify properties with trustworthy verdicts over unreliable channels which applies equally to the classification of mutation-immune properties.
Theorem 3
(Trustworthy Verdict Immunity Equivalence) Given a property \(\mathcal {L}\subseteq \varSigma ^\infty \), a trace mutation \(\mathcal {M}^k \subseteq \varSigma ^* \times \varSigma ^*\), a truth domain \(\mathbb {V}\), and an evaluation function  is immune to \(\mathcal {M}^k\) iff all verdicts in \(\mathbb {V}\) are trustworthy over a channel with \(\mathcal {M}^k\).
is immune to \(\mathcal {M}^k\) iff all verdicts in \(\mathbb {V}\) are trustworthy over a channel with \(\mathcal {M}^k\).
Proof
The proof is trivially derived from Definitions 12 and 15. If for all pairs \({(\sigma ,\sigma ') \in \mathcal {M}^k}\) and for all verdicts \({v \in \mathbb {V}}\) it is true that  implies
implies  , then for all pairs \({(\sigma ,\sigma ') \in \mathcal {M}^k}\) and all verdicts \(v \in \mathbb {V}\) it must be true that
, then for all pairs \({(\sigma ,\sigma ') \in \mathcal {M}^k}\) and all verdicts \(v \in \mathbb {V}\) it must be true that  . \(\square \)
. \(\square \)
Corollary 2
(Trustworthy Verdict True-False Immunity Equivalence) Given a property \(\mathcal {L}\subseteq \varSigma ^\infty \), and a trace mutation \(\mathcal {M}^k \subseteq \varSigma ^* \times \varSigma ^*\), \(\mathcal {L}\) is true-false immune to \(\mathcal {M}^k\) iff all verdicts in \(\mathbb {B}_{3}\) are trustworthy over a channel with \(\mathcal {M}^k\).
Proof
The proof follows directly from Definition 13 and Theorem 3. For a property to be true-false immune to a mutation, it must be immune for the \(\mathbb {B}_{3}\) truth domain. If all verdicts in a domain are trustworthy for a property and mutation, then the property is immune to that mutation. \(\square \)
7 Classification for mutation immunity
In this section, we update the monitorability-focused refinement of the safety-liveness taxonomy, recently introduced by Peled and Havelund [49]. This classification is designed so that its delineations between classes align well with questions of monitorability. This makes it better suited for our purposes than the more established Safety-Progress Hierarchy [20]. We are interested in classifying \(\omega \)-regular properties that are immune to trace mutations from unreliable channels.
7.1 The FR/FS classification
Peled and Havelund classify properties by whether they are Finitely Refutable (FR) or Finitely Satisfiable (FS) [49]. An \(\omega \)-regular property \(\mathcal {L}\subseteq \varSigma ^\omega \) must be one of the following.
-
Always Finitely Refutable (AFR) iff
 \({\exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and
\({\exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and 
-
Sometimes Finitely Refutable (SFR) iff
 \({\exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and
\({\exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and 
-
Never Finitely Refutable (NFR) iff
 \({\not \exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and
\({\not \exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and 
Additionally, \(\mathcal {L}\) must be one of the following.
-
Always Finitely Satisfiable (AFS) iff
 \({\exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and
\({\exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and 
-
Sometimes Finitely Satisfiable (SFS) iff
 \({\exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and
\({\exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and 
-
Never Finitely Satisfiable (NFS) iff
 \({\not \exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and
\({\not \exists \alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and 
The definitions for AFR, NFR, AFS, and NFS map directly to the classic definitions of safety and liveness properties, and their duals, guarantee and morbidity. The authors of [49] show that all \(\omega \)-regular properties are included in both \({{{\mathbf {\mathtt{{{AFR}}}}}}\cup {{\mathbf {\mathtt{{{SFR}}}}}}\cup {{\mathbf {\mathtt{{{NFR}}}}}}}\) and \({{{\mathbf {\mathtt{{{AFS}}}}}}\cup {{\mathbf {\mathtt{{{SFS}}}}}}\cup {{\mathbf {\mathtt{{{NFS}}}}}}}\).
-
Liveness (NFR)—A property \(\mathcal {L}\subseteq \varSigma ^\omega \) is a liveness property iff for all finite prefixes \({\alpha \in \varSigma ^*}\) there exists an infinite suffix \({\beta \in \varSigma ^\omega }\) such that \({\alpha \cdot \beta \in \mathcal {L}}\).
-
Morbidity (NFS)—A property \(\mathcal {L}\subseteq \varSigma ^\omega \) is a morbidity property iff for all finite prefixes \({\alpha \in \varSigma ^*}\) there exists an infinite suffix \({\beta \in \varSigma ^\omega }\) such that \({\alpha \cdot \beta \notin \mathcal {L}}\).
-
Safety (AFR)—A property \(\mathcal {L}\subseteq \varSigma ^\omega \) is a safety property iff for all infinite traces \({\sigma \notin \mathcal {L}}\) there exists a finite trace \({\alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and for all infinite suffixes \({\beta \in \varSigma ^\omega }\) \({\alpha \cdot \beta \notin \mathcal {L}}\)
-
Guarantee (AFS)—A property \(\mathcal {L}\subseteq \varSigma ^\omega \) is a guarantee property iff for all traces \({\sigma \in \mathcal {L}}\) there exists a finite prefix \({\alpha \in \varSigma ^*}\) such that \({\alpha \sqsubseteq {} \sigma }\) and for all infinite suffixes \({\beta \in \varSigma ^\omega }\) \({\alpha \cdot \beta \in \mathcal {L}}\)
The FR/FS classification is defined by the intersections between pairs of FR and FS classes. These intersections are shown in Fig. 2, which also labels the intersection \({{\mathbf {\mathtt{{{SFR}}}}}}\cap {{\mathbf {\mathtt{{{SFS}}}}}}\) as Quaestio, which are the \(\omega \)-regular properties not covered by the liveness, morbidity, safety, and guarantee classes. In the figure, each of NFR, NFS, AFR, and AFS is shown as a stadium shape with their intersections in the corners. The \({{\mathbf {\mathtt{{SFR}}}}} \cap {{\mathbf {\mathtt{{SFS}}}}}\) class surrounds the stadia and is also represented in the center of the diagram.
7.2 Additional property classes
We introduce five classes of properties that overlap with the classes from the FR/FS taxonomy. These are Proximate, Tolerant, Permissive, Inclusive, and Exclusive. We propose language-theoretic definitions for these classes and locate them within the context of the FR/FS framework.
The FR/FS classification provides the basis for a framework for relating properties that are immune to a trace mutation to properties that are monitorable under ideal conditions. However, the original FR/FS classes do not precisely define properties with mutation immunity in many cases. We must define smaller property classes within the framework to identify the properties with trustworthy verdicts over channels with the mutations from Definitions 7-10.
Figure 3 shows the FR/FS classification with the additional property classes indicated. In the figure, each area is numbered for ease of reference. Each area may represent multiple classes (if they overlap) and each class may be include multiple areas. For example, Liveness (NFR) Properties are represented in the figure by areas 1, 7, 8, 12, 13, and 16. Inclusion Properties, on the other hand, are represented in only area 12.
7.2.1 Proximate properties
Proximate Properties, which we denote Prox, are properties where the duplication of a symbol may change whether or not a trace satisfies or violates the property. For example, \(L[\![Xp]\!]\) is Proximate, since the trace \(\langle \{\lnot p\},\{p\},\cdots \rangle \) satisfies the property but \(\langle \{\lnot p\},\{\lnot p\},\{p\},\cdots \rangle \) does not. The intuition behind the name “Proximate” is that these properties depend, in some way, on the proximity of two parts of the trace. In Figure 3, areas 9, 10, 14, and 15 contain only Proximate Properties, and areas 5, 6, 8, and 13 include Proximate Properties but not only Proximate Properties.
Proximate Properties are related to the dual of a class usually called closed under stuttering [55], or stutter-invariant [50]. Stutter-invariant Properties are those in which any satisfying trace still satisfies the property when symbols are repeated. Proximate is not exactly the dual of stutter-invariant, as Proximate Properties are affected only by finite stuttering. This includes most, but not all, LTL formulae that contain the next (X) operator. For example, \(L[\![GF(p \wedge Xq)]\!]\) is not Proximate because finite duplication of symbols cannot cause a satisfying trace to violate the property. Note that the presence of next (X) in an LTL formula is not sufficient to prove inclusion in Prox but the absence of X guarantees that the formula is out of Prox.
Definition 16
(Proximate Properties) A given property \(\mathcal {L}\subseteq \varSigma ^\omega \) is a Proximate Property (\(\mathcal {L}\in {{\mathbf {\mathtt{{{Prox}}}}}}\)) iff  such that either \({\alpha \cdot \langle x \rangle \cdot \mu \in \mathcal {L}}\), and \({\alpha \cdot \langle x, x \rangle \cdot \mu \notin \mathcal {L}}\), or \({\alpha \cdot \langle x \rangle \cdot \mu \notin \mathcal {L}}\), and \({\alpha \cdot \langle x, x \rangle \cdot \mu \in \mathcal {L}}\).
such that either \({\alpha \cdot \langle x \rangle \cdot \mu \in \mathcal {L}}\), and \({\alpha \cdot \langle x, x \rangle \cdot \mu \notin \mathcal {L}}\), or \({\alpha \cdot \langle x \rangle \cdot \mu \notin \mathcal {L}}\), and \({\alpha \cdot \langle x, x \rangle \cdot \mu \in \mathcal {L}}\).
7.2.2 Tolerant properties
Tolerant Properties, which we denote by the abbreviation \({{\mathbf {\mathtt{{{Tolr}}}}}}\), are properties where satisfying traces will still satisfy the property with any finite string inserted into the trace. For example, \(L[\![Fp]\!]\) is a Tolerant Property because adding any finite string to a satisfying trace (say, \(\langle \{p\},\cdots \rangle \)) cannot cause the trace to violate the property. The intuition behind the name “Tolerant” is that the properties tolerate the insertion of a finite string. Tolerant Properties are shown in Fig. 3 as areas 1, 7, 12, and 16.
Definition 17
(Tolerant Properties) A given property \(\mathcal {L}\subseteq \varSigma ^\omega \) is a Tolerant Property (\(\mathcal {L}\in {{\mathbf {\mathtt{{{Tolr}}}}}}\)) iff  \({(\alpha \cdot \mu \in \mathcal {L}) \rightarrow (\alpha \cdot \beta \cdot \mu \in \mathcal {L})}\).
\({(\alpha \cdot \mu \in \mathcal {L}) \rightarrow (\alpha \cdot \beta \cdot \mu \in \mathcal {L})}\).
Tolerant is a subclass of Liveness and is disjoint from Proximate. That Tolerant is disjoint from Proximate is obvious, and we show that it is a subclass of Liveness in Theorem 4. Areas 8 and 13 in Fig. 3 represent Liveness Properties that are not Tolerant. A consequence of the differences between Definitions 16 and 17 is that \({{{\mathbf {\mathtt{{NFR}}}}} \cap {{\mathbf {\mathtt{{{Prox}}}}}}\subset {{\mathbf {\mathtt{{NFR}}}}} \setminus {{\mathbf {\mathtt{{{Tolr}}}}}}}\), however. An example of NFR property that is not Tolerant, but also is not Proximate is \(L[\![F(p \wedge Xq)]\!]\). A Proximate Property that is not Tolerant is \(L[\![F(p \wedge Xq \wedge XXp)]\!]\). An exact characterization of the properties \({{{\mathbf {\mathtt{{NFR}}}}} \setminus ({{\mathbf {\mathtt{{{Prox}}}}}}\cup {{\mathbf {\mathtt{{{Tolr}}}}}})}\) is unknown and left for future work.
Theorem 4
(Tolerant is a Subclass of Liveness) \({{\mathbf {\mathtt{{{Tolr}}}}}}\subset {{\mathbf {\mathtt{{{NFR}}}}}}\)
Proof
We must consider two cases: if the property is infinitely satisfied, or finitely satisfied.
-
1.
Case 1 (infinite satisfaction): In that case the infinite suffix of the trace \(\mu \in \varSigma ^\omega \) determines that \(\alpha \cdot \mu \in \mathcal {L}\) for any \(\alpha \in \varSigma ^*\). This is what Sistla called an absolute liveness property which are a subset of liveness properties [55].
-
2.
Case 2 (finite satisfaction): Suppose, a property \({\mathcal {L}_{2}\subseteq \varSigma ^\omega }\) where the finite prefix determines satisfaction. For clarity, we separate this finite portion into two parts \({\alpha ,\beta \in \varSigma ^*}\) such that
 . We will prove by contradiction. Now assume there exists a finite trace \({\gamma \in \varSigma ^*}\) and an infinite suffix \({\mu _f \in \varSigma ^\omega }\) such that \({\alpha \cdot \gamma \cdot \beta \cdot \mu _f \notin \mathcal {L}_{2}}\). If
. We will prove by contradiction. Now assume there exists a finite trace \({\gamma \in \varSigma ^*}\) and an infinite suffix \({\mu _f \in \varSigma ^\omega }\) such that \({\alpha \cdot \gamma \cdot \beta \cdot \mu _f \notin \mathcal {L}_{2}}\). If  , then \(\mathcal {L}_{2}\) is finitely refutable and not a Liveness property. Otherwise, \({\exists \mu _t \in \varSigma ^\omega }\) such that \({\alpha \cdot \gamma \cdot \beta \cdot \mu _t \in \mathcal {L}_{2}}\). If that is true, then it must be that
, then \(\mathcal {L}_{2}\) is finitely refutable and not a Liveness property. Otherwise, \({\exists \mu _t \in \varSigma ^\omega }\) such that \({\alpha \cdot \gamma \cdot \beta \cdot \mu _t \in \mathcal {L}_{2}}\). If that is true, then it must be that  which is the definition of a Liveness property.
which is the definition of a Liveness property.
\(\square \)
7.2.3 Permissive properties
Permissive Properties, which we denote by the abbreviation \({{\mathbf {\mathtt{{{Perm}}}}}}\), are properties where violating traces will still violate the property with any finite string inserted into the trace. For example, \(L[\![Gp]\!]\) is a Permissive Property because adding any finite string to a violating trace (say, \(\langle \{\lnot p\},\cdots \rangle \)) cannot cause the trace to satisfy the property. The intuition behind the name “Permissive” is that the properties permit the insertion of a string (like tolerant, but negative). Permissive Properties are shown in Fig. 3 as areas 1, 2, 3, and 4.
Definition 18
(Permissive Properties) A given property \(\mathcal {L}\subseteq \varSigma ^\omega \) is an Permissive Property (\(\mathcal {L}\in {{\mathbf {\mathtt{{{Perm}}}}}}\)) iff  \({(\alpha \cdot \mu \notin \mathcal {L}) \rightarrow (\alpha \cdot \beta \cdot \mu \notin \mathcal {L})}\).
\({(\alpha \cdot \mu \notin \mathcal {L}) \rightarrow (\alpha \cdot \beta \cdot \mu \notin \mathcal {L})}\).
Permissive is a subclass of Morbidity and is disjoint from Proximate. That Permissive is disjoint from Proximate is obvious, and we show that it is a subclass of Morbidity in Theorem 5. Areas 5 and 6 in Fig. 3 represent Morbidity Properties that are not Permissive. A consequence of the differences between Definitions 16 and 18 is that \({{{\mathbf {\mathtt{{NFS}}}}} \cap {{\mathbf {\mathtt{{{Prox}}}}}}\subset {{\mathbf {\mathtt{{NFS}}}}} \setminus {{\mathbf {\mathtt{{{Perm}}}}}}}\), however. An example of an NFS property that is not Permissive, but also is not Proximate is \(L[\![G(p\;U q)]\!]\). A Proximate Property that is not Permissive is \(L[\![G(p \rightarrow Xq)]\!]\). Like with Tolerant and Proximate, an exact characterization of the properties \({{{\mathbf {\mathtt{{NFR}}}}} \setminus ({{\mathbf {\mathtt{{{Prox}}}}}}\cup {{\mathbf {\mathtt{{{Perm}}}}}})}\) is unknown and left for future work.
Theorem 5
(Permissive is a Subclass of Morbidity) \({{\mathbf {\mathtt{{{Perm}}}}}}\subset {{\mathbf {\mathtt{{{NFS}}}}}}\)
Proof
The proof is equivalent to that for Theorem 4 but for Morbidity instead of Liveness. \(\square \)
7.2.4 Inclusion properties
Inclusion Properties, which we denote by the abbreviation Incl, are always satisfied by the presence of a finite set of symbols. For example, \(L[\![Fp]\!]\) is an Inclusion Property because its satisfaction depends only on the presence of one symbol where p holds. Intuitively, Inclusion Properties are restricted to those that can be expressed as LTL formulae of the form Fp where p is propositional, or disjunctions of Inclusion Property formulae with Fp or Gq where p and q are propositional. Inclusion Properties are shown in Fig. 3 as area 12.
Definition 19
(Inclusion Properties) A given property \(\mathcal {L}\subseteq \varSigma ^\omega \) is an Inclusion Property (\(\mathcal {L}\in {{\mathbf {\mathtt{{{Incl}}}}}}\)) iff there exists a finite set of symbols \(S \subseteq \varSigma \) such that  .
.
Theorem 6
(Inclusion is a Subclass of Tolerant and Disjoint from Morbidity) \({{{\mathbf {\mathtt{{{Incl}}}}}}\subset {{\mathbf {\mathtt{{{Tolr}}}}}}\setminus {{\mathbf {\mathtt{{{NFS}}}}}}}\)
Proof
Clearly, \(\mathcal {L}\in {{\mathbf {\mathtt{{{Tolr}}}}}}\ \forall \mathcal {L}\in {{\mathbf {\mathtt{{{Incl}}}}}}\). Given a property \(\mathcal {L}\in {{\mathbf {\mathtt{{{Incl}}}}}}\), any trace \(\sigma \in \mathcal {L}\) will still satisfy the property with additional symbols. It is also obvious that \(\mathcal {L}\notin {{\mathbf {\mathtt{{{NFS}}}}}}\ \forall \mathcal {L}\in {{\mathbf {\mathtt{{{Incl}}}}}}\), since it must be possible to satisfy \(\mathcal {L}\) by the inclusion of a finite set of symbols. \(\square \)
7.2.5 Exclusion properties
Exclusion Properties, which we denote by the abbreviation Excl, are always violated by the presence of a finite set of symbols. For example, \(L[\![G(\lnot p)]\!]\) is an Exclusion Property because its satisfaction depends only on the absence any state where p holds. Intuitively, Exclusion Properties are restricted to those that can be expressed as LTL formulae of the form Gp where p is propositional, or conjunctions of Exclusion Property formulae with Fp or Gq where p and q are propositional. Exclusion Properties are shown in Fig. 3 as area 3.
Definition 20
(Exclusion Properties) A given property \(\mathcal {L}\subseteq \varSigma ^\omega \) is an Exclusion Property (\(\mathcal {L}\in {{\mathbf {\mathtt{{{Excl}}}}}}\)) iff there exists a finite set of symbols \(S \subseteq \varSigma \) such that  .
.
Theorem 7
(Exclusion is a Subclass of Permissive and Disjoint from Liveness) \({{\mathbf {\mathtt{{{Excl}}}}}}\subset {{\mathbf {\mathtt{{{Perm}}}}}}\setminus {{\mathbf {\mathtt{{{NFR}}}}}}\)
Proof
Like for Theorem 6, \({\mathcal {L}\in {{\mathbf {\mathtt{{{Perm}}}}}}\ \forall \mathcal {L}\in {{\mathbf {\mathtt{{{Excl}}}}}}}\). Given a property \(\mathcal {L}\in {{\mathbf {\mathtt{{{Excl}}}}}}\), any trace \(\sigma \notin \mathcal {L}\) will still violate the property with additional symbols. It is also obvious that \({\mathcal {L}\notin {{\mathbf {\mathtt{{{NFR}}}}}}\ \forall \mathcal {L}\in {{\mathbf {\mathtt{{{Excl}}}}}}}\), since it must be possible to violate \(\mathcal {L}\) by the inclusion of a finite set of symbols. \(\square \)
8 Classifying immune properties
In this section, we classify trustworthy verdicts in the \(\mathbb {B}_{3}\) truth domain for properties monitored over unreliable channels. As shown in Sect. 6, this classification also serves to categorize properties that are immune to the trace mutations from those unreliable channels. To classify properties, we use the augmented FR/FS classification introduced in Sect. 7. We limit our study to the mutations introduced in Sect. 4.
Table 1 shows trustworthy verdicts in \(\mathbb {B}_{3}\) for each FR/FS class of properties and each of the four mutations from Sect. 4. In the table, a ✓ indicates that the verdict is trustworthy, a ✗ means that the verdict is not trustworthy, and a—denotes that the verdict is not possible for the given property class. The table also includes an example property for each class. For example, the first row in Table 1 shows the results for the \({{\mathbf {\mathtt{{{SFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}\) class, an example of which is the LTL property \(Fp \wedge Gq\). The leftmost three cells show the results for the Loss mutation. The cells show that the \(\top \) verdict is not possible for \({{\mathbf {\mathtt{{{SFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}\) Properties, the \(\bot \) verdict is trustworthy (for the Permissive subclass), and the \({{\varvec{?}}}\) verdict is not trustworthy.
Most of the property classes for which verdicts are trustworthy are subclasses of the original FR/FS classes defined in Sect. 7.2. For these, we annotate the ✓ mark to indicate the precise subclass. A ✓\(^p\) indicates the verdict is trustworthy for only Permissive properties. A ✓\(^t\) indicates the verdict is trustworthy for only Tolerant properties. A ✓\(^i\) denotes that the verdict is trustworthy for only Inclusive Properties. A ✓\(^e\) denotes that the verdict is trustworthy for only Exclusive Properties. A ✓\(^x\) indicates the verdict is trustworthy for the given property class excluding Proximate Properties.
8.1 Channels with loss
Only the unmonitorable class \({{\mathbf {\mathtt{{{NFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}\) is immune to Loss, but \(\textit{true}{}\) and \(\textit{false}{}\) verdicts are trustworthy over certain properties. Loss is interesting because it is the only mutation from Definitions 7-10 for which some properties have both trustworthy and non-trustworthy verdicts.
Theorem 8
(Over Channels with Loss, True is Trustworthy only for Tolerant Properties) Given a property \(\mathcal {L}\in {{\mathbf {\mathtt{{{Tolr}}}}}}\), for all pairs \({(\sigma ,\sigma ') \in \textit{Loss}^1}\),  . Given a property \({\mathcal {L}\subseteq (\varSigma ^\omega \setminus {{\mathbf {\mathtt{{{Tolr}}}}}})}\), there exists a pair \({(\sigma ,\sigma ') \in \textit{Loss}^1}\) such that
. Given a property \({\mathcal {L}\subseteq (\varSigma ^\omega \setminus {{\mathbf {\mathtt{{{Tolr}}}}}})}\), there exists a pair \({(\sigma ,\sigma ') \in \textit{Loss}^1}\) such that  .
.
Proof
We will show that \(\textit{true}\) is trustworthy for exactly the properties \({{\mathbf {\mathtt{{{Tolr}}}}}}{}\). We must show that \({\forall \mathcal {L}\in {{\mathbf {\mathtt{{{Tolr}}}}}}}\) there cannot exist a pair of traces \({(\sigma ,\sigma ') \in \textit{Loss}^1}\) such that  . Or, to restate using Definition 1, \({\sigma ' \cdot \mu _{t} \in \mathcal {L}}\) for all infinite suffixes \({\mu _{t} \in \varSigma ^\omega }\) and there exists an infinite suffix \({\mu _{f} \in \varSigma ^\omega }\) such that \({\sigma \cdot \mu _{f} \notin \mathcal {L}}\). We will prove by contradiction.
. Or, to restate using Definition 1, \({\sigma ' \cdot \mu _{t} \in \mathcal {L}}\) for all infinite suffixes \({\mu _{t} \in \varSigma ^\omega }\) and there exists an infinite suffix \({\mu _{f} \in \varSigma ^\omega }\) such that \({\sigma \cdot \mu _{f} \notin \mathcal {L}}\). We will prove by contradiction.
From Definition 7, since \(\sigma \) and \(\sigma '\) must not be equal (or they must result in the same verdict), there exist finite traces \({\alpha , \beta \in \varSigma ^*}\) and a symbol \({\exists x \in \varSigma }\) such that \({\sigma = \alpha \cdot \langle x \rangle \cdot \beta }\) and \({\sigma ' = \alpha \cdot \beta }\). So, we assume there exist a pair of finite traces \({(\alpha \cdot \langle x \rangle \cdot \beta ,\alpha \cdot \beta ) \in \textit{Loss}^1}\) such that, for all infinite suffixes \({\mu _t \in \varSigma ^\omega }\), \({\alpha \cdot \beta \cdot \mu _t \in \mathcal {L}}\) and there exists an infinite suffix \({\mu _f \in \varSigma ^\omega }\) such that \({\alpha \cdot \langle x \rangle \cdot \beta \cdot \mu _f \notin \mathcal {L}}\). For this to be true, it must be that there exists an infinite suffix \({\mu \in \varSigma ^\omega }\) such that \({\alpha \cdot \beta \cdot \mu \in \mathcal {L}}\) and \({\alpha \cdot \langle x \rangle \cdot \beta \cdot \mu \notin \mathcal {L}}\). Since \(\beta \cdot \mu \) appears in both traces, we can simplify to say that there exists an infinite suffix \({\mu \in \varSigma ^\omega }\) such that \({\alpha \cdot \mu \in \mathcal {L}}\) and \({\alpha \cdot \langle x \rangle \cdot \mu \notin \mathcal {L}}\). However, this is the complement of Tolerant Properties from Definition 17, which we have explicitly excluded. \(\square \)
Theorem 9
(False is Trustworthy only for Permissive Properties over Channels with Loss) Given a property \(\mathcal {L}\in {{\mathbf {\mathtt{{{Perm}}}}}}\), for all pairs \({(\sigma ,\sigma ') \in \textit{Loss}^1}\),  . Given a property \({\mathcal {L}\subseteq (\varSigma ^\omega \setminus {{\mathbf {\mathtt{{{Perm}}}}}})}\), there exists a pair \({(\sigma ,\sigma ') \in \textit{Loss}^1}\) such that
. Given a property \({\mathcal {L}\subseteq (\varSigma ^\omega \setminus {{\mathbf {\mathtt{{{Perm}}}}}})}\), there exists a pair \({(\sigma ,\sigma ') \in \textit{Loss}^1}\) such that  .
.
Proof
The proof is identical to that for Theorem 9, but for \(\textit{false}\) and Permissive Properties. \(\square \)
Theorem 10
(\({{\mathbf {\mathtt{{{NFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}\) Properties are Vacuously Immune to All Mutations) Given a property \(\mathcal {L}\in {{\mathbf {\mathtt{{{NFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}\), for any finite traces \({\sigma ,\sigma ' \in \varSigma ^*}\) it is always true that  .
.
Proof
The proof is trivial, since  for any finite trace \(\sigma \in \varSigma ^*\). \(\square \)
for any finite trace \(\sigma \in \varSigma ^*\). \(\square \)
8.2 Channels with corruption
Corruption is the only trace mutation we examine for which no properties, apart from those in \({{\mathbf {\mathtt{{{NFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}\), have trustworthy verdicts. This result is not surprising, since corruption can change any symbol in the alphabet to any other symbol. Corruption cannot change the length of the original trace, so we first show that this does not limit the properties for which the mutation may affect the monitoring verdict.
Lemma 1
(Strings of the Same Length Must Be Able to Result in Different Verdicts) Given a property \(\mathcal {L}\subseteq \varSigma ^\omega \), if there exist two finite strings \({s,s' \in \varSigma ^*}\) such that  , then there must exist two finite strings of the same length
, then there must exist two finite strings of the same length  such that
such that  .
.
Proof
First, suppose a property \({\mathcal {L}\in \varSigma ^\omega }\) such that there exist finite traces \({s,s' \in \varSigma ^*}\) such that  , and for all pairs of finite traces of equal length
, and for all pairs of finite traces of equal length  .
.
If all traces of the same length yield the same verdict, then one of s or \(s'\) must be longer than the other (which one does not matter). Assume \({|s| > |s'|}\). There are three cases:
-
1.
If
 then, from Definition 1, \({s' \cdot \mu \in \mathcal {L}}\) for all infinite suffixes \(\mu \in \varSigma ^\omega \). However, for all traces of the same length
then, from Definition 1, \({s' \cdot \mu \in \mathcal {L}}\) for all infinite suffixes \(\mu \in \varSigma ^\omega \). However, for all traces of the same length  , we assume that
, we assume that  , so there must be a prefix of s where the verdict is \(\top \), but this is a contradiction.
, so there must be a prefix of s where the verdict is \(\top \), but this is a contradiction. -
2.
The same logic applies if
 .
. -
3.
If
 , then either
, then either  or
or  . Suppose that
. Suppose that  , as the same argument applies for both verdicts. Then for all finite suffixes \({t \in \varSigma ^*}\) such that \(s'\) concatenated with t is the same length as s, \({|s' \cdot t| = |s|}\), it must be that \({(s' \cdot t) \in \mathcal {L}}\). However, by Definition 1, there exists an infinite suffix \({\mu \in \varSigma ^\omega }\) such that \((s' \cdot \mu ) \notin \mathcal {L}\). Then, there must be either a finite suffix the same length as t,
, as the same argument applies for both verdicts. Then for all finite suffixes \({t \in \varSigma ^*}\) such that \(s'\) concatenated with t is the same length as s, \({|s' \cdot t| = |s|}\), it must be that \({(s' \cdot t) \in \mathcal {L}}\). However, by Definition 1, there exists an infinite suffix \({\mu \in \varSigma ^\omega }\) such that \((s' \cdot \mu ) \notin \mathcal {L}\). Then, there must be either a finite suffix the same length as t,  where
where  or
or  , which is a contradiction.
, which is a contradiction.
\(\square \)
Theorem 11
(If Multiple Verdicts are Possible for a Property, Then None are Trustworthy Over Channels with Corruption) Given a property \(\mathcal {L}\subseteq \varSigma ^\omega \), for all verdicts \({v \in \mathbb {B}_{3}}\), if there exist two finite traces \({s,s' \in \varSigma ^*}\) such that  and
and  , then there exists a pair of traces \({(\sigma ,\sigma ') \in \textit{Corruption}^1}\) such that
, then there exists a pair of traces \({(\sigma ,\sigma ') \in \textit{Corruption}^1}\) such that  and
and  .
.
Proof
Suppose two finite traces with different verdicts  . From Lemma 1 it must be possible for \({|s| = |s'|}\). Clearly, from Definitions 8 and 11, there exists a number \({k \in \mathbb {N}}\) such that \({(s,s') \in \textit{Corruption}^k}\), since any finite string may appear on the left side of the pair and applying Corruption an arbitrary number of times can transform a string to any other string of the same length. From Corollary 1, a verdict is trustworthy for \(\textit{Corruption}^1\) iff it is trustworthy for \(\textit{Corruption}^k\). \(\square \)
. From Lemma 1 it must be possible for \({|s| = |s'|}\). Clearly, from Definitions 8 and 11, there exists a number \({k \in \mathbb {N}}\) such that \({(s,s') \in \textit{Corruption}^k}\), since any finite string may appear on the left side of the pair and applying Corruption an arbitrary number of times can transform a string to any other string of the same length. From Corollary 1, a verdict is trustworthy for \(\textit{Corruption}^1\) iff it is trustworthy for \(\textit{Corruption}^k\). \(\square \)
8.3 Channels with stutter
Many works on temporal logic have examined the effects of stuttering. Lamport argued for the omission of the next (X) operator in temporal logic, and demonstrated that traces with repeating symbols could not be differentiated without it [44]. The difference between prior work on stuttering and ours is that Definition 9 includes only finite stuttering, while other works have allowed for infinite repetition of a symbol [5, 50, 55]. This difference has significant consequences for what properties are immune to the mutation.
Theorem 12
(All Non-Proximate Properties are Immune to Stutter) Given a property \({\mathcal {L}\!\subseteq \! (\varSigma ^\omega \setminus {{\mathbf {\mathtt{{{Prox}}}}}})}\), for all pairs \({(\sigma ,\sigma ') \!\in \! \textit{Stutter}^1}\), it must be true that  .
.
Proof
The proof follows directly from Definitions 9 and 16. For all non-Proximate Properties, \({\mathcal {L}\in (\varSigma ^\omega \setminus {{\mathbf {\mathtt{{{Prox}}}}}})}\) and for all finite prefixes \({\alpha \in \varSigma ^*}\) for all infinite suffixes \({\forall \beta \in \varSigma ^\omega }\) and for all symbols \({x \in \varSigma }\), either \({\alpha \cdot \langle x \rangle \cdot \beta \in \mathcal {L}}\), and \({\alpha \cdot \langle x, x \rangle \cdot \beta \in \mathcal {L}}\), or \({\alpha \cdot \langle x \rangle \cdot \beta \notin \mathcal {L}}\), and \({\alpha \cdot \langle x, x \rangle \cdot \beta \notin \mathcal {L}}\). Clearly, \(\textit{true}\) is trustworthy, since for all pairs \((\sigma ,\sigma ') \in \textit{Stutter}^1\), if \({\sigma ' \cdot \mu \in \mathcal {L}}\) for all infinite suffixes \({\mu \in \varSigma ^\omega }\), then \({\sigma \cdot \mu \in \mathcal {L}}\). By the same logic, \(\textit{false}\) is trustworthy. If there exist infinite suffixes \({\mu _t,\mu _f \in \varSigma ^\omega }\) such that \({\sigma ' \cdot \mu _t \in \mathcal {L}}\) and \({\sigma ' \cdot \mu _f \notin \mathcal {L}}\), then \({\sigma \cdot \mu _t \in \mathcal {L}}\) and \({\sigma \cdot \mu _f \notin \mathcal {L}}\), so \({{\varvec{?}}}\) is also trustworthy. By Theorem 3 such a property is immune. \(\square \)
8.4 Channels with out-of-order
Properties that are immune to OutOfOrder are limited to subclasses of Liveness and Morbidity. The Inclusion and Exclusion classes defined in Sect. 7 are limited to properties where satisfaction or violation depend on the presence of specific symbols.
Theorem 13
(Inclusion and Exclusion Properties are Immune to OutOfOrder) Given a property \({\mathcal {L}\in {{\mathbf {\mathtt{{{Incl}}}}}}\cup {{\mathbf {\mathtt{{{Excl}}}}}}}\), for all pairs of finite traces \({(\sigma ,\sigma ') \in \textit{OutOfOrder}^1}\), it must be true that  .
.
Proof
The proof follows directly from Definitions 10, 19 and 20. By Definition 19, given a property \(\mathcal {L}\in {{\mathbf {\mathtt{{{Incl}}}}}}\), for all traces in that property \({s \in \mathcal {L}}\) there exists a set of symbols \({X \subseteq \varSigma }\) such that for an infinite trace \(\sigma \in \varSigma ^\omega \), \(\sigma \in \mathcal {L}\) iff all of the symbols in X are in \(\sigma \). By Definition 10, for all pairs of finite traces \({(\sigma ,\sigma ') \in \textit{OutOfOrder}^1}\) there cannot exist a symbol \({x \in \varSigma }\) such that \({x \in \sigma '}\) and \({x \notin \sigma }\). Since all pairs \({(\sigma ,\sigma ') \in \textit{OutOfOrder}^1}\) must contain the same symbols, they must result in the same verdicts. The same logic applies for Definition 20 and violation, rather than satisfaction, of the property. \(\square \)
Theorem 14
(No Verdicts are Trustworthy for Non-Inclusion, Non-Exclusion Properties Over Channels with OutOfOrder) Given a property \({\mathcal {L}\subseteq (\varSigma ^\omega \setminus ({{\mathbf {\mathtt{{{Incl}}}}}}\cup {{\mathbf {\mathtt{{{Excl}}}}}}))}\), for all verdicts \({v \in \mathbb {B}_{3}}\) there exists a pair of traces \({(\sigma ,\sigma ') \in \textit{OutOfOrder}^1}\) such that  and
and  , except in the case where \(\mathcal {L}\in {{\mathbf {\mathtt{{{NFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}\) and \(v = {{\varvec{?}}}\), since that is the only possible verdict for such properties.
, except in the case where \(\mathcal {L}\in {{\mathbf {\mathtt{{{NFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}\) and \(v = {{\varvec{?}}}\), since that is the only possible verdict for such properties.
Proof
The proof, again, follows directly from Definitions 10, 19 and 20. Consider a property \({\mathcal {L}\subseteq (\varSigma ^\omega \setminus ({{\mathbf {\mathtt{{{Incl}}}}}}\cup {{\mathbf {\mathtt{{{Excl}}}}}}))}\). Then, there must exist two infinite traces \({\sigma ,\sigma ' \in \varSigma ^\omega }\) such that \({\sigma \in \mathcal {L}}\) and \({\sigma ' \notin \mathcal {L}}\) where all symbols \({s \in \varSigma }\) occur in both string \({s \in \sigma }\) and \({s \in \sigma '}\). In that case, there are two possibilities.
-
1.
Satisfaction or violation depend on infinite strings. In that case, either both satisfaction and violation depend on infinite strings, so \({\mathcal {L}\in {{\mathbf {\mathtt{{{NFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}}\) and the verdict is always \({{\varvec{?}}}\), or only one depends on infinite strings and the other is covered by the second case.
-
2.
Satisfaction or violation depend on symbol order. In that case, by Definition 10, there exists a pair of finite traces \({(\sigma ,\sigma ') \in \textit{OutOfOrder}^1}\) such that \({\sigma \in \mathcal {L}}\) and \({\sigma ' \notin \mathcal {L}}\).
\(\square \)
8.5 Utility of mutation immune properties
Many properties that are immune to the Stutter and OutOfOrder mutations or have trustworthy verdicts in the presence of Loss are useful. To show the importance of these properties, we provide a classification of property specification patterns from Dwyer, Avrunin, and Corbett’s survey [28]. This analysis shows that the most common patterns are monitorable over some unreliable channels.
Table 2 shows the property specification patterns from [28] and where they fit in the updated FR/FS classification. Note that we only list patterns in the global scope as these patterns account for 78.9% of all the properties in the survey. In the table, the Pattern column gives the name of the pattern, Class gives the classification of that pattern in the updated FR/FS taxonomy, and Occurrence gives the incidence of that pattern in the global scope in the original study [28].
All of the patterns in Table 2 are immune to at least Stutter, and most are immune to or have trustworthy verdicts over other mutations. The Absence, Universality, Existence, and Bounded Existence patterns are all either Inclusive or Exclusive Properties. These patterns are immune to Stutter and OutOfOrder and have trustworthy verdicts over Loss and make up 37.2% of the global-scope properties from [28]. The Precedence and Precedence Chain patterns, which make up 56.8% of global-scope properties, are non-Proximate and immune to Stutter. The Response and Response Chain patterns, which only make up 5.9% of global-scope properties, are in \({{\mathbf {\mathtt{{{NFR}}}}}}\cap {{\mathbf {\mathtt{{{NFS}}}}}}\), which means they are non-monitorable and trivially immune to all mutations.
The property classification in this section is valuable for quickly identifying properties that can be monitored over channels with the Loss, Corruption, Stutter, and OutOfOrder mutations. However, custom mutations that more precisely model an unreliable channel must be analyzed separately. This requires a decision procedure that can accommodate any mutation. By Rice’s Theorem, monitorability over unreliable channels is undecidable in the general case where the language may require a Turing Machine to express. Most properties of interest, however, including those expressible as LTL, are \(\omega \)-regular. We now provide a decision procedure for those properties expressible by an NBA.
9 Deciding immunity for \(\omega \)-regular properties
To determine the immunity of an \(\omega \)-regular property to a trace mutation, we must construct automata that capture the notion of uncertainty from \(\mathbb {B}_{3}\). Bauer et al. defined a simple process to build a \(\mathbb {B}_{3}\) monitor using two DFAs in their work on \(\hbox {LTL}_3\) [13]. We will examine these DFAs to decide if the property is true-false immune to the trace mutation.
Two DFAs are needed to represent the \(\mathbb {B}_{3}\) output of the monitor, since each DFA can only accept or reject a trace. In the monitor, if one DFA rejects the trace then the verdict is \(\bot \), if the other rejects the trace then the verdict is \(\top \) and if neither reject then the verdict is \({{\varvec{?}}}\). It is not possible for both DFAs to reject due to how they are constructed.
The construction procedure for the monitor begins by complementing the property. A language of infinite words \(\mathcal {L}\) is represented as an NBA \({\mathcal {A}_\mathcal {L}= (Q,\varSigma ,q_0,\delta ,F_{\mathcal {L}})}\), for example, an LTL formula can be converted to an NBA by tableau construction [56]. The NBA is then complemented to form \({\overline{\mathcal {A}_\mathcal {L}} = (\overline{Q},\varSigma ,\overline{q_0},\overline{\delta },\overline{F_{\mathcal {L}}})}\).
Remark 1
The upper bound for NBA complementation is \(2^{O(n \log n)}\), so it is cheaper to complement an LTL property and construct its NBA if starting from temporal logic [43].
To form the monitor, create two NFAs based on the NBAs and then convert them to DFAs. The two NFAs are defined as \({\mathcal {A} = (Q,\varSigma ,q_0,\delta ,F)}\) and \({\overline{\mathcal {A}} = (\overline{Q},\varSigma ,\overline{q_0},\overline{\delta },\overline{F})}\) The new accepting states are the states from which an NBA accepting state is reachable. That is, we populate the accepting states so that  , and
, and  . The two NFAs are then converted to DFAs via subset construction. The verdict for a finite trace \(\sigma \) is then given as the following function
. The two NFAs are then converted to DFAs via subset construction. The verdict for a finite trace \(\sigma \) is then given as the following function  .
.
Definition 21
(\(\mathbb {B}_{3}\) Monitor Verdict) Given a property \(\mathcal {L}\subseteq \varSigma ^{\omega }\) , derive \(\mathbb {B}_{3}\) monitor DFAs \(\mathcal {A}\) and \(\overline{\mathcal {A}}\). The \(\mathbb {B}_{3}\) verdict for a string \(\sigma \in \varSigma ^*\) is the following.

Example
Figure 1b shows the NBA \(\mathcal {A}_\mathcal {L}\) that accepts the infinite-string language of the LTL formula \(\varphi = G(a \rightarrow F \lnot a) \vee F b\). To construct an \(\hbox {LTL}_3\) monitor for \(\varphi \), we must first complement this NBA, then use the two NBAs to create NFAs and finally DFAs.
Figure 4a shows the NBA \(\overline{\mathcal {A}_\mathcal {L}}\) that accepts the language \(L[\![\lnot \varphi ]\!]\) and is the complement of \(\mathcal {A}_\mathcal {L}\) in Fig. 1b. To obtain monitor DFAs, the states and transitions from these NBAs are used to construct NFAs with new accepting conditions, and then the NFAs are determinized. Figure 4b, c shows the simplified monitor DFAs for \(L[\![\varphi ]\!]\) and \(L[\![\lnot \varphi ]\!]\), respectively. The monitor reaches a \(\top \) verdict if the input trace prefix contains a symbol where b holds; otherwise, the verdict is \({{\varvec{?}}}\).
We can now restate Definition 13 using monitor automata. This new definition will allow us to construct a decision procedure for a property’s immunity to a mutation.
Theorem 15
(True-False Immunity to Unreliable Channels for \(\omega \)-Regular Properties) Given an \(\omega \)-regular language \({\mathcal {L}\subseteq \varSigma ^{\omega }}\), derive \(\mathbb {B}_{3}\) monitor DFAs \({\mathcal {A} = (Q,\varSigma ,q_0,\delta ,F)}\) and \({\overline{\mathcal {A}} = (\overline{Q},\varSigma ,\overline{q_0},\overline{\delta },\overline{F})}\). \(\mathcal {L}\) is true-false immune to a trace mutation \({\mathcal {M}^k \subseteq \varSigma ^* \times \varSigma ^*}\) iff for all pairs of finite traces in the mutation \({(\sigma ,\sigma ') \in \mathcal {M}^k}\), it must be that \((\sigma \notin \text {L}(\mathcal {A}) \Leftrightarrow \sigma ' \notin \text {L}(\mathcal {A}))\) and \({(\sigma \notin \text {L}(\overline{\mathcal {A}}) \Leftrightarrow \sigma ' \notin \text {L}(\overline{\mathcal {A}}))}\).
Proof
By Definition 13 we need only show that  is equivalent to \((\sigma \notin \text {L}(\mathcal {A}) \Leftrightarrow \sigma ' \notin \text {L}(\mathcal {A}))\) and \({(\sigma \notin \text {L}(\overline{\mathcal {A}}) \Leftrightarrow \sigma ' \notin \text {L}(\overline{\mathcal {A}}))}\). There are three cases: \(\bot \), \(\top \), and \({{\varvec{?}}}\). For \(\bot \) and \(\top \) it is obvious from Definition 21 that the verdicts are derived from exclusion from the languages of \(\mathcal {A}\) and \(\overline{\mathcal {A}}\). As there are only three possible verdicts, this also shows the \({{\varvec{?}}}\) case. \(\square \)
is equivalent to \((\sigma \notin \text {L}(\mathcal {A}) \Leftrightarrow \sigma ' \notin \text {L}(\mathcal {A}))\) and \({(\sigma \notin \text {L}(\overline{\mathcal {A}}) \Leftrightarrow \sigma ' \notin \text {L}(\overline{\mathcal {A}}))}\). There are three cases: \(\bot \), \(\top \), and \({{\varvec{?}}}\). For \(\bot \) and \(\top \) it is obvious from Definition 21 that the verdicts are derived from exclusion from the languages of \(\mathcal {A}\) and \(\overline{\mathcal {A}}\). As there are only three possible verdicts, this also shows the \({{\varvec{?}}}\) case. \(\square \)
We say that an automaton is immune to a trace mutation in a similar way to how a property is immune. To show that a property is true-false immune to a mutation, we only need to show that its \(\mathbb {B}_{3}\) monitor automata are also immune to the property. Note that, since the implication is both directions, we can use either language inclusion or exclusion in the definition.
Definition 22
(Finite Automaton Immunity) Given a finite automaton \({\mathcal {A} = (Q,\varSigma ,q_0,\delta ,F)}\) and a trace mutation \({\mathcal {M}^k \subseteq \varSigma ^* \times \varSigma ^*}\), \(\mathcal {A}\) is immune to \(\mathcal {M}^k\) iff for all pairs of finite traces in the mutation \({(\sigma ,\sigma ') \in \mathcal {M}^k}\), it must be that \({\sigma \in \text {L}(\mathcal {A}) \Leftrightarrow \sigma ' \in \text {L}(\mathcal {A})}\).
With this definition we can provide a decision procedure for the monitorability of an \(\omega \)-regular property over an unreliable channel. The procedure will check the immunity of the \(\mathbb {B}_{3}\) monitor automata to the mutations from the channel, as well as the property’s monitorability. If the DFAs are both immune to the mutations and the property is monitorable, then the property is monitorable over the unreliable channel.
10 Decision procedure for finite automaton immunity
We propose Algorithm 1 for deciding whether a DFA is immune to a trace mutation. The algorithm is loosely based on Hopcroft and Karp’s near-linear algorithm for determining the equivalence of finite automata [37].

Algorithm 1 checks if the DFA \(\mathcal {A}\) is immune to the mutation M, where \(\mathcal {A}\) represents part of the \(\mathbb {B}_{3}\) monitor for a property and M is a relation given by \(\mathcal {M}^1\) in Definition 11. The intuition behind Algorithm 1 is to follow transitions for pairs of unmutated and corresponding mutated strings in M and verify that they lead to the same acceptance verdicts. More specifically, Algorithm 1 finds sets of states which must be equivalent for the DFA to be immune to a given mutation. The final verdict of immune is found by checking that no equivalence class contains both final and non-final states. If an equivalence class contains both, then there are some strings for which the verdict will change due to the given mutation.
If all mutations required only a string of length one, the step at Lines 7 and 8 could follow transitions for pairs of single symbols. However, mutations like \(\textit{OutOfOrder}\) require strings of at least two symbols, so we must follow transitions for short strings. We express this idea of a minimum length for a mutation in the \(\textit{minLength} : 2^{\varSigma ^* \times \varSigma ^*} \rightarrow \mathbb {N}\) function. For mutations in Sect. 4, \(\textit{minLength}(\textit{Loss}) = \textit{minLength}(\textit{Corruption}) = \textit{minLength}(\textit{Stutter}) = 1\) and \(\textit{minLength}(\textit{OutOfOrder}) = 2\). Note that \(\textit{minLength}\) for unions must increase to permit the application of both mutations on a string. For example, \(\textit{minLength}(\textit{Loss}\cup \textit{Corruption}) = 2\). This length guarantees that each string has at least one mutation, which is sufficient to show immunity by Theorem 2.
The algorithm works as follows. We assume a mutation can occur at any time, so we begin by following transitions for pairs of mutated and unmutated strings from every reachable state (stored in the set R). On Lines 5-10, for each pair \((\sigma ,\sigma ')\) in M and for each reachable state, we compute the states \(q_1\) and \(q_2\) reached from \(\sigma \) (respectively, \(\sigma '\)). The map E contains equivalence classes, which we update for \(q_1\) and \(q_2\) to hold the set containing both states. The pair of states is also added to the worklist T, which contains equivalent states from which string suffixes must be explored.
The loop on Lines 11-20 then explores those suffixes. It takes a pair of states \((q_1,q_2)\) from the worklist and follows transitions from those states to reach \(n_1\) and \(n_2\). If \(n_1\) and \(n_2\) are already marked as equivalent to other states in E or aren’t marked as equivalent to each other, those states are added to the worklist, and their equivalence classes in E are merged. If at the end, there is an equivalence class with final and non-final states, then \(\mathcal {A}\) is not immune to M.
Theorem 16
(Immunity Procedure Correctness) Algorithm 1 is sound and complete for any DFA and prefix-assured mutation. That is, given a DFA \({\mathcal {A} = (\varSigma , Q, q_0, \delta , F)}\), and a mutation, M, \({\textsc {Immune}(\mathcal {A},M) \Leftrightarrow \mathcal {A}}\) is immune to M.
Proof
By Definition 22, this is equivalent to showing that \({\textsc {Immune}(\mathcal {A},M) \Leftrightarrow }\) \({(\forall (\sigma ,\sigma ') \in M,\ \sigma \in \text {L}(\mathcal {A}) \Leftrightarrow \sigma ' \in \text {L}(\mathcal {A}))}\).
We will prove the \(\Rightarrow \) direction (soundness) by contradiction. Suppose at the completion of the algorithm that all sets in E contain only final or non-final states, but that \(\mathcal {A}\) is not immune to M. There is at least one pair \((\sigma _b,\sigma _b') \in M\) where one leads to a final state, and one does not. If Algorithm 1 had checked this pair then these states would be in an equivalence class in E. Since the loop on Line 7 follows transitions for pairs in M of length \(\textit{minLength}(M)\), the reason \((\sigma _b,\sigma _b')\) was not checked must be because \(|\sigma _b| \ne \textit{minLength}(M)\). The length of \(\sigma _b\) must be greater than \(\textit{minLength}(M)\) since strings shorter than \(\textit{minLength}(M)\) cannot be mutated by M. Since M is prefix-assured, there must be a pair  that are prefixes of \((\sigma _b,\sigma _b')\). The loop on Line 11 will check \({(\sigma \cdot s,\sigma ' \cdot s)\ \forall s \in \varSigma ^*}\). Therefore, it must be the case that there exist two different finite suffixes
that are prefixes of \((\sigma _b,\sigma _b')\). The loop on Line 11 will check \({(\sigma \cdot s,\sigma ' \cdot s)\ \forall s \in \varSigma ^*}\). Therefore, it must be the case that there exist two different finite suffixes  and \({\sigma _b' = \sigma ' \cdot u}\). However, if \(t \ne u\) then \({(\sigma _b,\sigma _b') \in M^k}\) for some \(k > 1\), so \(\mathcal {A}\) is immune to \(M^1\) but not \(M^k\), but from Theorem 2 this is a contradiction.
and \({\sigma _b' = \sigma ' \cdot u}\). However, if \(t \ne u\) then \({(\sigma _b,\sigma _b') \in M^k}\) for some \(k > 1\), so \(\mathcal {A}\) is immune to \(M^1\) but not \(M^k\), but from Theorem 2 this is a contradiction.
We prove the \(\Leftarrow \) direction (completeness) by induction. We will show that if \(\mathcal {A}\) is immune to M then no set in E, and no pair in T will contain both final and non-final states. The base case at initialization is obviously true since every set in E contains only one state and T is empty. The induction hypothesis is that at a given step i of the algorithm if \(\mathcal {A}\) is immune to M then every set in E and every pair in T contains only final or non-final states.
At step \(i+1\), in the loop starting at Line 7, E and T are updated to contain states reached by following \(\sigma \) and \(\sigma '\). Clearly, if \(\mathcal {A}\) is immune to M then these states must be both final or non-final since we followed transitions from reachable states for a pair in M. In the loop on Line 11, \(n_1\) and \(n_2\) are reached by following the same symbol in the alphabet from a pair of states in T. If \(\mathcal {A}\) is immune to M, the strings leading to that pair of states must both be in, or both be out of the language. So, extending both strings by the same symbol in the alphabet creates two strings that must both be in or out of the language. These states reached by following these strings are added to T on Line 20.
On Lines 17 and 19, the two sets in E corresponding to \(n_1\) and \(n_2\) are merged. Since both sets must contain only final or non-final states, and one-or-both of \(n_1\) and \(n_2\) are contained in them, the union of the sets must also contain only final or non-final states. \(\square \)
Theorem 17
(Immunity Procedure Complexity) Algorithm 1 is Fixed-Parameter Tractable. That is, given a DFA \(\mathcal {A} = (\varSigma , Q, q_0, \delta , F)\), and a mutation, M, its maximum running time is \(|Q|^{O(1)}f(k)\), where f is some function that depends only on some parameter k.
Proof
The run-time complexity of Algorithm 1 is \(O(n)O(m^l\ f(M))\) where \({n = |Q|}\), \({m = |\varSigma |}\), \({l = \textit{minLength}(M)}\), and f is a function on M. First, Lines 4, 7, 8, 9, 10, 12, 13, 15, 16, 17, 18, 19, and 20 execute in constant time, while each of Lines 2, 3, and 21 run in time bounded by n.
The initialization loop at Line 5 runs once for each pair in the mutation where the length of \(\sigma \) is bounded by \(\textit{minLength}(M)\). This count is \(m^l\) times a factor f(M) determined by the mutation. For example, \(f(\textit{Loss}) = l\) because each \(\sigma \) is mutated to remove each symbol in the string. Critically, this factor f(M) must be finite, which it is for the mutations \(\mathcal {M}^1\). The loop at Line 6 runs in time bounded by n, so the body of the loop is reached at most \(m^l f(M) n\) times.
The loop at Line 11 may run at most \(m^l f(M) + n\) times. The loop continues while the worklist T is non-empty. Initially, T has \(m^l f(M)\) elements. Each time Line 13 runs, an element is removed from the worklist. For an element to be added to T, it must contain states corresponding to sets in E which differ. When this occurs, those two corresponding sets are merged, so the number of unique sets in E is reduced by at least one. Therefore, the maximum number of times Line 20 can be reached and an element added to T is n. \(\square \)
Note that, in practice, \(\textit{minLength}(M)\) is usually small (often only one), so Algorithm 1 achieves near linear performance in the size of the FA. The size of the alphabet has an effect, but it is still quadratic.
11 Related work
Unreliable channels have been acknowledged in formal methods research for some time. For example, Lamport suggested in 1983 that temporal logics without next operators were immune to stutter [44]. More recent works by Purandare et al. [53] and Lomuscio et al. [47] applied the principle suggested by Lamport for performance optimizations.
In this section, we describe related work in three areas. First, on works examining unreliable channels in RV, second, on the study of unreliable channels as they relate to Communicating Finite State Machines (CFSMs), and finally, on other definitions of monitorability.
11.1 Runtime verification
RV seeks to decide whether a trace generated by the execution of a program satisfies a specification, often expressed in a temporal logic like LTL [9]. Most RV methods assume an ideal trace, but the topic of unreliable channels is of growing interest in the field.
Work has been done to show which properties are verifiable on a trace with mutations and to express degrees of confidence when they are not. Stoller et al. used Hidden Markov Models (HMMs) to compute the probability of a property being satisfied on a lossy trace [58]. Their definition of lossy included a “gap” marker indicating where symbols were missing. They used HMMs to predict the missing states where gaps occurred and aided their estimations with a learned probability distribution of state transitions. Joshi et al. introduced an algorithm to determine if a specification could be monitored soundly in the presence of a trace with transient loss, meaning that eventually it contained successfully transmitted events [40]. They defined monotonicity to identify properties for which the verdicts could be relied upon once a decision was made.
Garg et al. introduced a first-order logic with restricted quantifiers for auditing incomplete policy logs [34]. The authors used restricted quantifiers to allow monitoring policies that would, in principle, require iterating over an infinite domain. Basin et al. also specified a first-order logic for auditing incomplete policy logs [12]. Basin et al. also proposed a semantics and monitoring algorithm for Metric Temporal Logic (MTL) with freeze quantifiers that was sound and complete for unordered traces [11]. Their semantics was based on a three-value logic, and the monitoring algorithm was evaluated over ordered and unordered traces. All three of these languages used a three value semantics (\(t, f, \bot \)) to model a lossy trace, where \(\bot \) represented missing information.
Leuker et al. introduced a technique for a Stream Runtime Verification (SRV) over incomplete traces [45]. They defined an abstract form of the TeSSLa SRV language and showed how it could be used to obtain sound verdicts on traces with well-defined gaps. Abstract verdicts were clearly delineated from concrete ones, so that imprecise results could not be confused for incorrect results. Their work assumed that missing values were within a known range and that gaps were identifiable.
Li et al. examined out-of-order data arrival in Complex Event Processing (CEP) systems and found that SASE [62] queries processed using the Active Instance Stack (AIS) data structure would fail in several ways [46]. They proposed modifications to AIS to support out-of-order data and found acceptable experimental overhead to their technique.
Baader, Bauer, and Tiu examined the complexity of regular language inclusion and exclusion of a finite trace with lost symbols [7]. They modeled traces as patterns where missing sequences were replaced with variables and considered both the linear case, where variables were unique, and the non-linear case, where they could repeat. The authors showed that, for languages specified as an NFA, linear exclusion was solvable in polynomial time while non-linear exclusion was PSPACE-Complete. For inclusion, they found that both the linear and non-linear cases were PSPACE-Complete.
Runtime verification in the presence of noise has been studied in the context of Analog and Mixed Signal (AMS) components, also referred to as mixed signal circuits. These integrate analog circuits and digital circuits, e.g., such a component can transform an analog signal to a digital signal. Wang et al. describe using runtime verification in combination with Monte Carlo simulation (called statistical runtime verification) to analyze Jitter [60]. Jitter is defined as the deviation in time between a noisy signal and an ideal one. A related concept is the notion of system instability, where control outputs oscillate permanently while inputs are constant. Halbwachs et al. proposed a method to verify the stability of systems using heuristics to check strongly connected components of an operator network [36].
11.2 Communicating finite state machines
Several works in information theory have modeled the problem of unreliable communication channels in CFSMs [17]. CFSM communication channels are treated as unbounded first-in first-out (FIFO) buffers between Finite State Machines (FSMs), which is a Turing complete model of computation for a class of infinite-state systems called simple reactive programs [61]. Simple reactive programs are data independent and are useful for modeling communication protocols like the Alternating Bit Protocol [10] and High-level Data Link Control (HDLC) [38]. CFSMs also form the basis of protocol specification languages such as Estelle [18], and Description Language (SDL) [16]. CFSMs with unreliable communications channels are no longer Turing complete, and a number of useful properties have been shown to hold in such cases.
Finkel introduced his notion of completely specified protocols to show that they are a class of machines for which the termination problem is decidable [32]. He defined a completely specified protocol as a CFSM where any FSM can receive any message in any local state and can stay in that state, and he showed that protocols using lossy FIFO channels are examples of such protocols. Abdulla and Jonsson later provided algorithms for deciding the termination problem for protocols on lossy FIFO buffers, as well as algorithms for some safety and eventuality properties [2].
Cécé et al. expanded this examination of unreliable FIFO channels in CFSMs by considering channels with insertion errors, duplication errors, and a combination of insertion, duplication, and lossy errors [19]. Their work defined insertion errors in FIFO buffers to be equal to our general notion of noisy traces, but their duplication errors were restricted to consecutive duplicates. They showed that noisy errors on a communication channel between two FSMs decrease the expressive power of the system more than lossy errors, while consecutive duplication errors do not decrease its expressive power at all.
Iyer and Narasimha introduced probability to the notion of lossy communications channels [39]. They argue that this is a more realistic notion of loss, as hardware reliability statistics are often known. Their work included algorithms for solving probabilistic notions of reachability and model checking. That is, given a channel with a known probability of loss, they asked whether a global state in the CFSM was reachable with a certain probability and tolerance, and whether a Propositional Temporal Logic (PTL) property was true with a certain probability and tolerance. Baier and Engelen proved that the set of message sequences on a probabilistic lossy channel that satisfy an LTL property could be decided with probability 1 if the probability of message loss was at least 1/2 [8]. Abdulla et al. proved that, if the probability of message loss was less than 1/2 then the same problem was undecidable [1].
Peng and Makki introduced Lossy Communicating Finite State Machines (LCFSMs) to simplify protocol modeling for lossy channels [51]. Traditionally, loss in unreliable communications channels has been modeled using the addition of extra CFSMs which consume messages. The authors argued that this leads to messy CFSM specifications which obfuscate the protocol being modeled. They introduced a delete action to allow the removal of these extra CFSMs.
11.3 Other definitions of monitorability
Some other definitions of monitorability exist which are outside the scope of this work. These solutions either assume partial knowledge of the monitored system or concern monitoring multiple systems simultaneously.
Sistla, Žefran, and Feng defined monitorability and strong monitorability for partially observable stochastic systems modeled as HMMs [57]. Gondi, Patel, and Sistla had already introduced this notion in their work on external monitoring of \(\omega \)-regular properties of stochastic systems [35], but the later work focused on formalizing the concept and on internal monitoring. In these works, properties to be monitored are given as deterministic Streett automata [54] and a model of the system is supplied as a HMM. This varies from definitions of monitoring where only a trace of the output symbols from the monitored system is assumed to be known.
Sistla et al. use Acceptance Accuracy (AA) and Rejection Accuracy (RA) to define monitorability and strong monitorability, and define them as properties of both a monitored formula and a monitored system. AA is given as the probability that a monitor accurately returns a positive verdict (accepts) for a formula and a system model, while RA is given as the probability that a monitor accurately returns a negative verdict (rejects) for a formula and a system model. Sistla et al. thus define that a system is strongly monitorable with respect to a formula if there exists a monitor such that both the AA and RA are 1. They then define that a system is monitorable with respect to a formula if there exists a monitor(s) such that accuracies arbitrarily close to 1 may be achieved. The authors conclude that all properties that can be represented as Streett automata are considered externally monitorable for finite state systems and safety properties are also strongly monitorable.
Agrawal and Bonakdarpour first proposed monitoring hyperproperties and introduced a notion of monitorability for such properties [4]. Hyperproperties are sets of sets of traces where monitoring requires reasoning about many prefixes simultaneously. The authors introduce a three-valued semantics for the hyperproperty specification language HyperLTL [23] and define monitorable classes in that logic. Stucki et al. proposed incorporating partial or complete knowledge of the system into monitoring hyperproperties [59]. They showed that monitoring hyperproperties without such information is infeasible in general and refined Agrawal and Bonakdarpour’s definition of hyperproperty monitorability to incorporate computability of the monitor.
Francalanza, Aceto, and Ingolfsdottir defined monitorability for \(\mu \)-Hennessy-Milner Logic (\(\mu \)HML), a branching time logic for RV based on the modal \(\mu \)-calculus [33]. They characterized what properties of \(\mu \)HML are monitorable and gave a method to synthesize monitors for those properties. Aceto et al. later introduced a hierarchy of monitorable fragments for \(\mu \)HML and established different guarantees for each fragment [3].
12 Conclusions and future work
The mutations from Definitions 7 to 10 are useful abstractions of common problems in communication. However, in many cases, they are stronger than is needed as practitioners may have knowledge of the channel that constrains the mutations. For example, on Mars Science Laboratory , messages contain sequence numbers which can be used to narrow the range of missing symbols. Although the property classification from Sect. 8 cannot be used for custom mutations, mutations can be easily defined and then properties can be tested for immunity using Algorithm 1. Custom mutations should avoid behavior that requires long strings to mutate, however, as this causes exponential slowdown. Future work should incorporate a decision procedure for trustworthy verdicts that can be used for custom mutations.
Well-designed mutations like those from Definitions 7–10 can be checked quickly. However, the method relies on \(\mathbb {B}_{3}\) monitor construction to obtain DFAs, and the procedure to create them from an NBA is in 2EXPSPACE. We argue that this is an acceptable cost of using the procedure since it is done offline and a monitor must be derived to check the property in any case. Future work should explore ideas from the study of monitorability [27, 49] to find a theoretical bound on deciding immunity and to explore algorithms that do not require monitor construction.
Another avenue for improving our work is to incorporate partial system models to reduce the range of unmutated strings as in gray-box monitoring [59]. Currently, the definition of immunity to a mutation requires that any string (using the alphabet) could be mutated. For many systems, this is more general than is needed, and constraining unmutated strings can allow for more properties to be considered immune and therefore monitorable.
Our definition of monitorability also assumes that every verdict must be trustworthy for a mutation, but some properties may be useful to monitor where only some verdicts are trustworthy. This is similar to how Weak Monitorability relaxes the requirement from Classical Monitorability that every execution may reach a true or false verdict. It may be interesting to define a notion of Weak Monitorability over Unreliable Channels that only requires true and false to be trustworthy.
The ability to check properties expressible by NBAs for monitorability over unreliable channels allows RV to be considered for applications where it would have previously been ignored. To arrive at this capability, we first needed to define monitorability over unreliable channels using both existing notions of monitorability and a new concept of mutation immunity. We proved that immunity to a single application of a mutation is sufficient to show immunity to any number of applications of that mutation, and we defined true-false immunity using \(\mathbb {B}_{3}\) semantics. The FR/FS classification provided a framework that we extended to categorize the properties that are immune to common mutations. In some cases, we found that properties had trustworthy verdicts when monitored over an unreliable channel, despite not being immune to the mutation from that channel.
We believe unreliable communication is an important topic for RV and other fields that rely on remote systems.
References
Abdulla, P., Baier, C., Iyer, P., Jonsson, B.: Reasoning about probabilistic lossy channel systems. In: International Conference on Concurrency Theory (CONCUR’20), LNCS, vol. 1877, pp. 320–333. Springer (2000)
Abdulla, P.A., Jonsson, B.: Verifying programs with unreliable channels. Inf. Comput. 127(2), 91–101 (1996). https://doi.org/10.1006/inco.1996.0053
Aceto, L., Achilleos, A., Francalanza, A., Ingólfsdóttir, A., Lehtinen, K. (2019). Adventures in monitorability: from branching to linear time and back again. In: Symposium on Principles of Programming Languages (POPL’19), vol. 3. ACM Press. https://doi.org/10.1145/3290365
Agrawal, S., Bonakdarpour, B.: Runtime verification of k-safety hyperproperties in HyperLTL. In: Computer Security Foundations Symposium (CSF’16), pp. 239–252. IEEE (2016). https://doi.org/10.1109/CSF.2016.24
Alpern, B., Demers, A.J., Schneider, F.B.: Safety without stuttering. Inf. Process. Lett. 23(4), 177–180 (1986). https://doi.org/10.1016/0020-0190(86)90132-8
ARM Limited (2019) Embedded trace macrocell architecture specification.http://infocenter.arm.com/help/index.jsp?topic=/com.arm.doc.ihi0014q/
Baader, F., Bauer, A., Tiu, A.: Matching trace patterns with regular policies. In: International Conference on Language and Automata Theory and Applications (LATA’09), LNAI, vol .5457, pp. 105–116. Springer (2009). https://doi.org/10.1007/978-3-642-00982-2_9
Baier, C., Engelen, B.: Establishing Qualitative Properties for Probabilistic Lossy Channel Systems, LNCS, vol. 1601, pp 34–52. Springer (1999) https://doi.org/10.1007/3-540-48778-6_3
Barringer, H., Goldberg, A., Havelund, K., Sen, K.: Rule-based runtime verification. In: Verification, Model Checking, and Abstract Interpretation (VMCAI’04), LNCS, vol. 2937, pp. 44–57. Springer (2009)
Bartlett, K.A., Scantlebury, R.A., Wilkinson, P.T.: A note on reliable full-duplex transmission over half-duplex links. Commun. ACM 12(5), 260–261 (1969). https://doi.org/10.1145/362946.362970
Basin, D., Klaedtke, F., Zălinescu, E.: Runtime verification of temporal properties over out-of-order data streams. In: Computer Aided Verification (CAV’17), LNCS, vol. 10426, pp. 356–376. Springer(2017). https://doi.org/10.1007/978-3-319-63387-9_18
Basin, D.A., Klaedtke, F., Marinovic, S., Zalinescu, E.: Monitoring compliance policies over incomplete and disagreeing logs. In: International Conference on Runtime Verification (RV’12), LNCS, vol. 7687, pp. 151–167. Springer (2012). https://doi.org/10.1007/978-3-642-35632-2_17
Bauer, A., Leucker, M., Schallhart, C.: Monitoring of real-time properties. In: Foundations of Software Technology and Theoretical Computer Science (FSTTCS’06), LNCS, vol. 4337, pp. 260–272. Springer (2006). https://doi.org/10.1007/11944836_25
Bauer, A., Leucker, M., Schallhart, C.: Comparing LTL semantics for runtime verification. J. Logic Comput. 20(3), 651–674 (2010). https://doi.org/10.1093/logcom/exn075
Bauer, A., Leucker, M., Schallhart, C.: Runtime verification for LTL and TLTL. ACM Trans. Softw. Eng. Methodol. 20(4), 14:1-14:64 (2011). https://doi.org/10.1145/2000799.2000800
Belina, F., Hogrefe, D., Sarma, A.: SDL with Applications from Protocol Specification. Prentice-Hall, Inc (1991)
Brand, D., Zafiropulo, P.: On communicating finite-state machines. J. ACM 30(2), 323–342 (1983). https://doi.org/10.1145/322374.322380
Budkowski, S., Dembinski, P.: An introduction to Estelle: a specification language for distributed systems. Comput. Netw. ISDN Syst. 14(1), 3–23 (1987). https://doi.org/10.1016/0169-7552(87)90084-5
Cécé, G., Finkel, A., Iyer, S.P.: Unreliable channels are easier to verify than perfect channels. Inf. Comput. 124(1), 20–31 (1996). https://doi.org/10.1006/inco.1996.0003
Chang, E., Manna, Z., Pnueli, A.: Characterization of temporal property classes. In: International Colloquium on Automata, Languages and Programming (ICALP’92), LNCS, vol. 623, pp. 474–486. Springer (1992)
Chen, Z., Wu. Y., Wei. O., Sheng. B.: Deciding weak monitorability for runtime verification. In: International Conference on Software Engineering (ICSE’18), pp. 163–164. ACM Press (2018). https://doi.org/10.1145/3183440.3195077
Cimatti, A., Tian, C., Tonetta, S.: Assumption-based runtime verification with partial observability and resets. In: International Conference on Runtime Verification (RV’19), LNCS, vol. 11757, pp. 165–184. Springer (2019). https://doi.org/10.1007/978-3-030-32079-9_10
Clarkson, M.R., Finkbeiner, B., Koleini, M., Micinski, K.K., Rabe, M.N., Sánchez, C.: Temporal logics for hyperproperties. In: International Conference on Principles of Security and Trust (POST’14), LNCS, vol. 8414, pp. 265–284. Springer (2014). https://doi.org/10.1007/978-3-642-54792-8_15
d’Amorim, M., Roşu, G.: Efficient monitoring of \(\omega \)-languages. In: Computer Aided Verification (CAV’05), LNCS, vol. 3576, pp. 364–378. Springer (2005). https://doi.org/10.1007/11513988_36
Diekert, V., Gastin, P.: First-Order Definable Languages, pp. 261–306. Amsterdam University Press (2008). https://doi.org/10.2307/j.ctt46mv83.12
Diekert, V., Leucker, M.: Topology, monitorable properties and runtime verification. Theoret. Comput. Sci. 537, 29–41 (2014). https://doi.org/10.1016/j.tcs.2014.02.052
Diekert, V., Muscholl, A., Walukiewicz, I.: A note on monitors and büchi automata. In: International Colloquium on Theoretical Aspects of Computing (ICTAC’15), LNCS, vol. 9399, pp. 39–57. Springer (2015).https://doi.org/10.1007/978-3-319-25150-9_3
Dwyer, M., Avrunin, G., Corbett, J.: Patterns in property specifications for finite-state verification. In: International Conference on Software Engineering (ICSE’99), pp. 411–420. ACM Press (1999)
Edwards, C.D., Bell, D.J., Gladden, R.E., Ilott, P.A., Jedrey, T.C., Johnston, M.D., Maxwell, J.L., Mendoza, R., McSmith, G.W., Potts, C.L., Schratz, B.C., Shihabi, M.M., Srinivasan, J.M., Varghese, P., Sanders, S.S., Denis, M.: Relay support for the mars science laboratory mission. In: Conference on Aerospace, pp. 1–14. IEEE (2013). https://doi.org/10.1109/AERO.2013.6497325
Falcone, Y., Fernandez, J.C., Mounier, L.: Runtime verification of safety-progress properties. In: International Conference on Runtime Verification (RV’09), LNCS, vol. 5779, pp. 40–59. Springer (2009). https://doi.org/10.1007/978-3-642-04694-0_4
Falcone, Y., Fernandez, J.C., Mounier, L.: What can you verify and enforce at runtime? Int. J. Softw. Tools Technol. Transf. 14(3), 349–382 (2012). https://doi.org/10.1007/s10009-011-0196-8
Finkel, A.: Decidability of the termination problem for completely specified protocols. Distrib. Comput. 7(3), 129–135 (1994). https://doi.org/10.1007/BF02277857
Francalanza, A., Aceto, L., Ingolfsdottir, A.: Monitorability for the Hennessy-Milner logic with recursion. Formal Methods Syst. Des. 51(1), 87–116 (2017). https://doi.org/10.1007/s10703-017-0273-z
Garg, D., Jia, L., Datta, A.: olicy auditing over incomplete logs: Theory, implementation and applications. In: Conference on Computer and Communications Security (CCS’11), pp. 151–162. ACM Press (2011). https://doi.org/10.1145/2046707.2046726
Gondi, K., Patel, Y., Sistla, A.P.: Monitoring the full range of \(\omega \)-regular properties of stochastic systems. In: Verification, Model Checking, and Abstract Interpretation (VMCAI’09), LNCS, vol. 5403, pp. 105–119. Springer (2009). https://doi.org/10.1007/978-3-540-93900-9_12
Halbwachs, N., Héry, J.F., Laleuf, J.C., Nicollin, X.: Stability of discrete sampled systems. In: International Symposium on Formal Techniques in Real-Time and Fault-Tolerant Systems (FTRTFT’20), LNCS, vol. 1926, pp. 1–11. Springer (2000). https://doi.org/10.1007/3-540-45352-0_1
Hopcroft, J.E., Karp, R.M.: A Linear Algorithm for Testing Equivalence of Finite Automata, Technical Report. Cornell University (1971)
ISO, IEC 13239:2002, : Information Technology—Telecommunications and Information Exchange Between Systems—High-Level Data Link Control (HDLC) Procedures Standard, International Organization for Standardization, Geneva, CH (2002)
Iyer, P., Narasimha, M.: Probabilistic lossy channel systems. In: International Joint Conference on Theory and Practice of Software Development (TAPSOFT’97), LNCS, vol. 1214, pp. 667–681. Springer(1997). https://doi.org/10.1007/BFb0030633
Joshi, Y., Tchamgoue, G.M., Fischmeister, S.: Runtime verification of LTL on lossy traces. In: Symposium on Applied Computing (SAC’17), pp. 1379–1386. ACM Press (2017). https://doi.org/10.1145/3019612.3019827
Kauffman, S., Havelund, K., Fischmeister, S.: Monitorability over unreliable channels. In: International Conference on Runtime Verification (RV’19), LNCS, vol. 11757, pp. 256–272. Springer (2019).https://doi.org/10.1007/978-3-030-32079-9_15
Kupferman, O., Vardi, M.Y.: Model checking of safety properties. Formal Methods Syst. Des. 19(3), 291–314 (2001a). https://doi.org/10.1023/A:1011254632723
Kupferman, O., Vardi, M.Y.: Weak alternating automata are not that weak. ACM Trans. Comput. Logic 2(3), 408–429 (2001b). https://doi.org/10.1145/377978.377993
Lamport, L.: What good is temporal logic? IFIP Congress Elsevier Inf. Process. 83, 657–668 (1983)
Leucker, M., Sánchez, C., Scheffel, T., Schmitz, M., Thoma, D.: Runtime verification for timed event streams with partial information. In: International Conference on Runtime Verification (RV’19), LNCS, vol. 11757, pp. 273–291. Springer (2019). https://doi.org/10.1007/978-3-030-32079-9_16
Li, M., Liu, M., Ding, L., Rundensteiner, E.A., Mani, M.: Event stream processing with out-of-order data arrival. In: International Conference on Distributed Computing Systems Workshops (ICDCSW’07), pp. 67–67. IEEE(2007). https://doi.org/10.1109/ICDCSW.2007.35
Lomuscio, A., Penczek, W., Qu, H.: Partial order reductions for model checking temporal epistemic logics over interleaved multi-agent systems. In: Interantional Conference on Autonomous Agents and Multiagent Systems (AAMAS’10), pp. 659–666. ACM Press (2010). https://doi.org/10.3233/FI-2010-276
Lozes, É., Villard, J.L.: Reliable contracts for unreliable half-duplex communications. In: Web Services and Formal Methods (WS-FM’12), LNCS, vol. 7176, pp. 2–16. Springer (2012). https://doi.org/10.1007/978-3-642-29834-9_2
Peled, D., Havelund, K.: Refining the safety–liveness classification of temporal properties according to monitorability. In: Models, Mindsets, Meta: The What, the How, and the Why Not? Essays Dedicated to Bernhard Steffen on the Occasion of His 60th Birthday, LNCS, vol. 11200, pp. 218–234. Springer (2019). https://doi.org/10.1007/978-3-030-22348-9_14
Peled, D., Wilke, T.: Stutter-invariant temporal properties are expressible without the next-time operator. Inf. Process. Lett. 63(5), 243–246 (1997). https://doi.org/10.1016/S0020-0190(97)00133-6
Peng, W., Makki, K.: Lossy communicating finite state machines. Telecommun. Syst. 25(3), 433–448 (2004). https://doi.org/10.1023/B:TELS.0000014793.19622.0e
Pnueli, A., Zaks, A.: PSL model checking and run-time verification via testers. In: Formal Methods (FM’06), LNCS, vol. 4085, pp. 573–586. Springer (2006). https://doi.org/10.1007/11813040_38
Purandare, R., Dwyer, M.B., Elbaum, S.: Monitor optimization via stutter-equivalent loop transformation. In: International Conference on Object Oriented Programming Systems Languages and Applications (OOPSLA’10), pp. 270–285. ACM Press (2010). https://doi.org/10.1145/1869459.1869483
Safra, S.: On the complexity of \(\omega \)-automata. In: Annual Symposium on Foundations of Computer Science, pp. 319–327. IEEE (1988). https://doi.org/10.1109/SFCS.1988.21948
Sistla, A.P.: Safety, liveness and fairness in temporal logic. Formal Aspects Comput. 6(5), 495–511 (1994). https://doi.org/10.1007/BF01211865
Sistla, A.P., Clarke, E.M.: The complexity of propositional linear temporal logics. J. ACM 32(3), 733–749 (1985). https://doi.org/10.1145/3828.3837
Sistla, A.P., Žefran, M., Feng, Y.: Monitorability of stochastic dynamical systems. In: Computer Aided Verification (CAV’11), LNCS, vol. 6806, pp. 720–736. Springer (2011). https://doi.org/10.1007/978-3-642-22110-1_58
Stoller, S.D., Bartocci, E., Seyster, J., Grosu, R., Havelund, K., Smolka, S.A., Zadok, E.: Runtime verification with state estimation. In: International Conference on Runtime Verification (RV’11), LNCS, vol. 7186, pp. 193–207. Springer (2011). https://doi.org/10.1007/978-3-642-29860-8_15
Stucki, S., Sánchez, C., Schneider, G., Bonakdarpour, B.: Gray-box monitoring of hyperproperties. In: Formal Methods (FM’19), LNCS, vol. 11800, pp. 406–424. Springer (2019). https://doi.org/10.1007/978-3-030-30942-8_25
Wang, Z., Zaki, M.H., Tahar, S.: Statistical runtime verification of analog and mixed signal designs. In: International Conference on Signals, Circuits and Systems (SCS’09), pp. 1–6. IEEE (2009). https://doi.org/10.1109/ICSCS.2009.5412620
Wolper, P.: Expressing interesting properties of programs in propositional temporal logic. In: Symposium on Principles of Programming Languages (POPL’86), pp. 184–193. ACM Press (1986). https://doi.org/10.1145/512644.512661
Wu, E., Diao, Y., Rizvi, S.: High-performance complex event processing over streams. In: International Conference on Management of Data (SIGMOD’06), pp. 407–418. ACM Press (2006). https://doi.org/10.1145/1142473.1142520
Acknowledgements
The authors would like to thank Rajeev Joshi for his early contributions to the work and the reviewers for their many helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research performed by the second author was carried out at Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.
Rights and permissions
About this article
Cite this article
Kauffman, S., Havelund, K. & Fischmeister, S. What can we monitor over unreliable channels?. Int J Softw Tools Technol Transfer 23, 579–600 (2021). https://doi.org/10.1007/s10009-021-00625-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10009-021-00625-z





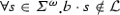 , and
, and .
.


















 . We will prove by contradiction. Now assume there exists a finite trace
. We will prove by contradiction. Now assume there exists a finite trace  , then
, then  which is the definition of a Liveness property.
which is the definition of a Liveness property. then, from Definition
then, from Definition  , we assume that
, we assume that  , so there must be a prefix of s where the verdict is
, so there must be a prefix of s where the verdict is  .
. , then either
, then either  or
or  . Suppose that
. Suppose that  , as the same argument applies for both verdicts. Then for all finite suffixes
, as the same argument applies for both verdicts. Then for all finite suffixes  where
where  or
or  , which is a contradiction.
, which is a contradiction.