Introduction

The electrode transformations of many organic compounds occurring at the electrode surface are commonly accompanied by adsorption phenomena [1]. Of these, special attentions attract the surface redox processes in which both compounds of a given redox couple are strongly immobilized on the electrode surface [1–6]. Given all the attention to the surface redox reactions, the application of voltammetry for probing the chemistry of redox proteins has recently emerged as an especially simple and powerful method of investigating biologically relevant redox-active compounds [7–10]. By simple adsorption of the redox protein sample onto the surface of some suitable lipophilic electrode, insights into the processes of electron transfer and protein–protein interactions can be obtained from experiments performed in common voltammetric set-up [7–10]. Very often, the electron transfer steps by various organic compounds and proteins, studied in thin-film or protein-film voltammetric scenarios, are coupled by chemical reactions [1, 4, 7, 11, 12]. Besides, lots of cases exist where the two electron transfer steps by the surface confined systems are bridged by an irreversible chemical reaction [1]. If we consider a surface electron transfer–chemical reaction (EC) mechanism for example, and if the product of the first electron step can be converted chemically to another electroactive specie, then we assign these reactions to follow the surface electron transfer–chemical reaction–electron transfer (ECE) mechanistic pathway. Although this reaction mechanism is quite complex, it is a widespread pathway of many proteins [7] and other important compounds in organic electrochemistry [1, 7, 13–19]. For example, the product of the first electron transfer step can undergo protonation, elimination, substitution, or reorganization reaction to give second electroactive specie [1, 13–19]. As the most familiar among the voltammetric techniques, the cyclic voltammetry is commonly used for characterization of electrochemically active systems following the ECE pathway [7, 13–16, 18, 19]. In recent two decades, however, numerous studies have demonstrated that square-wave voltammetry (SWV) is an exceptionally suitable technique for investigating the surface electrode reactions coupled by chemical reactions [1–6, 11, 12, 17]. Its unique advantages, such as high scan rate, large signal amplitude, efficient ability to discriminate against the charging current, and the possibility to get insight into both half-reactions of the redox process, make the SWV one of the most advanced members in the family of the pulse voltammetric techniques [1, 20]. In our recent works, we presented numerous theoretical studies under conditions of SWV in order to get insight into the features of various single electron transfer steps that are coupled by chemical reactions [1, 4–6, 11, 12, 21]. We have shown that SWV enables both thermodynamic and kinetic characterization of the surface electrode reactions that are coupled by chemical reactions in a very elegant way [1]. In this study, we extend the theoretical treatments of complex two-step electrode reactions under conditions of SWV [21] by considering the surface ECE electrode mechanism. The performed simulations address the surface redox steps featuring slow, modest, and fast electron transfer. The effect of the chemical kinetics and the electron transfer kinetics to the shape and position of the SW voltammetric responses brings diversity of interesting situations, which mainly depend on the rate of the chemical step but also on the differences in the standard redox potentials of both electron transfer steps. We give several hints to recognize qualitatively the surface ECE reaction in situations where both redox steps have identical or different values of their standard redox potentials. Also, hints are given for the determination of the kinetic parameters of the chemical reaction and those of the electron transfer steps.

The mathematical solutions of this mechanism are represented as integral equations, and they can be applied to any chronoamperometric technique. The numerical solutions in this work are adapted to the conditions of SWV. It is worth to mention that the initial theoretical considerations of an ECE mechanism under conditions of SWV, by redox reactions taking place from dissolved state, have been given by O’Dea et al. [17].

Mathematical model and simulation details

The considered surface ECE redox mechanism is presented by following reaction scheme:

$$A_{\left( {{\text{adsorbed}}} \right)} + ne^ - \rightleftarrows B_{\left( {{\text{adsorbed}}} \right)} + Y\xrightarrow{{k_{\text{f}} }}C_{\left( {{\text{adsorbed}}} \right)} + ne^ - \rightleftarrows D_{\left( {{\text{adsorbed}}} \right)} $$
(1)

It is assumed that all redox active participants in the electrode mechanism 1 are irreversibly immobilized (adsorbed) on the electrode surface, and there are no interactions between the adsorbed species. The molecules of all oxidized and reduced electroactive species are assumed to be strongly adsorbed on the electrode surface, following a Langmuir isotherm. It is also assumed that the adsorption constants of all adsorbed species have identical values. By Y, it is assigned an electrochemically inactive reactant, whose bulk concentration in solution is much higher than the initial concentration of all adsorbed electroactive species, so the chemical step in the reaction mechanism 1 can be considered to be of pseudo-first order [1]. k f (s−1) is a pseudo-first-order chemical rate constant order, commonly defined as k f = k f′c(Y), where k f′ is the real chemical rate constant (mol−1 cm3 s−1), and c(Y) is the molar concentration of the reactant Y. During the voltammetric experiment, the mass transport of all species is neglected. The electrode mechanism 1 is mathematically represented by the following set of equations:

$${d\Gamma {\left( A \right)}} \mathord{\left/ {\vphantom {{d\Gamma {\left( A \right)}} {dt}}} \right. \kern-\nulldelimiterspace} {dt} = { - I_{1} } \mathord{\left/ {\vphantom {{ - I_{1} } {{\left( {nFS} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {nFS} \right)}}$$
(2)
$${d\Gamma {\left( B \right)}} \mathord{\left/ {\vphantom {{d\Gamma {\left( B \right)}} {dt}}} \right. \kern-\nulldelimiterspace} {dt} = {I_{1} } \mathord{\left/ {\vphantom {{I_{1} } {{\left( {nFS} \right)} - k_{{\text{f}}} \Gamma {\left( B \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {nFS} \right)} - k_{{\text{f}}} \Gamma {\left( B \right)}}$$
(3)
$${d\Gamma {\left( C \right)}} \mathord{\left/ {\vphantom {{d\Gamma {\left( C \right)}} {dt}}} \right. \kern-\nulldelimiterspace} {dt} = { - I_{2} } \mathord{\left/ {\vphantom {{ - I_{2} } {{\left( {nFS} \right)} + k_{{\text{f}}} \Gamma {\left( B \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {nFS} \right)} + k_{{\text{f}}} \Gamma {\left( B \right)}}$$
(4)
$${d\Gamma {\left( D \right)}} \mathord{\left/ {\vphantom {{d\Gamma {\left( D \right)}} {dt}}} \right. \kern-\nulldelimiterspace} {dt} = {I_{2} } \mathord{\left/ {\vphantom {{I_{2} } {{\left( {nFS} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {nFS} \right)}}$$
(5)

with the following initial and boundary conditions

$$t = 0;\,\Gamma {\left( A \right)} = \Gamma {\left( A \right)} * ;\,\Gamma {\left( B \right)} = \Gamma {\left( C \right)} = \Gamma {\left( D \right)} = 0$$
(6)
$$t > 0;\,\Gamma {\left( A \right)} + \Gamma {\left( B \right)} + \Gamma {\left( C \right)} + \Gamma {\left( D \right)} = \Gamma {\left( A \right)} * .$$
(7)

Here, Γ (A), Γ (B), Γ (C), and Γ (D) are the initial surface concentrations of the species A, B, C, and D, respectively, while Γ (A)* is the total surface concentration of all species. Γ is a symbol of the surface concentration of particular specie that is a function of time t. I is the symbol of the current, S is the electrode surface area, F is the Faraday constant, while n is a number of exchanged electrons in an elementary act of electrochemical transformation (it is assumed that α and n are equal for both electrochemical steps in reaction mechanism 1). The solutions of Eqs. 2–5 were obtained by means of Laplace transformations. The solutions for the surface concentrations of the electroactive species A, B, C, and D in a form of integral equations read:

$$\Gamma {\left( A \right)} = \Gamma {\left( A \right)} * - {\int\limits_0^t {\frac{{I_{1} {\left( \tau \right)}}}{{nFS}}} }d\tau$$
(8)
$$\Gamma {\left( B \right)} = {\int\limits_0^t {\frac{{I_{1} {\left( \tau \right)}}}{{nFS}}\exp {\left[ { - k_{{\text{f}}} {\left( {t - \tau } \right)}} \right]}d\,\tau } }$$
(9)
$$\Gamma {\left( D \right)} = {\int\limits_0^t {\frac{{I_{2} {\left( \tau \right)}}} {{nFS}}} }d\,\tau $$
(10)

The solution for the surface concentration of C comes directly from condition 7, and it is:

$$\Gamma {\left( C \right)} = \Gamma {\left( A \right)} * - \Gamma {\left( A \right)} - \Gamma {\left( B \right)} - \Gamma {\left( D \right)}$$
(11)

or

$$\Gamma {\left( C \right)} = {\int\limits_0^t {\frac{{I_{1} {\left( \tau \right)}}}{{nFS}}d\tau - {\int\limits_0^t {\frac{{I_{1} {\left( \tau \right)}}}{{nFS}}\exp {\left[ { - k_{{\text{f}}} {\left( {t - \tau } \right)}} \right]}d\tau - {\int\limits_0^t {\frac{{I_{2} {\left( \tau \right)}}}{{nFS}}d\tau } }} }} }$$
(12)

Considering the Buttler–Volmer formalism [1], at the electrode surface the following conditions apply:

$$\frac{{I_{1} }}{{nFS}} = k_{{s,1}} \exp {\left( { - \alpha \phi _{1} } \right)}{\left[ {\Gamma {\left( A \right)} - \exp {\left( {\phi _{1} } \right)}\Gamma {\left( B \right)}} \right]}$$
(13)
$$\frac{{I_{2} }}{{nFS}} = k_{{s,2}} \exp {\left( { - \alpha \phi _{2} } \right)}{\left[ {\Gamma {\left( C \right)} - \exp {\left( {\phi _{2} } \right)}\Gamma {\left( D \right)}} \right]}$$
(14)

where k s,1 (s−1) and k s,2 (s−1) are the heterogeneous electron exchange rate constant corresponding to the standard redox potential of first \(E_{A{\text{/}}B}^{{\text{\rlap{--} o}}} \) and second \(E_{C{\text{/}}D}^{{\text{\rlap{--} o}}} \) electron transfer steps of the electrode reaction 1, respectively. α is the cathodic electron transfer coefficient, while \(\phi _1 = \frac{{nF}}{{RT}}(E - E_{A{\text{/}}B}^{{\text{\rlap{--} o}}} )\) and \(\phi _2 = \frac{{nF}}{{RT}}(E - E_{C{\text{/}}D}^{{\text{\rlap{--} o}}} )\) are the dimensionless relative electrode potentials. Substituting Eqs. 8 and 9 into Eq. 13 and Eqs. 10 and 12 into Eq. 14 yields:

$$\frac{{I_{1} }}{{nFS}} = k_{{s,1}} \exp {\left( { - \alpha \phi _{1} } \right)}{\left[ {\Gamma {\left( A \right)} * - {\int\limits_0^t {\frac{{I_{1} {\left( \tau \right)}}}{{nFS}}d\tau } } - \exp {\left( {\phi _{1} } \right)}{\int\limits_0^t {\frac{{I_{1} {\left( \tau \right)}}}{{nFS}}{\text{exp}}{\left[ {{\text{ - }}k_{{\text{f}}} {\left( {t - \tau } \right)}} \right]}d\tau } }} \right]}$$
(15)
$$\frac{{I_2 }}{{nFS}} = k_{s,2} \exp \left( { - \alpha \phi _2 } \right)\left[ {\int\limits_0^t {\frac{{I_1 \left( \tau \right)}}{{nFS}}d\tau } - \int\limits_0^t {\frac{{I_1 \left( \tau \right)}}{{nFS}}{\text{exp}}\left[ {{\text{ - }}k_{\text{f}} \left( {t - \tau } \right)} \right]d\tau } - \int\limits_0^t {\frac{{I_2 \left( \tau \right)}}{{nFS}}d\tau } - \exp \left( {\phi _2 } \right)\int\limits_0^t {\frac{{I_2 \left( \tau \right)}}{{nFS}}d\tau } } \right]$$
(16)

Integral Eqs. 15 and 16 are general mathematical solutions of the surface ECE electrode mechanism under chronoamperometric conditions. Numerical solution of Eqs. 15 and 16 adopted for SWV was obtained according to the method of Nicholson and Olmstead [22]. For numerical solutions, the time increment d was defined as d = 1/(50f), where f is the frequency of the potential modulation. It means that each SW half-period τ/2 was divided into 25 increments. The numerical solutions of Eqs. 15 and 16 read:

$${\text{ $ \Psi $ }}_1 = \frac{{K_1 \exp \left( { - \alpha \phi _{1,m} } \right) - \frac{{K_1 \exp \left( { - \alpha \phi _{1,m} } \right)}}{{50}}\sum\limits_{j = 1}^{m - 1} {\Psi _{1,j} } - \lambda ^{ - 1} K_1 \exp \left[ {\phi _{1,m} \left( {1 - \alpha } \right)} \right]\sum\limits_{j = 1}^{m - 1} {\Psi _{1,j} M_j } }}{{1 + \frac{{K_1 \exp \left( { - \alpha \phi _{1,m} } \right)}}{{50}} + \lambda ^{ - 1} K_1 M_1 \exp \left[ {\phi _{1,m} \left( {1 - \alpha } \right)} \right]}}$$
(17)
$${\text{ $ \Psi $ }}_2 = \frac{{\frac{{K_2 \exp \left( { - \alpha \phi _{2,m} } \right)}}{{50}}\sum\limits_{j = 1}^m {\Psi _{1,j} } - \lambda ^{ - 1} K_2 \exp \left( { - \alpha \phi _{2,m} } \right)\sum\limits_{j = 1}^m {{\text{ $ \Psi $ }}_{1,j} M_j } - \frac{{K_2 \exp \left( { - \alpha \phi _{2,m} } \right)}}{{50}}\left[ {1 + \exp \left( {\phi _{2,m} } \right)} \right]\sum\limits_{j = 1}^{m - 1} {{\text{ $ \Psi $ }}_{2,j} } }}{{1 + \frac{{K_2 \exp \left( { - \alpha \phi _{2,m} } \right)}}{{50}}\left[ {1 + \exp \left( {\phi _{2,m} } \right)} \right]}}$$
(18)

K 1 and K 2 are the dimensionless electron transfer kinetic parameters for the first and the second redox steps, respectively. These dimensionless kinetic parameters are defined as K 1 = k s,1/f, and K 2 = k s,2/f, where f is the SW signal frequency. By Ψ1 = I 1 /[nFSfΓ(A)*] and Ψ2 = I 2 /[nFSfΓ(A)*], we assign the dimensionless currents of the first and the second redox steps, respectively, while λ is the dimensionless chemical parameter defined as λ = k f/f. The numerical integration factor M is defined as \(M_j = \exp \left( { - \lambda \frac{j}{{50}}} \right) - \exp \left( { - \lambda \frac{{\left( {j + 1} \right)}}{{50}}} \right)\).

The overall dimensionless current for the reaction mechanism 1 is defined as:

$$\Psi = \Psi _1 + \Psi _2 .$$

The square-wave signal is a train of cathodic and anodic pulses superimposed on a staircase potential ramp. The height of each cathodic and anodic pulse is equal and designated as the square-wave amplitude E sw. Additionally, the SW signal is characterized by the staircase potential step ΔE and frequency f of the pulses [1].

For checking the accuracy and correctness of the model, the results of the surface ECE mechanism have been compared with those of a simple one-step surface redox reaction, i.e.:

$$A_{\left( {{\text{ads}}} \right)} + ne^ - \rightleftarrows B_{\left( {{\text{ads}}} \right)} $$
(19)

The procedure for numerical simulations of reaction 19 is described elsewhere [1].

If the value of the chemical parameter λ by the ECE mechanism was very small (i.e., λ < 0.000005), the theoretical voltammograms of surface ECE reaction 1 and that of simple surface redox reaction 19 were identical. This finding serves as strong evidence for the correctness of the theoretical surface ECE model.

All the simulations have been performed with the MATHCAD software.

Results and discussions

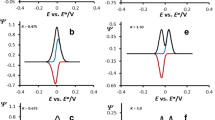
Theoretical net SW voltammograms of the surface ECE reaction are bell-shaped curves, whose features are strongly dependent on the value of the dimensionless chemical parameter λ, as well as on the dimensionless redox kinetic parameters K 1 and K 2, the number of exchanged electrons in both steps n 1 and n 2, the electron transfer coefficients α 1 and α 2 (for sake of simplicity, it is assumed that n = n 1 = n 2, and α = α 1 = α 2), the temperature T, and the potential modulation parameters (frequency f, amplitude E sw, and potential step ΔE). Like by the surface EC mechanism [1], the features of the theoretical SW voltammograms obtained for this specific surface ECE system are strongly dependent on the magnitude of the chemical rate constant. When considering the effect of chemical reactions, it is very important to note that any variations from reversible behaviour are related not to the absolute magnitude of the pseudo-first-order rate constant for the chemical reaction (k f) but to the value of this rate constant relative to the time scale of the experiment. For example, decreasing the time scale of the experiment also decreases the time available for the chemical reaction, and hence, the effect of the chemical reaction will be diminished. In addition to the rate of chemical step, the features of the theoretical SWV voltammograms of the surface ECE mechanism are strongly affected by one “virtual” thermodynamic parameter (E f) that is defined as the potential difference in the standard redox potentials between two electron transfer steps, i.e., \(E_{\text{f}} = E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \). The current SW voltammetric response depends strongly upon the relative values of the standard redox potentials of the two electron transfer reactions. For a “two-electron” reduction, if the standard redox potential of the second electron transfer step in reaction scheme 1 is at least 80 mV more negative than that of the first reduction step, then the two well-separated processes can generally be resolved. However, if the standard redox potential of the second reduction step is more positive or the same as that of the first reduction step, then a single “two-electron” reduction will be observed, as the second reduction will occur at the potential required for the first reduction step. If the value of the standard redox potential of the second reduction step \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \) is 20 mV to 80 mV more negative than the value of standard redox potential of the first reduction step \(E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \), then one observes two poorly separated processes featuring shouldering effects. All these situations are nicely portrayed in Fig. 1.

Fig. 1
figure 1

Theoretical square-wave voltammograms simulated for various differences in the standard redox potentials between the first and the second reduction step of a surface ECE reaction. Number of electrons n 1 = n 2 = 2, the electron transfer coefficients α = α 1 = α 2 = 0.5, temperature T = 298 K, amplitude E sw = 60 mV, potential step ΔE = 10 mV. The value of the kinetic parameters were K 1 = 0.1 and K 2 = 0.1, while the value of the chemical parameter was λ = 0.1

Full size image

In light of the discussion at Fig. 1 and in order for easier understanding of the theoretical results, it is useful to elaborate two different situations in respect to the differences of the standard redox potentials of the two electron transfer steps:

  1. A)

    The energy of occurring of the second electron transfer step is smaller or equal to that of the first electron transfer step, or \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \).

  2. B)

    The energy of the electron transfer for the second step is more negative at least for −90 mV or further than that of the first step, or \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \leqslant - 90\,{\text{mV}}\).

Case A: \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \)

If the standard redox potential of the second reduction step \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \) is more positive or equal to that of the first reduction step \(E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \), then a single SW voltammetric reduction process is expected to be observed, as the second reduction step will occur at the potential required for the first reduction. This situation is commonly observed for electroactive molecules that can exist as more than one isomer; for example, cis and trans isomers of transition metal complexes, but it is also frequently met by some proteins and other important biomolecules [7, 13–19]. The features of the SW voltammetric responses in such scenario will significantly depend on the value of the chemical kinetic parameter λ, but they will be also affected by the values of the electron transfer kinetic parameters K 1 and K 2 of the two reduction steps. Shown in Fig. 2 are theoretical SW voltammograms simulated for n 1 = n 2 = 2, α 1 = α 2 = 0.5, T = 298 K, and several values of the chemical parameter λ, in the situation where the kinetics of both electrochemical steps fall within the region of quasireversible electron transfer (i.e. K 1 = K 2 = 0.1) [1, 21]. In this situation, a single voltammetric peak is observed, which height increases by initial increasing of the value of the chemical parameter λ. The cause for this feature can be inscribed to one pseudo-catalytic phenomenon that takes place during the chemical step of the ECE reaction [1]. In the course of the anodic pulses of the SW excitation signal, the product of the first redox step B can be converted via the chemical reaction to C, but to some extent (depending mainly on the value of λ) will be turned back (reoxidized) to the initial reactant A, since both processes occur at the same potential. As the chemical reaction in mechanism 1 converts B to C, there will be additional reduction of A to form B during the measuring voltammetric time, in order to reestablish the equilibrium disturbed by the chemical reaction. As a consequence of this, additional amount of B will be created, that will contribute continuously for the current increase of the second electron transfer step. This gives rise to pronounced currents at the second redox step, which contributes considerably to the overall increase of the response of the ECE reaction, in situation when \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \). If the chemical parameter λ gets values λ > 0.1, then steady-state type of voltammograms are observed.

Fig. 2
figure 2

Case A, \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \). Effect of the chemical parameter to the features of theoretial SW voltammograms. The value of the kinetic parameters were K 1 = 0.1 and K 2 = 0.1, while the values of the chemical parameter λ = 0.000001 (black line), 0.01 (blue line) and 0.05 (red line). The potential step was ΔE = 4 mV, while the other simulation parameters were same as those in Fig. 1

Full size image

Even if \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \), however, the SW voltammograms of a surface ECE mechanism may feature complex shapes, depending of the value of the kinetic parameter of the second electron transfer step. Shown in Fig. 3 are several situations, which have been simulated for a constant value of the first redox step K 1 (K 1 falling within the quasireversible region), and several values of K 2 for the second redox step. In such a scenario, depending on the value of K 2, one can observe a single SW peak (curve 5 at Fig. 3), a shouldered SW peak (curves 3 and 4 at Fig. 3), or even two well-separated peaks when the value of K 2 falls within irreversible region (curves 1 and 2 at Fig. 3).

Fig. 3
figure 3

Case A, \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \). Effect of the kinetics of the second redox step to the features of the SW voltammograms. K 2 = 0.0001 (1), 0.001 (2), 0.01 (3), 0.025 (4), and 0.05 (5). The value was K 1 = 0.1, while the chemical parameter was λ = 0.1. The potential step was ΔE = 4 mV, while the other simulation parameters were same as those in Fig. 1

Full size image

In case of \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \), a very interesting situation is observed when the value for the kinetic parameter of the first redox step K 1 falls within the region of fast electron transfer (see Fig. 4a). As the value of K 1 increases from 0.1 to 100 for example, the theoretical SW voltammetric responses feature shapes from a single peak, passing via split SW peaks, and finishing again in a shouldered SWV peak in the regions of very high values of K 1. For a simple comparison, increasing of the kinetic parameter K by the simple surface reaction (reaction scheme II) leads to splitting of the net SW peak in two peaks, whose potential separation increases proportionally by increasing of K (see Fig. 4b) [1, 3, 21]. Obviously, the last (Fig. 4b) is completely different behaviour of that presented at Fig. 4a. Indeed, the complex featuring of the SWV current responses shown in Fig. 4a can be again inscribed to some extent to the effect of the rate of the chemical step to the features of both redox steps in mechanism 1.

Fig. 4
figure 4

Case A, \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \). Effect of the kinetics of the first redox step to the features of the theoretical SW voltammograms. The value of K 2 = 0.1, while the chemical parameter was λ = 0.1. The voltammograms in b are simulated for a simple surface redox reaction. The potential step was ΔE = 4 mV, while the other simulation parameters were same as those in Fig. 1

Full size image

The effects of the chemical kinetic parameter λ to the features of theoretical SWV responses, simulated for K 1 and K 2 values falling both within the region of very fast electron transfer, are shown in Fig. 5. As mentioned previously, the splitting of the net SWV peaks into two peaks is main attribute of the surface reactions featuring very fast electron transfer kinetics [1, 3]. If we are present in the region of split SW peaks, the increase of the chemical kinetic parameter λ from 0.0001 to 0.025 produces an increase of the height of both split peaks, and small decreasing of the potential separation between the split twin peaks in the same time (see the curves at Fig. 5a). The further increase of the value of λ from 0.05 to 0.1 leads to fast merging of the split peaks, which ends to a situation of existence of two dissimilar SWV peaks: the peak at more positive potentials reaches maximal height for λ = 0.1 (see the red curve at Fig. 5b), while the other peak at more negative potentials is much smaller, getting a constant height that is independent on the value of λ (see the red, blue, green and brown curves at Fig. 5b, for example). Further increase of the value of the dimensionless chemical parameter λ from 0.15 to 1 results in decreasing of the height of the peak at more positive potentials and shifting of its position toward more positive values, which is followed by appearing of a new smaller SWV peak in-between of the two already existing peaks (see the blue and green curves at Fig. 5b). Finally, when the chemical parameter λ gets values bigger than 1, the voltammetric curve consists of three well-separated SW peaks (see the lowest brown curve at Fig. 5b, for example). This situation is thereafter not additionally affected by the further increase of λ. The features of the ECE reaction shown in Fig. 5 can serve as a reliable qualitative criterion for distinguishing the surface ECE from the simple surface redox reaction. In this case, altering the concentration of reactant Y can mimic experimentally the theoretical effect of λ presented in Fig. 5. It is worth mentioning that altering of the SW frequency can also give the same effect. However, since the frequency affects simultaneously all kinetic parameters (K 1, K 2 and λ), it is not recommendable to apply frequency analysis for getting qualitative conclusions in such a case, due to the complexity of the output results that might be got. Nevertheless, the situations presented in Figs. 3, 4 and 5 give several hints of how complex this redox mechanism can be in the real experiments.

Fig. 5
figure 5

Case A, \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \). Effect of the kinetics of the chemical reaction to the features of the theoretical SW voltammograms in case when the kinetics of the both redox step are very fast. The value of K 1 = 5, K 2 = 5, while the values of the chemical parameters are given in the legends. The potential step was ΔE = 4 mV, while the other simulation parameters were same as those in Fig. 1

Full size image

Case B: \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \leqslant - 90\,{\text{mv}}\)

If the standard redox potential of the second reduction step \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \) is at least −90 mV or more negative than that of the first reduction step \(E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \), then usually, two nicely separated SW voltammetric reduction processes will be observed. In such case, the heights of both SW peaks will be significantly affected by the chemical parameter λ: as the value of λ increases, the intensity of the first reduction peak decreases, while the intensity of the SW peak for the second redox process at more negative potentials increases (see Fig. 6). The behavior of the first SW peak at more positive potentials will be the same as that for a surface EC mechanism [1]. The height of the first SWV peak is decreasing due to the effect of irreversible chemical reaction that “consumes” the product B during the measuring time of the experiment. The height of the second SW peak (i.e., the peak at more negative potentials) will be dependent upon the rate of the chemical reaction and the time of the voltammetric experiment, ranging from no-peak situation (for λ < 0.000005) to the normal surface redox process, when λ > 0.5. The behavior and the shape of the second SWV peak qualitatively resemble those of a surface chemical reaction-electron transfer (CE) reaction [1, 12].

Fig. 6
figure 6

Case B, \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) ≤ −90 mV. Effect of the chemical parameter to the features of theoretial SW voltammograms in situation where \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) = −150 mV. The value of the kinetic parameters were K 1 = 0.1 and K 2 = 0.1, while the values of the chemical parameter λ = 0.000001 (1), 0.005 (2), 0.02 (3), and 10 (4). The potential step was ΔE = 4 mV, while the other simulation parameters were same as those in Fig. 1

Full size image

In case when \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \leqslant - 90\,{\text{mV}}\), the SW voltammetric outputs might feature various remarkable shapes depending on the value of the chemical parameter λ and the magnitudes of the kinetic parameters of the first and the second electron transfer steps K 1 and K 2. Shown in Fig. 7a–c are several situations simulated for λ = 0.1 and several different values of electrode kinetic parameters K 1 and K 2. As it can be seen from Fig. 7, the voltammograms in such case can feature two, three, or even four SW peaks (i.e., two pairs of split twin peaks), which mainly depends on the magnitudes of electrode kinetic parameters K 1 and K 2.

Fig. 7
figure 7

Case B, \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) ≤ −90 mV. Effect of the kinetics of both redox steps to the features of the theoretical SW voltammograms, in the case where \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) = −150 mV. The value of the chemical parameter was λ = 0.1, ΔE = 4 mV, while other simulations parameters were same as those in Fig. 1

Full size image

If the kinetics of electron transfer of the first redox step is very fast, then a very interesting situation exists when the magnitude of the chemical kinetic parameter λ increases. Shown in Fig. 8 are several SW voltammograms simulated for K 1 = 5 (very fast electron transfer), K 2 = 0.1, and several values of the chemical kinetic parameter λ. If the magnitude of the chemical parameter λ is very small (i.e., very slow chemical step), the first SW peak at more positive potentials is featuring splitting shape (see Fig. 8a). The splitting phenomenon of the net SW peak is usually caused by the skew of forward and backward current components on the potential scale, as the value of the dimensionless kinetic parameter K falls in the region of very fast electron transfer [1, 23, 24]. Note that this phenomenon can be explored for very elegant thermodynamic and kinetic characterization of the electron transfer rate constant, and it is discussed in detail elsewhere [1, 3]. As the value of chemical parameter λ increases, the heights of the split SWV twin peaks also enhance, while the intensity of the second SWV redox process at more negative potentials increases significantly (see Fig. 8b). When the value of the chemical parameter λ gets values higher than 0.01, the symmetry of the split twin peaks starts to be disturbed (Fig. 8c). The decreasing of the height of the anodic peak of the twin-peak-featuring process is a direct consequence of consuming of B and its conversion to C via the increased rate of the chemical reaction. At the end, for big values of the chemical parameter λ (i.e., λ > 0.1), the splitting phenomenon by the first SWV redox process completely disappears (Fig. 8d), since the backward compound of the first process is being completely “consumed” via the chemical transformation of B to C.

Fig. 8
figure 8

Case B, \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) ≤ −90 mV. Effect of the chemical kinetic parameter λ to the features of the theoretical SW voltammograms in case when the kinetics of the first redox step is very fast. \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) = −150 mV, K 1 = 5, K 2 = 0.1, while other simulations parameters were same as those in Fig. 1

Full size image

In the real experiments, increasing of the concentration of the electrochemically inactive reagent Y can mimic the situation presented in Fig. 8. This is a very important item, since it gives hint to distinguish the surface ECE mechanism from the similar two-step surface electron transfer-electron transfer (EE) mechanism [21].

It is worth mentioning that, in a situation when the SW voltammetric curves of both electron transfer steps are partially overlapped, i.e., when the difference \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) is roughly −20 to −80 mV (see second situation at Fig. 1), then the behavior of the ECE mechanism is rather complex. In such case, it is recommendable to use a very small potential step (0.1 to 1 mV, for example) or derivative voltammetric modes in order to obtain nicely resolved voltammetric peaks that can be further analyzed.

Conclusions

Given all the complexity of the studied surface ECE mechanism, it is always useful to find simple qualitative diagnostic criteria to distinguish the surface ECE mechanism (reaction mechanism 1) from a simple surface electron-transfer reaction (reaction mechanism 19) [1, 3] and from a simple surface two-step EE mechanism [1, 21].

In the situation of existence of single SW voltammogram (i.e., when \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \)), the effect of the concentration of the electroinactive reactant Y (involved in the chemical step of reaction mechanism 1) to the features of the SW voltammograms is crucial parameter to distinguish the surface ECE from a simple surface reaction 19. Let us recall that the chemical parameter λ by surface ECE mechanism is defined as λ = k f/f. Because the chemical rate constant k f is of pseudo-first order, commonly defined as k f = k f′c(Y), [where k f′ is the real chemical rate constant (mol−1 cm3 s−1)], we can see that the value of the chemical parameter λ can be affected via the concentration of the reactant Y-c(Y). This is a very important item since it implicates that the increasing of the concentration of Y in the solution can experimentally reproduce the theoretical effect of the dimensionless chemical parameter λ shown in Fig. 2. Consequently, in a real experimental situation where \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \), the increase of the height of the SW voltammetric peak current, produced by increasing of the concentration of the electroinactive chemical reactant Y, can serve as first indicator for qualitative recognition of the surface ECE mechanism and for distinguishing it from the simple surface reaction mechanism 19.

In case of existence of two well-separated SW peaks (i.e., when \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) ≤ −90 mV), one can again obtain qualitative hints for recognizing of the surface ECE mechanism by increasing the concentration of the electroinactive reactant Y. While the increasing of the height of the second SWV peak and the decreasing of the intensity of the first SWV peak by increasing of c(Y) can serve as a simple criterion for recognizing of the surface ECE mechanism (see Fig. 6), the disappearance of the split SW twin peaks phenomenon by increasing of c(Y) (see Fig. 8) is a strong evidence for distinguishing the surface ECE from the surface EE mechanism [1, 21].

Another interesting question by this complex redox mechanism is to find methods for the determination of the kinetic parameters of both redox steps and for assessing of the kinetics of chemical step. Considering the situation of existence of single SW voltammogram (i.e., when \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta \geqslant E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \)), the methodologies of “quasireversible maximum” [1] and “split SW peaks” [1, 3] cannot give unanimous hints about the values of the standard rate constants of the two electron transfer steps involved in reaction mechanism 1. In such case, by applying of the methodologies described in [1] and [3], one gets always some intermediate values of k s,1 and k s,2.

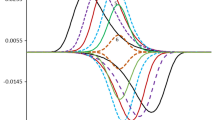
If, however, both redox steps of the surface ECE mechanism are nicely separated (i.e., when \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) ≤ −90 mV), then for the second redox step in reaction mechanism 1, one can determine the kinetic parameters of the electron transfer step by applying both the method of “quasireversible maximum” and “split SW peaks” [1]. For the first electron transfer step of the surface ECE mechanism, however, one should explore the method of “quasireversible maximum”, since in this case the position of the quasireversible maximum does not depend on the value of chemical parameter λ (see Fig. 9, for example). The SW splitting phenomenon should not be used for estimation of the kinetics of electron transfer of the first redox step since the potential separation of the split SW peaks in this case is affected to some extent of the magnitude of chemical parameter λ (see Fig. 8 for example).

Fig. 9
figure 9

Effect of the chemical kinetic parameter ∴*λ to the phenomenon of quasireversible maximum recorded for the first reduction step on the log(K 1). λ = 0.0001 (1), 0.005 (2), 0.1 (3), and 10 (4). The other simulation parameters were same as those in Fig. 1

Full size image

For the estimation of the rate constant of the chemical reaction k f′ by the surface ECE mechanism, one should make at best the analysis of the height of the peak current of the second voltammetric peak Ψnet,p,2 vs. the logarithm of the concentration of Y similar to that shown in Fig. 10. The theoretical dependence between Ψnet,p,2 and log(λ) has a sigmoidal shape with a large linear part, the slope of which depends on the electron transfer coefficient α 2 (see Fig. 10). The linear equation corresponding to the linear parts of the theoretical curves presented in Fig. 10 can be used for the determination of the chemical rate constant k f, providing that the value of the electron transfer coefficient of the second step α 2 is already known. For the determination of α 2, one is recommended to use the procedure developed in our most recent article [25].

Fig. 10
figure 10

Case B, \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) ≤ −90 mV. The effect of the chemical kinetic parameter λ to the peak current of the second reduction step. The value of the electron transfer coefficient of the second step was α 2 = 0.3 (1), 0.5 (2), and 0.7 (3). \(E_{{C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}}^\theta - E_{{A \mathord{\left/ {\vphantom {A B}} \right. \kern-\nulldelimiterspace} B}}^\theta \) = −150 mV, while the other simulation parameters were same as those in Fig. 1

Full size image

At the end, it is worth mentioning that the scan rate analysis (or frequency analysis) by this complex mechanism can also have important application. Since the second electron transfer step depends on how much of the intermediate B is chemically converted to intermediate C, the peak currents will be strongly affected by the scan rate. At very high scan rate, the chemical reaction and the second electron transfer step can be effectively suppressed by rapid re-conversion of B back to starting material A. This type of analysis can also give hints for qualitative recognition of the surface ECE mechanism.