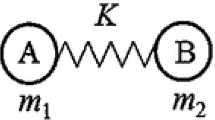Optimizing a coarse-grained space for approximate normal-mode vibrations of molecular heterodimers

Abstract

We applied the method of coarse-graining the intermolecular vibrations to molecular heterodimers assembled by double hydrogen bonding. This method is based on principal component analysis, by which the original atomic displacement vectors are projected onto a lower-dimensional space spanned by a basis set of translations, librations, and intramolecular vibrations of the constituent molecules. Compared with homodimers, the following points are particularly noted: (1) alignment of the constituent molecules in a non-symmetric atomic arrangement of the whole system and (2) the scheme of reordering the bases to construct an optimal coarse-grained space. We tested three schemes for reordering the intramolecular vibration vectors to determine that the best one is equivalent to size reduction based on the singular value decomposition. The coarse-graining analysis affords three parameters, Φ_intra, Φ_inter, and Φ_app, which are relevant to the mechanical nature of the molecular assembly. The Φ_intra values account for the internal stiffness of molecules, while the Φ_inter values are true stiffness constants of the intermolecular force and show a good correlation with the association energies of the dimers. The Φ_app values are the apparent intermolecular stiffness smaller than Φ_inter, as a result of compensation for neglecting intramolecular vibrations. All these values are consistent with each other under the coupled oscillator model, showing that the present coarse-graining analysis is valid for heterodimers as well as homodimers.

Introduction

Material properties are governed by both molecular structure and the packing of molecular species in the solid state; hence, the design, synthesis, and modification of novel materials with unique physicochemical properties are a significant pursuit for crystal engineering in many fields [1,2,3]. Indeed, crystal polymorphs, which possess identical chemical compositions but exist in different molecular arrangements and/or conformations, display distinct physical and chemical properties, including energetic properties and bioavailability [4,5,6,7]. Therefore, polymorphism has been an important consideration in many fields, including pharmaceuticals [8], food science [9], dyes/pigments [10], and organic electronics [11]. Although it is not always possible to observe a sufficient number of polymorphs and pseudopolymorphs [12,13,14,15], researchers have employed sophisticated techniques to this problem, including cocrystallization [16,17,18,19,20] and salification [21,22,23]. Furthermore, in recent years, the elastic or plastic behavior of molecular crystals, some of which may involve local changes in molecular arrangement, has attracted increasing attention [24]. For these reasons, analyzing supramolecular synthons or heterojunctions in molecular assemblies, in terms of elastic body mechanics, is of considerable importance [25]. The nature of intermolecular forces is typically reflected in the vibrational modes of molecular assemblies, especially in the low-frequency (LF) region. Recently, several spectroscopic methods, including terahertz absorption [26,27,28,29,30], Raman scattering [31,32,33,34], and resonant two-photon ionization [35,36,37], have been used to directly observe LF-mode vibrations. These methods cover the detection of hydrogen bonding, van der Waals interactions, overall molecular distortion, and libration in systems such as hydrated sugars, nucleobase pairs, and crystal polymorphs of some drugs.

Currently, the number of reports on normal-mode analysis of large molecular assemblies such as crystals is increasing [38,39,40,41]. Several high-level quantum chemical calculations with explicit full-atom representation have proven to be quite successful [42,43,44,45,46]. However, strict atomistic models often face problems related to the computational cost of the associated calculations. Unlike the intramolecular vibrations observed by infrared spectroscopy, no appropriate simple models are available for intermolecular vibrations. What makes it difficult to reduce the computational cost is the non-negligible coupling among the intermolecular and intramolecular vibrations in LF-mode vibrations. In an attempt to reduce the computational cost while maintaining high accuracy, we have been developing a method of coarse-graining atomic displacement vectors for normal vibrational modes [47,48,49,50]. From the coarse-grained displacement vector and frequency for each vibrational mode, we can evaluate the stiffness constant of intermolecular hydrogen bonds. To date, we have demonstrated that this size-reduction method is appropriate for reproducing homodimers that are assembled through double hydrogen bonding. For an assembly composed of rigid molecules, in which only small coupling among the intra- and intermolecular vibrations is expected, the displacement vectors can be sufficiently represented in a coarse-grained space spanned by twelve bases corresponding to translational and rotational motions of the constituent molecules [47]. For an assembly with an LF-mode intramolecular vibration, such as methyl libration, the inclusion of certain vibration modes in the coarse-grained space drastically improves the representation of the original vibration motions [48].

For molecular homodimers that consist of two identical molecules, maintaining an appropriate symmetry (centric, two-fold, mirror), the construction of the coarse-grained space is rather straightforward: one can select the intramolecular vibrations (alternately from two units in the assembly) in increasing order of frequency until the dimension reaches the number of the LF-mode vibrations of the original system. However, the situation is not that simple for heterodimers that consist of two different molecules or two identical molecules in a non-symmetric orientation. It is necessary to overcome this inevitable problem to apply our idea of coarse-graining to molecular crystals and other assemblies. In this paper, we describe our attempt to analyze the vibrations of 21 homo- and heterodimers that are composed of six different molecules (Fig. 1). The results are examined using a fidelity index that we have proposed to evaluate the quality of the coarse-grained space [50]. In addition, based on the coupled oscillator model, we demonstrate that the intermolecular vibrations can be understood in terms of rigid-body mechanics, but far beyond the conventional pseudodiatomic model.

Fig. 1

Molecular structures of monomers studied. Formic acid (FA), acetic acid (AA), trichloroacetic acid (TC), formamide (AD), formamidine (AN), and urea (UR) are abbreviated as indicated

Theory

For the Hessian analysis of molecular vibration, the displacement vectors C are obtained by diagonalizing the mass-weighted Hessian matrix (M^−1/2 KM^−1/2) with the eigenvalue matrix Ω that contains the corresponding frequency ω.

$$ \left({\mathbf{M}}^{-1/2}{\mathbf{KM}}^{-1/2}\right)\left({\mathbf{M}}^{1/2}\mathbf{C}\right)=\left({\mathbf{M}}^{1/2}\mathbf{C}\right){\boldsymbol{\Omega}}^2 $$

(1)

The mass-weighted displacement (MWD) vectors W are prepared by multiplying M^1/2 with C and normalized with matrix L⁻¹, where L² is the modal mass matrix [51]. The hat (^) on C, W, etc., denotes that these matrixes are normalized at least with respect to each column.

$$ \left\{\begin{array}{l}\hat{\mathbf{W}}={\mathbf{M}}^{1/2}\hat{\mathbf{C}}{\mathbf{L}}^{-1}\\ {}{\mathbf{L}}^2={\hat{\mathbf{C}}}^{\mathrm{T}}\mathbf{M}\hat{\mathbf{C}}\end{array}\right. $$

(2)

The dimensions of the mass (M) and stiffness (K) matrixes are 3 N × 3 N, where N is the number of constituent atoms. Size reduction based on the idea of principal component analysis (a priori Karhunen-Loève analysis) leads to the following formulation [47].

$$ \left({\boldsymbol{\Gamma}}^{1/2}{\boldsymbol{\Phi} \boldsymbol{\Gamma}}^{1/2}\right)\left({\boldsymbol{\Gamma}}^{1/2}\boldsymbol{\Xi} \right)=\left({\boldsymbol{\Gamma}}^{1/2}\boldsymbol{\Xi} \right){\boldsymbol{\Omega}}^2 $$

(3)

The matrices Γ⁻¹ and Φ, which were named after the GF method [52], contain coarse-grained inertial loads and force constants, respectively. These matrices are given by basis transformation from the Cartesian to an internal coordinate system, using a transformation matrix (coarse-graining matrix) B (3 N × n), which is composed of a reduced number of atomic displacement vectors (n ≤ 3N) as basic motions [49]. The coarse-grained displacement $\hat{\boldsymbol{\Xi}}$ is constructed using $\hat{\mathbf{C}}$ (3 N × n), which is a partial matrix of the original displacement vectors, in case n < 3 N.

$$ {\boldsymbol{\Gamma}}^{-1}\kern.5em \equiv \kern.5em {\mathbf{B}}^{\mathrm{T}}\mathbf{MB}\kern1.8em \left(n\times n\right) $$

(4)

$$ \boldsymbol{\Phi} \kern.5em \equiv \kern.5em {\mathbf{B}}^{\mathrm{T}}\mathbf{KB}\kern2.16em \left(n\times n\right) $$

(5)

$$ \hat{\boldsymbol{\Xi}}\equiv \kern.5em {\boldsymbol{\Gamma} \mathbf{B}}^{\mathrm{T}}\mathbf{M}\hat{\mathbf{C}}\kern1.8em \left(n\times n\right) $$

(6)

Again, the coarse-grained MWD vectors (columns in U) are prepared by multiplying Γ^1/2 with Ξ and normalized with matrix Λ⁻¹, where Λ² is the modal mass matrix under the reduced dimensions of motions.

$$ \left\{\begin{array}{l}\hat{\mathbf{U}}\kern.5em \equiv \kern.5em {\boldsymbol{\Gamma}}^{-1/2}\hat{\boldsymbol{\Xi}}{\boldsymbol{\Lambda}}^{-1}\left(n\times n\right)\\ {}{\boldsymbol{\Lambda}}^2\kern.5em \equiv \kern.5em {\hat{\boldsymbol{\Xi}}}^{\mathrm{T}}{\boldsymbol{\Gamma}}^{-1}\hat{\boldsymbol{\Xi}}\kern2.28em \left(n\times n\right)\end{array}\right) $$

(7)

If the set of frequencies for normal mode vibrations are determined either computationally or experimentally, the force constants can be obtained under the reduced dimension of the selected motions (a partial matrix of Ω² is used if n < 3 N). This set of force constants, combined with the appropriate information concerning inertial loads, such as molecular weight or moment of inertia, can reproduce the eigenfrequencies in the LF region with comparable accuracy to that derived from the original calculations or measurements.

$$ \boldsymbol{\Phi} ={\boldsymbol{\Gamma}}^{-1/2}\hat{\mathbf{U}}{\boldsymbol{\Omega}}^2{\hat{\mathbf{U}}}^{\mathrm{T}}{\boldsymbol{\Gamma}}^{-1/2}\kern2.04em \left(n\times n\right) $$

(8)

It is more convenient to convert Φ into $\tilde{\boldsymbol{\Phi}}$ by applying weighting factors N^1/2, so that we can compare the stiffness constants of different molecules with various molecular weights using the same standard. The matrix N^1/2 is defined so that N^1/2Γ⁻¹ N^1/2 gives the molecular weight (M_m) and the tensor of inertia (I_m) of the m-th (m = I, II, ..., X) molecular unit [47].

$$ \left\{\begin{array}{c}\kern4.25em \overset{\sim }{\Phi}={\mathrm{N}}^{1/2}\Phi {\mathrm{N}}^{1/2}\\ {}{\mathrm{N}}^{1/2}{\Gamma}^{-1}{\mathrm{N}}^{1/2}=\left(\begin{array}{c}{M}_{\mathrm{I}}\mathrm{E}\\ {}O\\ {}\begin{array}{c}\\ {}\\ {}\end{array}\end{array}\kern0.5em \begin{array}{c}\begin{array}{c}O\\ {}{\mathrm{I}}_{\mathrm{I}}\\ {}\end{array}\\ {}\\ {}\end{array}\kern0.5em \begin{array}{c}\\ {}\\ {}\begin{array}{c}\ddots \\ {}\\ {}\end{array}\end{array}\kern0.5em \begin{array}{c}\\ {}\\ {}\begin{array}{c}\\ {}{M}_{\mathrm{x}}\mathrm{E}\\ {}O\end{array}\end{array}\kern0.5em \begin{array}{c}\\ {}\\ {}\begin{array}{c}\\ {}O\\ {}{\mathrm{I}}_{\mathrm{x}}\end{array}\end{array}\right)\end{array}\right. $$

(9)

For the sake of simplicity, $\tilde{\boldsymbol{\Phi}}$ is denoted Φ in the rest of this paper.

For a given molecular assembly, its LF-mode vibrations can be approximately represented as a linear combination of six basic motions, namely, three translations (T_mx, T_my, T_mz) and three librations (R_mx, R_my, R_mz), for the m-th constituent molecule (hereafter called “unit m”), if they are substantially regarded as rigid bodies. For a molecular dimer (m = I or II), for example, the twelve basic motions in total are contained in the matrix B^°, each column of which is implicitly normalized but not necessarily orthogonalized.

$$ \left\{\begin{array}{l}{\mathbf{B}}^{\circ }=\left(\begin{array}{cc}{\mathbf{B}}_{{\mathrm{I}}^{\circ }}& O\\ {}O& {\mathbf{B}}_{{\mathrm{I}\mathrm{I}}^{\circ }}\end{array}\right)\\ {}{\mathbf{B}}_{{\mathrm{m}}^{\circ }}=\left({\mathbf{T}}_{\mathrm{m}\mathrm{x}}\kern0.24em {\mathbf{T}}_{\mathrm{m}\mathrm{y}}\kern0.24em {\mathbf{T}}_{\mathrm{m}\mathrm{z}}\kern0.24em {\mathbf{R}}_{\mathrm{m}\mathrm{x}}\kern0.24em {\mathbf{R}}_{\mathrm{m}\mathrm{y}}\kern0.24em {\mathbf{R}}_{\mathrm{m}\mathrm{z}}\right),\kern0.36em \mathrm{m}=\mathrm{I}\kern0.24em \mathrm{or}\kern0.24em \mathrm{I}\mathrm{I}\end{array}\right) $$

(10)

When the molecules have non-negligible flexibility, matrix B should additionally contain some displacement vectors b_I,1, b_I,2, b_I,3, ... b_I,kI and b_II,1, b_II,2, b_II,3, ... b_II,kII, the intramolecular vibration modes of units I and II, respectively [48]. When all the intramolecular vibrations are included in the basis set (i.e., k_I = 3 N_I-6; k_II = 3 N_II-6), the eigenvectors are virtually identical to those obtained from the original Hessian matrix represented in the Cartesian coordinate system. However, when the number of bases is restricted to a certain number, the order of incorporating bases should be carefully selected to optimize the coarse-grained space. In other words, for the column numbers {j | 1 < j < 3(N_I + N_II)} of matrix B, it is necessary to determine a new series of column vectors using permutation mapping σ (Eq. 12).

$$ \overset{\sim }{\mathbf{B}}=\left({\mathbf{B}}^{\circ}\kern0.36em {\mathbf{b}}_1\cdots {\mathbf{b}}_{k_{\mathrm{I}}+{k}_{\mathrm{I}\mathrm{I}}}\right),\kern0.48em {\mathbf{b}}_j=\left(\begin{array}{c}{\mathbf{b}}_{\mathrm{I},\sigma (j)}\\ {}O\end{array}\right)\kern0.24em \mathrm{or}\kern0.24em \left(\begin{array}{c}O\\ {}{\mathbf{b}}_{\mathrm{I}\mathrm{I},\sigma (j)}\end{array}\right) $$

(11)

$$ \sigma =\left(\begin{array}{c}1\\ {}\sigma (1)\end{array}\begin{array}{c}2\\ {}\sigma (2)\end{array}\begin{array}{c}\cdots \\ {}\end{array}\begin{array}{c}j\\ {}\sigma (j)\end{array}\begin{array}{c}\cdots \\ {}\end{array}\begin{array}{c}3\left({N}_{\mathrm{I}}+{N}_{\mathrm{I}\mathrm{I}}\right)\\ {}\sigma \left(3\left({N}_{\mathrm{I}}+{N}_{\mathrm{I}\mathrm{I}}\right)\right)\end{array}\right)\kern0.36em $$

(12)

The squared elements of Ξ represent contributions from the basic motions and individual intramolecular vibrations to the normal mode vibration of the entire molecular system. To maintain Ξ as a regular matrix, the row dimension of B should coincide with that of C. Therefore, for a given truncated C that contains displacement vectors of selected vibration modes, it is necessary to retain the suitable components of the basis transformation matrix, so that every displacement vector is satisfactorily represented as a linear combination of the column vectors of $\tilde{\mathbf{B}}.$ The tilde (~) on B, C, etc. denotes that they are partial matrixes of the original ones.

$$ \tilde{\mathbf{C}}\simeq \tilde{\mathbf{B}}\hat{\boldsymbol{\Xi}}\kern.5em \left(3N\times n\right) $$

(13)

The construction of the $\tilde{\mathbf{B}}$ matrix requires selection of the b_m,k vector, which is accomplished by extracting eigenvectors for the normal mode vibrations of an isolated single molecule as a model of the unit m (hereafter called “model m”). However, the structure of the model may change slightly after forming an assembly, especially when hydrogen bonding is involved. To remove the arbitrariness in choosing the coordination axes of the monomer, we determined the orientation of the models so that their principal axes of inertia coincide with those of the corresponding units arranged in the assembly (Fig. 2). Such an alignment is more important in handling heterodimers than in homodimers to minimize the error that may arise from the decreased symmetry. In addition, the definition of the coordinate system of the assembly is important because the coarse-grained force constants such as Φ_Tx,Tx correspond to the directions in a given coordinate. In the present study, we defined the xy plane as the least-square plane of the four atoms participating in the double hydrogen bond and the x-axis as the average of two hydrogen-bonding vectors projected onto the xy plane.

Fig. 2

Definition of terms used in this work (e.g., TC + AD dimer). Normal mode analysis is performed for an assembly that consists of two molecular units. Each model of the units is calculated independently, after which its orientation is adjusted to the corresponding unit in the assembly so that their principal axes (arrows in red, green, and blue) coincide

To obtain an appropriate permutation mapping σ, we examined three ways of augmenting the matrix B, where the twelve basic motions are preferentially arranged in the original order (Fig. 3). First, similar to a previous study regarding homodimers [50], we incorporated the vectors in increasing order of the frequency of intramolecular vibration (mapping #1). Because the dimensions of the intramolecular vibration differ between the two units, the vectors cannot be alternately acquired from the two models. Second, we noted the elements of Ξ as a measure of the contributions of the bases to reproduced atomic displacement vectors in C (Eq. 13) (mapping #2). Third, we noted the elements of U as a measure of the contributions of the MWD bases to the reproduced atomic MWD vectors in W (mapping #3). This permutation reorders j such that the sum of squared (σ(j), k) components of U (1 < k < j) is the maximum of {U_{σ(j) k}² | σ(j) < k < 3(N_I + N_II)}.

Fig. 3

Flowchart for constructing the coarse-grained space. The cards titled mappings #1, #2, and #3 can replace each other to compare the validity of those methods for selecting the bases

When we note the selected atomic displacement vectors contained in C, the MWD vectors are calculated using Eq. 14.

$$ \left\{\begin{array}{l}\overset{\sim }{\mathbf{W}}\kern1.5em \equiv \kern.5em {\mathbf{M}}^{1/2}{\overset{\sim }{\mathbf{C}}\overset{\sim }{\mathbf{L}}}^{-1}\\ {}{\overset{\sim }{\mathbf{L}}}^2\kern.5em \equiv \kern.5em {\overset{\sim }{\mathbf{C}}}^{\mathrm{T}}\mathbf{M}\overset{\sim }{\mathbf{C}}\end{array}\right) $$

(14)

Substituting C in Eq. 14 with that in Eq. 13, we can obtain the MWD vectors $\left(\overline{\mathbf{W}}\right)$reproduced in the coarse-grained space.

$$ {\displaystyle \begin{array}{l}\overline{\mathbf{W}}\equiv {\mathbf{M}}^{1/2}\tilde{\mathbf{B}}\hat{\boldsymbol{\Xi}}{\boldsymbol{\Lambda}}^{-1}\\ {}\kern0.84em ={\mathbf{M}}^{1/2}\tilde{\mathbf{B}}{\boldsymbol{\Gamma}}^{1/2}\hat{\mathbf{U}}\end{array}} $$

(15)

The quality of the coarse-grained space can be evaluated by comparing the MWD vectors on the original atomistic Cartesian coordinate bases with those reproduced on the reduced bases. We previously proposed the severest criterion F₄, which is the determinant of the correlation matrix R. The matrix R can be further rewritten as the product of ${\tilde{\mathbf{L}}}^{-1}$ and Λ, and the diagonal elements are the ratio of the reproduced modal masses to the original ones.

$$ \mathbf{R}\kern.5em \equiv \kern.5em {\overset{\sim }{\mathbf{W}}}^{\mathrm{T}}\overline{\mathbf{W}}={\overset{\sim }{\mathbf{L}}}^{-1}\boldsymbol{\Lambda} $$

(16)

$$ {F}_4=\det \left(\mathbf{R}\right) $$

(17)

If the matrix $\overline{\mathbf{W}}$ is identical to $\tilde{\mathbf{W}}$, the matrix R is equal to the unit matrix E, meaning that F₄ is maximized to unity when the coarse-grained space is complete to describe the normal-mode vibrations of the assembly. Therefore, $\tilde{\mathbf{W}}$ is properly approximated by $\overline{\mathbf{W}},$ which is further rewritten from Eq. 15 into its singular value decomposition (SVD), where $\tilde{\mathbf{H}}$ is a partial matrix containing MWD bases modified by Löwdin symmetry orthogonalization, J is an orthonormal matrix, and ρ^1/2 is a set of singular values.

$$ \left\{\begin{array}{l}\overset{\sim }{\mathbf{W}}\kern1em \simeq \overline{\mathbf{W}}\equiv \overset{\sim }{\mathbf{H}}{\rho}^{1/2}{\mathbf{J}}^{\mathrm{T}}\\ {}\overset{\sim }{\mathbf{H}}\kern1.5em \equiv \kern.5em {\mathbf{M}}^{1/2}\overset{\sim }{\mathbf{B}}{\boldsymbol{\Gamma}}^{1/2}\\ {}{\mathbf{J}}^{\mathrm{T}}\kern.5em \equiv \kern.5em {\rho}^{-1/2}\hat{\mathbf{U}}\end{array}\right) $$

(18)

By definition of SVD theory, the square of singular values is obtained by diagonalizing ${\overline{\mathbf{W}}\overline{\mathbf{W}}}^{\mathrm{T}}$ (Eq. 19). Consequently, $\tilde{\mathbf{H}}$ is a partial matrix of $\hat{\mathbf{H}},$ an orthonormal matrix that diagonalizes ${\overline{\mathbf{W}}\overline{\mathbf{W}}}^{\mathrm{T}},$ of which the eigenvalues are the diagonal elements of UU^T, namely, unity.

$$ \rho ={\hat{\mathbf{H}}}^{\mathrm{T}}\left({\overline{\mathbf{W}}\overline{\mathbf{W}}}^{\mathrm{T}}\right)\hat{\mathbf{H}}={\hat{\mathbf{U}}\hat{\mathbf{U}}}^{\mathrm{T}} $$

(19)

In a coarse-grained space, some of the eigenvalues of ${\overline{\mathbf{W}}\overline{\mathbf{W}}}^{\mathrm{T}}$ become substantially zero (rank deficient), meaning that we can pick up some non-zero singular values (ρ_i) that can properly approximate $\tilde{\mathbf{W}}$ based on Eq. 18. The singular value is given by Eq. 20, which is actually an indicator maximized when selecting the intramolecular vibration vector in mapping #3.

$$ {\rho}_i\kern.5em \simeq \kern.5em {\left({\overset{\sim }{\mathbf{U}}\overset{\sim }{\mathbf{U}}}^{\mathrm{T}}\right)}_{ii}=\sum \limits_m^i{U_{im}}^2 $$

(20)

The above formulation supports the use of mapping #3 in reordering matrix B. Mapping #2 also appears rational to some extent, but the non-orthonormality of the Ξ matrix shows that the diagonal elements of Ξ^TΞ cannot be singular values of any form of SVD.

Computational details

According to the formulation described in the “Theory” section, we modified our in-house program to calculate the Φ matrix, so that it is applicable to heterodimers. The molecules shown in Fig. 1 were used to construct 21 combinations, including 6 homodimers and 15 heterodimers (Fig. 4). The geometry of these dimers was optimized using the Hartree-Fock method with the 6-311G** basis set and subsequently subjected to normal vibration analysis at the same level of calculation. The energies of the monomers and dimers were used to calculate the dimerization energy (E_assoc) according to Eq. 21,

$$ {E}_{\mathrm{assoc}}=\left({E}_{\mathrm{model}\ \mathrm{I}}+{E}_{\mathrm{model}\ \mathrm{I}\mathrm{I}}\right)-{E}_{\mathrm{assembly}} $$

(21)

where E_{model I} and E_{model II} are the energies of models I and II, and E_assembly is that of the dimer. The basis set superpositional error was corrected by the counterpoise method. These molecular orbital calculations were performed in the GAUSSIAN 09 W programs [53]. Visualization of the molecules was performed with Jmol ver.14.4.0 [54].

Fig. 4

Molecular structures of homo- and heterodimers studied

Results and discussion

As a representative heterodimer, the results of TC + AD are described here. Figure 5 plots the fidelity index (F₄ in Eq. 17) as a function of the dimension of the coarse-grained space that was constructed according to methods #1–3 in the “Theory” section. In Fig. 5a, where the bases were arranged in increasing frequency order, the F₄ value swings between high and low levels at random, indicating that the bases were not properly selected, especially for the space of less than 25 dimensions. In Fig. 5b, where the bases were arranged in decreasing (Ξ^ΤΞ)_ii order, the F₄ value seems much improved, maintaining a sufficiently high level, although there are moderate depressions at 20, 24, 27, and 32 dimensions. As shown in Fig. 5c, where the bases were arranged in decreasing (U^ΤU)_ii order, the F₄ value maintains a high level as well, and the depression at 24–27 dimensions was significantly improved. As mentioned in the “Theory” section, the sorting scheme of mapping #3 seems quite reasonable, so that we can properly construct a coarse-grained space for a given dimension, although there are some occasional collapses. Such collapses imply a serious unsatisfactory basis set, namely, a lack of a certain vibrational motion crucial to the normal mode vibrations, which is partly due to the restriction of Ξ and U to square matrixes. For all reordering methods, the fidelity index is extremely low when the dimension is 12, which can be explained by the lack of C–C bond libration (#1 vibration mode of TC model).

Fig. 5

Fidelity index (blue lines, right axis) and stiffness constants Φ_Tx,Tx (■),Φ_Ty,Ty (●), and Φ_Tz,Tz (▲) (black lines, left axis) for TC + AD dimer as a function of the dimension of the coarse-grained space that was constructed by a mapping #1, b mapping #2, and c mapping #3

As demonstrated previously, we are interested in intermolecular stiffness with respect to a double hydrogen bond direction, namely, the diagonal element of Φ with respect to T_x, T_y, and T_z motions. Figure 5 overlays the elements Φ_Tx,Tx, Φ_Ty,Ty, and Φ_Tz,Tz as a function of the column dimension of B [55]. The line graph shows a stepwise increment with the increasing number of bases employed. This discontinuity indicates that the translational motions of the two units are coupled with a limited number of intramolecular vibrations: in a poor basis set, an apparent stiffness with respect to this motion is to some extent underestimated to compensate for the neglected intramolecular flexibility [49]. The step height between the neighboring plots is a measure of coupling with the added vibration mode. Similar to the case already reported for homodimers, the continuity of Φ elements is not greatly disturbed, even if the fidelity index sharply decreases, except for the 12-dimensional space, which lacks an essential basis responsible for the molecular flexibility. Thus, we can define the minimum coarse-graining dimension to be 13 for the TC + AD case.

Similar results were obtained for the other homo- and heterodimers, suggesting that reordering mapping #3 was reliable for constructing the coarse-grained space. The results of the Φ_Tx,Tx plots against the dimension of the space, together with the fidelity index F₄, are shown in Fig. S1. For all dimers, the trend of the Φ_Tx,Tx plot was similar to that of TC + AD, and the F₄ value remained at a moderately high level in many dimensions. For the dimers that contain either AA or TC, there was an LF vibration mode that strongly contributed from intramolecular C–C libration mode; hence, the minimum coarse-grained space comprised 13 dimensions. For AA+AA, AA+TC, and TC + TC dimers, the minimum dimensionality was 14. For the other dimers, coarse-graining in the 12-dimensional space afforded a sufficiently high value for the fidelity index.

Figure 6a displays a heatmap representation of the full matrix U for a dimer composed of TC and AD before reordering. The column index i designates a consecutive number of translations (1 ≤ i ≤ 3), librations (4 ≤ i ≤ 6), and normal mode vibrations (7 ≤ i ≤ 42) of the TC + AD dimer, while the row index j designates a consecutive number of translations and librations, as well as normal mode vibrations of TC (1 ≤ j ≤ 6, 13 ≤ j ≤ 30) and AD (7 ≤ j ≤ 12, 31 ≤ j ≤ 42). We can see from this figure that the modes of unit motion largely contribute to the mode of vibration of the assembly, while it becomes clearer when the rows are reordered according to the basis set selection scheme, mapping #3 (Fig. 6b). For example, the #5 vibrational mode of the dimer (i = 11) is predominantly attributed to T_x motions of TC (j = 1) and AD (j = 7) with an opposite sign, together with an additional contribution from the R_z motion of AD (j = 12). This can be visually understood from the molecular model (Fig. 7a), which shows that the #5 vibration is attributed to the stretching mode between TC and AD, although the center of mass is quite biased toward the TC side; hence, it is well approximated with the T_x motion of the AD model (Fig. 7b). In other words, regarding the TC + AD dimer, the #5 vibration directly reflects information about the intermolecular force of their double hydrogen bonding.

Fig. 6

Heatmap of the matrix U for TC + AD dimer. a Bases arranged by frequency for each model; b bases arranged by selected order using mapping #3. Enlarged versions of original figures are given in Figs. S2 and S3

Fig. 7

Schematic representation of the molecular motion for a #5, c #9, and e #12 vibration modes of TC + AD dimer; b T_x motion of AD; d #3, and f #6 vibration modes of TC

Figure 6b shows that the T_x motions of TC and AD also contribute to the #13, #15 (Fig. 7c), and #18 (Fig. 7e) vibrations of the dimer, and the main components of those vibrations are the R_z motion of AD (j = 12), #3 mode of TC (j = 15) (Fig. 7d), and #6 mode of TC (j = 18) (Fig. 7f), respectively. Consequently, these intramolecular vibrations are moderately coupled with the T_x motions of the constituent units through hydrogen bonding. As described earlier, this type of coupling is responsible for the stepwise behavior of the Φ plot. This is easily understood if one imagines that the assembly is approximated as a series connection of springs, where the apparent force constant is underestimated because of the neglect of the coupled springs. After dissolving all of the contributions from coupled springs, we can obtain the true force constant of the spring of interest. Regarding the intermolecular hydrogen bonding interactions discussed in this study, we denote the apparent stiffness in the minimum coarse-grained space (mostly, the fidelity index >0.8) as Φ_app and the true stiffness in the full-dimensional space as Φ_inter [48]. Table 1 summarizes the values of Φ_app and Φ_inter for all molecular dimers studied.

Table 1 Values of force constants (in N m⁻¹) for Φ_app (left) and Φ_inter (right)

Concerning the physical meaning of the step height of the Φ graphs, we previously proposed an analysis of intermolecular vibrations based on a coupled oscillator model that contains a series connection of three springs. The formulation of Φ_intra (Eq. 22) was initially derived from the rigorous treatment of a symmetric four-body model and later proved to approximately hold for an asymmetric model. According to Eq. 22, we can estimate the intramolecular stiffness Φ_intra averaged over TC and AD. For example, this value is calculated to be 115 N m⁻¹ using Eq. 22, with values of Φ_app = 35.4 N m⁻¹ and Φ_inter = 44.1 N m⁻¹. Table 2 summarizes the average intramolecular stiffness for all the dimers studied. The diagonal items in this table are the values from homodimers, namely, intramolecular stiffness intrinsic to respective molecules, and some of them are refinements of our previous report [48, 56]. TC exhibits an extremely low value (86.2 N m⁻¹), probably because of its flexible C–Cl bond as compared with a C-H bond. Conversely, AD gave the highest value (370 N m⁻¹) among the six molecules, reflecting its rigid skeleton supported by extended π-conjugation.

$$ {\varPhi}_{\mathrm{intra}}=\frac{\varPhi_{\mathrm{inter}}^2-{\left({\varPhi}_{\mathrm{inter}}-{\varPhi}_{\mathrm{app}}\right)}^2}{2\left({\varPhi}_{\mathrm{inter}}-{\varPhi}_{\mathrm{app}}\right)} $$

(22)

Table 2 Intramolecular stiffness of molecular dimers derived from Eq. 22

The idea of the averaged intramolecular stiffness is applied to the individual one for each contribution of the intramolecular vibration mode taken into account in the n-th step. In Eq. 23, ${\tilde{\varPhi}}_{\mathrm{app},n}$ and ${\tilde{\varPhi}}_{\mathrm{intra},n}$ are the apparent stiffness and newly contributed intramolecular stiffness, respectively, in the dimension of n.

$$ {\varPhi}_{\mathrm{intra},n}=\frac{\varPhi_{\mathrm{app},n}^2-{\left({\varPhi}_{\mathrm{app},n}-{\varPhi}_{\mathrm{app},n-1}\right)}^2}{2\left({\varPhi}_{\mathrm{app},n}-{\varPhi}_{\mathrm{app},n-1}\right)} $$

(23)

Here, we define ${\varPhi}_{\mathrm{ser}}^{-1}$ as the sum of ${\varPhi}_{\mathrm{intra},n}^{-1}$ over n from the minimum to the full dimensions of the coarse-grained space. This corresponds to the synthetic compliance of a series connection of springs.

$$ {\varPhi}_{\mathrm{ser}}^{-1}=\sum \limits_n^{3N}{\varPhi}_{\mathrm{intra},n}^{\kern0.6em -1} $$

(24)

Interestingly, the plot of Φ_ser against Φ_intra shows excellent linearity over all 21 dimers, with an incline of nearly 1 (incline = 0.999; intercept = −15.0 N m⁻¹; R² = 0.999) (Fig. 8). This result suggests that the internal stiffness of the molecule is well explained by a series connection of springs, for each of which the force constant is Φ_intra,n: for a coarse-grained space with a small dimension, most springs are “locked” to behave as rigid bodies and the apparent stiffness of the entire coupled oscillator is somewhat smaller than the true Φ_inter. As the dimension increases, the rigid bodies are “unlocked” to behave as springs and the apparent stiffness approaches the true value of Φ_inter.

Fig. 8

Correlation between Φ_ser (synthetic stiffness based on a series connection model of springs) and Φ_intra (averaged intramolecular stiffness)

The Φ_inter values reflect the intrinsic nature of intermolecular interactions, namely, hydrogen bonding interactions in the present case. Therefore, we can expect some relationship between the Φ_inter and the association energy of the dimer, E_assoc. The smallest and largest association energies among those studied were 36.7 (AN+AN) and 63.5 (TC + AN) kJ mol⁻¹, respectively, in which dimers had the smallest and largest Φ_inter values of 29.3 and 51.9 N m⁻¹. Figure 9 shows that both values demonstrate a moderate positive correlation, with an incline of 9.4 × 10⁻⁴ N m⁻¹/J mol⁻¹ and an intercept of − 5.7 N m⁻¹ (R² = 0.903). It seems natural but not quite obvious that the more the assembly is energetically favored, the higher the intermolecular stiffness is. In other words, E_assoc and Φ_inter are independent parameters that determine the depth and curvature of the potential curve. The unit of the incline can be converted to mol m⁻², implying that the inverse square root of this value indicates a distance somewhat characteristic to these series of double hydrogen-bonded dimers. Based on the harmonic oscillator model, we can propose a simple relationship (Eq. 25) between energy E and distance D. A characteristic distance D₀ can then be defined as the half-width of the hypothetical quadratic potential curve at E = 0, which is a measure of the positional tolerance of the constituent molecules. The linear relationship in Fig. 9 affords an average D₀ value of 1.9 Å for the series of double hydrogen-bonded dimers in this study. This index might change depending on the nature of intermolecular interactions, including π-stacking, van der Waals forces, and hydrogen bonding.

$$ \left\{\begin{array}{l}E=\frac{1}{2}{N}_{\mathrm{A}}{\varPhi}_{\mathrm{inter}}{D}^2-{E}_{\mathrm{assoc}}\\ {}{D}_0=\sqrt{\frac{2{E}_{\mathrm{assoc}}}{N_{\mathrm{A}}{\varPhi}_{\mathrm{inter}}}}\end{array}\right. $$

(25)

Fig. 9

Correlations among Φ_inter, Φ_app, and E_assoc

For Φ_app, conversely, there was an appreciable deviation from the least-square line (line not shown). In view of the nature of the Φ_app, which is the apparent stiffness that has been modified by coupling with intramolecular vibrations, it seems natural that it shows no apparent correlation with Φ_inter. The discrepancy between Φ_app and Φ_inter is attributed to the following reasons: (i) the stretching mode vibration of a molecular dimer is not always pure antisymmetric translational motion, but rather a mixture of shearing, libration, and so on; (ii) neglect of the intrinsic flexibility of the constituent molecules causes serious errors in calculating the force constant. For reason (i), contributions other than antisymmetric translation became appreciably large when the symmetry axes of the monomers did not coincide with the direction of hydrogen bonding. Even though a moderately symmetric AA+AA dimer is employed, the stretching mode has a nearly 20% contribution from R_z + R_z motion, and the situation seems similar for all the dimers studied in this paper. The effect arising from reasons (i) and (ii) will be highlighted by a comparison of the Φ_app with the force constant Φ_PDA derived from pseudodiatomic approximation (PDA), in which each constituent molecule is regarded as a frozen rigid body with a given molecular weight [57]. The force constant Φ_PDA can be calculated with the angular frequency ω_stretch for stretch mode vibration and the reciprocal masses Γ_I and Γ_II, which are the inverse of the molar masses of M_I and M_II, respectively. Because of its simplified derivation, it is often pointed out that there is only a poor correlation between the force constants based on PDA and the association energy [58]. Figure 10(a) shows a plot of the Φ_PDA values against the Φ_app, demonstrating sizable deviation from the diagonal line, although there is a moderate correlation with the homodimer data.

$$ {\varPhi}_{\mathrm{PDA}}=\frac{\omega_{\mathrm{stretch}}^2}{\varGamma_{\mathrm{I}}+{\varGamma}_{\mathrm{I}\mathrm{I}}} $$

(26)

Fig. 10

a Comparison of Φ_PDA vs. Φ_app; b comparison of Φ_COM vs. Φ_app

Next, we attempt to obtain an explicit representation of the coupling of vibration with respect to the inter- and intramolecular stiffness. To this end, we have previously employed a four-body coupled oscillator model (COM) composed of four masses, A, B, C, D, and springs between them (Fig. S4). One monomer is approximated with a weight M_I equally distributed on A and B, and a spring with a force constant of Φ_intra,I. Another monomer with a weight of M_II is represented by a similar oscillator composed of C and D connected with a spring of Φ_intra,II. The two oscillators are connected with a spring with a force constant of Φ_inter (<<Φ_intra,I, Φ_intra,II) between B and C, and the four bodies are constrained to one-dimensional movement. Diagonalization of the mass-weighted Hessian matrix of this model is performed, where the reciprocal masses Γ_I and Γ_II again give us a set of squared angular frequencies as eigenvalues. The lowest non-zero solution, ω_LF², corresponds to a vibration mode primarily attributed to the stretching of B–C. Meanwhile, high-frequency solutions ω_HF(ap)² and ω_HF(ip)² correspond to the anti-phase and in-phase vibrations, respectively, localized at the A-B and C-D pairs. Eq. 28 allows us to calculate an apparent force constant Φ_COM for the spring between B and C. This procedure assumes consolidation of the oscillators A–B and C–D pairs, but moves far beyond the simple pseudodiatomic approximation, in that we can properly take into account the intramolecular stiffness of the constituent molecules.

$$ \left(\begin{array}{cccc}{\varGamma}_{\mathrm{I}}{\varPhi}_{\mathrm{intra},\mathrm{I}}& -{\varGamma}_{\mathrm{I}}{\varPhi}_{\mathrm{intra},\mathrm{I}}& 0& 0\\ {}-{\varGamma}_{\mathrm{I}}{\varPhi}_{\mathrm{intra},\mathrm{I}}& {\varGamma}_{\mathrm{I}}\left({\varPhi}_{\mathrm{intra},\mathrm{I}}+{\varPhi}_{\mathrm{inter}}\right)& -\sqrt{\varGamma_{\mathrm{I}}{\varGamma}_{\mathrm{I}\mathrm{I}}}{\varPhi}_{\mathrm{inter}}& 0\\ {}0& -\sqrt{\varGamma_{\mathrm{I}}{\varGamma}_{\mathrm{I}\mathrm{I}}}{\varPhi}_{\mathrm{inter}}& {\varGamma}_{\mathrm{I}\mathrm{I}}\left({\varPhi}_{\mathrm{intra},\mathrm{I}\mathrm{I}}+{\varPhi}_{\mathrm{inter}}\right)& -{\varGamma}_{\mathrm{I}\mathrm{I}}{\varPhi}_{\mathrm{intra},\mathrm{I}\mathrm{I}}\\ {}0& 0& -{\varGamma}_{\mathrm{I}\mathrm{I}}{\varPhi}_{\mathrm{intra},\mathrm{I}\mathrm{I}}& {\varGamma}_{\mathrm{I}\mathrm{I}}{\varPhi}_{\mathrm{intra},\mathrm{I}\mathrm{I}}\end{array}\right)U=U\left(\begin{array}{cccc}0& & & O\\ {}& {\omega}_{\mathrm{LF}}^2& & \\ {}& & {\omega}_{\mathrm{HF}\left(\mathrm{ap}\right)}^2& \\ {}O& & & {\omega}_{\mathrm{HF}\left(\mathrm{ip}\right)}^2\end{array}\right) $$

(27)

$$ {\varPhi}_{\mathrm{COM}}=\frac{\omega_{\mathrm{LF}}^2}{\varGamma_{\mathrm{I}}+{\varGamma}_{\mathrm{I}\mathrm{I}}} $$

(28)

Because it is difficult for the eigenvalue equation, Eq. 27, to derive an analytical solution in the case of a heterodimer, we numerically calculated the Φ_COM values for all 21 dimers. Figure 10(b) shows an excellent correlation between Φ_COM and Φ_app, meaning that Φ_app can be explained by the lowest-frequency mode of the coupled oscillator model. In a coarse-grained space with the minimum dimension, Φ_app corresponds to the stiffness of the intermolecular force, but is to some extent underestimated to compensate for the neglected intramolecular flexibility. As the number of bases increases, the contributions from the monomers are gradually decoupled. Thus, the force constant approaches Φ_inter, which is the true stiffness of the central spring.

Conclusions

In this study, we developed a method of coarse-graining the intermolecular vibrations of molecular heterodimers assembled by double hydrogen bonding. In contrast to our previous study on homodimers, the coarse-grained space for heterodimers needs to be constructed with special care so that all normal-mode vibrations can be reproduced with a fidelity that is as high as possible at every dimension adopted. To this end, we tested three schemes of reordering the intramolecular vibration vectors to determine the best method to note the contributions of such vectors to the mass-weighted displacement in the coarse-grained space. This method is shown to be equivalent to the size-reduction of the MWD matrix based on singular value decomposition. Using this method, we successfully obtained the apparent stiffness constants at each dimension, resulting in a monotonously increasing stepwise graph. The stepwise behavior is rationalized in terms of the mechanics of a series connection of springs, which accounts for the internal flexibility of a molecule. The true stiffness constants of the intermolecular force were obtained at the high-dimension limit of the coarse-grained space. Interestingly, the true stiffness constants show a good correlation with the association energies of the dimers, based on which we have proposed a new parameter (a characteristic distance D₀) to evaluate the nature of the interaction. The set of stiffness constants, Φ_intra and Φ_inter, obtained for each dimer are consistent enough to reproduce the Φ_app based on the coupled oscillator model, showing that the model is valid, far beyond the pseudodiatomic model, for heterodimers as well as homodimers. The present work provides a firm foundation for our coarse-graining theory with application to the mechanical properties of molecular crystals and other heterogeneous molecular assemblies.