Abstract
The continuous-wave saturation (CWS) behavior of several measureable parameters in an EPR spectrum of a nitroxide free radical is carried out theoretically and tested experimentally with 15N-d17-4-Hydroxy-2,2,6,6-tetramethylpiperidine 1-oxyl in 60% aqueous-glycerol solutions from 273 to 340 K. The theory explicitly includes spin relaxation due to electron spin exchange and dipole–dipole interactions, but no other spectral diffusion pathways of paramagnetic relaxation. A primary objective of this work was to study the CWS of the dispersion signal induced by spin exchange and dipole–dipole interactions, a signal that is superimposed upon the absorption. This was rendered possible because, using modern least-squares fitting methods, the two signals may also be separated to high precision. Using a new rigorous theory, theoretical spectra were simulated and were also separated into absorption and dispersion components. The absorption components, both experimental and theoretical, may be analyzed using the traditional Bloch equations and compared with literature results. The dispersion components may only be analyzed by direct comparison of parameters derived from the theoretical and experimental spectra. A comparison of the amplitudes of the absorption and the dispersion components provides a severe test of the theory and the experimental results are good agreement with the theory. The experimental values of \({T}_{1}\) both from The Bloch equations and the direct comparison of the absorption components were comparable to the limited and scattered literature results where both pulsed- and CWS methods were employed. From the theory, the same value of \({T}_{1}\) was found from the CWS of the Lorentzian line width and the doubly-integrated intensity; however, there were discrepancies in the values of \({T}_{1}\) for these two parameters experimentally.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This is the first of a series of papers in quest of a deeper understanding of the effects of Heisenberg spin exchange (HSE) and dipole–dipole (DD) interactions on saturated EPR spectra of nitroxide free radicals (nitroxides) in solution. See Table 1 for a summary of abbreviations, notes, and acronyms. We extend further our theory [1,2,3,4,5] to an arbitrary value of the circularly-polarized magnetic induction of the microwave field, \({H}_{1}\), and compare the theoretical predictions with experimental results obtained from the nitroxide 4-hydroxy-2,2,6,6-tetramethylpiperidine-d17-1-15N-oxyl (15D-Tempol). Here, our focus is on nitroxides executing rapid rotational and translation motion yielding spectra in the motional-narrowed regime. Our goal is to understand the spin-relaxation behavior of nitroxides in solution in view of recent discoveries of interesting spectral properties of nitroxides where HSE and DD interactions which, at increasing concentration, \(C\), (M) induce signals that are admixtures of absorptive and dispersive terms: e.g., see [6, 7] and references therein. When we refer to “signals”, we mean the components of the EPR spectrum observed out-of-phase with \({H}_{1}\), normally observed with a modern EPR spectrometer employing automatic frequency control. Thus the designation dispersion in this context is distinct from its historical meaning of being the in-phase signal. Recent work offers a different viewpoint of this mixed shape of resonance lines [5]. These admixtures are a result of transfer of spin coherence by HSE, DD, or both. Thus, for 14N nitroxides, instead of three pure absorption lines observed at low \(C\), three spin modes [2, 6, 7] result at higher \(C\). The modes at high- and low-fields, (hf and lf) are comprised of two components, one absorption plus one dispersion while the central-line (cf) only shows only the absorption. Furthermore, as HSE increases, intensity of the absorption contributions to the lf and hf modes is transferred to the cf mode [8]. Finally, the lf and hf absorption components change from absorption to emission [6, 7]. For 15N nitroxides, the lf and hf are each comprised of one absorption and one dispersion. This work will also address the complex effect of inhomogeneous broadening (IHB) due to proton (deuteron) hyperfine structure (hfs) on the saturation behavior of nitroxides in the presence or absence of HSE and/or DD. For convenience, we mostly refer to protons in the text when it is clear that we mean either isotope. There has been considerable work on all of these aspects except for the dispersion. See, for example the review by Marsh and coworkers and references therein [9]. A problem that its already complicated by hfs, HSE, and DD [6] is further complicated because of the addition of another dimension, \({H}_{1}\). Fortunately, the reader may consult [9] as well as clear expositions of the various complicating factors in two recent books that detail the progress to date by Salikhov [2] (theory) and by Marsh [10] (theory and experimental methods). Both books provide a wealth of references and historical perspective.
It’s been 55 years since McConnell’s group at Stanford published their seminal work on nitroxides [12]. See, for example, [13] for a summary of the fundamental advances in the field replete with history and images of many of the principal contributors. The practical applications of nitroxide spin probes that have developed over this time span, and continue to be developed—just in biology and chemistry—is impractical to summarize because of its sheer abundance. Fortunately, a series of reviews of the advances have been available regularly: e.g., [14,15,16]. Useful reviews of continuous wave saturation (CWS) and other EPR techniques to study exchange processes and distances in membranes were given in [9] and [10]. Because of their practical use for studies of in vivo EPR imaging, relaxation times have been measured for a number of isotopically-substituted nitroxides [17]. Similar studies focused on the role of electron spin relaxation for Overhauser dynamic nuclear polarization [18,19,20,21,22,23,24,25].
Aside from their practical uses in chemistry and biology, nitroxides offer a unique testing ground for our understanding of interacting spins in liquids because they: (a) are stable and may be studied over wide ranges of temperatures in solvents of different viscosities and polarities; (b) have well defined hfs patterns that are precisely known [11] and variable by changing solvent polarity, nitroxide structure, and deuteron substitution; (c) afford precise variation of the spin diffusion due to HSE and DD from being negligible to one or the other being dominate; and, (d) offer two distinct regions of hfs and therefore, two intermediate zones [6]. The term “intermediate zone” refers to rates of transfer of spin coherence that are comparable to hyperfine coupling constants. Thus we refer to the proton or nitrogen intermediate zone when the rate of transfer of spin coherence is comparable to either \({\gamma a}_{\mathrm{p}}\) or \({\gamma A}_{0}\), where \({a}_{\mathrm{p}}\) or \({A}_{0}\) are the hyperfine coupling constants, in gauss, due to the protons or the nitrogen, respectively.
The feature that is completely new in this line of investigation is the role of the transfer of spin coherence that provokes line shifts and dispersion components [2]. The line shifts are beyond the scope of the present work, but are potentially very interesting because they arise not only from either HSE or DD [6] but also from the interaction of \({H}_{1}\) [3].
See a recent publication [26] for a brief summary of the development and uses of CWS and motives for pursuing the method further. Because the dispersion and absorption components may be reproducibly and accurately separated [6, 27], the saturation behavior of each component may be studied independently by CWS. Specifically, the saturation of the dispersion component may now be studied by CWS because it is separated from the much larger absorption. It would be difficult by pulsed methods because the recovery to equilibrium of both signals would be superimposed.
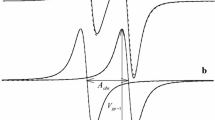
It has been 67 years since Portis published his pioneering paper on spin relaxation of F-centers as measured by continuous-wave saturation (CWS) of EPR of IHB spectra of F-centers [28]. Portis studied the CWS of the maximum amplitude of the absorption and showed that its unusual saturation behavior could be understood if the signal were comprised of individual Lorentzian resonance lines distributed over many resonance fields due to hyperfine coupling to neighboring magnetic nuclei. Portis coined the term “spin packet” which refers to an individual resonance line of Lorentzian shape with full-width at half-height line width, \(\Delta {H}_{1/2}^{L}\), that saturates according to the Bloch formalism, the “homogeneous case”
where \({H}_{1}\) is the effective value of the circularly-polarized magnetic induction and \({K}_{\mathrm{peak}}\) is the slope of the amplitude \(Y({H}_{0})\) in the unsaturated region; i.e., for \({H}_{1}^{2}{T}_{1}{T}_{2}\ll 1\) which we call “small \({H}_{1}\).” \({T}_{2}=2/\left[\gamma {\left(\Delta {H}_{1/2}^{L}\right)}_{0}\right]\) where subscript 0 denotes \(\left({H}_{1}\to 0\right)\). Experimental determination of \({H}_{1}\) depends on factors discussed in detail in [26] and references therein. In (1), \(\gamma\) is the gyromagnetic ratio of the free electron, \(H\) and \({H}_{0}\) are the swept- and resonance-magnetic fields, respectively. In Portis’ model, it is assumed that \({T}_{1}\) and \({T}_{2}\) are the same for all spin packets. The spin packets are distributed over an IHB profile to form a manifold of overlapping, unresolved Lorentzian lines.
To compare with theory, Portis assumed an IHB profile of Gaussian shape (Gaussian), leading to the convolution of a Lorentzian and Gaussian, the Voigt, to represent the spectrum [11, 28].
The familiar Voigt [11], used in various fields of physics [29], is defined by the single parameter, \(\chi\) as follows:
where \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) and \({\Delta H}_{\mathrm{pp}}^{\mathrm{G}}\) are the peak-to-peak Lorentzian line widths of the spin packets and of the Gaussian profile, respectively in a first-derivative presentation. Experimentally, Portis plotted the CWS of the maximum of the absorption in the center of the Voigtian line as well as the CWS of the height of the signal in-phase with \({H}_{1}\), the “normal” dispersion, which showed no saturation. Schematic representations of the Voigt comprised of spin packets abound in the literature. See, for example, Fig. 2 of [28] (non-derivative) or Fig. 1 of [6] (derivative). This latter schematic also includes dispersion components due to HSE and provides a graphical definition of the peak-to-peak height of the Voigt, denoted by \({V}_{\mathrm{pp}}\), and the peak-to-peak line width of the Voigt, \({\Delta H}_{\mathrm{pp}}^{0}\). In this work, these quantities will carry an index, when needed, to refer to a particular manifold or to distinguish between HSE and DD.
Portis assumed that there were no interactions between the spin packets and that \(\chi \to \infty\). He also established the fact that the spin packet was Lorentzian to high precision, justifying the use of the Lorentzian CWS, Eq. (1) [28]. The lack of interactions between the spin packets implies that transfer of spin coherence was absent.
Castner [30] studied the CWS of \({V}_{\mathrm{pp}}\) of the spectrum of the \({V}_{\mathrm{K}}\) center. He also assumed the Voigt and no spin diffusion, however, maintained a finite value of \(\chi\) to successfully describe CWS. The two authors studied the height of the symmetric EPR absorption in its non-derivative (Portis) or derivative (Castner) presentation; neither studied the integrated intensity which is given in Eq. (17) of [30].
Wolf [31] extended the work of Portis and Castner by including an unknown mechanism of spectral diffusion only controllable over a limited range by varying the temperature. He did not include transfer of spin coherence.
These three works suffered from the lack of a detailed knowledge of the hfs and in Wolf’s case, a lack of knowledge of the diffusion process and the omission of a treatment of transfer of spin coherence. Nitroxides treated with modern theories suffer from none of these deficiencies.
Modern workers have a tremendous advantage that allows us to separate the absorption and dispersion components of each line separately even if they are severely overlapping even to the extent that separate lines are not visually evident in the spectrum. The program Lowfit, which is described further below, is our method of effecting this separation. The significance of this separation is that we have a method to study the absorption component using the long established Bloch formulation of spin relaxation. The study of the dispersion components is now made possible by rigorous theories such as the one in the next section.
From the Bloch formalism, the first-derivative spectrum of a homogeneous line, the peak-to-peak line width, \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\), varies with \({H}_{1}\) as follows [26, 32]:
where the subscript 0 means the limit as \({H}_{1}\) goes to zero. \({T}_{2}=\underset{C\to 0}{\mathrm{lim}}2/\left[\sqrt{3}\upgamma {{\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\left(C\right)}_{0}\right]\) while the peak-to-peak height is given by [26, 32]
The CWS of \({V}_{\mathrm{pp}}\) or \({\Delta H}_{\mathrm{pp}}^{0}\) for an IHB manifold are not described by (3) or (4), respectively; however, provided that spin packets do not interact, the CWS for the doubly integrated intensity of the first-derivative spectrum, \(I\), does have the same form as that for a homogeneous line (Eq. 11 of [26]) as follows:
where \({K}_{\mathrm{I}}\) is the slope of \(I\) at small \({H}_{1}\).
Equations (3–5) are appropriate to the absorption components, only. A priori, Eqs. (3–5) are not expected to describe the CWS of real nitroxides except at \(C\to\) 0.
Let us summarize the argument in [26] that (5) applies to IHB spectra for \(C\to\) 0. Because each spin packet is independent of the others, it saturates as (5). \(I\) is the sum of the doubly-integrated intensities of all of spin packets, thus \(I\) also saturates according to (5). This same conclusion has been reach by others [9] based on the Voigt convolution [9]. The simpler argument given here shows that the assumption of a Voigt is unnecessary for \(C\to\) 0; it is true for any IHB profile, indeed for resolved or powder spectra.
A similar argument applies to fitting a CWS of \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) to (3) for \(C\to\) 0 even for IHB spectra. We assume that all of the spin packets in a given manifold have the same line width at \(C\to\) 0. Each spin packet broadens according to (3) so each spin packet continues to have the same width; thus the average width extracted from fit to a Voigt also follows (3). Here, the requirement of a Voigt line is explicit and therefore less general than the application of (5) which is valid for any line shape.
In the literature, it is generally accepted that for \(C\) > 0, in the presence of HSE, that the forms of CWS Eqs. (3) and (5) may be correctly applied to IHB spectra and give effective values of \({T}_{1}\), \({T}_{1}^{\mathrm{eff}}\), [9]. The implicit use of (3) for the CWS of \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) for IHB nitroxides in refs [33, 34] are examples; however, those authors used a different approach to obtain \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\). In other work, the CWS of \(I\) is used to obtain \({T}_{1}^{\mathrm{eff}}\) [9]. Whether these approaches to obtain \({T}_{1}^{\mathrm{eff}}\) are born out experimentally in the context of a rigorous theory is beyond the scope of this paper, but is obviously an important conjecture worthy of study. We shall see that under the assumptions of our theory, \({T}_{1}^{\mathrm{eff}}\) obtained from the absorption component of theoretical spectra shows that this conjecture is reasonable except in proton intermediate zones. See Table 4 below. In the theory developed here, the only relaxation pathways that are specifically included are due to HSE and/or DD.
A straightforward method to obtain \(I\) is to numerically integrate the spectrum twice, a necessary procedure for spectra not describable by an analytic line shape, for example slow motion or powder spectra. However, for fast motion nitroxide spectra such as those in Fig. S4 that are accurate Voigts, the accuracy is improved by at least an order of magnitude by using the parameters \(\chi\), \({V}_{\mathrm{pp}}\) and \({\Delta H}_{\mathrm{pp}}^{0}\) to compute \(I\) employing Eq. (35) of [11]. For noisy spectra the improvement is even greater. For a dramatic demonstration of this latter point, see Fig. 11 of [35].
In a comprehensive experimental and theoretical treatment of CWS in liquids that included the effects of HSE, Eastman et al. [34] studied the tetracyanoethylene anion radical (TCNE-) under conditions in which DD was negligible. Earlier studies of HSE of radicals in solution at low \({H}_{1}\) are cited in refs. 1–7 of [34]. At low concentrations, where HSE was negligible, they observed the expected nine well separated narrow lines of relative intensities near 1:4:10:16:19:16:10:4:1 spaced by \({A}_{0}\). Defining the spin exchange rate constant \({K}_{\mathrm{ex}}\) such that the frequency of spin exchange, \({\omega }_{\mathrm{ex}}\), is \({\omega }_{\mathrm{ex}}={K}_{\mathrm{ex}}C\), those authors showed that for slow exchange, \({K}_{\mathrm{ex}}C\ll {\gamma A}_{0}\), the effective spin–lattice relaxation time of the \(k\)th line with statistical weight of the \({\phi }_{k}\) was as follows:
Here \(k\) labels the projection of the nitrogen nuclear quantum numbers. \({T}_{1k}^{\mathrm{eff}}\) governs the CWS of each well separated Lorentzian line according to Eqs. (3)–(5) and depends on \(k\) if \({\phi }_{k}\) varies with \(k\) as was the case with TCNE-. In this example, \({\phi }_{k}\) = 1:4:10:16:19:16:10:4:1, each divided by 81. \({T}_{10}\) is the spin–lattice relaxation time directly to the lattice of each line, assumed to be independent of \(k\).
For nitroxides without protons, labelling the lines with the projection of the nitrogen spin quantum number, \(M\), \({\phi }_{M}=1/\left(2I+1\right)\) yields
Equations (6) and (7) have the simple physical interpretation that \({T}_{1M}^{\mathrm{eff}}\) is reduced by HSE from \({T}_{10}\) through the relaxation pathways provided by the non-resonant lines. The application of (7) to Fremy’s salt, which contains no protons, was carried out in [36] assuming that the spectrum was approximately Lorentzian using the CWS of the linewidth, (3), to obtain \({T}_{1\mathrm{cf}}^{\mathrm{eff}}\). Except for Fremy’s salt, all nitroxides are IHB.
To simplify the presentation, we discuss N equivalent protons which applies directly to radicals such as di-tert-butylnitroxide (DTBN) and 2,2,6,6-tetramethyl-4-oxopiperidine-1-oxyl (Tempone). For small \({H}_{1}\), this simplified hfs yields spectra that are excellent approximations to those derived from the true hfs for most nitroxides for \(\chi\) < 2 [11]. We demonstrate below that the same holds for saturated spectra by comparing CWS of Tempone vs. 4-hydroxy-2,2,6,6-tetramethylpiperidine 1-oxyl (Tempol). The advantage of this restriction is that a concrete, clearer exposition may be presented, maintaining the essential physical content. Our calculations are applicable to any hfs, so this simplified presentation does not affect the results for other hfs.
The IHB (\({\Delta H}_{\mathrm{pp}}^{\mathrm{G}})\) of spectra obtained with a modern EPR spectrometer is dominated by field modulation and hfs due to protons [37]. The former is treated in [37] and the latter by Eq. (2) of [11] from which, for \(N\) equivalent protons (deuterons),
where \(\alpha\) is a constant, near unity, to account for the small difference between the hyperfine pattern and the Gaussian. For Tempol, \(\sqrt{\alpha }=1.04\) [11].
The studies of the saturation of nitroxide spectra leading to (6) and (7) were limited to the effects of HSE on \({\Delta H}_{pp}^{L}\), using the square of (3) to fit the data to a straight line [36]. Those studies, and almost all others until 1997, dealt only with the line width until a paper appeared [38] that fundamentally changed the way we approached the studies of HSE and DD. In [38], an HSE-induced dispersion signal that is superimposed upon the traditionally studied absorption signal [39,40,41,42], was demonstrated to be capable of independently finding \({K}_{\mathrm{ex}}C\) to a precision rivalling that of line width studies.
This opened the door to the separation of HSE and DD [27, 43]. Another independent method to separate HSE and DD by comparing the concentration broadening of 14N versus 15N nitroxides was developed in [44].
The use of Lowfit to obtain \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\), \(I\), \({V}_{\mathrm{pp}}\) and \({V}_{\mathrm{disp}}\), and \(I\) is rather involved, thus we provide a detailed example involving an experimental spectrum in the Supplemental Information. We highlight one technical problem due to a mismatch of the cavity often encountered with lossy solvents [45]. This mismatch, introduces some normal in-phase dispersion signal into the normally detected out-of-phase signal. \({V}_{\mathrm{disp}}/{V}_{\mathrm{pp}}\) due to the mismatch, which we term “instrumental dispersion,” has the same sign and magnitude for all three (two) manifolds, either positive or negative depending on the conditions. This allows us to correct for the instrumental dispersion for 14N by subtracting \({V}_{\mathrm{disp}}^{\mathrm{cf}}/{V}_{\mathrm{pp}}^{\mathrm{cf}}\) from the other two ratios yielding two independent values of corrected \({V}_{\mathrm{disp}}^{\mathrm{man}}/{V}_{\mathrm{pp}}^{\mathrm{man}}\), giving us a means to assess the systematic errors.
Unfortunately, for 15N, we only have two such ratios giving us just one corrected value, denoted simply as \({V}_{\mathrm{disp}}\), as follows:
Our summary thus far has considered dominate HSE. Now, let us consider the case of dominant DD. The spectra are qualitatively similar to those in Fig. 1 except that the dispersion is negative; i.e., corrected \({V}_{\mathrm{disp}}^{\mathrm{lf}}<0\) and \({V}_{\mathrm{disp}}^{\mathrm{hf}}>0\). The reason for this difference in sign is that the transfer of phase coherence occurs without a phase change for HSE while for DD there is a change of phase of 180° [2]. Because they are of opposite sign, \({V}_{\mathrm{disp}}^{\mathrm{DD}}+{V}_{\mathrm{disp}}^{\mathrm{HSE}}\) can vanish over a (narrow) range of diffusion coefficients, \(D\). This interesting effect has been observed experimentally with 14pD-Tempone at approximately 180 K and with 15pD-Tempone at approximately 283 K in 70 wt% aqueous glycerol, see Fig. 13 of [27]. Line shifts toward the center from HSE, which have proved to be a valuable resource for separating HSE and DD and for studying re-collision during one encounter can be large, especially when \({K}_{\mathrm{ex}}C\cong {\gamma A}_{o}.\) See Table 2 of [7]. For DD, these shifts are outward, but they are marginally measureable and have not yet proved to be of quantitative use. See Fig. 12 of [43] where just a hint of outward shift is discernable near \({V}_{\mathrm{disp}}^{\mathrm{DD}}+{V}_{\mathrm{disp}}^{\mathrm{HSE}}\) = 0 before being overcome by the inward shift due to HSE.
CWS of \({V}_{\mathrm{pp}}\) for \({\gamma T}_{1}\) = 10 G−1 and \({\gamma T}_{2}\) = 1.67 G−1. Tempol pattern (squares) and Tempol pattern with \({a}_{\mathrm{p}}\) = 0 (circles); i.e., a Lorentzian. The two CWS are normalized to the same \({V}_{\mathrm{pp}}\) and the solid lines are fits to Eq. (4)
Taking into account the sign change upon transfer of spin coherence, HSE and DD are treated theoretically on a similar footing at low \({H}_{1}\). Within this framework we are able to think about the two interactions in broad terms but must keep in mind that DD shows very much smaller identifiable changes in the spectra. It’s important to keep in mind that the extent of line broadening provoked by DD is limited by the solid state, closely packed value of 49 G/M [43] while only about one-half of this value has been found experimentally [27]. Thus, in varying \(D\) over a wide range from where HSE vs. DD is predominate, most measureable effects are dominated by HSE, see Fig. 2a of [44] and Fig. 7 of [27]. Finally, in comparing three methods mentioned above to obtain the relative contribution of HSE versus DD, the results were different for the three methods, outside of experimental error, although the broad features were reasonable, see Figs. 4, 6, and 7 of [44].
Another complication in studying DD arose when corrected values of \({V}_{\mathrm{disp}}^{\mathrm{lf}}/{V}_{\mathrm{pp}}^{\mathrm{lf}}\) and \(-{V}_{\mathrm{disp}}^{\mathrm{hf}}/{V}_{\mathrm{pp}}^{\mathrm{hf}}\) were linear and equal to each other as functions of \(C\) up to about 30 mM, but they did not extrapolate to the origin [27]. The negative intercept [27] was nicely explained by Marsh [46] who showed that the pseudosecular electron–nuclear dipolar interaction also induced transfer of spin coherence for isolated nitroxides, albeit small and over a limited range of the diffusion coefficient.
In summary, at low \({H}_{1}\), the theory of HSE has been amply confirmed by experiment, including the effect of re-collisions of the same pair during one encounter [47, 48]. We felt modestly confident of our understanding of HSE at small \({H}_{1}\) [6] and anticipated gaining a deeper understanding of the behavior of the absorption and dispersion components due to HSE under saturating conditions. On the other hand, our understanding of DD is not yet complete, either at low \({H}_{1}\) or under saturating conditions.
To recap the motivation for this work, we strive to learn how to study spin relaxation in systems where transfer of spin coherence is significant using continuous wave EPR with a typical standard CW spectrometer. To achieve this goal, we separate the absorption and dispersion components of experimental or theoretical spectra. We study the absorption components with the long established Bloch expressions (3)–(5) to permit comparison with literature results. We then study these same absorption components with the rigorous theory (17) and, in addition, study the saturation of the dispersion components.
A guide to procedures in this paper is as follows: all theoretical spectra are simulated using (17), next section. These spectra are then fit with Lowfit to obtain the theoretical parameters \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\), \(I\), \({V}_{\mathrm{pp}}\) and \({V}_{\mathrm{disp}}\). These same parameters are then obtained from the experimental spectra. The CWS of the absorption components \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) and \(I\) are then analyzed with the Bloch formulation utilizing (3) and (5), respectively, after establishing that the CWS of \({V}_{\mathrm{pp}}\) yields poor values of \({T}_{1}\). All four parameters \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\), \(I\), \({V}_{\mathrm{pp}}\), and \({V}_{\mathrm{disp}}\) are analyzed by direct comparison with (17). \({T}_{1}\) derived from the absorption parameters obtained from \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) and \(I\) using the Bloch approach and the direct comparison may be compared with each other and with the literature. \({V}_{\mathrm{disp}}\) may only be obtained with a rigorous theory such as (17) and there are no literature values.
2 Theory
2.1 General Formulation of the Spectral Manifestations of HSE and DD Interactions
The shape of the EPR spectrum of a radical with hyperfine structure due to an arbitrary number of magnetic nuclei in a relatively dilute solution is given by the following kinetic equations (e.g., [4] and references therein:
here \({M}_{k}^{-}={M}_{kx}-i{M}_{ky}\), \({M}^{-}=\sum {M}_{k}^{-}\), \({M}_{z}=\sum {M}_{kz}\) and,
where
where \(\omega =\gamma {H}_{0}\) and \({J}^{\left(n\right)}\left(x\right)\) are spectral densities of the correlation functions for the dipole–dipole interaction, chapter 8 [49].
The expressions (12) – (14) are obtained under the assumption that \(\omega \ge {10}^{11}\) \({s}^{-1}\) to satisfy the condition that \(\omega {\tau }_{\mathrm{D}}\gg 1\) and at the same time, \({a}_{\mathrm{p}}{\tau }_{\mathrm{D}}\ll 1\); here the characteristic time \({\tau }_{\mathrm{D}}={b}^{2}\)/2D, with b the distance of closest approach between colliding paramagnetic radicals and D the diffusion coefficient of a single radical. Under these conditions the dipole–dipole interaction contribution terms practically do not depend on the index (\(k\)) of the hyperfine structure line (see Eq. (4.21) [50]).
In (10), the subscript \(k\) refers to the \(k\)th hyperfine component (e.g., for nitroxides: the nitrogen or one line in the proton superhyperfine structure); \(M_{k}^{ - }\) is the transverse magnetization, \({\varphi }_{k}\) is the statistical weight, \({T}_{2k}\) is the transverse relaxation time when \(C\to 0\), and \({\omega }_{k}\) is the resonance frequency of that component. The three rate constants in (11) are: spin dephasing, \({K}_{\mathrm{ex},\mathrm{sd}}\); spin coherence transfer to the observed spin from the colliding spin, \({K}_{\mathrm{ex},\mathrm{sct}}\); and spin excitation transfer during the bimolecular collision, \({K}_{\mathrm{ex},\mathrm{set}}\), respectively. Frequency shifts due to the same interacting pair colliding multiple times during a single encounter [47, 48, 50, 51] are denoted by\({\delta }_{k}\).
In general, the rate constants \({K}_{\mathrm{ex},\mathrm{sd}}\), \({K}_{\mathrm{ex},\mathrm{sct}}\), and \({K}_{\mathrm{ex},\mathrm{set}}\) may be different; however, if during the bimolecular collisions all spin dependent interactions of paramagnetic particles can be neglected except HSE, the three are equal [41], a condition known as equivalent HSE. HSE between nitroxides is known to fulfill this requisite [2]; thus, the following assumes that \({K}_{\mathrm{ex},\mathrm{sd}}\) = \({K}_{\mathrm{ex},\mathrm{sct}}\),= \({K}_{\mathrm{ex},\mathrm{set}}\) = \({K}_{\mathrm{ex}}\).
The intrinsic longitudinal spin lattice relaxation time is given by
where
Note that the definition of \({T}_{1}\) (15) describes the direct relaxation to the lattice of a spin in the excited state. Other relaxation pathways are limited to those offered by HSE and/or DD. Often the same symbol is used in the literature to denote an effective relaxation rate. In the present theory, at \(C\to\) 0 \({1/T}_{1d}\) = 0; however, calculations show that \({1/T}_{1d}\) is small for all \(C\) under the conditions of this experiment. Therefore, in practice, \({T}_{1}={T}_{10}\). Note that the present theory does not include other relaxation mechanisms at \(C\to\) 0, for example nitrogen nuclear spin flips of rate \({T}_{n}^{-1}\) [52]. In the event that these relaxation pathways and perhaps others become important, then a relaxation rate measured at \(C\to\) 0 would not be equal to a relaxation directly to the lattice. Within the context of the present theory, \({T}_{1}\) is expected to remain constant as functions of \(C\) and \(T\).
The details of the solution of Eq. (10) in the steady state, \(\partial {M}_{k}/\partial t\) = 0, (10) for equivalent HSE are solved in the Supplemental Information.
2.2 Solutions of the Kinetic Equations for Nitroxides
The spectra predicted by Eqs. (S6) and (S7) in the Supplementary Information are quite general encompassing hyperfine interactions due to any set of magnetic nuclei. For nitroxides, these nuclei are 15N (14N), protons (deuterons), 13C and occasionally others. Here, we specialize to the most common spin probe that is composed of only one nitrogen nucleus, a number of the order of 12 or more protons and/or deuterons and ignore all others.
The familiar EPR spectrum consists of \(2I+1\) manifolds inhomogeneously broadened by protons (deuterons), spaced by the isotropic coupling constant, \(\gamma {A}_{0}\) where \(I\) is the nuclear spin of the nitroxide.
Solutions of Eq. (10) are presented via the values of \({S}_{i}\) Eqs. (S6, S7) of the Supplemental Information which have the form:
where
In (17), \(M\) is summed over the nitrogen manifolds and \(m\) over the proton hfs. Note that, in writing \({W}_{1k}={W}_{1M}\), we have assumed that all of the proton lines in manifold \(M\) have the same value of \({T}_{1}\).
For the case of \(N\) equivalent protons, the resonance frequency of the \(m\)th proton line with respect to the center of each nitrogen manifold is given by
and the statistical weight is given by the binomial coefficients:
For the general case,
For deuterons or other magnetic nuclei, (21) is carried out by the computer by constructing a “stick” diagram beginning with the 1st nucleus and placing \(2{I}_{1}+1\) sticks spaced by \({a}_{1}\). Then for each successive nucleus the next layer of sticks is imposed on the previous layer, etc. For \(N\) equivalent protons, for example, each successive layer results in a stick overlaying previous ones and leads to (19) and (20). In this work, (21) is used for the Tempol pattern and for deuterated nitroxides to demonstrate the validity of using the simpler pattern under the conditions of our experiment.
All calculations in this paper are performed with the rigorous theory, (10, 17). The resulting spectra are fit with Lowfit which yields the parameters to plot the CWS.
2.3 Notation
It is instructive to compare CWS found from the rigorous results from (17) to those assuming \({a}_{\mathrm{p}}\) = 0, the homogeneous case.
The notation has changed twice since the work in 2010 [1]. The first change, in 2016, [53] was noted in [6]. The original notation was preserved in [6, 27, 44]. The second change is in this work as follows:
and
where the left-hand side (LHS) is the notation of [6, 27, 44, 53] and the quantities in the right-hand side are defined in (12) and (13). Note that, unlike previous notations, \({T}_{\mathrm{dd},\mathrm{sct}}^{-1}\) is a rate, not a rate constant; i.e., the concentration \(C\) is included in this rate.
2.4 Measureable Parameters at \({{\varvec{H}}}_{1}\) \(\to\) 0
For \({H}_{1}\) \(\to\) 0, in the absence of protons, the measureable parameters \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\) and \({V}_{\mathrm{disp}}/{V}_{\mathrm{pp}}\) are given in this notation as follows:
and
where the + or − sign refers to the lf or hf, respectively. For saturated spectra, the effective spin–lattice relaxation time is the new measureable parameter. Foreseeing our experimental results that show that \({T}_{1\mathrm{lf}}\ne {T}_{1\mathrm{hf}}\), we have extended Eq. (7) in the Supplemental Information for the case of 15N as follows:
where the factor 1/2 gives the statistical weight of one of the 15N manifolds and \(\overline{{T }_{1}}=\left[{T}_{1\mathrm{lf}}+{T}_{\mathrm{lf}}\right]/2\). Interchange of the lf and hf gives the other relationship. Generalization of (15) yields
2.4.1 Approximations
The rates in (24)–(26) may be simplified in two limits. In the high-viscosity limit (HVL), [49] where \({J}^{(1)}\left({\omega }_{0}\right)={J}^{(2)}\left(2{\omega }_{0}\right)=0\), \({\left({T}_{\mathrm{dd},\mathrm{sd}}\right)}^{-1}=5{\left({T}_{\mathrm{dd}}\right)}^{-1}\), \({\left({T}_{\mathrm{dd},\mathrm{sct}}\right)}^{-1}=4{\left({T}_{\mathrm{dd}}\right)}^{-1}\), and \({\left({T}_{\mathrm{dd},\mathrm{set}}\right)}^{-1}=2{\left({T}_{\mathrm{dd}}\right)}^{-1}\). In the low-viscosity limit (LVL), \({J}^{(0)}\left(0\right)\):\({J}^{(1)}\left({\omega }_{0}\right)\):\({J}^{(2)}\left({2\omega }_{0}\right)\) = 6:1:4; see after (VIII. 79) of [49]. We have argued the HVL is more appropriate and have shown that the difference in the HVL and LVL is rather small. See Fig. 5 of [44].
Thus, for the HVL, the important measurable parameters become
For small \({H}_{1}\), Eq. (29) is in accord with simulations for \(C\) = 0 and \(C\gg \gamma {a}_{\mathrm{p}}/{K}_{\mathrm{ex}}\), outside of the proton intermediate zone. In the HVL, (26) becomes
where plus or minus sign in (29) corresponds to lf or hf, respectively.
2.5 Theoretical Spectra and CWS Curves
2.5.1 Negligible HSE and DD
To illustrate the content of our theory, we present some results and conclusions from the theory by way of simulations using (17) for \(C\to 0\), approximated by \(C\) = 10–6 M. These simulations of spectra are then fit with Lowfit to obtain the pertinent parameters. We call these the theoretical parameters with the understanding that they represent the content of Eq. (17) only to the precision afforded by the fits. All of the simulated spectra in this subsection share the following parameters 15 N; \({A}_{0}\) = 23.7 G, \({\gamma T}_{1}\) = 10, 3.33, and 1.67\({\mathrm{G}}^{-1}\); \({\gamma T}_{2}=1.67 {\mathrm{G}}^{-1}\); \({K}_{\mathrm{ex}}C\) and \({W}_{\mathrm{dd}}C\) negligible.
The validity of our approach rests upon the fidelity of the theoretical spectrum shape to the Voigt. It is well known that at small \({H}_{1}\), the Voigt shape is insensitive to the particular hyperfine pattern for most nitroxides unless \(\chi\) > 2 [11]. Is this property maintained throughout the saturated region? We may answer this question by comparing spectra with the same Voigt shape and width; i.e., the same values of \({T}_{2}\) and \(\chi\) but different hfi. As a test, we simulate two patterns. Pattern 1: H-Tempone with 12 equivalent protons, \({a}_{\mathrm{p}}\) = 0.40 G. For small \({H}_{1}\) this is the same spectrum treated in Fig. 1 of [6]. Pattern 2: 10 inequivalent protons with, \({a}_{\mathrm{p}}\) = 0.44 G (6H), 0.36 G (2H), and 0.48 G (2H), where the integers in the parentheses are the number of equivalent protons. We term this latter pattern “Tempol” for convenience because it encompasses the major values of \({a}_{p}\) and gives the correct value of \(\Delta {H}_{\mathrm{pp}}^{\mathrm{G}}\) = 1.4 G for Tempol in water [11]. From Eq. (2) of [11], adopting the values of \(\sqrt{\alpha }\) = 1.04 for Tempol pattern and 1.03 for Tempone, the same value of \(\Delta {H}_{\mathrm{pp}}^{\mathrm{G}}\) = 1.4 G is obtained for the two nitroxides and therefore, the same value of \(\chi =2.0\), somewhat below the value of \({\chi }_{\mathrm{incip}}=2.3\) where proton structure may begin to be perceived [11]. Thus, the treatment of this pattern here and in [6] tests the theory for significant IHB.
The output of Lowfit is by default based on \(\chi\) derived from the Universal Nitroxide pattern given in Table 5 of [11]. To correct to other patterns, Eqs. (11) and (7a) of [11] are used. A summary of the values of \({T}_{1}\) and \({T}_{2}\) obtained by the fits are given in Table 2. The maximum discrepancy in \({T}_{2}\), 1.6%, occurs for \(\gamma {T}_{1}\) = 1.67 G−1 which is a factor of more than 13 shorter than our experimental values. At \(\gamma {T}_{1}\) = 10 G−1, still a factor of 2 faster than experiment, the error is negligible. The maximum discrepancies in \({T}_{1}\) from the CWS of either \({\mathrm{\Delta H}}_{pp}^{L}\) or \(I\) are 2–3%, which occur for short values of input \(\gamma {T}_{1}\) = 1.67 G−1. For a more realistic value of \(\gamma {T}_{1}\) = 10 G−1 the discrepancies are negligible. As expected, the values of \({T}_{1}\) from the CWS of \({V}_{\mathrm{pp}}\) are very poor. In summary, fit values of the relaxation times in the absence of spin diffusion for typical experimental conditions are negligibly different than the theoretical values and for faster times, are different by a few percent.
Plots of the CWS of \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\), \(I\), and \({V}_{\mathrm{pp}}\) for Tempone and Tempol are exhibited in Fig. S1 of the Supplemental Information.
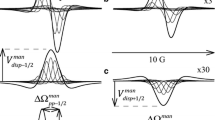
It is instructive to compare the CWS of \({V}_{\mathrm{pp}}\) for a Lorentzian line and an IHB line as shown in Fig. 1 which corresponds to \({\gamma T}_{1}\) = 10 G−1. The squares are for the Tempol pattern and circles for the same pattern except \({a}_{p}\) = 0; i.e., a Lorentzian. The two CWS are normalized to the same maximum \({V}_{\mathrm{pp}}\), \({V}_{\mathrm{pp}}^{\mathrm{max}}\), and the lines are fits to Eq. (4). The fit to the \({a}_{\mathrm{p}}\) = 0 case shows a maximum discrepancy of 1.6 × 10–9 \({V}_{\mathrm{pp}}^{\mathrm{max}}\) demonstrating that Eq. (9) is very accurate in the limit of \({a}_{\mathrm{p}}\) = 0. Let us define \({H}_{1}^{\mathrm{max}}\) as the value of \({H}_{1}\) at \({V}_{\mathrm{pp}}^{\mathrm{max}}\). It is clear that \({H}_{1}^{\mathrm{max}}\) increases due to IHB; i.e., it gives a first impression that \({T}_{1}\) is shorter due to IHB when in fact they have the same values of \({T}_{1}\) and \({T}_{2}\). The CWS of \({V}_{\mathrm{pp}}\) yields the correct values for the homogeneous case but not for the IHB. Note that this effect is not due to a greater number of relaxation pathways for the IHB spectrum because there is no spin diffusion. We see that the fit of the IHB case is visually rather a good fit; however, the output value \({T}_{1}\) is more than a factor of two too short. In short, a reasonable fit to a CWS and/or the values \({H}_{1}^{max}\) do not necessarily reveal a difference in spin relaxation.
Note that for nitroxides in liquids of low viscosity, Eq. 4 is expected to give a reasonable visual fit, because the values of \(\chi\) are relatively small for unresolved lines [11]. Contrast this with CWS in solids or high-viscosity fluids where unresolved lines with values of \(\chi\) much larger are often encountered, [9, 28, 30, 31, 54], and fits to Eq. (4) are very poor.
2.5.2 Appreciable HSE and/or DD
Some very interesting effects on the CWS are predicted by Eq. (17) at large values of \({K}_{\mathrm{ex}}C\) and \({H}_{1}\) [2, 3] that we shall detail in future publications. In this work, we confine our theoretical presentation to values of \({K}_{\mathrm{ex}}C/\gamma\) < 1.6 G and \({W}_{\mathrm{dd}}C/\gamma\) < 0.40 G, comparable to our experimental conditions.
Spectra were simulated as a function of \({H}_{1}\) by (17) for 15N with \({A}_{0}\)= 23.74 G employing typical parameters, \({K}_{\mathrm{ex}}/\gamma\) = 100 G/M and \({W}_{\mathrm{dd}}/\gamma\) = 25 G/M at \(C\) = 0, 0.5, and 16 mM. Input parameters of \({T}_{2}\) and \({T}_{1}\), similar to the values observed in the experiment, different for lf and hf, are given in Table 3. These spectra are IHB by 12 equivalent deuterons (nuclear spin 1, 25 lines) with \({a}_{\mathrm{d}}\) = 0.061 G, similar to the experiment, which yields, \({\Delta H}_{\mathrm{pp}}^{\mathrm{G}}\) = 0.359 G, Eq. (8). Spectra were also simulated with 12 equivalent protons (nuclear spin 1/2, 13 lines) with \({a}_{\mathrm{p}}\) = 0.0996 G which yields the same value of \({\Delta H}_{\mathrm{pp}}^{\mathrm{G}}\), Eq. (8). The maximum value of \(\chi\) is \(\chi =2.4\). Under all conditions, the spectra and the parameters extracted from the CWS are negligibly different for the two isotopes; thus, for the purpose of simulating theoretical spectra either pattern may be used. Note that \(C\) = 0.5 and 16 mM yield \({K}_{\mathrm{ex}}C/\gamma\) = 0.05 and 1.6 G, respectively compared with \(\gamma {a}_{\mathrm{p}}\) = 0.0992 G; i.e., just below and above the proton intermediate zone, respectively. Note that for \(C\to\) 0, these results are examples of negligible spin coherence transfer presented in the previous section; nevertheless, they are included in Tables 4 and 5 for comparison. The simulation assumed different \({T}_{1}\) values for low-, \({T}_{1\mathrm{lf}}\), and high-field, \({T}_{1\mathrm{hf}}\), lines. The kinetic Eq. (10) can be easily generalized to the case of different spin–lattice relaxation times of spins belonging to different components of the spectrum. Their solution in stationary conditions is found by standard methods. In the case of different \({T}_{1}\), this solution is more cumbersome than Eqs. (17, 18). Thus, we do not give it here.
Figure 2 shows the effects of saturation on the absorption and dispersion components for \(C\) = 16 mM: i.e., \({W}_{\mathrm{dd}}C/\gamma\) = 0.40 G (a and b) and \({K}_{\mathrm{ex}}C/\gamma\) = 1.6 G (c and d). The unsaturated components at small \({H}_{1}\) are shown for a DD and for c HSE. The saturated components (\({H}_{1}\) = 0.49 G) are shown in b and d respectively. In Fig. 2, the observed spectra (not shown) would be the sums of the two components. In b and d, both the absorptions and the dispersions are saturated, but the dispersions less so, as may be judged by the relative heights of the two components. For clarity, the dispersion components are amplified relative to the absorption components as indicated and the baselines are truncated.
Absorption and dispersion components of theoretical spectra of 16 mM Tempone with dominate DD, a and b and with dominate HSE, c and d. The spectra from which these components were derived (not shown) are the sum of the two components. Parts a and c are simulated at low \({H}_{1}\) and b and d at a saturating \({H}_{1}\) = 0.49 G. The baselines are truncated for clarity. The dispersions are amplified relative to the absorptions as indicated near their baselines. At high \({H}_{1}\) = 0.49 G, both the absorptions and the dispersions are saturated; however, the dispersion component less so. Compare the relative heights of the two components in b and d with those in a and b
The broadening of all components by saturation may be appreciated comparing a with b and c with d. Furthermore, it is evident that the hf components are saturated less by comparing the relative heights of the lf and hf absorption components in a vs. b and c vs. d. This is due to the fact that \({{T}_{1\mathrm{hf}}T}_{2\mathrm{hf}}\) < \({T}_{1\mathrm{lf}}{T}_{2\mathrm{lf}}\) for both the HSE and DD series.
2.5.2.1 CWS of \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\)
Typical CWS of the lf of \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}(C)\) are presented in the Supplemental Information. The theoretical values of \({{\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\left(C\right)}_{0}\) obtained from fitting simulated spectra are tabulated in columns 3 and 4 of Table 4. From Table 3, employing \({{\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\left(0\right)}_{0}=2/\gamma \sqrt{3}{T}_{2}\), we may calculate the input values of \({{\Delta H}_{\mathrm{pplf}}^{\mathrm{L}}\left(0\right)}_{0}\) = 0.149 G and \({{\Delta H}_{\mathrm{pplf}}^{\mathrm{L}}\left(0\right)}_{0}\) = 0.189 G for the HSE series and \({{\Delta H}_{\mathrm{pplf}}^{\mathrm{L}}\left(0\right)}_{0}\) = 0.425 G and \({{\Delta H}_{\mathrm{pplf}}^{\mathrm{L}}\left(0\right)}_{0}\) = 1.05 G for the DD series. Comparing these input values with those in columns 3 and 4 for \(C\to\) 0, the first row of the HSE or DD series, we see that the output (theoretical) and input values are identical. This verifies that our method of simulating and fitting to a Voigt produces accurate values of \({T}_{2}\). The final two columns of Table 4 show the approximate values assuming no protons. The values in Table 4 derived from the Universal and the correct map are within 1% of one another.
In Table 4, the discrepancies between the theoretical values and the other two methods are shown when they are > 1%; otherwise, the absence of parenthetical values indicates that the discrepancies are less than 1%. For the two non-zero values of \(C\), significant discrepancies are noted between the true and approximate values as computed from Eq. (28). This is fully expected because Eq. (28) assumes no protons. Nevertheless, apart from the proton intermediate zone, where 6–10% discrepancies in the HSE series are incurred, the discrepancies are very small. For the 16-mM results in the HSE series, they amount to only 1–2% and in the DD series they are negligible.
The fits of \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\) also yield values of \({T}_{1M}^{\mathrm{eff}}\) which are denoted by \({T}_{1M}^{\mathrm{eff}}\left(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\right)\) and tabulated in columns 3 and 4 of Table 5. For \(C\) = 0, the errors are negligible when the correct map is employed; use of the Universal map leads to errors of 6 and 8% for lf or hf, respectively. The fits to Eq. (3) of all CWS are excellent except for those for \(C\) = 0.5 mM, HSE where \({K}_{\mathrm{ex}}C/\gamma\) = 0.05 G. Note that values of \({T}_{1}^{\mathrm{eff}}\) are available from the Bloch formulation but not the rigorous theory, (10, 17), because they are not an input (true) parameter. Results in the first and third rows and from Sect. 2.5.1 show that the Bloch and rigorous theory are the same for \(C\to\) 0. For \(C>\) 0, no comparison between the two theories is possible. Comparison of the CWS generated by (10, 17) and the fit to the Bloch Eq. (3), shown visually in Fig. S2 shows that, outside the intermediate proton zone, \(C=\) 0.5 mM, the curves are essentially identical. The discrepancies between the rigorous theory and the fit to (3) is less than 1% for both HSE and DD.
Similarly, the discrepancies between the CWS of \(I\), shown in Fig. 3e, f below, are very small, less than 2% in the intermediate proton zone, and 1.2% elsewhere.
CWS of the lf of \({V}_{\mathrm{pp}}\) (a, b), \({V}_{\mathrm{disp}}\) (c, d), and \(I\) (e, f). The HSE series is depicted in a, c, e; the DD in b, d, and f. \(C\) = 0, circles; 0.5, squares; and 16 mM, triangles. All of the parameters are in arbitrary units; however, their relative values are indicated. In b, for example, Gain a × 6, means that the amplification is 6 times that in a. For clarity, the values are normalized to the same \(C\); i.e., the increase in intensity due to an increase in \(C\), which would be observed in the experiment, is discounted
In summary, CWS of the absorption components calculated from (10, 17) are fit to high precision by the Bloch formulations, yielding values of \({T}_{1\mathrm{lf}}\) and \({T}_{1\mathrm{hf}}\) that are same for \(C\to\) 0. Estimates of the values of \({T}_{1}^{\mathrm{eff}}\) observed in an experiment are only available from the Bloch formulation, unless simulations using (10, 17) of the CWS are found that are within about 2% of the observed values. We have not found such simulations for this first experiment because both \(C\) and \(I\) are rather small and lack the interesting effects alluded to in the first sentence of Sect. 2.5.2. Thus, in the following sections through Sect. 4.2, we develop in detail \({T}_{1}^{\mathrm{eff}}\). In Sect. 4.3, we demonstrate the direct use of (10, 17) to analyze the same experimental data.
2.5.2.2 CWS of \({V}_{\mathrm{pp}}\), \({V}_{\mathrm{disp}}\), and \(I\)
Figure 3 displays CWS of the lf of \({V}_{pp}\) (a and b), \({V}_{\mathrm{disp}}\) (c and d), and \(I\) (e and f). The HSE series is depicted in a, c, and e; the DD in b, d, and f. All of the parameters are in arbitrary units; however, their relative values are indicated. In b, for example, Gain a × 6, means that the amplification is 6 times that in a. For clarity, the values are normalized to the same \(C\); i.e., the increase in intensity due to an increase in \(C\) that would be observed in the experiment is discounted. In Fig. 3 only every other computed point is displayed; also, the line through the \({V}_{disp}\) data is interpolated to guide the eye. The symbols are the theoretical values and the solid lines are fits of \({V}_{\mathrm{pp}}\) to Eq. (4) and \(I\) to Eq. (5). The parameters \({{\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\left(0\right)}_{0}\) in these fits are taken from columns 5 and 6 of Table 4. It is important to be able to use the intercepts because they yield more precise values of \({{\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\left(0\right)}_{0}\) in an experiment. The fits in Fig. 3 yield values of \({\gamma T}_{1\mathrm{lf}}^{\mathrm{eff}}\left({V}_{\mathrm{pp}}\right)\) and \({\gamma T}_{1\mathrm{lf}}^{\mathrm{eff}}\left(I\right)\), respectively, where the parameter in the parentheses indicates the CWS that is fit. The values of \({\gamma T}_{1lf}^{eff}\left(I\right)\) are tabulated in columns 5 and 6 of Table 5; the values of \({\gamma T}_{1\mathrm{lf}}^{\mathrm{eff}}\left({V}_{\mathrm{pp}}\right)\) are in error by about a factor of 2 and are not reported. Approximate values of \({\gamma T}_{1\mathrm{lf}}^{\mathrm{eff}}\) were computed from Eq. (30), which assumes no protons, employing the input values given in Table 3. These are reported in columns 7 and 8 of Table 5. Columns 3 and 4 report values of \({T}_{1}^{\mathrm{eff}}\left(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\right)\), which were alluded to in the previous section.
In Fig. 3 it is apparent that the dispersion component saturates less readily than the absorption component which we have already noted in Fig. 2. Figure 3 depicts the behavior of the lf lines; for hf, the sign of each of the dispersion components is the opposite and the results are similar.
In Table 5, at \(C\) = 0, the input values (Table 3), those from CWS(\({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\)), CWS(\(I\)), and the no-proton approximation are all negligibly different which shows that the simulations, the fits, and Eq. (30) are consistent. For DD, only small differences are noted for all \(C\), however, for HSE, the theoretical values obtained from CWS(\({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\)) and CWS(\(I\)) for \(C\) = 0.5 mM are significantly different (19–23%) which is expected because \({K}_{\mathrm{ex}}C\) = 0.05 impinges on \(\gamma {a}_{\mathrm{p}}\) = 0.0992 G. At \(C\) = 16 mM they are also different (17%) where \({K}_{\mathrm{ex}}C\) = 1.6 G. Interestingly, the no-proton estimates in this intermediate proton zone are about half-way between the CWS(\({\Delta H}_{\mathrm{pp}}^{L}\)) and CWS(\(I\)) results.
In contemplating Fig. 3, note that the range of \({H}_{1}\), up to 0.49 G, is more than three times what we were able to achieve while maintaining critical coupling of the cavity in this study of a lossy solvent. Therefore, much of the detail seen in Fig. 3 is not available in the present experiment. Under ideal conditions, our spectrometer is capable of producing values \({H}_{1}\), up to 0.9 G.
3 Materials and Methods
4-Hydroxy-2,2,6,6-tetramethylpiperidine-d17-1-15N-oxyl (purity 95%) was prepared from isotope-enriched triacetonamine-15N-d17 according to literature procedures [55]. Triacetonamine-15N was prepared from 15NH4Cl (isotope enrichment 99.9%) according to the method by Pirrwitz and Schwarz [56] with minor modifications [57]. Glycerol (98%) and distilled water were used to prepare 60 wt% aqueous glycerol (60%AG). Samples from [6] stored in a refrigerator at 3 °C were used. As detailed in [6], a stock nitroxide solution with \(C\) = 50 mM was prepared gravimetrically and serially diluted. Non-degassed samples were drawn into 50-µL disposable pipettes and sealed at both ends with a flame. The samples extended through the entire cavity as described in [26]. References to \({H}_{1}\) mean effective values for a line sample in this configuration [26]. Only concentrations 0.03, 0.5, 5.0, 9.0, and 16.0 mM were used in this work.
EPR spectra were obtained at X-band at temperatures of 273, 298, 315, 340 K using a Bruker EMX Plus spectrometer equipped with a SHQ 4122 cavity and a standard temperature controller from Oxford, which had an accuracy of 0.1 K. Recording parameters of the CW EPR spectra are: modulation amplitude \({a}_{\mathrm{m}}=\) 0.1 G, modulation frequency \({f}_{\mathrm{m}}=\) 100 or 10 kHz, time constant 5.12 ms, conversion time 40 ms, field sweep 50 G, and resolution 50 mG. The CWS were obtained up to 31.7 mW while preserving the critical coupling of the resonator. The conversion from the power incident on the critically coupled cavity, \(P\), to \({H}_{1}\) was detailed in [26] using a standard sample of Fremy’s salt. By measuring the Q-value with the present samples in the cavity, the conversion is given by \({H}_{1}=1.1\sqrt{P}\) with \(P\) in W and \({H}_{1}\) in G.
4 Experimental Results
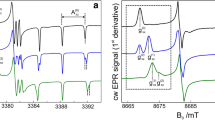
Figure 4 displays typical experimental spectra for \(C\) = 16 mM obtained at 315 K: at a \({H}_{1}\) = 6.2 mG and b 200 mG. The amplification of the low-power spectrum a relative to the higher-power spectrum b is × 17 as indicated. The amplitudes of the dispersion components are amplified × 3 to show these components more clearly. In a we see that instrumental dispersion, with a positive amplitude is superimposed upon the dispersion due to HSE and DD because \({V}_{\mathrm{disp}}^{\mathrm{lf}}/{V}_{\mathrm{pp}}^{\mathrm{lf}}\) > −\({V}_{\mathrm{disp}}^{\mathrm{hf}}/{V}_{\mathrm{pp}}^{\mathrm{hf}}\) for these components. In b we note an even more severe instrumental dispersion yielding a positive value of \({V}_{\mathrm{disp}}^{\mathrm{hf}}/{V}_{\mathrm{pp}}^{\mathrm{hf}}\) where it ought to be negative. The corrected values, by use of Eq. (9), yields \({V}_{\mathrm{disp}}^{\mathrm{lf}}/{V}_{\mathrm{pp}}^{\mathrm{lf}}\) = − \({V}_{\mathrm{disp}}^{\mathrm{hf}}/{V}_{\mathrm{pp}}^{\mathrm{hf}}\) for both lines in a as well as in b. We observe that \({V}_{disp}\) saturates less readily than \({V}_{\mathrm{pp}}\) in agreement with the theory, Figs. 3 and 4. Although it is not readily apparent on the scale of 4, the line widths in b are larger than those in a as expected. Similarly, it is not apparent that the nitrogen hyperfine spacing is larger in a than in b because the difference is less that the width of the printed line, but it is readily measureable.
Experimental absorption and overlaying dispersion component of 16-mM 15D-Tempol in 60 wt% aqueous glycerol at 315 K. a \({H}_{1}\) = 6.2 mG; b \({H}_{1}\) = 200 mG. c, d are the respective residuals. The baselines are truncated for clarity. For clarity, the spectrum is not shown: it is the sum of the two components and the residual. Note that \({V}_{\text{disp}}^{\text{hf}}\) for hf at the higher power is positive due to the larger instrumental dispersion; i.e., the cavity mismatch is more severe at the higher power. The corrected value, by use of Eq. (9), for both lines would be the normal \({V}_{\mathrm{disp}}^{\mathrm{hf}}\) < 0 as is expected for this HSE-dominated spectrum. The amplification of the low-power spectrum a relative to the higher-power spectrum b is × 16 as indicated
The experiments were performed with modulation frequency, \({f}_{\mathrm{m}}\) = 100 kHz; however, one brief experiment compared the CWS of \(C\) = 0.05 mM at 10 kHz to assure that slow passage was maintained. See [26] and references therein. The most sensitive comparison is made with \({V}_{\mathrm{pp}}\) despite the fact that we do not expect accurate results for \({T}_{1}\) from the CWS of this parameter. The values of \({{\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\left(C\right)}_{0}\) are the same to within 1 mG at the two frequencies, thus a difference in \({H}_{1}^{\mathrm{max}}\) is due to a difference in \({T}_{1}\). Figure 5 shows the results for the lf; the hf results are similar. The solid lines are fits to Eq. (3) of the 100-kHz data and the dashed lines to the 10-kHz data. These fits are approximate because the lines are IHB; however, they serve to guide the eye. Our conclusion is that the 273 K CWS appears to saturate less readily at 100 kHz most likely due to the lack of time to respond to the saturation \({H}_{1}\) at the higher frequency. At the other temperatures, the coincidence at the two frequencies is satisfactory. This same conclusion applies to the hf.
CWS of \({V}_{\mathrm{pp}}\) of the lf of \(C\) = 0.5 mM normalized to unity, taken with modulation frequency 100 kHz, circles and 10 kHz, squares at 273 K, a; 298 K, b; 315 K, c; and 340 K, d, respectively. The solid lines are fits to (3) for \({f}_{\mathrm{m}}\) = 100 kHz and the dashed for 10 kHz, where \({f}_{\mathrm{m}}\) is the modulation frequency. The fits are approximate for these IHB spectra; however, they serve to guide the eye. The values of \({{\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\left(C\right)}_{0}\) are independent of \({f}_{\mathrm{m}}\) to high precision, \(\sim\) 1 mG. The hf show similar behavior
For unsaturated spectra, the well documented procedures [6, 27, 43, 44] to separate HSE and DD were employed to find the rate constants given in Table 6. In earlier studies, we employed a single value of small \({H}_{1}\), whereas here, we improved the precision of the measurements by measuring the intercepts of CWS as described in [26]. As an example, Fig. 6 illustrates the improvement in precision for \({{\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\left(C\right)}_{0}\). The rate constants tabulated in Table 6 are within experimental uncertainty of the fit values in [6] for the three coincident temperatures. Values obtained from the “two-point method” [6] are consistently somewhat above these values. The uncertainties are larger here due to a smaller number of concentrations studied.
CWS of \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) for \(C\) = 0.03 mM at a 273 K, b 298 K, c 315 K, and d 340 K; circles, lf and squares, hf. These fits were good with \(r=\) 0.976 (273 K, hf), 0.994 (273 K, lf), 0.996 (298 and 340 K, hf), and 0.999 for all other temperatures and lines. Note the gain in precision from finding the intercepts, \({{\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\left(0\right)}_{0}\), from which to calculate values of \({T}_{2}\) rather than relying on the value at one small \({H}_{1}\)
For experimental CWS results given in Tables 7, 8, 9, 10 and 11, the output from Lowfit was corrected using the correct Tempol map [11].
4.1 Negligible HSE and DD
These results were obtained from the sample at \(C\) = 0.03 mM approximating \(C\to\) 0. We use the notation \(C\to\) 0 to refer to these results. As expected, the dispersion amplitudes were negligible. Figures 7 and 8 show the CWS of \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) and \(I\), the doubly-integrated intensity, respectively. The correlation coefficients, \(r\), are given in the captions, showing that the fits of \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\) are good and those of \(I\), are excellent. From Fig. 6, we obtain values of \({{\Delta H}_{\mathrm{pplf}}^{\mathrm{L}}\left(0\right)}_{0}\), Table 7, from which values of \({T}_{2}\) are obtained, Table 8.
From Fig. 7, we see that values of the product \({T}_{2}{T}_{1}\) are different for lf and hf, at all temperatures. The fits of \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) to (2) yield \({T}_{10\mathrm{lf}}\), \({T}_{10\mathrm{hf}}\), and \({\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}(0)}_{0}\) from which \({T}_{2}=2/\left[\sqrt{3}\upgamma {\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}(0)}_{0}\right].\) The fits of \(I\) to (5), after fixing the values of the values of \({T}_{2}\) obtained from Fig. 5, yield another set of \({T}_{10lf}\), \({T}_{10hf}\), and the parameter \({K}_{I}\) which is proportional to the doubly-integrated intensity for the unsaturated spectra. Table 9 tabulates the results from the CWS of \(I\). Details of the variation of \({K}_{I}\) with temperature are not presented; however, it is near that predicted by the Boltzmann factor.
CWS of \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) at a 273, b 298, c, 315, and d, 340 K. Circles, 0.03; squares, 5; stars, 9; and triangles, 16 mM. The solid lines are eye-fit theoretical curves, Eq. (17), with the parameters given in Table 12. At each temperature, \({T}_{10}\), \({T}_{2}\), \({K}_{\mathrm{ex}}\), and \({W}_{\mathrm{dd}}\) are maintained constant. Fits to the Bloch approach, Eq. (3), pass through data well within the size of the symbols and therefore are not shown
We observe that values of \({T}_{1}\) are very different when derived from the CWS of \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) or \(I\), in stark contrast to the results in Table 2. Observe that these differences may not be attributed to complications near the deuteron intermediate zone which is \({a}_{\mathrm{d}}\) = 0.06 G compared with the largest value of \({K}_{\mathrm{ex}}C/\gamma\) = 0.003 G.
4.2 Appreciable HSE and DD
The experimental CWS for \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) and \(I\) for \(C\) = 0.5, 5, 9, and 16 mM are plotted in Fig. 9, symbols. Except for one outlier, the Bloch fits to those data are even better than these quantities for \(C\to\) 0 in Figs. 7 and 8 respectively, with \(r\) near 0.999 for \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) and 0.9999 for \(I\) over all concentrations. There was one outlier at \({H}_{1}\) = 0.062 where Lowfit did not find a fit to a Voigt and thus is invalid. Eliminating this point in the fit to the CWS resulted in \(r\) = 0.999; including it, \(r\) = 0.993. These Bloch fits are not shown because the differences in the fits and the data are imperceptible on this scale, but the results are given in Tables 10 and 11.
The solid lines are direct comparisons with the rigorous theory which are described in the following section.
4.3 Direct Comparison of the CWS with the Rigorous Theory
This approach allows us to directly compare experimental CWS and rigorous CWS from Eqs. (10, 17) for any parameter that we wish to measure, not being constrained to just \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\) and \(I\). In Figs. 9, 10, 11, the solid lines are obtained by simulating spectra using (10, 17), fitting them with Lowfit, and constructing the CWS. The parameters \({T}_{10}\) and \({T}_{2}\) for lf and hf, and \({K}_{\mathrm{ex}}\), and \({W}_{\mathrm{dd}}\) were varied to find the best overall fit to all of the data according to our judgement. To obtain the eye fits, we begin with the parameters in Table 6. We were able to constrain \({T}_{10}\) and \({T}_{2}\) to constant values independent of \(C\). The direct comparison offers the advantage of exploiting \({V}_{\mathrm{pp}}\) and \({V}_{\mathrm{disp}}\) which are more rapidly varying functions of \({T}_{1}{T}_{2}{H}_{1}^{2}\) than \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\) or \(I\), therefore, more sensitive to global fitting. Note that for most concentrations and temperatures, \({V}_{\mathrm{pp}}\) attains a maximum or nearly a maximum, whereas for \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\) or \(I\) we must rely on less definitive regions of \({H}_{1}\). We have not yet attempted the type of curve-fitting analysis in Sect. 4.2 for \({V}_{\mathrm{disp}}\). Note that a severe test of the theory, is the CWS of \({V}_{\mathrm{disp}}\). The ratio \({V}_{\mathrm{disp}}/{V}_{\mathrm{pp}}\) relies not only on the correct dependence on \({H}_{1}\), but also the correct values of \({K}_{\mathrm{ex}}\) and \({W}_{\mathrm{dd}}\). Counterbalancing these advantages is that the uncertainties are more difficult to estimate.
CWS of \({V}_{\mathrm{disp}}\) with the same symbols and conditions as in Fig. 8 except that, for clarity, the values are amplified relative to Fig. 10 by the factors indicated. Importantly, the solid lines are given by the same values of the parameters in Table 12 as the fits to the other parameters. In particular, the experimentally accessible parameters \({V}_{\mathrm{disp}}/{V}_{\mathrm{pp}}\) are predicted by (17) rather well
The parameters obtained by direct comparison are tabulated in Table 12.
Figures 10, 11, 12 are in arbitrary units; in Fig. 9, the quantities are all on the same scale and the same is true in Fig. 10. In Fig. 11, the results for \({V}_{\mathrm{disp}}\) are amplified relative to those in Fig. 10 by the factors shown as Gains. For example, at 273 K, the values of \({V}_{\mathrm{disp}}\), Fig. 11a, are about 100 times less intense than the corresponding values of \({V}_{\mathrm{pp}}\), Fig. 10a. It is astonishing that such small signals may be separated from the overall signal, but that fact is at the heart of being able to use the dispersion signal effectively.
The eye fits to \({V}_{\mathrm{pp}}\) are rather impressive, considering the constraints, rivaling those in Fig. 5, except at 273 K. More impressive, in view of the fact that it’s the first time that it has been studied, the eye fits to \({V}_{\mathrm{disp}}\), again with the exception of 273 K, are remarkably good, showing that the theory predicts the ratio \({V}_{\mathrm{disp}}/{V}_{\mathrm{pp}}\) both as functions of \({T}_{10}\), \({T}_{2}\), \({K}_{\mathrm{ex}}\), and \({W}_{\mathrm{dd}}\), as well as \({H}_{1}\).
A criticism of the measurements at 100 kHz at 273 K, is that Fig. 5a shows that \({H}_{1}^{\mathrm{max}}\) is larger at 100 kHz than at 10 kHz. Measurements at 5 kHz, not shown, are the same as those at 10 kHz. In Fig. 10a, we expect that a small part of the discrepancies in \({H}_{1}^{\mathrm{max}}\) is due to passage effects; however, correction of these discrepancies would move the experimental points to even lower \({H}_{1}^{\mathrm{max}}\) by a small amount and would increase the true discrepancies. Thus the discrepancies in Fig. 10a demand an explanation that we cannot yet provide.
5 Discussion
This project to investigate each component of a spectrum separately, with or without HSE/DD interactions, is feasible because all of the lines, experimental and theoretical, are excellent Voigts which may be fit to high precision. Fortunately, in extending the theory and experiments to saturating values of \({H}_{1}\) the lines continue to be excellent Voigts. This is not to say that an analysis would be impossible by other means, only that a rapid, automated procedure to deal with large numbers of samples and spectra opens the door to feasible extensive investigations. Furthermore, because the absorption and dispersion components are orthogonal functions, they may be separated to high precision, even when the latter is very much smaller that the former.
Equipped with values of \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\), \(I\), \({V}_{\mathrm{pp}}\), and \({V}_{\mathrm{disp}}\), we employ two approaches to estimate \({T}_{2}\) and \({T}_{1}\) from the CWS. Approach 1 employs fitting the CWS of \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\) and \(I\), theoretical and experimental, to the Bloch Eqs. (3) and (5). This procedure is justified because, when applied to theoretical spectra, the results are the same as the known input values to Eq. (10, 17) for \(C\to\) 0, Table 2. This approach offers the advantage of objective and consistent estimates of \({T}_{2}\) and \({T}_{1}\) together with objective estimates of the errors in the usual manner [58]. Because \({V}_{\mathrm{pp}}\) from the Bloch approach yields values of \({T}_{1}\) that are in error by about a factor of two is a significant disadvantage. Approach 2 compares the CWS, experimental (symbols) and theoretical (lines), Eq. (17), of all four parameters searching for a global fit, by eye. An advantage is that \({V}_{\mathrm{pp}}\) is directly measureable from the spectrum with good precision at small rates of transfer of coherence transfer (small \(C\)). Because \({V}_{\mathrm{pp}}\) is a more rapidly varying function of \({H}_{1}\) than \(\Delta {H}_{\mathrm{pp}}^{\mathrm{L}}\) and \(I\) leading to more confidence in the fits. Perhaps more importantly, approach 2 affords the only way to study the CWS of dispersion. The significantly lower precision in finding correct eye fits and no objective way to access the uncertainties in \({T}_{10}\) will make it difficult to distinguish different models of spin relaxation; i.e., different spin relaxation mechanisms in the kinetic equations.
In applications where only relative values of \({T}_{1}^{\mathrm{eff}}\) are needed, the Bloch approach for \({V}_{\mathrm{pp}}\) may be useful; however, one would need the relative values of \({T}_{2}\) because \({T}_{1}^{\mathrm{eff}}\cdot {T}_{2}\) determines the saturation.
The ability to study the CWS of \({V}_{\mathrm{disp}}\) was our primary motive to revive the CWS method to study \({T}_{10}\). In contemplating studies of \({V}_{\mathrm{disp}}\), we frankly did not know what to expect in light of Portis’ observation that the in-phase dispersion showed no saturation while the absorption saturated readily [28]. We wondered if the relatively small values of \({H}_{1}\) available from a standard commercial spectrometer, especially with low Q-values due to lossy samples, would be sufficient to observe the saturation? Preliminary studies and this work (Fig. 11) proves the viability of this approach; however, we observe that at higher values of \(C\) and/or less viscous solvents where shorter values of \({T}_{10}\) are expected, it may be more difficult. We currently do not have a physical view of the saturation of the dispersion, much less an appropriate trial fit function. However, the theory, Eqs. (10, 17), predicts its behavior with surprising accuracy keeping in mind that the eye fits that reproduce the CWS of \({V}_{\mathrm{pp}}\) yield the fits to \({V}_{\mathrm{disp}}\) without any further adjustment. Stated differently, the same value of \({T}_{1}\) describes the saturation of both the absorption and the dispersion. Even at 273 K, Fig. 11a, which shows poor fits at higher values of \({H}_{1}\), are intriguingly similar at lower values.
5.1 Predictions of the Theory
5.1.1 Values of \({T}_{10}\)
From the theory, we have learned that Eqs. (3) and (5), which are derived assuming Lorentzian lines, may be used to fit IHB spectral lines in the limit of \(C\to\) 0; i.e., in the absence of HSE or DD. Thus, \({T}_{1}\) derived from the CWS of \({\Delta H}_{\mathrm{pp}}\) or from \(I\) for \(C\to\) 0 is the same theoretically. See Table 2 and the first rows of the HSE or DD series, Table 5. This result was expected from the simple arguments given in the Introduction. This validates our approach of presenting theoretical results from fitting theoretical simulations and encourages us to take theoretical results for \(C\) > 0 to be valid.
5.1.2 Values of \({T}_{1}\)
Except for the intermediate proton zone for HSE the theoretical values of \({T}_{1}^{\mathrm{eff}}({\Delta H}_{\mathrm{pp}}^{\mathrm{L}})\) ≈ \({T}_{1}^{\mathrm{eff}}\left(I\right)\), Table 5. Fig. S3 of the Supplemental Information is a plot of these theoretical results. Note that \({T}_{1}^{\mathrm{eff}}\) decreases very rapidly at low \(C\). For DD, \({T}_{1}^{\mathrm{eff}}({\Delta H}_{\mathrm{pp}}^{L})\) ≈ \({T}_{1}^{\mathrm{eff}}\left(I\right)\) for all \(C\); however, keep in mind that the rates of transfer of spin coherence are significantly smaller. For HSE in the intermediate proton zone, perhaps just by numerical accident, the no-proton approximation lies about midway between the other two.
Both CWS(\({\Delta H}_{\mathrm{pp}}^{L}\)), e.g. [33] and CWS(\(I\)) e.g. [59] have been proposed as methods to obtain \({T}_{1}^{\mathrm{eff}}\). Which, if either, is correct under the rather simple assumptions of Eq. (17)? The no-proton approximation is expected to yield values of \({T}_{1}^{\mathrm{eff}}\) that are longer than if protons are included because the latter provides more relaxation pathways. This expectation argues against using CWS(\(I\)); however, we do not yet have enough information to exclude it.
The theory offers us the opportunity to carry out global fits under conditions that we may specify. For example, the eye fits in Figs. 9, 10, 11 and 12, which assume that, at a given temperature, the same values of \({T}_{10}\), \({T}_{2}\), \({K}_{\mathrm{ex}}\), and \({W}_{\mathrm{dd}}\) govern the CWS of all four parameters, \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\), \(I\), \({V}_{\mathrm{pp}}\), and \({V}_{\mathrm{disp}}\) are not perfect, but promising. One could relax any one of these in search of a better fit, or introduce a new parameter in the future to test. These eye fits are tedious and subjective, but may provide clues to improve the theory or the experimental design.
5.2 Results from the Experiments for Absorption
5.2.1 Values from Pulse vs. CWS Measurements
Our literature search did not find results where both CWS and pulsed EPR measurements of Tempol in the same solvent carried out by the same lab. In fact, although our search was not as rigorous for other nitroxides, we did not come across any such data for any spin probe-solvent pair. The only data that we found employing the two approaches for Tempol were in toluene which are displayed in Fig. 12. The solid circles show values of \({T}_{1}^{-1}\) derived from CWS \(({\Delta H}_{\mathrm{pp}}^{\mathrm{L}})\) and the open circles derived from IR. The straight line is a fit to the combined data. Note that Figs. 13 are presented on linear scales permitting a better visual comparison of the data than log scales which are often used. Figures 13 do not yet show that pulsed and CWS data are the same because more data is required to assess the matter. They only show that the results from CWS are reasonable.
Spin–lattice relaxation rates derived from CWS(\({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\)), circles, and from CWS(\(I\)), squares. The straight lines are linear fits; closed symbols lf, open, hf. a compares the present results those of [33], who employed CWS(\({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\)) of pd-Tempone in toluene-d8 as a function of temperature. b compares the present results with those of [52] derived from combined measurements of SR-EPR and SR-ELDOR, triangles, in a series of water and glycerol. The dashed lines are smooth curves to guide the eye
5.2.2 Values of \({T}_{10}\)
Reducing \(C\to\) 0 yields \({T}_{10}\) provided that relaxation pathways other than HSE/DD are not effective; however, [52] has provided evidence that nitrogen nuclear spin flips at rate \({T}_{1n}^{-1}\) begin to compete with \({T}_{10}^{-1}\) for \({\tau }_{\mathrm{R}}\) \(>\) 0.1 ns. Taken at face value, Fig. 3 of [52] shows that \({T}_{1}^{\mathrm{eff}}\to {T}_{10}\) only at 340 K; at lower temperatures, \({T}_{10}\) would be longer after taking into account \({T}_{1n}\). In other words, because our present theory does not include \({T}_{1n}\), as T decreases, our values of \({T}_{1}^{-1}\) may be increasingly smaller than the data points in Fig. 13.
Figure 13 compares the values of \({T}_{10}\) from the present work with some from the literature: a CWS and b time domain. Rotational correlation times were computed from the data collected in [6] maintaining the full spectral densities; e.g., Eq. (5.61) of [10]. The results were averaged over 5 concentrations 0.2–40 mM. The value of \({\tau }_{R}\) for 315 K was found by interpolation between 298 and 323 K.
In considering Fig. 13a, we note that we used a standard sample of Fremy’s salt to calibrate our values of \({H}_{1}\), as described in detail in [26] which employs the same values of \({T}_{10}\) used in Hwang’s work, [33]. The estimated relative accuracy between our values of \({T}_{10}\) and those of Hwang is about 5%. Therefore, despite the fact that the accuracy of \({T}_{10}\) was estimated to be 20–30% [61], the relative values are comparable within 5%. We observe that at low values of \({\tau }_{\mathrm{R}}^{-1}\), our values (circles) of \({T}_{10}^{-1}({\Delta H}_{\mathrm{pp}}^{\mathrm{L}})\) are in excellent agreement with those of [33] but, as the relaxation rate increases above about 1 \({\mathrm{\mu s}}^{-1}\), the literature values are more in line with our values of \({T}_{10}^{-1}(I)\). Note that in Fig. 13a, the difference in \({T}_{10}^{-1}({\Delta H}_{\mathrm{pp}}^{\mathrm{L}})\) for lf and hf is minimal while for \({T}_{10}^{-1}(I)\) it is significant and increasing with rotational rate. While Fig. 13 shows that the relaxation rates of pd-Tempone in toluene and of pd-Tempol in 60%AG are comparable, they cannot definitively support the reliability of either \({T}_{10}^{-1}({\Delta H}_{\mathrm{pp}}^{\mathrm{L}})\) or \({T}_{10}^{-1}(I)\).
Figure 13b compares the present results those of [52] derived from combined time-domain measurements of saturation recovery-EPR and saturation recovery-ELDOR in a series of water/glycerol mixture, triangles. The dashed lines are smooth curves to guide the eye through the data of [52] as well as our data for \({T}_{1}^{-1}({\Delta H}_{\mathrm{pp}}^{\mathrm{L}})\), circles. Here, the full 20–30% uncertainty in \({H}_{1}\) in our measurements comes into play. Nevertheless, the overall agreement is reasonable keeping in mind that the ordinate is a linear scale, unlike the majority of literature data that are presented on a log scale. A preliminary observation is that time-domain data have more straightforward interpretations but that CWS data are more reproducible. Of course, reproducibility and accuracy can be quite different. This point is amply demonstrated by the difference between \({T}_{1}^{-1}({\Delta H}_{\mathrm{pp}}^{\mathrm{L}})\) and \({T}_{1}^{-1}(I)\) which are derived from the same sample and both from high quality fits to the CWS. We understand that the interpretation of \({T}_{1}^{-1}({\Delta H}_{\mathrm{pp}}^{\mathrm{L}})\) or \({T}_{1}^{-1}(I)\) even at \(C\) = 0.03 mM depends critically on a detailed understanding of possible relaxation pathways other than HSE/DD; however, we do not yet understand why the two modes of measurement would lead to different results.
5.2.3 Values of \({T}_{1\mathrm{lf}}^{\mathrm{eff}}/{T}_{1\mathrm{hf}}^{\mathrm{eff}}\)
In early work [62], \({T}_{1}^{\mathrm{eff}}\) was measured using the saturation-recovery technique (SR) for all three lines of 0.16 mM Tempol in sec-butyl benzene as a function of temperature. The values of \({T}_{1\mathrm{lf}}^{\mathrm{eff}}/{T}_{1\mathrm{hf}}^{\mathrm{eff}}\) showed no correlation with \(T\), yielding a mean value of 1.1 ± 0.2. In the same work, no significant difference in \({T}_{1}^{\mathrm{eff}}\) was reported for Tempone and pD-Tempone. For 15N Tempone, \({T}_{1\mathrm{lf}}^{\mathrm{eff}}/{T}_{1\mathrm{hf}}^{\mathrm{eff}}\) = 1.0 ± 0.2.
We are unaware of other work, employing either CWS or pulsed measurements that have reported \({T}_{1\mathrm{lf}}^{\mathrm{eff}}/{T}_{1\mathrm{hf}}^{\mathrm{eff}}\) in Tempol; however, more modern work using SR or IR revealed small but significant differences in three other nitroxides [17]. From IR, differences in \({T}_{1\mathrm{lf}}/{T}_{1\mathrm{hf}}\) were found that were not significantly different from rather different nitroxide structure, deuteration, or 15N enrichment. See column 4 of Table 3 in [17]. Combining all of their room temperature data, we find from those data, \({T}_{1\mathrm{lf}}/{T}_{1\mathrm{hf}}\) = 1.22 ± 0.03.
In this work, forming \({T}_{1\mathrm{lf}}^{\mathrm{eff}}/{T}_{1\mathrm{hf}}^{\mathrm{eff}}\) from Tables 8, 9, 10 and 11, one finds minor variations with \(T\) and \(C\). Furthermore, there is no correlation with \({f}_{\mathrm{m}}\). Combining all data, \({T}_{1\mathrm{lf}}^{\mathrm{eff}}/{T}_{1\mathrm{hf}}^{\mathrm{eff}}\) = 1.01 ± 0.05 from CWS(\({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\)), 1.3 ± 0.2 from CWS(\(I\)), and 1.15 ± 0.07 from the eye fits. This aspect supports the validity of CWS(\(I\)).
In summary, the pulsed EPR measurements [17] and various approaches to analyzing CWS in this work both show small, systematic departures of \({T}_{1\mathrm{lf}}/{T}_{1\mathrm{hf}}\) from unity of similar magnitude.
6 Conclusions
A theory was presented that allows the study of the CWS of any parameter derived from the EPR spectrum. The parameters readily available experimentally without fitting are \({\Delta H}_{\mathrm{pp}}^{\mathrm{spc}}\), the line width of the combined absorption and the dispersion and \({V}_{\mathrm{pp}}^{\mathrm{spc}}\), the amplitude of the combination, neither of which is very useful as the lines become broader. With fitting, \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\), \(I\), \({V}_{\mathrm{pp}}\), and \({V}_{\mathrm{disp}}\) may be studied. We have shown that the Bloch fits to CWS of \({V}_{\mathrm{pp}}\) are rather good, but yield values of \({T}_{1}\) that are wrong by 100% or more in the examples considered here. Furthermore, as exemplified by Fig. 1, comparison of empirical parameters based on a percentage change in \({V}_{\mathrm{pp}}^{\mathrm{spc}}\) from the linear behavior at small \({H}_{1}\) must be done with great care. Experimentally, at \(C\) = 0.03 mM where HSE or DD are negligible, \({T}_{10}\) is comparable with literature values, but the values derived from CWS of \(I\) or \({\Delta H}_{pp}\) are different from one another. For \(C\) > 0, using fits to the Bloch Eqs. (3) or (5) to obtain values of \({T}_{1\mathrm{hf}}^{\mathrm{eff}}\) as has been proposed in the literature [33, 59], yield values that are reasonable, but the values derived from \(I\) or of \({\Delta H}_{\mathrm{pp}}^{\mathrm{L}}\) are different. From eye fits, the CWS of \({\mathrm{V}}_{\mathrm{disp}}\) may be estimated and is in reasonable agreement with theory except at 273 K at higher values of \({H}_{1}.\)
References
K.M. Salikhov, Appl. Magn. Reson. 38, 237–256 (2010)
K.M. Salikhov, Fundamentals of Spin. Exchange Story of a Paradigm Shift (Springer, Geneva, 2019)
K.M. Salikhov, Appl. Magn. Reson. 723, 1074–1087 (2018)
K.M. Salikhov, I.T. Khairuzhdinov, J. Exp Theor Phys 128, 684–699 (2019)
K.M. Salikhov, Appl. Magn. Reson. 51, 297–325 (2020)
B.L. Bales, M.M. Bakirov, R.T. Galeev, I.A. Kirilyuk, A.I. Kokorin, K.M. Salikhov, Appl. Magn. Reson. 48, 1399–1445 (2017)
B.L. Bales, M. Peric, Appl. Magn. Reson. 48, 175–200 (2017)
B.L. Bales, M. Peric, J. Phys. Chem. A 106, 4846–4854 (2002)
D. Marsh, T. Páli, and P.I. Horváth, in Spin Labeling: The Next Millennium, L.J. Berliner, Editor. (Kluwer Academic Publishers, New York, Boston, Dordrecht, London, Moscow, 2002)
D. Marsh, Spin-Label Electron Paramagnetic Resonance Spectroscopy (CRC Press, Taylor & Francis Group, Boca Raton, 2020)
B.L. Bales, in Biological Magnetic Resonance, L.J. Berliner and J. Reuben, Editors. (Plenum, New York, 1989)
T.J. Stone, T. Buckman, P.L. Nordio, H.M. McConnell, Proc. Natl. Acad. Sci. USA 54, 1010–1017 (1965)
G.I. Likhtenshtein, Nitroxides. Brief History, Fundamentals, and Recent Developments (Springer, Cham, 2020)
L.J. Berliner (ed.), Spin Labeling: The Next Millennium. Biological Magnetic Resonance, vol. 14 (Kluwer Academic Publishers, New York, 2002), p. 444
L.J. Berliner, Spin Labeling: Theory and Applications (Plenum Publishing Corporation, New York, 1989)
L.J. Berliner, Spin Labeling II: Theory and Applications (Academic Press, New York, 1979)
J.R. Biller, V. Meyer, H. Elajaili, G.M. Rosen, J.P.Y. Kao, S.S. Eaton, G.R. Eaton, J. Magn. Reson. 212, 370–377 (2011)
J.R. Biller, J.E. McPeak, S.S. Eaton, G.R. Eaton, Appl. Magn. Reson. 49, 1235–1251 (2018)
A. Overhauser, Phys. Rev. 89, 689–700 (1953)
A. Overhauser, Phys. Rev. 92, 477 (1953)
R.D. Bates, W.S. Drozdoski, J. Chem. Phys. 67, 4038 (1977)
B.D. Armstrong, S. Han, J. Chem. Phys. 127, 10458 (2007)
M.J. Prandolini, V.P. Denysenkov, M. Gafurov, S. Lyubenova, B. Endeward, M. Bennati, T.E. Prisner, Appl. Magn. Reson. 34, 399–407 (2008)
D. Sezer, M. Gafurov, M.J. Prandolini, V.P. Denysenkov, T.F. Prisner, Phys. Chem. Chem. Phys. 11, 6638–6653 (2009)
M.T. Tuerke, M. Bennati, Appl. Magn. Reson. 43, 129–138 (2012)
M.M. Bakirov, K.M. Salikhov, M. Peric, R.N. Schwartz, B.L. Bales, Appl. Magn. Reson. 50, 919–942 (2019)
M. Peric, B.L. Bales, M. Peric, J. Phys. Chem. A 116, 2855–2866 (2012)
A.M. Portis, Phys. Rev. 91, 1071–1078 (1953)
A.S. AlOmar, Optik 225, 165533–165544 (2021)
T.G. Castner Jr., Phys. Rev. 115, 1506–1515 (1959)
E.L. Wolf, Phys. Rev. 142, 555–569 (1966)
C.P. Poole Jr., Electron Spin Resonance: A Comprehensive Treatise on Experimental Techniques, 2nd edn. (Dover, Mineola, 1996)
J.S. Hwang, R.P. Mason, L.-P. Hwang, J.H. Freed, J. Phys. Chem. 79, 489–511 (1975)
M.P. Eastman, R.G. Kooser, M.R. Das, J.H. Freed, J. Chem. Phys. 51, 2690 (1969)
B.L. Bales, Cell Biochem. Biophys. 75, 171–184 (2017)
M.P. Eastman, G.V. Bruno, J.H. Freed, J. Chem. Phys. 52, 321–327 (1970)
B.L. Bales, M. Peric, M.T. Lamy-Freund, J. Magn. Reson. 132, 279–286 (1998)
B.L. Bales, M. Peric, J. Phys. Chem. B 101, 8707–8716 (1997)
J.D. Currin, Phys. Rev. 126, 1995 (1962)
D. Kivelson and K. Ogan, in Advances in Magnetic Resonance, J.S. Waugh, Editor. (Academic Press, New York, 1974)
Y.N. Molin, K.M. Salikhov, K.I. Zamaraev, Spin Exchange. Principles and Applications in Chemistry and Biology (Springer, New York, 1980)
K.I. Zamaraev, Y.N. Molin, K.M. Salikhov, Spin Exchange. (Nauka, Siberian branch, Novosibisk. Russian Edition., 1977)
B.L. Bales, M. Meyer, S. Smith, M. Peric, J. Phys. Chem. A 113, 4930–4940 (2009)
B.L. Bales, M. Meyer, M. Peric, J. Phys. Chem. A 118, 6154–6162 (2014)
B.L. Bales, M. Peric, I. Dragutan, J. Phys. Chem. A 107, 9086–9098 (2003)
D. Marsh, J. Magn. Res. 277, 86–94 (2017)
B.L. Bales, M. Meyer, S. Smith, M. Peric, J. Phys. Chem. A 112, 2177–2181 (2008)
M.R. Kurban, M. Peric, B.L. Bales, J. Chem. Phys. 129, 064501-1-064501–10 (2008)
A. Abragam, Principles of Nuclear Magnetism (Oxford University Press, London, 1986)
K.M. Salikhov, A.G. Semenov, Y.D. Tsvetkov, Electron Spin Echo and Its Applications (Nauka, Novosibirsk, 1976). (in Russian)
K.M. Salikhov, J. Magn. Reson. 63, 271–279 (1985)
B.H. Robinson, D.A. Haas, C. Mailer, Science 263, 490–493 (1994)
K.M. Salikhov, M.M. Bakirov, R.T. Galeev, Appl. Magn. Reson. 47, 1095–1122 (2016)
M.K. Bowman, H. Hase, L. Kevan, J. Magn. Reson. 22, 23–32 (1976)
K. Yamada, Y. Kinoshita, T. Yamasaki, H. Sadasue, F. Mito, M. Nagai, S. Matsumoto, M. Aso, H. Suemuni, K. Sakai, H. Utsumi, Arch. Pharm. Chem. Life Sci. 341, 548–553 (2008)
J. Pirrwitz, D. Schwarz, (DDR Patent, 222017 A1 (WP C 07 D/260 901 6).)
L.A. Shundrin, I.A. Kirilyuk, I.A. Grigor’ev, Mendeleev Commun. 24, 298–300 (2014)
P.R. Bevington, Data Reduction and Error Analysis for the Physical Sciences (McGraw-Hill, New York, 1969)
D. Marsh, Spin Labeling. Theory and Applications (Plenum Publishing Corporation, New York, 1989)
R.N. Schwartz, L.L. Jones, M.K. Bowman, J. Phys. Chem. 83, 3429 (1979)
R.G. Kooser, W.V. Volland, J.H. Freed, J. Chem. Phys. 50, 5243–5257 (1969)
P.W. Percival, J.S. Hyde, J. Magn. Reson. 23, 249–257 (1976)
Acknowledgements
We are grateful to our colleagues from Kazan Zavoisky Physical-Technical Institute, Prof. M. Bowman and Dr. A.G. Maryasov for numerous fruitful discussions. M.M.B. and I.T.K. acknowledge financial support from the government assignment for FRC Kazan Scientific Center of RAS. K.M.S. acknowledges also support by the Russian Science Foundation (Project No. 20-63-46034).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Bakirov, M.M., Khairutdinov, I.T., Salikhov, K.M. et al. The Effect of Power Saturation on the Line Shapes of Nitroxide Spin Probes Under the Influence of Spin-Exchange and Dipole–Dipole Interactions Studied by CW EPR. Appl Magn Reson 53, 1275–1315 (2022). https://doi.org/10.1007/s00723-021-01461-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00723-021-01461-9