A Simple, Accurate Method to Determine the Effective Value of the Magnetic Induction of the Microwave Field from the Continuous Saturation of EPR Spectra of Fremy’s Salt Solutions. Representative values of $T_{1}$

Abstract

A simple protocol to measure the effective value of the circularly polarized magnetic induction of the microwave field is proposed and demonstrated employing continuous-wave saturation of a standard sample of Fremy’s salt measured under specified conditions. The fact that the doubly integrated intensity of first-derivative spectra is invariant with respect to the line shape is used to take into account the non-Lorentzian line shape to study the peak-to-peak intensity or the line width. Corrections for the use of line- rather than point-samples are developed.

1 Introduction

Continuous-wave saturation curves (CWS) of radicals in solution have been employed in the past to measure $T_{1}$ before time-domain methods became available [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. Unlike the time-domain methods, a precise value of the circularly polarized magnetic induction of the microwave field, $H_{1}$, is needed but CWS measurements are inherently simpler; especially in recent years when software has been developed to automatically vary precisely the microwave power incident on the resonator, $P$, acquire and store a spectrum, retune the cavity, and repeat the sequence over a series of $P$. Furthermore, CWS is available to labs that are not equipped with pulsed-EPR spectrometers.

Our interest in the spin-relaxation behavior of nitroxides in solution has been stimulated by recent discoveries of interesting spectral properties of these free radicals as a function of their concentration where Heisenberg spin exchange (HSE) and dipole–dipole (DD) interactions introduce signals that are admixtures of absorptive and dispersive terms. See [16, 17] and references therein. Thus, instead of three pure absorption lines observed at low concentration, three spin modes [16, 17] result at higher concentrations. The modes at high- and low-fields, are comprised of two components, one absorption plus one dispersion while the central-line shows only one component, an absorption. Furthermore, as HSE increases, intensity of the absorptive contributions to the low- and high-field lines is transferred to the central absorption line. Finally, the low- and high-field lines change from absorption to emission [16, 17]. Extensive studies of these phenomena have been published recently at low microwave powers to understand the line width ($1/T_{2} )$ behavior in the presence of complicated hyperfine structures due to protons and deuterons [16, 18] and references therein. Importantly, even severely overlapping resonances, past the point of coalescence into a single line, may be separated into the individual five components, three absorptive and two dispersive, each of which may studied with CWS separately. This provides another motive to use CWS. Pulsed methods are confined to measuring $T_{1}$ of the absorption-dispersion mixtures, not the separated components.

Now our attention has turned to the effects of HSE and DD as well as other variables on $T_{1}$. Studying HSE by EPR is a powerful method to study bi-molecular encounters [19] and re-encounters [20]. Its power derives from the fact that the interaction is very short range, occurring only during the short time in which the overlap of unpaired spin orbitals between the two colliding radicals is significant [19].

Therefore, to undertake an ambitious program to measure $T_{1}$ with numerous samples under a variety of conditions, we decided to revive the CWS method with a view to easily prepared samples. Our focus is on the standard X-band EPR spectrometer employing a TE₁₀₂ or TE₁₀₄ cavity, glassware to control the temperature, $T$, and magnetic field modulation of frequency, $f_{\text{m}}$, with a maximum amplitude, $a_{\text{m}}$, from coils mounted on the cavity producing a modulation-field that varies with position within the cavity. With this focus, it is easier to present the material. In addition, it is the setup mostly used by researchers who are not EPR experts. Nevertheless, our procedure might be extended to apply to other setups. To ensure accurate sample placement, a “line-sample” extending all the way through the cavity is preferable to a point-sample. It is easier to prepare the former than the latter and provides better signal-to-noise ratios (SNR) due to the increased filling factor.

The well-known relationship between $P$ and $H_{1} ,$$H_{1}$$\propto$$\sqrt P$ [2, 3, 21,22,23,24] hides the fact that the problem of determining $H_{1}$ at a given point within the sample and summing the resultant spectra for an extended sample is not trivial. The reader is referred to Ref. [22] and references therein for an exhaustive discussion of the various problems. The primary purpose of this paper is to propose a protocol to accurately measure the effective value of $H_{1}$ for a particular experimental setup. With our focus on nitroxide radicals in solution, we have selected solutions of Fremy’s salt, peroxlyamine disulfonate (PADS), rather than a solid. PADS is readily available, cheap, relatively stable and yields narrow EPR lines leading to good SNR. In fact, we exploit the instability of PADS at elevated temperatures to vary the concentration without disturbing the sample.

PADS has been extensively studied, both in solution [3, 4, 8,9,10,11,12,13,14] and solid phases [5,6,7, 15] since the early days of EPR. Unlike most other nitroxide spin probes, PADS resonance absorption lines are not complicated by unresolved proton or deuteron hyperfine structure and, thus, were anticipated to have a Lorentzian profile. Nevertheless, it has been reported [9, 8], and confirmed here, that the line shape deviates from Lorentzian due to a Gaussian component whose origin is still not satisfactorily explained. The same problem occurs with all nitroxides largely because of unresolved hyperfine structure due to protons, deuterons, and other magnetic nuclei. To study spin relaxation, the Lorentzian component must be separated from the Gaussian, an old problem in many branches of science where the information of interest lies in a Lorentzian line that is broadened by perturbations that, in many cases, are Gaussian, which produces a Voigt line shape [25]. The history of the problem, the separation of the Gaussian and Lorentzian components of the Voigt and the corrections of various parameters obtained from the EPR are treated in depth in Ref. [25]. As we shall see, of primary importance in CWS is the doubly integrated intensity of the first-derivative resonance line, $I$. Obtaining the correct value of $I$ is important because it varies by more than a factor of three from a Gaussian to a Lorentzian. Briefly, for non-experts in EPR, the intensity in the wings of a Lorentzian is larger than that of a Gaussian; for a Voigt, the intensity is intermediate [25]. By quantifying the variation of the intensity in the wings, a value of the Voigt parameter, Eq. (6), below is obtained. The method was first developed by measuring four points on the spectrum, the two corresponding to the maximum and minimum of the first-derivative spectrum and two more in the wings at the point where the Gaussian and Lorentzian differ the most [25]. Later [26], least-squares fitting to all of the points provide significantly better precision and afforded reliable estimates of the errors. There are three pertinent peak-to-peak line widths of the first-derivative spectrum: the observed, $\Delta H_{\text{pp}}^{\text{obs}}$, the Lorentzian, $\Delta H_{\text{pp}}^{\text{L}}$, and the Gaussian, $\Delta H_{\text{pp}}^{\text{G}}$, line widths, respectively.

All previous studies of PADS have assumed a Lorentzian shape; thus, the values of $T_{2}$ reported were extracted from $\Delta H_{\text{pp}}^{\text{obs}}$, assuming a Lorentzian line shape, using for the first derivative of the resonance signal $T_{2} = 2/\left[ {\sqrt 3 \gamma \Delta H_{\text{pp}}^{\text{obs}} (0)} \right]$ or $T_{2} = 2/\left( {\gamma \Delta H_{1/2}^{\text{obs}} (0)} \right)$ for the non-derivative spectrum, respectively, where $\Delta H_{1/2}^{\text{obs}} (0)$ is the full-width between half-maximum points of the non-derivative signal, $\gamma$ is the gyromagnetic ratio of the electron, and the zero means the limit as $H_{1} \to 0$. Thus, rather than listing the published values of $T_{2}$, we summarize in Table 1 the values of $\Delta H_{\text{pp}}^{\text{obs}} (0)$, the observed line widths. The PADS concentration is denoted by [PADS].

Table 1 Relaxation times of PADS derived from CWS in aqueous solutions of 0.05 M K₂CO₃ except as noted

To simplify the presentation, we shorten such phrases as “the first-derivative resonance line of Lorentzian shape” to just a “Lorentzian.” Similarly, with Gaussian and Voigt shapes. For example, we say “PADS is not Lorentzian” to mean “the resonance lines of the EPR spectrum of PADS are not of Lorentzian shape.”

Two concerns about the interpretation of CWS results are the influence of modulation sidebands [9] and passage effects [1]. In the present case, we show in Sect. 5.5 that neither of these pose a problem.

This work is novel in three respects. (1) We fit all spectra to a Voigt shape, permitting the use of all of the points of the spectrum rather than a few selected points. (2) We show that when spin diffusion may be neglected, the CWS of $I$ is described by the CWS of Lorentzian shape, independent of actual line shape. (3). We place on solid ground the concept of an effective value of $H_{1}$ by showing that the line shape of the sum of the Lorentzian spectra that make up the observed spectrum for a line sample is nearly Lorentzian and that the same CWS is observed for the line sample as for a point sample using an effective value of $H_{1}$.

These three matters which may not be familiar to some workers are carefully treated so that our arguments may be scrutinized. Those readers uninterested in those details may go directly to the protocol, given in two forms in Sects. 6.1 and 6.2. The procedure is quite simple and, for standard EPR spectrometers, should occupy less than an afternoon.

2 Theory

2.1 CWS of Lorentzian Lines

The saturation of a Lorentzian line is treated in many places; see, for example the textbook presentation in Ref. [21]. Defining the saturation factor, $s$, as

$$s = \left( {1 + \left( {H_{1} } \right)^{2} \gamma^{2} T_{1} T_{2} } \right)^{ - 1} ,$$

(1)

$\Delta H_{\text{pp}}^{\text{L}}$ varies with $H_{1}$ as

$$\Delta H_{\text{pp}}^{\text{L}} \left( {H_{1} } \right) = \Delta H_{\text{pp}}^{\text{L}} \left( 0 \right)s^{ - 1/2} ,$$

(2)

and the peak-to-peak line height ($V_{\text{pp}} )$ as

$$\frac{{V_{\text{pp}} }}{{H_{1} }} = \frac{{V_{\text{pp}} (H_{1}^{0} )}}{{H_{1}^{0} }}s^{3/2}$$

(3)

The doubly integrated intensity of the first-derivative spectrum ($I)$ is given by [25]

$$I = \frac{1}{2}F \cdot V_{\text{pp}} \left( {\Delta H_{\text{pp}}^{\text{obs}} } \right)^{2}$$

(4)

where the factor $F = 2\pi /\sqrt 3 = 3.63$ for the Lorentzian. Thus, from Eqs. (2) and (3), we find

$$\frac{I}{{H_{1} }} = \frac{{I(H_{1}^{0} )}}{{H_{1}^{0} }}s^{1/2}$$

(5)

In Eqs. (3) and (5), $H_{1}^{0}$ is any value below saturation where $s$ is negligibly different than unity.

We shall refer to the mode of measurement, $M$, as the CWS of $\Delta H_{\text{pp}}^{\text{L}}$, $V_{\text{pp}}$, or $I.$

All previous CWS studies of PADS have assumed that the Lorentzian line shape adequately describes the resonance lines, employing Eqs. (2) and (3) using $\Delta H_{\text{pp}}^{\text{obs}}$ rather than $\Delta H_{\text{pp}}^{\text{L}}$ to study $T_{2}$ and $T_{1}$. For other line shapes, neither (2) nor (3) is correct; however, under the conditions of negligible spin diffusion, Eq. (5) is correct, applicable to any arbitrary line shape, including those that are partially resolved. This can be seen by appealing to the spin packet model of inhomogeneously broadened lines [23, 24]. Each spin packet, which is Lorentzian and is assumed to be characterized by the same $T_{2}$, does obey Eqs. (2) and (3) and because $I = \mathop \sum \nolimits I_{j}$ where $I_{j}$ is the doubly integrated intensity of the $i$ th spin packet, the sum also obeys Eq. (5).

For most nitroxides, each line in the spectrum is accurately described by the Voigt that is characterized uniquely by the Voigt parameter as follows: [25]

$$\chi = \Delta H_{\text{pp}}^{\text{G}} /\Delta H_{\text{pp}}^{\text{L}}$$

(6)

Methods to obtain $\chi$ as well as $\Delta H_{\text{pp}}^{\text{G}}$ and $\Delta H_{\text{pp}}^{\text{L}}$ separately from least-squares fits of experimental or theoretical spectra have been available for many years; [26] thus, Eq. (2) may be used for a Voigt shape by extracting $\Delta H_{\text{pp}}^{\text{L}}$ from the measured $\Delta H_{\text{pp}}^{\text{obs}}$. For $\chi \to \infty$ the Gaussian shape is obtained where $F$ = $\sqrt {\pi e/8}$ = 1.03 [25]. For intermediate values of $\chi$, $F$ in Eq. (4) is obtained from Eq. (34) of Ref. [25].

Equations (2, 3, and 5) apply to a point-sample because $H_{1}$ varies with position. Let us assume for convenience the common arrangement which has the point-sample in the center of the TE₁₀₂ cavity where $H_{1}$ has its maximum value, $H_{1\rm{max} }$.

As supported by a large literature [2, 21, 22, 27, 28], the accepted relationship between the power incident on the cavity, $P$, and $H_{1\rm{max} }$ is as follows:

$$H_{1\rm{max} } = \varGamma_{\rm{max} } \sqrt {QP} = K_{1\rm{max} } \sqrt P$$

(7)

where $\varGamma_{\rm{max} }$ and $K_{1\rm{max} }$ are constants and $Q$ is the loaded quality-factor of the cavity. Note that Eq. (7) supposes a critically coupled cavity; if this is not the case, a correction factor is needed [9].

In what follows, we show that by employing effective values of $H_{1}$, equations of the same forms as (2) and (3) approximate well the CWS of samples that are not points, but “lines” (in cylindrical tubes of small diameter). Thus, we may write

$$H_{1} = \varGamma \sqrt {QP} = K_{{1{\text{M}}}} \sqrt P$$

(8)

where $H_{1} = \xi_{\text{M}} H_{1\rm{max} }$, $\varGamma = \xi_{\text{M}} \varGamma_{\rm{max} }$, and $K_{{1{\text{M}}}} = \xi_{\text{M}} K_{1\rm{max} }$ are effective values which depend on the mode of measurement denoted by the subscript $M$. $\varGamma$ is related to the conversion efficiency, e.g., Ref. [22]. For a point-sample yielding a Lorentzian, $\xi_{\text{M}}$ = 1 for all three modes, but for line-samples, they differ from one another.

Rewriting Eq. (2), employing Eq. (8), we have

$$\Delta H_{\text{pp}}^{\text{L}} = \Delta H_{\text{pp}}^{\text{L}} \left( 0 \right)\left( {1 + \left( {K_{{1\Delta H_{\text{pp}}^{\text{L}} }} \sqrt P } \right)^{2} \frac{2}{{\sqrt 3 \Delta H_{\text{pp}}^{\text{L}} \left( 0 \right)}}\gamma T_{1} } \right)^{1/2}$$

(9)

where $K_{{1\Delta H_{\text{pp}}^{\text{L}} }} = \xi_{{\Delta H_{\text{pp}}^{\text{L}} }} K_{1\rm{max} }$ with $\gamma T_{2} = 2/\sqrt 3 \Delta H_{\text{pp}}^{\text{L}} \left( 0 \right)$.

Recognizing that the slope of $V_{\text{pp}}$ with respect to $H_{1}$, $K_{\text{pp}}$, in the unsaturated region is given by $K_{\text{pp}} = V_{\text{pp}} \left( {H_{1}^{0} } \right)/H_{1}^{0}$, Eq. (3) may be written as follows

$$V_{\text{pp}} = K_{\text{pp}} \frac{{K_{{1V_{\text{pp}} }} \sqrt P }}{{\left( {1 + \left( {K_{{1V_{\text{pp}} }} \sqrt P } \right)^{2} \dfrac{2}{{\sqrt 3 \Delta H_{\text{pp}}^{\text{L}} \left( 0 \right)}}\gamma T_{1} } \right)^{3/2} }}$$

(10)

where $K_{{1V_{\text{pp}} }} = \xi_{{V_{\text{pp}} }} K_{1\rm{max} }$.

Similarly, from Eq. (5), $I$ varies as

$$I = K_{\text{I}} \frac{{K_{{1{\text{I}}}} \sqrt P }}{{\left( {1 + \left( {K_{{1{\text{I}}}} \sqrt P } \right)^{2} \dfrac{2}{{\sqrt 3 \Delta H_{\text{pp}}^{\text{L}} \left( 0 \right)}}\gamma T_{1} } \right)^{1/2} }}$$

(11)

where $K_{\text{I}}$ is the slope of $I$ with respect to $H_{1}$ at small $H_{1}$ and $K_{{1{\text{I}}}} = \xi_{\text{I}} K_{1\rm{max} }$. Observe that at large values of $\sqrt P$, $I$ becomes independent of $\sqrt P$.

2.2 The effective $H_{1}$ for a line-sample: Lorentzian shape

Do values of $\xi_{{\Delta H_{\text{pp}}^{\text{L}} }}$, $\xi_{{V_{\text{pp}} }}$, and $\xi_{\text{I}}$ exist such that Eqs. (9–11) produce the same CWS for a line-sample that they do for a point-sample using $\xi_{{\Delta H_{\text{pp}}^{\text{L}} }} = \xi_{{V_{\text{pp}} }} = \xi_{\text{I}} = 1$? It would not be surprising if this question could not be answered in the affirmative, because summing spectra from different points along the line-sample involves adding spectra at different levels of saturation; i.e., different values of $\Delta H_{\text{pp}}^{\text{L}}$. What line shape does this sum produce? Past workers have tacitly assumed that the CWS due to this composite spectrum could be treated with a Lorentzian form. From Eq. (4), the values of $V_{\text{pp}}$ for spectra away from the central point are enhanced as the inverse square of $\Delta H_{\text{pp}}^{\text{obs}}$ compared with that at the central point because of the smaller $\Delta H_{\text{pp}}^{\text{obs}}$. Furthermore, they are also enhanced because the values of $I$ are larger in relation to the central values because they are saturated less.

To answer these questions, we sum over the line to yield the resulting spectrum as follows:

$$Y^{\prime }_{\text{sum}} = \mathop \int \limits_{0}^{a} Y^{\prime } \left( x \right){\text{d}}x$$

(12)

where $a$ is the wide dimension of the cavity, traversed by the line-sample, which is usually oriented vertically in a standard spectrometer. At point $x$, the spectrum is given by Eq. (3.10) of Ref. [21] or as Eq. (8), section C of chapter 13 of Ref. [29] as follows:

$$Y^{\prime } \left( x \right) = - Ca_{\text{m}} (x)a_{1} (x)H_{1\rm{max} } \frac{{\left( {H - H_{0} } \right)\gamma T_{2} s^{2} }}{{\left[ {1 + s\left( {H - H_{0} } \right)^{2} \gamma^{2} T_{2}^{2} } \right]^{2} }}$$

(13)

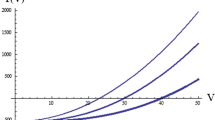
In Eq. (13), the amplitude of the field modulation varies as $a_{\text{m}} \left( x \right) = a_{\text{m}} \sin^{2} \left( {\pi x/a} \right)$ [28], and that of the circularly polarized magnetic induction as $a_{1} (x)H_{1\rm{max} } = a_{1} H_{1\rm{max} } \sin \left( {\pi x/a} \right)$ [28], and C is an arbitrary overall gain constant. Equation (13) supposes that $a_{\text{m}} \left( x \right)$ is small enough to avoid broadening. Equation (12) was solved numerically for $T_{1}$ = $T_{2}$ = 0.33 μs for different values of $H_{1\rm{max} }$. Perhaps surprisingly, the resulting sum spectra were accurately Lorentzian even when significantly saturated. For example, at $H_{1\rm{max} }$ = 0.24 G, where $\left( {\gamma H_{1\rm{max} } } \right)^{2} T_{1} T_{2}$ = 1.94, where $s$ = 0.340 for the central point, the fit to a Lorentzian yields $r$ = 0.99997 and a maximum ratio of residual to $V_{\text{pp}}$ of 0.009. Fitting all such spectra yields values of $V_{\text{pp}}$ and $\Delta H_{\text{pp}}^{\text{L}}$ from which $I$ may be calculated from Eq. (4). For convenience, $K_{1\rm{max} }$ is set to unity so that $\xi_{\text{M}} = K_{{1{\text{M}}}}$. Figure 1a shows the results of these calculations of the CWS of $\Delta H_{\text{pp}}^{\text{L}}$ for point and line samples. The lines through the points are the fits to Eq. (9) with $T_{1}$ = 0.33 μs and $\xi_{{\Delta H_{\text{pp}}^{\text{L}} }}$ = 1 for both sample types, yielding $K_{{1\Delta H_{\text{pp}}^{\text{L}} }}$ = 0.8518 ± 0.0031. The saturation of the line sample is less than that of the point-sample, as expected. Figure 1b shows the same data except with $\xi_{{\Delta H_{\text{pp}}^{\text{L}} }}$ = 0.8518 for the line sample, demonstrating that the line sample behaves as a point sample with an effective field $H_{1} = 0.8518H_{1\rm{max} }$. For $V_{\text{pp}}$ and $I$, the CWS are different if plotted against $\sqrt P$, not shown, but Figs. 2 and 3 show that coincident curves are obtained with $\xi_{{V_{\text{pp}} }}$ = 0.8620 ± 0.0022 and $\xi_{I}$ = 0.9013 ± 0.0008, respectively. The uncertainties are fit errors. Values of $V_{\text{pp}}$ and $I$ are given in arbitrary units (AU) because of the gain factor. Because the correct value of $H_{1}$ is given by mode $I$, to use the other modes to find the effective value of $H_{1}$, we must multiply the fit value of $K_{{1\Delta H_{\text{pp}}^{\text{L}} }}$ by the factor $\zeta_{{\Delta H_{\text{pp}}^{\text{L}} }} = K_{{1{\text{I}}}} /K_{{1\Delta H_{\text{pp}}^{\text{L}} }}$ = 1.058 ± 0.004 and of $K_{{1V_{\text{pp}} }}$ by $\zeta_{{V_{\text{pp}} }} = K_{{1{\text{I}}}} /K_{{1V_{\text{pp}} }}$ = 1.046 ± 0.003. Note that Eq. (13) is equivalent to Eq. (2) of Eaton et al. [28].

Fig. 1

CWS of $\Delta H_{\text{pp}}^{\text{L}}$ for a point-sample, squares, and line samples, circles, with a$\xi_{{\Delta H_{\text{pp}}^{\text{L}} }}$ = 1 for both samples and b with $\xi_{{\Delta H_{\text{pp}}^{\text{L}} }}$ = 0.8518 for the line-sample. What appears to be a single line is the overlay of two lines that are fits of the data to Eq. (9)

Fig. 2

CWS of $V_{\text{pp}}$ for a point-sample, squares, and line samples, circles, with $\xi_{{V_{\text{pp}} }}$ = 0.8620 for the line-sample. Two overlaying lines that appear to be a single line are fits of the data to Eq. (10)

Fig. 3

CWS of $I$ for a point-sample, squares, and line samples, circles, with $\xi_{I}$ = 0.9013 for the line-sample. Two overlaying lines that appear to be a single line are fits of the data to Eq. (11)

Freed and coworkers [9] found $\xi$ = 0.87 experimentally by comparing the CWS of a small sample of PADS to a line-sample. Eaton and coworkers verified the use of Eq. 13 experimentally by observing that the same results were obtained from a point- and line-sample; however, without considering the non-Lorentzian line shape. In Ref. [13], the problems of varying $H_{1}$ and $a_{\text{m}}$ were avoided by utilizing a sample placement passing the sample through the center of the broad face of the cavity; however, also assuming a Lorentzian.

3 A proposed protocol to measure $H_{1}$

To interpret the CWS to obtain values of $T_{1}$ from a radical of interest, it is clear that an accurate value of the effective $K_{1}$ is needed. The purpose of this work is to propose a simple method to determine $K_{1}$ by measuring the saturation behavior of an aqueous line sample of Fremy’s salt, peroxylamine disulfonate (PADS). We assume a value of $T_{1}$ = 0.33 μs taken from literature values, Table 1. This approach is similar to that of Ref. [28]. The determination of $K_{1}$ can be no more accurate than that of $T_{1}$ estimated to be 20–30% by Freed and coworkers [9]. A reasonable question is as follows: what is the point in studying carefully the effects of line-samples and non-Lorentzian line shapes for the calibration knowing that the best we can do is 20–30%? Our answer is two-fold. The first is that relative values of $T_{1}$ from different labs will be of good accuracy, estimated below to be 3.5–5%. Furthermore, conclusions may be drawn from relative values of $T_{1}$ due to changes in experimental parameters; for example, see Refs. [1, 2] and references therein. The second reason is that with modern time-domain methods continuing to develop [30], perhaps more accurate values of $T_{1}$ for PADS will be forthcoming from which values of $K_{1}$ and $T_{1}$ may be updated.

The proposed standard sample is as follows: air-saturated, 0.3-mM PADS in aqueous solution of 50-mM K₂CO₃ measured at 298 K, with magnetic-field modulation of frequency, $f_{\text{m}}$ = 100 kHz of amplitude $a_{\text{m}}$ = 0.1 G. The other parameters, receiver gain, time constant, and sweep time, may be chosen in the usual manner to provide a faithful spectrum [31].

To illustrate the protocol, we detail measurements of the standard sample sealed into 50-μL disposable capillaries filled so that the solutions pass through the entire cavity.

It is clear that the protocol will only directly apply to samples that mimic the PADS sample with fidelity. A line-sample of a radical of interest in 50-mM K₂CO₃ aqueous solution with the same geometry may be computed from the second equality in Eq. (8), provided that the $Q$ is the same. If there are significant differences in the values of $Q$ between the standard sample and the sample of interest, for example with a change of solvent or glassware, then measurements of $Q$ and the use of the first equality in Eq. (8) would be needed.

4 Experimental

PADS was purchased from Sigma-Aldrich and used as received. A stock solution of nominal 0.5-mM concentration was prepared by weight in aqueous 50-mM K₂CO₃ (TatChimProduct, 98%). Samples were sealed into 50-μL disposable capillaries filled so that the solutions pass through the entire cavity. The PADS purity was determined to be 60% by comparing its value of $I$ with that of a freshly prepared aqueous sample of protonated 2,2,6,6-tetramethyl-4-oxopiperidine-1-oxyl (Sigma 97%) below saturation. The quoted concentrations are those determined gravimetrically multiplied by 0.6. Thus, the stock solution fulfills the required 0.3 mM concentration for the standard sample. The spectra were obtained with a Bruker EMX plus spectrometer in Kazan at X-band (9.47 GHz) with nitrogen-flow temperature stabilization of precision 0.1 K; field-sweep width, 50 G; receiver gain, 1000; time constant, 5.12 ms; conversion time, 40 ms; and resolution, 1000 points. The Q value was measured at 33 dB ($P =$ 0.1 mW) using Bruker’s software EPR Acquisition. See section 7.5 of Ref. [22] for a discussion of this method and others. The authors outline some possible problems and conclude that for high-Q, the estimation is “fairly accurate.” In addition to the standard protocol to calibrate $H_{1}$, experiments were conducted varying the temperature, the oxygen concentration, the concentration of PADS, modulation frequency, and modulation amplitude. The concentration of PADS was serially reduced by heat quenching [32] as described below. In addition to air-saturated samples, oxygen or argon was bubbled through the standard solution for 30 min before filling and sealing the capillaries. We call these Air, Oxygen, and Argon samples, respectively. All of the data in this study were obtained with a critically coupled cavity; thus, Eq. (8) is valid as written.

The spectra were fit and analyzed by the program Lowfit, which searches for the minimum least-squares difference in the spectrum and a theoretical model of a Gaussian–Lorentzian sum function taking advantage of the fact that such a sum function is an excellent approximation to the Voigt shape [26]. $\Delta H_{\text{pp}}^{\text{L}}$ and $\Delta H_{\text{pp}}^{\text{G}}$ are obtained separately [26]. Accurate values of $I$, are obtained from the fit parameters using Eq. (34) of Ref. [25]. Lowfit includes both absorption and dispersion terms in the fit allowing correction for small dispersion admixtures due to a slightly unbalanced microwave bridge, as described in Ref. [20]. Corrections due to the contribution to the Gaussian line width by field modulation were carried out; [33], however, these amounted to only 4%, at most, of the intrinsic values of $\Delta H_{\text{pp}}^{\text{G}}$ and fall within the uncertainty of $\Delta H_{\text{pp}}^{\text{G}}$.

Fits of the CWS were performed with the Levenberg–Marquardt algorithm using Kaleidagraph (2457 Perkiomen Ave, Reading, PA 19606). The algorithm is accurate, efficient, and rapid provided that the estimates of the parameters are reasonably close to their final values. The values of the best-fit parameters are output with error estimates of the variables and the correlation coefficient, $r$ [34]. The fits shown in Figs. 1, 2, 3, 5, and 6 are performed and the fit curves plotted in considerably less than 1 s.

5 Results

5.1 The line shape of PADS

That the spectral lines of PADS are not Lorentzian was noted many years ago [8] by visually comparing them with those of the Gaussian and Lorentzian line shapes of equal $V_{\text{pp}}$ and $\Delta H_{\text{pp}}^{\text{obs}}$. Later [9], the departure from Lorentzian was tabulated. By fitting the spectra to a Voigt, the departure from a Lorentzian may be quantified, and using all of the spectral points the precision may be improved by an order of magnitude or much more in case of noisy spectra. For a dramatic demonstration of this point, see Fig. 11 of Ref. [35].

Figure 4a shows that $\Delta H_{\text{pp}}^{\text{G}}$ is a constant as a function of the PADS concentration, for all three lines, which is presented because there was a report [8] that the lines became increasingly Gaussian with decreasing concentration. Figure 4a shows no significant variation for concentrations down to 1.2 × 10⁻⁵ M, a factor of 79 lower than 95 × 10⁻⁵ M used in the previous paper [8]. Figure 4b shows that $\Delta H_{\text{pp}}^{\text{G}}$ is also constant with respect to $\sqrt P$. This result is important because it shows that saturation only affects the Lorentzian component of the Voigt.

Fig. 4

a Mean values and sd (error bars) of $\Delta H_{\text{pp}}^{\text{G}}$ averaged over 20 values of $\sqrt P$ for each of the three lines in the spectra versus PADS concentration. The mean value of $\Delta H_{\text{pp}}^{\text{G}}$ over the 480 measurements, placed near the origin for clarity, is shown by the solid square. b$\Delta H_{\text{pp}}^{\text{G}}$ vs. $\sqrt P$ for the same series. These data are from the heat quench experiment with an Air sample. Further data are given in Table 9

This work has not clarified the origin of the inhomogeneous broadening; however, there was a suggestion that it arose from hyperfine coupling with K⁺ ions during ion pairing [36]. We may rule out magnetic field inhomogeneity because faithful Lorentzian shapes of other free radicals were observed with the same magnet used to observe the non-Lorentzian shape of PADS [9]. Modulation sidebands may be ruled out because $\Delta H_{\text{pp}}^{\text{G}}$ is the same for $f_{m}$ = 100- and 10-kHz in this study.

5.2 Demonstration of the Protocol. Calibration of $K_{{ 1 {\text{M}}}}$ for the Kazan EPR Spectrometer

For one of the standard samples, Figs. 5, 6, 7 show typical CWS of $V_{\text{pp}}$, $I$, and $\Delta H_{\text{pp}}^{\text{L}}$, respectively. The lines in Fig. 7 are fits to Eq. (9) with fixed $T_{1}$ = 0.33 μs to obtain values of $K_{{1\Delta H_{\text{pp}}^{\text{L}} }}$ and $\Delta H_{\text{pp}}^{\text{L}} \left( 0 \right)$. The lines in Figs. 5 and 6 are fits to Eqs. (10) and (11), respectively, fixing $T_{1}$ = 0.33 μs and $T_{2} = 2/\left[ {\sqrt 3 \gamma \Delta H_{\text{pp}}^{\text{L}} (0)} \right]$, to find $K_{{1V_{\text{pp}} }}$ and $K_{\text{pp}}$ in Fig. 5 and $K_{{1{\text{I}}}}$ and $K_{\text{I}}$ in Fig. 6. The fit parameters for this sample are given in Tables 2, 3, and 4. The low-, center-, and high-field lines are denoted, lf, cf, and hf, respectively. The linear fits in the linear region, shown in the insets to Figs. 5 and 6, are precise for both $V_{\text{pp}}$ and $I$ as shown by the values of $r$ given in the respective captions, attesting to the remarkable linearity of $\sqrt P$ in the Bruker hardware and the precision obtained by least-squares fitting of the spectra. The values of $V_{\text{pp}}$, Fig. 6, for hf are slightly smaller than for cf and lf which are equal to one another, because $\Delta H_{\text{pp}}^{\text{L}}$ for hf is larger, Fig. 7 and Table 4; however, the values of $I$ in Fig. 6 are the same as expected.

Fig. 5

Main plot: CWS of $V_{\text{pp}}$ of the standard sample: lf, circles; cf, squares; and hf, diamonds. The lines are least-squares fits to Eq. (10) with parameters in Table 2. The arrow demarks the stable fitting range of $\sqrt P$. Inset: linear region where straight lines fit the data with $r$ = 0.99996, 0.99989, 0.99983

Fig. 6

Main plot: CWS of $I$ of the standard sample; symbols are the same as in Fig. 5. The lines are least-squares fits to Eq. (11) with parameters in Table 3. Inset: linear region where straight lines fit the data with $r$ = 0.9996, 0.9992, 0.9996

Fig. 7

Saturation of $\Delta H_{\text{pp}}^{\text{L}}$, the Lorentzian component of the Voigt line shape. Symbols are the same as in Fig. 5. The lines are least-squares fits to Eq. (9) with parameters in Table 4. What appears to be a single line is the overlay of two lines fit to lf and cf

Table 2 Fit parameters and fit errors for $V_{\text{pp}}$, Fig. 5

Table 3 Fit parameters and fit errors for doubly integrated intensity, $I$, Fig. 6

Table 4 Fit parameters and fit errors for $\Delta H_{\text{pp}}^{\text{L}}$, Fig. 7

The procedure for Sample 1 was repeated with 7 others from two stock solutions measured at different times. One of the samples was stored in the refrigerator for 1 month before being measured again. The mean values and standard deviation (sd) of 24 measurements (3 lines, 8 CWS) are $K_{{1{\text{I}}}}$ = 0.820 ± 0.025, $K_{{1\Delta H_{\text{pp}}^{\text{L}} }}$ = 1.02 ± 0.023, and $K_{{1V_{\text{pp}} }}$ = 0.905 ± 0.009. Note that the precision of $K_{{1V_{\text{pp}} }}$ is nearly three times that of the other two. The correct value of the effective $K_{1}$ is given by $K_{{ 1 {\text{I}}}}$. Therefore, if we wish to use the other modes to find the effective value of $H_{1}$, we must multiply the fits value of $K_{{1V_{\text{pp}} }}$ by $\zeta_{{V_{\text{pp}} }} = K_{{1{\text{I}}}} /K_{{1V_{\text{pp}} }}$ = (0.820 ± 0.025)/(0.905 ± 0.009) = 0.906 ± 0.029 and to use $\Delta H_{\text{pp}}^{\text{L}}$, multiply $K_{{\Delta H_{\text{pp}}^{\text{L}} }}$ by $\zeta_{{\Delta H_{\text{pp}}^{\text{L}} }} = K_{{ 1 {\text{I}}}} /K_{{1\Delta H_{\text{pp}}^{\text{L}} }}$ = (0.820 ± 0.025)/(1.02 ± 0.023) = 0.804 ± 0.030. For the Voigt line shape of the standard sample of PADS, we may find $H_{1}$ from the correction factors $\zeta_{\text{M}}$ as follows:

$$H_{1} = \zeta_{\text{M}} K_{{1{\text{M}}}} \sqrt P$$

(14)

Which are summarized in Table 5 together with the results for a Lorentzian line-sample.

Table 5 Values of $\zeta_{\text{M}}$ for $H_{1} = \zeta_{\text{M}} K_{{ 1 {\text{M}}}} \sqrt P$

Values in the penultimate column of Table 5 pertain to the standard samples taking into account the Voigt shape of PADS. For other samples of PADS as functions of concentration, oxygen concentration, and temperatures other than those of the standard sample, only the mode $I$ is applicable because the line shapes change with all three variables.

5.3 Value of $\varGamma$ Kazan EPR

The mean value and sd of $Q$ = (1.86 ± 0.11) × 10³ was obtained from four samples, each removed and replaced in the cavity twice, for a total of 8 measurements. From Eq. (1), with $Q^{1/2}$ = 43.1 ± 1.2, we compute $\varGamma$ = 0.0190 ± 0.0008 G/W^1/2 for the Kazan EPR.

5.4 Representative values of $T_{1}$ for PADS

With the value of $K_{1} = K_{{ 1 {\text{I}}}}$ calibrated for the Kazan EPR spectrometer, we briefly explore the dependence of $T_{1}$ and $T_{2}$ on temperature; oxygen concentration; modulation amplitude and frequency; and PADS concentration. In all that follows, the mode $I$ is used to determine $T_{1}$ and the mode $\Delta H_{\text{pp}}^{\text{L}}$ for $T_{2}$.

5.5 Dependence on modulation frequency and amplitude

Table 6 tabulates $T_{1}$ and $T_{2}$ for different combinations of $f_{\text{m}}$ and $a_{\text{m}}$ for a standard sample, showing that there is no significant difference for any of the combinations.

Table 6 Dependence of $T_{1}$ and $T_{2}$ on modulation amplitude and frequency

For the simple theory of Eqs. (2) (3) and (5) to apply, the thermal equilibrium of the spins within a spin packet must be maintained during the magnet-field sweep through resonance, a condition known as slow passage [1]. When the field is modulated, this condition is met as follows: [1]

$$\frac{{H_{1} }}{{2\pi a_{\text{m}} f_{\text{m}} }} \gg \sqrt {T_{1} T_{2} }$$

(15)

For PADS, $s$ is significantly different from unity when $H_{1} \approx$ 0.05 G, thus for values of $a_{\text{m}}$ and $f_{\text{m}}$ in Table 6, the LHS of Eq. (15) varies from 0.8 to 8 μs while the RHS is about 0.3 μs. Therefore, slow passage is expected to be fulfilled for all four of the modulation combinations and the fact that the values of $T_{1}$ are consistent over these combinations confirms this expectation. In Tables 6 and 8, the values of $T_{2}$ are mean values over the three lines, ignoring the small differences, that are shown explicitly in Tables 4 and 7.

Table 7 Dependence of T₁ and T₂ on temperature and oxygen concentration

5.6 Dependence on temperature and oxygen concentration

The results for $T_{1}$ and $T_{2}$ are given in Table 7. $T_{2}$ for lf and cf are within experimental uncertainty and are averaged. $T_{1}$ are averaged over the three lines. Uncertainties are the average fit errors and sd added in quadrature. Both $T_{1}$ and $T_{2}$ decrease with increasing oxygen concentration and with increasing temperature.

5.7 Dependence on the PADS concentration

One of the Argon samples and one of the Air samples were studied at 298 K at different PADS concentrations by heat quenching at 340 K for short time intervals to thermally degrade the PADS [32]. The samples were not disturbed during the process. This is a strategy similar to that utilized in Ref. [32]. The total quench time and values of $T_{1}$ and $T_{2}$ are given in Tables 8 and 9. In the absence of oxygen, the concentration is reduced by about 60% at 80 min of quenching, while with an Air sample, it is reduced by about 77%; thus, PADS is somewhat more stable at 340 K in the absence of oxygen. For PADS concentrations higher than those in Table 8, see Table 1 of Ref. [3].

Table 8 $T_{1}$ and $T_{2}$ at 298 K vs PADS concentration. Argon Sample

Table 9 $T_{1}$ and $T_{2}$ at 298 K vs PADS concentration. Air sample

5.8 Dependence on the microwave power range

The parameters from a least-squares fit can depend on the fit window [26]. Therefore, it is important to document the dependence of $K_{1}$ on the fit range. Taking as an example, the CWS in Fig. 5, we fit the same curve over different ranges to different maximum values of $\sqrt P$ yielding the results tabulated in Table 10. The percent discrepancy is given in the third column, showing that an accurate calibration is effected using any range up to one of the five maximum values of $\sqrt P$ in Fig. 5, demarked by the arrow. Because values of $K_{{1V_{\text{pp}} }}$ are expected to vary with the setup, these power ranges are only a guideline; however, this range is for $s$ from 0.45 to 0.83, independent of $K_{{1V_{\text{pp}} }}$. Because the fit range is robust, one may be guided by the appearance of the CWS and fit to several maximum powers near the CWS peak to confirm the invariance of the results.

Table 10 Dependence of $K_{{1V_{\text{pp}} }}$ on power range of the CWS^a

6 Discussion

6.1 Protocol to calibrate $H_{1}$ using parameters derived from the Voigt shape of PADS

Any mode of CWS may be used, employing the final column of Table 5; however, we recommend the mode $V_{\text{pp}}$ which is straightforward to measure and is more precise than either $\Delta H_{\text{pp}}^{\text{L}}$ or $I$. Thus, the CWS of $V_{\text{pp}}$ is fit to Eq. (10) with $T_{1}$ = 0.33 μs to find $K_{{1V_{\text{pp}} }}$ and the resulting value of $H_{1}$ is computed from Eq. (14) with $\zeta_{{V_{\text{pp}} }}$ = 0.906 ± 0.029. The uncertainty in $K_{{1V_{\text{pp}} }}$, including that due to the fit window, Table 10, is about 1.5%. Adding this to the 3.2% uncertainty for $\zeta_{{V_{\text{pp}} }}$ in quadrature gives about 3.5%. Therefore, $H_{1}$ may be determined with a precision of about 3.5% for a given value of Q.

6.2 Protocol to calibrate $H_{1}$ using parameters measured directly from the spectrum of PADS

We routinely fit all nitroxide spectra to a Voigt, check to see if it is an excellent fit using the criterion that the maximum residual between the fit and the spectrum be less than 1% of $V_{\text{pp}}$. For example, see Fig. 20 of Ref. [18]. Therefore, for us, it is just as easy to measure and compute $V_{\text{pp}}$, $\Delta H_{\text{pp}}^{\text{L}}$, $F$, and $I$ as it is to measure $\Delta H_{\text{pp}}^{\text{obs}}$ and $V_{\text{pp}}$. Nevertheless, we recognize that many, maybe most labs are not set up to do that and wish to calibrate $H_{1}$. With that in mind, we fit the CWS of $V_{\text{pp}}$ to Eq. (10) to obtain $K_{{1V_{\text{pp}} }}^{*}$ using $\Delta H_{\text{pp}}^{\text{obs}} \left( 0 \right)$ rather than $\Delta H_{\text{pp}}^{\text{L}} \left( 0 \right)$, where the asterisk denotes using the former rather than the latter. The ratio $K_{{1V_{\text{pp}} }}^{*} /K_{{1V_{\text{pp}} }}$ = 1.07 ± 0.02; therefore, the corrected values of $K_{{1V_{\text{pp}} }}$ = $K_{{1V_{\text{pp}} }}^{*} /(1.07 \pm 0.02)$. Thus, the CWS of $V_{\text{pp}}$ is fit to Eq. (10) with $T_{1}$ = 0.33 μs to find $K_{{1V_{\text{pp}} }}^{*}$ and the effective value of $H_{1}$ is computed from Eq. (14) with $\zeta *_{{V_{\text{pp}} }}$ = 0.847 ± 0.031, given in the final row of Table 5. The precision will depend on the errors in obtaining $\Delta H_{\text{pp}}^{\text{obs}}$ and $V_{\text{pp}}$ which must be estimated in each case.

We reiterate that to find reliable values of $T_{1}$ for other radicals the mode $I$ must be used. Indeed, we are able to use $V_{\text{pp}}$ to calibrate $H_{1}$ for PADS because its line shape does not differ radically from the Lorentzian allowing the use of the Lorentzian CWS to fit the results. For Voigt shapes with larger values of $\chi$ the CWS of $V_{\text{pp}}$ does not remotely conform to the Lorentzian CWS as can be appreciated by examining, for example, the results of Portis [23] where the CWS reaches a plateau and does not decrease or Castner [24], where it does reach a maximum but decreases more slowly than the Lorentzian. For further insight into problems associated with the saturation of inhomogeneously broadened lines, see also, Ref. [37].

We have proposed that the standard sample be measured at 298 K; however, there may be setups without temperature control. For those, a measurement of $T$ will permit a corrected value of $T_{1}$ to use in the calibration by interpolation in Table 7. We have proposed using air-saturated samples; however, deoxygenated samples could be used employing $T_{1}$ = 0.475 ± 0.019 μs for the Argon sample (Table 8) in Eqs. (9–11) to fit the CWS.

6.3 Update the Results

In the event that a more accurate value of $T_{1}$ becomes available, the results in this paper may be scaled by recognizing that the same value of $s$ is obtained for $T_{{1{\text{adj}}}} K_{{1{\text{adj}}}}^{2}$ = 0.33 μs $K_{1}^{2}$, where $T_{{1{\text{adj}}}}$ and $K_{{1{\text{adj}}}}^{{}}$ are the new, more accurate values and $K_{1}$ is the previously calibrated value; therefore

$$K_{{1{\text{adj}}}} = \sqrt {\frac{{0.33\mu {\text{s}}}}{{T_{{1{\text{adj}}}} }}} K_{1}$$

(16)

We have presented values of $T_{1}$ and $T_{2}$ as functions of several parameters. It is beyond the scope of this paper to discuss these results in detail; however, we do note that they decrease as a function of increasing oxygen and/or increasing PADS concentration, as expected, Tables 7, 8, 9. They also decrease with increasing $T$ for these rather low PADS concentrations. Under all conditions, $T_{1}$ > $T_{2}$.

6.4 CWS to increase precision

A benefit to CWS studies is an increased precision of parameters pertinent to the unsaturated region. Typically, one runs a saturation curve on a sample with a selected set of parameters; $T$, solvent, concentration, etc., and then picks a prudent value of $P$ to avoid saturation [31]. Then the experiment is run at that power, but considerable information is lost by not running a CWS. Using Fig. 5 to illustrate, perhaps a worker would select $\sqrt P$ = 0.02 G^1/2 as the prudent value. Then, to measure $\Delta H_{\text{pp}}^{\text{L}}$, for example, looking at Fig. 7, we see that the results are quite noisy, so much so that the difference between the three lines is not significant although from the 3rd column of Table 3, we see that the difference in $\Delta H_{\text{pp}}^{\text{L}}$ between hf versus the other two is small, but significant. Fitting a CWS not only increases the statistics but also profits from the increased SNR at higher powers. To improve the precision at a single value of $P$ one could measure the spectrum $N$ times gaining a factor $N^{1/2}$ in the precision [34], but all at the same SNR; thus, the gain in precision for the same acquisition time is less. Similar remarks apply to the slope of $V_{\text{pp}}$, $K_{\text{pp}}$, and the slope of $I$, $K_{\rm I}$. See the insets to Figs. 5 and 6. Thus, to compare the relative concentrations of radicals in two solutions, one may use all of the points to obtain $K_{\rm I}$ instead of the usual method of comparing them at one power for each sample. A similar use of CWS was employed by Eaton and co-workers to get better values of proton hyperfine coupling constants [28].

7 Conclusions

We have proposed and demonstrated a protocol to calibrate the effective value of $H_{1}$ by measuring and fitting the CWS of a standard sample of PADS. The demonstration was for the case of a line-sample extending all of the way through a TE₁₀₂ cavity with a particular configuration of the sample and temperature control glassware, so for changes in any of these, a new calibration would be necessary. For this demonstration, the calibration would permit the measurement of $T_{1}$ to a precision of about 3.5% if the sample of interest is in aqueous solution and careful sample placement ensures reproducible values of $Q$. For other solvents, measurements of $Q$ are necessary and, using our results as a guide, the uncertainty in $\sqrt Q$, 2.8%, adding in quadrature to the 3.5%, would increase the uncertainty to about 5%. Note that this estimate includes only random errors in the measurement of $Q$. These uncertainties are estimated from the fitting errors in the least-squares fits and the sd of repeated measurements. They do not include the uncertainty in the supposed value of $T_{1}$ = 0.33 μS. If a more accurate value of $T_{1}$ for the standard sample were to become available, Eq. (16) would allow corrected values of past measurements to be obtained.