The Dobryakov–Lebedev Relation Extended to Partially Resolved EPR Spectra

Abstract

The Dobryakov–Lebedev relation (Sov Phys Doklady 13:873, 1969), which relates the line width of the first-derivative of a Gaussian–Lorentzian convolution to the line widths of its Gaussian and Lorentzian components for an unresolved EPR line, is extended to resolved lines. Applying this extension to nitroxide-free radicals in solutions of low-viscosity solvents offers an opportunity to study interactions of the spins with the microwave field and spin–spin interactions previously inaccessible except by tedious numerical methods.

1 Introduction

Spectral lines complicated by inhomogeneous broadening (IHB) by various factors in several branches of experimental physics have been studied for many years and their study still is an active field. See [1] and references therein. Lifetime broadening effects, approximated by the Lorentzian profile ($L$), are often of direct interest, while the IHB is often approximated by a Gaussian profile ($G$). Appeals to the convolution between L and G, the Voigt ($V$) [2, 3], are abundant in the literature [1]. The convolution offers a method to separate L and G, to study each separately. While $V$ is a justifiable approximation to simulated or experimental spectra, it is computationally expensive; for each point in the line, the convolution integral must be calculated and repeated until a satisfactory match between the experiment and fit may be found [4]. It is not surprising, therefore, that there has been a chronic and continuing interest in developing rapid, accurate methods to approximate $V$. See [1], and references therein. See Table 1 for a list of definitions, abbreviations, and acronyms.

Table 1 Definitions, abbreviations, notes, and acronyms

In EPR studies of nitroxide free radicals (nitroxides), the weighted sum of $G$ and $L$, the SumF, Eq. (2) below, has proved to be an excellent approximation to experiment line shapes [5, 6]. Both $V$ and SumF provide exact descriptions of the line in both extremes, $L$ or $G$, and differ from each other by less than 0.7%. Keeping in mind that both $V$ and SumF are approximations, there are some reasons to prefer SumF to $V$ for reasons as described in Sect. 4.3.

In this paper, we restrict ourselves to nitroxide-free radicals executing rapid tumbling and translation in solution; however, nitroxides tumbling in solids can show motionally narrowed spectra similar to these presented here; e.g., Ref. [7]. Color centers in solids [8] and trapped electrons in glasses [9] are also amenable to study with the $\mathrm{DL}$. Furthermore, the methods developed here might find use in other organic-free radicals whose spectra are IHB. All nitroxides, except Fremy’s salt, are IHB and the vast majority of the spectra in the nitroxide literature are unresolved [4]. Therefore, in most cases, deconvolution of $V$ is routine [4]. This contribution addresses the few, but important cases in which the spectra are partially resolved. In practice only protonated nitroxides show resolution.

We present experimental data derived from the nitroxide 4-hydroxy-2,2,6,6-tetramethylpiperidine-1-oxyl (Tempol). To refer to per-deuterated Tempol, which we do not investigate here, we use the acronym d-Tempol and for the ¹⁵N-enriched versions, we use ¹⁵N Tempol or ¹⁵N d-Tempol. We present theoretical results from a model nitroxide with hyperfine coupling to 12 equivalent protons which we call Tempone.

For readers who are not experts in EPR studies of nitroxides, please see the series edited by Berliner [10,11,12] and a recent textbook [13].

2 Theory

In modern EPR, because magnetic-field modulation followed by phase-sensitive detection is used to increase the signal-to-noise ratio [14], the spectra are almost always presented as first-derivatives as they are in this paper. In a first-derivative spectrum, defining the peak-to-peak line widths of $G$ and $L$ as $\Delta {H}_{\mathrm{pp}}^{G}$ and $\Delta {H}_{\mathrm{pp}}^{L}$, respectively, we define the $V$-parameter as follows:

$$\chi =\frac{{\Delta H}_{\mathrm{pp}}^{G}}{{\Delta H}_{\mathrm{pp}}^{L}} .$$

(1)

The shape of $V$ is uniquely defined by $\chi$ [4].

EPR is one of the many fields that have benefited from evaluating $V$ by approximate methods. In common with other fields, its unresolved spectral lines may be modeled to high precision by a sum of $L$ and $G$, denoted by $\mathrm{SumF}$, Eq. (2) [5, 6]:

$$\mathrm{SumF}=I\left[\eta L+\left(1-\eta \right)G\right],$$

(2)

where, $\eta$, the mixing coefficient gives the fraction of the doubly integrated intensity, $I$, due to $L$. SumF makes no physical sense it is just a convenient, accurate fit function. The two functions are given as follows:

$$L=\frac{-8\sqrt{3}}{\pi {\left(\Delta {H}_{\mathrm{pp}}^{0}\right)}^{2}}\frac{\xi }{{\left(3+{\xi }^{2}\right)}^{2}},$$

(3)

$$G=\frac{-4}{\sqrt{2\pi }{\left(\Delta {H}_{\mathrm{pp}}^{0}\right)}^{2}}\xi {e}^{-{\xi }^{2}/2},$$

(4)

where $\Delta {H}_{\mathrm{pp}}^{0}$, common to both $G$ and $L$, is the peak-to-peak line width of the IHB line and:

$$\xi =2\frac{H-{H}_{0}}{\Delta {H}_{\mathrm{pp}}^{0}},$$

(5)

where $H$ is the swept magnetic field and ${H}_{0}$ is the resonance field of one of the three (two) nitrogen hyperfine lines due to ¹⁴N (¹⁵N) nitroxides. We use the term “line” to mean one of these nitrogen hyperfine lines. The term “proton lines” refers to resolved or unresolved proton hyperfine lines.

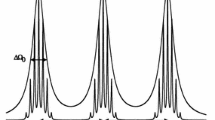
Figure 1 shows such an IHB line defining $\Delta {H}_{\mathrm{pp}}^{0}$ and ${V}_{\mathrm{pp}}$, the peak-to-peak height. ${V}_{\mathrm{pp}}$ may be found by observing that at $\xi =1$, $\mathrm{SumF}$ = ${V}_{\mathrm{pp}}$/2. Evaluating the constants, we find:

Fig. 1

a Simulated total spectrum, the superposition of 13 Lorentzian proton hyperfine lines of binomial intensity, of which only 9 are perceptible on this scale. Parameters of the simulation: ${a}_{1}$ = 0.400 G and ${N}_{1}$ = 12. $\Delta {H}_{\mathrm{pp}}^{L}$ = 0.72 G displayed with a magnetic field sweep-range of 10.00 G. $\Delta {H}_{\mathrm{pp}}^{G}$ = 1.44 G is found from Eq. (8), thus $\chi$ = 1.44 G/0.720 G = 2.00 b The residual, defined to be the spectrum minus the fit, amplified by a factor of 10, shows broad lines with overlying narrower lines in the center. c The residual for a simulation (not shown) with the same pattern but $\Delta {H}_{\mathrm{pp}}^{L}$ = 0.98 G, $\chi$ = 1.465 amplified by a factor of 10, shows broad lines and no overlying narrower lines. The measurable parameters from the fit, $\Delta {H}_{\mathrm{pp}}^{0}$ and ${V}_{\mathrm{pp}}$, are defined. The DL predicts $\Delta {H}_{\mathrm{pp}}^{0}$ = 1.844 G, while the fit yields 1.842 ± 0.001 G. The true $\Delta {H}_{\mathrm{pp}}^{0}$ = 1.864 G

$${V}_{\mathrm{pp}}=\frac{I}{{\left(\Delta {H}_{\mathrm{pp}}^{0}\right)}^{2}}\left[1.936-1.384\eta \right].$$

(6)

Equations (2)–(6) refer to each of the three (two) lines of an EPR spectrum. In this paper, we restrict our development to ¹⁴N nitroxides at low values of the concentration, $C$. This implies that the lines overlap negligibly and spin–spin interactions that yield spin–spin induced dispersion lines [15] are small. Furthermore, we limit our theory and experimental results to small values of ${H}_{1}$, the amplitude of circularly polarized magnetic induction of the microwave field, so that saturation effects are small. Our software, Lowfit, to analyze IHB includes line overlap explicitly and dispersion terms so that future work is not limited to low $C$ and ${H}_{1}$. See Ref. [16] for details.

In one important aspect, EPR is quite different from other fields. In practice, with modern spectrometers, $\Delta {H}_{\mathrm{pp}}^{G}$, is dominated by (a) magnetic field modulation and (b) hyperfine structure. For (a), see Ref. [17] where a simple expression is developed to express $\Delta {H}_{\mathrm{pp}}^{G}$ induced by field modulation. For alternative treatments, see Refs. [18] and [19].

For (b), accurately known proton hyperfine coupling constants, ${a}_{j}$, perhaps corrected for slight solvent and temperature dependences, are used to construct hyperfine patterns of “sticks’ upon which L are imposed as described in Ref. [4]. For these patterns, and others complicated by hyperfine coupling with magnetic nuclei other than protons, $\Delta {H}_{\mathrm{pp}}^{G}$ is twice the square-root of the second moment [4] computed from the following:

$$\Delta {H}_{\mathrm{pp}}^{G}=2\sqrt{\sum \alpha {I}_{j}\left({I}_{j}+1\right){N}_{j}{a}_{j}^{2}/3},$$

(7)

where ${a}_{j}$ is the hyperfine coupling constant for the jth set of ${N}_{j}$ equivalent nuclei of nuclear spin ${I}_{j}$ and $\alpha$ is a constant, near unity, to account for the small difference between the hyperfine pattern and $G$ [4]. For most nitroxides, the only important nuclei are protons and deuterons. Here, we are considering only protons, thus:

$$\Delta {H}_{\mathrm{pp}}^{G}=\sqrt{\sum \alpha {N}_{j}{a}_{j}^{2}}.$$

(8)

The task of extracting ${\Delta H}_{\mathrm{pp}}^{L}$ from the larger ${\Delta H}_{\mathrm{pp}}^{0}$ for nitroxides undergoing rapid tumbling in fluids was rendered routine 32 years ago for most spin probes in most experiments. Unlike some other fields, in EPR we require only about 2.5 digits of accuracy, modest compared with higher accuracies needed in other fields [1].

In employing SumF, confusion may arise because of the use of the words “Gaussian” and “Lorentzian” in two entirely different contexts. First, they are used to form the fit function SumF, where the line width of both is the overall width $\Delta {H}_{\mathrm{pp}}^{0}$. Second, they are used to describe the widths of the two components of $V$ where the widths are $\Delta {H}_{\mathrm{pp}}^{G}$ and $\Delta {H}_{\mathrm{pp}}^{L}$, respectively. In the first context, the functions are used to define the line shape but are not meaningful physically.

In summary, $\Delta {H}_{\mathrm{pp}}^{G}$ may be calculated from known values of ${a}_{j}$ [4] and the measured value of the amplitude of the field modulation [17].

Although not strictly required, the simple analytical relationship between the line widths discovered by Dobryakov and Lebedev [20] has facilitated investigations tremendously over the last 32 years [13, 21]. For a discussion of why this is so, see Ref. [4]. Curiously, the simplicity of the Dobryakov–Lebedev relation (DL) [20], Eq. (9), is fortuitous because they measured first-derivative spectra and formulated the DL in terms of the equivalent of $\Delta {H}_{\mathrm{pp}}^{L}$ and $\Delta {H}_{\mathrm{pp}}^{G}$. For the non-derivative presentation or higher harmonics of the field modulation, DL is more complicated [6, 22]. It has been 52 years since the publication in English of the, DL [20], and its utility continues unabated to this day [1]:

$${\left(\frac{\Delta {H}_{\mathrm{pp}}^{G}}{\Delta {H}_{\mathrm{pp}}^{0}}\right)}^{2}+\left(\frac{\Delta {H}_{\mathrm{pp}}^{L}}{\Delta {H}_{\mathrm{pp}}^{0}}\right)=1.$$

(9)

2.1 Theoretical Nitroxide Spectra IHB by Protons

Figure 1a shows a simulation of one of three ¹⁴N lines for Tempone assuming no interactions between the spins. The pattern is defined by ${a}_{1}$ = 0.400 G and ${N}_{1}$ = 12 with the spectrum displayed on a magnetic field sweep of 10.00 G. Of the 13 proton lines of binomial intensity, only 9 are perceptible on this scale. At X-band, the spacing of the proton lines is negligibly different from 0.400 G. From Eq. (8), the input values yield $\Delta {H}_{\mathrm{pp}}^{G}$ = 1.44 G assuming $\sqrt{\alpha }$ = 1.04 [4]. Each $L$ proton line is assumed to have the same peak-to-peak width $\Delta {H}_{\mathrm{pp}}^{L}$ = 0.720 G; i.e., each has the same value of ${T}_{2}$. Although one might expect different values of ${\Delta H}_{\mathrm{pp}}^{L}$ would result for different proton lines due to anisotropic proton coupling tensors; the difference has been found to be small; for example, [23,24,25,26]. For examples of simulations compared with experimental lines, see, for example, Figs. 2 and 3 of [4]. Experimentally, in solution, the lack of interactions is traditionally assured by lowering $C$ until no further line width change may be measured. This is denoted $C\to 0$. From the input parameters, $\chi$ = 2.00 and from the DL, the predicted $\Delta {H}_{\mathrm{pp}}^{0}$ = 1.844 G. The fit to SumF yields $\eta$ = 0.59292 and $\Delta {H}_{\mathrm{pp}}^{0}$ = 1.842 ± 0.001 G, and direct measurement, 1.864 G.

Overlying the line in Fig. 1 is the fit to the SumF; however, the two are imperceptibly different on this scale. The residual, defined to be the spectrum minus the fit, amplified by a factor of 10, is displayed in Fig. 1b. At the lower end of the sweep, the residual is negative; i.e., the spectrum is less intense (more $G$) than the fit, in this case by 0.3%. The residual from another simulation with the same pattern, but $\Delta {H}_{\mathrm{pp}}^{L}$ = 0.98 G which results in $\chi$ = 1.465, appears in Fig. 1c. The residual in Fig. 1b is characterized by broad lines with overlying narrower lines in the central region, while, for the more $L$ spectrum, Fig. 1c, the broad lines persist, but the narrow lines do not. The narrow lines presage incipient resolution as $\chi$ increases and, as we shall see, begin to dominate the residual as $\chi$ increases. The ratio of maxima of the broad residual lines to ${V}_{\mathrm{pp}}$ are 0.3%, well within the criterion for an excellent fit [15]. Fitting the same spectrum to $V$ would yield almost the same results because the $V$ and the SumF differ by, at most, 0.7% [6]. The problem with this latter fit is, despite being an excellent fit, the value of $\chi$ = 2.58 is in error by 29%. From Eq. (9), we find $\Delta {H}_{\mathrm{pp}}^{L}$ = 0.590 G, rather than the input value of 0.72 G, an error of − 18%. For those who would prefer to fit IHB with $V$, excellent fits lead to large errors in $\Delta {H}_{\mathrm{pp}}^{L}$ above $\chi$ = 2 which would have to be corrected by some scheme for careful work. As we move to values of $\chi$ ~ 5, the errors incumbent with $V$ become worse. More discussion of this is given in Sect. 4.3.

2.2 Partially Resolved Nitroxide EPR Spectra

Figure 2 displays simulations of one of three ¹⁴N lines for Tempol with proton coupling constants ${a}_{1}$ = 0.460 G(6H), ${a}_{2}$ = 0.290 G(2H), ${a}_{3}$ = 0.430 G(2H), and ${a}_{4}$ = 0.063 G(2H), where the numbers of equivalent protons, ${N}_{j}$, are given in the parentheses [4, 27]. For the 4th set, ${a}_{4}$ = 0.063 G incorporates the small IHB due to one small coupling of 0.07 G and six of coupling 0.02 G, respectively [27]. From Eq. (8), $\Delta {H}_{\mathrm{pp}}^{G}$ = 1.400 G using the value of $\alpha$ = 1.08 [4]. In a $\Delta {H}_{\mathrm{pp}}^{L}$ = 0.1596 G and b 0.1141 G, yielding from Eq. (1) $\chi$ = 8.77 and $\chi$ = 12.2, respectively. Parameters defining the heights of the fits, the extremum values of the spectra and of the residual are indicated. Clearly, there is no way to apply the DL to these spectra: there is no $\Delta {H}_{\mathrm{pp}}^{0}$ and no clear way to study selected points on the spectra to approximate $\chi$ in the manner of [4]. Nevertheless, we have discovered that these resolved lines may be fit to SumF. These simulations also assume no interactions between the spins.

Fig. 2

Simulated spectra of one of three ¹⁴N lines for Tempol with proton coupling constants ${a}_{1}$ = 0.460 G(6H), ${a}_{2}$ = 0.290 G(2H), ${a}_{3}$ = 0.430 G(2H), and ${a}_{4}$ = 0.063 G(2H), where the numbers of equivalent protons are given in the parentheses. From Eq. (8), $\Delta {H}_{\mathrm{pp}}^{G}$ = 1.400 G using the known value of $\alpha$ = 1.08 [4] a $\Delta {H}_{\mathrm{pp}}^{L}$ = 0.1596 G and b 0.1141 G, yielding from Eq. (1) $\chi$ = 8.77 and $\chi$ = 12.2, respectively. The corresponding residuals are shown in c and d. The peak-to-peak line width of the fits are a 1.51 G and b 1.50 G, respectively, while the values of $\Delta {H}_{\mathrm{pp}}^{0}$ computed from the input values using the DL are a 1.47 G and b 1.46 G, respectively

Those fits to SumF are given by the solid lines through the spectra in Fig. 2a and b while c and d are the corresponding residuals. Let us define the peak-to-peak line width of the fit as $\Delta {H}_{\mathrm{pp}}^{\mathrm{fit}}$ (not labeled) and ask what relationship it has to the DL prediction of $\Delta {H}_{\mathrm{pp}}^{0}$? Following the procedure outlined for Tempone in the final paragraph of the previous section, we find that $\Delta {H}_{\mathrm{pp}}^{\mathrm{fit}}$ = a 1.51 G and b 1.50 G, respectively, while the DL values are a 1.47 G and b 1.46 G, respectively. The spectra presented in Fig. 2 were designed to emphasize the features of resolved lines; however, they are more resolved than the best resolved experimental spectrum in this study where the largest value of $\chi$ = 4.7 ± 0.2. They are also outside of the range of the Tempol map given in Fig. 3.

Fig. 3

Maps from the SumF mixing parameter, $\eta$, to the Voigt parameter, $\chi$. Dashed line Tempone and solid line, Tempol. Error bars from estimated uncertainties in fits to simulations. The largest values of $\chi$ in all of the experiments in this study are 4.7 ± 0.2

2.2.1 Maps for Unresolved and Resolved Nitroxide Spectra

By simulating a series of spectra at different values of $\chi$ and fitting them with the SumF, one generates a series of pairs of values of $\chi$ and $\eta$, i.e., the Tempol map. For unresolved spectra, this procedure reproduces the map that we have always used [4]. The same procedure produces the Tempone map where examples of spectra and fits are shown in Figs. 1 and 4a, below. These maps are displayed in Fig. 3, for Tempone, dashed line, and for Tempol, solid line. The error bars are the estimated errors from the fits in the usual manner [28]. The map for any nitroxide may be constructed in this manner that extends into the resolved region. ${V}_{\mathrm{fit}}$ may be taken equal to ${V}_{\mathrm{pp}}$ by assuring that its value yields the correct input value of $I$ which is easily done following the procedure in Sect. 8 of [4]. Briefly, $I=\frac{1}{2}F\left(\chi \right)\left({{\Delta H}_{\mathrm{pp}}^{0}}^{2}{V}_{\mathrm{pp}}\right)$; thus, $F\left(\chi \right)$ is formed to give the correct (input) value of $I$. This ability to extract $\chi$ and $F$ gives us access to all of the correction procedures in Ref. [4]. Note that the maps in Fig. 3 vary continuously across the transitions from unresolved to resolved lines. For Tempol, the average discrepancy between $\Delta {H}_{\mathrm{pp}}^{\mathrm{fit}}$ and $\Delta {H}_{\mathrm{pp}}^{0}$ is 17 mG or a percentage discrepancy of 1%.

Fig. 4

Simulated spectra, (Eq. (13) of [15]), of one of three ¹⁴N lines for Tempone with proton coupling constant ${a}_{p}$ = 0.0996 G (12H), ${\gamma T}_{1}^{-1}$ = 0.02300 and ${\gamma T}_{2}^{-1}$ = 0.0500 G a ${H}_{1}$ = 10^–4, b 0.0201, c, 0.0401, and d 0.0501 G. $C\to 0$. For ${H}_{1}$ = 10^–4 G, ${{\Delta H}_{\mathrm{pp}}^{L}\left(\mathrm{O}\right)}_{0}$ = 0.0577 G

The maps and values of $F$ are given in Tables 2 and 3. Although values of $\chi$ for Tempone are given to cover a range of resolved spectra, as far as we know, a resolved spectrum has not yet been observed.

Table 2 Tempol map

Table 3 Tempone map

Theoretically, we may generate the maps by varying the input values of ${\Delta H}_{\mathrm{pp}}^{L}$ or ${a}_{j}$ or both. The DL makes it trivial to simulate a series of spectra that all have the same value of ${\Delta H}_{\mathrm{pp}}^{0}$ which is convenient for some purposes. For example, we simulated the spectrum leading to Fig. 1c in one step, not having to simulate by trial and error. Any combination of these inputs yields the identical map.

2.2.2 Effect of Small Saturating Powers

Figure 4 shows some simulated results of applying saturating microwave power to one of three ¹⁴N lines for Tempone with proton coupling constant ${a}_{1}$ = 0.0996 G, ${N}_{1}$ = 12, ${\gamma T}_{1}^{-1}$ = 0.02300 and ${\gamma T}_{2}^{-1}$ = 0.0500 G a ${H}_{1}$ = 10^–4, b 0.0201, c, 0.0401, and d 0.0501 G. For ${H}_{1}$ = 10^–4, ${{\Delta H}_{\mathrm{pp}}^{L}\left(\mathrm{0}\right)}_{0}$ = 0.0577 G. These spectra were simulated using Eq. (13) of [15] in the absence of interactions. We observe that as ${\Delta H}_{\mathrm{pp}}^{L}$ increases and saturation sets in, the resolution becomes less as expected. Figure 4 was prepared with a rather small value of ${{\Delta H}_{\mathrm{pp}}^{L}\left(\mathrm{0}\right)}_{0}$ = 0.577 G so that the effects may be visualized. See Table 4 for details. Reminder: ${{\Delta H}_{\mathrm{pp}}^{L}\left(\mathrm{C}\right)}_{{H}_{1}}$ denotes the value of ${\Delta H}_{\mathrm{pp}}^{L}$ at $C\to 0$ measured at ${H}_{1}$. The value of $\alpha$ is nominal [4]; all of the values in Table 4 depend on the choice of that parameter. One minor problem with obtaining precision fitting to $V$ is that $\alpha$ is taken to be unity. Comparing the ${H}_{1}$ = 0.0001 G with the input values shows that differences in input versus output for the unsaturated spectrum are found only in the 3rd digit. $\Delta {H}_{\mathrm{pp}}^{G}$ is produced to 4 digits, although in practice it is only measurable to 2.5 digits. This demonstrates that line shifts with ${H}_{1}$, which would be reflected in the values of $\Delta {H}_{\mathrm{pp}}^{G}$, are negligible in the absence of spin diffusion. Note that ${\Delta H}_{\mathrm{pp}}^{0}$ increases by only 6% while ${\Delta H}_{\mathrm{pp}}^{L}$ increases by 78%. Errors are always inevitable in using changes in ${\Delta H}_{\mathrm{pp}}^{0}$ to estimate changes in ${\Delta H}_{\mathrm{pp}}^{L}$, even in deuterated nitroxides [16], but this illustrates that moving into the resolved regime exacerbates the problem.

Table 4 Variation of line widths and $V$-parameter with ${H}_{1}$, $C$ = 0

3 Experimental

3.1 Methods

The nitroxide spin probe 4-hydroxy-2,2,6,6-tetramethylpiperidine-1-oxyl (Tempol) was purchased from Molecular Probes, Inc. Decane (99+%, Batch # 10417HB) was purchased from Sigma Aldrich. All the chemicals were used as received. A 5.0-mM stock solution of Tempol was prepared by weight in decane which was then diluted to obtain 0.1- and 0.5-mM solutions. Samples were drawn into open-ended polytetrafluoroethylene (PTFE-ID: AWG21) tubing obtained from Zeus. The tubing was then folded in half, and the open ends were sealed with Seal-Ease plastic clay from Clay Adams, Inc. The tubing, folded end down, was then placed into a quartz tube made by Wilmad Glass Co, with a hole in the bottom. Finally, the quartz tube was inserted in the quartz dewar insert of a Bruker N₂ temperature controller, that is placed in the microwave cavity (ER 4119HS, TE₀₁₁) of a Buker EMXPlus EPR spectrometer. The microwave source was a 200-mW Gunn dual oscillator. In this arrangement, N₂ was used to control the sample temperature and displace the oxygen, reducing the line width [29]. The temperature of the samples was elevated to 45 °C to hasten the exchange of oxygen until no further line-width reduction was noted, typically requiring about an hour, before setting the temperature to the desired values. Field modulation was applied at 100 kHz with an amplitude of 0.1 G.

3.2 Preview of Some Possible Experimental Applications

The purpose of the following preliminary experimental measurements is twofold: (a) demonstrate that fitting real spectra to SumF leads to viable results that are in keeping with what is expected, and (b) provide insight into possible experimental programs. To simplify the discussion, we assume that DD is negligible. It makes no difference in our conclusions; however, in previous work with alkanes [30], we found negligible dipole–dipole coupling for d-Tempone in decane at − 20 °C. In the more viscous alkane, squalane, we found [31] that HSE dominates the spin–spin interactions for Tempone at $T/\eta$ = 24 K/cP, accounting for 96% of the broadening For Tempol in decane at − 27 °C, $T/\eta$ = 114 K/cP [30], a factor of ~ 5 larger, from which we may conclude that HSE dominates in the present experiment.

3.2.1 Varying the Temperature

Figure 5 shows spectra taken of 0.1 mM Tempol at − 27 and 32 °C. The upper traces display the spectra with fits (overlying dots every 20th point). The second traces show, on an expanded scale, the cf spectra and fits, while the third traces show the residuals. $\Delta {H}_{\mathrm{pp}}^{L}$ determined from the Tempol map, Table 3, are within experimental uncertainties for the three nitrogen lines. After averaging, $\Delta {H}_{\mathrm{pp}}^{L}$ = 0.270 ± 0.012 G at − 27 °C and 0.402 ± 0.002 G at 32 °C. The heights are displayed on the same scale, demonstrating that the residual forms a major part of the spectrum at − 27 °C and less so at 32 °C. Thus, at − 27 °C, ${V}_{\mathrm{res}}$ ~ 0.65 ${V}_{\mathrm{fit}}$ and ${V}_{\mathrm{fit}}$ ~ 0.65 ${V}_{\mathrm{spc}}$; at 32 °C, ${V}_{\mathrm{res}}$ ~ 0.13 ${V}_{\mathrm{fit}}$ and ${V}_{\mathrm{fit}}$ ~ ${V}_{\mathrm{spc}}$. In the past [16], we have proposed that the ratio ${V}_{\mathrm{res}}/{V}_{\mathrm{spc}}$ be less than 1% for a line to be considered a good $V$ in the case of unresolved lines. Obviously, for resolved lines, this criterion cannot apply, and the question of whether an experimental line in Fig. 5 is considered to be a good $V$ needs to be redefined. To reiterate our remarks in Sect. 2.2.2, ${\Delta H}_{\mathrm{pp}}^{L}$ increases by approximately 49% while that of ${\Delta H}_{\mathrm{pp}}^{0}$ decreases by 3% upon changing the temperature from − 27 to 32 °C.

Fig. 5

Experimental EPR spectra of 0.1 mM Tempol at a − 27 and b 32 °C at $\sqrt{P}$ = 0.025 W^1/2. Top traces, solid lines, spectra, overlying dots, fits, displaying every 20th point. Second traces, the cf spectra and fits, presented on an expanded magnetic sweep width. Third traces, residuals. The heights are displayed on the same scale

The changes in the spectra in Fig. 5 are mostly due to an increase in ${\Delta H}_{\mathrm{pp}}^{L}$ as the temperature increases; see Fig. 6. However, for this to be strictly true, $C$ would need to be small enough for HSE to be negligible and $\sqrt{P}$ would need to be small enough for the line broadening to be negligible or comparable at the two temperatures. Furthermore, both non-negligible values of HSE and or $\sqrt{P}$ provoke line shifts, the former is well known [32], the latter proposed theoretically but as yet unconfirmed experimentally [33]. These effects are likely to be quite small at $C$ = 0.1 mM and $\sqrt{P}$ = 0.025 W^1/2 but perhaps not negligible. More work is needed to quantify these effects, and as we move forward, we shall investigate if the residuals are more sensitive to them than are the spectra.

Fig. 6

Line widths vs temperature of 0.1 mM Tempol in n-decane. Circles, lf; diamonds, cf; and triangles, hf, taken at $\sqrt{P}$ = 0.025 W^1/2

Figure 6 displays the variation in the line widths as a function of temperature showing the dramatic difference in the directly measurable width, $\Delta {H}_{\mathrm{pp}}^{0}$, and the desired width $\Delta {H}_{\mathrm{pp}}^{L}$. The melting point of decane is − 29.7 °C [34]; therefore, the lowest data at − 32 °C are in the super-cooled region. Attempts to supercool to − 36 °C resulted in a frozen sample.

Not only is there a significant quantitative difference in $\Delta {H}_{\mathrm{pp}}^{0}$, and $\Delta {H}_{\mathrm{pp}}^{L}$, but also the qualitative behavior is different. While $\Delta {H}_{\mathrm{pp}}^{0}$ decreases slightly with temperature, $\Delta {H}_{\mathrm{pp}}^{L}$ increases slightly. Comparing Figs. 5 and 6, we notice that while $\Delta {H}_{\mathrm{pp}}^{0}$ and $\Delta {H}_{\mathrm{pp}}^{L}$ vary little, the residual varies significantly. Thanks to the DL, the width $\Delta {H}_{\mathrm{pp}}^{G}$ is trivially available so that is plotted in Fig. 6 as well. As expected, the major contribution to $\Delta {H}_{\mathrm{pp}}^{0}$ is provided by $\Delta {H}_{\mathrm{pp}}^{G}$. The modest decrease in $\Delta {H}_{\mathrm{pp}}^{G}$ and the modest increase in $\Delta {H}_{\mathrm{pp}}^{L}$, contrive to decrease $\chi$ significantly, from 4.7 ± 0.2 to 3.22 ± 0.01, a factor of ~ 1.5. Note that in Fig. 5, the decrease in ${V}_{\mathrm{res}}{/V}_{\mathrm{fit}}$ is considerable larger, by a factor of ~ 5.

These preliminary data were obtained at a constant $\sqrt{P}$ = 0.025 W^1/2. Significant improvement in the precision of these data would have been obtained by measuring a continuous-wave saturation curve (CWS) of $\Delta {H}_{\mathrm{pp}}^{L}$; i.e., by plotting $\Delta {H}_{\mathrm{pp}}^{L}$ against ${H}_{1}$. Finding the intercept of the CWS, by fitting the curve to Eq. (9) of [15], as suggested in Ref. [15] and illustrated in Fig. 9, below offers significant improvement in the precision of ${{\Delta H}_{\mathrm{pp}}^{L}\left(\mathrm{C}\right)}_{0}$.

3.2.2 Varying the Concentration: HSE

Figure 7 shows the effect of raising the concentration of Tempol from $C$ = 0.1 to 0.5 mM. It is well-known that HSE increases the linewidths which is expected to reduce the resolution; however, concentration-dependent measurements are considerably more interesting than that as discussed in depth recently [16]. Briefly, the less intense proton lines are broadened the most; the proton lines move toward one another; and intra line HSE introduces HSE-induced signals with the form of dispersion signals [16]. This produces an interesting situation where the shifts tend to reduce $\Delta {H}_{\mathrm{pp}}^{G}$ and therefore $\chi$ while the broadening increases ${\Delta H}_{\mathrm{pp}}^{L}$ also reducing $\chi$. By measuring the two CWS, shown in Fig. 9, and fitting them to Eq. (9) of [15], the intercepts yield the following values: ${{\Delta H}_{\mathrm{pp}}^{L}\left(0.1 \, \mathrm{mM}\right)}_{0}$ = 0.313 ± 0.006 G and ${{\Delta H}_{\mathrm{pp}}^{L}\left(0.5 \, \mathrm{mM}\right)}_{0}$ = 0.372 ± 0.001 G. These are mean values and standard deviations of two runs at each concentration. The change in the residual is less dramatic for increasing $C$, Fig. 7, than it is for increasing $T$, Fig. 5.

Fig. 7

Experimental EPR spectra of the cf of Tempol in n-decane at − 27 °C of a $C$ = 0.1 mM and b 0.5 mM. Top traces, spectra and fits. Lower traces, the residuals. Relative heights are on the same scale. $\sqrt{P}$ = 0.014 W^1/2

3.2.3 Varying the Microwave Power

Figure 8 shows the effect of applying saturating microwave power, $P$, to a sample of 0.1 mM Tempol in decane at − 27 °C. To get an idea of the difference in $\sqrt{P}$ = 0.025 and 0.014 W^1/2, compare Figs. 5a and 8a, especially the residuals.

Fig. 8

Experimental EPR spectra of the cl of 0.1 mM Tempol in n-decane at − 27 °C a $\sqrt{P}$ = 0.014 W^1/2 and b $\sqrt{P}$ = 0.159 W^1/2. Top traces, spectra and fits. Lower traces, the residuals

It is well-known that the proton lines broaden as microwave power saturation sets in Refs. [14, 15, 35]. Therefore, the decrease in resolution evident as $P$ is increased is expected; however, the situation is potentially considerably more interesting than that. Because HSE provides relaxation pathways to non-resonant lines [36], the effective relaxation rates of the proton line are expected to vary from one line to another. This has not been observed in nitroxides as yet; however, the reduction in the effective spin relaxation rate due to pathways between nitrogen lines was observed long ago [36]. Furthermore, a recent theory [33] predicts that the proton and the nitrogen lines shift as saturation sets in, an effect not yet observed experimentally.

Figure 9 shows CWS of ${\Delta H}_{\mathrm{pp}}^{L}$ for 0.1 and 0.5 mM Tempol. Each sample was measured twice, shown by triangles or circles; filled, 0.5 mM or open, 0.1 mM. The abscissa, $\sqrt{P}$, is proportional to ${H}_{1}$ [8, 14, 35, 37]. The solid lines are fits to Eq. (9) of Ref. [15] following a method proposed therein. There are four fit lines, two for each concentration, but the two for 0.5 mM are coincident on this scale and the two for 0.1 mM, nearly so. The experiments for Fig. 6 were collected for $C$ = 0.1 mM at a constant $\sqrt{P}$ =  0.025 W^1/2, where the 0.1 mM data (open circles) show considerable scatter both between the two runs and with respect to the fits to the CWS. From the fits, ${{\Delta H}_{\mathrm{pp}}^{L}\left(0.1 \, \mathrm{mM}\right)}_{0}$ = 0.314 ± 0.009 G for one run and 0.311 ± 0.007 G for the other. As an estimate of the intercept of the 0.1 mM sample, not using the CWS, we average the 14 points for both runs for $\sqrt{P}$ < 0.02 W^1/2 and obtain ${{\Delta H}_{\mathrm{pp}}^{L}\left(0.1 \, \mathrm{mM}\right)}_{0}$ = 0.322 ± 0.036 G for the mean and standard deviation. If we had measured just one point at $\sqrt{P}$ = 0.02 W^1/2 we would have obtained ${{\Delta H}_{\mathrm{pp}}^{L}\left(0.1 \, \mathrm{mM}\right)}_{0}$ = 0.278 with no better way to estimate the uncertainty than the difference between the two runs ± 0.002 G. The discrepancy between the measurement of one point versus either the intercept of the fit or averaging 14 points is about 13%. For the higher concentration, ${{\Delta H}_{\mathrm{pp}}^{L}\left(0.5 \, \mathrm{mM}\right)}_{0}$ = 0.372 ± 0.001 G. Figure 9 is included, even though treatment of the CWS to obtain values of ${T}_{1}$ is beyond the scope of this paper, because it illustrates dramatically the advantage of obtaining a CWS even though one is only interested in the intercept.

Fig. 9

Experimental saturation broadening of ${\Delta H}_{\mathrm{pp}}^{L}$ of the cf of Tempol at − 27 °C. The open circles and triangles are two runs of 0.1 mM and the closed circles and triangles are two of 0.5 mM. The four solid lines are fits to Eq. (9) of [15]. The two for 0.5 mM are indistinguishable on this scale and the two for 0.1 mM are nearly so; this latter despite significant scatter at low powers

Our intention with Fig. 9 was to illustrate the advantage of measuring CWS, and leave it there. However, we find it quite interesting that the fits to the two concentrations in Fig. 9 are practically parallel; i.e., the shapes of the CWS are similar. Indeed, the fits also yield a quantity proportional to the product ${T}_{1}{T}_{2}$ [15, 35]. From the fits, ${T}_{1}{T}_{2}$ $\propto$ 15.8 ± 1.5 and 15.4 ± 1.9 for the two runs of 0.1 mM and 15.6 ± 0.5 and 15.8 ± 0.4 for the two at 0.5 mM. The magnitudes of these products depend on the proportionality constant between $\sqrt{P}$ and ${H}_{1}$ [15], so their absolute values are not available absent that calibration. However, the interesting (shocking!) thing is that all four values are equal, well within the estimates of the uncertainties. Qualitatively, we can see that because ${T}_{1}{T}_{2}$ is the same for both concentrations and ${T}_{2}$ is larger for 0.1 mM (smaller ${{\Delta H}_{\mathrm{pp}}^{L}(C)}_{0}$), ${T}_{1}$ is smaller for 0.1 mM. In other words, saturation sets in at lower values of $\sqrt{P}$ for the lower concentration as expected.

4 Discussion

4.1 Analyzing Spectra with Resolved Proton Hyperfine Structure

We have shown that an experimental partially resolved line may be analyzed in the same manner as an unresolved IHB line as detailed in Ref. [4]. A fit of the spectrum to SumF yields $\eta$, ${V}_{\mathrm{pp}}$ and $\Delta {H}_{\mathrm{pp}}^{0}$. For a particular nitroxide, one uses the proper map to get $\chi$ and the DL to obtained $\Delta {H}_{\mathrm{pp}}^{L}$ and $\Delta {H}_{\mathrm{pp}}^{G}$. If the line is unresolved, the same procedure applies and the transition from unresolved to resolved is seamless, (Fig. 3). This is a crucial feature because varying experimental parameters such as $T$, $C$, $P$, pressure, oxygen concentration, may involve spectra that are unresolved under some conditions and resolved under others. Furthermore, because $\Delta {H}_{\mathrm{pp}}^{L}$ is often different for lf and hf, both resolved and unresolved can appear in the same spectrum. See Fig. 8 of [16] that nearly fulfills this expectation. With $\chi$ in hand, all of the correction procedures in Ref. [4] are available. An important procedure is to obtain an accurate estimate of $I$ from noisy lines, perhaps overlapping, using a sweep width of the order of several line widths, not nearly enough to account for the long tail of the $L$ [14]. The value of this cannot be overestimated.

4.2 Why Study Resolved Spectra

In a paper published 45 years ago, Backer, et al. [38] used a nitroxide with resolved structure to study oxygen concentrations in a biological system. More modern work has been carried out by, for example, Hyde [39] and Halpern [40] and their co-workers as well as others [41]. Empirical parameters, for example, that are defined in Fig. 2 of [39], were calibrated to obtain the oxygen concentrations. These procedures were effective but labor intensive. By the methods described here, they would be amenable to rapid, automated analysis.

Other than for oximetry, a reasonable question is as follows: why go to the trouble to analyze partially resolved proton hyperfine patterns when one can simply buy deuterated nitroxides where resolution has never been observed? In most studies, where the purpose of an investigation is to study other systems, without being troubled by unresolved spectra, there is none, except perhaps the cost. Nevertheless, as an example, when Lee and Shetty [7] studied ¹⁵N d-Tempol, they intended to compare the results with Tempol but were dissuaded when they learned that spectra due to the latter were resolved. Those authors did not reveal their motive to study the protonated radical; could it be that they were curious if ${\Delta H}_{\mathrm{pp}}^{L}$ was equal in deuterated versus non-deuterated nitroxides? We are curious; thus, this will be one of our first investigations.

To appreciate a more compelling interest in resolved lines, we note that a nitroxide has two regions of hyperfine spacing: that of the proton structure and of the nitrogen. Interesting theoretical and experimental questions arise when the HSE frequency [16] and/or ${H}_{1}$ [33] become comparable with the hyperfine spacings. One of our honorees called the latter effects due to ${H}_{1}$ “peculiar [33].”

To be more concrete, let us express our interest in analyzing resolved spectra by appealing to [16], which is a compendium of most of what we know about studying HSE and DD at small ${H}_{1}$. References therein show the progress through the years. First, from the experimental perspective, see Fig. 8 in Ref. [16], similar to Fig. 7b of this paper, except before we used ¹⁵N H-Tempol in 60 wt% aqueous glycerol. We were able to fit the 2017 spectrum to SumF, but were not able to use the data from it and other resolved spectra because we didn’t know how to analyze them. Because of that, in Fig. 11a, which are plots of ${\Delta H}_{\mathrm{pp}}^{L}$ vs $C$, the points from the protonated radical stopped well short of the origin. In contrast, the points for the deuterated radical in Fig. 11b were available down to very near the origin. We concluded that the slopes for D and H were the same but the intercepts were different; however, this conclusion required that the linear dependence would extend to lower values of $C$ where we had no data. Should we expect that ${\Delta H}_{\mathrm{pp}}^{L}$ vs $C$ is indeed linear all the way to the origin? After all, that assumption has been the bedrock of finding ${{\Delta H}_{\mathrm{pp}}^{L}\left(\mathrm{0}\right)}_{0}$ and therefore ${T}_{2}$ [30, 42,43,44,45].

Now, let us see what the theory tells us by examining Fig. 3 of [16]. There, we see that the theory contradicts this bedrock. The values of ${\Delta H}_{\mathrm{pp}}^{L}$ near the origin are significantly smaller than those predicted by a linear fit to higher concentrations. If the detail near the origin is missed, and the data at higher $C$ is used to find the intercept, the value of ${{\Delta H}_{\mathrm{pp}}^{L}\left(0\right)}_{0}$ is too large; i.e., ${T}_{2}$ is too small. The change in slope of ${\Delta H}_{\mathrm{pp}}^{L}$ near the origin predicted by theory has never been observed experimentally, except for a hint of this result in Fig. 3 of [44] based on a single point, obviously not conclusive. That one result was obtained with 16-doxylstearic acid methyl ester, which does have large proton couplings resulting in $\chi \approx 5$, but still yields spectra that are unresolved, because of a fortuitous combination of ${a}_{j}$ [46]. Other than that, we have never worked at low concentrations with a nitroxide with proton spacings that are large enough to produce resolved spectra. This is tantamount to saying we have not measured $d{\Delta H}_{\mathrm{pp}}^{L}/dC$ near the origin in resolved spectra to compare them with those obtained at higher values of $C$.

A similar situation occurs for DD, except that values of $d{\Delta H}_{\mathrm{pp}}^{L}/dC$ near the origin are smaller than a linear extrapolation from higher $C$, Fig. 4 of [16]. For DD, the values of ${T}_{2}$ deduced from a linear extrapolation would be too large.

The experimental and theoretical considerations are more complex than this brief summary can detail [16], chiefly due to dispersion signals induced by HSE or DD between proton lines of the same nitrogen line. These can become quite large as $C$ increases until they begin to cancel one another. See Ref. [16] for details. Our purpose is not to reiterate the details, only to justify our interest.

Without going into detail, varying $T$ and ${H}_{1}$ are also complicated. Changing $T$ of any sample where HSE/DD are not negligible, brings an interplay between HSE/DD and broadening due to rotational motion that is complicated. We know, in principle, how to separate the two mechanisms, but one must work near $C\to 0$ and one must have values of ${a}_{j}$ that are large enough to measure the departures of the curves from linearity. Interestingly, according to theory, very similar complications enter as ${H}_{1}$ is increased into the saturation region and when $C$ increases; lines shift and broaden. It appears that both of these may be studied experimentally. Compare Figs. 7 and 8.

We have not mentioned the study of line shifts, although they have proved to be quite useful to study collisions [32] 43,44,45 and re-collisions [30, 47] in the reaction cage and to study free volume [48]. That would take us far afield of the present purpose to demonstrate that resolved lines may be analyzed. From the experimental plots, Figs. 5, 7, and 8, it appears that the shifts of the nitrogen lines for resolved spectra will be just as easy to study as those for unresolved lines. It also appears to be promising to study proton line shifts, although as yet, this avenue has not been pursued. We just mention that there are two possible approaches to study proton line shifts: (a) average shifts from fits or (b) individual shifts. Obviously, (b) is more difficult but considerably more revealing.

Obviously, a couple of points in each experimental case presented here, where we change $T$, $C$ and ${H}_{1}$, cannot be analyzed in detail yet. With the correct experiments, following the procedures developed through the years, we are encouraged that results near the origin of $C$ and ${H}_{1}$ may be correctly analyzed. In short, our brief exploratory experimental work demonstrates the feasibility of doing more complete experiments.

Let us mention one more consideration in an experimental program to study resolve spectra near $C\to 0$. One needs to vary $C$ in increments small enough so that ${K}_{\mathrm{ex}}C$ is small compared with ${\gamma a}_{j}$ a region that shows resolution. For typical nitroxides like Tempol or Tempone, ${K}_{\mathrm{ex}}\sim 100\mathrm{G}/\mathrm{M}$ in alkanes, thus to get enough points near the origin, one needs increments of $C$, $\delta C$, of about 4 mM or less for Tempol and 1 mM for Tempone. There is no problem in principle to carry out these experiments; however, in practice, a large number of spectra must be analyzed. To analyze a large number of spectra by methods employed by early workers [27, 49, 50] which involved simulating a spectrum, comparing it with the experimental spectrum, and proceeding by trial and error to find satisfactory fits, is prohibitively labor intensive. While this worked in the old days when there was no other choice, it is impractical for ambitious programs involving numerous spectra. The situation to study deuterated nitroxides is simplified in that the spectra are unresolved; however, near $C$ = 0, where ${a}_{d}=0.153{a}_{p}$ [4], which would require $\delta C\sim$ 0.6 mG or 0.15 mG or less, for d-Tempone or d-Tempol, respectively.

4.3 Voigts, SumFs, and Patterns

It is clear that $\mathrm{SumF}$ or $V$ which have no structure are only approximations to patterns. This is true even if the patterns are unresolved as in Fig. 1. In the unresolved case, the rationale for using an inappropriate fit function is that it yields accurate values for the average values of ${\Delta H}_{\mathrm{pp}}^{L}$ and may be automated. It is clear that an unresolved line cannot have much more information than its position, height, width, and shape. For resolved spectra, more information becomes available so what is the rationale to continue to fit with $\mathrm{SumF}$ or $V$? If accurate average values of ${\Delta H}_{\mathrm{pp}}^{L}$ are sufficient for the goals of an experiment, then because of the validity of the DL, the same advantages of speed and automation are available. Furthermore, in some experiments, both resolved and unresolved spectra may be encountered and the present methods allow the entire series of measurements to be analyzed with the same model. If more information is desired, spectral simulation becomes an option; however, the transition from unresolved to resolved spectra may present a problem.

We speculate that a further benefit of fitting partially resolved spectra with $\mathrm{SumF}$ or $V$ will be the availability of the residuals as assets as discussed in Sect. 4.4.

We turn to the question of whether $\mathrm{SumF}$ is an appropriate fit function for patterns in EPR. Most unresolved nitroxides may be fit to excellent precision by $\mathrm{SumF}$; thus, because $V$ and $\mathrm{SumF}$ are the same within a maximum discrepancy of 0.7% [6], $V$ also would provide an excellent fit [1].

Why not use $V$ routinely to fit nitroxide spectra? Our excuse 32 years ago [4] was that $V$ was prohibitively slow in computing, comparing, and adjusting until a proper fit could be found. We used a roomful of primitive personal computers to do the analysis running overnight, transferred the data to a cassette, and repeated the process night after night; thus, we adopted the SumF and have used it ever since [16]. In EPR, the argument that the computations take too long is not as compelling now that the computing power available to use on the desktop is enormous, following, more or less, Moore’s Law [51]. Thus, we offer another rational to continue with the SumF. We recognize that speed is of great importance in some fields, where real-time analysis is desired but probably not in EPR.

We have already seen from Fig. 1 that $V$ gives values of $\Delta {H}_{\mathrm{pp}}^{L}$ that are 18% too small while $\mathrm{SumF}$ gives results that are utterly negligible. This is for a spectrum with a rather small value of $\chi$ = 2 where one must amplify the residuals by a factor of 10 to see them well. This large difference in precision is not because $\mathrm{SumF}$ is a superior fit function, rather it is because it has been calibrated to that particular pattern. Because one could fit just as well with $V$, one probably could figure out a way to map the output values of $\chi$ obtained from $V$ to those that would yield precise values of $\Delta {H}_{\mathrm{pp}}^{L}$. One would have to do this for every pattern, although this is not as formidable as it may sound: there are many nitroxides, but only a handful of different patterns [4]. We have not done this, and would be interested to see the results of a worker who would undertake this exercise. Let us assume that this exercise would be successful. For us, $V$ would lose its charm as a physically sound model and become merely a different, phenomenological approach to estimate $\Delta {H}_{\mathrm{pp}}^{L}$. For $\mathrm{SumF}$, correcting output parameters has always been straightforward for unresolved spectra by constructing the correct map for each nitroxide especially for $\chi$ > 2 [4]. Now, for resolved spectra, the same is true.

4.4 Is the Residual a Potential Resource?

Here, we speculate that the residual from fits of resolved or nearly resolved spectra may be of significant utility, perhaps in some cases more so than the spectrum. From this work, we have noticed that a more sensitive method to judge if $C$ is low enough to avoid HSE/DD would be to monitor ${V}_{\mathrm{res}}$ rather than the traditional $\Delta {H}_{\mathrm{pp}}^{0}$. This speculation comes from a comparison of the spectra and the residuals in Figs. 5, 7, and 8. For example, in Fig. 5, the decrease in $\chi$ is about a factor of 1.5 while that in ${V}_{\mathrm{res}}{/V}_{\mathrm{fit}}$ is by a factor ~ 5.

The experimental residuals are symmetrical and show sharp lines whose intensities vary significantly with the conditions. Comparing the theoretical Fig. 2c with the experimental Fig. 5a, second trace, one notices not just the lines but similar “bumps” in both residuals. These bumps could be a quite sensitive test of the correspondence of the theory and the experiment, especially useful in fine tuning values of ${a}_{j}$.

5 Conclusions

Resolved nitroxide spectra may be fit with SumF and the DL employed to extract accurate values of ${\Delta H}_{\mathrm{pp}}^{L}$ and all of the quantities that depend on it. Brief experimental measurements show that such fits are feasible for real spectra and yield what we expect when we change $T$, $C$, and ${H}_{1}$ which offers opportunities to study challenging experimental conditions which were previously inaccessible except by tedious numerical means.

Appendix: Criterion for Incipient Resolution

The criterion for incipient resolution has always been subjective, defined as the value of $\chi$ where a visual distortion of an IHB occurs. Before, we observed the peak of the line and decided if it was a normal smooth curve or not.

Figure 10 shows a series of simulated Tempol spectra at $\chi$ = a 1.17, b 2.54, c 2.98, d 3.44, e 4.13, and f 5.29. The residuals are amplified as indicated; for example, in b, the residual has been amplified by a factor of 7.55. In our opinion, a practiced eye may discern incipient resolution in c at a glance, without any fitting. The insert shows the peak region in more detail. d with its insert shows a definite distortion that anyone may discern. This criterion is still subjective; however, once we decide, we may quantify it by specifying the ratio ${V}_{\mathrm{res}}/{V}_{\mathrm{pp}.}$ For c, $\chi$ = 2.98, ${V}_{\mathrm{res}}/{V}_{\mathrm{pp}.}$ = 0.02. If it becomes important, one could subtract the broad resonances evident in Fig. 1c to be more precise because it is the narrow residual lines that yield the information.

Fig. 10

A series of simulated Tempol spectra at $\chi$ = a 1.17, b 2.54, c 2.98, d 3.44, e 4.13, and f 5.29. The residuals are amplified as indicated; for example, in b, the residual has been amplified by a factor of 7.55