Detailed Analysis of Manifestations of the Spin Coherence Transfer in EPR Spectra of ¹⁴N Nitroxide Free Radicals in Non-Viscous Liquids

Abstract

Manifestations of the spin coherence transfer induced by the exchange and dipole–dipole interactions between spin probes in dilute solutions in the electron paramagnetic resonance (EPR) spectra have been studied. The perturbation theory of manifestations of the spin coherence transfer in the EPR spectra of nitroxide free radicals elaborated by one of the authors Salikhov (Applied Magnetic Resonance 38:237–256, 2010) has been generalized with allowance for the super hyperfine structure of the EPR spectra. For ¹⁴N nitroxide radicals, the total EPR spectrum was presented as a sum of three independent components in the case of slow and intermediate spin coherence transfer rates. The shapes of these components were found. The side components of the EPR spectrum contain the absorption and dispersion contributions and, as a result, have the asymmetric (mixed) shapes. These asymmetric components can be presented as J = J _absorption ± p J _dispersion. The p value is found for the arbitrary super hyperfine structure of the spectrum. In the slow and intermediate spin coherence transfer rate regime, the parameter p is independent of the super hyperfine interactions in the nitroxide radicals, but the shapes of J _absorption and J _dispersion terms depend on the super hyperfine structure of the nitrogen components of the nitroxide EPR spectrum and on the spin coherence transfer rate. It is confirmed theoretically that a good strategy to evaluate the spin coherence transfer rate from the EPR spectra is using the dispersion contribution to the shape of the EPR spectra of nitroxide free radicals. An algorithm is suggested and tested for determining the spin coherence transfer and spin decoherence rates.

1 Introduction

It is well known that the short-range exchange interaction between spin probes (paramagnetic particles) in dilute solutions induces the bimolecular process of the exchange of spin states of colliding particles: the spin exchange. By studying this process, one can obtain useful information about the frequency of bimolecular collisions in complex systems, the overlap of the electron wave functions, which is of great importance for the interpretation of the electron transfer between donor and acceptor molecules (see [1–6]).

The spin exchange rate can be determined using the methods of electron paramagnetic resonance (EPR) spectroscopy. The bimolecular spin exchange transforms the shape of the EPR spectra of spin probes remarkably: it broadens the components of the EPR spectra, shifts these components, can produce the exchange narrowing of EPR spectra, and some of the EPR spectrum components can become asymmetric [1–3, 5, 6]. Thus, in principle, the spin exchange rate can be determined by analyzing the shape of the EPR spectra. However, in addition to the exchange interaction, the long-range dipole–dipole interaction can also change the states of spin probes. Both interactions affect the shape of the EPR spectrum causing the spin-probe concentration-dependent transformations of the spectrum shape. Another important interaction, which also affects significantly the EPR spectrum, is the hyperfine interaction of the unpaired electrons with magnetic nuclei.

Nitroxide free radicals are among favorite spin probes used for studying the spin exchange. Keeping this in mind, in the course of our considerations below, including numerical simulations of the EPR spectra, we refer to solutions of ¹⁴N nitroxide radicals. These considerations can be properly projected to ¹⁵N nitroxide radicals and other paramagnetic particles. There were developed several algorithms for determining the spin exchange rates using the EPR data (see [1–6]). The conventional algorithm (see [4–6]) is based on the following observations. Components of the EPR spectra exhibit the concentration-dependent broadening and shifts of the EPR lines at the low-spin probe concentration. At high concentration, all components of the EPR spectrum converge to the narrow single line at the gravity center of the spectrum. However, this algorithm disregards some specific manifestations of the spin exchange in the EPR spectrum shape. In the presence of the spin exchange, the shape of EPR spectra components can be a sum of absorption and dispersion terms [1, 4, 5]. For example, the EPR spectrum of two side (nitrogen) hyperfine components of the ¹⁴N nitroxide radical has the asymmetric shape. Note that the conventional algorithm does not treat correctly the dipole–dipole interaction between spin probes: it ignores the spin coherence transfer induced by this interaction. According to the conventional theory, the dipole–dipole interaction in non-viscous solutions produces only the spin decoherence [7, Ch. 8, Eqs. (VIII. 79, VIII. 89)]. However, in Refs. ([8, Eqs. (4.20, 4.75)], [9]), it was shown by Salikhov that the dipole–dipole interaction also causes the spin coherence transfer alongside with the exchange interaction. It is worth mentioning that in non-viscous solutions, the contributions of the exchange and dipole–dipole interactions to the spin decoherence rate are added, while their contributions to the spin coherence transfer rate are subtracted [1, 8, 9].

One more problem arises due to the hyperfine structure of the spin probe EPR spectra. For example, in the case of nitroxide radicals, the EPR spectra have the hyperfine structure induced by nitrogen nucleus and other magnetic nuclei (protons, deuterons, ¹³C). There are three (in the case of ¹⁴N) well-resolved nitrogen hyperfine components, which belong to the subensembles of nitroxide radicals with different projections of the nitrogen nuclear spins (m = +1, 0, −1 for ¹⁴N). Each nitrogen component has the resolved/unresolved hyperfine structure induced by the interaction of the unpaired electron with other magnetic nuclei. This super hyperfine structure and overlapping of the nitrogen components provide additional problems for determining the bimolecular spin exchange rates.

The EPR manifestations of the spin exchange between nitroxide radicals were comprehensively investigated experimentally. The relevant results are reviewed in Refs. [4–6]. Recently, Bales and coworkers (see [2, 3, 6, 10]) developed a new approach for determining the spin exchange rate using EPR data based on the theoretical observation by Salikhov that due to the coherence transfer, the components of EPR spectra can become asymmetric and can be presented as a sum of absorption and dispersion contributions [4, 5]. Bales and coworkers tested this theoretical prediction and demonstrated in experiments that the determination of the dispersion contribution to the shape of EPR spectra is a reliable method to determine the spin coherence transfer rate.

For a model nitroxide free radical, the rigorous theoretical analysis of manifestations of the exchange and dipole–dipole interactions in the shape of the nitroxide radical EPR spectrum was presented in Ref. [1]. Only the hyperfine interaction with the nitrogen nuclear spin was considered, while the super hyperfine structure of the EPR spectrum induced by the interaction with all other magnetic nuclei except nitrogen was ignored. In the case of the slow spin exchange (slow spin coherence transfer), the shape of EPR spectra of ¹⁴N nitroxides was presented as a sum of three independent components. The side components of the spectrum are asymmetric. These asymmetric components contain the absorption and dispersion contributions. The dispersion contribution to the EPR spectrum was determined quantitatively using the perturbation theory for the non-degenerate case.

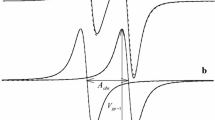
In real systems, the nitrogen hyperfine components of the EPR spectra of nitroxide radicals have the additional super hyperfine structure (see Fig. 1).

Fig. 1

Schematic presentation of the EPR spectrum for a model ¹⁴N-nitroxide radical with six equivalent protons

As it is shown in Fig. 1, nitrogen nuclei and protons lead to the hyperfine splitting of the EPR lines in different scales: the splitting by the nitrogen nucleus is much larger than the splitting due to protons. Therefore, it is justified to introduce two characteristic spin concentrations: C ₀ and C*. They correspond to the characteristic spin exchange rates, K _ex C (K _ex is the spin exchange rate constant), determined by the conditions (1/3) K _ex C ₀ = ∆Ω ₀ and (1/3) K _ex C* = a _N, respectively (see Fig. 1). When C < C ₀, the nitrogen components manifest the inhomogeneous broadening induced by the super hyperfine interaction, since the spin exchange inside the nitrogen components (the spin exchange between super hyperfine components) is relatively slow in this spin concentration range. Therefore, the effect of the spin exchange on the EPR spectrum at C < C ₀ has to be analyzed carefully. In the spin concentration range C ₀ < C < C*, the spin exchange rate is fast enough to collapse each nitrogen component into the exchange narrowed homogeneous line. Qualitatively, the manifestations of the spin exchange in the EPR spectra of nitroxide radicals in the presence of the super hyperfine structure are well known (see [4, 5] chapter 3). For example, for the water solution of the stable free radical 2,2,6,6-tetramethyl-4-oxopiperidine-1-oxyl (TANONE) in the range of intermediate concentrations (0.4 ÷1.7) × 10⁻² M/L (C ₀ < C < C*), the linewidth depends on the spin concentration linearly, but the linewidth has the non-linear part at very low concentrations C < 0.3 × 10⁻² M/L (C < C ₀) (see Fig. 3.5 in [5] and the discussion therein). Manifestations of the spin exchange in EPR spectra of nitroxide free radicals in the slow (C < C ₀) and intermediate spin exchange rate (C ₀ < C < C*) regimes were studied in the solution of di-tert-butylnitroxide (DTBN) [10]. It was shown that the spin exchange leads to the broadening, shift, and eventual collapse of the lines forming the 19-line proton hyperfine pattern of the central nitrogen component, which corresponds to the nitrogen nuclear spin projection m = 0.

The aim of this work is to generalize the perturbation theory approach [1] for nitroxide radicals to the concentration region C < C* with allowance for the super hyperfine interaction of the unpaired electron. As expected, in the intermediate concentration range C ₀ < C < C*, the EPR spectrum of nitroxide radicals can be described using the theoretical model [1] with minor modifications of the spin packet linewidths in a group of lines corresponding to one value of the nitrogen nuclear spin projection number m = 0, ±1. Our main goal was to generalize the perturbation theory approach [1] for nitroxide radicals into the concentration range C < C ₀. In this slow spin exchange case, it is shown that the total EPR spectrum of ¹⁴N nitroxide radicals is also a sum of three independent components. The shape of these components is determined by the super hyperfine structure of nitrogen components and by the spin exchange rate inside these components alongside with the spin exchange between nitrogen components. Note that the spin exchange inside nitrogen components was treated exactly. The dispersion contribution to the nitrogen components of the EPR spectra in the case of the slow spin coherence transfer was found analytically. In good approximation, the amplitude of the dispersion contribution to the spectrum does not depend on the super hyperfine structure of the nitrogen components, and it is equal to the value obtained in Refs. [1, 4, 5] disregarding the super hyperfine structure. The shape of the dispersion contribution and the shape of the absorption contribution in the range C < C ₀ depend on the super hyperfine structure of the nitrogen components. The perturbation theory approach results were tested in numerical experiments. The EPR spectra were simulated with a given set of parameters which describe the spin exchange and the dipole–dipole interactions as well as the hyperfine interactions with the nitrogen nucleus and the super hyperfine interactions. Following the theory developed in Ref. [1] and in this work, we suggest an algorithm for determining the spin decoherence and spin coherence transfer rates. We tested the algorithm by analyzing the simulated EPR spectra. The rates can be further tuned by the numerical simulations of the EPR spectra. To facilitate these simulations, we present the known general kinetic equations for the transverse components of the magnetization. When the dipole–dipole contribution to the shape of the EPR spectrum is negligible, the solution of the kinetic equations is well known. In the case of non-viscous solutions, these kinetic equations can be solved with allowance for the dipole–dipole interaction and the exchange interaction (see also [9]). Here, we present expressions which describe the shape of the EPR spectrum nitrogen components in the range C < C ₀ with allowance for the exchange, dipole–dipole, and the super hyperfine interactions. Note that these results can be properly applied to solutions of ¹⁵N nitroxide free radicals and other paramagnetic particles.

2 Theoretical Consideration

2.1 Arbitrary Concentration of Spin Probes

We consider a dilute solution of paramagnetic particles (spin probes) with the electron spin S = 1/2. We assume that g _k is the statistical weight of the kth hyperfine component of their EPR spectrum. We denote the transverse component of the electron spin magnetization of that particles which belong to the kth hyperfine component with the resonance frequency ω _k and the transverse relaxation time T _2k as M _k− = M _kx  − iM _ky . Phenomenologically, the spin exchange affects the magnetic resonance spectra similar to the chemical exchange. The following kinetic equations for M _k− with allowance for the exchange and dipole–dipole interactions were obtained in the rotating frame (see [1], [4, Eq. (2.72)], [8, Eqs. (4.20, 4.75)]):

$$ {\text{d}}M_{k - } /{\text{d}}t = ( - i(w_{k} + \delta_{k} - w) \, - \varGamma_{0k} ) \, M_{k - } - \, W_{k} M_{k - } + g_{k} \sum {V_{kn} M_{n - } - iw_{1} M_{kz} .} $$

(1)

Here, δ _k is the additional shift of the resonance frequency induced by the interference of the exchange and hyperfine interactions (see [5, 10]). The kinetic coefficient Γ _0k  = 1/T _2k gives the intrinsic homogeneous (alternating) linewidth of the kth spin packet [11]. The terms with W _k and V _kn describe the spin decoherence (W) and the spin coherence transfer (V) induced by the exchange and dipole–dipole interactions between spin probes. The last term describes the magnetization motion induced by the alternating magnetic field with the frequency ω and amplitude B ₁, while ω ₁ = γB ₁ is the Rabi frequency. Note that during the simulation of EPR spectra in low B ₁ fields, when the saturation effect can be ignored, the longitudinal magnetizations in Eq. (1) can be replaced by their equilibrium values M _k0 = g _k M ₀.

According to [1, 4, 5, 8, 9], we have

$$ W_{k} = K_{\text{ex}} C \, + \sum {g_{n} /T_{{2{\text{dd}}}} \left( {k,n} \right),} $$

(2)

$$ V_{kn} = K_{\text{ex}} C - \, 1/T_{{2{\text{dd}}}}^{{\prime }} \left( {k,n} \right). $$

(3)

Here, K _ex C is the spin exchange rate. The 1/T _dd terms arise from the dipole–dipole interaction, and they are given by the following expressions [7–9]:

$$ 1/T_{{2{\text{dd}}}} \left( {k,n} \right) = \left( {1/6} \right)\kappa^{2} C \, (J^{0} \left( 0 \right) \, + \, \left( {1/4} \right)J^{0} (\omega_{k} - \omega_{n} ) \, + \, \left( {9/2} \right)J^{1} (\omega_{n} ) \, + \, 9J^{1} (\omega_{k} ) \, + \, \left( {9/4} \right)J^{2} (\omega_{k} + \omega_{n} )) \equiv K_{\text{dsd}} \left( {k,n} \right) \, C, $$

$$ 1/T'_{{2{\text{dd}}}} \left( {k,n} \right) \, = \, \left( {1/12} \right)\kappa^{2} C \, (J^{0} \left( 0 \right) \, + J^{0} (\omega_{k} - \omega_{n} ) \, + \, 9J^{1} (\omega_{n} ) \, + \, 9J^{1} (\omega_{k} )) \equiv K_{\text{dsct}} \left( {k,n} \right) \, C. $$

(4)

Here, κ ² = (3/4) g ⁴ β ⁴/h ², g is the g-factor of the nitroxide radical, β is the Bohr magneton, and J ^q(ω) are spectral densities of the correlation functions for the dipole–dipole interaction ([7], ch.VIII).

The continuous-wave EPR spectrum shape is given by:

$$ J_{\text{EPR}} = - \text{Im} \sum {M_{k - } } , $$

where M _k− is the steady-state solution of Eq. (1)

$$ ( - i(w_{k} + \delta_{k} - w) \, - \varGamma_{0k} ) \, M_{k - } - W_{k} M_{k - } + \, g_{k} \sum {V_{kn} M_{n - } = iw_{1} g_{k} M_{0} .} $$

(5)

Solution of Eq. (5) can be easily found if the dipole–dipole contributions to W and V are negligible. Indeed, in Eqs. (2, 3), the contribution of the spin exchange to W _k and V _kn is supposed to be independent of the hyperfine components, W _k  = W, V _kn  = V. Moreover, for the spin exchange, W = V = K _ex C. In this case, Eq. (5) has the form:

$$ ( - i(w_{k} + \delta_{k} - w) \, - \varGamma_{0k} ) \, M_{k - } - VM_{k - } + \, g_{k} V\sum {M_{n - } = iw_{1} g_{k} M_{0} .} $$

(5a)

The value of the total transverse magnetization $M_{ - } = \sum {M_{k - } }$ is obtained straightforwardly from Eq. (5a). The corresponding result is presented below [see Eq. (9a)].

With allowance for the dipole–dipole contribution to the spin decoherence and the spin coherence transfer, the solution of Eq. (5) is not so straightforward, since the dipole–dipole contribution to W _k and V _kn depends, in principle, on the hyperfine components. However, these equations are simplified in the case of non-viscous solutions when the characteristic time of the translational mutual diffusion of spin probes τ _D = r ²₀ /D is short enough, so that the fast motion condition is fulfilled: a _N τ _D ≪ 1, where r ₀ is the collision radius of two spin probes, D is the coefficient of their mutual translational diffusion. Under this condition, the power densities J ^(q)(x) in Eq. (4) can be approximated as:

$$ J^{(0)} (w_{k} - w_{n} ) \approx J^{(0)} \left( 0 \right), \, J^{(1)} (w_{k} ) \approx J^{(1)} (w_{n} ) \approx J^{(1)} (\omega ), \, J^{(2)} (w_{k} + w_{n} ) \approx J^{(2)} (2\omega ). $$

In this case of the fast motion of spin probes, Eqs. (2–4) are reduced to:

$$ W_{k} \approx W = K_{\text{ex}} C + 1/T_{{2{\text{dd}}}} \equiv \left( {K_{\text{ex}} + K_{\text{dsd}} } \right) \, C \equiv K_{\text{sd}} C, $$

$$ V_{kn} \approx V = K_{\text{ex}} C - 1/T_{{2{\text{dd}}}}^{{\prime }} \equiv \left( {K_{\text{ex}} - \, K_{\text{dsct}} } \right) \, C \equiv K_{\text{sct}} C, $$

(6)

$$ K_{\text{dsd}} = \left( {1/24} \right)\kappa^{2} (5J^{0} \left( 0 \right) + 54J^{1} (\omega_{0} ) + 9J^{2} (2\omega_{0} )), $$

$$ K_{\text{dsct}} = \left( {1/6} \right)\kappa^{2} (J^{0} \left( 0 \right) + 9J^{1} (\omega_{0} )). $$

Note that W − V = 1/T _2dd + 1/T′_2dd = (3/8) κ ² C (J ⁰(0) + 10 J ¹(ω ₀) + J ²(2ω ₀)).

Here, parameters K _dsd and K _dsct are introduced, which describe the contribution of the dipole–dipole interaction to the spin decoherence and to the spin coherence transfer, respectively. Formally, these coefficients appear like the spin exchange rate constant K _ex [see Eq. (6)]. However, note that the effect of the long-range dipole–dipole interaction is not considered as a result of binary collisions of spin probes.

For numerical simulations, it is necessary to estimate scales of possible values of the spin decoherence and spin coherence transfer kinetic parameters. The binary collision rate Z can be estimated using the Smolukhovskii result: Z = 4 π r ₀ D C, where r ₀ is the collision radius of two spin probes and D is their mutual diffusion coefficient. To estimate the spin exchange rate, we assume that the exchange interaction is switched on suddenly at the collision of two spin probes. For this sudden collision approximation, the maximum spin exchange rate constant is expected to be K _ex = 2 π r ₀ D [4, 5]. If the concentration C is measured in mM/L, then K _ex = 2 π r ₀ D 10⁻⁶ N _A, s⁻¹ L/mM. In the EPR experiments, it is convenient to use the unit gauss (G) of the magnetic field strength. Thus, K _ex = 2 π r ₀ D 10⁻⁶ N _A/(1.76·10⁷) ≈ 2 r ₀ D 10¹¹, G L/mM. Here, N _A is Avogadro’s number. For example, for realistic molecular kinetic parameters r ₀ = 0.7 nm, D = 10⁻⁵ cm²/s, one obtains K _ex = 0.15 G L/mM. In the course of numerical simulations, we will use K _ex around this value. The contribution of the dipole–dipole interaction to the spin decoherence and spin coherence transfer rates was calculated numerically using expressions for J ^(q)(ω) in [7, Eqs. (VIII.109, VIII.114)]. The results of these numerical calculations are presented in Fig. 2. The dashed line shows K _ex = 2 π r ₀ D. Figure 2 shows that in non-viscous liquids, when D ~ 10⁻⁶–10⁻⁵ cm²/s, the dipole–dipole interaction contribution to the spin dephasing and to the spin coherence transfer is much less than the contribution of the exchange interaction (the spin exchange). Note that K _dsd and K _dsct are almost equal when D ~ 10⁻⁶–10⁻⁵ cm²/s, K _dsd ≈ K _dsct (see Fig. 2).

Fig. 2

Dependence of K _dsd, G L/mM (solid line) and K _dsct, G L/mM (dotted line), K _ex, G L/mM (dashed line) on the two spin probes mutual diffusion coefficient. Parameters used in these simulations: a _N = 16 G, r ₀ = 0.7 nm, and ω ₀ = 3400 G

Thus, in non-viscous liquids, Eq. (5) can be written as (compare with Eq. (5a)):

$$ ( - i(w_{k} + \delta_{k} - w) \, - \varGamma_{0k} ) \, M_{k - } - W \, M_{k - } + \, g_{k} V\sum {M_{n - } = iw_{1} g_{k} M_{0} ,} $$

or

$$ ( - i(w_{k} + \delta_{k} - w) \, - \varGamma_{0k} ) \, M_{k - } - \, K_{\text{sd}} C \, M_{k - } + \, g_{k} K_{\text{sct}} C \, M_{ - } = iw_{1} g_{k} M_{eq} . $$

(7)

Here, M ₋ = ΣM _n− is the total transverse magnetization. Solving Eq. (7), we find:

$$ J_{\text{EPR}} = - \text{Im} M_{ - } = - w_{1} M_{eq} \text{Re} \{ F(\omega )\} . $$

(8)

Here

$$ F(w) = G\left( \omega \right)/\left( {1 \, + \, V \, G\left( \omega \right)} \right), $$

(9)

$$ G(w) = \sum {g_{k} /( - i(w_{k} + \delta_{k} - w) \, - \, (\varGamma_{0k} + \, W)),} $$

where V = K _ex C − K _dsct C and W = K _ex C + K _dsd C are the spin coherence transfer and spin decoherence rates induced by the exchange and dipole–dipole interactions, respectively.

When the dipole–dipole interaction is negligible, the EPR spectrum is given by the expression:

$$ J_{\text{EPR}} = - w_{1} M_{eq} \text{Re} \{ G_{ex} (\omega )/(1 \, + \, K_{ex} C \, G_{ex} (\omega ))\} , $$

(9a)

$$ G_{ex} (w) = \sum {g_{k} /( - i(w_{k} + \delta_{k} - w) - (\varGamma_{0k} + \, K_{ex} C)).} $$

Equation (9a) is well known in the spin exchange problem (see [4, 5, 12]). The result given by Eq. (9) is the generalization of the conventional theory of the spin exchange and its manifestations in EPR spectroscopy: Eq. (9) includes the spin exchange and dipole–dipole interaction contributions to the spin dynamics.

Theoretical results presented above make it possible to simulate the EPR spectra of spin probes in dilute solutions and to analyze their transformations when the spin concentration changes. Below we will use Eqs. (8, 9) for simulating spectra.

There are two concentration-dependent parameters W and V, which affect the shape of the EPR spectrum. The parameter W is the concentration-dependent contribution to the width of Lorentzian spin packets, which form the G(ω) function. The form of this function is determined by the distribution of the resonance frequencies ω _k  = ω ₀ + Δ _k . When this inhomogeneous distribution of resonance frequencies has the Gaussian form, the function G(ω) has the Voigt form (see [6]). When the spin coherence transfer is ignored, V = 0, all EPR lines in the G(ω) demonstrate the concentration broadening equal to W. The spin coherence transfer with the rate V changes the observed spectrum Re(F(ω)). The coherence transfer (non-zero rate V) leads to mixed resonance line shapes, changes the concentration broadening of the resonance lines, shifts the lines, leads to the collapse of the EPR spectrum into one homogeneous line. If the dipole–dipole interaction gives the negligible contribution, the exchange narrowed line is observed at the fast spin exchange case. If the dipolar contribution is not negligible, the collapsed line manifests the concentration-dependent dipolar broadening. It is worth to note that the dipolar broadening of the spectrum W − V = 1/T _2dd + 1/T′_2dd under the condition of the spectrum collapse, when K _sct C > a _N, is larger than the dipolar spin decoherence rate 1/T _2dd. The last observation arises from the fact that the exchange and dipole–dipole interactions transfer the spin coherence with different signs. Indeed, V = (K _ex − K _dsct) C [see Eq. (6)].

To demonstrate these qualitative statements concerning the spin probe concentration dependence of the EPR spectrum shape, we present some results of numerical simulations for ¹⁴N nitroxide radicals (Fig. 3). During these simulations, we assumed that the super hyperfine structure of the nitrogen components is described by the Gaussian distribution. If the nitroxide radical has 5–10 or even more protons with close hyperfine interaction constants, in good approximation the distribution of the frequencies induced by the super hyperfine interaction with protons can be described by the Gaussian function, f _m (∆) = (1/Sqrt[2 π σ])exp(−(∆−a _N m)²/(2 σ)), where m = −1, 0, 1 (projections of the ¹⁴N nuclear spin), a _N m is the resonance frequency shift induced by the hyperfine interaction with the nitrogen nuclear spin and σ is the dispersion of the ∆ distribution. Note that the width ΔΏ ₀ of the Gaussian nitrogen component of the spectrum (see Fig. 1) can be characterized by the square root of dispersion, σ ^1/2.

Fig. 3

Numerical simulations of the EPR spectrum (left) and its derivative (right) of ¹⁴N nitroxide radicals for several concentrations of spins. The following parameters were used in these calculations: a _N = 16 G, g = 2, σ = 0.12 G ², Γ _0k  = 0.2 G, W = V = K _ex C = 0.1 C G (dashed lines); K _ex = 0.05 G L/mM, K _dsd = 0.011 G L/mM, K _dsct = 0.009 G L/mM (solid lines), C is concentration of radicals in mM/L units, B is the external magnetic field strength

Figure 3 shows that in the slow spin exchange regime, the spectrum has three components corresponding to projections of the ¹⁴N nuclear spin. We present the results of simulations for two model situations. In one case, we assume that the dipole–dipole interaction contribution can be neglected compared to the exchange interaction contribution, so that W = V = K _ex C (dashed curves in Fig. 3). In another case, we suppose that the dipole–dipole interaction contribution decreases the spin coherence transfer rate V and increases the spin decoherence rate W (solid curves in Fig. 3).

Figure 3 shows the well-known concentration-dependent features of EPR spectra in solutions: at low concentration the EPR lines broaden and shift, at high concentration they converge into a single line at the center of gravity of the spectrum. When the spin exchange interaction gives the major contribution and the dipole–dipole interaction can be ignored, at high concentration, the EPR spectrum consists of a single narrow homogeneously broadened line (dashed curves in Fig. 3 demonstrate the exchange narrowing effect). When the spin exchange and dipole–dipole interactions contribute to the spin dynamics, at high-spin concentration, the EPR spectrum consists of one homogeneously broadened line and it has the concentration broadening equal to W − V = 1/T _2dd + 1/T′_2dd, so that the line width increases with the spin concentration due to the dipole–dipole interaction contribution (see solid curves in Fig. 3).

For the ¹⁴N containing nitroxide radical, the central component is symmetric, while side components (low- and high-field ones) are asymmetric, since they contain dispersion contributions.

2.2 Low Concentration (Slow Spin Exchange) Case

Equations (8, 9) make it possible to simulate EPR spectra for any concentration of paramagnetic particles and for any hyperfine structure of the EPR spectra. Note that Eqs. (8, 9) include exchange and dipole–dipole interactions contributions to the spin decoherence and the spin coherence transfer. Thus, in principle, by varying the parameters W, V in Eq. (9), one can find the best-fit parameters, which reproduce the experimental curves.

However, for practical applications of the theory for the interpretation of the experimental results, it is desirable to find some approximate solutions of the problem which are relevant to different spin coherence transfer rates.

As it was discussed above, there are three characteristic ranges of the nitroxide free radical concentrations:

• C < C ₀ (K _sct C < 3 ΔΏ ₀), slow spin coherence transfer;

• C ₀ < C < C* (3 ΔΏ ₀ < K _sct C < 3 a _N), intermediate spin coherence transfer rate;

• C > C*, (K _sct C > 3 a _N), fast spin coherence transfer.

In the cases of slow and intermediate coherence transfer rate, there is a small parameter V/a _N < 1. Thus, one can apply the perturbation theory to specify the general shape of the EPR spectrum given by Eqs. (8, 9).

For concentrations, when (1/3) V < a _N and neglecting the super hyperfine interaction with all magnetic nuclei except for the nitrogen nucleus, in [1, 4, 5], the problem of the coupled motion of the spin magnetizations of all nitrogen components was reduced to the problem of the spin magnetization motion of the uncoupled (quasi-independent) components but with renormalized parameters of the homogeneous broadening of the spin packets and their resonance frequencies. The analogous strategy can also be implemented in the general case when the nitrogen components of the EPR spectrum have the additional super hyperfine structure due to the interaction with magnetic nuclei except nitrogen. In this work, at nitroxide radical concentrations, when (1/3) V < a _N, the total EPR spectrum has been presented as a sum of the uncoupled components even in the presence of the super hyperfine splitting. Therefore, the theory was generalized with allowance for the super hyperfine structure of EPR spectra of nitroxide radicals.

In the case C → 0, the nitroxide radicals demonstrate the EPR spectrum which has, as a rule, resolved hyperfine components corresponding to three projections of ¹⁴N nuclear spin, m = 1, 0, −1 (see Fig. 1). At low nitroxide radical concentration, the spin coherence transfer rate can be much less than the splitting between the nitrogen hyperfine components, i.e., (1/3) V < a _N. Under this condition the effect of the spin coherence transfer between radicals, which belong to different nitrogen hyperfine components, on the shape of the EPR spectrum can be analyzed using the perturbation theory for non-degenerate resonance frequencies with respect to the small parameter V/a _N. However, the spin coherence transfer between radicals inside the definite nitrogen component corresponds to degenerate or quasi-degenerate case. This situation is in detail considered in the “Appendix” (see below). Here, the final expressions for the three quasi-independent components of the EPR spectrum are presented (see also [1, 4, 5]):

$$ \begin{aligned} J_{1} &= - \text{Re} \{ \left( {1 \, + iV/\left( {a_{\text{N}} } \right)} \right) \, \ll G(\omega_{0} + a_{\text{N}} - \, \left( {1/6} \right) \, g_{n} \left( {V^{2} /a_{\text{N}} } \right) \, + \, \delta_{{{\text{ex}},1n}}\\ &\quad + \Delta_{n} - \, \omega , \, W + \varGamma_{01} )\gg /(1 \, + \, \left( {V/3} \right) \hfill \\ &\ll G(\omega_{0} + a_{N} - \, \left( {1/6} \right) \, g_{n} \left( {V^{2} /a_{\text{N}} } \right) \, + \, \delta_{{{\text{ex}},1n}} + \Delta_{n} - \, \omega , \, W + \varGamma_{01} )\gg )\}, \hfill \\ \end{aligned} $$

$$ J_{0} = - \text{Re} \{ \ll G(\omega_{0} + \Delta_{n} - \omega ,W + \varGamma_{00} )\gg /(1 \, + \, \left( {V/3} \right)\ll G(\omega_{0} + \Delta_{n} - \, \omega ,W + \varGamma_{00} )\gg )\} , $$

(10)

$$ \begin{aligned} J_{ - 1} &= - \text{Re} \{ \left( {1 \, {-}iV/\left( {a_{\text{N}} } \right)} \right)\ll G(\omega_{0} - a_{\text{N}} + \, \left( {1/6} \right) \, g_{n} \left( {V^{2} /a_{\text{N}} } \right) \, + \, \delta_{{{\text{ex}}, - 1n}} \\ &\quad + \Delta_{n} - \omega ,W + \varGamma_{0 - 1} )\gg /(1 + \left( {V/3} \right) \hfill \\ \ll G(\omega_{0} - a_{\text{N}} + \, \left( {1/6} \right) \, g_{n} \left( {V^{2} /a_{\text{N}} } \right) + \delta_{{{\text{ex}}, - 1n}} + \Delta_{n} - \omega ,W + \varGamma_{0 - 1} )\gg )\} , \hfill \\ \end{aligned} $$

where

$$ \ll \,G\left( {x_{n} ,y}\, \right)\gg\,= \sum {g_{n} /\left( { - ix_{n} - \, y} \right),} $$

ω ₀ is the Larmor precession frequency of the radical unpaired electron spin in the external magnetic field B, g _n is the statistical weight of the nth super hyperfine component inside the nitrogen component of the EPR spectrum of nitroxide radicals, δ _ex,mn is the shift of the resonance frequency induced by the exchange interaction during collisions [13], and Δ _n is the shift of the resonance frequency induced by magnetic buclei except nitrogen. We expect that the dependence of the shift δ _ex,mn on the super hyperfine splitting can be ignored, so that δ _ex,mn  ≈ δ _ex,m , it depends only on the nitrogen nuclear spin orientation. To simplify discussion in numerical simulations below, we ignore this frequency shift and put δ _ex,m  = 0.

Note that the frequency shifts ±g _n (1/6) (V ²/a _N) of the side nitrogen components [see J ₁ and J ₋₁, Eq. (10)] describe the tendency of these components to collapse at the center of gravity of the EPR spectrum due to the spin coherence transfer between its different nitrogen components. These line shifts underestimate real shifts, since they were derived by neglecting the exchange narrowing of each nitrogen component of the EPR spectrum when (1/3) V → ∆Ω ₀. When all proton hyperfine lines collapse and give a single line, these frequency shifts should be equal to the shifts in the intermediate spin coherence transfer case, where they are ±(1/6) (V ²/a _N) (see [1, 4, 5] and Eq. (11) below). Thus, the line shifts should change from ±g _n (1/6) (V ²/a _N) to ±(1/6) (V ²/a _N) when V increases from zero to 3 ∆Ω ₀. In fact, these line shifts are the most important in the region V ≈ 3∆Ω ₀. Numerical simulations presented in Sect. 3 support the assumption that in the case of slow spin coherence transfer, in Eq. (10), the frequency shifts ±g _n (1/6) (V ²/a _N) can be substituted by ±(1/6) (V ²/a _N) not only at V → 3∆Ω ₀ but at all V (V < 3∆Ω ₀) values. Thus, in the slow spin coherence transfer case, the three quasi-independent components of the EPR spectrum are approximated as:

$$ \begin{aligned} J_{1} &= - \, \text{Re} \{ \left( {1 \, + iV/\left( {a_{\text{N}} } \right)} \right) \, \ll G(\omega_{0} + a_{\text{N}} - \left( {1/6} \right)\left( {V^{2} /a_{\text{N}} } \right) \, + \, \delta_{{{\text{ex}},1n}} + \Delta_{n} - \omega , \, W + \varGamma_{01} )\gg /(1 + \left( {V/3} \right) \, \hfill \\ &\ll G(\omega_{0} + a_{\text{N}} - \left( {1/6} \right) \, \left( {V^{2} /a_{\text{N}} } \right) + \delta_{{{\text{ex}},1n}} + \Delta_{n} - \omega ,W + \varGamma_{01} )\gg )\} , \hfill \\ \end{aligned} $$

$$ J_{0} = - \text{Re} \{ \ll G(\omega_{0} + \Delta_{n} - \omega ,W + \varGamma_{00} )\gg /(1 + \left( {V/3} \right)\ll G(\omega_{0} + \Delta_{n} - \omega ,W + \varGamma_{00} )\gg )\} , $$

(10a)

$$ \begin{aligned} J_{ - 1}& = - \text{Re} \{ \left( {1 - iV/\left( {a_{\text{N}} } \right)} \right)\ll G(\omega_{0} - a_{\text{N}} + \left( {1/6} \right) \left( {V^{2} /a_{\text{N}} } \right) + \Delta_{n} - \omega ,W + \varGamma_{0 - 1} )\gg /(1 + \left( {V/3} \right) \, \hfill \\ &\ll G(\omega_{0} - a_{\text{N}} + \left( {1/6} \right) \left( {V^{2} /a_{\text{N}} } \right) + \delta_{ex, - 1} + \Delta_{n} - \omega ,W + \varGamma_{0 - 1} )\gg )\} . \hfill \\ \end{aligned} $$

The shape of the nitroxide radical EPR spectrum (Eq. (10)) can be simplified further for the intermediate concentration regime C ₀ < C < C* when the spin coherence transfer rate exceeds the inhomogeneous broadening of the nitrogen components of the spectrum. In this case, all spins in the nitrogen component have the same resonance frequency and the additional shift of the side components should be ±(1/6) (V ²/a _N) as it was already shown in [1, 4, 5]. Thus, in the intermediate concentration regime C ₀ < C < C*, Eq. (10) is reduced to the model situation considered in Ref. [1]. In this intermediate spin concentration case, the EPR spectrum is a sum of three components given by equations:

$$ J_{m} \approx - (w_{1} /3)\text{Re} \left\{ {_{{}} \left( {1 \, + {\text{im}}\left( {V/a_{\text{N}} } \right)} \right) \, G_{m} /\left( {1 + \left( {1/3} \right) \, VG_{m} } \right)} \right\},\quad m = 0,\; \pm 1, $$

$$ G_{1} = 1/\left( { - i\left( {\omega_{0} + a_{\text{N}} + \delta_{{{\text{ex}},1}} - \left( {1/6} \right)\left( {V^{2} /a_{\text{N}} } \right) - \omega } \right) - \left( {W + 3\langle \Delta^{2} \rangle /V + \varGamma_{01} } \right)} \right), $$

(11)

$$ G_{0} = 1/\left( { - i\left( {\omega_{0} - \omega } \right) - \left( {W + 3\langle \Delta^{2} \rangle /V + \varGamma_{00} } \right)} \right), $$

$$ G_{ - 1} = 1/\left( { - i\left( {\omega_{0} - a_{\text{N}} + \, \delta_{{{\text{ex}}, - 1}} + \left( {1/6} \right)\left( {V^{2} /a_{\text{N}} } \right) - \omega } \right) - \left( {W + 3\;\langle \Delta^{2} \rangle /V + \varGamma_{0 - 1} } \right)} \right). $$

Equation (11) coincides with results obtained in Ref. [1] for the model relevant for this intermediate spin coherence rate situation. The only minor difference concerns the line width. In Eq. (11), there appears an additional contribution 3‹Δ²›/V to the line width, which describes the contribution of the spin coherence transfer inside the nitrogen component. Note that the spin coherence transfer rate inside the nitrogen component is V/3 and ‹Δ²› is the dispersion of the super hyperfine interaction-induced distribution of the resonance frequencies. If this distribution is a Gaussian, then ‹Δ²› = σ.

Thus, Eqs. (10a, 11) show that in the low spin concentration case, the components of the EPR spectrum can be presented in the form:

$$ J_{m} = - (w_{1} /3)\text{Re} \left\{ {\left( {1 + {\text{im}}\left( {V/a_{\text{N}} } \right)} \right)G_{m} /\left( {1 \, + \, \left( {1/3} \right) \, VG_{m} } \right)} \right\}, $$

where

$$ G_{m} = \sum {g_{n} /( - i(\omega_{0} + \, ma_{\text{N}} + \, \delta_{{{\text{ex}},m}} {-}m\left( {1/6} \right)\left( {V^{2} /a_{\text{N}} } \right) + \Delta_{n} - w){-}W - \varGamma_{0m} ) \equiv A_{m} + i\Delta_{m} } $$

(12)

in the case of the slow spin coherence transfer regime (Eq. (10a)) or

$$ G^{\prime }_{m} = 1/( - i(\omega_{0} + ma_{\text{N}} + \delta_{{{\text{ex}},m}} {-}m\left( {1/6} \right)\left( {V^{2} /a_{\text{N}} } \right) - w){-}W - 3\langle \Delta^{2} \rangle /V - \varGamma_{0m} ) \equiv A{\prime }_{m} + i\Delta {\prime }_{m} ,\quad m = 0, \pm 1, $$

(12a)

in the case of an intermediate spin coherence transfer rate (Eq. (11)).

The results presented above show that in the case of the low spin concentration, the amplitude of the dispersion contribution does not depend on the super hyperfine structure of the nitrogen EPR spectrum components of the nitroxide radicals. In fact, the same amplitude was found in [1] under the assumption that there is no super hyperfine structure of the nitrogen components. However, the shape of the dispersion contribution as well as the shape of the absorption contribution depends on the super hyperfine structure. In the absence of the super hyperfine structure, the absorption and dispersion contributions are given by the real and imaginary parts of the Lorentzian form (1/(1 + iz)). In the case of the Gaussian distribution of the super hyperfine structure, the shape of the dispersion contribution is given by the imaginary part of the Voigt form [see Eq. (12)]. At the same time, the shape of the absorption contribution is not given simply by the real part A _m of the Voigt form even in the limit of very low concentrations. These statements are valid only for the very low concentrations, at C → 0. In the general case of the spin coherence transfer, in particular for spin concentrations around C ₀, the absorption and dispersion contributions to the EPR signal are not described by simple functions like the Lorentzian or Voigt forms.

2.3 Fast Spin Coherence Transfer Case, K _sct C ≫ a _N

At high concentrations, when V > 3 a _N, Eq. (10) is not valid. Under this condition, one has to use the general solution given by Eqs. (8, 9). However, in this limit case, the exchange narrowing effect operates and the total EPR spectrum of the nitroxide free radical appears as the Lorentzian absorption curve with the concentration-dependent dipolar broadening W − V = 1/T _2dd + 1/T′_2dd [see Eq. (6)]:

$$ J_{\text{EPR}} \cong w_{1} M_{0} \left( {W{-}V + \varGamma + 2a_{\text{N}}^{2} /\left( {3V} \right)} \right)/\left( {\left( {\omega_{0} - \omega } \right)^{2} + \left( {W{-}V + \varGamma + 2a_{\text{N}}^{2} /\left( {3V} \right)} \right)^{2} } \right). $$

(13)

Here, Γ = (1/3) (Γ ₀₁ + Γ ₀₀ + Γ _0-1), and a term 2 a ²_N /(3V) gives the spin coherence transfer contribution to the linewidth [4, 5].

3 Potential of the Approximate Solutions (Eqs. (10, 11)): Numerical Simulations

Thus, we derived the exact theoretical expressions (Eqs. (8, 9)) which describe the EPR spectrum of spin probes with allowance for the effects of the exchange, dipole–dipole, and hyperfine interactions. For three characteristic nitroxide free radical concentration ranges, approximate equations were proposed to describe the shape of the EPR spectra of the ¹⁴N nitroxide free radicals in the limit cases of the slow spin coherence transfer (Eqs. (10, 10a)), intermediate spin coherence transfer rate (Eq. (11)) and the fast spin coherence transfer (Eq. (13)). Note that Eq. (9) was obtained long ago in the spin exchange theory (see [5, 11]). The approximate solution relevant to the intermediate spin coherence transfer in the case of nitroxide radicals (Eq. (11)) was considered earlier in [1]. The fast spin coherence transfer case (Eq. (13)) is rather trivial and well known. A non-trivial aspect is that the dipolar broadening in this limit is equal not to the dipolar contribution to the spin decoherence, W, but to the dipolar contributions to spin decoherence and spin coherence transfer effects, W − V. Note that the dipolar contribution to W − V is larger than that to W, since V < 0 for the dipole–dipole interaction. Note that the last observation is relevant to the well-known result: the line broadening induced by the dipole–dipole interaction between like spins is larger than the dipolar broadening between unlike spins [7]. The new result of this work is the theoretical description of the nitrogen components of the EPR spectrum of the nitroxide radicals in the case of the slow coherence transfer (Eqs. (10, 10a)) when the spin coherence transfer transforms dramatically the shapes of nitrogen components of the spectrum.

The potential of the approximate solutions of the problem for different concentration regions was revealed by computer simulations of the EPR spectra. For the chosen set of magnetic resonance and kinetic parameters, a _N, σ, Γ _0k, K _sct, K _sd, we simulated the EPR spectrum using the exact theory (Eq. (9)) and the approximate theories (Eqs. (10, 10a, 11)) and compared the results of these computer experiments.

The key point of the approximate theories (Eqs. (10, 10a, 11)) is the reduction of the kinetic equations which describe the coupled motion of the hyperfine component magnetizations to the non-coupled motion of new variables (eigenvectors of the problem, i.e., definite combinations of the hyperfine component magnetizations). The EPR spectrum was presented as a sum of the three independent contributions.

It was assumed in the numerical simulations that the super hyperfine interactions with many protons lead to the Gaussian distribution of the resonance frequency shift Δ. In this case

$$ \begin{aligned} G(x,y) = \left( {1/\left( {2\pi \sigma } \right)^{1/2} } \right)\int {{\text{d}}\Delta } \exp \left( { - \Delta^{2} /\left( {2\sigma } \right)} \right)(1/(i(x + \, \Delta ) \, - y)) \hfill \\ = (1/(2\pi \sigma )^{1/2} )\int {{\text{d}}\Delta } \exp ( - \Delta^{2} /(2\sigma )) \, [ - \, y/((x \, + \Delta )^{2} + \, y^{2} ) - i(x \, + \Delta )/((x \, + \Delta )^{2} + \, y^{2} )]. \hfill \\ \end{aligned} $$

The real part of G(x, y) has the form of the symmetric absorption curve and the imaginary part has the form of the asymmetric dispersion curve.

At V = 0, e.g., at the zero radical concentration, the shape of each nitrogen hyperfine component is described by the real part of G(x, y) Eq. (12) with proper values of x and y [see Eqs. (10, 10a)]. Note that Re G(x, y) is the convolution of the Lorentzian profile 1/((x + Δ)² + y ²) and the Gaussian distribution f(Δ) representing homogeneous and inhomogeneous broadenings, respectively. This convolution is known as the Voigt form [6]. However, when the concentration increases, i.e. V ≠ 0, the spin exchange and dipole–dipole interaction effects are manifested in the shape of the EPR spectrum. Equations (10, 10a, 11) show that at V ≠ 0, the dispersion part of G(x, y) contributes to the shape of the EPR spectrum components, and as a consequence, the low- and high-field (side) components become asymmetric containing absorption and dispersion contributions.

To test the approximate Eqs. (10, 10a, 11), the EPR spectrum of the ¹⁴N nitroxide radical was simulated at different nitroxide free radical concentrations and a certain set of parameters (Fig. 4). Note that the intrinsic line widths Γ _0k are different for the nitrogen components [11]. The analytical expressions presented above allow to consider this fact. However, in our numerical simulations, we will suppose that those intrinsic line widths are equal, since their difference does not affect the contribution of the dispersion term to the spectrum components. They only broaden the absorption and dispersion terms of the spectrum components.

Fig. 4

Comparison of the spectra simulated using the exact solution Eqs. (8, 9) (dashed curves) and the sum of three components calculated using Eq. (10) (thin curves) and Eq. (10a) (thick curves). Parameters used in these simulations are: a _N = 16 G, g = 2, σ = 0.1 G ², W = V = K _ex C = 0.1 C G (C is measured in mM/L), Γ _0k  = 0.2 G

For the parameters used in the simulations in Fig. 4, the estimated values of the characteristic concentrations are C ₀ ≈ 30 mM/L, C* ≈ 80 mM/L.

These figures make it possible to conclude the following: In the very low concentration range 0 < C < 30 mM/L, the approximate Eqs. (10, 10a) give the EPR spectra which totally coincide with the exact spectrum. In the intermediate concentration range 30 mM/L < C < 80 mM/L, the approximate Eqs. (10, 10a) give the EPR spectra which are close to the exact spectrum. Thus, the perturbation theory (Eqs. (10, 10a)) does reasonably well describe the shape of the EPR spectrum of the ¹⁴N nitroxide radicals in the case of the slow and intermediate rate spin coherence transfer. At concentration C = 150 mM/L, the condition K _sct C < 3 a _N is not fulfilled, so that, as expected, the perturbation theory fails to describe the EPR spectrum shape.

Approximate Eqs. (10) and (10a) give close results (see Fig. 4). We consider Eq. (10a) as more preferable than Eq. (10). As it was pointed out above, Eq. (10a) overestimate the shifts of the side nitrogen components at very low-spin concentrations when the spin coherence transfer is also very slow. The frequency shifts under consideration are the second-order effect compared with a _N, namely, they can be estimated as a _N (K _sct C ₀/a _N)² < a _N. Therefore, at low nitroxide free radical concentration, this particular shift of the resonance frequencies is of minor importance. The situation changes when the spin concentration increases and the spin coherence transfer leads to the collapse of the proton hyperfine structure of the nitrogen components of the EPR spectrum. In this spin concentration range, Eq. (10) underestimates the line shifts under consideration. Equation (10) disregards the decrease in the super hyperfine interaction-induced inhomogeneous broadening of the nitrogen components and the shifts of the side nitrogen components as a whole to the center of gravity of the spectrum when the spin concentration increases. When the concentration increases, the frequency shift of the side nitrogen component as a whole should be equal to (1/6)a _N (K _sct C*/a _N)², while Eq. (10) contains less shifts for each individual proton hyperfine line inside the nitrogen component. It can be seen from the simulated spectra for C = 60, 80, 100 mM/L (Fig. 4) that approximate Eq. (10a) gives the better result concerning the position of the maxima of the side nitrogen components than Eq. (10). To highlight the last feature, the inset in Fig. 4 shows the behavior of simulated spectra near the maximum of the high-field nitrogen component.

At the spin concentrations C > C ₀, the nitrogen components of the EPR spectrum became the exchange narrowed homogeneously broadened lines. As a result in the concentration range C ₀ < C < C*, one can ignore the super hyperfine structure of the spectrum. For this case, the perturbation theory of the EPR spectrum of the nitroxide radical was developed in Ref. [1] [see Eq. (11)]. Equation (11) is simplified version of the perturbation theory result given by Eq. (10a). Note that Eq. (10a) considers explicitly the spin coherence transfer between super hyperfine structure lines inside nitrogen components, while in Eq. (11), the super hyperfine structure is ignored. We compared the spectra simulated using Eqs. (9), (10a), and (11) (Fig. 5).

Fig. 5

Comparison of the spectra simulated using the exact solution Eq. (9) (dashed curves) and the sum of three components calculated using Eq. (10a) (thick curves) and Eq. (11) (thin curves). Parameters used in these simulations are: a _N = 16 G, g = 2, σ = 0.1 G ², W = V = K _ex C = 0.1 C G (C is measured in mM/L), Γ _0k  = 0.2 G

Figure 5 shows that at concentrations C > 40 mM/L, the spectra calculated using the simplified Eq. (11) reproduce completely those simulated using the Eq. (10a). In the intermediate spin concentration region, which is 20 mM/L < C<100 mM/L for the parameters chosen for Fig. 5, the approximation Eq. (11) describes reasonably well the shape of the spectrum. Figure 6 shows the shapes of the quasi-independent components of the EPR spectrum simulated by Eq. (10a).

Fig. 6

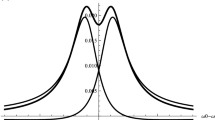
Simulated (Eq. (10a)) independent components of the EPR spectrum of the ¹⁴N nitroxide radical (a) and the derivative of the total EPR spectrum (b). The spectra are simulated with the following parameters: a _N = 16 G, g = 2, σ = 0.12 G ², W = V = 0.1 C G, C = 30 mM/L, and Γ _0k  = 0.2 G

Figure 6 shows that the side components have the asymmetric shape. They can be presented as a sum of the symmetric absorption contribution and the asymmetric dispersion contribution. Due to this asymmetry, the positive (max) and negative (min) amplitudes of the derivatives of the side components are not equal. This fact is used below to determine the contribution of the dispersion to the signal using the algorithm presented in [1].

4 Determination of the Kinetic Parameters V and W from the EPR Spectra

Discussion presented above provides an approach for analyzing the concentration transformations of the nitroxide EPR spectrum shape. Our approach is based on the paradigm developed by Bales and coworkers (see [2, 3, 10]). They elaborated a procedure for determining the spin exchange rate by analyzing the dispersion contribution to the shape of the EPR spectrum. In our work, we accept their main idea to use the dispersion contribution for determining the spin coherence transfer rate, i.e., for determining the kinetic parameter V. However, we implement this general idea in a different way based on the further development of the theoretical description of the spin concentration dependence of the shape of the EPR spectrum presented in this work (see also [1]).

The derivative of the spectrum is detected in the EPR experiment. We suggest the following steps for determining the spin coherence transfer rate V and the spin decoherence rate W. First, we find the value of the spin coherence transfer rate V from the dispersion contribution to the side components of the nitroxide radicals EPR spectrum using the algorithm developed in Ref. [1]. Second, the spin decoherence rate W is determined from the spin concentration broadening of the nitrogen components of the spectrum at the intermediate spin concentrations when 3∆Ω ₀ < V < 3a _N. Third, we suggest to simulate the EPR spectrum using the determined parameters V and W. By comparing the simulated spectrum with the spectrum detected in the experiment, one has to decide whether these parameters should be tuned further or not. Thus, our speculations concerning the analysis of the shape of the EPR spectrum and its spin concentration dependence based on the perturbation theory can give the optimal probe values of the kinetic parameters W and V in the course of the iterative procedure for determining exact values of these kinetic parameters.

To illustrate this approach, we performed the computer experiments with the model ¹⁴N nitroxide radical. For the computer simulations, we take the nitroxide radical with 12 equivalent protons. Note that in this case, the proton hyperfine structure can be described by the Gaussian distribution of the resonance frequencies. The kinetic parameters V and W are proportional to the spin concentration:

$$ V = K_{\text{sct}} C\quad {\text{and}}\quad W = K_{\text{sd}} C, $$

(14)

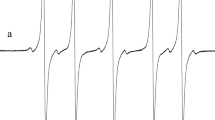
where K _sct is the spin coherence transfer rate constant and K _sd is the spin decoherence rate constant, both induced by the exchange and dipole–dipole interactions between radicals. For the chosen values of the decoherence and the spin coherence transfer rate constants, we simulate the EPR spectrum using Eq. (9). The spin concentration was varied during these computer simulations (Fig. 7).

Fig. 7

Simulated EPR spectrum derivative of the model ¹⁴N nitroxide radical with 12 protons. Parameters used in these simulations are: a _N = 16 G, a _P = 0.2 G, Γ _0k  = 0.2 G, K _ex = 0.1 G L/mM, K _dsct = K _dsd = 0: C = 10 mM/L (a) and C = 20 mM/L (b)

Figure 7 shows that the side nitrogen components of the spectra are asymmetric. According to Ref. [1] and discussion above, in the spin concentration region 3∆Ω ₀ < K _sct C < 3a _N, the dispersion contribution to the spectrum, J = Abs + p Dis, can be found from the measured ratio r = M _max/M _min (see Fig. 5 in Ref. [1]). The results obtained in [1] (Eq. (24) and Fig. 5) lead to the approximate equation:

$$ p = \frac{{\sqrt 3 (1 - \sqrt {2\left| r \right| - 1} )}}{2} $$

(15)

Using Eq. (15), one finds the dispersion contribution p

$$ p = - \, mV/a_{\text{N}} = - \, mK_{\text{sct}} C/a_{\text{N}} ,\quad m = 1,\;0,\; - 1. $$

(16)

Equations (15, 16) were obtained in Ref. [1], when the super hyperfine structure of the EPR spectrum was ignored. Therefore, they are valid in the intermediate concentration case C ₀ < C < C*. However, in this work, we showed that Eq. (16) gives the correct dispersion contribution p over the whole slow and intermediate rate spin coherence transfer region C < C* (K _sct C < 3a _N) even in the presence of the super hyperfine structure of the nitrogen components of the EPR spectrum of the nitroxide radical. Encouraged with the last observation we apply also Eq. (15) to the whole region 0 < K _sct C < 3 a _N of the slow and intermediate rate spin coherence transfer regimes. We consider the fact that the spin coherence transfer between super hyperfine structure lines inside the nitrogen components does not create an asymmetry of the nitrogen compounds as a whole. Therefore, we found the dispersion contribution p under the conditions 0 < K _sct C < 3a _N using Eq. (15), and then using Eq. (16), we determined the spin coherence transfer rate and rate constants.

For illustration, we find the p value for the spectra shown in Fig. 7.

At concentration 10 mM/L from Fig. 7, one has $r_{1} = \frac{{\max_{1} }}{{\min_{1} }} = \frac{0.672943}{ - 0.629748} = - 1.06859$ for the low-field component and r ₋₁ = (max₃)/(min₃) = 0.6297/(−0.6729) = −0.936. for the high-field component. From Eq. (19) for these r values, we find $p_{1} = - 0.05751$ and p ₋₁ = 0.057. Using Eq. (16), we find K _sct C = 0.92 G, K _sct = 0.092 G L/mM. The spectra in Fig. 7 were simulated using K _sct = 0.1 G L/mM. We see that K _sct = 0.092 G L/mM obtained as output is 8 % less than the spin coherence transfer rate constant used as the input parameter for simulation.

For C = 20 mM/L, the dispersion contribution should increase two times compared to the C = 10 mM/L case. From the spectrum in Fig. 7 for C = 20 mM/L, r ₁ = −1157 and r₋₁ = −0.864. From Eq. (15), we find p ₁ = 0.127, p ₋₁ = −0.127. Using Eq. (16), we obtain the output K _sct = 0.102 G L/mM almost coinciding with the value K _sct = 0.1 G L/mM used in the EPR spectra simulations. Note that according to the results presented above, r ₁ r ₋₁ = 1. In the case when the intrinsic line widths of the nitrogen components are equal, this is evident and expected result. Less evident is that this relation r ₁ r ₋₁ = 1 is valid for any values of the intrinsic line widths Γ _0k.

We simulated and analyzed the EPR spectrum for two model situations: neglecting the dipole–dipole contribution (closed circles in Fig. 8) and taking it into account (open circles in Fig. 8). First, we performed the computer experiment with a chosen set of input parameters, including the input coherence transfer rate V = K _sct C and the spin decoherence rate W = K _sd C: using exact Eq. (9), we obtained experimental spectra. Second, following the algorithm outlined above, we found the parameters r ₁ and r ₋₁ for the derivatives of these spectra. Then, using Eqs. (15, 16), we determined the spin coherence transfer rate which we call as the output value of the K _sct C.

Fig. 8

Correlation between the input and output spin coherence transfer rate V = K _sct C used as the input of the computer simulation of the EPR spectrum and the value of the kinetic parameter K _sct C obtained by analyzing the dispersion contribution to the simulated EPR spectrum component. The bisector is shown as the solid line. Parameters used in these simulations are: Γ _k  = 0.2 G, a _N = 16 G, g = 2, number of protons = 12, a _P = 0.2 G, K _ex = 0.05 G L/mM, K _dsct = K _dsd = 0 (open triangles); K _ex = 0.05 G L/mM, K _dsct = 0.005 G L/mM, K _dsd = 0.006 G L/mM (open circles); K _ex = 0.05 G L/mM, K _dsct = 0.01 G L/mM, K _dsd = 0.012 G L/mM (closed circles)

If the algorithm used for determining the parameter V from the EPR spectrum data on the basis of Eqs. (15, 16) would be ideal, the plot in Fig. 8 is expected to be a straight line—a bisector. Any deviations from the bisector characterize errors in the determination of the spin coherence transfer rate following our algorithm. Figure 8 shows that the data from the computer experiment belong to the bisector in the low-spin concentration region. Thus, the spin coherence transfer rate V can be determined by measuring the parameter r = M _max/M _min in the region of low-spin concentration. It was discussed above that there are two characteristic spin concentrations. The concentration C ₀ characterizes the collapse of the super hyperfine structure of the EPR spectrum. It occurs when the spin coherence transfer rate inside nitrogen components is equal to the inhomogeneous broadening induced by the super hyperfine interactions: (1/3)K _ex C ₀ = ∆Ω ₀ (see Fig. 1). In the numerical simulations (Fig. 8), K _ex = 0.05 G L/mM, ∆Ω ₀ = 0.35 G. Thus, in this case, C ₀ = 20 mM/L. It is shown in Fig. 8 that the spin coherence transfer rates obtained by analyzing the simulated spectra belong to the bisector up to the spin concentration of about 30–40 mM/L. At the higher spin concentrations, the data of V obtained from analysis of the simulated spectra deviate from the bisector considerably. The output rate starts to deviate from the bisector even earlier (at lower spin concentration) if both, the dipole–dipole and the exchange interactions, contribute (compare closed and open circles data with open triangles data in Fig. 8). This deviation is explained by the effect of the overlapping of the nitrogen components of the EPR spectrum. The parameter r = M _max/M _min is very sensitive to this overlapping.

The consideration of the spectrum shape at different concentration ranges shows that the spin decoherence rate W and the spin coherence transfer rate V determine directly the widths of the spectrum components in the intermediate concentrations C ₀ < C < C*. According to the theory developed in this work, in the intermediate spin concentration range, the peak-to-peak distances should manifest the linear concentration dependence. From Eq. (11) (see also [1]), the peak-to-peak distances in the EPR spectrum derivative for the components are:

$$ \Delta \varOmega_{\text{m}} = f\left( p \right) \, \Delta \varOmega_{{0{\text{m}}}} , $$

(17)

where

$$ \Delta \varOmega_{{ 0 {\text{m}}}} = W - V/3 \, + 3\langle \Delta^{2} \rangle /V + \varGamma_{{ 0 {\text{m}}}} \equiv \varGamma \left( C \right) \, + \, \varGamma_{{ 0 {\text{m}}}} , $$

(18)

$$ f\left( p \right) = 2 \cdot 3^{1/2} \left( {1 + p^{2} } \right)^{1/3} \text{Im} \left( {\left( {1 \, + ip} \right)^{1/3} /p} \right). $$

When the dispersion does not contribute to the spectrum, i.e., p = 0, then f(p) = 2·3^−1/2 = 1.1547.

To check these expectations, we simulated the EPR spectra again and found the peak-to-peak distances for their derivatives. The simulations were done for the same set of the input parameters as in Fig. 8. For the simulated spectra, the peak-to-peak distance and the concentration-dependent part of the line widths Γ(C) were calculated. If our algorithm is valid, the output Γ(C) should coincide with the input value. The results of the computer experiments and analysis of the simulated spectra are shown in Fig. 9.

Fig. 9

Correlation between the input and output values of the concentration-dependent part of the line width Г(C) of the low-field component of the ¹⁴N nitroxide radical. Parameters used in these simulations are: Γ ₁ = 0.2 G, a _N = 16G, g = 2, number of protons = 12, a _P = 0.2 G, K _ex = 0.05 G L/mM, K _dsct = K _dsd = 0 (open triangles), K _ex = 0.05 G L/mM, K _dsct = 0.005 G L/mM, K _dsd = 0.006 G L/mM (open squares), K _ex = 0.05 G L/mM, K _dsct = 0.01 G L/mM, K _dsd = 0.012 G L/mM (closed squares)

Figure 9 shows that in the concentration range (30, 100 mM/L), the data of the analysis of the simulated EPR spectra are close to the bisector. Thus, our algorithm gives reliable results for determining the concentration-dependent spin decoherence rate Г(C).

Figure 9 shows the non-linear spin concentration dependence of the line width at low concentrations C < C ₀ and at high concentrations C ≈ C* (K _sct C* = 3a _N). These deviations are expected. At very low concentrations, the exchange narrowing of individual nitrogen components interferes with the exchange broadening due to the spin exchange between different nitrogen components. At high concentrations, the exchange broadening interferes with the collapse of the whole spectrum into one homogeneous line.

Note that the line width Г(C) contains contributions of the spin exchange and dipole–dipole interactions. The separation of these contributions was comprehensively considered in [1].

5 Concluding Remarks

The shape of the EPR spectra of the spin probes depends on the spin decoherence and spin coherence transfer between probes induced by the exchange and dipole–dipole interactions between spins. However, manifestations of these interactions in the EPR experiments depend on other interactions, e.g., the hyperfine interaction of unpaired electrons with magnetic nuclei. In this work, we analyzed comprehensively the manifestations of the exchange and dipole–dipole interactions in the EPR spectrum in non-viscous solutions of ¹⁴N containing spin probes (nitroxide free radicals). This work is closely related with [1], where this problem was studied under the assumption that the super hyperfine structure of the EPR spectrum due to the interaction with all magnetic nuclei except for of nitrogen can be ignored. Here, the theory was extended to include into consideration all magnetic nuclei of the spin probes. The consideration was focused on the case of the slow spin coherence transfer. It was shown that the side components of the EPR spectrum contain the absorption and dispersion terms: J _EPR = Abs + p Dis, and p = −m K _sct C/a _N (m = 1, −1 for the left- and right-hand nitrogen components, respectively) independent of the super hyperfine structure due to magnetic nuclei except for nitrogen. This observation provides a way for determining the spin coherence transfer rate by analyzing the dispersion contribution to the side nitrogen components of the EPR spectrum at the low-spin probe concentration.

The spin decoherence leads to broadening of the resonance lines. However, the shapes of the dispersion term as well as the shape of the absorption contribution depend on the super hyperfine structure. Therefore, the concentration-dependent spin decoherence rate can be determined from the concentration broadening but only in the intermediate range of the spin probe concentration. An algorithm was proposed and tested for determining the rates of the spin coherence transfer and spin decoherence induced by the exchange and dipole–dipole interactions between spin probes in dilute solutions. The algorithm was tested by the results of the computer experiments: numerical simulations of the EPR spectra and the determination of the spin coherence transfer and spin decoherence rates by analyzing the simulation data using the algorithm suggested. We hope that this algorithm will be useful when studying the spin exchange process.

Appendix

1.1 Perturbation Theory of the EPR Spectrum Shape of ¹⁴N Nitroxide Radicals

We consider the solution of the ¹⁴N nitroxide radicals. The hyperfine interaction with nitrogen nuclei in nitroxides is much larger than the super hyperfine interaction with other magnetic nuclei. In this case at the low radical concentration (C → 0), the expected EPR spectrum is shown schematically in Fig. 1. There are three bands which correspond to the projections of the nitrogen nuclear spins, m = +1, 0, −1. Each of these bands has an additional super hyperfine structure due to the interaction of unpaired electrons with other (except for nitrogen) magnetic nuclei (protons, deuterons, ¹³C). The widths of these bands ∆Ω ₀ (see Fig. 1) are less than the distances between centers of these bands, ∆Ω ₀ < a _N. The spin coherence transfer terms V _kn in Eqs. (1, 7) connect magnetizations of the subensemble of nitroxides with different resonance frequencies. In the wide range of the radical concentrations, the transition terms V _kn can be much less than the nitrogen hyperfine splitting, (1/3) K _ex C < a _N. In this case, the spin coherence transfer between spins which belong to different nitrogen EPR spectrum bands can be treated in the framework of the perturbation theory for non-degenerate resonance frequencies. Under the same condition, the spin exchange inside nitrogen components of the EPR spectrum corresponds to the quasi-degenerate case.

The EPR spectrum shape is found from the solution of the system of Eq. (7) in the rotating frame for the partial transverse magnetizations M _k :

$$ ( - i(\omega_{k} + \delta_{k} - \omega) - \varGamma_{k} ) \, M_{k} - W \, M_{k} + g_{k} VM = i\omega_{1} g_{k} M_{0} , $$

(19)

where W = K _ex C + 1/T _2dd, V = K _ex C − 1/T′_2dd.

We divide all subensembles of nitroxide radicals into three groups which correspond to three projections of the ¹⁴N nuclear spins, m = 1, 0, −1, while a set of numbers {n} characterizes all super hyperfine structure components in each nitrogen component of the EPR spectrum (see Fig. 1). Then, in Eq. (19), k ≡ {m, n}, M _k  ≡ M _mn  = {M _1n , M _0n , M _−1n }, g _k  ≡ g _m g _n  = (1/3)g _n . In these notations, we rewrite Eq. (19) as:

$$ ( - i(\omega_{1n} + \delta_{1n} - \omega) \, - \varGamma_{01} )M_{1n} - \, W \, M_{1n} + \left( {1/3} \right) \, g_{n} V \, \left( \sum {M_{1n} } + {\sum {\varvec M_{0n} } + \sum {\varvec M_{ - 1n} } } \right) = i {\omega_{1} M_{1n,eq} ,} $$

$$( - i(\omega_{0n} + \delta_{0n} - \omega) - \varGamma_{00} ) \, M_{0n} - W \, M_{0n} + \left( {1/3} \right) \, g_{n} V \, \left(\sum M_{0n} + \sum \varvec M_{1n} + \sum \varvec M_{ - 1n} \right) = i\omega_{1} M_{0n,{\text{eq}}},$$

(20)

$$ {( - i(\omega_{ - 1n} + \delta_{ - 1n} - \omega) \, - \varGamma_{0 - 1} ) \, M_{ - 1n} - W \, M_{ - 1n} + \, \left( {1/3} \right) \, g_{n} V \, \left( {\sum { M_{ - 1n} + \sum {\varvec M_{1n} + \sum {\varvec M_{0n} } } } } \right) = i\omega_{1} M_{0 - 1n, \, eq} }. $$

In these equations, the terms marked in bold italic describe the spin exchange between spins with sufficiently large difference of their resonance frequencies. Their contributions to the solution of Eq. (20) can be found using the perturbation theory for the non-degenerate case. In the approximation, linear over V the partial magnetizations M _1n , M_0n , and M _−1n and the right-hand sides of Eq. (20) take the form:

$$ M*_{mn} \left( {\omega_{mn} } \right) = M_{mn} \left( {\omega_{mn} } \right) + i\left( {1/3} \right)g_{n} V\sum {M_{pq} \left( {\omega_{pq} } \right)/\left( {\omega_{mn} - \, \omega_{pq} } \right) \, \quad (p \ne m).} $$

(21)

The right-hand side of Eq. (20) is transformed analogously:

$$ M*_{mn,eq} = \, g_{mn} \left( {1 \, + iV\sum {g_{pq} /\left( {\omega_{mn} - \, \omega_{pq} } \right)} } \right)M_{eq} = \, M_{eq} \left( {1/3} \right)g_{n} \left( {1 + i\left( {1/3} \right)V\sum {g_{q} /\left( {\omega_{mn} - \, \omega_{pq} } \right))} } \right)\quad \, (p \ne m). $$

(22)

Due to the spin coherence transfer between different nitrogen components, the resonance frequencies shift as:

$$ \omega *_{mn} = \omega_{mn} - \, g_{mn} V^{2} \sum {g_{pq} /(\omega_{mn} - \omega_{pq} )\quad \, (p \ne m).} $$

(23)

In Eqs. (21–23), the denominators of 1/(ω _mn  − ω _pq ) are the difference of the resonance frequencies of spins, which belong to different nitrogen components of the EPR spectrum. We assume that the difference (ω _mn  − ω _pq ) is mainly determined by the hyperfine interaction with nitrogen: (ω _1n  − ω _0q ) ≅ a _N, (ω _0n  − ω _−1q ) ≅ a _N, (ω _1n  − ω _−1q ) ≅ 2 a _N. With this approximation, Eqs. (21–23) take the forms:

$$ M*_{1n} \left( {\omega_{mn} } \right) \cong M_{1n} \left( {\omega_{mn} } \right) \, + i\left( {1/3} \right) \, g_{n} \left( {V/a_{N} } \right)\sum {M_{0q} \left( {\omega_{pq} } \right) \, + i\left( {1/3} \right) \, g_{n} \left( {V/\left( {2a_{N} } \right)} \right)\sum {M_{ - 1q} \left( {\omega_{pq} } \right),} } $$

$$ \begin{aligned} M*_{0n} \left( {\omega_{mn} } \right) \cong M_{0n} \left( {\omega_{mn} } \right) \, {-}i\left( {1/3} \right) \, g_{n} \left( {V/a_{N} } \right) \, \sum {M_{1q} \left( {\omega_{pq} } \right) \, + i\left( {1/3} \right) \, g_{n} \left( {V/a_{N} } \right)\sum {M_{ - 1q} \left( {\omega_{pq} } \right),} } \hfill \\ M*_{ - 1n} \left( {\omega_{mn} } \right) \cong M_{ - 1n} \left( {\omega_{mn} } \right) \, {-}i\left( {1/3} \right) \, g_{n} \left( {V/\left( {2a_{N} } \right)} \right)\sum {M_{1q} \left( {\omega_{pq} } \right) \, {-}i\left( {1/3} \right) \, g_{n} \left( {V/a_{N} } \right)\sum {M_{0q} \left( {\omega_{pq} } \right),} } \hfill \\ \end{aligned} $$

$$ M_{z} *_{1n, \, eq} = \, g_{n} \left( {1/3} \right) \, \left( {1 + i\left( {1/2} \right)\left( {V/a_{\text{N}} } \right)} \right) \, M_{eq} , $$

$$ M_{z} *_{0n, \, eq} = \, g_{n} \left( {1/3} \right) \, M_{eq} , $$

(24)

$$ M_{z} *_{ - 1n,eq} = \, g_{n} \left( {1/3} \right) \, \left( {1 \, - i\left( {1/2} \right) \, \left( {V/a_{\text{N}} } \right)} \right) \, M_{eq} , $$

$$ \omega*_{1n} = \omega_{1n} - \, \left( {1/2} \right) \, g_{n} \left( {V^{2} /a_{\text{N}} } \right), $$

$$ \omega*_{0n} = \omega_{0n} , $$

$$ \omega*_{ - 1n} = \omega_{ - 1n} + \left( {1/2} \right) \, g_{n} \left( {V^{2} /a_{\text{N}} } \right). $$

Thus, for the small parameter (1/3) V/a _N < 1, Eq. (20) takes the form of the uncoupled equations for the transverse magnetizations of the nitrogen hyperfine components:

$$ ( - i(\omega*_{1n} + \delta_{1n} - \omega) \, {-} \, W \, - \varGamma_{1} ) \, M*_{1n} + \, \left( {1/3} \right) \, g_{n} V \, M*_{1} = \, g_{n} i\omega_{1} \left( {1/3} \right) \, \left( {1 + i\left( {1/2} \right) \, \left( {V/a_{N} } \right)} \right) \, M_{eq} , $$

$$ ( - i(\omega*_{0n} + \delta_{0n} - \omega) \, {-} \, W \, - \varGamma_{0} ) \, M*_{0n} + \, \left( {1/3} \right) \, g_{n} V \, M*_{0} = \, g_{n} i\omega_{1} \left( {1/3} \right) \, M_{eq} , $$

(25)

$$ ( - i(\omega*_{ - 1n} + \delta_{ - 1n} - \omega) \, {-} \, W \, - \varGamma_{ - 1} ) \, M*_{ - 1n} + \, \left( {1/3} \right) \, g_{n} V \, M*_{ - 1} = \, g_{n} i\omega_{1} \left( {1/3} \right) \, \left( {1 - i\left( {1/2} \right) \, \left( {V/a_{N} } \right)} \right) \, M_{eq} , $$

where M*₁ = Σ M*_1n , M*₀ = Σ M*_0n , M*₋₁ = Σ M*_−1n .

These equations give:

$$ M*_{1n} = \, (g_{n} / \, ( - i(\omega*_{1n} + \delta_{1n} - \omega){-}W \, - \varGamma_{01} )) \, (i\omega_{1} \left( {1/3} \right) \, \left( {1 + i\left( {1/2} \right) \, \left( {V/a_{N} } \right)} \right) \, M_{eq} - \left( {1/3} \right) \, V \, M*_{1} ), $$

$$ M*_{0n} = \, (g_{n} / \, ( - i(\omega*_{0n} + \delta_{0n} - \omega){-}W - \varGamma_{00} )) \, (i\omega_{1} \left( {1/3} \right) \, M_{eq} - \left( {1/3} \right) \, VM*_{0} ), $$

$$ M*_{ - 1n} = (g_{n} / \, ( - i(\omega*_{ - 1n} + \delta_{ - 1n} - \omega){-}W \, - \varGamma_{0 - 1} )) \, (i\omega_{1} \left( {1/3} \right) \, \left( {1 - i\left( {1/2} \right) \, \left( {V/a_{N} } \right)} \right) \, M_{eq} - \left( {1/3} \right) \, V \, M*_{ - 1} ). $$

The magnetizations M*₁, M*₀, and M*₋₁ can be found straightforwardly:

$$ M*_{m} = C_{m} G_{m} /\left( {1 \, + \, \left( {1/3} \right)VG_{m} } \right), $$

(26)

where

$$ G_{m} = \sum {g_{n} / ( - i(\omega *_{mn} + \delta_{mn} - \omega ) \, {-} \, W \, - \varGamma_{0m} ),} $$

$$ C_{m} = (i\omega_{1} \left( {1/3} \right) \, \left( {1 + im\left( {1/2} \right) \, \left( {V/a_{N} } \right)} \right) \, M_{eq} ,\quad m = + 1,0,\; - 1. $$

(27)

In the EPR experiments, one observes the total transverse magnetization M = M ₁ + M ₀ + M ₋₁. In the approximation, linear over V/a _N [see Eqs. (21, 24)]

$$ M_{1} \cong M*_{1} {-}i\left( {1/3} \right) \, \left( {V/a_{\text{N}} } \right) \, M*_{0} {-}i\left( {1/3} \right) \, \left( {V/2a_{\text{N}} } \right) \, M*_{ - 1} , $$

$$ M_{0} \cong M*_{0} + i\left( {1/3} \right) \, \left( {V/a_{\text{N}} } \right) \, M*_{1} {-}i\left( {1/3} \right) \, \left( {V/a_{\text{N}} } \right) \, M*_{ - 1} , $$

$$ M_{ - 1} \cong M*_{ - 1} + i\left( {1/3} \right) \, \left( {V/\left( {2a_{\text{N}} } \right)} \right) \, M*_{1} + i\left( {1/3} \right)\left( {V/a_{\text{N}} } \right) \, M*_{0} . $$

Thus, the EPR spectrum is given:

$$ J = - \text{Im} \left\{ M \right\} = J_{1} + \, J_{0} + \, J_{ - 1} , $$

$$ \begin{aligned} J_{m} = - \text{Im} \left\{ {(1 \, + {\text{im}}\left( {1/2} \right)\left( {V/a_{\text{N}} } \right)M*_{m} } \right\} \cong - \left( {1/3} \right)\text{Im} \{ i\omega_{1} \left( {1 + im\left( {V/a_{\text{N}} } \right)} \right)G_{m} /\left( {1 + \left( {1/3} \right) \, V \, G_{m} } \right)\} \, \hfill \\ { = } - (\omega_{1} /3)\text{Re} \left\{ {_{{}} \left( {1 \, + im \, \left( {V/a_{\text{N}} } \right)} \right) \, G_{m} /\left({1\,+ \,\left({1/3} \right)\,V\,G_{m}} \right)} \right\}. \hfill \\ \end{aligned} $$

(28)

$$ G_{m} = \sum { g_{n} /( - i(\omega *_{mn} + \delta_{mn} - \omega ){-}W \, - \varGamma_{0m} ).} $$