Numeric Calculation of Antiferromagnetic Resonance Frequencies for the Noncollinear Antiferromagnet

Abstract

We present an algorithm for the numeric calculation of antiferromagnetic resonance frequencies for the noncollinear antiferromagnets of general type. This algorithm uses general exchange symmetry approach (Andreev and Marchenko, Sov. Phys. Usp. 130:39, 1980) and is applicable for description of low-energy dynamics of an arbitrary noncollinear spin structure in weak fields. Algorithm is implemented as a MatLab and C$++$ program codes, available for download. Program codes are tested against some representative analytically solvable cases.

1 Introduction

Antiferromagnetic ordering is observed at low temperatures in a vast amount of crystals. In the simplest case, magnetic ions can be grouped into two sublattices with antiparallel average spins yielding the collinear antiferromagnetic structure. However, such collinear structures do not cover all possible types of antiferromagnetic order: one can easily imagine magnets with more than two sublattices or helicoidal structures, which cannot be deduced to a finite number of sublattices at all. Numerous examples of such systems are known, e.g., three-sublattice “triangular” antiferromagnetic order in CsNiCl$_3$ and RbNiCl$_3$ [2, 3], 12-sublattices ordering in an Mn$_3$Al$_2$Ge$_3$O$_{12}$ garnet [4, 5], spiral ordering in LiCu$_2$O$_2$ [6–8], and complicated multi-$\mathbf {k}$ structure in strongly frustrated pyrochlore magnet Gd$_2$Ti$_2$O$_7$ [9].

Electron spin resonance (antiferromagnetic resonance, AFMR) is a powerful and sensitive tool to study low-energy dynamics of the magnetically ordered systems. By exciting uniform oscillations (i.e., $k=0$ spin waves) of the ordered spin structure one can investigate its properties: orientation of the ordered structure with respect to the crystal, strength of the anisotropic interactions fixing this orientation, and various spin-reorientation transitions. Due to high-energy resolution of microwave AFMR spectrometry, spin-wave spectrum details at $\mathbf {k}=0$ can be quite routinely determined with accuracy up to 5 mkeV (corresponding to the resolution of 1 GHz), thus strongly complimenting powerful inelastic magnetic neutron scattering techniques at low energies.

However, interpretation of the antiferromagnetic resonance data for complicated magnetic structures is sometimes difficult. Antiferromagnetic resonance frequencies for a collinear structure can be calculated relatively easily in a two-sublattice model [10]. Similar calculations for a noncollinear magnets are much less general: many-sublattice model calculations using a mean-field theory approach are very cumbersome [11]; standard (Holstein–Primakoff like) spin-wave theory approach to many-sublattice antiferromagnets is also complicated (e.g., [12, 13]). Moreover, analytical solution of these equations is usually out of the question for general mutual orientation of the magnetic field and sublattice magnetizations. Numeric calculations of spin-wave spectra are also known, see e.g., SpinW library by Tóth [14], but they rely on strongly model-dependent microscopic hamiltonian.

Some of these difficulties can be overcome using an exchange symmetry approach developed in [1]. This approach allows to build up general hydrodynamic description of low-energy dynamics of an antiferromagnet. It was successfully applied for various magnetic systems [3, 5, 8, 15–17]. However, analytical solution for f(H) dependency (which is the characteristic observable in antiferromagnetic resonance experiment) remains complicated, if possible at all, for arbitrary direction of magnetic field.

In the present manuscript, we describe numeric approach to the solution of dynamic equations within framework of exchange symmetry approach [1] in the arbitrary case. The developed algorithm is implemented in program codes, available on the authors homepage [18].

2 Brief Basics of Exchange Symmetry Approach and Derivation of Dynamic Equations

First, we briefly recall necessary equations of exchange symmetry theory [1] to be used in our calculations. The main limitation of this theory is that distortions of the ordered spin structure are small, which limits its applicability to the low fields $H\ll H_{\mathrm{ex}} \simeq J/(g\mu _\mathrm{B})$. In particular, this limitation excludes from consideration various phase transitions with complete restructuring of the order parameter (collinear–noncollinear transitions, various magnetization plateaus phases, etc.). Under this assumption, any noncollinear magnetic structure can be described by three unitary orthogonal vectors $\mathbf {l}_{1,2,3}$ (e.g., planar structure with a wavevector $\mathbf {k}$ can be described as $\mathbf {S}(\mathbf {r})={\mathbf {l}}_1 \cos (\mathbf {k} \mathbf {r})+{\mathbf {l}}_2 \sin (\mathbf {k} \mathbf {r})$, with ${\mathbf {l}}_3={\mathbf {l}}_1\times {\mathbf {l}}_2$). All static properties and low-energy dynamics of this structure can be described by its Lagrangian with Lagrangian density (we use here notations of Refs. [8, 19])

$$\begin{aligned} \mathcal{L}=\sum _i \frac{I_i}{2} \left( \dot{\mathbf {l}}_i +\gamma \left[ \mathbf { l}_i \times \mathbf { H} \right] \right) ^2 - U_\mathrm{A}(\left\{ {\mathbf {l}}_i\right\} ) \end{aligned}$$

(1)

here $\gamma$ is a free electron gyromagnetic ratio and $U_\mathrm{A}$ is the energy of anisotropy. Constants $I_i\ge 0$ are related to susceptibilities as $\mathbf {M}=\frac{\partial \mathcal{L}}{\partial \mathbf {H}}$: magnetic susceptibilities for the field applied along ith vector are $\chi _1=\gamma ^2(I_2+I_3)$, $\chi _2=\gamma ^2(I_1+I_3)$, $\chi _3=\gamma ^2(I_1+I_2)$.

Anisotropy energy should be invariant under crystal symmetry transformation, its exact form depends on the symmetry of the particular crystal and on the exchange symmetry of the ordered phase; relationship between $I_i$ constants is also fixed by symmetry of the susceptibilities tensor for a given spin structure. Some examples for the known analytically solvable cases are given in Appendix. Note that $I_i$ constants and exact form of the anisotropy energy are the only parameters of this approach. Once they are deduced only the formal operations remains.

First, static equilibrium position $\mathbf {l}_i^{(0)}$ have to be found by minimization of potential energy density

$$\begin{aligned} {\Pi }=-\sum _i \frac{I_i}{2} \gamma ^2 \left[ \mathbf { l}_i \times \mathbf { H} \right] ^2 + U_\mathrm{A}(\left\{ {\mathbf {l}}_i\right\} ) \end{aligned}$$

(2)

Second, frequencies of small oscillations near equilibrium have to be deduced. We suppose here that these oscillations are parameterized by some three non-degenerate variables $\left\{ \phi _\alpha \right\}$, e.g., Euler angles or other suitable variables. For the sake of simplicity we take that all of $\phi _\alpha =0$ at equilibrium position. Potential energy has a quadratic minimum at the equilibrium, thus when looking for small oscillations we can replace potential energy by its quadratic expansion. This substitution explicitly excludes possible problems of a numeric algorithm due to the finite accuracy of minimum determination. Lagrangian density is then

$$\begin{aligned} \mathcal{L}=\sum _i \frac{I_i}{2} \left( \dot{\mathbf {l}}_i\right) ^2 +\gamma \sum _i I_i\left( {\dot{\mathbf {l}}}_i\cdot \left[ {\mathbf {l}}_i\times \mathbf {H}\right] \right) -\frac{1}{2}\sum _{\beta ,\delta }\left( \frac{\partial ^2 \Pi }{\partial \phi _\beta \partial \phi _\delta }\right) _{0}\phi _\beta \phi _\delta \end{aligned}$$

(3)

here $(\ldots )_0$ index means that derivative is calculated at equilibrium position.

To obtain dynamic equations linear in $\phi _\alpha$ or its time derivatives, $\mathbf {l}_i$ have to be expanded up to second order in $\phi _\alpha$:

$$\begin{aligned} \mathbf {l}_i=\, & {} \mathbf {l}_i^{(0)}+ \sum _\beta \left( \frac{\partial \mathbf {l}_i}{\partial \phi _\beta }\right) _0\phi _\beta +\frac{1}{2}\sum _{\beta ,\delta }\left( \frac{\partial ^2\mathbf {l}_i}{\partial \phi _\beta \partial \phi _\delta }\right) _0\phi _\beta \phi _\delta \\ \dot{\mathbf {l}}_i= & {} \sum _\beta \left( \frac{\partial {\mathbf {l}}_i}{\partial \phi _\beta }\right) _{0} \dot{\phi }_\beta +\sum _{\beta ,\delta }\left( \frac{\partial ^2\mathbf {l}_i}{\partial \phi _\beta \partial \phi _\delta }\right) _0\phi _\beta \dot{\phi }_\delta , \end{aligned}$$

then with linear over $\phi _\alpha$ accuracy

$$\begin{aligned} \frac{\partial \mathcal{L}}{\partial \phi _\alpha }=\, & {} \gamma \sum _{i, \beta \ne \alpha } \left( \left( \frac{\partial {\mathbf {l}}_i}{\partial \phi _\beta }\right) _0 \cdot \left[ \left( \frac{\partial {{\mathbf {l}}_i}}{\partial \phi _\alpha }\right) _0\times \mathbf {H}\right] \right) {\dot{\phi }}_\beta \\&+\gamma \sum _{i,\beta } I_i \dot{\phi }_\beta \left( \frac{\partial ^2\mathbf {l}_i}{\partial \phi _\alpha \partial \phi _\beta }\right) _0\cdot \left[ \mathbf {l}_i^{(0)}\times \mathbf {H}\right] - \sum _\beta \left( \frac{\partial ^2 \Pi }{\partial \phi _\alpha \partial \phi _\beta }\right) _{0}\phi _\beta \end{aligned}$$

and so forth.

Variation of the action results in three Euler–Lagrange equations

$$\begin{aligned} \frac{\mathrm{d} }{\mathrm{d}t}\frac{\partial \mathcal{L}}{\partial \dot{\phi }_\alpha }-\frac{\partial \mathcal{L}}{\partial \phi _\alpha }=0 \end{aligned}$$

(4)

By summing up all terms and by substituting uniform harmonic oscillations $\phi _\beta =\phi _\beta ^{(0)} \mathrm{e}^{\imath \omega t}$ we obtain equations on oscillation amplitudes $\phi _\beta ^{(0)}$. Required degeneracy of these equations results in the condition $\mathrm{det}\mathcal{M}=0$ where matrix $\mathcal{M}$ of the linear equations is defined as

$$\begin{aligned} \mathcal{M}_{\alpha \beta }= & {} -\omega ^2 \sum _i I_i \left( \left( \frac{\partial {\mathbf {l}}_i}{\partial \phi _\alpha }\right) _{0} \cdot \left( \frac{\partial {\mathbf {l}}_i}{\partial \phi _\beta }\right) _{0}\right) \nonumber \\&+2\imath \omega \gamma \sum _i I_i \left( \left( \frac{\partial {\mathbf {l}}_i}{\partial \phi _\alpha }\right) _0 \cdot \left[ \left( \frac{\partial {{\mathbf {l}}_i}}{\partial \phi _\beta }\right) _0\times \mathbf {H}\right] \right) +\left( \frac{\partial ^2 \Pi }{\partial \phi _\alpha \partial \phi _\beta }\right) _{0} \end{aligned}$$

(5)

The equation det$\mathcal{M}=0$ results in real cubic equation for $\omega ^2$, all complex coefficients will sum to zero. Solution of this equation yields eigenfrequencies of small oscillations we sought for.

Experimental observation of these small oscillations in standard magnetic resonance experiment is, in fact, observation of the absorption of microwave radiation of certain polarization. Thus, information about oscillation of magnetization $\mathbf {m}(t)=\mathbf {m}\mathrm{e}^{\imath \omega t}$ is important as well. It can be calculated straightforwardly as $\mathbf {M}=\frac{\partial \mathcal{L}}{\partial \mathbf {H}}=\mathbf {M}_0+\mathbf {m} \mathrm{e}^{\imath \omega t}$, oscillating magnetization vector is

$$\begin{aligned} \mathbf {m}=\, & {} \imath \gamma \omega \sum _{i,\beta }I_i \left[ \left( \frac{\partial \mathbf {l}_i}{\partial \phi _\beta }\right) _0\times \mathbf {l}_i^{(0)}\right] \phi _\beta ^{(0)}\nonumber \\&- \gamma ^2 \sum _{i,\beta }I_i\left( \left( \left( \frac{\partial \mathbf {l}_i}{\partial \phi _\beta }\right) _0\cdot \mathbf {H}\right) \mathbf {l}_i^{(0)}+\left( \mathbf {l}_i^{(0)}\cdot \mathbf {H}\right) \left( \frac{\partial \mathbf {l}_i}{\partial \phi _\beta }\right) _0\right) \phi _\beta ^{(0)} \end{aligned}$$

(6)

complex form of $\mathbf {m}$ describes circular or elliptical precession of magnetization: $\mathbf {m}(t)=\left( \mathbf {u}+\imath \mathbf {v}\right) \mathrm{e}^{\imath \omega t}$ means that real magnetization is $\mathbf {u} \cos \omega t-\mathbf {v} \sin \omega t$. Average square of longitudinal and transverse components of the oscillating magnetization can be used as a simple indicator of excitation conditions

$$\begin{aligned} \langle {\mathbf {m}}^2\rangle= & {} \frac{1}{2}({\mathbf {u}}^2+{\mathbf {v}}^2)\end{aligned}$$

(7)

$$\begin{aligned} \langle m_{||}^2 \rangle= & {} \frac{1}{2}((\mathbf {u}\cdot \mathbf {n})^2+(\mathbf {v}\cdot \mathbf {n})^2)\end{aligned}$$

(8)

$$\begin{aligned} \langle m_{\perp }^2\rangle= & {} \langle {\mathbf {m}}^2\rangle -\langle m_{||}^2 \rangle \end{aligned}$$

(9)

here $\mathbf {n}$ is a unitary vector in the applied field direction. Being interested in only the polarization of oscillating magnetization, we will norm its square averaged (if non-zero) to unity: $\langle {\mathbf {m}}^2\rangle =1$.

Determination of the initial guesses for the model parameters is case dependent. We will note here that equation det$\mathcal{M}=0$ allows one to scale all parameters of $\mathcal{M}$ arbitrary. This means that (unless one is particulary interested to reproduce both static and dynamical properties without scaling coefficients) one of the coefficients (one of $I_i$ constants or one of the coefficients in anisotropy energy expansion) can be set to unity for convenience. Second, the $\mathcal{M}$ matrix simplifies for zero-field problem (its complex part vanishes) which could help to find zero-field gaps in AFMR spectrum. Another possible simplification is softening of the AFMR modes, which commonly appears at spin reorientation transition. In this case, $\omega =0$ and det$\mathcal{M}=0$ reduces to det$( \frac{\partial ^2 \Pi }{\partial \phi _\alpha \partial \phi _\beta })_{0}=0$. Finally, at high fields one of the AFMR modes is field independent and its frequency can be calculated [20], while field-dependent mode linear asymptotes are (we assume that $\chi _3=\gamma ^2(I_1+I_2)$ is the largest susceptibility)

$$\begin{aligned} \omega _2\,= \,& {} \gamma H\\ \omega _3\,=\, & {} \sqrt{1-2\frac{I_3(I_1+I_2)}{(I_1+I_3)(I_2+I_3)}}\gamma H=\sqrt{1-\frac{(\chi _1+\chi _2-\chi _3)\chi _3}{\chi _1\chi _2}}\gamma H \end{aligned}$$

In the limiting case of $I_1=I_2$ ($\chi _1=\chi _2<\chi _3$), $\omega _3=\frac{I_1-I_3}{I_1+I_3}\gamma H = \frac{\chi _3-\chi _1}{\chi _1} \gamma H$. Alternatively, $I_i$ constants can be deduced from the susceptibility measurements.

3 Solving Dynamic Equations Numerically

Below we describe briefly details of algorithm implementations. MatLab script and C$++$ source files along with compiled Win32 executable file can be downloaded at [18]. More detailed information is presented in the electronic supplementary materials of this manuscript.

3.1 Search for Equilibrium

We define orientation of $\lbrace {\mathbf {l}}_i\rbrace$ vectors by Euler angles $\theta$, $\phi$ and $\psi$. Minimization can be performed with any suitable standard numeric minimization procedure. However please note that numeric procedures always look for local minimum. Thus, to find a global minimum, one has to perform preliminary search for a starting approximation with minimal potential energy $\Pi$ over some grid in the Euler angles space. On the other hand, it could be of interest to follow a particular local minimum evolution with field, which allows one to model response from different magnetic domains. MatLab implementation uses global minimum search only, C$++$ implementation allows one to follow local minimum on user choice.

From this point, we assume that desired equilibrium position $\lbrace {\mathbf {l}}_i^{(0)}\rbrace$ is found. Dynamic equations are obtained by varying action $S=\int \mathcal{L} \mathrm{d}V \mathrm{d}t$ and they can be written down as any suitable variable. Euler angles are, generally, not the best choice for dynamics equation as they suffer from “gimbal lock” problem: one of the degrees of freedom will be lost if at some moment ${\mathbf {l}}_3||Z$. To avoid this problem we used two approaches for calculation of eigenfrequencies: (i) to recalculate our problem to the frame of reference which is definitely free from the “gimbal lock”, or (ii) to use other set of variables for dynamic equations. First approach was implemented in MatLab code, second approach was implemented in C$++$ code.

3.2 Solving Dynamics Equation, MatLab Implementation Details

First approach was applied in MatLab environment using the Symbolic Math Toolbox, as it provides functions for manipulating symbolic math equations and lets analytically perform differentiation, simplification and transforms. All these opportunities allow us to consider not only quadratic terms in the anisotropy energy $U_\mathrm{A}$, but also take into consideration its higher orders in accordance with symmetry theory, if necessary. GlobalSearch class is used as well for obtaining global minimum point of potential energy $\Pi$ and finding equilibrium position $\lbrace {\mathbf {l}}_i^{(0)}\rbrace$.

First, we rotate laboratory reference frame in such a way that $\theta =\phi =\psi =\pi /6$ for equilibrium position of $\lbrace {\mathbf {l}}_i\rbrace$ vectors. The choice of angle equal to $\pi /6$ is fairly arbitrary, it is chosen simply to exclude “gimbal lock” problem. Herewith, recalculation of vector components of the external magnetic field and transformation of the anisotropy energy to new coordinates is needed. If $A = \lbrace a_{\alpha \beta } \rbrace$ is the matrix of this rotation, $B = A^{-1} = \lbrace b_{\alpha \beta } \rbrace$ is the inverse matrix, then in new frame of references

$$\begin{aligned} H^{'}_{\alpha } = \sum _\beta a_{\alpha \beta } H_{\beta } \end{aligned}$$

(10)

$$\begin{aligned} \tilde{U}_A(\lbrace l^{\alpha }_i \rbrace ) = U_\mathrm{A} \Bigl ( \Bigl \lbrace \sum _\beta b_{\alpha \beta } l^{\beta }_i \Bigr \rbrace \Bigr ) \end{aligned}$$

(11)

Here, $\mathbf {H} = \left\{ H_{\alpha } \right\}$ and $\mathbf {H'} = \lbrace H^{'}_{\alpha } \rbrace$ are vectors of the external magnetic field in the basic and transformed frames of references correspondingly, $\tilde{U}_A(\lbrace l^{\alpha }_i \rbrace )$ is the anisotropy energy written in new frame of references.

Second, we use parametrization of Euler angles for description of small oscillations near the equilibrium position in transformed frame of references, because in such case “gimbal lock” problem is avoided. As magnetic vectors components $\lbrace l^{\alpha }_i \rbrace$ are known functions of $\theta$, $\phi$, $\psi$ parameters, there are no any problems to obtain the values of first derivatives of $\lbrace l^{\alpha }_i \rbrace$ vectors and the values of first and second derivatives of potential energy $\Pi$ at $\lbrace {\mathbf {l}}_i^{(0)}\rbrace$ position. These values are used for calculations of oscillations eigenfrequencies from the equation det$\mathcal{M}=0$ according to Eq. (5).

Complete algorithm is divided into few steps:

• 1. We start from specified start field $H=H_{\mathrm{start}}$ applied in the specified direction.

• 2. We look for global minimum of potential energy $\Pi$ and find a new equilibrium position at field H. Information on equilibrium position (Euler angles, potential energy at equilibrium, projections of $\lbrace \mathbf {l}_i^{(0)}\rbrace$ vectors on the field direction, longitudinal and transverse susceptibilities) is saved.

• 3. Components of vector $\mathbf {H'}$ (see Eq. (10)) and anisotropy energy $\tilde{U}_\mathrm{A}$ (Eq. 11) in transformed frame of references are obtained.

• 4. Matrix $\mathcal{M}$ (see Eq. (5)) is calculated and det$\mathcal{M}=0$ equation is solved for eigenfrequencies. Results are saved.

• 5. Eigenvectors and average values of projections of oscillating magnetization vector along and transverse to external magnetic field for all oscillation modes are found and saved.

• 6. Field is increased by specified increment $H_{\mathrm{step}}$. If the field does not reach its goal value $H_{\mathrm{stop}}$, we continue with Step 2.

All input parameters including anisotropy energy function $U_\mathrm{A}$ in general case, $\chi _i$ and $\gamma$ coefficients, magnetic field direction, variation boundaries, increment of the value of magnetic field are specified in MatLab script. Calculation results are saved in three files correspondingly with static properties (equilibrium position, energy at equilibrium, projections of $\lbrace \mathbf {l}_i^{(0)}\rbrace$ vectors on the field direction, longitudinal and transverse susceptibilities), oscillation eigenfrequencies and eigenvectors together with average projections of oscillating magnetization vector along and transverse to the magnetic field.

3.3 Solving Dynamics Equation, C$++$ Implementation Details

MatLab environment allows big flexibility and allows one to avoid a lot of routine operations. However, it requires commercial software and, being an interpreter, is somewhat slower than a properly compiled program. Thus, we propose an alternative implementation in C$++$ language along with flexible executable program.

For the sake of flexibility we will consider only quadratic terms in anisotropy energy

$$\begin{aligned} U_\mathrm{A}=\mathop {{\sum {'}}}\limits _{i, j, \alpha ,\beta } a_{ij}^{\alpha ,\beta }~ l_i^{\alpha } l_j^{\beta } \end{aligned}$$

(12)

here $\mathop {{\sum {'}}}\limits _{}$ sign means that each $l_i^{\alpha } l_j^{\beta }$ combination is counted only once during summation (which formally means $i \le j$ and, for the case $i=j$, $\alpha \le \beta$). Higher orders of anisotropy can be included in the program code in a straightforward way, if necessary. This restriction allows to read all $a_{ij}^{\alpha \beta }$ coefficients from easily editable plain text ini-file and to simplify all derivative calculations for minimum search routine and for dynamics equation derivation, e.g.,

$$\begin{aligned} \frac{\partial U_\mathrm{A}}{\partial x}=\mathop {{\sum {'}}}\limits _{i, j, \alpha ,\beta } a_{ij}^{\alpha ,\beta } \left( \frac{\partial l_i^{\alpha }}{\partial x} l_j^{\beta }+ l_i^{\alpha } \frac{\partial l_j^{\beta }}{\partial x}\right) \end{aligned}$$

(13)

here x is some variable of choice.

Numerical Recipes [21] frprmn routine is used to find an equilibrium position. We continue calculations in the same frame of references attached to the crystal, but small oscillations near the equilibrium are described as a small rotations of $\left\{ {\mathbf {l}}_i\right\}$ vectors parameterized by vector of small rotations $\mathbf {\phi }=(\phi _x,\phi _y,\phi _z)$. Length of this vector is rotation angle and its direction defines rotation axis, at equilibrium position $\phi =0$. Up to quadratic terms in $\phi$ transformation of $\left\{ {\mathbf {l}}_i\right\}$ can be described as:

$$\begin{aligned} {\mathbf {l}}_i={\mathbf {l}}_i^{(0)}+\left[ \mathbf {\phi }\times \mathbf {l}_i^{(0)}\right] +\frac{1}{2}\left[ \mathbf {\phi }\times \left[ \mathbf {\phi }\times \mathbf {l}_i^{(0)}\right] \right] +\underline{O}(\phi ^3) \end{aligned}$$

(14)

This parametrization is free from “gimbal lock”. Note that there are non-zero second-order derivatives $\frac{\partial ^2\mathbf {l}_i}{\partial \phi _\alpha \partial \phi _\beta }$ which have to be taken into account when calculating Hessian matrix $\frac{\partial ^2 \Pi }{\partial \phi _\alpha \partial \phi _\beta }$. This allows complete calculation of oscillations of eigenfrequencies.

Once eigenfrequencies are known, complex oscillation vectors $\mathbf {\phi }$ are found as zero-eigenvalue eigenvectors of $\mathcal{M}$ matrix using standard jacobi procedure from Numerical Recipes [21]. This allows to compute complex oscillating magnetization vector $\mathbf {m}$ (see Eq. (6)) and its average projections on the field direction and on the direction transverse to the field.

Complete algorithm looks as follows:

• 1. We start from specified start field $H=H_{\mathrm{start}}$ applied in the specified direction.

• 2. We look for a new equilibrium position at field H. According to user choice we either look for global minimum or for a local minimum close to some initial approximation (specified initial approximation at first point or previous equilibrium position). Information on equilibrium position (Euler angles, projections of ${\mathbf {l}}_i$ on the field direction and longitudinal susceptibility) is saved.

• 3. Matrix $\mathcal{M}$ (see Eq. (5)) is calculated and det$\mathcal{M}=0$ equation is solved for eigenfrequencies. Results are saved.

• 4. Oscillating complex magnetization components and average longitudinal and transverse components of the oscillating magnetization for all oscillation modes are found and saved.

• 5. Field is increased by specified increment $H_{\mathrm{step}}$. If the field does not reach its goal value $H_{\mathrm{stop}}$, we continue with Step 2.

All input parameters including anisotropy energy coefficients (Eq. 12), $I_i$ and $\gamma$ coefficients, magnetic field direction and limiting boundaries are specified in a text ini-file. Calculation results are saved in three files with static properties (equilibrium position, energy at equilibrium, longitudinal and transverse susceptibilities), oscillation eigenfrequencies and eigenvectors correspondingly.

3.4 Application to the Test Examples

Fig. 1

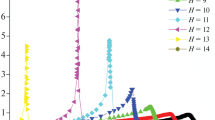
Application of the numeric algorithms to the test example of Mn$_3$Al$_2$Ge$_3$O$_{12}$. Model parameters reproduce 1.2 K experimental data of Ref. [5] and are listed in the “Appendix”. On all panels closed symbols are the results of MatLab-implemented algorithm, open symbols are the results of C$++$-implemented algorithm. Left panel $\mathbf {H}||[111]$, bold solid lines are analytical solution; right panel $\mathbf {H}||[100]$, curves are guide to the eye

We tested our algorithms against test cases described in Appendix. Example of the numerically computed AFMR f(H) dependence is shown in Fig. 1, detailed test protocols are included in supplementary material.

Test routine included: application to the test cases with known analytical results for f(H), computation at the equivalent field orientations for cubic crystal, computation of the f(H) curve at canted field orientation. We have found that numeric results coincide with known analytical solutions, both implementations of the algorithm yield the same results, no “gimbal lock” cases occurs.

Some minor instabilities of the numeric procedures were noted in highly degenerate cases (coincidence of resonance frequencies for different modes or presence of a zero-frequency mode), but they affect only less important output data. We found that sometimes determination of the frequency for $\omega =0$ mode, which is not experimentally observable, is faulty or excitation condition determination is sometimes uncertain for the degenerate modes. Determination of the static properties and f(H) curves for $f\ne 0$ was not affected by these issues.

4 Conclusion

We present an algorithm for numerical solution of antiferromagnetic resonance frequencies for a noncollinear antiferromagnet of a general type within framework of the exchange symmetry theory [1]. Algorithm is implemented in the available MatLab and C$++$ codes (including ready-to-use compiled win32 executable) [18] and implementations are tested against known analytically solvable models.

Appendix: Analytically Solvable Models Used as Test Cases

We recall here some of the known examples of application of exchange symmetry theory to low-energy dynamics of noncollinear antiferromagnets. These analytical solutions were used as test cases to ascertain correctness of numeric algorithms.

The first test example is an antiferromagnet on a triangular lattice CsNiCl$_3$ [3]. In the ordered phase of this magnet, spins form a planar 120$^\circ$ structure. High symmetry of triangular lattice leaves single invariant in the anisotropy energy $U_\mathrm{A}=\beta ({l_{3}^z})^2$, here z-axis is normal to hexagonal plane and vector ${\mathbf {l}}_3$ is the normal to the plane of the planar spin structure, $\beta >0$ as at zero-field spin plane is orthogonal to the hexagonal crystallographic plane. Magnetic susceptibility normal to the spin plane dominates: $\chi _3>\chi _2=\chi _1$ (i.e., $I_3<I_1=I_2$). Two of the zero-field frequencies are zero, non-zero zero-field frequency is $\omega _{0}=\gamma \sqrt{\frac{I_1-I_3}{I_1+I_3}\beta }=\gamma \sqrt{\frac{\chi _3-\chi _1}{\chi _1}\beta }$. As the field is applied along z-axis spin plane reorients at the field $H_0=\sqrt{\frac{\beta }{\gamma ^2 (I_1-I_3)}}=\sqrt{\frac{\beta }{\chi _3-\chi _1}}$. Magnetic resonance frequencies at $\mathbf {H}||z$ are given by equations:

$$\begin{aligned} H<H_0&:\omega _1^2=\omega _{0}^2+\left( \gamma H\right) ^2\\& \quad\omega _2=\omega _3=0\\ H>H_0&:&\omega _{1,2}=\sqrt{\left( \frac{I_1}{I_1+I_3} \gamma H \right) ^2-\omega _{10}^2}\pm \frac{I_3}{I_1+I_3}\gamma H\\&=\sqrt{\left( \frac{\chi _3}{2\chi _1}\gamma H \right) ^2-\omega _{0}^2}\pm \frac{2\chi _1-\chi _3}{2\chi _1}\gamma H\\&\omega _3=0 \end{aligned}$$

Because of simplicity of anisotropy energy, this problem can be solved analytically at arbitrary field orientation, see Ref. [3] for details.

To reproduce experimental results of Ref. [3], we take for our modeling $\beta =1$ kOe$^2$, $\gamma =18.8 \frac{10^9 \mathrm{rad}~ \mathrm{s}^{-1}}{\mathrm{kOe}}$ (3.0 GHz kOe$^{-1}$ in frequency units), $I_1=I_2=8.77\times 10^{-6} \frac{ \mathrm{kOe}^2}{(10^9 \mathrm{rad}~\mathrm{s}^{-1})^2}$ and $I_3=9.75\times 10^{-7}\frac{ \mathrm{kOe}^2}{(10^9 \mathrm{rad}~\mathrm{s}^{-1})^2}$.

Second, we consider 12-sublattice antiferromagnet Mn$_3$Al$_2$Ge$_3$O$_{12}$ [5]. Here, $I_1=I_2$ because of the cubic symmetry, anisotropy energy $U_\mathrm{A}=\lambda [l_{2z}^2-l_{1z}^2+\frac{2}{\sqrt{3}}(l_{1x}l_{2x}-l_{1y}l_{2y})]$ ($\lambda >0$) (we use notations of Ref. [22]). At zero-field plane of the spiral structure is orthogonal to one of the $\langle 111\rangle$ directions. Oscillation eigenfrequencies can be found at $\mathbf {H}||[111]$:

$$\begin{aligned} \omega _{1,2}= & {} \sqrt{ \left( \frac{I_1}{I_1+I_3}\gamma H\right) ^2+\frac{4}{3}\frac{\lambda }{(I_1+I_3)}} \pm \frac{I_3}{I_1+I_3}\gamma H\\= & {} \sqrt{ \left( \frac{\chi _3}{2\chi _1}\gamma H\right) ^2+\frac{4}{3}\frac{\lambda }{\chi _1}\gamma ^2} \pm \frac{2\chi _1-\chi _3}{2\chi _1}\gamma H \\ \omega _3= & {} \sqrt{\frac{8}{3}\frac{\lambda }{I_1}}=\gamma \sqrt{\frac{8}{3}\frac{2\lambda }{\chi _3}} \end{aligned}$$

To reproduce experimental results of Ref. [5], we take for our modeling $\lambda =1$ kOe$^2$, $\gamma =17.6\frac{10^9 \mathrm{rad}~\mathrm{s}^{-1}}{\mathrm{kOe}}$ (2.80 GHz kOe$^{-1}$), $I_1=I_2=1.42\times 10^{-5}\frac{ \mathrm{kOe}^2}{(10^9~\mathrm{rad}~~ \mathrm{s}^{-1})^2}$, $I_3=7.99\times 10^{-6}\frac{ \mathrm{kOe}^2}{(10^9 \mathrm{rad}~\mathrm{s}^{-1})^2}$. Results of the modeling for this case are shown at the Fig. 1.

Finally, it is a spiral magnet LiCu$_2$O$_2$ [8]. Despite the orthorhombic symmetry $I_1=I_2$ as there is no anisotropy in the plane of the spiral structure, $U_\mathrm{A}=\frac{A}{2}l_{3z}^2+\frac{B}{2} l_{3y}^2$ ($A\le B \le 0$). It turns out that in the case of LiCu$_2$O$_2$ A and B constants in anisotropy energy are close within 1 %. Thus, normal to the spin plane $\mathbf {l}_3$ rotates almost freely in the (yz) plane. One of the oscillation frequencies corresponds to the rotation in the plane of spiral structure and is always zero since phase of the helix can be changed at no energy cost. Two other modes have non-zero zero-field frequencies

$$\begin{aligned} \omega _{10}^2= & {} -\frac{A}{I_1+I_3}=-\gamma ^2 \frac{A}{\chi _1}\\ \omega _{20}^2= & {} \frac{B-A}{I_1+I_3}=\gamma ^2\frac{B-A}{\chi _1}<\omega _{10}^2\\ \end{aligned}$$

For LiCu$_2$O$_2$ $\chi _3>\chi _1$, in this case at $\mathbf {H}||z$ vector $\mathbf {l}_3$ always remains aligned along z and non-zero oscillation frequencies are

$$\begin{aligned} \omega _{1,2}^2= & {} \frac{\omega _{10}^2+\omega _{20}^2}{2}+ \gamma ^2 H^2\frac{I_3^2+I_1^2}{\left( I_3+I_1\right) ^2}\\&\pm \sqrt{\left( \frac{\omega _{10}^2-\omega _{20}^2}{2}\right) ^2+4\frac{\gamma ^4H^4 I_1^2I_3^2}{\left( I_1+I_3\right) ^4}+2\frac{\gamma ^2 H^2 (\omega _{10}^2+ \omega _{20}^2)I_3^2}{\left( I_1+I_3\right) ^2}} \end{aligned}$$

At $\mathbf {H}||x$ spin plane rotates orthogonally to the magnetic field at some critical field. Critical field $H_{\mathrm{cx}}=\frac{\omega _{10}}{\gamma }\sqrt{\frac{I_1+I_3}{I_1-I_3}}=\frac{\omega _{10}}{\gamma }\sqrt{\frac{\chi _1}{\chi _3-\chi _1}}$ and oscillation frequencies are

$$\begin{aligned}H<H_{\mathrm{cx}}:\\\omega _1^2=\, & {} \omega _{10}^2+\gamma ^2 H^2\\ \omega _2^2=\, & {} \omega _{20}^2\\H>H_{\mathrm{cx}}:\\ \omega _{1,2}^2=\, & {} \frac{\omega _{20}^2-2\omega _{10}^2}{2} +\frac{I_1^2+I_3^2}{\left( I_1+I_3\right) ^2}\gamma ^2 H^2 \\&\pm \sqrt{\frac{\omega _{20}^4}{4}+ 2\gamma ^2 H^2\frac{\left( \omega _{20}^2-2\omega _{10}^2\right) I_3^2}{\left( I_1+I_3\right) ^2} +4\frac{\gamma ^4 H^4 I_1^2 I_3^2}{\left( I_1+I_3\right) ^4}} \end{aligned}$$

To reproduce experimental results of Ref. [8], we take for our modeling $\gamma =17.59\frac{10^9 \mathrm{rad}~ \mathrm{s}^{-1}}{\mathrm{kOe}}$ (corresponds to 2.80 GHz kOe$^{-1}$), $A=-1$ kOe$^2$, $B=-0.99$ kOe$^2$, $I_1=I_2=1.85\times 10^{-7}\frac{ \mathrm{kOe}^2}{(10^9~\mathrm{rad}~\mathrm{s}^{-1})^2}$, $I_3=6.18\times 10^{-8}\frac{ \mathrm{kOe}^2}{(10^9 \mathrm{rad}~\mathrm{s}^{-1})^2}$

The detailed comparison of the modeled curves with analytical predictions is given in a supplementary material.