Photothermal interactions in a semiconducting rotating plate with voids and temperature-dependent properties under dual phase lag model

Abstract

The current manuscript focuses on the photo-thermoelastic interactions in a rotating plate with a porous structure and temperature-dependent properties. The analysis is performed using the dual phase lag theory and by considering a two-dimensional isotropic homogeneous plate. The upper surface of the plate experiences the application of a mechanical source, while the lower surface of the plate is insulated thermally. The application of the normal mode technique enables the derivation of analytical expressions for various field variables such as displacement, stress, change in volume fraction field, carrier density and temperature within the physical domain. Numerical computations are performed for a plate composed of silicon material and the results are represented graphically with the support of MATLAB software to demonstrate the consistency of the obtained results. To outline the influences of rotation, photothermal transport process, temperature-dependent properties and void parameters on the physical fields, certain collations are presented. Some specific cases of interest have also been deducted.

1 Introduction

Because of the advancement of nuclear reactors, electromagnetic lasers, X-ray machines and other technologies, generalized theories of thermoelasticity are getting a lot of attention from various researchers and engineers. The generalized theories of thermoelasticity utilize hy-perbolic-type heat conduction equation and allow for thermal signals propagating with finite speeds. Lord and Shulman [1] were the pioneers of the first non-classical generalized theory, termed as L-S theory of generalized thermoelasticity, which incorporates a relaxation time in Fourier’s law of heat conduction. The anisotropic situation was then included in L-S theory by Dhaliwal and Sherief [2]. Tzou [3] proposed dual phase lag (DPL) theory of generalized thermoelasticity. He extended Fourier’s law $\vec {q}=-K\vec {\nabla } T$ of heat conduction to the equation $\vec {q}(R, t+\tau _{q})=-K\vec {\nabla } T(R, t+\tau _{T})$, with two different phase lags, where the temperature gradient $\vec {\nabla } T$ at a spatial location R of the material at time $t+\tau _{T}$ corresponds to the heat flux vector $\vec {q}$ at the same position at another time $t+\tau _{q}$ and K is the thermal conductivity of the material. The relaxation time $\tau _{T}$ highlights the micro-structural interactions such as phonon scattering and phonon-electron interactions and is called the phase-lag of the temperature gradient, while other relaxation time $\tau _q$ emphasizes fast transitory effects of the thermal inertia, which is termed as the phase lag of the heat flux. The Fourier’s law in the dual phase lag model is identical to the classical Fourier’s law if we take $\tau _{q}=\tau _{T}=0$.

The qualitative and stability aspects of the dual phase lag theory were examined by Quintanilla and Racke [4]. They analyzed the connection between the two distinct phase lags, namely $\tau _{q}$ and $\tau _{T}$. Kalkal et al. [5] scrutinized the thermoviscoelastic disturbances in a homogeneous isotropic thick plate using the eigenvalue approach to analyze the impacts of the fractional order parameter, viscosity and time. Under DPL model of generalized thermoelasticity, Allam and Tayel [6] examined the effect of nonhomogeneity parameter on a functionally graded thermoelastic rectangular thin plate. By utilizing dual phase lag theory of generalized thermoelasticity, various authors [7,8,9] made significant advancements in the field of generalized thermoelasticity. Peng et al. [10] developed a modified nonlocal thermoviscoelastic model by combining the dual phase lag heat conduction model and the fractional-order strain model and investigated the transient response of a viscoelastic microplate subjected to a sinusoidal thermal loading. Abouelregal et al. [11] examined thermo-magnetic interactions in a viscoelastic micropolar thermoelastic medium under dual phase lag theory of generalized thermoelasticity. Recently, Zenkour et al. [12] investigated the thermoelastic response of biological tissue subjected to thermal shock using an advanced thermal conduction theory known as refined three-phase-lag (TPL) theory of generalized thermoelasticity.

In our surroundings, semiconductor materials exist that have great importance in renewable sources of energy i.e. in the solar cell industry. When a sample of semiconductor material is illuminated by a beam of sunlight or laser beam, the electron–hole pairs are generated which scatter through the crystal from the place of their generation to region of lower excess-pair concentration and produce carrier density (plasma) waves that are similar to thermal waves. In general, when a semiconductor is heated, its electrons are released from its atoms, raising the temperature of the semiconductor and as a result, the electron resistance of the semiconductor decreases. Photothermal and photoacoustic sciences have played a crucial role in the development of semiconductors and microelectronic structures as they allow for the measurement of important parameters such as thermal diffusivity, temperature, surface thickness, sound velocity and specific heat. Todorovic [13] investigated the dynamic elastic bending contribution of the photoacoustic and photothermal signals as a function of modulation frequency including the propagation processes of the plasma, thermal and elastic waves. A complete analytical solution of photothermal deflection spectroscopy for the measurement of thermal conductivities in an anisotropic material was presented by Jeon et al. [14]. Song et al. [15] studied the elastic disturbances in semiconducting cantilevers under laser excitation and obtained the 3-D response for the carrier density and temperature distribution using Green function method. Utilizing normal mode analysis, Lotfy [16] discussed the impact of hydrostatic initial stress, two-temperature and activation coupling parameters under the photothermal process of semiconducting medium. Hobiny and Abbas [17] investigated the problem of photothermal waves in an unbounded semiconductor medium with a cylindrical cavity. Kilany et al. [18] studied the influences of rotation, void and photothermal parameters in a semiconducting thermoelastic half-space in the context of L-S theory. Zenkour [19] defined a unified theory of coupled photo-thermoelasticity to investigate the multi-time-derivative heat formulae. The photogenerated transport processes were examined by El-Sapa et al. [20], when a microelongated elastic non-local semiconductor thermoelastic medium is considered. Under the influence of a moving mechanical load, Deswal et al. [21] scrutinized the effects of gravity, diffusion, time, magnetic field and Hall current on a photothermoelastic semiconducting medium.

A continuum elastic body with voids refers to a porous solid material, where the matrix materials are elastic and the volume of the material contains small pores or voids. Linear and non-linear theories of elastic solids with voids have deliberated applications in several fields such as geological and biological material sciences, rocks, drugs, soils, medical device industry and the petroleum industry. Cowin and Nunziato [22] developed the linear theory of elastic materials with voids and studied the mechanical behaviour of porous materials. The basic idea of the above theory is that the bulk density of the continuum body is presented by the product of the change in volume fraction field and density field of the matrix material. Iesan [23] developed a theory of thermoelastic materials with voids, where the constitutive equations were derived based on the balance law of energy, the entropy production inequality and the invariance requirements under superposed rigid body motions. It was also discussed that the transverse wave vibrates without affecting the porosity and temperature distribution of the material. Deswal and Hooda [24] scrutinized the effects of voids, rotation parameter and magnetic field in the context of two-temperature generalized thermoelasticity. Othman and Hilal [25] studied the effects of gravity and voids in a thermoelastic medium under various theories of generalized thermoelasticity. By employing the generalized theory of thermoelasticity with one relaxation time, Gunghas et al. [26] studied two-dimensional deformations in a nonhomogeneous thermoelastic porous medium with gravity, whose surface is subjected to a thermal load. Under various theories of generalized thermoelasticity, Othman et al. [27] studied the effects of voids and temperature-dependent properties on a generalized thermo-microstretch solid half-space.

In most of the studies, modulus of elasticity, coefficient of thermal expansion, Poisson’s ratio and thermal conductivity are considered to be constants instead of temperature dependent, which restrict the materiality of the solutions obtained to certain ranges of temperature. Keeping this in mind, Tang [28] presented the stress formulation of thermoelasticity with temperature-dependent properties and showed that if a simply connected body has a uniform temperature change and has no surface tractions in the absence of body forces, then all the stress components are identically zero throughout the body. Othman [29] studied the behaviour of two-dimensional solutions in a generalized thermoelastic medium with temperature dependence of the elastic modulus on the reference temperature. By employing Laplace and Fourier transform techniques, Kumar and Devi [30] scrutinized the effects of voids, thermal conductivity and temperature-dependent properties on the field variables. Using three different theories, Othman and Edeeb [31] investigated the effect of temperature-dependent properties on thermoelastic porous medium with rotation. Alharbi et al. [32] studied the effects of temperature-dependent properties, voids and internal heat source on a micropolar thermoelastic medium in the context of three phase lag theory. Mirparizi and Razavinasab [33] applied the modified Green-Lindsay theory to analyze thermo-electro-magneto-elasticity in a functionally graded disk that considers temperature-dependent material properties. Barak and Dhankhar [34] analyzed thermomechanical interactions in a non-homogeneous fiber-reinforced thermoelastic medium with temperature-dependent properties.

In the present investigation, the dual phase lag theory of generalized thermoelasticity is applied to analyze disturbances in a rotating photothermal semiconducting plate that includes voids and has temperature-dependent properties. Using normal mode analysis, exact expressions are derived for various field variables, including normal stress, normal displacement, temperature, change in volume fraction field and carrier density. These field variables are computed numerically with the help of MATLAB programming for a silicon crystal-like material and the obtained numerical results are displayed graphically. Some collations are presented to delineate the effects of photothermal transport process, rotation and void parameters on normal stress, normal displacement, temperature, change in volume fraction field and carrier density. The impacts of temperature-dependent properties and time on the physical fields are also displayed.

Although numerous studies have been conducted to observe the transitory disturbances caused by different parameters in a thermoelastic medium, the work in its current form has not been studied by any researcher till date. The analysis of issues involving rotation, voids, temperature-dependent properties and photothermoelasticity may be done effectively with the help of the current formulation. The novelty of this research stems from the examination of more parameters on different field quantities in response of the mechanical load. The findings of this research can be applied to laser resurfacing, vessel lesion treatment, laser surgery, material science, biomechanical science, earthquake engineering and solid mechanics. Inspired by the broad spectrum of potential applications discussed above across various fields, we are motivated to investigate the dynamical distributions in a photothermoelastic rotating plate with voids and temperature-dependent properties.

2 Fundamental equations

Following Kilany et al. [18] and Iesan [23], the constitutive relations and field equations for an isotropic, homogeneous semiconducting rotational medium with voids and temperature-dependent properties in the absence of body forces can be expressed as:

(a) Constitutive equations

$$\begin{aligned} & \sigma _{ij}=2\mu e_{ij} +(\lambda e_{kk}-\beta \theta +b_{v}\phi _{v}-\delta _{n}N)\delta _{ij}, \end{aligned}$$

(1)

$$\begin{aligned} & e_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}), \end{aligned}$$

(2)

$$\begin{aligned} & g=-w_{v}\dot{\phi }_{v}-\xi \phi _{v}-b_{v}e_{kk}+n\theta , \end{aligned}$$

(3)

$$\begin{aligned} & h_{i}=\alpha \phi _{v,i}, \end{aligned}$$

(4)

where $\lambda$ and $\mu$ are the well known Lame’s elastic constants, $\beta =(3\lambda +2\mu ) \alpha _t$, $\alpha _t$ is the coefficient of linear thermal expansion, $\sigma _{ij}$ are the components of stress, $e_{ij}$ are the components of strain, $u_{i}$ are the components of displacement vector $\vec {u}$, $h_i$ are the components of equilibrated stress, $\theta =T-T_0$ is the temperature in which T denotes the absolute temperature, $T_{0}$ is the reference temperature of the medium in its natural state assumed to be $|\frac{\theta }{T_0}|\ll 1$, $\delta _{n}$ is the difference of deformation potential of conduction and valence band such that $\delta _{n}=(3\lambda +2\mu ) d_n$, $d_n$ is coefficient of electronic deformation, $e = e_{kk}$ is the cubical dilatation, $\phi _v$ is the change in volume fraction field, $\alpha$, $w_{v}$, $b_v$ and $\xi$ are the void material constants, n is thermo-void coefficient, g is the intrinsic equilibrated body force, N is the carrier density and $\delta _{ij}$ is the Kronecker delta function.

(b) Carrier density (plasma wave) equation

$$\begin{aligned} & D_{E}\nabla ^2 N-\frac{N}{\tau }+\kappa \theta =\frac{\partial N}{\partial t}, \end{aligned}$$

(5)

where, $\displaystyle \kappa =\dfrac{1}{\tau }\dfrac{\partial \displaystyle N_{0}}{\partial T}$, $N_{0}$ is the equilibrium carrier concentration at temperature T, $D_{E}$ is the carrier diffusion coefficient and $\tau$ is the photo-generated carrier life time.

(c) Equation of motion in the rotating frame (Schoenberg and Censor [35])

$$\begin{aligned} & \sigma _{ji,j}=\rho [\ddot{{\vec {u}}}+(\vec {\Omega }\times \vec {\Omega }\times \vec {u})+ (2\vec {\Omega }\times \dot{\vec {u}})]_{i}, \end{aligned}$$

(6)

where $\rho$ is the mass density and it is assumed that the whole body is rotating with an angular velocity $\vec {\Omega }$. Due to accelerated frame of reference, the equation of motion has two additional terms: $(\vec {\Omega }\times \vec {\Omega }\times \vec {u})$ is the centripetal acceleration due to time varying motion only and $(2\vec {\Omega }\times \dot{\vec {u}})$ is Coriolis acceleration due to moving reference frame.

(d) Heat conduction equation (Tzou [3])

$$\begin{aligned} & K\left( 1+\tau _{T}\frac{\partial }{\partial t}\right) \theta _{,ii}=\left( 1+\tau _{q}\frac{\partial }{\partial t}+\eta \frac{\tau _{q}^2}{2}\frac{\partial ^2 }{\partial t^2}\right) \left( \rho C_{E}\frac{\partial \theta }{\partial t}+\beta T_{0}\frac{\partial e}{\partial t}+nT_{0}\frac{\partial \phi _{v}}{\partial t}\right) -\frac{E_{g}}{\tau }N, \end{aligned}$$

(7)

where $C_{E}$ is the specific heat at constant strain, K is the thermal conductivity, $E_{g}$ is the energy gap of the semiconductor, $\tau _T$ and $\tau _q$ are phase lags of temperature gradient and heat flux respectively and $\eta$ is the unifying parameter. Moreover, the use of unifying parameter $\eta$ in Eq. (7) makes this fundamental equation valid for the two different theories of generalized thermoelasticity:

Case I: Lord-Shulman (LS) theory: $\tau _{T}=0$ and $\eta =0$.

Case II: Dual phase lag (DPL) theory: $\tau _{q}-\tau _{T}>0$ and $\eta =1$.

(e) Balance of equilibrated force

$$\begin{aligned} & h_{i,i}+g=\rho \chi \ddot{\phi }_{v}, \end{aligned}$$

(8)

where $\chi$ is the equilibrated inertia.

In the above relations, $i,j,k=1,2,3$, comma represents derivative with respect to spatial variable and a superposed dot denotes derivative with respect to time t.

Moreover, our motive is to investigate the effect of temperature-dependent parameters on the physical fields. Therefore, we suppose that

$$\begin{aligned} & (\lambda ,\;\mu ,\;\beta ,\;\delta _{n},\;\kappa ,\;E_{g},\;D_{E},\;\alpha ,\;b_{v},\;\xi ,\;w_{v},\;n,\chi )\nonumber \\ & \quad \qquad = f(\alpha ^*)(\lambda _{0},\;\mu _{0},\;\beta _{0},\;\delta _{n_0},\;\kappa _{0},\;E_{g_0},\;D_{E_0},\;\alpha _{0},\;b_{v_0},\;\xi _{0},\;w_{v_0},\;n_{0},{\chi }_{0}), \end{aligned}$$

(9)

where $\lambda _{0},\;\mu _{0},\;\beta _{0},\;\delta _{n_0},\;\kappa _{0},\;E_{g_0},\;D_{E_0},\;\alpha _{0},\;b_{v_0},\;\xi _{0},\;w_{v_0},\;n_{0}$ and $\chi _{0}$ are constants, $f(\alpha ^*)$ is a given non-dimensional function of temperature such that $f(\alpha ^*)=1-\alpha ^*T_{0}$ and $\alpha ^*$ is an empirical material constant. In case of without temperature-dependent properties, we have $f(\alpha ^*)=1$.

3 Formulation of the problem

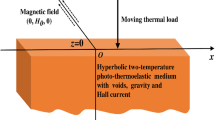
In the current manuscript, we consider a rotating homogeneous isotropic semiconducting plate with voids and temperature-dependent properties under DPL model, occupying the region $-d\le x \le d$, $-\infty \le y\le \infty$. The origin of the rectangular cartesian co-ordinate system (x, y, z) is taken on the middle surface of the plate. The yz-plane is chosen to coincide with the middle surface and the x-axis is normal to it along the thickness of the plate. The fundamental state of the considered medium is undisturbed and initially at uniform temperature $T_0$. The surfaces of plate are given by $x=\pm d$ in which the upper surface $(x=d)$ of the plate is subjected to the action of a mechanical load and the lower surface $(x=-d)$ of the plate is laid on a rigid foundation and is thermally insulated. We choose y-axis in the direction of wave propagation so that all the particles on a line parallel to z-axis are equally displaced, therefore all the field quantities are independent of the z-coordinate. The plate is rotating about z-axis with uniform angular velocity $\vec {\Omega }$. The geometry of the problem is shown in Fig. 1.

Fig. 1

Geometry of the problem

Under the above considerations, we may write the displacement vector $\vec {u}$, angular velocity $\vec {\Omega }$, temperature $\theta$, carrier density N and change in volume fraction field $\phi _{v}$ as:

$$\begin{aligned} & \vec {u}= (u,v,0), \; u=u(x,y,t), \;v=v(x,y,t), \; \vec {\Omega }=(0,0,\Omega ), \;\theta = \theta (x,y,t),\nonumber \\ & N=N(x,y,t) ~~~\text {and}~~~\phi _{v}=\phi _{v}(x,y,t). \end{aligned}$$

(10)

Using expressions (9) and (10), constitutive relation (1) provides the stress components in the form:

$$\begin{aligned} & \sigma _{xx}=\alpha _{1}\left[ D_{1}\frac{\partial u}{\partial x}+\lambda _{0}\frac{\partial v}{\partial y} -\beta _{0} \theta +b_{v_0}\phi _{v}-\delta _{n_0} N\right] , \end{aligned}$$

(11)

$$\begin{aligned} & \sigma _{yy}=\alpha _{1}\left[ \lambda _{0}\frac{\partial u}{\partial x}+D_{1}\frac{\partial v}{\partial y}-\beta _{0} \theta +b_{v_0}\phi _{v}-\delta _{n_0} N\right] , \end{aligned}$$

(12)

$$\begin{aligned} & \sigma _{xy}=\alpha _{1}\mu _{0} \left[ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right] , \end{aligned}$$

(13)

where $D_{1} = \lambda _{0}+2\mu _{0}$ and $\alpha _{1}=1-\alpha ^*T_{0}$.

Taking into consideration expressions (3), (4), (9) and (11)–(13), the governing equations (5)–(8) are converted to:

$$\begin{aligned}&\alpha _{1}D_{E_0}\nabla ^2N-\frac{N}{\tau }+\alpha _{1}\kappa _{0} \theta =\frac{\partial N}{\partial t}, \end{aligned}$$

(14)

$$\begin{aligned}&\alpha _{1}\left[ D_{1}\frac{\partial ^2 u}{\partial x^2}+\mu _{0}\frac{\partial ^2 u}{\partial y^2}+D_{2}\frac{\partial ^2 v}{\partial x\partial y}-\beta _{0}\frac{\partial \theta }{\partial x}+b_{v_0}\frac{\partial \phi _ v}{\partial x}-\delta _{n_0}\frac{\partial N}{\partial x}\right] =\rho \left( \frac{\partial ^2 u}{\partial t^2}-\Omega ^2u-2\Omega \frac{\partial v}{\partial t}\right) , \end{aligned}$$

(15)

$$\begin{aligned}&\alpha _{1}\left[ D_{1}\frac{\partial ^2 v}{\partial y^2}+\mu _{0}\frac{\partial ^2 v}{\partial x^2}+D_{2}\frac{\partial ^2 u}{\partial x\partial y}-\beta _{0}\frac{\partial \theta }{\partial y}+b_{v_0}\frac{\partial \phi _ v}{\partial y}-\delta _{n_0}\frac{\partial N}{\partial y}\right] =\rho \left( \frac{\partial ^2 v}{\partial t^2}-\Omega ^2v+2\Omega \frac{\partial u}{\partial t}\right) , \end{aligned}$$

(16)

$$\begin{aligned}&\left( 1+\tau _{q}\frac{\partial }{\partial t}+\eta \frac{\tau _{q}^2}{2}\frac{\partial ^2}{\partial t^2}\right) \left( \rho C_{E}\frac{\partial \theta }{\partial t}+\alpha _{1}\beta _{0}T_{0}\frac{\partial e}{\partial t} +\alpha _{1}n_{0}T_{0}\frac{\partial \phi _{v}}{\partial t}\right) -\alpha _1\frac{E_{g_0}}{\tau }N\nonumber \\&\quad \qquad =K\left( 1+\tau _{T}\frac{\partial }{\partial t}\right) \nabla ^2\theta , \end{aligned}$$

(17)

$$\begin{aligned}&\alpha _{0}\nabla ^2\phi _{v}-w_{v_0}\frac{\partial \phi _{v}}{\partial t}-\xi _{0}\phi _{v}-b_{v_0}\left( \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) +n_{0}\theta =\rho \chi _{0}\frac{\partial ^2\phi _{v}}{\partial t^2}, \end{aligned}$$

(18)

where

$$\begin{aligned} \displaystyle \nabla ^2\cong \frac{\partial ^2}{\partial {x^2}}+\frac{\partial ^2}{\partial {y^2}}.\; \end{aligned}$$

For convenience in the subsequent analysis, we will introduce the following non-dimensional variables:

$$\begin{aligned} & (x',y',u',v')=\frac{1}{C_{T}t^*}(x,y,u,v),\ \ (t', \tau _{q}', \tau _{T}')=\frac{1}{t^*}( t, \tau _{q}, \tau _{T}),\ \ \sigma _{ij}'=\frac{\sigma _{ij}}{\mu _{0}},\nonumber \\ & \theta '=\frac{\beta _{0}}{\lambda _{0}+2\mu _{0}}\theta ,\ \ N'=\frac{\delta _{n0}}{\lambda _{0}+2\mu _{0}}N, \ \ \phi _{v}'=\frac{\chi _{0}}{\lambda _{0}+2\mu _{0}} \phi _{v},\ \ \Omega '=t^{*}\Omega , \nonumber \\ & \text {with} \ \ t^{*}=\frac{K}{\rho C_{E}C_{T}^2} \ \ \text {and}\ \ C_{T}^2=\frac{\lambda _{0}+2\mu _{0}}{\rho }. \end{aligned}$$

(19)

Now, with the help of the non-dimensional quantities defined in (19), expressions (11)–(13) and the Eqs. (14)–(18) become (dropping the prime notation)

$$\begin{aligned} & \sigma _{xx}=\alpha _{1}\left[ D_{3}\frac{\partial u}{\partial x}+D_{4}\frac{\partial v}{\partial y} -D_{3}\theta +D_{5}\phi _{v}-D_{3} N\right] , \end{aligned}$$

(20)

$$\begin{aligned} & \sigma _{yy}=\alpha _{1}\left[ D_{4}\frac{\partial u}{\partial x}+D_{3}\frac{\partial v}{\partial y} -D_{3}\theta +D_{5}\phi _{v}-D_{3} N\right] , \end{aligned}$$

(21)

$$\begin{aligned} & \sigma _{xy}=\alpha _{1}\left[ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right] , \end{aligned}$$

(22)

$$\begin{aligned} & (\nabla ^2-D_{6}-D_{7}\frac{\partial }{\partial t})N+D_{8}\theta =0, \end{aligned}$$

(23)

$$\begin{aligned} & \alpha _{1}\left[ \frac{\partial ^2 u}{\partial x^2}+D_{9}\frac{\partial ^2 u}{\partial y^2}+D_{10}\frac{\partial ^2 v}{\partial x\partial y}-\frac{\partial \theta }{\partial x}+D_{11}\frac{\partial \phi _ v}{\partial x}-\frac{\partial N}{\partial x}\right] =\frac{\partial ^2 u}{\partial t^2}-\Omega ^2u-2\Omega \frac{\partial v}{\partial t},\end{aligned}$$

(24)

$$\begin{aligned} & \alpha _{1}\left[ \frac{\partial ^2 v}{\partial y^2}+D_{9}\frac{\partial ^2 v}{\partial x^2}+D_{10}\frac{\partial ^2 u}{\partial x\partial y}-\frac{\partial \theta }{\partial y}+D_{11}\frac{\partial \phi _ v}{\partial y}-\frac{\partial N}{\partial y}\right] =\frac{\partial ^2 v}{\partial t^2}-\Omega ^2v+2\Omega \frac{\partial u}{\partial t}, \end{aligned}$$

(25)

$$\begin{aligned} & \left( 1+\tau _{T}\frac{\partial }{\partial t}\right) \nabla ^2\theta =\left( 1+\tau _{q}\frac{\partial }{\partial t}+\eta \frac{\tau _{q}^2}{2}\frac{\partial ^2}{\partial t^2}\right) \left( \frac{\partial \theta }{\partial t}+D_{12}\frac{\partial e}{\partial t}+D_{13}\frac{\partial \phi _{v}}{\partial t}\right) -D_{14}N, \end{aligned}$$

(26)

$$\begin{aligned} & \left( \nabla ^2-D_{15}-D_{16}\frac{\partial }{\partial t}-D_{17}\frac{\partial ^2}{\partial t^2}\right) \phi _{v}-D_{18}\left( \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) +D_{19}\theta =0, \end{aligned}$$

(27)

where

$$\begin{aligned} & D_{2}=\lambda _{0}+\mu _{0},\ \ \ \ \ D_{3}=\frac{D_{1}}{\mu _{0}},\ \ \ \ \ D_{4}=\frac{\lambda _{0}}{\mu _{0}},\ \ \ \ D_{5}=\frac{b_{v_0}D_{3}}{\chi _{0}},\ \ D_{6}=\frac{ t^*{^2}C_{T}^2}{D_{E_0}\alpha _{1}\tau },\\ & D_{7}=\frac{t^*C_{T}^2 }{D_{E_0}\alpha _{1}},\ \ D_{8}=\frac{\kappa _{0}t^*{^2}\delta _{n_{0}}C_{T}^2 }{\beta _{0}D_{E_0}},\ \ D_{9}=\frac{1}{D_{3}}, \ \ D_{10}=\frac{D_{2}}{D_{1}}, \ \ \ \ D_{11}=\frac{b_{v_0}}{\chi _{0}},\\ & D_{12}=\frac{t^*\alpha _{1}\beta _{0}^2 T_{0}}{\rho K},\ \ D_{13}=\frac{n_{0}\alpha _{1}\beta _{0} T_{0}}{\rho \chi _{0}C_{E}},\ \ D_{14}=\frac{E_{g_0}\alpha _{1}\beta _{0}}{\tau \rho \delta _{n_{0}} C_{E}},\ \ D_{15}=\frac{ t^*{^2}C_{T}^2\xi _{0}}{\alpha _{0}}, \\ & D_{16}=\frac{ t^*w_{v_0}C_{T}^2}{\alpha _{0}},\ \ D_{17}=\frac{ \rho \chi _{0}C_{T}^2}{\alpha _{0}},\; D_{18}=\frac{b_{v_0}\chi _{0} t^*{^2}C_{T}^2}{\alpha _{0}D_{1}},\; D_{19}=\frac{ n_{0}\chi _{0}t^*{^2}C_{T}^2}{\alpha _{0}\beta _{0}}. \end{aligned}$$

Now, we introduce the potential functions $\Phi (x,y,t)$ and $\Psi (x,y,t)$, which are related to the displacement components u(x, y, t) and v(x, y, t) as:

$$\begin{aligned} & u=\frac{\partial \Phi }{\partial x}+\frac{\partial \Psi }{\partial y}, \ \ v=\frac{\partial \Phi }{\partial y}-\frac{\partial \Psi }{\partial x}. \end{aligned}$$

(28)

With the help of (28), expressions (20)–(22) and Eqs. (23)–(27) convert to:

$$\begin{aligned} & \sigma _{xx}=\alpha _{1}\left[ D_{3}\frac{\partial ^2 \Phi }{\partial x^2}+D_{4}\frac{\partial ^2 \Phi }{\partial y^2}+2\frac{\partial ^2 \Psi }{\partial x\partial y} -D_{3}\theta +D_{5}\phi _{v}-D_{3} N\right] , \end{aligned}$$

(29)

$$\begin{aligned} & \sigma _{yy}=\alpha _{1}\left[ D_{3}\frac{\partial ^2 \Phi }{\partial y^2}+D_{4}\frac{\partial ^2 \Phi }{\partial x^2}-2\frac{\partial ^2 \Psi }{\partial x\partial y} -D_{3}\theta +D_{5}\phi _{v}-D_{3} N\right] , \end{aligned}$$

(30)

$$\begin{aligned} & \sigma _{xy}=\alpha _{1}\left[ \frac{\partial ^2 \Psi }{\partial y^2}-\frac{\partial ^2 \Psi }{\partial x^2}+2\frac{\partial ^2 \Phi }{\partial x\partial y}\right] , \end{aligned}$$

(31)

$$\begin{aligned} & (\nabla ^2-D_{6}-D_{7}\frac{\partial }{\partial t})N+D_{8}\theta =0, \end{aligned}$$

(32)

$$\begin{aligned} & \left( \alpha _{1}\nabla ^2-\frac{\partial ^2}{\partial t^2}+\Omega ^2\right) \Phi -2\Omega \frac{\partial \Psi }{\partial t}-\alpha _{1}\theta +D_{20}\phi _{v}-\alpha _{1}N=0, \end{aligned}$$

(33)

$$\begin{aligned} & \left( D_{21}\nabla ^2-\frac{\partial ^2}{\partial t^2}+\Omega ^2\right) \Psi +2\Omega \frac{\partial \Phi }{\partial t}=0, \end{aligned}$$

(34)

$$\begin{aligned} & \left( 1+\tau _{q}\frac{\partial }{\partial t}+\eta \frac{\tau _{q}^2}{2}\frac{\partial ^2}{\partial t^2}\right) \left( \frac{\partial \theta }{\partial t}+D_{12}\frac{\partial }{\partial t}(\nabla ^2\Phi )+D_{13}\frac{\partial \phi _{v}}{\partial t}\right) \nonumber \\ & \quad -D_{14}N-\left( 1+\tau _{T}\frac{\partial }{\partial t}\right) \nabla ^2\theta =0, \end{aligned}$$

(35)

$$\begin{aligned} & \left( \nabla ^2-D_{15}-D_{16}\frac{\partial }{\partial t}-D_{17}\frac{\partial ^2}{\partial t^2}\right) \phi _{v}-D_{18}\nabla ^2\Phi +D_{19}\theta =0, \end{aligned}$$

(36)

where

$$\begin{aligned} \displaystyle D_{20}=\frac{\alpha _{1}b_{v_0}}{\chi _{0}},\ \ D_{21}=\frac{\alpha _{1}}{D_{3}}. \end{aligned}$$

4 Normal mode analysis

The normal mode technique is utilized to obtain exact solutions without making any assumed limitations on the physical variables that are present in the governing equations of the considered problem. This technique involves decomposing the solution of the physical quantities into normal modes. Essentially, the normal mode technique seeks to express the solution in the Fourier transformed domain. As a result, the physical variables being analyzed can be expressed in terms of normal modes, using the following format:

$$\begin{aligned} & \left[ \Phi ,\Psi ,N,\theta ,\phi _{v},\sigma _{ij}\right] (x,y,t)=\left[ \Phi ^*,\Psi ^*,N^*,\theta ^*,\phi _{v}^*,\sigma _{ij}^*\right] (x) \exp {(\omega t+ \iota my) }, \end{aligned}$$

(37)

where $\Phi ^*,\ \Psi ^*,\ N^*,\ \theta ^*, \ \phi _{v}^*$ and $\sigma _{ij}^*$ are the amplitudes of the physical quantities, $\omega$ is the angular frequency, m is the wave number in y-direction and $\iota$ is the imaginary unit.

Substituting the expression (37) into Eqs. (32)–(36), we attain the following set of equations:

$$\begin{aligned} & D_{8}\theta ^*+(D^2+B_{11})N^*=0, \end{aligned}$$

(38)

$$\begin{aligned} & (D^2+B_{12})\Phi ^*+B_{13}\Psi ^*-\theta ^*+B_{14}\phi _{v}^*- N^*=0, \end{aligned}$$

(39)

$$\begin{aligned} & B_{16}\Phi ^*+(D^2+B_{15})\Psi ^*=0, \end{aligned}$$

(40)

$$\begin{aligned} & \left( B_{17}(D^2-m^2)-B_{18}\right) \theta ^*-B_{19}(D^2-m^2)\Phi ^*-B_{20}\phi _{v}^*+D_{14}N^*=0, \end{aligned}$$

(41)

$$\begin{aligned} & (D^2+B_{21})\Phi _{v}^*-D_{18}(D^2-m^2)\Phi ^*+D_{19}\theta ^*=0, \end{aligned}$$

(42)

where

$$\begin{aligned} & D \cong \frac{\partial }{\partial x},\quad B_{11} = -(m^2+D_{6}+D_{7}\omega ),\quad B_{12} = \frac{\Omega ^2-\omega ^2}{\alpha _{1}}-m^2,\quad B_{13} = \frac{-2\Omega \omega }{\alpha _{1}},\\ & B_{14}=\frac{D_{20}}{\alpha _{1}},\ \ \ B_{15}=\frac{\Omega ^2-\omega ^2}{D_{21}}-m^2,\ \ \ B_{16}=\frac{2\Omega \omega }{D_{21}},\ \ \ B_{17}=(1+\tau _{T}\omega ), \\ & B_{18}= \left( 1+\tau _{q}\omega +\eta \frac{\tau _{q}^2\omega ^2}{2}\right) \omega , \ \ B_{19}=B_{18}D_{12},\ \ \ B_{20}=B_{18}D_{13},\\ & B_{21}=- \left( m^2+D_{15}+D_{16}\omega +D_{17}\omega ^2\right) . \end{aligned}$$

Eliminating the functions $\Phi ^*,\ \Psi ^*, \ N^*,\ \theta ^*$ and $\phi _{v}^*$ from Eqs. (38)–(42), we get the following differential equation of order ten

$$\begin{aligned} & [D^{10}+I_{1}D^8+I_{2}D^6+I_{3}D^4+I_{4}D^2+I_{5}](\Phi ^*, \Psi ^*, N^*, \theta ^*, \phi _{v}^*)=0, \end{aligned}$$

(43)

where

$$\begin{aligned} & I_{1}=\frac{(E_{15}E_{21}+E_{14}E_{22}-E_{11}E_{25}-E_{12}E_{24})}{(E_{14}E_{21}-E_{11}E_{24})},\\ & I_{2}=\frac{(E_{16}E_{21}+E_{15}E_{22}+E_{14}E_{23}-E_{11}E_{26}-E_{12}E_{25}-E_{13}E_{24})}{(E_{14}E_{21}-E_{11}E_{24})},\\ & I_{3}=\frac{(E_{17}E_{21}+E_{16}E_{22}+E_{15}E_{23}-E_{11}E_{27}-E_{12}E_{26}-E_{13}E_{25})}{(E_{14}E_{21}-E_{11}E_{24})},\\ & I_{4}=\frac{(E_{17}E_{22}+E_{16}E_{23}-E_{12}E_{27}-E_{13}E_{26})}{(E_{14}E_{21}-E_{11}E_{24})},\\ & I_{5}=\frac{(E_{17}E_{23}-E_{13}E_{27})}{(E_{14}E_{21}-E_{11}E_{24})},\\ & E_{11}=D_{8}C_{25}-C_{15}C_{23},\;E_{12}=C_{11}C_{25}+C_{15}C_{24}-C_{16}C_{23},\;E_{13}=C_{12}C_{25}+C_{16}C_{24},\\ & E_{14}=-C_{15}B_{16},\; E_{15}=C_{25}-C_{15}C_{21}-C_{16}B_{16},\;E_{16}=C_{13}C_{25}+C_{15}C_{22}-C_{16}C_{21},\\ & E_{17}=C_{14}C_{25}+C_{16}C_{22},\;E_{21}=D_{8}C_{23},\;E_{22}=C_{31}C_{23}+C_{25}C_{32}-D_{8}C_{24},\\ & E_{23}=C_{33}C_{25}-C_{31}C_{24},\;E_{24}=D_{8}B_{17},\;E_{25}=D_{8}C_{21}+C_{31}B_{17},\\ & E_{26}=C_{31}C_{21}-D_{8}C_{22}+C_{25}D_{19},\;E_{27}=C_{34}C_{25}-C_{31}C_{22},\;C_{11}=(B_{12}+B_{15})D_{8},\\ & C_{12}=(B_{12}B_{15}-B_{13}B_{16})D_{8},\; C_{13}=B_{11}+B_{15}-D_{8}, \;C_{14}=B_{11}B_{15}-D_{8}B_{15},\\ & C_{15}=D_{8}B_{14},\; C_{16}=D_{8}B_{14}B_{15},\; C_{21}=B_{17}B_{11}-B_{17}m^2-B_{18}, \\ & C_{22}=B_{17}B_{11}m^2+B_{18}B_{11}+D_{14}D_{8},\;C_{23}=B_{19}D_{8},\; C_{24}=B_{19}D_{8}m^2,\\ & C_{25}=B_{20}D_{8},\; C_{31}=B_{21}D_{8},\; C_{32}=D_{8}D_{18},\;C_{33}=-D_{8}D_{18}m^2,\;C_{34}=B_{11}D_{19}. \end{aligned}$$

Eq. (43) can be factorized as:

$$\begin{aligned} (D^2-\lambda _1^2)(D^2-\lambda _2^2)(D^2-\lambda _3^2)(D^2-\lambda _4^2)(D^2-\lambda _5^2)(\Phi ^*,\ \Psi ^*,\ N^*,\ \theta ^*, \ \phi _{v}^* )(x)=0, \end{aligned}$$

(44)

where $\lambda _n^2\;(n=1,2,3,4,5)$ are the roots of the characteristic equation of (43).

Now, the solution of Eq. (44) can be written as

$$\begin{aligned} (\Phi ^*, \ \Psi ^*, \ N^*, \ \theta ^*, \ \phi _{v}^*)(x)= & \sum _{i=1}^{5} \left[ (H_{1i}, 1, H_{2i}, H_{3i}, H_{4i})M_i(m,\omega )\text{ exp }(\lambda _ix)\right. \nonumber \\ & \left. +(N_{1i}, 1, N_{2i}, N_{3i}, N_{4i})G_i(m,\omega )\text{ exp }(-\lambda _ix)\right] , \end{aligned}$$

(45)

where $M_i$ and $G_i$ are arbitrary constants depending upon m and $\omega$.   $H_{ji}$   $\text {and}$ $\;N_{ji}\;(j=1,2,3,4; \quad i=1,2,3,4,5)$ are the coupling parameters among $\Phi ^*$, $\Psi ^*$, $N^*$, $\theta ^*$ and $\phi _{v}^*$. The values of coupling parameters are obtained from Eqs. (38)–(42) and are given as:

$$\begin{aligned} & H_{1i}=\frac{-(\lambda _i^2+B_{15})}{B_{16 }},\;H_{2i}=-\frac{(E_{11}\lambda _i^4+E_{12}\lambda _i^2+E_{13})H_{1i}}{E_{14}\lambda _i^6+E_{15}\lambda _i^4+E_{16}\lambda _i^2+E_{17}},\;H_{3i}=\frac{-(\lambda _i^2+B_{11})H_{2i}}{D_{8}},\;\\ & H_{4i}=\frac{D_{18}(\lambda _i^2-m^{2})H_{1i}-D_{19}H_{3i}}{(\lambda _i^2+B_{21})},\; \;\\ & N_{1i}=\frac{-(\lambda _i^2+B_{15})}{B_{16}},\;N_{2i}=-\frac{(E_{11}\lambda _i^4+E_{12}\lambda _i^2+E_{13})N_{1i}}{E_{14}\lambda _i^6+E_{15}\lambda _i^4+E_{16}\lambda _i^2+E_{17}},\;N_{3i}=\frac{-(\lambda _i^2+B_{11})N_{2i}}{D_{8}},\;\\ & N_{4i}=\frac{D_{18}(\lambda _i^2-m^{2})N_{1i}-D_{19}N_{3i}}{(\lambda _i^2+B_{21})},\; \; \; (i=1,2,3,4,5). \end{aligned}$$

Based on the solution given in (45), the components of displacement (28) and stresses (29)–(31) can be expressed in the following form:

$$\begin{aligned} ({{u^*}, {v^*}, \sigma _{xx}^*}, {\sigma _{yy}^*}, {\sigma _{xy}^*})(x)= & \sum _{i=1}^{5} \left[ (H_{5i}, H_{6i}, H_{7i}, H_{8i}, H_{9i}) M_i(m,\omega )\exp (\lambda _ix) \right. \nonumber \\ & \left. +(N_{5i}, N_{6i}, N_{7i}, N_{8i}, N_{9i}) G_i(m,\omega )\exp (-\lambda _ix) \right] , \end{aligned}$$

(46)

where

$$\begin{aligned} & H_{5i}=(\lambda _i H_{1i}+\iota m ),\quad H_{6i}=(\iota m H_{1i}-\lambda _i ),\\ & H_{7i}=\alpha _{1}\left( (D_{3}\lambda _i^2-m^2D_{4})H_{1i}+2\iota m\lambda _{i} -D_{3}H_{3i}+D_{5}H_{4i}-D_{3}H_{2i}\right) ,\\ & H_{8i}=\alpha _{1}\left( (D_{4}\lambda _i^2-m^2D_{3})H_{1i}-2\iota m\lambda _{i}-D_{3}H_{3i}+D_{5}H_{4i}-D_{3}H_{2i}\right) ,\\ & H_{9i}=-\alpha _{1}\left( 2\iota m\lambda _{i}H_{1i}(\lambda _i^2+m^2)\right) ,\\ & N_{5i}=(-\lambda _i N_{1i}+\iota m ),\; N_{6i}=(\iota m N_{1i}+\lambda _i ),\\ & N_{7i}=\alpha _{1}\left( (D_{3}\lambda _i^2-m^2D_{4})N_{1i}-2\iota m\lambda _{i}-D_{3}N_{3i}+D_{5}N_{4i}-D_{3}N_{2i}\right) ,\\ & N_{8i}=\alpha _{1}\left( (D_{4}\lambda _i^2-m^2D_{3})N_{1i}+2\iota m\lambda _{i}-D_{3}N_{3i}+D_{5}N_{4i}-D_{3}N_{2i}\right) ,\\ & N_{9i}=\alpha _{1}2\iota m\lambda _{i}N_{1i}(\lambda _i^2+m^2). \end{aligned}$$

5 Application: mechanical load

A mechanical load $\sigma _0(y,t)$ is imposed on the upper surface $x=d$ of the considered rotating semiconducting thermoelastic plate with voids and temperature-dependent properties as shown in Fig. 1. The lower surface $x=-d$ of the plate is thermally insulated. The constants $M_{i}$ and $G_{i}\;(i=1,2,3,4,5)$ will be determined by imposing appropriate boundary conditions.

Case I: Boundary conditions on the upper surface of the plate

(i) Mechanical conditions:

As the upper surface $x=d$ of the plate is subjected to a mechanical load, the mechanical boundary conditions on the upper surface of the plate are written as:

$$\begin{aligned} & \sigma _{xx}(d,y,t)=-\sigma _0(y,t), \end{aligned}$$

(47)

$$\begin{aligned} & \sigma _{xy}(d,y,t)=0, \end{aligned}$$

(48)

where $\sigma _0(y,t)$ is a given function of y and t representing the applied mechanical load such that $\sigma _0= \sigma _0^*\exp (\omega t+\iota my)$, the constant $\sigma _0^*$ is the strength of the mechanical load.

(ii) Thermal condition:

The upper surface $x=d$ of the plate is kept at a uniform temperature $T_0$ i.e. the temperature distribution $(\theta =T-T_0)$ must vanish at the bounding surface, i.e.

$$\begin{aligned} & \theta (d,y,t)=0. \end{aligned}$$

(49)

(iii) Void condition:

The change in volume fraction field is supposed to be zero on the upper surface $x=d$ of the plate, i.e.

$$\begin{aligned} & \phi _v(d,y,t)=0. \end{aligned}$$

(50)

(iv) Plasma excitation condition:

The excitation process occurs during the transport process on the surface $x=d$ of plate with finite recombination probability, such that it can be represented by the carrier density in the following form:

$$\begin{aligned} {D_{E}}\frac{\partial N}{\partial x}(d,y,t)=sN(d,y,t), \end{aligned}$$

(51)

where s is the recombination velocity.

Case II: Boundary conditions on the lower surface of the plate

(i) Mechanical conditions:

The lower surface of the plate is laid on a rigid foundation i.e. normal and tangential components of displacement vanish at the lower surface $x=-d$ of the plate. So, the mechanical boundary conditions on the lower surface of the plate are written as:

$$\begin{aligned} & u(-d,y,t)=0, \end{aligned}$$

(52)

$$\begin{aligned} & v(-d,y,t)=0. \end{aligned}$$

(53)

(ii) Thermal condition:

The lower surface of plate i.e. the surface $x=-d$, is assumed to be thermally insulated. Therefore, the corresponding boundary condition is given by:

$$\begin{aligned} & \frac{\partial \theta }{\partial x}(-d,y,t)=0. \end{aligned}$$

(54)

(iii) Void condition:

The change in volume fraction field is constant on the lower surface $x=-d$ of the plate, i.e.

$$\begin{aligned} & \frac{\partial \phi _v }{\partial x}(-d,y,t)=0. \end{aligned}$$

(55)

(iv) Plasma excitation condition:

At the surface $x=-d$ of the plate with finite recombination probability, the excitation process takes place during the transport process. This process can be described by the carrier density in the following form:

$$\begin{aligned} {D_{E}}\frac{\partial N}{\partial x}(d,y,t)=sN(d,y,t), \end{aligned}$$

(56)

where s is the recombination velocity.

Taking into account the non dimensional expressions for all the field variables from (45) and (46) and applying the normal mode technique defined in expression (37), the above boundary conditions reduce to a non homogeneous system of ten equations, which can be written as:

$$\begin{aligned} \sum _{j=1}^{10}X_{ij}Y_j=Z_i\;\;(i=1,2,3,\cdots ,10), \end{aligned}$$

(57)

where

$$\begin{aligned} & X_{1j}=H_{7j}\exp (\lambda _jd),\quad X_{2j}=H_{9j}\exp (\lambda _jd),\quad X_{3j}=H_{3j}\exp (\lambda _jd),\\ & X_{4j}=H_{4j}\exp (\lambda _jd),\quad X_{5j}=H_{2j}(\lambda _j-L)\exp (\lambda _jd),\quad X_{6j}=H_{51}\exp (-\lambda _jd),\\ & X_{7j}=H_{6j}\exp (-\lambda _jd),\quad X_{8j}=\lambda _jH_{3j}\exp (-\lambda _jd),\quad X_{9j}=\lambda _j H_{4j}\exp (-\lambda _jd),\\ & X_{10j}=H_{2j}(\lambda _j-L)\exp (-\lambda _jd),\\ & X_{1j+5}=N_{7j}\exp (-\lambda _jd),\quad X_{2j+5}=N_{9j}\exp (-\lambda _jd),\quad X_{3j+5}=N_{3j}\exp (-\lambda _jd),\\ & X_{4j+4}=N_{4j}\exp (-\lambda _jd),\quad X_{5j+5}=N_{2j}(-\lambda _j-L)\exp (-\lambda _jd),\quad X_{6j+5}=N_{5j}\exp (\lambda _jd),\\ & X_{7j+5}=N_{6j}\exp (\lambda _jd),\quad X_{8j+5}=(\lambda _j)N_{3j}\exp (\lambda _jd),\quad X_{9j+5}=(-\lambda _j)N_{4j}\exp (\lambda _jd),\\ & X_{10j+5}=N_{2j}(-\lambda _j-L)\exp (\lambda _jd),\quad L=\frac{st^*C_{T}}{D_{E}},\\ & Y_j=M_j,\quad Y_{j+5}=G_j,\quad Z_1={-\sigma _0},\quad Z_i=0,\quad (i=2,3,\dots ,10; \quad j=1,2,3,4,5). \end{aligned}$$

Now, we get the values of $M_{j}$ and $G_{j}\;(j=1,2,3,4,5)$ with the help of matrix inversion method. Using these values in the expressions (45) and (46), which when substituted in (37), provides the exact expressions of the field variables.

6 Significant cases

6.1 Ignoring void effect

If the void effect is neglected, the material constants due to the presence of voids will disappear from the medium and the above problem reduces to that of a problem of a semiconducting rotating plate with temperature-dependent properties. This is achieved by setting $\alpha =w_{v}=b_v=\xi =\chi =n=0$ in both the constitutive relations and field equations. Considering the above necessary modifications and following a procedure similar to the general case, we derive a set of equations analogous to Eqs. (38)–(41), as follows:

$$\begin{aligned} & D_{8}\theta ^*+(D^2+B_{11})N^*=0, \end{aligned}$$

(58)

$$\begin{aligned} & (D^2+B_{12})\Phi ^*+B_{13}\Psi ^*-\theta ^*- N^*=0, \end{aligned}$$

(59)

$$\begin{aligned} & B_{16}\Phi ^*+(D^2+B_{15})\Psi ^*=0, \end{aligned}$$

(60)

$$\begin{aligned} & \left( B_{17}(D^2-m^2)-B_{18}\right) \theta ^*-B_{19}(D^2-m^2)\Phi ^*+D_{14}N^*=0, \end{aligned}$$

(61)

By eliminating the functions $\Phi ^*,\ \Psi ^*, \ N^*\$and$\ \theta ^*$ from the equations mentioned above, we arrive at an eight-order differential equation given by:

$$\begin{aligned} & [D^{8}+I'_{1}D^6+I'_{2}D^4+I'_{3}D^2+I'_{4}](\Phi ^*,\ \Psi ^*,\ N^*,\ \theta ^*)=0, \end{aligned}$$

(62)

where

$$\begin{aligned} & I'_{1}=\frac{(C_{11}B_{17}+D_{8}C_{21}-C_{23})}{D_{8}B_{17}}, \quad I'_{2}=\frac{(C_{12}B_{17}+C_{11}C_{21}-D_{8}C_{22}-C_{13}C_{23}+C_{24})}{D_{8}B_{17}},\\ & I'_{3}=\frac{(C_{12}C_{21}-C_{11}C_{22}-C_{14}C_{23}+C_{13}C_{24})}{D_{8}B_{17}}, \quad I'_{4}=\frac{(C_{14}C_{24}-C_{12}C_{22})}{D_{8}B_{17}}. \end{aligned}$$

Now, Eq. (62) can be factorized as:

$$\begin{aligned} (D^2-{\lambda '_{1}}^2)(D^2-{\lambda '_{2}}^2)(D^2-{\lambda '_{3}}^2)(D^2-{\lambda '_{4}}^2)(\Phi ^*,\ \Psi ^*,\ N^*,\ \theta ^*)(x)=0, \end{aligned}$$

(63)

where ${\lambda '_{n}}^2\;(n=1,2,3,4)$ are the roots of the characteristic equation of (62).

Now, the solution of Eq. (63) can be written as:

$$\begin{aligned} (\Phi ^*,\ \Psi ^*,\ N^*,\ \theta ^*)(x)= & \sum _{i=1}^{4}\left[ (H'_{1i},\ 1, \ H'_{2i},\ H'_{3i})M'_i(m,\omega ) \exp ({\lambda '_{i}}x) \right. \nonumber \\ & \left. + (N'_{1i},\ 1,\ N'_{2i},\ N'_{3i})G'_i(m,\omega )\exp (-{\lambda '_{i}}x)\right] , \end{aligned}$$

(64)

where $M'_{i}$ and $G'_{i}$ are arbitrary constants depending upon m and $\omega$. $H'_{ij}$ and $\;N'_{ij}\;(i=1,2,3,4;j=1,2,3)$ are the coupling parameters among $\Phi ^*$, $\Psi ^*$, $N^*$ and $\theta ^*$. The values of coupling parameters are obtained from Eqs. (58)–(61) and are given as:

$$\begin{aligned} & H'_{1i}=\frac{-({\lambda '_{i}}^2+B_{15})}{B_{16}},\quad H'_{2i}=-\frac{(D_{8}{\lambda '_{i}}^4+C_{11}{\lambda '_{i}}^2+C_{12})H'_{1i}}{{\lambda '_{i}}^4+C_{13}{\lambda '_{i}}^2+C_{14}},\\ & H'_{3i}=\frac{-({\lambda '_{i}}^2+B_{11})H'_{2i}}{D_{8}},\quad N'_{1i}=\frac{-({\lambda '_{i}}^2+B_{15})}{B_{16}},\\ & N'_{2i}=-\frac{(D_{8}{\lambda '_{i}}^4+C_{11}{\lambda '_{i}}^2+C_{12})N'_{1i}}{{\lambda '_{i}}^4+C_{13}{\lambda '_{i}}^2+C_{14}},\\ & N'_{3i}=\frac{-({\lambda '_{i}}^2+B_{11})N'_{2i}}{D_{8}},\quad (i=1,2,3,4). \end{aligned}$$

In view of solution (64), the components of displacement and stress take the following form:

$$\begin{aligned} ({{u^*},\ {v^*},\ \sigma _{xx}^*},\ {\sigma _{yy}^*},\ {\sigma _{xy}^*})(x)= & \sum _{i=1}^{5} \left[ (H'_{4i},\ H'_{5i},\ H'_{6i},\ H'_{7i},\ H'_{8i}) M'_i(m,\omega )\exp ({\lambda '_{i}}x) \right. \nonumber \\ & \left. +(N'_{4i},\ N'_{5i},\ N'_{6i},\ N'_{7i},\ N'_{8i}) G'_i(m,\omega )\exp (-{\lambda '_{i}}x)\right] , \end{aligned}$$

(65)

where

$$\begin{aligned} & H'_{4i} = ({\lambda '_{i}} H'_{1i}+\iota m),\ \ H'_{5i} = (\iota m H'_{1i}-{\lambda '_{i}}), \\ & H'_{6i} = \alpha _{1}\left( (D_{3}{\lambda '_{i}}^2-m^2D_{4})H'_{1i}+2\iota m\lambda '_{i}-D_{3}(H'_{3i}-H'_{2i})\right) , \\ & H'_{7i} = \alpha _{1}\left( (D_{4}{\lambda '_{i}}^2-m^2D_{3})H'_{1i}-2\iota m\lambda '_{i}-D_{3}(H'_{3i}-H'_{2i})\right) , \\ & H'_{8i} =- \alpha _{1}\left( 2\iota m{\lambda '_{i}}({\lambda '_{i}}^2+m^2)H'_{1i}\right) , \\ & N'_{4i} = (-{\lambda '_{i} }N'_{1i}+\iota m),\ \ N'_{5i} = (\iota m N'_{1i}+{\lambda '_{i}}),\\ & N'_{6i} = \alpha _{1}\left( (D_{3}{\lambda '_{i}}^2-m^2D_{4})N'_{1i}-2\iota m\lambda '_{i}-D_{3}(N'_{3i}-N'_{2i})\right) , \\ & N'_{7i} = \alpha _{1}\left( (D_{4}{\lambda '_{i}}^2-m^2D_{3})N'_{1i}+2\iota m\lambda '_{i}-D_{3}(N'_{3i}-N'_{2i})\right) ,\\ & N'_{8i}=\alpha _{1}2\iota m\lambda '_{i}({\lambda '_{i}}^2+m^2)N'_{1i}. \end{aligned}$$

By excluding the boundary conditions associated with the void effect from (47)–(56) and considering the other appropriate boundary conditions, we obtain a non-homogeneous system of eight equations given as:

$$\begin{aligned} \sum _{j=1}^{8}X'_{ij}Y'_j=Z'_i,\;\;(i=1,2,\cdots ,8), \end{aligned}$$

(66)

where

$$\begin{aligned} & X'_{1j}=H'_{6j}\exp (\lambda '_jd),\quad X'_{2j}=H'_{8j}\exp (\lambda '_jd),\quad X'_{3j}=H'_{3j}\exp (\lambda '_jd),\\ & X'_{4j}=H'_{2j}(\lambda '_j-L)\exp (\lambda '_jd),\quad X'_{5j}=H'_{4j}\exp (-\lambda '_jd),\\ & X'_{6j}=H'_{5j}\exp (-\lambda '_jd),\quad X'_{7j}=\lambda '_jH'_{3j}\exp (-\lambda '_jd),\\ & X'_{8j}=H'_{2j}(\lambda '_j-L)\exp (-\lambda '_jd),\\ & X'_{1j+4}=N'_{6j}\exp (-\lambda '_jd),\quad X'_{2j+4}=N'_{8j}\exp (-\lambda '_jd),\\ & X'_{3j+4}=N'_{3j}\exp (-\lambda '_jd),\quad X'_{4j+4}=N'_{2j}(-\lambda '_j-L)\exp (-\lambda '_jd),\\ & X'_{5j+4}=N'_{4j}\exp (\lambda '_jd),\quad \quad X'_{6j+4}=N'_{5j}\exp (\lambda '_jd),\\ & X'_{7j+4}=N'_{3j}(\lambda '_j)\exp (\lambda '_jd),\quad X'_{8j+4}=N'_{2j}(-\lambda '_j-L)\exp (\lambda '_jd),\quad \\ & L=\frac{st^*C_{T}}{D_{E}},\quad Y'_j=M'_j,\quad Y'_{j+4}=G'_j, \quad Z'_1={-\sigma _0},\\ & Z'_i=0,\quad (i=2,3,\ldots ,8, \quad j=1,2,3,4). \end{aligned}$$

Following the similar procedure as in the main case, the exact expressions of the field variables can be derived for a semiconducting rotating plate with temperature-dependent properties.

6.2 Ignoring rotational effect

If we also neglect the rotational effect in the aforementioned case by setting the rotation parameter $\Omega$ to zero, the expressions for the normal stress, normal displacement, temperature distribution and carrier density can be obtained as in general case. Furthermore, if we also neglect the photothermal effect in the medium, the results will coincide with those of Allam and Tayel [6] (without nonhomogeneity effects) with appropriate changes in the boundary conditions.

6.3 Without temperature-dependent properties

If we remove the effect of temperature-dependent properties from the considered medium i.e. $\alpha ^*=0.0$, then we are left with the resulting problem of a photothermoelastic semiconducting rotating plate under dual phase lag theory. Additionally, if we assume the solid medium as half space instead of a plate, our results would correspond to those obtained by Kilnay et al. [18] with appropriate modifications in the boundary conditions and the theory employed.

7 Computational results and discussion

In order to study the impact of rotation, temperature-dependent properties, time, void and photothermal parameters on the field variables, a numerical analysis is carried out with the help of computer programing software MATLAB. We have followed Kilany et al. [18] for a silicon crystal-like material with the physical data listed in Table 1.

Table 1 Values of physical constants

All the physical variables are displayed in graphs with the thickness of plate $-1.0\le x\le 1.0$ at time $t= 0.1$. By utilizing the above-mentioned numerical values, we have depicted the effects of rotation, photothermal parameter, void parameter, temperature-dependent properties and time on the considered field variables. For convenience, we have classified the figures into five different groups:

Group I: Figure 2a–e examine the effect of angular velocity on the distribution of physical quantities for three different values of rotation parameter as $\Omega = 0.01$ (solid line), $\Omega = 0.02$ (dashed line) and $\Omega = 0.03$ (dotted line).

Group II: Figure 3a–e are presented to depict the effect of photothermal transport process on the variations of field variables versus the thickness of the plate, by considering three different values of $D_E$ (Carrier diffusion coefficient).

Group III: Figure 4a–e depict the effect of void parameter $b_v$ on the two dimensional variations of the considered field variables for three different values of parameter $b_v=1.13849\times 10^{10}$ (solid line), $b_v=3.13849\times 10^{10}$ (dashed line) and $b_v=5.13849\times 10^{10}$ (dotted line).

Group IV: Figure 5a–e are plotted to scrutinize the effect of temperature-dependent properties on the variations of the physical field variables. The solid line represents the plots of field variables corresponding to the temperature-dependent properties and the dashed line corresponds to the plots without temperature-dependent properties.

Group V: Figure 6a–e are aimed at exploring the influence of time as $t=0.1$ (solid line), $t=0.3$ (dashed line) and $t=0.5$ (dotted line), on the considered physical quantities.

7.1 Group I: Effect of rotation

Group I consists of Fig. 2a–e. Figure 2a elucidates the variation of normal stress $\sigma _{xx}$ with the thickness of plate for three different values of angular velocity $\Omega$. The variations are having the starting points with maximum non-zero values at the upper surface of the plate, which complies fairly well with the boundary condition. The distribution experiences a similar pattern for all the considered values of the rotation parameter. Also, it is noted from the plot that the increasing value of rotation parameter acts to decrease the numerical values of normal stress $\sigma _{xx}$. The variation of normal displacement u has been displayed in Fig. 2b for three different values of the rotation parameter. It is evident from the plot that on the rigid base at $x=-1.0$, normal displacement u is zero, which complies fairly well with the assumed boundary condition. The maximum magnitude of normal displacement is found to be on the upper surface $(x=1.0)$ of the plate, which may be attributed to the fact that the upper surface of the plate is subjected to a mechanical load. Also, it is observed from the plot that the rotation parameter has a decreasing effect on the magnitude of the normal displacement u. Figure 2c gives the comparison of temperature distribution $\theta$ for three different values of angular velocity $\Omega$. The temperature distribution behaves similarly for all the values of rotation parameter $\Omega$, albeit with varying magnitudes. The figure also demonstrates that an increase in the value of rotation parameter leads to a decrease in the magnitude of the temperature distribution. This observation highlights the noticeable decreasing effect of rotation on the profile of temperature distribution $\theta$.

The transient effects of rotation parameter on the volume fraction field $\phi _v$ have been shown in Fig. 2d. The plot illustrates that the change in volume fraction field $\phi _{v}$ has three different initial values corresponding to three different values of angular velocity $\Omega$ at the lower surface of the plate $(x=-1.0)$. Increasing values of rotation cause a decrease in the magnitude of $\phi _v$. The change in volume fraction field $\phi _v$ is zero at the upper surface of the plate for all the three different values of rotation parameter, which agrees well with the real situation. Figure 2e indicates the qualitative behaviour of carrier density N. We can observe from the figure that field variable N has different numerical values on the lower surface of the plate $(x=-1.0)$. The maximum value of carrier density N is found at location $x=0.2$ of the plate. Moreover, rotation parameter $\Omega$ has a decreasing effect on N.

7.2 Group II: Effect of photothermal transport process

This group comprises Fig. 3a–e. Figure 3a illuminates the variations of normal stress $\sigma _{xx}$ under the effect of photothermal parameter $D_{E}$. For all the three values of $D_{E}$, $\sigma _{xx}$ starts with different positive values on the lower surface of the plate and attains its maximum value in the locality of source i.e. on the upper surface of the plate $(x=1.0)$, which confirms the assumed boundary condition. It is clear from the plot that $\sigma _{xx}$ is tensile in nature for all the considered values of photothermal parameter $D_{E}$. Moreover, it is easy to observe that $D_{E}$ has an increasing effect on $\sigma _{xx}$. The effect of parameter $D_{E}$ on normal displacement u is shown in Fig. 3b. The values of normal displacement start with magnitude zero at $x=-1.0$ and are found to be maximum on the upper surface of the plate for the three values of photothermal parameter $D_{E}$, which is in accordance with the boundary condition. Also, $D_{E}$ has a decreasing impact on the normal displacement.

Figure 3c depicts the variations of temperature distribution $\theta$ for three different values of $D_{E}$. The medium is initially at uniform temperature $T_0$. As no thermal load is imposed on the upper surface $(x=1.0)$ of the plate, therefore temperature deviation $(\theta =T-T_0)$ vanishes at the upper surface of the plate i.e. reference temperature $(T_0)$ of the medium is maintained. The numerical values of $\theta$ for $D_E =2.5\times 10^{-3}$ are larger than those for $D_{E} =3.5\times 10^{-3}$ and $D_{E} =5.5\times 10^{-3}$. The qualitative behaviour of the temperature distribution $\theta$ is similar for every value of $D_{E}$ but experiences a decreasing impact of photothermal parameter. The distribution of change in volume fraction field $\phi _{v}$ with respect to distance x for all the three values of $D_{E}$ has been shown in Fig. 3d. It is manifested from the figure that the change in volume fraction field is directly proportional to $D_{E}$. Increment in photothermal parameter $D_{E}$ is responsible for the increase in the magnitude of change in volume fraction field $\phi _v$. The dynamic effect of photothermal parameter $D_{E}$ on the variation of carrier density N is depicted in Fig. 3e. It can be observed from the graph that the numerical values of the carrier density N are large for larger values of $D_{E}$. This shows that $D_{E}$ has an increasing effect on N.

7.3 Group III: Effect of voids

This group includes Fig. 4a–e. Figure 4a is drawn to present the variation of normal stress $\sigma _{xx}$ for the three different values of void parameter $b_{v}$. It is observed from the plot that the upper surface of the plate $x=1.0$ is subjected to the action of a mechanical load, therefore, normal stress $\sigma _{xx}$ should have a non-zero value near the location of the application of the load. Also, normal stress follows a similar trend for the three considered values of $b_{v}$ and attains larger values with the increasing values of $b_{v}$. Figure 4b shows the variations of normal displacement u with thickness x. It is clearly depicted in the plot that normal displacement is directly proportional to the void parameter $b_{v}$. It is also observed from the graph that normal displacement u is zero at the lower surface $(x=-1.0)$ of the plate, which is completely in agreement with the boundary condition.

The significant effect of void parameter $b_{v}$ on the distribution of temperature $\theta$ is depicted in Fig. 4c. It is observed from the plot that temperature behaves like a decreasing function of the void parameter $b_{v}$. Figure 4d illuminates that the void parameter acts to increase the magnitude of change in volume fraction field $\phi _{v}$. It is evident from the plot that the change in volume fraction field initiates with zero magnitude at the upper surface of the plate and shows its maximum impact within the region $-0.2 \le x \le 0.6$. In Fig. 4e, three curves of carrier density are drawn with respect to thickness of the plate for three different values of void parameter $b_{v}$. A comparison of the curves shows that the maximum effect of void parameter $b_{v}$ is appearing in the range $-1 \le x \le 0.4$ and if we move away from this range, this impact starts vanishing. Another observation from this figure is that an increase in the value of $b_{v}$ results in decrement in the values of carrier density function N.

Fig. 2

Effect of rotation parameter $\Omega$ on the field variables

Fig. 3

Effect of photothermal parameter $D_E$ on the field variables

Fig. 4

Effect of void parameter $b_v$ on the field variables

Fig. 5

Effect of temperature-dependent parameter $\alpha ^*$ on the field variables

Fig. 6

Effect of time t on the field variables

7.4 Group IV: Effect of temperature-dependent properties

In this group, Fig. 5a–e are plotted to demonstrate the effect of temperature-dependent properties on the considered field variables. Figure 5a exhibits the distribution of normal stress $\sigma _{xx}$ with the thickness of plate in two cases (with temperature-dependent properties and without temperature-dependent properties). Values of normal stress indicate a significant difference for the two cases. On the upper surface of the plate, the values of normal stress are found to be maximum, which may be attributed to the fact that the upper surface of the plate is subjected to a mechanical load, which is physically reasonable. The distribution of normal displacement u is plotted in Fig. 5b. The curve of normal displacement u without temperature-dependent properties is lower as compared to that with temperature-dependent properties, which clearly shows an increasing effect of $\alpha ^*$ on the normal displacement. For both the cases, normal displacement u has a value zero on the lower surface of the plate, likely due to the lower surface of the plate is being supported by a rigid foundation. Figure 5c reveals the dynamic effect of temperature-dependent properties on the temperature distribution $\theta$ of the plate with thickness x. The absolute values of temperature $\theta$ exhibit a notable increase in the range $-1 \le x \le 0.12$ when temperature-dependent properties are considered, in contrast to when these properties are not taken into account. This observation indicates that temperature-dependent properties have an enhancing influence on the temperature $\theta$ within this range. However, beyond this range, temperature-dependent properties have a diminishing impact on the temperature $\theta$.

Figure 5d shows the transient effect of temperature-dependent properties on the volume fraction field $\phi _{v}$. The difference in the numerical values of $\phi _{v}$ for both the cases is quite observable from the plot. The solution curves follow a similar pattern of variation in the whole range $-1 \le x \le 1$. It can be noticed from the figure that absolute values of change in volume fraction field are large in presence of temperature-dependent properties in comparison to its absence, which indicates an increasing effect of $\alpha ^*$ on $\phi _{v}$. Figure 5e reveals the profile of carrier density N for the two different cases ( presence and absence of temperature-dependent properties). The profile curves have different starting values $5.3604\times 10^{-4}$ and $7.7188\times 10^{-4}$ on the lower surface of the plate for with and without temperature-dependent properties respectively. It is clear from the figure that the flow of variations for both the media is similar in the whole range. Also, the presence of temperature dependency in the medium is having a decreasing impact on this field variable.

7.5 Group V: Effect of time

This group consists of Fig. 6a–e, from which Fig. 6a shows the effect of time on the variation of normal stress $\sigma _{xx}$. It attains its maximum values 0.9, 1.03 and 1.18 for $t=0.1, 0.3$ and 0.5 respectively and sharply decreases continuously to reach the lower surface of the plate. For all the three different values of time t, normal stress is maximum in the vicinity of the source i.e. at the upper surface $x=d$ of plate, which is physically plausible. It is clear from the plot that $\sigma _{xx}$ is directly proportional to the values of time t. The effect of time t on normal displacement u is shown in Fig. 6b. The magnitude of variation in normal displacement u for small values of t is small in comparison to large values of t, which shows that time has an increasing effect on u and this effect disappears on the lower surface of the plate. Figure 6c is plotted to scrutinize the effect of time on temperature distribution $\theta$ for three different values of t. It is noted that the difference among the magnitudes of temperature distribution $\theta$ for different values of t is remarkable on the lower surface of the plate. This difference disappears gradually as it goes to the upper surface of the plate. It is also found that the magnitude of temperature distribution $\theta$ is large for larger values of t. This shows that the time has an increasing effect on $\theta$.

The variation in change in volume fraction field $\phi _{v }$ has been exhibited in Fig. 6d for the three values of time t. For all the values of t,  the volume fraction field starts with some non-zero values on the lower surface of the plate. As we move away from the lower surface of the plate towards the upper surface, these values approach zero on the upper surface of the plate, which acts in accordance with the assumed boundary conditions. Additionally, it is evident that the volume fraction field $\phi _{v}$ exhibits an increasing effect of time t. Figure 6e is drawn to show the variant of carrier density N for three values of time $(t=0.1, 0.3$ and 0.5). Carrier density N has large values when $t=0.5$ as compared to the case when $t=0.1$ and $t= 0.3,$ which clearly indicates that time has an increasing effect on the carrier density N, which complies well with the real situation. The figure also displays that the profile of carrier density N is similar in all the three cases having non-zero values on the lower as well as the upper surface of the plate, which observes fairly well with the boundary condition.

8 Concluding remarks

In this research work, we have inspected the normal stress, normal displacement, temperature distribution, change in volume fraction field and carrier density in a homogeneous, isotropic photothermoelastic rotatory plate with voids and temperature-dependent properties. The problem is negotiated in the framework of normal mode analysis under DPL model, when a mechanical load is imposed on the upper surface of the plate. The impacts of rotation, photothermal parameter $D_{E, }$ void parameter $b_{v}$, temperature-dependent parameter $\alpha ^*$ and time are examined on the field variables. According to the above theoretical, numerical and graphical representations, some conclusions emerge as follows:

• The presence of rotation parameter $\Omega$ plays a considerable role in the variations of all the physical fields. It has a decreasing effect on all the field quantities.

• The effect of photothermal parameter has significantly appeared on all the field variables. It has an increasing effect on normal stress, change in the volume fraction field and carrier density while it acts to decrease the magnitudes of normal displacement and temperature distribution.

• Void parameter $b_v$ has an increasing effect on normal stress, normal displacement and change in the volume fraction field, while it has a decreasing effect on carrier density and temperature distribution.

• All the physical variables are significantly affected by the temperature-dependent properties. These properties have an increasing effect on the normal displacement and change in volume fraction field, while the reverse happens on carrier density N. However, it has a mixed kind of effect on normal stress and temperature distribution.

• All the field variables are directly proportional to the time. We obtain a noticeable increasing effect of time on all the physical quantities in the restricted region of a plate of thickness 2d.

• As expected, all the physical quantities are continuous and satisfy the boundary conditions.

9 Applications of the model

The theory of thermoelasticity in a semiconducting rotating plate with voids and temperature-dependent properties has a wide range of applications in various fields, including astronautics, aeronautics, nuclear reactors, soil dynamics, high particle accelerators, earthquake engineering and the study of nanomaterial behaviour. Photothermal semiconducting media have significant applications in physics, geophysics, television circuits, automatic control systems, sound and motion picture technology, copying and recording equipment and particularly in solar cells and semiconducting polymer nanocomposites, which offer mechanical flexibility and lower fabrication costs. The combination of photothermal properties and semiconducting capabilities makes these materials valuable in industry, biophysics, structural engineering and chemical engineering.

Voids have significant effects in many scientific fields, particularly in geophysics and geology. Researchers have shown a keen interest in understanding how voids influence materials in the presence of thermoelasticity. This research aims to detect the effects caused by voids, especially regarding how materials respond to external changes. The method used in this study applies to a broad spectrum of problems in thermoelasticity, thermodynamics and photothermoelasticity. The normal mode technique has become a standard method for studying the dynamics of biological molecules. It is used to identify and characterize the slowest motions in macromolecular systems, which are inaccessible.