Dynamics of a compressed Euler–Bernoulli beam on an elastic foundation with a partly prescribed discrete spectrum

Abstract

In this paper, the dynamics of a compressed Euler-Bernoulli beam on a Winkler elastic foundation under the action of an external nonlinear force, which models a wind force, is studied. The beam is assumed to be long, and the lower part of its spectrum is prescribed. An asymptotic method is proposed to find the parameters of the beam, in order to have this prescribed lower part of the spectrum. All these parameters are necessary to guarantee the stability of the beam and to avoid resonances between the low frequency modes. These modes have special spatial supports that exclude a direct interaction between them. It is shown that the Galerkin system describing the time evolution can be decomposed into a system of almost independent equations which describes n independent nonlinear oscillators. Each oscillator has its own phase and frequency. It is shown that interaction between oscillators can exist only through high frequency modes.

1 Introduction

The axially loaded Euler–Bernoulli beam resting on an elastic Winkler foundation is a simple mechanical model for a large class of engineering structures, which are long and slender, and for which it is possible to ignore the effects of rotary inertia and shear deformation. In many practical applications it is useful to construct such a beam with given (lower part of the) spectrum for the natural eigenfrequencies. Some examples on how to avoid undesirable resonances in mechanical structures using “the principles of passive modification and active control” are considered in [1]. Other examples are the “determination of parameters in a numerical model for a structure such that the first natural eigenfrequencies coincide with experimental data for these frequencies”, see for instance [2,3,4,5,6] . Similar examples can be found in the geophysical sciences, where researchers are dealing with the reconstruction of the internal structure of the Earth from data on toroidal and spheroidal oscillations [7], or in the field of the identification of structural damage from frequency data (see [8,9,10,11]). Also the determination of loads acting on elastic beams or plates during the vibrations of the structure are of interest in practical applications [12, 13]. In [14] the authors show that for certain mass per unit length distributions and for flexural stiffness variations in axially loaded Rayleigh beams, there exist fundamental closed form solutions of the governing differential equations. The obtained results can serve as "benchmark solutions for various numerical methods and also provide valuable insights into the design of such beams if they are required to vibrate at or away from a pre-specified frequency range". In this paper, we consider one of these inverse problems for an axially compressed Euler–Bernoulli beam resting on an elastic Winkler foundation. The beam is under the action of an external weak, nonlinear force which models a wind force (see [15,16,17]). This model can be useful, for example, to analysis the dynamic behavior of hull structures in wind turbine. In [18] a one-dimensional model for an offshore wind turbine was proposed. The main characteristic of the model is an Euler–Bernoulli beam with a constant cross-section of area and with variable sectional density and longitudinal force along the axial direction of the beam. In our model we take into account the variation of the beam rigidity in axial direction. The approach as suggested in this paper can be seen as a first step in developing a method which helps to design a spectrum for a construction which leads to a predictable dynamic behaviour. Through the design the so-obtained oscillation modes, which are the most important ones for the beam dynamics, can then be controlled by active or passive controls. To solve the problem an asymptotic approach is proposed, which makes it possible to show that the high-frequency modes (corresponding to the free vibrations of the linear beam) lead to small (in terms of norm) contributions to the solution (despite possible resonances). Therefore, it is possible to design part of the spectrum containing only a limited number of low frequency modes (the frequency threshold can be estimated). Instead of methods as suggested in [7, 13], where the beam’s rigidity and linear mass density vary along the longitudinal coordinate, we propose a method which uses only variations in the rigidity of the beam. We choose the beam rigidity as a piecewise constant function that is bounded on N small intervals separated by non-small distances. First we solve the problem for large L, and $N=1$. This problem plays the role of a reference problem. Using a variational principle, explicit formulas, and Euler’s approach for a critical compressive force, we construct eigenfunctions, which decay exponentially in space. In the general case for $N> 1$, we divide up the beam into N sections, each of which is described by a reference problem. Due to exponential decay, the resulting functions satisfy the differential equation and boundary conditions with high exponential accuracy. There are no resonances between the constructed modes, since the effect of mode overlap is exponentially small. For several types of spectra examples for finding the beam parameters are given, and an algorithm of beam design with a partly prescribed spectrum is described in detail. The paper is organized as follows. In Sect. 2 we state the problem. In the Sect. 3 we show that the problem is well posed. In Sect. 4 we outline the main ideas on how to get the desirable dynamics of the beam. Further, in Sect. 5 we formulate the spectrum design problem. In Sect. 6, we give the proof for the main theorem, and formulate an algorithm that allows us to design a beam with a partly prescribed spectrum. In Sect. 7, we consider nonlinear effects. Finally, Sect. 8 contains a discussion and some concluding remarks.

2 Statement of the problem

The equation describing the dynamics of an Euler–Bernoulli beam on a Winkler foundation is given by:

$$\begin{aligned} m_0 u_{tt} + ( D(x) u_{xx})_{xx} + T_0 u_{xx} + K u= f(u_t), \end{aligned}$$

(1)

where u(x, t) is the beam transverse displacement, $x \in [0, L]$ is the longitudinal coordinate, L is the length of the beam, $t >0$ is the time, $m_0=A\rho$ is the mass of the beam per unit length, A is the beam’s cross-sectional area, $\rho$ is the beam’s material density, $D(x)=EI(x)$ or $D(x)=E(x)I$ is a non-heterogeneous beam rigidity, I is the moment of the cross-section area, E is the Young’s modulus of the beam material, $T_0>0$ is the longitudinal compressive force, $f(u_t)$ is a smooth function, which defines nonlinear forces acting on the beam, and K is the Winkler elastic foundation coefficient. Note that we keep the beam’s cross-sectional area constant and vary the moment of the cross-sectional inertia. The force $f(u_t)$ may have the following form (see [15,16,17, 19]):

$$\begin{aligned} f(u_t)= a_1 u_t + a_2 u_t^3, \end{aligned}$$

(2)

where $a_i$ are coefficients. These coefficients can have arbitrary signs, however, to provide existence of solutions of the problem, and to avoid an unbounded energy growth, it is necessary to fulfill the following condition (see [15, 19]):

$$\begin{aligned} a_2 <0. \end{aligned}$$

(3)

We will not consider the trivial linear case $a_2=0$, where the energy is bounded for $a_1<0$, and unbounded for $a_1>0$. The initial conditions have the following form

$$\begin{aligned} u(x, 0)=u_0(x), \quad u_t(x, 0)=u_1(x), \end{aligned}$$

(4)

where $u_0, u_1$ are smooth functions. We consider a problem for a beam, which has a length L with a free boundary at $x=L$, and a clamped boundary at $x=0$. Then, the following boundary conditions hold:

$$\begin{aligned} u_{x} (x,t) = u(x,t) =0, \quad x=0,\quad t\ge 0, \end{aligned}$$

(5)

and

$$\begin{aligned} & u_{xx} (x,t)=0, \quad x=L,\quad t\ge 0 \end{aligned}$$

(6)

$$\begin{aligned} & (D(x)u_{xx}(x,t))_x+ T_0 u_{x}(x,t)=0, \quad x=L,\quad t\ge 0. \end{aligned}$$

(7)

These conditions can be obtained by a variation of a natural Lagrangian ${{\mathcal {L}}}[u]= \frac{1}{2} \int _0^L (Du_{xx}^2 -T_0 u_x^2 +Ku^2) dx$ associated with the problem. We suppose that D(x) is a smooth positive function:

$$\begin{aligned} D(x) > 0, \quad x \in [0, L]. \end{aligned}$$

(8)

Notice that the differential equation (1), and the given initial and boundary conditions can be transformed to a dimensionless form when we rescale the variables. For the rescaling, the following choice is made: $x={\bar{x}}L$, $u={\bar{u}}L$, $L={\bar{L}}\sqrt{A}$, $D(x)=E_mI_m {\overline{D}} (x) =D_m {\overline{D}} (x)$, $t={\bar{t}}\frac{1}{c_0}$, $c_0^2=\frac{E_m}{A\rho }$, $\bar{T_0}=\frac{T_0}{AE_m}$, ${\bar{K}}=\frac{K}{Ac_0^2\rho }$. Also it is possible to consider the case when $D(x)=E_mI(x) {\overline{D}} (x)$ or $D(x)=E(x)I_m {\overline{D}} (x)$. Here $I_m$ and $E_m$ are the maximum values of the beams moment of the cross-sectional area, and Young’s modulus of the beam’s material, respectively. For simplification, the bars are omitted, and the final equation then takes the form:

$$\begin{aligned} ( D(x) u_{xx})_{xx} + T_0 u_{xx} + K u + m_0 u_{tt} = \epsilon f(u_t) \, \end{aligned}$$

(9)

where $m_0=1$, and $\epsilon >0$ is a small parameter.

3 The well-posedness of the problem

3.1 General estimate of energy

We are looking for solutions u(x, t) of the weakly nonlinear initial-boundary value problem (IBVP) defined by (1)–(7), which are bounded in $\textbf{L}^2[0, L]$. Under certain conditions on f existence of such solutions follows from an a priori estimate, which gives a limit from above for the beam energy. We use the following standard notation

$$\begin{aligned} (u, v)=\int _{0}^{L} u(x) v(x) dx, \quad \Vert u \Vert = (u, u)^{1/2}. \end{aligned}$$

Let us introduce the dissipation functional

$$\begin{aligned} P[u_t]=\int _0^L p(u_t(x,t)) dx, \end{aligned}$$

where $p(u_t)= a_1 u_t^2/2 + a_2 u_t^4/4$.

Multiplying the left and the right hand sides of (1) by $u_t$, and by integrating by parts, one obtains

$$\begin{aligned} \frac{d E[u(\cdot ,t)]}{dt}=\epsilon P[u_t], \end{aligned}$$

(10)

where

$$\begin{aligned} E[u]= E_{kin}[u_t] + E_{pot}[u], \end{aligned}$$

is the beam energy which is a sum of the kinetic and the potential energies:

$$\begin{aligned} E_{kin}[u_t]= & \frac{m_0}{2} \Vert u_t\Vert ^2,\\ E_{pot}[u]= & \frac{1}{2}\left( \int _0^L D(x)u_{xx}^2 dx - T_0 \Vert u_x\Vert ^2 + K\Vert u\Vert ^2\right) . \end{aligned}$$

Equation (10) implies that

$$\begin{aligned} E[u(x,t)]=E[u(x,0)] + \epsilon \int _0^t P[u_s]ds. \end{aligned}$$

(11)

Lemma I

Assume that condition (3) holds. Then, for $\epsilon >0$ one has

$$\begin{aligned} \Vert u_t(\cdot , t)\Vert ^2, \ \Vert u_x(\cdot , t)\Vert ^2, \Vert u(\cdot , t)\Vert ^2 < {{\bar{C}}} + \epsilon C_0 t, \quad \forall t>0, \end{aligned}$$

(12)

where a positive constant ${{\bar{C}}}$ depends on the norms $\Vert u_0\Vert , \ \Vert u_1 \Vert$ of the initial data and a positive constant $C_0$ depends on $a_1$ and $a_2$.

This Lemma provides us a priori estimates of the $L_2$-norms of u and $u_t$, which show that solutions of (1) exist for all times t if the initial data have bounded $L_2$-norms, that is,

$$\begin{aligned} \Vert u_0\Vert , \ \Vert u_1 \Vert < c_0. \end{aligned}$$

Proof

Condition (3) implies the uniform in v estimate $p(v) < C_1$ for some $C_1 \ge 0$. Therefore, $P[u_t] < C_1 L$. Then Eq. (11) implies

$$\begin{aligned} 2E[u(x,t)] < 2 E[u(x,0)] + \epsilon C_1 L t \end{aligned}$$

(13)

which completes the proof of the estimate.

3.2 Estimate of kinetic energy for stable beams

Under additional assumptions on the properties of the beam, we can improve the estimate in Lemma I, and obtain estimates which are uniform in time. The functional of the potential energy is not necessarily positively definite, but if the beam is linearly stable then

$$\begin{aligned} E_{pot} \ge {{\bar{C}}}_0 \Vert u\Vert ^2, \end{aligned}$$

(14)

for some ${{\bar{C}}}_0>0$. This condition means that the parameters D(x), K, $T_0$ are chosen such that the potential energy is positive for all beam forms and the Euler instability is absent. Let us introduce the time averages:

$$\begin{aligned} \langle f \rangle _T = T^{-1} \int _0^T f(s) ds, \ T>0. \end{aligned}$$

Under condition (14) we are able to estimate the time averages of $E_{kin}$ for large times $T \le c\epsilon ^{-1}$. To do this, let us rewrite (11) as

$$\begin{aligned} E_{kin}[u(x,t)] -E_{kin} [u(x,0)] =\Delta E_{pot} + \epsilon \int _0^t P(u_s) ds, \end{aligned}$$

where

$$\begin{aligned} \Delta E_{pot} = E_{pot}[u(x,0)] - E_{pot}[u(x,t)] \le E_{pot}[u(x,0)]=C_1. \end{aligned}$$

Condition (14) and the last equation imply that

$$\begin{aligned} T^{-1} \bigl (E_{kin}[u_t(x,t)] -E_{kin} [u(x,0)]\bigr ) \le T^{-1} E_{pot}[u(x,0] + \epsilon T^{-1} a_1 \int _0^T P(u_s) ds, \end{aligned}$$

which in turn, leads to

$$\begin{aligned} \epsilon \frac{|a_2|}{4} \Bigl \langle \int _0^L u_t^4 dx \Bigr \rangle _T \le R_T, \end{aligned}$$

(15)

where

$$\begin{aligned} R_T= \frac{\epsilon a_1}{2} \Bigl \langle \int _0^L u_t^2 dx \Bigr \rangle _T + T^{-1} E_0, \end{aligned}$$

and

$$\begin{aligned} E_0= E_{kin} [u_t(x,t)]\vert _{t=0} + E_{pot}[u(x,0] \end{aligned}$$

where $E_0$ is the initial beam energy. Now we use the Schwarz inequality

$$\begin{aligned} \int _0^L u_t^2 dx \le L^{1/2} \left( \int _0^L u_t^4 dx \right) ^{1/2}. \end{aligned}$$

By using this inequality and (15), one obtains

$$\begin{aligned} \frac{|a_2|}{4L} \langle \Vert u_t\Vert ^4 \rangle _T \le \frac{a_1}{2} \langle \Vert u_t\Vert ^2 \rangle _T + \epsilon ^{-1} T^{-1} E_0. \end{aligned}$$

(16)

This inequality shows that $\Vert u_t\Vert ^2$ is less than the maximal positive root $y_0$ of the polynomial $Q(y)=\frac{|a_2|}{4\,L} y^2 - \frac{a_1}{2} y - \epsilon ^{-1} T^{-1} E_0$. This root is

$$\begin{aligned} y_2(T)= L |a_2|^{-1} \Bigl (a_1 + \sqrt{a_1^2 + \epsilon ^{-1} T^{-1} E_0 |a_2| L^{-1} } \Bigr ). \end{aligned}$$

Therefore,

$$\begin{aligned} E_{kin}[u_t(x, T)] \le \frac{ m_0 y_2(T) }{2}. \end{aligned}$$

(17)

Note that this estimate is uniform in $\epsilon$ for times $T \in I_{\epsilon }=(\epsilon ^{-1} \tau _{min}, +\infty )$, where $\tau _{min}$ is a constant independent of $\epsilon >0$. To obtain the estimate for $T < \epsilon ^{-1} \tau _{min}$, we use equation (10) which, under condition $a_2<0$, implies that

$$\begin{aligned} \frac{dE[u(\cdot ,t)]}{dt} \le \epsilon a_1 \Vert u_t\Vert ^2 = \frac{2a_1 \epsilon }{m_0} E_{kin}[u(x\cdot ,t)]. \end{aligned}$$

Now, we use the condition that $E_{pot}\ge 0$. Then, the last inequality gives

$$\begin{aligned} \frac{dE[u(\cdot ,t)]}{dt} \le \frac{2a_1 \epsilon }{m_0} E[u(x\cdot ,t)], \end{aligned}$$

and therefore,

$$\begin{aligned} E[u(\cdot ,t)] \le E[u(x\cdot ,0)] \exp \Bigl (\frac{2a_1 \epsilon }{m_0} t\Bigr ), \end{aligned}$$

(18)

that, in turn, gives us uniform in $\epsilon >0$ estimate of the energy E[u(x, t)] for all $t \in (0,\epsilon ^{-1} \tau _{min})$. The estimates (17 ) and (18) lead to the following Lemma II:

Lemma II

Under the condition (14), and for $T>0$ we have

$$\begin{aligned} E_{kin}[u_t(\cdot , T)] \le {{\bar{C}}}_E, \end{aligned}$$

(19)

where a positive constant ${{\bar{C}}}_E$ is uniform in T, $\epsilon >0$.

This Lemma and inequality (15) allow us to obtain the following corollary.

Corollary

For $t \in I_{\epsilon }$ and for stable beams satisfying (14), one has

$$\begin{aligned} E_{pot}[u(x,t)] < C_{pot}, \end{aligned}$$

(20)

where positive constants $C_{pot}, C_2, C_4$ can depend on initial data and parameters but are uniform in $\epsilon >0$.

Proof

Let us observe that on the interval $I_{\epsilon }$ the quantity $y_2(T)$ is uniform in $\epsilon$. To derive estimate (20) for $E_{pot}$, we note that

$$\begin{aligned} \frac{dE_{kin}}{dt} + \frac{dE_{pot} }{dt} \le a_1 \epsilon \Vert u_t\Vert ^2, \end{aligned}$$

and, as a result by integration over [0, t], one obtains

$$\begin{aligned} E_{pot}(t) \le E(0) + a_1 t \epsilon \langle \Vert u_t\Vert ^2 \rangle _t, \end{aligned}$$

and thus, by Lemma II, for $t \in I_{\epsilon }$ one has (20).

4 The main idea on how to get the desirable large time behavior of the beam

We would like to get the desirable large time behaviour of the beam and avoid resonances. Let us consider a hyperbolic nonlinear equation in a Hilbert space $\textbf{H}$ with an inner product (, ) and norm $\Vert \ \Vert$:

$$\begin{aligned} u_{tt}= -\textbf{L} u +\epsilon F(u_t), \end{aligned}$$

(21)

where $\textbf{L}$ is a linear positively definite self-adjoint operator, and $\epsilon >0$ is small. The function F is smooth and for sufficiently large $\Vert u_t\Vert$ the function F satisfies

$$\begin{aligned} |(F(u_t), u_t) |<C, \end{aligned}$$

(22)

where $C>0$ is a constant. Equation (22) holds for the cubic nonlinearity (2) if $a_2<0$. In fact, then F is a map $u \rightarrow a_1 u_t^2 + a_2 u_t^3$ and $|(F, u_t)|=\bigl | \int _0^L (a_1 u_t^2 + a_2 u_t^4 )dx\bigr |$. Let $r=u_t^2$. For $a_2 <0$ the parabola $p(r)=a_1 r + a_2 r^2$ has the maximum at $r_0 = a_1 (2|a_2|)^{-1}$. Therefore, in this case $C=L a_1^2 (4 |a_2|^{-1})$. In our case the Hilbert space $\textbf{H}$ consists of all measurable functions u(x) satisfying the boundary conditions (5), (6), and (7) such that $\int _0^L u_{xx}^2 dx$ is bounded (i.e. lie in the Sobolev space $W_{2,2}[0,L]$). The corresponding inner product is $(u,v)=\int _0^L u(x)v(x) dx$. Sometimes, it is hard to find exact eigenfunctions of $\textbf{L}$. Suppose, however, that we can find approximating eigenfunctions such that

$$\begin{aligned} \lambda _j \phi _j=\textbf{L} \phi _j + h_j, \quad j \in [m]=\{1,2,\ldots , m\}, \end{aligned}$$

(23)

where the functions $\phi _j$ are orthonormal, $\lambda _j >0$, and where $h_j$ are small corrections:

$$\begin{aligned} \Vert h_j \Vert \ll \epsilon \quad \forall j \in [m]. \end{aligned}$$

(24)

Moreover, suppose that there is a spectral barrier

$$\begin{aligned} (\textbf{L}u, u) \le - R \Vert u\Vert \quad \forall u \in \textbf{H} \end{aligned}$$

(25)

where $R \gg \lambda _m> \lambda _{m-1}>...>\lambda _1>0$. This spectral barrier property helps us to analyse all evolution equations with dissipative effects [20]. We can represent solutions u of Eq. (21) by

$$\begin{aligned} u=\sum _{j=1}^m X_j(t)\phi _j +{\tilde{u}}, \quad ({\tilde{u}}, \phi _j)=0, \ \forall j \in [m]. \end{aligned}$$

where the term ${\tilde{u}}$ is orthogonal in $L_2$-norm to all approximating eigenfuctions $\phi _j$. Then the finite dimensional Galerkin system

$$\begin{aligned} \frac{d^2 X_j}{dt^2}= -\lambda X_j + \left( F\big (\sum _{n=1}^m \frac{dX_n(t)}{dt} \phi _n \big ), \phi _j \right) \end{aligned}$$

(26)

serves as a good approximation for the exact solutions as will turn out in Sect. 7. Note that typically, in order to solve a weakly nonlinear evolution equation, people use a Galerkin basis consisting of eigenfunctions of a linear operator associated with the linear part of the equation. However, we can use any orthogonal (and even non-orthogonal ) basis in $L_2[0, L]$. In our case it is convenient to use a basis consisting of the localized approximating eigenfunctions (which, as we will see, are orthogonal up to exponentially small terms) plus all remaining localized and non-localized eigenfunctions. In fact, for sufficiently small $\epsilon >0$ one can show (see Sect. 7) that $\Vert {\tilde{u}}\Vert$ remains small for all sufficiently large t. This means that, for example, a beam affected by a wind load can become unstable only under action of low frequency modes, therefore, to provide stability, we should design the spectrum with prescribed low frequency modes. The main idea in the construction of the functions $\phi _j$ (providing the stability) is that the product of the functions $\phi _i \phi _j$ is exponentially small that allows us to avoid resonances between low frequency modes, whereas resonances between high frequency modes do not lead to large growth of amplitudes in $\Vert u\Vert$. So, if we are able to construct the operator $\textbf{L}$ with prescribed spectrum $\lambda _j$ for the approximating eigenfunctions and the spectral barrier for $\textbf{L}$, we will be able to get the desirable large time behaviour of the system. The approximating eigenfunctions are called quasimodes [21]. In mechanical engineering problems, interactions between quasimodes and exact eigenfunctions are nontrivial, as it was first noted in the seminal work [21]. In this work, V.I. Arnold also notes that quasimodes are more convenient to describe the large time dynamics than the use of eigenfunctions. Following these ideas, in the next sections we find quasimodes satisfying (for $L\gg 1$) the spectral problem with an exponential accuracy of $O\big (\exp (-cL)\big )$, where $c>0$ depends on the beam parameters, but is uniform in L.

5 The spectrum design problem and the main result

Let us first consider the case when $\epsilon =0$. Then, we apply the Fourier method by taking

$$\begin{aligned} u(x,t)=U(x) \exp (i \omega t), \end{aligned}$$

which leads to a linear operator $\textbf{L}$ associated with our problem, that is,

$$\begin{aligned} \textbf{L} U= (D(x) U_{xx})_{xx} + T_0 U_{xx} +KU, \end{aligned}$$

(27)

and the following boundary conditions are satisfied:

$$\begin{aligned} U_{x}= & 0, \quad U=0 \quad \text{ for } \quad x=0, \end{aligned}$$

(28)

$$\begin{aligned} U_{xx}= & 0, \quad (D(x)U_{xx})_x + T_0 U_x=0 \quad \text{ for } \quad x=L. \end{aligned}$$

(29)

And so, we obtain a spectral problem which is defined by the equation

$$\begin{aligned} \textbf{L} U = \lambda U, \end{aligned}$$

(30)

and the boundary conditions (28), (29). We consider the following spectrum design problem (SDP).

Let $\lambda _i \in (0, \lambda _{max})$ be given different numbers for $i=1, \ldots , m$. Consider a beam with parameters $T_0$, D(x), K, and $L\gg 1$ such that there exist quasimodes $\phi _j$ satisfying the following equations with an exponential accuracy:

$$\begin{aligned} \textbf{L} \phi _j= \lambda _j \phi _j + h_j, \end{aligned}$$

(31)

where

$$\begin{aligned} \Vert h_j\Vert < c_1 \exp (-c_0 L), \quad j=1,\ldots , m, \end{aligned}$$

(32)

where $c_0, c_1$ are positive constants uniform in L as $L \gg 1$. If $\phi$ is orthogonal to all quasimodes, i.e.,

$$\begin{aligned} (\phi , \phi _j)=0 \quad j=1,\ldots , m \end{aligned}$$

(33)

then

$$\begin{aligned} (\textbf{L} \phi , \phi ) \ge \Delta \Vert \phi \Vert ^2. \end{aligned}$$

(34)

Property (34) implies that the spectrum of the operator $\textbf{L}$ restricted to the subspace of functions orthogonal in $\textbf{H}=L_2[0, L]$ to all quasimodes, lies in the domain

$$\begin{aligned} D_{\Delta }= \{\lambda \in {{\mathbb {R}}}: \quad \lambda > \Delta \}, \end{aligned}$$

where $\Delta \gg \lambda _{max}>0$. This statement means that the numbers $\lambda _i$ for $i=1, \ldots , m$ define the main beam oscillation frequencies. At the same time, the possible oscillations for the remaining beam frequencies will be sharply damped by the force $f(u_t)$. In fact, the critical level for spectrum truncation can be defined via the damping terms and the Galerkin method. In fact, the modes with large frequencies damp out faster (this is shown in Sect. 7).

Our main result is as follows:

Theorem

The SDP problem has a solution if $\delta =\max _{i}\lambda _i/\Delta$ is small enough. There is an algorithm to find $T_0, D(x), K$, and L.

Note that, without loss of generality, we can assume that

$$\begin{aligned} \Delta =1, \quad \lambda _i=\delta {\hat{\lambda }}_i, \end{aligned}$$

(35)

where ${\hat{\lambda }}_i >0$ are of order 1. In fact, we always can change $T_0$, D(x), K and L to realise (35) (by multiplying all parameters with appropriate coefficients).

Note that the corresponding frequencies $\omega _j$ of the free beam oscillations (for $\epsilon =0$) can be found by simple expressions, i.e.,

$$\begin{aligned} \omega _j= \sqrt{ -\lambda _j/m_0}. \end{aligned}$$

(36)

We will refer to designed modes and frequencies as a low frequency spectrum LS, and to the remaining part of the spectrum as a high frequency spectrum HS. All non-localized modes lie in the high frequency domain.

6 Proof and Algorithm

Let us first consider the simplest case when $m=1$. We take a beam with a piece-wise constant rigidity D(x) which is symmetric around the midpoint at $x=L/2$. Around this midpoint a narrow soft layer for $x \in (L/2-L_0, L/2+L_0)$ of the length $2L_0 \ll L$ with a small rigidity $D_0$ is located, while the remaining part of the beam has a high rigidity $D_1$. To analyse the spectrum of the beam, we apply an asymptotic approach by using small dimensionless parameters $L_0/L$ and $D_0/D_1$. We use the parameter $K>0$ in order to obtain $\lambda _1 >0$ and to satisfy condition (34). The value for $T_0$ can be taken arbitrary, but it is related to the choice for $D_0$. Let $K > \lambda _1$, ${\tilde{\lambda }}_1 =\lambda _1- K$, and let us take $D_0 ={{\bar{D}}}_0 +{\tilde{D}}_0$, where ${{\bar{D}}}_0 =T_0 (L_0/\pi )^2$. To simplify the analysis, we introduce the coordinate shift $x \rightarrow x-L/2$ and extend the beam to an infinite beam (see step 1 in Sect. 6.1, where we find an auxiliary eigenfunction (mode) which decreases exponentially as $|x -L/2| \gg 1$). To create a spectral barrier $\Delta$ and a design it will turn out that the Euler instability plays an important role. Consider the auxiliary spectral problem

$$\begin{aligned} & D_0 w_{xxxx} + T_0 w_{xx} ={\tilde{\lambda }} w, \end{aligned}$$

(37)

$$\begin{aligned} & w(\pm L_0)=0, \quad w_x(\pm L_0)=0. \end{aligned}$$

(38)

For $D_0={{\bar{D}}}_0$ we have a solution $w=1+\cos (kx)$ with ${\tilde{\lambda }}=0$ corresponding to the Euler instability for (37). To obtain a small ${\tilde{\lambda }}={\tilde{\lambda }}_1 \ne 0$, we perturb $D_0={{\bar{D}}}_0$ by a small term ${\tilde{D}}_0$ of the order $\delta$ (see also step 2 in Sect. 6.1 and Eq. (64)). Then all other eigenvalues ${\tilde{\lambda }}$ are larger than $\Delta \gg \delta$. We expect that inside the soft layer the quasimode $\phi _j$ is close to w. To describe the asymptotic solutions $\phi$ outside the soft layer in the domain $x >L_0$, we consider the following auxiliary spectral problem

$$\begin{aligned} \begin{aligned}&D_1 W_{xxxx} + T_0 W_{xx} ={\tilde{\lambda }} W, \\&\quad W( L_0)=0, \quad W_x( L_0)=0,\\&\quad W_{xx}(+\infty )=0, \quad W_{xxx}(+\infty )=0, \end{aligned} \end{aligned}$$

(39)

and a similar problem in the domain $x < -L_0$. For large $D_1$ we can remove the term $T_0 W_{xx}$. Then for ${\tilde{\lambda }}={\tilde{\lambda }}_1 <0$ we obtain exponentially decreasing solutions W of problem (39):

$$\begin{aligned} \exp (-r (x-L_0)) \big (C_1 \cos ( {{\bar{r}}}(x-L_0)) + C_1 \sin ( {{\bar{r}}}(x-L_0)) \big ), \end{aligned}$$

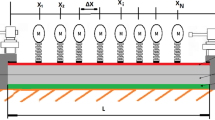
where $r \approx (|{\tilde{\lambda }}_1|/D_1)^{1/4}$ and ${{\bar{r}}}=r/\sqrt{2}$. To obtain an even quasimode $\phi _1$, we match slightly perturbed functions w and W at $x=L_0$ to provide smoothness of the solutions. This construction shows that we need the parameter K to satisfy the condition $\lambda _j >0$ for quasimode eigenvalues (which in turn provides the real valued frequencies of the beam oscillations). We also need $T_0$ to design the spectral barrier $\Delta$. So, a single soft layer allows us to design the frequency of a single, low frequency quasimode (see Figs. 1, 2). The amplitude of this mode should be smaller than $C \exp (-a|x-x_c|)$, where $x_c=L/2$ and $a=O\bigl (D_1^{-1/4}\bigr )>0$ is the attenuation coefficient. We thus should take $L \gg D_1^{1/4}$.

For $m >1$ we find m localized approximating eigenfunctions by these auxiliary eigenmodes. Here the beam consists of m narrow layers of rigidity $D_0$ and intermediate large layers of rigidity $D_i$, $i=1,2,\ldots ,m$. Let us consider for example the case $m=3$. In this case we take three soft narrow layers located at $x_c=4, 10, 17$ (see Figs. 3, 4). Each layer generates the corresponding well localized exponentially decreasing approximating modes $\phi _1, \phi _2, \phi _3$. These modes interact weakly because the products $\phi _i \phi _j(x)$ are small for $i \ne j$ and for sufficiently large $D_i$ leading to small inner products involved in the Galerkin truncation procedure.

6.1 Step 1: the auxiliary problem

Fig. 1

Beam with prescribed spectrum for the case $m=1$

As a first step, we consider the case $m=1$. The system under investigation is shown in Fig. 1. We will consider the case when $f(u_t)=0$. The following auxiliary problem for the infinite beam is as follows:

$$\begin{aligned} (D(x)u_{xx})_{xx} + T_0 u_{xx}={\tilde{\lambda }} u, \quad x \in (-\infty , +\infty ) \end{aligned}$$

(40)

where ${\tilde{\lambda }}=\lambda -K$, and

$$\begin{aligned} u(x), u_x(x) \rightarrow 0, \quad x \rightarrow \pm \infty . \end{aligned}$$

(41)

We choose D(x) as follows:

$$\begin{aligned} D(x)= & D_1, \quad |x| > L_0, \\ D(x)= & D_0 \quad |x| < L_0, \end{aligned}$$

where $D_1 \gg D_0 >0$. Before starting the computations, it is useful to remark that we are looking for eigenfunctions with minimal eigenvalues ${\tilde{\lambda }}$. The variational principle for the eigenfunctions u has the form

$$\begin{aligned} L[u]=\int _{-\infty }^{+\infty } \bigl (D(x) u_{xx}^2 -T_0 u_x^2\bigr )dx ={\tilde{\lambda }} \rightarrow \min \end{aligned}$$

(42)

under the boundary conditions (41) and the condition

$$\begin{aligned} \int _{-\infty }^{+\infty } u^2(x) dx=1. \end{aligned}$$

Note that D(x) is an even function. Then we observe that without loss of generality, we can assume that a function, which is a solution of the variational problem (42) is even in x, or is odd in x. In fact, we can represent u as a sum of odd and even functions: $u=u^{-}+ u^{+}$. All integrals of the form $\int _{-\infty }^{+\infty } u^{+} u^{-}$, $\int _{-\infty }^{+\infty } u^{+}_x u^{-}_x$ and $\int _{-\infty }^{+\infty } D(x) u^{+}_{xx} u^{-}_{xx}$ arising in the variational principle are equal to zero. Then it is easy to see that either the even part $u^+$ or the odd part $u^{-}$ gives no less ${\tilde{\lambda }}$ value with respect to u. So, due to this observation, we can consider even or odd solutions u, and this simplifies the computations. We consider even solutions; for odd ones the computations are similar. Let us note that minimal ${\tilde{\lambda }}$ values will occur for even solutions. Odd solutions lie in the zone of high frequencies. To avoid singularities, we make the substitution $v_{xx}=u$. Then by integrating the obtained equation (40) two times with respect to x, and by taking into account the boundary conditions (41) as $x\rightarrow \pm \infty$ we obtain:

$$\begin{aligned} & D(x)v_{xxxx} + T_0 v_{xx}={\tilde{\lambda }} v + c_1 + c_2 x, \quad x \in (-\infty , +\infty ), \end{aligned}$$

(43)

$$\begin{aligned} & v_{xx}(x), v_{xxx}(x) \rightarrow 0, \quad x \rightarrow \pm \infty , \end{aligned}$$

(44)

where $c_i$ are constants of integration. For ${\tilde{\lambda }} \ne 0$ (if ${\tilde{\lambda }}=0$ we can always obtain ${\tilde{\lambda }} \ne 0$ by a small perturbation of $T_0$) we introduce a transformation ${\tilde{v}}=v - {\tilde{\lambda }}^{-1}(c_1 +c_2 x)$ yielding (we omit the tilde in the notation for v):

$$\begin{aligned} & D(x)v_{xxxx} + T_0 v_{xx}={\tilde{\lambda }} v, \quad x \in (-\infty , +\infty ), \end{aligned}$$

(45)

$$\begin{aligned} & v_{xx}(x), v_{xxx}(x) \rightarrow 0, \quad x \rightarrow \pm \infty . \end{aligned}$$

(46)

Suppose that

$$\begin{aligned} \beta _0=T_0^2 + 4D_0{\tilde{\lambda }} >0, \quad \beta _1=T_0^2 + 4D_1{\tilde{\lambda }} <0. \end{aligned}$$

(47)

The second condition leads to solutions which are exponentially decreasing in x as $x \rightarrow +\infty$.

If the solution v is even with respect to x, for $|x| < L_0$ then one obtains

$$\begin{aligned} v_{in}(x, \lambda )=C_1 \cosh (k_{+} x) + C_2 \cos (k_{-}x), \end{aligned}$$

(48)

where

$$\begin{aligned} k_{\pm } = \left( \frac{ \mp T_0 + \sqrt{T_0^2 + 4{\tilde{\lambda }} D_0}}{2 D_0} \right) ^{1/2}. \end{aligned}$$

For $|x| > L_0$ one has

$$\begin{aligned} v_{out}(x, {\tilde{\lambda }})=\exp (-a (x-L_0)) g(x, {\tilde{\lambda }}), \end{aligned}$$

(49)

where

$$\begin{aligned} g(x, {\tilde{\lambda }})=C_3 \cos (\gamma (x-L_0)) + C_4 \sin (\gamma (x-L_0)). \end{aligned}$$

Due to (47) for large $D_1$ one has

$$\begin{aligned} a \approx \gamma = \frac{1}{2} \left( \frac{\sqrt{|T_0^2 + 4{\tilde{\lambda }} D_1|}}{D_1} \right) ^{1/2}. \end{aligned}$$

Note that $a,\gamma =O\bigl (D_1^{-1/4}\bigr )$ for large $D_1$. This outer solution $v_{out}(x)$ is exponentially decreasing as $x \rightarrow +\infty$. To find $C_i$ (for $i=1,2,3,4$) and ${\tilde{\lambda }}$ we use the following matching conditions for the inner solution $v_{in}$ and the outer solution $v_{out}$ at $x=\pm L_0$:

$$\begin{aligned} D_x^p v_{in}(x, {\tilde{\lambda }})=D_x^p v_{out}(x, {\tilde{\lambda }}), \quad D_x=d/dx, \end{aligned}$$

for $p=0,1,2, 3$. Computing the derivatives, we obtain the following linear algebraic system:

$$\begin{aligned} \textbf{A} \textbf{C}=O, \end{aligned}$$

(50)

where $\textbf{C}=(C_1, C_2, C_3, C_4)^{T}$, and $O=(0,0,0,0)^{T}$, and $\textbf{A}$ is a $4\times 4$ matrix with entries $a_{ij}$ defined by

$$\begin{aligned} a_{11}= & \cosh (k_{+} L_0), \ a_{12}=\cos (k_{-} L_0), \end{aligned}$$

(51)

$$\begin{aligned} a_{21}= & k_{ +} \sinh (k_{+}L_0), \ a_{22}= - k_{-} \sin (k_{-}L_0), \end{aligned}$$

(52)

$$\begin{aligned} a_{31}= & k_{ +}^2 C_1 \cosh (k_{+} L_0) \ a_{32}=- k_{ -}^2 \cos (k_{-} L_0), \end{aligned}$$

(53)

$$\begin{aligned} a_{41}= & k_{ +}^3 C_1 \sinh (k_{+} L_0), \ a_{42}= k_{-}^3 \sin (k_{-} L_0), \end{aligned}$$

(54)

where $k_{\pm }$ depend on ${\tilde{\lambda }}$, and the other entries $a_{ij}$ satisfy the estimates

$$\begin{aligned} & a_{13}=1, \ a_{14}=0, \quad a_{23}, a_{24}=O\bigl (D_1^{-1/4}\bigr ), \\ & a_{33}, a_{34}=O\bigl (D^{-1/2}\bigr ), \quad a_{43}, \ a_{44}=O\bigl (D_1^{-3/4}\bigr ). \end{aligned}$$

The linear system (50) has nontrivial solutions if the determinant of $\textbf{A}$ is equal to zero. Using that $D_1\gg 1$, and the definitions and estimates for $a_{ij}$, we obtain that system (50) can be reduced to the study of a characteristic equation defined by the conditions $D_x^2 v_{in}(x)=D_x^3 v_{in}(x)=0$ at $x=L_0$. This reduced system is

$$\begin{aligned} k_{ +}^2 C_1 \cosh (k_{+}({\tilde{\lambda }}) L_0) - k_{ -}^2 C_2 \cos (k_{ -}({\tilde{\lambda }}) L_0)= & 0, \end{aligned}$$

(55)

$$\begin{aligned} k_{ +}^3 C_1 \sinh (k_{ +}(\lambda ) L_0) + k_{-}^3 C_2 \sin (k_{-}{\tilde{\lambda }}) L_0)= & 0, \end{aligned}$$

(56)

and leads to the following characteristic equation for ${\tilde{\lambda }}$ (see also Fig. 5):

$$\begin{aligned} \sin (k_{-}({\tilde{\lambda }}) L_0) = - b({\tilde{\lambda }}) \tanh (k_{+}({\tilde{\lambda }}) L_0) \cos (k_{ -}({\tilde{\lambda }}) L_0), \end{aligned}$$

(57)

where $b({\tilde{\lambda }}) =k_{ +}({\tilde{\lambda }})/ k_{-} ({\tilde{\lambda }})$. Note that the roots of this equation (57) are always real because they are eigenvalues of the following self-adjoint problem on $[-L_0, L_0]$:

$$\begin{aligned} & D_0 u_{xxxx} + T_0 u_{xx} ={\tilde{\lambda }} u, \end{aligned}$$

(58)

$$\begin{aligned} & u_{x}(x)=u(x)=0, \quad x=\pm L_0, \end{aligned}$$

(59)

associated to the Lagrangian

$$\begin{aligned} {{\mathcal {L}}}[u]=\frac{1}{2}\int _{-L_0}^{L_0} \bigl (D_0 u_{xx}^2 - T_0 u_{x}^2\bigr ) dx. \end{aligned}$$

In fact, the boundary conditions (59) are a consequence of the equations (55) and (56), which express the fact that $D_x^2 v_{in}(x)=0$, $D_x^3 v_{in}(x)=0$ at $x=\pm L_0$ which in turn is equivalent to (59) since $D_x^2 v_{in}(x)=u(x)$ for $x \in (-L_0, L_0)$. Note that problem (58)–(59) can be derived, in a similar way, for odd solutions, and that the boundary conditions (59) for this problem can be obtained by variational arguments.

Moreover, we should satisfy the conditions (47). It is sufficient to satisfy the first condition $\beta _0 >0$ by taking ${\tilde{\lambda }}<0$ only, because the second condition $\beta _1<0$ can be automatically satisfied by a choice $D_1\gg D_0$. Equation (57) has a countable set of real roots and we are looking for the minimal negative root. We vary $D_0$, $T_0$ and $L_0$ (see Fig. 6). Note that then for odd solutions of (58)–(59) the corresponding values ${\tilde{\lambda }}$ are larger in magnitude.

Fig. 2

An example of a spectrum, where a single frequency is designed

Fig. 3

The rigidity D(x), which will generate a spectrum with a single localized eigenfunction, corresponding to eigenvalue $\lambda _1=\delta$. The remaining spectrum is separated far away from $\lambda _1$ (see Fig. 1). The parameters are $L=20, L_0=1, T_0=1$, $\delta =0.5$, $K=3\delta$, and $D_1=10$. The values $D_{0,j}$ are obtained by formula (64)

Fig. 4

An example of a spectrum, where we design the first 3 eigenvalues

Fig. 5

The rigidity D(x), which will generate a linear beam operator with three localized eigenfunctions with the prescribed eigenvalues $\lambda _1=\delta , \lambda _2=2\delta , \lambda _3=5\delta$. The parameters are $L=20, L_0=1, T_0=1$, $\delta =0.5$, $K=3\delta$, $D_1=10$. The values $D_{0,j}$ are obtained from formula (64)

So, we obtain a solution $u(x,{\tilde{\lambda }})=v_{xx}(x,{\tilde{\lambda }})$ of Eq. (40), which is exponentially decreasing as $x \rightarrow \infty$, that is, for $x \rightarrow \infty$ the function $u(x, {\tilde{\lambda }})$ behaves like:

$$\begin{aligned} |u(x, {\tilde{\lambda }})| < C \exp \bigl (-c_0 {{\bar{D}}}_1^{-1/4} x\bigr ), \end{aligned}$$

(60)

where $C, c_0$ are positive constants uniform in $D_1$. This solution is even in x.

6.2 Step 2: combining solutions in layers

The idea is illustrated in Figs. 1, 2, 3 and 4. We choose D(x) as a piecewise constant function, with n equidistant local minima. The wells for D are separated by distances $2L_1$, and the well widths are $2L_0$. We suppose that

$$\begin{aligned} L_1/L_0 \gg 1. \end{aligned}$$

We choose

$$\begin{aligned} D(x)= & D_{0, j}, \quad x \in I_j, \\ D(x)= & D_1, \quad x \notin \cup I_j, \end{aligned}$$

where $I_j=[a_j, b_j]$ are intervals with boundaries $a_j=L_1(j-1/2) + 2L_0(j-1)$, $b_j=a_j + 2L_0$. We set $L_1 D_1^{-1/2}\gg 1$. Under this condition the decreasing tails of the functions $\phi _{(j)}(x)$ will be exponentially small. Further we describe how to choose $T_0, D_{0,j}$, K, and how to construct approximating eigenfunctions $\phi _j(x)$. We can assume that the prescribed spectrum has the form (35), where $\delta >0$ is a small parameter. Let us consider the spectral problem (58)–(59) on the $j^{th}$-interval $I_j=(a_j, b_j)$ with $D_0=D_{0, j}$:

$$\begin{aligned} & D_{0,j} u_{xxxx}^{(j)} + T_0 u^{(j)}_{xx} ={\tilde{\lambda }}_j u^{(j)}, \quad a_j< x < b_j \end{aligned}$$

(61)

$$\begin{aligned} & u_{x}^{(j)}(x)=u^{(j)}(x)=0, \quad \text {for} \ x=a_j, b_j. \end{aligned}$$

(62)

Let us fix $L_0, T_0>0$. Then, by using the properties of the corresponding Lagrangian we can observe that for sufficiently large $D_{0, j}$ the corresponding eigenvalue ${\tilde{\lambda }}_j$ is positive, and for $D_{0, j}$ close to zero we have negative ${\tilde{\lambda }}_j$. Therefore, there exist a $D_{0, j}$ (close to the value that defines the Euler instability) and a $K^{*}>0$ such that ${\tilde{\lambda }}=\delta \lambda _j - \delta K^{*}<0$. Note that the value of $D_{0,j}$ can be computed by using a perturbation approach, similar as in quantum mechanics, see [22]. First we find the value $D_{0,j}={{\bar{D}}}_{0}$ such that ${\tilde{\lambda }}_j=0$. In this case the solution inside the soft zone has the form $u_{0,j}= 1 + \cos (k_0(x-{{\bar{x}}}_j))$, where $k_0=\pi /L_0$ and ${{\bar{x}}}_j$ is the center of jth zone. This solution exists if ${{\bar{D}}}_0 k_0^4 - T_0 k_0^2=0$, thus, ${{\bar{D}}}_0= T_0 (L_0/\pi )^2$. Let $D_{0,j}={{\bar{D}}}_0 + {\tilde{D}}_{0,j}$, where ${\tilde{D}}_{0,j}$ is a small correction of the order $\delta$. Consider the perturbed problem

$$\begin{aligned} & ({{\bar{D}}}_0 + {\tilde{D}}_{0,j}) u_{xxxx} + T_0 u_{xx}={\tilde{\lambda }}_j u, \\ & u_x(\pm L_0)=u(\pm L_0)=0, \end{aligned}$$

where the term ${\tilde{D}}_{0,j} u_{xxxx}$ is a perturbation. According to perturbation theory, we have

$$\begin{aligned} {\tilde{\lambda }}_j =\frac{ {\tilde{D}}_{0,j} \Vert {u_{0,j}}_{xx}\Vert ^2 }{\Vert u_{0,j}\Vert ^2} +O(\delta ^2). \end{aligned}$$

(63)

We note that $\Vert u_{0,j}\Vert ^2=L_0$ and $\Vert {u_{0,j}}_{xx}\Vert ^2=k_0^4 3L_0/2$. We substitute these values into (63) and obtain

$$\begin{aligned} D_{0,j} \approx T_0(L_0/\pi )^2 + \frac{ 2\delta }{3} {\tilde{\lambda }}_j (L_0/\pi )^4 + O(\delta ^2). \end{aligned}$$

(64)

We set $K=\delta K^{*}$. The remaining part of the spectrum is separated and lies above the barrier $\Delta _0=O(1)$, where $\Delta _0$ is independent of $\delta$. Observe that this whole construction is independent of $D_1$.

Now we can use the obtained functions $u^{(j)}$ to construct approximating eigenfunctions $\psi _j$. First we extend $u^{(j)}(x)$ defined on $I_j=(a_j, b_j)$ on a larger interval $W_j=(a_j-L_1, b_j+L_1)$, where $L_1 \gg D_1^{1/3}$, as it was done in step 1. The obtained function we denote by $\phi _j$. Furthermore, we construct an extension of these functions on the whole interval [0, L] as follows:

$$\begin{aligned} {\hat{\psi }}_j(x)=\phi ^{(j)}(x) \ \text {for} \ x \in W_j, \quad {\hat{\psi }}_j(x)=0, \ \text {for} \ x \notin W_j. \end{aligned}$$

These functions are not continuous although discontinuities at the edges of $W_j$ are exponentially small and are of the order $\exp (-c_0 D_1^{1/6})$, with $c_0 >0$. We can introduce a convolution with a mollifier $\chi _{\kappa }$ to obtain smooth $\psi _j$’s, which are approximating eigenfunctions up to exponentially small $h_j$: $\Vert h_j\Vert < c \exp (-c_0 D_1^{1/4})$.

Remind that a mollifier $\chi (x)$ is a $C^{\infty }$ smooth, non-negative function with a bounded support $(-1, 1)$ such that $\int _{-\infty }^{\infty } \chi (x) dx=1$, and the convolution of f(x) with a small parameter $\kappa >0$ is defined by the following convolution

$$\begin{aligned} f_{st}(x)= \int _{-\infty }^{\infty } f(x-y) \chi _{\kappa } (y) dy, \end{aligned}$$

where $\chi _{\kappa }(y)=\kappa ^{-1} \chi (y/\kappa )$. We set

$$\begin{aligned} \phi _j(x) = \int _{y=0}^L {\hat{\psi }}_j(x-y) \chi _{\kappa }(y) dy. \end{aligned}$$

It is clear that the functions $\phi _j$ are orthogonal just because their supports are disjunct for sufficiently small $\kappa >0$. The boundary conditions are also satisfied for small $\kappa$ because the functions ${\hat{\psi }}_j$ have supports $S_j$, which lie strictly within the interval [0, L], and at $x=0$ and $x=L$ all derivatives of ${\hat{\psi }}_j$ are equal to zero.

Fig. 6

This plot shows that for an appropriate choice of $D_0, L_0$ and $T_0$ we can obtain Eq. (57), which has a single root ${\tilde{\lambda }}$ in the interval $(-T_0^2/4D_0, 0]$. The curve F is the plot of the map ${\tilde{\lambda }} \in (-T_0^2/4D_0, 0] \rightarrow - b({\tilde{\lambda }}) \tan (k_{+}({\tilde{\lambda }}) L_0) \cos (k_{ -}( {\tilde{\lambda }}) L_0)$ and the curve G is the plot of the function $\sin (k_{ -}({\tilde{\lambda }}) L_0)$. The parameters are $T_0=8, D_0=1$ and $L_0=1$

6.3 Justification of the construction and proof of the estimate (34)

For the boundary conditions (28) and (29) at $x=0$ and $x=L$ it is assumed that

$$\begin{aligned} L^3 \ll D_1 \ll L^4, \quad L \gg 1. \end{aligned}$$

(65)

To justify the construction of the eigenfunctions and to prove the estimate (34), we start by noting that the quadratic form defined by the operator $\textbf{L}$ is equal to the Lagrangian:

$$\begin{aligned} (\textbf{L} \phi , \phi ) = {{\mathcal {L}}}[\phi ]. \end{aligned}$$

Suppose $\Vert \phi \Vert =1$. We decompose the Lagrangian into two contributions. The first one is a term induced by the hard domain H consisting of intervals where $D=D_1$, and the second one is a contribution given by soft intervals, where $D=D_0$. If $D_1 \gg 1$ and $L\gg 1$ then under condition (65) the contribution of the hard domain is much less than the contribution of the soft domain. Using this fact and using a priori estimates we show, in this subsection, that in the hard domain $|\phi |$ is small. Then the condition of orthogonality (33) implies that the scalar products $\int _{I_j} \phi \phi _j dx$ are close to zero in the jth interval $I_j$, where the jth approximating function is localized. Due to our choice of $D_{0,j}$ this implies that the contribution of the soft domain into the Lagrangian ${{\mathcal {L}}}[\phi ]$ is more than a constant of O(1), uniform in L.

To start, let us prove first an auxiliary lemma.

Lemma III

Let $\phi \in C^2[0, L]$ and $\phi _x(x_0)=0$ at a point $x_0 \in [-L_0, L_0]$. Then,

$$\begin{aligned} & |\phi _x(x)| \le |x-x_0|^{1/2} \Vert \phi _{xx}\Vert , \end{aligned}$$

(66)

$$\begin{aligned} & |\phi (x)- \phi (x_0)| \le |x-x_0|^{1/2} \Vert \phi _{x}\Vert . \end{aligned}$$

(67)

If $\phi (0)=\phi _x(0)=0$ then

$$\begin{aligned} \sup _{x \in [0,L]}|\phi (x)|^2 \le 2L^3 \Vert \phi _{xx}\Vert ^2, \end{aligned}$$

(68)

and

$$\begin{aligned} \sup _{x \in [0, L]} |\phi _x(x)|^2 \le L \Vert \phi _{xx}\Vert ^2. \end{aligned}$$

(69)

Proof

One has

$$\begin{aligned} {\tilde{\phi }}_x= \int _{x_0}^x {\tilde{\phi }}_{yy} dy. \end{aligned}$$

We apply the Cauchy–Schwarz inequality to the right hand side of this equation and obtain

$$\begin{aligned} |{\tilde{\phi }}_x(x)| \le |x-x_0|^{1/2}\left( \int _{x_0}^{x} {\tilde{\phi }}_{xx}^2 dx \right) ^{1/2} \le |x-x_0|^{1/2} \Vert {\tilde{\phi }}_{xx}\Vert , \end{aligned}$$

that proves (66). To prove (67), we write down

$$\begin{aligned} {\tilde{\phi }}(x) -{\tilde{\phi }}(x_0) = \int _{x_0}^{x} {\tilde{\phi }}_y dy. \end{aligned}$$

As above, one has

$$\begin{aligned} \left| \int _{x_0}^{x} {\tilde{\phi }}_y dy\right| \le |x-x_0|^{1/2} \Vert {\tilde{\phi }}_{x}\Vert \end{aligned}$$

that implies (67). To derive (68), we use (67) and (66). Let us note that according to (67)

$$\begin{aligned} |\phi (x)| \le L^{1/2} \Vert \phi _x\Vert . \end{aligned}$$

Due to (66) this implies

$$\begin{aligned} \Vert \phi _x(x)\Vert \le L^{1/2} \sup |\phi _{x}| \le L \Vert \phi _{xx}\Vert \end{aligned}$$

and we obtain (68). Estimate (69) follows from (66). And so the proof of Lemma III is completed.

We introduce ${{\mathcal {L}}}_{hard}$ and ${{\mathcal {L}}}_{soft}$, which denote the contributions of the hard and soft zones into the Lagrangian, respectively:

$$\begin{aligned} {{\mathcal {L}}}_{soft}[u]= & \int _{-L_0}^{L_0} \big (D_0 u_{xx}^2 - T_0 u_x^2 + K u^2 \big ) dx, \\ {{\mathcal {L}}}_{hard}[u]= & \int _{H} \big (D_1 u_{xx}^2 - T_0 u_x^2 + K u^2 \big ) dx, \end{aligned}$$

where the domain H is defined for those x for which $D(x)=D_1$. We also consider the contributions

$$\begin{aligned} {{\mathcal {L}}}_{hard, j}[u] = \int _{H_j} \Big (D_1 u_{xx}^2 - T_0 u_x^2 + K u^2 \Big ) dx, \end{aligned}$$

where $H_j=[x_{2j}, x_{2j+1}]$ denotes the jth hard interval, $j=0,1,...,m$, $x_0=0$, and $x_{2\,m+1}=L$. Similarly,

$$\begin{aligned} {{\mathcal {L}}}_{soft, j}[u] = \int _{H_j} \big (D_0 u_{xx}^2 - T_0 u_x^2 + K u^2 \big ) dx, \end{aligned}$$

where $S_j=[x_{2j+1}, x_{2j+2}]$ denotes the jth soft interval, $j=0,..., m-1$. Our next aim it to find lower bounds for $L_{hard}$ and $L_{soft}$.

Lemma IV

Under the condition (65) one has

$$\begin{aligned} {{\mathcal {L}}}_{hard} \ge \int _H \Bigl (\frac{D_1}{2} \phi _{xx}^2 + K\phi \Bigr )^2 dx. \end{aligned}$$

(70)

Proof

We use (69):

$$\begin{aligned} T_0 \Vert \phi _x\Vert ^2 \le T_0 L \max |\phi _x|^2 \le T_0 L^2 \Vert \phi _{xx}\Vert ^2. \end{aligned}$$

Note that due to (65)

$$\begin{aligned} T_0 L^2 \Vert \phi _{xx}\Vert ^2 \ll \frac{D_1}{2} \int _H \phi _{xx}^2 dx, \end{aligned}$$

and so, inequality (70) is proved.

Lemma V

The Lagrangian ${{\mathcal {L}}}_{soft, j}$ satisfies the estimate

$$\begin{aligned} {{\mathcal {L}}}_{soft, j} \ge - C_L R_j, \end{aligned}$$

(71)

with

$$\begin{aligned} R_j = \phi ^2(x_{2j+1}) + \phi ^2(x_{2j+2}) + \phi _x^2(x_{2j+1}) + \phi _x^2 (x_{2j+2}), \end{aligned}$$

where the constant $C_L>0$ is uniform in L.

Proof

Consider the minimization problem

$$\begin{aligned} \min _{\phi }\int _{x_{2j+1}}^{x_{2j+2}} \big (D_0 \phi _{xx}^2 dx -T_0 \phi _x + K \phi ^2 \big ) dx, \end{aligned}$$

under the boundary conditions

$$\begin{aligned} \phi (x)= & A_i, \quad x=x_{2j+1}, \quad \phi (x)=B_i, \quad x=x_{2j+2}, \\ \phi _x(x)= & {\tilde{A}}_i, \quad x=x_{2j+1}, \quad \phi (x)={\tilde{B}}_i, \quad x=x_{2j+2}. \end{aligned}$$

The function $\phi$ satisfies the Euler equation

$$\begin{aligned} D_0 \phi _{xxxx} + T_0 \phi _{xx} + K \phi =0. \end{aligned}$$

We solve this equation under the aforementioned boundary conditions. Due to our choice for $D_0, T_0$, and K, the solutions have the form

$$\begin{aligned} \phi =C_1 \cos (k_+ x) + C_2 \cos (k_{-} x) + C_3 \sin (k_+ x) + C_4 \sin (k_{-} x), \end{aligned}$$

where

$$\begin{aligned} k_{\pm }^2 =\frac{ T_0 \pm \sqrt{T_0^2 - 4 D_0 K}}{2D_0}. \end{aligned}$$

By substituting these solutions into the boundary conditions, we obtain a system of linear algebraic equations for $C=(C_1, C_2, C_3, C_4)^{tr}$:

$$\begin{aligned} \textbf{M} C= A, \quad A=(A_i, {\tilde{A}}_i, B_i, {\tilde{B}}_i)^{tr}, \end{aligned}$$

where matrix $\textbf{M}$ is non-degenerate: $\det \textbf{M} \ne 0$. Therefore, $\Vert C \Vert \le c_0 \Vert A\Vert =c_0 R$, where $c_0>0$ is a constant uniform in L (because all parameters of this minimisation problem are independent of L). This last estimate for the norm of C completes the proof of Lemma V.

The Lemmas III–V are used to prove the next lemma.

Lemma VI

Let condition (65) be satisfied. Then, in the rigid zone H the function $\phi$ satisfies the following estimate

$$\begin{aligned} \sup _{x \in H} |\phi (x)| \le c_0 L^{3/2} D_1^{-1/2} \rho , \end{aligned}$$

(72)

where $c_0$ is a positive constant uniform in $L\gg 1$ and in $\rho ={{\mathcal {L}}}[\phi ]^{1/2}$.

Proof

One has

$$\begin{aligned} {{\mathcal {L}}}_{hard} [\phi ] + {{\mathcal {L}}}_{soft} [\phi ] =\rho ^2. \end{aligned}$$

Using the Lemmas IV and V, we obtain

$$\begin{aligned} \int _H \Bigl (\frac{D_1}{2} \Vert \phi _{xx}\Vert ^2 + K\Vert \phi \Vert ^2 \Bigr )dx - C_L {{\bar{R}}} \le \rho ^2, \end{aligned}$$

where

$$\begin{aligned} {{\bar{R}}} = \sum _{j=0}^{m-1} R_j. \end{aligned}$$

Lemma III gives the following estimate:

$$\begin{aligned} {{\bar{R}}} \le m c_2 L^3 \Vert \phi _{xx}\Vert ^2, \end{aligned}$$

where $c_2 >0$ is a constant uniform in L. Combining the previous estimates and taking into account (65) one obtains

$$\begin{aligned} D_1 \int _H \phi _{xx}^2 dx \le c_5 \rho ^2, \end{aligned}$$

where $c_5 >0$ is uniform in L. Consider the interval $[0, x_0]$. On this interval (we take into account the boundary conditions (28)) one has

$$\begin{aligned} |\phi _x(x)|^2 \le |L| \int _{0}^{x_0} \phi _{xx}^2 dx, \quad x \in [0, x_0], \end{aligned}$$

(73)

and thus

$$\begin{aligned} |\phi (x)| \le L \max _{x \in [0, x_0]} |\phi _x(x)| \le L^{3/2} \int _H \phi _{xx}^2 dx, \end{aligned}$$

(74)

which implies that

$$\begin{aligned} |\phi (x)| \le D_1^{-1/2} L^{3/2} \rho . \end{aligned}$$

(75)

This proves (72) on the first hard interval. We can extend this estimate to the first soft interval $[x_0, x_1]$ by Lemma III. Further, we continue by induction, for example,

$$\begin{aligned} |\phi _x(x) -\phi _x(x_1)|^2 \le |L| \int _{x_1}^{x_2} \phi _{xx}^2 dx, \quad x \in [x_1, x_2], \end{aligned}$$

(76)

and thus

$$\begin{aligned} |\phi (x)-\phi (x_1)| \le L \max _{x \in [x_1, x_2]} |\phi _x(x)| \le L^{3/2} \int _H \phi _{xx}^2 dx, \end{aligned}$$

(77)

and estimate (72) follows. And so, Lemma VI is proved.

The remaining part of the proof of (34) is based on Lemma VI. According to Lemma VI, since $\phi$ satisfies the estimate (72) in the hard zone H the relation $(\phi , \phi _j)=0$ implies that

$$\begin{aligned} \int _H \phi (x) \phi _j(x) dx < D_1^{-1/2} L^{3/2} \rho \end{aligned}$$

(78)

as $L \rightarrow \infty$. Let $I_j$ denote the jth soft interval. Note that by our construction of $\phi _j$ one has

$$\begin{aligned} \sup _{x \in I_k} |\phi _j(x)| < C_1 \exp (- c_7 D_1^{1/4}), \quad k \ne j, \end{aligned}$$

where $C_1, c_7>0$ are uniform in L.

Then (33) implies that $\phi$ and $\phi _j$ are almost orthogonal in the soft interval $I_j$:

$$\begin{aligned} \int _{I_j} \phi (x) \phi _j(x) dx = O(L^{-s}), \quad s>0, \quad L \rightarrow \infty . \end{aligned}$$

(79)

Then we have

$$\begin{aligned} \phi = C_j \phi _j + {\tilde{\phi }}, \end{aligned}$$

where

$$\begin{aligned} \int _{I_j} {\tilde{\phi }}(x) \phi _j(x) dx=0, \quad |C_j| < O(L^{-s}), \end{aligned}$$

(80)

and

$$\begin{aligned} \int _{I_j} {\tilde{\phi }}(x)^2 >1/2 \end{aligned}$$

(81)

for large $L\gg 1$. By (80) and (81) we can estimate ${{\mathcal {L}}}_{soft}[\phi ]$ as follows:

$$\begin{aligned} {{\mathcal {L}}}_{soft}[\phi ] > c_7 (O(L^{-2s}) \rho + {{\mathcal {L}}}_{soft}[{\tilde{\phi }}], \end{aligned}$$

(82)

where $c_7$ is uniform in L. Due to (80) the term ${\tilde{\phi }}$ is almost orthogonal to the Euler critical mode, and we have

$$\begin{aligned} {{\mathcal {L}}}_{soft}[{\tilde{\phi }}]> c_8\Vert {\tilde{\phi }}\Vert ^2 > c_9, \end{aligned}$$

where $c_8, c_9 >0$ are constants uniform in $\delta >0$ and L, where $\delta$ is defined in the SDP theorem at the end of Sect. 5. Then by (81) we obtain that

$$\begin{aligned} {{\mathcal {L}}}_{soft}[\phi ] > c_7 (O(L^{-2s}) + c_9. \end{aligned}$$

(83)

Thus,

$$\begin{aligned} \rho = {{\mathcal {L}}}[\phi ]> {{\mathcal {L}}}_{soft}[\phi ] > c_7 (O(L^{-2s}) + c_9, \end{aligned}$$

(84)

and for large L we obtain inequality (34) with $\rho >c_{10}$, which is uniform in $\delta$ and L. And so, the Theorem at the end of Sect. 5 is proved.

7 Nonlinear effects and resonances

7.1 An estimate for the averaged kinetic energy

In this short subsection, we use the a priori estimate (17) for the kinetic energy $E_{kin}=\frac{m\Vert u_{t}\Vert ^2}{2}$ as obtained in Lemma II. This estimate shows that the growth of the $L_2$-norm $\Vert u\Vert$ can be described by the low frequency modes only. Let us represent the solution u as a sum of a low frequency part and a high frequency part: $u= u^{(l)} + u^{(h)},$ where for the high frequency term $u^{(h)}$ one has

$$\begin{aligned} \Vert u_t^{(h)} \Vert > \Delta \Vert u^{(h)} \Vert , \end{aligned}$$

(85)

where $\Delta >0$ is a parameter. For example, if $u^{(h)}$ is a sum of harmonics

$$\begin{aligned} u^{(h)} = \sum _{j} \exp ( i \omega _j t) \psi _j(x), \end{aligned}$$

where $\psi _j$ form a system of orthogonal functions, then $\Delta > \min |\omega _j|$. Inequality (85) and estimate (17) give

$$\begin{aligned} \Vert u^{(h)} (\cdot , t)\Vert \le \Delta ^{-1} y_2(t). \end{aligned}$$

(86)

So, the averaged contribution of high frequency modes is proportional to $\Delta ^{-1}$(since $y_2(t)$ is bounded). A similar result can be obtained by using asymptotic approximations of the solutions, which we study in the next subsection.

7.2 Asymptotic approximations of the solutions

In this section, we consider the weakly nonlinear dynamics of beams for which the spectrum of the corresponding linear oscillations satisfy the properties as described in the previous two sections. As will turn out in this section internal resonances between low frequency modes will not occur, and when high frequency modes are involved the corresponding resonances are less important in the sense that the amplitudes of the involved modes are relatively small. To describe the resonances, we apply the asymptotic representation for the solutions, and we obtain an infinite Galerkin system

$$\begin{aligned} m_0\frac{d^2 X_j}{dt^2} + m_0 \omega _j^2 X_j= \epsilon \bigl ( f(u_t),\psi _j \bigr ), \end{aligned}$$

(87)

for $j=1, 2,...$ on a time interval of order $\frac{1}{\epsilon }$. In (87) $f(u_t)$ is given by (2). $X_j(t)$ can be rewritten in

$$\begin{aligned} X_j(t) =A_j(\tau ) \sin (\omega _j t +\phi _n(\tau )), \end{aligned}$$

where $\tau =\epsilon t$ is a slow time, and where $A_j$ and $\phi _j$ are the unknown amplitude and phase respectively. Here $X_j$ are Fourier coefficients of the function u(x, t) : $X_j(t)= (u(\cdot , t), \psi _j)$. Then, for $A_j$ we obtain (see [23])

$$\begin{aligned} 2 m_0 \omega _j \frac{dA_j}{d\tau }= \bigl ( f(u_t),\psi _j \bigr ) + O(\epsilon ). \end{aligned}$$

(88)

By integrating (88) with respect to $\tau$, we obtain

$$\begin{aligned} 2m_0(A_j(\tau )-A_j(0))= \epsilon \omega _j^{-1} \int _0^{\epsilon ^{-1} \tau } \bigl ( f(u_t),\psi _j \bigr ) ds + O(\epsilon ). \end{aligned}$$

(89)

We apply the Schwarz and Hölder inequalities to obtain a rough estimate of the right hand side in (88)

$$\begin{aligned} & |(u_t, \psi _j)| \le \Vert u_t\Vert ^2, \ \\ & |(u_t^3, \psi _j)| \le \left( \int _0^L |u_t|^4 dx \biggr )^{4/3} \biggl (\int _0^L |\psi _j|^4 dx \right) ^{1/4}. \end{aligned}$$

Then, by using these estimates and (89) we have

$$\begin{aligned} |A_j(\tau )-A_j(0)| \le \textrm{const}\, \omega _j^{-1}\left\langle |a_1| \Vert u_t\Vert + c_j |a_3|\left( \int _0^L |u_t|^4 dx \right) ^{4/3} \right\rangle _{\epsilon ^{-1} \tau }, \end{aligned}$$

(90)

where $\langle f \rangle _T$ denotes the time average of the function f over the interval [0, T]:

$$\begin{aligned} \langle f \rangle _T =T^{-1} \int _0^T f(t) dt. \end{aligned}$$

According to Lemma II and the Corollary after Lemma II, we have on the interval $I_{\epsilon }$ (as defined in Lemma II)

$$\begin{aligned} |A_j(\tau )-A_j(0)| \le C_5 \omega _j^{-1}, \end{aligned}$$

(91)

for some $C_5 >0$, i.e., the contributions of the high frequency modes are small.

Let us consider the resonances in more detail. Let us denote by $\omega _j$, $\psi _j$ the frequencies and eigenfunctions lying in the low frequency spectrum $\textbf{LS}$, and let us denote by ${\tilde{\omega }}_j$, ${\tilde{\psi }}_j$ the frequencies and eigenfunctions lying in the high frequency spectrum zone $\textbf{HS}$. Let us consider the dynamics of $A_j$ with $j \in \textbf{LS}$ and let us study possible resonance effects in this dynamics. Then, by the standard analysis (see, for example, [17]) we obtain that the following different situations might occur:

3HL: an internal resonance induced by three high frequency modes and a single localized one:

$$\begin{aligned} |{\tilde{\omega }}_{k_1} \pm {\tilde{\omega }}_{k_2} \pm {\tilde{\omega }}_{k_1} \pm \omega _j| < c \epsilon , \quad \end{aligned}$$

(92)

where $j \in \textbf{LS},k_1,k_2, k_3 \in \textbf{HS}$. This effect is proportional to

$$\begin{aligned} R_{j k_1, k_2, k_3} =\int _0^L \phi _{k_1} \phi _{k_2} \phi _{k_3} \psi _ j dx; \end{aligned}$$

2H2L: an internal resonance induced by two high frequency modes and two localized ones:

$$\begin{aligned} |{\tilde{\omega }}_{k_1} \pm {\tilde{\omega }}_{k_2} \pm \omega _{i} \pm \omega _j| < c \epsilon , \quad \end{aligned}$$

(93)

where $i,j \in \textbf{LS},k_1,k_2 \in \textbf{HS}$. This effect is proportional to

$$\begin{aligned} R_{j k_1, k_2, k_3} =\int _0^L \phi _{k_1} \phi _{k_2} \psi _{i} \psi _j dx; \end{aligned}$$

H3L: an internal resonance induced by a high frequency mode and three localized ones:

$$\begin{aligned} |{\tilde{\omega }}_{k} \pm \omega _{i_1} \pm \omega _{i_2} \pm \omega _j| < c \epsilon , \quad \end{aligned}$$

(94)

where $k\in \textbf{HS},j,i_1,i_2 \in \textbf{LS}$. This effect is proportional to

$$\begin{aligned} R_{j i_1, i_2, k} =\int _0^L \phi _{k} \psi _{i_1} \psi _{i_2} \psi _{j}dx; \end{aligned}$$

4 L: an internal resonance, which involves localized low frequency modes only:

$$\begin{aligned} | \omega _{i_1} \pm \omega _{i_2} \pm \omega _{i_3} \pm \omega _j| < c \epsilon , \quad \end{aligned}$$

(95)

where $j,i_1,i_2, i_3 \in \textbf{LS}$. This effect is proportional to

$$\begin{aligned} R_{j i_1, i_2, k} =\int _0^L \psi _{i_1} \psi _{i_2} \psi _{i_3} \psi _{j}dx. \end{aligned}$$

Let us consider these cases. The resonance 3HL is possible because the sum or differences of three high frequencies may be small, however, the coefficient $R_{j k_1 k_2, k_3}$ is proportional to the small dimensionless parameter $\theta =L_0/L$ (because the function $\psi _j$ is localized in the layer with width $L_0$).

The resonance 2H2L is also possible. The function $\psi _i \psi _j$ is exponentially small for $i\ne j$, and the coefficient $R_{j j k_2, k_3}$ is proportional to $\theta$.

The resonance H3L is impossible because it can only exist under the condition that $i_1=i_2=j$ but then the resonance condition (94) does not hold.

At last, the resonance 4 L can occur for $i_1=i_2=i_3=j$ and it gives the main contribution, which is larger then all other remaining resonances. This can be shown as follows. We can obtain a general rough estimate for the high frequency resonance contributions. If we truncate the Galerkin system to the low frequency localized modes only, we have

$$\begin{aligned} m_0 \frac{d^2 X_j}{dt^2}= - m_0\omega _j^2 X_j + \epsilon \big (f(u_t^{tr}), \psi _j \big ). \end{aligned}$$

(96)

where $u^{tr}=\sum _{j=1}^{m} X_j \psi _j$, $j=1,2, ..., m$. This system can be simplified. In fact, as it was mentioned above, the products $\psi _j \psi _i$ with $i \ne j$ are small. Thus, taking into account the main resonaces 4 L only, and removing small terms, we obtain a truncated Galerkin system consisting of m independent equations, which describe m independent nonlinear oscillators (of the Rayleigh type):

$$\begin{aligned} m_0\frac{d^2 X_j}{dt^2}= - m_0 \omega _j^2 X_j + {{\bar{a}}}_1 \frac{dX_j(t)}{dt} + {{\bar{a}}}_2 \Big (\frac{dX_j(t)}{dt}\Big )^3, \end{aligned}$$

(97)

where $\omega _j$ are prescribed frequencies and the coefficients ${{\bar{a}}}_j$ are equal to

$$\begin{aligned} {{\bar{a}}}_1=a_1, \quad {{\bar{a}}}_2= a_2 \int _0^L \psi _j^4 dx. \end{aligned}$$

8 Conclusions and discussion

In this paper, the dynamics of a compressed Euler–Bernoulli beam on an elastic foundation under the action of an external force, which models a wind force, is studied. The elastic foundation has a few, small, constant soft parts, and a few, large and constant hard parts. The beam is assumed to be long, and the lower part of its spectrum is prescribed. An asymptotic method on how to find the beam’s parameters which ensure the prescribed lower part of the spectrum, is presented. This method uses the following parameters: a spatially heterogeneous rigidity, a compressive longitudinal force, and a coefficient of the elastic Winkler foundation. The value of the compressive longitudinal force must be less than the critical Euler force. All these parameters are critically important to provide the stability of the beam and the absence of resonances between low frequency modes. These modes have special spatial supports that exclude a direct interaction between them. So, the Galerkin system describing the significant part of the time evolution of the beam can be given by a system of almost independent equations, which describes m independent nonlinear oscillators. Each oscillator has its own phase and frequency. Interactions between oscillators can take place only through high frequency modes. Although the direct impact of the remaining high frequency modes is weak, we can expect interesting possible effects such as synchronization or desynchronization of the main localized modes via these weak interactions. This problem will be considered and studied in a future research project. Since it was not within the scope of this paper, the asymptotic approach as presented in this paper, has not been justified mathematically. However, it should be observed that all approximations satisfy the partial differential equation (9) and the initial conditions (4) up to order $\epsilon ^2$ for times t of order $\epsilon ^{-1}$. To prove mathematically that the approximations as obtained in this paper are also order $\epsilon$ accurate for times t up to order $\epsilon ^{-1}$, one can follow the analysis as given in [15] for a weakly nonlinear wave equation or in [24] for a weakly nonlinear wave equation on an elastic foundation, or in [25] for a weakly nonlinear beam equation on an elastic foundation, or in [26] for a weakly nonlinear plate equation on an elastic foundation. For the constructed approximations of the solutions of the initial-boundary value problem for (9) a similar, mathematical analysis as given in [15, 24,25,26] can be given, and it can be shown that the asymptotic approximations of the solutions are order $\epsilon$ accurate for times t of order $\epsilon ^{-1}$ (for $\epsilon$ sufficiently small). Also to validate the obtained analytic results a numerical calculation of the beam frequencies was performed for the case considered in Sect. 6.1. For the computations, the parameters of the beam presented in Fig. 3 were taken. The computations were performed with the help of ANSYS 2022 using the calculation module “Modal”. In Table 1 the magnitudes of the first 6 natural frequencies are presented. As can be observed the difference between the numerical and analytical results are small.

Table 1 Values of the frequencies