Non-conforming Trefftz finite element implementation of orthotropic Kirchhoff plate model based on consistent couple stress theory

Abstract

This work proposes a new 4-node non-conforming plate element for static and dynamic analyses of small-scale orthotropic thin plates within the consistent couple stress theory. By applying the Kirchhoff thin plate bending constraint to the three-dimensional consistent couple stress elasticity, the non-classical orthotropic thin plate model is established and the Trefftz functions are derived. Then, the new element is formulated in a straightforward manner based on the generalized conforming theory, by taking the obtained Trefftz functions as the basic function for construction and employing a novel set of point conforming conditions to enforce the compatibility requirement in weak sense. Several benchmark examples are examined and the results show that the element has good numerical accuracy and mesh-distortion tolerance in prediction of the size-dependent bending behavior of the small-scale orthotropic thin plates.

1 Introduction

Orthotropic thin plates are among the most used industrial structural components and can be found in various engineering fields due to their superior properties. And now, with the vigorous development of the material science and manufacturing technology, the application of orthotropic plate structures in micro- and nano-devices is becoming more and more extensive. Previous research results fully demonstrate that the mechanical behavior of the structure at small scale is size dependent and the commonly used classical continuum theory which lacks an internal length scale is incapable of incorporating this dependence. Considering that the continuum theory is generally more feasible and more efficient than the molecular/atomistic simulation theory in practical engineering problems, many researchers have addressed the non-classical high-order continuum theories, such as the strain gradient theory [1], the couple stress theory [2], the nonlocal theory [3], the micromorphic theory [4] and the combination of them. Accurate description of the size effects using the high-order continuum theory in general requires a certain number of internal material length-scale parameters (MLSPs). However, it is not a simple matter to calibrate these material parameters experimentally, because these parameters do not necessarily have clear physical meaning. Therefore, the high-order continuum theory containing fewer internal length-scale parameters is more preferred in practical applications.

The couple stress theory is one of the high-order continuum theories that have concise expressions and relatively explicit physical interpretations, and has drawn great attentions from scholars since the pioneering work [5]. At present, there are two different versions of the couple stress theory that require only one additional length-scale parameter for isotropic materials. The first one is the widely used modified couple stress theory (MCST) proposed by Yang et al. [6]. This theory is obtained by introducing a presumptive equilibrium condition of moments of couples into the classical C¹ couple stress theory, which is, respectively, explored by Toupin [2], Mindlin and Tiersten [7], and Koiter [8] and is often referred to as TMK-CST, to enforce the couple stress tensor to be symmetric. Accordingly, only the symmetric part of curvatures is considered to have contribution to the deformation energy. Over the past decades, many researchers have used this theory to well analyze and design thin plate structures at small scales. For instance, Tsiatas and his cooperators [9, 10] solved the bending problems of the isotropic and orthotropic Kirchhoff plates based on the MCST by using the fundamental solution method and the analog equation method; Akgöz and Civalek [11] analyzed the mechanical response of the thin plates resting on elastic medium using the MCST; Fang et al. [12] established the model for free vibration and transient response of rotating functionally graded microplates based on the MCST; Kim et al. [13] investigated the bending, free vibration and buckling response of functionally graded porous thin microplates based on the MCST. More comprehensive information on this topic can be found in the literature reviews [14, 15]. It is found that the TMK-CST and the MCST cannot describe the pure bending deformation of a plate properly [16]. In particular, the MCST is based on the torsion deformation rather than the curvature bending, and thus predicts no couple stresses and no size effect for the pure bending of the plate into a spherical shell.

The second version of the couple stress theory that contains one additional length-scale parameter for isotropic materials is the consistent couple stress theory (CCST) proposed by Hadjesfandiari and Dargush [17]. In this development, the couple stress tensor is proved to be skew-symmetric and accordingly, only the skew-symmetric part of the gradient of the rotation is considered in the deformation energy. It is reported in [17] that the CCST can overcome the inconsistent deficiencies of the TMK-CST and MCST which are primarily caused by the indeterminacy of the spherical part of the couple stress tensor. One can easily observe that the assumption of skew-symmetry of the couple stress tensor in the CCST is the exactly opposite of that in the MCST. In some ways, these two theories can be regarded as two distinct cases that degenerated from the TMK-CST. It is interesting to notice that there is still some debate as to which of these two theories is more reasonable [18, 19]. Despite the controversy, the CCST has also seen an increasing application in past years [20,21,22,23,24]. Recently, the CCST has been successfully employed to analyze micro-/nano-thin beam, plate and shell structures. For instance, Alavi et al. [25] developed a linear size-dependent Timoshenko beam model based on the CCST; Wu and Hu [26] proposed a unified formulation of various size-dependent plate theories on the basis of the CCST for analyses of functionally graded microplates embedded in an elastic medium; Qu et al. [27] presented a plate model based on the CCST using the series expansion theory for studying the size effect in high-frequency analysis; Ji and Li [28] investigated the size-dependent electromechanical coupling response in circular microplate based on the CCST; Dehkordi and Beni [29] performed the electromechanical free vibration analysis of single-walled conic nanotube; Wang and Li [30] studied the synergistic effect of the memory-size-microstructure on thermoelastic damping of a microplate based on the CCST; Ajri et al. [31] analyzed the non-stationary free vibration and nonlinear dynamic behavior of viscoelastic nano-plates based on the CCST.

As mentioned above, with the growing applications of orthotropic micro-thin plates with complex geometric shapes, accurately simulating their size-dependent mechanical responses becomes particularly important. The theoretical approaches provide insights into the mechanism of micro-/nano-structures, but their scope of application is very limited. Therefore, the robust numerical methods are urgently needed in analyzing real engineering problems. The finite element method (FEM), as one of the most accepted numerical simulation tools in industrial community, has clearly become an attractive option for this task. In recent years, efforts have been devoted to the development of finite element models based on the CCST. To name a few, we mentioned the penalty element formulation for plane strain problem proposed by Chakravarty et al. [32], the Lagrangian multiplier element formulation for plane strain problems proposed by Darrall et al. [33], the mixed element formulation for dynamic analysis proposed by Deng and Dargush [34] and the mixed element formulation for anisotropic centrosymmetric materials proposed by Pedgaonkar et al. [35]. The plate elements developed based on the plate models are generally more popular than solid elements in dealing with the orthotropic thin plate structures with complex geometry because of their better computation efficiency. However, there are very few works regarding the plate elements based on the CCST. In particular, to our best knowledge, no orthotropic thin plate element based on the CCST has been reported in the opening studies. Therefore, more efforts are needed on this topic. In addition to the FEM, there are some other numerical methods having been employed to analyze the consistent couple stress problems, such as the boundary element method (BEM) [36,37,38] and the Ritz spline method [39], but these methods are not as practical and convenient as the FEM.

The main objective of this work is to develop a robust quadrilateral 4-node 12-DOF (degree of freedom) plate element with high numerical accuracy and mesh-distortion tolerance for efficient analysis of orthotropic thin plates within the framework of the CCST. It is well known that in the finite element implementation of the C¹ couple stress theories, including the TMK-CST, MCST and CCST, meeting the higher-order continuity requirement will not only give rise to the great difficulties in construction compatible shape functions, but also make the element’s performance very sensitive to mesh distortion. On the other hand, if the higher-order continuity requirement is ignored in the element construction, the convergence property of the finite element cannot be guaranteed. Therefore, how to relax the continuity requirement reasonably and how to effectively improve element’s capability in distorted meshes are the focus of the present development. To this end, the generalized conforming Trefftz element method, which has been successfully applied to the plate models based on the classical continuum theory [40, 41] as well as the plate models based on the MCST [42,43,44], is adopted as the underlying foundation for element development. This method blends the attributes of the Trefftz element method [45,46,47,48,49], in that the Trefftz functions which can satisfy the related differential governing equations are used as the basis for formulating shape functions, with the usual displacement-based FEM. With respect to the present concerned problem, the required Trefftz functions are derived by directly introducing the thin plate assumptions into the three-dimensional (3D) consistent couple stress elasticity. Moreover, given that the Trefftz functions generally violate the continuity requirement between adjacent elements, the generalized conforming theory [50] is employed to impose the continuity requirement in a relaxed way to ensure the computational convergence of the non-conforming element. For purpose of evaluating the new element’s performance, a series of numerical examples are examined in some of which the analytical reference solutions are derived. As demonstrated by the numerical results that, the new plate element can correctly simulate the size-dependent bending responses of the orthotropic thin microplates, exhibiting good numerical precision and low susceptibility to mesh distortion.

The remainder of the paper are organized as follows. After the Introduction, the non-classical orthotropic Kirchhoff plate bending model based on the CCST is established and the Trefftz functions are derived in Sect. 2. The construction process of the new element is presented in Sect. 3, and the numerical tests are carried out in Sect. 4. Finally, the paper is concluded in Sect. 5.

2 The orthotropic thin plate model based on CCST

2.1 The basic equation of the new plate model

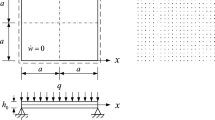
Figure 1 illustrates the schematic representation of the orthotropic micro-thin plate with thickness h subjected to the transverse distributed load at its top surface. The mid-surface of the plate is defined as the reference plane, representing the Cartesian coordinates x and y along the two material principal directions, respectively. Besides, z denotes the transverse direction oriented from the bottom to the top $\left( {{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2} \le z \le {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} \right)$. Assuming that the plate experiences the bending deformation without the membrane stretching effects, the three displacements u, v and w with respect to above the Cartesian coordinate system can be expressed as

$$u = - z\psi_{x} \left( {x,y} \right),\;\;v = - z\psi_{y} \left( {x,y} \right),\;\;w = w\left( {x,y} \right)$$

(1)

in which the plate rotations $\psi_{x}$ and $\psi_{y}$ are given in accordance with the Kirchhoff thin plate assumption by

$$\psi_{x} \left( {x,\;y} \right) = \frac{{\partial w\left( {x,\;y} \right)}}{\partial x},\;\;\psi_{y} \left( {x,\;y} \right) = \frac{{\partial w\left( {x,\;y} \right)}}{\partial y}$$

(2)

Fig. 1

The orthotropic thin plate based on the CCST

By inserting Eq. (1) into the strain–displacement relations in the CCST [17], the nonzero strain components are obtained:

$$\varepsilon_{xx} = \frac{\partial u}{{\partial x}} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }},\;\;\varepsilon_{yy} = \frac{\partial v}{{\partial y}} = - z\frac{{\partial^{2} w}}{{\partial y^{2} }},\;\;\varepsilon_{xy} = \frac{1}{2}\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right) = - z\frac{{\partial^{2} w}}{\partial x\partial y}$$

(3)

while the nonzero mechanical rotations are determined by

$$\omega_{x} = \frac{1}{2}\left( {\frac{\partial w}{{\partial y}} - \frac{\partial v}{{\partial z}}} \right) = \frac{\partial w}{{\partial y}},\;\;\;\omega_{y} = \frac{1}{2}\left( {\frac{\partial u}{{\partial z}} - \frac{\partial w}{{\partial x}}} \right) = - \frac{\partial w}{{\partial x}}$$

(4)

which further give rise to the nonzero mean curvatures in the CCST:

$$\kappa_{xy} = - \kappa_{yx} = \frac{1}{2}\left( {\frac{{\partial \omega_{x} }}{\partial y} - \frac{{\partial \omega_{y} }}{\partial x}} \right) = \frac{1}{2}\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)$$

(5)

Within the framework of the CCST, the force–stresses should satisfy the following equilibrium equations:

$$\left\{ {\begin{array}{*{20}c} {\frac{{\partial \sigma_{xx} }}{\partial x} + \frac{{\partial \sigma_{yx} }}{\partial y} + \frac{{\partial \sigma_{zx} }}{\partial z} + f_{x} = \rho \ddot{u}} \\ {\frac{{\partial \sigma_{xy} }}{\partial x} + \frac{{\partial \sigma_{yy} }}{\partial y} + \frac{{\partial \sigma_{zy} }}{\partial z} + f_{y} = \rho \ddot{v}} \\ {\frac{{\partial \sigma_{xz} }}{\partial x} + \frac{{\partial \sigma_{yz} }}{\partial y} + \frac{{\partial \sigma_{zz} }}{\partial z} + f_{z} = \rho \ddot{w}} \\ \end{array} } \right.$$

(6)

in which ρ is the density; $\ddot{u}$, $\ddot{v}$ and $\ddot{w}$ are the three acceleration components; and $f_{x}$, $f_{y}$ and $f_{z}$ are the external body force loads. Note that these body force loads are equal to zero for the plate bending problem discussed in the present work. Besides, the force–stresses should also meet the following balance equations together with the couple stresses [17]:

$$\left\{ {\begin{array}{*{20}c} {\frac{{\partial \mu_{xz} }}{\partial x} + \frac{{\partial \mu_{yz} }}{\partial y} + \sigma_{xy} - \sigma_{yx} = 0} \\ {\frac{{\partial \mu_{yx} }}{\partial y} + \frac{{\partial \mu_{zx} }}{\partial z} + \sigma_{yz} - \sigma_{zy} = 0} \\ {\frac{{\partial \mu_{xy} }}{\partial x} + \frac{{\partial \mu_{zy} }}{\partial z} - \sigma_{xz} + \sigma_{zx} = 0} \\ \end{array} } \right.$$

(7)

It is interesting to notice that the force–stress tensor in the CCST [17] is allowed to be asymmetric and in general can be decomposed into symmetric part and skew-symmetric part, in which the symmetric part $\sigma_{(\;)}$ is defined as

$$\sigma_{{\left( {xx} \right)}} = \sigma_{xx} ,\;\;\sigma_{{\left( {yy} \right)}} = \sigma_{yy} ,\;\;\sigma_{{\left( {zz} \right)}} = \sigma_{zz}$$

(8)

$$\sigma_{{\left( {xy} \right)}} = \sigma_{{\left( {yx} \right)}} = \frac{{\sigma_{xy} + \sigma_{yx} }}{2},\;\;\sigma_{{\left( {yz} \right)}} = \sigma_{{\left( {zy} \right)}} = \frac{{\sigma_{yz} + \sigma_{zy} }}{2},\;\;\sigma_{{\left( {xz} \right)}} = \sigma_{{\left( {zx} \right)}} = \frac{{\sigma_{xz} + \sigma_{zx} }}{2}$$

(9)

while the skew-symmetric part $\sigma_{[\;]}$ is given by

$$\sigma_{{\left[ {xx} \right]}} = 0,\;\;\sigma_{{\left[ {yy} \right]}} = 0,\;\;\sigma_{{\left[ {zz} \right]}} = 0$$

(10)

$$\sigma_{{\left[ {xy} \right]}} = - \sigma_{{\left[ {yx} \right]}} = \frac{{\sigma_{xy} - \sigma_{yx} }}{2},\;\;\sigma_{{\left[ {yz} \right]}} = - \sigma_{{\left[ {zy} \right]}} = \frac{{\sigma_{yz} - \sigma_{zy} }}{2},\;\;\sigma_{{\left[ {xz} \right]}} = - \sigma_{{\left[ {zx} \right]}} = \frac{{\sigma_{xz} - \sigma_{zx} }}{2}$$

(11)

Thereby, substituting Eqs. (8–11) back into Eqs. (6 and 7) and neglecting the external body loads yield

$$\left\{ {\begin{array}{*{20}c} {\frac{{\partial \sigma_{{\left( {xx} \right)}} }}{\partial x} + \frac{{\partial \sigma_{{\left( {yx} \right)}} }}{\partial y} + \frac{{\partial \sigma_{{\left( {zx} \right)}} }}{\partial z} + \frac{{\partial \sigma_{{\left[ {yx} \right]}} }}{\partial y} + \frac{{\partial \sigma_{{\left[ {zx} \right]}} }}{\partial z} = \rho \ddot{u}} \\ {\frac{{\partial \sigma_{{\left( {xy} \right)}} }}{\partial x} + \frac{{\partial \sigma_{{\left( {yy} \right)}} }}{\partial y} + \frac{{\partial \sigma_{{\left( {zy} \right)}} }}{\partial z} + \frac{{\partial \sigma_{{\left[ {xy} \right]}} }}{\partial x} + \frac{{\partial \sigma_{{\left[ {zy} \right]}} }}{\partial z} = \rho \ddot{v}} \\ {\frac{{\partial \sigma_{{\left( {xz} \right)}} }}{\partial x} + \frac{{\partial \sigma_{{\left( {yz} \right)}} }}{\partial y} + \frac{{\partial \sigma_{{\left( {zz} \right)}} }}{\partial z} + \frac{{\partial \sigma_{{\left[ {xz} \right]}} }}{\partial x} + \frac{{\partial \sigma_{{\left[ {yz} \right]}} }}{\partial y} = \rho \ddot{w}} \\ \end{array} } \right.$$

(12)

and

$$\left\{ {\begin{array}{*{20}c} {\frac{{\partial \mu_{xz} }}{\partial x} + \frac{{\partial \mu_{yz} }}{\partial y} + 2\sigma_{{\left[ {xy} \right]}} = 0} \\ {\frac{{\partial \mu_{yx} }}{\partial y} + \frac{{\partial \mu_{zx} }}{\partial z} + 2\sigma_{{\left[ {yz} \right]}} = 0} \\ {\frac{{\partial \mu_{xy} }}{\partial x} + \frac{{\partial \mu_{zy} }}{\partial z} + 2\sigma_{{\left[ {zx} \right]}} = 0} \\ \end{array} } \right.$$

(13)

The symmetric part of the force–stress is the work conjugate pair of strain and can be obtained from the strain using the constitutive relation, while the skew-symmetric part of force–stress is determined from the couple stress using Eq. (13). Besides, the couple stress is the work conjugate pair of the mean curvature. However, it should be pointed out that due to the introduction of Kirchhoff thin plate assumption in the model, the force–stress and couple stress which are directly calculated by substituting the nonzero strain and mean curvature given in Eqs. (3 and 5) into the 3D constitutive equations will violate the equilibrium equations and stress boundary conditions. Therefore, the following alternative process is employed to identify them.

First, the symmetric parts of the three in-plane force–stress components are determined by substituting the relevant strains given in Eq. (3) into the orthotropic constitutive equations of the plane stress state:

$$\sigma_{{\left( {xx} \right)}} = \frac{{E_{x} }}{{1 - \nu_{xy} \nu_{yx} }}\varepsilon_{xx} + \frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\varepsilon_{yy} = - z\left( {\frac{{E_{x} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)$$

(14)

$$\sigma_{{\left( {yy} \right)}} = \frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\varepsilon_{xx} + \frac{{E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\varepsilon_{yy} = - z\left( {\frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)$$

(15)

$$\sigma_{{\left( {xy} \right)}} = 2G_{xy} \varepsilon_{xy} = - 2G_{xy} z\frac{{\partial^{2} w}}{\partial x\partial y}$$

(16)

in which $E_{x} ,\;E_{y} ,\;\nu_{xy} ,\;\nu_{yz} ,\;G_{xy}$ are the engineering material constants with respect to the two in-plane material principal directions.

Second, the nonzero couple stresses are determined by directly inserting the mean curvatures given in Eq. (5) into constitutive relationships as follows:

$$\mu_{xy} = - \mu_{yx} = - 8G_{xy} l^{2} \kappa_{xy} = - 4G_{xy} l^{2} \nabla^{2} w$$

(17)

where $\nabla^{2}$ is the Laplace operator. Note that the assumption proposed in [35] that only one MLSP as denoted by l is required for orthotropic materials is adopted here. Therefore, by virtue of Eq. (13), the skew-symmetric parts of the force–stresses are deduced:

$$\sigma_{{\left[ {xy} \right]}} = - \sigma_{{\left[ {yx} \right]}} = 0$$

(18)

$$\sigma_{{\left[ {xz} \right]}} = - \sigma_{{\left[ {zx} \right]}} = - 2G_{xy} l^{2} \frac{\partial }{\partial x}\left( {\nabla^{2} w} \right)$$

(19)

$$\sigma_{{\left[ {yz} \right]}} = - \sigma_{{\left[ {zy} \right]}} = - 2G_{xy} l^{2} \frac{\partial }{\partial y}\left( {\nabla^{2} w} \right)$$

(20)

Afterward, substituting Eqs. (14–16) and Eqs. (18–20) into the first two equations shown in Eq. (12) leads to

$$\sigma_{{\left( {zx} \right),z}} = z\left( { - \rho \frac{{\partial \ddot{w}}}{\partial x} + \frac{{E_{x} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} + 2G_{xy} \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}} \right)$$

(21)

$$\sigma_{{\left( {zy} \right),z}} = z\left( { - \rho \frac{{\partial \ddot{w}}}{\partial y} + \frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} + \frac{{E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial y^{3} }} + 2G_{xy} \frac{{\partial^{3} w}}{{\partial x^{2} \partial y}}} \right)$$

(22)

By integrating Eqs. (21 and 22) along the plate thickness direction and making the derived shear components of the force–stress meet the zero-value boundary conditions at the plate’s top and bottom surfaces, the following expressions can be obtained:

$$\sigma_{zx} = \left( {\frac{{z^{2} }}{2} - \frac{{h^{2} }}{8}} \right)\left( { - \rho \frac{{\partial \ddot{w}}}{\partial x} + \frac{{E_{x} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} + 2G_{xy} \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}} \right)$$

(23)

$$\sigma_{zy} = \left( {\frac{{z^{2} }}{2} - \frac{{h^{2} }}{8}} \right)\left( { - \rho \frac{{\partial \ddot{w}}}{\partial y} + \frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} + \frac{{E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial y^{3} }} + 2G_{xy} \frac{{\partial^{3} w}}{{\partial x^{2} \partial y}}} \right)$$

(24)

from which we can also get

$$\sigma_{{\left( {zx} \right)}} = \left( {\frac{{z^{2} }}{2} - \frac{{h^{2} }}{8}} \right)\left( { - \rho \frac{{\partial \ddot{w}}}{\partial x} + \frac{{E_{x} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} + 2G_{xy} \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}} \right) - 2G_{xy} l^{2} \frac{\partial }{\partial x}\left( {\nabla^{2} w} \right)$$

(25)

$$\sigma_{{\left( {zy} \right)}} = \left( {\frac{{z^{2} }}{2} - \frac{{h^{2} }}{8}} \right)\left( { - \rho \frac{{\partial \ddot{w}}}{\partial y} + \frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} + \frac{{E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{3} w}}{{\partial y^{3} }} + 2G_{xy} \frac{{\partial^{3} w}}{{\partial x^{2} \partial y}}} \right) - 2G_{xy} l^{2} \frac{\partial }{\partial y}\left( {\nabla^{2} w} \right)$$

(26)

It is worth noticing that both the $\sigma_{{\left( {zx} \right)}}$ and $\sigma_{{\left( {zy} \right)}}$ are the functions of the coordinates, although their work conjugated shear strains $\varepsilon_{zx}$ and $\varepsilon_{zy}$ are equal to zero due to the assumed displacement fields given by Eq. (1).

Last, substituting Eqs. (19, 20, 25 and 26) back into the third one in Eq. (12) and performing the integration along the plate thickness give rise to

$$\begin{gathered} \sigma_{zz} = - \left( {\frac{{z^{3} }}{6} - \frac{{zh^{2} }}{8}} \right)\left( { - \rho \nabla^{2} \ddot{w} + \frac{{E_{x} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{2\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + 4G_{xy} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \frac{{E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}\frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) \\ + z\rho \ddot{w} + 4zG_{xy} l^{2} \nabla^{2} \nabla^{2} w + {\text{C}} \\ \end{gathered}$$

(27)

where C is a function independent of z to be determined. Making use of the boundary conditions that the value of the force–stress $\sigma_{zz}$ is zero at the bottom surface and is equal to q at the top surface, the function C can be derived and the following equation is delivered:

$$\rho h\ddot{w} - \frac{{\rho h^{3} }}{12}\nabla^{2} \ddot{w} + \left( {D_{x} + D_{l} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\left( {H + D_{l} } \right)\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \left( {D_{y} + D_{l} } \right)\frac{{\partial^{4} w}}{{\partial y^{4} }} = q$$

(28)

in which

$$D_{x} = \frac{{h^{3} }}{12}\frac{{E_{x} }}{{1 - \nu_{xy} \nu_{yx} }},\;\;\;D_{y} = \frac{{h^{3} }}{12}\frac{{E_{y} }}{{1 - \nu_{xy} \nu_{yx} }},\;\;\;H = \frac{{h^{3} }}{12}\left( {\frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }} + 2G_{xy} } \right),\;\;\;D_{l} = 4G_{xy} l^{2} h$$

(29)

For static bending problems, Eq. (28) becomes

$$\left( {D_{x} + D_{l} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\left( {H + D_{l} } \right)\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \left( {D_{y} + D_{l} } \right)\frac{{\partial^{4} w}}{{\partial y^{4} }} = q$$

(30)

One can easily observe that Eqs. (28 and 30) can degenerate into the ones of the classical orthotropic Kirchhoff plate bending model by simply setting l to zero.

Moreover, the bending moments and couple moments of the present orthotropic thin plate can be defined as by

$$M_{xx} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {z\sigma_{xx} {\text{d}} z} ,\;\;\;M_{yy} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {z\sigma_{yy} {\text{d}} z} ,\;\;\;M_{xy} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {z\sigma_{xy} {\text{d}} z,\;\;\;M_{yx} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {z\sigma_{yx} {\text{d}} z} }$$

(31)

$$Y_{xy} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\mu_{xy} {\text{d}} z} ,\;\;\;Y_{yx} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\mu_{yx} {\text{d}} z}$$

(32)

Since the nonzero force–stresses and couple stresses have been expressed as the functions of w, the bending moments and couple moments can also be expressed in terms of w.

2.2 The Trefftz functions of the new plate model

As previously mentioned, the Trefftz FEM is an effective method to improve the element’s numerical accuracy in the distorted mesh. The main idea of the Trefftz FEM is to use the Trefftz functions which can satisfy the governing equations of the concerned problem as the basis function for element construction. In order to develop a robust Trefftz-type plate element to analyze the proposed non-classical thin plate model based on the CCST, the required Trefftz functions are introduced in this section. For the sake of simplicity, only the Trefftz functions of the static problems are derived for element construction and their effectiveness in dynamic problems will be carefully assessed in the numerical tests.

The solutions of Eq. (30) that is an inhomogeneous partial differential equation can be obtained by, respectively, deriving the particular solution $\tilde{w}$ which satisfies

$$\left( {D_{x} + D_{l} } \right)\frac{{\partial^{4} \tilde{w}}}{{\partial x^{4} }} + 2\left( {H + D_{l} } \right)\frac{{\partial^{4} \tilde{w}}}{{\partial x^{2} \partial y^{2} }} + \left( {D_{y} + D_{l} } \right)\frac{{\partial^{4} \tilde{w}}}{{\partial y^{4} }} = q$$

(33)

and the homogeneous solution $\hat{w}$ which is deduced by solving

$$\left( {D_{x} + D_{l} } \right)\frac{{\partial^{4} \hat{w}}}{{\partial x^{4} }} + 2\left( {H + D_{l} } \right)\frac{{\partial^{4} \hat{w}}}{{\partial x^{2} \partial y^{2} }} + \left( {D_{y} + D_{l} } \right)\frac{{\partial^{4} \hat{w}}}{{\partial y^{4} }} = 0$$

(34)

From the point of view of analytical solution, it is essential to consider the particular solution. But for the finite element construction, it is actually possible not to use the particular solution. This is because in most cases in the FEM, the external loads need to be equivalently translated into a series of nodal loads by some means. Neglecting the particular solution in the construction process of the Trefftz-type element does bring approximation to some extent which may make the performance of the element slightly degraded, but it also helps make the element formula more concise. Based on the latter consideration, in this work, only the homogeneous solution part is used as the basis function for element construction while the particular solution part is not considered.

Since Eq. (34) has the same form as the classical orthotropic Kirchhoff plate bending model, the solution of Eq. (34) can be easily derived from that of the classical orthotropic Kirchhoff plate [51, 52] by replacing the corresponding material parameters. Thereby, the fourteen items of the homogeneous solutions which are expressed in polynomial form are introduced directly without providing their detailed derivation procedure:

$$\hat{w}^{1} = 1,\;\;\;\hat{w}^{2} = x,\;\;\;\hat{w}^{3} = y,\;\;\;\hat{w}^{4} = x^{2} ,\;\;\;\hat{w}^{5} = xy,\;\;\;\hat{w}^{6} = y^{2}$$

(35)

$$\hat{w}^{7} = x^{3} ,\;\;\;\hat{w}^{8} = x^{2} y,\;\;\;\hat{w}^{9} = xy^{2} ,\;\;\;\hat{w}^{10} = y^{3} ,\;\;\;\hat{w}^{11} = x^{3} y,\;\;\;\hat{w}^{12} = xy^{3}$$

(36)

$$\hat{w}^{13} = \left( {D_{y} + D_{l} } \right)x^{4} - \left( {D_{x} + D_{l} } \right)y^{4} ,\;\;\;\hat{w}^{14} = \left( {H + D_{l} } \right)\left( {x^{4} + y^{4} } \right) - 3\left( {D_{x} + 2D_{l} + D_{y} } \right)x^{2} y^{2}$$

(37)

These solutions can guarantee the completeness of fourth order and are linearly independent with each other. Then, by substituting Eqs. (35–37) into the relevant equations discussed in Sect. 2.1, the corresponding solutions of the displacements, plate rotations, strains, mechanical rotations, mean curvatures, force–stresses and couple stresses can be derived.

Finally, it should be emphasized once again that these solutions are obtained by solving the static bending problems of the Kirchhoff plate based on the CCST. Thus, their reasonability and validity in dynamic problems should be carefully verified.

3 Generalized conforming Trefftz plate element

3.1 The element interpolation function

As shown in Fig. 2, the four nodes of the quadrilateral plate element are represented by 1 ~ 4 while 5 ~ 8 denote the midpoints of four edges. The plate element has one transverse displacement DOF and two plate rotation DOFs per node and its nodal DOF vector is expressed by

$${\mathbf{q}}^{e} = \left[ {\begin{array}{*{20}c} {w_{1} } & {\psi_{x1} } & {\psi_{y1} } & {w_{2} } & {\psi_{x2} } & {\psi_{y2} } & {w_{3} } & {\psi_{x3} } & {\psi_{y3} } & {w_{4} } & {\psi_{x4} } & {\psi_{y4} } \\ \end{array} } \right]^{T}$$

(38)

Fig. 2

The new 4-node microplate element based on the CCST

Considering that the Trefftz functions of the problem concerned have already been derived in the previous section, the transverse displacement field of the plate element can be initially assumed to be a linear combination of these Trefftz functions:

$$w = \sum\limits_{i = 1}^{14} {\hat{w}^{i} \alpha_{i} }$$

(39)

and accordingly, the plate rotation fields are given by

$$\psi_{x} = \sum\limits_{i = 1}^{14} {\hat{\psi }_{x}^{i} \alpha_{i} } ,\;\;\;\;\psi_{y} = \sum\limits_{i = 1}^{14} {\hat{\psi }_{y}^{i} \alpha_{i} }$$

(40)

in which $\hat{\psi }_{x}^{i}$ and $\hat{\psi }_{y}^{i}$ are obtained by inserting $\hat{w}^{i}$ into Eq. (2). Then, the two in-plane displacement fields u and v can also be obtained in accordance with Eq. (1). For brevity, they can be expressed in the following vector form:

$${\mathbf{u}} = \left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} = {\mathbf{U}}{\varvec{\upalpha}}$$

(41)

in which

$${{{\upalpha}}} = \left[ {\begin{array}{*{20}c} {\alpha_{1} } & {\alpha_{2} } & {\alpha_{3} } & {...} & {\alpha_{14} } \\ \end{array} } \right]^{T}$$

(42)

$${\mathbf{U}} = \left[ {\begin{array}{*{20}c} { - z{\hat{\psi}}_{x}^{1} } & { - z{\hat{\psi}}_{x}^{2} } & { - z{\hat{\psi}}_{x}^{3} } & {...} & { - z\hat{\psi }_{x}^{14} } \\ { - z\hat{\psi }_{y}^{1} } & { - z\hat{\psi }_{y}^{2} } & { - z\hat{\psi }_{y}^{3} } & {...} & { - z\hat{\psi }_{y}^{14} } \\ {\hat{w}^{1} } & {\hat{w}^{2} } & {\hat{w}^{3} } & {...} & {\hat{w}^{14} } \\ \end{array} } \right]$$

(43)

Correspondingly, the nonzero strains are determined as

$${{\varvec{\upvarepsilon}}} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {2\varepsilon_{xy} } \\ \end{array} } \right\} = {\mathbf{E}}{\varvec{\upalpha}}$$

(44)

with

$${\mathbf{E}} = \left[ {\begin{array}{*{20}c} {\hat{\varepsilon }_{xx}^{1} } & {\hat{\varepsilon }_{xx}^{2} } & {\hat{\varepsilon }_{xx}^{3} } & {...} & {\hat{\varepsilon }_{xx}^{14} } \\ {\hat{\varepsilon }_{yy}^{1} } & {\hat{\varepsilon }_{yy}^{2} } & {\hat{\varepsilon }_{yy}^{3} } & {...} & {\hat{\varepsilon }_{yy}^{14} } \\ {2\hat{\varepsilon }_{xy}^{1} } & {2\hat{\varepsilon }_{xy}^{2} } & {2\hat{\varepsilon }_{xy}^{3} } & {...} & {2\hat{\varepsilon }_{xy}^{14} } \\ \end{array} } \right]$$

(45)

where $\hat{\varepsilon }_{xx}^{i}$, $\hat{\varepsilon }_{yy}^{i}$ and $\hat{\varepsilon }_{xy}^{i}$ are calculated by inserting $\hat{w}^{i}$ into Eq. (3); the nonzero mean curvatures are given by

$${{\varvec{\upkappa}}} = \left\{ {\begin{array}{*{20}c} { - \kappa_{xy} } \\ { - \kappa_{yx} } \\ \end{array} } \right\} = {\mathbf{X}}{\varvec{\upalpha}}$$

(46)

with

$${\mathbf{\bf X}} = \left[ {\begin{array}{*{20}c} { - \hat{\kappa }_{xy}^{1} } & { - \hat{\kappa }_{xy}^{2} } & { - \hat{\kappa }_{xy}^{3} } & {...} & { - \hat{\kappa }_{xy}^{14} } \\ { - \hat{\kappa }_{yx}^{1} } & { - \hat{\kappa }_{yx}^{2} } & { - \hat{\kappa }_{yx}^{3} } & {...} & { - \hat{\kappa }_{yx}^{14} } \\ \end{array} } \right]$$

(47)

where $\hat{\kappa }_{xy}^{i}$ and $\hat{\kappa }_{yx}^{i}$ are obtained by inserting $\hat{w}^{i}$ into Eq. (5).

In most cases, the final variables to be solved in the FE equation system are the element nodal DOFs. Therefore, it is necessary to establish the relationship between the coefficient vector ${{\varvec{\upalpha}}}$ and the element nodal DOF vector ${\mathbf{q}}^{e}$. It is a feasible and easy scheme to determine this relationship by only considering the point conforming conditions. However, due to the incompatibility of the above Trefftz functions at the element boundary, it generally cannot strictly meet the displacement continuity requirement between elements. It should be pointed out that meeting the compatibility requirement is an important factor to ensure the convergence of finite element, and thus, reasonable measures are needed to enforce the necessary compatibility conditions. To this end, the generalized conforming theory proposed by Long et al. [50] is employed here. In this concept, the compatibility requirement is satisfied in a weak sense and the resulting element can be regarded as a kind of limiting conforming model, which means that the element gradually changes from the non-conforming model into the conforming one with the mesh refinement. A generalized conforming scheme consisting of fourteen point conforming conditions has been proposed in [40] for constructing classical thin plate element. Recently, this scheme has also been successfully applied to the development of the thin plate/shell elements based on the MCST [42, 43]. Because both the plate models based on the CCST and MCST need to meet the C¹ continuity requirement of w, this scheme can be directly applied to this work without special modification. The fourteen conforming conditions in this scheme are described as below.

First, the value of the assumed transverse displacement field at the four nodes should be equal to the corresponding nodal DOF:

$$w\left( {x_{i} ,y_{i} } \right) = w_{i} ,\;\;\left( {i = 1\sim 4} \right)$$

(48)

in which $w\left( {x_{i} ,y_{i} } \right)$ denotes the displacement calculated by substituting the coordinates $\left( {x_{i} ,y_{i} } \right)$ of the point i into Eq. (39). Besides, the following point conforming conditions for transverse displacement are also considered:

$$w\left( {x_{5} ,y_{5} } \right) + w\left( {x_{7} ,y_{7} } \right) = w_{5} + w_{7}$$

(49)

$$w\left( {x_{6} ,y_{6} } \right) + w\left( {x_{8} ,y_{8} } \right) = w_{6} + w_{8}$$

(50)

where the items on the right-hand sides are determined by

$$w_{i + 4} = \frac{1}{2}w_{i} + \frac{1}{2}w_{j} + \frac{{L_{ij} }}{8}\psi_{si} - \frac{{L_{ij} }}{8}\psi_{sj} ,\;\;\;\left( {ij = 12,\;23,\;34,\;41} \right)$$

(51)

in which $\psi_{si}$ and $\psi_{sj}$ are the plate tangential rotations at the end nodes of the edge ij and can be transformed from the corresponding nodal plate rotation DOFs; $L_{ij}$ is the length of the edge.

Second, as illustrated in Fig. 2, the conforming conditions for plate normal rotation along the edge at the points with local parametric coordinates $\xi = \pm {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 3}} \right. \kern-0pt} 3}$ are considered:

$$\psi_{n} \left( {x_{k} ,y_{k} } \right) = \psi_{nk} ,\;\;\left( {k = A_{i} \;{\text{and}}\;B_{i} ,\;\;i = 1\sim 4} \right)$$

(52)

where $\psi_{n} \left( {x_{k} ,y_{k} } \right)$ is calculated in accordance with the assumed plate rotation fields given in Eq. (40) and $\psi_{nk}$ is interpolated by

$$\psi_{nk} = \frac{{1 - \xi_{k} }}{2}\psi_{ni} + \frac{{1 + \xi_{k} }}{2}\psi_{nj} ,\;\;\left( {k = A_{i} \;{\text{and}}\;B_{i} ,\;\;ij = 12,\;23,\;34,\;41} \right)$$

(53)

in which $\psi_{ni}$ and $\psi_{nj}$ are the plate normal rotations at the end nodes of the edge ij and determined by the corresponding nodal plate rotation DOFs.

After imposing the foregoing fourteen conforming conditions to the assumed deformation fields given in Eqs. (39 and 40), we can get the relationship between ${{\varvec{\upalpha}}}$ and ${\mathbf{q}}^{e}$:

$${{\varvec{\uplambda}}}{\varvec{\upalpha }} = {\varvec{\Lambda}}{\mathbf{q}}^{e}$$

(54)

where the detailed expressions of the matrices ${{\varvec{\uplambda}}}$ and ${{\varvec{\Lambda}}}$ are summarized in Appendix 1 for the sake of brevity. Thereby, we can rewrite Eq. (41) as the interpolation form of ${\mathbf{q}}^{e}$:

$${\mathbf{u}} = {\mathbf{U}}{\varvec{\uplambda}}^{- 1} {\varvec{\Lambda}}{\mathbf{q}}^{e} = {\mathbf{N}}_{u} {\mathbf{q}}^{e}$$

(55)

Correspondingly, we have the strain and mean curvature:

$${\varvec{\upvarepsilon}} ={\mathbf{E}}{\varvec{\uplambda }}^{ - 1} {\varvec{\Lambda}}{\mathbf{q}}^{e} = {\mathbf{B}}_{\varepsilon } {\mathbf{q}}^{e}$$

(56)

$${{\varvec{\upkappa}}} = {\mathbf{X}}{\varvec{\uplambda}}^{ - 1} {\varvec{\Lambda}}{\mathbf{q}}^{e} = {\mathbf{B}}_{\kappa } {\mathbf{q}}^{e}$$

(57)

from which the symmetric part of the force–stress and the couple stress can be further obtained by virtue of Eqs. (14–17):

$${{\varvec{\upsigma}}}_{{{\text{sym}}}} = \left\{ {\begin{array}{*{20}c} {\sigma_{{\left( {xx} \right)}} } \\ {\sigma_{{\left( {yy} \right)}} } \\ {\sigma_{{\left( {xy} \right)}} } \\ \end{array} } \right\} = {\mathbf{D}}_{\varepsilon } {\mathbf{B}}_{\varepsilon } {\mathbf{q}}^{e}$$

(58)

$${{\varvec{\upmu}}} = \left\{ {\begin{array}{*{20}c} {\mu_{xy} } \\ {\mu_{yx} } \\ \end{array} } \right\} = {\mathbf{D}}_{\kappa } {\mathbf{B}}_{\kappa } {\mathbf{q}}^{e}$$

(59)

where

$${\mathbf{D}}_{\varepsilon } = \left[ {\begin{array}{*{20}c} {\frac{{E_{x} }}{{1 - \nu_{xy} \nu_{yx} }}} & {\frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}} & 0 \\ {\frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}} & {\frac{{E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}} & 0 \\ 0 & 0 & {\begin{array}{*{20}c} {} \\ {} \\ \end{array} G_{xy} } \\ \end{array} } \right]$$

(60)

$${\mathbf{D}}_{\kappa } = \left[ {\begin{array}{*{20}c} {8G_{xy} l^{2} } & 0 \\ 0 & {8G_{xy} l^{2} } \\ \end{array} } \right]$$

(61)

3.2 The final element formulation

The virtual work principle will be employed to derive the final finite element formulation. As previously mentioned, the skew-symmetric part of the force–stress does not contribute to the deformation energy in the CCST, so that this part is not considered in the virtual work principle. In addition, by assuming that the plate is only subjected to external force loads on its top surface and lateral surface and the effect of micro-inertia [44] is neglected, the virtual work principle of the present plate bending problem can be given as

$$\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\int_{\Omega } {\delta {\mathbf{u}}^{T} \rho {\ddot{\bf u}}{\text{d}} \Omega } {\text{d}} z} + \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\int_{\Omega } {\left( {\delta {{\varvec{\upvarepsilon}}}^{T} {{\varvec{\upsigma}}}_{{{\text{sym}}}} + \delta {{\varvec{\upkappa}}}^{T} {{\varvec{\upmu}}}} \right){\text{d}} \Omega } {\text{d}} z} - \int_{\Omega } {\delta {\mathbf{u}}^{T} {\mathbf{f}}{\text{d}} \Omega } - \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\int_{\Gamma } {\delta {\mathbf{u}}^{T} {\mathbf{t}}{\text{d}} \Gamma } {\text{d}} z} = 0$$

(62)

in which $\Omega$ denotes the domain of the plate mid-surface bounded by $\Gamma$, f and t are the force loads acting on the top surface and lateral surface of the plate, respectively. It should be noted that the additional energy terms generated by the displacement incompatibility have been ignored in Eq. (62), which inevitably introduces some error. However, the numerical examples discussed later in this paper demonstrate that the error caused by this approximation is very small and the convergence property of the element is guaranteed due to the generalized conforming theory.

By inserting Eqs. (55–59) into Eq. (62) and applying the variational statement, the finite element equation system at the element level is established:

$${\mathbf{M}}^{e} {\ddot{\bf q}}^{e} + {\mathbf{K}}^{e} {\mathbf{q}}^{e} = {\mathbf{Q}}^{e}$$

(63)

in which ${\mathbf{M}}^{e}$ is element mass matrix:

$${\mathbf{M}}^{e} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\int_{\Omega } {\rho {\mathbf{N}}_{u}^{T} {\mathbf{N}}_{u} {\text{d}} \Omega } {\text{d}} z}$$

(64)

${\mathbf{K}}^{e}$ is element stiffness matrix:

$${\mathbf{K}}^{e} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\int_{\Omega } {\left( {{\mathbf{B}}_{\varepsilon }^{T} {\mathbf{D}}_{\varepsilon } {\mathbf{B}}_{\varepsilon } + {\mathbf{B}}_{\kappa }^{T} {\mathbf{D}}_{\kappa } {\mathbf{B}}_{\kappa } } \right){\text{d}} \Omega } {\text{d}} z}$$

(65)

${\mathbf{Q}}^{e}$ is the element equivalent load vector:

$${\mathbf{Q}}^{e} = \int_{\Omega } {{\mathbf{N}}_{u}^{T} {\mathbf{f}}{\text{d}} \Omega } + \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\int_{\Gamma } {{\mathbf{N}}_{u}^{T} {\mathbf{t}}{\text{d}} \Gamma } {\text{d}} z}$$

(66)

Next, the corresponding global mass matrix M, stiffness matrix K and load vector Q can be simply obtained through matrix assembly. Moreover, for the free vibration analysis, the nature frequency $\theta$ and mode shape ${\mathbf{q}}^{\theta }$ can be solved by considering the following equation:

$$\left( {{\mathbf{K}} - \theta^{2} {\mathbf{M}}} \right){\mathbf{q}}^{\theta } = {\mathbf{0}}$$

(67)

4 Numerical validation

In order to fully test the performance of the new element in analyzing the size-dependent mechanical response of thin plates in the framework of the CCST, a series of numerical examples, including five static ones and three free vibration ones, are analyzed. The analytical solutions of some of these examples are relatively easy to obtain and summarized in Appendix 2, while for the others the derivation of the analytical solution is not a trivial task; thus, the numerical values obtained from refined meshes are provided as the reference values for comparison. In these tests, the relative errors are defined as

$$e_{w} = \left| {\frac{{w - w_{{{\text{ref}}}} }}{{w_{{{\text{ref}}}} }}} \right|,\;\;\;e_{M} = \left| {\frac{{M - M_{{{\text{ref}}}} }}{{M_{{{\text{ref}}}} }}} \right|,\;\;\;e_{\theta } = \left| {\frac{{\theta - \theta_{{{\text{ref}}}} }}{{\theta_{{{\text{ref}}}} }}} \right|$$

(68)

4.1 The static bending problems

4.1.1 The patch test of plate bending

The patch test is commonly used to numerically verify the convergence property of the non-conforming element. As illustrated in Fig. 3, the orthotropic thin plate with the thickness h = 0.02 mm is divided into several elements with irregular shapes. The engineering material constants with respect to the material principal directions are given by

$$E_{x} = 10E_{y} = 100{\text{MPa}},\;\;G_{xy} = 0.5E_{y} , \, \nu_{xy} = 0.25,\;\;\;l = 20\;{\mu m}$$

(69)

Fig. 3

The patch test (unit: mm)

In order to produce a deformation state where the bending moments and couple moments are constant, the transverse displacements and plate rotations at the plate boundary nodes which are determined using the following functions are adopted as the prescribed boundary conditions:

$$w = 1 + x + y + x^{2} + y^{2} + xy, \, \psi_{x} = 1 + 2x + y, \, \psi_{y} = 1 + 2y + x$$

(70)

The computations are operated by using two typical distorted meshes as given in Fig. 3 which, respectively, contain one concave quadrilateral element or degenerate triangular element. The numerical results show that the element can pass the patch test strictly, demonstrating that the computation convergence of the new element is guaranteed.

4.1.2 The square plate

Figure 4 depicts the thin square plate under uniformly distributed transverse load q. The plate boundaries are completely simply supported or clamped. The span is L = 10 mm and thickness is h = 0.1 mm. Because of symmetry, only one quarter of the plate is modeled using the plate element. First, the plate is assumed to be made of isotropic material with E = 10.92GPa and ν = 0.3. The convergence results of the dimensionless central deflection and bending moment for different MLSPs are summarized in Tables 1 and 2, while the convergence plots of the relative errors are provided in Fig. 5. Second, the orthotropic case is considered with the material parameters $E_{x} = 10E_{y} ,\;\;G_{xy} = 0.5E_{y} ,$$\nu_{xy} = 0.25$. The numerical results are listed in Tables 3 and 4, and the corresponding convergence plots are shown in Fig. 6. It is obvious that the numerical results of the new element converge into the reference values very quickly. Besides, the distributions of the transverse deflection and bending moment along the path AB calculated using 16 × 16 elements are presented in Fig. 7, from which one can clearly see that the element captures the size dependence very well. As the MLSP l increases, the thin plate becomes more stiffer, resulting smaller maximum displacement and moment.

Fig. 4

The model and typical mesh of the square plate

Table 1 The convergence of dimensionless central deflection and bending moment of the simply supported isotropic square plate

Table 2 The convergence of dimensionless central deflection and bending moment of the clamped isotropic square plate

Fig. 5

The relative errors of central deflection and bending moment of the isotropic square plate

Table 3 The convergence of dimensionless central deflection and bending moment of the simply supported orthotropic square plate

Table 4 The convergence of dimensionless central deflection and bending moment of the clamped orthotropic square plate

Fig. 6

The relative errors of central deflection and bending moment of the orthotropic square plate

Fig. 7

The distributions of the deflection and bending moment along the path AB of the orthotropic square plate

4.1.3 The circular plate

As shown in Fig. 8, the static bending behavior of the circular plate when subjected to uniformly distributed transverse load q is evaluated. The plate radius is R = 5 mm and thickness is h = 0.1 mm. By taking advantage of symmetry, only one quarter is simulated using 3 × N × N elements. The convergence results of the normalized central deflection and bending moment of the isotropic plate with E = 10.92GPa and ν = 0.3 are plotted in Fig. 9, while those of the clamped orthotropic circular plate with $E_{x} = 10E_{y} ,\;\;G_{xy} = 0.5E_{y} , \, \nu_{xy} = 0.25$ are provided in Fig. 10. Note that the expressions of the analytical reference solutions used in this test are summarized in Appendix 2. It is shown again that the new element has good convergence in predicting the displacement and bending moment when simulating the size-dependent response of the microplate based on the CCST.

Fig. 8

The model and typical mesh of the circular plate

Fig. 9

The relative errors of central deflection and bending moment of the isotropic circular plate

Fig. 10

The relative errors of central deflection and bending moment of the clamped orthotropic circular plate

4.1.4 The test for distortion sensitivity

As shown in Fig. 11, this test also involves the static deformation of the clamped orthotropic square plate under uniformly distributed transverse load with span L = 10 mm and thickness h = 0.1 mm. However, different with the cases discussed in Sect. 4.1.2, the two principal material directions are defined as along the diagonal directions of the plate. Due to symmetry, one quarter of the plate which is a triangular region is modeled by using three elements. In order to investigate the sensitivity of the new element to mesh distortion, the mesh node P is artificially moved from its original position along the path AO to a new position P’ for generating a mesh with severe distortion. In particular, when the parameter ${\Delta }$ is larger than ${5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0pt} 6}$, the element BOCP degenerates into a concave quadrangle. Figure 12 gives the variation of the deflection at the point O versus the parameter ${\Delta }$, in which the results have been normalized by $w_{{{\Delta } = 0}}$. It can be observed that the maximum deviation is less than 8%, revealing that the element has good tolerance to mesh distortion. Moreover, it also reveals that the MLSP l does not have obvious influence on the element’s distortion sensitivity.

Fig. 11

The model of the distortion sensitivity test (unit: mm)

Fig. 12

The results of the distortion sensitivity test

4.1.5 The L-shaped plate with hole

For assessing the element’s performance in analyzing structures with irregular shapes, as shown in Fig. 13, the orthotropic L-shaped plate with hole subjected to a uniformly distributed transverse load is considered. The plate is clamped at the left end, while the other edges are free. The thickness is h = 0.1 mm and the material parameters are given by

$$E_{x} = 60700{\text{MPa, }}E_{y} = 24800{\text{MPa}},\;\;G_{xy} = 12000{\text{MPa}}, \, \nu_{xy} = 0.23$$

(71)

Fig. 13

The L-shaped plate with hole and typical mesh with N = 1

Figure 13 illustrates the basic mesh used for the FE computation and this basic mesh will be refined by dividing each element into N × N elements. The convergence results of the dimensionless deflection at the point A for different MLSPs are listed in Table 5. Since it is almost impossible to derive the analytical solution, the results obtained by using a fine mesh composed of 16,384 elements are employed as the reference values. As is evident in Table 5 that the element still has good convergence when simulating complex plate structures. Besides, the distribution of the displacement over the whole structure is provided in Fig. 14. It can be seen that, with the increase in the MLSP, the deformation of the plate gradually decreases, indicating that the plate becomes stiffer.

Table 5 The convergence of deflection at the point A of the L-shaped plate with hole

Fig. 14

The distribution of dimensionless displacement of the L-shaped plate with hole

4.2 The free vibration problems

4.2.1 The square plate

This test involves the free vibration analysis of the square plate with edge length L = 10 mm and thickness h = 0.1 mm. Different with the static analysis, the whole structure is modeled by using N × N new elements. First, the isotropic case is considered with the material parameters E = 169GPa, ρ = 2332 kg/m³ and ν = 0.3. Tables 6 and 7 show the convergence results of the plate’s dimensionless natural frequency under simply supported constraint and clamped constraint, respectively. Besides, the convergence plots are shown in Fig. 15. Next, the orthotropic case is analyzed by assuming the following parameters

$$E_{x} = 60700{\text{MPa, }}E_{y} = 24800{\text{MPa}},\;\;G_{xy} = 12000{\text{MPa}}, \, \nu_{xy} = 0.23, \, \rho = 2000{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}$$

(72)

Table 6 The convergence of natural frequency of the simply supported isotropic square plate

Table 7 The convergence of natural frequency of the clamped isotropic square plate

Fig. 15

The relative errors of natural frequency of the isotropic square plate

The numerical results are provided in Tables 8 and 9. The relative errors are shown in Fig. 16. In addition, the variations of the nature frequency of the orthotropic plate versus the MLSP obtained using 32 × 32 elements are plotted in Fig. 17. It is shown that the new element also exhibits good convergence in the free vibration analysis. In addition, it can also be observed from the numerical results that the increase in the MLSP leads to the increase in the natural frequency, proving the effectiveness of the element in capturing the size effects in dynamic analysis.

Table 8 The convergence of natural frequency of the simply supported orthotropic square plate

Table 9 The convergence of natural frequency of the clamped orthotropic square plate

Fig. 16

The relative errors of natural frequency of the orthotropic square plate

Fig. 17

The dimensionless nature frequency of the orthotropic square plate

Fig. 18

The relative errors of natural frequency of the orthotropic circular plate

4.2.2 The circular plate

In this test, the free vibration of the orthotropic circular plate is analyzed with the material parameters given by Eq. (72). The whole region of the circular plate is modeled, simulating each quarter of the plate using the same mesh strategy as in Sect. 4.1.3. The convergence results of the nature frequency are summarized in Tables 10 and 11. The corresponding plots of the relative errors are provided in Fig. 18. Besides, the variations of the nature frequency versus the MLSP calculated using 12 × 16 × 16 elements are plotted in Fig. 19. This test demonstrates again that the new element shows good numerical accuracy in predicting the size-dependent dynamic responses of the small-scale orthotropic plate based on the CCST.

Table 10 The convergence of natural frequency of the simply supported orthotropic circular plate

Table 11 The convergence of natural frequency of the clamped orthotropic circular plate

Fig. 19

The dimensionless nature frequency of the orthotropic circular plate

4.2.3 The L-shaped plate with hole

The free vibration behavior of the L-shaped plate with hole which has been discussed in Sect. 4.1.5 is investigated. The density of the material is $\rho = 2000{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}$. The meshes used here are the same as in the static problem. The convergence results of dimensionless nature frequency for different MLSPs are summarized in Table 12. Besides, the influences of the MLSP on the nature frequency and mode shape are shown in Figs. 20 and 21, respectively. It is evident that the numerical results adequately demonstrate the validness of the element in simulating the dynamic response of plate with complex shapes.

Table 12 The convergence of natural frequency of the L-shaped plate with hole

Fig. 20

The dimensionless nature frequency of the L-shaped plate with hole

Fig. 21

The vibration mode shape of the L-shaped plate with hole

5 Conclusions

A new non-conforming Trefftz-type 4-node 12-DOF plate element is developed for analysis of the small-scale orthotropic thin plates in the framework of the CCST [17]. This is accomplished via two main steps. First, to derive the desired Trefftz functions, the non-classical orthotropic thin plate bending model is established by incorporating the Kirchhoff thin plate bending assumption into the 3D consistent couple stress elasticity and converting the governing differential equations into one single equation. Second, the obtained Trefftz functions are adopted as the basic functions for formulating the non-conforming quadrilateral plate element and a novel set of point conforming conditions based on the generalized conforming theory [50] is used to enforce the C¹ interelement compatibility requirement in weak sense. The element construction procedure is straightforward and the final element expression is concise. The numerical results reveal that the element can always exactly pass the patch test even though it is in badly distorted shape, demonstrating that the convergence property of the new non-conforming element is guaranteed. Besides, it is also shown that the element can provide satisfactory performances in capturing the size effect of the small-scale orthotropic thin plate with complex geometry, exhibiting good convergence rate and low susceptibility to mesh distortion.

Appendices

Appendix 1

The matrix ${{\varvec{\uplambda}}}$ in Eq. (54) is composed of two parts, as follows:

$${{\varvec{\uplambda}}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\uplambda}}}^{w} } \\ {{{\varvec{\uplambda}}}^{\psi } } \\ \end{array} } \right]$$

(73)

The first submatrix ${{\varvec{\uplambda}}}^{w}$ is expressed as

$${{\varvec{\uplambda}}}^{w} = \left[ {\begin{array}{*{20}c} {\hat{w}^{1} \left( {x_{1} ,y_{1} } \right)} & {\hat{w}^{2} \left( {x_{1} ,y_{1} } \right)} & \cdots & {\hat{w}^{14} \left( {x_{1} ,y_{1} } \right)} \\ {\hat{w}^{1} \left( {x_{2} ,y_{2} } \right)} & {\hat{w}^{2} \left( {x_{2} ,y_{2} } \right)} & \cdots & {\hat{w}^{14} \left( {x_{2} ,y_{2} } \right)} \\ {\hat{w}^{1} \left( {x_{3} ,y_{3} } \right)} & {\hat{w}^{2} \left( {x_{3} ,y_{3} } \right)} & \cdots & {\hat{w}^{14} \left( {x_{3} ,y_{3} } \right)} \\ {\hat{w}^{1} \left( {x_{4} ,y_{4} } \right)} & {\hat{w}^{2} \left( {x_{4} ,y_{4} } \right)} & \cdots & {\hat{w}^{14} \left( {x_{4} ,y_{4} } \right)} \\ {\hat{w}^{1} \left( {x_{5} ,y_{5} } \right) + \hat{w}^{1} \left( {x_{7} ,y_{7} } \right)} & {\hat{w}^{2} \left( {x_{5} ,y_{5} } \right) + \hat{w}^{2} \left( {x_{7} ,y_{7} } \right)} & \cdots & {\hat{w}^{14} \left( {x_{5} ,y_{5} } \right) + \hat{w}^{14} \left( {x_{7} ,y_{7} } \right)} \\ {\hat{w}^{1} \left( {x_{6} ,y_{6} } \right) + \hat{w}^{1} \left( {x_{8} ,y_{8} } \right)} & {\hat{w}^{2} \left( {x_{6} ,y_{6} } \right) + \hat{w}^{2} \left( {x_{8} ,y_{8} } \right)} & \cdots & {\hat{w}^{14} \left( {x_{6} ,y_{6} } \right) + \hat{w}^{14} \left( {x_{8} ,y_{8} } \right)} \\ \end{array} } \right]$$

(74)

while the second part ${{\varvec{\uplambda}}}^{\psi }$ is given by

$${{\varvec{\uplambda}}}^{\psi } = {\mathbf{T}}_{n} {{\varvec{\Phi}}}$$

(75)

in which

$${{\varvec{\Phi}}} = \left[ {\begin{array}{*{20}c} {\hat{\psi }_{x}^{1} \left( {x_{A1} ,y_{A1} } \right)} & {\hat{\psi }_{x}^{2} \left( {x_{A1} ,y_{A1} } \right)} & {...} & {\hat{\psi }_{x}^{14} \left( {x_{A1} ,y_{A1} } \right)} \\ {\hat{\psi }_{y}^{1} \left( {x_{A1} ,y_{A1} } \right)} & {\hat{\psi }_{y}^{2} \left( {x_{A1} ,y_{A1} } \right)} & {...} & {\hat{\psi }_{y}^{14} \left( {x_{A1} ,y_{A1} } \right)} \\ \vdots & \vdots & \ddots & {...} \\ {\hat{\psi }_{x}^{1} \left( {x_{B4} ,y_{B4} } \right)} & {\hat{\psi }_{x}^{2} \left( {x_{B4} ,y_{B4} } \right)} & {...} & {\hat{\psi }_{x}^{14} \left( {x_{B4} ,y_{B4} } \right)} \\ {\hat{\psi }_{y}^{1} \left( {x_{B4} ,y_{B4} } \right)} & {\hat{\psi }_{y}^{2} \left( {x_{B4} ,y_{B4} } \right)} & {...} & {\hat{\psi }_{y}^{14} \left( {x_{B4} ,y_{B4} } \right)} \\ \end{array} } \right]$$

(76)

and

$${\mathbf{T}}_{n} = \left[ {\begin{array}{*{20}c} {{\mathbf{T}}_{1} } & {} & {} & {} \\ {} & {{\mathbf{T}}_{2} } & {} & {} \\ {} & {} & {{\mathbf{T}}_{3} } & {} \\ {} & {} & {} & {{\mathbf{T}}_{4} } \\ \end{array} } \right],\;\;\; {\mathbf{T}}_{i} = \left[ {\begin{array}{*{20}c} { - \frac{{y_{ij} }}{{L_{ij} }}} & {\frac{{x_{ij} }}{{L_{ij} }}} & {} & {} \\ {} & {} & { - \frac{{y_{ij} }}{{L_{ij} }}} & {\frac{{x_{ij} }}{{L_{ij} }}} \\ \end{array} } \right],\;\;\;\left( {ij = 12,\;23,\;34,\;41} \right)$$

(77)

where $x_{ij} = x_{i} - x_{j}$ and $y_{ij} = y_{i} - y_{j}$.

The matrix ${{\varvec{\Lambda}}}$ in Eq. (54) takes the form

$${{\varvec{\Lambda}}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\Lambda}}}^{w} } \\ {{{\varvec{\Lambda}}}^{\psi } } \\ \end{array} } \right]$$

(78)

in which

$${{\varvec{\Lambda}}}^{w} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {} & {} & {} & {} & {} & {} & {} & {} & {} \\ {} & {} & {} & 1 & 0 & 0 & {} & {} & {} & {} & {} & {} \\ {} & {} & {} & {} & {} & {} & 1 & 0 & 0 & {} & {} & {} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & 1 & 0 & 0 \\ \frac{1}{2} & { - \frac{{x_{12} }}{8}} & { - \frac{{y_{12} }}{8}} & \frac{1}{2} & {\frac{{x_{12} }}{8}} & {\frac{{y_{12} }}{8}} & \frac{1}{2} & { - \frac{{x_{34} }}{8}} & { - \frac{{y_{34} }}{8}} & \frac{1}{2} & {\frac{{x_{34} }}{8}} & {\frac{{y_{34} }}{8}} \\ \frac{1}{2} & {\frac{{x_{41} }}{8}} & {\frac{{y_{41} }}{8}} & \frac{1}{2} & { - \frac{{x_{23} }}{8}} & { - \frac{{y_{23} }}{8}} & \frac{1}{2} & {\frac{{x_{23} }}{8}} & {\frac{{y_{23} }}{8}} & \frac{1}{2} & { - \frac{{x_{41} }}{8}} & { - \frac{{y_{41} }}{8}} \\ \end{array} } \right]$$

(79)

and ${{\varvec{\Lambda}}}^{\psi }$ is given by

$${{\varvec{\Lambda}}}^{\psi } = \left[ {\begin{array}{*{20}c} {{{\varvec{\Lambda}}}_{11}^{\psi } } & {{{\varvec{\Lambda}}}_{12}^{\psi } } & {} & {} \\ {} & {{{\varvec{\Lambda}}}_{22}^{\psi } } & {{{\varvec{\Lambda}}}_{23}^{\psi } } & {} \\ {} & {} & {{{\varvec{\Lambda}}}_{33}^{\psi } } & {{{\varvec{\Lambda}}}_{34}^{\psi } } \\ {{{\varvec{\Lambda}}}_{41}^{\psi } } & {} & {} & {{{\varvec{\Lambda}}}_{44}^{\psi } } \\ \end{array} } \right]$$

(80)

with

$${{\varvec{\Lambda}}}_{ii}^{\psi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{{1 + {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}}}{{2L_{ij} }}y_{ij} } & {\frac{{1 + {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}}}{{2L_{ij} }}x_{ij} } \\ 0 & { - \frac{{1 - {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}}}{{2L_{ij} }}y_{ij} } & {\frac{{1 - {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}}}{{2L_{ij} }}x_{ij} } \\ \end{array} } \right],\;\;\; {{\varvec{\Lambda}}}_{ij}^{\psi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{{1 - {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}}}{{2L_{ij} }}y_{ij} } & {\frac{{1 - {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}}}{{2L_{ij} }}x_{ij} } \\ 0 & { - \frac{{1 + {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}}}{{2L_{ij} }}y_{ij} } & {\frac{{1 + {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}}}{{2L_{ij} }}x_{ij} } \\ \end{array} } \right]$$

(81)

where $ij = 12,\;23,\;34,\;41$.

Appendix 2

As previously discussed, the analytical solutions of some of the numerical tests are relatively easy to obtain and these are summarized in this section.

With respect to the static bending behavior of the square thin plate under uniformly distributed transverse load q, the deflection of the simply supported orthotropic case can be obtained using the Navier method:

$$w = \frac{{16qL^{4} }}{{\pi^{6} }}\sum\limits_{n = 1}^{\infty } {\sum\limits_{m = 1}^{\infty } {\frac{1}{mn}\frac{{\sin \frac{m\pi }{L}x\sin \frac{n\pi }{L}y}}{{\left( {D_{x} + D_{l} } \right)m^{4} + 2\left( {H + D_{l} } \right)m^{2} n^{2} + \left( {D_{y} + D_{l} } \right)n^{4} }}} }$$

(82)

in which L is the edge length of the square plate. Then, by substituting Eq. (82) into the definitions given in Sect. 2, the resultants can be also obtained. From Eq. (82), the deflection of the simply supported isotropic case is delivered:

$$w = \frac{{16qL^{4} }}{{\left( {D + D_{l} } \right)\pi^{6} }}\sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\frac{1}{mn}\frac{{\sin \frac{m\pi }{L}x\sin \frac{n\pi }{L}y}}{{\left( {m^{4} + 2m^{2} n^{2} + n^{4} } \right)}}} }$$

(83)

Note that it is difficult to derive the solution of the clamped orthotropic square plate analytically, only that of the clamped isotropic case is provided by using the superposition method [53]:

$$w = \frac{q}{{8\left( {D + D_{l} } \right)}}\left[ {\left( {\frac{{L^{2} }}{4} - x^{2} } \right)\left( {\frac{{L^{2} }}{4} - y^{2} } \right) - \frac{{L^{3} }}{2}\left( {\sum\limits_{n = 1,3...}^{\infty } {\frac{{A_{n} Y_{n} }}{{n^{2} }}\frac{{\cos \frac{n\pi x}{L}}}{{\cosh^{2} \frac{n\pi }{2}}} + \sum\limits_{m = 1,3...}^{\infty } {\frac{{A_{m} X_{m} }}{{m^{2} }}\frac{{\cos \frac{m\pi y}{L}}}{{\cosh^{2} \frac{m\pi }{2}}}} } } \right)} \right]$$

(84)

in which

$$X_{m} = L\sinh \frac{m\pi }{2}\cosh \frac{m\pi x}{L} - 2x\cosh \frac{m\pi }{2}\sinh \frac{m\pi x}{L}$$

(85)

$$Y_{n} = L\sinh \frac{n\pi }{2}\cosh \frac{n\pi y}{L} - 2y\cosh \frac{n\pi }{2}\sinh \frac{n\pi y}{L}$$

(86)

and the coefficients $A_{n}$ and $A_{m}$ are determined in accordance with the boundary conditions and summarized in Table

Table 13 The coefficients used in Eq. (84)

13.

Besides, the reference frequency of the free vibration of the simply supported isotropic square plate is given by

$$\theta_{mn} = \pi^{2} \left(\frac{{m^{2} }}{{L^{2} }} + \frac{{n^{2} }}{{L^{2} }}\right)\sqrt {\frac{{D[1 + 24(1 - \nu )\frac{{l^{2} }}{{h^{2} }}]}}{{\rho h + \frac{\rho }{12}h^{3} \pi^{2} (\frac{{m^{2} }}{{L^{2} }} + \frac{{n^{2} }}{{L^{2} }})}}} ,\;\;\;m\;{\text{and}}\;n = 1,2,3 \ldots$$

(87)

With respect to the static bending behavior of the circular thin plate under uniformly distributed transverse load q, the deflection of the clamped orthotropic case can be obtained:

$$w = \frac{{q\left( {R^{2} - r^{2} } \right)^{2} }}{{8\left[ {3\left( {D_{x} + D_{l} } \right) + 2\left( {H + D_{l} } \right) + 3\left( {D_{y} + D_{l} } \right)} \right]}}$$

(88)

in which R is the radius of the circular plate and $r^{2} = x^{2} + y^{2}$. From Eq. (88), the deflection of the clamped isotropic case is further deduced:

$$w = \frac{q}{{64\left( {D + D_{l} } \right)}}\left( {R^{2} - r^{2} } \right)^{2}$$

(89)

In addition, the deflection of the simply supported isotropic circular plate is given by

$$w = \frac{{qR^{4} }}{{64\left( {D + D_{l} } \right)\left[ {\left( {1 + \nu } \right)D + 2D_{l} } \right]}}\left( {{\text{A}}\frac{{r^{4} }}{{R^{4} }} + {\text{B}}\frac{{r^{2} }}{{R^{2} }} + {\text{C}}} \right)$$

(90)

with

$${\text{A}} = \left( {1 + \nu } \right)D + 2D_{l} {,}\;\;\;{\text{B}} = - 2\left( {3 + \nu } \right)D - 8D_{l} {,}\;\;\;{\text{C}} = \left( {5 + \nu } \right)D + 6D_{l}$$

(91)