Damaged composite structural strength enhancement under elevated thermal environment using shape memory alloy fiber

Abstract

The damaged laminated composite structural strength and repair action due to functional material reinforcement is investigated mathematically in this research using a higher-order displacement field model. The effect of a crack on the frequency responses is predicted numerically using the finite element (FE) approach. The reduction in total structural strength due to the crack and elevated temperatures are computed using the proposed model. Further, the enhancement of parent structural strength/stiffness is achieved by reinforcing the shape memory alloy (SMA). Moreover, the damage repair and improved frequency are achieved through activated SMA under a temperature range. The numerical model efficacy is established by conducting the convergence and adequate comparison studies. The study of the cracked laminate is verified for different temperature ranges, with and without SMA fiber. Additionally, a few experimental frequencies of intact and damaged composite panels have been carried out for comparison to gain confidence in the proposed model. Finally, several numerical examples are solved by varying the important structural input parameters (material and geometry) and their influences discussed in detail.

1 Introduction

Composite materials play a prominent role in engineering design and positively affect the applications of several sectors like automobile, aerospace, marine, acoustics, etc. The composite structural stiffness is reduced due to inherent damages, i.e., cracks, delamination, edge dislocations, etc. These defects in the composite create safety concerns and a reduction in their total structural stiffness. The reinforcement of SMA in laminates significantly improves the structural strength and subsequently, the stiffness. By its enormous properties, it is clear that SMA has an excellent ability to improve the laminated structural stiffness. However, paying close attention to composite shells embedded with SMA is a long way off. In the recent past, a number of works have been reported examining the vibration characteristics of laminate with and without crack. In addition, the effect of SMA reinforcement on these laminated composites has been reported and discussed in the following lines. Leissa [1] has studied the free vibration characteristics of rectangular intact plates for different boundary conditions using the Ritz method. A similar analysis has been carried out by Liew et al. [2] for the laminate with edge and central crack by considering the accurate domain decomposition method. Lee et al. [3] investigated the vibration behavior of the centrally cracked isotropic and orthotropic rectangular plate by using the Rayleigh method, and Brethee [4] performed the same in commercial FE tool, i.e., ANSYS. Fujimoto [5] reported the experimental eigenvalue and the analytical cases for the plate structure with central crack via a hybrid finite element method (FEM). The FE model of both cantilever and simply supported square plate for the different crack lengths and positions was analyzed and verified experimentally [6]. Ritz method has been adopted by Huang et al. [7] to perform the natural frequency responses of a side cracked rectangular plate. In continuation to earlier research Ritz method in association with the classical plate theory (CPT) [8] has been adopted to analyze the simply supported cracked rectangular plates numerically for the prediction of free vibration responses. Asadigorji et al. [9] adopted the CPT kinematics to model the rectangular laminated composite plate consisting of multiple cracks. The eigenvalue responses for the square plate with internal cracks in various locations of the laminated composite are presented by Huang et al. [10]. The numerical and experimental frequency analysis of the laminated composite plate under elevated temperature and the hygrothermal environment are discussed in [11]. The free vibration frequencies of a thin rectangular isotropic plate with surface and internal cracks are computed analytically under the thermal environment in [12]. The flat stiffened plate and beam structural frequencies with side crack are modeled using CPT in [13] using the Ritz method. The natural frequency of a cantilever glass fiber and carbon-reinforced polymer composites (GFRPCs and CFRPCs) are investigated in [14] using the commercial FE tool (ANSYS platform). The frequency responses of piezoelectric bonded composite plates with cracks have been studied by adopting the minimum energy principle [15]. The vibration behavior of stiffened cracked plate is predicted numerically in [16] via the first-order shear deformation theory (FSDT) and higher-order deformation theory (HSDT), respectively. A partially cracked carbon–boron laminated composite plate is investigated [17] for the free natural frequency analysis using classical laminated plate theory for different end boundaries (clamped and simple support). Imran et al. [18] discussed various analytical and the experimental approaches for the evaluation of the natural frequency considering multiple boundary conditions. Li [19] focused on the layer-wise theory (LWT) application for the modeling of the laminated composite structures and their applications. Gayen et al. [20] have deliberately reviewed the safety and future research prospects of cracked structural functional graded materials (FGM) components. The free vibration frequency responses of Graphite/Epoxy composite plate embedded with Shape memory alloy (SMA) are obtained by solving the general governing equation via FE steps in [21]. The natural frequencies of clamped glass fiber composite beams with integrated SMA wires are studied experimentally and verified with the analytical results in [22]. Lau [23] reported the dynamic responses of SMA bonded composite beam theoretically considering different values of prestrain and verified with the experimental data to establish the models’ accuracy. The free vibration frequency and their corresponding mode shapes of SMA bonded laminated composite under an elevated thermal environment are investigated in [24] by using different mid-plane theories (CPT and FSDT). The effect of the axial load of prestrained SMA wires is studied in [25]. The natural frequency of the laminated sandwich composite structure embedded with SMA wires is examined in [26] using the 3D FEM model. The free vibration frequencies characteristics of SMA embedded laminated composite are investigated experimentally in [27] by varying the volume fractions. The bonding effectiveness between the SMA wire and the host material are verified in [28] under the static and dynamic loading for the determination of overall performances of the hybrid composite laminates. Additionally, a few structural models have been introduced in the past to address the large deformation (nonlinearity in geometry or due to loading) cases of various geometrical shapes, i.e., the large amplitude vibration of cylindrical shell panels in [29]. Further, the nonlinear frequency responses of the post-buckled composite structure embedded with SMA fiber were investigated via Green Lagrange type nonlinear strain in the framework of the HSDT [30]. The discrete singular convolution (DSC) method in association with the FSDT has been adopted in [31] to analyze the free vibration frequencies of the laminated composites. The free vibration frequencies of the skew laminated composite plates embedded with SMA fiber are reported in [32] under the temperature loading. The one-dimensional Brinson’s model is used to predict the thermo-mechanical behavior of shape memory alloy wires. The governing equations are generated using FSDT and solved using a numerical method called the generalized differential quadrature method (GDQ). A micromechanical model is developed to investigate the fracture behavior and the influence of the contact region caused by the impact of implanted SMA wires on composite plates. [33]. Tensile behavior of SMA (Ni–Ti) fiber-reinforced (SMAFR) Ti–Al laminated composites is presented [34]. Muwafaq Mohmmed Ali et al. [35] investigated thermal frequency analysis using ANSYS–ADPL software and experimental results considering the hybridized laminated composite material with E-glass fibers integrated with shape memory alloy wires. John et al. [36] utilized strain energy perturbations on a composite plate to investigate the natural frequency modulation using SMA wires. The applications of SMA in the engineering field have been reviewed [37]. The current global situation on development and application of NiTi smart material SMA is reviewed [38] and the self-healing behavior of SMA is presented [39] using nano-capsules. Additionally, the dynamic analysis of silica nanoparticles under seismic load is examined in [40]. The ZnO nanofibers effect on the smart and mechanical properties of concrete is studied in [41]. Similarly, the free vibration responses of double smart nano-beam system are presented in [42]. The theoretical analysis of functionally graded SMA is investigated [43] under thermal conditions. The thermomechanical properties of SMA (Ni–Ti) and shape memory polymers (SMP) are discussed in [44].

The literature review indicates that the study initially focused on the effect of the natural frequency with various crack positions on the composite structures being modeled through either CPT or the FSDT types of mid-plane kinematics. Further, the frequency analysis of the SMA bonded layered composite structure is too much limited in the published domain. To the authors’ knowledge, no literature has been reported yet on SMA reinforcement to enhance the damaged structural stiffness including the environmental effect. Thus, the current research plans investigate the fundamental frequency of cracked laminated composite reinforced with SMA fiber. In this regard, a generic mathematical model based on the HSDT is prepared to predict the free vibration frequency characteristics of cracked layered structures reinforced with SMA under elevated temperatures. Initially, Hamilton’s principle is used to derive the model’s governing equation. The structural equation is modified to a discrete form to reduce the equation order using the isoparametric finite element technique. The numerical results are obtained using in-house developed MATLAB code based on the derived mathematical model. Further, the solution stability and exactness are established by comparing the available published data with the current numerical results. In addition, the current model efficacy is checked further by comparing in-house experimental frequency responses. For the experimental purpose, a few laminated panels are fabricated and an initial crack is introduced for the recording, as well as for comparison purpose. The experimental validation under elevated temperature demonstrates the proposed model’s validity under the variable environmental conditions. Some numerical experimentations are conducted by changing the structural input parameters (curvature ratio and geometrical shapes) including the SMA volume fractions, SMA pre-strain, shell geometries, different end boundaries, and crack ratios (c/a) to show the model applicability.

2 Mathematical formulation

2.1 Geometrical representation

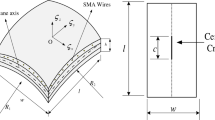
The cracked composite layered shell panel embedded with SMA is considered in the curvilinear coordinate system $\left( {\varsigma_{x} ,\varsigma_{y} ,\varsigma_{z} } \right)$ as shown in Fig. 1. The laminate consists of a finite number of layers nl with equal thickness and arbitrarily oriented at an angle θ. The laminated composite shell panel of length l and width b has been assumed on the global $\varsigma_{x}$- and $\varsigma_{y}$-axes. The thickness h of the laminated composite is considered through the $\varsigma_{z}$-direction. The longitudinal crack of length c is assumed at the center of the laminate. The curvature of the shell panel is defined as R₁ and R₂ in the $\varsigma_{x}$ and $\varsigma_{y}$ direction. The different shell geometries can be obtained by varying the radius of curvature and are listed in Table 1.

Fig. 1

Geometrical representation of laminated shell panel embedded with SMA

Table 1 Shell geometries and their notations, including curvatures

2.2 Strain–displacement relations

The higher-order shear deformation mid-plane kinematics has been adopted for the current SMA bonded damaged layered composite to maintain the necessary shear stress/strain continuity. Additionally, third-order theories offer an improvement in accuracy over the available lower-order kinematics and eradicate the use correction factor.

Now, the global displacement field model of the panel is assumed in the following form [45]:

$$ \begin{gathered} U_{\varsigma x} = u_{{p\varsigma_{x} }} + u_{{q\varsigma_{x} }} \varsigma_{z} + u_{{r\varsigma_{x} }} \varsigma_{z}^{2} + u_{{s\varsigma_{x} }} \varsigma_{z}^{3} , \hfill \\ U_{\varsigma y} = u_{{p\varsigma_{y} }} + u_{{q\varsigma_{y} }} \varsigma_{z} + u_{{r\varsigma_{y} }} \varsigma_{z}^{2} + u_{{s\varsigma_{y} }} \varsigma_{z}^{3} , \hfill \\ U_{\varsigma z} = u_{{p\varsigma_{z} }} , \hfill \\ \end{gathered} $$

(1)

where $u_{{p\varsigma_{x} }} = U_{{\varsigma_{x} }} \left( {\varsigma_{x} ,\varsigma_{y} ,t} \right)$; $u_{{p\varsigma_{y} }} = U_{{\varsigma_{y} }} \left( {\varsigma_{x} ,\varsigma_{y} ,t} \right)$; $u_{{p\varsigma_{z} }} = U_{{\varsigma_{z} }} \left( {\varsigma_{x} ,\varsigma_{y} ,t} \right)$; $u_{{q\varsigma_{x} }} = \left( {\frac{{\partial U_{{\varsigma_{x} }} }}{{\partial \varsigma_{z} }}} \right)$; $u_{{q\varsigma_{y} }} = \left( {\frac{{\partial U_{{\varsigma_{y} }} }}{{\partial \varsigma_{z} }}} \right)$; $u_{{r\varsigma_{x} }} = \frac{1}{2}\left( {\partial^{2} U_{{\varsigma_{x} }} /\partial \varsigma_{z}^{2} } \right)$; $u_{{r\varsigma_{y} }} = \frac{1}{2}\left( {\partial^{2} U_{{\varsigma_{y} }} /\partial \varsigma_{z}^{2} } \right)$; $u_{{s\varsigma_{x} }} = \frac{1}{6}\left( {\partial^{3} U_{{\varsigma_{y} }} /\partial \varsigma_{z}^{3} } \right)$; $u_{{s\varsigma_{y} }} = \frac{1}{6}\left( {\partial^{3} U_{{\varsigma_{y} }} /\partial \varsigma_{z}^{3} } \right)$.

In the above relations $u_{{p\varsigma_{x} }}$, $u_{{p\varsigma_{y} }}$, $u_{{p\varsigma_{z} }}$ are displacement parameters at midplane $\varsigma_{z}$ = 0, in all the three-axis directions, i.e., $\varsigma_{x}$, $\varsigma_{y}$, and $\varsigma_{z}$, respectively. The rotation of the normal to the mid surface is denoted by $u_{{q\varsigma_{x} }}$ and $u_{{q\varsigma_{y} }}$ about the $\varsigma_{x}$- and $\varsigma_{y}$-axes, respectively. The higher-order deformation parameters are represented by $u_{{r\varsigma_{x} }}$, $u_{{r\varsigma_{y} }}$, $u_{{s\varsigma_{x} }}$, and $u_{{s\varsigma_{y} }}$.

$$ \left\{ \lambda \right\} = \left[ H \right]\left\{ {\lambda_{n} } \right\} , $$

(2)

$$ \left\{ {\lambda_{n} } \right\} = \left\{ {U_{\varsigma x} U_{\varsigma y} U_{\varsigma z} } \right\}^{T} , $$

$$ \left\{ {\lambda_{n} } \right\} = \left\{ {u_{{p\varsigma_{x} }} u_{{p\varsigma_{y} }} u_{{p\varsigma_{z} }} u_{{q\varsigma_{x} }} u_{{q\varsigma_{y} }} u_{{r\varsigma_{x} }} u_{{r\varsigma_{y} }} u_{{s\varsigma_{x} }} u_{{s\varsigma_{y} }} } \right\}^{T} , $$

(3)

and, $[H] = \left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 0 &\quad {\varsigma_{z} } &\quad 0 &\quad {\varsigma_{z}^{2} } &\quad 0 &\quad {\varsigma_{z}^{3} } &\quad 0 \\ 0 &\quad 1 &\quad 0 &\quad 0 &\quad {\varsigma_{z} } &\quad 0 &\quad {\varsigma_{z}^{2} } &\quad 0 &\quad {\varsigma_{z}^{3} } \\ 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ \end{array} } \right]$.

The linear strain–displacement relation is stated as [46]:

$$ \{ \varepsilon \} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\left( {\partial U_{{\varsigma_{x} }} /\partial \varsigma_{x} } \right) + \left( {U_{{\varsigma_{z} }} /R_{{\varsigma_{x} }} } \right)} \\ {\left( {\partial U_{{\varsigma_{y} }} /\partial \varsigma_{y} } \right) + \left( {U_{{\varsigma_{z} }} /R_{{\varsigma_{y} }} } \right)} \\ {\left( {\partial U_{{\varsigma_{x} }} /\partial \varsigma_{\varsigma y} } \right) + \left( {\partial U_{{\varsigma_{y} }} /\partial \varsigma_{\varsigma x} } \right) + \left( {2U_{{\varsigma_{z} }} /R_{{\varsigma_{xy} }} } \right)} \\ {\left( {\partial U_{{\varsigma_{y} }} /\partial \varsigma_{z} } \right) + \left( {\partial U_{{\varsigma_{z} }} /\partial \varsigma_{y} } \right) - \left( {U_{{\varsigma_{x} }} /R_{{\varsigma_{x} }} } \right)} \\ {\left( {\partial U_{{\varsigma_{x} }} /\partial \varsigma_{z} } \right) + \left( {\partial U_{{\varsigma_{z} }} /\partial \varsigma_{x} } \right) - \left( {U_{{\varsigma_{y} }} /R_{{\varsigma_{y} }} } \right)} \\ \end{array} } \right\} .$$

(4)

2.3 Constitutive relations

The thermoelastic constitutive relations of an SMA-reinforced laminated composite structure (assumed to be in the initial state and not bend due to its own weight/external loading) are assumed identical to [47]:

$$ \left\{ \sigma \right\}^{k} = \left[ Q \right]^{k} \left\{ {\varepsilon - \alpha \times \Delta T} \right\}^{k} + \left( {V_{f}^{k} } \right)\left\{ {\sigma_{RS} } \right\}^{k} , $$

(5)

$$ \left\{ \sigma \right\}^{k} = \left\{ {\left[ Q \right]^{k} \left\{ \varepsilon \right\}^{k} - \left[ Q \right]^{k} \left\{ \alpha \right\}^{k} \Delta T} \right\} + \left\{ {\left( {V_{f}^{k} } \right)\left\{ {\sigma_{RS} } \right\}^{k} } \right\} , $$

(6)

where $\Delta T$ is the change in temperature along with the thickness of the kth composite layer. The matrix $\left[ Q \right]$ is the reduced transformed elastic constant matrix, $\alpha$ is the thermal expansion coefficient, the volume fraction of SMA represented by V_f, $\left\{ \sigma \right\}$ is stress, $\left\{ {\sigma_{RS} } \right\}$ is the recovery stress, strain is denoted by $\varepsilon$.

2.4 Strain energy equations

The total strain energy is defined as

$$ \{ U\} = \{ U_{\varepsilon } \} - \{ U_{T} \} + \{ U_{RS} \} , $$

(7)

where $\{ U\}$ is the total strain energy $\{ U_{\varepsilon } \}$, $\{ U_{T} \}$ and $\{ U_{RS} \}$ are stated as strain energy due to mechanical, thermal, and recovery forces.

The strain energy induced due to them in recovery and in-plane thermal forces are calculated as:

$$ \{ U_{RS} \} = \iint {\{ \overline{\varepsilon }_{G} \}^{T} [D_{{G_{RS} }} ]\{ \overline{\varepsilon }_{G} \} d\varsigma_{x} d\varsigma_{y} } , $$

(8)

$$ \{ U_{T} \} = \iint {\{ \overline{\varepsilon }_{G} \}^{T} [D_{{G_{T} }} ]\{ \overline{\varepsilon }_{G} \} d\varsigma_{x} d\varsigma_{y} } , $$

(9)

$$ \left\{ {U_{\varepsilon } } \right\} = \frac{1}{2}\iint {\sum\limits_{k = 1}^{3} {\left[ {\int\limits_{{Z_{k - 1} }}^{{Z_{k} }} {\left\{ \varepsilon \right\}^{T} \left\{ {\sigma_{\varepsilon } } \right\}d\varsigma_{z} } } \right]} }d\varsigma_{x} d\varsigma_{y} . $$

(10)

Here, the stress due to mechanical load is represented as $\left\{ {\sigma_{\varepsilon } } \right\}$.where, $[D_{{G_{RS} }} ]$ and $[D_{{G_{T} }} ]$ are material property matrix due to recovery and thermal loads, respectively, and $\{ \overline{\varepsilon }_{G} \}$ is the corresponding geometric strain vector.

The recovery force (FRS) generated in the layered composite reinforced with SMA due to temperature change is given by:

$$ F_{RS} = \left\{ {N_{{x_{RS} }} \,\,N_{{y_{RS} }} \,\,N_{{xy_{RS} }} \,\,0\,\,0} \right\}^{T} = \sum\limits_{k = 1}^{3} {\int\limits_{{Z_{k - 1} }}^{{Z_{k} }} {\left( {V_{f}^{k} } \right)\left\{ {\sigma_{RS} \,\,0\,\,0\,\,0\,\,0} \right\}^{T} } d\varsigma_{z} } . $$

(11)

In-plane thermal forces (F_T) are calculated as:

$$ F_{T} = \left\{ {N_{{x_{T} }} \,\,N_{{y_{T} }} \,\,N_{{xy_{T} }} \,\,0\,\,0} \right\}^{T} = \sum\limits_{k = 1}^{3} {\int\limits_{{Z_{k - 1} }}^{{Z_{k} }} {\left( {V_{f}^{k} } \right)\left\{ {\sigma_{T} \,\,0\,\,0\,\,0\,\,0} \right\}^{T} } \,} d\varsigma_{z} . $$

(12)

2.5 Kinetic energy

The kinetic energy ($K_{EG}$) of the composite shell embedded with SMA is obtained using:

$$ K_{EG} = \frac{1}{2}\iint {\left\{ {\sum\limits_{k = 1}^{3} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\rho \left\{ {\dot{\lambda }} \right\}^{T} \left\{ {\dot{\lambda }} \right\}} } d\varsigma_{z} } \right\}}d\varsigma_{x} d\varsigma_{y} , $$

(13)

$$ \begin{aligned} K_{EG} = & \frac{1}{2}\int\limits_{A} {\left\{ {\sum\limits_{k = 1}^{3} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ {\dot{\lambda }_{n} } \right\}^{T} [H]^{T} (\rho )^{k} [H]\left\{ {\dot{\lambda }_{n} } \right\}} } d\varsigma_{z} } \right\}dA} \\ = & \frac{1}{2}\int\limits_{A} {\left\{ {\dot{\lambda }_{n} } \right\}^{T} [m]^{k} \left\{ {\dot{\lambda }_{n} } \right\}dA} , \\ \end{aligned} $$

(14)

$$ [m]^{k} = \sum\limits_{k = 1}^{3} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {[H]^{T} \rho^{k} } [H]d\varsigma_{z} } , $$

where $\rho$, $[H]$, and [m]^k represent the density, thickness coordinate matrix and inertia matrix, respectively.

2.6 External work done

The expression for work done ($\Delta W_{D}$) due to the thermal load, recovery load, and the externally applied mechanical loading can be expressed as

$$ \begin{aligned} \Delta W_{D} = & \iint {\left\{ {\lambda_{n} } \right\}^{T} \left\{ {F_{M} } \right\}d\varsigma_{x} d\varsigma_{y} } + \iint {\left\{ {\lambda_{n} } \right\}^{T} \left\{ {F_{T} } \right\}d\varsigma_{x} d\varsigma_{y} } + \iint {\left\{ {\lambda_{n} } \right\}^{T} \left\{ {F_{RS} } \right\}d\varsigma_{x} d\varsigma_{y} } . \\ \end{aligned} $$

(15)

Solving the above expression gives

$$ \Delta W_{D} = \left\{ {\lambda_{n} } \right\}^{T} \left\{ {F_{M} } \right\} + \left\{ {\lambda_{n} } \right\}^{T} \left\{ {F_{T} } \right\} + \left\{ {\lambda_{n} } \right\}^{T} \left\{ {F_{RS} } \right\}, $$

(16)

where $\Delta W_{M}$ = $\left\{ {\lambda_{n} } \right\}^{T} \left\{ {F_{M} } \right\}$,$\Delta W_{T}$ = $\left\{ {\lambda_{n} } \right\}^{T} \left\{ {F_{T} } \right\}$ and $\Delta W_{RS}$$\left\{ {\lambda_{n} } \right\}^{T} \left\{ {F_{RS} } \right\}$.

Substituting $\Delta W_{M}$,$\Delta W_{T}$ and $\Delta W_{RS}$ in Eq. (16):

$$ \Delta W_{D} = \Delta W_{M} + \Delta W_{T} + \Delta W_{RS} , $$

(17)

where {F_M}, {F_T} and {F_RS} are the mechanical, thermal and recovery load vector.

2.7 Finite element formulation

Finite element method (FEM) steps are used for computational purposes to convert the continuous structural model to a discrete form. In this study, a nine-noded isoperimetric quadrilateral Lagrangian element with nine degrees of freedom per node is used.

The linear mid-plane strain vector in terms of the nodal displacement vector, with finite element approximation, can be written as [48]

$$ \left\{ {\lambda_{0} } \right\} = \sum\limits_{i = 1}^{9} {N_{i} \left\{ {\lambda_{ni} } \right\}} , $$

(18)

where $\left\{ {\lambda_{0} } \right\}$ is the elemental displacement, N_i is the shape function of the ‘ith’ node, and $\left\{ {\lambda_{ni} } \right\} = \left\{ {u_{{p\varsigma_{xi} }} u_{{p\varsigma_{yi} }} u_{{p\varsigma_{zi} }} u_{{q\varsigma_{xi} }} u_{{q\varsigma_{yi} }} u_{{r\varsigma_{xi} }} u_{{r\varsigma_{yi} }} u_{{s\varsigma_{xi} }} u_{{s\varsigma_{yi} }} } \right\}^{T}$ is the nodal displacement vector.

The linear mid-plane strain vector in terms of the nodal displacement vector is rewritten as

$$ \left\{ {\overline{\varepsilon }} \right\} \, = \, \left[ B \right]\left\{ {\lambda_{n} } \right\},\;\;\left\{ {\overline{\varepsilon }_{G} } \right\} \, = \, \left[ {B_{G} } \right]\left\{ {\lambda_{ni} } \right\} , $$

(19)

where [B] and [B_G] are the strain–displacement matrices obtained after introducing the differential operator and nodal polynomial functions, respectively [49] (provided in the Appendix).

2.7.1 Elemetal stiffness matrix

The element-wise strain energy stored in the SMA-reinforced composite panel is computed as:

$$ (U_{\varepsilon } )_{El} = \frac{1}{2}\iint {\left( {\left( {\left[ B \right]\left\{ {\lambda_{ni} } \right\}} \right)^{T} \left[ D \right]\left( {\left[ B \right]\left\{ {\lambda_{ni} } \right\}} \right)} \right)_{El} d\varsigma_{x} d\varsigma_{y} } . $$

(20)

The elemental stiffness matrix $[K_{L} ]_{El} \,$ is:

$$ [K_{L} ]_{El} \, = \int_{ - 1}^{1} {\int_{ - 1}^{1} {[B]^{T} \left[ D \right][B]} } \left| J \right|d\xi d\eta . $$

(21)

2.7.2 Elemental geometric stiffness matrix

The elemental strain energy stored in the composite strengthened SMA embedded structure under the impact of the in-plane thermal loading using Eqs. (8) and (9) is stated as:

$$ \{ U_{T} \}_{El} = \frac{1}{2}\left\{ {\lambda_{ni} } \right\}^{T} [K_{{G_{T} }} ]_{El} \left\{ {\lambda_{ni} } \right\} , $$

(22)

$$ \{ U_{RS} \}_{El} = \frac{1}{2}\left\{ {\lambda_{ni} } \right\}^{T} [K_{{G_{RS} }} ]_{El} \left\{ {\lambda_{ni} } \right\} . $$

(23)

The elemental geometric stiffness matrix of thermal stress $[K_{GT} ]_{{^{El} }}$ is represented as:

$$ [K_{{G_{T} }} ]_{El} \, = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {[B_{G} ]^{T} [D_{{G_{T} }} ][B_{G} ]\left| J \right|d\xi d\eta } } . $$

(24)

The elemental geometric stiffness matrix of recovery stress $[K_{{G_{RS} }} ]_{{^{El} }}$ is represented as:

$$ [K_{{G_{RS} }} ]_{El} \, = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {[B_{G} ]^{T} [D_{{G_{RS} }} ][B_{G} ]\left| J \right|d\xi d\eta } } . $$

(25)

2.7.3 Elemental force matrix

The elementwise work done due to mechanical, thermal, and recovery load is represented as:

$$ W_{El} = \iint {\left\{ {\lambda_{ni} } \right\}^{T} \left\{ {F_{M} } \right\}_{El} } + \iint {\left\{ {\lambda_{ni} } \right\}^{T} \left\{ {F_{T} } \right\}}_{El} + \iint {\left\{ {\lambda_{ni} } \right\}^{T} \left\{ {F_{RS} } \right\}}_{El} , $$

(26)

where $\left\{ {F_{M} } \right\}_{El}$, $\left\{ {F_{T} } \right\}_{El}$ and $\left\{ {F_{RS} } \right\}_{El}$ are mechanical, thermal, recovery load vectors and the corresponding equations are represented as:

$$ \left\{ {F_{M} } \right\}_{El} = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {[N]^{T} \left\{ q \right\}\left| J \right|d\xi d\eta } } , $$

(27)

$$ \left\{ {F_{T} } \right\}_{El} = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left( {\int\limits_{ - h/2}^{ + h/2} {[B_{G} ]^{T} [H_{G} ]^{T} [Q]\left\{ {\varepsilon_{Th} } \right\}d\varsigma_{z} } } \right)} } \left| J \right|d\xi d\eta , $$

(28)

$$ \left\{ {F_{RS} } \right\}_{El} = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left( {\int\limits_{ - h/2}^{ + h/2} {[B_{G} ]^{T} [H_{G} ]^{T} \left\{ {\sigma_{RS} } \right\}\left( {V_{f} } \right)d\varsigma_{z} } } \right)} } \left| J \right|d\xi d\eta . $$

(29)

2.7.4 Elemental mass matrix

The elementwise kinetic energy of laminate can be expressed as:

$$ \left( {K_{EG} } \right)_{El} = \frac{1}{2}\int {\int {\left\{ {\dot{\lambda }_{0} } \right\}^{T} [m]^{k} \left\{ {\dot{\lambda }_{n} } \right\}\,} } d\varsigma_{x} d\varsigma_{y} . $$

(30)

The elemental mass matrix $[M]_{El}$ is expressed as:

$$ [M]_{El} = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {[N]^{T} [m][N]\left| J \right|d\xi d\eta } } . $$

(31)

2.7.5 Governing equations

The equivalent governing equation for the SMA-reinforced composite curved panel obtained using the variational principle is:

$$ \delta \int\limits_{{t_{1} }}^{{t_{2} }} {(\left( {K_{EG} } \right)_{El} - ((U_{\varepsilon } )_{El} + \{ U_{T} \}_{El} + \{ U_{RS} \}_{El} + W_{El} ))dt = 0} , $$

(32)

$$ [K]\left\{ \lambda \right\} + [K_{G} ]\left\{ \lambda \right\} + [M]\left\{ {\ddot{\lambda }} \right\} = \left\{ {F_{M} } \right\} + \left\{ {F_{T} } \right\} - \left\{ {F_{RS} } \right\} , $$

(33)

where $[K]$ and $[M]$ are the overall stiffness and mass matrices of the system. Similarly, $\left\{ {F_{M} } \right\}$,$\left\{ {F_{T} } \right\}$, $\left\{ {F_{RS} } \right\}$ and $\left\{ {\ddot{\lambda }} \right\}$ are the global form of system force and the acceleration vectors, respectively. Additionally, $[K_{G} ]$ represents the geometry stiffness matrix obtained from the distorted form structure due to the excess temperature loading and its detail can be seen in [30].

2.7.6 Free vibration equations

The equilibrium equation of free vibration is represented as:

$$ \left( {\left[ K \right] + \left[ {K_{G} } \right]} \right)\left\{ \lambda \right\} + \left[ M \right]\left\{ {\ddot{\lambda }} \right\} = 0 . $$

(34)

It is rewritten in eigenvector form as:

$$ \left( {\left[ K \right] + \left[ {K_{G} } \right] - \omega_{a}^{2} \left[ M \right]} \right)\left\{ \phi \right\} = 0 , $$

(35)

where $\omega_{a}^{{}}$ and $\phi$ are the eigenvalues and eigenvectors, respectively.

2.8 Crack formation and discretization

A centrally placed crack through the thickness of a laminated composite shell is formulated for numerical analysis. The crack dimensions are considered on the global $\varsigma_{x}$- and $\varsigma_{y}$- axes, and the schematic view of the composite shell panel with crack is shown in Fig. 1. Initially, the first quadrant is discretized via a nine-noded quadrilateral isoparametric element with nine degrees of freedom at each node. Following the same, the first quadrant is mirrored by using an algorithm developed in MATLAB code to acquire the second quadrant. Then the complete view of discretization for the shell panel is obtained by swapping the model about the x-axis shown in Fig. 2.

Fig. 2

Mesh discretization view of laminated composite

2.9 Boundary conditions

The boundary conditions (BC) aid the solution sets of equations by eradicating rigid body motion and decreasing the total number of unknowns, which improves computational efficacy. Hence, Eq. (35) is solved to get the natural frequency data by assuming different sets of end boundary conditions, i.e., CCCC—clamped, SSSS—simply supported, CFFF—cantilever, SCSC—both opposite sides simply supported and clamped, CFCF—both opposite sides clamped and free. The descriptions of the necessary boundary conditions are specified in Table 2.

Table 2 Boundary conditions and displacement values at edges

3 Materials and methods

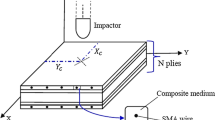
The four-layered laminated plates are fabricated by woven glass fiber (610 GSM) and epoxy (Lapox L12 and K6 hardener) via the popular hand layup technique for the subsequent experimentation (refer to Fig. 3). The detailed step-by-step fabrication process, curing, and required sample preparation can be seen in [50]. Furthermore, the experimental properties are recorded using the steps outlined in the references to concise the explanation [51]. The obtained properties utilized for the experimental frequency analysis of the composite plate are: E₁₁ = 8.01 GPa, E₂₂ = 7.95 GPa, G₁₂ = 2.09 GPa, ѵ = 0.17, ρ = 1587 kg/m³, α = 5 × 10^{–6 1}/°C. After fabrication and property evaluation of these laminates, the specimens are kept in a cantilever boundary condition by a fixture, and an accelerometer (Model no-352C03) is mounted on the laminate panels. An impact hammer (Model No: 086C03) is used to excite an initial shake to the laminate, and the accelerometer records the analogue acceleration signals. Further, the c-DAQ (Model no-c-DAQ-9178) is used to convert the recorded analogue signals to digital signals. The virtual programming platform, i.e., LabVIEW has been utilized the digital form of the frequency responses of the cracked structure is converted into frequency responses via fast Fourier transformations. The actual experimental setup including the associated components for the frequency analysis is shown in Fig. 4. Similarly, the free vibrations of the cracked composite plate under a thermal environment (using lab-scale thermal chamber) are recorded at the temperature difference (ΔT) of 15 °C and 25 °C, respectively. Thus, the experimental natural frequency responses of a laminated composite plate with crack (longitudinal and transverse) under ambient and thermal environments are recorded.

Fig. 3

Materials and fabricated laminated composites

Fig. 4

Experimental test rig for frequency analysis

4 Results and discussion

Further, the physical form of the model is formulated into a mathematical model by utilizing the HSDT method. Then, with the help of FEM, the current model is converted into a computer code and evaluated for the numerical values. The higher-order Finite element model efficacy was investigated by computing the frequency responses of a laminated cracked composite bonded with intelligent material (SMA) at elevated temperatures. Convergence tests for all possible outcomes of cracked laminated composite with and without SMA mated panel, including the thermal Effect is exposed. The model’s validity is verified by comparing the obtained numerical results with the available reference data, and experimental validation is performed. The calculated results and the effects of input parameters on modal responses are thoroughly discussed in the upcoming sections.

4.1 Convergence

The consistency and stability of the obtained natural frequency values are compared for the various mesh sizes. Then, optimal mesh density is selected for the comparison. The convergence analysis for a simply supported cracked laminated composite square plate without SMA (0.1 × 0.1 m, h/a = 0.001 m) has been considered. The frequency values have shown a good agreement at 3 × 3 mesh density, i.e., 72 elements, and diverged hereafter. The difference between the frequency values decreases as the number of elements increases. The convergence results are shown in Table 3. Secondly, the thermal frequency responses of a simply supported laminated composite plate embedded with SMA wires (0.381 × 0.305 × 0.0013 m) have been considered for convergence analysis and found good agreement with the results. The convergence analysis is shown in Table 4, and 3 × 3 mesh density is adopted for this case. The current convergence results show that the natural frequency values indicate a decrease with an increase in elements. It is clear that after a certain range of mesh density, the difference between them is pretty slight, and the deviation is negligible. Increasing the number of elements also gives accurate results, considering the computational time. Thus, it is preferred to adopt (3 × 3), i.e., 72 element mesh, for better outcomes for all the case.

Table 3 Convergence analysis of the natural frequency of layered composite square plate with a central crack

Table 4 Convergence analysis of natural frequency for composite plate embedded with SMA Natural Frequency (rad/sec)

4.2 Validation

Based on the convergence analysis, the model is being extended to perform a validation test for the frequency parameters of cracked laminate. The validation has been done for the numerical and experimental cases for the cracked laminate without SMA under ambient conditions and laminate plate with SMA under thermal conditions. Initially, the obtained numerical values for the cracked laminated composite plate without SMA are compared for validation with the published research data [52] and validated, where the crack is given centrally to the composite plate and considering the (h/a) = 0.01, v = 0.3 and for various crack ratios (c/a). Material properties of the plate are considered from [52]. Comparison results of the validation are given in Table 5.

Table 5 Validation of natural frequency of layered composite square plate with a central crack

A simply supported layered composite plate embedded with SMA is considered, and the dimensions, material properties, and structural input parameters such as SMA material properties, recovery stress, and SMA young’s modulus are obtained from reference [53] for computational purposes. The natural frequency responses of the laminated composite reinforced by SMA wires are numerically obtained for the SMA volume fractions and prestrain as V_f = 10% and ε_pre = 3%. Therefore, the numerical values of natural frequency (rad/sec) are obtained and compared with published data [53] and found in good agreement. The comparison results are shown in Table 6.

Table 6 Validation of thermal frequency of laminated composite plate embedded with SMA

Then, the free vibration analysis for the cracked composite plate was experimentally validated with numerical values under ambient and thermal environments for cantilever boundary conditions. Dimensions for the plate are considered as (0.145 × 0.15 × 0.0023 m) where, crack length is 0.05 m and experimentally evaluated material properties for the composite plate are E₁₁ = 8.01 GPa, E₂₂ = 7.956 GPa, G₁₂ = 2.09 GPa, ѵ = 0.17, ρ = 1587 kg/m³ and α = 5 × 10^–6 1/°C. The frequency analysis for the fabricated layered composite plate under ambient temperature is performed and compared with numerical results for two different cases of crack orientation (longitudinal and transverse). Similarly, the cracked laminated plate is analyzed for free vibrations under a thermal environment, and the temperature difference (ΔT) is set at 15 °C and 25 °C, respectively. From the obtained results, the present numerical results are close to the experimental data for both ambient and thermal conditions. The experimental validation results for the ambient condition of the cracked composite plate are shown in Fig. 5a and b, whereas for the thermal conditions, i.e., (ΔT = 15 °C and ΔT = 25 °C) are shown in Fig. 6a and b, respectively. However, the obtained experimental results deviated from the expected line (≤ 10%) for the natural frequency at 3^rd mode under both thermal conditions.

Fig. 5

Experimental validation of free vibration of the cracked composite plate in ambient condition

Fig. 6

Experimental validation free vibration of cracked laminated composite with elevated temperature

4.3 Additional examples

Finally, the eigenfrequencies of the numerical model are further investigated by considering various structural design parameters such as curvature ratio, boundary conditions, shell geometries, crack ratios, and the volume fraction and prestrain of SMA for the computation of new results. The dimensions of the composite plate are 0.6 m × 0.4 m × 0.005 m, where the crack length (c) is 0.1 m in the center by considering simply supported boundary conditions. The stacking sequence is [0°/90°/90°/0°/0°/90°/90°/0°], curvature ratio is (R/a = 50), and it is analyzed for elevated temperature up to 150 °C (Reference temperature is considered as 21 °C). The material properties for the Epoxy-Graphite and SMA are given in Table 7. The corresponding modulus of elasticity and recovery stress values of SMA [54] are shown in Fig. 7a and b, respectively. These structural/geometrical parameters and material properties are considered throughout these additional examples if not stated otherwise.

Table 7 Thermo-mechanical properties of laminate embedded with SMA

Fig. 7

Recovery stress and Modulus of Elasticity of SMA for Heating case [54]

4.3.1 Effect of prestrain of SMA under elevated temperature

The effect of SMA prestrain and variable temperature ranges have significant impact on the structural modulus and the constraint layer stresses. This prestrain allows the parent structure to resist additional loads or to improve their stiffnesses. The influence of prestrain at various temperature ranges and the thermal frequency responses of curved panels with crack have been investigated in this example. The solutions are computed for the variable prestrain by considering two volume fractions of SMA, i.e., V_f = 10%, and V_f = 20%, as well as different shell geometries GS-C and GS-E, respectively. The frequency responses are shown in Fig. 8(a)-(d). The natural frequency of cracked composite shell panels embedded with shape memory alloy wires is analyzed under a thermal environment ranging from 30 °C to 150 °C. The thermal frequency data of GS-C and GS-E increase while the prestrain increases. The pattern obtained for all the responses plotted in the graph is quite similar for both shell geometries. However, a significant difference can be observed after a certain temperature range, i.e., the curve falls after an apparent rise. The obtained results explain that the SMA fiber actively contributes to modifying structural stiffness up to a specific temperature range and then behaves irresponsive.

• The frequency values for SMA volume fraction V_f = 10%: the rise of the curve continues till 60 °C for ε_pre = 1% and ε_pre = 2% prestrain and 100 °C. Similarly, ε_pre = 3%, a slight downward trend of the curve for both GS-C: Fig. 8a and GS-E: Fig. 8c geometries, respectively.

• The natural frequency values of SMA volume fraction V_f = 20%: the curve indicates a hike of responses till 70 °C for ε_pre = 1%, 90 °C for ε_pre = 2% and 120 °C for ε_pre = 3% prestrain. Further, a slight drop of the frequency parameter is seen for the curve for both GS-C (Fig. 8b) and GS-E (Fig. 8d) geometries.

• The natural frequency values of SMA V_f = 0% and ε_pre = 0%; there is a decline in the curve until up to 150 °C for both GS-C and GS-E geometries.

• The overall frequency enhanced an amount of 5% while SMA volume fractions (V_f) increase from 10 to 20% irrespective of all values of prestrain and shell geometries, i.e., GS-C and GS-E, respectively.

Fig. 8

Natural frequency values of GS-C & GS-E cracked panels by varying Pre-strain of SMA under Thermal environment. (for V_f = 10%, and V_f = 20%)

4.3.2 Effect of volume fraction of SMA under elevated temperature

Because of their high densities, SMA wires improve the stiffness of fiber-reinforced cracked composite panels and improve final responses due to their inherent intelligence when exposed to temperature. The volume fraction of shape memory alloy wire in the composite plays a major role in the resulting frequency values under thermal conditions. The natural frequency values obtained by varying volume fractions of SMA i.e., V_f = 0%, V_f = 10%, V_f = 15%, V_f = 20% with respect to both the prestrain ε_pre = 1% and ε_pre = 3% by considering GS-C and GS-E geometries under thermal environment ranging from 30 °C to 120 °C as shown in Fig. 9a–d. It is clear that the SMA improves overall structural strength due to its unique inherent pseudo elastic property, regardless of geometry or environmental effects.

• The eigenvalues for SMA prestrain ε_pre = 1%; the curve shows a clear spike till 60 °C for V_f = 10%, 70 °C for V_f = 15% and 80 °C for V_f = 20% of volume fractions for both GS-C: Fig. 9a and GS-E: Fig. 9c geometries.

• The eigenvalues for SMA prestrain ε_pre = 3%; the curve shown a clear spike till 100 °C for V_f = 10%, 110 °C for V_f = 15% and 120 °C for V_f = 20% of volume fractions for both GS-C: Fig. 9b and GS-E: Fig. 9d geometries.

• The eigenvalues of SMA V_f = 0% and ε_pre = 0%; there is an apparent dip throughout the curve up to 150 °C for both GS-C and GS-E geometries.

• The percentage improvement of natural frequency is 4% while the prestrain (ε_pre) of the SMA increases from 1 to 3% irrespective of all volume fractions and shell geometries (GS-C and GS-E).

Fig. 9

Natural frequency values of GS-C & GS-E cracked panels by varying volume fraction of SMA under Thermal environment. (ε_pre = 1% and ε_pre = 3%)

4.3.3 Effect of curvature ratio under elevated temperature

The strength of the composite panel depends on the curvature ratio, and the steadiness can be examined with different curvature ratios. The effect of SMA upon the current model is also studied in this example. Furthermore, the impact of the curvature ratio on the SMA-reinforced cracked composite panel on the outcomes can be studied. Two cases of volume fraction and prestrain of SMA, i.e., V_f = 10%, ε_pre = 3% and V_f = 20%, ε_pre = 1% by varying the curvature ratios are (i.e., R/a = 20, 30, 40, 50) is considered for the natural frequency analysis for both the shell geometries GS-C and GS-E under elevated temperatures up to 150 °C as shown in Fig. 10a–d. As the curvature ratio increases, the composite structure becomes flatter, and the stretching energy is reduced compared to the bending for the flat panel.

• The free vibration of the layered composite structure considering the composition of volume fraction and prestrain (V_f = 10%, ε_pre = 3%) of SMA, the curve has shown a sharp hike up to 100 °C and then a gradual decrease in the frequency throughout the curve for all the curvature ratios (R/a). It is noticeable that the obtained curves are pretty similar for both GS-C: Fig. 10a and GS-E: Fig. 10c geometries.

• The free vibration of the composite panel considering the proportion of volume fraction and prestrain (V_f = 20%, ε_pre = 1%) of SMA; the curve has shown a sharp hike up to 70 °C and then a gradual decline in the eigenvalues through the curve for all the curvature ratios (R/a). The obtained arcs are similar for GS-C: Fig. 10b and GS-E: Fig. 10d geometries.

Fig. 10

Natural frequency values of GS-C & GS-E cracked panels by varying curvature ratio under Thermal environment (considering V_f = 10%, ε_pre = 3% and V_f = 20%, ε_pre = 1%)

4.3.4 Effect of boundary conditions under elevated temperature

The necessary boundary conditions transform the physical form of the structure to mathematical form and reduce the number of unknowns. The natural frequency values for a few boundary conditions have been analyzed in the study. Considering volume fraction and prestrain (V_f = 10%, ε_pre = 3%) of SMA under elevated temperature for both GS-C and GS-E geometries shown in Fig. 11a and b. The cracked composite panel’s natural frequency with various end boundary conditions (i.e., CCCC, SCSC, CFFF, CFCF) is considered for the analysis. The obtained curves are pretty similar and follow a similar pattern for GS-C and GS-E’s shell geometries. Clamped condition (CCCC) has been the highest, and cantilever condition (CFFF) has been the lowest in terms of the eigenvalues for GS-C and GS-E.

• The free vibration values for both CCCC and SCSC, the curve has risen to 60 °C and then shown a slight decline throughout the curve for both the geometries GS-C and GS-E.

• The free vibration for CFCF has shown an apparent rise till 110 °C and gradual fall afterward. And this boundary condition showed a consistent increase comparatively with other boundary conditions. Also, the application of SMA is active up to 110 °C for both the geometries GS-C and GS-E.

• The free vibration values of the CFFF boundary condition have shown an apparent fall from an initial point to throughout the curve for both the geometries GS-C and GS-E.

Fig. 11

Natural frequency values of GS-C & GS-E cracked panels by varying Boundary conditions under Thermal environment (CCCC, SCSC, CFFF, CFCF)

4.3.5 Effect of shell geometry under elevated temperature

The geometry of the shell panels is used to classify them rather than their load-bearing capacity. Furthermore, geometrical shapes provide additional stiffness and improve stiffness parameters. The natural frequency analysis of the SMA bonded cracked composite layered shell panel is analyzed under thermal environment for all the shell geometries (i.e., GS-A, GS-B.GS-C, GS-D, GS-E) considering both cases of volume fraction and pre-strain of SMA, i.e., V_f = 10%, ε_pre = 3% and V_f = 20%, ε_pre = 1% shown in Fig. 12a and b.

• The frequency values of the first case, i.e., V_f = 10%, ε_pre = 3%, have shown an evident rise in the curve up to 100 °C for all shell geometries, and then the slope decreased gradually till the end of the curve.

• The frequency values of the second case, i.e., V_f = 20%, ε_pre = 1%. All shell geometries have shown a rise up to 70 °C and then have declined throughout the curve.

Fig. 12

Natural frequency values of cracked panels with SMA by varying all shell geometries under thermal environment. (considering V_f = 10%, ε_pre = 3% and V_f = 20%, ε_pre = 1%

4.3.6 Effect of crack ratio under elevated temperature

The layered composite structure embedded with shape memory alloy wires without any crack is analyzed for the free vibration analysis. The crack length is varied based on crack ratio, i.e., c/a ratio, where ‘c’ is known as crack length and considered crack ratios ((c/a) = 0, 0.25, 0.5, 0.75, 1). The effect of crack on the composite structure can be clearly studied for the panels GS-C and GS-E, as shown in Fig. 13a and b, respectively. The volume fraction and prestrain of SMA in the structure V_f = 10%, ε_pre = 3% under simply supported boundary conditions are considered. This analysis shows a clear understanding of the behavior of cracked laminate under elevated temperatures. The comparison study of the composite laminate with crack ratios and without crack is analyzed. It is understood that the frequency values decrease as the crack length increases, and the maximum frequency values have been obtained for the laminate without a crack. This analysis also found that the presence of SMA on the laminate can help the material stiffen up to a specific temperature range afterward the application of SMA is deactivated. The obtained results are shown in a similar pattern for both the geometries. The natural frequency responses are indirectly proportional to the crack ratio (c/a).

• The frequency values have raised up to 100 °C when there is no crack given to the material, and the SMA is active and obtained highest frequency values for both the cases and lowest frequency values are recorded for crack ratio (c/a = 1).

• Thereafter the frequency values raised up to 110 °C for c/a = 0.25, 120 °C for c/a = 0.5, 130 °C for both c/a = 0.75 and c/a = 1. Then, after a slight decline in the curve in all the above cases after the particular temperature range. These results show the composite’s SMA activation, which creates a balanced stiffness opposite to the crack. This is due to the inherent capacity of pseudo-elastic smart material SMA

Fig. 13

Natural frequency values of cracked laminate with SMA by varying crack ratios (c/a) under thermal environment. (considering V_f = 10%, ε_pre = 3% and V_f = 20%, ε_pre = 1%)

5 Conclusions

This study uses a higher-order polynomial model to analyze the cracked layered composite shell panel’s finite element thermal frequency responses embedded with SMA fibers. The numerical results are computed using a homemade computer (MATLAB) code based on the current mathematical model. Using Hamilton’s principle, the state space equation of motion is derived, and isoparametric FE steps further reduce the order. A series of numerical experiments were used to validate the model’s efficacy and stability. Furthermore, the model’s accuracy was confirmed by comparing cracked laminated composite’s predicted numerical frequency responses with experimental values for ambient and thermal conditions. Finally, the model has been engaged to compute different numbers of numerical examples considering the variable structural geometrical parameters, boundary conditions, shell geometries, volume fraction and prestrain of SMA, crack ratios (c/a), and influence of elevated temperature. The obtained results are discussed for the current model, and the analytical observations from these results are listed below:

• The validation and convergence cases indicate that the current numerical solution stability and accuracy follow the good agreement.

• These examples show that structural stiffness is directly proportional to the volume fraction of SMA. However, it is limited to a specific temperature range before SMA is inactive. Similarly, the pre-strain of SMA and its respective recovery stress contribute to an increase in overall structural stiffness under elevated temperature.

• This study proposes a unique approach, i.e., the natural frequency analysis of cracked laminate by reinforcing smart material SMA. The detailed analysis of various parameters has been deliberately discussed individually.

• SMA plays a significant role in improving laminate stiffness and the results obtained are in the desired line and exhibited the impact of shape memory alloy over the cracked shell panel.

Appendix

Individual terms of matrix [B]:

[B]_1,1 = $\partial /\partial x$, [B]_1,3 = $1/R_{x}$, [B]_2,2 = $\partial /\partial y$, [B]_2,3 = $1/R_{y}$, [B]_3,1 = $\partial /\partial y$, [B]_3,2 = $\partial /\partial x$, [B]_3,3 = $2/R_{xy}$, [B]_4,1 = $- 1/R_{x}$, [B]_4,3 = $\partial /\partial x$, [B]_4,4 = 1, [B]_5,2 = $- 1/R_{y}$, [B]_5,3 = $\partial /\partial x$, [B]_5,5 = 1, [B]_6,4 = $\partial /\partial x$, [B]_7,5 = $\partial /\partial y$, [B]_8,4 = $\partial /\partial y$, [B]_8,5 = $\partial /\partial x$, [B]_9,4 = $- 1/R_{x}$, [B]_9,6 = 2, [B]_10,5 = $- 1/R_{y}$, [B]_10,7 = 2, [B]_11,6 = $\partial /\partial x$, [B]_12,7 = $\partial /\partial y$, [B]_13,6 = $\partial /\partial y$, [B]_13,7 = $\partial /\partial x$, [B]_14,6 = $- 1/R_{x}$, [B]_14,8 = 2, [B]_15,7 = $- 1/R_{y}$, [B]_15,9 = 2, [B]_16,8 = $\partial /\partial x$, [B]_17,9 = $\partial /\partial y$, [B]_18,8 = $\partial /\partial y$, [B]_18,9 = $\partial /\partial x$,[B]_19,8 = $- 1/R_{x}$, [B]_20,9 = $- 1/R_{y}$.

Individual terms of matrix [B_G]:

[B_G]_1,1 = $\partial /\partial x$, [B_G]_1,3 = $1/R_{x}$, [B_G]_2,1 = $\partial /\partial y$, [B_G]_3,2 = $\partial /\partial x$, [B_G]_4,2 = $\partial /\partial y$, [B_G]_4,3 = $1/R_{y}$, [B_G]_5,1 = $- 1/R_{x}$, [B_G]_5,3 = $\partial /\partial x$, [B_G]_6,2 = $- 1/R_{y}$, [B_G]_6,3 = $\partial /\partial y$, [B_G]_7,4 = $\partial /\partial x$, [B_G]_8,4 = $\partial /\partial y$, [B_G]_9,5 = $\partial /\partial x$, [B_G]_10,5 = $\partial /\partial y$, [B_G]_11,4 = $- 1/R_{x}$, [B_G]_12,5 = $- 1/R_{y}$, [B_G]_13,6 = $\partial /\partial x$, [B_G]_14,6 = $\partial /\partial y$, [B_G]_15,7 = $\partial /\partial x$, [B_G]_16,7 = $\partial /\partial y$, [B_G]_17,6 = $- 1/R_{x}$, [B_G]_18,7 = $- 1/R_{y}$, [B_G]_19,8 = $\partial /\partial x$, [B_G]_20,8 = $\partial /\partial y$, [B_G]_21,9 = $\partial /\partial x$, [B_G]_22,9 = $\partial /\partial y$, [B_G]_23,8 = $- 1/R_{x}$, [B_G]_24,9 = $- 1/R_{y}$.