1 Introduction

In recent years, carbon nanotubes (CNTs) have become promising structures for diverse fields such as medicine, engineering, and agriculture due to their advantageous mechanical, thermal, electrical, and chemical characteristics, leading to many practical applications, such as nano-electro-mechanical systems, nano-devices for drug delivery, and chemical nanosensors [1,2,3,4,5,6,7,8,9,10,11]. As reported by other researchers, continuum-based theories have been used to study the mechanical behavior of CNTs because techniques such as molecular dynamic simulations are expensive and time-consuming [12,12,13,14,15,16].

Once the dimensions of structures become very small, the size effect should be taken into account in both theoretical and experimental investigations [16,17,18,19,20,21,22,23]. It is worth mentioning that classical continuum elasticity [24,25,26] is not capable of predicting the mechanical behavior of nano- and micro-structures because it does not take into account size effects. Thus, different non-classical continuum elasticity theories, including nonlocal elasticity [27,28,29,30], modified couple stress theory [31,32,33,34], and strain gradient theory (SGT) [35,36,37,38,39], have been developed for capturing the size effects in nano- and micro-structures. However, the nonlocal elasticity presented by Eringen [40] has been applied to investigate the size-dependent mechanical response of nano-beams [41, 42] and nano-plates [43,44,45,46].

Understanding the vibration characteristics of nanostructures is still a substantial area of study for many researchers. In the last decades, significant attention has been devoted to mechanical vibration and stability of single and multi-walled CNTs [12, 28, 47,48,49,50,51,52,53,54,55,56,57,58], nanoplates [43, 45, 59,60,61,62,63,64,65,66], and nanoshells [67,68,69,70,71,72,73]. In the work presented by Thai [74], bending, buckling, and vibration of Euler–Bernoulli nanobeams were investigated using the nonlocal theory of Eringen. In that study, Hamilton’s principle was used to extract the equations of motion and boundary conditions, which were solved analytically. Concerning Euler–Bernoulli beam theory with the consideration of the von Kármán geometric nonlinearity, Gheshlaghi and Hasheminezhad [75] investigated the effects of surface energy on the nonlinear vibration of micro- and nanobeams. Hao and Jian [76] analyzed the effects of internal moving viscoelastic fluid on the natural frequency of SWCNTs with clamped–clamped end conditions using the differential quadrature method and with consideration of the constitutive equation of a viscoelastic fluid via a Maxwell non-Newtonian fluid model. Lu et al. [77] developed a size-dependent sinusoidal shear deformation beam model to assess the free vibration of nanobeams utilizing strain gradient theory, in which the influences of the nonlocal parameter, material length scale parameter, slenderness ratio, and shear deformation were studied. Ghadiri et al. [78] researched free vibration analysis of functionally graded rotating nanobeams considering surface effects using the nonlocal theory of Eringen. Ansari and Arash [79] analyzed the vibration of double-walled carbon nanotubes using a nonlocal elastic shell model taking into account the van der Waals forces between tubes. They studied the effects of nonlocal parameters, layerwise boundary conditions, and geometrical parameters on the natural frequencies of the double-walled carbon nanotubes. Considering first-order shear deformation theory, Imani Aria and Friswell [80] presented a nonlocal finite element model for the analysis of free vibration of functionally graded (FG) nanobeams, in which the material properties were assumed to obey a power-law function. Based on Euler–Bernoulli beam model and nonlocal theory, Zhang et al. [81] analyzed the transverse vibration of double-walled carbon nanotubes resting on a viscoelastic foundation subjected to a longitudinal magnetic field. Xu et al. [82] carried out research on free vibrations of a double-walled carbon nanotube taking into account van der Waals effects between the inner and outer tubes; the results obtained from their study showed the effects of different boundary conditions, including cantilever, fixed-simple, and fixed–fixed. Atashafrooz et al. [83] carried out the vibration and instability analysis of carbon nanotubes conveying nano-flow taking into account surface effects according to the nonlocal strain gradient theory. Taking Gurtin–Murdoch's theory into account, they derived the nonlocal governing equations of motion using Hamilton's principle, solved by Galerkin's approach. In their study, the effects of the nonlocal parameters, surface effects, and Knudsen number on the natural frequency and critical flow velocity of carbon nanotubes were examined. Ansari et al. [84] carried out an analysis of the torsional vibration of carbon nanotubes utilizing the strain gradient theory and molecular dynamics simulations to capture the size effects. In that study, the governing equation and boundary conditions were deduced using Hamilton's principle, and solved by the generalized differential quadrature method. Also, they carried out molecular dynamic simulations for carbon nanotubes with different aspect ratios and boundary conditions. Taking nonlocal elasticity and the Timoshenko beam model into account, Wang et al. [85] studied the influences of the nonlocal parameter, axial load, and elastic medium on flexural waves in carbon nanotubes.

Investigation of curved pipes conveying fluid considering extensible [86] and inextensible [87] theories is difficult compared to straight pipes [88, 89] because of the configuration of the curved pipes. Therefore, less effort has been devoted to research on the dynamics and stability of fluid-conveying curved pipes in both large-scale and small-scale structures, and most of the existing literature is associated with the dynamic behavior of straight ones. In early studies performed by Chen [90,91,92], a linear model and exact solution for the analysis of in-plane and out-of-plane vibration and stability of fluid-conveying curved pipes was reported based on the “conventional” inextensible theory in which the initial forces due to the centrifugal and pressure forces produced by the internal fluid are neglected. Afterward, Misra et al. [87] proposed a “modified” inextensible theory which consists of the assumption of inextensibility of the centerline of the tube as in the conventional inextensible theory, but the steady-state initial forces due to the centrifugal and pressure forces are also taken into consideration. As reported more recently, Dini et al. [93] analyzed hygro-thermo-mechanical vibration and stability of curved double-walled carbon nanotubes conveying fluid, using Eringen’s nonlocal theory and the “conventional” inextensible theory. They examined the influences of different chirality, van der Waals interaction coefficient, nonlocal parameter, magnetic field, and visco-elastic foundation coefficients on the natural frequencies and stability of the curved carbon nanotubes. Malikan et al. [94] studied the dynamic response of non-cylindrical curved viscoelastic SWCNTs using nonlocal strain gradient elasticity, wherein a modified shear deformation beam theory was utilized to extract the governing equations of motion, solved by the Galerkin analytical method. In another work, Karami and Farid [95] introduced a new formulation for curved CNTs containing flowing fluid to investigate their in-plane free vibration using Eringen’s nonlocal elasticity theory and the finite element method, wherein the influences of the nonlocal parameter and the curvature of the pipe on the natural frequency and critical flow velocity were studied. Tang et al. [96] performed a three-dimensional vibration analysis of curved micro-pipes conveying fluid with fixed–fixed end conditions by employing the modified couple stress theory and Hamilton’s principle. Regarding the inextensible theory of curved pipes, Ghavanloo et al. [97] performed a free vibration analysis of fluid-conveying curved CNTs embedded in a viscoelastic foundation, modeled as a linear elastic cylindrical tube. In their study, they discretized the nonlocal equations of motion with the aid of the finite element method and obtained the natural frequencies by solving a quadratic eigenvalue problem. In another work, Mehdipour et al. [98] reported an elastic beam model for nonlinear vibration of a CSWCNT embedded in a Pasternak elastic medium utilizing the nonlocal continuum mechanics.

To the best of the authors’ knowledge, in the available literature there has been no attempt toward analyzing the in-plane and out-of-plane thermo-mechanical vibrations of curved single-walled carbon nanotubes conveying fluid based on nonlocal elasticity and the “modified” inextensible theory. The modified inextensibility of the tube developed by Misra et al. [87] has not been considered heretofore by other researchers to analyze the dynamical behavior of curved nano-beams. Thus, after deriving the governing equations using Hamilton’s principle, the differential quadrature method is applied to the nonlocal equations of motion and boundary conditions to obtain the natural frequencies of the CSWCNT for clamped–clamped end conditions. Finally, the effects of the nonlocal parameter, thermal and magnetic fields, fluid velocity, angle of the tube, and elastic foundation coefficients on the vibration response of the CSWCNT are reported.

2 Electrodynamic Maxwell’s relations

In this Section, Maxwell’s relations are presented. Taking \({\varvec{J}}\) as the current density, \({\varvec{h}}\) as the distributing vector of the magnetic field, \({\varvec{e}}\) as strength vector of the electric field, and \(\eta\) as magnetic permeability, Maxwell’s equations for an elastic body are given by [99, 100]:

$${\varvec{J}}=\nabla \times {\varvec{h}},$$
(1.1)
$$\nabla \times {\varvec{e}}=-\eta \frac{\partial {\varvec{h}}}{\partial t},$$
(1.2)
$$\nabla .{\varvec{h}}=0,$$
(1.3)
$${\varvec{e}}=-\eta \left(\frac{\partial {\varvec{U}}}{\partial t}\times {\varvec{H}}\right),$$
(1.4)
$${\varvec{h}}=\nabla \times \left({\varvec{U}}\times {\varvec{H}}\right)$$
(1.5)

wherein \(\nabla =\frac{\partial }{\partial x}{{\varvec{e}}}_{{\varvec{x}}}+\frac{1}{r}\frac{\partial }{\partial \theta }{{\varvec{e}}}_{{\varvec{\theta}}}+\frac{\partial }{\partial z}{{\varvec{e}}}_{{\varvec{z}}}\) is the Laplace operator in cylindrical coordinates and \(\left({{\varvec{e}}}_{{\varvec{x}}},{{\varvec{e}}}_{{\varvec{\theta}}},{{\varvec{e}}}_{{\varvec{z}}}\right)\) are the base vectors. For the present analysis, the magnetic and displacement fields in cylindrical coordinates \(\left(x,\theta ,z\right)\) are, respectively, considered as vectors \({\varvec{H}}=\left(0,{H}_{\theta },0\right)\) and \({\varvec{U}}=\left(u,w,v\right)\). Therefore,

$${\varvec{J}}=\nabla \times {\varvec{h}}=\frac{{H}_{\theta }}{{r}^{2}}\left(\frac{{\partial }^{2}v}{\partial {\theta }^{2}}\right){{\varvec{e}}}_{{\varvec{x}}}+\frac{{H}_{\theta }}{{r}^{2}}\left(\frac{\partial v}{\partial \theta }\right){{\varvec{e}}}_{{\varvec{\theta}}}-\frac{{H}_{\theta }}{{r}^{2}}\left(\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right){{\varvec{e}}}_{{\varvec{z}}}$$
(2)

in which \(u(\theta ,t)\), \(w(\theta ,t)\), and \(v(\theta ,t)\) indicate displacement components of the mid-surface in the radial, circumferential and axial directions \((x, \theta ,z)\), respectively. Therefore, \({\varvec{f}}\) is Lorentz’s force which may be expressed as follows:

$${\varvec{f}}={f}_{x}{{\varvec{e}}}_{{\varvec{x}}}+{f}_{\theta }{{\varvec{e}}}_{{\varvec{\theta}}}+{f}_{z}{{\varvec{e}}}_{{\varvec{z}}}=\eta \left({\varvec{J}}\times {\varvec{H}}\right)=\frac{\eta {H}_{\theta }^{2}}{{r}^{2}}\left(\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right){{\varvec{e}}}_{{\varvec{x}}}+\frac{\eta {H}_{\theta }^{2}}{{r}^{2}}\left(\frac{{\partial }^{2}v}{\partial {\theta }^{2}}\right){{\varvec{e}}}_{{\varvec{z}}}$$
(3)

in which \({f}_{x}\), \({f}_{\theta }\), and \({f}_{z}\) are Lorentz’s forces in the radial, circumferential, and axial direction, respectively.

3 Nonlocal elasticity theory

As introduced by Eringen [40, 101], the stress at a reference point \(x\) is assumed to be a function of the strain field at every point \({x}^{^{\prime}}\) in an elastic body \(V\). According to Eringen’s study, the basic equations of nonlocal theory for a linear and homogeneous elastic solids may be given as follows:

$${\sigma }_{ij}(x)=\int \alpha \left(\left|x-{x}^{^{\prime}}\right|,\mu \right){C}_{ijkl}{\varepsilon }_{kl}\left({x}^{^{\prime}}\right)dV\left({x}^{^{\prime}}\right),\quad \forall x\in V,$$
(4.1)
$${\sigma }_{ij,j}=0,$$
(4.2)
$${\varepsilon }_{ij}=\frac{1}{2}\left({u}_{i,j}+{u}_{j,i}\right)$$
(4.3)

where \({C}_{ijkl}\) is the elastic modulus tensor for classical isotropic elasticity, \({\sigma }_{ij}\) and \({\varepsilon }_{ij}\) are the stress and strain tensors at point \(x\), respectively, \({u}_{i}\) is the displacement vector, \(\alpha \left(\left|x-{x}^{^{\prime}}\right|, \mu \right)\) is the nonlocal modulus or attenuation function incorporating into the constitutive equations the nonlocal effects at the reference point \(x\) produced by local strain at the source \({x}^{^{\prime}},\) \(\left|x-{x}^{^{\prime}}\right|\) is the distance in Euclidean form, and \(\mu\) is a material constant that depends on the internal (e.g., lattice parameter, granular size, the distance between C–C bonds) and external characteristic lengths (e.g., crack length, wavelength) [102]. A simplified equation in differential form is used as a basis of all nonlocal constitutive formulations because the integral constitutive Eq. (4.1) is difficult to solve. Therefore, a nonlocal differential equation based on Eq. (4.1) is defined as:

$$\left(1-{\mu }^{2}{l}^{2}{\nabla }^{2}\right){\varvec{\sigma}}={\varvec{C}}:{\varvec{\varepsilon}}, \mu ={e}_{0}a/l$$
(5)

wherein ‘\(:\)’ represents the double dot product. The parameter \(\left({e}_{0}a\right)\) is the scale coefficient leading to small-scale effects on the response of the nano-scaled structures.

4 Thermo-mechanical vibration of nonlocal CSWCNT model

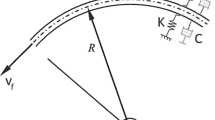
As shown in Fig. 1, a curved carbon nanotube with curvature \(R\), mass per unit length \({m}_{t}\), elastic modulus \(E\), moment of inertia \(I\), and cross-sectional area \(A\) is considered, and it is embedded in a Kelvin–Voigt elastic foundation which consists of a spring and a damper in parallel. It contains flowing fluid with mass per unit length \({m}_{f}\) and constant velocity \({v}_{f}\). Based on the curved Euler–Bernoulli beam theory, the circumferential strain for the CSWCNT can be expressed as [103]:

Fig. 1
figure 1

Schematic of a curved single-walled carbon nanotube conveying fluid

Full size image
$${\varepsilon }_{\theta \theta }={\varepsilon }^{0}+x{k}^{0}, {\varepsilon }^{0}=\frac{1}{R}\left[-u+\frac{\partial w}{\partial \theta }\right], {k}^{0}=\frac{1}{{R}^{2}}\left(\frac{\partial w}{\partial \theta }+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right).$$
(6)

Also, the nonlocal constitutive Eq. (5) can be approximated for the CSWCNT as follows:

$${\sigma }_{\theta \theta }-{\mu }^{2}{\nabla }^{2}{\sigma }_{\theta \theta }=E{\varepsilon }_{\theta \theta }$$
(7)

in which \({\sigma }_{\theta \theta }\) and \({\varepsilon }_{\theta \theta }\) are circumferential stress and circumferential strain, respectively. Given the assumption that there is no extension of the centerline of the CSWCNT, then \(u\) and \(w\) can be related by [91]:

$$u=\frac{\partial w}{\partial \theta }.$$
(8)

The strain energy of the CSWCNT (\(\prod_{t}\)) is given by [92]:

$$\prod_{t} = \int\limits_{0}^{\alpha } {\left[ {M_{N} \left( {R\phi - \frac{{\partial^{2} v}}{{\partial \theta^{2} }}} \right) + M_{Z} \left( {\frac{{\partial^{2} u}}{{\partial \theta^{2} }} + \frac{\partial w}{{\partial \theta }}} \right) + M_{T} \left( {\frac{\partial v}{{\partial \theta }} + R\frac{\partial \phi }{{\partial \theta }}} \right)} \right]Rd\theta }$$
(9)

where \(\alpha\) and \(\phi\) are the total angle of the CSWCNT and twist angle, respectively. Also, \(M_{i}\) is the bending moment in the nanotube which can be given by [92]:

$${M}_{N}-\frac{{\mu }^{2}}{{R}^{2}}\frac{{{\partial }^{2}M}_{N}}{\partial {\theta }^{2}}=\frac{EI}{{R}^{2}}\left[R\phi -\frac{{\partial }^{2}v}{\partial {\theta }^{2}}\right],$$
(10.1)
$${M}_{z}-\frac{{\mu }^{2}}{{R}^{2}}\frac{{{\partial }^{2}M}_{z}}{\partial {\theta }^{2}}=\frac{EI}{{R}^{2}}\left[\frac{\partial w}{\partial \theta }+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right],$$
(10.2)
$${M}_{T}-\frac{{\mu }^{2}}{{R}^{2}}\frac{{{\partial }^{2}M}_{T}}{\partial {\theta }^{2}}=\frac{GJ}{{R}^{2}}\left[R\frac{\partial \phi }{\partial \theta }+\frac{\partial v}{\partial \theta }\right].$$
(10.3)

Also, the work done by external forces is:

$${W}_{ext}={W}_{m}+{W}_{kv}+{W}_{T}$$
(11)

in which \({W}_{m}\), \({W}_{kv}\), and \({W}_{T}\) are the work done by the external magnetic field, the Kelvin–Voigt viscoelastic foundation, and thermal loading, respectively, expressed as

$${W}_{m}={\int }_{0}^{\alpha }\left({f}_{x}u+{f}_{z}v\right)Rd\theta,$$
(12.1)
$${W}_{kv}={\int }_{0}^{\alpha }\left(-{P}_{kv}^{u}u-{P}_{kv}^{v}v\right)Rd\theta,$$
(12.2)
$${W}_{T}=\frac{1}{2}{\int }_{0}^{\alpha }\left(\frac{{N}_{T}}{{R}^{2}}\right)\left[{\left(\frac{\partial u}{\partial \theta }\right)}^{2}+{\left(\frac{\partial v}{\partial \theta }\right)}^{2}\right]Rd\theta$$
(12.3)

in which \({N}_{T}=EA\epsilon \Delta T\) is the normal force induced by a temperature change \(\Delta T\), and \(\epsilon\) is the thermal expansion coefficient. Also, in Eq. (12.2) we have

$${P}_{kv}^{u}={C}_{kv}\frac{\partial u}{\partial t}+{K}_{kv}u ; {P}_{kv}^{v}={C}_{kv}\frac{\partial v}{\partial t}+{K}_{kv}v.$$
(13)

The kinetic energy of the CSWCNT \(\left({K}_{t}\right).\) can be given by

$$K_{t} = \frac{{m_{t} }}{2}\mathop \smallint \limits_{0}^{\alpha } \left\{ {\left[ {\left( {\frac{{\partial u}}{{\partial t}}} \right)^{2} + \left( {\frac{{\partial w}}{{\partial t}}} \right)^{2} + \left( {\frac{{\partial v}}{{\partial t}}} \right)^{2} } \right]} \right\}Rd\theta.$$
(14)

Also, the kinetic energy of the flowing fluid \(\left({K}_{f}\right)\) is defined as [92]:

$$K_{f} = \frac{{m_{f} }}{2}\mathop \smallint \limits_{0}^{\alpha } \left[ {v_{f}^{2} + \left( {\frac{{\partial u}}{{\partial t}}} \right)^{2} + \left( {\frac{{\partial w}}{{\partial t}}} \right)^{2} + \left( {\frac{{\partial v}}{{\partial t}}} \right)^{2} + 2v_{f} \frac{{\partial w}}{{\partial t}} + \frac{{2v_{f} }}{R}\left( {\frac{{\partial u}}{{\partial \theta }} + w} \right)\frac{{\partial u}}{{\partial t}} + \frac{{2v_{f} }}{R}\frac{{\partial v}}{{\partial t}}\frac{{\partial v}}{{\partial \theta }} + \frac{{v_{f}^{2} }}{{R^{2} }}\left( {\frac{{\partial u}}{{\partial \theta }} + w} \right)^{2} + \frac{{v_{f}^{2} }}{{R^{2} }}\left( {\frac{{\partial v}}{{\partial \theta }}} \right)^{2} } \right]Rd\theta.$$
(15)

The nonlocal governing equations and boundary conditions of the CSWCNT can be derived from Hamilton’s principle based on the following relation:

$$\int\limits_{0}^{t} {\delta \left( {W_{ext} + K_{t} + K_{f} - \prod_{f} - \prod_{t} } \right)dt = 0}.$$
(16)

It is worth mentioning that the potential energy of the fluid is zero (\(\prod_{f} = 0\)) because the fluid is incompressible. By substituting Eqs. (9) and (11)–(15) into Eq. (16) and using Eq. (8), integrating by parts and setting the coefficients of \(\delta w,\delta v\), and \(\delta \phi\) to zero, the nonlocal equations of motion are obtained as

$$\delta w: \frac{1}{R}\frac{{\partial }^{3}{M}_{z}}{\partial {\theta }^{3}}+\frac{1}{R}\frac{\partial {M}_{z}}{\partial \theta }+{m}_{f}R\left[\frac{{\partial }^{4}w}{\partial {\theta }^{2}\partial {t}^{2}}-\frac{{\partial }^{2}w}{\partial {t}^{2}}\right]+2{m}_{f}{\vartheta }_{f}\left[\frac{{\partial }^{2}w}{\partial {\theta }^{3}\partial t}+\frac{{\partial }^{2}w}{\partial \theta \partial t}\right]+\frac{{m}_{f}{\vartheta }_{f}^{2}}{R}\left[\frac{{\partial }^{4}w}{\partial {\theta }^{4}}+2\frac{{\partial }^{2}w}{\partial {\theta }^{2}}+w\right]+R\frac{\partial {P}_{kv}^{u}}{\partial \theta }-R\frac{\partial {f}_{x}}{\partial \theta }+\frac{N}{R}\frac{{\partial }^{4}w}{\partial {\theta }^{4}}+{m}_{t}R\left[\frac{{\partial }^{4}w}{\partial {\theta }^{2}\partial {t}^{2}}-\frac{{\partial }^{2}w}{\partial {t}^{2}}\right]=0,$$
(17.1)
$$\delta v: \frac{1}{R}\frac{{\partial }^{2}{M}_{N}}{\partial {\theta }^{2}}+\frac{1}{R}\frac{\partial {M}_{T}}{\partial \theta }-{m}_{f}R\frac{{\partial }^{2}v}{\partial {\theta }^{2}}-2{m}_{f}{\vartheta }_{f}\frac{{\partial }^{2}v}{\partial \theta \partial t}-\frac{{m}_{f}{\vartheta }_{f}^{2}}{R}\frac{{\partial }^{2}v}{\partial {\theta }^{2}}-R{P}_{kv}^{v}+{f}_{z}R-\frac{N}{R}\frac{{\partial }^{2}v}{\partial {\theta }^{2}}-{m}_{t}R\frac{{\partial }^{2}v}{\partial {t}^{2}}=0,$$
(17.2)
$$\delta \phi : -{M}_{N}+\frac{\partial {M}_{T}}{\partial \theta }=0.$$
(17.3)

Combining Eq. (17) with Eq. (10) and after some manipulations, the nonlocal equations of motion for in-plane vibration and out-of-plane vibration can be given as follows.

4.1 In-plane vibration

$$\left[1-{\mu }^{2}\left(\frac{{m}_{f}{v}_{f}^{2}}{EI}+\frac{N}{EI}-\frac{\eta A{R}^{2}{H}_{\theta }^{2}}{EI}\right)\right]\frac{{\partial }^{6}w}{\partial {\theta }^{6}}+\left[2-\frac{{\mu }^{2}{m}_{f}{v}_{f}^{2}}{EI}-\left({\mu }^{2}-{R}^{2}\right)\left(\frac{{m}_{f}{v}_{f}^{2}}{EI}\right)-{\mu }^{2}\frac{{K}_{kv}{R}^{2}}{EI}-\frac{\eta A{R}^{2}{H}_{\theta }^{2}}{EI}+\frac{N{R}^{2}}{EI}\right]\frac{{\partial }^{4}w}{\partial {\theta }^{4}}+\left[1-\left({\mu }^{2}-{R}^{2}\right)\frac{{m}_{f}{v}_{f}^{2}}{EI}+\frac{{m}_{f}{v}_{f}^{2}{R}^{2}}{EI}+\frac{{K}_{kv}{R}^{4}}{EI}\right]\frac{{\partial }^{2}w}{\partial {\theta }^{2}}+\frac{{m}_{f}{v}_{f}^{2}{R}^{2}}{EI}w-\frac{{R}^{2}{\mu }^{2}\left({m}_{t}+{m}_{f}\right)}{EI}\frac{{\partial }^{6}w}{\partial {\theta }^{4}\partial {t}^{2}}-\frac{{R}^{4}\left({m}_{t}+{m}_{f}\right)}{EI}\frac{{\partial }^{2}w}{\partial {t}^{2}}+\frac{{R}^{2}\left({m}_{t}+{m}_{f}\right)\left({\mu }^{2}+{R}^{2}\right)}{EI}\frac{{\partial }^{4}w}{\partial {\theta }^{2}\partial {t}^{2}}-\frac{2R{m}_{f}{v}_{f}{\mu }^{2}}{EI}\frac{{\partial }^{6}w}{\partial {\theta }^{5}\partial t}-\frac{2R{m}_{f}{v}_{f}\left({\mu }^{2}-{R}^{2}\right)}{EI}\frac{{\partial }^{4}w}{\partial {\theta }^{3}\partial t}+\frac{2{R}^{3}{m}_{f}{v}_{f}}{EI}\frac{{\partial }^{2}w}{\partial \theta \partial t}-{\mu }^{2}\frac{{C}_{kv}{R}^{2}}{EI}\frac{{\partial }^{5}w}{\partial {\theta }^{4}\partial t}+\frac{{C}_{kv}{R}^{4}}{EI}\frac{{\partial }^{3}w}{\partial {\theta }^{2}\partial t}+\Pi \left(\frac{{\partial }^{4}w}{\partial {\theta }^{4}}+2\frac{{\partial }^{2}w}{\partial {\theta }^{2}}+w\right)-{\mu }^{2}\Pi \left(\frac{{\partial }^{6}w}{\partial {\theta }^{6}}+2\frac{{\partial }^{4}w}{\partial {\theta }^{4}}+\frac{{\partial }^{2}w}{\partial {\theta }^{2}}\right)=0.$$
(18)

4.2 Out-of-plane vibration

$$\frac{EI}{{R}^{2}}\left[R\varphi -\frac{{\partial }^{2}v}{\partial {\theta }^{2}}\right]-\frac{GJ}{{R}^{2}}\left[R\frac{{\partial }^{2}\phi }{\partial {\theta }^{2}}+\frac{{\partial }^{2}v}{\partial {\theta }^{2}}\right]=0,$$
(19.1)
$$\left[1+\frac{{\mu }^{2}}{{R}^{2}}\left(\frac{\eta A{H}_{\theta }^{2}{R}^{2}}{EI}-\frac{{m}_{f}{v}_{f}^{2}{R}^{2}}{EI}-\frac{N{R}^{2}}{EI}\right)\right]\frac{{\partial }^{4}v}{\partial {\theta }^{4}}+\left[-\frac{GJ}{EI}-\frac{{m}_{f}{v}_{f}^{2}{R}^{2}}{EI}-{\mu }^{2}\frac{{K}_{kv}{R}^{2}}{EI}-\frac{\eta A{H}_{\theta }^{2}{R}^{2}}{EI}+\frac{N{R}^{2}}{EI}\right]\frac{{\partial }^{2}v}{\partial {\theta }^{2}}-\left[1+\frac{GJ}{EI}\right]R\frac{{\partial }^{2}\phi }{\partial {\theta }^{2}}-\frac{{R}^{2}{\mu }^{2}\left({m}_{t}+{m}_{f}\right)}{EI}\frac{{\partial }^{4}v}{\partial {\theta }^{2}\partial {t}^{2}}-\frac{2{\mu }^{2}{m}_{f}{v}_{f}R}{EI}\frac{{\partial }^{4}v}{\partial {\theta }^{3}\partial t}+\frac{{R}^{4}\left({m}_{t}+{m}_{f}\right)}{EI}\frac{{\partial }^{2}v}{\partial {t}^{2}}+\frac{2{m}_{f}{v}_{f}{R}^{3}}{EI}\frac{{\partial }^{2}v}{\partial \theta \partial t}-{\mu }^{2}\frac{{C}_{kv}{R}^{2}}{EI}\frac{{\partial }^{3}v}{\partial {\theta }^{2}\partial t}+\frac{{K}_{kv}{R}^{4}}{EI}v+\frac{{C}_{kv}{R}^{4}}{EI}\frac{\partial v}{\partial t}+\Pi \left(\frac{{\partial }^{2}v}{\partial {\theta }^{2}}\right)-{\mu }^{2}\Pi \left(\frac{{\partial }^{4}v}{\partial {\theta }^{4}}\right)=0.$$
(19.2)

It is notable that \(\Pi\) is the steady-state combined force depending on the fluid flow velocity. In the modified-inextensible theory, in which \(\Pi\) is taken into account, the internal flow is only subject to a Coriolis force, whereas in the conventional inextensible theory, the internal flow is subject to the centrifugal, and Coriolis forces and the combined force \(\Pi\) is negligible. If both ends of the CSWCNT are supported and the gravity effect is ignored, then \(\Pi =-{v}_{f}^{2}\) [87]. Moreover, if the nonlocal parameter \(\mu\) is neglected and the effects of the thermal loading, magnetic field, and elastic foundation are absent, Eqs. (18) and (19) reduce to those obtained by Misra et al. [87]. Hence, by introducing the following dimensionless parameters:

$$\bar{w} = \frac{w}{R},~~\bar{v} = \frac{v}{R},~~\bar{\mu } = \frac{\mu }{R},~~\beta = \frac{{m_{f} }}{{m_{t} + m_{f} }},~~\vartheta = \sqrt {\frac{{m_{f} }}{{EI}}} Rv_{f} ,~~\tau = \sqrt {\frac{{EI}}{{m_{t} + m_{f} }}} \frac{t}{{R^{2} }}~,~~\bar{K}_{{kv}} = \frac{{K_{{kv}} R^{4} }}{{EI}},~~\bar{C}_{{kv}} = \frac{{C_{{kv}} R^{2} }}{{\sqrt {EI\left( {m_{t} + m_{f} } \right)} }}~,~~K = \frac{{GJ}}{{EI}}~,~~\bar{N} = \frac{{N_{T} R^{2} }}{{EI}}~,~~\bar{H}_{\theta } = \frac{{\eta AR^{2} H_{\theta }^{2} }}{{EI}},$$
(20)

the nonlocal equations of motion for the CSWCNT are given in dimensionless form as follows:

4.3 In-plane vibration

$$\left[1-{\overline{\mu }}^{2}\left({\vartheta }^{2}+\overline{N }-{\overline{H} }_{\theta }\right)\right]\frac{{\partial }^{6}\overline{w}}{\partial {\theta }^{6}}+\left[2-{\overline{\mu }}^{2}{\vartheta }^{2}-\left({\overline{\mu }}^{2}-1\right){\vartheta }^{2}-{\overline{\mu }}^{2}{\overline{K} }_{kv}+\overline{N }-{\overline{H} }_{\theta }\right]\frac{{\partial }^{4}\overline{w}}{\partial {\theta }^{4}}+\left[1-\left({\overline{\mu }}^{2}-1\right){\vartheta }^{2}+{\vartheta }^{2}+{\overline{K} }_{kv}\right]\frac{{\partial }^{2}\overline{w}}{\partial {\theta }^{2}}+{\vartheta }^{2}\overline{w }-{\overline{\mu }}^{2}\frac{{\partial }^{6}\overline{w}}{\partial {\theta }^{4}\partial {\tau }^{2}}+\left({\overline{\mu }}^{2}+1\right)\frac{{\partial }^{4}\overline{w}}{\partial {\theta }^{2}\partial {\tau }^{2}}-\frac{{\partial }^{2}\overline{w}}{\partial {\tau }^{2}}-2{\overline{\mu }}^{2}\vartheta \sqrt{\beta }\frac{{\partial }^{6}\overline{w}}{\partial {\theta }^{5}\partial \tau }-2\left({\overline{\mu }}^{2}-1\right)\vartheta \sqrt{\beta }\frac{{\partial }^{4}\overline{w}}{\partial {\theta }^{3}\partial \tau }+2\vartheta \sqrt{\beta }\frac{{\partial }^{2}\overline{w}}{\partial \theta \partial \tau }-{\overline{\mu }}^{2}{\overline{C} }_{kv}\frac{{\partial }^{5}\overline{w}}{\partial {\theta }^{4}\partial \tau }+{\overline{C} }_{kv}\frac{{\partial }^{3}\overline{w}}{\partial {\theta }^{2}\partial \tau }+\Pi \left(\frac{{\partial }^{4}\overline{w}}{\partial {\theta }^{4}}+2\frac{{\partial }^{2}\overline{w}}{\partial {\theta }^{2}}+\overline{w }\right)-{\overline{\mu }}^{2}\Pi \left(\frac{{\partial }^{6}\overline{w}}{\partial {\theta }^{6}}+2\frac{{\partial }^{4}\overline{w}}{\partial {\theta }^{4}}+\frac{{\partial }^{2}\overline{w}}{\partial {\theta }^{2}}\right)=0.$$
(21)

4.4 Out-of-plane vibration

$$\frac{{\partial }^{2}\overline{v}}{\partial {\theta }^{2}}-\phi +K\left(\frac{{\partial }^{2}\phi }{\partial {\theta }^{2}}+\frac{{\partial }^{2}\overline{v}}{\partial {\theta }^{2}}\right)=0,$$
(22.1)
$$\left[1+{\overline{\mu }}^{2}\left({\overline{H} }_{\theta }-{\vartheta }^{2}-\overline{N }\right)\right]\frac{{\partial }^{4}\overline{v}}{\partial {\theta }^{4}}+\left[-K-{\overline{\mu }}^{2}{\overline{K} }_{kv}+{\vartheta }^{2}-{\overline{H} }_{\theta }+\overline{N }\right]\frac{{\partial }^{2}\overline{v}}{\partial {\theta }^{2}}-\left(1+K\right)\frac{{\partial }^{2}\phi }{\partial {\theta }^{2}}+{\overline{K} }_{kv}\overline{v }-{\overline{\mu }}^{2}\frac{{\partial }^{4}\overline{v}}{\partial {\theta }^{2}\partial {\tau }^{2}}-2{\overline{\mu }}^{2}\vartheta \sqrt{\beta }\frac{{\partial }^{4}\overline{v}}{\partial {\theta }^{3}\partial \tau }+\frac{{\partial }^{2}\overline{v}}{\partial {\tau }^{2}}+2\vartheta \sqrt{\beta }\frac{{\partial }^{2}\overline{v}}{\partial \theta \partial \tau }-{\overline{\mu }}^{2}{\overline{C} }_{kv}\frac{{\partial }^{3}\overline{v}}{\partial {\theta }^{2}\partial \tau }+{\overline{C} }_{kv}\frac{\partial \overline{v}}{\partial \tau }+\Pi \left(\frac{{\partial }^{2}\overline{v}}{\partial {\theta }^{2}}\right)-{\overline{\mu }}^{2}\Pi \left(\frac{{\partial }^{4}\overline{v}}{\partial {\theta }^{4}}\right)=0.$$
(22.2)

The clamped–clamped boundary conditions are also described as follows.

In-plane vibration

Out-of-plane vibration

(23)

\(\left.\begin{array}{c}w=0\\ u=0\\ \frac{\partial u}{\partial \theta }=0\end{array}\right\} at \theta =0, \alpha ;\)

\(\left.\begin{array}{c}v=0\\ \frac{\partial v}{\partial \theta }=0\\ \phi =0\end{array}\right\} at \theta =0, \alpha ;\)

5 Differential quadrature method

Recently, the differential quadrature method (DQM) has been increasingly utilized for solving linear and nonlinear partial differential equations and is steadily emerging as an important discretization technique [100,101,106]. One of the most eminent benefits of the DQM is that it can yield extremely precise approximations with a few grid points, becoming a promising choice in comparison to different numerical solution techniques [107, 108]. The DQM has been successfully applied to diverse problems, introducing detailed formulations to solve linear and nonlinear differential equations [108]. The nature of the DQM is that the partial derivatives of a function of a space variable at a given point are approximated by a weighted linear summation of the function values at all discrete points in the domain. Consequently, the nth order derivative of function \(f(x)\) at a discrete point \({x}_{i}\) can be obtained by the weighted linear sum of the function values as [109]

$${\left.\frac{{d}^{n}f}{d{x}^{n}}\right|}_{x={x}_{i}}=\sum_{j=1}^{N}{A}_{ij}^{\left(n\right)}f({x}_{j});\quad ( i=\mathrm{1,2},\dots ,N)$$
(24)

where \({A}_{ij}^{(n)}\) is the weighting coefficient of the nth order derivative and \(N\) is the number of grid points. For the first derivative, the weighting coefficients can be obtained by [109]

$${A}_{ij}^{\left(1\right)}=\frac{L({x}_{i})}{({x}_{i}-{x}_{j})L({x}_{j})};\quad (i,j=\mathrm{1,2},\dots ,N; i\ne j)$$
(25)

in which \(L({x}_{i})\) is given as:

$$L({x}_{i})=\prod_{j=1, j\ne i}^{N}({x}_{i}-{x}_{j}).$$
(26)

For the second-order and higher-order derivatives, the weighting coefficients are approximated as [109]

$${A}_{ij}^{\left(n\right)}=n\left({A}_{ii}^{\left(n-1\right)}{A}_{ij}^{\left(1\right)}-\frac{{A}_{ij}^{\left(n-1\right)}}{({x}_{i}-{x}_{j})}\right); (i,j=\mathrm{1,2},\dots ,N; i\ne j ; n=\mathrm{2,3},\dots ,N-1),$$
(27)
$${A}_{ii}^{\left(n\right)}=-\sum_{j=1, j\ne i}^{N}{A}_{ij}^{\left(n\right)}; (i,j=\mathrm{1,2},\dots ,N; n=\mathrm{2,3},\dots ,N-1).$$
(28)

An effective method for selecting the grid points is obtained by employing the following equation:

$${r}_{i}=a+\frac{1}{2}\left[1-cos\left(\frac{\left(i-1\right)\pi }{N-1}\right)\right](b-a); (i=\mathrm{1,2},\dots ,N)$$
(29)

where \(a\) and \(b\) are the first and last interval. A set of algebraic equations is given by applying the DQM to the nonlocal equations of motion and associated boundary conditions. Therefore, Eqs. (21) and (22) are approximated by using DQM as follows.

5.1 In-plane vibration

$$\sum_{j=1}^{N}\left\{\left[1-{\overline{\mu }}^{2}\left({\vartheta }^{2}+\overline{N }-{\overline{H} }_{\theta }\right)-{\overline{\mu }}^{2}\Pi \right]{A}_{ij}^{(6)}+\left[2-{\overline{\mu }}^{2}{\vartheta }^{2}-\left({\overline{\mu }}^{2}-1\right){\vartheta }^{2}-{\overline{\mu }}^{2}{\overline{K} }_{kv}+\overline{N }-{\overline{H} }_{\theta }+\Pi (1-{2\overline{\mu }}^{2})\right]{A}_{ij}^{(4)}+\left[1-\left({\overline{\mu }}^{2}-1\right){\vartheta }^{2}+{\vartheta }^{2}+{\overline{K} }_{kv}+\Pi (2-{\overline{\mu }}^{2})\right]{A}_{ij}^{(2)}\right\}{W}_{j}+\sum_{j=1}^{N}\left\{-{\overline{\mu }}^{2}{A}_{ij}^{\left(4\right)}+\left({\overline{\mu }}^{2}+1\right){A}_{ij}^{\left(2\right)}\right\}{\ddot{W}}_{j}+\sum_{j=1}^{N}\left\{-2{\overline{\mu }}^{2}\vartheta \sqrt{\beta }{A}_{ij}^{\left(5\right)}-2\left({\overline{\mu }}^{2}-1\right)\vartheta \sqrt{\beta }{A}_{ij}^{\left(3\right)}+2\vartheta \sqrt{\beta }{A}_{ij}^{\left(1\right)}-{\overline{\mu }}^{2}{\overline{C} }_{kv}{A}_{ij}^{\left(4\right)}+{\overline{C} }_{kv}{A}_{ij}^{\left(2\right)}\right\}{\dot{W}}_{j}+\left({\vartheta }^{2}+\Pi \right){W}_{i}-{\ddot{W}}_{i}=0.$$
(30.1)

5.2 Out-of-plane vibration

$$\sum_{j=1}^{N}\left\{\left(1+K\right){B}_{ij}^{\left(2\right)}{V}_{j}+K{C}_{ij}^{\left(2\right)}{\phi }_{j}\right\}-{\phi }_{i}=0,$$
(30.2)
$$\sum_{j=1}^{N}\left\{\left[1+{\overline{\mu }}^{2}\left({\overline{H} }_{\theta }-{\vartheta }^{2}-\overline{N }\right)-{\overline{\mu }}^{2}\Pi \right]{B}_{ij}^{\left(4\right)}+\left[-K-{\overline{\mu }}^{2}{\overline{K} }_{kv}+{\vartheta }^{2}-{\overline{H} }_{\theta }+\overline{N }+\Pi \right]{B}_{ij}^{\left(2\right)}\right\}{V}_{j}-\sum_{j=1}^{N}\left(1+K\right){C}_{ij}^{\left(2\right)}{\phi }_{j}+\sum_{j=1}^{N}\left\{-{\overline{\mu }}^{2}{B}_{ij}^{\left(2\right)}{\ddot{V}}_{j}+\left(-2{\overline{\mu }}^{2}\vartheta \sqrt{\beta }{B}_{ij}^{\left(3\right)}+2\vartheta \sqrt{\beta }{B}_{ij}^{\left(1\right)}-{\overline{\mu }}^{2}{\overline{C} }_{kv}{B}_{ij}^{\left(2\right)}\right){\dot{V}}_{j}\right\}+{\ddot{V}}_{i}+{\overline{C} }_{kv}{\dot{V}}_{i}+{\overline{K} }_{kv}{V}_{i}=0$$
(30.3)

By applying DQM in the domain and boundary, a set of equations is obtained as follows:

$$\left[\begin{array}{cc}{K}_{dd}& {K}_{db}\\ {K}_{bd}& {K}_{bb}\end{array}\right]\left\{ \begin{array}{c}\left\{{U}_{d}\right\}\\ \left\{{U}_{b}\right\}\end{array} \right\}+\left[\begin{array}{cc}{C}_{dd}& {C}_{db}\\ {C}_{bd}& {C}_{bb}\end{array}\right]\left\{ \begin{array}{c}\left\{{\dot{U}}_{d}\right\}\\ \left\{{\dot{U}}_{b}\right\}\end{array} \right\}+\left[\begin{array}{cc}{M}_{dd}& {M}_{db}\\ {M}_{bd}& {M}_{bb}\end{array}\right]\left\{ \begin{array}{c}\left\{{\ddot{U}}_{d}\right\}\\ \left\{{\ddot{U}}_{b}\right\}\end{array} \right\}=0$$
(31)

wherein the subscript \(b\) denotes elements associated with the boundary points, whereas subscript \(d\) indicates elements related to internal points. Also, the dot denotes differentiation with respect to time. The solution of Eq. (31) is assumed as

$$\left\{U\right\}=\left\{\overline{U}\right\}\mathrm{exp }(\omega \tau )$$
(32)

where \(\left\{ {\overline{U}} \right\} = \left\{ { \begin{array}{*{20}c} {\left\{ {\overline{U}_{d} } \right\}} \\ {\left\{ {\overline{U}_{b} } \right\}} \\ \end{array} } \right\}\) is an undetermined function of amplitude, and \(Im\left( \omega \right)\) is the natural frequency of the CSWCNT. Substituting Eq. (32) into Eq. (31), a homogeneous equation is obtained,

$$\left({\omega }^{2}\left[M\right]+\omega \left[C\right]+[K]\right)\left\{{\overline{U} }_{d}\right\}=0,$$
(33)

in which

$$M={M}_{dd}-{M}_{db}{K}_{bb}^{-1}{K}_{bd}; C={C}_{dd}-{C}_{db}{K}_{bb}^{-1}{K}_{bd}; K={K}_{dd}-{K}_{db}{K}_{bb}^{-1}{K}_{bd}.$$
(34)

A non-trivial solution of Eq. (33) is achieved by setting the determinant of the coefficient matrix equal to zero, that is

$$det\left({\omega }^{2}\left[M\right]+\omega \left[C\right]+[K]\right)=0.$$
(35)

The natural frequencies of the fluid-conveying CSWCNT exposed to thermal and magnetic loadings can be obtained by approximating the eigenvalues of Eq. (35).

6 Simulation results and discussion

6.1 Verification of the GDQ method

The convergence of the GDQ method is first examined for a reliable solution. Regarding Fig. 2, a convergence investigation is performed to determine the 3rd mode natural frequency of the CSWCNT. It is obvious that once a sufficient number of nodes (\({N}_{GDQ}\)) is utilized, the natural frequency of the CSWCNT does not change remarkably. Therefore, the number of nodes \({N}_{GDQ}=20\) is considered for assurance and increasing the accuracy of results. It can be observed that the GDQ method can produce highly accurate approximations with a few grid points compared to other numerical methods.

Fig. 2
figure 2

The convergence of grid points for the 3rd mode in-plane natural frequency, (\(\alpha =\uppi ,\upbeta =0.5, \overline{\upmu }={\overline{\mathrm{K}} }_{\mathrm{kv}}={\overline{\mathrm{C}} }_{\mathrm{kv}}=\overline{\mathrm{N} }={\overline{\mathrm{H}} }_{\uptheta }=0\))

Full size image

In addition, it is necessary to verify and confirm the GDQ method by comparing results with those given by Ref. [87] for in-plane and out-of-plane vibrations. To this end, the results are represented in Fig. 3 for a curved tube conveying fluid (\(\beta =0.5\)) in the absence of thermal loading, magnetic field, an elastic foundation (\(\overline{\mu }={\overline{K} }_{kv}={\overline{C} }_{kv}=\overline{N }={\overline{H} }_{\theta }=0\)), and a total angle \(\alpha =\pi\). Also, it should be pointed out that in all simulation results the clamped–clamped end conditions are considered for both in-plane and out-of-plane motions. It is obvious from Fig. 3 that the results obtained from the GDQ method are in a good agreement with those obtained by Ref. [87], showing the high precision of the GDQ.

Fig. 3
figure 3

Dimensionless frequency versus dimensionless flow velocity for in-plane and out-of-plane motions: a comparison between the present method and Ref. [87], (\(\alpha =\uppi ,\upbeta =0.5, \overline{\upmu }={\overline{\mathrm{K}} }_{\mathrm{kv}}={\overline{\mathrm{C}} }_{\mathrm{kv}}=\overline{\mathrm{N} }={\overline{\mathrm{H}} }_{\uptheta }=0\))

Full size image

It should be pointed out that in the “conventional” inextensible theory, where the steady-state combined force \(\Pi\) is ignored, the influence of internal flow on the natural frequencies includes the centrifugal and Coriolis forces. Nevertheless, in the “modified” inextensible theory which considers the steady-state combined force \(\Pi\), the internal flow exerts only a Coriolis force. In the absence of gravity and when both ends of the CSWCNT are supported, the combined force is considered as \(\Pi =-{\vartheta }^{2}\) [87], and so the terms related to the combined force cancel out those arising from the centrifugal force [87]. Therefore, in the “modified” inextensible theory presented here, the CSWCNT does not lose stability as the flow velocity increases, whereas in the “conventional” inextensible theory used by Dini et al. [93] and Chen [90,91,92] the natural frequency decreases by increasing the flow velocity, vanishing at a certain critical velocity for both in-plane and out-of-plane motions, implying the onset of a static buckling-type instability.

6.2 Frequency analysis of the CSWCNT

In this Section, the size-dependent dynamical behavior for in-plane and out-of-plane vibrations of a CSWCNT conveying fluid is presented. Numerical studies are carried out to examine the effects of the nonlocal parameter, thermal loading, magnetic field, elastic foundation, and velocity of the fluid on the dimensionless in-plane and out-of-plane natural frequencies of the CSWCNT. To this end, the following dimensionless parameters are assumed for the calculations:

$$\overline{\mu } = 0.2, \beta = \overline{N} = 0.5, \overline{C}_{kv} = \overline{K}_{kv} = \overline{H}_{\theta } = 1, K = R = 1, \alpha = \pi.$$

To study the effects of the total angle and flow velocity, Fig. 4 reveals how the 3rd mode natural frequency of the CSWCNT varies for different values of the angle and flow velocity. As shown, it is clear that as the angle and flow velocity increase, the CSWCNT becomes more flexible and the dimensionless in-plane and out-of-plane natural frequencies are reduced. In addition, it can be concluded that the values of the natural frequency for out-of-plane motion are significantly lower than for in-plane motion.

Fig. 4
figure 4

The effects of total angle and flow velocity on the 3rd mode natural frequency of the CSWCNT conveying fluid: a in-plane vibration, b out-of-plane vibration, (\(\overline{\upmu }=0.2,\upbeta =\overline{\mathrm{N} }=0.5, {\overline{\mathrm{K}} }_{\mathrm{kv}}={\overline{\mathrm{C}} }_{\mathrm{kv}}=1\))

Full size image

The dimensionless natural frequency for different modes versus the dimensionless flow velocity is plotted in Fig. 5 which reveals the effects of nonlocal parameters on the frequency of the CSWCNT. Increasing the nonlocal parameters leads to decreasing the dimensionless in-plane and out-of-plane natural frequencies which results in a reduction in the stiffness of the system. A comparison between the in-plane and out-of-plane vibrations shows that the values of the natural frequency for in-plane vibrations are higher than those obtained for out-of-plane vibrations.

Fig. 5
figure 5

The effects of nonlocal parameters on the dimensionless natural frequency of the CSWCNT conveying fluid: a in-plane vibration, b out-of-plane vibration, (\(\alpha =\uppi ,\upbeta =\overline{\mathrm{N} }=0.5, {\overline{\mathrm{K}} }_{\mathrm{kv}}={\overline{\mathrm{C}} }_{\mathrm{kv}}={\overline{\mathrm{H}} }_{\uptheta }=1\))

Full size image

Figure 6 depicts the effects of the thermal field on the dimensionless natural frequency of the CSWCNT for both in-plane and out-of-plane motions. It can be observed from Fig. 6 that the dimensionless in-plane and out-of-plane natural frequencies decrease by raising the thermal field, leading to declining stiffness of the system.

Fig. 6
figure 6

The effects of the thermal field on the dimensionless natural frequency of the CSWCNT conveying fluid: a in-plane vibration, b out-of-plane vibration, (\(\alpha =\uppi , \overline{\upmu }=0.2,\upbeta =0.5, {\overline{\mathrm{K}} }_{\mathrm{kv}}={\overline{\mathrm{C}} }_{\mathrm{kv}}={\overline{\mathrm{H}} }_{\uptheta }=1\))

Full size image

The effects of magnetic field intensity on the dimensionless natural frequency of the CSWCNT conveying fluid for both in-plane and out-of-plane motions are plotted in Fig. 7. It is obvious that an increase in the magnetic field intensity leads to a growth in the dimensionless in-plane and out-of-plane natural frequencies which results in raising the stiffness of the system.

Fig. 7
figure 7

The effects of the magnetic field on the dimensionless natural frequency of the CSWCNT conveying fluid: a in-plane vibration, b out-of-plane vibration, (\(\alpha =\uppi , \overline{\upmu }=0.2,\upbeta =\overline{\mathrm{N} }=0.5, {\overline{\mathrm{K}} }_{\mathrm{kv}}={\overline{\mathrm{C}} }_{\mathrm{kv}}=1\))

Full size image

To realize the effects of the damping and stiffness coefficients of the Kelvin–Voigt elastic foundation, Fig. 8 shows how the natural frequency of the CSWCNT varies concerning different values of the flow velocity. As depicted in Fig. 8, it is obvious that once stiffness and damping coefficients are chosen as \({\overline{K} }_{kv}=8\) and \({\overline{C} }_{kv}=1\) (i.e., \({\overline{K} }_{kv}>{\overline{C} }_{kv}\)), the dimensionless natural frequency is increased for both in-plane and out-of-plane motions, leading to an increase in the stiffness of the CSWCNT. Also, considering stiffness and damping coefficients as \({\overline{K} }_{kv}=1\) and \({\overline{C} }_{kv}=8\) (i.e., \({\overline{C} }_{kv}>{\overline{K} }_{kv}\)) results in a reduction in the dimensionless in-plane and out-of-plane natural frequencies, meaning that the CSWCNT becomes more flexible.

Fig. 8
figure 8

The effects of the visco-elastic foundation on the dimensionless natural frequency of the CSWCNT conveying fluid: a in-plane vibration, b out-of-plane vibration, (\(\alpha =\uppi , \overline{\upmu }=0.2,\upbeta =\overline{\mathrm{N} }=0.5, {\overline{\mathrm{H}} }_{\uptheta }=1\))

Full size image

7 Conclusions

The paper aimed to develop a curved Euler–Bernoulli beam model based on nonlocal elasticity to examine in-plane and out-of-plane motions of a curved single-walled carbon nanotube conveying fluid and subjected to thermal loading and magnetic field. The “modified” inextensible theory was used in which the extension of the centerline of the tube is assumed to be negligible, but the initial or steady-state combined force due to the centrifugal and pressure forces is taken into account. The in-plane and out-of-plane nonlocal equations of motion and boundary conditions were derived using Hamilton’s principle. The GDQ method was utilized to obtain the natural frequencies of in-plane and out-of-plane vibrations. A comparison study was performed to verify the method and results with those given in the literature and increase the accuracy of the results. It was observed that the GDQ method can produce highly accurate approximations with a few grid points compared to other numerical methods. The effects of the small-scale parameter, total angle, flow velocity, thermal loading, elastic medium, and magnetic field were evaluated on the in-plane and out-of-plane motions. In the light of the foregoing observations, it can be inferred that the natural frequency of the CSWCNT conveying fluid is sensitive to the changes in the nonlocal parameter, thermal loading, magnetic field intensity, flow velocity, angle, and elastic medium coefficients. It was evident that for both in-plane and out-of-plane motions the natural frequency is decreased by raising the small-scale parameter and thermal loading, whereas it increases by raising the magnetic field intensity. Furthermore, it was observed that the dimensionless in-plane and out-of-plane natural frequencies decrease with increasing the flow velocity and total angle, leading to a reduction in the stiffness of the system. In addition, by using the “modified” inextensible theory for the nonlocal elasticity of Eringen, it was predicted that the CSWCNT supported at both ends does not lose stability with an increase in the flow velocity, as reported also by Misra et al. using classical elasticity.