On the free vibration and design optimization of a shape memory alloy hybrid laminated composite plate

Abstract

A shape memory alloy (SMA) is a temperature-dependent smart material that can be used to tune the stiffness of structures in a thermal environment. In the present article, vibrations of hybrid laminated composite plates reinforced with shape memory alloy fibers under temperature change are studied. Parametric free vibration analysis is conducted to study the effect of the SMA volume fraction, SMA fibers prestrain, length-to-width ratio, and thickness-to-length ratio on the fundamental natural frequency and critical thermal buckling temperature of the hybrid plate subject to fully clamped and fully simply supported boundary conditions. With the objective of maximizing the fundamental natural frequency of the hybrid plate, for the first time, simultaneously, the optimum stacking sequence of the hybrid plate and the best layers to embed the shape memory alloy fibers are found. Interestingly, the study shows that the notion of embedding SMA fibers in the composite plate does not guarantee an increase in the fundamental natural frequency. Depending on the stacking sequence and the layers in which the SMA fibers are embedded, adverse effects might happen. It is shown that inserting the SMA fibers in layers close to the mid-plane maximizes the fundamental natural frequency of the plate.

1 Introduction

Shape memory alloys (SMAs) have attracted the attention of many scientists due to their unique functional properties. The two most well-known properties of SMAs are their shape memory effect and their super-elasticity, which are regaining a predetermined shape after unloading and heating and exhibiting a large amount of recoverable inelastic deformation after unloading, respectively [1,2,3].

Embedding SMA fibers in composites is one of the most promising advances in aerospace, marine, and civil engineering [4]. The dynamic analysis of composite structures reinforced with SMA fibers has long attracted the attention of researchers. Rogers et al. used SMA wires to control the frequency of a graphite/epoxy laminated beam based on active strain energy tuning and active property tuning [5]. Birman [6] studied the effect of composite and SMA stiffeners on the stability of composite cylindrical shells and rectangular plates subjected to compressive load. It was concluded that in plates and long shallow shells, SMA stiffeners are more efficient than composite ones. Finite element analysis was carried out by Lau [7] to obtain the vibrational characteristic of SMA composite beams with various boundary conditions. It was shown that the natural frequencies and the damping ratio of smart composite beams with SMA fibers increase as the temperature rises. Park et al. [8] studied the vibrational behavior of thermally buckled composite plates reinforced with SMA fibers. They showed that using SMA fibers in composite plates increases their critical temperature. Zhang et al. [9] studied the dynamic characteristics of a laminated composite plate containing a woven SMA layer and unidirectional SMA wires both experimentally and theoretically. Using a finite element method, Kuo et al. [10] showed that inserting SMA fibers in the mid-plane of a laminated composite plate improves its buckling load. Kim et al. [11] numerically studied the low-velocity impact behavior of composite plates reinforced with thin films of SMA. Asadi et al. [12, 13] studied free vibration of a shape memory alloy hybrid composite (SMAHC) beam and the thermal stability of a geometrically imperfect SMAHC plate reinforced with SMA. They showed that by proper use of SMA fibers, the thermal bifurcation could be delayed and thermal post-buckling deflection can be controlled. Dehkordi et al. [14] performed a nonlinear transient dynamic analysis on a sandwich plate with a flexible core and laminated composite sheets with embedded SMA wires. They proposed a mixed layerwise and equivalent single-layer model and used Brinson’s constitutive model for SMA fibers. Using the Ritz method, Mahabadi et al. [15] studied the effect of the orientation of reinforcing SMA fibers on the fundamental natural frequency of an SMAHC plate. Developing a meshless method, Nazari et al. [16] performed the free vibration analysis of a hybrid sandwich composite plate consisting of shape memory alloy wires, functionally graded face sheets, and fiber-reinforced composite core. They showed that the thickness of these layers and the angle of the embedded SMA wires affect the fundamental natural frequency of this hybrid plate. Nekouei et al. [17] presented a semi-analytical solution for the free vibration of SMAHC conical shells. They showed that using SMA fibers has significant effect on increasing the fundamental natural frequency of SMAHC conical shells.

Although considerable research has been devoted to the dynamic analysis of structures reinforced by SMA fibers, optimization of reinforced hybrid composite structures has not been studied extensively in the literature. Shokuhfar et al. [18] used the response surface method and optimized an SMAHC plate under low-velocity impact in order to minimize the maximum transverse deflection of the plate. Park et al. [19] conducted the optimal design of a variable-twist proprotor by maximizing its twist actuation. They used an SMAHC to change the built-in twist. They embedded SMA fibers neither in the outermost nor in the mid-layers; the fibers were inserted in other layers. Salim et al. [20] studied the thermal buckling and free vibration of an SMAHC cylindrical shell and used a genetic algorithm to find the optimum stacking sequence which maximizes the shell’s fundamental natural frequency. Kamarian and Shakeri [21] used the first-order shear deformation theory (FSDT), Brinson’s model, and generalized differential quadrature solution method to obtain the critical buckling temperature of rectangular and skew SMAHC plates. They used the firefly algorithm to find the optimum stacking sequence that leads to a maximum critical buckling temperature of the skew plate. In [20, 21], the SMA fibers were inserted in the outermost layers and only the best stacking sequence is obtained.

To the best of the authors’ knowledge, optimization of an SMAHC plate to maximize its natural frequency has not been addressed in the available literature yet. In the present study, using a genetic algorithm based on free vibration, optimization of nickel–titanium SMA fibers arrangements in an eight-layered rectangular composite plate is carried out. The one-dimensional Brinson model [22] is used to simulate the behavior of the SMA fibers. To obtain the free vibrational response of the SMAHC plate, the FSDT and the Ritz method are utilized. In the first section of the numerical results, the effect of various parameters on the fundamental natural frequency is studied. Using a genetic algorithm, the study is concluded by the optimization process. With the aim of maximizing the fundamental natural frequency, for the first time and simultaneously the best stacking sequence of the SMAHC plate and the best two layers to insert the SMA fibers are obtained.

2 Theoretical development

2.1 Problem description

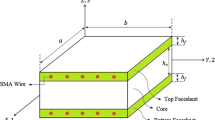
Figure 1 shows an eight-layered SMAHC plate of length a, width b, and thickness h in the x-, y-, and z-directions, respectively. The global Cartesian coordinate system (x, y, z) is located in the middle plane of the plate. The angle between the fiber’s orientation and the x-axis is denoted by $\theta$. The study is carried out for two different boundary conditions of fully clamped (CCCC) and fully immovable simply supported (SSSS). SMA fibers are inserted along the composite fibers. In the schematic Fig. 1, the SMA fibers are located in the outermost layers, even though they can be inserted in any other layers.

Fig. 1

Schematic of an SMAHC plate along with the coordinate system

2.2 Problem formulation

2.2.1 Brinson’s constitutive model

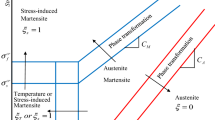
On the basis of the simplified one-dimensional Brinson model [22], the total martensitic fraction $(\zeta )$ is the sum of the stress-induced martensitic fraction ($\zeta _\mathrm{s}$) and the temperature-induced martensitic fractions ($\zeta _\mathrm{T}$) [23],

$$\begin{aligned} \zeta =\zeta _\mathrm{s} +\zeta _\mathrm{T}. \end{aligned}$$

(1)

According to the Reuss scheme, Young’s modulus of the SMA fibers, $E_\mathrm{s}$, is defined as

$$\begin{aligned} E_\mathrm{s} (\zeta )=\frac{E_\mathrm{A} }{1+\left( \frac{E_\mathrm{A} }{E_\mathrm{M} }-1\right) \zeta _\mathrm{s} }, \end{aligned}$$

(2)

where $E_\mathrm{A}$ and $E_\mathrm{M}$ are Young’s modulus of the SMA in the pure austenite and pure martensitic phase, respectively [23]. The recovery stress ($\sigma ^\mathrm{{r}}$) can be calculated based on the strain ($\varepsilon$), the thermoelastic coefficient ($\Theta$), the difference in temperature from its reference value ($\Delta T$), the maximum recoverable strain of the SMA fibers ($\varepsilon _\mathrm{L}$) and Young’s modulus of the SMA fibers as follows [24]:

$$\begin{aligned} \sigma ^\mathrm{{r}}=E_\mathrm{s} (\zeta )(\varepsilon -\varepsilon _\mathrm{L} \zeta _\mathrm{s} )+\Theta \,\Delta T. \end{aligned}$$

(3)

Under the conditions of $T>A_\mathrm{s}$ and $C_\mathrm{A} (T-A_\mathrm{f} )<\sigma ^\mathrm{{r}}<C_\mathrm{A} (T-A_\mathrm{s})$, the martensitic fractions during the heating stage, phase transformation, can be approximated by the following kinetics cosine formulation

$$\begin{aligned} \zeta= & {} \frac{\zeta _{0} }{2}\left[ {\cos \left( {\frac{\pi }{A_\mathrm{f} -A_\mathrm{S} }\left( T-A_\mathrm{S} -\frac{\sigma ^\mathrm{{r}}}{C_\mathrm{A} }\right) } \right) +1} \right] , \end{aligned}$$

(4)

$$\begin{aligned} \zeta _\mathrm{S}= & {} \zeta _\mathrm{S_{0} } \frac{\zeta }{\zeta _{0} }, \end{aligned}$$

(5)

$$\begin{aligned} \zeta _\mathrm{T}= & {} \zeta _{T_{0} } \frac{\zeta }{\zeta _{0} }, \end{aligned}$$

(6)

where T is the temperature, the constant $C_\mathrm{A}$ is the gradient of the curve of critical stress for the reverse phase transformation, and the subscript 0 stands for the initial state. $A_\mathrm{s}$ and $A_\mathrm{f}$ are the austenitic start and finish temperatures, respectively. During the heating stage for $T>A_\mathrm{s}$ and $C_\mathrm{A} (T-A_\mathrm{f} )<\sigma ^\mathrm{{r}}<C_\mathrm{A} (T-A_\mathrm{s})$, recovery stress and martensitic fractions can be obtained by solving Eqs. (3)–(6) simultaneously [22].

2.2.2 Laminated Composite plate

Considering the multicell mechanics approach [25], at a given martensitic fraction, the effective thermomechanical properties of an SMAHC plate, i.e., Young’s modulus (E), shear modulus (G), Poisson’s ratio ($\nu$), linear thermal expansion coefficient ($\alpha$) and mass density ($\rho$), can be estimated by Eqs. (7)–(15):

$$\begin{aligned} E_{11}= & {} E_\mathrm{s} (\zeta )V_\mathrm{s} +E_\mathrm{1m} (1-V_\mathrm{s} ), \end{aligned}$$

(7)

$$\begin{aligned} E_{22}= & {} E_\mathrm{2m} \left[ {(1-\sqrt{V_\mathrm{s} } )+\frac{\sqrt{V_\mathrm{s} } }{1-\sqrt{V_\mathrm{s} } \left( 1-\frac{E_\mathrm{2m} }{E_\mathrm{s} (\zeta )}\right) }} \right] , \end{aligned}$$

(8)

$$\begin{aligned} G_{12}= & {} G_{13} =G_\mathrm{12m} \times \left[ {1-\sqrt{V_\mathrm{s} } +\frac{\sqrt{V_\mathrm{s} } }{1-\sqrt{V_\mathrm{s} } \left( 1-\frac{G_\mathrm{12m} }{G_\mathrm{s} (\zeta )}\right) }} \right] , \end{aligned}$$

(9)

$$\begin{aligned} G_{23}= & {} \frac{G_\mathrm{23m} }{1-\sqrt{V_\mathrm{s} } (1-\frac{G_\mathrm{23m} }{G_\mathrm{s} (\zeta )})}, \end{aligned}$$

(10)

$$\begin{aligned} G_\mathrm{s} (\zeta )= & {} \frac{E_\mathrm{s} (\zeta )}{2(1+\nu _\mathrm{12s} )}, \end{aligned}$$

(11)

$$\begin{aligned} \nu _{12}= & {} \nu _\mathrm{12s} V_\mathrm{s} +\nu _\mathrm{12m} (1-V_\mathrm{s} ), \end{aligned}$$

(12)

$$\begin{aligned} \alpha _{1}= & {} \frac{V_\mathrm{s} \alpha _\mathrm{s} E_\mathrm{s} (\zeta )+(1-V_\mathrm{s} )\alpha _\mathrm{1m} E_\mathrm{1m} }{E_{11} }, \end{aligned}$$

(13)

$$\begin{aligned} \alpha _{2}= & {} \frac{E_\mathrm{2m} }{E_{22} }\left[ {\alpha _\mathrm{2m} (1-\sqrt{V_\mathrm{s} } )+\frac{\alpha _\mathrm{2m} \sqrt{V_\mathrm{s} } -\sqrt{V_\mathrm{s} } (\alpha _\mathrm{2m} -\alpha _\mathrm{s} )}{1-\sqrt{V_\mathrm{s} } \left( 1-\frac{E_\mathrm{2m} }{E_\mathrm{s} (\zeta )}\right) }} \right] , \end{aligned}$$

(14)

$$\begin{aligned} \rho= & {} \rho _\mathrm{s} V_\mathrm{s} +\rho _\mathrm{m} (1-V_\mathrm{s} ), \end{aligned}$$

(15)

where the subscripts m and s stand for the composite and the SMA fibers, respectively, and $V_\mathrm{s}$ denotes the volume fraction of SMA fibers.

Following the FSDT assumptions, the displacement components can be written as:

$$\begin{aligned} \begin{array}{l} u(x,y,z,t)=u_{0} (x,y,z,t)+z\phi _{x} (x,y,t), \\ v(x,y,z,t)=v_{0} (x,y,z,t)+z\phi _{y} (x,y,t), \\ w(x,y,z,t)=w_{0} (x,y,t), \\ \end{array} \end{aligned}$$

(16)

in which $u_{0}$, $v_{0}$, and $w_{0}$ are displacements of the mid-plane ($z=0$) in the x-, y-, and z-directions, respectively. Furthermore, $\phi _{x}$ and $\phi _{y}$ represent the rotations of the transverse normal of the mid-plane about the y- and x-axes, respectively [26]. The linear strain–displacement relationships are

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {\varepsilon _{xx} } \\ {\varepsilon _{yy} } \\ \end{array} }} \\ {\gamma _{yz} } \\ {\gamma _{xz} } \\ \end{array} }} \\ {\gamma _{xy} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\varepsilon _{xx}^{(0)} } \\ {\begin{array}{l} \varepsilon _{yy}^{(0)} \\ \gamma _{yz}^{(0)} \\ \end{array}} \\ {\gamma _{xz}^{(0)} } \\ {\gamma _{xy}^{(0)} } \\ \end{array} }} \right\} +z\left\{ {{\begin{array}{*{20}c} {\varepsilon _{xx}^{(1)} } \\ {\begin{array}{l} \varepsilon _{yy}^{(1)} \\ \gamma _{yz}^{(1)} \\ \end{array}} \\ {\gamma _{xz}^{(1)} } \\ {\gamma _{xy}^{(1)} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\frac{\partial u_{0} }{\partial x}} \\ {\frac{\partial v_{0} }{\partial y}} \\ {\phi _{y} +\frac{\partial w_{0} }{\partial y}} \\ {{\begin{array}{*{20}c} {\phi _{x} +\frac{\partial w_{0} }{\partial x}} \\ {\frac{\partial u_{0} }{\partial y}+\frac{\partial v_{0} }{\partial x}}\\ \end{array} }} \\ \end{array} }} \right\} +z\left\{ {{\begin{array}{*{20}c} {\frac{\partial \phi _{x} }{\partial x}} \\ {\frac{\partial \phi _{y} }{\partial y}} \\ 0 \\ {{\begin{array}{*{20}c} 0 \\ {\frac{\partial \phi _{x} }{\partial y}+\frac{\partial \phi _{y} }{\partial x}} \\ \end{array} }} \\ \end{array} }} \right\} , \end{aligned}$$

(17)

where $\varepsilon _{xx}$ and $\varepsilon _{yy}$ are the normal strains and $\gamma _{yz}$, $\gamma _{xz}$, and $\gamma _{xy}$ are the shear strains. For an SMAHC plate under thermal loading, the constitutive law can be written as [12]

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {\sigma _{xx} } \\ {\sigma _{yy} } \\ \end{array} }} \\ {\tau _{yz} } \\ {\tau _{xz} } \\ \end{array} }} \\ {\tau _{xy} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} {{\overline{Q}}_{11} } &{} {{\overline{Q}}_{12}} &{} 0 &{} 0&{} {{\overline{Q}}_{16} } \\ {{\overline{Q}}_{12} } &{} {{\overline{Q}}_{22} } &{} 0 &{}0&{} {{\overline{Q}}_{26} } \\ 0 &{} 0 &{} {{\overline{Q}}_{44} } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {{\overline{Q}}_{55} } &{} 0 \\ {{\overline{Q}}_{16} } &{} {{\overline{Q}}_{26} } &{} 0 &{}0&{} {{\overline{Q}}_{66} } \\ \end{array} }} \right] \left( {\left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {\varepsilon _{xx} } \\ {\varepsilon _{yy} } \\ \end{array} }} \\ {\gamma _{yz} } \\ {\gamma _{xz} } \\ \end{array} }} \\ {\gamma _{xy} } \\ \end{array} }} \right\} -\Delta T\left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {\alpha _{xx} } \\ {\alpha _{yy} } \\ \end{array} }} \\ 0 \\ 0 \\ \end{array} }} \\ {2\alpha _{xy} } \\ \end{array} }} \right\} } \right) +V_\mathrm{s} \left\{ {{\begin{array}{*{20}c} {\sigma _{x}^\mathrm{{r}} } \\ {{\begin{array}{*{20}c} {\sigma _{y}^\mathrm{{r}} } \\ 0 \\ \end{array} }} \\ 0 \\ {\sigma _{xy}^\mathrm{{r}} } \\ \end{array} }} \right\} , \end{aligned}$$

(18)

where $\sigma _{xx}$ and $\sigma _{yy}$ are the normal stresses, $\tau _{yz}$, $\tau _{xz}$, and $\tau _{xy}$ are the shear stresses, and ${\bar{Q}}_{ij}$ are the components of the transformed reduced stiffness matrix, relations for the computation of which are mentioned in Appendix A.

In view of the FSDT, multiplying the first, second, and fifth rows of Eq. (18) by (1, z) and integrating the results in the z-direction leads to

$$\begin{aligned} \left[ {\begin{array}{l} N_{xx} \\ N_{yy} \\ N_{xy} \\ M_{xx} \\ M_{yy} \\ M_{xy} \\ \end{array}} \right] =\left[ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {\begin{array}{l} A_{11} \\ A_{12} \\ A_{16} \\ B_{11} \\ B_{12} \\ B_{16} \\ \end{array}} &{} {\begin{array}{l} A_{12} \\ A_{22} \\ A_{26} \\ B_{12} \\ B_{22} \\ B_{26} \\ \end{array}} \\ \end{array} }} &{} {\begin{array}{l} A_{16} \\ A_{26} \\ A_{66} \\ B_{16} \\ B_{26} \\ B_{66} \\ \end{array}} \\ \end{array} }} &{} {\begin{array}{l} B_{11} \\ B_{12} \\ B_{16} \\ D_{11} \\ D_{12} \\ D_{16} \\ \end{array}} \\ \end{array} }} &{} {\begin{array}{l} B_{12} \\ B_{22} \\ B_{26} \\ D_{12} \\ D_{22} \\ D_{26} \\ \end{array}} &{} {\begin{array}{l} B_{16} \\ B_{26} \\ B_{66} \\ D_{16} \\ D_{26} \\ D_{66} \\ \end{array}} \\ \end{array} }} \right] \left[ {\begin{array}{l} \varepsilon _{xx}^{(0)} \\ \varepsilon _{yy}^{(0)} \\ \gamma _{xy}^{(0)} \\ \varepsilon _{xx}^{(1)} \\ \varepsilon _{yy}^{(1)} \\ \gamma _{xy}^{(1)} \\ \end{array}} \right] -\left[ {\begin{array}{l} N_{xx}^\mathrm{{T}} \\ N_{yy}^\mathrm{{T}} \\ N_{xy}^\mathrm{{T}} \\ M_{xx}^\mathrm{{T}} \\ M_{yy}^\mathrm{{T}} \\ M_{xy}^\mathrm{{T}} \\ \end{array}} \right] +\left[ {\begin{array}{l} N_{xx}^\mathrm{{r}} \\ N_{yy}^\mathrm{{r}} \\ N_{xy}^\mathrm{{r}} \\ M_{xx}^\mathrm{{r}} \\ M_{yy}^\mathrm{{r}} \\ M_{xy}^\mathrm{{r}} \\ \end{array}} \right] , \end{aligned}$$

(19)

where the resultant force (N), the resultant moment (M), the thermal resultant force ($N^\mathrm{{T}}$), the thermal moment resultant ($M^\mathrm{{T}}$), the resultant force induced by the recovery stress ($N^\mathrm{{r}}$), and the moment resultant induced by the recovery stress ($M^\mathrm{{r}}$) of the kth layer with the fiber orientation of $\theta _{k}$ with respect to the $x-$axis, as shown in Fig. 1, can be written as

$$\begin{aligned}&\left[ {\left\{ {\begin{array}{l} N_{xx} \\ N_{yy} \\ N_{xy} \\ \end{array}} \right\} ,\left\{ {\begin{array}{l} M_{xx} \\ M_{yy} \\ M_{xy} \\ \end{array}} \right\} } \right] =\sum \limits _{k=1}^\mathrm{NL} {\int \limits _{h_{k-1} }^{h_{k} } {\left\{ {{\begin{array}{*{20}c} {\sigma _{xx} } \\ {\sigma _{yy} } \\ {\tau _{xy} } \\ \end{array} }} \right\} \,} (1,z)\,\,} \text {d}z, \end{aligned}$$

(20)

$$\begin{aligned}&\left[ {\left\{ {\begin{array}{l} N_{xx}^\mathrm{{T}} \\ N_{yy}^\mathrm{{T}} \\ N_{xy}^\mathrm{{T}} \\ \end{array}} \right\} ,\left\{ {\begin{array}{l} M_{xx}^\mathrm{{T}} \\ M_{yy}^\mathrm{{T}} \\ M_{xy}^\mathrm{{T}} \\ \end{array}} \right\} } \right] =\sum \limits _{k=1}^\mathrm{NL} {\int \limits _{h_{k-1} }^{h_{k} } {\left[ {\begin{array}{l} {\begin{array}{*{20}c} {{\bar{Q}}_{11} } &{} {{\bar{Q}}_{12} } &{} {{\bar{Q}}_{16} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\bar{Q}}_{12} } &{} {{\bar{Q}}_{22} } &{} {{\bar{Q}}_{26} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\bar{Q}}_{16} } &{} {{\bar{Q}}_{26} } &{} {{\bar{Q}}_{66} } \\ \end{array} } \\ \end{array}} \right] } } \nonumber \\&\quad \times \left[ {{\begin{array}{*{20}c} {\begin{array}{l} \cos ^{2}\theta _{k} \\ \sin ^{2}\theta _{k} \\ 2\sin \theta _{k} \cos \theta _{k} \\ \end{array}} &{} {\begin{array}{l} \sin ^{2}\theta _{k} \\ \cos ^{2}\theta _{k} \\ -2\sin \theta _{k} \cos \theta _{k} \\ \end{array}} \\ \end{array} }} \right] \times \left[ {\begin{array}{l} \alpha _{11} \\ \alpha _{22} \\ \end{array}} \right] \Delta T(1,z)\,\text {d}z, \end{aligned}$$

(21)

$$\begin{aligned}&\left[ {\left\{ {\begin{array}{l} N_{xx}^\mathrm{{r}} \\ N_{yy}^\mathrm{{r}} \\ N_{xy}^\mathrm{{r}} \\ \end{array}} \right\} ,\left\{ {\begin{array}{l} M_{xx}^\mathrm{{r}} \\ M_{yy}^\mathrm{{r}} \\ M_{xy}^\mathrm{{r}} \\ \end{array}} \right\} } \right] =\sum \limits _{k=1}^\mathrm{NL} {\int \limits _{h_{k-1} }^{h_{k} } {\sigma ^\mathrm{{r}}V_{s} } \left[ {\begin{array}{l} \cos ^{2}\theta _{k} \\ \sin ^{2}\theta _{k} \\ \sin \theta _{k} \cos \theta _{k} \\ \end{array}} \right] \,(1,z)\,\text {d}z}. \end{aligned}$$

(22)

In the principal coordinates of the plate, the components of the extensional matrix ($A_{ij}$), the coupling matrix $(B_{ij})$, and the bending stiffness matrix ($D_{ij}$) are as follows [27]

$$\begin{aligned} \begin{array}{l@{\qquad }l} A_{ij} =\sum \limits _{k=1}^\mathrm{NL} {({\bar{Q}}_{ij} )_{k} [h_{k} -h_{k-1} ]} &{} (i,j=1,2,6),\\ A_{ij} =\frac{5}{4}\sum \limits _{k=1}^\mathrm{NL} {({\bar{Q}} _{ij} )_{k} [h_{k} -h_{k-1} -\frac{4}{3}(h_{k}^{3} -h_{k-1}^{3} )\frac{1}{h^{2}}]} &{} (i,j=4,5),\\ B_{ij} =\frac{1}{2}\sum \limits _{k=1}^\mathrm{NL} {({\bar{Q}} _{ij} )_{k} [h_{k}^{2} -h_{k-1}^{2} ]} &{} (i,j=1,2,6),\\ D_{ij} =\frac{1}{3}\sum \limits _{k=1}^\mathrm{NL} {({\bar{Q}} _{ij} )_{k} [h_{k}^{3} -h_{k-1}^{3} ]} &{} (i,j=1,2,6),\\ \end{array} \end{aligned}$$

(23)

where $h_{k}$ is the distance of the kth layer upper surface from the mid-plane and $N\!L$ is the number of layers. It should be noted that to compensate for the inaccuracy of constant shear strain and shear stress across the thickness, a shear correction factor of 5/6 is used in this study.

2.3 Solution method

The Ritz method is used to acquire the fundamental natural frequency of the SMAHC plate. Assuming an undamped small amplitude periodic motion, the displacement field may be written as

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {u_{0} (x,y,t)=\sum \nolimits _{n=1}^N {\sum \nolimits _{m=1}^M {U_{mn} \text {e}^{i\omega t}u_{m} (x)u_{n} (y)} } }, \\ {v_{0} (x,y,t)=\sum \nolimits _{n=1}^N {\sum \nolimits _{m=1}^M {V_{mn} \text {e}^{i\omega t}v_{m} (x)v_{n} (y)} } }, \\ {w_{0} (x,y,t)=\sum \nolimits _{n=1}^N {\sum \nolimits _{m=1}^M {W_{mn} \text {e}^{i\omega t}w_{m} (x)w_{n} (y)} } }, \\ {\phi _{x} (x,y,t)=\sum \nolimits _{n=1}^N {\sum \nolimits _{m=1}^M {X_{mn} \text {e}^{i\omega t}x_{m} (x)x_{n} (y)} } }, \\ {\phi _{y} (x,y,t)=\sum \nolimits _{n=1}^N {\sum \nolimits _{m=1}^M {Y_{mn} \text {e}^{i\omega t}} } y_{m} (x)y_{n} (y)}, \\ \end{array} }} \right. \end{aligned}$$

(24)

where $U_{mn} ,V_{mn} ,W_{mn} ,X_{mn}$, and $Y_{mn}$ are unknown coefficients to be determined and $u_{m}$, $u_{n}$, $v_{m}$, $v_{n}$, $w_{m}$, $w_{n}$, $x_{m}$, $x_{n}$, $y_{m}$, and $y_{n}$ are the assumed functions which satisfy the geometric boundary conditions. The displacement field must be substituted in the energy functions. The kinetic energy, K, is

$$\begin{aligned} K=\frac{1}{2}\int \limits _{\Omega _{0} } {\left\{ {\left. {\int _{-\frac{h}{2}}^{\frac{h}{2}} {\rho \left[ {\left( \frac{\partial u}{\partial t}\right) ^{2}+\left( \frac{\partial v}{\partial t}\right) ^{2}+\left( \frac{\partial w}{\partial t}\right) ^{2}} \right] } \text {d}z} \right\} } \right. } \text {d}x\text {d}y, \end{aligned}$$

(25)

Substituting the displacement components from Eq. (16) into Eq. (25) and some mathematical manipulation yields

$$\begin{aligned} K= & {} \frac{1}{2}\int \limits _{\Omega _{0} } {\left[ {I_{2} \left( \left( \frac{\partial \phi _{x} }{\partial t}\right) ^{2}+\left( \frac{\partial \phi _{y} }{\partial t}\right) ^{2}\right) +I_{1} \left( \frac{\partial u_{0} }{\partial t}\frac{\partial \phi _{x} }{\partial t}+\frac{\partial v_{0} }{\partial t}\frac{\partial \phi _{y} }{\partial t}\right) } \right. }\nonumber \\&\quad \left. {+I_{0} \left( \left( \frac{\partial u_{0} }{\partial t}\right) ^{2}+\left( \frac{\partial v_{0} }{\partial t}\right) ^{2}+\left( \frac{\partial w_{0} }{\partial t}\right) ^{2}\right) } \right] \,\text {d}x\text {d}y, \end{aligned}$$

(26)

where the inertia terms $I_{0}$, $I_{1}$, and $I_{2}$ are defined as

$$\begin{aligned} I_{i} =\int _{-\frac{h}{2}}^{\frac{h}{2}} {\rho z^{i}\text {d}z} \quad (i=0,1,2). \end{aligned}$$

(27)

The total strain energy due to bending, U, is

$$\begin{aligned} U=\frac{1}{2}\int \limits _{\Omega _{0} } {\left\{ {\left. {\int _{-\frac{h}{2}}^{\frac{h}{2}} {[\sigma _{xx} \varepsilon _{xx} +\sigma _{yy} \varepsilon _{yy} +\sigma _{xy} \gamma _{xy} +\sigma _{xz} \gamma _{xz} +\sigma _{yz} \gamma _{yz} } ]\text {d}z} \right\} } \right. } \text {d}x\text {d}y. \end{aligned}$$

(28)

The work done by external forces, V, as presented by [28] is

$$\begin{aligned} V= & {} \frac{1}{2}\int \limits _{\Omega _{0} } {\left[ {\hat{N}_{x}} \left( \frac{\partial w}{\partial x}\right) ^{2}+{\hat{N}_{y} } \left( \frac{\partial w}{\partial y}\right) ^{2}+2{\hat{N}_{xy} } \left( \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}\right) \right] } \text {d}x\text {d}y, \end{aligned}$$

(29)

$$\begin{aligned} \hat{N}= & {} N^\mathrm{{r}}-N^\mathrm{{T}}, \end{aligned}$$

(30)

where $\hat{N}$ stands for the resultant force induced by applying uniform thermal loads on the SMA fibers. The CCCC and SSSS boundary conditions and their corresponding assumed displacement fields are as follows:

• Immovable simply supported plate

  • Boundary conditions

  $$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {u_{0} (0,y)=0,\,\,u_{0} (a,y)=0,\,\,u_{0} (x,0)=0,\,\,u_{0} (x,b)=0;\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\ {v_{0} (0,y)=0,\,\,v_{0} (a,y)=0,\,\,v_{0} (x,0)=0,\,\,v_{0} (x,b)=0;\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\ {w_{0} (0,y)=0,\,\,w_{0} (a,y)=0,\,\,w_{0} (x,0)=0,\,\,w_{0} (x,b)=0;\,\,\,\,\,\,\,\,} \\ {\phi _{y} (0,y)=0,\,\,\phi _{y} (a,y)=0,\,\,\phi _{x} (x,0)=0,\,\,\phi _{x} (x,b)=0;\,\,\,\,\,\,\,\,\,\,\,\,} \\ {M_{x} (0,y)=0,\,\,M_{x} (a,y)=0,\,\,M_{y} (x,0)=0,\,\,M_{y} (x,b)=0} \\ \end{array} }} \right. \end{aligned}$$

  (31)

  • Assumed displacement field

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {u_{0} \left( x,y,t\right) =\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {U_{mn} \text {e}^{i\omega t}\sin \left( \frac{m\pi }{a}x\right) \sin \left( \frac{n\pi }{b}y\right) ,} } } \\ {v_{0} \left( x,y,t\right) =\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {V_{mn} \text {e}^{i\omega t}\sin \left( \frac{m\pi }{a}x\right) \sin \left( \frac{n\pi }{b}y\right) ,} } } \\ {w_{0} \left( x,y,t\right) =\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {W_{mn} \text {e}^{i\omega t}\sin \left( \frac{m\pi }{a}x\right) \sin \left( \frac{n\pi }{b}y\right) ,} } } \\ {\phi _{x} \left( x,y,t\right) =\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {X_{mn} \text {e}^{i\omega t}\cos \left( \frac{m\pi }{a}x\right) \sin \left( \frac{n\pi }{b}y\right) ,} } } \\ {\phi _{y} \left( x,y,t\right) =\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {Y_{mn} \text {e}^{i\omega t}\sin \left( \frac{m\pi }{a}x\right) \cos \left( \frac{n\pi }{b}y\right) } } } \\ \end{array} }} \right. \end{aligned}$$

(32)

• Clamped plate

  • Boundary conditions

  $$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {u_{0} (0,y)=0,\,\,u_{0} (a,y)=0,\,\,u_{0} (x,0)=0,\,\,u_{0} (x,b)=0;\,\,\,\,\,} \\ {v_{0} (0,y)=0,\,\,v_{0} (a,y)=0,\,\,v_{0} (x,0)=0,\,\,v_{0} (x,b)=0;\,\,\,\,\,} \\ {w_{0} (0,y)=0,\,\,w_{0} (a,y)=0,\,\,w_{0} (x,0)=0,\,\,w_{0} (x,b)=0;} \\ {\phi _{x} (0,y)=0,\,\,\phi _{x} (a,y)=0,\,\,\phi _{x} (x,0)=0,\,\,\phi _{x} (x,b)=0;\,\,\,\,} \\ {\phi _{y} (0,y)=0,\,\,\phi _{y} (a,y)=0,\,\,\phi _{y} (x,0)=0,\,\,\phi _{y} (x,b)=0\,\,\,} \\ \end{array} }} \right. \end{aligned}$$

  (33)

  • Assumed displacement field

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {u_{0} (x,y,t)=\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {U_{mn} \text {e}^{i\omega t}x^{m}(x-a)y^{n}(y-b),} } \,} \\ {v_{0} (x,y,t)=\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {V_{mn} \text {e}^{i\omega t}x^{m}(x-a)y^{n}(y-b),} } \,\,} \\ {w_{0} (x,y,t)=\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {W_{mn} \text {e}^{i\omega t}x^{m}(x-a)y^{n}(y-b),} } } \\ {\phi _{x} (x,y,t)=\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {X_{mn} \text {e}^{i\omega t}x^{m}(x-a)y^{n}(y-b),} }} \\ {\phi _{y} (x,y,t)=\sum \nolimits _{n=1}^{\bar{{N}}} {\sum \nolimits _{m=1}^{\bar{{M}}} {Y_{mn} \text {e}^{i\omega t}x^{m}(x-a)y^{n}(y-b)} }} \\ \end{array} }} \right. \end{aligned}$$

(34)

To form the mass and stiffness matrices, the Lagrangian functional $L:=K-(U+V)$ is formed [29]. Taking into consideration Eqs. (17)–(23), the assumed displacement fields are substituted in the equations of the strain energy, kinetic energy, and work done by external forces, namely Eqs. (26), (28), and (29), respectively. The stationary value of L is obtained by differentiating it with respect to the unknown coefficients of the displacement field:

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {\frac{\partial (K-(U+V))}{\partial U_{mn} }=0}, \\ {\frac{\partial (K-(U+V))}{\partial V_{mn} }=0}, \\ \end{array} }} \\ {\frac{\partial (K-(U+V))}{\partial W_{mn} }=0}, \\ {\frac{\partial (K-(U+V))}{\partial X_{mn} }=0}, \\ \end{array} }} \\ {\frac{\partial (K-(U+V))}{\partial Y_{mn} }=0}, \\ \end{array} }} \right. \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(m=1,2,...,\bar{{M}};\,n=1,2,...,\bar{{N}}), \end{aligned}$$

(35)

which yields a matrix eigenvalue problem in terms of the variable column vector $\mathbf{X }$ as follows:

$$\begin{aligned}{}[K]\mathbf{X }=\omega ^{2}[M]\mathbf{X }, \end{aligned}$$

(36)

where

$$\begin{aligned} \mathbf{X }=\{U_{mn} ,V_{mn} ,W_{mn} ,X_{mn} ,Y_{mn}\}. \end{aligned}$$

(37)

The detailed derivations of stiffness and mass matrices are provided in Appendix B. The approximate natural frequencies are the square roots of the eigenvalues of $[M]^{-1}[K]$. The coefficients of the Ritz expansion mode shapes give the corresponding eigenvectors.

2.4 Optimization procedure

A genetic algorithm is an optimization method that emanates from natural biological evolution. It operates on the potential solutions, called population, to create better solutions at each generation by utilizing operators that exist in nature, called crossover and mutation. These operators help in finding better-suited answers to the problem than the initial solutions; this means an improvement in the approximated solutions. Each individual of the population is called a chromosome.

In the present study, a genetic algorithm is utilized to find the best stacking sequence of the SMAHC plate and the best two layers in which the SMA fibers should be inserted to maximize the fundamental natural frequency of the SMAHC plate. The assumed chromosomes contain the angle of fibers in each layer and the layer numbers with SMA fibers. In this study, the number of both population and generations is considered to be 100. In the optimization process, fifty percent of the population is selected randomly for mutation. For each one of these chromosomes, the mutation operator randomly picks two genes. Selected genes can be either the angle or the layer number. In the former case, the angle of the layer is replaced by its complement, and in the latter case, a new random number is reproduced. The crossover operator selects 70 percent of the population based on a tournament selection and creates new chromosomes out of them. In each selection stage, three chromosomes are picked, and the one with the highest fundamental natural frequency is chosen as the first parent. By repeating the same procedure, the second parent is selected. By combining the selected chromosomes, two new chromosomes are produced. The procedure of optimization is displayed in the flowchart shown in Fig. 2.

Fig. 2

Flowchart of the genetic algorithm code

3 Results and discussion

3.1 Comparative studies

The proposed method is verified by comparing the fundamental natural frequency of three cases with those available in open literature studies [12, 27,28,29,30,31,32,33,34,35,36,37,38].

Case 1) An SSSS rectangular laminated composite plate with the stacking sequence of [0/90/90/0].

The dimensionless material and geometric properties are

$$\begin{aligned} \rho= & {} 1600\,(\text {kg/m}^{3}),\,\,\frac{E_{1} }{E_{2} }=40,\,\,\frac{E_{2} }{E_{3} }=1,\,\,\frac{G_{12} }{E_{2} }=\frac{G_{13} }{E_{2} }=0.6,\,\,\frac{G_{23} }{E_{2} }=0.5, \\&\quad \nu _{12} =\nu _{13} =\nu _{23} =0.25,\,\,\frac{a}{b}=1,\,\,\frac{a}{h}=50. \end{aligned}$$

In Table 1, the dimensionless fundamental natural frequency, ${\overline{\omega }} =\omega \,b^{2}{\sqrt{\rho / {E_{2} }} } / h$, obtained from the present study and those reported by [27,28,29,30,31,32,33] are listed.

Case 2) A CCCC square laminated composite plate with the stacking sequence of [0/90/0].

The dimensionless material and geometric properties are

$$\begin{aligned} \rho= & {} 1586\,(kg/m^{3}),\,\,\frac{E_{1} }{E_{2} }=40,\,\,\frac{E_{2} }{E_{3} }=1,\,\,\frac{G_{12} }{E_{2} }=\frac{G_{13} }{E_{2} }=0.6,\,\,\frac{G_{23} }{E_{2} }=0.5, \\&\quad \nu _{12} =\nu _{13} =\nu _{23} =0.25,\,\,\frac{a}{b}=1,\,\,\frac{a}{h}=1000. \end{aligned}$$

The dimensionless fundamental natural frequency is defined as $\bar{{\omega }}=\omega \times {b^{2}\sqrt{{12\rho (1-\nu _{12} \nu _{21} )} / {E_{2} h^{2}}} } / {\pi ^{2}}$. The dimensionless fundamental natural frequencies obtained by the present and [34,35,36] studies are listed in Table 2. RBF and 1D-IRBFN stand for the radial basis function and the one-dimensional integrated RBF networks, respectively. Tables 1 and 2 show that the results of the present study are in good correlation with the published data as the maximum discrepancy between the results reaches 0.36 % and 1.0% for SSSS and CCCC plates, respectively.

Table 1 Comparison of the dimensionless fundamental natural frequency of an SSSS laminated composite plate

Table 2 Comparison of the dimensionless fundamental natural frequency of a CCCC laminated composite plate

Case 3) An eight-layered composite square plate under thermal loading with SSSS boundaries.

Using the material properties given in Table 3, the critical buckling temperatures are compared with [12, 37, 38] in Table 4. The reference temperature is $20^{\circ }\hbox {C}$.

Table 3 Lamina material properties ($G_{12} =G_{13} =G_{23}$) [37]

Table 4 Comparison of the critical buckling temperature of two different stacking sequences $(a/h = 100, a/b = 1)$

3.2 Parametric studies

In this section, the effects of various material and geometric parameters on the fundamental natural frequency and critical buckling temperature of an eight-layered SMAHC plate are investigated. In the present study, a NiTi/graphite/epoxy rectangular laminated plate with the total thickness, length, and width of 0.02 (m), 1 (m), and 1 (m), respectively, is studied. The symmetric stacking sequence of $[0/90/90/0]_{S}$ is considered. The thermomechanical properties of graphite/epoxy and NiTi fibers are listed in Table 5. The default values for the volume fraction and prestrain of SMA fibers are 0.15 and 0.01, respectively. SMA fibers are inserted uniformly in layers 1 and 8, aligned with the graphite fibers. The reference temperature is considered $20\,^{\circ }\hbox {C}$.

Table 5 Thermomechanical properties of graphite/epoxy and NiTi fibers

3.2.1 Effect of SMA fibers prestrain

The effects of prestrain on the fundamental natural frequency of the SMAHC plate are depicted in Fig. 3. At low temperatures, the generated recovery stress of SMA fibers is not enough to increase the stiffness significantly. On the other hand, since the SMA fibers have higher density compared with the original plate, the increase in mass due to inserting the SMA fibers outweighs the increase in stiffness, which in turn decreases the frequency. As the temperature increases above the austenite start temperature, the generated recovery stress of SMA fibers rises significantly, which dramatically increases the stiffness of the plate. This stiffness rise outweighs the increase in the mass, which results in increasing the natural frequency and postpones the buckling to higher temperatures. This increasing trend for natural frequency continues up to the austenite finish temperature. After that, the effect of rising the temperature on softening the plate dominates the stiffening effect of the recovery stress. Hence, the fundamental natural frequency decreases.

The critical thermal buckling temperatures of the SSSS and CCCC laminated composite plate for various prestrains are listed in Table 6. It can be concluded that reinforcing a composite plate with SMA fibers postpones critical thermal buckling of the plate to a higher temperature. Furthermore, increasing the SMA prestrain dramatically increases both the fundamental natural frequency and the critical buckling temperature. The increase in stiffness of a reinforced laminated composite plate with the SSSS boundary condition is more than that of a similar plate with the CCCC support, which is due to higher structural stiffness of the clamped supported plate in comparison with the simply supported one.

Fig. 3

Influence of SMA fibers prestrain and increasing temperature on the fundamental natural frequency of the a SSSS and b CCCC rectangular plate

Table 6 Critical thermal buckling temperature of the rectangular SMAHC plate for different SMA

3.2.2 SMA fibers volume fraction

For three different values of SMA fibers volume fraction, the fundamental natural frequency and thermal buckling temperature are illustrated in Fig. 4. It can be observed that increasing the volume fraction of the SMA fibers affects the fundamental natural frequency and postpones the thermal buckling. The more SMA fibers are inserted in the plate, the more the recovery stress is generated. On the other hand, this will increase the mass of the plate, which is a limiting factor that affects the value of the natural frequency. Table 7 specifies the critical thermal buckling temperature of the plate for four values of volume fractions of SMA fibers. It can be observed that inserting the SMA fibers in the SSSS and CCCC plates is more effective in the former one.

Fig. 4

Influence of SMA fibers volume fraction and increasing temperature on the fundamental natural frequency of the a SSSS and b CCCC rectangular plate

Table 7 Influence of SMA fibers volume fraction on the critical thermal buckling temperature of the rectangular SMAHC plate

3.2.3 Geometrical parameters

Variations in the fundamental natural frequency of the plate versus temperature for various length-to-width ratios, a/b, are depicted in Fig. 5. For each aspect ratio, both the laminated composite and the SMAHC plates are studied. In this section, the length is held constant. Keeping the length constant while decreasing the width is equivalent to a fewer number of SMA fibers for the rectangular plate in comparison with the square one. Thus, the generated recovery stress and mass of the rectangular plate are less than the square one with the same length. Given the results of Fig. 5, it can be concluded that this decrease in stiffness has outweighed the reduction in mass. The critical thermal buckling temperatures for different aspect ratios are presented in Table 8. For either type of the boundary conditions, increasing the aspect ratio decreases the critical temperature, though this effect is more pronounced for the SSSS plate. As the width of the rectangular plate grows, the percentage change in the critical thermal buckling temperature due to embedding the SMA fibers further increases.

Fig. 5

Influence of aspect ratio and increasing temperature on the fundamental natural frequency of the a SSSS and b CCCC plate (dash line: without SMA fibers, straight line: with SMA fibers)

Table 8 Critical thermal buckling temperature ($^{\circ }$C) of the laminated composite plate for different aspect ratios of plate

The fundamental natural frequency of the SMAHC plate is computed for various thickness-to-length ratios, h/a. Figure 6 shows the variation in the fundamental natural frequency versus temperature for two cases of the laminated composite and SMAHC plate. As the thickness decreases, the effect of embedding the SMA fibers in the laminated composite plate becomes more noticeable. In the case that thermal buckling occurs at a temperature below the austenitic start temperature, the SMA fibers do not affect the fundamental natural frequency of the plate. For instance, the SSSS plate with the thickness-to-length ratio of 0.005 thermally buckles at $34\,^{\circ }\hbox {C}$, which is before the activation of the SMA fibers. The results presented in Table 9 show that for either type of boundary conditions, increasing the thickness postpones the thermal buckling to a higher temperature, which is more noticeable for the SSSS plate.

Fig. 6

Influence of thickness-to-length ratio and increasing temperature on the fundamental natural frequency of the a SSSS and b CCCC plate (dash line: without SMA fibers, straight line: with SMA fibers)

Table 9 Influence of inserting SMA fibers on the critical thermal buckling temperature of the rectangular plate with different thickness-to-length ratios

3.3 Optimization

3.3.1 Comparative optimization study

In this section, to obtain the maximum fundamental natural frequency, the best stacking sequence and the best two layers to embed the SMA fibers are generated using the genetic algorithm. To verify the optimization process, for an eight-layered graphite epoxy composite square plate, the proposed stacking sequence is compared with [40, 41] which used the layerwise optimization approach and the complex method, respectively. To find the best stacking sequence, the orientation angle varied between $-\,90^{\circ }$ and $90^{\circ }$ with an increment of $5^{\circ }$. The mechanical properties of the graphite epoxy composite are given as

$$\begin{aligned} E_\mathrm{L} =138\,(\text {GPa}),\,\,E_\mathrm{T} =8.96\,(\text {GPa}),\,G_{\mathrm {LT}}=7.1\,\,(\text {GPa}),\,\,\nu _{\mathrm {LT}} =0.3,\,\,\frac{a}{b}=1. \end{aligned}$$

In Table 10, for a square plate with SSSS boundary conditions, the maximum dimensionless frequency, $\bar{{\omega }}=\omega \,a^{2}(\frac{12(1-\nu _{\mathrm {LT}} \nu _{\mathrm {TL}} )\rho }{E_{\mathrm {T}} h^{3}})^{\frac{1}{2}}$, obtained by the present study is compared with [40, 41]. It is concluded that the maximum fundamental natural frequency obtained by the genetic algorithm is close to the results of [40, 41]. The stacking sequences of the present study and [40] are essentially the same.

Table 10 Optimization of stacking sequence for SSSS square plate

3.3.2 Optimization results

For square and rectangular eight-layered SMAHC plates with SSSS and CCCC boundary conditions, the best and worst two layers to insert the SMA fibers and their corresponding stacking sequences are obtained. For the optimization, like the comparative study, the orientation angle increment is $5^{\circ }$. The dimensions of the square and rectangular plates are $1\,(\text {m})\times 1\,(\text {m})\times 0.02\,(\text {m})$, and $1.5\,(\text {m})\times 1\,(\text {m})\times 0.02\,(\text {m})$, respectively. The mechanical properties of the SMAHC plate are listed in Table 5. The volume fraction and prestrain of the SMA fibers are 0.15 and 0.05, respectively.

The results of the optimization study are provided in Figs. 7, 8, Tables 11 and 12. It can be observed that the best layers to insert the SMA fibers are the closest ones to the mid-plane. The reason is embedding the SMA fibers in layers with the highest stiffness; i.e., the vicinity of the mid-plane maximizes the fundamental natural frequency since the plate’s mass is independent of the SMA fiber locations. Comparing the fundamental natural frequency of the worst layup of the SMAHC plate and the best stacking sequence of the laminated composite plate leads to a very important and unforeseen result: inserting the SMA fibers in a laminated composite plate does not guaranty a higher fundamental natural frequency and might cause an adverse effect. Thus, optimizing the stacking sequence and finding the best layers to insert the SMA fibers are essential.

As an example, for the CCCC rectangular plate, the fundamental natural frequency of the worst layup of the SMAHC case is 920.3 rad/s, which is below the frequency of the best case of the laminated composite plate without SMA fibers, which is $1152.1\,\text{ rad/s }$.

The obtained results for both types of boundary conditions and shapes are compared in Table 13. Since the optimization is intrinsically a random process, it is possible that the genetic algorithm sticks to a local optimum which is still close to the global one. An apparent example is the obtained optimum stacking sequence for the simply supported square plate with the optimum sequence of $[45/45/45/40(\text {SMA})]_\mathrm{S}$; due to the symmetry of the shape and boundary conditions, it is expected that the orientation of the middle layers be $45^{\circ }$. The fundamental natural frequency of the $[45/45/45/45(\text {SMA})]_\mathrm{S}$ square plate is $806.3\,\text{ rad/s }$, which is very close to the $806.2\, \text{ rad/s }$ of the found local optimum solution.

As was discussed in the Introduction [20, 21] embedded the SMA fibers in the outermost layers. Just for the sake of comparison, for the same SSSS square plate, the stacking of $[45(\text {SMA})/45/45/45]_\mathrm{S}$ yields the fundamental natural frequency of 788.7 rad/s, which is smaller than the obtained optimum one. It can also be observed that reinforcing the plate with SMA fibers increases the fundamental natural frequency of the simply supported plates more than for the clamped ones. For the studied SMAHC rectangular simply supported plate, using the optimum stacking sequences and optimum layers for inserting the SMA fibers increases the fundamental natural frequency by approximately 57%.

Fig. 7

Genetic algorithm results for the square plate: a SSSS without SMA, b SSSS with SMA, c CCCC without SMA, d CCCC with SMA

Table 11 Best and worst combination of the stacking sequences and layers to insert the SMA fibers for the square plate

Fig. 8

Genetic algorithm results for the rectangular plate: a SSSS without SMA, b SSSS with SMA, c CCCC without SMA, d) CCCC with SMA

Table 12 Best and worst combination of the stacking sequences and layers to insert the SMA fibers for the rectangular plate

Table 13 Comparison of maximum fundamental frequency obtained by the genetic algorithm

4 Conclusion

In the present study, vibrations of rectangular laminated composite plates reinforced with shape memory alloy fibers under temperature change are studied. In order to simulate the behavior of the SMA fibers and account for the generated recovery stress in the martensitic phase transformation, the one-dimensional Brinson model is employed. Furthermore, to obtain the fundamental natural frequency of the hybrid laminated composite plate, the first-order shear deformation theory and the Ritz method are used. Parametric studies on the influence of the SMA fibers volume fraction and prestrain as well as the plate aspect and thickness-to-length ratios on the structure’s fundamental natural frequency and critical thermal buckling temperature are carried out. After that, a genetic algorithm is utilized to find, for the first time and simultaneously, the optimum stacking sequence and the best layers to insert the SMA fibers, which maximize the fundamental natural frequency of the plate. Through comparative studies, both the solution method, Ritz, and optimization procedure, genetic algorithm, are validated. The main concluding remarks are summarized as follows:

• Increase in either the prestrain or volume fraction of the SMA fibers affects the fundamental natural frequency and increases the critical buckling temperature dramatically.

• Reinforcing laminated composite plates with SMA fibers is more efficient in the simply supported plates compared to the fully clamped ones.

• A square SMAHC plate has higher fundamental frequencies than a rectangular one with the same length.

• Decreasing the thickness-to-length ratio increases the effect of inserting SMA in the cases that their thermal buckling occurs after the austenitic start temperature.

• Inserting SMA fibers in a laminated composite plate does not necessarily increase the fundamental natural frequency of the structure. Improper selection of the stacking sequence and the layers in which the SMA fibers are embedded might reduce the natural frequency of the laminated composite plate.

• For the purpose of maximizing the fundamental natural frequency, the best layers to insert the SMA fibers are the ones closest to the mid-plane.

Appendices

Appendix A

The reduced stiffness matrix ($Q_{ij}$) and the transformed reduced stiffness matrix (${\bar{Q}}_{ij}$) of the kth layer with the fiber orientation of $\theta _{k}$ are

$$\begin{aligned} Q_{11}= & {} \frac{E_{11} }{1-\nu _{12} \nu _{21} },\,\,Q_{22} =\frac{E_{22} }{1-\nu _{12} \nu _{21} },\,\,Q_{12} =Q_{21} =\frac{\nu _{21} E_{11} }{1-\nu _{12} \nu _{21} }, \nonumber \\&\quad Q_{44}=G_{23} ,\,\,Q_{55} =G_{13} ,\,\,Q_{66} =G_{12},\nonumber \\ {\bar{Q}}_{11}= & {} Q_{11} \cos ^{4}\theta _{k} +2(Q_{12} +2Q_{66} )\sin ^{2}\theta _{k} \cos ^{2}\theta _{k} +Q_{22} \sin ^{4}\theta _{k}, \nonumber \\ {\bar{Q}}_{12}= & {} (Q_{11} +Q_{22} -4Q_{66} )\sin ^{2}\theta _{k} \cos ^{2}\theta _{k} +Q_{12} (\cos ^{4}\theta _{k} +\sin ^{4}\theta _{k} ), \nonumber \\ {\bar{Q}}_{22}= & {} Q_{11} \sin ^{4}\theta _{k} +2(Q_{12} +2Q_{66} )\sin ^{2}\theta _{k} \cos ^{2}\theta _{k} +Q_{22} \cos ^{4}\theta _{k}, \nonumber \\ {\bar{Q}}_{16}= & {} -\cos \theta _{k} \sin ^{3}\theta _{k} Q_{22} +\cos ^{3}\theta _{k} \sin \theta _{k} Q_{11}, \nonumber \\&\quad -\sin \theta _{k} \cos \theta _{k} (\cos ^{2}\theta _{k} -\sin ^{2}\theta _{k} )(Q_{12} +2Q_{66} ), \nonumber \\ {\bar{Q}}_{26}= & {} -\cos ^{3}\theta _{k} \sin \theta _{k} Q_{22} +\cos \theta _{k} \sin ^{3}\theta _{k} Q_{11} \nonumber \\&\quad +\cos \theta _{k} \sin \theta _{k} (\cos ^{2}\theta _{k} -\sin ^{2}\theta _{k} )(Q_{12} +2Q_{66} ), \nonumber \\ {\bar{Q}}_{66}= & {} (Q_{11} +Q_{22} -2Q_{12} )\cos ^{2}\theta _{k} \sin ^{2}\theta _{k} +Q_{66} (\cos ^{2}\theta _{k} \sin ^{2}\theta _{k} )^{2}, \nonumber \\ {\bar{Q}}_{44}= & {} Q_{44} \cos ^{2}\theta _{k} +Q_{55} \sin ^{2}\theta _{k}, \nonumber \\ {\bar{Q}}_{45}= & {} (Q_{55} -Q_{44} )\cos \theta _{k} \sin \theta _{k}, \nonumber \\ {\bar{Q}}_{55}= & {} Q_{55} \cos ^{2}\theta _{k} +Q_{44} \sin ^{2}\theta _{k}. \end{aligned}$$

(A.1)

Appendix B

The detailed derivations of stiffness and mass matrices are as follows:

$$\begin{aligned} \frac{\partial U}{\partial U_{mn}}= & {} \frac{1}{2}\int \limits _{\Omega _{0} } {[(B_{11} \text {e}^{i\omega t}u_{m,x} u_{n} +B_{16} \text {e}^{i\omega t}u_{m} u_{n,y} )(X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} )} \nonumber \\&\quad +(B_{12} \text {e}^{i\omega t}u_{m,x} u_{n} +B_{26} \text {e}^{i\omega t}u_{m} u_{n,y} )(Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} ) \nonumber \\&\quad +(B_{16} \text {e}^{i\omega t}u_{m,x} u_{n} +B_{66} \text {e}^{i\omega t}u_{m} u_{n,y} )(X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} \nonumber \\&\quad +Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )+(2A_{11} U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} +A_{12} V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} \nonumber \\&\quad +A_{16} (2U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} )\nonumber \\&\quad +B_{11} X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} +B_{12} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} \nonumber \\&\quad +B_{16} (X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )-N_{x}^\mathrm{{T}} +N_{x}^\mathrm{{r}} )(\text {e}^{i\omega t}u_{m,x} u_{n} )\nonumber \\&\quad +(A_{12} \text {e}^{i\omega t}u_{m,x} u_{n} +A_{26} \text {e}^{i\omega t}u_{m} u_{n,y} )(V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} ) \nonumber \\&\quad +(2A_{16} U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} +A_{26} V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} \nonumber \\&\quad +A_{66} (2U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} ) \nonumber \\&\quad +B_{16} X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} +B_{26} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y}\nonumber \\&\quad +B_{66} (X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )-N_{xy}^\mathrm{{T}} +N_{xy}^\mathrm{{r}} )(\text {e}^{i\omega t}u_{m} u_{n,y} ) \nonumber \\&\quad +(A_{16} \text {e}^{i\omega t}u_{m,x} u_{n}+A_{66} \text {e}^{i\omega t}u_{m} u_{n,y} )(V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} )]\text {d}x\text {d}y, \end{aligned}$$

(B.1)

$$\begin{aligned} \frac{\partial U}{\partial V_{mn}}= & {} \frac{1}{2}\int \limits _{\Omega _{0} } {[B_{12} \text {e}^{i\omega t}v_{m} v_{n,y} +B_{16} \text {e}^{i\omega t}v_{m,x} v_{n} )(X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} )} \nonumber \\&\quad +(B_{22} \text {e}^{i\omega t}v_{m} v_{n,y} +B_{26} \text {e}^{i\omega t}v_{m,x} v_{n} )(Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} ) \nonumber \\&\quad +(B_{26} \text {e}^{i\omega t}v_{m} v_{n,y} +B_{66} \text {e}^{i\omega t}v_{m,x} v_{n} )(X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )\nonumber \\&\quad +(A_{12} \text {e}^{i\omega t}v_{m} v_{n,y} +A_{16} \text {e}^{i\omega t}v_{m,x} v_{n} )(U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} ) \nonumber \\&\quad +(A_{12} U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} +2A_{22} V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} \nonumber \\&\quad +A_{26} (U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +2V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} ) \nonumber \\&\quad +B_{12} X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} +B_{22} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} \nonumber \\&\quad +B_{26} (X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )-N_{y}^\mathrm{{T}} +N_{y}^\mathrm{{r}} )(\text {e}^{i\omega t}v_{m} v_{n,y} ) \nonumber \\&\quad +(A_{26} \text {e}^{i\omega t}v_{m} v_{n,y} +A_{66} \text {e}^{i\omega t}v_{m,x} v_{n} )(U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} )\nonumber \\&\quad +(A_{16} U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} +2A_{26} V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} \nonumber \\&\quad +A_{66} (U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +2V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} )\nonumber \\&\quad +B_{16} X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} +B_{26} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} \nonumber \\&\quad +B_{66} (X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )-N_{xy}^\mathrm{{T}} +N_{xy}^\mathrm{{r}} )(\text {e}^{i\omega t}v_{m,x} v_{n} )]\text {d}x\text {d}y, \end{aligned}$$

(B.2)

$$\begin{aligned} \frac{\partial U}{\partial W_{mn}}= & {} \frac{1}{2}\int \limits _{\Omega _{0} } [ (k_{s} (A_{45} (2W_{kl} \text {e}^{i\omega t}w_{k} w_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k} y_{l} )\nonumber \\&\quad +A_{55} (2W_{kl} \text {e}^{i\omega t}w_{k,x} w_{l} +X_{kl} \text {e}^{i\omega t}x_{k} x_{l} )))(\text {e}^{i\omega t}w_{m,x} w_{n} ) \nonumber \\&\quad +(k_{s} (A_{45} (\text {e}^{i\omega t}w_{m} w_{n,y} )+A_{55} (\text {e}^{i\omega t}w_{m,x} w_{n} )))(X_{kl} \text {e}^{i\omega t}x_{k} x_{l} )\nonumber \\&\quad +(k_{s} (A_{44} (2W_{kl} \text {e}^{i\omega t}w_{k} w_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k} y_{l} ) \nonumber \\&\quad +A_{45} (2W_{kl} \text {e}^{i\omega t}w_{k,x} w_{l} +X_{kl} \text {e}^{i\omega t}x_{k} x_{l} )))(\text {e}^{i\omega t}w_{m} w_{n,y} )\nonumber \\&\quad +(k_{s} (A_{44} (\text {e}^{i\omega t}w_{m} w_{n,y} )+A_{45} (\text {e}^{i\omega t}w_{m,x} w_{n} )))(Y_{kl} \text {e}^{i\omega t}y_{k} y_{l} )]\text {d}x\text {d}y, \end{aligned}$$

(B.3)

$$\begin{aligned} \frac{\partial U}{\partial X_{mn}}= & {} \frac{1}{2}\int \limits _{\Omega _{0} } {[(B_{11} U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} +B_{12} V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} } \nonumber \\&\quad +B_{16} (U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} ) \nonumber \\&\quad +2D_{11} X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} +D_{12} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} \nonumber \\&\quad +D_{16} (2X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )-M_{x}^\mathrm{{T}} +M_{x}^\mathrm{{r}} )(\text {e}^{i\omega t}x_{m,x} x_{n} ) \nonumber \\&\quad +(D_{12} \text {e}^{i\omega t}x_{m,x} x_{n} +D_{26} \text {e}^{i\omega t}x_{m} x_{n,y} )(Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} )\nonumber \\&\quad +(B_{16} U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} +B_{26} V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} \nonumber \\&\quad +B_{66} (U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} )\nonumber \\&\quad +2D_{16} X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} +D_{26} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} \nonumber \\&\quad +D_{66} (2X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )-M_{xy}^\mathrm{{T}} +M_{xy}^\mathrm{{r}} )(\text {e}^{i\omega t}x_{m} x_{n,y} )\nonumber \\&\quad +(D_{16} \text {e}^{i\omega t}x_{m,x} x_{n} +D_{66} \text {e}^{i\omega t}x_{m} x_{n,y} )(Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} ) \nonumber \\&\quad +(B_{11} \text {e}^{i\omega t}x_{m,x} x_{n} +B_{16} \text {e}^{i\omega t}x_{m} x_{n,y} )(U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} )\nonumber \\&\quad +(B_{12} \text {e}^{i\omega t}x_{m,x} x_{n} +B_{26} \text {e}^{i\omega t}x_{m} x_{n,y} )(V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} ) \nonumber \\&\quad +(B_{16} \text {e}^{i\omega t}x_{m,x} x_{n} +B_{66} \text {e}^{i\omega t}x_{m} x_{n,y} )(U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} )\nonumber \\&\quad +(k_{s} A_{55} \text {e}^{i\omega t}x_{m} x_{n} )(W_{kl} \text {e}^{i\omega t}w_{k,x} w_{l} ) \nonumber \\&\quad +(k_{s} (A_{45} (W_{kl} \text {e}^{i\omega t}w_{k} w_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k} y_{l} )\nonumber \\&\quad +A_{55} (W_{kl} \text {e}^{i\omega t}w_{k,x} w_{l} +2X_{kl} \text {e}^{i\omega t}x_{k} x_{l} )))(\text {e}^{i\omega t}x_{m} x_{n} ) \nonumber \\&\quad +(k_{s} A_{45} \text {e}^{i\omega t}x_{m} x_{n} )(W_{kl} \text {e}^{i\omega t}w_{k} w_{l,y} +Y_{kl} \text {e}^{i\omega t}y_{k} y_{l} )]\text {d}x\text {d}y, \end{aligned}$$

(B.4)

$$\begin{aligned} \frac{\partial U}{\partial Y_{mn} }= & {} \frac{1}{2}\int \limits _{\Omega _{0} } {[(D_{12} \text {e}^{i\omega t}y_{m} y_{n,y} +D_{16} \text {e}^{i\omega t}y_{m,x} y_{n} )(X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} )} \nonumber \\&\quad +(B_{12} U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} +B_{22} V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} \nonumber \\&\quad +B_{26} (U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} )\nonumber \\&\quad +D_{12} X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} +2D_{22} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} \nonumber \\&\quad +D_{26} (X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} +2Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )-M_{y}^\mathrm{{T}} +M_{y}^\mathrm{{r}} )(\text {e}^{i\omega t}y_{m} y_{n,y} )\nonumber \\&\quad +(D_{26} \text {e}^{i\omega t}y_{m} y_{n,y} +D_{66} \text {e}^{i\omega t}y_{m,x} y_{n} )(X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} ) \nonumber \\&\quad +(B_{16} U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} +B_{26} V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} \nonumber \\&\quad +B_{66} (U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} ) \nonumber \\&\quad +D_{16} X_{kl} \text {e}^{i\omega t}x_{k,x} x_{l} +2D_{26} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l,y} \nonumber \\&\quad +D_{66} (X_{kl} \text {e}^{i\omega t}x_{k} x_{l,y} +2Y_{kl} \text {e}^{i\omega t}y_{k,x} y_{l} )-M_{xy}^\mathrm{{T}} +M_{xy}^\mathrm{{r}} )(\text {e}^{i\omega t}y_{m,x} y_{n} ) \nonumber \\&\quad (B_{12} \text {e}^{i\omega t}y_{m} y_{n,y} +B_{16} \text {e}^{i\omega t}y_{m,x} y_{n} )(U_{kl} \text {e}^{i\omega t}u_{k,x} u_{l} )\nonumber \\&\quad +(B_{22} \text {e}^{i\omega t}y_{m} y_{n,y} +B_{26} \text {e}^{i\omega t}y_{m,x} y_{n} )(V_{kl} \text {e}^{i\omega t}v_{k} v_{l,y} ) \nonumber \\&\quad +(B_{26} \text {e}^{i\omega t}y_{m} y_{n,y} +B_{66} \text {e}^{i\omega t}y_{m,x} y_{n} )(U_{kl} \text {e}^{i\omega t}u_{k} u_{l,y} +V_{kl} \text {e}^{i\omega t}v_{k,x} v_{l} )\nonumber \\&\quad +(k_{s} A_{45} \text {e}^{i\omega t}y_{m} y_{n} )(W_{kl} \text {e}^{i\omega t}w_{k,x} w_{l} +X_{kl} \text {e}^{i\omega t}x_{k} x_{l} ) \nonumber \\&\quad +(k_{s} A_{44} \text {e}^{i\omega t}y_{m} y_{n} )(W_{kl} \text {e}^{i\omega t}w_{k} w_{l,y} )\nonumber \\&\quad +(k_{s} (A_{44} (W_{kl} \text {e}^{i\omega t}w_{k} w_{l,y} +2Y_{kl} \text {e}^{i\omega t}y_{k} y_{l} ) \nonumber \\&\quad +A_{45} (W_{kl} \text {e}^{i\omega t}w_{k,x} w_{l} +X_{kl} \text {e}^{i\omega t}x_{k} x_{l} )))(\text {e}^{i\omega t}y_{m} y_{n} )]\text {d}x\text {d}y, \end{aligned}$$

(B.5)

$$\begin{aligned} \frac{\partial K}{\partial U_{mn} }= & {} \frac{-\omega ^{2}}{2}\int \limits _{\Omega _{0} } {\left[ {I_{1} (\text {e}^{i\omega t}u_{m} u_{n} X_{kl} \text {e}^{i\omega t}x_{k} x_{l} )+I_{0} (2\text {e}^{i\omega t}u_{m} u_{n} U_{kl} \text {e}^{i\omega t}u_{k} u_{l} )} \right] } \text {d}x\text {d}y, \end{aligned}$$

(B.6)

$$\begin{aligned} \frac{\partial K}{\partial V_{mn} }= & {} \frac{-\omega ^{2}}{2}\int \limits _{\Omega _{0} } {\left[ {I_{1} (\text {e}^{i\omega t}v_{m} v_{n} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l} )+I_{0} (2\text {e}^{i\omega t}v_{m} v_{n} V_{kl} \text {e}^{i\omega t}v_{k} v_{l} )} \right] } \text {d}x\text {d}y, \end{aligned}$$

(B.7)

$$\begin{aligned} \frac{\partial K}{\partial W_{mn} }= & {} \frac{-\omega ^{2}}{2}\int \limits _{\Omega _{0} } {\left[ {I_{0} (2\text {e}^{i\omega t}w_{m} w_{n} W_{kl} \text {e}^{i\omega t}w_{k} w_{l} )} \right] } \text {d}x\text {d}y, \end{aligned}$$

(B.8)

$$\begin{aligned} \frac{\partial K}{\partial X_{mn} }= & {} \frac{-\omega ^{2}}{2}\int \limits _{\Omega _{0} } {\left[ {I_{2} (2\text {e}^{i\omega t}x_{m} x_{n} X_{kl} \text {e}^{i\omega t}x_{k} x_{l} )+I_{1} (U_{kl} \text {e}^{i\omega t}u_{k} u_{l} \text {e}^{i\omega t}x_{m} x_{n} )} \right] } \text {d}x\text {d}y, \end{aligned}$$

(B.9)

$$\begin{aligned} \frac{\partial K}{\partial Y_{mn} }= & {} \frac{-\omega ^{2}}{2}\int \limits _{\Omega _{0} } {\left[ {I_{2} (2\text {e}^{i\omega t}y_{m} y_{n} Y_{kl} \text {e}^{i\omega t}y_{k} y_{l} )+I_{1} (V_{kl} \text {e}^{i\omega t}v_{k} v_{l} \text {e}^{i\omega t}y_{m} y_{n} )} \right] } \text {d}x\text {d}y, \end{aligned}$$

(B.10)

$$\begin{aligned} \frac{\partial V}{\partial W_{mn} }= & {} \frac{1}{2}\int \limits _{\Omega _{0} } {[{\hat{N}_{x}} 2\text {e}^{i\omega t}w_{m,x} w_{n} W_{kl} \text {e}^{i\omega t}w_{k,x} w_{l} +{\hat{N}_{y}} 2\text {e}^{i\omega t}w_{m} w_{n,y} W_{kl} \text {e}^{i\omega t}w_{k} w_{l,y} ]} \text {d}x\text {d}y. \end{aligned}$$

(B.11)

Using the above equations, the stiffness and mass matrices are computed as follows:

$$\begin{aligned} K= & {} \left[ {{\begin{array}{*{20}c} {\left( \frac{\partial U}{\partial U_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial U}{\partial U_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial U}{\partial U_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial U}{\partial U_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial U}{\partial U_{mn} }\right) _{Y_{kl} } } \\ {\left( \frac{\partial U}{\partial V_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial U}{\partial V_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial U}{\partial V_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial U}{\partial V_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial U}{\partial V_{mn} }\right) _{Y_{kl} } } \\ {\left( \frac{\partial V}{\partial W_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial U}{\partial W_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial U}{\partial W_{mn} }\right) _{W_{kl} } +\left( \frac{\partial V}{\partial W_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial U}{\partial W_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial U}{\partial W_{mn} }\right) _{Y_{kl} } } \\ {\left( \frac{\partial U}{\partial X_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial U}{\partial X_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial U}{\partial X_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial U}{\partial X_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial U}{\partial X_{mn} }\right) _{Y_{kl} } } \\ {\left( \frac{\partial U}{\partial Y_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial U}{\partial Y_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial U}{\partial Y_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial U}{\partial Y_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial U}{\partial Y_{mn} }\right) _{Y_{kl} } } \\ \end{array} }} \right] , \end{aligned}$$

(B.12)

$$\begin{aligned} M= & {} \left[ {{\begin{array}{*{20}c} {\left( \frac{\partial K}{\partial U_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial K}{\partial U_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial K}{\partial U_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial K}{\partial U_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial K}{\partial U_{mn} }\right) _{Y_{kl} } } \\ {\left( \frac{\partial K}{\partial V_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial K}{\partial V_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial K}{\partial V_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial K}{\partial V_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial K}{\partial V_{mn} }\right) _{Y_{kl} } } \\ {\left( \frac{\partial K}{\partial W_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial K}{\partial W_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial K}{\partial W_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial K}{\partial W_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial K}{\partial W_{mn} }\right) _{Y_{kl} } } \\ {\left( \frac{\partial K}{\partial X_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial K}{\partial X_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial K}{\partial X_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial K}{\partial X_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial K}{\partial X_{mn} }\right) _{Y_{kl} } } \\ {\left( \frac{\partial K}{\partial Y_{mn} }\right) _{U_{kl} } } &{} {\left( \frac{\partial K}{\partial Y_{mn} }\right) _{V_{kl} } } &{} {\left( \frac{\partial K}{\partial Y_{mn} }\right) _{W_{kl} } } &{} {\left( \frac{\partial K}{\partial Y_{mn} }\right) _{X_{kl} } } &{} {\left( \frac{\partial K}{\partial Y_{mn} }\right) _{Y_{kl} } } \\ \end{array} }} \right] . \end{aligned}$$

(B.13)