An analytical approach to the analysis of an electrically permeable interface crack in a 1D piezoelectric quasicrystal

Abstract

A plane problem is analysed for an electrically permeable crack in a bi-material composed of two semi-infinite 1D piezoelectric quasicrystals bonded together. The polarization direction coincides with the quasiperiodic direction of the materials and is orthogonal to the interface. Uniformly distributed phonon normal and shear in-plane stresses and also phason stress and electric displacement are applied at infinity. The matrix–vector representations for the phonon and phason stresses, the electrical displacement and for the derivatives of the phonon and phason displacements and electrical potentials jumps via the sectional-holomorphic vector-function are derived. Using these relations and satisfying the conditions at the crack faces, the problems of linear relationship are formulated and solved exactly. All required phonon and phason characteristics are given in the form of simple analytical expressions. A numerical analysis is carried out for two different 1D piezoelectric quasicrystals bonded together. The obtained results are presented in graph and table forms.

1 Introduction

Quasicrystals (QCs) differ from ordinary crystals and non-crystals by their high strength, high wear resistance, low heat-transfer, etc. These materials, found by Shechtman et al. [1] are nowadays extensively used in various areas of technology and engineering.

Because of the quasiperiodic symmetry of QCs, concepts of the high-dimensional space have been introduced instead of the classical crystallographic theory. The phonon field represents the lattice vibrations in QCs, and the phason field defines the quasiperiodic rearrangement of atoms. Both these fields are used to describe the elastic properties of QCs. One-dimensional (1D) QCs exhibit just one quasiperiodic axis, while the perpendicular plane reveals classical crystalline properties. Generalized elasticity theory of QCs and the state of the art is given in e.g. [2,3,4].

The crack problems in homogeneous QCs got due attention in the literature. Using the mathematical theory of elasticity of QCs , Fan et al. [5] and Li et al. [6] studied the moving screw dislocation and straight dislocation in one-dimensional (1D) hexagonal QCs. Enrico et al. [7] studied the linear crack problem in ten symmetric two-dimensional quasicrystals by using the Stroh method. Gao et al. [8] considered the problem of cubic quasicrystal media with an elliptic hole or a crack. Interaction between a semi-infinite crack and a straight dislocation in a decagonal quasicrystal has been analyzed in [9]. Liu et al. [10] studied the interaction of dislocations with cracks in one dimensional hexagonal QCs based on the analytic function theory. Li et al. [11] investigated the interaction of a screw dislocation with an elliptical hole in icosahedral quasicrystals. A one-dimensional hexagonal quasicrystal with a planar crack in an infinite medium was studied in [12]. Path-independent integrals for crack problems in quasicrystals with nonstationary conditions were derived in [13], and the method of crack path prediction under mixed-mode loading in 1D quasicrystals was developed in [14]. An effect of plasticity for a half-infinite Dugdale crack embedded in an infinite space of a one-dimensional hexagonal quasicrystal was studied in [15]. 3D exact analysis of the elastic field in an infinite medium for a two-dimensional hexagonal quasicrystal with a planar crack was performed in [16].

A thermo-elastic field in an infinite space of a two-dimensional hexagonal quasicrystal with a penny-shaped plane crack was studied in [17]. The thermo-elastic field in an infinite one-dimensional hexagonal quasicrystal space with a penny-shaped crack under anti-symmetric uniform heat fluxes was considered in [18]. Fundamental solutions of penny-shaped and half-infinite plane cracks in an infinite space of a one-dimensional hexagonal quasicrystal under thermal loading has been obtained in [19], and thermo-elastic Green’s functions for an infinite bi-material composed of one-dimensional hexagonal quasicrystals were found in [20]. Fundamental solutions for three-dimensional cracks in one-dimensional hexagonal piezoelectric quasicrystals were found in [21]. The problem of crack opening and closing in a soft-matter pentagonal and decagonal quasicrystal was considered in [22]. Shear cracks moving in one-dimensional hexagonal quasicrystalline materials were studied in [23].

Piezoelectricity is an important physical property of QCs. The piezoelectric QCs were investigated in papers [24,25,26,27]. Green’s functions of a one-dimensional quasicrystal bi-material with piezoelectric effect were investigated in [28]. A set of 3D general solutions to static problems of 1D hexagonal piezoelectric quasicrystals is obtained in [29] with use of displacement functions. Three-dimensional cracks in one-dimensional hexagonal piezoelectric quasicrystals were studied in [30], and a penny-shaped dielectric crack in the quasicrystal plate of the same structure was considered in [31]. Two collinear electrically permeable anti-plane cracks of equal length lying at the mid-plane of a one-dimensional hexagonal piezoelectric quasicrystal strip were investigated in [32]. Two asymmetrical limited permeable cracks emanating from an elliptical hole in one-dimensional hexagonal piezoelectric quasicrystals were considered in [33]. An anti-plane crack in a half-space of a one-dimensional piezoelectric quasicrystal was investigated in [34].

However, interface cracks in bi-material and multi-material components between different QC materials have not been sufficiently studied till now. As far as we know on this subject, an arbitrarily shaped electrically impermeable interface crack in a one-dimensional hexagonal thermo-electro-elastic quasicrystal bi-material was investigated in [35, 36] by an analytical-numerical method, and a crack between dissimilar one-dimensional hexagonal quasicrystals with piezoelectric effect under anti-plane shear and in-plane electric loadings was recently studied in [37].

The present paper is devoted to developing an exact analytical solution for an electrically permeable interface crack situated in the interface between two bonded one-dimensional hexagonal QCs with point group 6 mm [23]. Phonon and phason stress components, their intensity factors, and also crack displacement jumps are presented in a simple analytical form and illustrated graphically. The importance of the obtained solution is justified by the absence of sufficient analytical results on interface cracks in QCs and by the possibility of using the obtained equations and results for verifying of numerical solutions for similar problems in finite sized domains.

2 Formulation of the basic relations

For the linear elastic theory of QCs, the constitutive relations, equilibrium equations, and geometric equations of a 1D piezoelectric hexagonal QC with point group 6 mm without body forces and free charges can be expressed in the following form:

$$\begin{aligned} \sigma _{ij}= & {} c_{ijks} \varepsilon _{ks} -e_{sij} E_{s} +R_{ij3s} W_{3s} , \end{aligned}$$

(1)

$$\begin{aligned} D_{i}= & {} e_{iks} \varepsilon _{ks} +\xi _{is} E_{s} +\tilde{{e}}_{i3s} W_{3s} , \end{aligned}$$

(2)

$$\begin{aligned} H_{3i}= & {} R_{ks3i} \varepsilon _{ks} -\tilde{{e}}_{s3i} E_{s} +K_{3i3s} W_{3s}, \end{aligned}$$

(3)

$$\begin{aligned} \sigma _{ij,j}= & {} 0, D_{i,i} =0, H_{3i,i} =0, \end{aligned}$$

(4)

$$\begin{aligned} \varepsilon _{ij}= & {} \tfrac{1}{2}(u_{i,j} +u_{j,i} ), E_{i} =-\phi _{,i} , W_{3i} =W_{3,i} \end{aligned}$$

(5)

where $i, j, k, s=1$, 2, 3, and the denotation “,” represents the derivative operation for the space variables; $u_{i}$, $W_{3}$, and $\varphi$ are the phonon displacements, phason displacement, and electric potential, respectively, and the atom arrangement is periodic in the $x_{1}$–$x_{2}$ plane and quasiperiodic in the $x_{3}$-axis; $\sigma _{ij}$ and $\varepsilon _{ks}$ are the phonon stresses and strains, respectively; $H_{3i}$ and $W_{3i}$ are the phason stresses and strains, respectively; $D_{i}$ and $E_{i}$ are the electric displacements and electric fields, respectively, and the polarization direction is along the $x_{3}$-axis; $c_{ijks}$ and $K_{3j3s}$ are the elastic constants in the phonon and phason fields, respectively; $R_{ij3k}$ represent the phonon–phason coupling elastic constants; $e_{jks}$ and $\tilde{{e}}_{jks}$ are the piezoelectric constants in the phonon and phason fields, respectively; $\xi _{is}$ are the permittivity constants.

From (1)–(5) one gets the following governing equations:

$$\begin{aligned} \left\{ \begin{array}{c} \left( {c_{ijks} u_{k} +e_{sij} \varphi +R_{ij3s} W_{3} } \right) _{,si} =0,\\ \left( {e_{iks} u_{k} -\xi _{is} \varphi +\tilde{{e}}_{i3s} W_{3} } \right) _{,si} =0,\\ \left( {R_{ik3s} u_{k} +\tilde{{e}}_{i3s} \varphi +K_{3i3s} W_{3} } \right) _{,si} =0.\\ \end{array}\right. \end{aligned}$$

(6)

Next we introduce the following vectors:

$$\begin{aligned} {\mathbf{V}}=\left\{ \begin{array}{ccccc} u_{1}, &{} u_{2}, &{} u_{3}, &{} \varphi , &{} W_{3} \\ \end{array}\right\} ^{T}, {\mathbf{t}}=\left\{ \begin{array}{ccccc} \sigma _{31}, &{} \sigma _{32}, \sigma _{33}, &{} D_{3}, &{} H_{33} \\ \end{array}\right\} ^{T}, \end{aligned}$$

(7)

where the superscript T stands for the transposed matrix.

Performing the analysis presented in “Appendixes 1 and 2”, one arrives at the following representations:

$$\begin{aligned} \langle \mathbf{V}'(x_{1})\rangle= & {} {\varvec{\upomega }}^{+} (x_{1})-{\varvec{\upomega }}^{-}(x_{1}), \end{aligned}$$

(8)

$$\begin{aligned} {\mathbf{t}}^{(1)}(x_{1}, 0)= & {} \mathbf{G}{\varvec{\upomega }}^{+} (x_{1})- \bar{\mathbf{G}}{\varvec{\upomega }}^{-}(x_{1}) \end{aligned}$$

(9)

where the $5\times 5$ matrix ${\mathbf{G}}$ is defined in “Appendix 2” and ${\varvec{\upomega }}(z)$ is a vector-function analytic in the whole plane cut along $-b<x_{1}<b$, $x_{3}=0$.

Consider further the plane problem in the $x_{1}$–$x_{3}$ plane assuming all fields are independent on the coordinate $x_{2}$. We’ll use the contracted notation, whereby a pair of indices is changed into a single index according to the rule: $\underline{11}\rightarrow 1$, $\underline{22}\rightarrow 2$, $\underline{33}\rightarrow 3$, $\underline{23}$ or $\underline{32}\rightarrow 4$, $\underline{13}$ or $\underline{31}\rightarrow 5$, $\underline{12}$ or $\underline{21}\rightarrow 6$. The constitutive relations for 1D hexagonal piezoelectric QCs, referred to the Cartesian coordinate $(x_{1}, x_{2}, x_{3})$ with $(x_{1}, 0,x_{2})$ coincident with the periodic plane and $x_{3}$-axis identical to the quasiperiodic direction attain the form

The equilibrium and geometric equations in this case follow from (4) and (5), respectively.

The matrix G from Eq. (7) without the second row and column has in this case the following structure:

$$\begin{aligned} {\mathbf{G}}=\left[ \begin{array}{*{20}l} {ig_{11} } &{}\quad {g_{13}} &{}\quad {g_{14}} &{}\quad {g_{15} } \\ {g_{31} } &{}\quad {ig_{33}} &{}\quad {ig_{34}} &{}\quad {ig_{35}} \\ {g_{41} } &{}\quad {ig_{43}} &{}\quad {ig_{44}} &{}\quad {ig_{45}} \\ {g_{51} } &{}\quad {ig_{53}} &{}\quad {ig_{54}} &{}\quad {ig_{55}} \\ \end{array}\right] , \end{aligned}$$

(11)

where all $g_{ij}$ are real and ${g}_{31}=-{g}_{13}$, ${g}_{41}=-{g}_{14}$, ${g}_{51}=-{g}_{15}$, ${g}_{53}={g}_{35}$, ${g}_{43}={g}_{34}$, ${g}_{45}={g}_{54}$ holds true.

3 A single electrically permeable interface crack between two different 1D hexagonal piezoelectric QCs

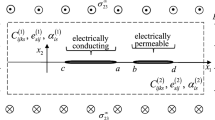
Consider a crack $-b\le x_{1} \;\le b$, $x_{3} \;=0$ in the interface between two semi-infinite 1D piezoelectric hexagonal quasicrystalline spaces with point group 6 mm (Fig. 1). It is assumed that uniform phonon ($\sigma ^{\infty },\tau ^{\infty })$ and phason $H^{\infty }$ stresses as well as electrical displacement $D^{\infty }$ are prescribed at infinity. It is assumed also that the crack is electrically permeable and all fields are independent on the coordinate $x_{2}$.

Fig. 1

A crack between two 1D piezoelectric QCs

In this case relations (8), (9) are valid with the matrix G defined by Eq. (9). The interface conditions have the following form:

$$\begin{aligned}&\sigma _{13}^{\pm } =0, \quad \sigma _{33}^{\pm } =0,\quad H_{33}^{\pm } =0, \left\langle \varphi \right\rangle =0,\quad \;\left\langle { D_{3} } \right\rangle =0\ \hbox {for}\ -b<x_{1} \;<b, \end{aligned}$$

(12)

$$\begin{aligned}&\left\langle {\sigma _{13} } \right\rangle =0,\;\quad \left\langle {\sigma _{33} } \right\rangle =0,\quad \left\langle {H_{33} } \right\rangle =0,\;\;\left\langle {u_{1} } \right\rangle =0,\;\;\left\langle {u_{3} } \right\rangle =0,\nonumber \\&\left\langle {W_{3} } \right\rangle =0,\,\;\left\langle \varphi \right\rangle =0,\;\left\langle { D_{3} } \right\rangle =0\ \hbox {for}\ x_{1} \;\notin (-b,b) \end{aligned}$$

(13)

where $\langle f \rangle$ means the jump of the function f over the material interface.

Because of the two last equations in (12) and (13) together with Eq. (8), one has

$$\begin{aligned} \left\langle \varphi ' \right\rangle =\left\langle {{V}'_{4} \left( {x_{1} } \right) } \right\rangle =\omega _{4}^{+} \left( {x_{1}} \right) -\omega _{4}^{-} \left( {x_{1} } \right) =0\ \hbox {for} \ x_{1} \in \left( {-\infty ;\;\infty } \right) . \end{aligned}$$

It means that the function $\omega _{4} (z)$ is analytic in the whole plane and

$$\begin{aligned} \omega _{4} (z)=\omega _{4}^{0} =const \end{aligned}$$

holds true.

Because of $x_{1} \;\notin (-b,b)$ one has ${\varvec{\upomega }}^{+}(x_{1})={\varvec{\upomega }}^{-}( {x_{1} }) ={\varvec{\upomega }}({x_{1}})$; then it follows from Eq. (3) that

$$\begin{aligned} {\mathbf{t}}^{(1)}(x_{1}, 0) = (\mathbf{G}-\bar{\mathbf{G}})\,{\varvec{\upomega }} ({x_{1} })\ \hbox {for}\ x_{1} \;\notin (-b,b) \end{aligned}$$

(14)

and

$$\begin{aligned} {\mathbf{t}}^{\infty }={{\mathbf{t}}^{\left( 1 \right) } \left( {x_{1} ,0} \right) } \bigg |_{x_{1} \rightarrow \infty } =\left( {{\mathbf{G}}-{\bar{{\mathbf{G}}}}} \right) {\varvec{\upomega }} (z)\bigg |_{z\rightarrow \infty }, \end{aligned}$$

(15)

where ${\mathbf{t}}^{\infty }=\left\{ {\tau ^{\infty }, \sigma ^{\infty }, D^{\infty },\;H^{\infty }} \right\} ^{T}$.

It follows from Eq. (15)

$$\begin{aligned} {\varvec{\upomega }}\left( z \right) \bigg |_{z\rightarrow \infty } =\left( {{\mathbf{G}}-{\bar{{\mathbf{G}}}}} \right) ^{-1}{\mathbf{t}}^{\infty } \end{aligned}$$

(16)

and, therefore,

$$\begin{aligned} \omega _{4}^{0} =\left\{ {\left( {{\mathbf{G}}-{\bar{{\mathbf{G}}}}}\right) ^{-1} {\mathbf{t}}^{\infty }} \right\} _{4} \end{aligned}$$

is the forth component of the vector (16).

By introducing the following vectors:

$$\begin{aligned} {\mathbf{Q}}=\left\{ {{\begin{array}{c} {\sigma _{31} } \\ {\sigma _{33} } \\ {H_{33} } \\ \end{array} }} \right\} , {\mathbf{e}}=\left\{ {{\begin{array}{c} {e_{1} } \\ {e_{3} } \\ {e_{5} } \\ \end{array} }} \right\} , {\varvec{\Psi }}=\left\{ {{\begin{array}{c} {\Psi _{1} } \\ {\Psi _{3} } \\ {\Psi _{5} } \\ \end{array} }} \right\} , \ \hbox {and the matrix} \ {\varvec{\uprho }}=\left[ {{\begin{array}{lll} {\rho _{11} } &{}\quad {\rho _{13} } &{}\quad {\rho _{15} } \\ {\rho _{31} } &{}\quad {\rho _{33} } &{}\quad {\rho _{35} } \\ {\rho _{51} } &{}\quad {\rho _{53} } &{}\quad {\rho _{55} } \\ \end{array} }} \right] \end{aligned}$$

(17)

with the components $e_{1} =0,\;e_{3} =2G_{34} \omega _{40} ,\;e_{5} =2G_{54} \omega _{40}$, $\Psi _{i} =\omega _{i}$, $\rho _{ij} =G_{ij}$ ($i, j=1$,3,5), the representation (9) without the second and forth equations can be written in the form

$$\begin{aligned} {\mathbf{Q}}^{(1)}(x_{1}, 0)=\mathbf{R} {\varvec{\Psi }}^{+}(x_{1}) -{\bar{{\mathbf{R}}}} {\varvec{\Psi }}^{-}(x_{1}). \end{aligned}$$

(18)

Further, the transformation of Eq. (18) will be performed similarly to the case of an electromechanical loading (Herrmann et al. [38]). Introducing a one line matrix ${\mathbf{S}}=[S_{1} ,S_{3} ,S_{5} ]$ and considering a product ${\mathbf{SQ}}^{(1)}(x_{1} ,0)$, the following relations can be obtained by use of Eqs. (9) and (18):

$$\begin{aligned}&\sigma _{33}^{(1)} (x_{1} ,0)+m_{j5} H_{33}^{(1)} (x_{1} ,0)+im_{j1} \sigma _{13}^{(1)} (x_{1} ,0)=\Omega _{j}^{+} (x_{1} )+\gamma _{j} \Omega _{j}^{-} (x_{1} )+\eta _{j}, \end{aligned}$$

(19)

$$\begin{aligned}&n_{j1} \left\langle {{u}'_{1} (x_{1} )} \right\rangle +in_{j3} \left\langle {{u}'_{3} (x_{1} )} \right\rangle +in_{j5} \left\langle {{W}'_{3} (x_{1} )} \right\rangle =\Omega _{j}^{+} (x_{1} )-\Omega _{j}^{-} (x_{1} ), \end{aligned}$$

(20)

where

$$\begin{aligned} \Omega _{j} (z)=n_{j1} \Psi _{1} (z)+i\{n_{j3} \Psi _{3} (z)+n_{j5} \Psi _{5} (z)\}, \end{aligned}$$

(21)

$\eta _{j} ={\mathbf{S}}_{j} {\mathbf{e}}=2(G_{34} +m_{j3} G_{54} )W_{40}$, $m_{j5} =S_{j5}$, $m_{j1} =-iS_{j1}$, $n_{j1} =Y_{j1}$, $n_{j3} =-iY_{j3}$, $n_{j5} =-iY_{j5}$, and $m_{jl} ,\,n_{jl}$ ($l=1,3,5$) are real, ${\mathbf{Y}}_{j} ={\mathbf{S}}_{j} {\varvec{\uprho }}$. Moreover, $\gamma _{j}$ and ${\mathbf{S}}_{j}^{T} =[S_{j1} ,S_{j3} ,S_{j5} ]$ ($j=1,3,5$) are, respectively, the eigenvalues and eigenvectors of the matrix $(\gamma \;{\varvec{\uprho }}^{T}+\bar{{\varvec{\uprho }}}^{T})$. The roots of the equation $\det (\gamma \;{\varvec{\uprho }}^{T} +\bar{{\varvec{\uprho }}}^{T})=0$ can be presented in the form

$$\begin{aligned} \gamma _{1} =\frac{1+\delta }{1-\delta }, \quad \gamma _{3} =\gamma _{1}^{-1} ,\quad \gamma _{5} =1, \end{aligned}$$

(22)

where

$$\begin{aligned} \delta ^{2}=\frac{g_{15}^{2} g_{33} +g_{13}^{2} g_{55} -2g_{15} g_{13} g_{35} }{g_{11} (g_{33} g_{55} -g_{35}^{2})}. \end{aligned}$$

(23)

It appears to be that $\delta ^{2}>0$ holds true for 1D piezoelectric QC bimaterials considered in this paper. In this case the properties of the coefficients $m_{jl} ,\,n_{jl}$ reported above are valid.

Taking into account that for $x_{1} \;\notin (-b,b)$ the relationships $\Omega _{j}^{+} (x_{1} )=\Omega _{j}^{-} (x_{1} )=\Omega _{j} (x_{1} )$ hold true, one has

$$\begin{aligned} (1+\gamma _{j} )\Omega _{j} (x_{1} )={\mathbf{S}}_{j} {\mathbf{Q}}^{(1)}(x_{1} ,0) \ \text {for}\ x_{1} \rightarrow \infty . \end{aligned}$$

(24)

But taking into account that the functions $\Omega _{j} (z)$ are analytic in the whole plane cut along $-b<x_{1} \;<b$, $x_{2} =0$, and by using that ${\mathbf{Q}}^{(1)}(x_{1} ,0)=[\tau ^{\infty }, \sigma ^{\infty },H^{\infty }]^{T}$ for $x_{1} \rightarrow \infty$, one has

$$\begin{aligned} \Omega _{j} (z)=(1+\gamma _{j} )^{-1}(im_{j1} \tau ^{\infty } +\sigma ^{\infty }+m_{j5} H^{\infty }-\eta _{j} ) \ \text {for}\ z\rightarrow \infty . \end{aligned}$$

(25)

By introducing new functions

$$\begin{aligned} \Theta _{j} (z)=\Omega _{j} (z)+(1+\gamma _{j} )^{-1}\eta _{j}, \end{aligned}$$

(26)

Eqs. (19), (20), and (25) are written in the form

$$\begin{aligned}&\sigma _{33}^{(1)} (x_{1} ,0)+m_{j5} H_{33}^{(1)} (x_{1} ,0)+im_{j1} \sigma _{13}^{(1)} (x_{1} ,0)=\Theta _{j}^{+} (x_{1} ) +\gamma _{j} \Theta _{j}^{-} (x_{1}), \end{aligned}$$

(27)

$$\begin{aligned}&n_{j1} \left\langle {{u}'_{1} (x_{1} )} \right\rangle +in_{j3} \left\langle {{u}'_{3} (x_{1} )} \right\rangle +in_{j5} \left\langle {{W}'_{3} (x_{1} )} \right\rangle =\Theta _{j}^{+} (x_{1}) -\Theta _{j}^{-} (x_{1} ), \end{aligned}$$

(28)

$$\begin{aligned}&\Theta _{j} (z)\vert _{z\rightarrow \infty } =(1+\gamma _{j} )^{-1}(im_{j1} \tau ^{\infty }+\sigma ^{\infty }+m_{j5} H^{\infty }). \end{aligned}$$

(29)

Satisfying the interface conditions (12) by using Eq. (27), one arrives at the following Riemann boundary value problem:

$$\begin{aligned} \Theta _{j}^{+} \left( {x_{1} } \right) +\gamma _{j} \,\Theta _{j}^{-} \left( {x_{1} } \right) =0\ \hbox {for}\ x_{1} \in \left( {-b,b} \right) , \end{aligned}$$

(30)

with the conditions at infinity (29).

According to [37], the solution of this problem has the following form:

$$\begin{aligned} \Theta _{j} (z)=X_{j} (z)(\sigma _{j}^{*} -i\tau _{j}^{*})(z-2ib\varepsilon _{j}), \end{aligned}$$

(31)

where $X_{j}(z)=(z+b)^{{-1/2+i\varepsilon }_{j}} (z-b)^{{-1/2+i\varepsilon }_{j}}$, $\sigma _{j}^{*} =\frac{1}{r_{j} }(\sigma ^{\infty }+m_{j5} H^{\infty }), \tau _{j}^{*} =-m_{j1} \tau ^{\infty }/r_{j}$, $r_{j}=(1+\gamma _{j})$, $\varepsilon _{j}= \frac{\mathrm{ln}\gamma _j}{2\pi }$ , $j=1$, 3, 5.

4 Determination of phonon and phason displacement jumps and stresses

Substituting (31) into Eq. (28), one gets

$$\begin{aligned}&n_{j1} \left\langle {{u}'_{1} (x_{1} ,0)} \right\rangle +i\left\{ {n_{j3} \left\langle {{u}'_{3} (x_{1} ,0)} \right\rangle +n_{j4} \left\langle {{W}'_{3} (x_{1} ,0)} \right\rangle } \right\} \nonumber \\&\quad =\frac{\gamma _{j}+1}{\gamma _{j}}(\sigma _{j}^{*}-i\tau _{j}^{*}) (x_{1}+b)^{{-1/2+i\varepsilon }_{j}}(x_{1}-b)^{{-1/2+i\varepsilon }_{j}} (x_{1}-2ib\varepsilon _{j}) \quad (j=1, 3, 5). \end{aligned}$$

(32)

By integrating this equation, one arrives at the formula

$$\begin{aligned}&n_{j1} \left\langle {u_{1} (x_{1} ,0)} \right\rangle +i\left\{ {n_{j3} \left\langle {u_{3} (x_{1} ,0)} \right\rangle +n_{j4} \left\langle {W_{3} (x_{1} ,0)} \right\rangle } \right\} \nonumber \\&\quad = \frac{\gamma _{j}+1}{\gamma _{j}}(\sigma _{j}^{*}-i\tau _{j}^{*}) \left( \frac{x_{1}+b}{x_{1}-b}\right) ^{{i\varepsilon }_{j}} \sqrt{x_{1}^{2}-b^{2}}\ \hbox {for}\ x_{1}\in (-b, b), \quad j=1, 3, 5. \end{aligned}$$

(33)

The analysis shows that for the considered class of QCs the relations $n_{51} =0$, $\varepsilon _{5} =0$, $\gamma _{5} =1$ are valid. Because of this, the equations

$$\begin{aligned}&n_{13} \left\langle {u_{3} (x_{1} ,0)} \right\rangle +n_{15} \left\langle {W_{3} (x_{1} ,0)} \right\rangle =\hbox {Im}\left\{ \frac{\gamma _{1}+1}{\gamma _{1}}(\sigma _{1}^{*}-i\tau _{1}^{*}) {\left( \frac{x_{1}+b}{x_{1}-b}\right) }^{{i\varepsilon }_{1}} \sqrt{x_{1}^{2}-b^{2}}\right\} , \end{aligned}$$

(34)

$$\begin{aligned}&n_{53} \left\langle {u_{3} (x_{1} ,0)} \right\rangle +n_{55} \left\langle {W_{3} (x_{1} ,0)} \right\rangle =-2i(\sigma _{5}^{*} -i\tau _{5}^{*} )\sqrt{x_{1}^{2} -b^{2}} \end{aligned}$$

(35)

can be derived from (33) for $x_{1}\in (-b, b)$.

These relations are a system of linear algebraic equations for $\langle {u_{3} (x_{1} ,0)} \rangle$ and $\langle {W_{3} (x_{1}, 0)} \rangle$ leading to the solution

$$\begin{aligned} \left\langle {u_{3} (x_{1} ,0)} \right\rangle= & {} \Delta ^{-1}\left\{ {n_{55} H_{1} (x_{1} )-n_{15} H_{2} (x_{1} )} \right\} , \nonumber \\ \left\langle {W_{3} (x_{1} ,0)} \right\rangle= & {} \Delta ^{-1}\left\{ {-n_{53} H_{1} (x_{1} )+n_{13} H_{2} (x_{1} )} \right\} , \end{aligned}$$

(36)

where $H_{1}(x_{1})=\{\frac{\gamma _{1}+1}{\gamma _{1}} (\sigma _{1}^{*}\cos \alpha +\tau _{1}^{*}\sin \alpha ) \sqrt{x_{1}^{2}-b^{2}}$, $H_{2} (x_{1} )=2\,\sigma _{5}^{*} \sqrt{b^{2}-x_{1}^{2}}$, $\alpha =\varepsilon _{1}\mathrm{ln}(\frac{b+x_{1}}{b-x_{1}})$, $\Delta =n_{13} n_{55} -n_{53} n_{15}$.

By means of relations (27) and (31) and in view of the properties of the matrix m the phonon and phason stresses for $x_{1}>b$ can be written in the form

$$\begin{aligned}&\sigma _{33}^{(1)} (x_{1} ,0)+m_{15} H_{33}^{(1)} (x_{1} ,0)+im_{11} \sigma _{13}^{(1)} (x_{1} ,0)\nonumber \\&\quad =(1+\gamma _{1}) \left( {\sigma _{1}^{*} -i\tau _{1}^{*}}\right) \left( {x_{1} -2ib\varepsilon _{1} } \right) (x_{1}+b)^{-1/2+i\varepsilon _{1}} (x_{1} -b)^{-1/2-i\varepsilon _{1} }+m_{15}H^{\infty }, \end{aligned}$$

(37)

$$\begin{aligned}&\sigma _{33}^{(1)} (x_{1} ,0)+m_{55} H_{33}^{(1)} (x_{1} ,0) =\frac{2\sigma _{5}^{*} x_{1} }{\sqrt{x_{1}^{2} -b^{2}}} +m_{55}H^{\infty }. \end{aligned}$$

(38)

The shear stress $\sigma _{13}^{(1)} (x_{1}, 0)$ can be found directly from (37) whilst (38) and the real part of (37) composes the system of two linear algebraic equations with respect to $\sigma _{33}^{(1)} (x_{1} ,0),\,\;H_{33}^{(1)} (x_{1} ,0)$, from which these functions can be easily found.

The intensity factors (IFs) at the point b are defined as [38]:

$$\begin{aligned} K_{1} +m_{15} K_{5} +im_{11} K_{2}= & {} \lim \limits _{x_{1} \rightarrow b+0} \sqrt{2\pi (x_{1} -b)} (x_{1} -b)^{i\varepsilon _{1}}\nonumber \\&\times [\sigma _{33}^{(1)} (x_{1},0) +m_{15} H_{33}^{(1)} (x_{1} ,0) +im_{11} \sigma _{13}^{(1)} (x_{1},0)], \end{aligned}$$

(39)

$$\begin{aligned} K_{1} +m_{55} K_{5}= & {} \lim \limits _{x_{1} \rightarrow b+0} \sqrt{2\pi \left( {x_{1} -b} \right) } \left[ {\sigma _{33}^{(1)} (x_{1} ,0) +m_{55}H_{33}^{(1)} (x_{1} ,0)} \right] . \end{aligned}$$

(40)

Using (37), (38), one gets for $x_{1} \rightarrow b+0$

$$\begin{aligned} K_{1} +m_{15} K_{5} -im_{11} K_{2}= & {} \sqrt{\frac{l\pi }{2}} \left( {1-2i\varepsilon _{1}}\right) [\sigma ^{\infty } +m_{15} H^{\infty }-im_{11} \tau ^{\infty }]e^{i\psi }, \end{aligned}$$

(41)

$$\begin{aligned} K_{1} +m_{55} K_{5}= & {} \sqrt{\frac{l\pi }{2}} \left( {\sigma ^{\infty } +m_{55} H^{\infty }}\right) , \end{aligned}$$

(42)

where $\psi = \varepsilon \mathrm{ln} l$, $\alpha =\frac{(\gamma _{1}+1)^{2}}{4\gamma _{1}}$, and $l=2b$ is the crack length. From the formulae (41), (42) the analytical expressions for $K_{1}$, $K_{2}$, and $K_{5}$ can be easily derived.

In some cases, the distribution of phonon and phason components over the whole bimaterial region is important to know. By considering the achievement of this purpose, Eqs. (A.11) and (A.20) we can write

$$\begin{aligned} {\mathbf{t}}^{(m)}(x_{1} ,x_{3} )=2Re\left\{ {{\mathbf{B}}^{(m)}\,{\varvec{\Lambda }} {\varvec{\upomega }}(z)} \right\} ,\ ({m} = 1,2) \end{aligned}$$

(43)

where ${\varvec{\Lambda }}=\left\{ \begin{array}{ll} \mathbf{D}^{-1} &{}\quad \hbox {for}\ x_{3} >0 \\ -\bar{\mathbf{D}}^{-1} &{} \quad \hbox {for}\ x_{3} <0 \\ \end{array}\right.$.

Using further (17) and (21), one gets

$$\begin{aligned} \omega _{i} (z)=\sum \limits _{j=1,3,5} {\kappa _{ij} } \Omega _{j} (z) (i=1, 3, 5), \end{aligned}$$

(44)

where ${\varvec{\upkappa }}={\mathbf{n}}_{0}^{-1}$, ${\mathbf{n}}_{0} =\left( \begin{array}{ccc} n_{11} &{}\quad in_{13} &{}\quad in_{15} \\ n_{31} &{}\quad in_{33} &{}\quad in_{35} \\ n_{51} &{}\quad in_{53} &{}\quad in_{55} \\ \end{array}\right)$.

Taking into account also that $\omega _{4} (z)=\omega _{4}^{0}$, Eq. (43) in the expanded form is written as

$$\begin{aligned} t_{i}^{(m)} (x_{1} ,x_{3} )=2Re\left\{ \sum \limits _{l=1,3,5} \left[ \Pi _{il}^{(m)} \,\Omega _{l} (z_{l}^{(m)})\right] +\omega _{4}^{0}\sum \limits _{j=1,3,4,5} \left( \Lambda _{j4} B_{ij}^{(m)}\right) \right\} \ (i=1, 3, 5), \end{aligned}$$

(45)

where $\Pi _{il}^{(m)} =\sum \nolimits _{j=1,3,4,5} {B_{ij}^{(m)} \sum \nolimits _{k=1,3,5} {\Lambda _{jk} } } \kappa _{kl}$.

The required phonon and phason stresses can be calculated with the formula (45) at any part of the upper ($m=1$) and lover ($m=2$) half planes.

5 Numerical results and discussion

Consider as upper and lower materials the piezoelectric QCs given in “Appendix 3”.

In Table 1, the values of the SIFs obtained from Eqs. (41), (42) for different variants of external phonon loading, $H^{\infty }=0$ and $b=10$ mm are presented. It can be seen from the second and third lines of this Table that, unlike a crack in a homogeneous QC, each separate nonzero external component produces nonzero values of all SIFs.

Table 1 The values of the SIFs $K_{1}$, $K_{2}$, and $K_{5}$ for different variants of external loading

Because of linearity of the considered problem, the SIFs for other values of $\sigma ^{\infty }, \tau ^{\infty }$ can be obtained by simple linear combinations of the obtained results. Some particular cases of such combinations leading to zero intensity factors of certain field components are shown in lines 4–6 of Table 1. It is seen from the presented results that the shear stress has more essential influence on the intensity factor of phason stress than the normal one.

In Fig. 2, the variations of the phonon normal displacement jump $\langle {u_{3} (x_{1} ,0)} \rangle$ along the crack region for $\sigma ^{\infty }=10$ MPa and $b=10$ mm are presented. Lines I, II, and III correspond to $H^{\infty }$ equal to 0 MPa, 1 MPa, and 2 MPa, respectively. It is seen from this Figure that positive external phason normal stress increases the phonon crack opening.

Similar results for the phason displacement jump $\langle W_{3} (x_{1} ,0)\rangle$ for the same loading and the crack length as in Fig. 2 are given in Fig. 3. Lines I, II, and III also correspond to the same values of $H^{\infty }$ as in Fig. 2. It is seen from this Figure that pure positive phonon normal stress induces a negative phason displacement jump (line I), and additional positive phason normal stress $H^{\infty }$ corrects this displacement jump to positive values.

Fig. 2

The variations of the phonon normal displacement jump $\langle u_{3} (x_{1}, 0)\rangle$ along the crack region for $\sigma ^{\infty }=10$ MPa and different values of $H^{\infty }$

Fig. 3

The phason displacement jump $\langle W_{3} (x_{1} ,0) \rangle$ for the same crack and loadings as in Fig. 2

The phason displacement jumps $\langle W_{3} (x_{1} ,0) \rangle$ for $\sigma ^{\infty }=10$ MPa, $b=10$ mm and different values of shear stress $\tau ^{\infty }$ are given in Fig. 4. Lines I, II, and III correspond to $\tau ^{\infty }$ equal to 0 MPa, 5 MPa, and 10 MPa, respectively. It is seen from this Figure that the phason displacement jump is symmetrical for $\tau ^{\infty }=0$ (line I), but application of nonzero shear stress of the same order as $\sigma ^{\infty }$ moderately influences this displacement jump leading to its symmetry losing (lines II and III).

Fig. 4

Phason displacement jump $\langle W_{3} (x_{1} ,0) \rangle$ for the mixed mode phonon loading

It is seen from the formulas (33)–(35) that the displacement jumps include oscillating terms. This means that some zones of crack faces interpenetration exist at the crack tips. For $\tau ^{\infty }=0$ these zones are extremely small, and they are invisible in Fig. 2. However, with increasing absolute values of $\tau ^{\infty }$, one of these zones grows and another one decreases. Such situation with the longer interpenetrations zone of the phonon normal displacement is demonstrated in Fig. 5. This Figure is obtained for $b=0.1$ m, $\sigma ^{\infty }=1$ MPa, and $\tau ^{\infty }$ equals to 0 (line I), $-40$ MPa (II), $-70$ MPa (III), and $-100$ MPa (IY). It can be seen that visible zones of the crack faces interpenetrations appear only for a rather large phonon shear field. Therefore, in most cases the considered model, even if it does not account for the contact zones at the crack faces, can be used in the sense suggested in Ref. [40].

Fig. 5

Phonon displacement jump $\langle u_{3} (x_{1} ,0) \rangle$ at the right crack tip for a relatively large phonon shear field

Fig. 6

Variation of the phonon shear stress $\sigma _{13}^{(1)} (x_{1}, 0)$ on the right crack continuation for $\sigma ^{\infty }=10$ MPa, $b=10$ mm and different $\tau ^{\infty }$

In Fig. 6, the variation of the phonon shear stress $\sigma _{13}^{(1)} (x_{1}, 0)$ on the crack continuation for $\sigma ^{\infty }=10$ MPa, $b=10$ mm, and different $\tau ^{\infty }$ are presented. Lines I, II, and III correspond to $\tau ^{\infty }$ equal to 0, 0.01 MPa, and 0.02 MPa, respectively. This Figure shows that the relatively small values of $\tau ^{\infty }$ with respect to $\sigma ^{\infty }$ have rather significant influence upon the near tip shear stress.

In Fig. 7, the distributions of the phason stress $H_{33}^{(1)} (x_{1}, x_{2})$ at the upper vicinity of the right crack tip ($x_{1} =0.01,\;x_{2} =0)$ are presented for the illustration of using the formula (45). The combination of materials was the same as earlier, and the normal phonon stress $\sigma ^{\infty }=10$ MPa was applied at infinity. The curves with markers represent the level lines of $H_{33}^{(1)} (x_{1} ,x_{2} )$, which demonstrate its variation in the mentioned region. Similar fields can be drawn with use of (45) for other phonon and phason stress components at any subdomain of the medium.

Fig. 7

Variation of the phason stress $H_{33}^{(1)} (x_{1}, x_{2})$ at the vicinity $0.0095\,m\le x_{1} \le 0.011$ m, $0\le x_{2} \le 0.0005$ m of the right crack tip

To confirm the correctness of the obtained solution, let us compare its particular case of identical lower and upper materials with the solution for an electrically permeable crack in the homogeneous 1D QC. Let us take the upper material of “Appendix 3” and $\sigma ^{\infty }=10$ MPa, $\tau ^{\infty }=0$, $H^{\infty }=0$, $b=10$ mm as both the upper and lower material. The values of $\langle u_{3} (0,0)\rangle$, $\langle W_{3} (0,0)\rangle$ appear to be equal $4.248\times 10^{-6}$ m and $1.241\times 10^{-5}$ m, respectively, by the presented approach, and $4.243\times 10^{-6}$ m and $1.280\times 10^{-5}$ m, respectively, by direct consideration of the crack in the homogeneous 1D QC. The stresses $\sigma _{33}^{(1)} (x_{1} ,0)$ on the crack continuation corresponding to these two cases completely agree with each other.

6 Conclusions

A plane problem for a tunnel electrically permeable crack $-b\le x_{1} \;\le b$, $x_{3} \;=0$ along the interface between two bonded semi-infinite 1D piezoelectric quasicrystalline spaces is considered. It is assumed that the atom arrangement is periodic in the $x_{1}$–$x_{2}$ plane and quasiperiodic in the $x_{3}$-direction, and the last axis represents the direction of polarization. Uniformly distributed phonon normal and shear in-plane stresses and, also, phason stress and electric displacement can be prescribed at infinity.

The matrix vector representations (8), (9) for the phonon and phason stresses and the electrical displacement and also for the derivatives of the phonon and phason displacements and electrical potentials jumps via the vector function, holomorphic in the whole complex plane except the crack region, are derived. Excluding from these relations the out of plane components and taking into account the electric permeability along the whole interface these representations are simplified and presented in the form (19), (20) and later as (27), (28). Using these relations and satisfying the conditions at the crack faces, a Riemann problem of linear relationship (30) is formulated. The exact solution of this problem is obtained. Simple analytical expressions for the phonon and phason displacement jumps along the crack region and also the phonon and phason stresses along the bonded parts of the material interface as well as their stress intensity factors are given.

A numerical analysis is carried out for the combination of different QCs from Ref. [26]. The obtained results for the phonon and phason components along the interface are presented in table and graph forms, and moreover their behaviour outside of the interface is analytically derived and graphically illustrated. The following valuable conclusions are drawn from these data:

• Unlike a crack in a homogeneous QC each separate nonzero external phonon component produces nonzero values of all stress intensity factors for a bimaterial case;

• Each component of phonon stress causes phason stress and displacement jump, and the influence of the phonon shear stress on the intensity factor of phason stress is more sensitive than the influence of the normal one.

Note that even though an oscillating singularity appears in the considered interface crack model, the zone of the crack faces interpenetration is extremely small for most loads. These zones became more visible only for a very large phonon shear field.

Finally, the results for a particular case of identical lower and upper materials of the QC bi-material are calculated and compared with those obtained for the corresponding homogeneous QC. A very good agreement of these results is revealed.

Appendices

Appendix 1: General solution of Eq. (6)

Assuming that all fields are independent on the coordinate $x_{2}$, the solution of Eq. (6) according to the method suggested in [41] can be presented in the form:

$$\begin{aligned} {\mathbf{V}}={\mathbf{a}}\;{\mathbf{f}}(z), \end{aligned}$$

(A.1)

where $z=x_{1} +p\,x_{3}$, and the vector ${\mathbf{a}} =[a_{1}, a_{2}, a_{3}, a_{4}]^{T}$ can be found from the relation

$$\begin{aligned} \left[ {{\mathbf{Q}}+p({\mathbf{E}}+{\mathbf{E}}^{T})+p^{2}{\mathbf{T}}}\right] \,{\mathbf{a}}=0. \end{aligned}$$

(A.2)

The elements of the $5\times 5$ matrices Q, E, and T are defined as

$$\begin{aligned} {\mathbf{Q}}=\left[ \begin{array}{lll} {c_{1jk1} } &{}\quad {e_{1j1} } &{}\quad {R_{1j31} } \\ {e_{1k1} } &{}\quad {-\xi _{11} } &{}\quad {\tilde{{e}}_{131} } \\ {R_{k131} } &{}\quad {\tilde{{e}}_{131} } &{}\quad {-K_{3131} } \\ \end{array}\right] , {\mathbf{E}}=\left[ \begin{array}{lll} {c_{1jk2} } &{}\quad {e_{21j1} } &{}\quad {R_{j132} } \\ {e_{1k2} } &{}\quad {-\xi _{12} } &{}\quad {\tilde{{e}}_{132} } \\ {R_{k231} } &{}\quad {\tilde{{e}}_{132} } &{}\quad {K_{3132} } \\ \end{array}\right] , {\mathbf{T}}=\left[ \begin{array}{lll} {c_{2jk2} } &{}\quad {e_{2j2} } &{}\quad {R_{j232} } \\ {e_{2k2} } &{}\quad {-\xi _{22} } &{}\quad {\tilde{{e}}_{232} } \\ {R_{k232} } &{}\quad {\tilde{{e}}_{232} } &{}\quad {K_{3232} } \\ \end{array}\right] . \end{aligned}$$

A nontrivial solution of Eq. (A.2) exists if p is a root of the equation

$$\begin{aligned} \det \,\left[ {{\mathbf{Q}}+p({\mathbf{E}}+{\mathbf{E}}^{T})+p^{2}{\mathbf{T}}} \right] =0. \end{aligned}$$

(A.3)

Since Eq. (A.3) has no real roots [42] we denote the roots of Eq. (A.3) with positive imaginary parts as $p_{\alpha }$ and the associated eigenvectors of (A.2) as ${\mathbf{a}}_{\alpha }$ (subscript $\alpha$ here and afterwards takes the numbers 1–5). The most general real solution of Eq. (6) can be presented as [42]

$$\begin{aligned} {\mathbf{V}}={\mathbf{A}}\,{\mathbf{f}}(z)+{\bar{{\mathbf{A}}}}\,{\bar{{\mathbf{f}}}}(\bar{{z}}), \end{aligned}$$

(A.4)

where ${\mathbf{A}}=[{{\mathbf{a}}_{1}, {\mathbf{a}}_{2}, {\mathbf{a}}_{3}, {\mathbf{a}}_{4}, {\mathbf{a}}_{5}}]$ is a matrix composed of eigenvectors, ${\mathbf{f}}(z)=[f_{1} (z_{1} ),f_{2} (z_{2} ), f_{3} (z_{3}), f_{4} (z_{4}), f_{5} (z_{5} )]^{\mathrm{T}}$ is an arbitrary vector function, $z_{\alpha } =x_{1} +p_{\alpha }\,x_{3}$, and the overbar stands for the complex conjugate.

Using Eqs. (1)–(3) the vector t introduced by Eq. (7) can be represented in the form

$$\begin{aligned} \mathbf{t}=\mathbf{B}\,\mathbf{f}'(z)+\bar{\mathbf{B}}\,\bar{\mathbf{f}}'(\bar{z}), \end{aligned}$$

(A.5)

where the $5\times 5$ matrix B is defined as

$$\begin{aligned} {\mathbf{B}}=[{{\mathbf{b}}_{1} ,{\mathbf{b}}_{2} ,{\mathbf{b}}_{3}, {\mathbf{b}}_{4} ,{\mathbf{b}}_{5}}] \end{aligned}$$

with

$$\begin{aligned} {\mathbf{b}}_{\alpha }= & {} ({\mathbf{R}}^{T}+p_{\alpha } {\mathbf{T}}){\mathbf{a}}_{\alpha }\ (\hbox {not summed over index}\ \alpha ) \end{aligned}$$

(A.6)

and

$$\begin{aligned} \mathbf{f}'(z)=\left[ {\frac{\mathrm{d}f_{1} (z_{1} )}{\mathrm{d}z_{1}}, \frac{\mathrm{d}f_{2} (z_{2} )}{\mathrm{d}z_{2} },\frac{\mathrm{d}f_{3} (z_{3} )}{\mathrm{d}z_{3}}, \frac{\mathrm{d}f_{4} (z_{4} )}{\mathrm{d}z_{4} },\frac{\mathrm{d}f_{5} (z_{5} )}{\mathrm{d}z_{5} }}\right] ^{T}. \end{aligned}$$

(A.7)

Appendix 2: Solution for a composite of two 1D hexagonal piezoelectric QCs with mixed boundary conditions at the interface

A bimaterial composed of two different semi-infinite 1D hexagonal piezoelectric quasicrystalline spaces $x_{3} >0$ and $x_{3} <0$, with properties defined by Eqs. (1)–(3) for each material, is considered (a cross-section orthogonal to the axis $x_{2}$ is shown in Fig. 1). We assume that the vector t is continuous across the whole bimaterial interface and the part $L=\{(-\infty ,-b)\cup (b,\infty )\}$ of the interface $-\propto< x_{1}<\propto$, $x_{3}=0$ is mechanically and electrically bounded, i.e. the boundary conditions at the interface $x_{3} =0$ are the following ones:

$$\begin{aligned}&{\mathbf{t}}^{(1)}(x_{1} ,0)={\mathbf{t}}^{(2)}(x_{1} ,0) \quad for \quad x_{1} \in (-\infty ,\infty ), \end{aligned}$$

(A.8)

$$\begin{aligned}&{\mathbf{V}}^{({\mathbf{1}})}(x_{1} ,0)={\mathbf{V}}^{(2)}(x_{1} ,0) \quad for\quad x_{1} \in L. \end{aligned}$$

(A.9)

In this case according to Eqs. (A.4), (A.5), the solution of Eqs. (6) can be written for each subdomain in the form

$$\begin{aligned}&{\mathbf{V}}^{(j)}(x_{1} ,x_{3} )={\mathbf{A}}^{(j)}\,{\mathbf{f}}^{(j)}(z) +{\bar{{\mathbf{A}}}}^{(j)}\,{\bar{{\mathbf{f}}}}^{(j)}(\bar{{z}}), \end{aligned}$$

(A.10)

$$\begin{aligned}&{\mathbf{t}}^{(j)}(x_{1} ,x_{3} )={\mathbf{B}}^{(j)}\,{\mathbf{f}'}^{(j)}(z) +{\bar{{\mathbf{B}}}}^{(j)}\,\bar{\mathbf{f}}'^{(j)}(\bar{{z}}), \end{aligned}$$

(A.11)

where $j=1$ for $x_{3}>0$ and $j=2$ for $x_{3}<0$; the vector functions ${\mathbf{f}}^{(1)}(z)$ and ${\mathbf{f}}^{(2)}(z)$ are analytic in the upper ($x_{3}>0$) and the lower ($x_{3}<0$) domains, respectively.

Equation (A.11) and the boundary condition (A.8) give

$$\begin{aligned} {\mathbf{B}}^{(1)}\,{\mathbf{f}'}^{(1)}(x_{1} )-{\bar{{\mathbf{B}}}}^{(2)} \,\bar{\mathbf{f}}'^{(2)}(x_{1})= {\mathbf{B}}^{(2)}\,\mathbf{f}'^{(2)} (x_{1} )-{\bar{{\mathbf{B}}}}^{(1)}\,\bar{\mathbf{f}}'^{(1)}(x_{1}) \ \hbox {for} \quad -\infty<x_{1} <\infty . \end{aligned}$$

(A.12)

The left-hand side of Eq. (A.12) is the boundary value of a function analytic in the domain $x_{3}>0$ and the right-hand side of Eq. (A.12) is a boundary value of another function analytic in the domain $x_{3}<0$. Equation (A.12) means that both functions can be analytically continued into the entire plane, i.e. they are equal for $x_{3}>0$ and $x_{3}<0$, respectively, to a function M(z) analytic in the whole plane. Taking into account that the phonon and phason stresses and the electric displacement are bounded at infinity one gets from Eq. (A.11) that $\mathbf{M} ({z})|_{{z}\rightarrow \propto }=\mathbf{M} ^{(\mathbf 0 )} =\mathbf{const }$. But it means that $\mathbf{M} ({z})=\mathbf{M} ^{(\mathbf 0 )}$ holds true in the whole plane. Thus from Eq. (A.12) it follows

$$\begin{aligned}&{\mathbf{B}}^{(1)}{\mathbf{f}}'^{(1)}\;(z)-{\bar{{\mathbf{B}}}}^{(2)}{\bar{{\mathbf{f}}}}'^{(2)} \;(\bar{{z}})=\mathbf{M} ^{(\mathbf 0 )}\ \hbox {for}\quad x_{3}> 0, \end{aligned}$$

(A.13)

$$\begin{aligned}&{\mathbf{B}}^{(2)}{\mathbf{f}}'^{(2)}\;(z)-{\bar{{\mathbf{B}}}}^{(1)}{\bar{{\mathbf{f}}}}'^{(1)} \;(\bar{{z}})=\mathbf{M} ^{(\mathbf 0 )}\ \hbox {for}\quad x_{3}< 0, \end{aligned}$$

(A.14)

where $\mathbf{M} ^{(\mathbf 0 )}$ is an arbitrary constant vector. Assuming that the eigenvalues are distinct and taking into account that the matrices in Eqs. (A.13), (A.14) are non-singular [40], one obtains

$$\begin{aligned} {\bar{{\mathbf{f}}}}'^{(2)}\;(\bar{{z}})= & {} ({\bar{{\mathbf{B}}}}^{(2)})^{-1} {\mathbf{B}}^{(1)}{\mathbf{f}}'^{(1)}\;(z)-({\bar{{\mathbf{B}}}}^{(2)})^{-1} {\mathbf{M}}^{{\mathbf{(0)}}}\ \hbox {for}\quad x_{3}>0,\nonumber \\ {\bar{{\mathbf{f}}}}'^{(1)}\;(\bar{{z}})= & {} ({\bar{{\mathbf{B}}}}^{(1)})^{-1} {\mathbf{B}}^{(2)}{\mathbf{f}}'^{(2)}\;(z)-({\bar{{\mathbf{B}}}}^{(1)})^{-1} {\mathbf{M}}^{{\mathbf{(0)}}}\ \hbox {for} \quad x_{3}< 0. \end{aligned}$$

(A.15)

Since ${\mathbf{f}}'^{(1)}\;(z)$ and ${\mathbf{f}}'^{(2)}\;(z)$ are arbitrary functions, one can set $\mathbf{M} ^{(\mathbf 0 )} =\mathbf 0$, and Eq. (A.15) gets the form

$$\begin{aligned} {\bar{{\mathbf{f}}}}'^{(2)}\;(\bar{{z}})= & {} ({\bar{{\mathbf{B}}}}^{(2)})^{-1} {\mathbf{B}}^{(1)}{\mathbf{f}}'^{(1)}\;(z)\ \hbox {for}\quad x_{3}> 0,\nonumber \\ {\bar{{\mathbf{f}}}}'^{(1)}\;(\bar{{z}})= & {} ({\bar{{\mathbf{B}}}}^{(1)})^{-1} {\mathbf{B}}^{(2)}{\mathbf{f}}'^{(2)}\;(z)\ \hbox {for}\quad x_{3}< 0. \end{aligned}$$

(A.16)

Consider further the vector

$$\begin{aligned} \left\langle {\mathbf{V}'}(x_{1}) \right\rangle ={\mathbf{V}'}^{(1)}(x_{1} ,0)-{\mathbf{V}'}^{(2)}(x_{1} ,0) \end{aligned}$$

(A.17)

of the derivatives of the jumps of phonon and phason displacements and electric potential across the material interface. By using Eqs. (A.10) and (A.16), it can be written as

$$\begin{aligned} \langle \mathbf{V}'(x_{1})\rangle =\mathbf{Df}'^{(1)}(x_{1}) +\bar{\mathbf{D}}\bar{f}'^{(1)}(x_{1}), \end{aligned}$$

(A.18)

with the definition ${\mathbf{D}}={\mathbf{A}}^{(1)}-{\bar{{\mathbf{A}}}}^{(2)} ({\bar{{\mathbf{B}}}}^{(2)})^{-1}{\mathbf{B}}^{(1)}$.

    From Eq. (A.11), the vector $\mathbf{t} ^{(1)}$ on the material interface can be written as

$$\begin{aligned} \mathbf{t}^{(1)}(x_{1}, 0)={\mathbf{B}}^{(1)}\,{\mathbf{f}'}^{(1)}(x_{1}) +{\bar{\mathbf{B}}}^{(1)}\,{\bar{\mathbf{f}}}'^{(1)}(x_{1}). \end{aligned}$$

(A.19)

Introducing the vector function ${\varvec{\upomega }}(z)$ by the formula

$$\begin{aligned} {\varvec{\upomega }}(z) =\left\{ \begin{array}{ll} \mathbf{D}\,\mathbf{N} (z) &{} \quad \hbox {for}\quad x_{3} >0 \\ -\bar{\mathbf{D}}\,\bar{\mathbf{N}}(z) &{} \quad \hbox {for}\quad x_{3} <0 \\ \end{array}\right. , \end{aligned}$$

(A.20)

with ${\mathbf{N}}(z)=[{f_{1}'^{(1)}(z),\,f_{2}'^{(1)}(z), \,f_{3}'^{(1)}(z),\,f_{4}'^{(1)}(z),f_{5}'^{(1)}(z)}]^{T}$, leads to the following expressions:

$$\begin{aligned} \langle \mathbf{V}'(x_{1})\rangle= & {} {\varvec{\upomega }}^{+} (x_{1})-{\varvec{\upomega }}^{-}(x_{1}), \end{aligned}$$

(A.21)

$$\begin{aligned} \mathbf{t}^{(1)}(x_{1}, 0)= & {} \mathbf{G}{\varvec{\upomega }}^{+} (x_{1})-\bar{\mathbf{G}}{\varvec{\upomega }}^{-}(x_{1}) \end{aligned}$$

(A.22)

where ${\mathbf{G}}={\mathbf{B}}^{(1)}{\mathbf{D}}^{-1}$ and ${\varvec{\upomega }}^{+} (x_{1} )={\varvec{\upomega }}(x_{1} +i0), {\varvec{\upomega }}^{-}(x_{1}) ={\varvec{\upomega }}(x_{1}-i0)$.

    Equations (A.21) and (A.22) can be used for the analysis of compositions of different semi-infinite 1D hexagonal piezoelectric quasicrystals with cracks at their interface.

Appendix 3: Constants of 1D piezoelectric QCs poling in the $x_{3}$-direction [28]

	Upper material	Lower material
Phonon elastic	$c_{11} =150$, $c_{12} =100$, $c_{13} =90$	$c_{11} =234.33$, $c_{12} =57.41$, $c_{13} =66.63$
constants (GPa)	$c_{33} =130$, $c_{44} =50$	$c_{33} =232.22$, $c_{44} =70.19$
Phason elastic constants (GPa)	$K_{1} =0.18$, $K_{2} =0.3$	$K_{1} =122$, $K_{2} =24$
Coupling constants (GPa)	$R_{1} =-1.50$, $R_{2} =1.20$, $R_{3} =1.20$	$R_{1} =R_{2} =R_{3} =0.8846$
Piezoelectric constants	$e_{31} =\tilde{{e}}_{15} =-0.160$, $e_{33} =0.347$,	$e_{31} =-4.4$, $e_{33} =18.6$, $e_{15} =11.6$
(C m$^{-2}$)	$e_{15} =-0.138$, $\tilde{{e}}_{33} =0.350$	$\tilde{{e}}_{15} =1.16$, $\tilde{{e}}_{33} =1.86$
Dielectric constants ($10^{-9}$ C$^{2}$ N$^{-1}$ m$^{-2}$)	$\xi _{11} =0.0826$, $\xi _{33} =0.0903$	$\xi _{11} =5$, $\xi _{33} =10$