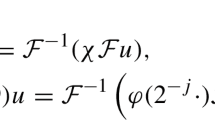Well-posedness and non-uniform dependence on initial data for the Fornberg–Whitham-type equation in Besov spaces

Abstract

In this paper, we first establish the local well-posedness for the Fornberg–Whitham-type equation in the Besov spaces $B^{s}_{p,r}({\mathbb {R}})$ with $1\le p,r\le \infty$ and $s> max\{1+\frac{1}{p},\frac{3}{2}\}$, which improve the previous work in Sobolev spaces $H^{s}({\mathbb {R}})= B^{s}_{2,2}({\mathbb {R}})$ with $s>\frac{3}{2}$ (Lai and Luo in J Differ Equ 344:509–521, 2023). Furthermore, we prove the solution is not uniformly continuous dependence on the initial data in the Besov spaces $B^{s}_{p,r}({\mathbb {R}})$ with $1\le p\le \infty$,$1\le r< \infty$ and $s> max\{1+\frac{1}{p},\frac{3}{2}\}$.

1 Introduction

The following Fornberg–Whitham (FW) equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \ W_{t}-W_{xxx}-W_{x}+\frac{3}{2}WW_{x}=\frac{9}{2}W_{x}W_{xx}+\frac{3}{2}WW_{xxx},\quad x\in {\mathbb {R}}, t >0,\\ \ W(x,0)=W_{0}(x),\quad x\in {\mathbb {R}},\\ \end{array}\right. } \end{aligned}$$

(1.1)

which was proposed by Fornberg and Whitham [1] as a model for breaking waves. Eq (1.1) has a peakon solution $W(t,x)=\frac{8}{9}e^{-\frac{1}{2}|x-\frac{4}{3}t|}$. We can rewrite (1.1) in non-local form

$$\begin{aligned} {\left\{ \begin{array}{ll} \ W_{t}+\frac{3}{2}WW_{x}=\partial _{x}(1-\partial _{x}^{2})^{-1}W,\quad x\in {\mathbb {R}}, t >0,\\ \ W(x,0)=W_{0}(x),\quad x\in {\mathbb {R}}.\\ \end{array}\right. } \end{aligned}$$

(1.2)

In this form, the FW equation was compared with the CH equation [2, 3]

$$\begin{aligned} W_{t}+WW_{x}=\partial _{x}\left( 1-\partial _{x}^{2}\right) ^{-1}\left( W^{2}+\frac{1}{2}W_{x}^{2}\right) . \end{aligned}$$

The CH equation has a bi-Hamiltonian structure and is completely integrable in the sense of Lax pair [2]. The local well-posedness and ill-posedness of the Cauchy problem for the CH equation in Sobolev spaces and Besov spaces have been studied in [4,5,6,7,8]. Moreover, the CH equation has more proposition, such as, global strong solution, wave breaking phenomena, global weak solutions and so on, we can find in [9,10,11,12,13,14,15,16]. Further, the non-uniform dependence of solution map for the CH equation in Sobolev spaces and Besov spaces have been investigated in many papers, see [17,18,19].

Unlike the CH equation, the FW equation (1.1) is non-integrable and lakes enough useful conserved quantities, which make it is difficult to study the properties of solutions to the equation. Recently, The local well-posedness of the Cauchy problem for the FW equation (1.1)in Sobolev spaces and Besov spaces are obtained in [20, 21]. And they demonstrated that the date-to-solution map is not uniformly continuous but Hölder continuity in some given topology and existence of weak solution to FW equation are investigated in [22,23,24].

Recently, Lai and Luo studied a shallow water wave equation called Fornberg–Whitham-type equation in [25],

$$\begin{aligned} W_{t}-W_{xxx}-kW_{x}+mWW_{x}=\frac{9}{2}W_{x}W_{xx}+\frac{3}{2}WW_{xxx}. \end{aligned}$$

(1.3)

and the non-local form

$$\begin{aligned} {\left\{ \begin{array}{ll} W_{t}+\frac{3}{2}WW_{x}=\partial _{x}(1-\partial _{x}^{2})^{-1}(kW+\frac{3-2m}{4}W^{2}),\quad x\in {\mathbb {R}}, t >0,\\ W(x,0)=W_{0}(x),\quad x\in {\mathbb {R}}.\\ \end{array}\right. } \end{aligned}$$

(1.4)

where $m>0$ and $m\ge 0$ are constants. which is viewed as a generalization of Eq. (1.1) and the structure of this equation the non-local term with both W and $W^{2}$ is complicated in comparison with the only W in (1.1). Especially, if $k=1$ and $m=\frac{3}{2}$, equation (1.4) is reduced to the classical FW equation (1.1).

In [25], the authers estiblished the local-well-posedness in Sobolev spaces $H^{s}({\mathbb {R}})$ with $s>\frac{3}{2}$ and study the blow-up phenomena of solutions. However, the local-well-posedness for equation in the Besov spaces $B^{s}_{p,r}({\mathbb {R}})$ with $1\le p,r\le \infty$ and $s> max\{1+\frac{1}{p},\frac{3}{2}\}$($H^{s}({\mathbb {R}})= B^{s}_{2,2}({\mathbb {R}})$ with $s>\frac{3}{2}$) has not been studied. In this paper, view the idea of [8, 18, 26], we will study the local well-posedness and non-uniform dependence on initial data for the Fornberg–Whitham-type equation (1.4) in Besov spaces.

The first results concerning the local well-posedness for Fornberg–Whitham-type equation (1.4) in Besov spaces. Which yields the following theorem.

Theorem 1.1

Let $1\le p,r\le \infty$ and $s> max\{1+\frac{1}{p},\frac{3}{2}\}$ and the initial date $u_{0} \in B^{s}_{p,r}({\mathbb {R}})$. Then, there exists a time $T>0$ such that the cauchy problem (1.4) has a unique solution $W\in E^{s}_{p,r}(T)$, and the map $W_{0}$ $\mapsto$ W is continuous from a neighborhood of $W_{0}$ in $B^{s}_{p,r}$ into

$$\begin{aligned} {\mathcal {C}}([0,T];B^{s^{\prime }}_{p,r}({\mathbb {R}}))\cap {\mathcal {C}}^{1}([0,T];B^{s^{\prime }-1}_{p,r}({\mathbb {R}})) \end{aligned}$$

$s^{\prime } < s$ when $r=+\infty$ whereas $s^{\prime } = s$ when $r<+\infty$. Furthermore, for all $t\in [0,T]$, we have

$$\begin{aligned} \Vert W(t)\Vert _{B^{s}_{p,r}({\mathbb {R}})}\le C \Vert W_{0}\Vert _{B^{s}_{p,r}({\mathbb {R}})}. \end{aligned}$$

(1.5)

From our well-posedness result, we know that the data-to-solution map $W_{0}$ $\mapsto$ W is continuous from any bounded subset of $B^{s}_{p,r}$ into $E^{s}_{p,r}(T)$, Moveover, by constructing the initial data, we can demonstrate the data-to-solution map of Eq. (1.4) is not uniformly continuous as follows.

Theorem 1.2

Let $s> max\{1+\frac{1}{p},\frac{3}{2}\}$ and $1\le p\le \infty$, $1\le r<\infty$. Then the data-to-solution map for Eq. (1.4) is not uniformly continuous from any bounded subset in $B^{s}_{p,r}({\mathbb {R}})$ into ${\mathcal {C}}([0,T];B^{s}_{p,r}({\mathbb {R}}))$. That is, there exists two sequences of solutions $W^{n}$ and $V^{n}$ such that

$$\begin{aligned}{} & {} \Vert W^{n}_{0}\Vert _{ B^{s}_{p,r}}+\Vert V^{n}_{0}\Vert _{ B^{s}_{p,r}}\lesssim 1,\quad \lim _{n\rightarrow \infty }\Vert W^{n}_{0}-V^{n}_{0}\Vert _{ B^{s}_{p,r}}=0, \\{} & {} \lim _{n\rightarrow \infty }\inf \Vert W^{n}(t)-V^{n}(t)\Vert _{ B^{s}_{p,r}}\gtrsim t,\quad t\in (0,T_{0}], \end{aligned}$$

with small positive time $T_{0}\le T$.

Remark

Note that when $p = 2, r = 2$, one has $B^{s}_{p,r}({\mathbb {R}})$ = $H^{s}(R)$. Thus, Theorem 1 and Theorem 2 imply that under the condition $u_{0}\in H^{s}(R)$ with $s>\frac{3}{2}$, we can obtain the local well-posedness(see [25]) and the non-uniform continuity for the data-to-solution map in sobolev spaces.

Notation

The symbol $A\lesssim B$ means that there is a uniform positive constant C independent of A and B such that $A\le CB.$

2 Preliminaries

Before proceeding, we recall the following properties in Besov spaces. In addition, we need to review the transport equation theory, which will be used in the paper.

Definition 2.1

(Littlewood–Paley Decomposition) There exists a couple of smooth functions $(\chi ,\varphi )$ valued in [0,1], such that $\chi$ is supported in the ball ${\mathcal {B}}\triangleq \{\xi \in {\mathbb {R}}:|\xi |\le \frac{4}{3}\}$, and $\varphi$ is supported in the ring ${\mathcal {C}}\triangleq \{\xi \in {\mathbb {R}}:\frac{3}{4}\le |\xi |\le \frac{8}{3}\}$. Moreover,

$$\begin{aligned}{} & {} \forall \xi \in {\mathbb {R}}^{d},\chi (\xi )+\sum _{j\ge 0}\varphi (2^{-j}\xi )=1,\\{} & {} \forall \xi \in {\mathbb {R}}^{d}\backslash \{0\},\sum _{j\in {\mathbb {Z}}}\varphi (2^{-j}\xi )=1,\\{} & {} |j-j'|\ge 2\Rightarrow \textrm{Supp}\varphi (2^{-j}\cdot )\cap \textrm{Supp}\varphi (2^{-j'}\cdot )=\varnothing ,\\{} & {} j\ge 1\Rightarrow \textrm{Supp}\chi (\cdot )\cap \textrm{Supp}\varphi (2^{-j}\cdot )=\varnothing . \end{aligned}$$

Then, we can define the nonhomogeneous dyadic blocks $\vartriangle _{j}$ and nonhomogeneous low frequency cut-off operator $S_{j}$ as follows:

$$\begin{aligned}{} & {} \vartriangle _{j}u=0,\quad j\le -2,\quad \triangle _{-1}u=\chi (D)u={\mathcal {F}}^{-1}(\chi {\mathcal {F}}u),\\{} & {} \vartriangle _{j}u=\varphi (2^{-j}D)u={\mathcal {F}}^{-1}(\varphi (2^{-j}\cdot ){\mathcal {F}}u),\quad if j\ge 0,\\{} & {} S_{j}u=\sum _{j'=-\infty }^{j-1}\vartriangle _{j'}u. \end{aligned}$$

Definition 2.2

[27] Let $s\in {\mathbb {R}}$ and $1<p,r\le \infty .$ The nonhomogeneous Besov space $B^{s}_{p,r}({\mathbb {R}}^{d})$ ($B^{s}_{p,r}$) consists of all tempered distribution u such that

$$\begin{aligned} \Vert u\Vert _{ B^{s}_{p,r}({\mathbb {R}}^{d})}\triangleq \Vert (2^{js}\Vert \vartriangle _{j}u\Vert _{L^{p}({\mathbb {R}}^{d})})_{j\in {\mathbb {Z}}}\Vert _{l^{r}({\mathbb {Z}})}<\infty . \end{aligned}$$

We introduce a function spaces $E^{s}_{p,r}(T)$ as follows.

$$\begin{aligned} E^{s}_{p,r}(T) {\left\{ \begin{array}{ll} {\mathcal {C}}([0,T];B^{s}_{p,r})\cap {\mathcal {C}}^{1}([0,T];B^{s-1}_{p,r}),\quad { if}\ r<\infty ,\\ {\mathcal {C}}_{w}([0,T];B^{s}_{p,\infty })\cap {\mathcal {C}}^{0,1}([0,T];B^{s-1}_{p,\infty }),\quad { if}\ r=\infty \\ \end{array}\right. } \end{aligned}$$

Therefore, we have the product laws as follows.

Lemma 2.1

[27]

• 1. Algebraic properties: $\forall s>0$, $B^{s}_{p,r}\cap L^{\infty }$ is a Banach algebra. $B^{s}_{p,r}$ is a Banach algebra $\Leftrightarrow B^{s}_{p,r}\hookrightarrow L^{\infty } \Leftrightarrow s>\frac{d}{p}$ or $s=\frac{d}{p},r=1$.

• 2. For any $s>0$ and $1\le p,r\le \infty$, there have

  $$\begin{aligned} \Vert uv\Vert _{ B^{s}_{p,r}} \le C(\Vert u\Vert _{ L^{\infty }} \Vert v\Vert _{ B^{s}_{p,r}}+\Vert v\Vert _{ L^{\infty }} \Vert u\Vert _{ B^{s}_{p,r}}). \end{aligned}$$

• 3. Let $1\le p,r\le \infty$ and $s>max\{{\frac{3}{2},1+\frac{d}{p}}\}.$ Then, we have

  $$\begin{aligned} \Vert uv\Vert _{ B^{s-2}_{p,r}}\le C \Vert u\Vert _{ B^{s-1}_{p,r}}\Vert v\Vert _{ B^{s-2}_{p,r}}. \end{aligned}$$

• 4. Density: $C_{c}^{\infty }$ is dense in $B^{s}_{p,r}$ $\Leftrightarrow 1\le p,r<\infty .$

• 5. Fatou lemma: If $\{u_{n}\}_{n\in N}$ is bounded in $B^{s}_{p,r}$ and $u_{n} \rightarrow u$ in $S^{\prime }$, then $u\in B^{s}_{p,r}$ and

  $$\begin{aligned} \Vert u\Vert _{ B^{s}_{p,r}}\le \liminf _{n\rightarrow \infty }\Vert u_{n}\Vert _{ B^{s}_{p,r}} \end{aligned}$$

• 6. Let $n\in {\mathbb {R}}$ and g be an $S^{n}$-multiplier. Then, the operator g(D) is continuous from $B^{s}_{p,r}$ to $B^{s-n}_{p,r}$.

Next, we give some useful results in the transport equation theory, which are crucial to show our main theorem.

Lemma 2.2

(Theorem 3.38, [27]) Assume $1\le p,r\le \infty$ and $s>-\frac{d}{p}$. Let v be a vector field such that $\nabla v\in L^{1}([0,T];B^{s-1}_{p,r})$ if $s>1+\frac{d}{p}$ or to $L^{1}([0,T];B^{\frac{d}{p}}_{p,r}\cap L^{\infty })$ otherwise. Suppose also that $f_{0}\in B^{s}_{p,r}$,$g\in L^{1}([0,T];B^{s}_{p,r})$ and the function $f\in L^{\infty }([0,T];B^{s}_{p,r})\cap {\mathcal {C}}([0,T];S^{\prime })$ solves the d-dimensional linear transport equations

$$\begin{aligned} \partial _{t}f+v\cdot \triangledown f=g,\quad f|_{t=0}=f_{0}. \end{aligned}$$

(2.1)

Then there exists a constant $C=C(d,p,r,s)$ such that the following statement hold:

• 1. If $r=1$ or $s\ne 1+\frac{d}{p}$, then

  $$\begin{aligned} \Vert f(s)\Vert _{ B^{s}_{p,r}}\le \Vert f_{0}\Vert _{ B^{s}_{p,r}} +\int _{0}^{t}\Vert g(\tau )\Vert _{ B^{s}_{p,r}}d\tau + C\int _{0}^{t}V_{p}(\tau )\Vert f(\tau )\Vert _{ B^{s}_{p,r}}d\tau \qquad \end{aligned}$$

  (2.2)

  or

  $$\begin{aligned} \Vert f(s)\Vert _{ B^{s}_{p,r}}\le Ce^{CV_{p}(t)} \left( \Vert f_{0}\Vert _{ B^{\sigma }_{p,r}}+\int _{0}^{t}e^{-CV_{p}(\tau )}\Vert g(\tau )\Vert _{ B^{s}_{p,r}}d\tau \right) , \end{aligned}$$

  (2.3)

  where $V_{p}(t)=\int _{0}^{t}\Vert \nabla v(\tau )\Vert _{ B^{\frac{d}{p}}_{p,r}\cap L^{\infty }}d\tau$ if $s< 1+\frac{d}{p}$ and $V_{p}(t)=\int _{0}^{t}\Vert \nabla v(\tau )\Vert _{ B^{s-1}_{p,r}}d\tau$ else.

• 2. If $f=v$, then for all $s>0$ the estimate (3.3) holds with

  $$\begin{aligned} V_{p}(t)=\int _{0}^{t}\Vert \triangledown v(s)\Vert _{ L^{\infty }({\mathbb {R}}^{d})}ds. \end{aligned}$$

• 3. If $r<+\infty$, then $f\in {\mathcal {C}}([0,T];B^{s}_{p,r})$. If $r=+\infty$, then $f\in {\mathcal {C}}([0,T];B^{s^{\prime }}_{p,r})$ for all $s^{\prime }<s$.

Lemma 2.3

[27](Existence and uniqueness) For $1\le p,r,p_{1}\le \infty$ and $s>-d\min \{\frac{1}{p^{\prime }},\frac{1}{p_{1}}\}$ with $\frac{1}{p}+\frac{1}{p^{\prime }}=1$. suppose that initial data $f_{0}\in B^{s}_{p,r}({\mathbb {R}})$,$g\in L^{1}([0,T];B^{s}_{p,r})$. Let v be a time-dependent vector field such that $v\in L^{\rho }([0,T];B^{-M}_{\infty ,\infty })$ for some $\rho>1, M>0$ and $\nabla v\in L^{1}([0,T];B^{\frac{d}{p}}_{p,r}\cap L^{\infty })$ if $s<1+\frac{d}{p_{1}}$ and $\nabla v\in L^{1}([0,T];B^{s-1}_{p_{1},r})$ if $s>1+\frac{d}{p}$ or $s=1+\frac{d}{p_{1}}$ and $r=1$. Then the Eq. (3.1) have a unique solution $f\in L^{\infty }([0,T];B^{s}_{p,r}\cap (\cap _{s^{\prime }<s}{\mathcal {C}}([0,T];B^{s^{\prime }}_{p,1}))$ and the inequalities in Lemma 2 hold true. Moreover, $r<\infty$, then we have $f\in {\mathcal {C}}([0,T];B^{s}_{p,1})$.

3 Local well-posedness

In this section, we will study the local well-posedness of the Cauchy problem (1.4) in Besov spaces. we divide four steps to prove the Theorem 1.1.

Step 1. Uniqueness and continuity with respect to the initial data $W_{0}$ are immediate consequence of the following Lemma:

Lemma 3.1

Assume $1\le p,r\le \infty$ and $s>\max \{1+\frac{1}{p}, \frac{3}{2}\}$. Let $W,V \in L^{\infty }([0,T];B^{s}_{p,r})\cap {\mathcal {C}}([0,T];S^{\prime })$ be two solutions of the Eq. (1.4) with initial data $W_{0}, V_{0} \in B^{s}_{p,r}$. Thus, for any $t\in [0,T]$, we have

$$\begin{aligned} \Vert W(t) - V(t)\Vert _{ B^{s-1}_{p,r}}\le \Vert W_{0} - V_{0}\Vert _{ B^{s-1}_{p,r}}e^{C\int _{0}^{t}(1 + \Vert W(\tau )\Vert _{ B^{s}_{p,r}} + \Vert V(\tau )\Vert _{ B^{s}_{p,r}})d\tau }, \end{aligned}$$

(3.1)

Proof

Let $U=W-V$, we can know that $W,V \in L^{\infty }([0,T];B^{s}_{p,r})\cap {\mathcal {C}}([0,T];S^{\prime })$, which implies $U \in {\mathcal {C}}([0,T];B^{s-1}_{p,r})$, and U is the solution of the following equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \ U_{t}+\frac{3}{2}WU_{x}=-\frac{3}{2}UV_{x} + \partial _{x}(1-\partial _{x}^{2})^{-1}(kU+\frac{3-2m}{4}U(W+V)),\\ \ U(x,0)=W_{0}-V_{0}.\\ \end{array}\right. } \end{aligned}$$

(3.2)

For $s>\frac{3}{2}$, Lemma 2.2 implies that

$$\begin{aligned}&\Vert U(t)\Vert _{ B^{s-1}_{p,r}}\le \Vert U_{0}\Vert _{ B^{s-1}_{p,r}} +\int _{0}^{t}\Vert \partial _{x}W\Vert _{ B^{s-2}_{p,r}}\Vert U\Vert _{ B^{s-1}_{p,r}}d\tau \nonumber \\&\quad + C\int _{0}^{t}(\Vert U\partial _{x}V\Vert _{ B^{s}_{p,r}} + \Vert \partial _{x}(1-\partial _{x}^{2})^{-1}(kU+\frac{3-2m}{4}U(W+V))\Vert _{ B^{s-1}_{p,r}})d\tau . \end{aligned}$$

(3.3)

The algebraic property for $B^{s-1}_{p,r}$ for $s>1+\frac{1}{p}$, we can obtain

$$\begin{aligned} \Vert U\partial _{x}V\Vert _{ B^{s-1}_{p,r}}\le C\Vert U\Vert _{ B^{s-1}_{p,r}}\Vert \partial _{x}V\Vert _{ B^{s-1}_{p,r}} \le C\Vert U\Vert _{ B^{s-1}_{p,r}}\Vert V\Vert _{ B^{s}_{p,r}}. \end{aligned}$$

(3.4)

Since the operator$(1-\partial _{x}^{2})^{-1}$ is a $S^{-2}$-multiplier, applying Lemma 2.1(6). We have

$$\begin{aligned}&\Vert \partial _{x}(1-\partial _{x}^{2})^{-1}(kU+\frac{3-2m}{4}U(W+V))\Vert _{ B^{s-1}_{p,r}} \nonumber \\&\quad \le C(\Vert U\Vert _{ B^{s-2}_{p,r}}+ \Vert U(W+V)\Vert _{ B^{s-2}_{p,r}}) \nonumber \\&\quad \le \Vert U\Vert _{ B^{s-1}_{p,r}} + C\Vert U\Vert _{ B^{s-1}_{p,r}}(\Vert W\Vert _{ B^{s}_{p,r}}+\Vert V\Vert _{ B^{s}_{p,r}}). \end{aligned}$$

(3.5)

Plugging (3.4), (3.5) into (3.3) gives

$$\begin{aligned} \Vert U(t)\Vert _{ B^{s-1}_{p,r}}\le \Vert U_{0}\Vert _{ B^{s-1}_{p,r}} + C\int _{0}^{t}\Vert U\Vert _{ B^{s-1}_{p,r}} (\Vert W\Vert _{ B^{s}_{p,r}}+\Vert V\Vert _{ B^{s}_{p,r}} + 1)d\tau . \end{aligned}$$

(3.6)

By using the Gronwall’s inequality, which yield the Lemma 3.1.

Step 2. Next, will start the proof of Theorem 1.1, which is motivated by the proof of the Cauchy problem about Camassa-Holm-type equation [7]. We can use the classical Friedrichs regularization method to construct approximate solution to Eq. (1.4).

Lemma 3.2

, Let $1\le p,r\le \infty$ and $s>\max \{1+\frac{1}{p}, \frac{3}{2}\}$. Assume $W^{0}=0$, there exist a sequence of smooth function $\{W^{n}\}_{n\in {\mathbb {N}}}$ solves the following linear transport equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \ \partial _{t}W^{n+1}+\frac{3}{2}W^{n}\partial _{x}W^{n+1}=\partial _{x}(1-\partial _{x}^{2})^{-1}(kW^{n}+\frac{3-2m}{4}(W^{n})^{2}),\\ \ W(x,0)=W_{0}(x).\\ \end{array}\right. } \end{aligned}$$

(3.7)

Then, we have $\{W^{n}\}_{n\in {\mathbb {N}}}$ is uniformly bounded in $E^{s}_{p,r}(T)$ and $\{W^{n}\}_{n\in {\mathbb {N}}}$ is a Cauchy sequence in ${\mathcal {C}}([0,T];B^{s-1}_{p,r})$.

Proof

From Lemma 2.2, we know that the Eq. (3.7) has a global solution $W^{n+1}\in E^{s}_{p,r}(T)$ with $s>\max \{1+\frac{1}{p}, \frac{3}{2}\}$ and the following inequality

$$\begin{aligned}&\Vert W^{n+1}(t)\Vert _{ B^{s}_{p,r}}\le Ce^{C\int _{0}^{t}\Vert W^{n}(\tau )\Vert _{ B^{s}_{p,r}}d\tau } \left( \Vert W_{0}\Vert _{ B^{s}_{p,r}} \right. \nonumber \\&\quad \left. + C\int _{0}^{t}e^{-C\int _{0}^{\tau }\Vert W^{n}(\tau ^{\prime })\Vert _{ B^{s}_{p,r}}d\tau ^{\prime }}\left( \Vert \partial _{x}(1-\partial _{x}^{2})^{-1}\left( kW^{n}+\frac{3-2m}{4}(W^{n})^{2}\right) \Vert _{ B^{s}_{p,r}}\right) d\tau \right) . \end{aligned}$$

(3.8)

We know that $B^{s}_{p,r}$, $B^{s-1}_{p,r}$ are Banach algebras and the embedding $B^{s}_{p,r}\hookrightarrow B^{s-1}_{p,r}\hookrightarrow L^{\infty }$ for $s>1 + \frac{1}{p}$. Note that the operator $(1-\partial _{x}^{2})^{-1}$ is a $S^{-2}$-multiplier. Thus, we have

$$\begin{aligned} \Vert \partial _{x}(1-\partial _{x}^{2})^{-1}\left( kW^{n}+\frac{3-2m}{4}(W^{n})^{2}\right) \Vert _{ B^{s}_{p,r}}\le C(\Vert W^{n}\Vert _{ B^{s}_{p,r}}+\Vert W^{n}\Vert _{B^{s}_{p,r}}^{2}).\qquad \end{aligned}$$

(3.9)

Thus, we can obtain

$$\begin{aligned}&\Vert W^{n+1}(t)\Vert _{ B^{s}_{p,r}}\le e^{C\int _{0}^{t}\Vert W^{n}(\tau )\Vert _{ B^{s}_{p,r}}d\tau } (\Vert W_{0}\Vert _{ B^{s}_{p,r}}\nonumber \\&\quad + C\int _{0}^{t}e^{-C\int _{0}^{\tau }\Vert W^{n}(\tau ^{\prime })\Vert _{ B^{s}_{p,r}}d\tau ^{\prime }}( \Vert W^{n}(\tau )\Vert _{ B^{s}_{p,r}}+\Vert W^{n}(\tau )\Vert _{ B^{s}_{p,r}}^{2})d\tau . \end{aligned}$$

(3.10)

If we choose $M^{n}(t)=\Vert W^{n}(t)\Vert _{ B^{s}_{p,r}} +1$, $M_{0}=\Vert W_{0}\Vert _{ B^{s}_{p,r}} +1$. Then, we have

$$\begin{aligned} M^{n+1}(t) \le e^{C\int _{0}^{t}M^{n}(\tau )d\tau }M_{0} + C\int _{0}^{t}e^{C\int _{\tau }^{t}M^{n}(t^{\prime })dt^{\prime }}( M^{n}(\tau ))^{2}d\tau . \end{aligned}$$

(3.11)

Fix $T>0$, such that $T\le \frac{1}{4CM_{0}}$, by induction, we can claim that

$$\begin{aligned} M^{n}(t) \le \frac{M_{0}}{1 - 2CM_{0}t }\le 2M_{0}, \quad \forall t\in [0,T]. \end{aligned}$$

(3.12)

Plugging (3.12) into (3.11), for any$0\le \tau <t\le \frac{1}{4CM_{0}}$, we have

$$\begin{aligned} e^{C\int _{\tau }^{t}M^{n}(t^{\prime })dt^{\prime }}\le e^{C\int _{\tau }^{t}\frac{M_{0}}{1 - 2CM_{0}t^{\prime } }dt^{\prime }}=\left( \frac{1 - 2CM_{0}\tau }{1 - 2CM_{0}t}\right) ^{\frac{1}{2}}. \end{aligned}$$

and

$$\begin{aligned} M^{n+1}(t)&\le \frac{M_{0}}{(1 - 2CM_{0}t)^{\frac{1}{2}}} + \frac{M_{0}^{2}}{(1 - 2CM_{0}t)^{\frac{1}{2}}}\int _{0}^{t}(1 - 2CM_{0}\tau )^{-\frac{3}{2}}d\tau \nonumber \\&= \frac{M_{0}}{(1 - 2CM_{0}t)^{\frac{1}{2}}} + \frac{M_{0}}{(1 - 2CM_{0}t)^{\frac{1}{2}}}\left\{ \frac{1}{(1 - 2CM_{0}t)^{\frac{1}{2}}}-1\right\} \nonumber \\&=\frac{M_{0}}{1 - 2CM_{0}t }\le 2M_{0}. \end{aligned}$$

(3.13)

Thus, $\{W^{n}\}_{n\in {\mathbb {N}}}$ is uniformly bounded in ${\mathcal {C}}([0,T];B^{s}_{p,r})$ and

$$\begin{aligned} \Vert W^{n}(t)\Vert _{ B^{s}_{p,r}}\le 2\Vert W_{0}\Vert _{ B^{s}_{p,r}},\quad \forall t\in [0,T]. \end{aligned}$$

(3.14)

Using the Eq. (3.7), we can easily showed that $\{\partial _{t}W^{n}\}_{n\in {\mathbb {N}}}$ is uniformly bounded in ${\mathcal {C}}([0,T];B^{s-1}_{p,r})$. Thus, the sequence $\{W^{n}\}_{n\in {\mathbb {N}}}$ is uniformly bounded in $E^{s}_{p,r}(T)$.

Step 3. we will prove that $\{W^{n}\}_{n\in {\mathbb {N}}}$ is a Cauchy sequence in ${\mathcal {C}}([0,T];B^{s-1}_{p,r})$. For any $n,j\in {\mathbb {N}}$, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \ \partial _{t}(W^{n+j+1}-W^{n+1})+\frac{3}{2}W^{n+j}\partial _{x}(W^{n+j+1}-W^{n+1})\\ =\frac{3}{2}(W^{n}-W^{n+j})\partial _{x}W^{n+1}+\\ \partial _{x}(1-\partial _{x}^{2})^{-1}[k(W^{n+j}-W^{n})+\frac{3-2m}{4}(W^{n+j}-W^{n})(W^{n+j}+W^{n})],\\ \ (W^{n+j+1}-W^{n+1})(x,0)=0.\\ \end{array}\right. }\qquad \end{aligned}$$

(3.15)

Applying Lemma 2.2 again, and the uniform boundedness of $W^{n}$, $B^{s-1}_{p,r}$ is a Banach algebra, we have

$$\begin{aligned} ~&\Vert W^{n+j+1}-W^{n+1}\Vert _{ B^{s}_{p,r}}\nonumber \\&\quad \le e^{C\int _{0}^{t}\Vert W^{n}(\tau )\Vert _{ B^{s}_{p,r}}d\tau } \int _{0}^{t}e^{-C\int _{0}^{\tau }\Vert W^{n}(\tau ^{\prime })\Vert _{ B^{s}_{p,r}}d\tau ^{\prime }}( \Vert W^{n+j}(\tau )-W^{n}(\tau )\Vert _{ B^{s-1}_{p,r}})d\tau \nonumber \\&\quad \le C\int _{0}^{t}( \Vert W^{n+j}(\tau )-W^{n}(\tau )\Vert _{ B^{s-1}_{p,r}})d\tau . \end{aligned}$$

(3.16)

Thus, employing the induction procedure, we can obtain

$$\begin{aligned} \Vert W^{n+j+1}-W^{n+1}\Vert _{ L_{T}^{\infty }(B^{s}_{p,r})}\le \frac{(TC)^{n+1}}{(n+1)!}\le C2^{-n}. \end{aligned}$$

(3.17)

Which implies that $\{W^{n}\}_{n\in {\mathbb {N}}}$ is a Cauchy sequence in ${\mathcal {C}}([0,T];B^{s-1}_{p,r})$.

Step 4. We prove the existence and uniqueness for Eq. (1.4) in Besov space.

Proof of Theorem 1.1

From Lemma 3.2, we know that the sequence$\{W^{n}\}_{n\in {\mathbb {N}}}$ is a Cauchy sequence in ${\mathcal {C}}([0,T];B^{s-1}_{p,r})$. Hence, $\{W^{n}\}_{n\in {\mathbb {N}}}$ converges to some limit function $W\in {\mathcal {C}}([0,T];B^{s-1}_{p,r})$. Now, we need to show that the limit function$W\in E_{p,r}^{s}(T)$ and solves Eq. (1.4). Because $\{W^{n}\}_{n\in {\mathbb {N}}}$ is uniformly bounded in $L^{\infty }([0,T];B^{s}_{p,r})$, we can deduce that $W\in L^{\infty }([0,T];B^{s}_{p,r})$ by the Fatou property for Besov spaces.

Thanks to

$$\begin{aligned} W^{n}\rightarrow W \quad in\quad {\mathcal {C}}([0,T];B^{s-1}_{p,r}) \end{aligned}$$

(3.18)

and the interpolation inequality, we have

$$\begin{aligned} W^{n}\rightarrow W \quad in\quad {\mathcal {C}}([0,T];B^{s^{\prime }}_{p,r})\quad for\quad any\quad s^{\prime }<s. \end{aligned}$$

Thus, it is a routine to pass the limit in Eq. (4.7) and show that W is a solution of Eq. (1.4).

For the case $r<\infty$, Lemma 2.2 tell us that $W\in {\mathcal {C}}([0,T];B^{s^{\prime }}_{p,r})$ for any$s^{\prime }<s$. Using Eq. (1.4), it is easy to obtain that $\partial _{t}W\in {\mathcal {C}}([0,T];B^{s-1}_{p,r})$ if $r<\infty$, and $\partial _{t}W\in {\mathcal {C}}([0,T];B^{s-1}_{p,r})$ otherwise. Thus, the solution$W\in E_{p,r}^{s}(T)$.

The continuity with respect to initial data for $s^{\prime }<s$ in

$$\begin{aligned} {\mathcal {C}}([0,T];B^{s^{\prime }}_{p,r}({\mathbb {R}}))\cap {\mathcal {C}}^{1}([0,T];B^{s^{\prime }-1}_{p,r}({\mathbb {R}})), \end{aligned}$$

can be get by Lemma 3.1 and interpolation property. For the case$s^{\prime }=s$ can be get though the viscosity approximation method for Eq. (1.4), The approximation solution $\{W_{\epsilon }\}_{\epsilon >0}$ converges uniformly in

$$\begin{aligned} {\mathcal {C}}([0,T];B^{s}_{p,r}({\mathbb {R}}))\cap {\mathcal {C}}^{1}([0,T];B^{s-1}_{p,r}({\mathbb {R}})) \end{aligned}$$

imply the continuity of the solutionW in $E_{p,r}^{s}(T)$. Then, we have finished the proof of Theorem 1.1. $\square$

4 Non-uniform continuous dependence

In this section, we will give the proof of Theorem 1.2. The local well-posedness result in Theorem 1.1 yield that the data-to-solution map is continuously dependence on the initial. Furthermore, we show that this data-to-solution map is not uniformly continuous in Besov space $B^{s}_{p,r}$ with $s> max\{1+\frac{1}{p},\frac{3}{2}\}$ and $1\le p\le \infty$, $1\le r<\infty$.

Next, we need to introduce smooth, radial cut-off functions to localize the frequency region. Let ${\widehat{\phi }}\in {\mathcal {C}}_{0}^{\infty }({\mathbb {R}})$ be an even, real-valued and non-negative function on ${\mathbb {R}}$ and satisfy

$$\begin{aligned} \widehat{\phi (\xi )}= {\left\{ \begin{array}{ll} \ 1, &{} if\,\,|\xi |\le \frac{1}{4}\\ \ 0, &{} if\,\,|\xi |\ge \frac{1}{2}.\\ \end{array}\right. } \end{aligned}$$

(4.1)

Next, we recall the following Lemma in [18]

Lemma 4.1

For any $p\in [1,\infty ]$, there exists a positive constant M such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\inf \Vert \phi ^{2}(x)\cos \left( \frac{17}{12}2^{-n}x\right) \Vert _{ L^{p}}\ge M. \end{aligned}$$

(4.2)

Proof

we can assume that $p\in [1,\infty )$. Using the Fourier inversion formula and the Fubini’s theorem, we see that

$$\begin{aligned} \Vert \phi \Vert _{L^{\infty }}=\sup _{x\in {\mathbb {R}}}\frac{1}{2\pi }\left|\int _{{\mathbb {R}}}{\widehat{\phi }}(\xi )\cos (x\xi )d\xi \right|\le \frac{1}{2\pi }\int _{{\mathbb {R}}}{\widehat{\phi }}(\xi )d\xi , \end{aligned}$$

(4.3)

where

$$\begin{aligned} \phi (0)=\frac{1}{2\pi }\int _{{\mathbb {R}}}{\widehat{\phi }}(\xi )d\xi >0. \end{aligned}$$

Since $\phi$ is a real-valued and continuous function on ${\mathbb {R}}$, then there exists some $\delta >0$ such that

$$\begin{aligned} \phi (x)\ge \frac{\phi (0)}{2},\quad x\in B_{\delta }(0). \end{aligned}$$

Therefore, we deduce

$$\begin{aligned} \Vert \phi ^{2}\cos \left( \frac{17}{12}2^{n}x\right) \Vert _{L^{p}}^{p}{} & {} \ge \frac{\phi (0)^{2}}{4}\int _{0}^{\delta }|\cos \left( \frac{17}{12}2^{n}x\right) |^{p}dx\\{} & {} =\frac{\delta }{4}\phi ^{2}(0)\frac{1}{2^n{\widetilde{\delta }}}\int _{0}^{2^n{\widetilde{\delta }}}|\cos x|^{p}dx \quad with \quad {\widetilde{\delta }}=\frac{17}{12\delta }.\\ \end{aligned}$$

With the following fact

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{2^n{\widetilde{\delta }}}\int _{0}^{2^n{\widetilde{\delta }}}|\cos x|^{p}dx=\frac{1}{\pi }\int _{0}^{\pi }|\cos x|^{p}dx. \end{aligned}$$

Hence, we conclude the desired result.

Lemma 4.2

Let $s\in {\mathbb {R}}$ and $(p,r)\in [1,\infty ]\times [0,\infty )$. Define the hight frequency function $f_{n}$ by

$$\begin{aligned} f_{n}=2^{-ns}\phi (x)\sin \left( \frac{17}{12}2^{n}x\right) ,\quad n\gg 1. \end{aligned}$$

Then for any $\sigma \in {\mathbb {R}}$ we have

$$\begin{aligned} \Vert f_{n}\Vert _{ B^{\sigma }_{p,r}}\le 2^{n(\sigma -s)}\Vert \phi \Vert _{L^{P}}. \end{aligned}$$

(4.4)

Proof

It is easy to compute that

$$\begin{aligned} {\widehat{f}}=2^{-ns-1}i\left[ {\widehat{\phi }}\left( \xi +\frac{17}{12}2^{n}\right) -{\widehat{\phi }}\left( \xi -\frac{17}{12}2^{n}\right) \right] , \end{aligned}$$

which implies

$$\begin{aligned} \textrm{supp } {\widehat{f}}_{n}\subset \left\{ {\xi \in {\mathbb {R}}:\frac{17}{12}2^{n}-\frac{1}{2}\le |\xi |\le \frac{17}{12}2^{n}+\frac{1}{2}}\right\} , \end{aligned}$$

we deduce

$$\begin{aligned} \triangle _{j}(f_{n})= {\left\{ \begin{array}{ll} \ f_{n},&{} if\mathop j=n,\\ \ 0, &{} if\mathop j\ne n.\\ \end{array}\right. } \end{aligned}$$

Hence, the definition of the Besov spaces tells us that the desired result.

Lemma 4.3

Let $s \in {\mathbb {R}}$ and $p\in [1,\infty ]$. Define the low frequency function $g_{n}$ by

$$\begin{aligned} g_{n}=\frac{12}{17}2^{-n}\phi (x),\quad n\gg 1. \end{aligned}$$

Then we have

$$\begin{aligned} \Vert g_{n}\Vert _{ B^{s}_{p,r}}\le C2^{-n}, \end{aligned}$$

other there exists a positive constant ${\widetilde{M}}$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\inf \Vert g_{n}\partial _{x}f_{n}\Vert _{ B^{s}_{p,\infty }}\ge {\widetilde{M}}. \end{aligned}$$

(4.5)

Proof

We know that

$$\begin{aligned} \textrm{supp}{\widehat{g}}_{n}\subset \left\{ \xi \in {\mathbb {R}}:0\le |\xi |\le \frac{1}{2}\right\} , \end{aligned}$$

combing $\textrm{supp}\varphi$, we can get

$$\begin{aligned} \widehat{\vartriangle _{j}(g_{n})}=\varphi (2^{-j}\cdot )\widehat{g_{n}}\equiv 0,\quad j\ge 0, \end{aligned}$$

therefore

$$\begin{aligned} \Vert g_{n}\Vert _{ B^{s}_{p,r}}=\frac{12}{17}2^{-s}\cdot 2^{-n}\Vert \vartriangle _{-1}\phi \Vert _{L^{p}}\le 2^{-n}\Vert \phi \Vert _{L^{p}}. \end{aligned}$$

Then, we have

$$\begin{aligned} \textrm{supp} \widehat{g_{n}\partial _{x}f_{n}}\subset \left\{ \xi \in {\mathbb {R}}:\frac{17}{12}2^{n}-1\le |\xi |\le \frac{17}{12}2^{n}+1\right\} , \end{aligned}$$

which implies

$$\begin{aligned} \triangle _{j}(g_{n}\partial _{x}f_{n})= {\left\{ \begin{array}{ll} \ g_{n}\partial _{x}f_{n},&{} if\mathop j=n,\\ \ 0,&{} if\mathop j\ne n.\\ \end{array}\right. } \end{aligned}$$

Using the definitions of $f_{n}$ and $g_{n}$, we have

$$\begin{aligned} \Vert g_{n}\partial _{x}f_{n}\Vert _{B^{s}_{p,\infty }}{} & {} =2^{ns}\Vert \triangle _{n}(g_{n}\partial _{x}f_{n})\Vert _{L^{p}}=2^{ns}\Vert g_{n}\partial _{x}f_{n}\Vert _{L^{p}}\\{} & {} =\Vert \phi ^{2}(x)\cos \left( \frac{17}{12}2^{n}x\right) +\frac{17}{12}2^{-n}\phi (x)\partial _{x}\phi (x)\sin \left( \frac{17}{12}2^{n}x\right) \Vert _{L^{p}}\\{} & {} \ge \Vert \phi ^{2}(x)\cos \left( \frac{17}{12}2^{n}x\right) \Vert _{L^{p}}-C2^{-n}. \end{aligned}$$

Thus, the Lemma 4.1 enables us to finish the proof of the Lemma 4.3.

Assume that $W^{n}$ is a solution of Eq. (1.4) with the initial data $W_{0}^{n}:= f_{n}(x)$. Then, we have the following estimate

Proposition 4.1

. Let (s,p,r) meet the condition in Theorem 1.2, we have for$j=\pm 1$

$$\begin{aligned} \Vert W^{n}\Vert _{ B^{s+j}_{p,r}}\le C2^{jn}, \end{aligned}$$

(4.6)

and

$$\begin{aligned} \Vert W^{n}-W_{0}^{n}\Vert _{ B^{s+j}_{p,r}}\le C2^{-\varepsilon _{s}n}, \end{aligned}$$

(4.7)

where $2\varepsilon _{s}=\min \{s-1-\frac{1}{p},2\}$.

Proof

The well-posedness result Theorem 1 insures that the solution $\{W^{n}\}_{n\in {\mathbb {N}}} \in {\mathcal {C}}([0,T];B^{s-1}_{p,r})$ with a lifespan $T\simeq 1$. Moreover, we have

$$\begin{aligned} \Vert W^{n}\Vert _{L_{T}^{\infty } (B^{s}_{p,r})}\le C\Vert W_{0}^{n}\Vert _{B^{s}_{p,r}}\le C, \end{aligned}$$

(4.8)

and the similar as (3.8), we have for any $t\in [0,T]$ and $j=\pm 1$,

$$\begin{aligned} ~&\Vert W^{n}(t)\Vert _{ B^{s+j}_{p,r}}\le \Vert W^{n}_{0}\Vert _{ B^{s+j}_{p,r}} \nonumber \\ {}&\qquad \quad + C\int _{0}^{t}( \Vert \partial _{x}(1-\partial _{x}^{2})^{-1}\left( kW^{n}+\frac{3-2m}{4}(W^{n})^{2}\right) \Vert _{ B^{s+k}_{p,r}})d\tau \nonumber \\ {}&\quad \le C\Vert W^{n}_{0}\Vert _{ B^{s+j}_{p,r}} + C\int _{0}^{t}( \Vert W^{n}\Vert _{ B^{s+j}_{p,r}}+\Vert W^{n}(t)\Vert ^{2}_{ B^{s+j}_{p,r}})d\tau . \end{aligned}$$

(4.9)

Applying the Gronwall’s inequality and (4.4), we have for all $t\in [0,T]$

$$\begin{aligned} \Vert W^{n}\Vert _{B^{s-1}_{p,r}}\le C2^{-n},\quad \Vert W^{n}\Vert _{B^{s+1}_{p,r}}\le C2^{n}. \end{aligned}$$

(4.10)

Since $s-\epsilon _{s}-1>\frac{1}{p}$, the embed property leads to

$$\begin{aligned} \Vert W^{n}\Vert _{L^{\infty }}\le C\Vert W^{n}\Vert _{B^{s-\epsilon _{s}-1}_{p,r}}. \end{aligned}$$

(4.11)

Now, we estimate $\Vert W^{n}-w_{0}^{n}\Vert _{B^{s}_{p,r}}$. Using the fundamental theorem of calculus we have

$$\begin{aligned} \Vert W^{n}-W_{0}^{n}\Vert _{B^{s}_{p,r}}\le \int _{0}^{t}\Vert \partial _{\tau }W^{n}(\tau )\Vert _{B^{s}_{p,r}}d\tau . \end{aligned}$$

(4.12)

Applying the Eq. (1.4), embed property and (4.4), we have

$$\begin{aligned} ~&\Vert W^{n}-W_{0}^{n}\Vert _{ B^{s}_{p,r}}\le C\int _{0}^{t}\Vert W^{n}\partial _{x}W^{n}\Vert _{ B^{s}_{p,r}}\nonumber \\ {}&\qquad +\int _{0}^{t}( \Vert \partial _{x}(1-\partial _{x}^{2})^{-1}\left( kW^{n}+\frac{3-2m}{4}(W^{n})^{2}\right) \Vert _{ B^{s+k}_{p,r}})d\tau \nonumber \\ {}&\quad \le C (\Vert W^{n}\Vert _{ B^{s}_{p,r}}\Vert \partial _{x}W^{n}\Vert _{ L^{\infty }}+\Vert W^{n}\Vert _{L^{\infty }}\Vert \partial _{x}W^{n}\Vert _{ B^{s}_{p,r}})\nonumber \\ {}&\qquad +C(\Vert W^{n}(t)\Vert _{ B^{s-1}_{p,r}}+\Vert W^{n}(t)\Vert ^{2}_{ B^{s-1}_{p,r}}) \nonumber \\ {}&\quad \le C(2^{-\epsilon _{s}n} + 2^{-(\epsilon _{s}+1)n}2^{n} + 2^{-n})\nonumber \\ {}&\quad \le C2^{-\epsilon _{s}n} + C2^{-n} \nonumber \\&\quad \le C2^{-\epsilon _{s}n}. \end{aligned}$$

(4.13)

The proof of this proposition is completed.

In order to prove that the nun-uniform continuous dependence result, we construct another sequence of approximate solutions to Eq. (1.4) with initial data

$$\begin{aligned} V_{0}^{n}=f_{n}+g_{n}. \end{aligned}$$

Proposition 4.2

. Let (s,p,r) meet the condition in Theorem 1.2. Assume $V^{n}$ is a solution of Eq. (1.4) with initial data $V_{0}^{n}$. Then, for all $t\in [0,T]$, we have

$$\begin{aligned} \Vert V^{n}-V_{0}^{n}+\frac{3}{2}t V_{0}^{n}\partial _{x}V_{0}^{n}\Vert _{ B^{s}_{p,r}}\le Ct^{2} + C2^{-\epsilon _{s}n}. \end{aligned}$$

(4.14)

Proof

Applying the Theorem 1.1 yields that the solution $V^{n}\in {\mathcal {C}}([0,T];B^{s}_{p,r})$ with $T\simeq 1$, and Lemma 4.2, Lemma 4.3, we have

$$\begin{aligned} \Vert V^{n}\Vert _{ B^{s+j}_{p,r}}\le C\Vert V_{0}^{n}\Vert _{ B^{s+j}_{p,r}}\le C(\Vert f_{n}\Vert _{ B^{s+j}_{p,r}}+\Vert g_{n}\Vert _{ B^{s+j}_{p,r}})\le C2^{jn}\quad for j=\pm 1,\nonumber \\ \end{aligned}$$

(4.15)

and

$$\begin{aligned} \Vert V_{0}^{n}\partial _{x}V_{0}^{n}\Vert _{ B^{s+j}_{p,r}}&\le C(\Vert V_{0}^{n}\Vert _{ B^{s+j}_{p,r}}\Vert \partial _{x}V_{0}^{n}\Vert _{L^{\infty }}+\Vert \partial _{x}V_{0}^{n}\Vert _{ B^{s+j}_{p,r}}\Vert V_{0}^{n}\Vert _{L^{\infty }}) \nonumber \\ {}&\le C2^{jn}+C2^{-n}2^{(j+1)n} \nonumber \\ {}&\le C2^{jn} \quad for j=0,\pm 1. \end{aligned}$$

(4.16)

Thus, we can obtain that

$$\begin{aligned} \Vert V^{n},V_{0}^{n},\frac{3}{2}V_{0}^{n}\partial _{x}V_{0}^{n}\Vert _{ B^{s-1}_{p,r}}\le C\Vert V^{n},V_{0}^{n},V_{0}^{n}\partial _{x}V_{0}^{n}\Vert _{ B^{s-\frac{1}{2}}_{p,r}}\le C2^{-\frac{1}{2}n}. \end{aligned}$$

(4.17)

Next, we estimate $\Vert \eta ^{n}\Vert _{ B^{s}_{p,r}}$, where $\eta ^{n}=V^{n}-V_{0}^{n}-tP_{0}^{n}$ with $P_{0}^{n}=-\frac{3}{2}V_{0}^{n}\partial _{x}V_{0}^{n}$. We know that $\eta ^{n}$ is a solution of the following equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \ \partial _{t}\eta ^{n}+\frac{3}{2}V^{n}\partial _{x}\eta ^{n}=-\frac{3}{2}tV^{n}\partial _{x}P_{0}^{n} -\frac{3}{2}(V^{n}-V_{0}^{n})\partial _{x}V_{0}^{n}\\ +t\partial _{x}(1-\partial _{x}^{2})^{-1}(kP_{0}^{n}+\frac{3-2m}{4}V^{n}P_{0}^{n}) \\ +\partial _{x}(1-\partial _{x}^{2})^{-1}\left[ \left( k+\frac{3-2m}{4}V^{n}\right) \eta ^{n}+kV_{0}^{n}+\frac{3-2m}{4}V^{n}V_{0}^{n}\right] , \\ \eta ^{n}(x,0)=0.\\ \end{array}\right. } \end{aligned}$$

(4.18)

Using Lemma 2.2 and (4.11), we have

$$\begin{aligned} \begin{aligned} \Vert V^{n}\partial _{x}P_{0}^{n}\Vert _{ B^{s-1}_{p,r}}&\le C(\Vert V^{n}\Vert _{ L^{\infty }}\Vert \partial _{x}P_{0}^{n}\Vert _{ B^{s-1}_{p,r}}+\Vert V^{n}\Vert _{ B^{s-1}_{p,r}}\Vert \partial _{x}P_{0}^{n}\Vert _{ L^{\infty }})\\&\le C(\Vert V^{n}\Vert _{ B^{s-1}_{p,r}}\Vert V_{0}^{n}\partial _{x}V_{0}^{n}\Vert _{ B^{s}_{p,r}}+\Vert V^{n}\Vert _{ B^{s}_{p,r}}\Vert \partial _{x}P_{0}^{n}\Vert _{ B^{s-1-\epsilon _{s}}_{p,r}}) \\&\le C2^{-n}+C2^{-\epsilon _{s}n} \end{aligned} \end{aligned}$$

(4.19)

and

$$\begin{aligned} \Vert V^{n}\partial _{x}P_{0}^{n}\Vert _{ B^{s}_{p,r}}\le & {} C(\Vert V^{n}\Vert _{ L^{\infty }}\Vert \partial _{x}P_{0}^{n}\Vert _{ B^{s}_{p,r}}+\Vert V^{n}\Vert _{ B^{s}_{p,r}}\Vert \partial _{x}P_{0}^{n}\Vert _{ L^{\infty }})\nonumber \\\le & {} C(\Vert V^{n}\Vert _{ B^{s-1}_{p,r}}\Vert V_{0}^{n}\partial _{x}V_{0}^{n}\Vert _{ B^{s+1}_{p,r}}+\Vert V^{n}\Vert _{ B^{s}_{p,r}}\Vert \partial _{x}P_{0}^{n}\Vert _{ B^{s-1}_{p,r}}) \nonumber \\\le & {} C \end{aligned}$$

(4.20)

Applying Lemma 2.2 again, we have

$$\begin{aligned} \Vert (V^{n}-V_{0}^{n})\partial _{x}V_{0}^{n}\Vert _{ B^{s-1}_{p,r}}\le & {} C\Vert V^{n}-V_{0}^{n}\Vert _{ B^{s-1}_{p,r}}\Vert \partial _{x}V_{0}^{n}\Vert _{ B^{s-1}_{p,r}} \nonumber \\\le & {} C2^{-n}, \end{aligned}$$

(4.21)

and

$$\begin{aligned} \begin{aligned}&\Vert (V^{n}-V_{0}^{n})\partial _{x}V_{0}^{n}\Vert _{ B^{s}_{p,r}}\\&\quad \le C(\Vert V^{n}-V_{0}^{n}\Vert _{ L^{\infty }}\Vert \partial _{x}V_{0}^{n}\Vert _{ B^{s}_{p,r}}+\Vert V^{n}-V_{0}^{n}\Vert _{ B^{s}_{p,r}}\Vert \partial _{x}V_{0}^{n}\Vert _{ L^{\infty }})\\&\quad \le C(\Vert V^{n}-V_{0}^{n}\Vert _{ B^{s-1}_{p,r}}\Vert V_{0}^{n}\Vert _{ B^{s+1}_{p,r}}+\Vert V^{n}-V_{0}^{n}\Vert _{ B^{s}_{p,r}}\Vert \partial _{x}V_{0}^{n}\Vert _{ B^{s-1}_{p,r}}) \\&\quad \le C. \end{aligned} \end{aligned}$$

(4.22)

Using the fact $B^{s-1}_{p,r}$ is a Banach algebra, and Lemma 2.2(6),the operator $(1-\partial _{x}^{2})^{-1}$ is $S^{-2}$-multiplier, we get

$$\begin{aligned} \begin{aligned}&\Vert \partial _{x}(1-\partial _{x}^{2})^{-1}\left( kP_{0}^{n}+\frac{3-2m}{4}V^{n}P_{0}^{n}\right) \Vert _{ B^{s-1}_{p,r}}\\ {}&\quad \le C\Vert P_{0}^{n}\Vert _{ B^{s-2}_{p,r}} + C\Vert V^{n}P_{0}^{n}\Vert _{ B^{s-2}_{p,r}}\\&\quad \le C\Vert P_{0}^{n}\Vert _{ B^{s-1}_{p,r}}+C\Vert V^{n}\Vert _{ B^{s-1}_{p,r}}\Vert P_{0}^{n}\Vert _{ B^{s}_{p,r}} \\&\quad \le C2^{-n}, \end{aligned} \end{aligned}$$

(4.23)

and

$$\begin{aligned} \begin{aligned}&\Vert \partial _{x}(1-\partial _{x}^{2})^{-1}\left( kP_{0}^{n}+\frac{3-2m}{4}V^{n}P_{0}^{n}\right) \Vert _{ B^{s}_{p,r}}\\ {}&\quad \le C\Vert P_{0}^{n}\Vert _{ B^{s-1}_{p,r}} + C\Vert V^{n}P_{0}^{n}\Vert _{ B^{s-1}_{p,r}}\\&\quad \le C\Vert P_{0}^{n}\Vert _{ B^{s-1}_{p,r}}+C\Vert V^{n}\Vert _{ B^{s-1}_{p,r}}\Vert P_{0}^{n}\Vert _{ B^{s}_{p,r}} \\&\quad \le C2^{-n}, \end{aligned} \end{aligned}$$

(4.24)

The same procedure of estimates as above, we also obtain

$$\begin{aligned} \begin{aligned}&\Vert \partial _{x}(1-\partial _{x}^{2})^{-1}\left[ \left( k+\frac{3-2m}{4}V^{n}\right) \eta ^{n}+kV_{0}^{n}+\frac{3-2m}{4}V^{n}V_{0}^{n}\right] \Vert _{ B^{s-1}_{p,r}}\\&\quad \le C\Vert \eta ^{n}\Vert _{ B^{s-2}_{p,r}} + C\Vert V^{n}\eta ^{n}\Vert _{ B^{s-2}_{p,r}} + C\Vert V_{0}^{n}\Vert _{ B^{s-2}_{p,r}} + C\Vert V^{n}V_{0}^{n}\Vert _{ B^{s-2}_{p,r}}\\&\quad \le C\Vert \eta ^{n}\Vert _{ B^{s-1}_{p,r}}+C2^{-n}, \end{aligned} \end{aligned}$$

(4.25)

and

$$\begin{aligned} \begin{aligned}&\Vert \partial _{x}(1-\partial _{x}^{2})^{-1}\left[ \left( k+\frac{3-2m}{4}V^{n}\right) \eta ^{n}+kV_{0}^{n}+\frac{3-2m}{4}V^{n}V_{0}^{n}\right] \Vert _{ B^{s}_{p,r}}\\ {}&\quad \le C\Vert \eta ^{n}\Vert _{ B^{s-1}_{p,r}} + C\Vert V^{n}\eta ^{n}\Vert _{ B^{s-1}_{p,r}} + C\Vert V_{0}^{n}\Vert _{ B^{s-1}_{p,r}} + C\Vert V^{n}V_{0}^{n}\Vert _{ B^{s-1}_{p,r}}\\&\quad \le C\Vert \eta ^{n}\Vert _{ B^{s-1}_{p,r}}+C2^{-n}, \end{aligned} \end{aligned}$$

(4.26)

Applying the Gronwall’s inequality and  (4.19), (4.21), (4.23), (4.25), we have

$$\begin{aligned} \Vert \eta ^{n}\Vert _{ B^{s-1}_{p,r}}\le Ct^{2}2^{-n} + C2^{-n\epsilon _{s}}. \end{aligned}$$

(4.27)

Applying the Gronwall’s inequality and  (4.19), (4.21), (4.23), (4.25), (4.27), we have

$$\begin{aligned} \Vert \eta ^{n}\Vert _{ B^{s}_{p,r}}\le Ct^{2} +Ct2^{-n}+ C\int _{0}^{t}\Vert \eta ^{n}(\tau )\Vert _{ B^{s-1}_{p,r}}d\tau \le Ct^{2} +C2^{-n\epsilon _{s}} \end{aligned}$$

(4.28)

Thus, we completed the proof of Proposition 4.2.

With the proposition 4.1, proposition 4.2, we gives the proof of Theorem 2.

Proof of the Theorem 1.2

Using The Lemma 4.3, we have

$$\begin{aligned} \Vert W_{0}^{n}-V_{0}^{n}\Vert _{ B^{s}_{p,r}}= \Vert g_{n}\Vert _{ B^{s}_{p,r}} \le C2^{-n}. \end{aligned}$$

(4.29)

Thus, we can obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert W_{0}^{n}-V_{0}^{n}\Vert _{ B^{s}_{p,r}}= 0. \end{aligned}$$

(4.30)

Moveover, we have

$$\begin{aligned} \begin{aligned} \Vert W^{n}-V^{n}\Vert _{ B^{s}_{p,r}}&= \Vert W^{n}-f_{n}-g_{n}-\eta ^{n}-tP_{0}^{n}\Vert _{ B^{s}_{p,r}} \\&\ge C\Vert tP_{0}^{n}\Vert _{ B^{s}_{p,r}}-C\Vert W^{n}-f_{n}\Vert _{ B^{s}_{p,r}}-C\Vert g_{n}\Vert _{ B^{s}_{p,r}}-C\Vert \eta ^{n}\Vert _{ B^{s}_{p,r}} \\&\ge Ct\Vert P_{0}^{n}\Vert _{ B^{s}_{p,r}}-Ct^{2} -C2^{-n\epsilon _{s}}. \end{aligned}\nonumber \\ \end{aligned}$$

(4.31)

Since

$$\begin{aligned} P_{0}^{n}=-\frac{3}{2}(f_{n}\partial _{x}f_{n} + f_{n}\partial _{x}g_{n} +g_{n}\partial _{x}f_{n}+g_{n}\partial _{x}g_{n}) \end{aligned}$$

by simple calculation, we can get

$$\begin{aligned} \begin{aligned}&\Vert (f_{n}\partial _{x}f_{n}\Vert _{B^{s}_{p,r}}\le \Vert f_{n}\Vert _{ L^{\infty }}\Vert f_{n}\Vert _{ B^{s+1}_{p,r}} +\Vert \partial _{x}f_{n}\Vert _{ L^{\infty }}\Vert f_{n}\Vert _{ B^{s}_{p,r}}\le C2^{-n\epsilon _{s}},\\&\Vert f_{n}\partial _{x}g_{n}\Vert _{B^{s}_{p,r}}\le \Vert f_{n}\Vert _{B^{s}_{p,r}}\Vert g_{n}\Vert _{B^{s+1}_{p,r}}\le C2^{-n},\\&\Vert g_{n}\partial _{x}g_{n}\Vert _{B^{s}_{p,r}}\le \Vert g_{n}\Vert _{B^{s}_{p,r}}\Vert g_{n}\Vert _{B^{s+1}_{p,r}}\le C2^{-n}.\\ \end{aligned} \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert W^{n}-V^{n}\Vert _{ B^{s}_{p,r}}\ge Ct\Vert g_{n}\partial _{x}f_{n}\Vert _{ B^{s}_{p,\infty }}-Ct^{2} -C2^{-n}. \end{aligned}$$

Thank to (4.5), we can get

$$\begin{aligned} \liminf _{n\rightarrow \infty }\Vert W^{n}-V^{n}\Vert _{ B^{s}_{p,r}}\gtrsim t, \quad t\in [0,T_{0}], \end{aligned}$$

(4.32)

for $T_{0}$ small enough. This completes the proof of Theorem 1.2.